Influence of Compression Rings on the Dynamic Characteristics and Sealing Capacity of the Combustion Chamber in Diesel Engines
Abstract
1. Introduction
2. Materials and Methods
2.1. Mathematical Model of the Compression Ring
2.1.1. Lubrication Oil Properties
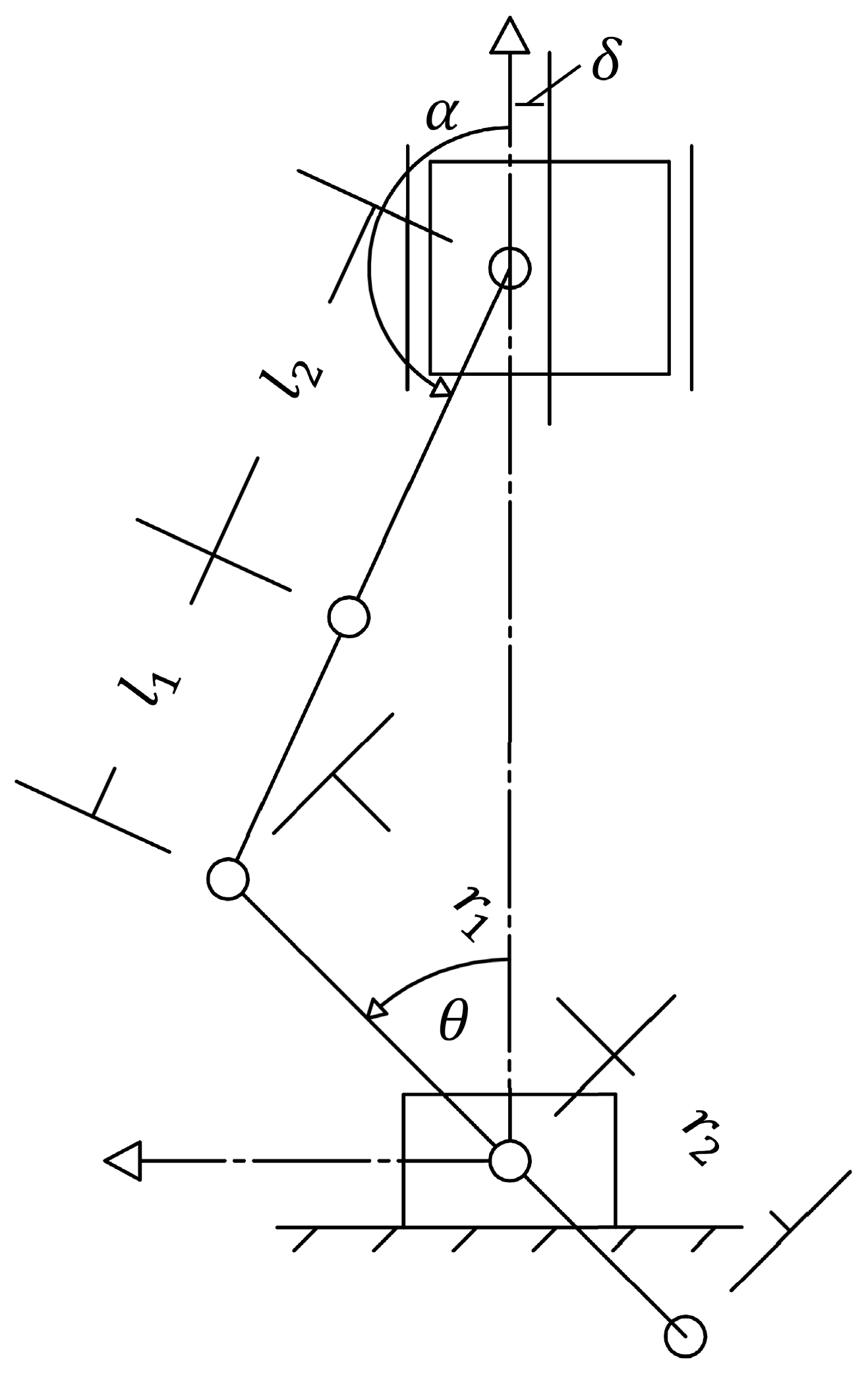
2.1.2. Kinematic Piston Model
2.1.3. Compression Ring Kinematics
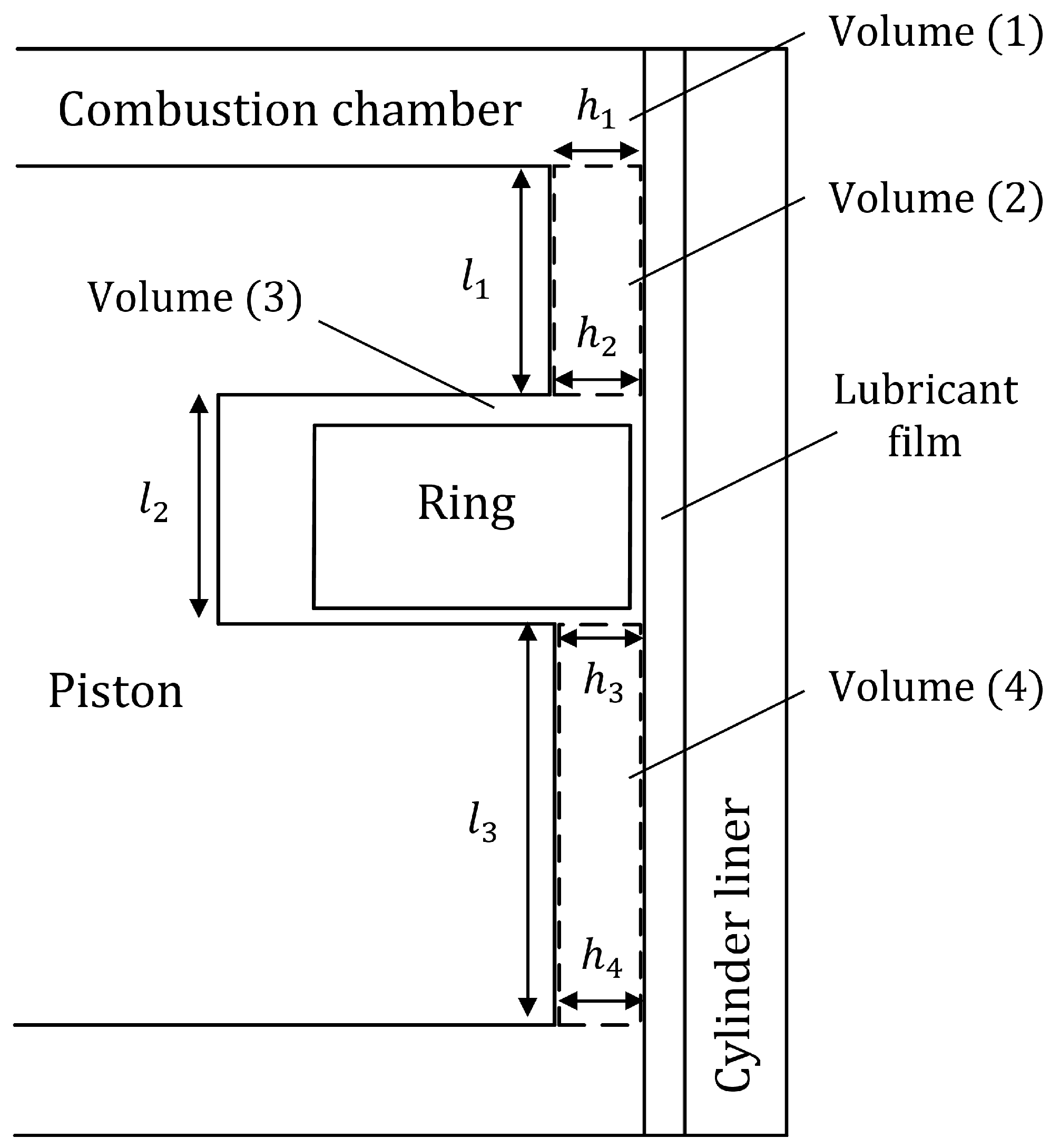
2.1.4. Gas Blow-By Model
2.1.5. Compression Ring Deformation Model
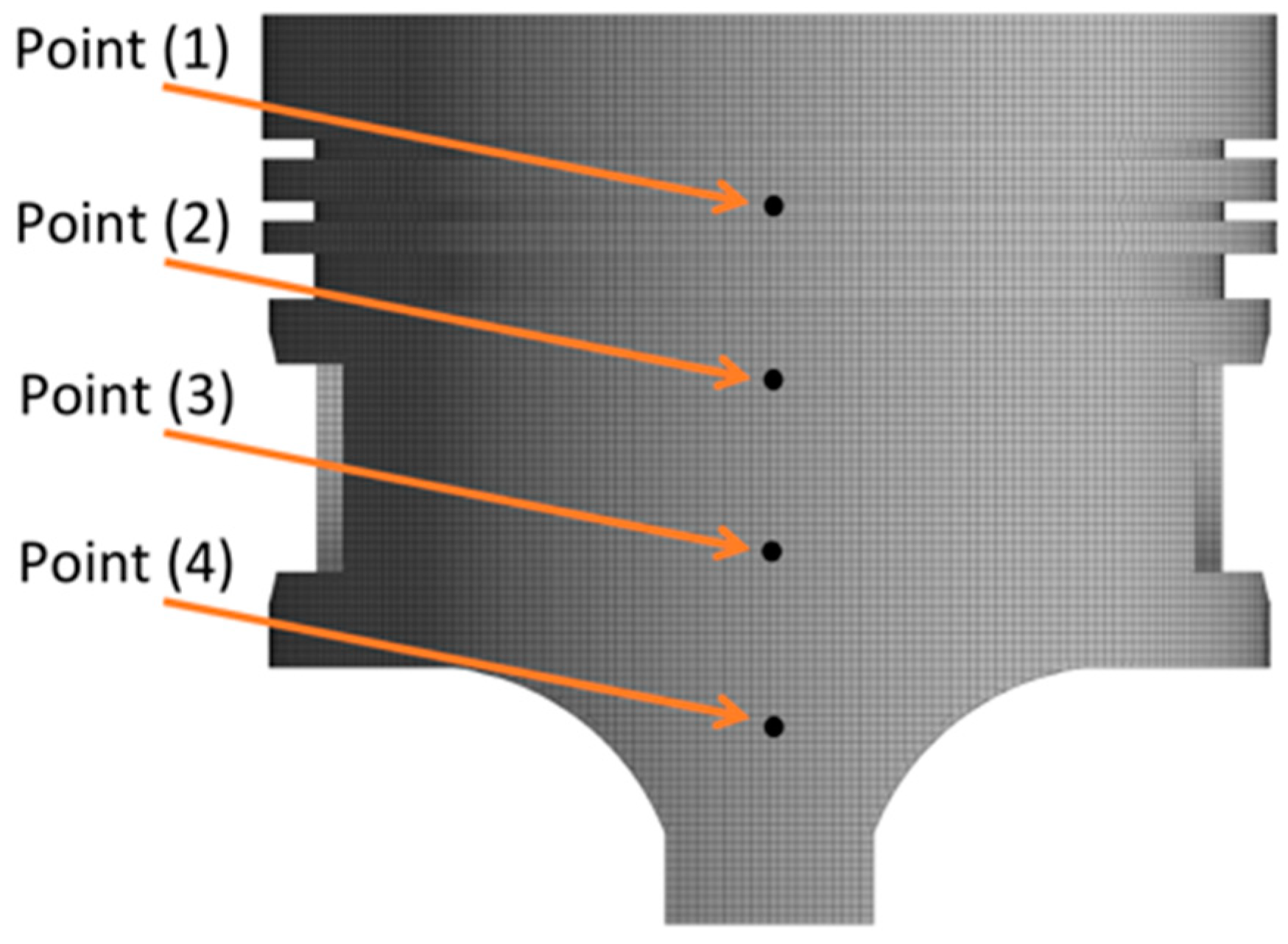
2.1.6. Piston Skirt Deformation Model
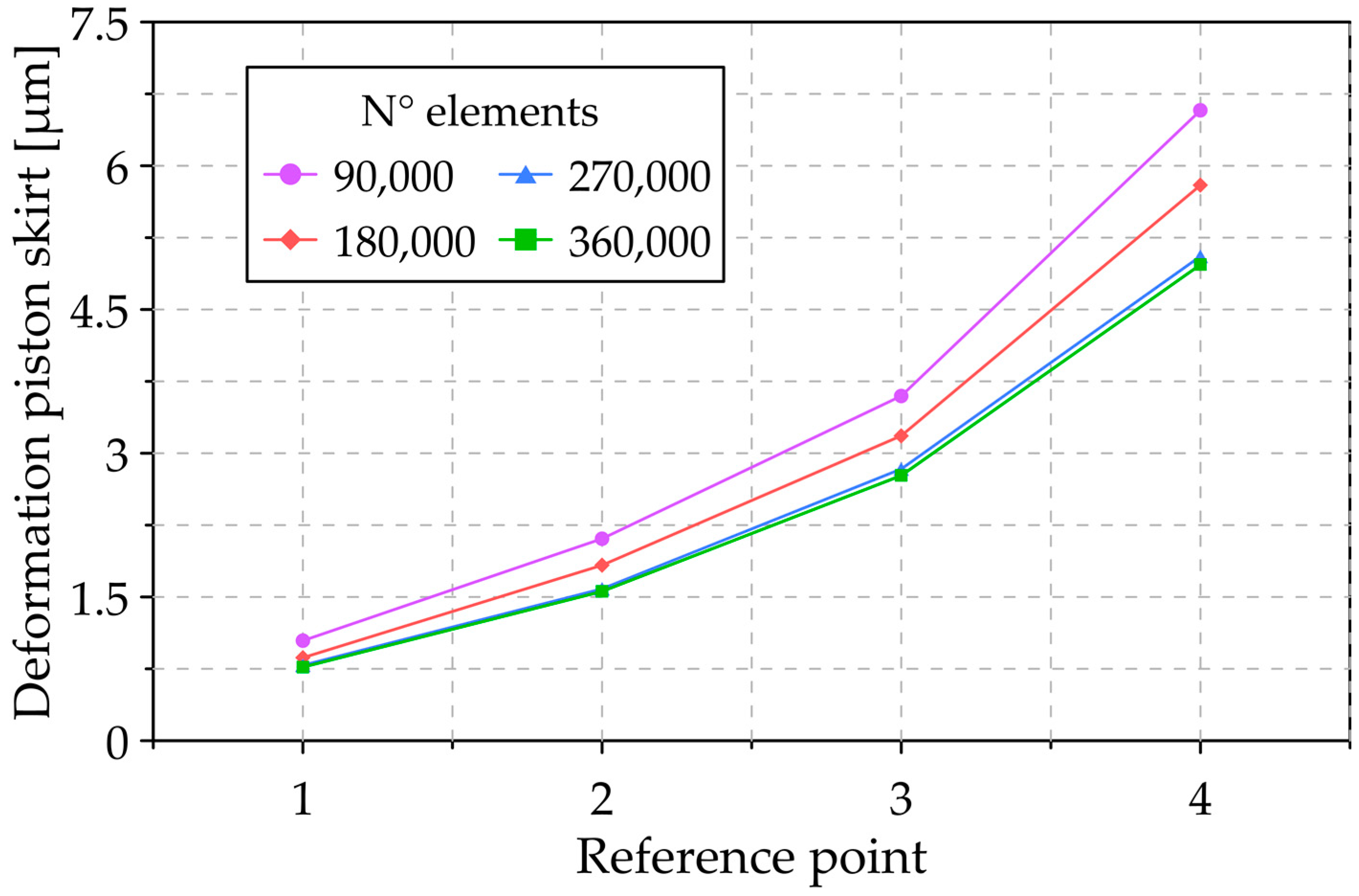
2.2. Numerical Methodology
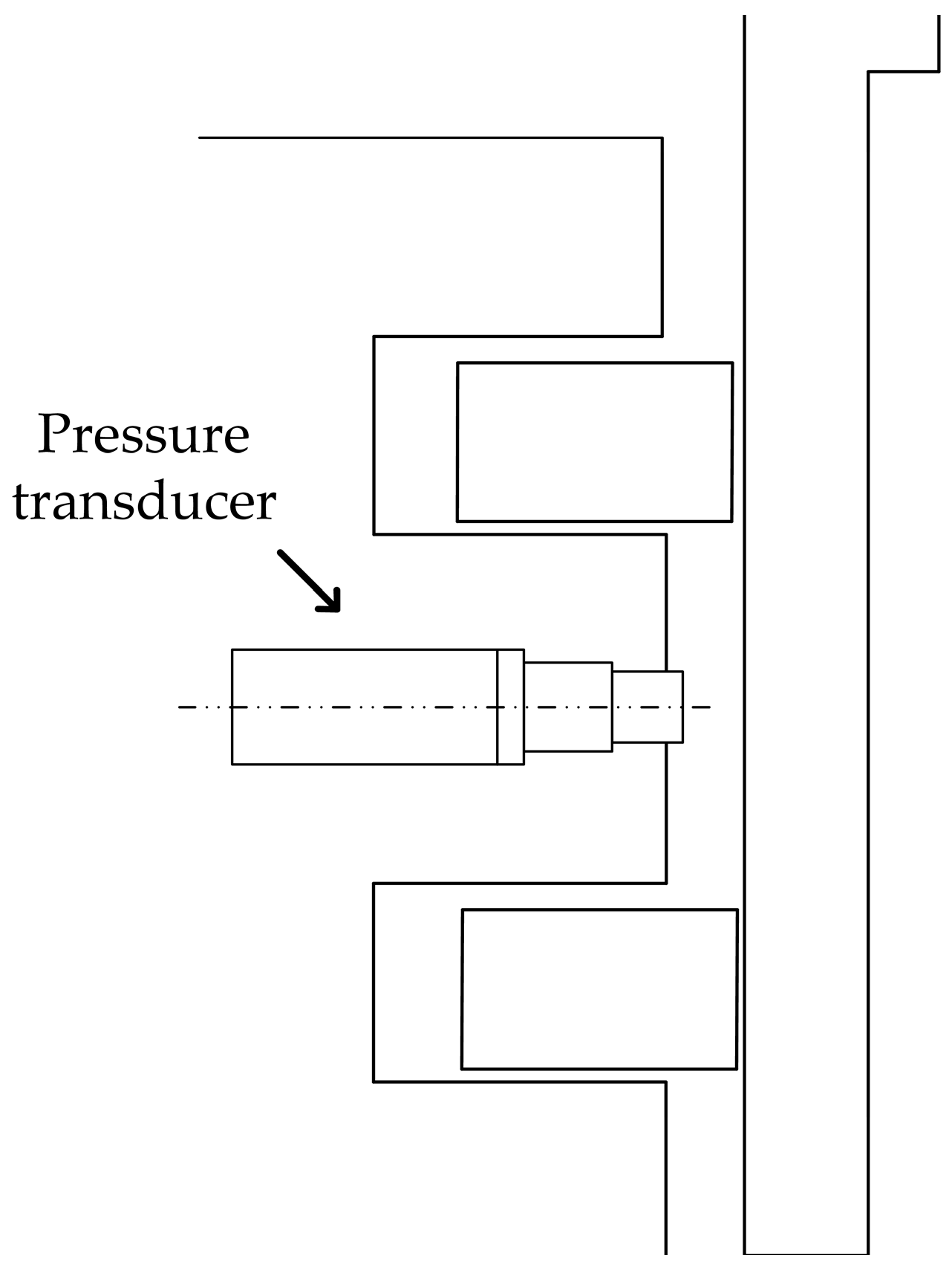
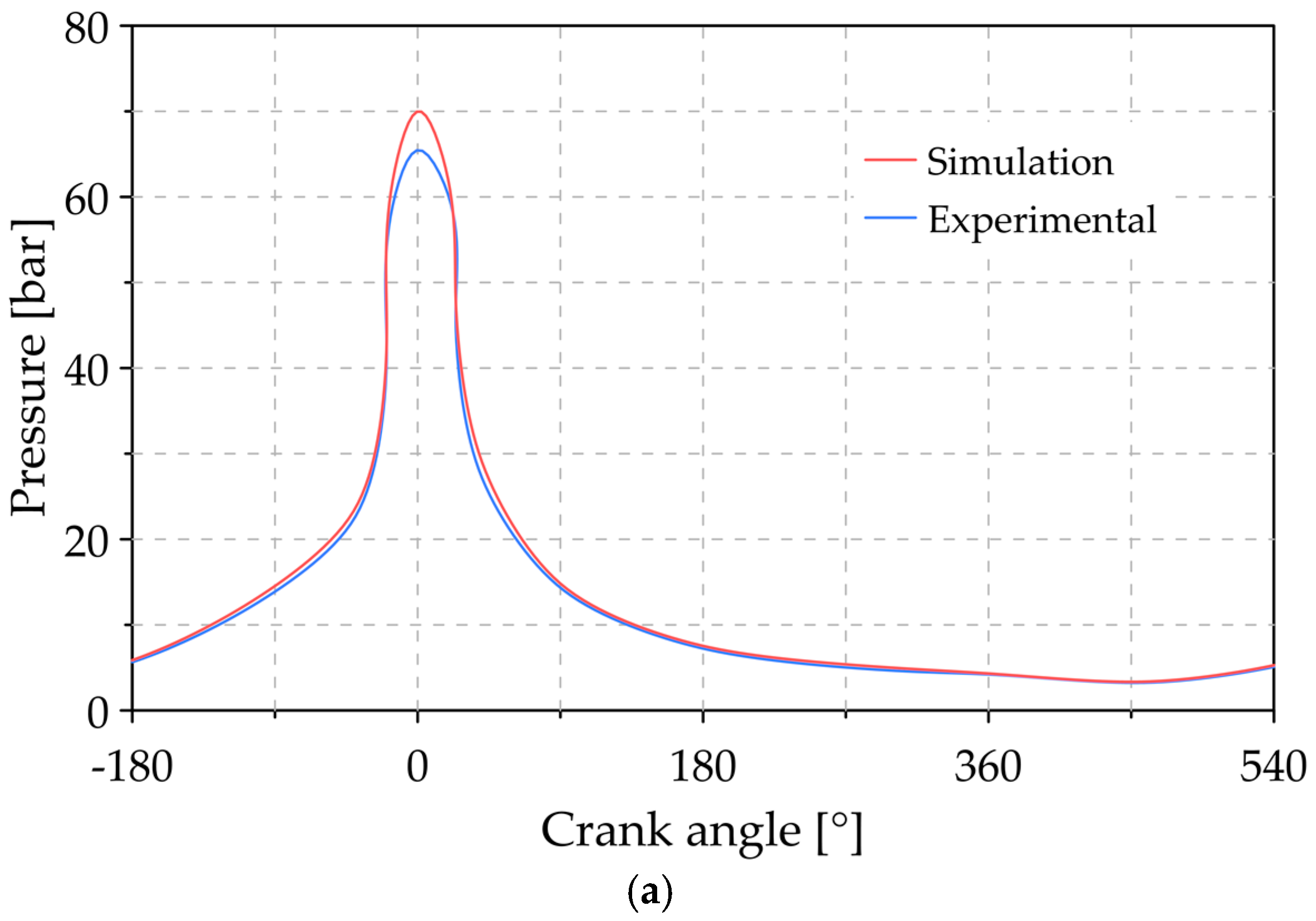
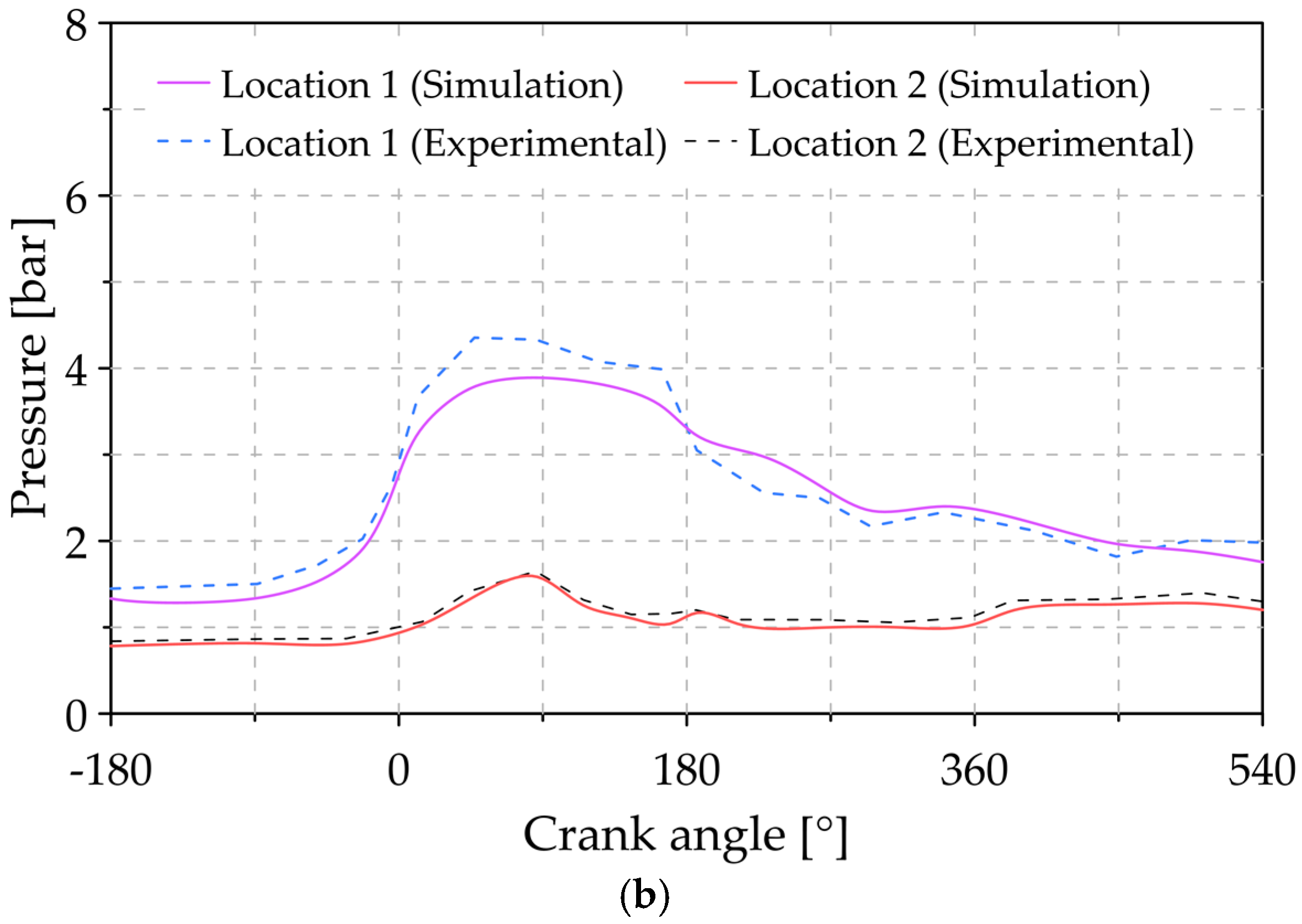
2.3. Experimental Validation
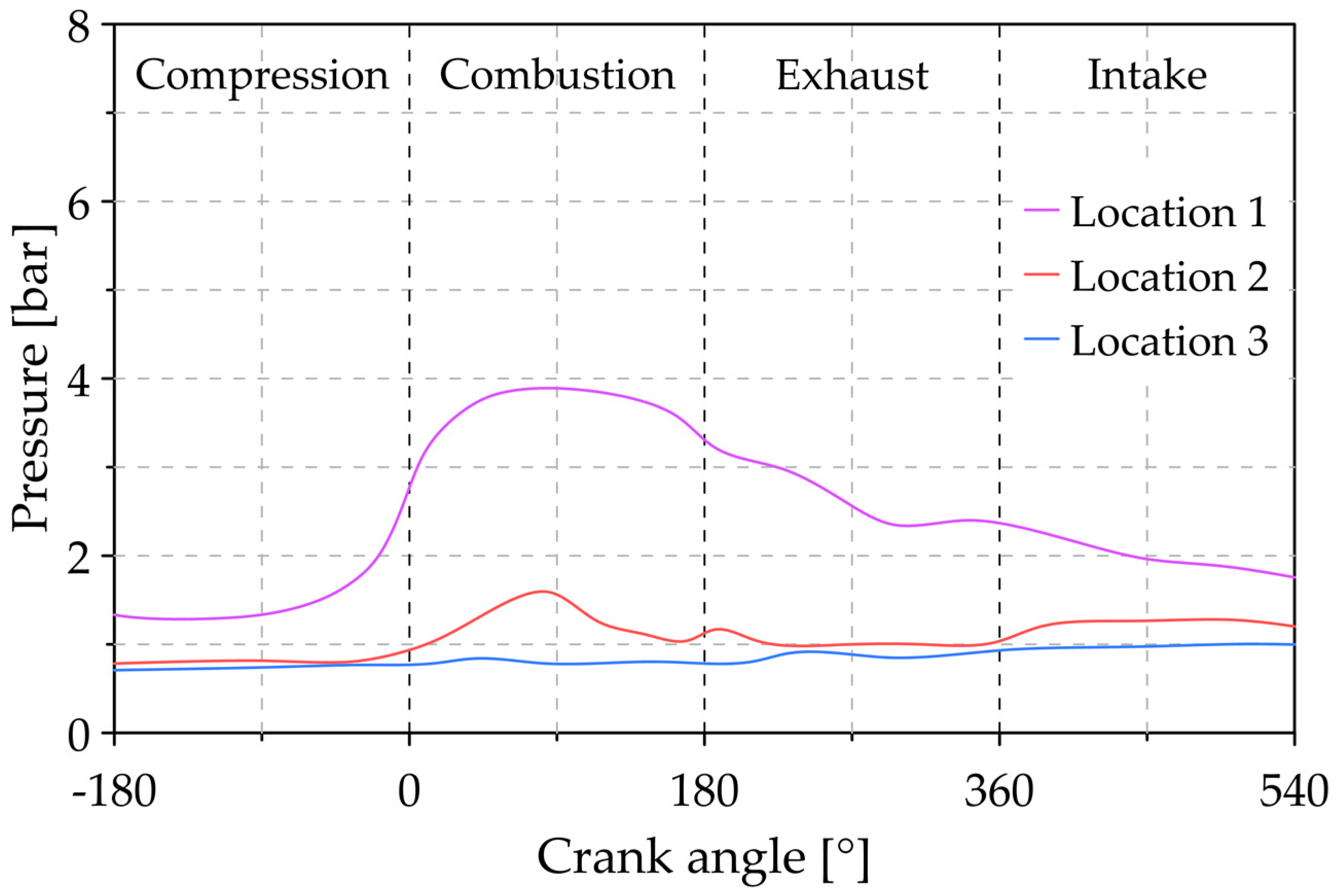
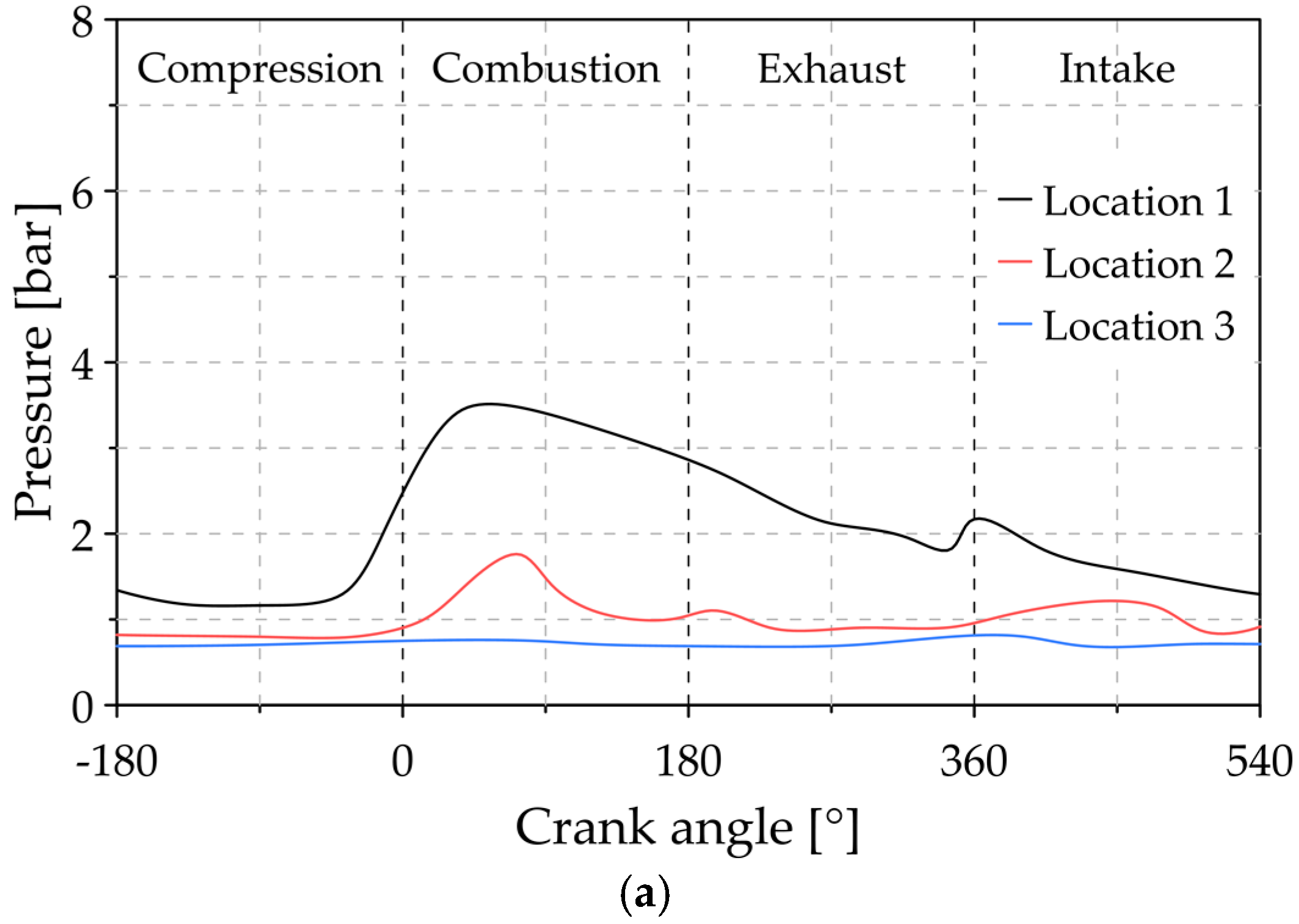
3. Results and Discussions
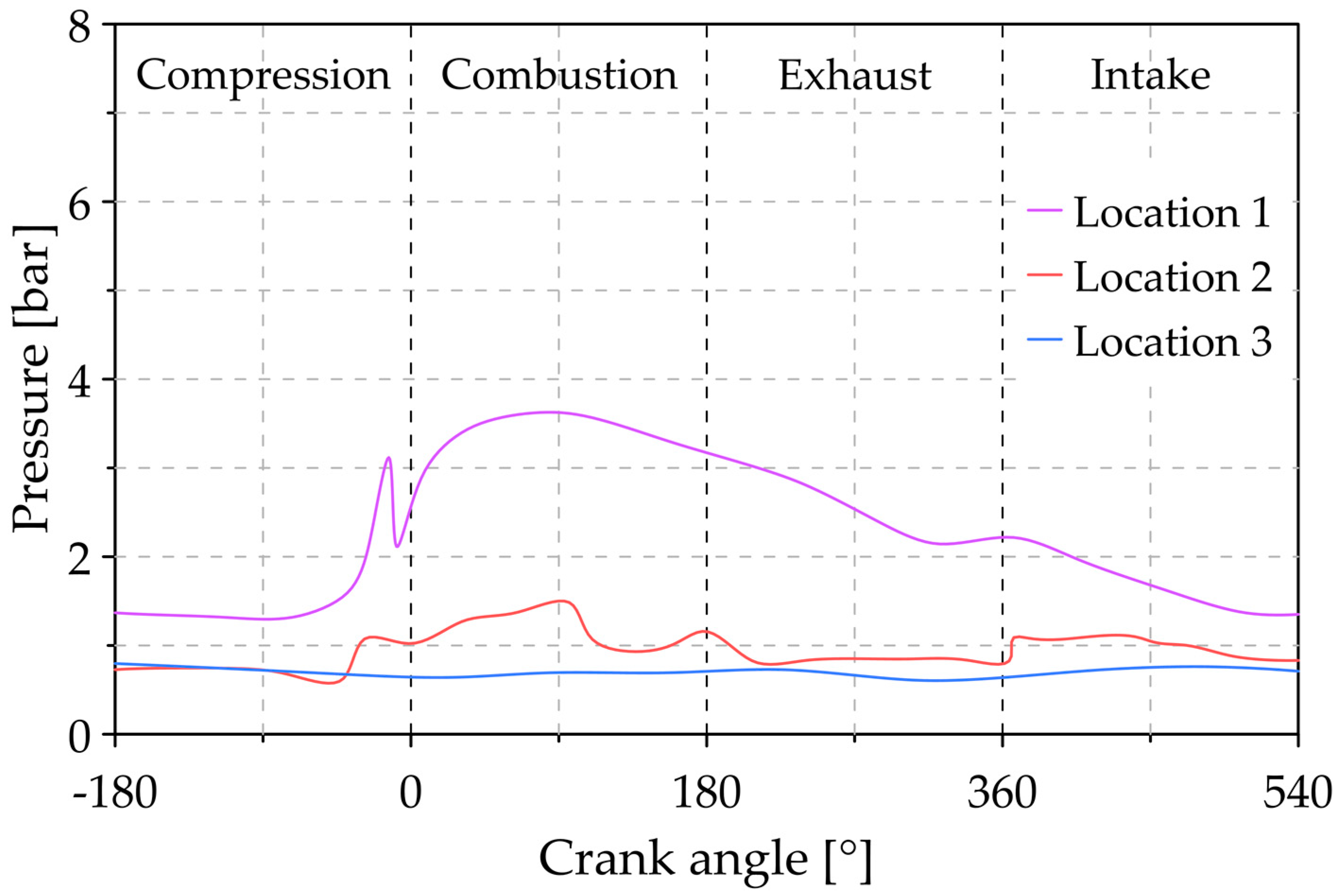
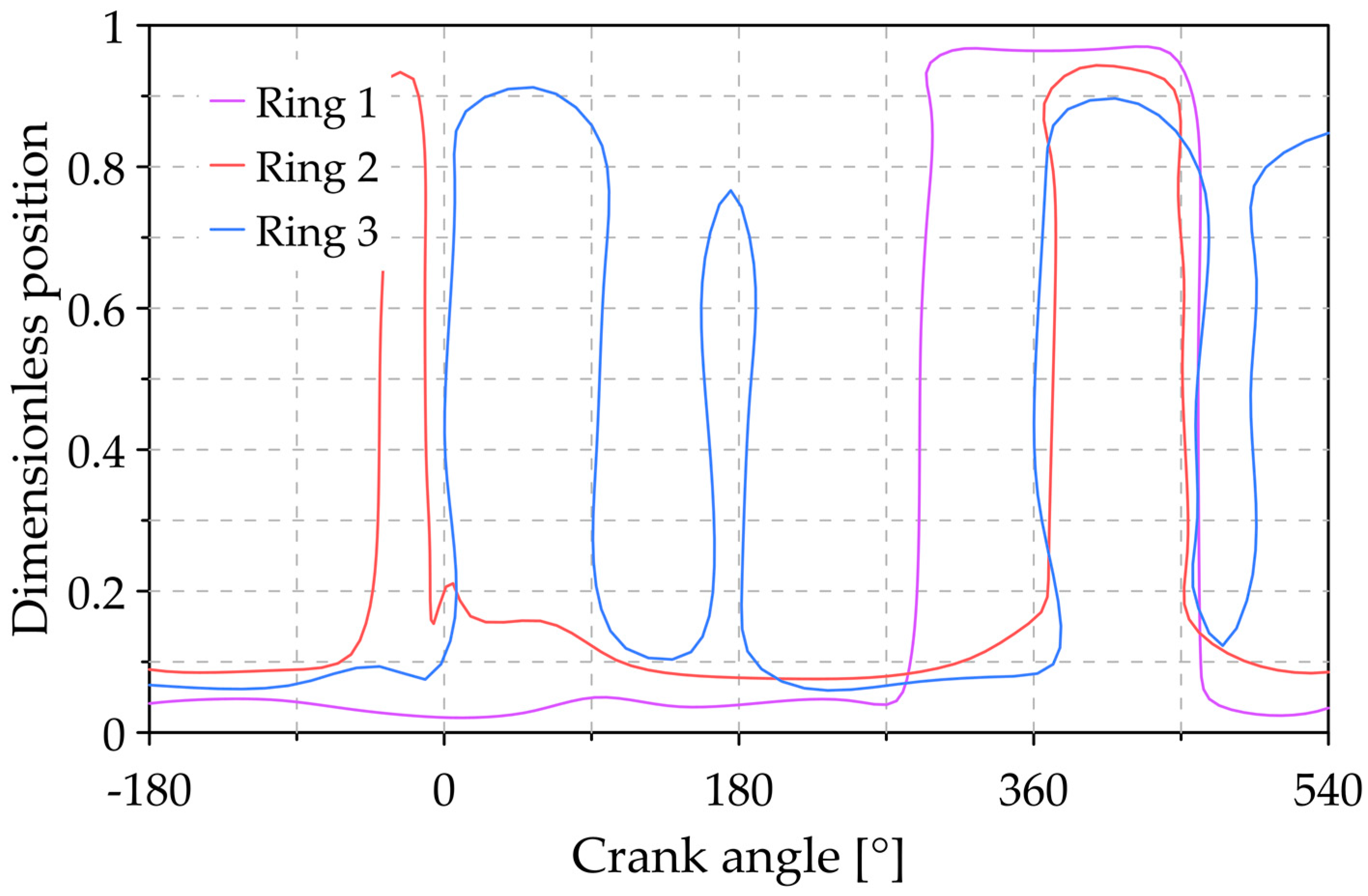
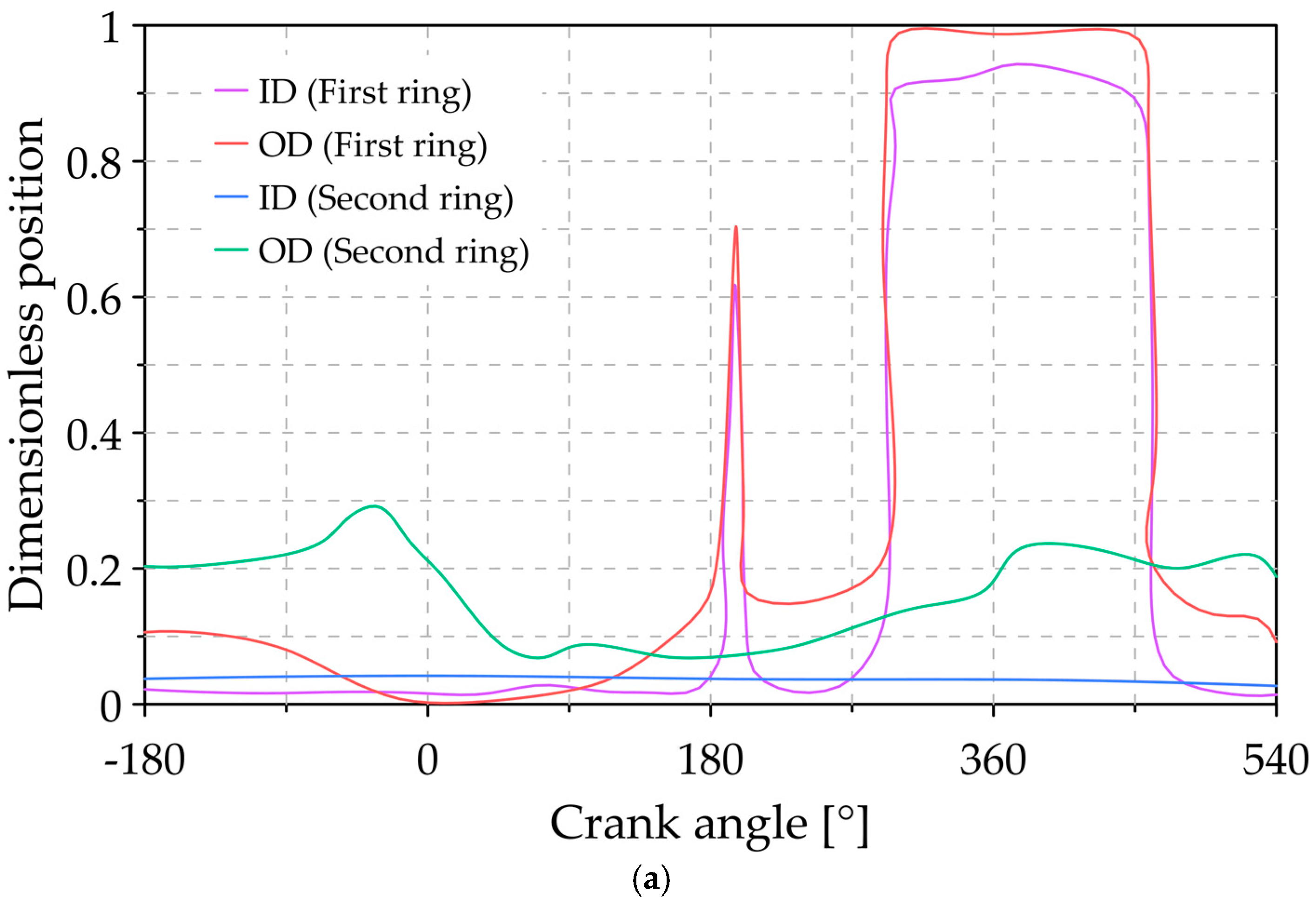
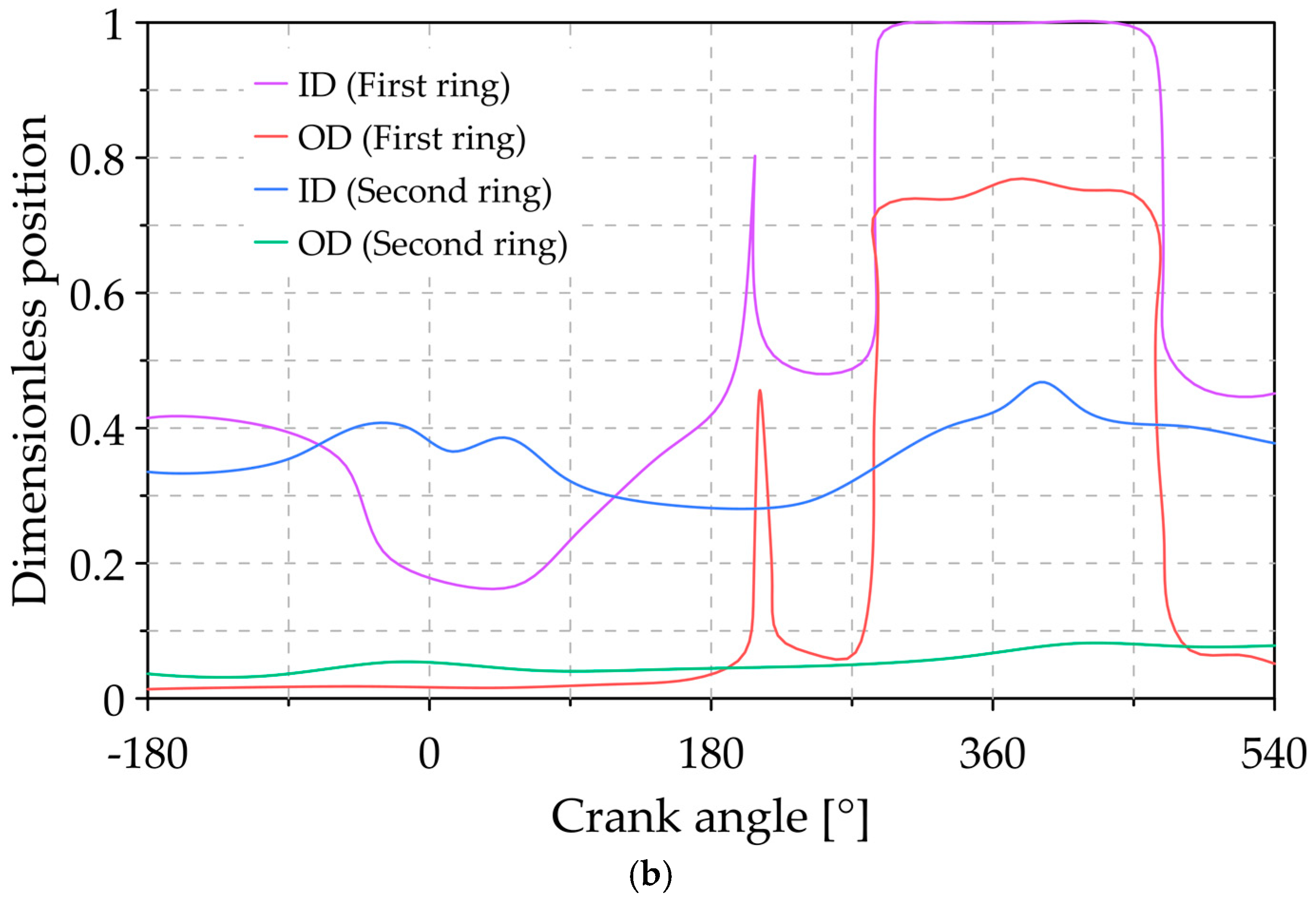
3.1. Analysis of the Reference Conditions
3.2. Analysis of the Influence of Ring Gap
3.3. Analysis of the Variation of the Mass of Compression Rings
3.4. Analysis of the Variation of the Twist Angle of Compression Rings
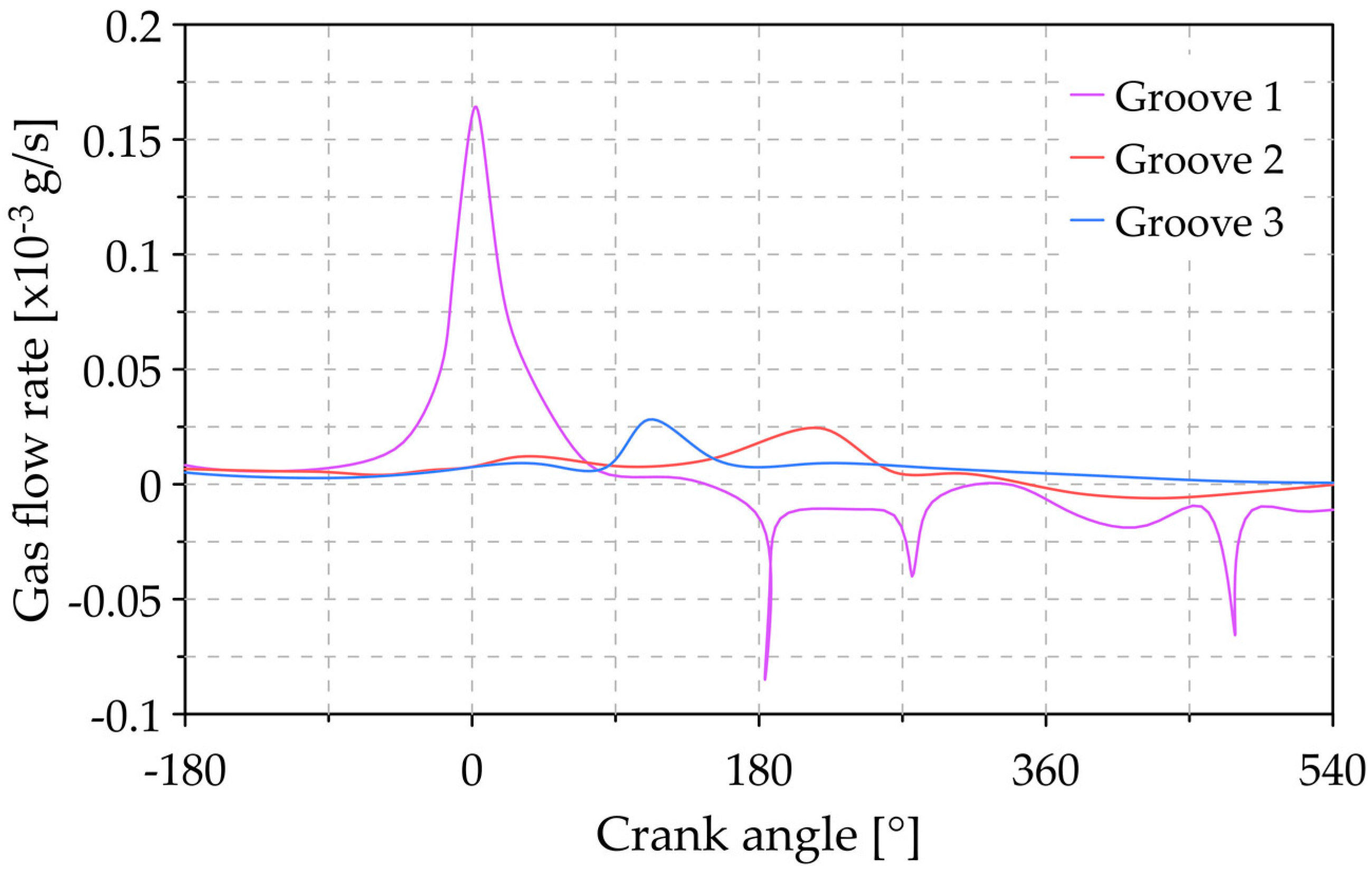
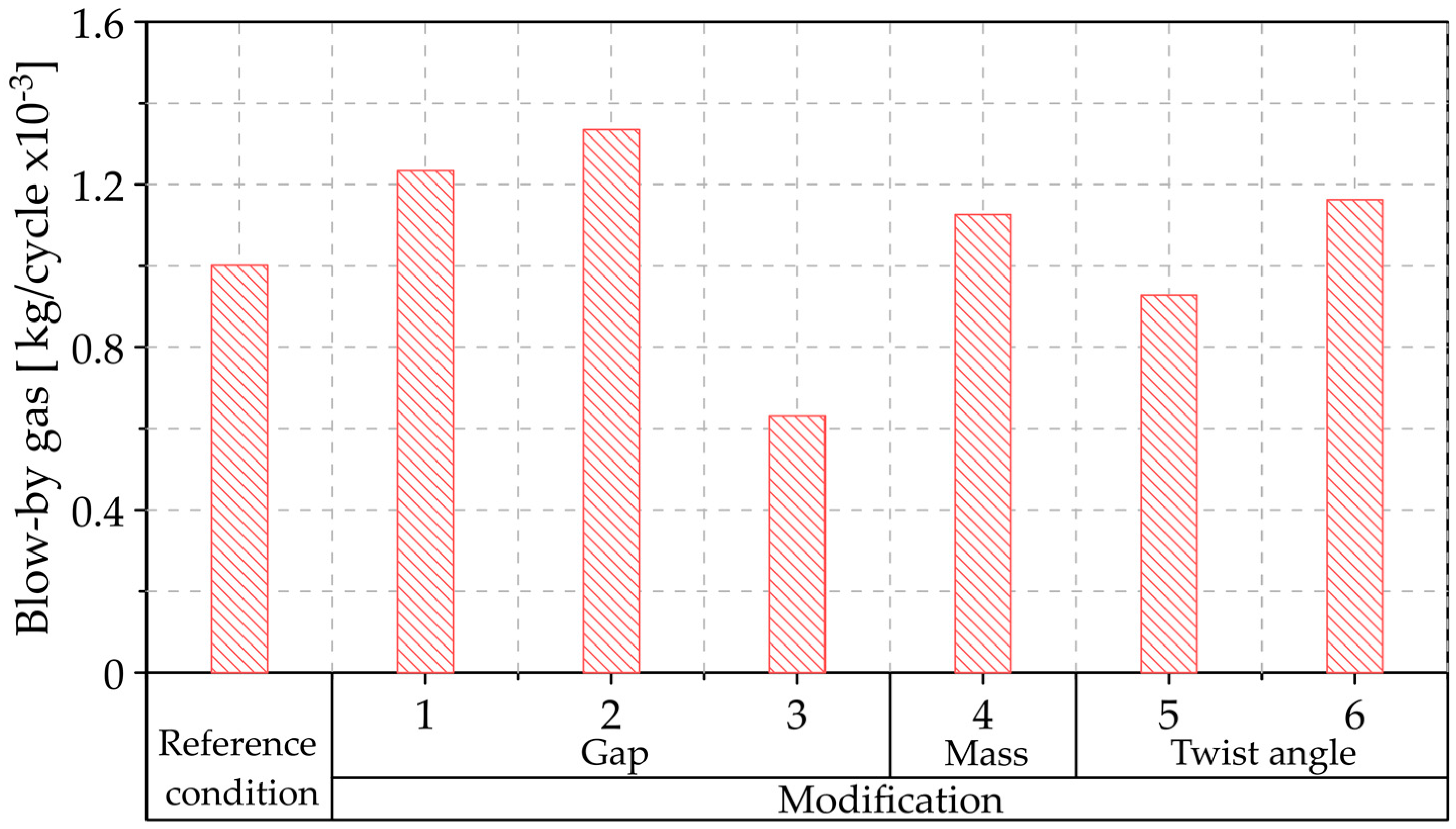
3.5. Analysis of the Variation of Blow-By Gas
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Nomenclature | |
| Internal combustion engine | |
| FEA | Finite element analysis |
| Temperature | |
| Pressure | |
| Model constant | |
| Acceleration | |
| Longitude | |
| Force | |
| Piston mass | |
| Hydrodynamic pressure | |
| Viscous shear stress | |
| Area | |
| Pressure flow factors | |
| Shear flow factor | |
| Thickness of the lubrication film | |
| Piezo-viscosity index | |
| Thermo-viscosity index | |
| Coefficient of asperity shear strength | |
| Asperity contact pressure | |
| Surface roughness | |
| Average asperity radius of curvature | |
| Asperity distribution | |
| The stribeck’s lubricant film ratio | |
| Equivalent Young’s modulus of elasticity | |
| Statistical function of lubricant film ratio | |
| Modulus of elasticity | |
| Poisson’s ratio | |
| Eccentricities of piston at the top of the skirt | |
| Eccentricities of piston at the bottom of the skirt | |
| Clearance between the cylinder liner and piston skirt | |
| Longitude of piston skirt | |
| Piston skirt deformation | |
| Limiting Eyring shear stress | |
| Effective asperity contact area | |
| Statistical function of the Stribeck’s lubricant film ratio | |
| Specific pressure of the piston ring on the cylinder wall | |
| Diameter of the ring | |
| Width of the ring | |
| Bending stress | |
| Shear factor due to local roughness | |
| Ring gap | |
| Length of the ring | |
| Stiffness torsion | |
| Inner diameter | |
| Outer diameter | |
| Mass flow | |
| Shear factor due to sliding velocity | |
| Gas constant | |
| Dynamic viscosity of the gas | |
| Sutherland’s number | |
| Ring gap area | |
| Discharge coefficient | |
| Compressibility factor | |
| Ratio of the specific heats | |
| Second moment of inertia of the area | |
| Cross-sectional area | |
| Radius of curvature of the ring | |
| Angular position of the ring | |
| Elastic compliance matrix | |
| Radial direction | |
| Axial direction | |
| Shear factor due to mean pressure | |
| Distance between the wrist pin and axis of the piston | |
| Greek Letters | |
| Density | |
| Coefficient of thermal expansion | |
| Viscosity | |
| Model constant | |
| Atmospheric piezo-viscosity coefficient | |
| Thermo-viscosity coefficient | |
| Displacement angle of the connecting rod | |
| Angular velocity | |
| Displacement angle of the crankshaft | |
| Ring twist angle | |
| Subscripts | |
| Environmental conditions | |
| Atmospheric | |
| Piston | |
| Connecting rod | |
| c | Crankshaft |
| Combustion gases | |
References
- Amador, G.; Duarte, J.F.; Rincon, A.; Fontalvo, A.; Bula, A.; Padilla, R.V.; Orozco, W. Characteristics of Auto-Ignition in Internal Combustion Engines Operated with Gaseous Fuels of Variable Methane Number. J. Energy Resour. Technol. Trans. ASME 2017, 139. [Google Scholar] [CrossRef]
- Ochoa, G.V.; Isaza-Roldan, C.; Duarte Forero, J. Economic and Exergo-Advance Analysis of a Waste Heat Recovery System Based on Regenerative Organic Rankine Cycle under Organic Fluids with Low Global Warming Potential. Energies 2020, 13, 1317. [Google Scholar] [CrossRef]
- Pavlovic, J.; Ciuffo, B.; Fontaras, G.; Valverde, V.; Marotta, A. How much difference in type-approval CO2 emissions from passenger cars in Europe can be expected from changing to the new test procedure (NEDC vs. WLTP)? Transp. Res. Part A Policy Pract. 2018, 111, 136–147. [Google Scholar] [CrossRef]
- Orozco, W.; Acuña, N.; Duarte, J. Characterization of Emissions in Low Displacement Diesel Engines Using Biodiesel and Energy Recovery System. Int. Rev. Mech. Eng. 2019, 13, 420–426. [Google Scholar] [CrossRef]
- Duarte, J.; Garcia, J.; Jiménez, J.; Sanjuan, M.E.; Bula, A.; González, J. Auto-Ignition Control in Spark-Ignition Engines Using Internal Model Control Structure. J. Energy Resour. Technol. Trans. ASME 2017, 139. [Google Scholar] [CrossRef]
- Allen, C.M.; Gosala, D.B.; Shaver, G.M.; McCarthy, J. Comparative study of diesel engine cylinder deactivation transition strategies. Int. J. Engine Res. 2019, 20, 570–580. [Google Scholar] [CrossRef]
- Oglieve, C.J.; Mohammadpour, M.; Rahnejat, H. Optimisation of the vehicle transmission and the gear-shifting strategy for the minimum fuel consumption and the minimum nitrogen oxide emissions. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2017, 231, 883–899. [Google Scholar] [CrossRef]
- Duarte, J.; Amador, G.; Garcia, J.; Fontalvo, A.; Vasquez Padilla, R.; Sanjuan, M.; Gonzalez Quiroga, A. Auto-ignition control in turbocharged internal combustion engines operating with gaseous fuels. Energy 2014, 71, 137–147. [Google Scholar] [CrossRef]
- Turnbull, R.; Mohammadpour, M.; Rahmani, R.; Rahnejat, H.; Offner, G. Coupled elastodynamics of piston compression ring subject to sweep excitation. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2017, 231, 469–479. [Google Scholar] [CrossRef]
- Morris, N.; Mohammadpour, M.; Rahmani, R.; Rahnejat, H. Optimisation of the piston compression ring for improved energy efficiency of high performance race engines. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2017, 231, 1806–1817. [Google Scholar] [CrossRef]
- Baker, C.; Theodossiades, S.; Rahmani, R.; Rahnejat, H.; Fitzsimons, B. On the Transient Three-Dimensional Tribodynamics of Internal Combustion Engine Top Compression Ring. J. Eng. Gas Turbines Power 2017, 139. [Google Scholar] [CrossRef]
- Hallouin, B.; Lasseux, D.; Senger, G. Gas flow through a bore-piston ring contact. Int. J. Engine Res. 2020. [Google Scholar] [CrossRef]
- Namazian, M.; Heywood, J.B. Flow in the Piston-Cylinder-Ring Crevices of a Spark-Ignition Engine: Effect on Hydrocarbon Emissions, Efficiency and Power; SAE Technical Papers; Society of Automotive Engineers: Warrendale, PA, USA, 1982. [Google Scholar]
- Furuhama, S.; Tada, T. On the Flow of Gas through the Piston-Rings: 2nd Report, the Character of Gas Leakage. Bull. JSME 1961, 4, 691–698. [Google Scholar] [CrossRef]
- Tomanik, E.; Sobrinho, R.M.S.; Zecchinelli, R. Influence Of Top Ring End Gap Types At Blow-By Of Internal Combustion Engines. SAE Tech. Pap. 1993. [Google Scholar] [CrossRef]
- Wannatong, K.; Chanchaona, S.; Sanitjai, S. Simulation algorithm for piston ring dynamics. Simul. Model. Pract. Theory 2008, 16, 127–146. [Google Scholar] [CrossRef]
- Keribar, R.; Dursunkaya, Z.; Flemming, M.F. An Integrated Model of Ring Pack Performance. J. Eng. Gas Turbines Power 1991, 113, 382–389. [Google Scholar] [CrossRef]
- Przesmitzki, S.; Tian, T. An Experimental Study of the Time Scales and Controlling Factors Affecting Drastic Blow-by Increases during Transient Load Changes in SI Engines. SAE Tech. Pap. 2008. [Google Scholar] [CrossRef]
- Iijima, N.; Miyamoto, T.; Takiguchi, M.; Kai, R.; Sato, M. An Experimental Study on Phenomena of Piston Ring Collapse. SAE Tech. Pap. 2002. [Google Scholar] [CrossRef]
- Tian, T. Dynamic behaviours of piston rings and their practical impact. Part 2: Oil transport, friction and wear of ring/liner interface and the effects of piston and ring dynamics. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2002, 216, 229–248. [Google Scholar] [CrossRef]
- Dowson, D.; Higginson, G.R. A Numerical Solution to the Elasto-Hydrodynamic Problem. J. Mech. Eng. Sci. 1959, 1, 6–15. [Google Scholar] [CrossRef]
- Yang, P.; Cui, J.; Jin, Z.M.; Dowson, D. Transient elastohydrodynamic analysis of elliptical contacts. Part 2: Thermal and Newtonian lubricant solution. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2005, 219, 187–200. [Google Scholar] [CrossRef]
- Roelands, C.J.A.; Winer, W.O.; Wright, W.A. Correlational Aspects of the Viscosity-Temperature-Pressure Relationship of Lubricating Oils (Dr In dissertation at Technical University of Delft, 1966). J. Lubr. Technol. 1971, 93, 209–210. [Google Scholar] [CrossRef]
- Houpert, L. New Results of Traction Force Calculations in Elastohydrodynamic Contacts. J. Tribol. 1985, 107, 241–245. [Google Scholar] [CrossRef]
- Perera, M.S.M.; Theodossiades, S.; Rahnejat, H. Elasto-multi-body dynamics of internal combustion engines with tribological conjunctions. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2010, 224, 261–277. [Google Scholar] [CrossRef]
- Consuegra, F.; Bula, A.; Guillín, W.; Sánchez, J.; Duarte Forero, J. Instantaneous in-Cylinder Volume Considering Deformation and Clearance due to Lubricating Film in Reciprocating Internal Combustion Engines. Energies 2019, 12, 1437. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Application of Average Flow Model to Lubrication between Rough Sliding Surfaces. J. Lubr. Technol. 1979, 101, 220–229. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Tripp, J.H. The Contact of Two Nominally Flat Rough Surfaces. Proc. Inst. Mech. Eng. 1970, 185, 625–633. [Google Scholar] [CrossRef]
- Teodorescu, M.; Balakrishnan, S.; Rahnejat, H. Integrated Tribological Analysis within a Multi- physics Approach to System Dynamics. Tribol. Interface Eng. Ser. 2005, 48, 725–737. [Google Scholar]
- Makartchouk, A. Diesel Engine Engineering: Thermodynamics, Dynamics, Design, and Control; CRC Press: Boca Raton, FL, USA, 2002; Volume 143. [Google Scholar]
- Tian, T.; Noordzij, L.B.; Wong, V.W.; Heywood, J.B. Modeling Piston-Ring Dynamics, Blowby, and Ring-Twist Effects. J. Eng. Gas Turbines Power 1998, 120, 843–854. [Google Scholar] [CrossRef]
- Lyubarskyy, P.; Bartel, D. 2D CFD-model of the piston assembly in a diesel engine for the analysis of piston ring dynamics, mass transport and friction. Tribol. Int. 2016, 104, 352–368. [Google Scholar] [CrossRef]
- Rahmani, R.; Theodossiades, S.; Rahnejat, H.; Fitzsimons, B. Transient elastohydrodynamic lubrication of rough new or worn piston compression ring conjunction with an out-of-round cylinder bore. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2012, 226, 284–305. [Google Scholar] [CrossRef]
- Lang, T.E. Vibration of Thin Circular Rings, Part 1; Jet Propulsion Laboratory: Pasadena, CA, USA, 1962.
- Sutherland, L.W. The viscosity of gases and molecular force. Philos. Mag. 1893, 36, 507–531. [Google Scholar] [CrossRef]
- Theaker, M.; Rahmani, R.; Rahnejat, H. Prediction of Ring-Bore Conformance and Contact Condition and Experimental Validation. In Proceedings of the ASME 2012 Internal Combustion Engine Division Spring Technical Conference, Piemonte, Italy, 6–9 May 2012; pp. 885–892. [Google Scholar]
- Zhu, D.; Hu, Y.-Z.; Cheng, H.S.; Arai, T.; Hamai, K. A Numerical Analysis for Piston Skirts in Mixed Lubrication: Part II—Deformation Considerations. J. Tribol. 1993, 115, 125–133. [Google Scholar] [CrossRef]
- Cantore, G.; Giacopini, M.; Rosi, R.; Strozzi, A.; Pelloni, P.; Forte, C.; Achiluzzi, M.; Bianchi, G.M.; Ceschini, L.; Morri, A. Validation of a combined CFD/FEM methodology for the evaluation of thermal load acting on aluminum alloy pistons through hardness measurements in internal combustion engines. Metall. Sci. Tecnol. 2011, 29, 16–25. [Google Scholar]
- Richardson, D.E. Comparison of Measured and Theoretical Inter-Ring Gas Pressure on a Diesel Engine; SAE Technical Papers; SAE International: Warrendale, PA, USA, 1996. [Google Scholar]
- Dursunkaya, Z.; Keribar, R.; Richardson, D.E. Experimental and Numerical Investigation of Inter-Ring Gas Pressures and Blowby in a Diesel Engine. SAE Tech. Pap. 1993. [Google Scholar] [CrossRef]
- Nikolakopoulos, P.G. Simulation of deposits effect on cylinder liner and influence on new and worn compression ring of a turbocharged DI engine. Simul. Model. Pract. Theory 2021, 106, 102195. [Google Scholar] [CrossRef]
- Delprete, C.; Selmani, E.; Bisha, A. Gas escape to crankcase: Impact of system parameters on sealing behavior of a piston cylinder ring pack. Int. J. Energy Environ. Eng. 2019, 10, 207–220. [Google Scholar] [CrossRef]
- Selmani, E.; Bisha, A. Engine Speed and Load on the Sealing Capacity of a Piston Ring-Pack. Eur. J. Eng. Res. Sci. 2020, 5, 304–313. [Google Scholar] [CrossRef]
- Cheng, C.; Schock, H.; Richardson, D. The dynamics of second ring flutter and collapse in modern diesel engines. J. Eng. Gas Turbines Power 2015, 137. [Google Scholar] [CrossRef]
- Tian, T. Dynamic behaviours of piston rings and their practical impact. Part 1: Ring flutter and ring collapse and their effects on gas flow and oil transport. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2002, 216, 209–228. [Google Scholar] [CrossRef]
- Kurbet, S.N.; Kumar, R.K. A finite element study of piston tilt effects on piston ring dynamics in internal combustion engines. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2004, 218, 107–117. [Google Scholar] [CrossRef]

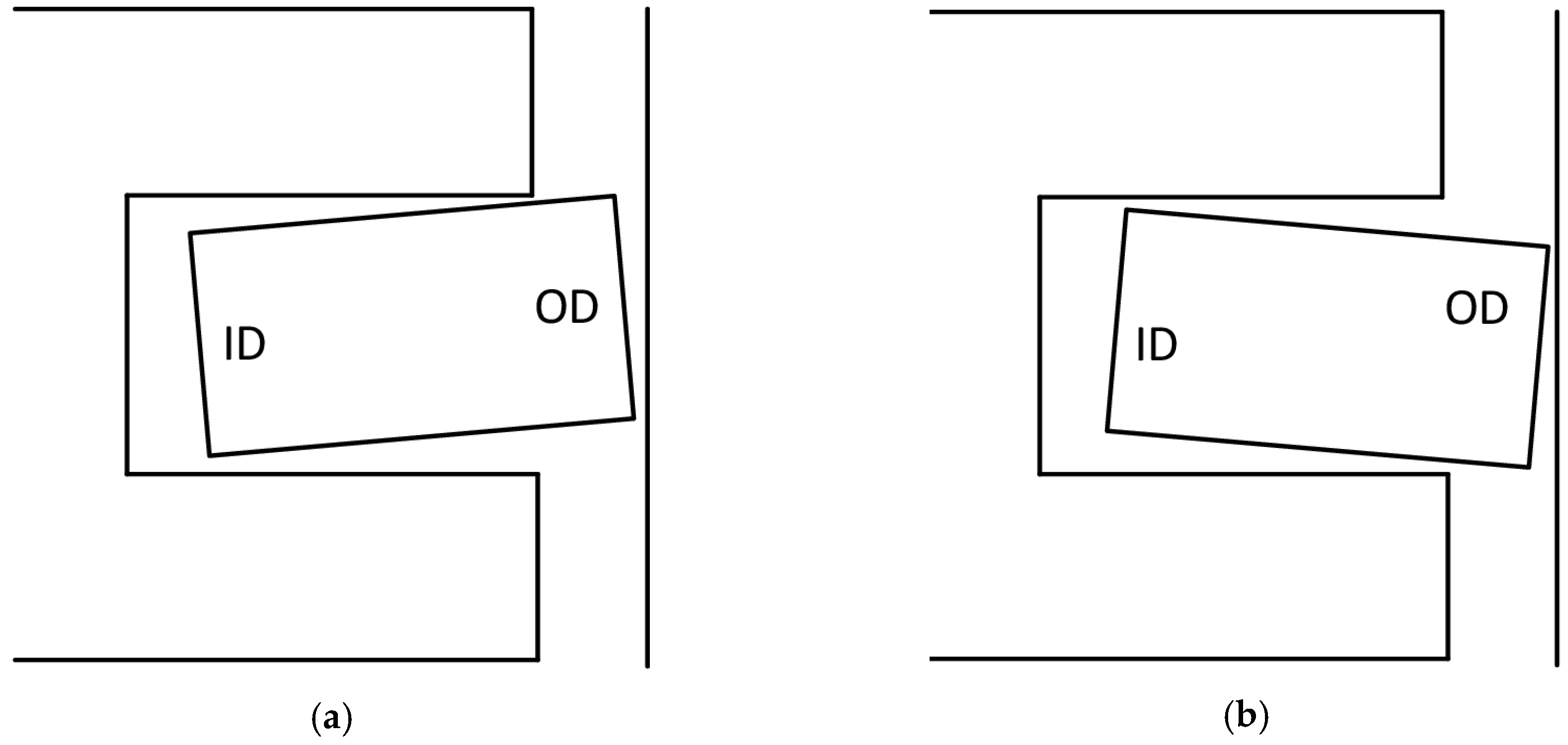
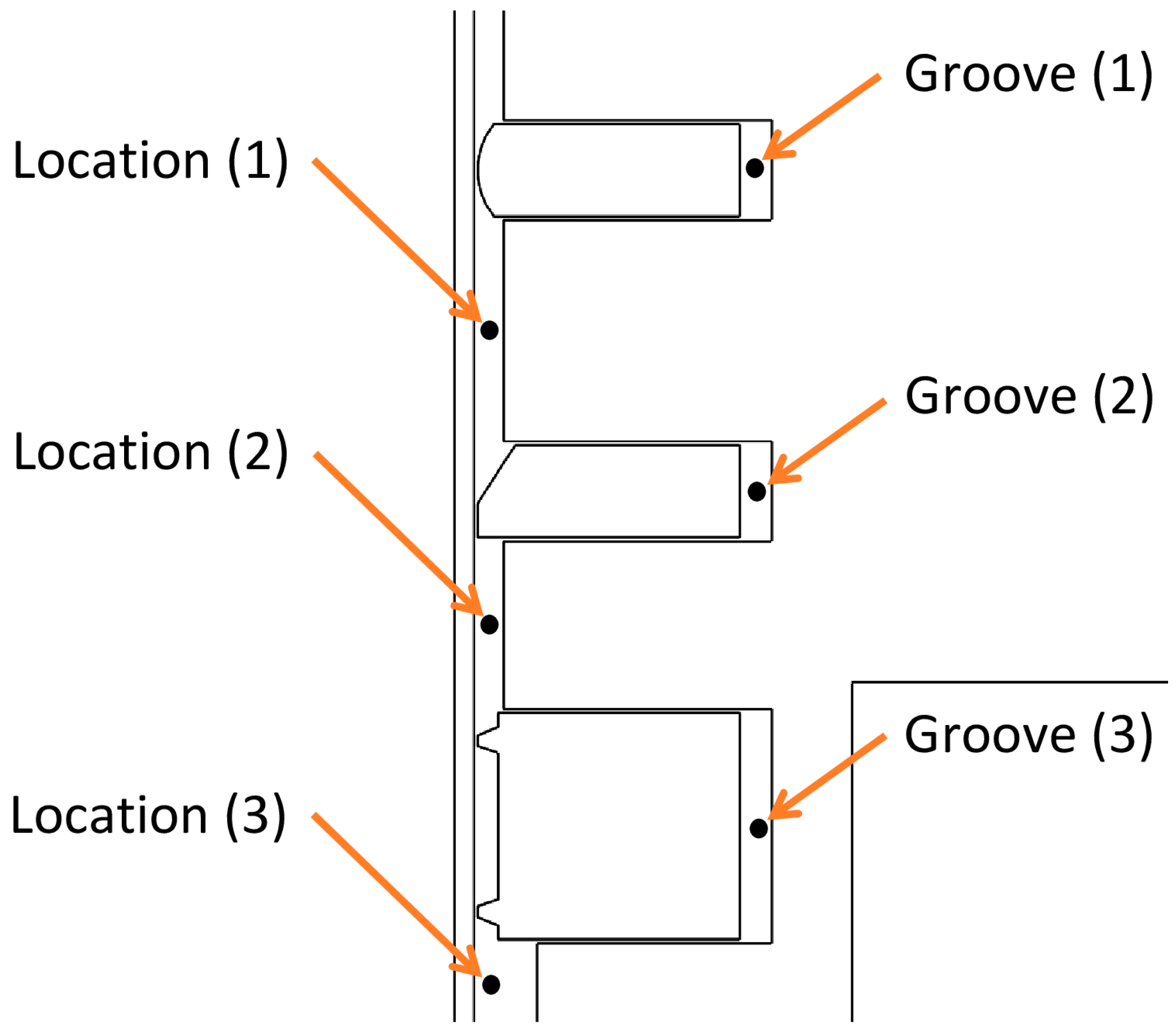

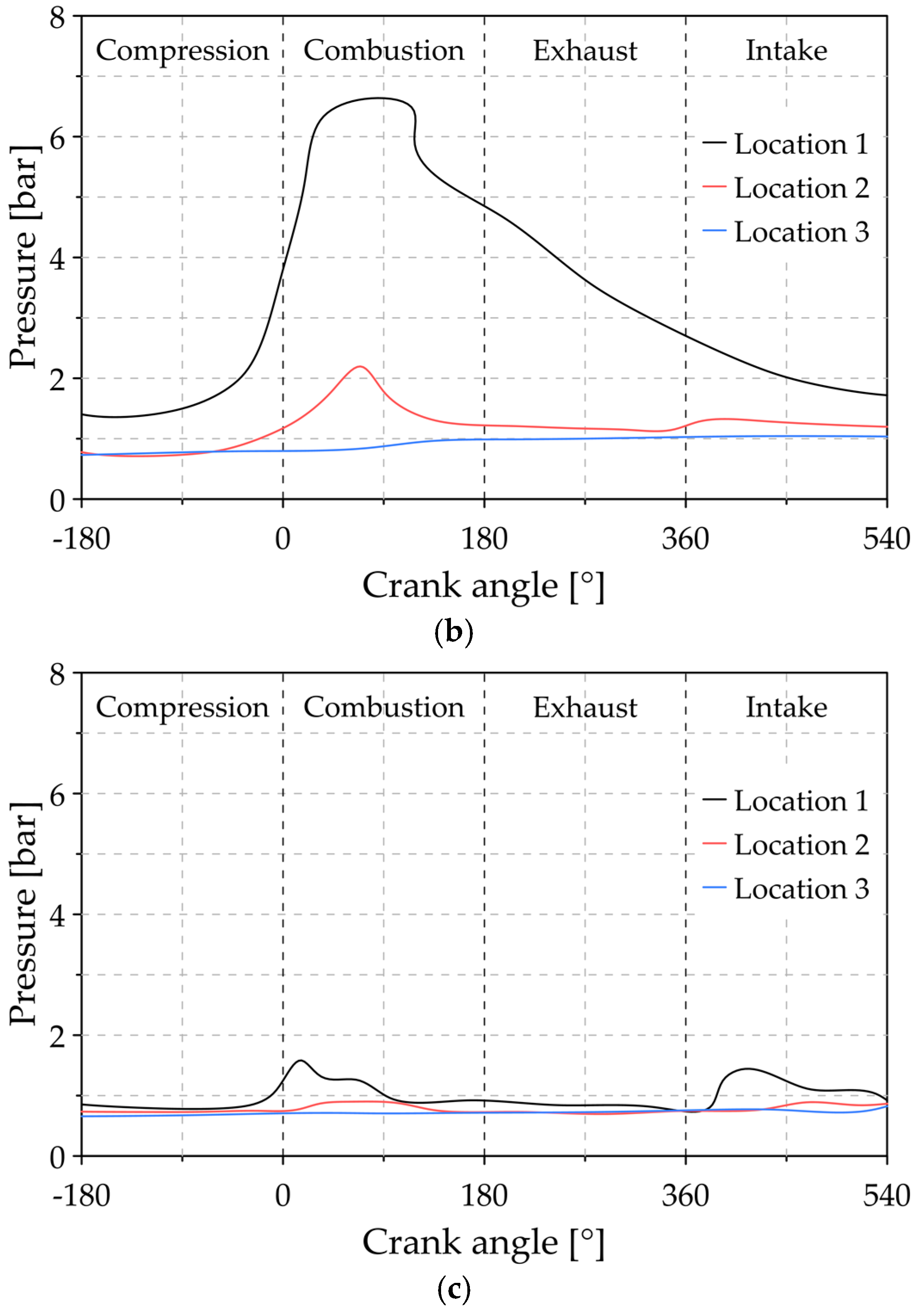
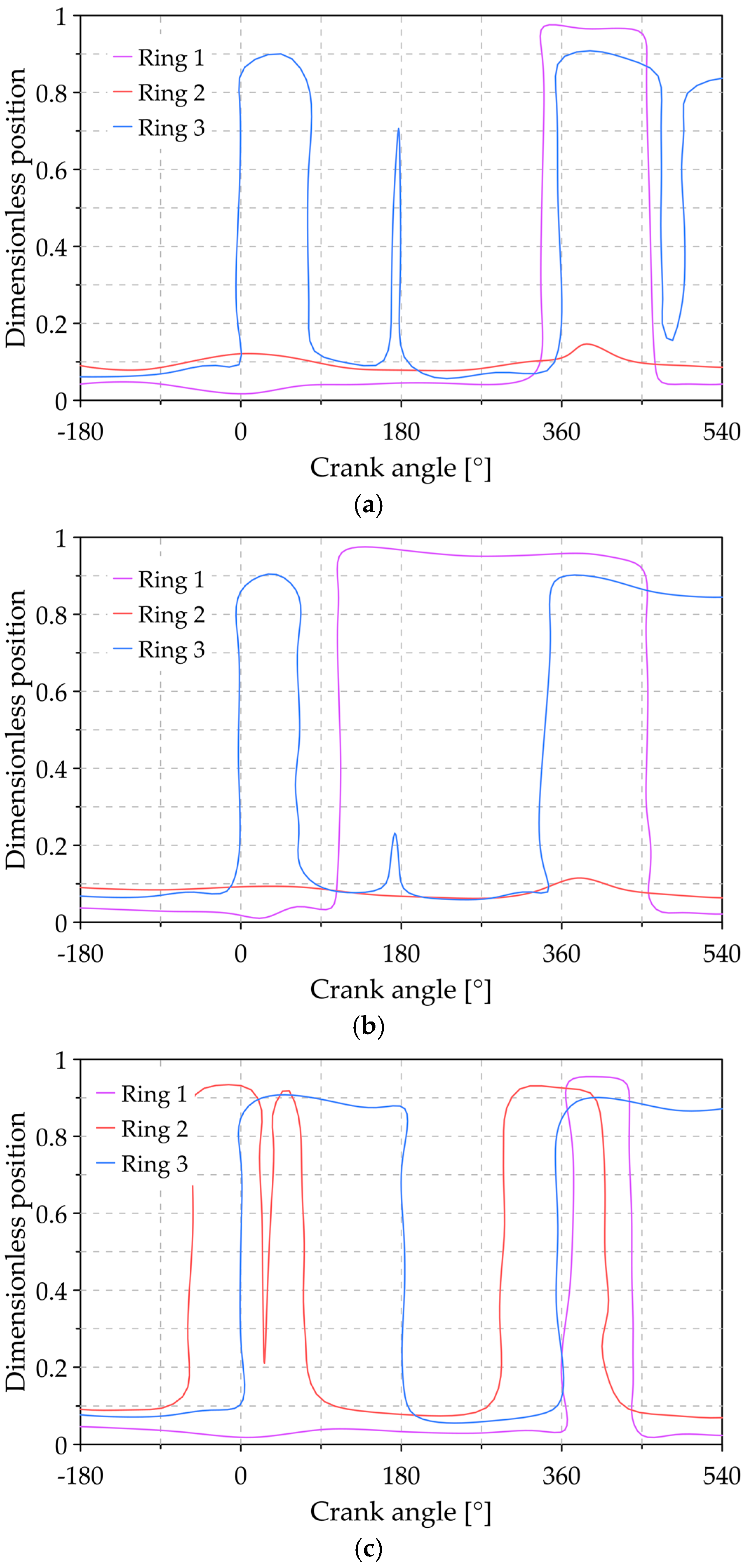
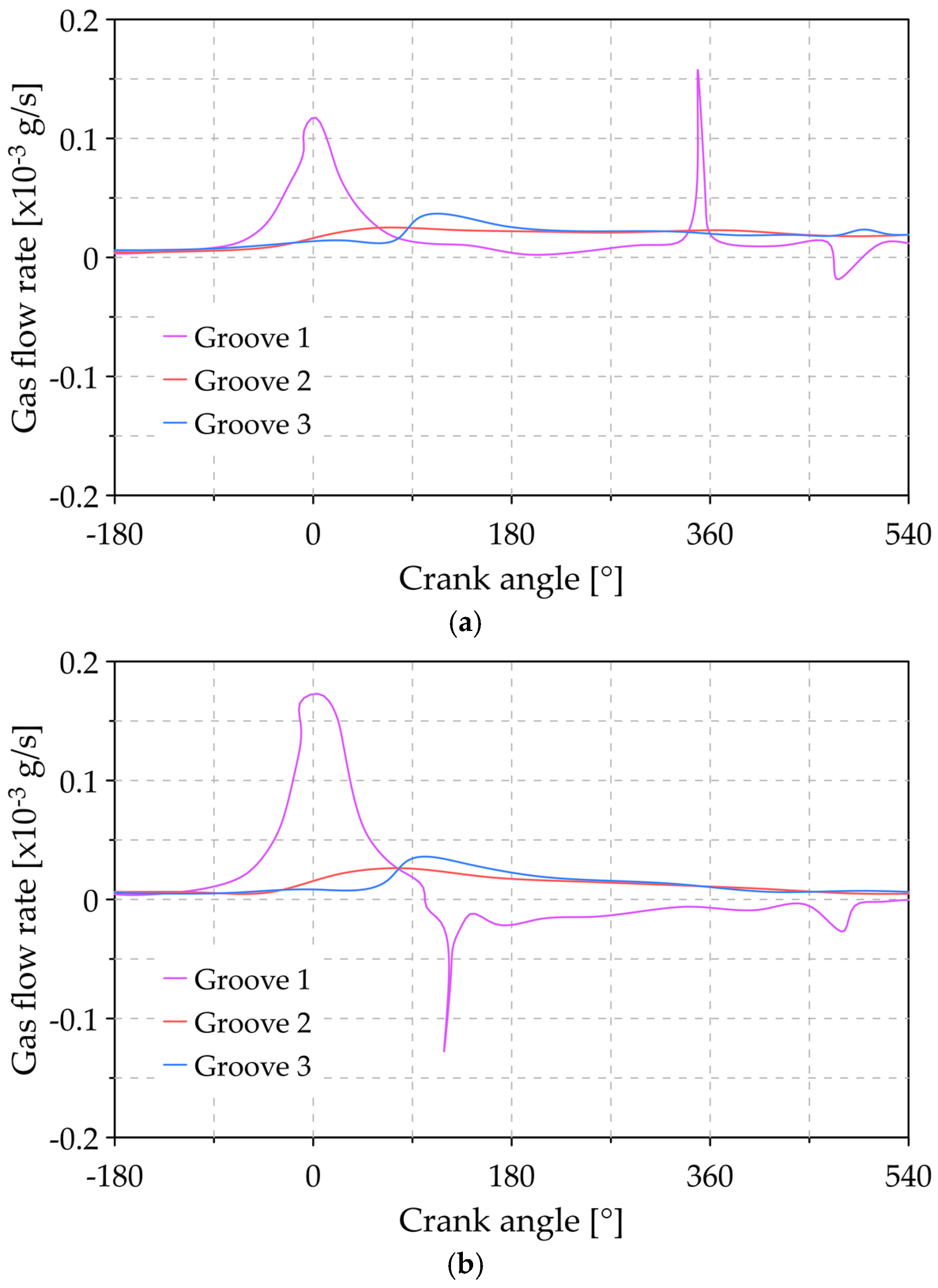
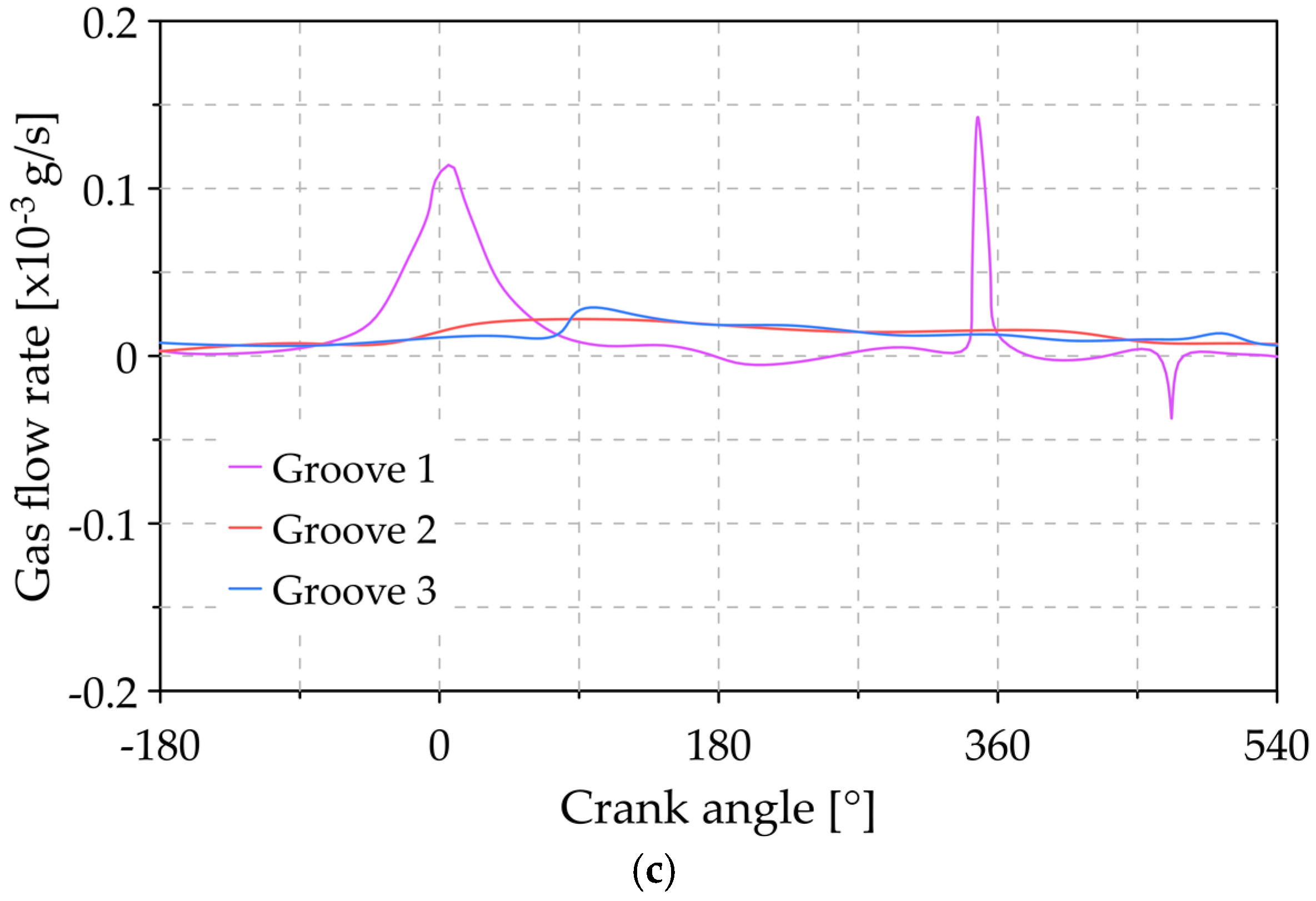
| Modification | Parameter | First Ring | Second Ring |
|---|---|---|---|
| 1 | Gap | −25% | +25% |
| 2 | +25% | ||
| 3 | −25% | −25% | |
| 4 | Mass | +50% | +50% |
| 5 | Twist angle | Positive | Positive |
| 6 | Negative | Negative |
| Model | SK-MDF300 |
|---|---|
| Manufacturer | SOKAN |
| Bore × stroke | 78 mm × 62.57 mm |
| Engine type | 1 cylinder |
| Maximum power | 4.6 hp at 3600 rpm |
| Cycle | 4 Strokes |
| Injection system | Direct injection |
| Displaced volume | 299 CC |
| Compression ratio | 20:1 |
| Intake system | Naturally Aspirated |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández-Comas, B.; Maestre-Cambronel, D.; Pardo-García, C.; Fonseca-Vigoya, M.D.S.; Pabón-León, J. Influence of Compression Rings on the Dynamic Characteristics and Sealing Capacity of the Combustion Chamber in Diesel Engines. Lubricants 2021, 9, 25. https://doi.org/10.3390/lubricants9030025
Hernández-Comas B, Maestre-Cambronel D, Pardo-García C, Fonseca-Vigoya MDS, Pabón-León J. Influence of Compression Rings on the Dynamic Characteristics and Sealing Capacity of the Combustion Chamber in Diesel Engines. Lubricants. 2021; 9(3):25. https://doi.org/10.3390/lubricants9030025
Chicago/Turabian StyleHernández-Comas, Brando, Daniel Maestre-Cambronel, Carlos Pardo-García, Marlen Del Socorro Fonseca-Vigoya, and Jhon Pabón-León. 2021. "Influence of Compression Rings on the Dynamic Characteristics and Sealing Capacity of the Combustion Chamber in Diesel Engines" Lubricants 9, no. 3: 25. https://doi.org/10.3390/lubricants9030025
APA StyleHernández-Comas, B., Maestre-Cambronel, D., Pardo-García, C., Fonseca-Vigoya, M. D. S., & Pabón-León, J. (2021). Influence of Compression Rings on the Dynamic Characteristics and Sealing Capacity of the Combustion Chamber in Diesel Engines. Lubricants, 9(3), 25. https://doi.org/10.3390/lubricants9030025








