Understanding Friction in Cam–Tappet Contacts—An Application-Oriented Time-Dependent Simulation Approach Considering Surface Asperities and Edge Effects
Abstract
:1. Introduction
2. Materials and Methods
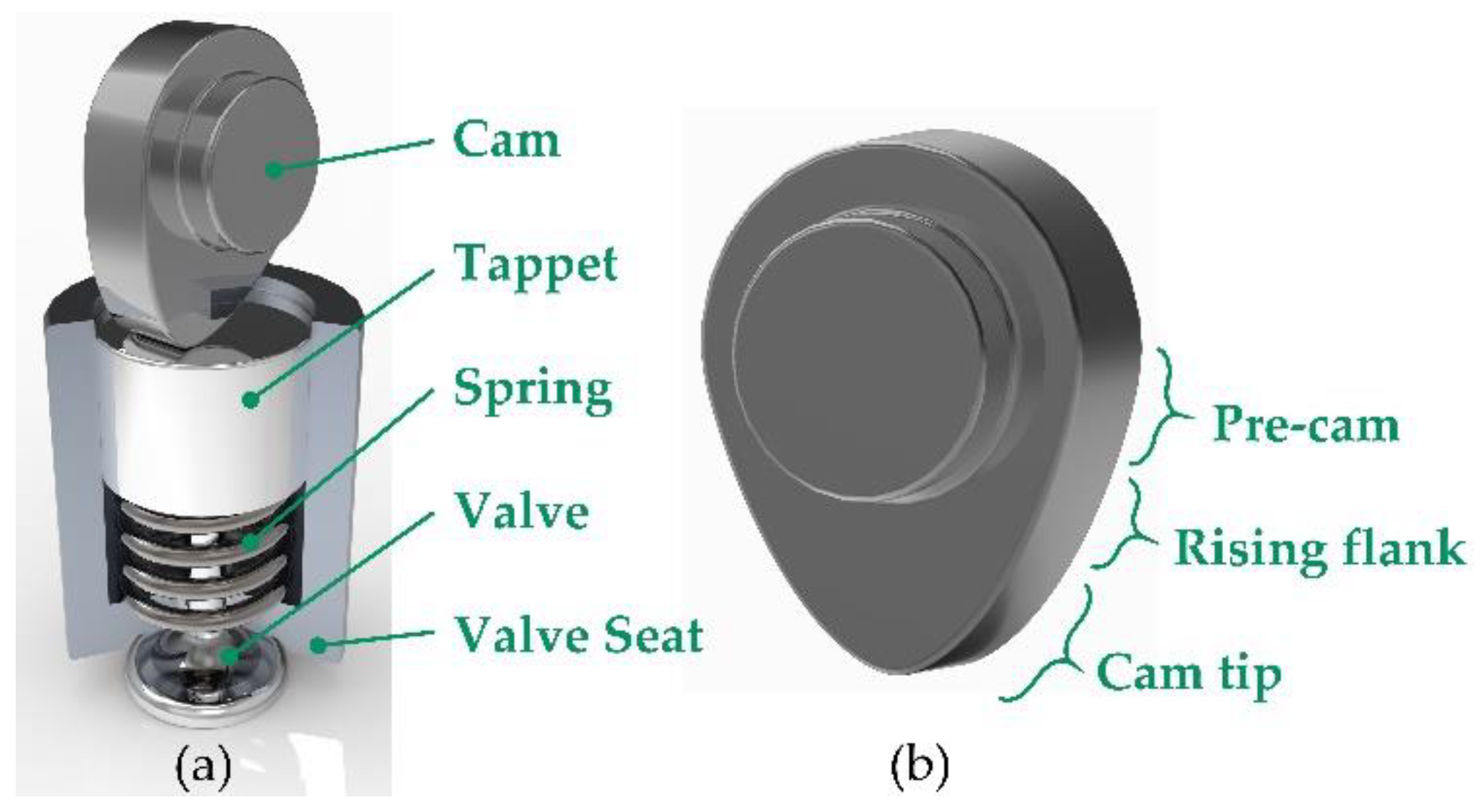
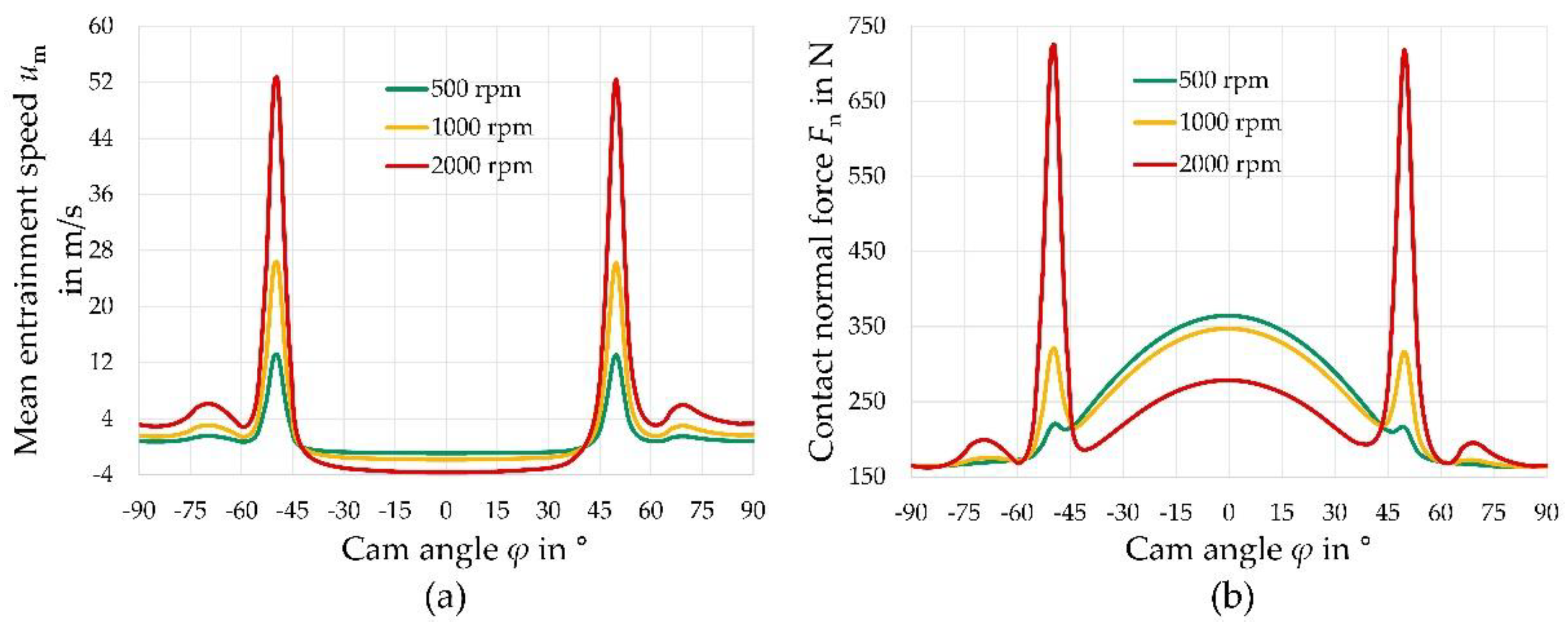
2.1. Load Spectrum of the Cam–Tappet Contact
2.2. Fluid Properites
2.3. Numerical Modelling
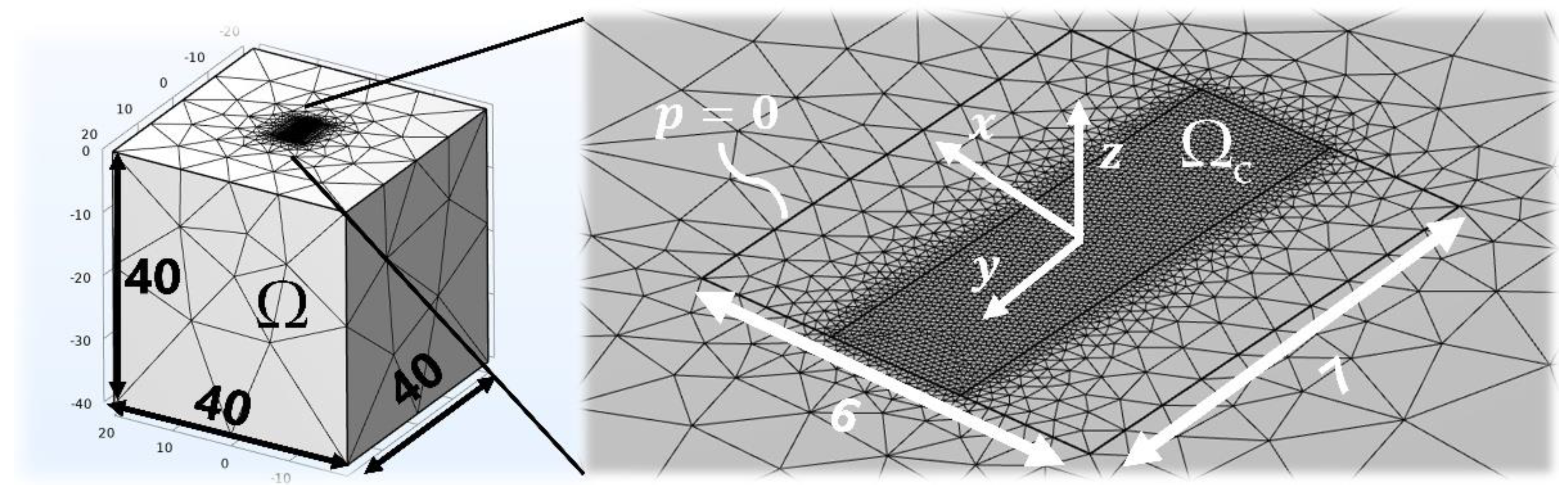
2.3.1. Dimensionless Scaling of the Contact Area
2.3.2. Hydrodynamics
2.3.3. Contact Mechanics
2.3.4. Equilibrium of Forces
2.3.5. Film Thickness Equation
2.3.6. Cavitation
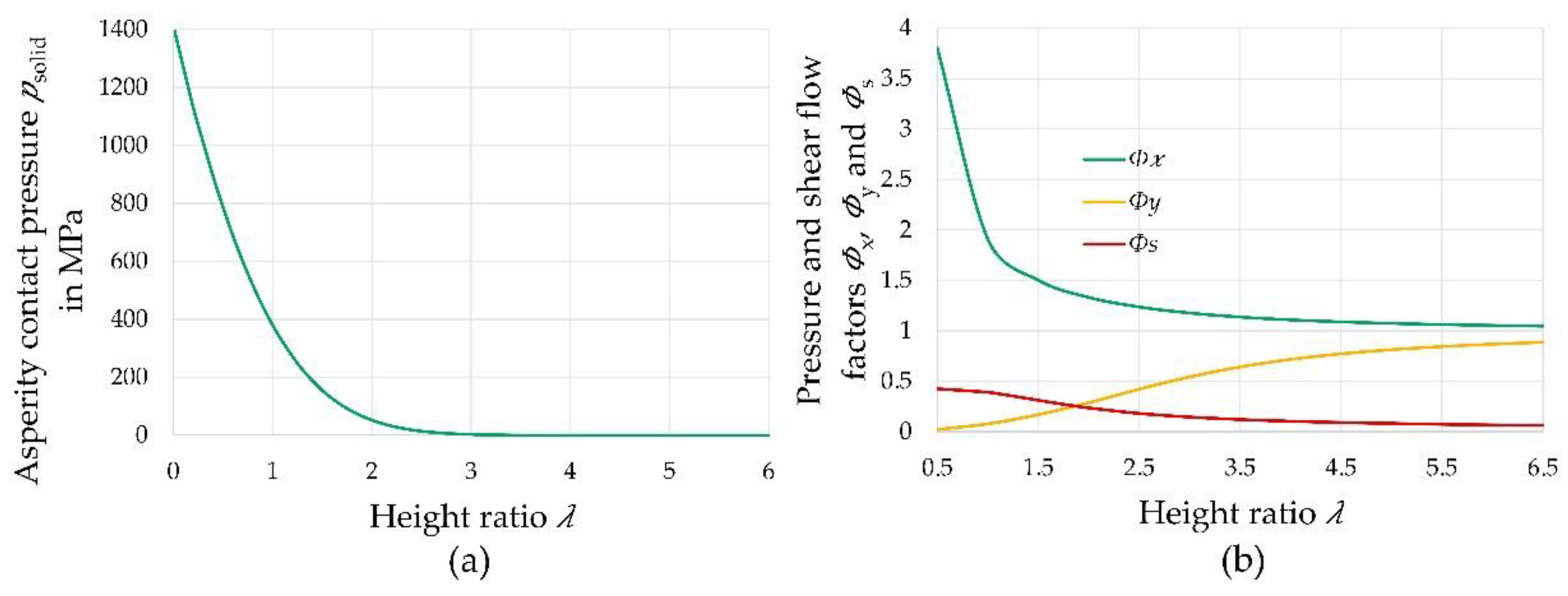
2.3.7. Mixed Lubrication
2.3.8. Numerical Implementation
2.4. Target Values of the Simulation
3. Results
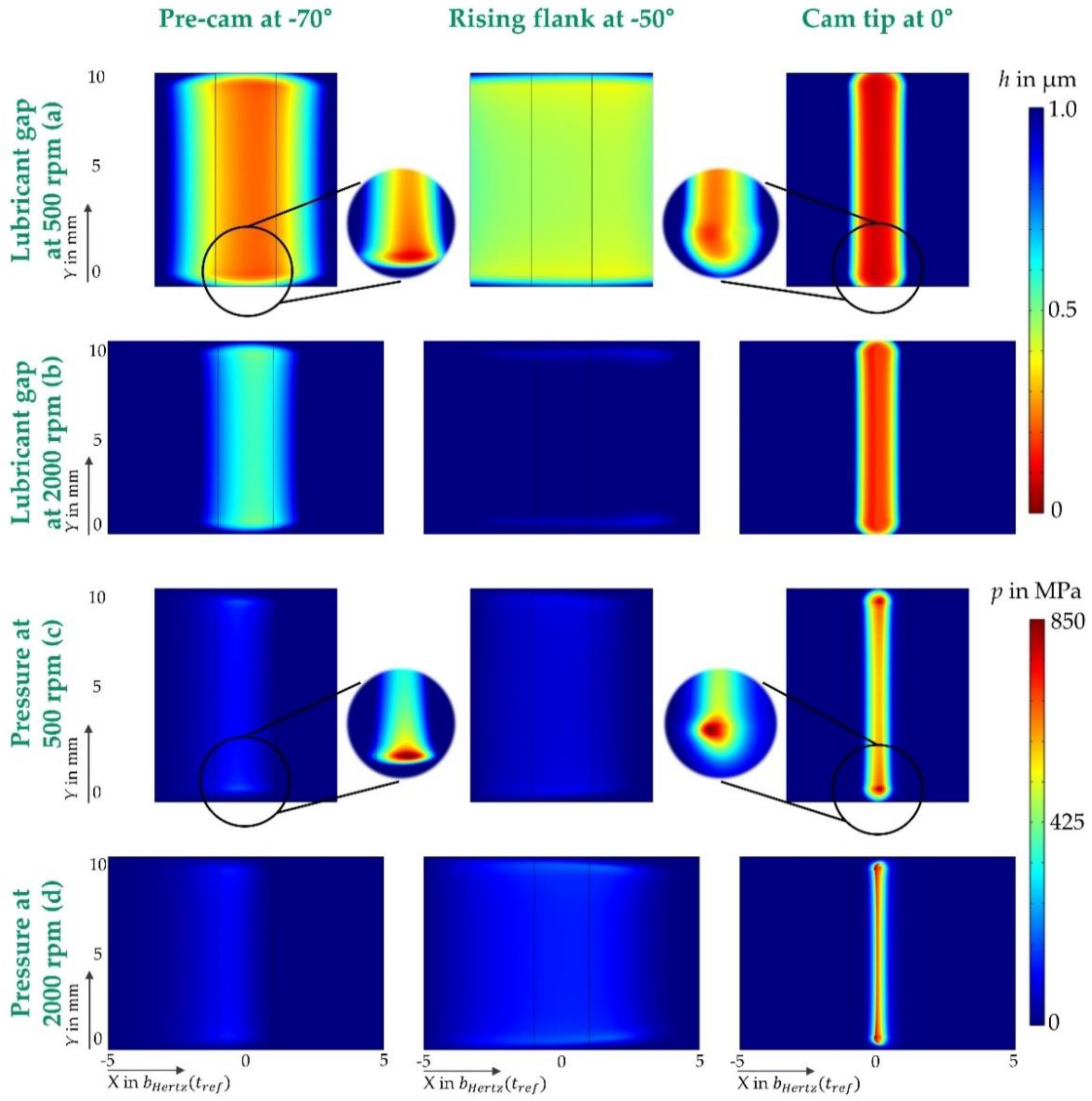
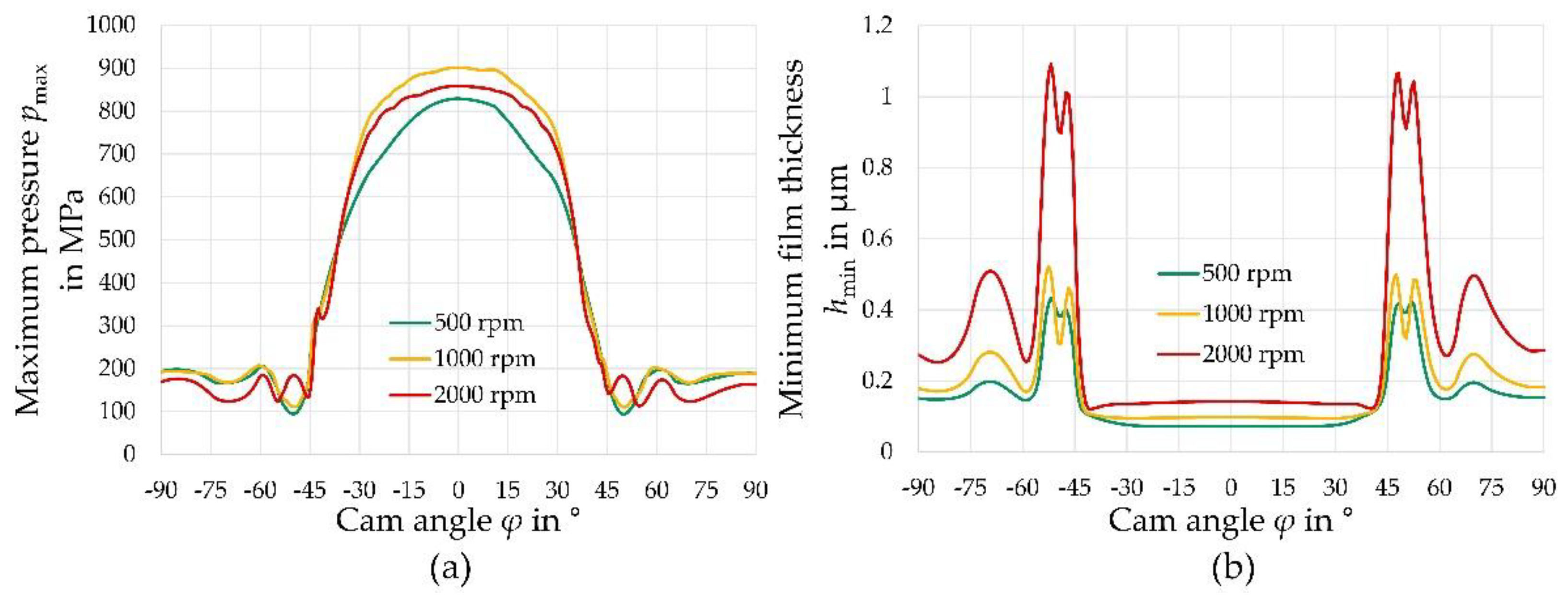
3.1. Pressure and Lubriant Gap Distribution
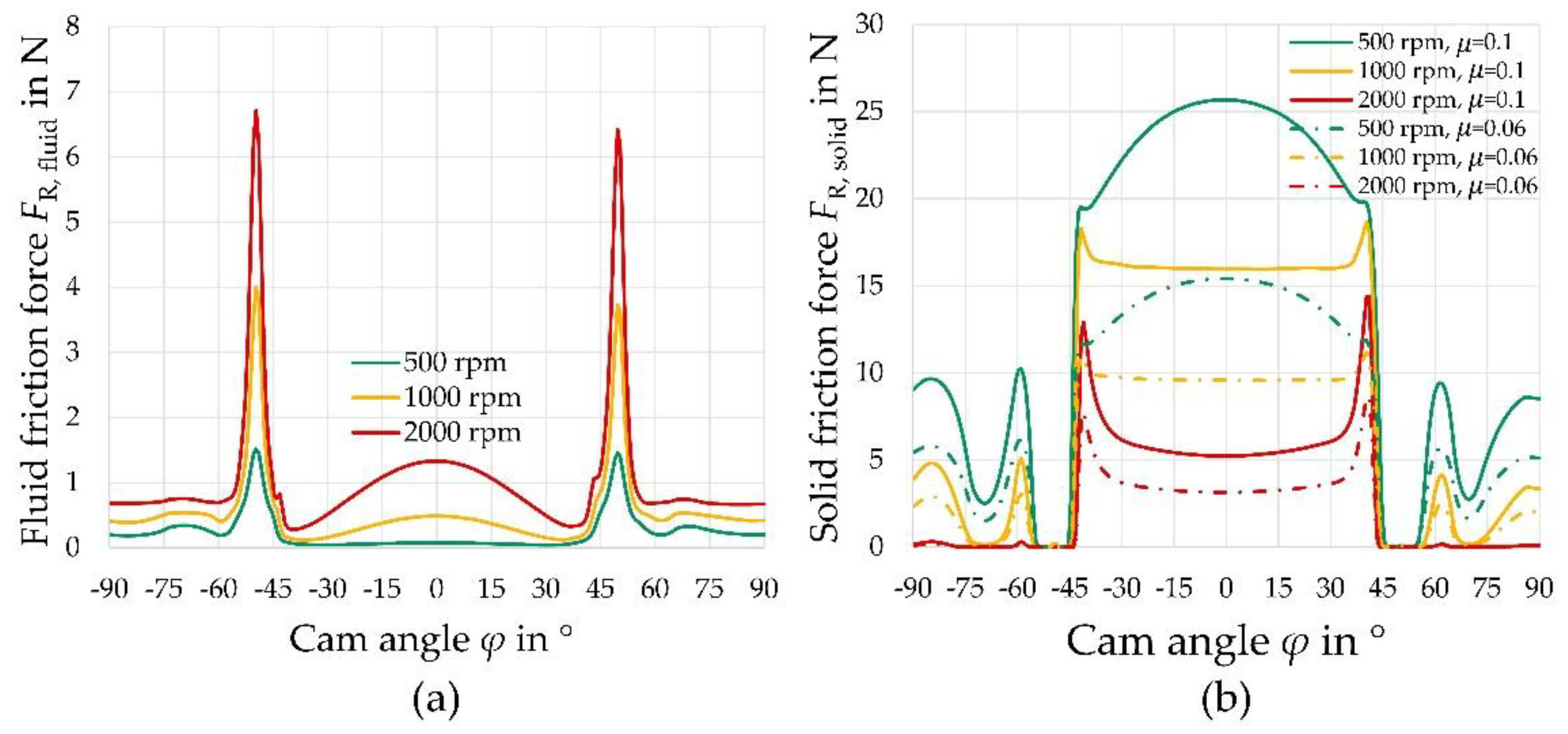
3.2. Friction in the Cam–Tappet Contact
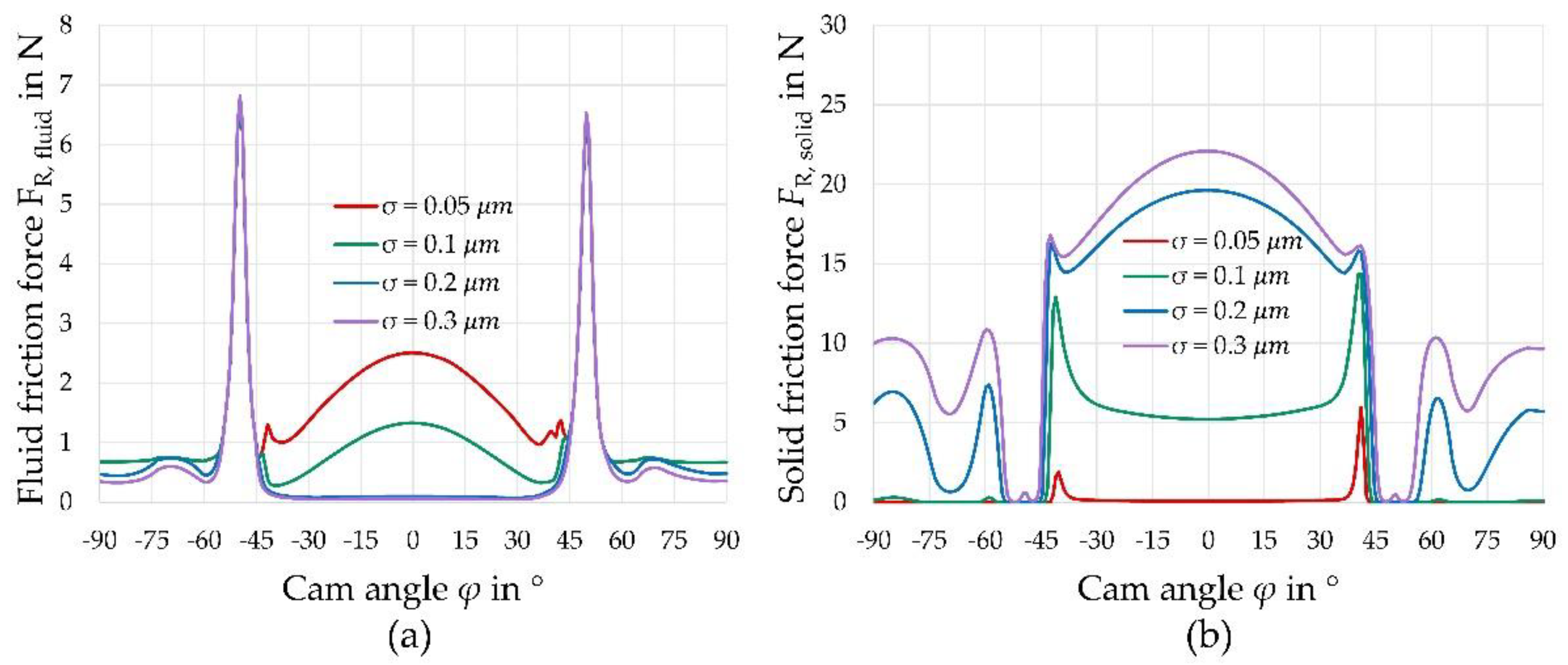
3.3. Influence of Surface Routhness on the Tribological Behaviour
4. Discussion
5. Conclusions
- Effects at the edges of the line contact appear to have an important influence on the tribological behavior. The narrower lubrication gap and the increased pressure at these areas suggest that the edge areas might contribute decisively to increased wear;
- The cam–tappet contact is in the mixed friction region, with the solid contact clearly dominating in the total friction force. The friction forces determined in the simulation agree well with those from experimental bench tests;
- The surface properties of cams and tappets have a considerable effect on the lubricant film structure and thus on the friction and wear behavior of the tribological system. The influence of roughness outweighs many other influencing factors, and thus deserves special attention;
- The selection of the simulation approach and the influencing variables should always be adapted to the aspect of the contact to be considered in order to find an optimal balance between accuracy and computational efficiency. The presented model is particularly suitable for the investigation of geometry adaptations and time-dependent friction force curves over the cycle.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Carreau parameter | |
| Herzian contact half-wide | |
| Elasticity tensor | |
| Speed correction factor | |
| Force correction factor | |
| Radius correction factor | |
| Function of the cam edge geometry | |
| Contact normal force | |
| Friction force | |
| Solid friction force | |
| Fluid friction force | |
| Critical shear stress | |
| Lubricant gap height | |
| Gap height with fluid | |
| Minimum lubricant gap height | |
| Dimensionless lubricant gap height | |
| Dimensionless distance between undeformed bodies | |
| Dimensionless contact length in y-direction | |
| Carreau parameter | |
| Hydrodynamic pressure | |
| Solid contact pressure | |
| Cavitation pressure | |
| Maximum pressure | |
| Dimensionless hydrodynamic pressure | |
| Dimensionless solid contact pressure | |
| Dimensionless total contact pressure | |
| Hertzian contact pressure | |
| Cam radius | |
| y-axis scaling factor | |
| Time | |
| Dimensionless time | |
| Mean entrainment velocity | |
| Coordinates | |
| Dimensionless coordinates | |
| Pressure viscosity coefficient | |
| Penalty function | |
| Ratio of the x and y correlation lengths | |
| Shear rate | |
| Dimensionless elastic deformation | |
| Strain tensor | |
| Viscosity | |
| Base viscosity | |
| Dimensionless viscosity | |
| Second plateau viscosity | |
| Viscosity of the liquid phase | |
| Fractional film content | |
| Lubricant gap height ratio | |
| Coefficient of friction | |
| Penalty factor | |
| Density | |
| Base density | |
| Density of the liquid phase | |
| Dimensionless density | |
| Stress tensor | |
| Shear stress | |
| Cam angle | |
| Term of the Reynolds equation | |
| Calculation area | |
| Central calculation area | |
| Nabla operator |
References
- Holmberg, K.; Erdemir, A. Influence of Tribology on Global Energy Consumption, Costs and Emissions. Friction 2017, 5, 263–284. [Google Scholar] [CrossRef]
- Holmberg, K.; Andersson, P.; Erdemir, A. Global Energy Consumption Due to Friction in Passenger Cars. Tribol. Int. 2012, 47, 221–234. [Google Scholar] [CrossRef]
- Holmberg, K.; Erdemir, A. The Impact of Tribology on Energy Use and CO2 Emission Globally and in Combustion Engine and Electric Cars. Tribol. Int. 2019, 135, 389–396. [Google Scholar] [CrossRef]
- Serrano, J.R.; Novella, R.; Piqueras, P. Why the Development of Internal Combustion Engines Is Still Necessary to Fight against Global Climate Change from the Perspective of Transportation. Appl. Sci. 2019, 9, 4597. [Google Scholar] [CrossRef] [Green Version]
- Kalghatgi, G. Is It Really the End of Internal Combustion Engines and Petroleum in Transport? Appl. Energy 2018, 225, 965–974. [Google Scholar] [CrossRef]
- Bae, C.; Kim, J. Alternative Fuels for Internal Combustion Engines. Proc. Combust. Inst. 2017, 36, 3389–3413. [Google Scholar] [CrossRef]
- Lee, P.; Zhmud, B. Low Friction Powertrains: Current Advances in Lubricants and Coatings. Lubricants 2021, 9, 74. [Google Scholar] [CrossRef]
- Ciulli, E.; Fazzolari, F.; Pugliese, G. Contact Force Measurements in Cam and Follower Lubricated Contacts. Front. Mech. Eng. 2020, 6, 601410. [Google Scholar] [CrossRef]
- Van Helden, A.K.; van der Meer, R.J.; van Staaden, J.J.; van Gelderen, E. Dynamic Friction in Cam/Tappet Lubrication. SAE Trans. 1985, 94, 224–231. [Google Scholar]
- Kano, M. Super Low Friction of DLC Applied to Engine Cam Follower Lubricated with Ester-Containing Oil. Tribol. Int. 2006, 39, 1682–1685. [Google Scholar] [CrossRef]
- Dobrenizki, L.; Tremmel, S.; Wartzack, S.; Hoffmann, D.C.; Brögelmann, T.; Bobzin, K.; Bagcivan, N.; Musayev, Y.; Hosenfeldt, T. Efficiency Improvement in Automobile Bucket Tappet/Camshaft Contacts by DLC Coatings—Influence of Engine Oil, Temperature and Camshaft Speed. Surf. Coat. Technol. 2016, 308, 360–373. [Google Scholar] [CrossRef]
- Marian, M.; Weikert, T.; Tremmel, S. On Friction Reduction by Surface Modifications in the TEHL Cam/Tappet-Contact-Experimental and Numerical Studies. Coatings 2019, 9, 843. [Google Scholar] [CrossRef] [Green Version]
- Mabuchi, Y.; Yamashita, T.; Izumi, H.; Sekikawa, T.; Nishimura, K.; Hirano, S.; Moriguchi, Y. Examination of the Axial Shape of the Automotive Valvetrain Cam for Engine Friction Reduction. Tribol. Trans. 2017, 60, 1088–1098. [Google Scholar] [CrossRef]
- Ai, X.; Yu, H. A Numerical Analysis for the Transient EHL Process of a Cam-Tappet Pair in I. C. Engine. J. Tribol. 1989, 111, 413–417. [Google Scholar] [CrossRef]
- Dowson, D.; Taylor, C.M.; Zhu, G. A Transient Elastohydrodynamic Lubrication Analysis of a Cam and Follower. J. Phys. D Appl. Phys. 1992, 25, A313–A320. [Google Scholar] [CrossRef]
- Messé, S.; Lubrecht, A.A. Transient Elastohydrodynamic Analysis of an Overhead Cam/Tappet Contact. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2000, 214, 415–425. [Google Scholar] [CrossRef]
- Lubrecht, A.A.; Venner, C.H. Elastohydrodynamic Lubrication of Rough Surfaces. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 1999, 213, 397–404. [Google Scholar] [CrossRef]
- Teodorescu, M.; Taraza, D.; Henein, N.A.; Bryzik, W. Simplified Elasto-Hydrodynamic Friction Model of the Cam-Tappet Contact. SAE Trans. 2003, 112, 1271–1282. [Google Scholar]
- Dowson, D.; Higginson, G.R. Elasto-Hydrodynamic Lubrication: International Series on Materials Science and Technology; Dowson, D., Higginson, G.R., Eds.; Pergamon Press: Oxford, UK; Elsevier: New York, NY, USA, 1977; ISBN 978-0-08-021302-6. [Google Scholar]
- Wang, J.; Yang, P. A Numerical Analysis for TEHL of Eccentric-Tappet Pair Subjected to Transient Load. J. Tribol. 2003, 125, 770–779. [Google Scholar] [CrossRef]
- Wang, J.; Venner, C.H.; Lubrecht, A.A. Influence of Surface Waviness on the Thermal Elastohydrodynamic Lubrication of an Eccentric-Tappet Pair. J. Tribol. 2013, 135, 021001. [Google Scholar] [CrossRef]
- Chong, W.; Teodorescu, M.; Rahnejat, H. Mixed Thermo-Elastohydrodynamic Cam-Tappet Power Loss in Low-Speed Emission Cycles. Int. J. Engine Res. 2014, 15, 153–164. [Google Scholar] [CrossRef] [Green Version]
- Raisin, J.; Fillot, N.; Vergne, P.; Dureisseix, D.; Lacour, V. Transient Thermal Elastohydrodynamic Modeling of Cam–Follower Systems: Understanding Performance. Tribol. Trans. 2016, 59, 720–732. [Google Scholar] [CrossRef]
- Habchi, W. Finite Element Modeling of Elastohydrodynamic Lubrication Problems; John Wiley & Sons: Hoboken, NJ, USA, 2018; ISBN 978-1-119-22514-0. [Google Scholar]
- Habchi, W.; Eyheramendy, D.; Vergne, P.; Morales-Espejel, G. A Full-System Approach of the Elastohydrodynamic Line/Point Contact Problem. J. Tribol. 2008, 130, 021501. [Google Scholar] [CrossRef]
- Wassim, H. Une Approche Éléments Finis avec Couplage fort des Problèmes de Lubrification Élastohydrodynamique: Application aux Fluides de très Faible Viscosité. Ph.D. Thesis, L’Institut National des Sciences Appliquées de Lyon, Lyon, France, 2008. Available online: http://docinsa.insa-lyon.fr/these/2008/habchi/these.pdf (accessed on 25 October 2021).
- Wu, W.; Wang, J.; Venner, C.H. Thermal Elastohydrodynamic Lubrication of an Optimized Cam–Tappet Pair in Smooth Contact. J. Tribol. 2016, 138, 021501. [Google Scholar] [CrossRef]
- Tsuha, N.A.H.; Nonato, F.; Cavalca, K.L. Formulation of a Reduced Order Model for the Stiffness on Elastohydrodynamic Line Contacts Applied to Cam-Follower Mechanism. Mech. Mach. Theory 2017, 113, 22–39. [Google Scholar] [CrossRef]
- Shirzadegan, M.; Almqvist, A.; Larsson, R. Fully Coupled EHL Model for Simulation of Finite Length Line Cam-Roller Follower Contacts. Tribol. Int. 2016, 103, 584–598. [Google Scholar] [CrossRef] [Green Version]
- Yu, C.; Meng, X.; Xie, Y. Numerical Simulation of the Effects of Coating on Thermal Elastohydrodynamic Lubrication in Cam/Tappet Contact. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2017, 231, 221–239. [Google Scholar] [CrossRef]
- Meng, X.; Yu, C.; Xie, Y.; Mei, B. Thermal Insulation Effect on EHL of Coated Cam/Tappet Contact during Start Up. Ind. Lubr. Tribol. 2018, 70, 917–926. [Google Scholar] [CrossRef]
- Lyu, B.; Meng, X.; Zhang, R.; Cui, Y. A Comprehensive Numerical Study on Friction Reduction and Wear Resistance by Surface Coating on Cam/Tappet Pairs under Different Conditions. Coatings 2020, 10, 485. [Google Scholar] [CrossRef]
- Marian, M.; Tremmel, S.; Wartzack, S. Microtextured Surfaces in Higher Loaded Rolling-Sliding EHL Line-Contacts. Tribol. Int. 2018, 127, 420–432. [Google Scholar] [CrossRef]
- Torabi, A.; Akbarzadeh, S.; Salimpour, M.; Khonsari, M.M. On the Running-in Behavior of Cam-Follower Mechanism. Tribol. Int. 2018, 118, 301–313. [Google Scholar] [CrossRef]
- Tang, H.; Wang, J.; Sun, N.; Zhu, J. Effect of Angular Speed of Cam on Oil Film Variation in the Line Contact Thermal EHL of a Cam-Tappet Pair. Ind. Lubr. Tribol. 2020, 72, 713–722. [Google Scholar] [CrossRef]
- Marian, M.; Orgeldinger, C.; Rothammer, B.; Nečas, D.; Vrbka, M.; Křupka, I.; Hartl, M.; Wimmer, M.A.; Tremmel, S.; Wartzack, S. Towards the Understanding of Lubrication Mechanisms in Total Knee Replacements—Part II: Numerical Modeling. Tribol. Int. 2021, 156, 106809. [Google Scholar] [CrossRef]
- Marian, M. Numerische Auslegung von Oberflächenmikrotexturen für geschmierte tribologische Kontakte; Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU): Erlangen, Germany, 2021. [Google Scholar]
- Weschta, M. Untersuchungen zur Wirkungsweise von Mikrotexturen in elastohydrodynamischen Gleit/Wälz-Kontakten. Ph.D. Thesis, Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Erlangen, Germany, 2017. [Google Scholar]
- Carreau, P.J. Rheological Equations from Molecular Network Theories. Trans. Soc. Rheol. 1972, 16, 99–127. [Google Scholar] [CrossRef]
- Bair, S. A Rough Shear-Thinning Correction for EHD Film Thickness. Tribol. Trans. 2004, 47, 361–365. [Google Scholar] [CrossRef]
- Roelands, C.J.A. Correlational Aspects of the Viscosity-Temperature-Pressure Relationship of Lubricating Oils. Ph.D. Thesis, TU Delft, Delft, The Netherlands, 1966. [Google Scholar]
- Lohner, T.; Ziegltrum, A.; Stemplinger, J.-P.; Stahl, K. Engineering Software Solution for Thermal Elastohydrodynamic Lubrication Using Multiphysics Software. Adv. Tribol. 2016, 2016, 6507203. [Google Scholar] [CrossRef] [Green Version]
- Hertz, H. Ueber die Berührung fester elastischer Körper. Journal für die reine und angewandte Mathematik 1882, 1882, 156–171. [Google Scholar] [CrossRef]
- Tan, X.; Goodyer, C.E.; Jimack, P.K.; Taylor, R.I.; Walkley, M.A. Computational Approaches for Modelling Elastohydrodynamic Lubrication Using Multiphysics Software. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2012, 226, 463–480. [Google Scholar] [CrossRef]
- Winkler, A.; Marian, M.; Tremmel, S.; Wartzack, S. Numerical Modeling of Wear in a Thrust Roller Bearing under Mixed Elastohydrodynamic Lubrication. Lubricants 2020, 8, 58. [Google Scholar] [CrossRef]
- Reynolds, O. On the Theory of Lubrication and Its Application to Mr. Beauchamp Tower’s Experiments, Including an Experimental Determination of the Viscosity of Olive Oil. Philos. Trans. R. Soc. Lond. 1886, 177, 157–234. [Google Scholar] [CrossRef]
- Marian, M.; Weschta, M.; Tremmel, S.; Wartzack, S. Simulation of Microtextured Surfaces in Starved EHL Contacts Using Commercial FE Software. Matls. Perf. Charact. 2017, 6, 165–181. [Google Scholar] [CrossRef]
- Zhao, Y.; Maietta, D.M.; Chang, L. An Asperity Microcontact Model Incorporating the Transition from Elastic Deformation to Fully Plastic Flow. J. Tribol. 2000, 122, 86–93. [Google Scholar] [CrossRef]
- Marian, M.; Grützmacher, P.; Rosenkranz, A.; Tremmel, S.; Mücklich, F.; Wartzack, S. Designing Surface Textures for EHL Point-Contacts—Transient 3D Simulations, Meta-Modeling and Experimental Validation. Tribol. Int. 2019, 137, 152–163. [Google Scholar] [CrossRef]
- Masjedi, M.; Khonsari, M.M. Film Thickness and Asperity Load Formulas for Line-Contact Elastohydrodynamic Lubrication With Provision for Surface Roughness. J. Tribol. 2012, 134, 011503. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H. Application of Average Flow Model to Lubrication between Rough Sliding Surfaces. J. Lubr. Technol. 1979, 101, 220–229. [Google Scholar] [CrossRef]
- The Finite Element Method for Fluid Dynamics, 7th ed.; Zienkiewicz, O.C.; Taylor, R.L.; Nithiarasu, P. (Eds.) Butterworth-Heinemann: Oxford, UK, 2014; ISBN 978-1-85617-635-4. [Google Scholar]
- Tribologie-Handbuch; Czichos, H.; Habig, K.-H. (Eds.) Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2015; ISBN 978-3-8348-1810-2. [Google Scholar]
- Habchi, W.; Vergne, P.; Bair, S.; Andersson, O.; Eyheramendy, D.; Morales-Espejel, G.E. Influence of Pressure and Temperature Dependence of Thermal Properties of a Lubricant on the Behaviour of Circular TEHD Contacts. Tribol. Int. 2010, 43, 1842–1850. [Google Scholar] [CrossRef]
- Liu, H.C.; Zhang, B.B.; Bader, N.; Venner, C.H.; Poll, G. Simplified Traction Prediction for Highly Loaded Rolling/Sliding EHL Contacts. Tribol. Int. 2020, 148, 106335. [Google Scholar] [CrossRef]
- Björling, M.; Habchi, W.; Bair, S.; Larsson, R.; Marklund, P. Towards the True Prediction of EHL Friction. Tribol. Int. 2013, 66, 19–26. [Google Scholar] [CrossRef] [Green Version]
| Base density | |
| Base viscosity | |
| Pressure viscosity coefficient | |
| Critical shear stress | |
| Second plateau viscosity | |
| Carreau parameter | 2.2 |
| Carreau parameter | 0.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orgeldinger, C.; Tremmel, S. Understanding Friction in Cam–Tappet Contacts—An Application-Oriented Time-Dependent Simulation Approach Considering Surface Asperities and Edge Effects. Lubricants 2021, 9, 106. https://doi.org/10.3390/lubricants9110106
Orgeldinger C, Tremmel S. Understanding Friction in Cam–Tappet Contacts—An Application-Oriented Time-Dependent Simulation Approach Considering Surface Asperities and Edge Effects. Lubricants. 2021; 9(11):106. https://doi.org/10.3390/lubricants9110106
Chicago/Turabian StyleOrgeldinger, Christian, and Stephan Tremmel. 2021. "Understanding Friction in Cam–Tappet Contacts—An Application-Oriented Time-Dependent Simulation Approach Considering Surface Asperities and Edge Effects" Lubricants 9, no. 11: 106. https://doi.org/10.3390/lubricants9110106
APA StyleOrgeldinger, C., & Tremmel, S. (2021). Understanding Friction in Cam–Tappet Contacts—An Application-Oriented Time-Dependent Simulation Approach Considering Surface Asperities and Edge Effects. Lubricants, 9(11), 106. https://doi.org/10.3390/lubricants9110106






