Study of Frictional Effects of Granite Subjected to Quasi-Static Contact Loading

Abstract

The rock fragmentation response to drilling, in particular percussive drilling, is important in order to improve the efficiency of such an operation. The resulting problem includes spherical contact between the drill bit and the material and therefore, a numerical analysis of frictional effects in quasi-static spherical indentation of Bohus granite is presented. The frictional coefficient between the indenter and the granite surface is accounted for in numerical simulations. A previously determined constitutive law is used for the purpose of numerical analyses. The latter consists of a Drucker-Prager plasticity model with variable dilation angle coupled with an anisotropic damage model. Since the tensile strength is random, Weibull statistics was considered. Using a frictionless contact model, the stress state of Bohus granite corresponding to the first material failure occurrence, observed in indentation experiments, was numerically determined. However, the frictional effects, which are of interest in this study, may lead to changes in the numerically established stress state and consequently the Weibull parameters should be recalibrated. The so-called Weibull stress decreases from 120 MPa for a frictionless contact to 75 MPa for frictional contact, and the Weibull modulus from 24 to 12. It is numerically observed that the predicted force-penetration response, using the new set of Weibull parameters, is not influenced by friction. Conversely, the predicted fracture pattern, in the case of frictional contact, is similar to the case of frictionless contact, but its size is somewhat larger. Last, a parametric study analyzing the dependence of the friction coefficient is carried out and no significant changes are detected. The novelty of the present findings concerns the fact that both an advanced damage description in combination with an advanced plasticity model, both implemented for finite element analyses, is used to analyze frictional effects at granite indentation.

1. Introduction

A large number of studies on the behavior of quasi-brittle materials under quasi-static or dynamic loadings is found in the literature [1,2,3,4,5,6,7,8,9,10,11,12,13]. For example, various circular flat-bottomed indenters with different sizes were used to quasi-statically indent rock materials [2]. The authors described that the fragmentation process could be separated into different stages based on the recorded force-penetration response. Other examples, which are relevant to this study, are the analyses by [5,7]. In the first one [5], the fracture pattern of Bohus granite (hard rock) due to spherical indentation loading during percussive drilling was investigated. A plasticity postulate similar to incompressible Drucker-Prager plasticity (with zero dilation angle) was combined with an anisotropic damage model to predict the fragmentation of the chosen rock material. In another study, [7], the same rock material was loaded by a circular flat punch. The theory of elasticity was considered, and the fracture mechanism was investigated. The model parameters were determined from experimental data. The Weibull distribution [14,15] was considered to describe the tensile strength of rock, and the parameters were calibrated from previously conducted three-point bend tests. Furthermore, in some other studies [16,17], it is mentioned that the dynamic compressive and tensile strength of brittle materials increase with loading rates. However, taking into account the small values of the effective volume in indentation testing, the rate effect should be less critical than the size effect [7].

In previous studies by the authors of this work, the mechanical behavior of Bohus granite rock blocks loaded by a spherical indenter was studied. The constitutive law was separated into an elastoplastic regime and tensile failure (mode-I fracture) response. The elasto-plastic behavior was captured by compressible plasticity, namely the Drucker-Prager law with variable dilation angle [10]. Any inelastic deformation, corresponding to the crushed material at high compressive pressures under the contact area as well as the region with multiple microcracks due to the shear stresses, was captured by such model. The plasticity parameters were calibrated based on quasi-oedometric compression tests [18]. It was suggested that a linear Drucker-Prager law was sufficient to describe the material behavior. One of the challenging points was determining a variable dilation angle rather than using zero dilatancy or a dilation angle equal to the friction angle (i.e., associated flow rule). For this purpose, the dilatancy was determined as a function of pressure based on quasi-oedometric compression test results. Later, quasi-static indentation tests were conducted, and the force-penetration response was recorded. Then the selected elastoplastic model was validated against acquired data of indentation tests. Moreover, the images provided by a high-speed camera, which was used to capture rock surface images, illustrated material removals, which was suggested to be due to ring and radial cracking on the surface outside the contact area.

To model tensile failure of Bohus granite, the present authors employed an anisotropic damage (DFH) model [19,20]. The DFH model accounts for tensile failure due to high stress state on the rock surface outside the contact area. This stress state may lead to cracking of the rock, and subsequently material removals on the specimen surface. These material removals were observed in the images provided by high-speed camera monitoring, and they corresponded to load-drops in the force-penetration response. It was suggested that the stress state at the first load-drop could be used to determine the tensile strength of the tested material. It was shown that this stress state varied between the experiments. Therefore, the granite tensile strength was treated as a random variable. In practice, Weibull statistics was employed, and the corresponding Weibull parameters were experimentally determined.

In this study, it is attempted to numerically investigate the frictional effects on the above-mentioned indentation experiment. The friction coefficient between the indenter and the rock specimen is first assumed to be equal to 0.4, and it is accounted for in finite element simulations. It should be stated that with such a value on the friction coefficient (and also for lower ones), the indentation contact problem is in practice fully adhesive [21]. A parametric study is then performed detailing the influence of the frictional behavior. Adding friction between the indenter surface and the rock surface led to relief of the stresses on the rock surface. In particular, the radial stress (i.e., first principal stress) level on the surface right outside the contact area is highly affected. As stated previously by the authors, this radial stress is the reason behind the first load-drop observed in the force-penetration response of the analyzed material. Consequently, the tensile strength of the material, determined based on this radial stress state at first load-drop, is also changing, and the distribution of tensile strength as well. Therefore, the Weibull parameters, namely the Weibull stress and the Weibull modulus are modified to adjust the new finite element results obtained when accounting for friction.

Last, the influence of friction on the force-penetration response and the fracture pattern of the rock are investigated. It can be summarized that the force-penetration curve is not influenced, and that the fracture pattern is similar to frictionless contact, but its size is somewhat larger. It should be mentioned that presently, a standard Coulomb law is used to model friction. This is believed to be sufficient for the present purpose but for future and more detailed studies, advanced models such as the ones by [22,23] could be useful to include in the analysis.

2. Elastoplastic Damage Model

The material of interest in this study is Bohus granite. It was attempted previously to determine a constitutive model for this material. The elasticity properties were determined from direct compression and tensile experiments [18]. To calibrate plasticity properties, quasi-oedometric experiments were conducted to establish a yield function for the studied material [10,18]. It should be mentioned that what is referred to as plasticity, in the present context, corresponds to irreversible deformations induced by frictional sliding of closed cracks except those due to tensile stress states (mode-I fracture). It was suggested by the authors that a linear Drucker-Prager law could be a good representation of yielding, since Bohus granite exhibits almost a linear pressure-dependent yield behavior [5]. The Drucker-Prager law is known as

$$F=q-p\tan \beta -d=0$$

(1)

where $F$ is the yield function, $d$ the cohesion, $\beta$ the friction angle and $q$ von Mises equivalent stress. It should be noted that pressure ($p$) is equal to the negative hydrostatic pressure.

$$p=-\frac{1}{3}trace\left(\mathbf{\sigma }\right)$$

(2)

where $\mathbf{\sigma }$ denotes the Cauchy stress tensor. The flow potential $G$ reads

$$G=q-p\tan \Psi$$

(3)

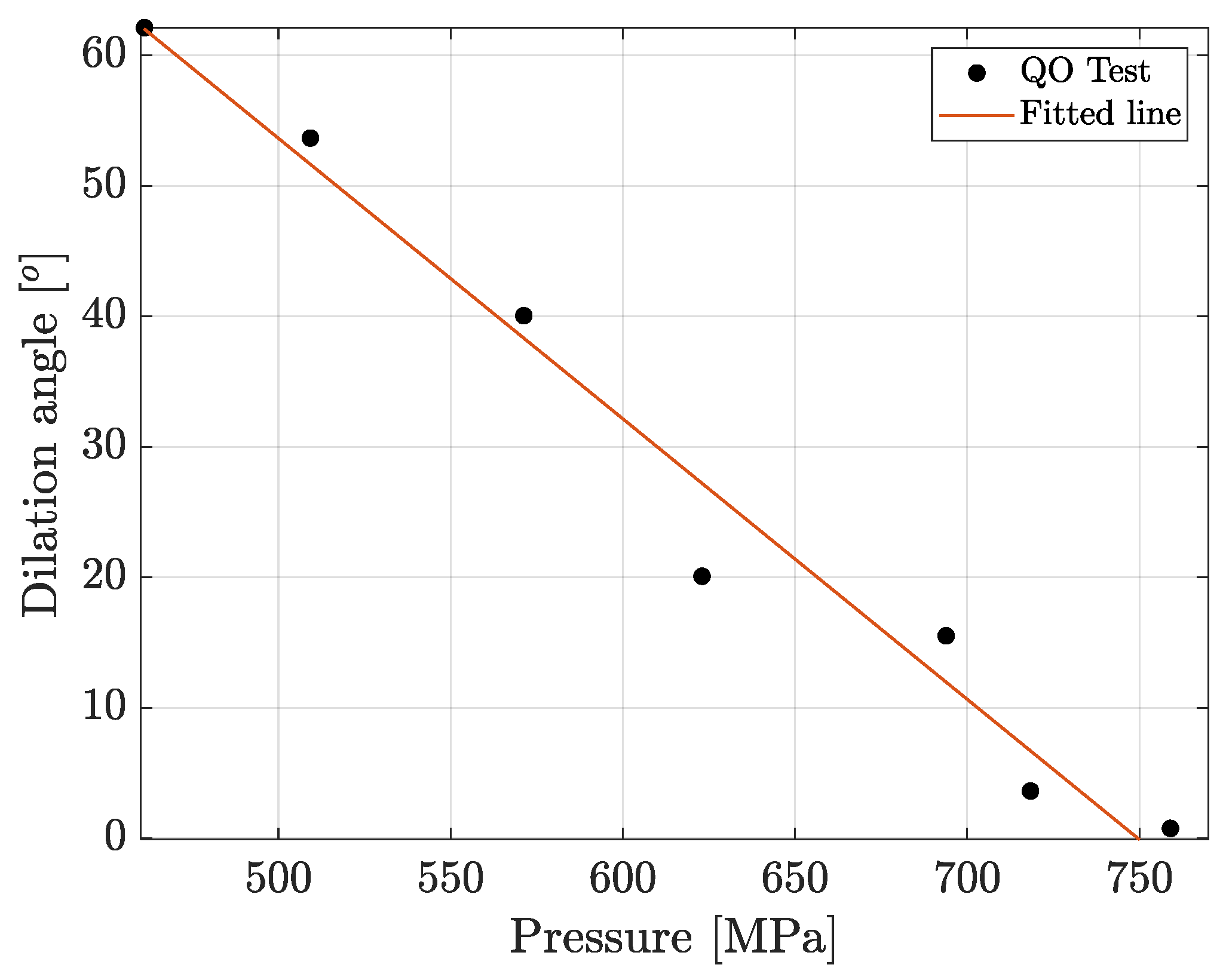
where $\Psi$ is the dilation angle, which is written as

$$\Psi ={\tan }^{-1}\left(\frac{3}{3\frac{{\dot{\epsilon }}_a^i}{{\dot{\epsilon }}_v^i}-1}\right)$$

(4)

where ${\dot{\epsilon }}_a^i$ is the inelastic axial strain rate, and ${\dot{\epsilon }}_v^i$ the inelastic volumetric strain rate. This equation expresses the dependence of the dilation angle with the ratio between the inelastic axial and volumetric strain increments, which was determined based on quasi-oedometric test results. The inelastic volumetric strain is related to the pressure. Therefore, the dilation angle is determined as a function of pressure, see Figure 1.

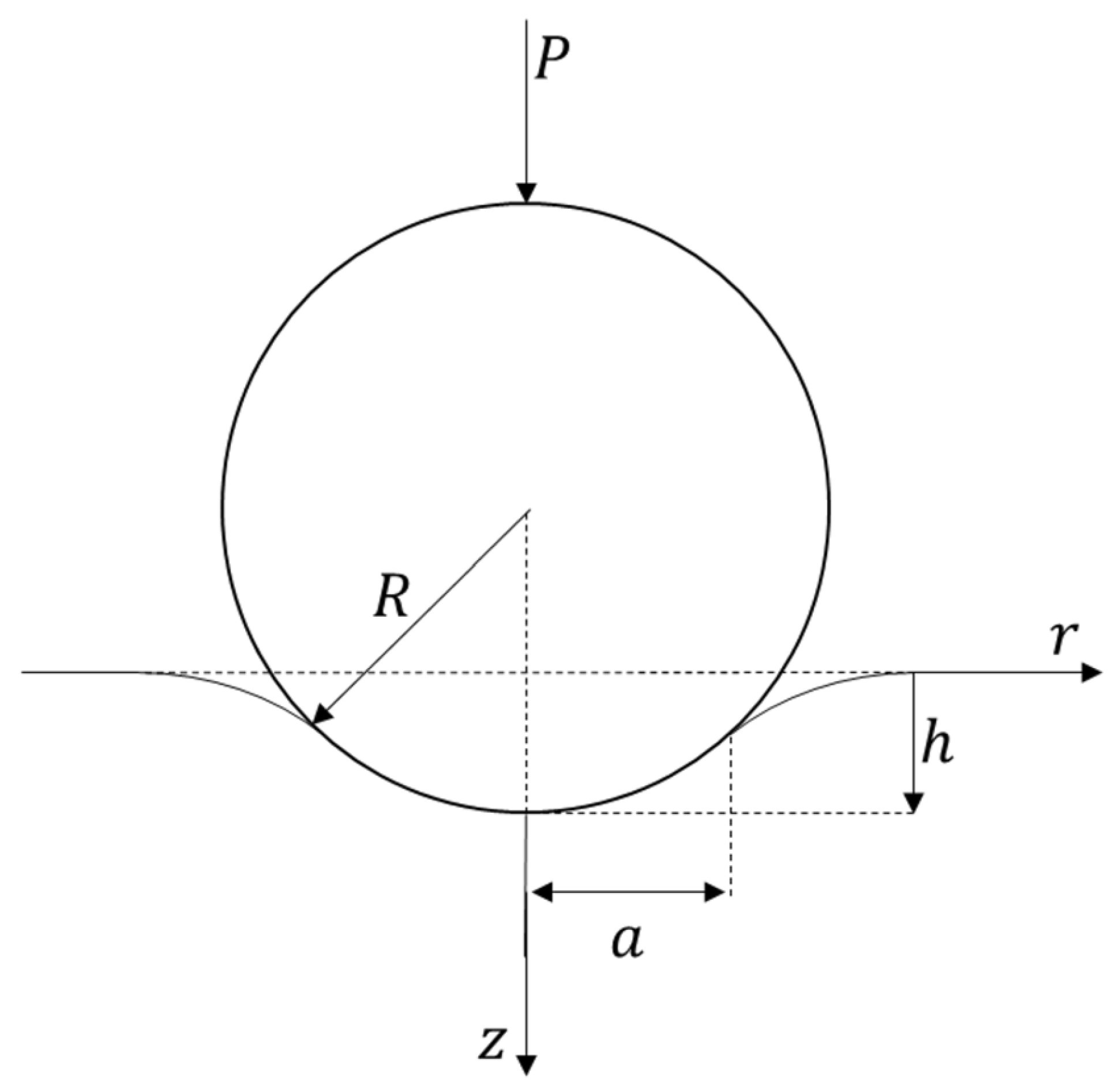
Following the constitutive modeling, quasi-static spherical indentation tests were performed [10]. Rock blocks of 15 cm × 15 cm × 15 cm were indented using a tungsten carbide spherical indenter. The size of the indenter was chosen equal to 12 mm. The experiments were carried out using a 100 kN servo-controlled testing machine. The load cell response of the testing machine was recorded during the test. Two linear variable displacement transducers (LVDTs) were used to measure the penetration depth. The tests were conducted in displacement control mode at a constant velocity of 5 μm/s. Then, the calibrated elastoplastic model was implemented numerically in the commercial finite element software Abaqus via a user material subroutine [24] in order to predict the force-penetration response of rock blocks indented by the tungsten carbide spherical indenter, see Figure 2.

The numerical model reproduced very well the experimentally measured force-penetration curves. Moreover, a high-speed camera was also used to monitor what happened to the rock block surface during indentation tests. It was found that the load-drops in the force-penetration response corresponded to material damage on the specimen surface. It is worth mentioning that a posteriori computed-tomography (CT) images did not reveal any substantial sub-surface cracking, see Figure 6 in [10].

As discussed in the previous paragraph, the irreversible deformation due to tensile stress states (i.e., tensile failure) was excluded [10]. Later on, the DFH model was used to account for tensile failure of the material [25]. The DFH model captures probabilistic features of Bohus granite by incorporating the Weibull distribution and weakest link theory for low loading rates [14,15,20]. Using a Poisson point-process framework, the weakest link assumption and a Weibull model, the failure probability reads

$$P_F=1-\exp \left[-Z_{eff}{\lambda }_t\left({\sigma }_F\right)\right]$$

(5)

where $Z_{eff}$ is the effective volume [26], and ${\lambda }_t$ the initiation density

$${\lambda }_t\left({\sigma }_F\right)={\lambda }_0{\left(\frac{{\sigma }_F}{S_0}\right)}^m$$

(6)

where $m$ is the Weibull modulus, $S_0^m/{\lambda }_0$ the Weibull scale parameter, and ${\sigma }_F$ the maximum tensile stress experienced by the material. The effective volume is written as

$$Z_{eff}=\underset{\Omega }{\overset{}{{\displaystyle \int }}}{\left(\frac{{\sigma }_1}{{\sigma }_F}\right)}^{m}dZ\mathrm{when}{\sigma }_F>0$$

(7)

where ${\sigma }_1$ is the maximum principal stress, ${\sigma }_F$ the maximum principal stress in the whole volume, and $\langle ·\rangle$ refers to the Macaulay brackets. The average failure stress ${\sigma }_w$ reads

$${\sigma }_w=S_0{\left({\lambda }_{0}Z{H}_m\right)}^{-\frac{1}{m}}\mathsf{\Gamma }\left(1+\frac{1}{m}\right)$$

(8)

where $\mathsf{\Gamma }$ is the Euler function of the second kind

$$\mathsf{\Gamma }\left(x\right)=\underset{0}{\overset{\infty }{{\displaystyle \int }}}\exp \left(-u\right)u^{x-1}du$$

(9)

The fracture strength in the DFH model is sensitive to the loading rate [27]. If the loading rate is low, the activation of the weakest defect in the material leads to the formation of a single crack. The initiation and growth of this crack is the reason behind material failure. Conversely, if the loading rate is high, stresses reach high levels since the stress rate is high. Therefore, there is enough time for multiple defects with various strengths to activate. Consequently, various cracks initiate and propagate, which leads to multiple fragmentation. The interested reader may refer to [19,20] for a detailed description.

As mentioned earlier, it was suggested [25] that indentation test data may be used to determine the tensile strength of Bohus granite. The first principal stress level corresponding to the first load-drop observed in the force-penetration curve was considered to be the tensile strength of the material. In practice, the first principal stress state at first load-drop was determined from numerical analyses. Since the first load-drop occurred at somewhat different indentation depths, the material tensile strength was considered to be a random variable and the Weibull distribution was considered. The Weibull modulus $m$ was determined based on the so-called Weibull plot, see Figure 3, in which several indentation experiments were considered. The effective volume was also determined from Equation (7). The material parameters found in [25] are summarized in

Table 1. Material parameters based on [25] in which the frictional effects were neglected.

Material Parameter
$E\left(\mathrm{GPa}\right)$	$52$
$\nu$	$0.25$
$\rho \left(\mathrm{kg}/{\mathrm{m}}^3\right)$	$2630$
$\beta {(}^{°})$	$51.7$
$d\left(\mathrm{MPa}\right)$	153.3
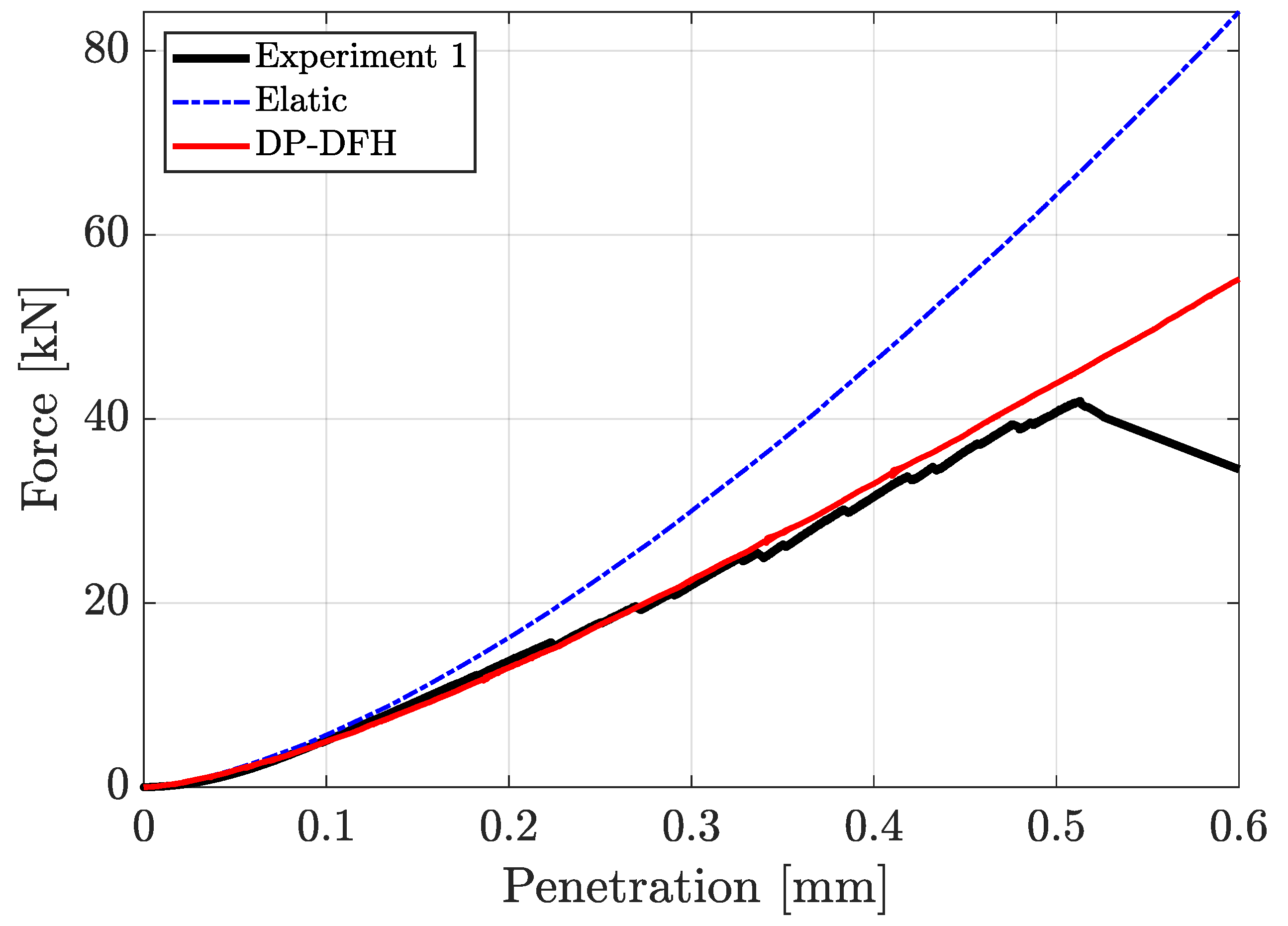
$\Psi {(}^{°})$ $m$ ${\sigma }_w\left(\mathrm{MPa}\right)$ $Z_{eff}\left({\mathrm{mm}}^3\right)$	Figure 1 24 120 1

. The experimental force-penetration response [10] as well as numerical simulation responses are reported in Figure 4. The DP-DFH (Drucker-Prager law coupled with the DFH damage model) and elastic models are compared with experimental results. The elastic and DP-DFH model parameters are gathered in Table 1. The results based on DP-DFH model are in good agreement with the experimental results. 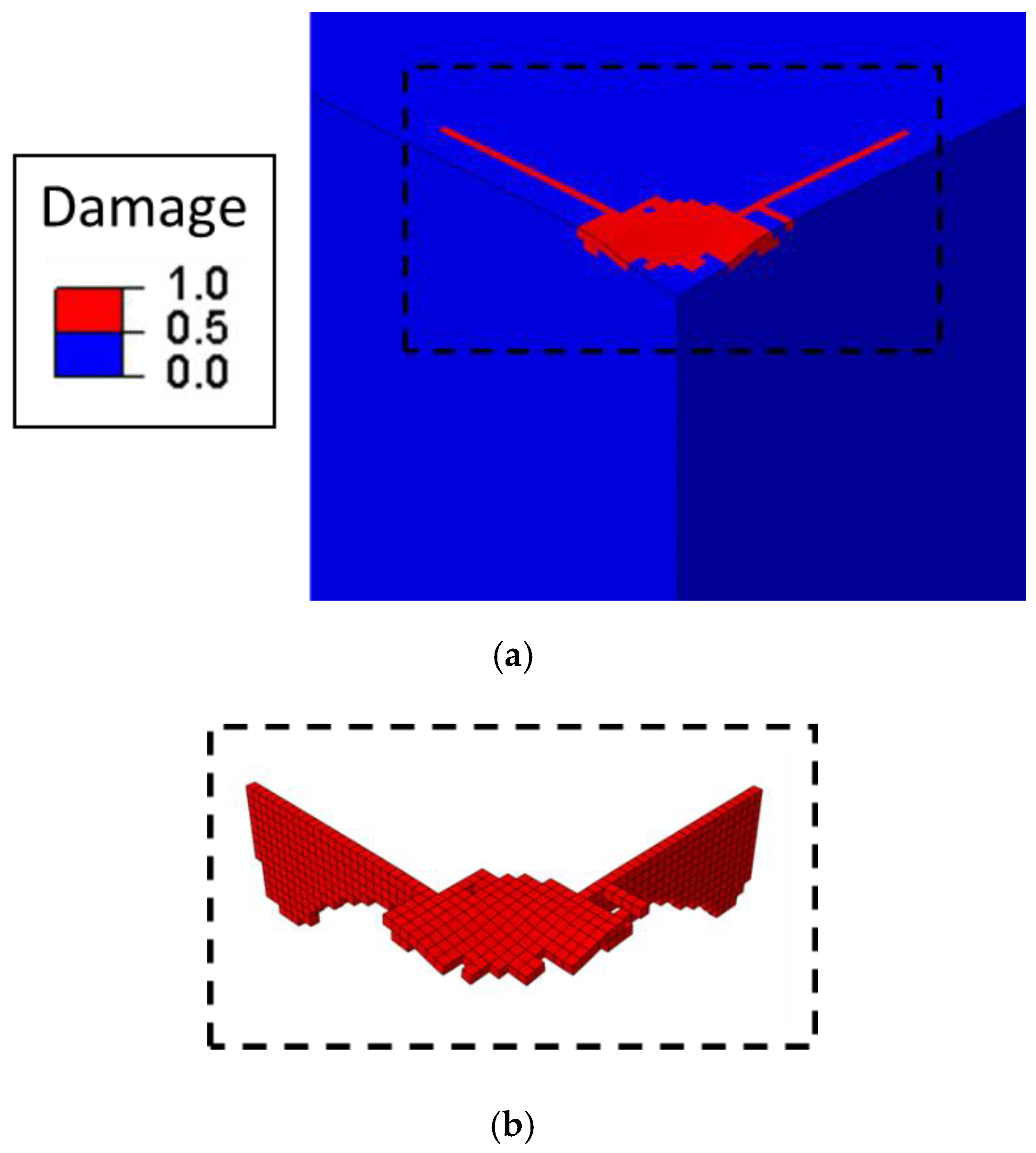Last, the numerically predicted fracture zone using the material parameters in Table 1 is depicted in Figure 5. This zone is in accordance with the experimental observations, CT images [10], in which the fracture zone was confined to the surface and radial cracks developed over a short distance into the material.

3. Finite Element Model

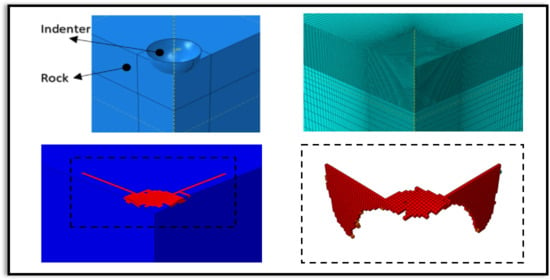
A brief summary of the finite element model is given in this section. Additional details of the numerical analysis are found in [25]. In the present case, the explicit version of Abaqus [24] was used. By means of symmetries, only one quarter of the rock block was modeled to reduce the computation time. The rock block geometry was meshed with 0.2 mm in length elements (Figure 6). The element type was linear reduced integration brick. The indenter was modeled as a 3D analytical rigid body since its elastic modulus is almost ten times larger than the granite elastic modulus. The rigid indenter was subjected to a vertical displacement with a constant velocity. The total contact force was also captured by monitoring the reaction force, which is an output variable in Abaqus. As a result, the force-penetration could be captured and compared to experimental data. The contact behavior was assumed to be governed by Coulomb law with a frictional coefficient $\mu$ varied in the analyses. With high values of the frictional coefficient, the indentation contact problem can be considered to be fully adhesive [21].

The employed constitutive model used in this work is the called DP-DFH model. The designation stands for the Drucker-Prager law coupled with the DFH damage model. The DP-DFH model was previously introduced in Abaqus via a VUMAT user material subroutine [20]. In Abaqus, the user-defined material model can be implemented in user subroutine VUMAT. This subroutine was used also in the present numerical analyses. Accordingly, the numerical investigation is not using the finite element package Abaqus in a standard manner but instead includes material subroutines developed by the authors, both as regards the plasticity model as well as the damage model. It is worth mentioning that all the material parameters are defined as inputs to the DP-DFH VUMAT subroutine. The simulation was divided into very small steps. At beginning of each step, the strain and stress states are known from the previous step as well as all the internal variables. The strain increments are then provided by Abaqus and the stress state should be updated by the user. This task is carried through the VUMAT subroutine. First, the trial stress state is predicted based on a pure elastic increment assumption. The predicted stress state is then corrected against the yield function. Subsequently, the principal stresses are determined based on the corrected stress state. If any principal stress (${\sigma }_i$) level reaches the material tensile strength, the corresponding damage parameter (${\omega }_i$) will develop. As the simulation continues, the damage variables change based on their growth law. The damage variable increases from zero, denoting intact material, to one, which means that the material is incapable of holding any tensile load in the corresponding direction ($0<{\omega }_i<1)$. Last, the stress state is updated by multiplying each (effective) principal stress ${\sigma }_i$ by $\left(1-{\omega }_i\right)$ [21].

As already mentioned above, the indentation procedure was numerically simulated in displacement-controlled manner with constant indenter velocity. To reduce the computation time, the indenter velocity was increased to some point without a significant change in the simulated results.

4. Frictional Study Results and Discussions

Quasi-static spherical indentation was already numerically simulated for a frictionless contact [25], and the numerical results were compared to experimental data. The DFH model inputs, specifically the Weibull parameters, were also needed in order to numerically predict the fracture pattern. The indentation test was simulated so that the stress state in the rock geometry was found. Then, the Weibull parameters were calibrated based on this stress state.

In this study, frictional effects are investigated in indentation tests. First, the DP parameters were the same as previously [10]. However, the Weibull parameters in the DFH model should be recalibrated since they were set based on simulated stress states. The friction coefficient between the indenter surface and the rock surface was first assumed equal to 0.4. This value was implemented in the finite element model and the stress state in the rock geometry was captured. Furthermore, several indentation experiments ($N=$9) were considered [10], and the first load-drop in each experiment was considered. It was previously observed that the first load-drop occurred at somewhat different indentation depths [10]. Therefore, the first load-drop depth is of probabilistic nature. Moreover, this load-drop is likely due to Hertzian (ring) cracking because of high tensile stresses (first principal stress) on the rock surface. Therefore, the first principal stress corresponding to each load-drop depth was required and determined from numerical simulations. Based on the finite element results, it is observed that the first principal stress level on the rock surface outside the contact area decreases due to frictional effects in combination with the fact that plastic deformation is confined to a small region close to the indenter. In fact, the stress level decreases by almost 40%. It should also be mentioned that the methodology used in this paper is valid for hard rocks with limited crushed zone as well as limited plasticity. Softer rocks with an extensive plastic region have different fragmentation responses and should be treated in a different manner [28].

The latter statement deserves some further explanation. The indentation response of an elastic-plastic material can generally be divided into three different regimes which are fully elastic, constrained plastic and fully plastic. The first regime occurs at the initial loading stage and the corresponding response can be predicted by Hertzian theory. As for regime two, the theoretical treatment is challenging due to uncertainty in size and shape of the evolving plastic zone. Regarding regime three, the plastic region is significant [28].

The plastic zone significantly changes the near field indentation stresses, while the far-field stresses seems to be little affected compared with the elastic case [29]. In some cases, including plasticity leads to circumferential tension right outside the contact region on the surface [30,31], in contrast to the elastic case in which the radial stress is tensile in the mentioned region. This change from radial tension under elastic condition to circumferential tension under elasto-plastic condition is mostly the reason behind the change of fracture pattern from a ring crack in a very brittle material such as glass to a radial crack in a semi-brittle material such as granite [32].

The contact response of hard rocks such as granite, which is of interest in this study, is of regime two with constraint plasticity. Therefore, the methodology used in this paper together with the assumptions made on the fragmentation response is mainly valid for the hard rocks that shows limited crushed zone and limited plasticity at indentation.

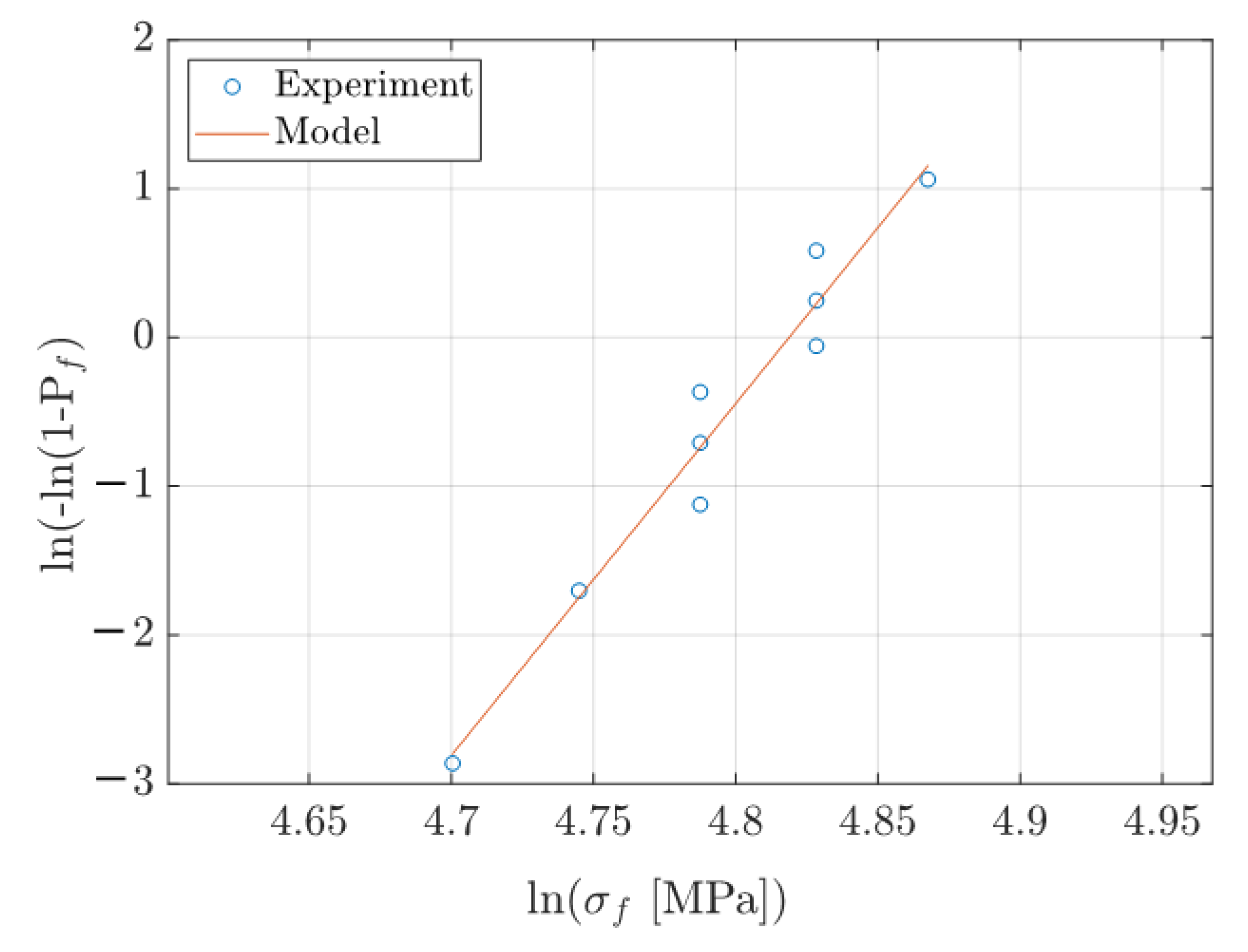
The first principal stress levels are assumed to be equal to the material failure strength. Then, the resulting failure strengths are sorted in ascending order, and the corresponding failure probability $P_f$ of the n-th test is calculated as

$$P_f=\frac{n-0.5}{N}$$

(10)

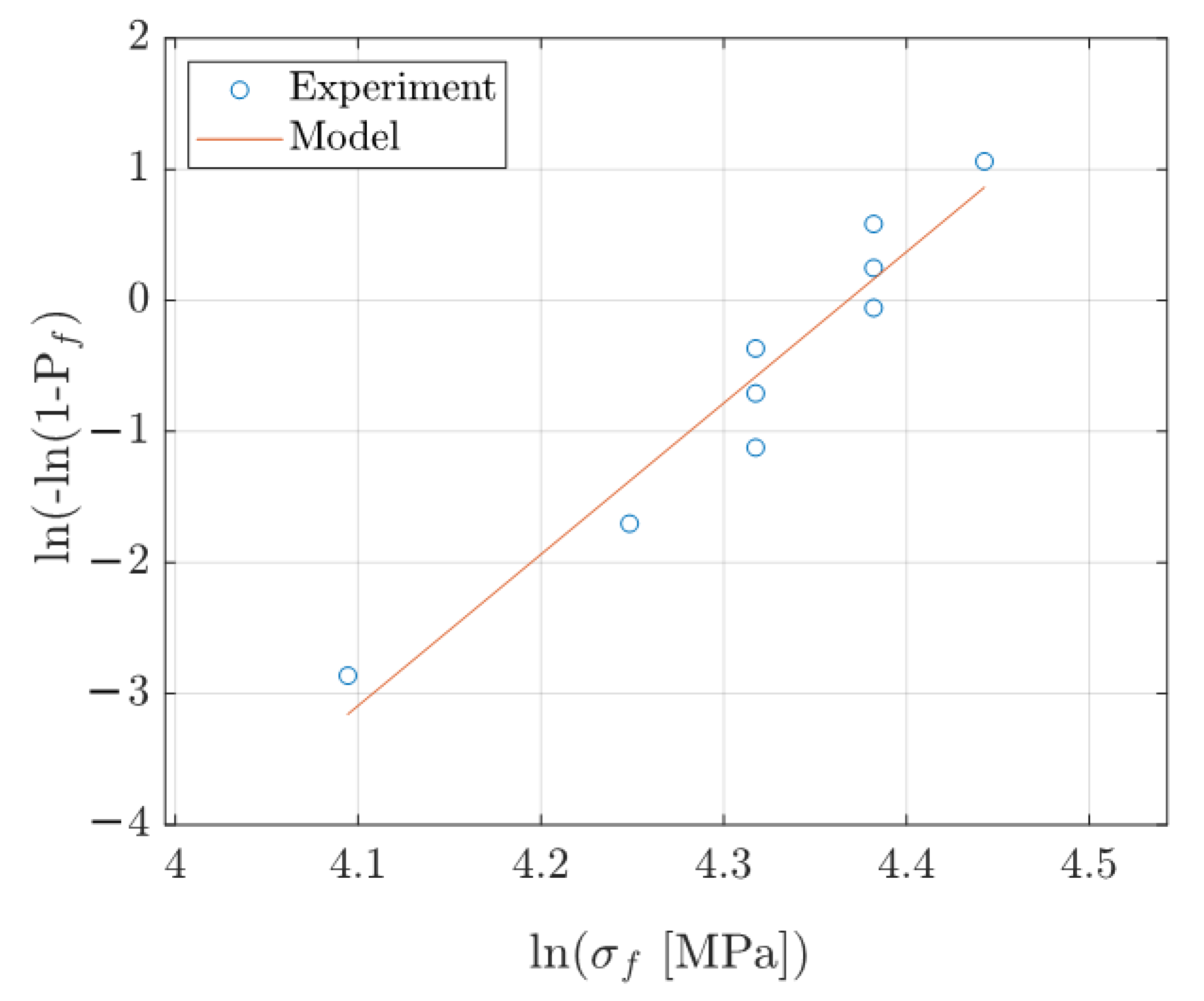
where $N$ is the total number of tests. The corresponding Weibull plot is reported in Figure 7. A linear regression is performed, and the slope of the fitted line gives the Weibull modulus $m$, here equal to 12. Last, the effective volume is calculated from Equation (7) and it is equal to 2 ${\mathrm{mm}}^3$. The new set of Weibull parameters obtained in the current study is listed in

Table 2. Weibull parameters used in DFH model. The friction coefficient was assumed equal to 0.4. The elastoplastic material parameters are the same as in Table 1.

Material Parameter
$m$	12
${\sigma }_w\left(\mathrm{MPa}\right)$	75
$Z_{eff}\left({\mathrm{mm}}^3\right)$	2

.

Using the new set of DFH parameters, the force-penetration response is reproduced. It is found that the force-penetration response is not influenced by frictional effects. Very early on, plasticity occurs under the indenter and controls material flow (see below). Moreover, the damage zone is shown in Figure 8 obtained by using Table 1 data as well as Table 2 data for comparison purposes. The indented surface of typical rock specimens is also shown. The fracture pattern for frictional contact is similar to that with frictionless contact. However, the fractured zone size increases somewhat due to different stress states and determined material strength parameters.

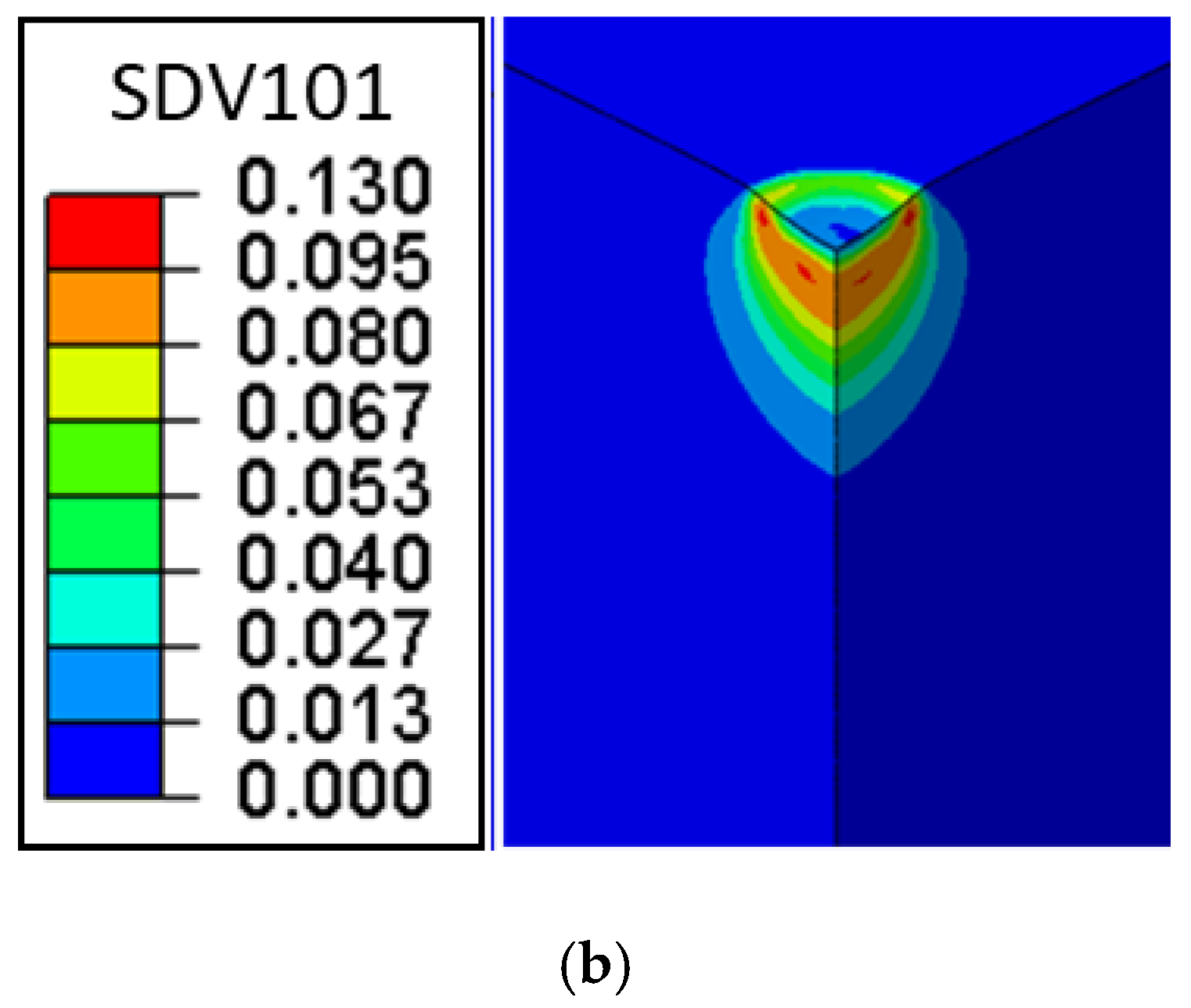
The equivalent plastic strain field generated by numerical simulations, using the plasticity model (DP), is compared between the frictionless case, Figure 9a, and the frictional case (µ = 0.4), Figure 9b. The plastically deformed region corresponds to the crushed material due to high hydrostatic pressures as well as the shear zone with multiple (closed) microcracks. The plastically deformed region was not affected by frictional effects. As a consequence, the effect of friction is very limited on the overall force-penetration response. It should be recalled that irreversible strains are modeled as plasticity in this study.

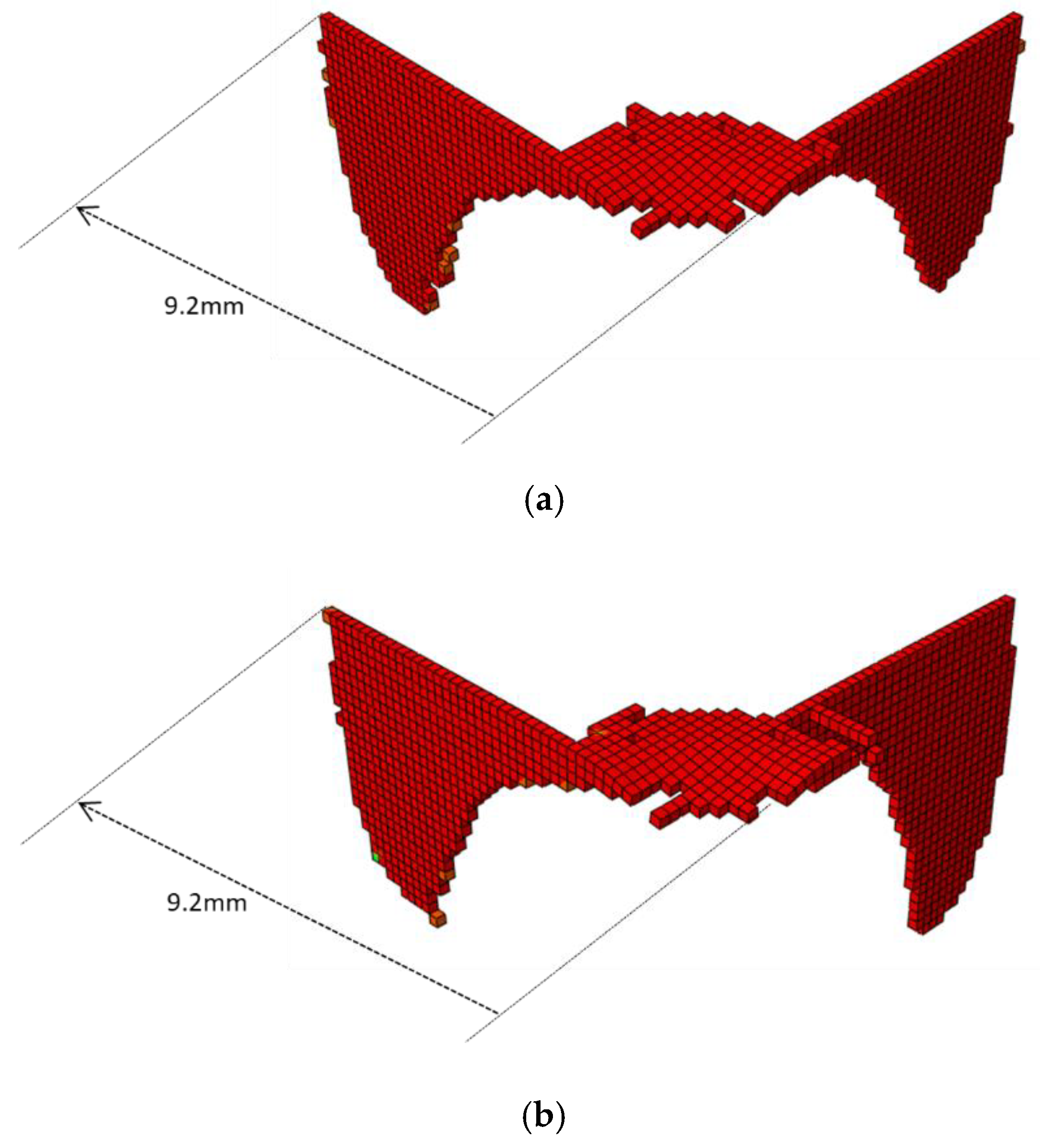
Last, a parametric study is performed for friction coefficients $\mu =$ 0.1, 0.2, 0.3 and 0.5. No substantial differences in force-penetration curves are observed. The Weibull modulus $m$ takes on approximately the same value (i.e., 12) in all nonzero friction coefficient cases. This is due to the fact that the stress state does not change much between these cases, as adhesive or close to adhesive contact is at issue (see discussion above). This is emphasized by the fracture patterns shown for friction coefficients $\mu =$ 0.1 and 0.5 in Figure 10. Clearly, the pattern for $\mu =$ 0.5 (and also for $\mu =$ 0.1) is very similar to the one for $\mu =$ 0.4 in Figure 8b. However, some intermediate effects are noticed for $\mu =$ 0.1 for which ${\sigma }_w$ is somewhat higher (80 MPa) than in the other cases (i.e., 75 MPa) and the fractured zone is slightly smaller than for $\mu =$ 0.4 and 0.5. From these results it can be concluded that frictional effects are sufficiently accounted for by performing an analysis with $\mu >$ 0.1 say. At higher values on the frictional coefficient global and local quantities remain the same.

5. Concluding Remarks

The material of interest in this study was Bohus granite. A Drucker-Prager (DP) law was chosen to predict any inelastic deformations except tensile failure (mode-I fracture). To model the latter, an anisotropic damage model was chosen. Since the material strength is heterogeneous, the tensile strength should be considered to be a random variable, which was described by Weibull statistics. Also, granite shows a size-dependent tensile strength [7], which is captured by the Weibull size effect using the effective volume concept. These features are included in the chosen damage model. In practice, the statistical inputs of the damage model, namely the Weibull parameters, are to be calibrated in order to numerically predict fragmentation.

In this work, frictional effects were investigated for quasi-static spherical indentation using the DP-DFH constitutive model. The DP parameters were determined in a previous work by the authors [10]. The DFH parameters, specifically the statistical inputs, were also previously determined [25]. However, the DFH statistical inputs were calibrated based on finite element modeling of indentation tests assuming frictionless contact between the indenter and the tested rock. The first load-drop observed in the force-penetration response recorded during indentation tests was considered to determine the Weibull parameters. This load-drop is likely due to high radial tensile stresses immediately outside the contact boundary. The stress state during the initial steps of the indentation test was thus required and determined via finite element simulations. The resulting stress state was then used to determine the statistical parameters. However, the stress state especially on the rock surface close to the contact region may be influenced by friction. Therefore, various friction coefficients were considered in the current finite element model. From the simulated stress states, the parameters were recalibrated. The Weibull stress dropped from 120 MPa for frictionless contact to ≈75 MPa for frictional contact cases, and the Weibull modulus from 24 to 12. The effective volume increased from 1 ${\mathrm{mm}}^3$ to 2${\mathrm{mm}}^3$.

It was numerically observed that friction does not affect the predicted force-penetration response of Bohus granite under indentation loading using the current set of Weibull parameters. Conversely, the fracture pattern predicted by considering a rather high nonzero friction coefficient is similar to that for frictionless contact, but its size is somewhat larger. Last, a parametric study for nonzero friction coefficients was performed and no significant changes in parameters or fracturing features were observed.

From a practical point of view, the results are directly relevant for drilling and cutting operations on hard rocks. A very important area for application is percussive drilling.