1. Introduction
The dynamics of systems affected by friction are most often studied in the context of friction-excited vibrations (FIV). Prominent examples for FIV in mechanical structures and machines range from brake systems [
1,
2,
3,
4], clutches [
5], drill strings [
6] to artificial hip joints [
7] and others. FIV often arise through positive energy feedback from a friction interface with the structure, i.e., through self-excitation [
8,
9,
10]. Sub-critical Hopf bifurcations [
11,
12] and isolated solution branches [
13,
14,
15] are a common observation in those systems, such that bi- and multi-stable systems have been reported numerously [
14,
16,
17]. The computation of those nonlinear responses (periodic, quasi-period orbits, chaotic trajectories) is a well-established field of research [
18,
19,
20,
21], mostly resulting in the identification of complicated bifurcation diagrams [
11,
13,
22,
23,
24]. The stability of the solutions is usually assessed by local Lyapunov-type stability metrics [
25,
26]. Hence, the stability statement is often a binary one that measures the state’s robustness against
small perturbations. However, the actual size of
permissible perturbations, i.e., those for which the trajectory would still return back to the state, is not given. In a multi-stable system configuration, the long term steady-state behavior thus depends on the choice of initial conditions or the size of instantaneous perturbations. Once the system enters another basin of attraction, severe jumping phenomena may occur. Typically, such jumps are related to a change from a stable steady sliding state to high-intensity periodic vibrations or stick-slip cycles [
27,
28,
29], or from one periodic solution to another periodic solution [
11].
This work investigates a rather novel technique denoted as basin stability to estimate the size of the system’s basins of attraction in a subset of the state space. The basins’ size estimation can then be considered a global stability metric, i.e., indicating how likely the system is to end up on one of the co-existing stable steady-states. Therefore, those probabilities add new insights to the rather binary stability statements derived from local perturbation-based approaches. We study a friction oscillator excited by a falling friction slope and a second oscillator excited through binary flutter instability. Our results indicate that the basin stability analysis is a robust and easily applicable model-agnostic technique. It can reveal the actual picture of the long-term behavior for a given set of perturbations, thus augmenting classical bifurcation and stability studies. Using the basin stability analysis, some solutions can even be ruled out if one can guarantee strict control over the instantaneous perturbations to system trajectories or operating conditions.
2. The Concept of Basin Stability
We study nonlinear dynamic systems
with the states
in the
N-dimensional state space. The long-term asymptotic behavior is denoted as
attractor [
30] throughout this work. Typically, the Lyapunov spectrum
is assessed to characterize the linear stability of a state
against small perturbations. For fixed points, the Lyapunov exponents are equivalent to the system’s eigenvalues derived from the complex eigenvalue analysis (CEA). The real parts of the eigenvalues indicate linear stability to a
small perturbation about the fixed point. The sizes of the real parts indicate the strength of attraction (
) or rejection (
) for stable or unstable directions in state space, respectively. However, the eigenvalues do not encode a piece of information about the permissible size of perturbations that are still attracted by the fixed point. While this is not an issue for systems that feature only a single stable solution, the situation is different for systems featuring multiple stable solutions. For these systems, local stability concepts may have only a limited validity: a non-small perturbation of a state can result in a jump to another attractor. Hence, global stability concepts are required to assess the size of permissible perturbations, i.e., to characterize the basins of attraction for all solutions. The basin of attraction
denotes the subset of states that converge to the same attracting set
. The basin boundaries are related to unstable solutions of the system which represent separatrices of the basins in state space. Depending on the size and shape of its basin, an attractor can be more or less robust against non-small perturbations. There are multiple ways to compute the basins of attraction, e.g., through Lyapunov functions [
31]. These methods are known for some canonical, low-dimensional, and well-studied systems. However, they are not readily available, or straight-forward to compute, for any generic and high-dimensional nonlinear dynamical system, such as frictional oscillators which are studied in this work.
The basin stability proposed by Menck et al. [
32,
33] is a global stability concept for complex systems that aims at measuring stability against non-small perturbations by a volume-based probabilistic approach. Conceptually, the basin stability measures the volumetric share of all basins of attraction in a hypervolume of the state space. For a computationally feasible solution, a distribution
of perturbations is drawn from a reference subset
of the state space, representing a set of states to which the system may be pushed to through non-small perturbations with
. For each perturbation, the steady-state behavior of the dynamical system is obtained through time-marching integrations. Then, the fraction of perturbed states that converged to the specific attractor
denotes an estimate for the basin stability
, i.e., [
32,
34]
Here,
denotes an indicator function that classifies a steady state solution
to belong to the attractor
. Therefore,
is an estimate for the volume share of the basin of attraction
given the reference subset
sampled by
[
32,
35]. Naturally, for a
k-multi-stable system, the basin stability values of all
k attractors add up to unity
. The size, i.e., the number of states, of the dynamical system to be studied by the basin stability is only limited by computational power for the Monte Carlo simulations. As the basin stability computation can be considered a repeated Bernoulli experiment [
32], the standard error of the basin stability estimate is
which can be used to find a subset
that ensures a low standard error. Recently, systems with fractal, riddled, and intermingled basin boundaries were studied [
33] indicating the robustness of the basin stability concept. All basin stability computations in this work were obtained from the open-source package
bSTAB [
36] available at
https://github.com/TUHH-DYN/bSTAB/tree/v1.0.
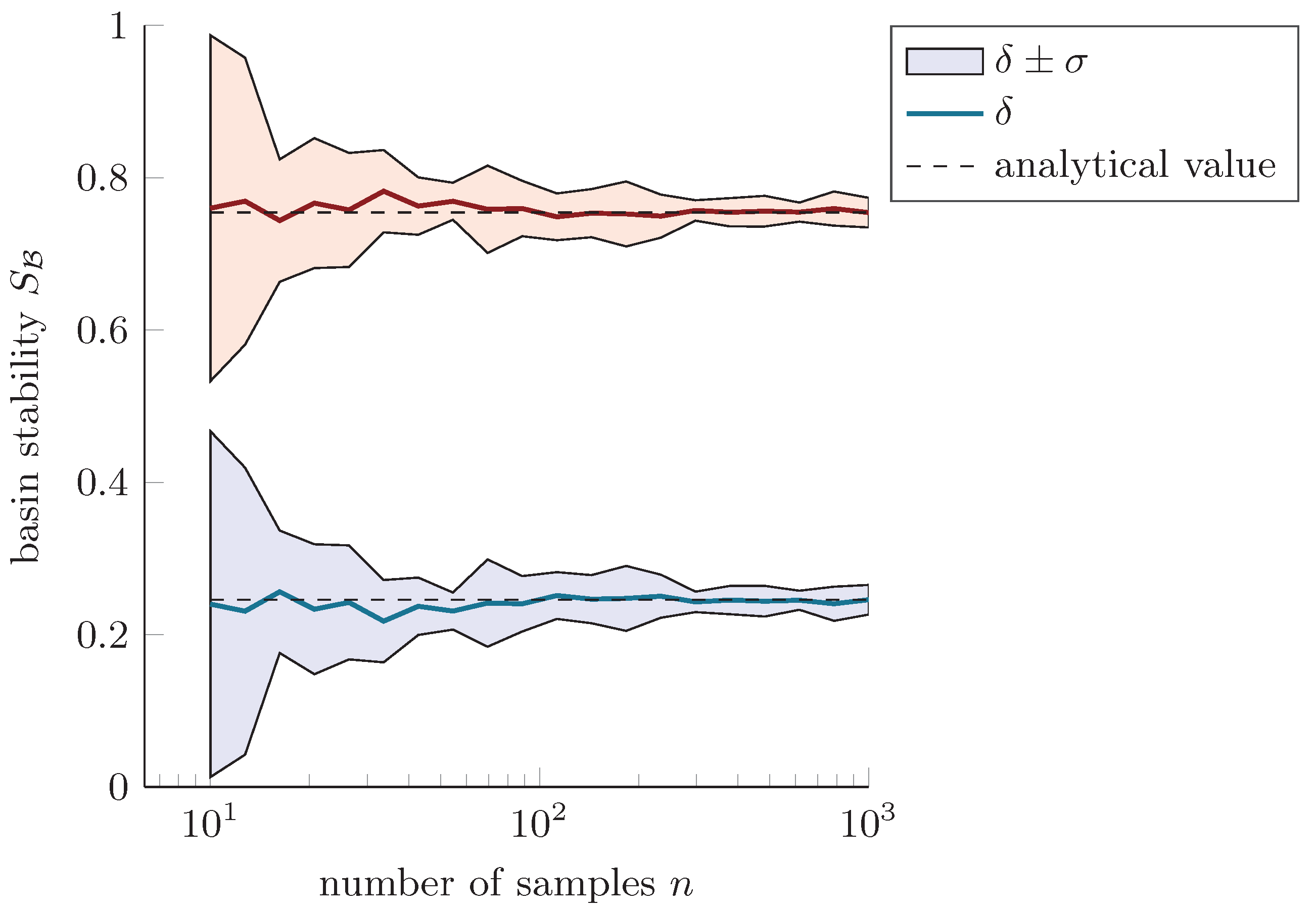
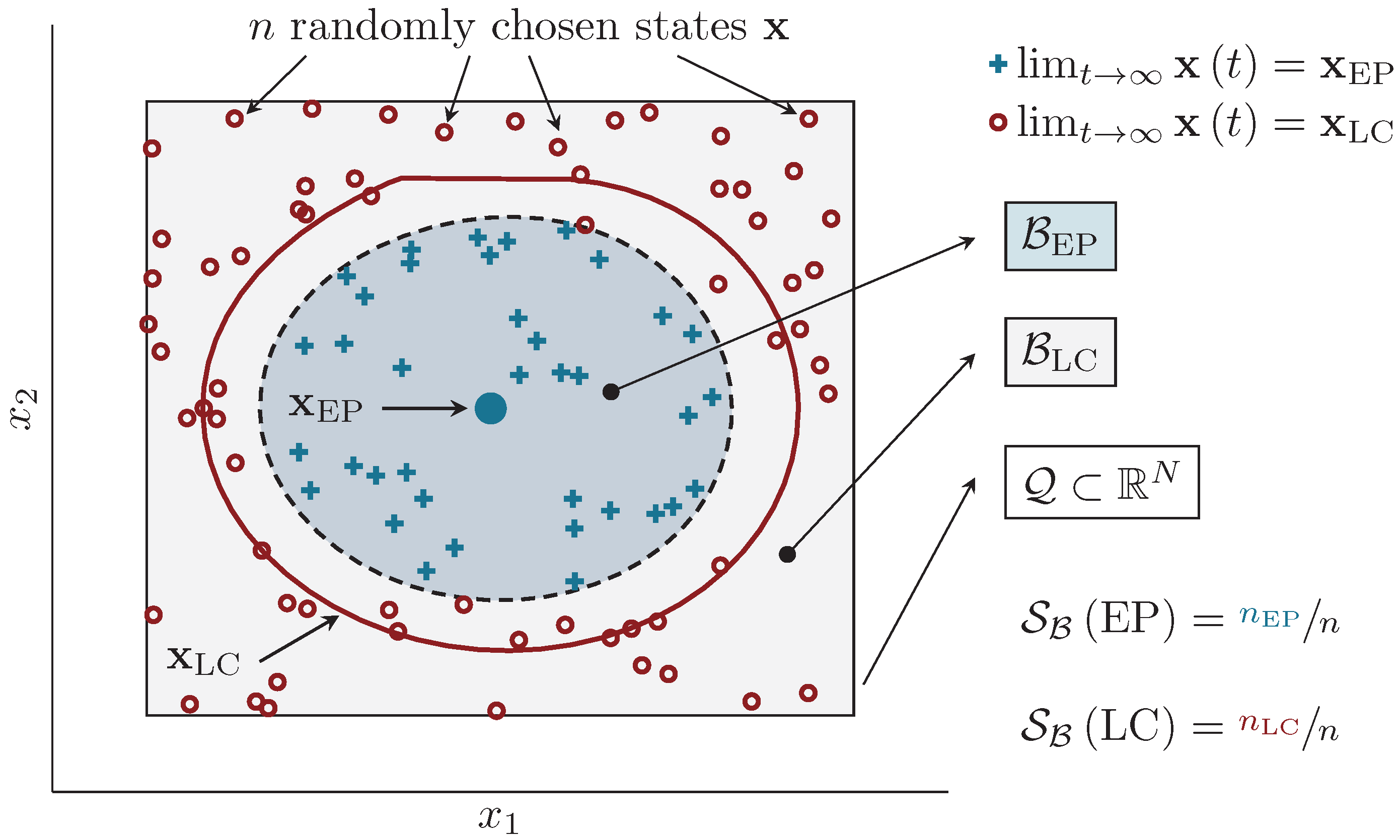
Figure 1 displays a schematic for illustrating the practical computation of basin stability values. A nonlinear dynamical system with two states
is studied (In fact, the system is the single-degree-of-freedom frictional oscillator to be discussed in
Section 3). The system exhibits three solutions: A stable equilibrium position (
), an unstable periodic orbit (
), and a stable limit cycle (
). The distribution of perturbations
is chosen such that all solutions are contained in
and
samples are drawn uniformly at random. The trajectories starting from
states in the basin
converge towards the equilibrium position, while
states are located in the basin
and thus converge to the stable limit cycle. As a result, the basin stability estimates are
and
, respectively. Because the separatrix, which is the unstable periodic orbit, is explicitly known for the system, the basin volumes can be determined analytically. The exact volumetric fractions of
and
in
are
and
, respectively. Therefore, the basin stability computed from
samples is a good approximation for the system at hand (
Appendix A.2 indicates that
samples are required for a very close approximation of the analytical results).
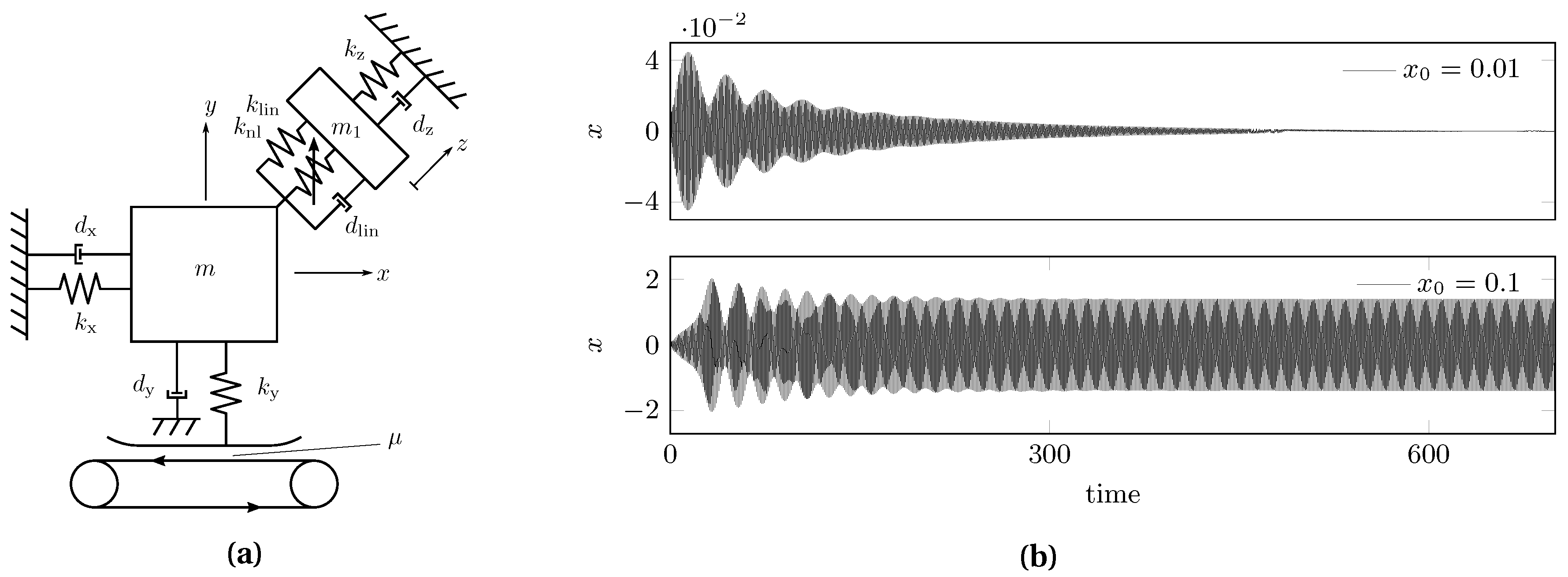
3. Bi-Stable Oscillator with Falling Friction Slope
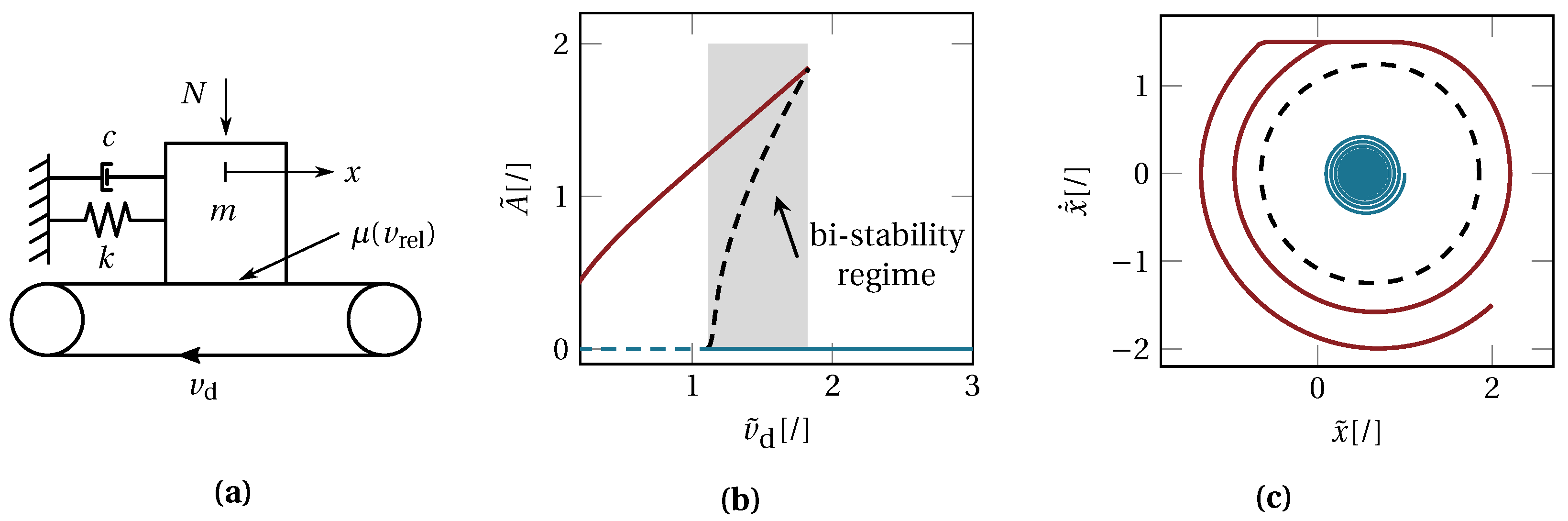
As a first system, we study the dynamics and the stability of a single-degree-of-freedom oscillator
, see
Figure 2a, with velocity-dependent friction as proposed by Papangelo et al. [
12]. Specifically, the friction characteristic
is a velocity-dependent weakening function
featuring the static friction coefficient
, the dynamic friction coefficient
, the reference velocity
and the contact normal load
N. The non-dimensional form of the equations of motion is obtained through normalization
of the quantities accordingly to the work of Papangelo et al. [
12]. The velocity-dependence introduces a dynamic instability that gives rise to friction-induced vibrations (FIV) for
. Moreover, the friction nonlinearity enables the system to exhibit a bi-stable behavior, such that a stable steady sliding state and a stable stick-slip cycle co-exist for a range of belt velocities
, see
Figure 2b. At
, the steady sliding state loses stability at a subcritical Hopf bifurcation point. In the bi-stability regime, and depending on the initial condition or instantaneous perturbations, the system will either end up in the low-energy steady sliding state, or on the high-intensity stick-slip cycle. Both solutions are locally stable and attractive, i.e., robust against small perturbations.
For this minimal system, the basin boundaries are directly accessible through the unstable periodic orbit (UPO). However, if this knowledge was not available, the probability of arriving on one of the two steady states would be unknown.
Figure 1 displays a sampling with
points uniform at random from
at
, and the resulting basin stability values
and
. Hence, for this
, it is more likely to arrive on the high-amplitude limit cycle solution than on the steady sliding fixed point.
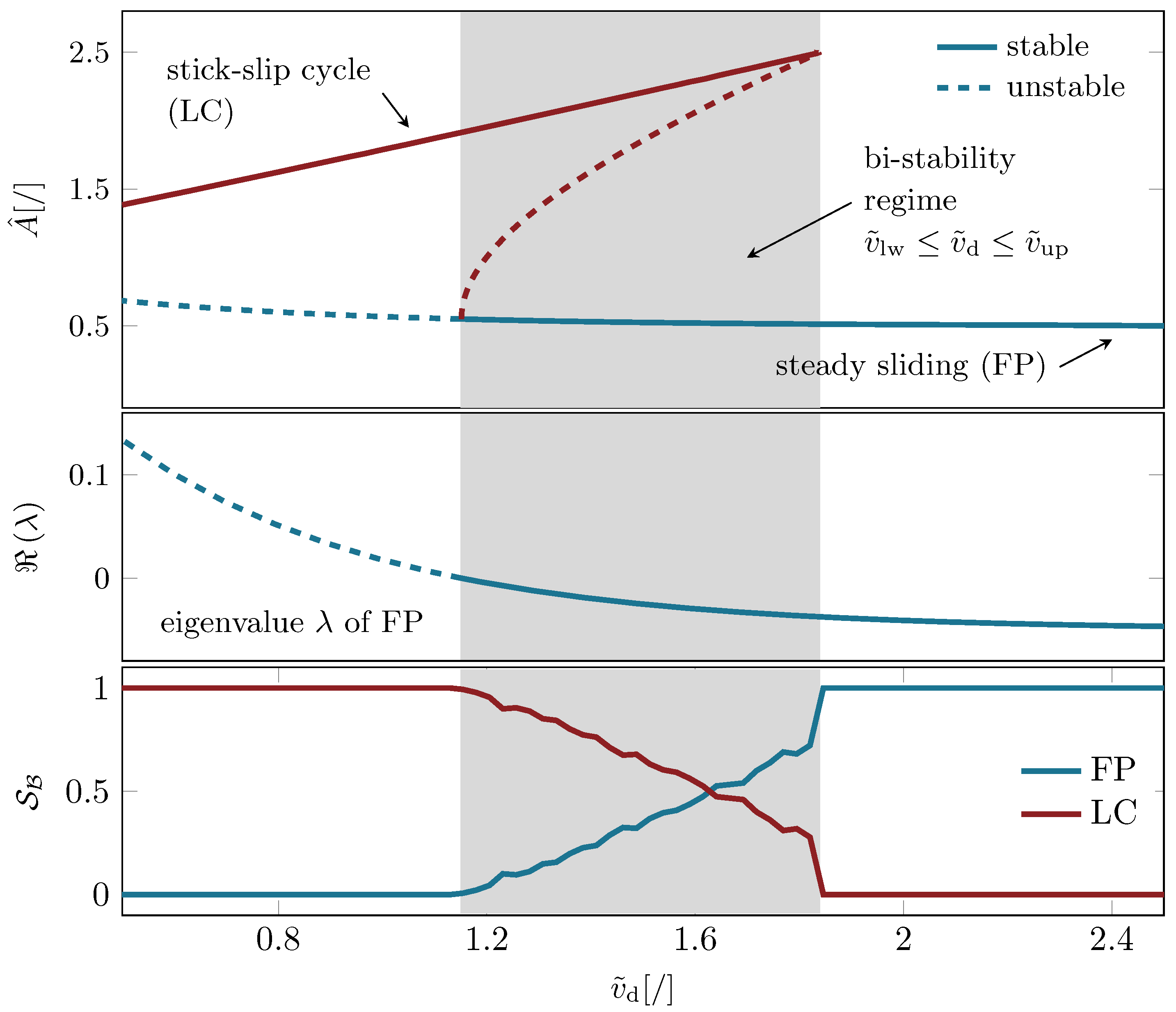
To complement the bifurcation diagram and the complex eigenvalue analysis, the basin stability of the fixed point and limit cycle solution is derived along the normalized belt velocity parameter. In particular, at each velocity value
initial conditions are drawn from a uniform random distribution in
, i.e., positive initial displacement and negative initial velocity.
Figure 3 depicts the eigenvalue’s real part and the basin stability. As
decreases, the real part grows until it crosses into the positive plane at
. This rather smooth behavior nicely indicates the transition into linear instability of the fixed point solution. However, the eigenvalues at the exemplary points
and
would not allow a statement about the system’s probability to converge to this solution instead of converging to the periodic orbit. Additionally, the eigenvalue obviously does not indicate the existence of the competing stable periodic solution in this parameter range. At this point the basin stability analysis comes into play: Below the Hopf bifurcation point, all trajectories converge to the periodic orbit, hence
, and above the bi-stability regime all trajectories converge to the globally stable fixed point, i.e.,
for
. For the chosen subset
, the periodic orbit is the dominating behavior in the lower parameter range of the bi-stable regime. For increasing relative velocity the probabilities, i.e., the basin stability values, are more balanced for arriving either on the LC or the FP. For
the fixed point is the more probable solution to arrive at. Therefore, the basin stability values add an important insight and complement the binary stability statements given by the eigenvalues. Using the basin stability, it is now possible to state
how stable a solution is against arbitrary and possibly
non-small perturbations. For more realistic systems, this statement may be of even larger value than the binary stability statement given by local metrics.
4. Bi-Stable Oscillator with Mode-Coupling
As a second system, we study a frictional oscillator [
8,
11], which (in contrast to the first system) experiences FIV through a mode-coupling instability. The system features a main oscillating mass that is in dry Coulomb-type frictional contact with a conveyer belt. A second mass is connected to the main mass through a nonlinear joint element in diagonal direction, thereby geometrically coupling the vertical and horizontal movement of the main mass. The relative sliding velocity is assumed to always be positive, such that no stick-slip cycles can arise. For the nonlinear joint element, a cubic stiffness nonlinearity
is chosen [
11]. The equations of motion and parameter values are given in
Appendix B and the model is displayed in
Figure 4.
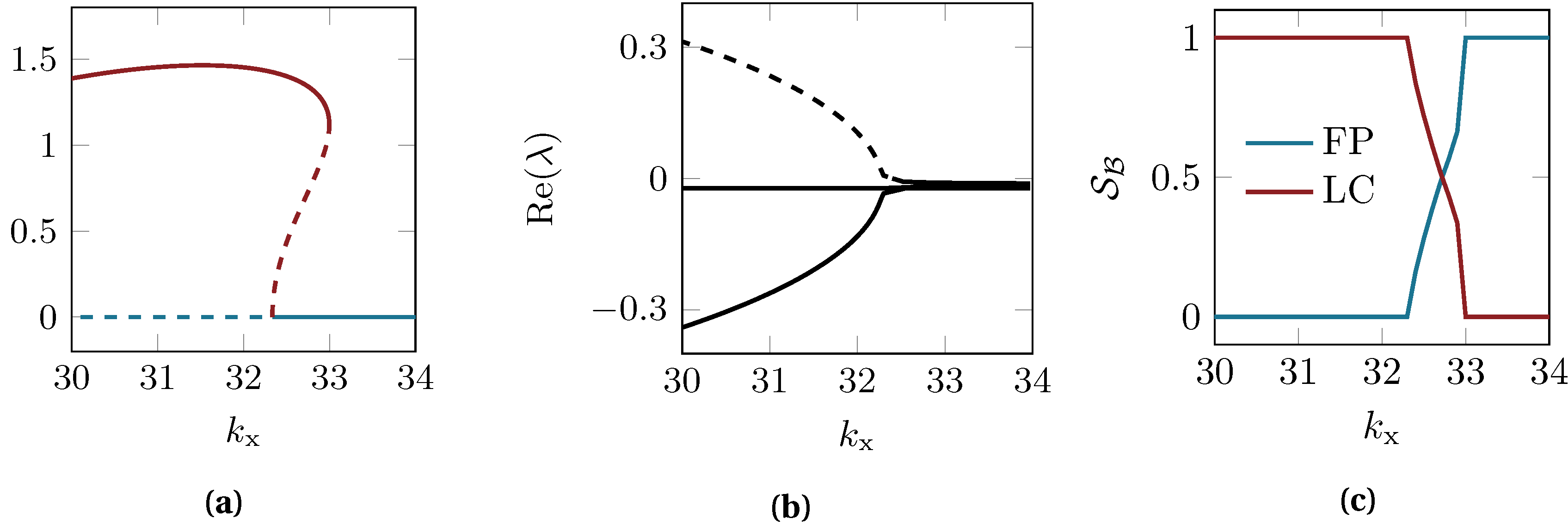
Previous studies have revealed the complicated bifurcation behavior of this system, including super- and sub-critical Hopf bifurcations as well as isolated solution branches [
11,
13,
14]. In this study, a variation of the horizontal stiffness
is performed. A sub-critical Hopf bifurcation point is found at
, see
Figure 5a. Below, a stable limit cycle and the unstable fixed point exist. Above this value there is a bi-stable range up to
with a co-existing stable limit cycle and the stable fixed point. The eigenvalues’ real parts in
Figure 5b exhibit the classical forking behavior that is related to the mode-coupling instability mechanism in this system. At the point of instability, one eigenvalue crosses into the positive plane. The basin stability
of both stable solutions is computed for
random initial conditions drawn from
(all other initial conditions are fixed to 0).
Figure 5c depicts the basin stability as a function of the horizontal stiffness. In the bi-stability range
the basin stability values indicate that the limit cycle solution is the dominating one for lower stiffness values. For larger stiffness values the fixed point solution is the most probable for our choice of
. Hence, within this rather short bi-stability range, a minor variation of the horizontal stiffness value would crucially affect the probability of arriving either on the low-energy steady-sliding state, or on the high-energy limit cycle, which may cause increased wear, audible vibrations and other effects in realistic systems. Such kind of statement about the global stability regarding non-small perturbations would not have been easily accessible through the bifurcation diagram or the local stability analysis.
These results are clearly related to the shape of the unstable periodic orbit, i.e., the separatrix of both basins of attraction. While the qualitative basin stability values for a variation in the initial conditions for
x would have been readable from the bifurcation diagram in
Figure 5a, this task quickly becomes complex once more degrees-of-freedom (DOFs) are considered. For example, let us consider a reference subset
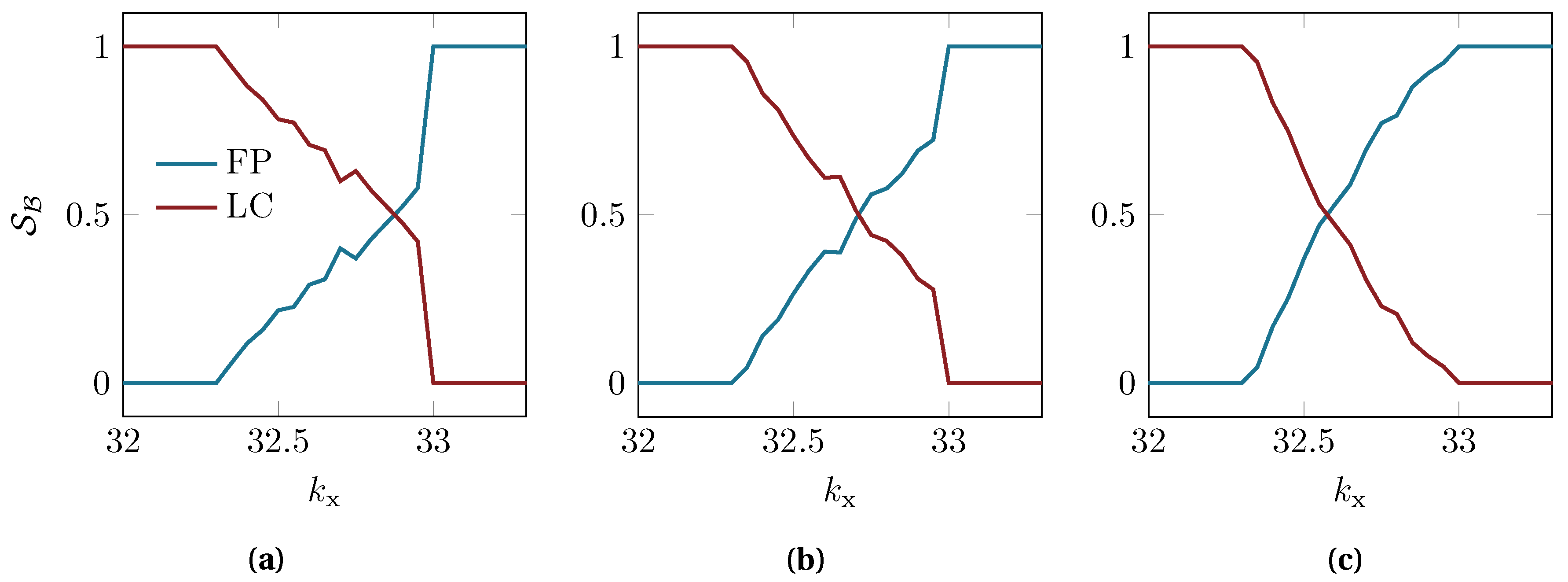
that captures certain variations for multiple DOFs, instead of variations for a single DOF as shown before.
Figure 6 displays the basin stability values for three different choices of
, i.e., different variations of the range of possible initial conditions:
In the first case, some initial variations in the horizontal position and large variations in the vertical displacement of the main mass are allowed. In the second case, variations in the initial velocities are studied, and in the third case also variations in the secondary mass’ initial conditions are considered. Such scenarios would quickly become impractical for studying permissible perturbations, i.e., the global stability of each solution, using bifurcation diagrams and subdividing the state space by the unstable solutions. The concept of basin stability automates this process through the Monte Carlo sampling, allowing for a easy-scaling and consistent estimation of the relevant basin volumes.
In fact, even though the three reference sets are very different in their value ranges, the resulting basin stability analysis displayed in
Figure 6 does not change qualitatively. The
turning point, i.e., the point after which the FP solution dominates over the LC solution for increasing values of
, changes only slightly: For
this point is found at
, while it is
and
for
and
, respectively. Hence, the basin stability is not very sensitive to the choice of
for this system. In a situation in which the overall qualitative behavior of the basin stability values may have seem obvious, the quantitative evaluation would have become difficult to obtain from the bifurcation diagrams. Especially for higher-dimensional systems and specific subset choices the basin stability analysis represents a highly robust approach to estimate the probability of arriving on either of the competing solutions, which we will illustrate in the next section.
5. Bi-Stable Oscillator with Isolated Periodic Solution
The third dynamical system studied in this work is a weakly damped variant of the system proposed in the previous section and sketched in
Figure 4. Here, the damping parameters are reduced by a factor of 10 to
. This system configuration has already been studied in [
13,
14] where the authors found an isolated solution branch resulting from the damping variation.
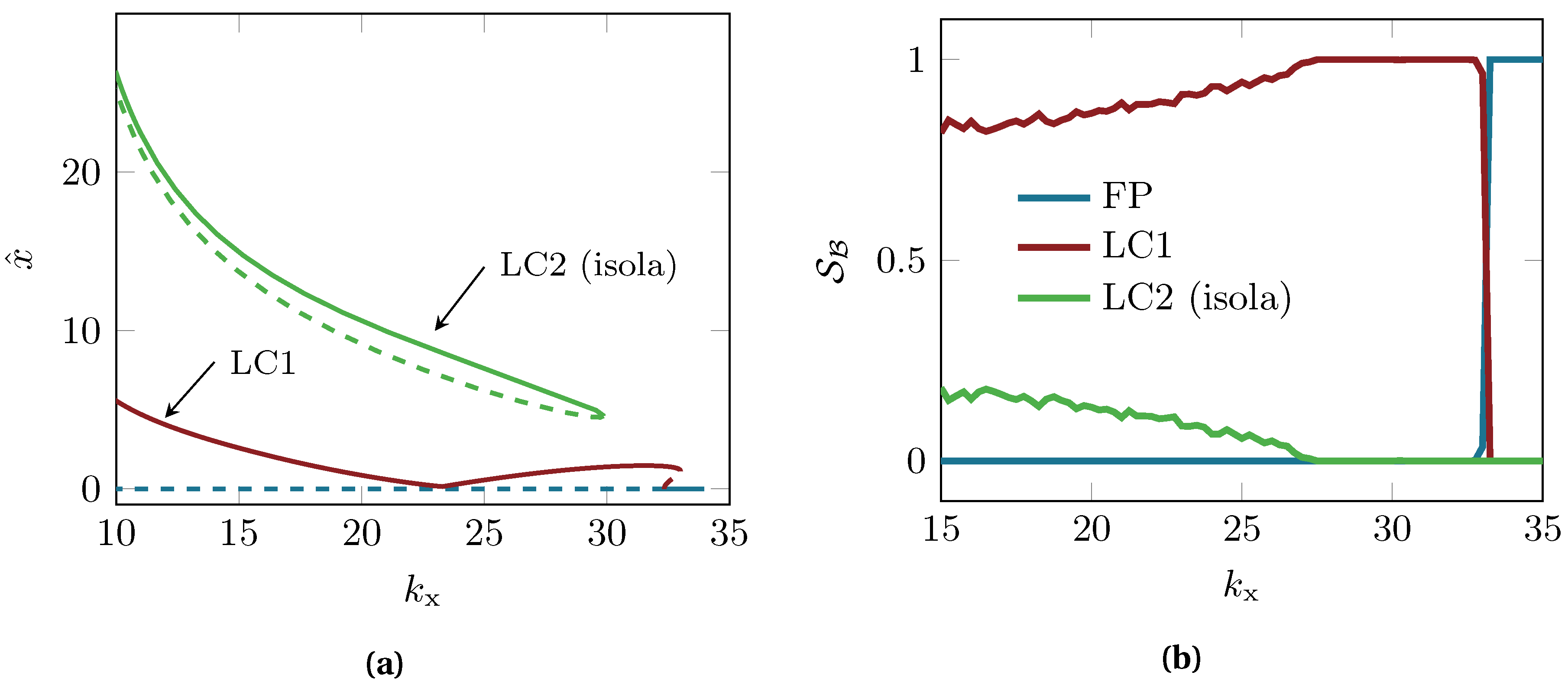
Figure 7a displays the bifurcation diagram for the horizontal stiffness
. The fixed point solution loses stability through a sub-critical Hopf bifurcation at
to a limit cycle solution, hereafter denotes as LC1. Interestingly, a second stable limit cycle solution is born for
, which is found to be an isolated branch [
14], hereafter denoted as LC2. That is, this solution is not connected to any other solution path. As a result, the system may jump from the fixed point solution to the first limit cycle for
, and then from the limit cycle to the isolated branch for
. Hence, within a rather narrow parameter range, two jumping phenomena between different solutions may occur. It is, therefore, of great interest to investigate the probability of arriving on either of those solutions for some prescribed set of initial conditions.
Figure 7b displays the basin stability values for both periodic orbits and the fixed point solution. For the reference subset, we arbitrarily chose
using
sampling points. For for the bi-stability range featuring the two periodic solutions LC1 and LC2 (
) the basin stability analysis reveals that LC1 is the by far most probable solution. A maximum of
of the trajectories converge to the isolated solution branch, while the remaining trajectories converge to the first periodic orbit. Particularly interesting is the parameter regime
. Here, the basin stability indicates that LC1 is globally stable, even though the stable isola still co-exists. However, due to the choice of
, no initial conditions were drawn for the basin related to LC2. Hence, if the range of initial conditions and perturbations can be quantified or limited for some specific system, the basin stability analysis can also help to rule out jumping phenomena between co-existing solutions.
Another interesting observation is the following: the basin stability values in this specific setting do not follow the qualitative trend of the respective amplitudes reported in
Figure 7a.
keeps increasing along the stiffness parameter, while the corresponding amplitude of the horizontal vibration amplitude shows a different behavior. Theoretically, it is clear that the vibration amplitudes do not relate to the size of the basins of attraction. However, on the first sight classical bifurcation diagrams may suggest that one solution is
more attractive if it has a larger vibration amplitude. At this point, the basin stability represents a technique to quantify the attractiveness in a highly consistent manner.
Lastly, we discuss our previous thought on the benefits of having a robust methodical approach to estimating the basin volumes through Monte Carlo sampling irrespective of the dynamical system at hand (so-called
model-agnostic techniques). Especially for such low-dimensional systems as shown before, one might raise the issue of using computation-heavy sampling methods, even though the basins of attraction are readily available once the bifurcation diagram is known.
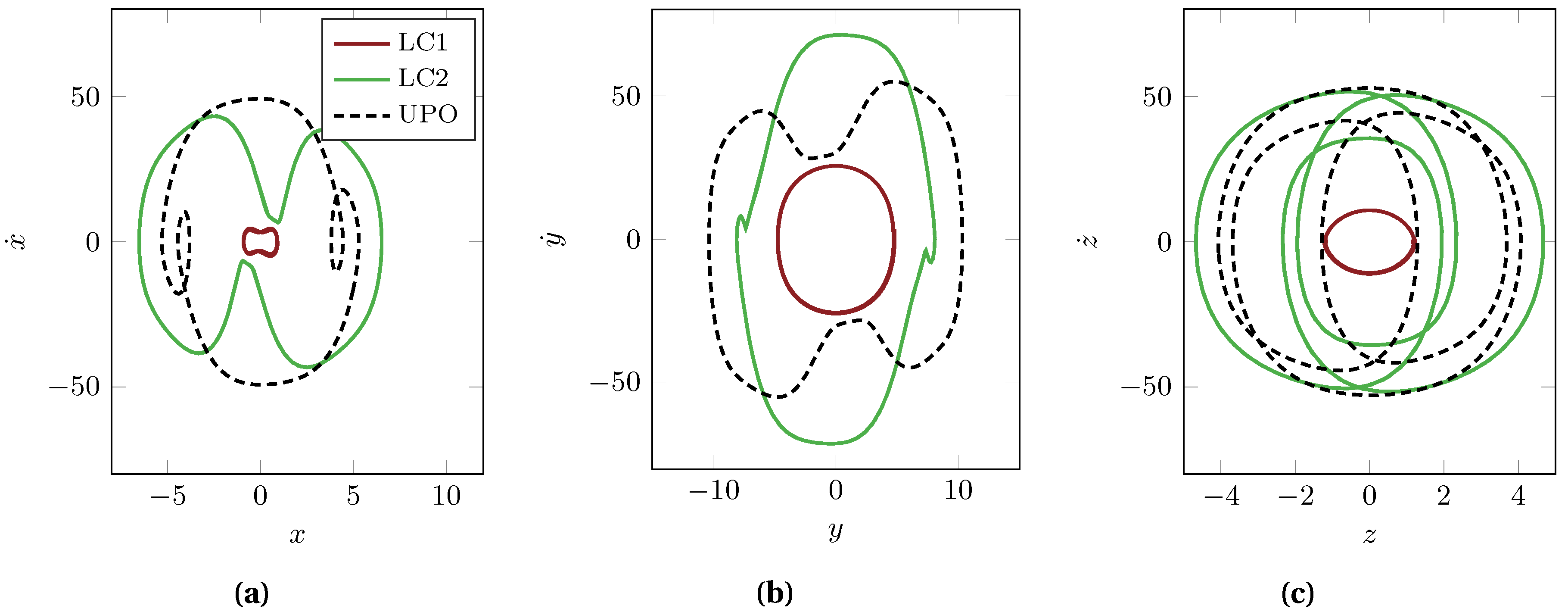
Figure 8 displays the state space of each DOF at
, hence in a configuration where the two periodic orbits co-exists. It becomes clear that even for this 3 DOF oscillator (6 states), the analytical calculation of the basin volumes can quickly become a challenge. There is no straight-forward way to computing the volumes in the six-dimensional space from the intertwined basins separated by the unstable orbits, especially looking at the
z coordinate. Therefore, the basin stability analysis is not only relevant for systems featuring larger number of states, but also for rather low-dimensional systems.