1. Introduction
Friction-induced vibrations (FIVs) are a peculiar type of oscillations generated by the friction acting between two bodies in relative motion. They consist of either the successions of stick and slip phases between the two bodies [
1], or of quasi-harmonic oscillations having an approximately sinusoidal displacement–time relation [
2,
3]. Although for some specific applications these kinds of vibrations are intentionally generated, such in the case of violin strings [
4] and singing wine glasses [
5], typically they are seen as a detrimental phenomenon, as in the cases of brake squeal [
6] or earthquakes [
7,
8].
Several methods exist for suppressing FIVs. One possibility is to reduce the friction force at the interface utilizing a lubricant. This method is efficient if friction is not required for the device to operate, such as in the case of hinge squeaking; however, it cannot be adopted for brake squeal mitigation, where high friction is strictly required. Most brake squeal suppression methods consist of increasing the system damping, which is obtained with various techniques [
6,
9]. Experimental observations also illustrated that isolating the natural frequencies of the brake system’s components at low frequencies tends to reduce the occurrence of audible brake squeal [
10]; however, in many cases, this strategy is not effective [
11]. For active methods for suppressing FIV, Cunefare and Graf [
12] proposed adopting a dither exciting the system at non-audible frequencies, which can suppress brake squeal. Papangelo and Ciavarella [
13] proposed to mitigate FIVs by normal load variation, for which they provided a closed-form solution.
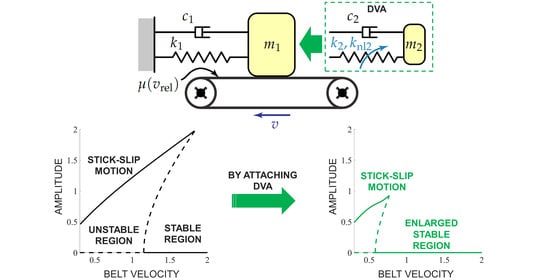
The dynamic vibration absorber (DVA) is a practical tool for suppressing undesired vibrations in several engineering applications. Its classical design [
14] consists of a mass attached to the host structure through a spring and a damper. By tuning its natural frequency in correspondence of the frequency to be damped, it is able to dynamically interact with the host structure dissipating vibration energy. It is successfully employed in several engineering fields for the suppression of various kinds of vibrations, such as flutter instabilities [
15,
16], rolling motions in ships [
17], helicopter rotor oscillations [
18] and machine tool vibrations [
19,
20]. Although DVAs are a mature technology, which was first proposed more than one hundred years ago [
17], to the authors’ knowledge, there are only a few and relatively recent studies addressing its implementation to suppress FIVs. Popp and Rudolph [
21] numerically and experimentally analyzed the performance of a DVA for FIV suppression; by utilizing a single-degree-of-freedom (DoF) primary system, they illustrated its beneficial effect. Chatterjee [
22] studied the stability properties of an undamped DVA attached to a two-DoF primary system. Very recently, Niknam and Farhang [
23] proposed a study similar to that of Chatterjee [
22], where they also provided some numerical simulations of the full system, missing in [
22]. Despite the promising results obtained in [
21,
22,
23], a clear tuning strategy of the DVA’s parameters for maximizing its performance is still missing. This paper aims to fill this gap by providing a precise tuning of the absorber parameters for optimizing stability properties and studying the behavior of the host system with the attached DVA while stability is lost.
The rest of the paper is organized as follows. In
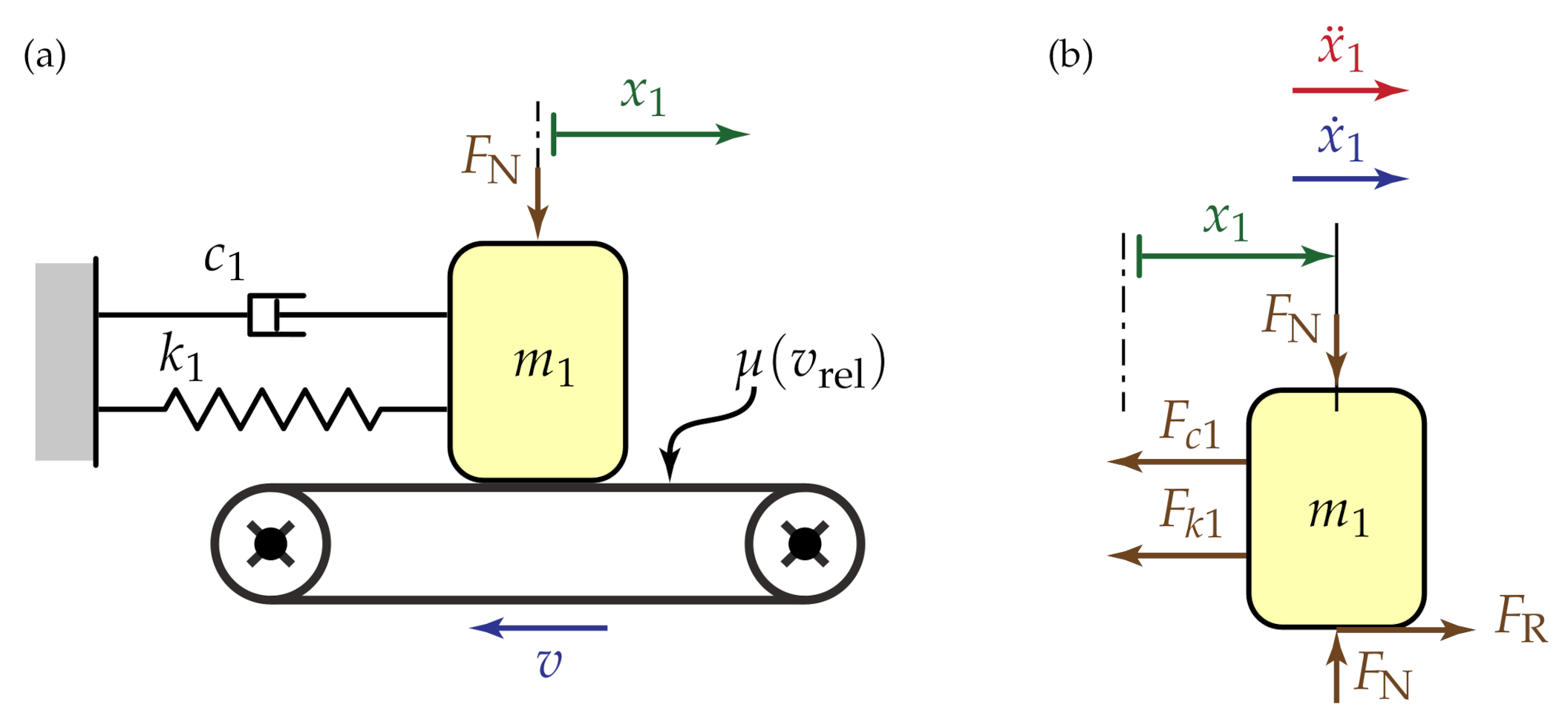
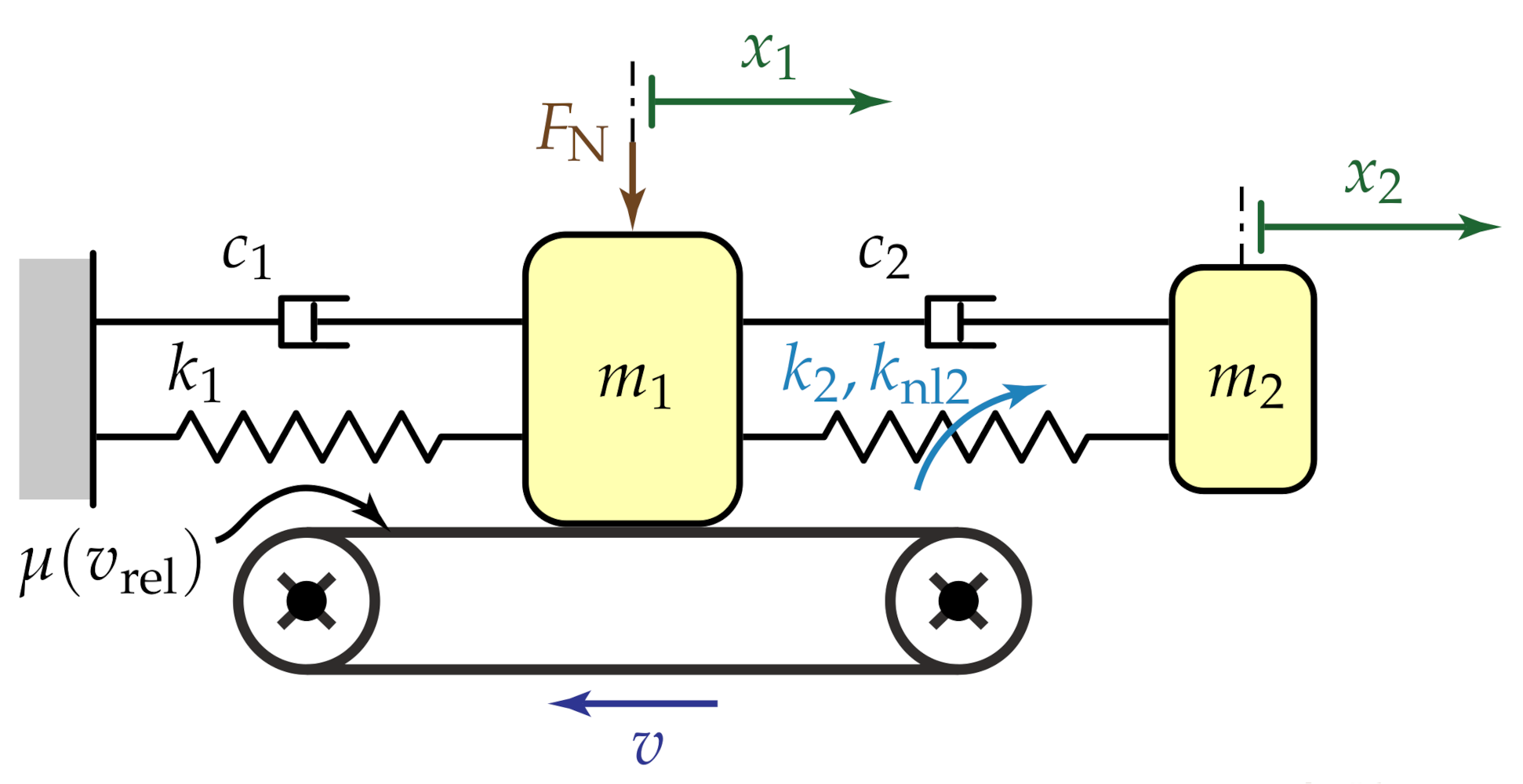
Section 2, the mechanical model, consisting of the host mass-on-moving-belt system and the attached DVA, is introduced. In
Section 3, the stability analysis of the host system, without and with the DVA, is performed, providing explicit equations for the optimal tuning of the absorber parameters. In
Section 4 and
Section 5, the bifurcations occurring at the loss of stability of the host system, without and with absorber, are analytically studied. Furthermore, the effect of the addition of a cubic term in the absorber’s restoring force is analytically investigated; analytical results are integrated by numerical simulation, illustrating the system’s behavior at high amplitudes. In
Section 6, conclusions about the benefits and limitations of the DVA are presented.
4. Bifurcation Analysis of the Host System without the DVA
The analysis performed in
Section 3 refers to the system linearized around its equilibrium. Therefore, it is able to describe its dynamics only in the vicinity of the equilibrium, while phenomena occurring when the stability is lost are overlooked. Additionally, it provides no information about the stable equilibrium’s robustness if the system is subject to non-small perturbations. To investigate the system behavior at the loss of stability and correctly evaluate the DVA performance, we reintroduce the nonlinear terms and analytically perform a bifurcation analysis of the system without and with DVA.
Considering the system in Equation (
5), we first center the system around its equilibrium point
by introducing the variable
, and then we expand it in Taylor series up to the third order, obtaining
For
, matrix
has complex conjugate eigenvalues
and eigenvectors
, which are reduced to
for
.
We then define the transformation matrix
we apply the transformation
and we pre-multiply Equation (
36) by
, leading to
where
For
,
,
is kept as a generic function of
v, since
is the critical term causing the instability. The system in Equation (
39) is in the so-called Jordan normal form.
By performing several transformations, namely transformation in complex form, near-identity transformation and transformation in polar coordinates, the bifurcation can be characterized through its normal form
where
Details of this standard procedure can be found in [
26]. Non-zero real equilibrium solutions of Equation (
41) correspond to periodic motion of the system in Equation (
5). Linearizing
around
, we obtain
which has solutions
The trivial solution
exists for any value
v and it is stable for
. Differently,
is real only if the argument of the square root in Equation (
44) is non-negative, which occurs for
. Since
, in all relevant cases
is positive (see Equation (
42)), which, as clearly explained in [
26], means that the bifurcation is subcritical. This implies that
corresponds to unstable solutions of Equation (
41). This result is in accordance with [
1].
A practical consequence of the subcritical character of the bifurcation is that the system, even within the stable region of the equilibrium (), can experience large oscillations. If the system, while in equilibrium, is subject to a sufficiently large perturbation, which makes it cross the unstable periodic solution in the phase space, it will leave its basin of attraction and it will reach another attractor, which in this case consists of stick–slip oscillations.
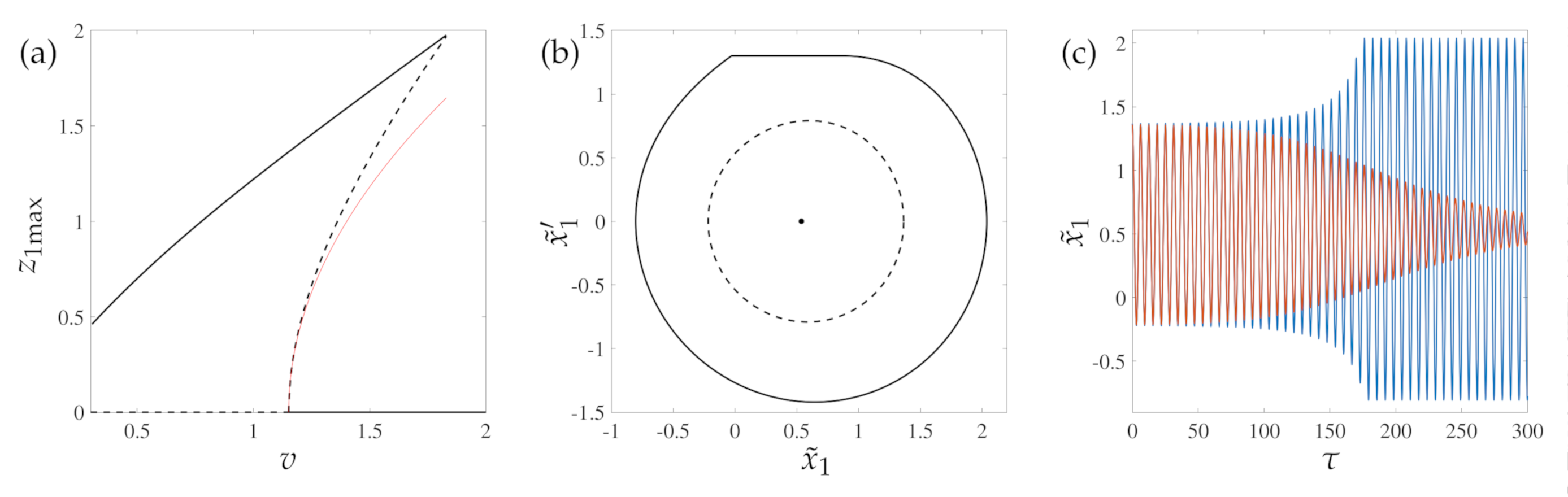
The bifurcation diagram in
Figure 8a clearly illustrates this scenario. The dashed line indicates a branch of unstable periodic solutions generated at the bifurcation (this branch was obtained through time reverse numerical simulations). The solid line, instead, marks the branch of stick–slip oscillation. The thin solid red line represents the branch of unstable periodic solutions obtained from the analytical computation. We remark on the excellent agreement of the analytically computed solution with the numerical one at low amplitudes. For
, the system presents two stable solutions, the trivial one and a stick–slip periodic solution, and an unstable periodic solution, as illustrated in
Figure 8b for
. Depending on the initial conditions, the system will either converge towards the trivial solution (red curve in
Figure 8c) or will undergo stick–slip oscillations (blue curve in
Figure 8c). Numerical solutions were computed utilizing the switch model proposed in [
4].
5. Bifurcation Analysis of the Host System with the DVA
To evaluate the DVA performance when stability is lost, we analyze the bifurcation behavior of the system with an attached DVA. The analysis is performed assuming that
and
are tuned approximately according to Equation (
25). An analysis of the eigenvalues of matrix
illustrates that at the loss of stability, if
and
are tuned approximately according to Equation (
25), a couple of complex conjugate eigenvalues leaves the left-hand side of the complex plane, meaning that their real parts become positive. This scenario corresponds to the occurrence of a Hopf bifurcation. We also notice that, if
and
, not one, but two couples of complex conjugate eigenvalues leave the left-hand side of the complex plane. Referring to the stability chart in
Figure 4a, the entire unstable region matrix
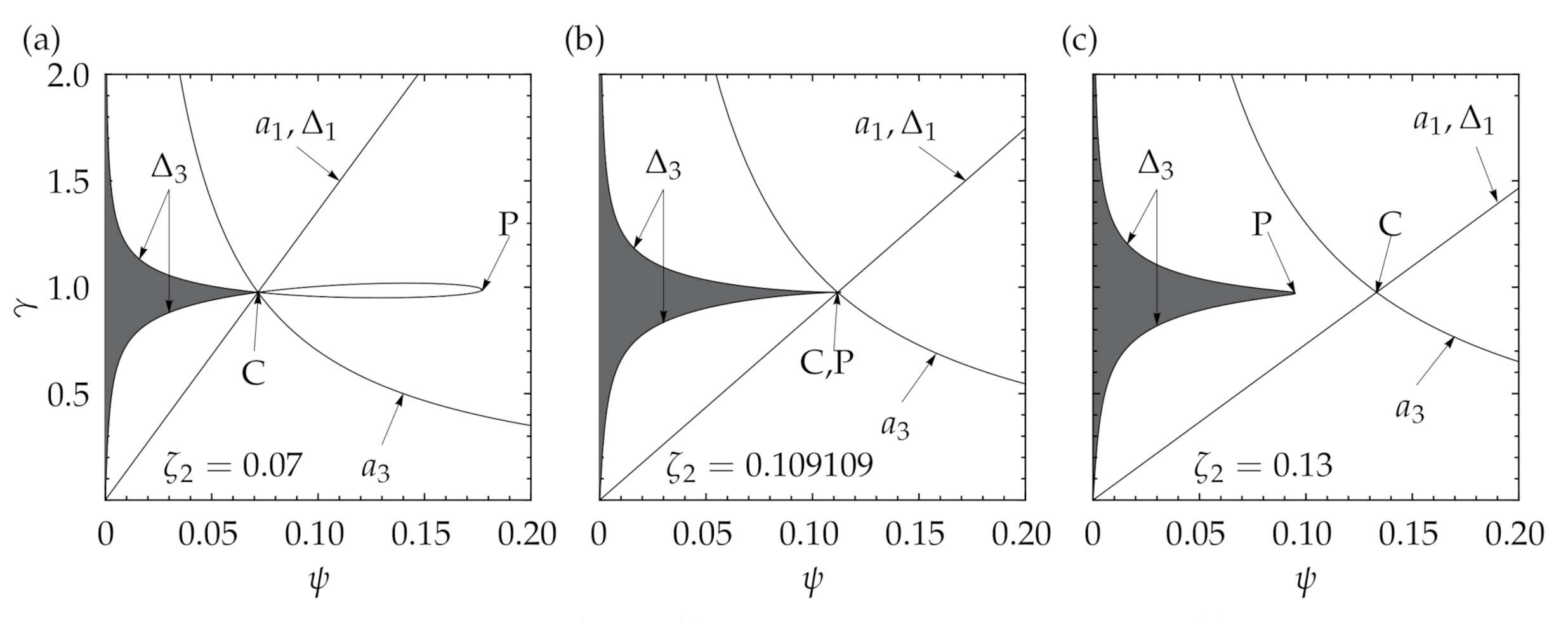
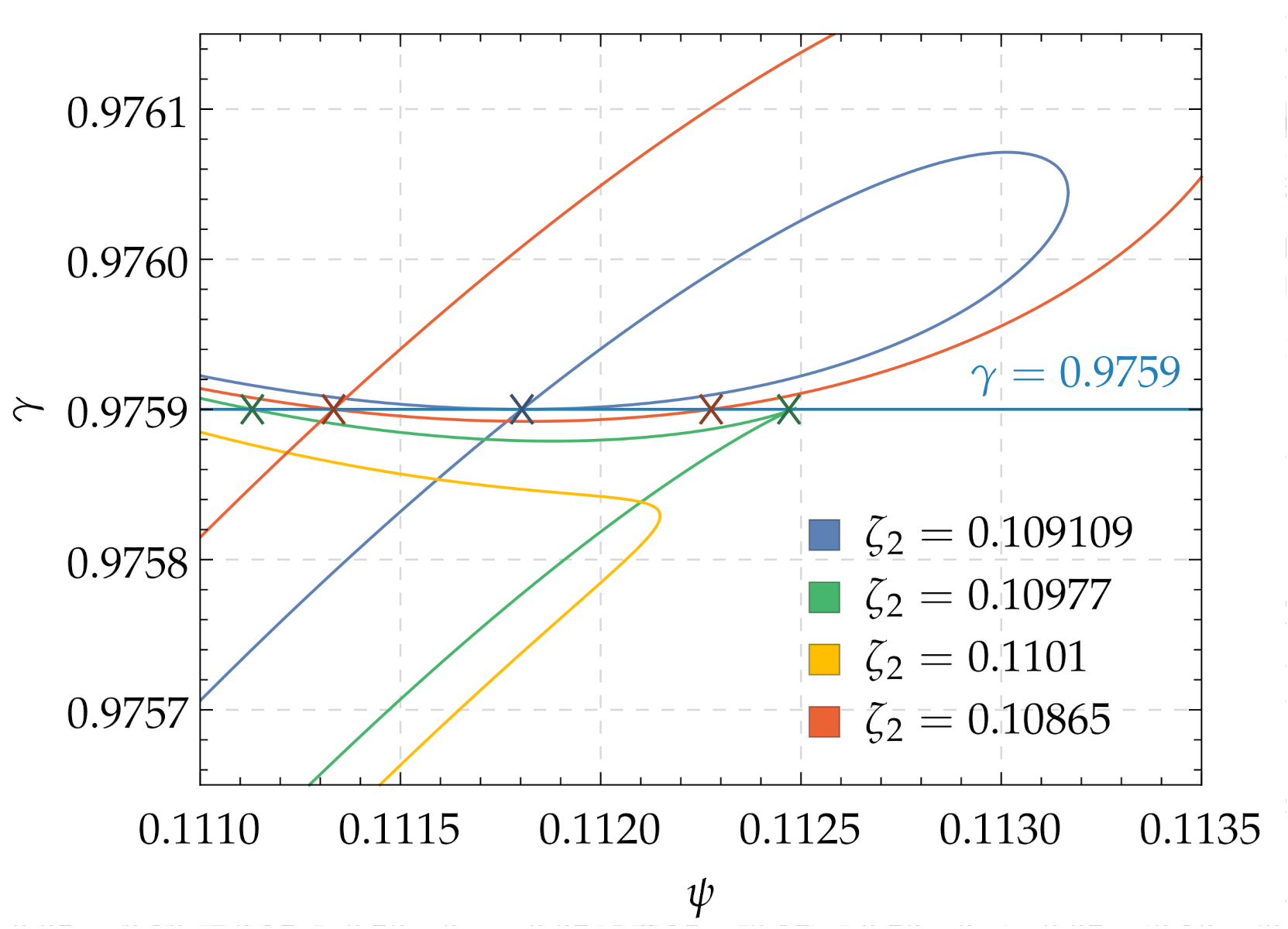
has only one couple of eigenvalues with positive real part, except in the loop delimited by Points C and P, where all four eigenvalues have positive real part. This scenario corresponds to a Hopf–Hopf (or double Hopf) bifurcation. In the following, the case of a single Hopf bifurcation is analyzed.
The first step of the analysis consists of transforming the system in Equation (
9) into first-order form, similar to Equation (
14), but including nonlinear terms up to the third order, which leads to
In the vicinity of the loss of stability,
has two couples of complex conjugate eigenvalues
and
. To decouple the linear part of the system, we define the transformation matrix
where
and
are two of the eigenvectors of
, and we apply the transformation
, obtaining
where
For the sake of brevity, the explicit formulation of is omitted here.
In the case of a single Hopf bifurcation, only
becomes positive at the loss of stability, while
remains negative. Therefore, only the first two equations of Equation (
47) are linearly related to the bifurcation, while
and
have minor local effect at the bifurcation. Next, we aim at reducing the dynamics of the system to the so-called
center manifold, which is a two-dimensional surface tangent at the bifurcation point to the subspace spanned by the two eigenvectors
and
related to the bifurcation. To do so, we approximate
and
by
and
, reducing the system to
where
j and
k are non-negative integers (more details on this procedure can be found in [
26]) and h.o.t. stands for higher order terms.
The system in Equation (
49) has the same form as Equation (
39); therefore, exactly the same steps can be performed to reduce the system to its normal form, that is
where [
26]
Imposing
,
and
, we obtain
Proceeding as done for the host system without DVA, we have that the non-trivial solutions of Equation (
50) is given by
where
. We notice that
is positive if the DVA is linear (
), which means that also in this case the bifurcation is subcritical, and it generates unstable periodic solutions. Analyzing other values of
and
, we verified that the subcritical characteristic persists for a relatively large parameter value range. The corresponding bifurcation diagram is illustrated in
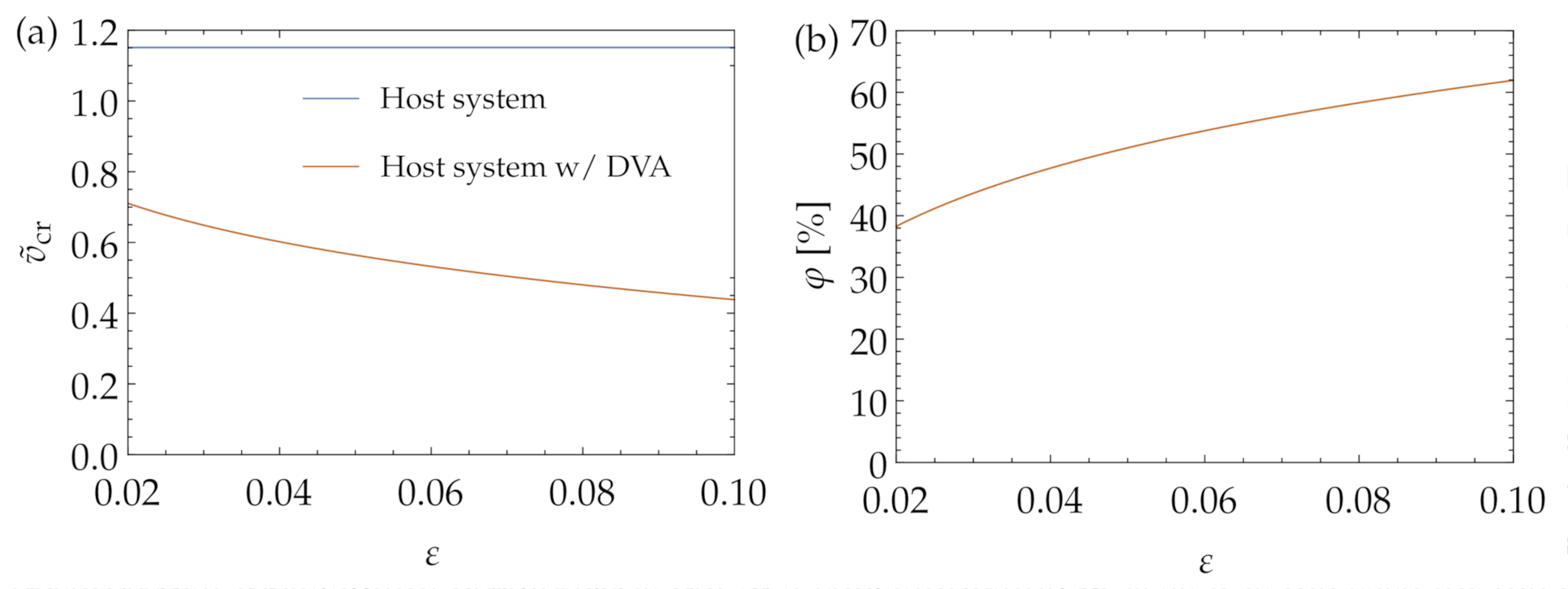
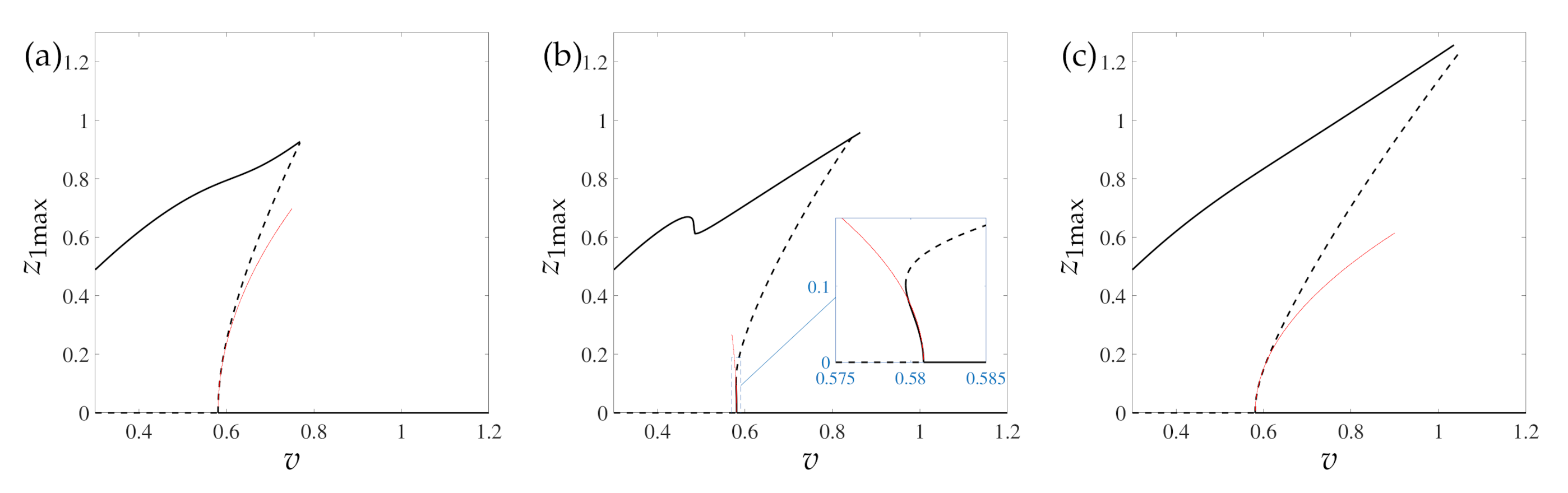
Figure 9a. Comparing
Figure 9a and
Figure 8a, we notice that, although the linear DVA does not change the characteristic of the bifurcation, the advantages in terms of vibrations suppression persist also in the nonlinear range. In fact, for the considered parameter values, in the host system without DVA, stick–slip oscillations exist for
, while, with the addition of the absorber, they are limited to the range
.
Equation (
52) suggests that, if
,
becomes negative, making therefore the bifurcation supercritical. This scenario is confirmed by the bifurcation diagram depicted in
Figure 9b, for
. Although at first sight it seems that the bifurcation is subcritical, the inset illustrates that the bifurcation is indeed supercritical; however, the branch of periodic solutions bends rapidly to the right in correspondence of a fold bifurcation, making the overall scenario similar to the case of
. The figure confirms the correctness of the analytical computation; nevertheless, it also points out that the performed local analysis is unable to capture the global behavior of the system, which is not qualitatively affected by the variation of the nonlinear characteristic of the DVA’s spring. Furthermore, we notice that the addition of the softening nonlinear spring enlarges the bistable range, making stick–slip oscillations exist up to
, instead of 0.768 as in the case of
.
Figure 9c illustrates the bifurcation diagram obtained for a hardening absorber’s spring (
). In this case, the range of existence of stick–slip oscillations is further enlarged, persisting up to
. We also remark that increasing the value of
above 0.01 or decreasing it below −0.01 provided only worse performance than those illustrated in
Figure 9. This result suggests that any low order nonlinearity of the absorber’s stiffness is detrimental concerning the DVA effectiveness. This finding is somehow surprising, considering that in similar applications the addition of a properly tuned nonlinear term in the DVA’s stiffness provided some advantages [
20,
25,
27].
Regarding
Figure 9b, we notice that the branch of stick–slip oscillations presents two folds for
. However, an analysis of the system’s steady state solutions before and after the folds did not reveal any particular detail relevant from an engineering point of view; therefore, the phenomenon was not analyzed in further detail. We also remark that, in
Figure 9b,c, the branches of stable and unstable solutions do not encounter each other at a well defined point, as happens in
Figure 8a, for instance. This is probably related to the fact that the branches of unstable solutions in
Figure 9 were obtained adopting the shooting method (employing
MatCont [
28], a
MATLAB-based toolbox for numerical continuation) of the system smoothed assuming that
is always positive. This assumption makes the considered system unable to exhibit stick–slip oscillations, but keeps it equivalent to the original system for
. In contrast, the stable branches were obtained from direct numerical simulations of the full system. Therefore, inaccuracies of the smoothed system in the proximity of the onset of stick–slip motions are possible.
As mentioned at the beginning of this section, for and , the system undergoes a Hopf–Hopf bifurcation. However, acknowledging the fact that the bifurcation analysis seems to be an inefficient tool for investigating the post-bifurcation behavior of the system, which is dominated by large amplitude oscillations, and considering that the analysis of such a bifurcation requires a significant analytical effort, the detailed investigation of this case is omitted in this study.