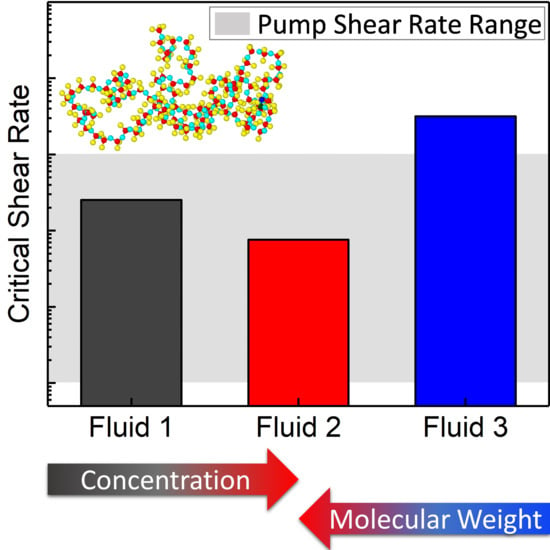
Critical Shear Rate of Polymer-Enhanced Hydraulic Fluids
Abstract
1. Introduction
2. Materials and Methods
2.1. Rheological Measurements
2.2. Molecular Dynamics Simulations
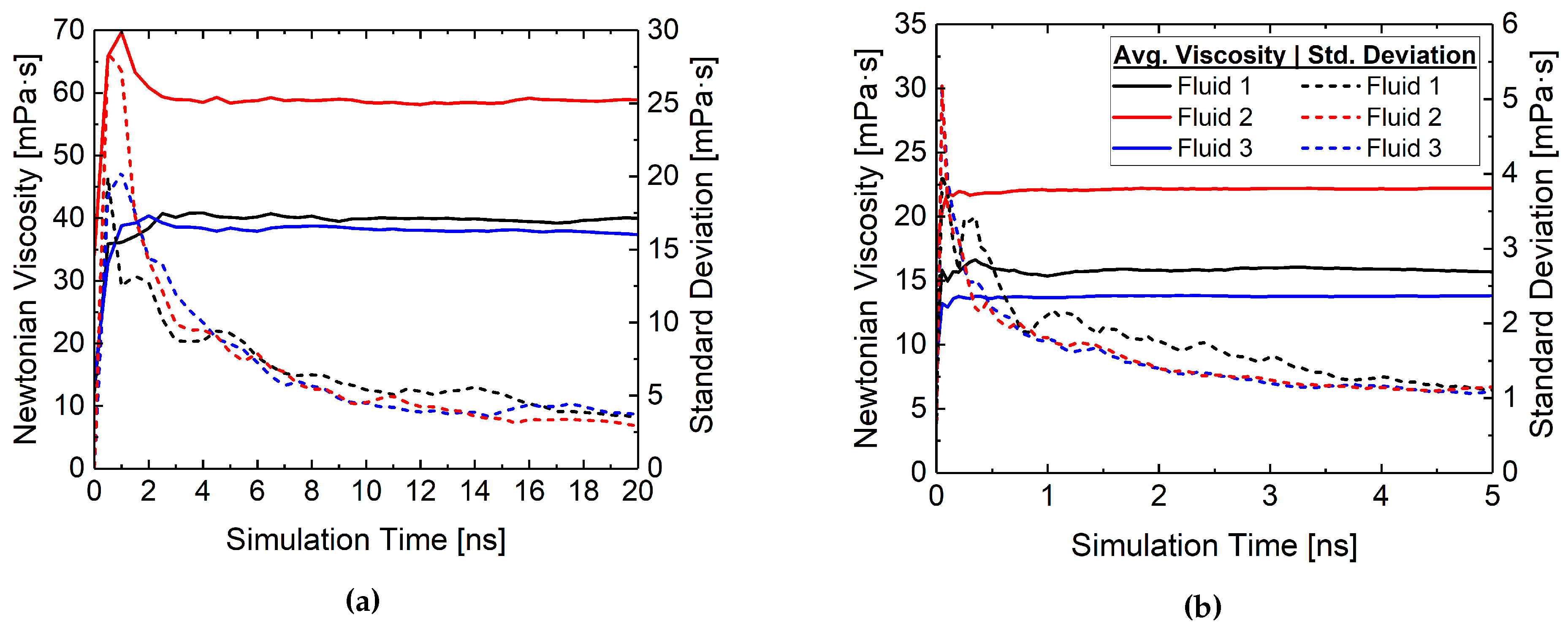
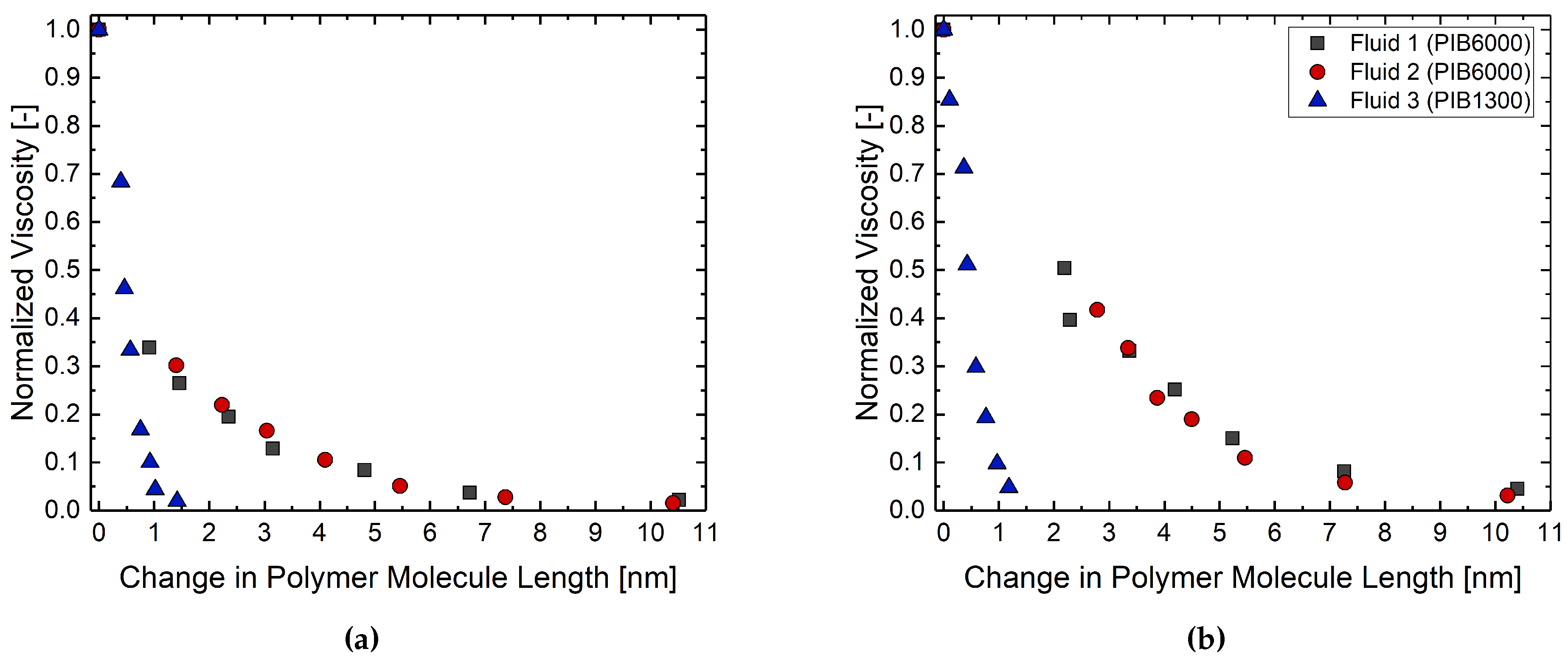
3. Results and Discussion
3.1. Fluid Identification and Formulation
3.2. Rheological Behavior
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| EMD | equilibrium molecular dynamics |
| GK | Green–Kubo |
| MD | molecular dynamics |
| NEMD | non-equilibrium molecular dynamics |
| NPT | isothermal–isobaric ensemble |
| NVE | canonical ensemble |
| NVT | microcanonical ensemble |
| PAO | polyalphaolefin |
| PAO2 | polyalphaolefin of 2 mm/s at 100 C |
| PAO4 | polyalphaolefin of 4 mm/s at 100 C |
| PAO8 | polyalphaolefin of 8 mm/s at 100 C |
| PIB | polyisobutylene |
| PIB1300 | polyisobutylene of 1300 g/mol |
| PIB6000 | polyisobutylene of 6000 g/mol |
| TraPPE | transferable potentials for phase equilibria |
| UA | united atom |
| VI | viscosity index |
| VM | viscosity modifier |
| Nomenclature | |
| concentration of polymer | |
| concentration of of solvent or base oil | |
| Boltzmann constant | |
| M | molecular weight |
| n | power-law exponent |
| pressure or stress tensor | |
| shear stress | |
| universal gas constant | |
| T | temperature |
| velocity of atoms in the x-direction | |
| V | volume |
| Weissenberg number | |
| shear viscosity of fluid | |
| Newtonian viscosity of fluid | |
| Newtonian viscosity of polymer | |
| Newtonian viscosity of solvent or base oil | |
| viscosity at infinite shear rate of fluid | |
| shear rate | |
| critical shear rate | |
| time constant or rotational relaxation time | |
| mass density | |
| density of polymer | |
| density of solvent or base oil | |
| flow gradient or momentum flux |
References
- McGuire, N.; Michael, P. Efficient hydraulic systems deliver the power. Tribol. Lubr. Technol. 2016, 72, 36. [Google Scholar]
- Michael, P.W.; Khalid, H.; Wanke, T. An Investigation of External Gear Pump Efficiency and Stribeck Values; Technical Report, SAE Technical Paper; SAE: Warrendale, PA, USA, 2012. [Google Scholar]
- Mettakadapa, S.; Bair, S.; Aoki, S.; Kobessho, M.; Carter, L.; Kamimura, H.; Michael, P.W. A fluid property model for piston pump case drain and pressure compensator flow losses. In Proceedings of the ASME/BATH 2015 Symposium on Fluid Power and Motion Control, Chicago, IL, USA, 12–14 October 2015; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2015. [Google Scholar]
- Görlitzer, H.; Alibert, M.; Herzog, S.; Neveu, C. Dependence of Pump Flow Rate on the Viscosity of High VI Hydraulics Fluids. In Proceedings of the 15th International Colloquium Tribology, Stuttgart/Ostfildern, Germany, 17–19 January 2006; Technische Akademie Esslingen: Ostfildern, Germany, 2006. [Google Scholar]
- Devlin, M.T.; Senn, J.; Turner, T.L.; Milner, J.; Jao, T.C. Reduction in axle oil operating temperatures by fluids with optimized torque transfer efficiencies. Lubr. Sci. 2006, 18, 7–23. [Google Scholar] [CrossRef]
- Michael, P.W.; Garcia, J.M.; Bair, S.S.; Devlin, M.T.; Martini, A. Lubricant Chemistry and Rheology Effects on Hydraulic Motor Starting Efficiency. Tribol. Trans. 2012, 55, 549–557. [Google Scholar] [CrossRef]
- Michael, P.; Cheekolu, M.; Panwar, P.; Devlin, M.; Davidson, R.; Johnson, D.; Martini, A. Temporary and Permanent Viscosity Loss Correlated to Hydraulic System Performance. Tribol. Trans. 2018, 61, 901–910. [Google Scholar] [CrossRef]
- Ver Strate, G.; Struglinski, M. Polymers as Lubricating-Oil Viscosity Modifiers; ACS Publications: Washington, DC, USA, 1991. [Google Scholar]
- Cai, G.; Zhang, L.; Ma, L.; Eli, W. Synthesis and characterization of polybutylacrylate viscosity index improver with anti-wear function. Lubr. Sci. 2015, 27, 209–216. [Google Scholar] [CrossRef]
- Martini, A.; Ramasamy, U.S.; Len, M. Review of Viscosity Modifier Lubricant Additives. Tribol. Lett. 2018, 66, 58. [Google Scholar] [CrossRef]
- Rizvi, S. A Comprehensive Review of Lubricant Chemistry, Technology, Selection, and Design; ASTM International: West Conshohocken, PA, USA, 2009. [Google Scholar]
- Holtzinger, J.; Green, J.; Lamb, G.; Atkinson, D.; Spikes, H. New method of measuring permanent viscosity loss of polymer-containing lubricants. Tribol. Trans. 2012, 55, 631–639. [Google Scholar] [CrossRef]
- Covitch, M.J. How polymer architecture affects permanent viscosity loss of multigrade lubricants. SAE Trans. 1998, 107, 1881–1894. [Google Scholar]
- Bezot, P.; Hesse-Bezot, C.; Faure, D.; Calvez, J. The effect of mechanical stress on four viscosity improver polymers. Lubr. Sci. 2000, 12, 301–312. [Google Scholar] [CrossRef]
- Bartz, W.J. Influence of viscosity index improver, molecular weight, and base oil on thickening, shear stability, and evaporation losses of multigrade oils. Lubr. Sci. 2000, 12, 215–237. [Google Scholar] [CrossRef]
- Wang, J.; Ye, Z.; Zhu, S. Topology-engineered hyperbranched high-molecular-weight polyethylenes as lubricant viscosity-index improvers of high shear stability. Ind. Eng. Chem. Res. 2007, 46, 1174–1178. [Google Scholar] [CrossRef]
- Campbell, K.; Erck, R.A.; Swita, M.; Cosimbescu, L. Multifunctional Tunable Polymethacrylates for Enhanced Shear Stability and Wear Prevention. ACS Appl. Polym. Mater. 2020. [Google Scholar] [CrossRef]
- Bhattacharya, P.; Ramasamy, U.S.; Krueger, S.; Robinson, J.W.; Tarasevich, B.J.; Martini, A.; Cosimbescu, L. Trends in thermoresponsive behavior of lipophilic polymers. Ind. Eng. Chem. Res. 2016, 55, 12983–12990. [Google Scholar] [CrossRef]
- Fenske, M.; Klaus, E.; Dannenbrink, R. Viscosity-Shear Behavior of Two Non-Newtonian Polymer-Blended Oils. In Proceedings of the Symposium on Methods of Measuring Viscosity at High Rates of Shear, Washington, DC, USA, 24 February 1950; ASTM International: West Conshohocken, PA, USA, 1951. [Google Scholar]
- ASTM International. D5621-20 Standard Test Method for Sonic Shear Stability of Hydraulic Fluids; ASTM International: West Conshohocken, PA, USA, 2020. [Google Scholar]
- Coordinating European Council. 45–99: Viscosity Shear Stability of Transmission Lubricants (Taper Roller Bearing Rig); Technical Report; Coordinating European Council: Brussels, Belgium, 2014. [Google Scholar]
- Cui, S.; Cummings, P.; Cochran, H.; Moore, J.; Gupta, S. Nonequilibrium molecular dynamics simulation of the rheology of linear and branched alkanes. Int. J. Thermophys. 1998, 19, 449–459. [Google Scholar] [CrossRef]
- Bair, S.; McCabe, C.; Cummings, P.T. Comparison of Nonequilibrium Molecular Dynamics with Experimental Measurements in the Nonlinear Shear-thinning Regime. Phys. Rev. Lett. 2002, 88, 058302. [Google Scholar] [CrossRef] [PubMed]
- Bair, S.S. High Pressure Rheology for Quantitative Elastohydrodynamics; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Panwar, P.; Len, M.; Gajghate, N.; Michael, P.; Martini, A. Fluid Effects on Mechanical Efficiency of Hydraulic Pumps: Dynamometer Measurements and Molecular Simulations. In Proceedings of the ASME/BATH 2019 Symposium on Fluid Power and Motion Control, Longboat Key, FL, USA, 7–9 October 2019; Volume FPMC2019-1712, p. 10. [Google Scholar]
- Kremer, K.; Grest, G.S. Dynamics of Entangled Linear Polymer Melts: A Molecular-Dynamics Simulation. J. Chem. Phys. 1990, 92, 5057–5086. [Google Scholar] [CrossRef]
- Mondello, M.; Grest, G.S. Viscosity Calculations of n-alkanes by Equilibrium Molecular Dynamics. J. Chem. Phys. 1997, 106, 9327–9336. [Google Scholar] [CrossRef]
- Mondello, M.; Grest, G.S.; Webb, E.B., III; Peczak, P. Dynamics of n-alkanes: Comparison to Rouse model. J. Chem. Phys. 1998, 109, 798–805. [Google Scholar] [CrossRef]
- Shimida, T.; Horng, P.L.; Porter, R.S. Broad Shear Range Viscometry of High Polymer Solutions: Polystyrene and Polyisobutene in Decalin. J. Rheol. 1980, 24, 783–797. [Google Scholar] [CrossRef]
- Zolper, T.J.; Seyam, A.M.; Chen, C.; Jungk, M.; Stammer, A.; Stoegbauer, H.; Marks, T.J.; Chung, Y.W.; Wang, Q. Energy efficient siloxane lubricants utilizing temporary shear-thinning. Tribol. Lett. 2013, 49, 525–538. [Google Scholar] [CrossRef]
- Tanner, R.I. Engineering Rheology; Oxford University Press: Oxford, UK, 2000; Volume 52. [Google Scholar]
- Rouse, P.E., Jr. A theory of the linear viscoelastic properties of dilute solutions of coiling polymers. J. Chem. Phys. 1953, 21, 1272–1280. [Google Scholar] [CrossRef]
- Rouse, P., Jr.; Sittel, K. Viscoelastic properties of dilute polymer solutions. J. Appl. Phys. 1953, 24, 690–696. [Google Scholar] [CrossRef]
- de Gennes, P.G. Reptation of a polymer chain in the presence of fixed obstacles. J. Chem. Phys. 1971, 55, 572–579. [Google Scholar] [CrossRef]
- De Gennes, P.G.; Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- de Gennes, P.G. Dynamics of fluctuations and spinodal decomposition in polymer blends. J. Chem. Phys. 1980, 72, 4756–4763. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F.; Edwards, S.F. The Theory of Polymer Dynamics; Oxford University Press: Oxford, UK, 1988; Volume 73. [Google Scholar]
- Mondello, M.; Grest, G.S.; Garcia, A.R.; Silbernagel, B.G. Molecular Dynamics of Linear and Branched Alkanes: Simulations and Nuclear Magnetic Resonance Results. J. Chem. Phys. 1996, 105, 5208–5215. [Google Scholar] [CrossRef]
- Ewen, J.P.; Gattinoni, C.; Thakkar, F.M.; Morgan, N.; Spikes, H.A.; Dini, D. A Comparison of Classical Force-Fields for Molecular Dynamics Simulations of Lubricants. Materials 2016, 9, 651. [Google Scholar] [CrossRef]
- Jadhao, V.; Robbins, M.O. Probing large viscosities in glass-formers with nonequilibrium simulations. Proc. Natl. Acad. Sci. USA 2017, 114, 7952–7957. [Google Scholar] [CrossRef]
- Jadhao, V.; Robbins, M.O. Rheological properties of liquids under conditions of elastohydrodynamic lubrication. Tribol. Lett. 2019, 67, 66. [Google Scholar] [CrossRef]
- Martin, M.G.; Siepmann, J.I. Transferable potentials for phase equilibria. 1. United-atom description of n-alkanes. J. Phys. Chem. B 1998, 102, 2569–2577. [Google Scholar] [CrossRef]
- Martin, M.G.; Siepmann, J.I. Novel configurational-bias Monte Carlo method for branched molecules. Transferable potentials for phase equilibria. 2. United-atom description of branched alkanes. J. Phys. Chem. B 1999, 103, 4508–4517. [Google Scholar] [CrossRef]
- Wick, C.D.; Martin, M.G.; Siepmann, J.I. Transferable potentials for phase equilibria. 4. United-atom description of linear and branched alkenes and alkylbenzenes. J. Phys. Chem. B 2000, 104, 8008–8016. [Google Scholar] [CrossRef]
- Dinpajooh, M.; Nitzan, A. Heat conduction in polymer chains with controlled end-to-end distance. J. Chem. Phys. 2020, 153, 164903. [Google Scholar] [CrossRef] [PubMed]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef] [PubMed]
- Reiher, W., III. Theoretical Studies of Hydrogen Bonding. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 1985. [Google Scholar]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- NOSÉ, S.U.I. A Molecular Dynamics Method for Simulations in the Canonical Ensemble. Mol. Phys. 2002, 100, 191–198. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical Dynamics: Equilibrium Phase-Space Distributions. Phys. Rev. A 1985, 31, 1695. [Google Scholar] [CrossRef] [PubMed]
- Maginn, E.J.; Messerly, R.A.; Carlson, D.J.; Roe, D.R.; Elliott, J.R. Best practices for computing transport properties 1. Self-diffusivity and viscosity from equilibrium molecular dynamics [article v1. 0]. Living J. Comput. Mol. Sci 2019, 1, 1–20. [Google Scholar] [CrossRef]
- Zhang, Y.; Otani, A.; Maginn, E.J. Reliable viscosity calculation from equilibrium molecular dynamics simulations: A time decomposition method. J. Chem. Theory Comput. 2015, 11, 3537–3546. [Google Scholar] [CrossRef] [PubMed]
- Ewen, J.; Heyes, D.; Dini, D. Advances in Nonequilibrium Molecular Dynamics Simulations of Lubricants and Additives. Friction 2018, 6, 349–386. [Google Scholar] [CrossRef]
- Todd, B.D.; Daivis, P.J. Nonequilibrium Molecular Dynamics: Theory, Algorithms and Applications; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Zhmud, B. Viscosity blending equations. Lube Mag. 2014, 121, 24–29. [Google Scholar]
- Fetters, L.J.; Graessley, W.; Kiss, A. Viscoelastic properties of polyisobutylene melts. Macromolecules 1991, 24, 3136–3141. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers; John Wiley & Sons: Hoboken, NJ, USA, 1980. [Google Scholar]
- Bair, S.; Winer, W.O. A quantitative test of the Einstein–Debye relation using the shear dependence of viscosity for low molecular weight liquids. Tribol. Lett. 2007, 26, 223. [Google Scholar] [CrossRef]
- Bird, R.B.; Curtiss, C.F.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids, Volume 2: Kinetic Theory; Wiley: Hoboken, NJ, USA, 1987. [Google Scholar]
- Grandelli, H.E.; Dickmann, J.S.; Devlin, M.T.; Hassler, J.C.; Kiran, E. Volumetric Properties and Internal Pressure of Poly (α-olefin) Base Oils. Ind. Eng. Chem. Res. 2013, 52, 17725–17734. [Google Scholar] [CrossRef]
- Rach, S.F.; Kühn, F.E. On the Way to Improve the Environmental Benignity of Chemical Processes: Novel Catalysts for a Polymerization Process. Sustainability 2009, 1, 35–42. [Google Scholar] [CrossRef]
- Carreau, P.J. Rheological equations from molecular network theories. Trans. Soc. Rheol. 1972, 16, 99–127. [Google Scholar] [CrossRef]

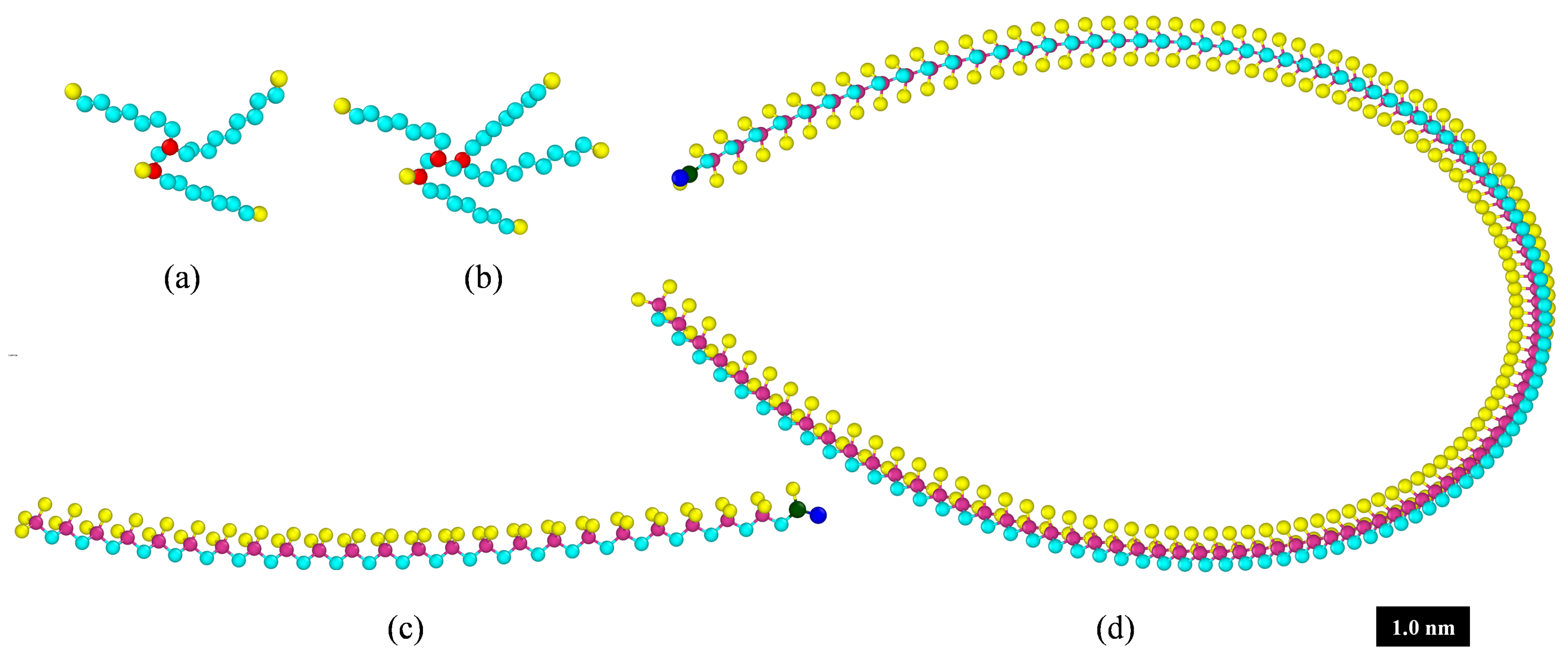

| Fluid ID | Fluid 1 | Fluid 2 | Fluid 3 |
|---|---|---|---|
| PAO4 | 88 wt.% | 84 wt.% | - |
| PAO8 | - | - | 88 wt.% |
| PIB1300 | - | - | 12 wt.% |
| PIB6000 | 12 wt.% | 16 wt.% | - |
| Fluid ID | Fluid 1 | Fluid 2 | Fluid 3 |
|---|---|---|---|
| Decene trimer, CH | 261 | 244 | - |
| Decene tetramer, CH | 196 | 168 | 386 |
| Polymer, PIB1300 (CH) | - | - | 22 |
| Polymer, PIB6000 (CH) | 5 | 6 | - |
| Temperature | Fluid ID | Viscosity (mPa·s) | |
|---|---|---|---|
| Experiment | Simulation | ||
| 50 C | Fluid 1 | 40.2 | 39.7 ± 4.0 |
| Fluid 2 | 62.3 | 58.9 ± 3.2 | |
| Fluid 3 | 35.45 | 38.6 ± 3.4 | |
| 80 C | Fluid 1 | 15.9 | 15.7 ± 1.1 |
| Fluid 2 | 22.3 | 23.1 ± 1.0 | |
| Fluid 3 | 13.5 | 14.3 ± 1.0 | |
| Temperature | Fluid ID | Critical Shear Rate (1/s) | |
|---|---|---|---|
| Experimental/Simulation | Prediction | ||
| 50 C | Fluid 1 | ||
| Fluid 2 | |||
| Fluid 3 | |||
| 80 C | Fluid 1 | ||
| Fluid 2 | |||
| Fluid 3 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panwar, P.; Michael, P.; Devlin, M.; Martini, A. Critical Shear Rate of Polymer-Enhanced Hydraulic Fluids. Lubricants 2020, 8, 102. https://doi.org/10.3390/lubricants8120102
Panwar P, Michael P, Devlin M, Martini A. Critical Shear Rate of Polymer-Enhanced Hydraulic Fluids. Lubricants. 2020; 8(12):102. https://doi.org/10.3390/lubricants8120102
Chicago/Turabian StylePanwar, Pawan, Paul Michael, Mark Devlin, and Ashlie Martini. 2020. "Critical Shear Rate of Polymer-Enhanced Hydraulic Fluids" Lubricants 8, no. 12: 102. https://doi.org/10.3390/lubricants8120102
APA StylePanwar, P., Michael, P., Devlin, M., & Martini, A. (2020). Critical Shear Rate of Polymer-Enhanced Hydraulic Fluids. Lubricants, 8(12), 102. https://doi.org/10.3390/lubricants8120102