Numerical Simulation of a Slipper Model with Multi-Lands and Grooves for Hydraulic Piston Pumps and Motors in Mixed Lubrication
Abstract
:1. Introduction
2. Theoretical Model
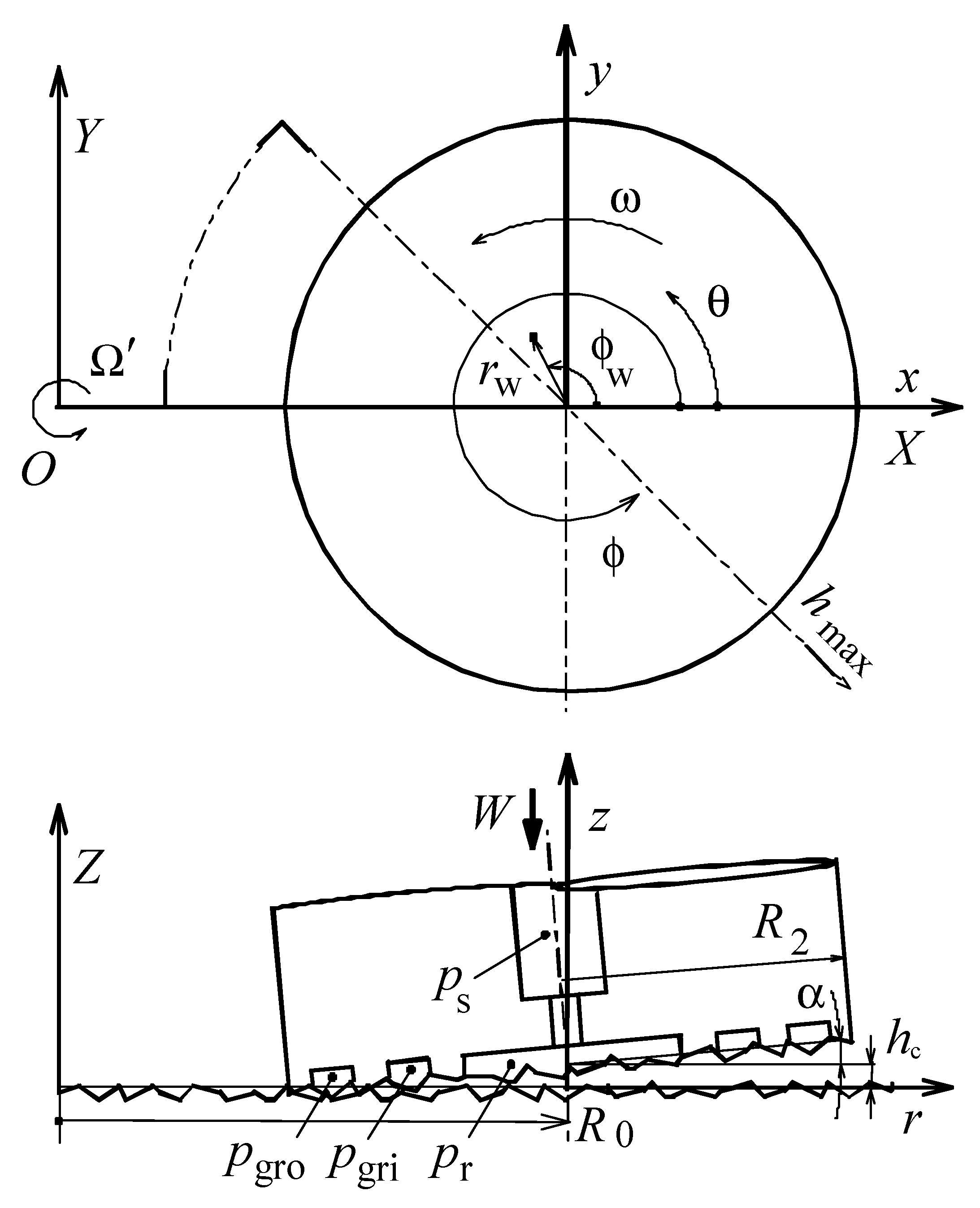
2.1. Basic Equations
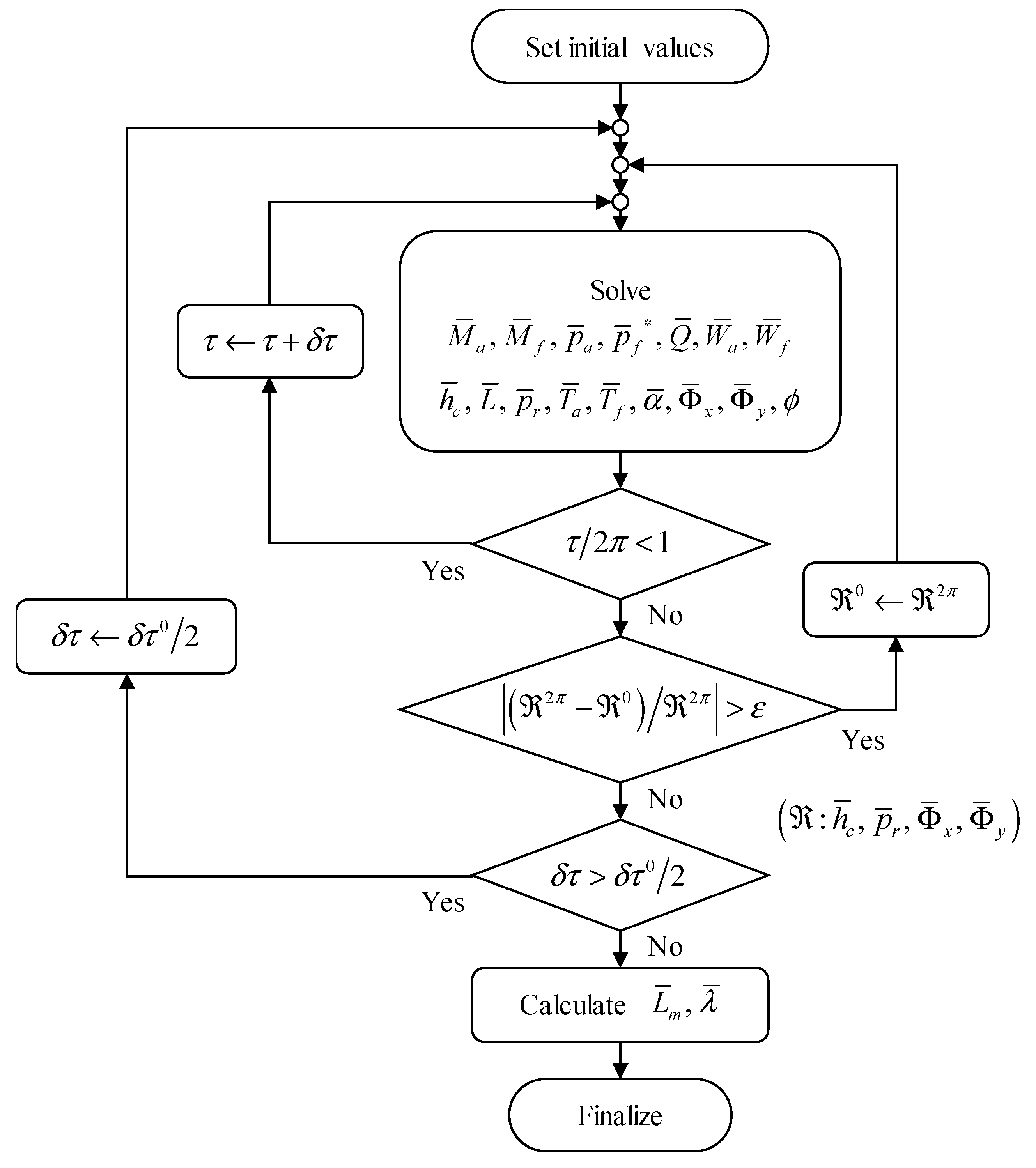
2.2. Calculation Procedure
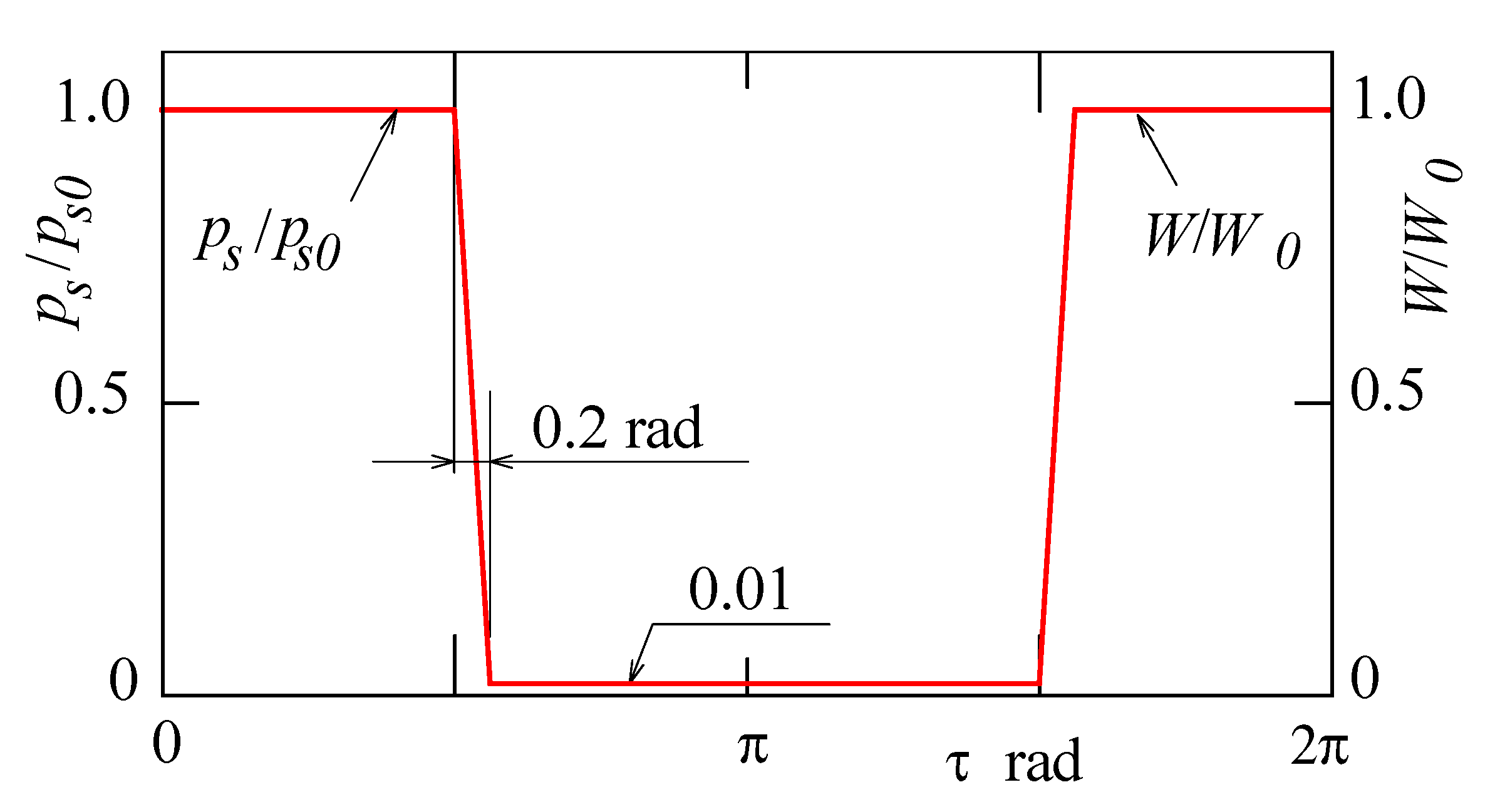
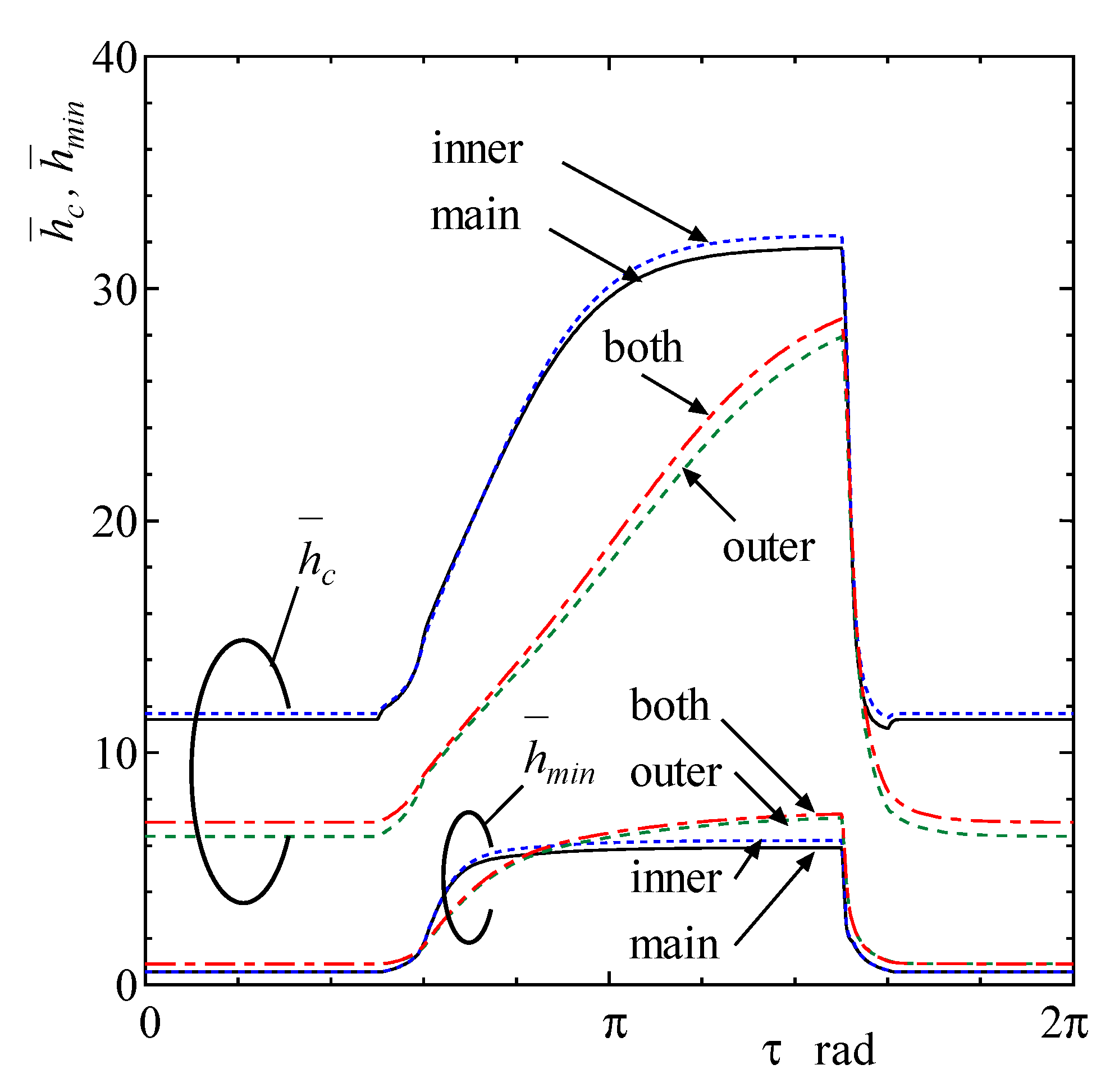
3. Results and Discussion
4. Discussion
5. Conclusions
Funding
Conflicts of Interest
Nomenclature
| inner radius ratio of main land, = | |
| outer radius ratio of main land, = | |
| inner radius ratio of inner land, = | |
| outer radius ratio of inner land, = | |
| inner radius ratio of outer land, = | |
| outer radius ratio of outer land, = | |
| separation | |
| equivalent elastic modulus, = | |
| H | representative clearance |
| hardness, = | |
| h | clearance, = |
| center thickness | |
| mean film thickness | |
| moment inertia, = | |
| bulk modulus | |
| power loss, = | |
| moment, = | |
| mass, = | |
| pressure, = | |
| ambient pressure, = | |
| recess pressure, = | |
| supply pressure, = | |
| Q | flow rate, = |
| leaked flow rate, = | |
| revolution radius | |
| representative radius | |
| coordinates, = r/R2, θ, z/H | |
| load eccentricity | |
| parameter, = | |
| friction torque, = | |
| recess volume, = | |
| load, = | |
| plasticity index | |
| coordinates | |
| coordinates | |
| pad inclination angle, = | |
| restrictor parameter, = | |
| equivalent radius of asperity summit | |
| hydrostatic balance ratio | |
| asperity density | |
| stiffness, = | |
| viscosity | |
| surface roughness, = | |
| standard deviation of asperity summit height | |
| time, = | |
| pad azimuth | |
| representative angular velocity | |
| disk angular velocity | |
| pad angular velocity | |
| Subscripts: | |
| a | asperity, contact |
| c | center |
| f | fluid |
| gri | inner groove |
| gro | outer groove |
| in | inner land |
| m | time-average |
| max | maximum |
| min | minimum |
| mn | main land |
| out | outer land |
| r | recess |
| 0 | reference, high pressure period |
| 1 | inside |
| 2 | outside |
Appendix A
Appendix B
References
- Shute, N.A.; Turnbull, D.E. Minimum power loss of hydrostatic slipper bearings for axial piston machines. Proc. Int. Conv. Lubr. Wear 1963, 6, 3–14. [Google Scholar]
- Böinghoff, O. Untersuchen zum Reibungsverhalten der Gleitschuhe in Schrägscheiben-Axialkolbenmascinen. VDI Forsch. 1977, 584, 1–46. [Google Scholar]
- Iboshi, N.; Yamaguchi, A. Characteristics of a slipper bearing for swash plate type axial piston pumps and motors: 1st report, theoretical analysis. Bull. Jpn. Soc. Mech. Eng. 1982, 25, 1921–1930. [Google Scholar] [CrossRef]
- Koç, E.; Hooke, C.J. Considerations in the design of partially hydrostatic slipper bearings. Tribol. Int. 1997, 30, 815–823. [Google Scholar] [CrossRef]
- Manring, N.D. The relative motion between the ball guide and slipper retainer within an axial-piston swash-plate type hydrostatic pump. J. Dyn. Syst. Meas. Control Trans. ASME 1999, 121, 518–523. [Google Scholar] [CrossRef]
- Suzuki, K.; Suzuki, M.; Sakurai, S.; Hemmi, M.; Kazama, T. Multi body dynamics of a slipper in swash plate type piston pumps and motors couples with hydrodynamic analysis of oil-film. Bull. Jpn. Soc. Mech. Eng. 2014, 80, FE0224. (In Japanese) [Google Scholar] [CrossRef]
- Schenk, A.; Ivantysynova, M.A. Transient thermoelastohydrodynamic lubrication model for the slipper/swashplate in axial piston machines. J. Tribol. Trans. ASME 2015, 137, 031701–031710. [Google Scholar] [CrossRef]
- Lin, S.; Hu, J. Tribo-dynamic model of slipper bearings. Appl. Math. Model. 2015, 39, 548–558. [Google Scholar] [CrossRef]
- Hashemi, S.; Kroker, A.; Bobach, L.; Bartel, D. Multibody dynamics of pivot slipper pad thrust bearing in axial piston machines incorporating thermal elastohydrodynamics and mixed lubrication model. Tribol. Int. 2016, 96, 57–76. [Google Scholar] [CrossRef]
- Bergada, J.M.; Watton, J.; Haynes, J.M.; Davies, D.L. The hydrostatic/hydrodynamic behaviour of an axial piston pump slipper with multiple lands. Meccanica 2010, 45, 58–602. [Google Scholar] [CrossRef]
- Chen, J.; Ma, J.; Li, J.; Fu, Y. Performance optimization of grooved slippers for aero hydraulic pumps. Chin. J. Aeronaut. 2016, 29, 814–823. [Google Scholar] [CrossRef] [Green Version]
- Schenk, A.T. Predicting Lubrication Performance between the Slipper and Swashplate in Axial Piston Hydraulic Machines. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2014. [Google Scholar]
- Kazama, T. Mathematical modeling of a multi-land slipper for swash-plate type axial piston pumps and motors. In Proceedings of the 5th China-Japan Joint Workshop on Fluid Power, Beijing, China, 23 July 2018; pp. 46–50. [Google Scholar]
- Tang, H.; Yin, Y.; Ren, Y.; Xiang, J.; Chen, J. Impact of the thermal effect on the load-carrying capacity of a slipper pair for an aviation axial-piston pump. Chin. J. Aeronaut. 2018, 31, 395–409. [Google Scholar] [CrossRef]
- Hashemi, S.; Friedrich, H.; Bobach, L.; Bartel, D. Validation of a thermal elastohydrodynamic multibody dynamics model of the slipper pad by friction force measurement in the axial piston pump. Tribol. Int. 2017, 115, 319–337. [Google Scholar] [CrossRef]
- Kazama, T. Thermohydrodynamic lubrication model applicable to a slipper of swashplate type axial piston pumps and motors (Effects of operating conditions). Tribol. Online 2010, 5, 250–254. [Google Scholar] [CrossRef]
- Yamaguchi, A.; Matsuoka, H. A mixed lubrication model applicable to bearing/seal parts of hydraulic equipment. J. Tribol. Trans. ASME 1992, 114, 116–121. [Google Scholar] [CrossRef]
- Kazama, T.; Yamaguchi, A. Application of a mixed lubrication model for hydrostatic thrust bearings of hydraulic equipment. J. Tribol. Trans. ASME 1993, 115, 686–691. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. 1996, 295, 300–319. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication. J. Lubr. Technol. Trans. ASME 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Application of average flow model to lubrication between rough sliding surfaces. J. Lubr. Technol. Trans. ASME 1979, 101, 220–230. [Google Scholar] [CrossRef]
- Kazama, T.; Yamaguchi, A. Experiment on mixed lubrication of hydrostatic thrust bearings for hydraulic equipment. J. Lubr. Technol. Trans. ASME 1995, 117, 399–402. [Google Scholar] [CrossRef]
- Kazama, T. Numerical simulation of a slipper model for water hydraulic pumps/motors in mixed lubrication. In Proceedings of the 6th JFPS International Symposium on Fluid Power, Tsukuba, Japan, 7–10 November 2005. [Google Scholar] [CrossRef]
- Kazama, T. Numerical simulation of a slipper with retainer for axial piston pumps and motors under swashplate vibration. JFPS Int. J. Fluid Power Syst. 2017, 10, 18–23. [Google Scholar] [CrossRef]


| Parameter | Value | Unit |
|---|---|---|
| 0.5 | ||
| 0.6 | ||
| 0.7 | ||
| 0.8 | ||
| 0.9 | ||
| 1 | ||
| 1 | GPa | |
| 100 | g | |
| 2.4 | ||
| 12.5 | mm | |
| 0.3 | mm | |
| 0.08 | ||
| 1.1 | ||
| 28 | mPa·s | |
| 875 | kg/m3 | |
| 1 | μm |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kazama, T. Numerical Simulation of a Slipper Model with Multi-Lands and Grooves for Hydraulic Piston Pumps and Motors in Mixed Lubrication. Lubricants 2019, 7, 55. https://doi.org/10.3390/lubricants7070055
Kazama T. Numerical Simulation of a Slipper Model with Multi-Lands and Grooves for Hydraulic Piston Pumps and Motors in Mixed Lubrication. Lubricants. 2019; 7(7):55. https://doi.org/10.3390/lubricants7070055
Chicago/Turabian StyleKazama, Toshiharu. 2019. "Numerical Simulation of a Slipper Model with Multi-Lands and Grooves for Hydraulic Piston Pumps and Motors in Mixed Lubrication" Lubricants 7, no. 7: 55. https://doi.org/10.3390/lubricants7070055




