Film Thickness and Shape Evaluation in a Cam-Follower Line Contact with Digital Image Processing
Abstract
:1. Introduction
2. Materials and Methods
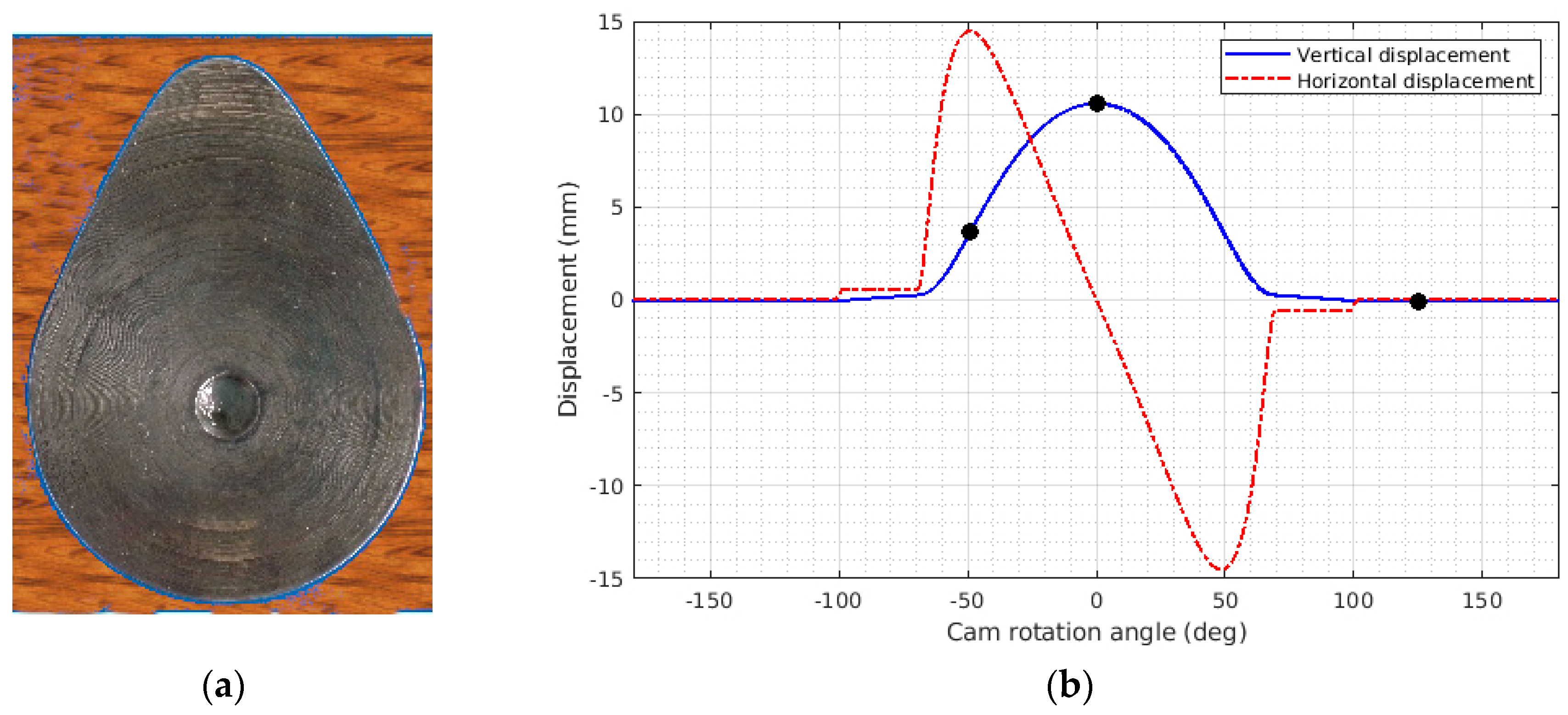
2.1. Experimental Test Rig
2.2. Film Thickness Measurement Procedures
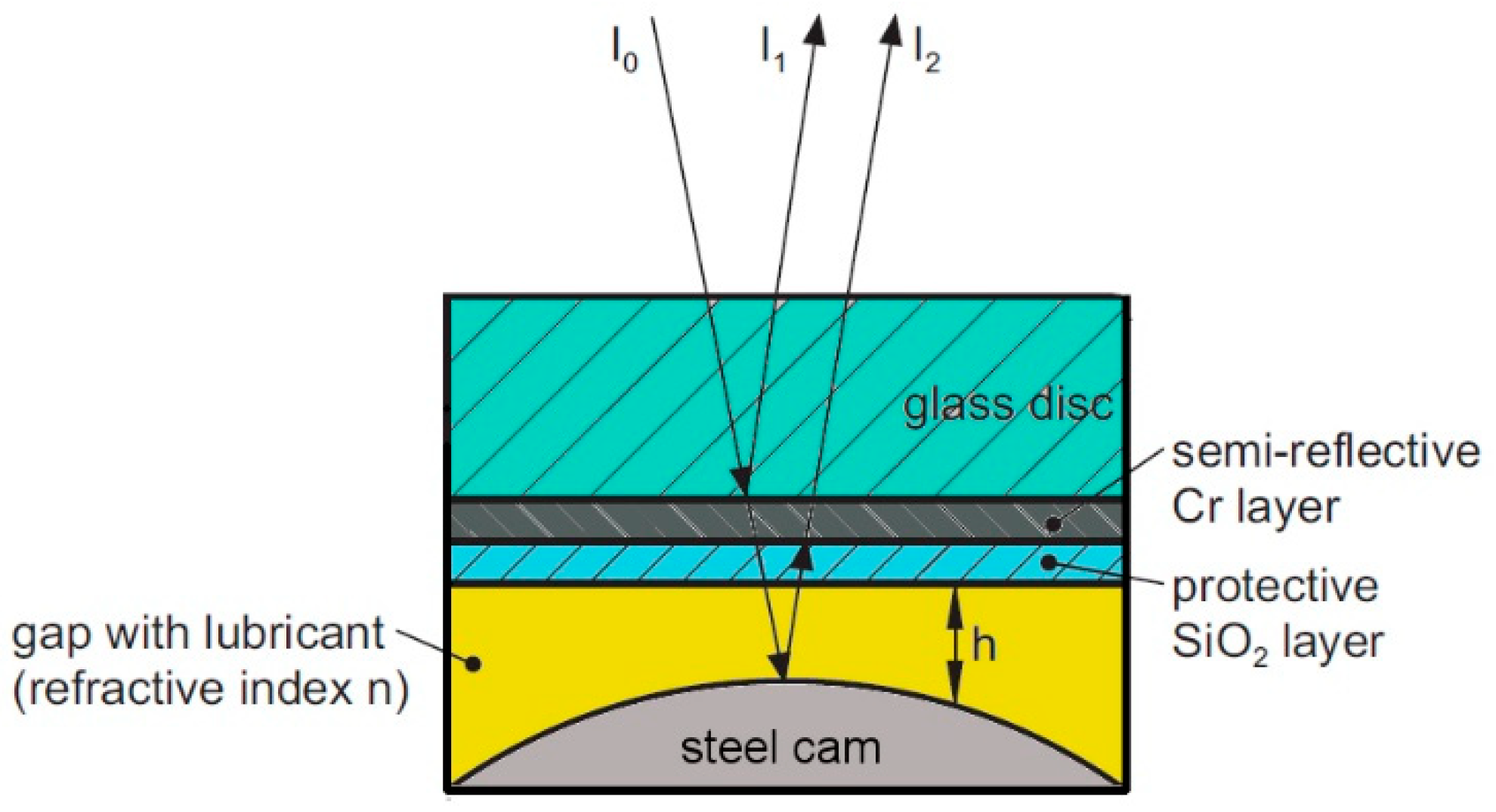
2.2.1. Fundamentals of Optical Interferometry
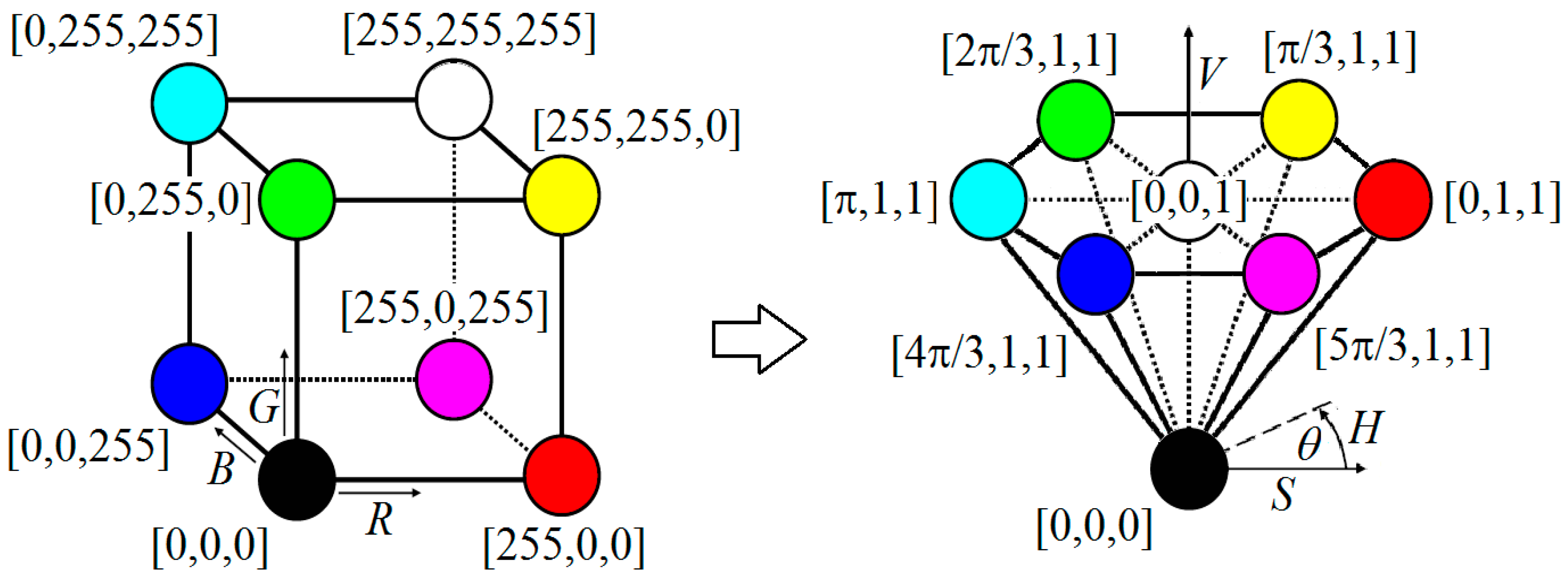
2.2.2. Color Spaces in Optical Interferometry
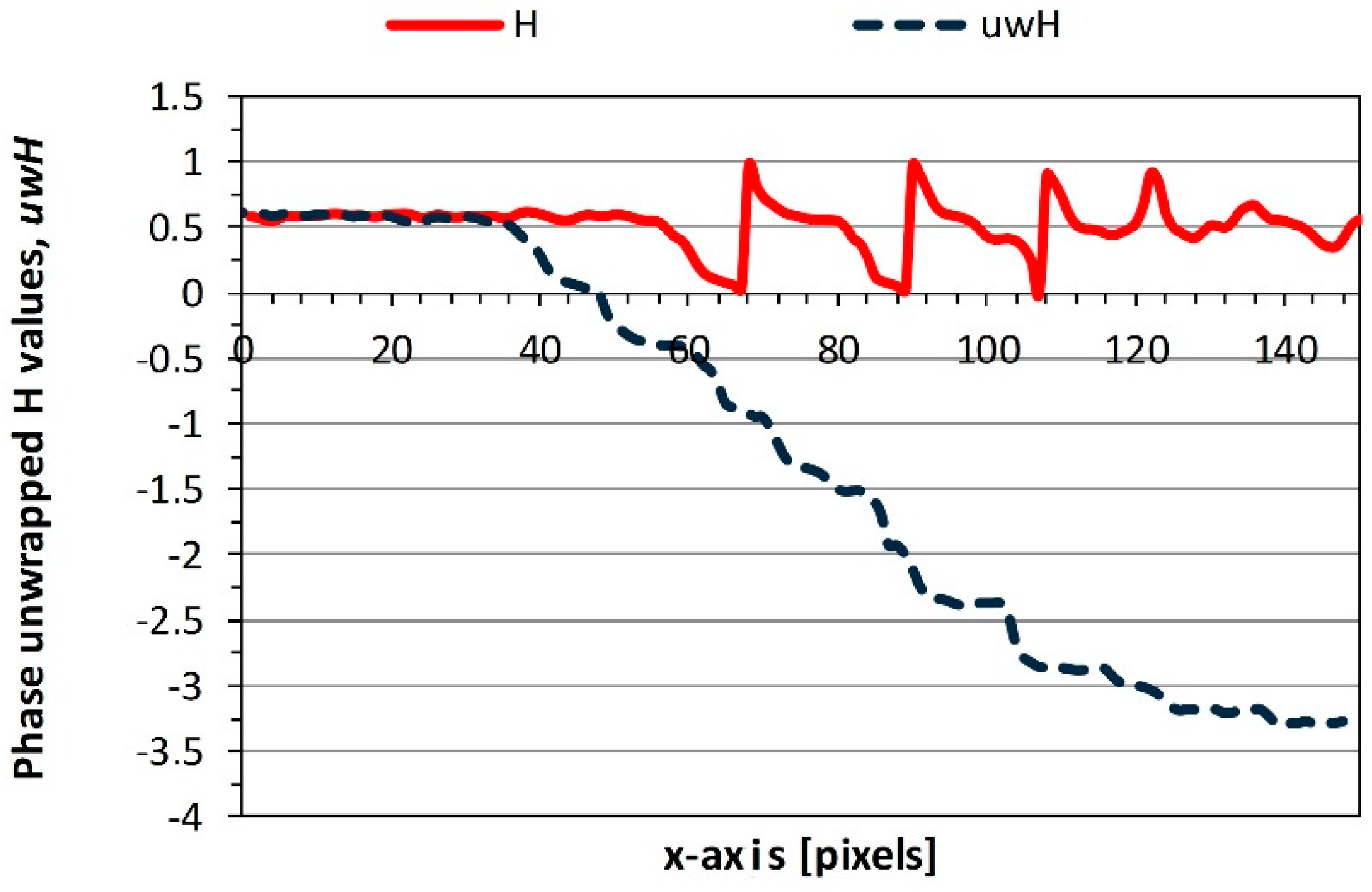
2.2.3. Elaboration of the Hue Signal
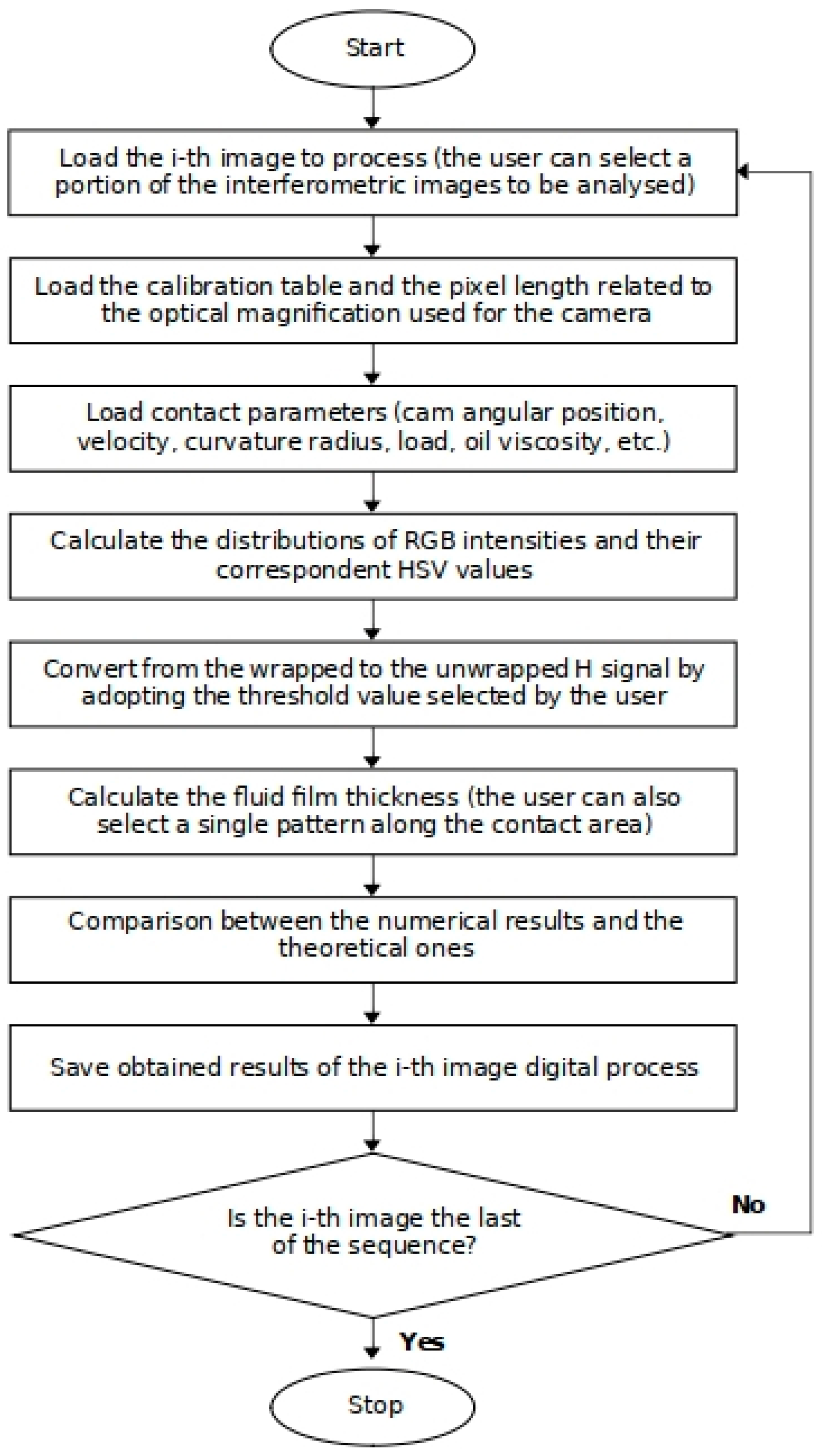
2.2.4. The Image Processing Program
3. Results
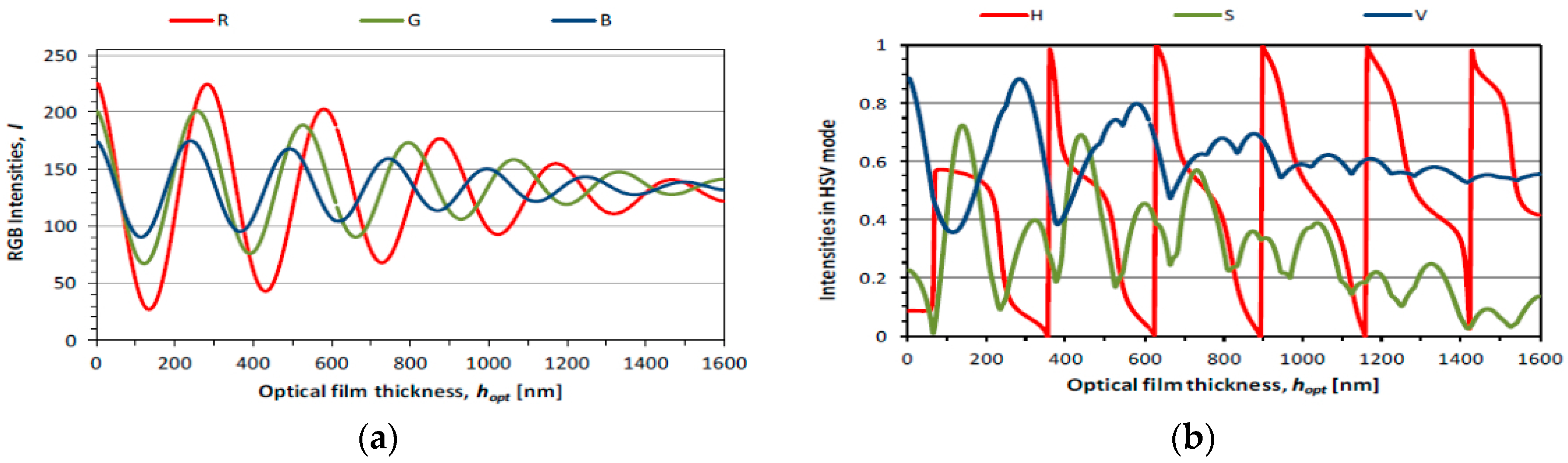
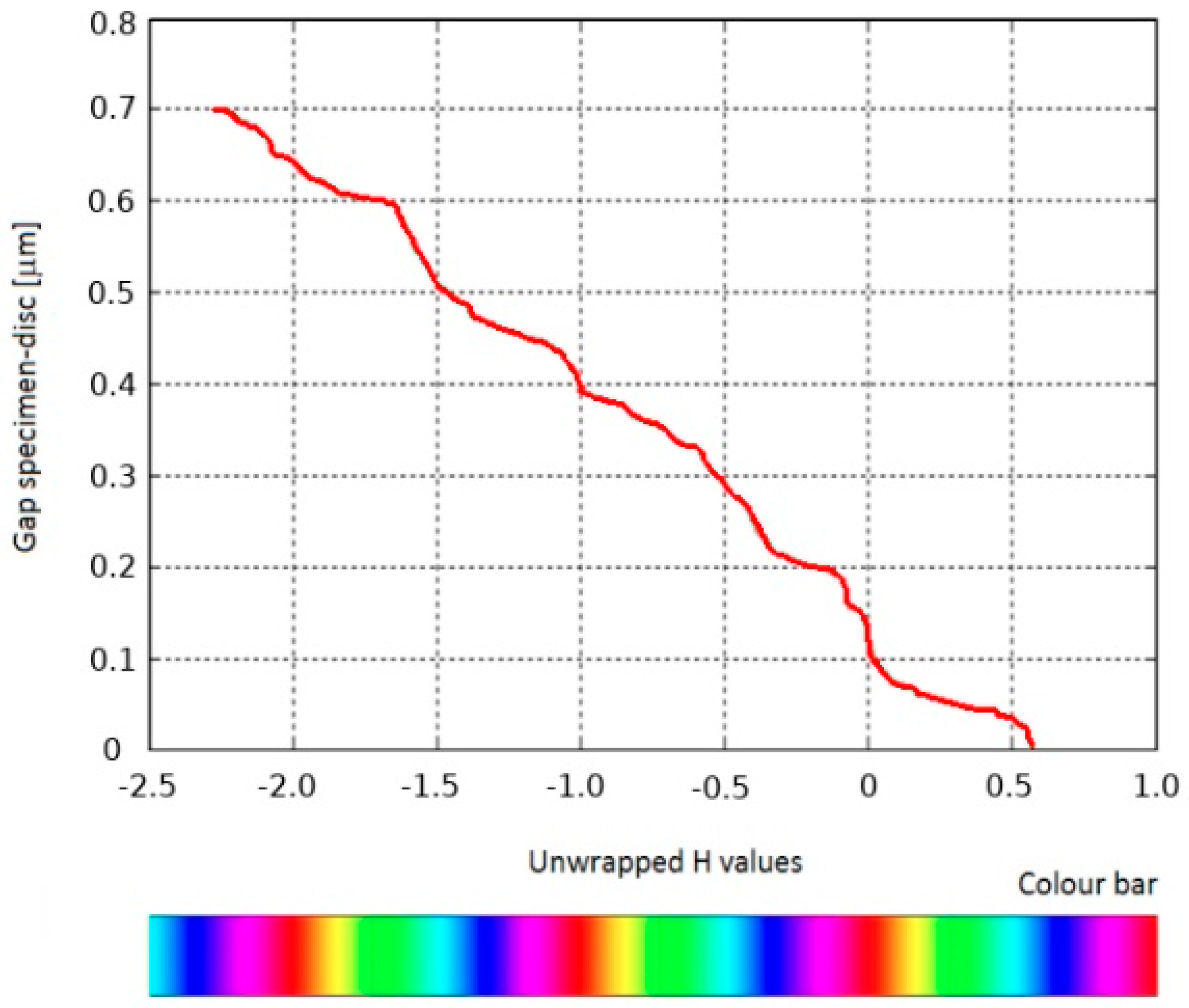
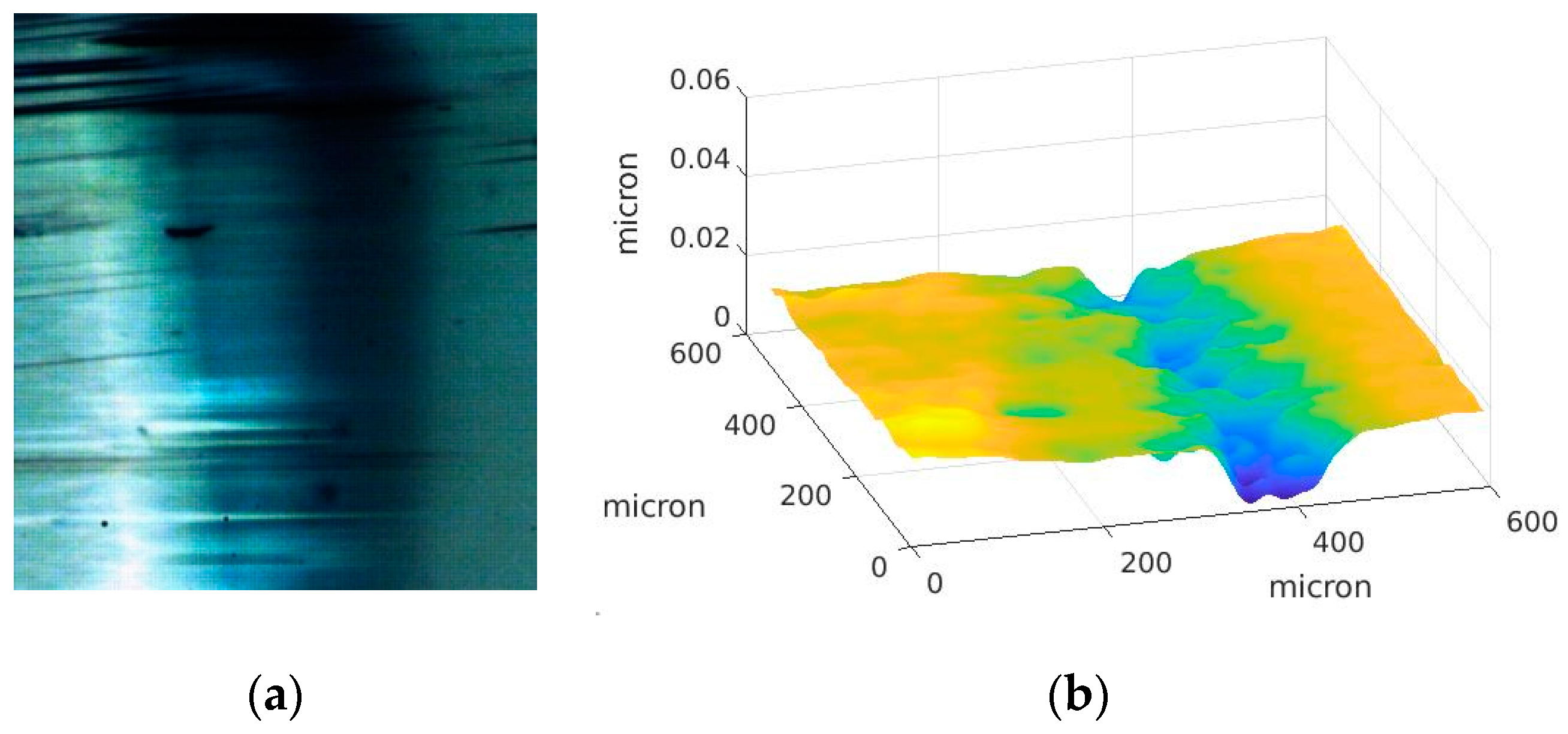
3.1. Calibration
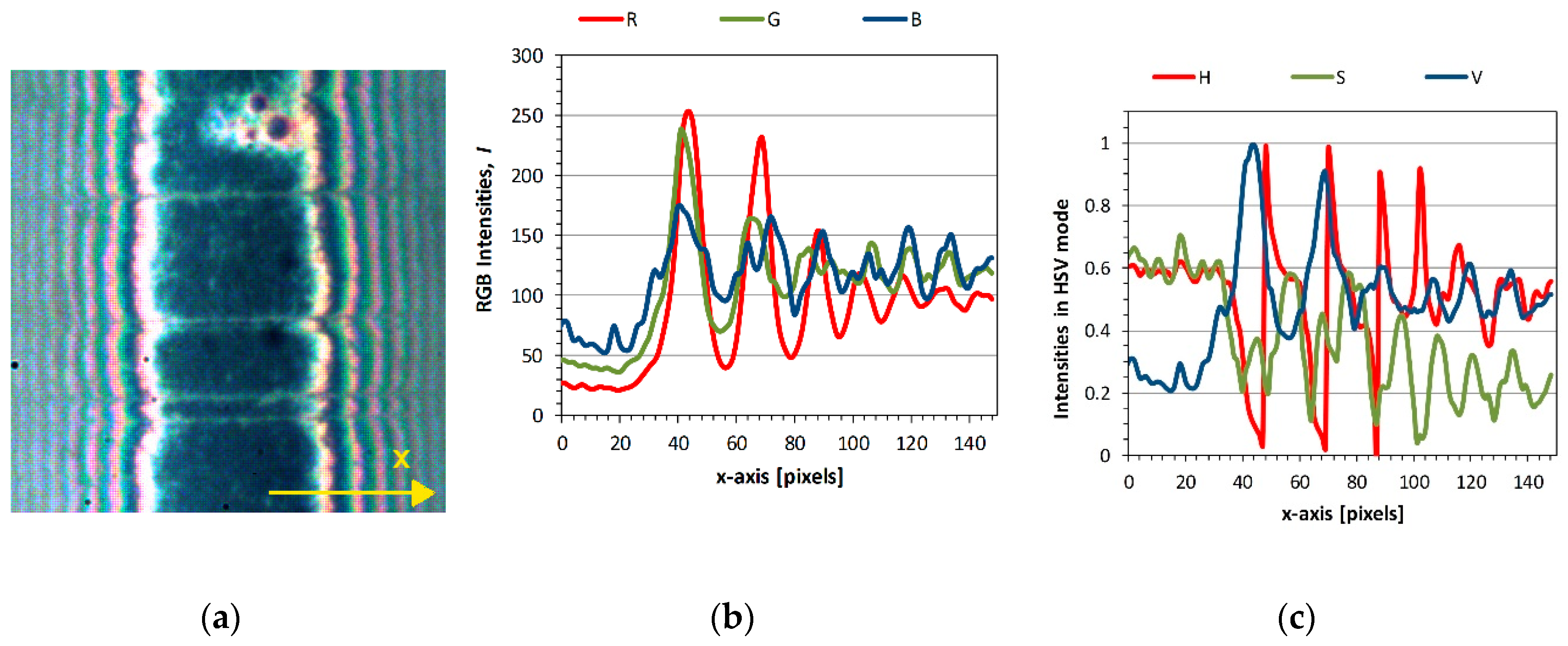
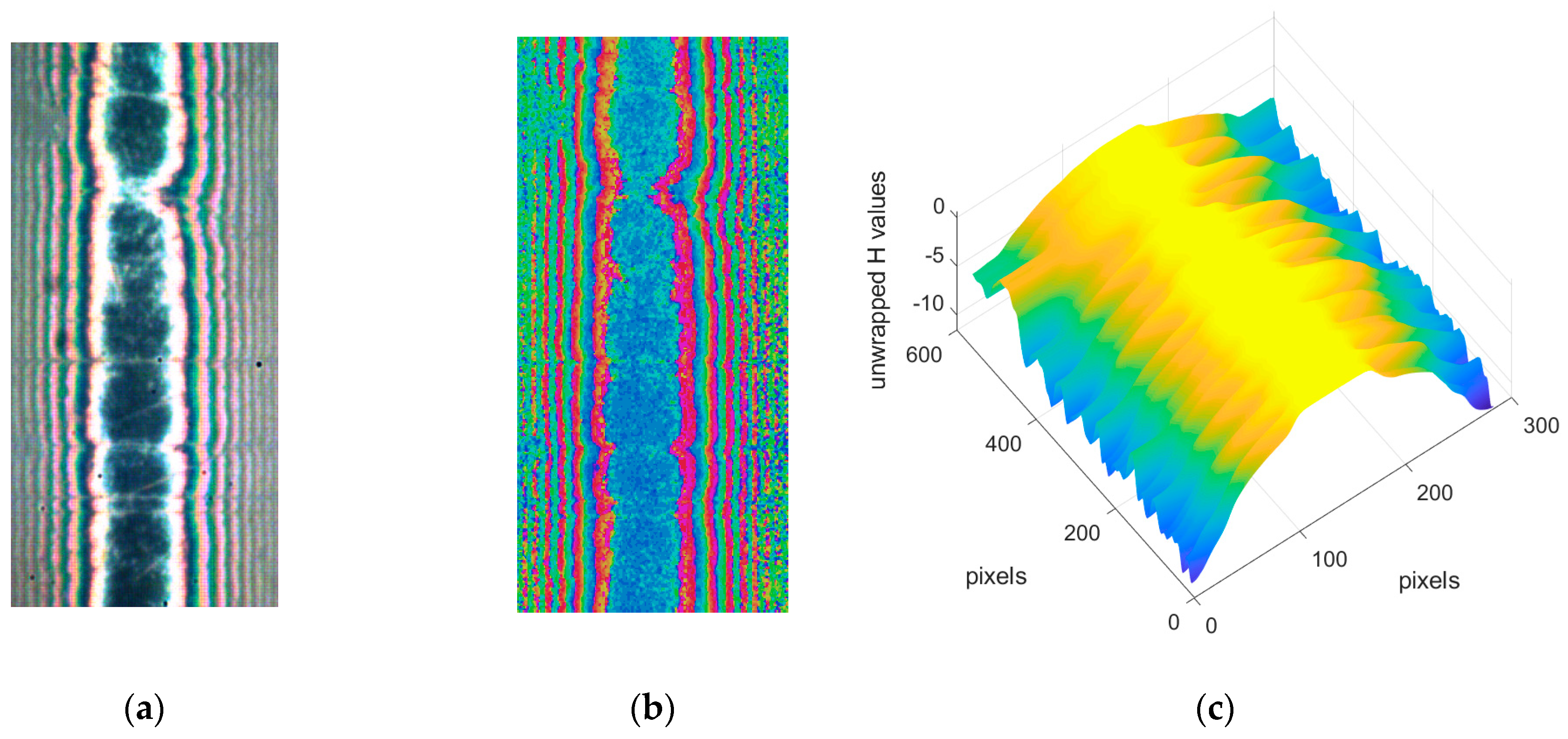
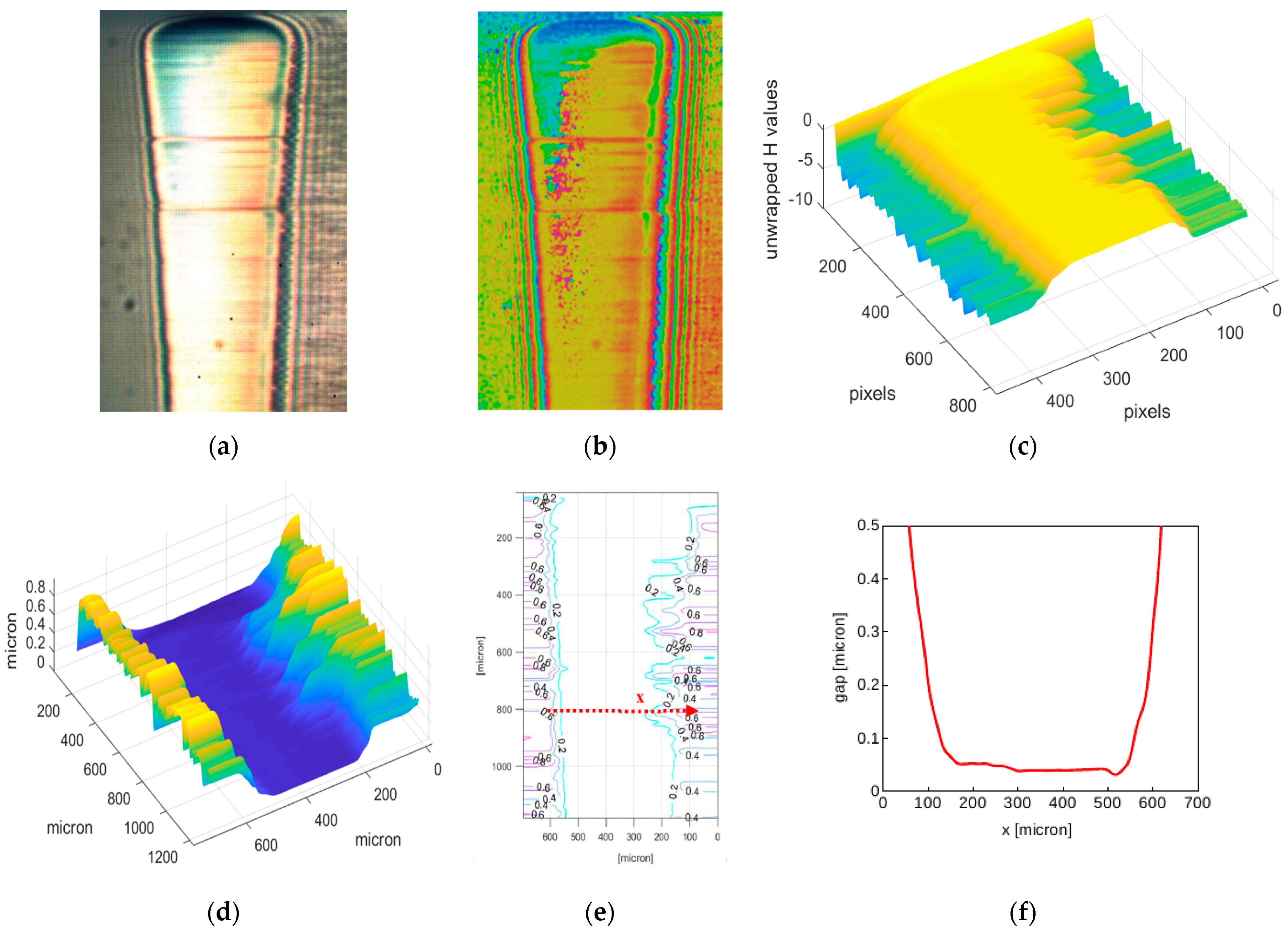
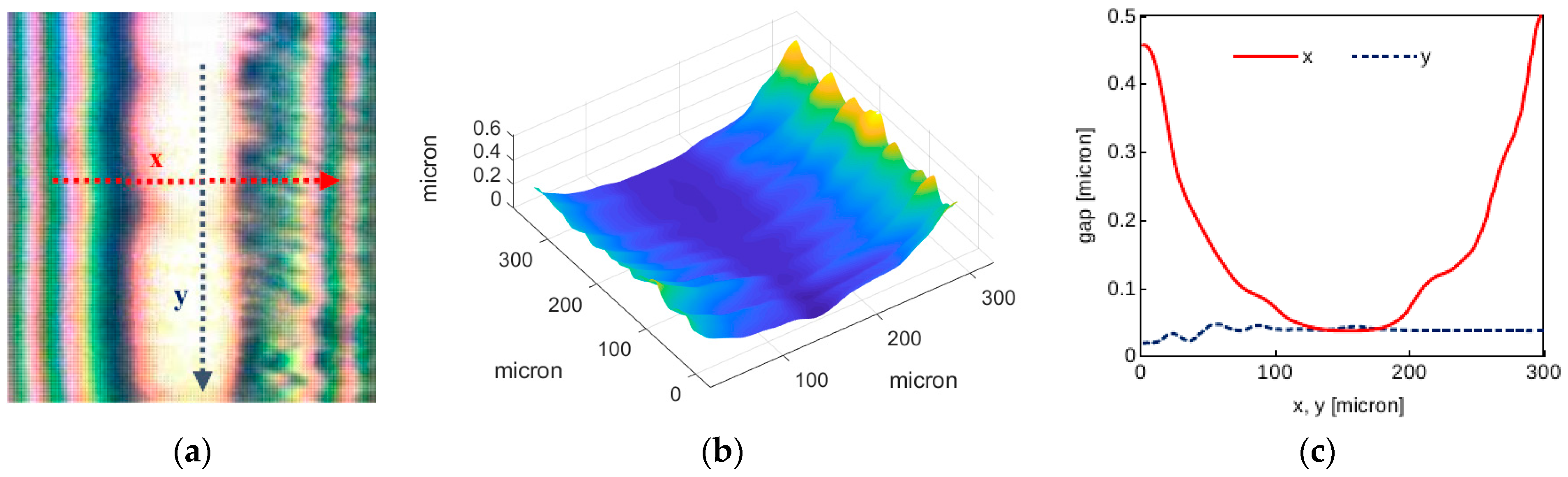
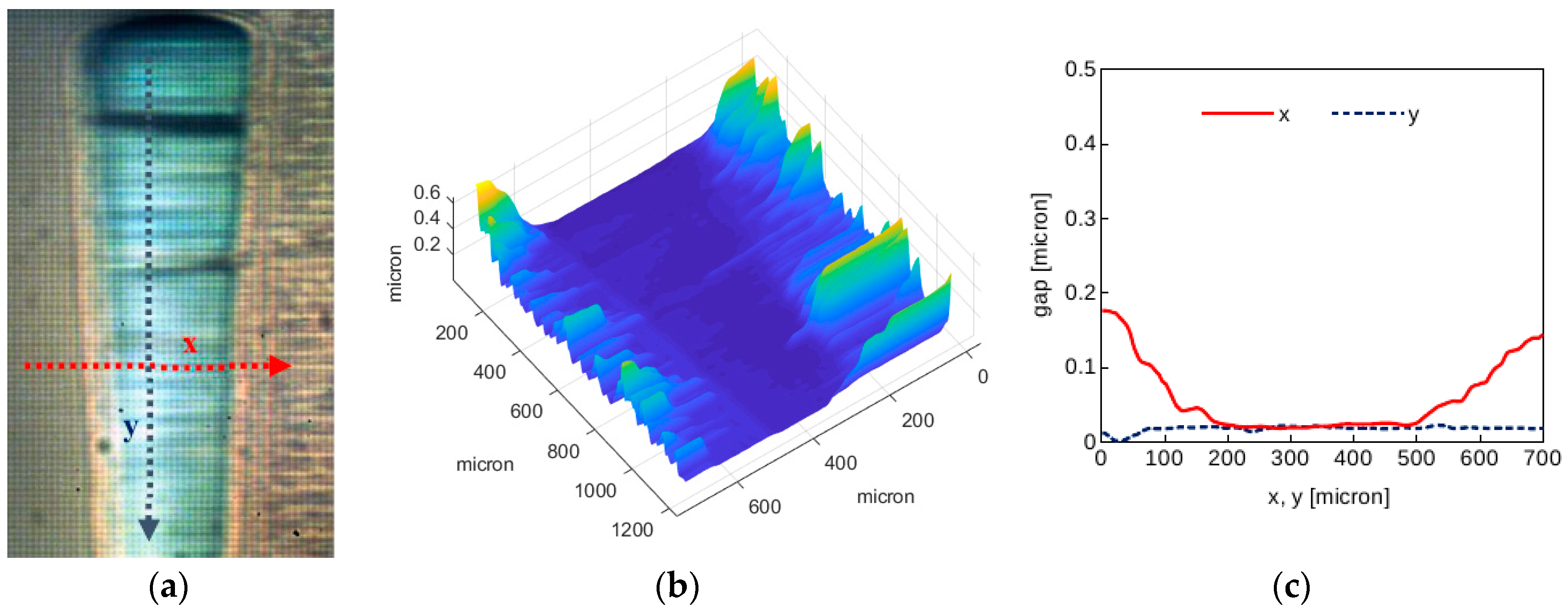
3.2. Sample Result for a Hertzian Contact
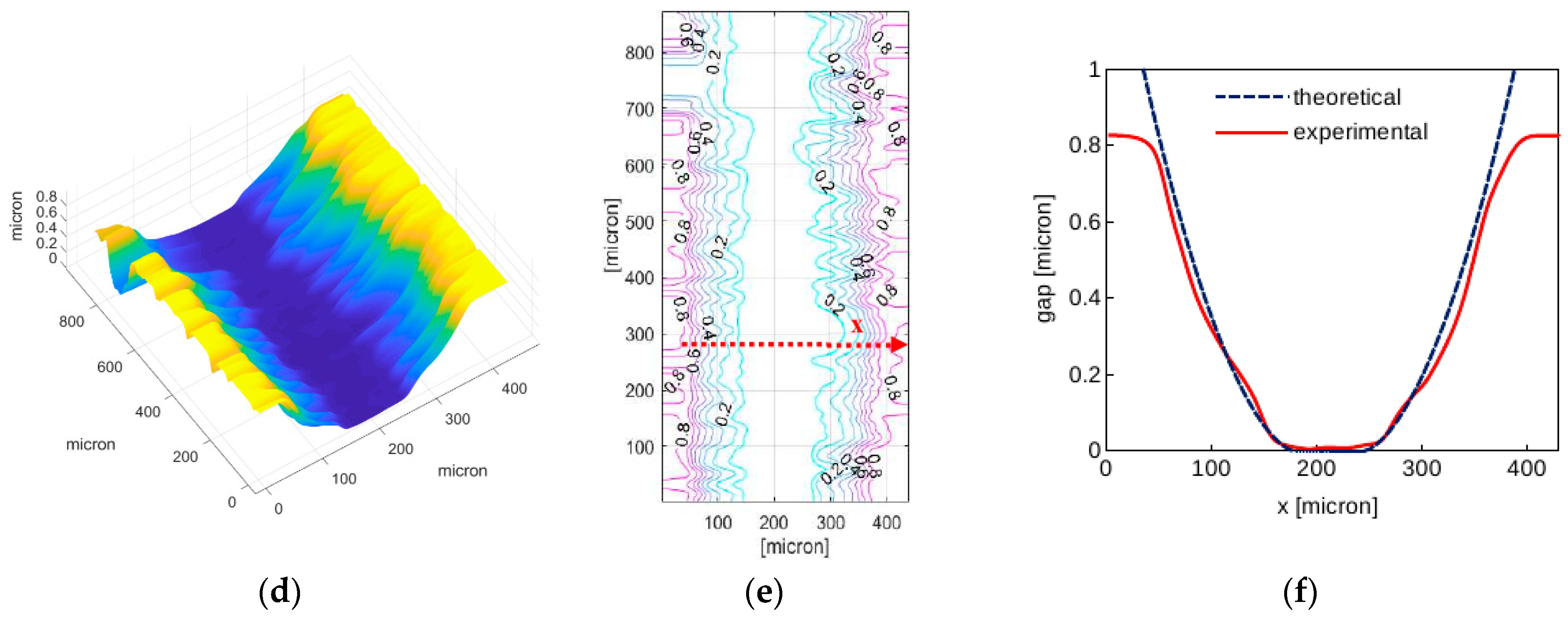
3.3. Sample Results for EHL Contacts
4. Discussion
5. Conclusions and Future Developments
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Ciulli, E. Non-steady state non-conformal contacts: Friction and film thickness studies. Meccanica 2009, 44, 409–425. [Google Scholar] [CrossRef]
- Myant, C.; Fowell, M.; Cann, P. The effect of transient motion on isoviscous-EHL films in compliant, point, contacts. Tribol. Int. 2014, 72, 98–107. [Google Scholar] [CrossRef]
- Ali, F.; Kaneta, M.; Křupka, I.; Hartl, M. Experimental and numerical investigation on the behavior of transverse limited micro-grooves in EHL point contacts. Tribol. Int. 2015, 84, 81–89. [Google Scholar] [CrossRef]
- Hamilton, G.M. The hydrodynamic of a cam follower. Tribol. Int. 1980, 13, 113–119. [Google Scholar] [CrossRef]
- van Leeuwen, H.; Meijer, H.; Schouten, M. Elastohydrodynamic film thickness and temperature measurements in dynamically loaded concentrated contacts: Eccentric cam–flat follower. In 13th Leeds–Lyon Symposium; Elsevier: Amsterdam, the Netherlands, 1987; pp. 611–625. [Google Scholar]
- Dowson, D.; Harrison, P.; Taylor, C.M.; Zhu, G. Experimental observation of lubricant film state between a cam and bucket follower using the electrical resistivity technique. In Proceedings of the Japan International Tribology Conference, Nagoya, Japan, 29 October–1 November 1990; pp. 119–124. [Google Scholar]
- Mufti, R.A. Experimental technique for evaluating valve train performance of a heavy duty diesel engine. Proc. IMECHE 2009, 223, 425–436. [Google Scholar] [CrossRef]
- Ma, L.; Luo, J.B. Thin film lubrication in the past 20 years. Friction 2016, 4, 280–302. [Google Scholar] [CrossRef] [Green Version]
- Gustafsson, L.; Höglund, E.; Marklund, O. Measuring Lubricant Film Thickness with Image Analysis. Proc. Inst. Mech. Eng. J J. Eng. Tribol. 1994, 208, 199–205. [Google Scholar] [CrossRef]
- Cann, P.M.; Spikes, H.A.; Hutchinson, J. The Development of a Spacer Layer Imaging Method (SLIM) for Mapping Elastohydrodynamic Contacts. Tribol. Trans. 1996, 39, 915–921. [Google Scholar] [CrossRef]
- Luo, J.B.; Wen, S.Z.; Huang, P. Thin film lubrication. Part I. Study on the transition between EHL and thin film lubrication using a relative optical interference intensity technique. Wear 1996, 194, 107–115. [Google Scholar] [CrossRef]
- Guo, F.; Wong, P.L. A multi-beam intensity-based approach for lubricant film measurements in non-conformal contacts. Proc. Inst. Mech. Eng. J J. Eng. Tribol. 2002, 216, 281–291. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, P. An Improved Interference Method for Measuring Lubricant Film Thickness Using Monochromatic Light. Tribol. Lett. 2017, 65, 120. [Google Scholar] [CrossRef]
- Kaneta, M.; Kanada, T.; Nishikawa, H. Optical interferometric observations of the effects of a moving dent on point contact EHL. ASME J. Tribol. 1997, 32, 69–79. [Google Scholar]
- Liu, H.C.; Guo, F.; Guo, L.; Wong, P.L. A dichromatic interference intensity modulation approach to measurement of lubricating film thickness. Tribol. Lett. 2015, 58. [Google Scholar] [CrossRef]
- Bai, Q.; Guo, F.; Wong, P.L.; Jiang, P. Online Measurement of Lubricating Film Thickness in Slider-on-Disc Contact Based on Dichromatic Optical Interferometry. Tribol. Lett. 2017, 65. [Google Scholar] [CrossRef]
- Marklund, O.; Gustafsson, L. Interferometry-based measurements of oil-film thickness. Proc. Inst. Mech. Eng. J. Eng. Tribol. 2001, 215, 243–259. [Google Scholar] [CrossRef]
- Hartl, M.; Krupka, I.; Poliscuk, R.; Liska, M. An Automatic System for Real-Time Evaluation of EHD Film Thickness and Shape Based on the Colorimetric Interferometry. Tribol. Trans. 1999, 42, 303–309. [Google Scholar] [CrossRef]
- Hartl, M.; Křupka, I.; Poliščuk, R.; Liška, M.; Molimard, J.; Querry, M.; Vergne, P. Thin Film Colorimetric Interferometry. Tribol. Trans. 2001, 44, 270–276. [Google Scholar] [CrossRef]
- Křupka, I.; Šperka, P.; Hartl, M.; Xue Jin, S.; Yang, C.X. Effect of real longitudinal surface roughness on lubrication film formation within line elastohydrodynamic contact. Tribol. Int. 2010, 43, 2384–2389. [Google Scholar] [CrossRef]
- Ciulli, E.; Draexl, T.; Stadler, K. Film thickness analysis for EHL contacts under steady-state and transient conditions by automatic digital image processing. Adv. Tribol. 2008, 2008, 325187. [Google Scholar] [CrossRef]
- Ciulli, E.; Fazzolari, F.; Piccigallo, B. Experimental study on circular eccentric cam–follower pairs. Proc. Inst. Mech. Eng. J J. Eng. Tribol. 2014, 228, 1088–1098. [Google Scholar] [CrossRef]
- Fazzolari, F.; Ciulli, E.; Vela, D. A novel instrumentation for contact force measurement in cam-follower pairs. In Proceedings of the 18th International Colloquium Tribology, Industrial and Automotive Lubrication, Esslingen, Germany, 10–12 January 2012. [Google Scholar]
- Pugliese, G.; Ciulli, E.; Fazzolari, F. Experimental aspects of a cam-follower contact. In Proceedings of the Accepted for Presentation to the 15th IFToMM World Congress, Krakow, Poland, 30 June–4 July 2019. [Google Scholar]
- Cameron, A.; Gohar, R. Theoretical and experimental studies of the oil film in lubricated point contact. Proc. R. Soc. A 1966, 291, 520–535. [Google Scholar]
- Eguchi, M.; Yamamoto, T. Film thickness measurement using white light spacer interferometry and its calibration by HSV color space. In Proceedings of the 5th International Conference on Tribology, Parma, Italy, 20–22 September 2006; pp. 20–22. [Google Scholar]
- Cameron, A. The Principles of Lubrication; Wiley: New York, NY, USA, 1966. [Google Scholar]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Marklund, O. Interferometric Measurements and Analysis with Applications in Elastohydrodynamic Experiments. Ph.D. Thesis, Lulea University of Technology, Luleå, Sweden, 1998. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2008. [Google Scholar]
- Berns, R.S.; Billmeyer, F.W.; Saltzman, M. Billmeyer and Saltzman’s Principles of Color. Technology; Wiley: New York, NY, USA, 2000; pp. 20–32. [Google Scholar]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciulli, E.; Pugliese, G.; Fazzolari, F. Film Thickness and Shape Evaluation in a Cam-Follower Line Contact with Digital Image Processing. Lubricants 2019, 7, 29. https://doi.org/10.3390/lubricants7040029
Ciulli E, Pugliese G, Fazzolari F. Film Thickness and Shape Evaluation in a Cam-Follower Line Contact with Digital Image Processing. Lubricants. 2019; 7(4):29. https://doi.org/10.3390/lubricants7040029
Chicago/Turabian StyleCiulli, Enrico, Giovanni Pugliese, and Francesco Fazzolari. 2019. "Film Thickness and Shape Evaluation in a Cam-Follower Line Contact with Digital Image Processing" Lubricants 7, no. 4: 29. https://doi.org/10.3390/lubricants7040029
APA StyleCiulli, E., Pugliese, G., & Fazzolari, F. (2019). Film Thickness and Shape Evaluation in a Cam-Follower Line Contact with Digital Image Processing. Lubricants, 7(4), 29. https://doi.org/10.3390/lubricants7040029






