Linear and Nonlinear Viscoelastic Modulus of Rubber

Abstract

We study the linear and nonlinear viscoelastic properties of two tire tread compounds. We discuss the difference in nonlinear response between the oscillatory tensile and shear modes. We also analyze strain relaxation (creep) data for the same systems. We discuss what type of measurements are most suitable for obtaining the viscoelastic modulus used in rubber friction calculations.

1. Introduction

Most practical applications of rubber materials involve large deformations, with strain in the range of 0.1–1. Rubber with filler particles is a highly nonlinear material, where the effective elastic modulus typically decreases by a factor of ≈10 with increasing strain from less ${10}^{-4}$ to 1. Most of the drop occurs already for a very small strain, typically below 0.1. The strong dependence on the strain amplitude is due to the breakup of the filler network [1,2,3,4,5,6,7,8,9,10,11,12,13]. That is, in the undeformed state, if the filler particle (volume) fraction is larger than ≈0.3, they form a percolating network in the rubber matrix. During deformation with large enough strain, this network is broken up, resulting in a strong reduction in the effective elastic modulus. This break up of the filler network with an increasing strain amplitude is also associated with a large increase in the dissipative response of the rubber compound.

An interesting idea for the low-strain extensional reinforcement of elastomers was proposed by Smith et al. [12]. They proposed that the reinforcement results from a nanoparticulate jamming-induced suppression in the composite Poisson ratio. This suppression forces an increase in rubber volume with extensional deformation, effectively converting a portion of the rubber’s bulk modulus into an extensional modulus.

There are different ways to probe the nonlinear viscoelastic properties of rubber materials, and here we compare the results of measurements using oscillatory strain in tension and shear modes. We also compare these results with the effective modulus obtained from strain relaxation (creep) measurements. We discuss what type of measurements are most suitable for obtaining the viscoelastic modulus for rubber friction calculations.

In Section 2 we review the theory of nonlinear response. In Section 3 we present the experimental methods used here, and in Section 4, our experimental results. Section 5 contains a discussion and Section 6 the summary and conclusion.

2. Theory

The nonlinear response theory shows that the relation between stress $\sigma \left(t\right)$ and strain $ϵ\left(t\right)$ during elongation or shear can be written as [14]

$$\begin{array}{c}\sigma \left(t\right)=\int d{t}_1{E}_1(t-t_1)ϵ\left(t_1\right)+\int d{t}_{1}d{t}_2{E}_2(t-t_1,t-t_2)ϵ\left(t_1\right)ϵ\left(t_2\right)\\ +\int d{t}_{1}d{t}_{2}d{t}_3{E}_3(t-t_1,t-t_2,t-t_3)ϵ\left(t_1\right)ϵ\left(t_2\right)ϵ\left(t_3\right)+\dots ,\end{array}$$

(1)

where causality requires that the response function $E_1$ is nonzero only when $t_1<t$, $E_2$ is nonzero only when $t_1<t$ and $t_2<t$, and so on.

For elongation of a rectangular strip (elongation force $F\left(t\right)$) with (undeformed) cross section $A_0$ and length $L_0$, and if $\sigma \left(t\right)$ is the engineering stress $F\left(t\right)/A_0$ then $ϵ\left(t\right)$ in Equation (1) is conveniently chosen as the linear strain $[L\left(t\right)-L_0]/L_0$, while if $\sigma \left(t\right)=F\left(t\right)/A\left(t\right)$ is the physical (or true) stress then $ϵ\left(t\right)$ is conveniently chosen as the logarithmic strain $\ln [L\left(t\right)/L_0]$: consider elongating a rubber strip with the original cross section $A_0$ and length $L_0$. If $\sigma \left(t\right)$ denote the engineering stress then the elongation force $F\left(t\right)=\sigma \left(t\right)A_0$ and the work to elongate is $U=\int F\left(t\right)dL=\int \sigma \left(t\right)A_0{L}_{0}dL/L_0=V_0\int \sigma \left(t\right)\dot{ϵ}\left(t\right)dt$ where $ϵ\left(t\right)=[L\left(t\right)-L_0]/L_0$ is the linear strain and $V_0$ the rubber volume. If $\sigma \left(t\right)$ denote the physical stress then $F\left(t\right)=\sigma \left(t\right)A\left(t\right)$ so that $U=\int \sigma \left(t\right)A\left(t\right)dL=\int \sigma \left(t\right)A\left(t\right)L\left(t\right)dL/L\left(t\right)=V_0\int \sigma \left(t\right)\dot{ϵ}\left(t\right)dt$ where $ϵ\left(t\right)=\ln [L\left(t\right)/L_0]$ is the logarithmic strain. Here we have assumed that there is no change in the volume during the deformation i.e., $V_0=A\left(t\right)L\left(t\right)=A_0{L}_0$. For small strain, as is well known, the logarithmic strain reduces to the linear strain.

There are various ways to study the nonlinear viscoelastic properties of rubber materials. One of the standard methods is to apply oscillatory strain, and gradual increasing of the strain amplitude. If the strain is given by $ϵ={ϵ}_0\cos \left(\omega t\right)$ then the sum in Equation (1) will have the form

$$\sigma \left(t\right)=\mathrm{Re}\left[Z_0(\omega ,{ϵ}_0)+Z_1(\omega ,{ϵ}_0)e^{i\omega t}+Z_2(\omega ,{ϵ}_0)e^{i2\omega t}+\dots \right]{ϵ}_0,$$

where $Z_n(\omega ,{ϵ}_0)$ ($n=0,1,2,\dots$) are complex valued functions of the frequency $\omega$ and the strain amplitude ${ϵ}_0$. For example,

$$Z_0=\frac{1}{2}{ϵ}_0{\int }_0^{\infty }d{t}_{1}d{t}_2{E}_2(t_1,t_2)e^{i\omega (t_1-t_2)}+\dots$$

$$\begin{array}{l}{Z}_1={\int }_0^{\infty }d{t}_1{E}_1\left(t_1\right)e^{i\omega t_1}+\frac{1}{4}{ϵ}_0^2{\int }_0^{\infty }d{t}_{1}d{t}_{2}d{t}_3{E}_3(t_1,t_2,t_3)\\ \times \left[e^{i\omega (t_1+t_2+t_3)}+e^{i\omega (t_1-t_2+t_3)}+e^{i\omega (t_1-t_2-t_3)}\right]+\dots \end{array}$$

Note that when ${ϵ}_0\to 0$ only the $Z_1$ term will be non-zero. If we write $Z_0=\left|Z_0\right|\exp \left(i{\varphi }_0\right)$, $Z_1=\left|Z_1\right|\exp \left(i{\varphi }_1\right)$, … we can also write

$$\sigma \left(t\right)=\left[|Z_0|\cos {\varphi }_0+|Z_1|\cos (\omega t+{\varphi }_1)+\left|Z_2\right|\cos (2\omega t+{\varphi }_2)+\dots \right]{ϵ}_0.$$

The dynamical mechanical analysis (DMA) instruments that we use give as the output the effective Young’s modulus $E(\omega ,{ϵ}_0)$ (or shear modulus) obtained from the stress component which oscillates with the same frequency as the (driving) strain, i.e.,

$$E(\omega ,{ϵ}_0)=Z_1(\omega ,{ϵ}_0),$$

which depends on the strain amplitude ${ϵ}_0$. For small strain amplitude, where the rubber responds linearly to the applied strain, $Z_1(\omega ,{ϵ}_0)$ is independent of the strain amplitude and equal to the (viscoelastic) linear response function $E\left(\omega \right)$.

We notice that the energy dissipation for one cycle of oscillating strain depends only on the response function $Z_1(\omega ,{ϵ}_0)$. This follows from the expression for the energy dissipation (per unit volume and for one period of oscillation) in response to the oscillating strain $ϵ\left(t\right)={ϵ}_0\cos \left(\omega t\right)$:

$$\begin{array}{cc}\hfill U& ={\int }_0^{T}dt\sigma \left(t\right)\dot{ϵ}\left(t\right)=\mathrm{Re}{\int }_0^{T}dt\sigma \left(t\right){ϵ}_0(-i\omega )e^{-i\omega t}\hfill \\ & =\frac{1}{2}\omega {ϵ}_0^2\mathrm{Im}{\int }_0^{T}dt\left(Z_1{e}^{i\omega t}+Z_1^{*}{e}^{-i\omega t}\right)e^{-i\omega t}\hfill \\ & =\frac{\omega T}{2}{ϵ}_0^2\mathrm{Im}{Z}_1=\pi {ϵ}_0^2\mathrm{Im}E(\omega ,{ϵ}_0)\hfill \end{array}$$

(2)

Here we have used that $Z_n{e}^{in\omega t}$ for $n\ne 1$ will give a vanishing contribution to the dissipated energy since the integrand in (2) will have the time dependency $e^{i(n\pm 1)\omega t}$ which will vanish when integrated over one period of the oscillating strain.

The quantity $E(\omega ,{ϵ}_0)$ is very important since it reduces to the (linear response) viscoelastic modulus $E\left(\omega \right)$ as ${ϵ}_0\to 0$, and it determines the dissipated energy (in response to the oscillatory strain $ϵ\left(t\right)={ϵ}_0\cos \left(\omega t\right)$) even in the nonlinear region. We also notice that for filled rubber compounds, the response to the harmonic drive $ϵ\left(t\right)={ϵ}_0\cos \left(\omega t\right)$ is often a nearly perfectly sinusoidal stress response, i.e., it lacks higher-order harmonics [15]. Still, $E(\omega ,{ϵ}_0)$ depends on the strain amplitude ${ϵ}_0$ and the viscoelastic modulus can be written approximately as

$$\mathrm{Re}E(\omega ,{ϵ}_0)\approx f\left({ϵ}_0\right)\mathrm{Re}E\left(\omega \right),$$

$$\mathrm{Im}E(\omega ,{ϵ}_0)\approx g\left({ϵ}_0\right)\mathrm{Im}E\left(\omega \right),$$

where $f\left({ϵ}_0\right)$ and $g\left({ϵ}_0\right)$ are two different function with $f\left(0\right)=g\left(0\right)=1$. Note that if $f\left({ϵ}_0\right)=g\left({ϵ}_0\right)$ then $E(\omega ,{ϵ}_0)$ would obey the Kramers–Kronig relation (see below), but it was shown in [16] that this is not the case. The fact that the harmonic drive results in a nearly perfectly sinusoidal response has been denoted as the “harmonic paradox”.

The presence of two different functions f and g in the expression for $E(\omega ,{ϵ}_0)$ indicates that the deformation of filled rubber involves some new channel of energy dissipation, different from that involving the rubber matrix. This new dissipation channel may involve slip of polymer chains on the surface of filler particles, or some rearrangement of polymer chains when filler particle are separated from each other when the filler network breaks up during the deformation of the rubber. We noticed that f and g depend on temperature in a different way from that of the rubber matrix.

Another experimental approach to study the viscoelastic response of polymers is stress or strain relaxation. In these experiments, at time $t=0$ a constant stress is applied (strain relaxation or creep), or a constant displacement (strain) is imposed (stress relaxation). This will result in a strain which increases with increasing time, or to stress, which decreases with time. For example, if $ϵ\left(t\right)={ϵ}_0\theta \left(t\right)$ (stress relaxation), where $\theta \left(t\right)$ is a step function, we get from Equation (1)

$$\begin{array}{c}\sigma \left(t\right)={\int }_0^{\infty }d{t}_1{E}_1(t-t_1){ϵ}_0+{\int }_0^{\infty }d{t}_{1}d{t}_2{E}_2(t-t_1,t-t_2){ϵ}_0^2\\ +{\int }_0^{\infty }d{t}_{1}d{t}_{2}d{t}_3{E}_3(t-t_1,t-t_2,t-t_3){ϵ}_0^3+\dots \end{array}$$

(3)

We can write this equation as

$$\sigma \left(t\right)=E_{\sigma }(t,{ϵ}_0){ϵ}_0.$$

In the linear response region, the stress relaxation modulus $E_{\sigma }\left(t\right)=E_{\sigma }(t,{ϵ}_0=0)$ and the modulus $E\left(\omega \right)=E(\omega ,{ϵ}_0=0)$ contain exactly the same information. At first this may seem surprising since $E\left(\omega \right)$ is a complex function, and, therefore, consists of two real functions, while $E\left(t\right)$ is a single real function. However, due to causality the real and imaginary part of $E\left(\omega \right)$ (as well for any other linear response function) satisfies the Kramers–Kronig relation, which in the present case takes the form

$$\mathrm{Re}E\left(\omega \right)=E(\infty )+\frac{2}{\pi }P{\int }_0^{\infty }d{\omega }^{\prime }\frac{{\omega }^{\prime }\mathrm{Im}E\left({\omega }^{\prime }\right)}{{\omega }^{{}^{\prime }2}-{\omega }^2},$$

(4)

where $E(\infty )$ equals $E\left(\omega \right)$ as $\omega \to \infty$, and where P stands for principal value. Therefore, given $\mathrm{Im}E\left(\omega \right)$ we can calculate $\mathrm{Re}E\left(\omega \right)$, i.e., there is only one independent function.

In the linear response limit, the relation between $E\left(\omega \right)$ and $E_{\sigma }\left(t\right)$ is easy to derive: If the strain is abruptly increased (at time $t=0$) from zero to ${ϵ}_0$ then

$$ϵ\left(\omega \right)={\int }_0^{\infty }dt{ϵ}_0{e}^{i\omega t-0^{+}t}=\frac{i{ϵ}_0}{\omega +i{0}^{+}},$$

where $0^{+}$ is an infinitesimal small positive number. In this case, the stress at time $t>0$ will be:

$$\sigma \left(t\right)=\frac{1}{2\pi }\int d\omega E\left(\omega \right)ϵ\left(\omega \right)e^{-i\omega t}=\frac{1}{2\pi }\int d\omega E\left(\omega \right)\frac{i{ϵ}_0}{\omega +i{0}^{+}}{e}^{-i\omega t}.$$

Comparing this to the definition $\sigma \left(t\right)=E_{\sigma }\left(t\right){ϵ}_0$ gives

$$E_{\sigma }\left(t\right)=-\frac{1}{2\pi i}\int d\omega E\left(\omega \right)\frac{1}{\omega +i{0}^{+}}{e}^{-i\omega t}$$

(5)

Here we note that causality requires that $E\left(\omega \right)$ can be represented using the following spectral decomposition (Prony series)

$$E\left(\omega \right)=E(\infty )-{\int }_0^{\infty }d\tau \frac{H_{\sigma }\left(\tau \right)}{1-i\omega \tau },$$

(6)

where $H_{\sigma }\left(\tau \right)$ is a real (and positive) function of relaxation time $\tau$. Substituting this into Equation (5) gives

$$E_{\sigma }\left(t\right)=E(\infty )-{\int }_0^{\infty }d\tau H_{\sigma }\left(\tau \right)\left(1-e^{-t/\tau }\right)$$

(7)

In the case where ${ϵ}_0$ is so large that the response is nonlinear, one cannot use Equation (5) to relate $E(\omega ,{ϵ}_0)$ to $E_{\sigma }(t,{ϵ}_0)$. However, it appears that it is still possible to write $E_{\sigma }(t,{ϵ}_0)$ in the form of Equation (7), where $H_{\sigma }$ now depends on ${ϵ}_0$ and then use Equation (6) to obtain an effective modulus which we denote as $E_{\sigma }(\omega ,{ϵ}_0)$.

In a strain relaxation (creep) experiment, at $t=0$ a constant stress ${\sigma }_0$ is applied and the time dependent strain $ϵ\left(t\right)$ is measured. To describe this one can introduce the strain relaxation modulus via

$$ϵ\left(t\right)=E_{ϵ}^{-1}(t,{\sigma }_0){\sigma }_0.$$

In the linear response limit $E_{ϵ}\left(t\right)=E_{ϵ}(t,{\sigma }_0=0)$ can be obtained from $E\left(\omega \right)$ by using that

$$\sigma \left(\omega \right)=\frac{i{\sigma }_0}{\omega +i{0}^{+}}.$$

Thus for $t>0$:

$$ϵ\left(t\right)=\frac{1}{2\pi }\int d\omega \frac{\sigma \left(\omega \right)}{E\left(\omega \right)}{e}^{-i\omega t}=\frac{1}{2\pi }\int d\omega \frac{1}{E\left(\omega \right)}\frac{i{\sigma }_0}{\omega +i{0}^{+}}{e}^{-i\omega t}.$$

Comparing this to the definition $ϵ\left(t\right)=E_{ϵ}^{-1}\left(t\right){\sigma }_0$ gives

$$\frac{1}{E_{ϵ}\left(t\right)}=-\frac{1}{2\pi i}\int d\omega \frac{1}{E\left(\omega \right)}\frac{1}{\omega +i{0}^{+}}{e}^{-i\omega t}.$$

(8)

Here we note that causality requires that $E^{-1}\left(\omega \right)$ can be represented using the following spectral decomposition (Prony series)

$$\frac{1}{E\left(\omega \right)}=\frac{1}{E(\infty )}+{\int }_0^{\infty }d\tau \frac{H_{ϵ}\left(\tau \right)}{1-i\omega \tau },$$

(9)

where $H_{ϵ}\left(\tau \right)$ is a real and positive. Substituting this into Equation (8) gives

$$\frac{1}{E_{ϵ}\left(t\right)}=\frac{1}{E(\infty )}+{\int }_0^{\infty }d\tau H_{ϵ}\left(\tau \right)\left(1-e^{-t/\tau }\right)$$

(10)

In the case where ${\sigma }_0$ is so large that the response is nonlinear one cannot use Equation (8) to relate $E(\omega ,{ϵ}_0)$ to $E_{ϵ}(t,{ϵ}_0)$. However, it appears, that it is still possible to write $E_{ϵ}(t,{ϵ}_0)$ on the form Equation (10), where $H_{ϵ}$ now depends on ${\sigma }_0$ and then use Equation (9) to obtain an effective modulus which we denote as $E_{ϵ}(\omega ,{ϵ}_0)$.

3. Experimental Procedure

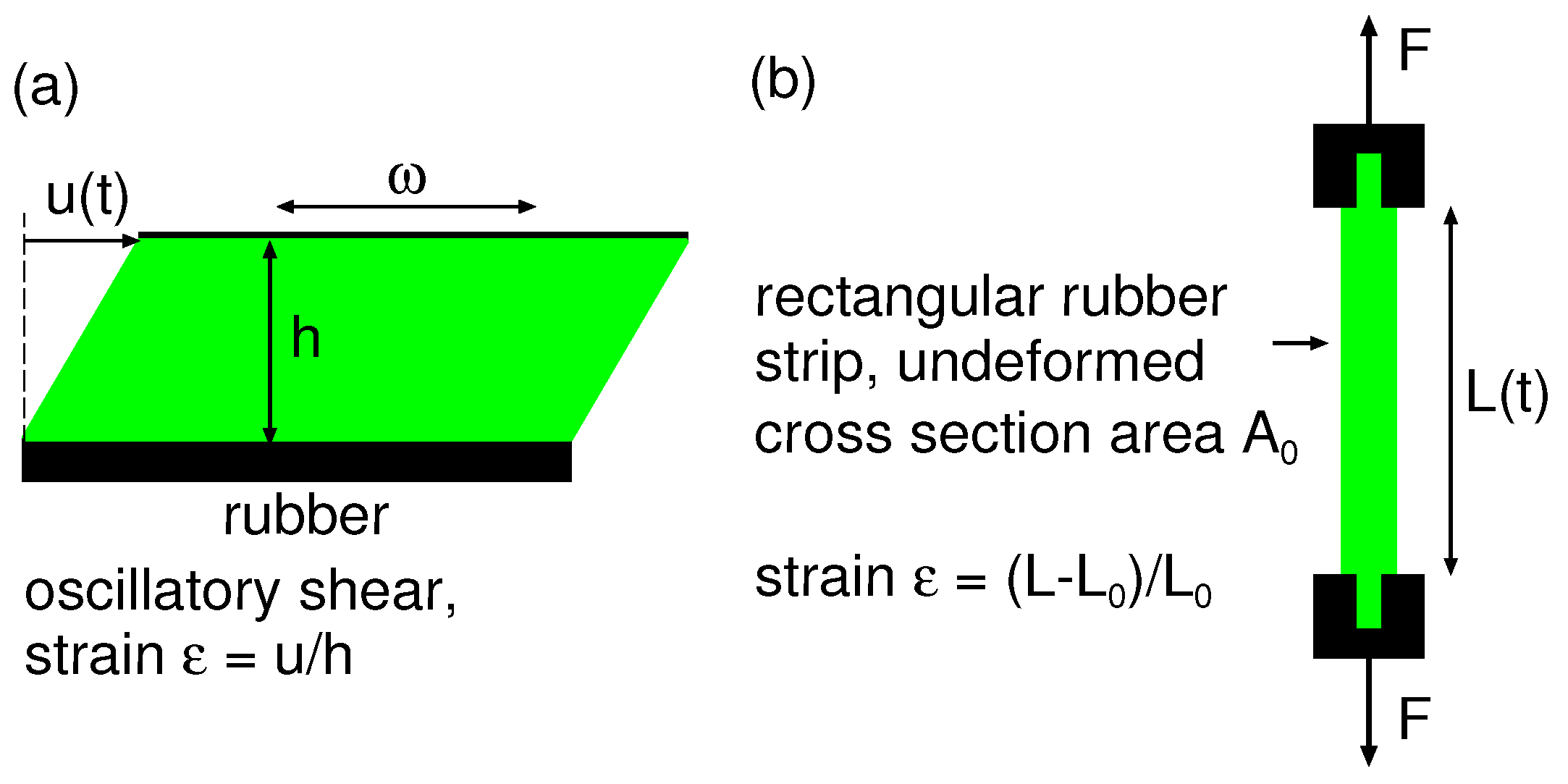
We performed measurements of the linear and nonlinear properties of two rubber compounds using the two experimental set-ups shown schematically in Figure 1. The first method was performed in shear mode on the Metravib dynamical mechanical analysis (DMA) instrument. To obtain the shear modulus $G(\omega ,{ϵ}_0)$ the upper plate in Figure 1a oscillates $u\left(t\right)=u_0\cos \left(\omega t\right)$ in a plane with the frequency $\omega$ and strain amplitude ${ϵ}_0=u_0/h$.

The strain sweep was performed at different temperatures ($T=-10$, 0, 20, 60 and $100{}^{\circ }\mathrm{C}$), and was carried out from shear strain 0.0001 to 1 at the frequency $f=10\mathrm{Hz}$. For each temperature, a new sample prepared from the same compound was used. Each sample was acclimatized in a DMA chamber for 10 min to achieve the desired temperature.

The second (home-built) set-up (Figure 1b) was used for strain relaxation (creep) measurements. At $t=0$ the rubber strip was elongated with the applied force F. The length $L\left(t\right)$ of the rubber strip increased with time due to viscoelastic deformations (creep). Before applying the force F, the rubber strip had a length $L_0$ and a cross section area $A_0$, and at time t the length and cross section area were $L\left(t\right)$ and $A\left(t\right)$, respectively, where $A_0{L}_0\approx A\left(t\right)L\left(t\right)$. We defined the effective Young’s modulus $E_{ϵ}(t,{\sigma }_0)$ so that $\sigma \left(t\right)=E_{ϵ}(t,{\sigma }_0)ϵ\left(t\right)$ where the strain $ϵ\left(t\right)=(L\left(t\right)-L_0)/L_0$ and the (physical) stress $\sigma \left(t\right)=F/A\left(t\right)=(F/A_0)(L\left(t\right)/L_0)=(F/A_0)(1+ϵ\left(t\right))={\sigma }_0(1+ϵ\left(t\right))$. Note that the physical stress depends on time, therefore $E_{ϵ}(t,{\sigma }_0)$ defined in this way is slightly different from the strain relaxation modulus defined in Section 2.

We also performed measurements of the viscoelastic master curve and strain sweeps in oscillatory tension mode using a Q800 DMA instrument produced by TA Instruments. In this case, we applied the oscillatory strain $ϵ\left(t\right)={ϵ}_1+{ϵ}_0\cos \left(\omega t\right)$, where the pre-strain ${ϵ}_1$ was chosen to be ${ϵ}_1=1.25{ϵ}_0$ so that the rubber strip remained straight during the whole oscillation cycle. For the master curve, we used very small strain amplitude, ${ϵ}_0=0.0004$, and in this case we are in the linear response region, where the modulus $E\left(\omega \right)$ is independent on the strain amplitude (and the pre-strain). However, the strain sweep does depend on the pre-strain so we cannot expect exactly the same results as in the shear mode where no pre-strain applied. Since the pre-strain contributes to the break-up of the filler network, and since the pre-strain increases in proportion to the dynamic strain amplitude, we expect faster strain softening with increasing strain amplitude for the strain sweep in tension compared to in shear mode. In addition, the shear strain $ϵ=u/h$ is not the same quantity as the strain in elongation $ϵ=(L-L_0)/L_0$; usually the shear strain is denoted by $\gamma$ rather than $ϵ$, but here we use the same notation for both quantities.

4. Experimental Results

Here we will present results for the linear and nonlinear response of two tire tread rubber compounds. Rubber compound A is a summer tire tread compound while the other compound C is a winter tread compound. Both compounds have a silica filler. The glass transition temperature, here defined as the temperature T where $\tan \delta \left(T\right)$ is maximal when studied at the frequency $\omega =0.01{\mathrm{s}}^{-1}$, are $T_{\mathrm{g}}=-30.4{}^{\circ }\mathrm{C}$ and $-47.2{}^{\circ }\mathrm{C}$ for compound A and C, respectively.

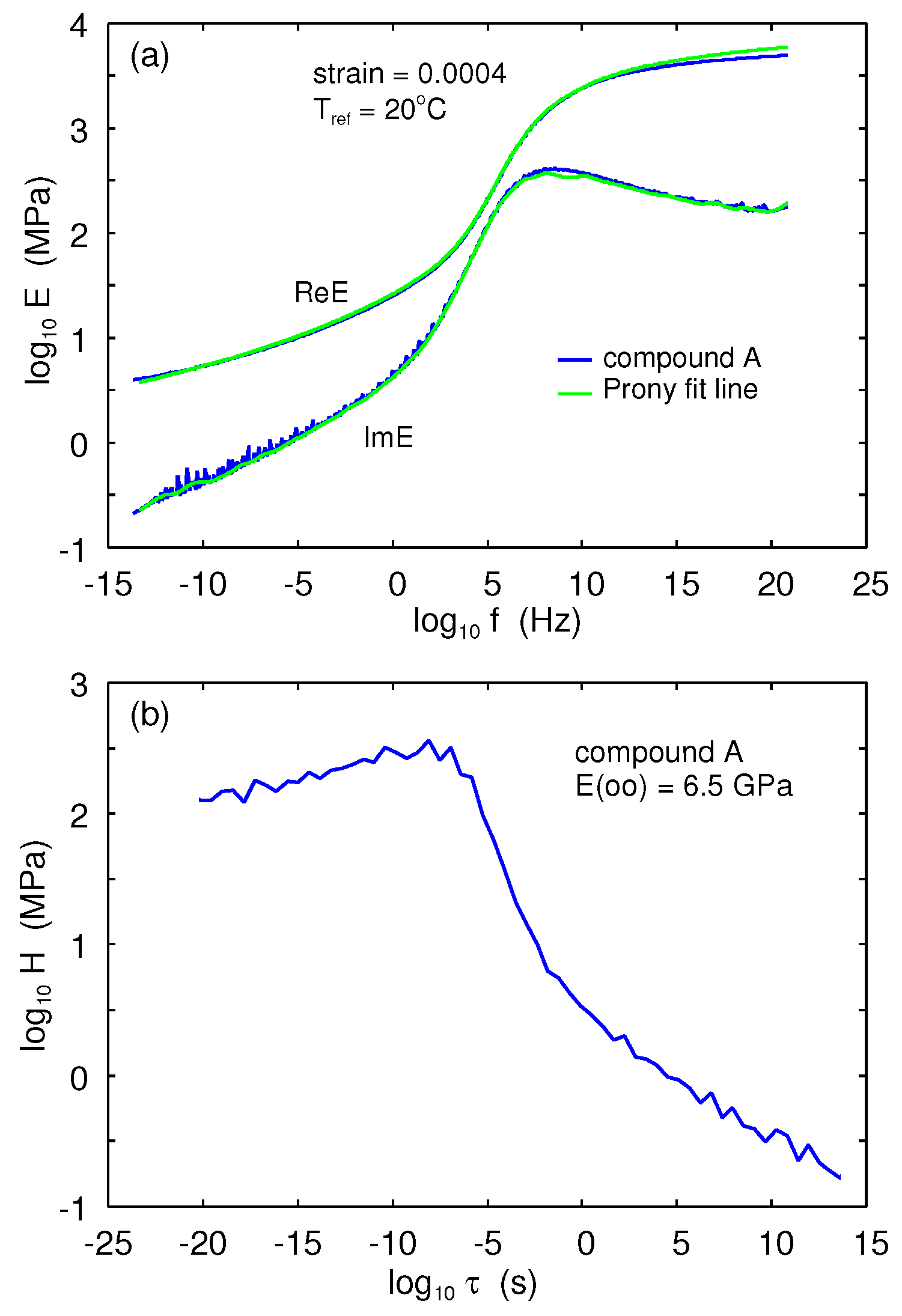
We measured the linear response of viscoelastic modulus in oscillatory strain (see Figure 2a) with a very small strain amplitude, $0.0004$ and a pre-strain $0.0005$. The measurements was done at several frequencies between $0.1\mathrm{Hz}$ and $100\mathrm{Hz}$, and for many temperatures. The measured frequency segments were shifted to obtain a smooth master curve (see Ref. [16] for more details). In Figure 2a the blue line is the master curve for compound A. The results of fitting the Prony series (Equation (6)) are also shown, where the spectral weight $H\left(\tau \right)$ is shown in Figure 2b. Clearly, both the real and imaginary part of the viscoelastic modulus can be fitted very well with the Prony series. This shows that the real and imaginary parts of the viscoelastic modulus obey the Kramers Kronig relation, as indeed expected, because of the small strain used in the measurements of viscoelastic modulus (linear response). However, when the effective modulus is measured at a higher strain the Prony series can no longer fit the measured data (not shown), as already shown in Ref. [16].

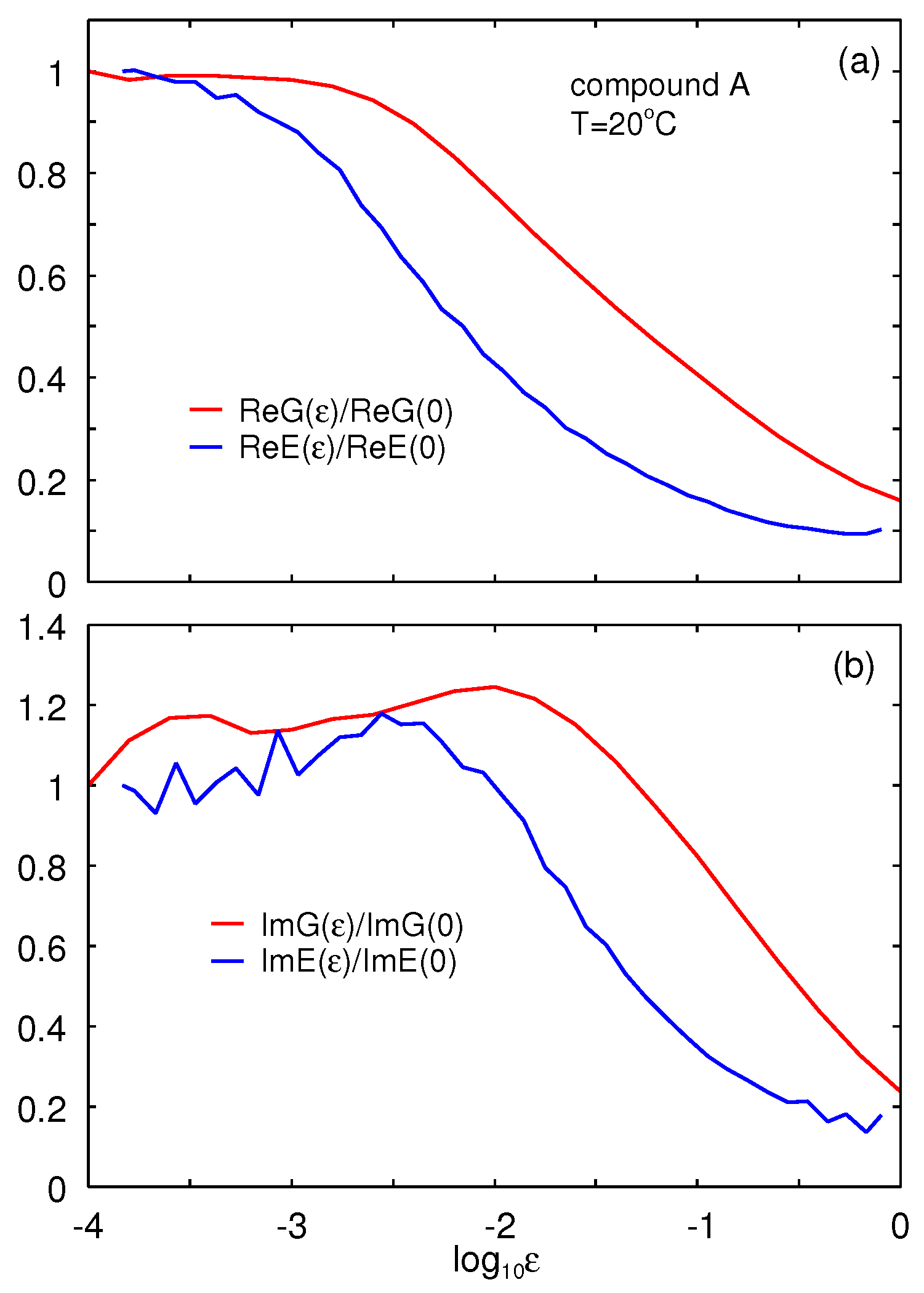
We measured the nonlinear viscoelastic response using strain sweeps in oscillatory tension and shear modes. In Figure 3 we show (a) the ratio $\mathrm{Re}G\left(ϵ\right)/\mathrm{Re}G\left(0\right)$ (red line) and $\mathrm{Re}E\left(ϵ\right)/\mathrm{Re}E\left(0\right)$ (blue line) as a function of the logarithm of the strain, and in (b) the same for the imaginary part of G and E. To measure the effective Young’s modulus E the rubber strip is pre-strained with an amplitude which is $25\%$ larger than the dynamical strain amplitude, i.e., pre-strain $=1.25{ϵ}_0$ if the dynamical strain is $ϵ\left(t\right)={ϵ}_0\cos \left(\omega t\right)$. This pre-strain increases with increasing amplitude of dynamical strain and may be the main reason why the strain softening occurs at smaller strain for the effective E-modulus than for the G-modulus. Note also that the strain in shear mode is defined differently than in tension.

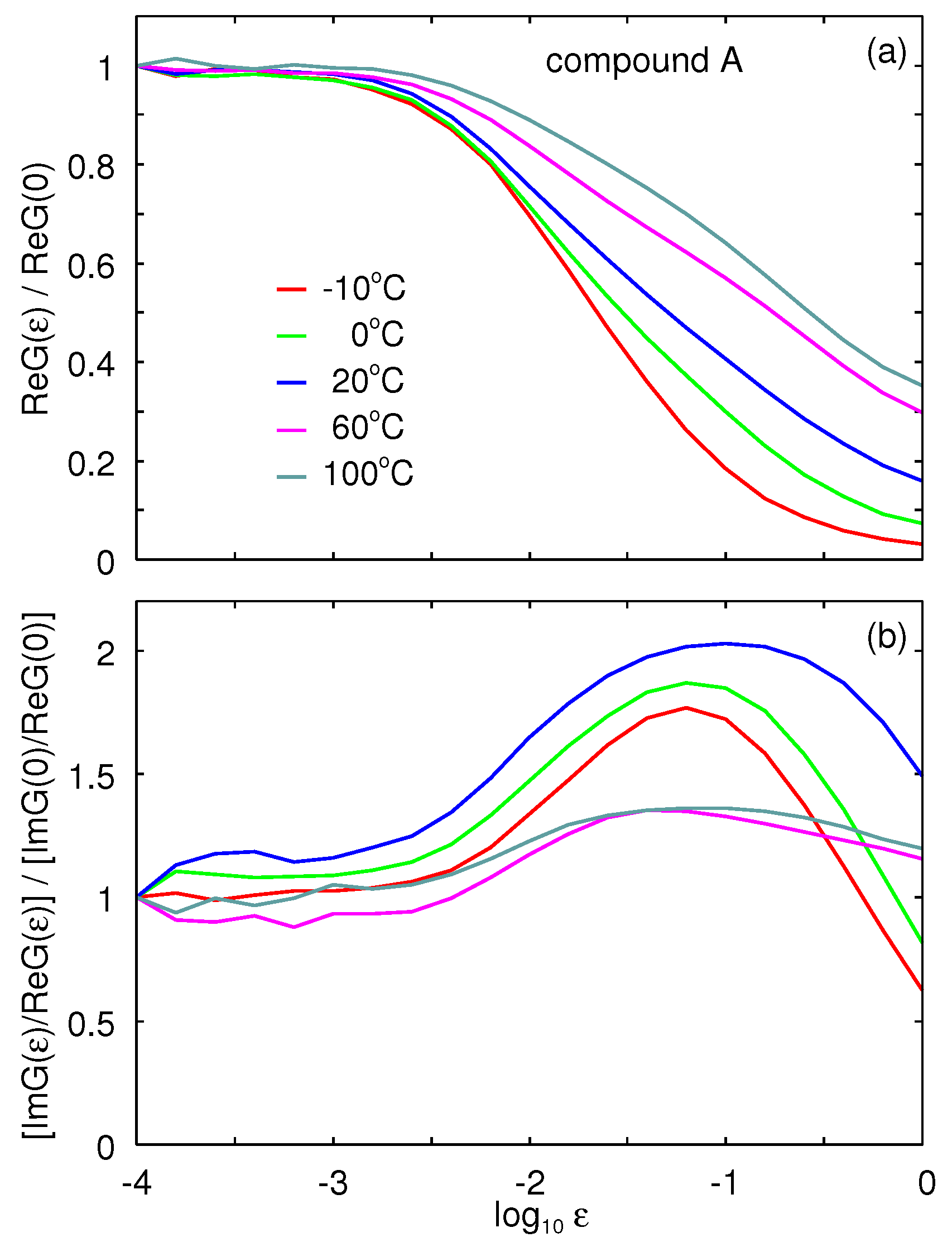
In Figure 4 we show the results obtained in shear for the ratio (a) $\mathrm{Re}G\left(ϵ\right)/\mathrm{Re}G\left(0\right)$ and (b) $\left[\mathrm{Im}G\right(ϵ)/\mathrm{Re}G(ϵ\left)\right]/\left[\mathrm{Im}G\right(0)/\mathrm{Re}G(0\left)\right]$ for the compound A. Note in (a) the strain softening which is strongest at the lowest temperature. Figure 4b shows that the energy dissipation is enhanced when the filler network is broken. Note also that the peak in $\left[\mathrm{Im}G\right(ϵ)/\mathrm{Re}G(ϵ\left)\right]/\left[\mathrm{Im}G\right(0)/\mathrm{Re}G(0\left)\right]$ is the highest for $T=20{}^{\circ }\mathrm{C}$.

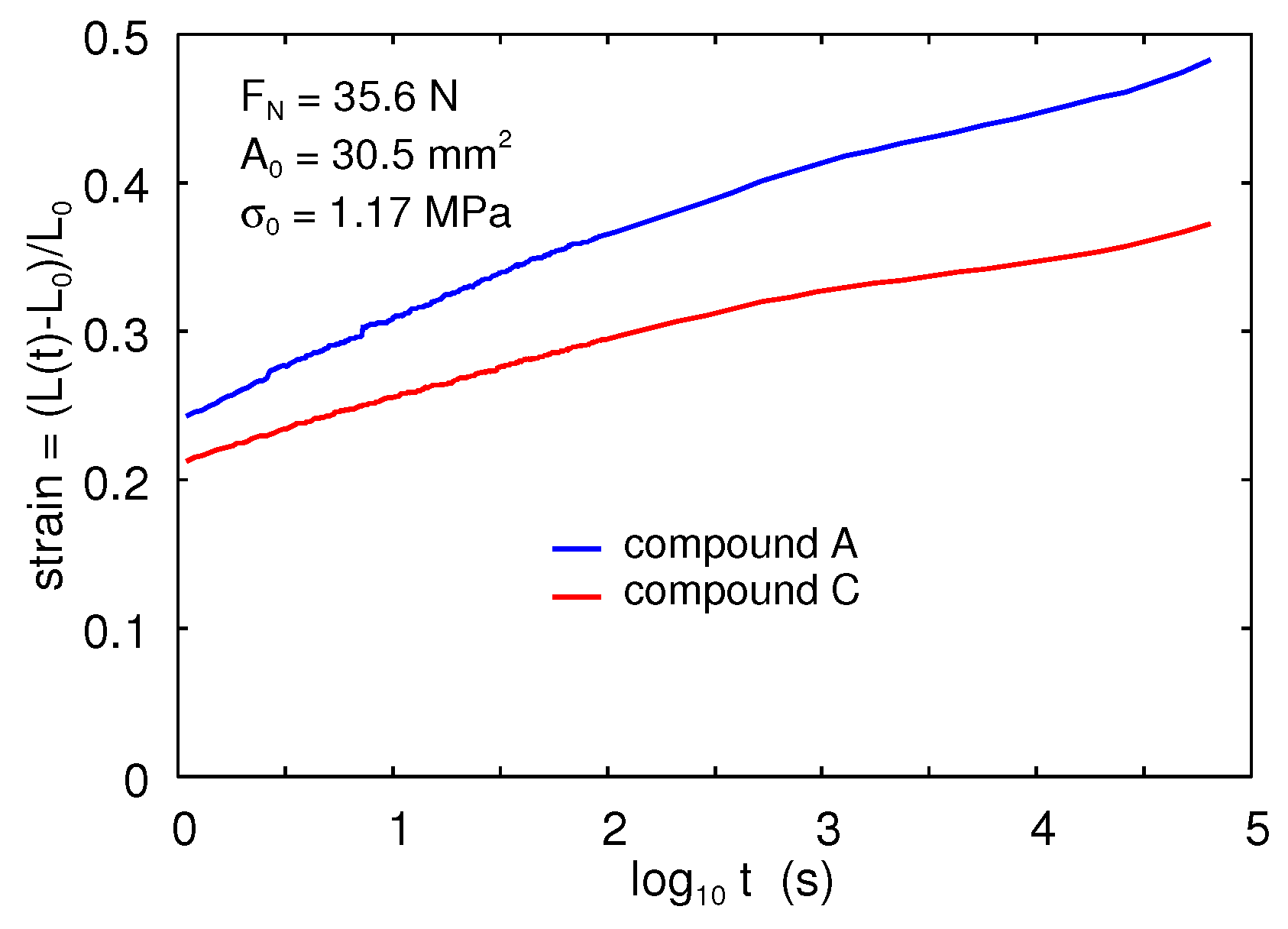
We also performed strain relaxation (creep) experiments. The red and blue lines in Figure 5 show the measured results for compounds C and A, respectively. Note that for short times, the strain is $ϵ\approx 0.24$ for compound A and $ϵ\approx 0.21$ for compound C.

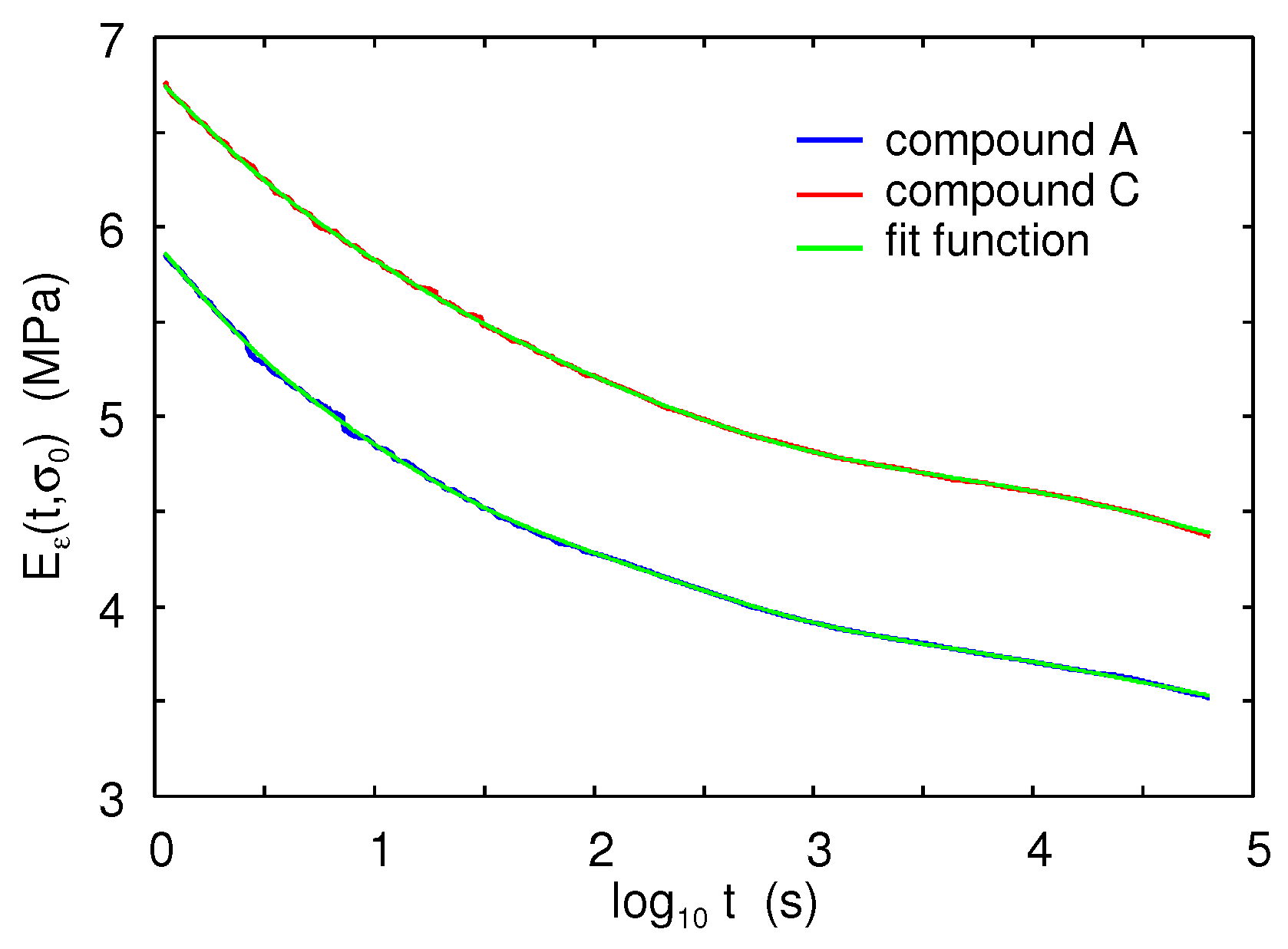
Figure 6 shows the time-dependence of the (nonlinear) strain relaxation modulus $E_{ϵ}(t,{\sigma }_0)$, as obtained from the experimental data in Figure 5 using $E_{ϵ}={\sigma }_0/ϵ\left(t\right)$ (or rather $E_{ϵ}=\sigma \left(t\right)/ϵ\left(t\right)$ where $\sigma \left(t\right)$ is the physical stress). The green lines are the fitted curves using the fit function in the form (10).

Now we will show that if we calculate the complex frequency-dependent modulus $E_{ϵ}(\omega ,{\sigma }_0)$ from (9) using the $H_{ϵ}\left(\tau \right)$, obtained by fitting $E_{ϵ}(t,{\sigma }_0)$ to the form (10) (green lines in Figure 6), then this does not agree with the result $E(\omega ,{\sigma }_0)$, obtained from the direct DMA measurement using oscillatory shear strain.

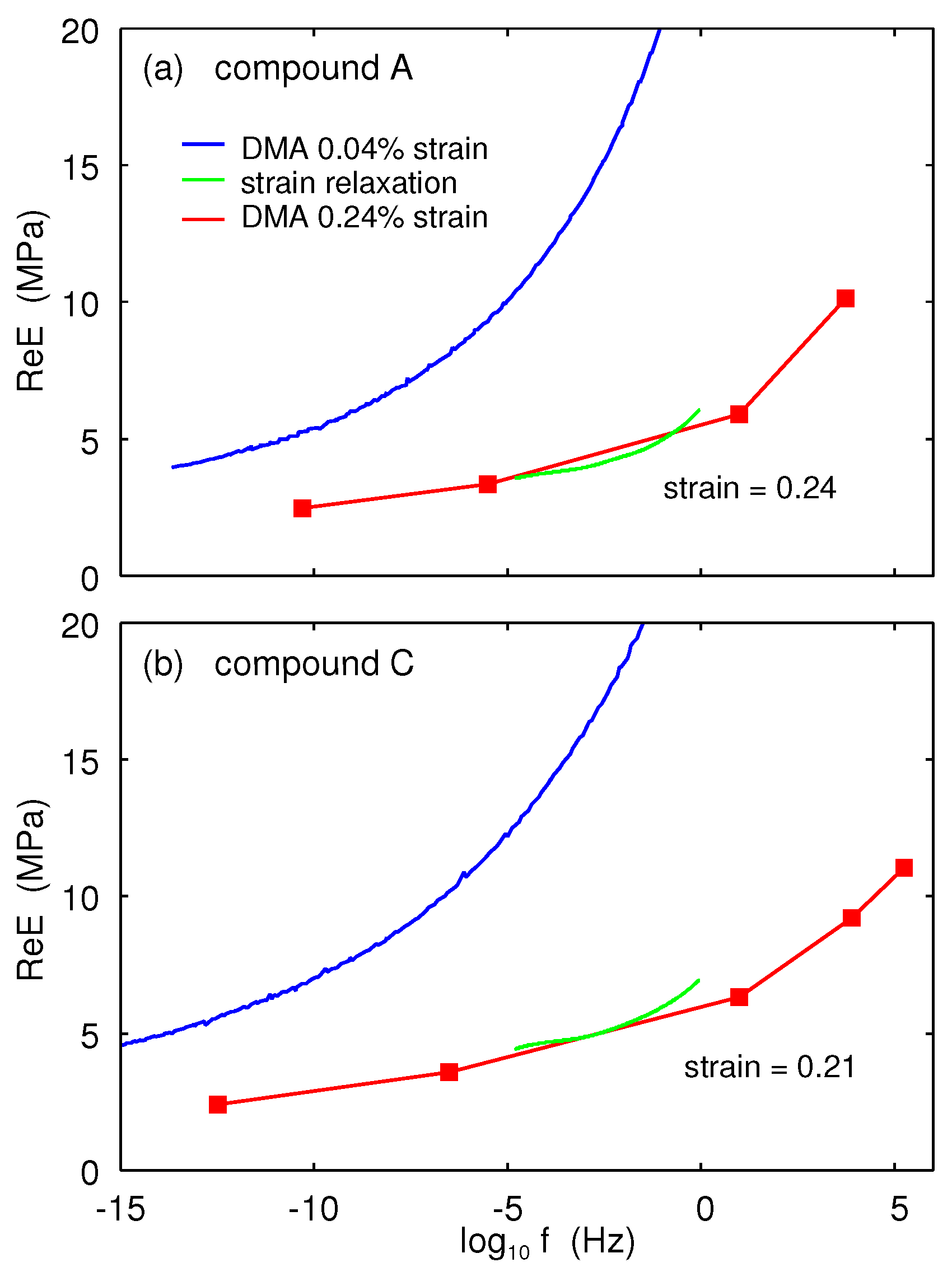
The blue lines in Figure 7 show the real part of the small-strain (0.0004) viscoelastic modulus $E\left(\omega \right)$ as a function of frequency for compound A (a) and C (b). The red lines were obtained from the measured (non-linear) shear modulus assuming $E=3G$ and the strain amplitude ${ϵ}_0=0.24$ in (a) and ${ϵ}_0=0.21$ in (b). (Note: we preferred to use the effective modulus obtained using $E=3G$ rather than the one measured directly in the oscillatory tension mode, since strain relaxation (creep) does not have a pre-strain so it is best to compare it with the effective modulus obtained from the shear modulus.) Also shown (green lines) are the real parts of the modulus for compounds A and C as obtained from the strain relaxation measurements using (9) with $H_{ϵ}(\tau ,{ϵ}_0)$, obtained as described above, from fitting the strain relaxation data to the fit function in the form (10). 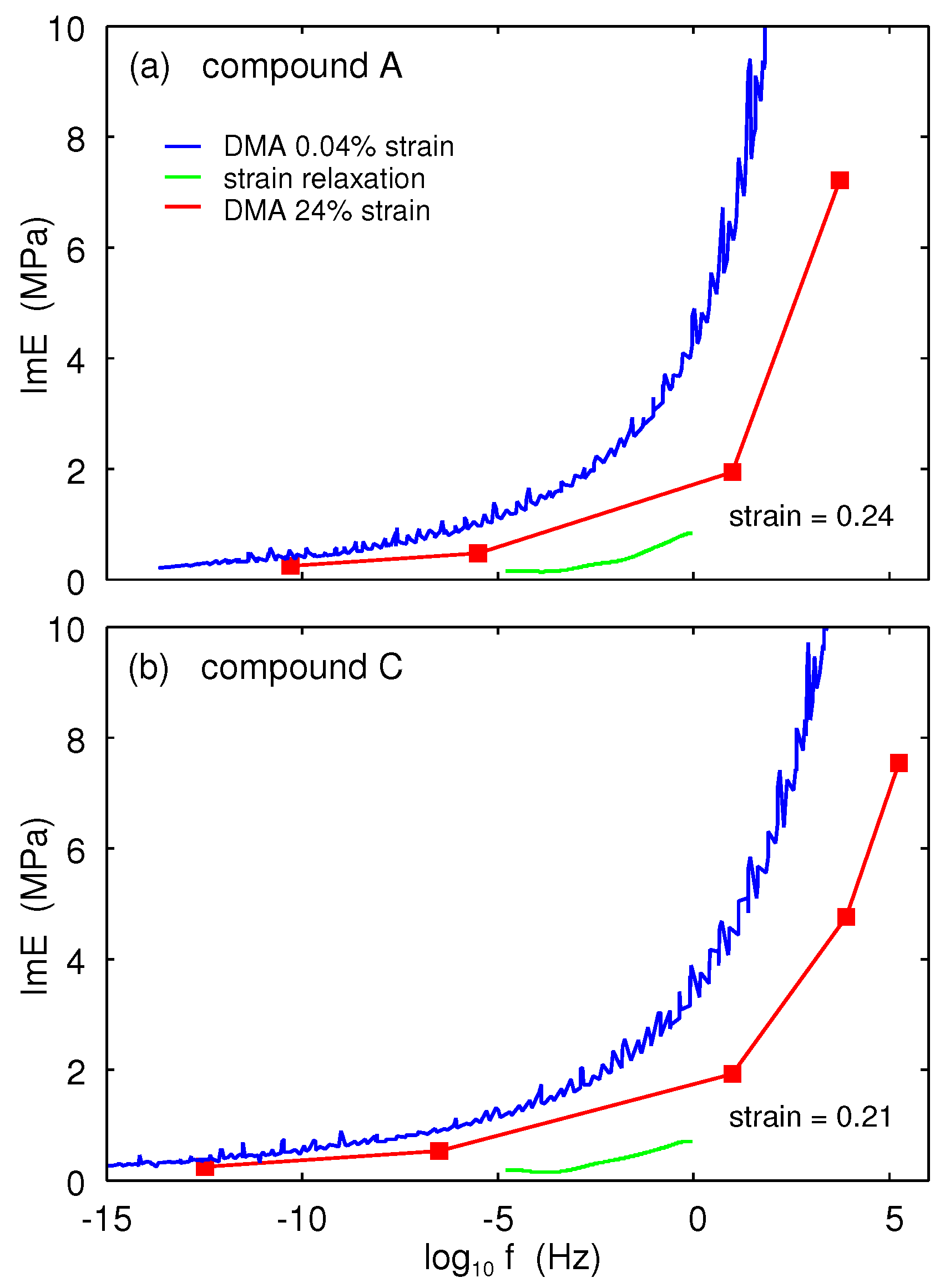In this case, the agreement between the two different procedures for obtaining the nonlinear function $\mathrm{Re}E(\omega ,{ϵ}_0)$ is quite good. However, for the imaginary part $\mathrm{Im}E(\omega ,{ϵ}_0)$, the two procedures give very different results. This is shown in Figure 8. Clearly, the direct measurement of $E(\omega ,{ϵ}_0)$ using oscillatory strain gives much higher energy dissipation than that obtained from the strain relaxation data. Note that for small strains, in the linear response region, both procedures give the same result for $\mathrm{Re}E\left(\omega \right)$ and $\mathrm{Im}E\left(\omega \right)$. This difference between the linear and non-linear case is due to the fact that in the non-linear region the Kramers–Kronig relation is not valid, and the non-linear E-modulus, as defined above, cannot be represented in the form of Equations (6) or (9).

5. Discussion

For rubber friction studies, where the viscoelastic properties of the rubber enter as an important input, the strain can be very large and it is important to include non-linearity in the viscoelastic response. However, in the analytical treatment of sliding friction, it is nearly impossible to include non-linearity in a completely rigorous way. One approach is to assume a linear relation between stress and strain in the theoretical derivations, but instead of using the small strain modulus $E\left(\omega \right)$, use an effective modulus $E(\omega ,ϵ)$ for a typical strain $ϵ$ involved in the problem of interest. For sliding friction on the road surfaces $ϵ\approx 1$, therefore, the information is needed on the non-linear response for very large strains.

Now, which is the best experimental way to obtain the large strain modulus? It depends on the application. In the linear response regime, all methods give the same result, so it does not matter whether the modulus is measured in shear (gives $G\left(\omega \right)$ and $E\left(\omega \right)\approx 3G\left(\omega \right)$) or tension (gives $E\left(\omega \right)$) mode or during strain or stress relaxation (gives $E_{\sigma }\left(t\right)$ or $E_{ϵ}\left(t\right)$, of which $E\left(\omega \right)$ can be obtained using Equations (6) + (7) or Equations (9) + (10)). However, as shown above for large strain, all these methods give different results.

For rubber friction on road surfaces, it is clear that a direct measurement of the viscoelastic modulus in response to oscillating applied strain is the best approach since the pulsating deformations acting on the rubber surface during sliding on the hard rough substrate surface (e.g., a road surface) are similar to the oscillatory deformations in the DMA experiment. In addition, in this case, the dissipated energy in response to strain oscillation is correctly described [see Equation (2)]. However, tensile measurements require pre-strain which breaks-up the filler network, which will affect the effective modulus. In rubber friction experiments, road asperities slide along the rubber surface and there is only very little pre-strain. This suggests that the shear modulus (obtained without pre-strain) is probably better than the modulus obtained in tension with pre-strain. An even better method was proposed in Ref. 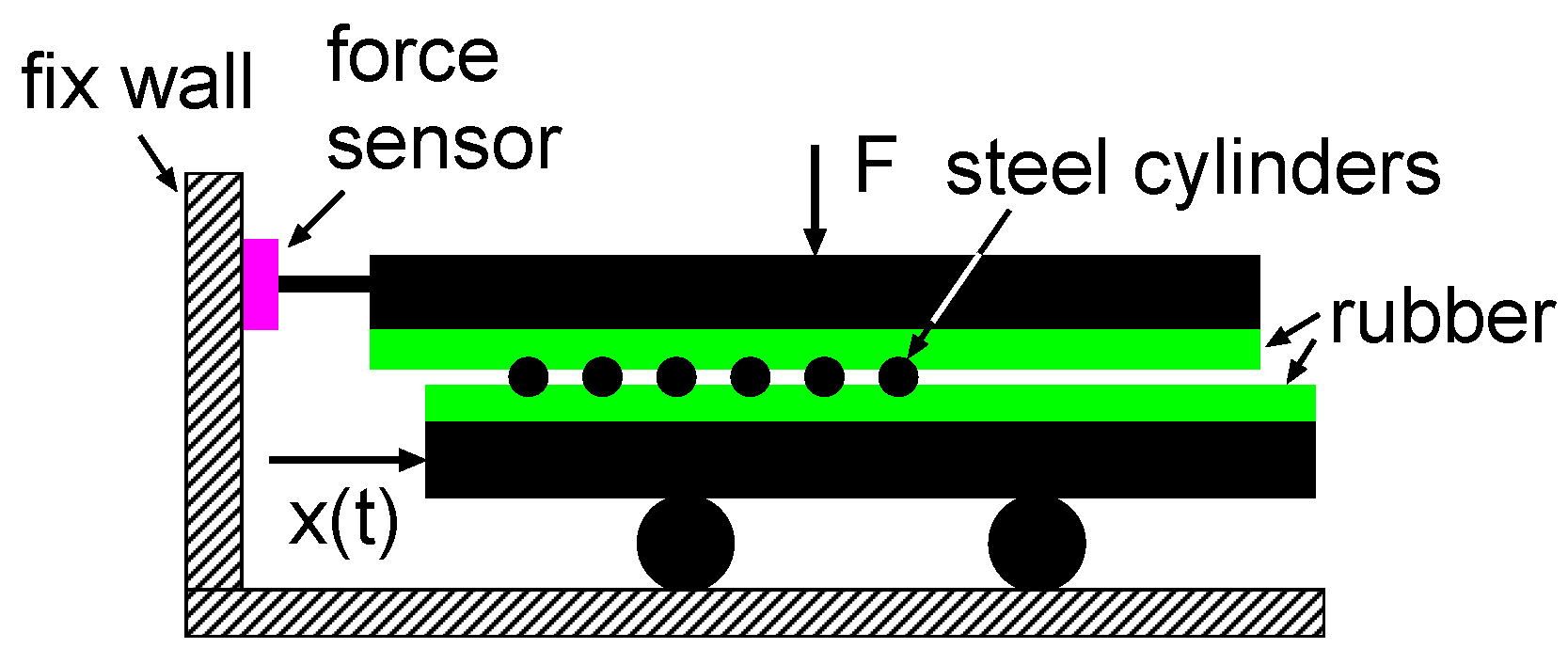[17] (see Appendix B in Ref. [17]). It involves rolling friction experiments (see Figure 9), where the associated deformations are very similar to when the asperities slide over the rubber surface.

In some other applications the non-linear E-modulus, measured during strain (or stress) relaxation, could be more suitable, e.g., to study the increase in contact area with time when a rubber block is loaded against a rough surface at time $t=0$ with a constant external load force (strain relaxation) or constant applied compression (stress relaxation) [18,19].

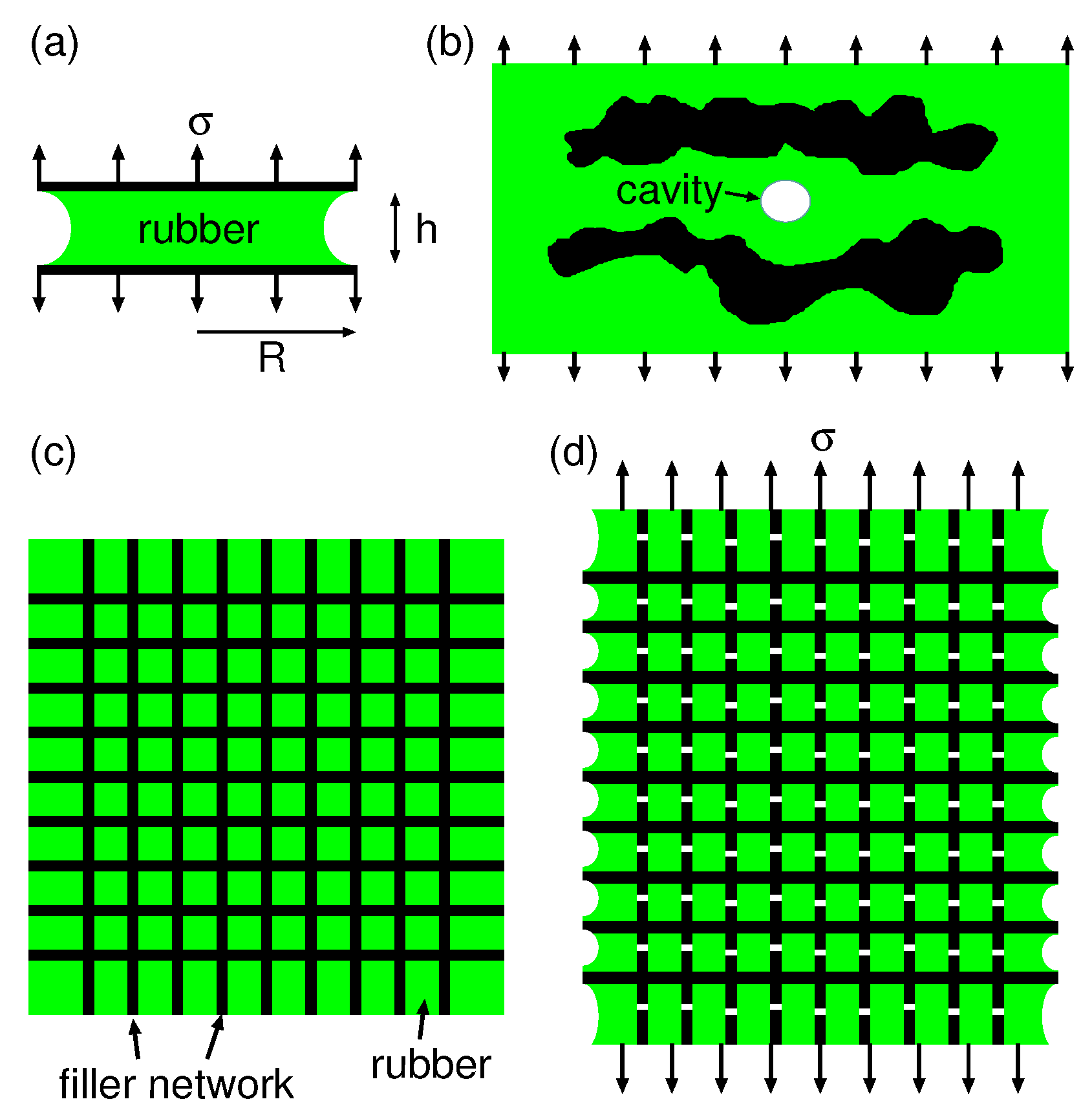
Many ideas have been presented for the increase in the low-strain rubber modulus when filler particles are added to rubber. Here we suggest that it may be due to a confinement effect as illustrated in Figure 10. It is well known that if a rubber sheet is confined between two rigid surfaces, the effective Young’s modulus increases due to the confinement. Thus, if the rubber sheet has the thickness h and is confined between circular rigid surfaces with radius R, then the effective Young’s modulus (Gent–Lindley equation) [20] $E_{\mathrm{eff}}\approx E(1+2S^2)$ where $S=R/2h$.

The confinement of rubber between filler cluster regions in rubber may have a similar effect on the low-strain modulus as the rigid sheets in Figure 10a. This is illustrated with an extreme case in Figure 10c,d where rigid sheets are embedded in the rubber matrix. We note that the sheets are under compression in the transverse direction while they are under tension in the direction of the applied stress. A filler particle cluster may be more stable under compression than under tension. Thus, as long as the applied stress is not too large the filler network may be stable in the transverse direction, giving a strong increase in the effective Young’s modulus due to the Gent–Lindley confinement effect. This picture of the enhancement in the low-strain modulus is similar to the suppression-in-the-composite-Poisson-ratio model proposed by Smith et al. [12].

The origin of the the enhancement in the low-strain modulus presented above is supported by recent experimental results for the formation of cavities in filled rubbers when a rubber slab is exposed to elongation. In this case it is observed [21,22] that cavitation start in regions between filler clusters (see Figure 10b), as expected because of the Gent-Lindley confinement effect since the negative pressure is highest in the central region between the cluster surfaces.

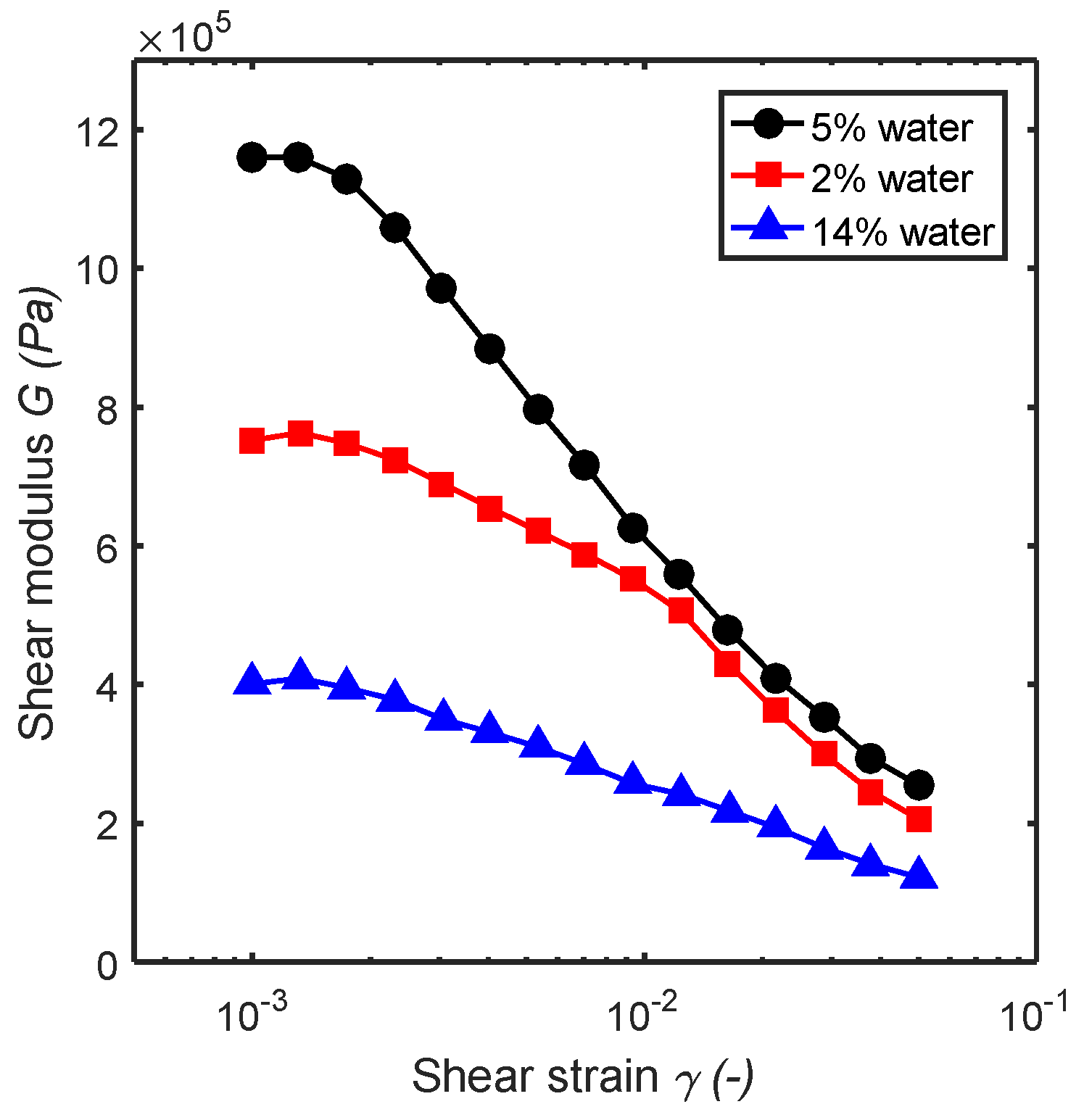
The strong drop in the effective modulus with increasing strain amplitude of filled rubber compounds is also observed for other particle systems. Thus, the effective shear modulus of (slightly) wet sand as a function of the strain amplitude is very similar to that of the filled rubber compounds [23,24]; see Figure 11. For slightly wet sand, water capillary bridges bind the sand grains together. Similarly, the filler particles in rubber interact with a weak attraction, of different physical origin than for sand. Note that the drop in shear modulus for sand occurs over a similar range of strain as for filled rubber compounds, and that the magnitude of the drop is similar. This strongly indicates the same physical origin of both phenomena. Here we note that the formal theory has been developed for granular materials which may also have implications for filled rubber compounds. This theory is based on Edwards statistical mechanics for jammed granular matter, see Refs. [25,26]. One difference is that for a granular material, such as sand, the thermal motion of the particles can be neglected, while the filler particles in rubber can be very small (of nanometer size) and in this case thermal motion cannot be neglected. The exact theory of the viscoelastic properties of filled rubber compounds still does not exist.

6. Summary and Conclusions

We have studied the linear and nonlinear viscoelastic properties of two tire tread compounds, and discussed the difference in the non-linear response between oscillatory tensile and shear modes. We have also analyzed strain relaxation data for the same systems. We have discussed which type of measurements is most suitable for obtaining the viscoelastic modulus to be used in rubber friction calculations.