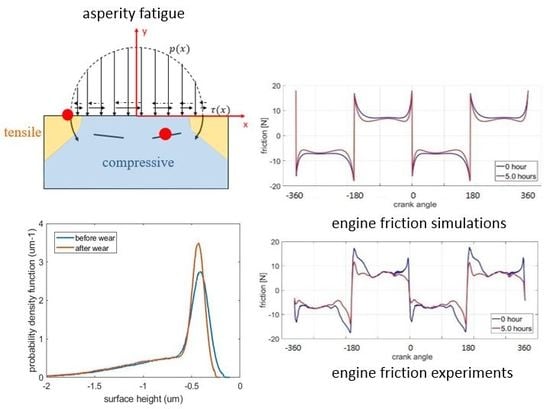
Both wear coefficient and friction change from the simulation are evaluated. For the tested surfaces, wear rate has relatively large magnitude at the beginning but gradually decreases to a constant. In addition, the simulation results also indicate that the constant wear rate for the steady state is proportional to external load if the external load is solely supported by the asperity contact. Therefore, the wear rate predicted with the fatigue mechanism employed here fits the Archard law [
23]. Friction for the entire engine cycle is calculated based on existing friction correlations [
21]. Different liner surface finishes are tested and compared with engine experimental results. Different cast iron liner finishes are utilized for both simulation and floating liner engine testing. The effectiveness of the asperity fatigue model is verified by the comparison between simulation results and experimental results, which show similar trends for engine friction change after break-in wear. The experimental friction measurements are obtained from floating liner engines (FLE). The detailed experimental setup was adequately described by Westerfield [
19]. The design of the FLE was originally provided by Takiguchi [
24,
25]. The FLE is a specialized internal combustion engine that allows measurement of friction contributions from the piston assembly while the engine is in operation.
3.1. Results of Liner Wear during Break-In Period
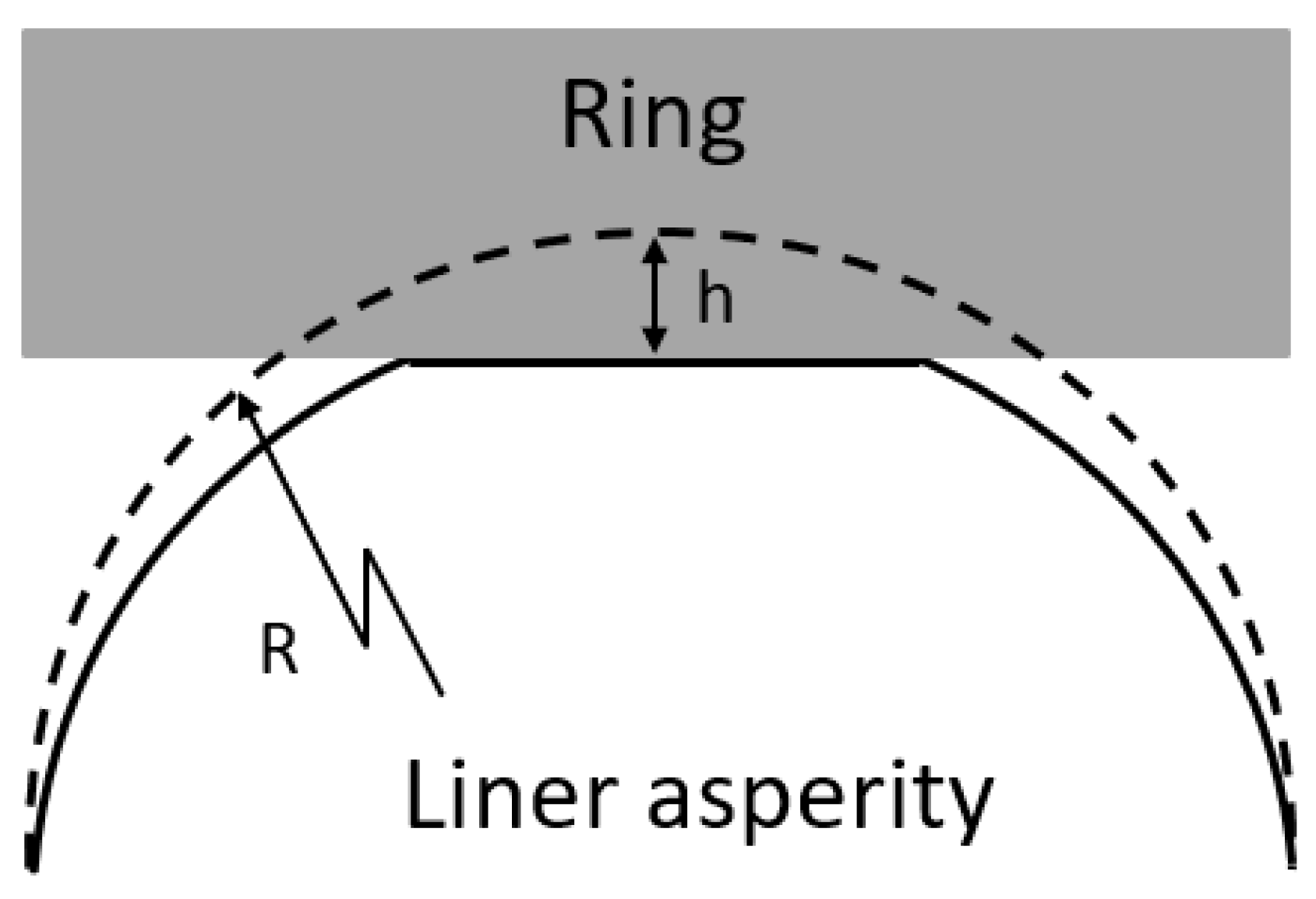
In this section, liner wear break-in simulation results are presented based on the asperity fatigue wear model. Liner surfaces with different finishes are tested to investigate the impact of roughness, denoted as GG07, GG09, GG21, GG28, and GG30, shown in
Figure 4 with the Daimler liner finish classification [
20]. The surfaces used here as the inputs of the wear model are generated numerically based on the real optical measurements [
26]. For each surface, the external nominal pressure varies from 1 MPa to 4 MPa in order to also study the effect of pressure on fatigue wear.
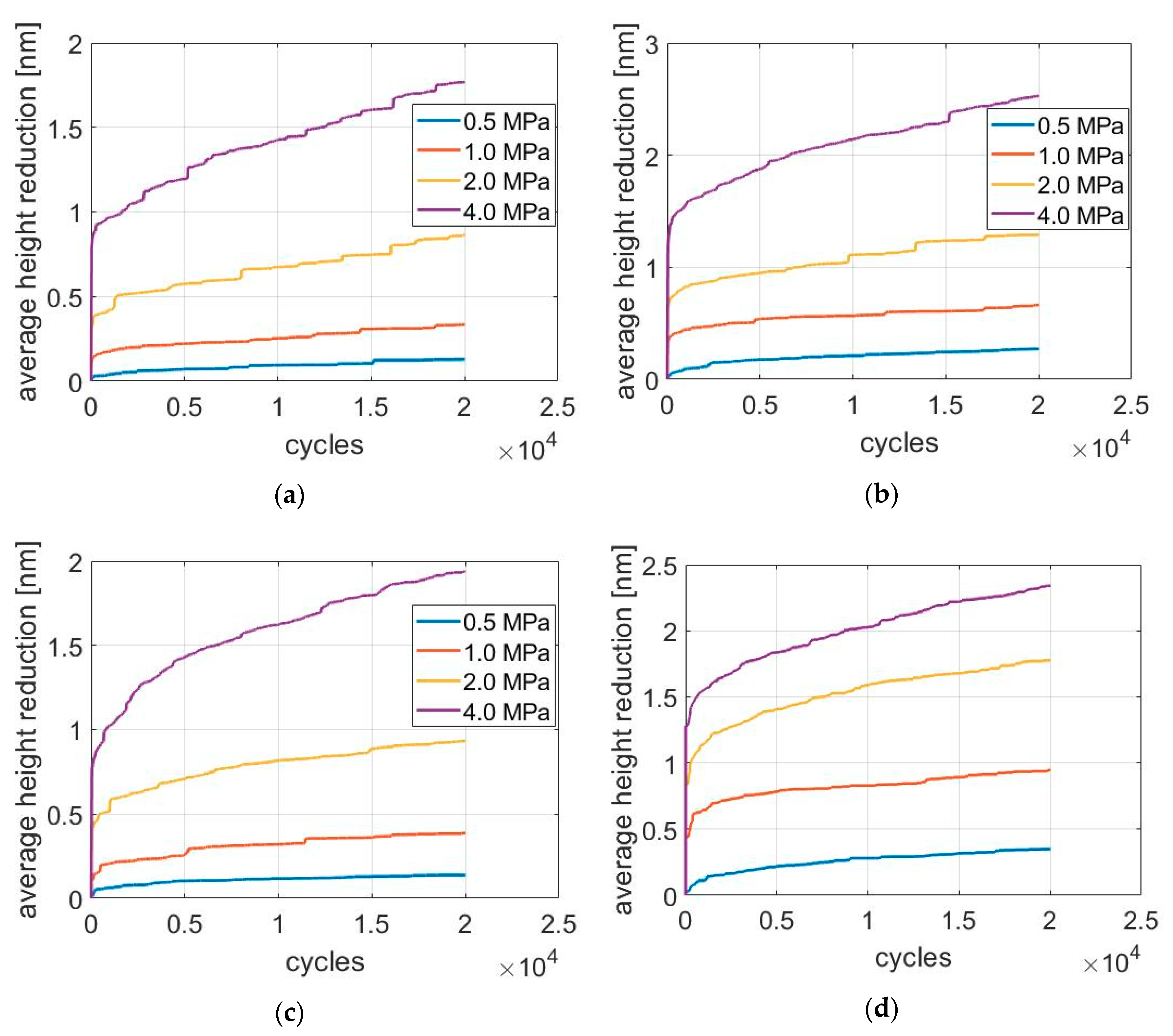
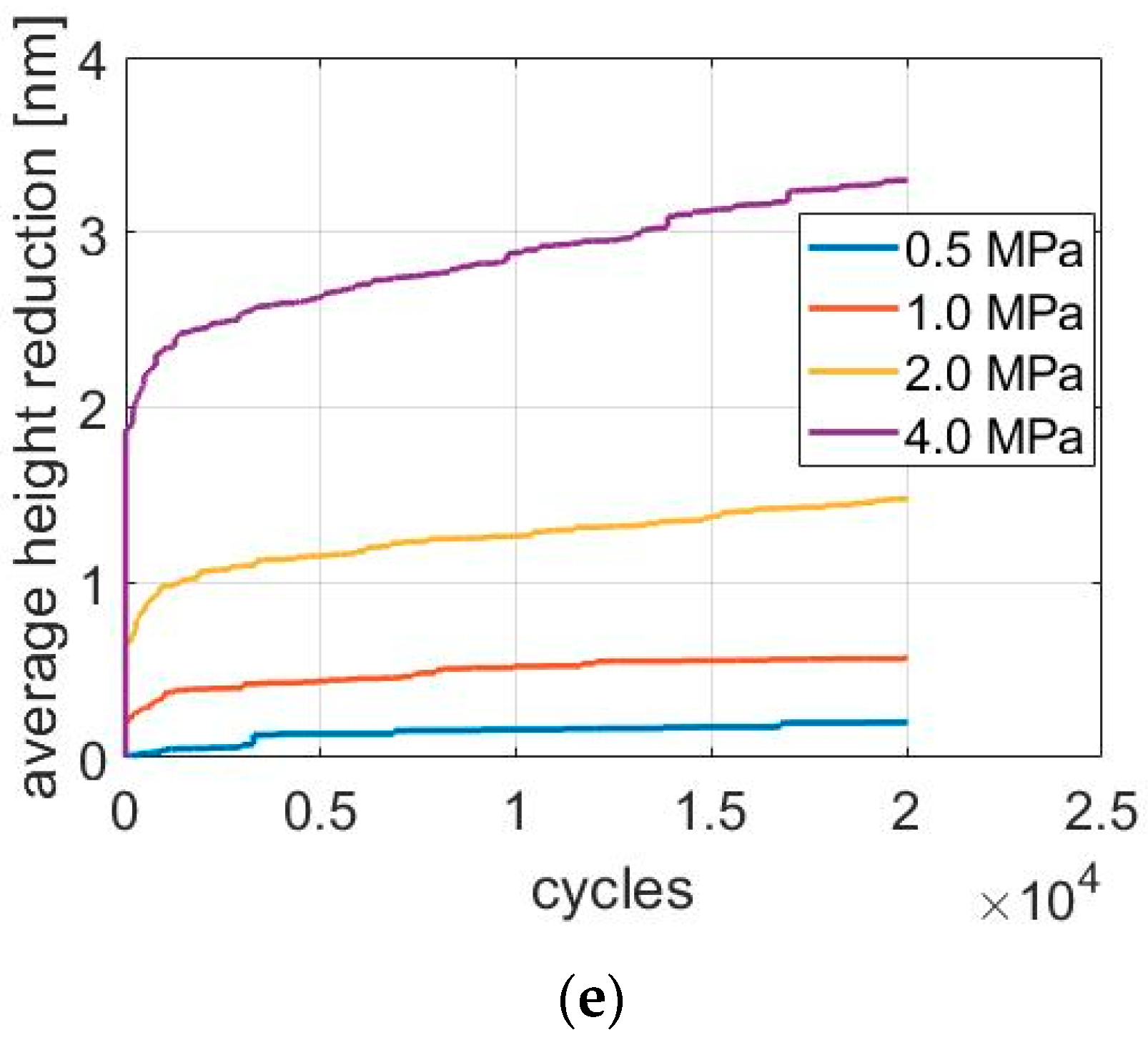
Figure 5 shows break-in wear as a function of time (number of sliding cycles) for all 5 liner finishes. Wear is evaluated by the average height reduction over the entire surface. According to the results of liner wear simulation, the wear rate of the liner is relatively large at the beginning, but gradually reduces to a steady value for all different nominal stresses. Moreover, the steady-state wear rate is proportional to normal pressure, as indicated in
Figure 6. The vertical axis is the steady-state wear rate, which is evaluated by the average surface height reduction over each thousand running cycles. For the wear of metallic materials, Archard’s law is a widely used correlation that quantitatively describes sliding wear and external parameters; the volume of wear debris for metal sliding is proportional to the product of normal load and sliding distance, but inversely proportional to the material hardness [
23,
27]:
In Equation (9), V is the volume of wear debris, and P, L, and H are external normal pressure, sliding distance, and material hardness, respectively. Here, k is the wear coefficient, which is a constant for a certain material with a specific surface finish. As one important mechanism in metal wear, asperity fatigue wear obeys Archard’s law. Therefore, it is reasonable and essential to calculate the wear coefficient of surfaces with different finishes, which is conventionally used as a parameter to evaluate wear resistance of a surface.
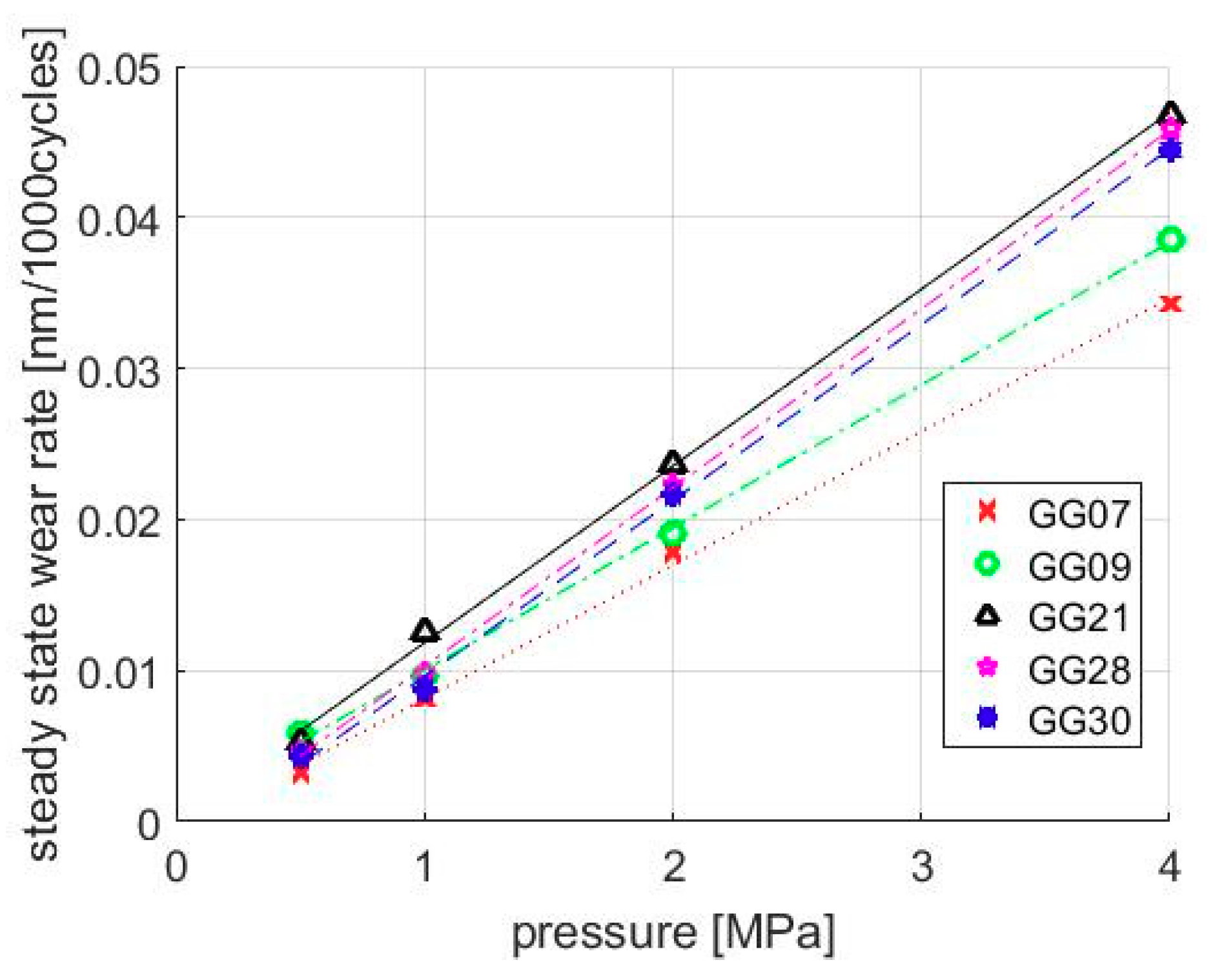
Corresponding to the constant slope in
Figure 6, the wear coefficient based on Equation (6) is presented in
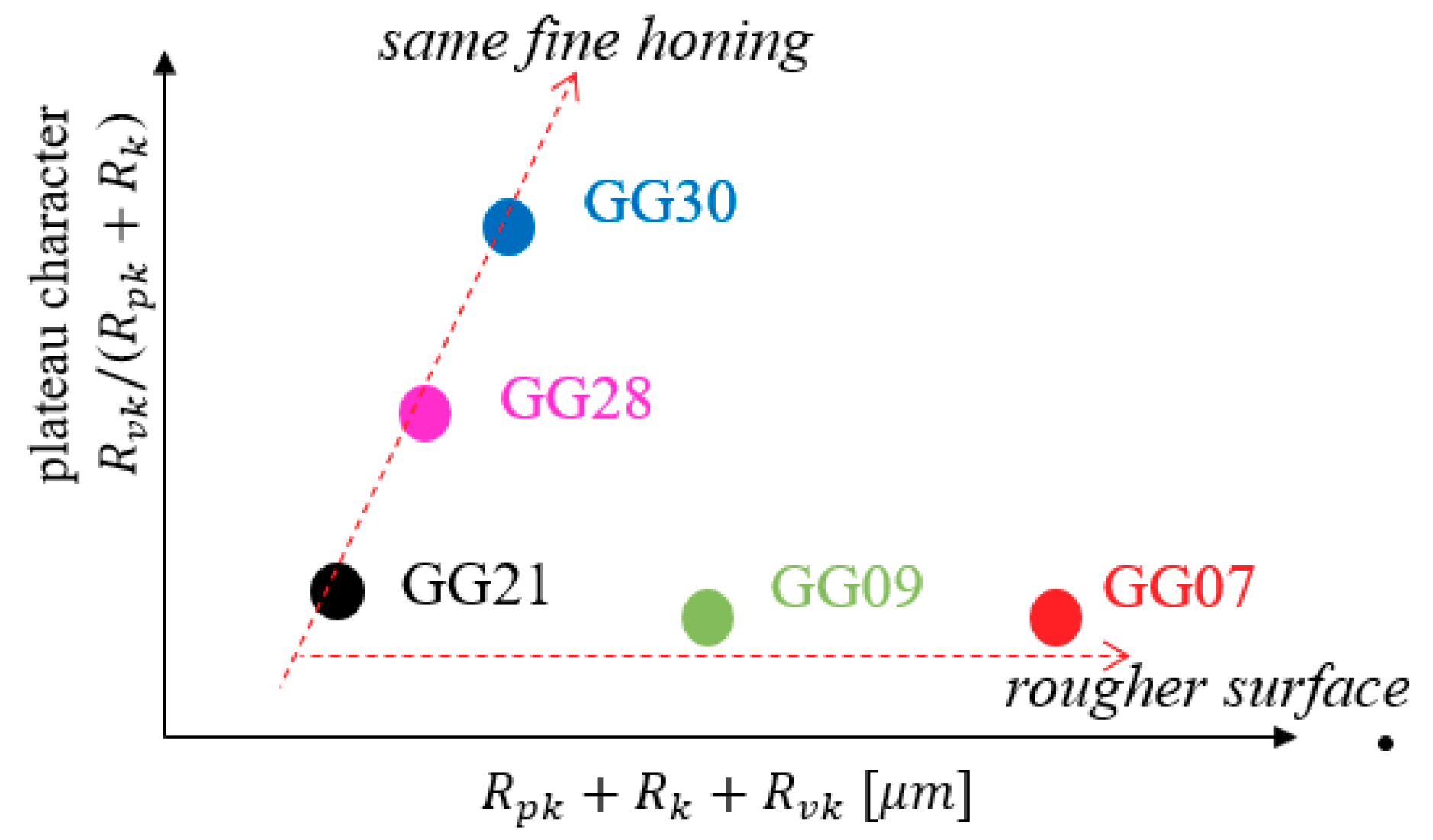
Table 2. It is essential to point out that the wear coefficients of GG21, GG28, and GG30 liner finishes have approximately the same value, indicating the steady-state wear rates of these surfaces are very close. The reason may be found from their manufacturing procedures. As illustrated in
Section 2.5, the only difference among GG21, GG28, and GG30 finishes is the height of the fine finish. Although the plateau ratios are different for these three surfaces because of the fine finish, plateau regions have the same roughness level. Additionally, the size and shape of contact asperities are statistically the same for the three finishes. Therefore, it is reasonable that their wear coefficients are so close. Furthermore, the results here imply that the steady-state asperity fatigue wear rate largely depends on the roughness level of the plateau region resulting from fine honing.
3.2. Further Investigations on the Effect of Surface Roughness
In the previous section, simulation results show that the wear rate of a surface depends greatly on its roughness level, especially the size and shape of contact asperities. In order to seek more detailed underlying correlations, additional simulations are conducted for break-in fatigue wear. In the following, the sizes of the asperities are varied artificially to examine the effect on the break-in behavior.
As inputs of the wear model, the roughness matrix representing a rough liner surface has specific resolutions in the sliding direction and circumferential direction, dx and dy. In this section, dx and dy are stretched by a factor of 0.5, 2, 4, and 8 to modify the size and slope of liner surface asperities. A larger stretched scale indicates flatter asperities. Other simulation parameters remain the same as previous simulations.
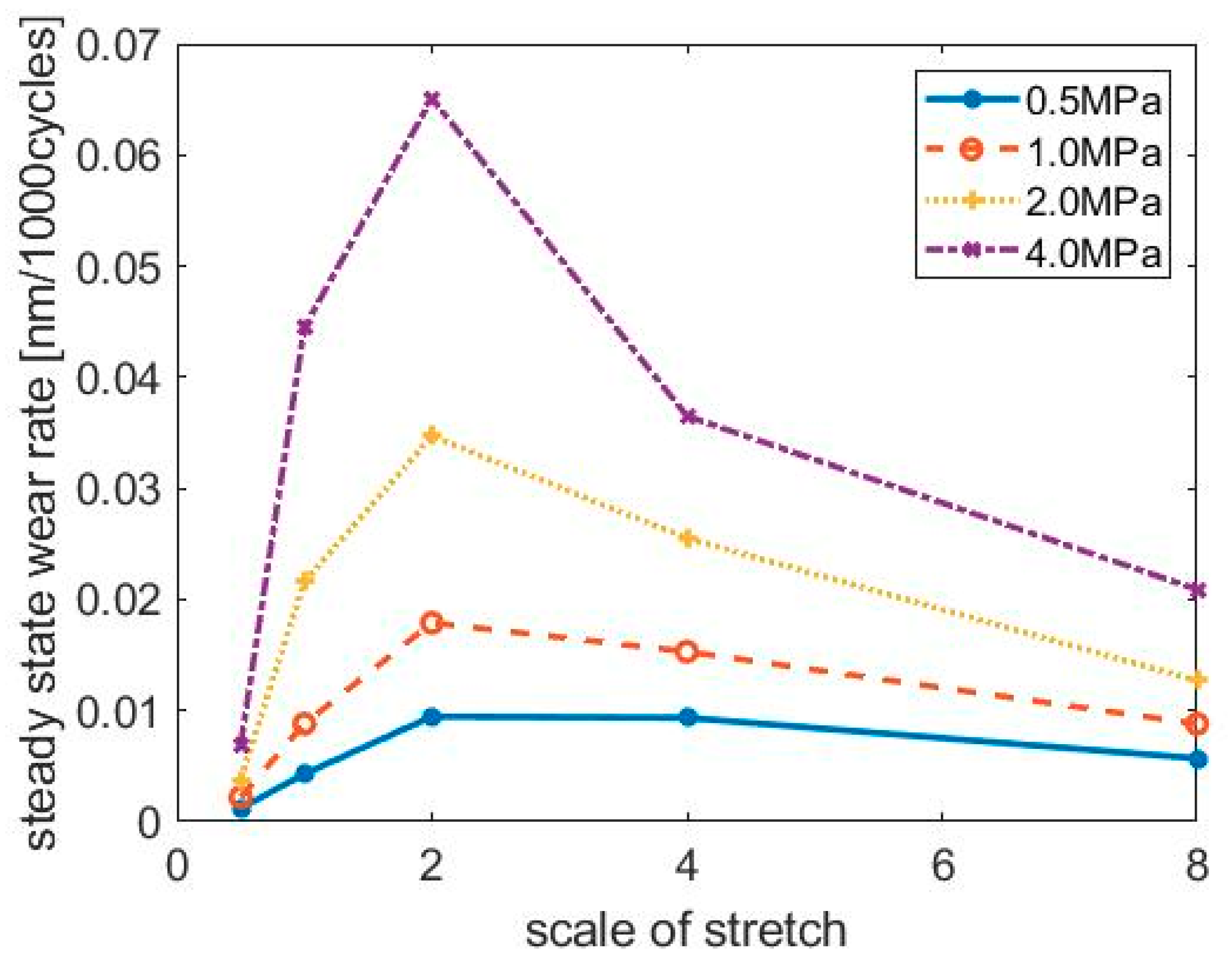
The steady-state wear rate under different stretched scales and normal pressures is summarized in
Figure 7. With a constant normal pressure, the steady-state wear rate first increases, then decreases as the size of the asperities increases. The maximum steady state wear rate for all normal pressures occurs with the stretched scale factor of 2. This interesting result indicates that an optimal asperity flatness can be achieved if the designer of the liner surfaces wants to minimize the break-in period.
Figure 8 qualitatively explains why the optimal asperity flatness and size exist.
As shown in
Figure 8, the original surface is modified with a stretch factor of 0.5 and 2, keeping the height of the asperities constant. In this simple analysis, it is assumed that all asperities have the same shape. Because asperities with a stretch factor of 0.5 have the smallest radius of curvature, according to Equations (1)–(3), the overlapping volume of this liner surface and the ring are the smallest, resulting in a low steady-state wear rate. As the asperities are continuously stretched, the overlapping volume also increases since the average contact pressure is reduced. However, because of the reduction of contact pressure on each asperity, the speed of crack propagation for both surface and subsurface cracks decreases. The two influencing factors, overlapping volume and crack propagation speed, are indeed competitive, as asperities are artificially enlarged with increasing stretch scale factor. If the effect of the crack propagation rate reduction takes the dominant position, the steady-state wear rate decreases. This is the reason why the maximum wear rate occurs at a certain asperity flatness level. One extreme case can help to understand this trend—when the liner surface is ideally smooth with only a single flat asperity, the contact pressure on this asperity is equal to the external nominal pressure. The external nominal pressure on the liner is usually far below the normal range of pressure leading to fatigue wear, resulting in the wear rate being almost zero.
3.3. Calculated Friction Change and Comparison with Experimental Results
The evolution of engine lubrication is studied and compared with experimental results through the friction under one complete cycle and the Stribeck curve. Plots of engine cycle friction can reflect friction variation within each engine cycle. The correlation between piston position and friction level is evaluated through various crank angles. The Stribeck curve is presented to illustrate how the friction coefficient evolves as the sliding speed changes. The theoretical calculation of friction is performed by both the model of hydrodynamic pressure and the model of dry contact. The wear process of different liner finishes is simulated by the asperity fatigue wear model, with friction curves plotted for surfaces before wear and after wear. The break-in FLE experiments were conducted at 80 °C with an engine speed of 400 rpm. The lubricant is a special high-temperature, high-shear (HTHS) oil with a viscosity of 1.4 mPa·s
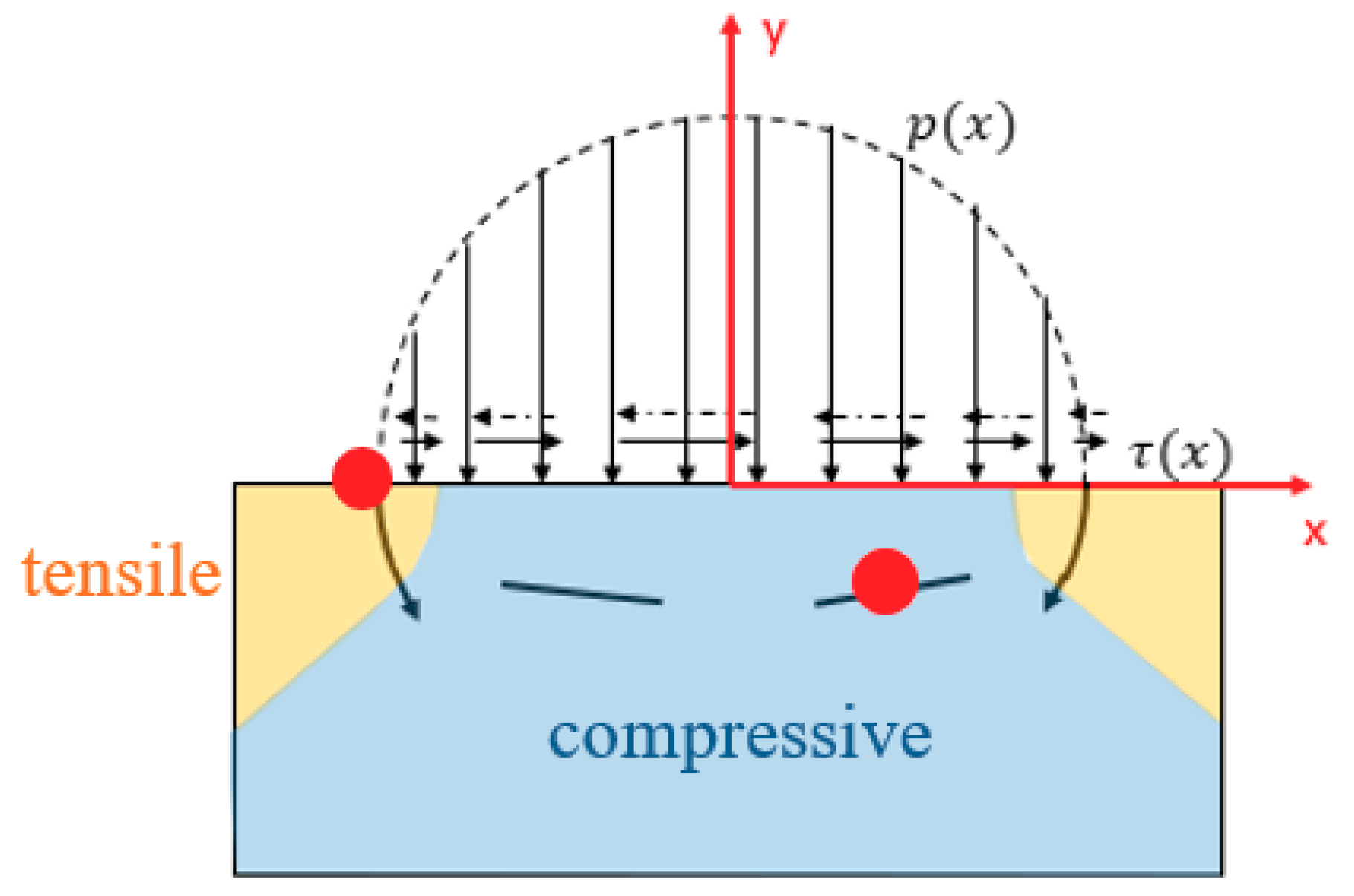
The correlations of hydrodynamic pressure, hydrodynamic shear stress, and contact pressure introduced in
Section 2.6 are utilized to obtain the friction curves for the entire engine cycle. The cycle model is a modified version of the published one [
28] and the major modification is the replacement of the hydrodynamic lubrication submodel with the correlation based on the results of the deterministic model, as described earlier [
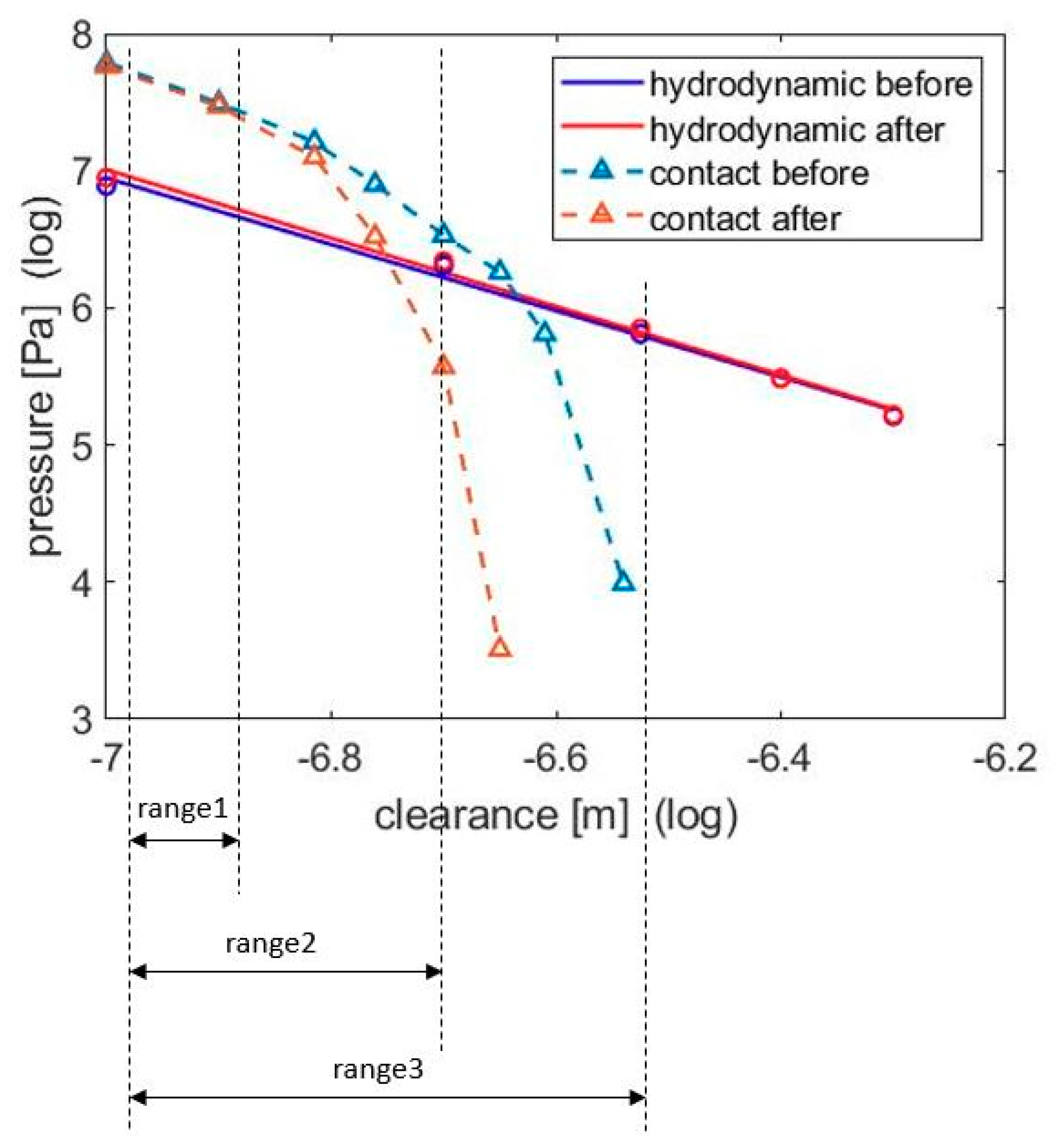
21]. As the ring liner clearance depends on the ring sliding speed, the friction also varies for each engine cycle, with the minimum friction value occurring during mid-stroke at low engine speed. Since the sliding speed is close to zero at the top dead center (TDC) and the bottom dead center (BDC), different engine speeds have similar friction magnitudes at the two positions. When the clearance reaches this smallest value, neither contact pressure nor hydrodynamic pressure show obvious change after wear. The simulated contact pressure and hydrodynamic pressure of the GG30 surface finish are plotted in
Figure 9 as functions of the ring liner clearance. The wear simulation of GG30 is performed using the asperity fatigue wear model, with a simulated duration of five hours, engine speed of 400 rpm, and external nominal pressure of 2 MPa. For simplicity, this nominal pressure is solely supported by the asperity contact in the wear model. Therefore, the wear rate should be considered as the upper bound estimation from the model because part of the ring load is supported by the hydrodynamic pressure in reality.
As shown in
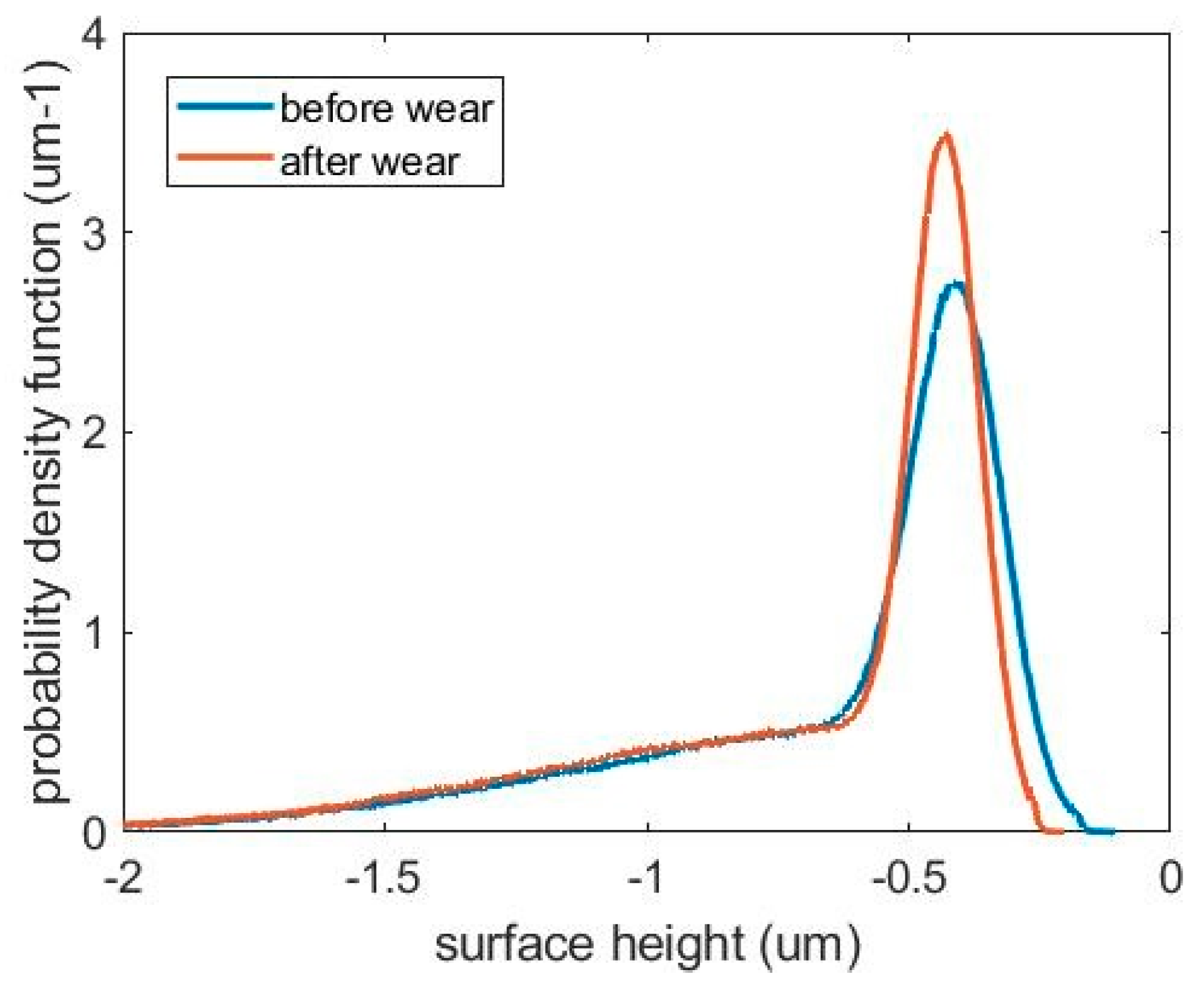
Figure 9, compared with the original surface, the surface after wear simulation has approximately the same hydrodynamic pressure, but the contact pressure is reduced because the asperities are flattened and gradually fractured. This can be further revealed in
Figure 10, which contains the height distribution curves for the liner surface before and after wear simulation. The clearance here in
Figure 9 is defined as the distance between the ring surface and the peak of the plateau. With a worn plateau, the contact pressure reduces after wear. When the ring liner clearance is small, the contact pressure changes little because only high asperities are fractured after 5 h break-in wear. A small clearance exists for low sliding conditions, especially when the piston moves to the top dead center or the bottom dead center. Range 1, range 2, and range 3 correspond to the ring liner clearance range when the engine speed is 100 rpm, 500 rpm, and 1000 rpm, respectively.
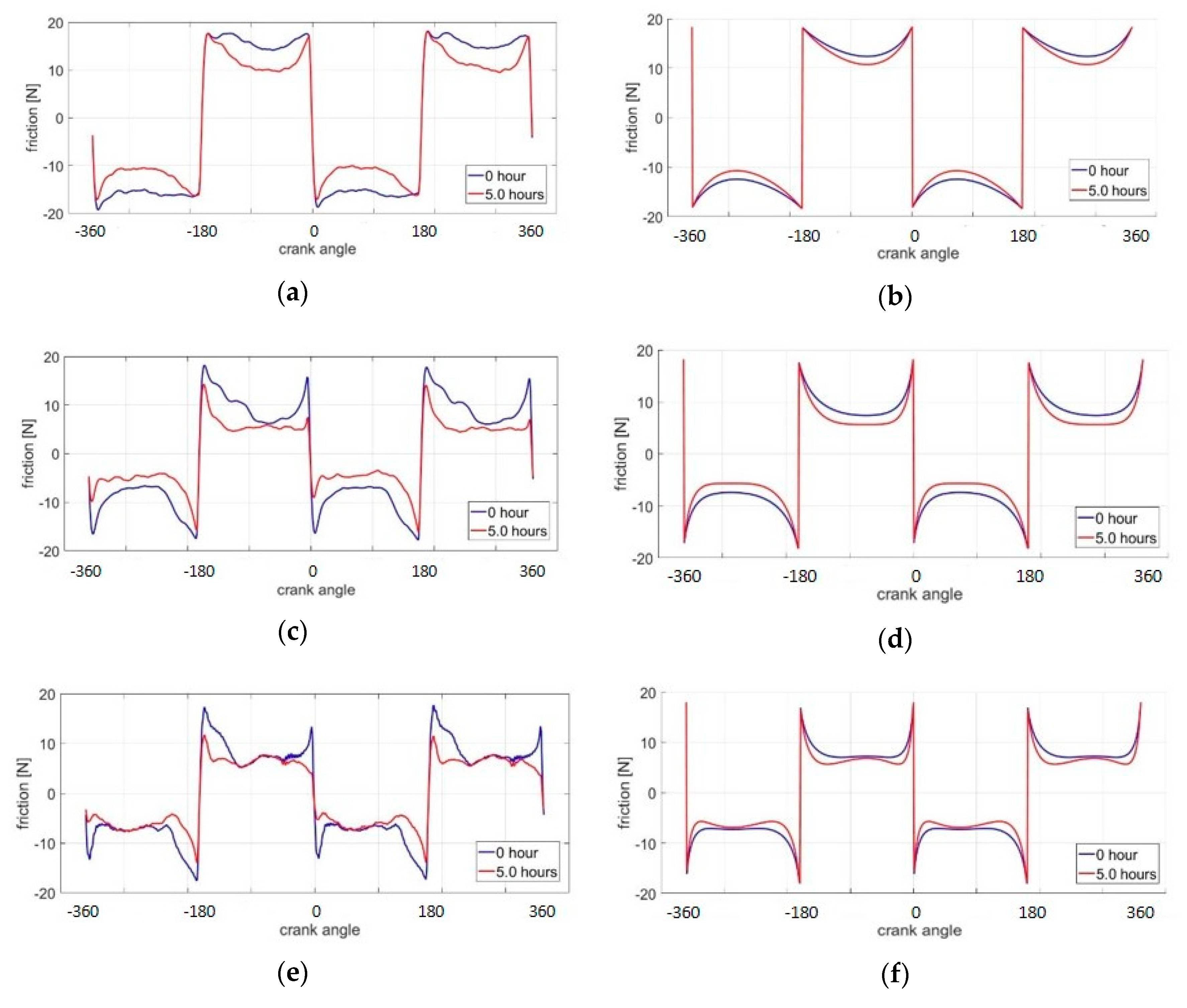
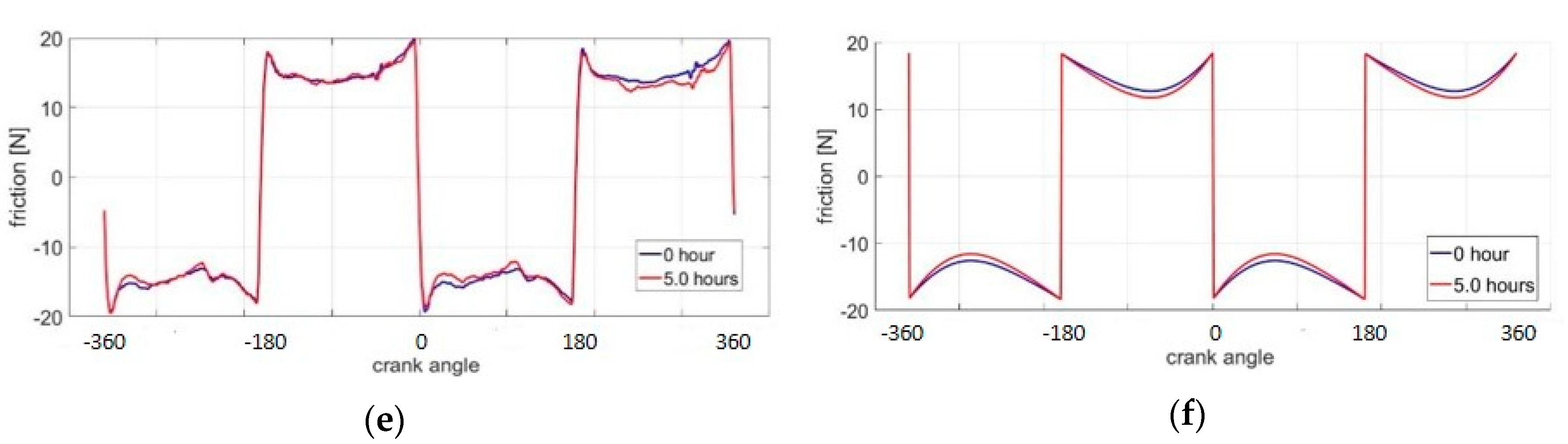
The pressure change shown in
Figure 9 is consistent with the friction curves in
Figure 11, in which the friction does not change much after wear near TDC and BDC. On the other hand, in the mid-stroke region, the ring may have different sliding velocities with different engine speeds. When the engine speed is 100 rpm, the contact pressure has a slight drop. This leads to the friction reduction after wear at mid-stroke in
Figure 11b; here, contact pressure is always the dominant factor, much more so than the hydrodynamic pressure. When the engine speed reaches 1000 rpm, the contact pressure is much lower than hydrodynamic pressure at the mid-stroke, for both conditions before and after wear. Therefore, as shown in
Figure 11f, the friction curves become almost overlapped in the middle. Compared with the friction measurements obtained experimentally, the relatively important trend between hydrodynamic pressure and contact pressure agrees well, as shown in
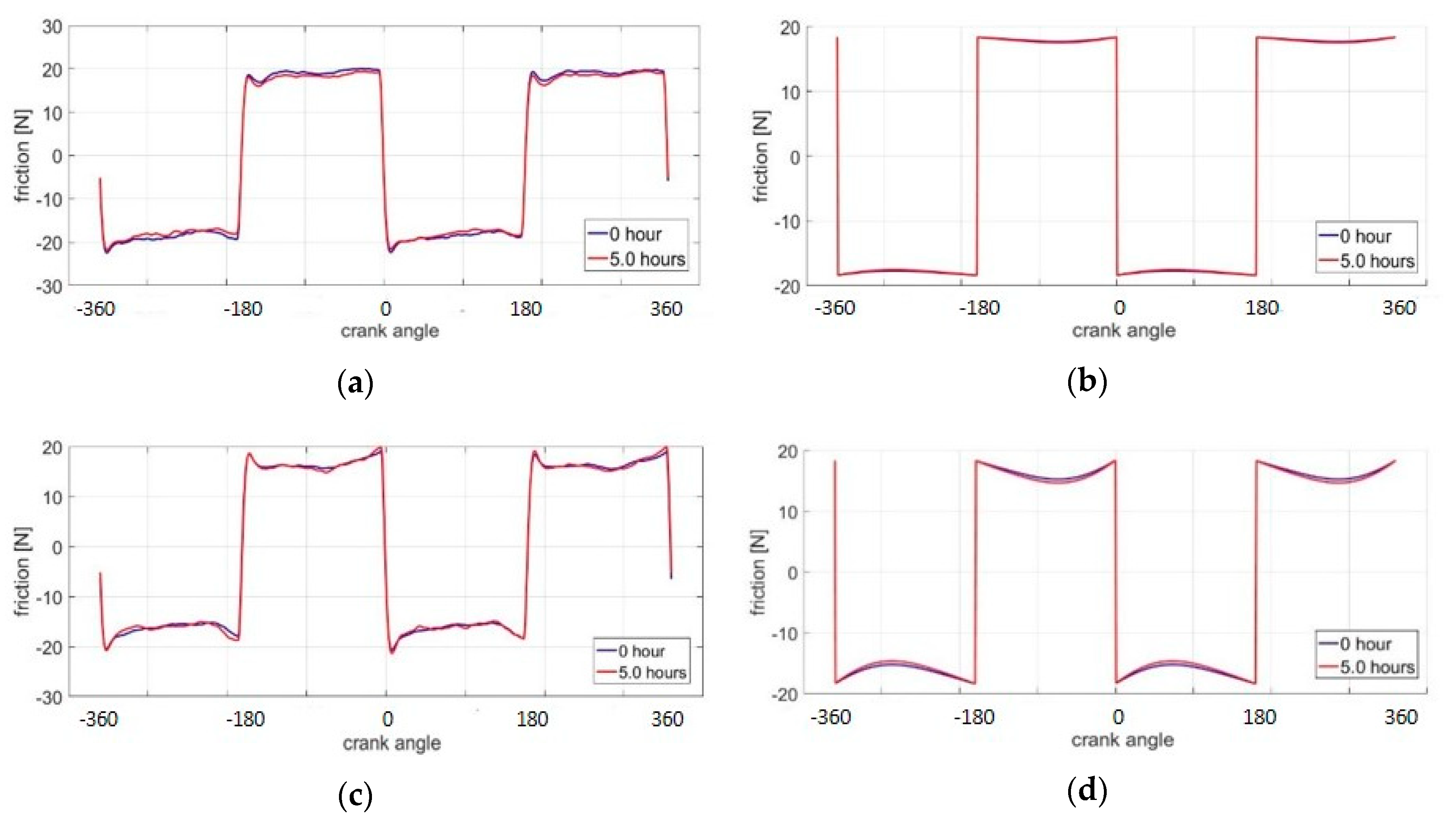
Figure 11. The engine cycle friction curves of GG07 are also obtained in
Figure 12. Unlike GG30, for GG07, the boundary lubrication dominates throughout the whole cycle across all engine speeds. This domination did not change much after 5 h of operation. Two factors may contribute to this difference with GG30. First, the combination of the range of engine speed and the lubricant viscosity does not allow the ring to escape the boundary-lubrication-dominated regime. Second, the average asperity size of GG07 is larger than for GG30, resulting in a lower asperity fatigue wear rate, as mentioned in the previous section. Therefore, the surface topology change for GG07 is also slower, resulting in a less remarkable friction drop for GG07 after wear than for GG30. The experimental measurements also support this difference between GG07 and GG30.
One important mismatch between simulation and experiment is the magnitude of friction drop in GG30. Especially for the engine speed of 100 rpm, the friction drop in the mid-stroke region is larger than the predicted result. As hydrodynamic friction is not dominant at low engine speeds, this indicates that the predicted contact pressure drop is smaller than in experimental measurements. Therefore, the break-in wear rate is also underestimated. One reason for the underestimation of fatigue wear rate comes from the assumption of low yield when calculating crack propagation. However, the plastic regions around cracks are not always small compared with crack lengths. With the extended plastic regions, cracks can propagate faster than predicted in this fatigue model, leading to higher wear rate and more dramatic friction drop. The other possible error source is the assumption that asperity fatigue wear is uniform over the entire liner surface, while in reality asperity contact is different along the stroke during break-in.
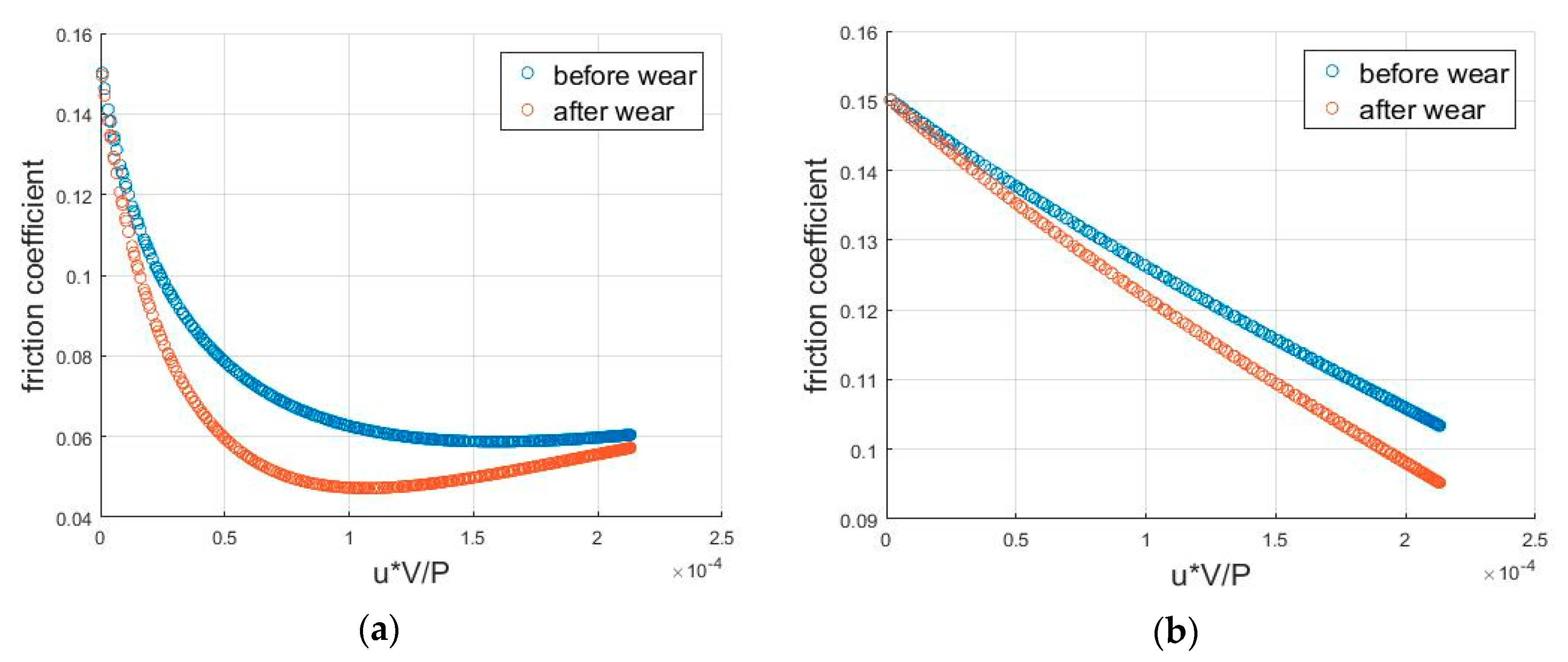
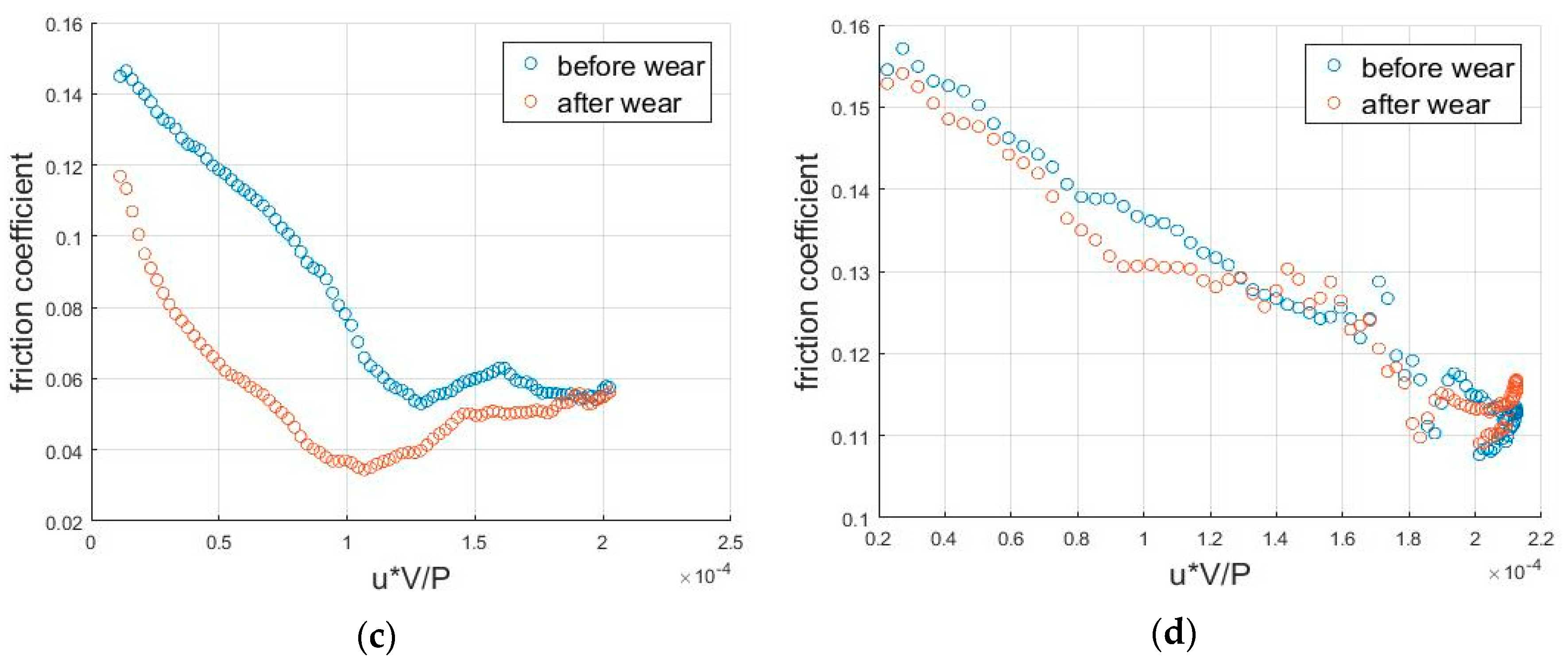
Besides the engine cycle friction plots, the Stribeck curve reflecting the friction coefficient as a function of sliding speed is also plotted in
Figure 13. When the sliding speed is low (boundary lubrication), friction is mainly caused by solid contact. As the sliding speed increases, hydrodynamic friction gradually makes a more significant contribution, so that it changes into mixed friction. If the speed keeps increasing, the two surfaces are separated further and hydrodynamic force becomes the only friction source. Because of the increase of the shear rate, the friction increases again. For GG07, because the surface is rougher, it needs a larger sliding velocity to enter the hydrodynamic lubrication condition, which is beyond the range of engine speed.