Theoretical and Experimental Investigations on Transient Run-Up Procedures of Journal Bearings Including Mixed Friction Conditions
Abstract
:1. Introduction
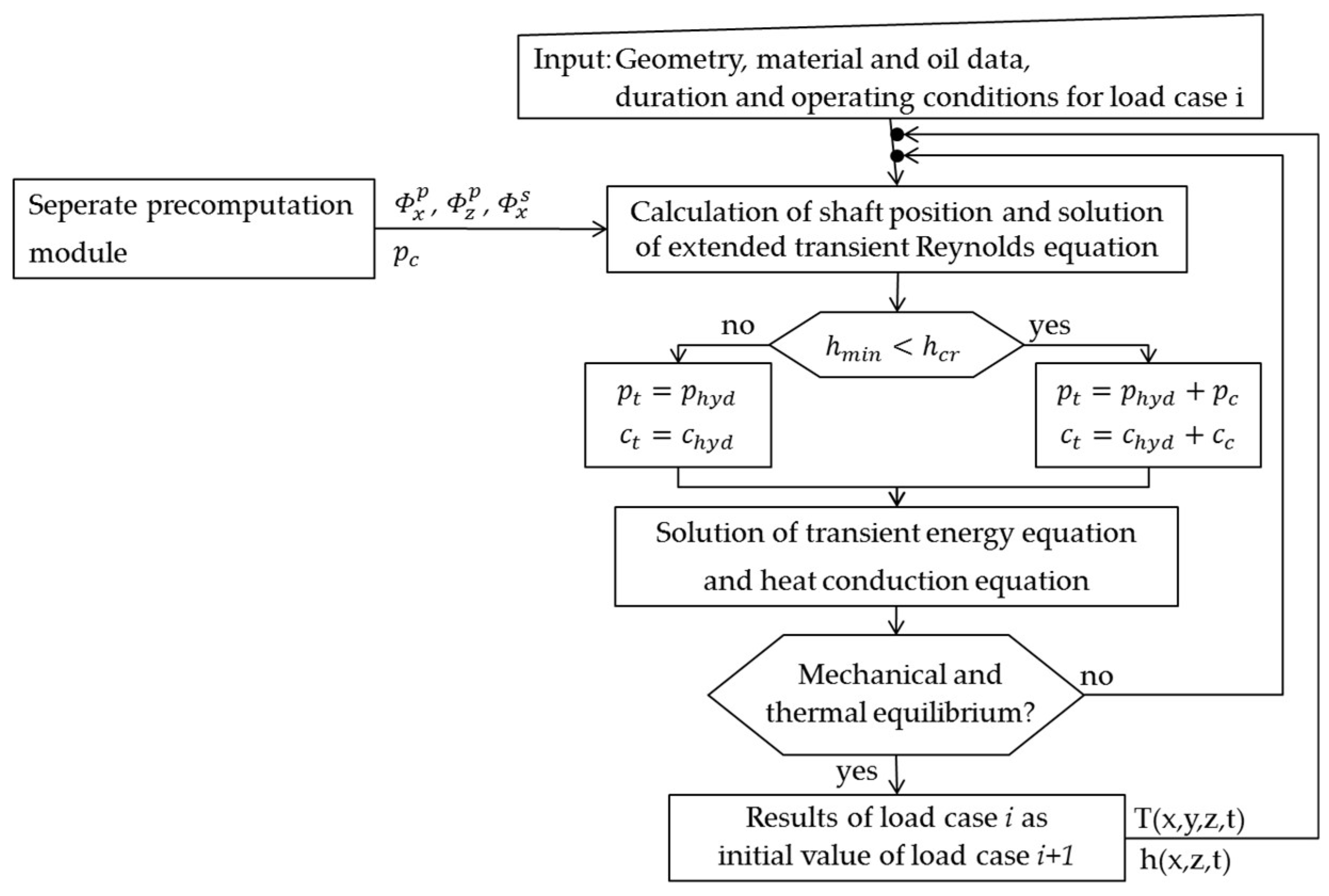
2. Theoretical Analysis
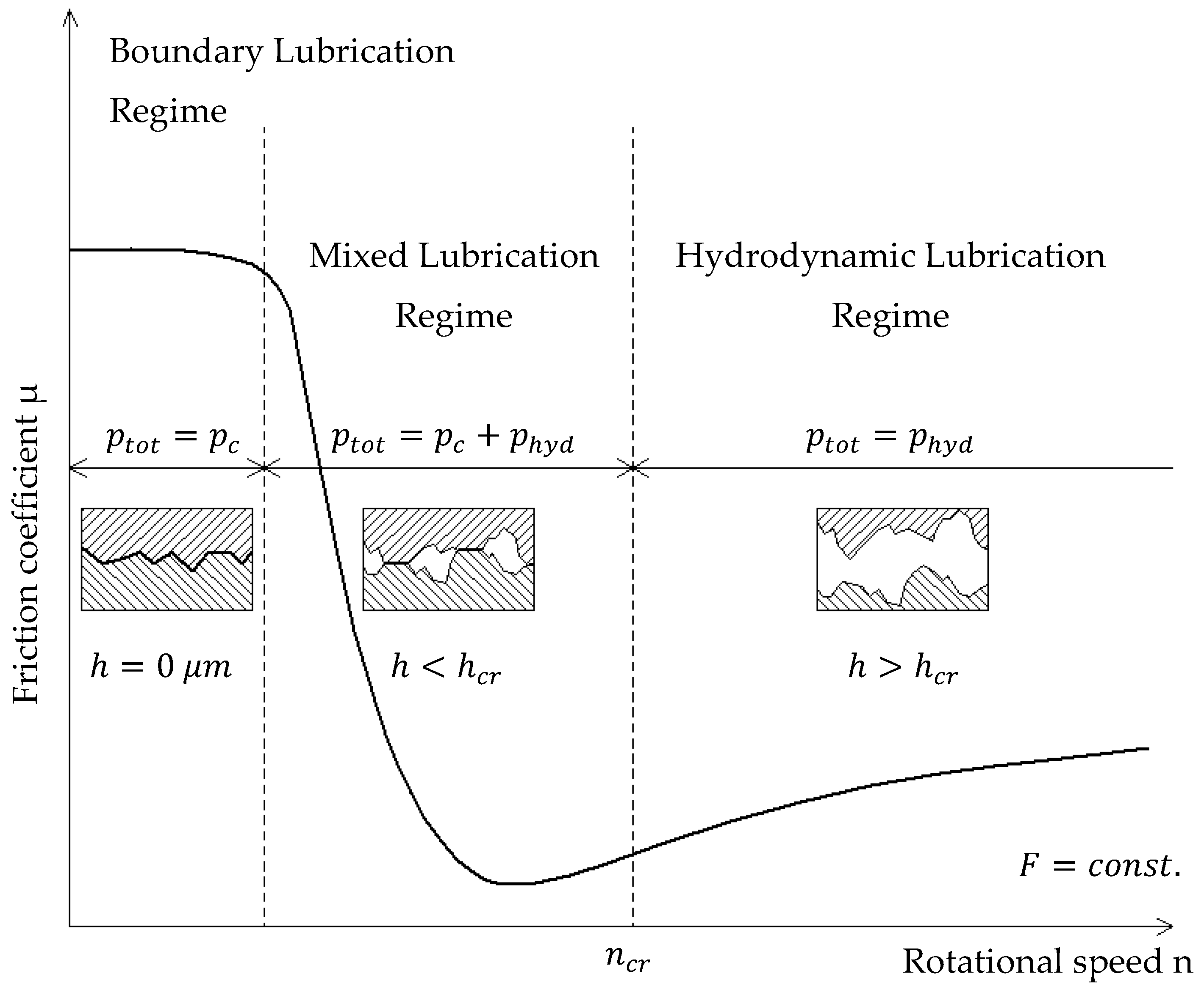
2.1. Mixed Lubrication Model
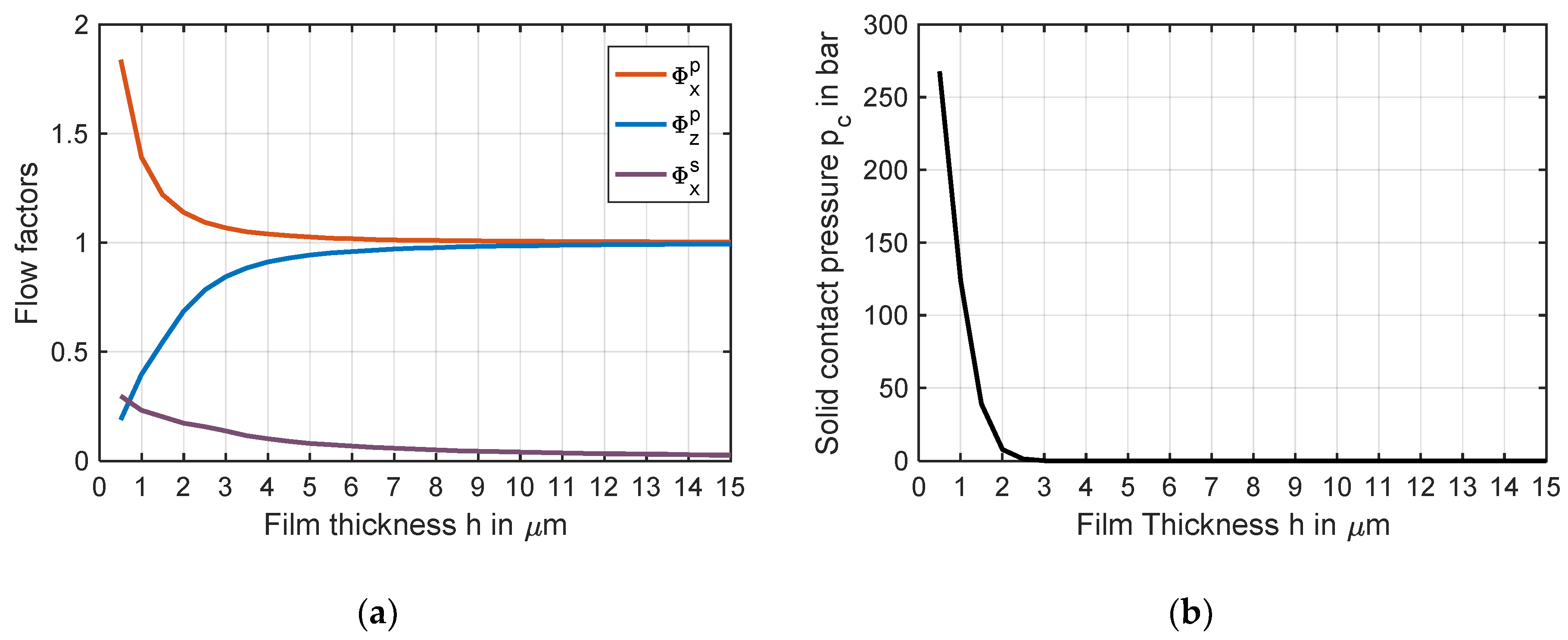
2.1.1. Hydrodynamic Pressure
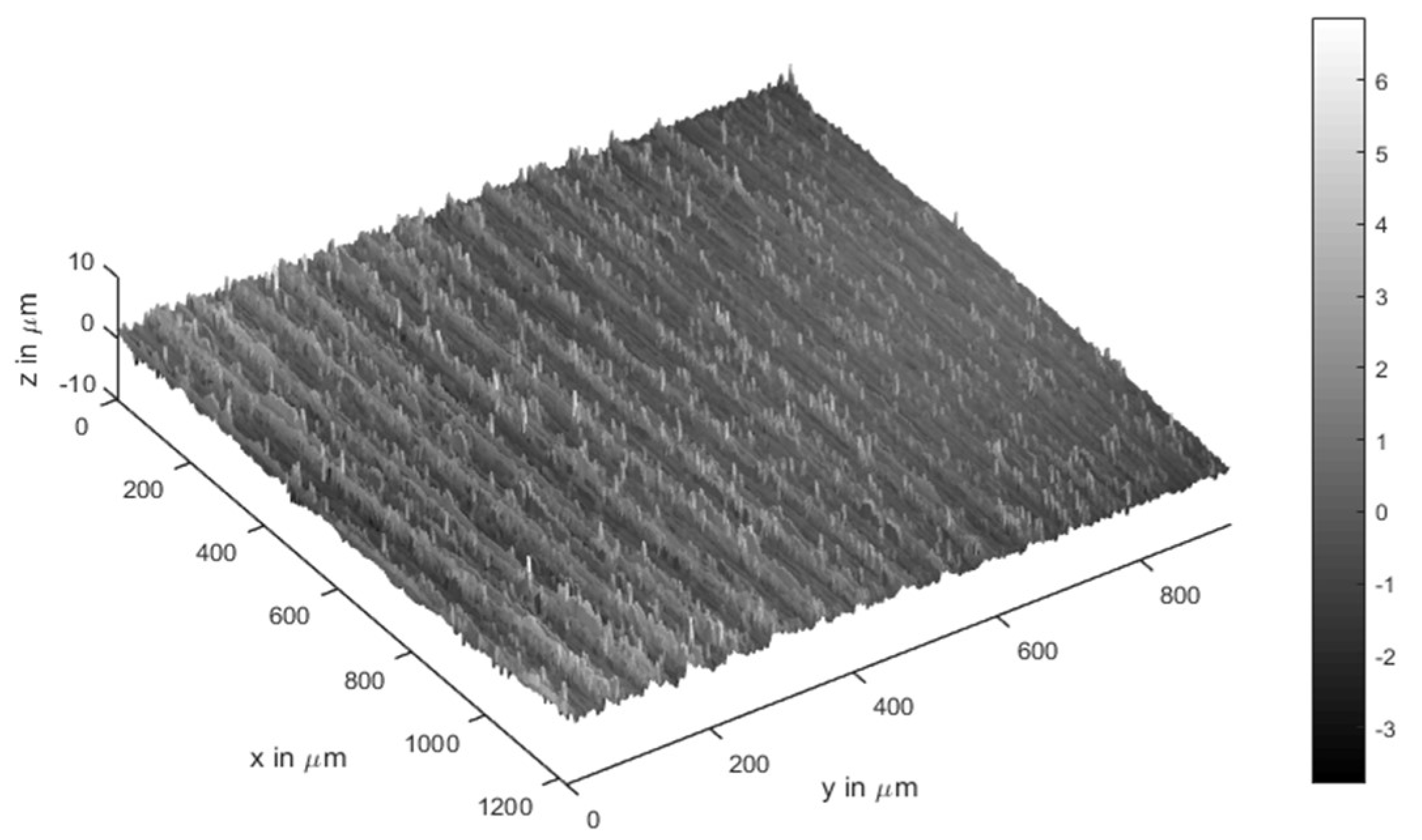
2.1.2. Solid Contact Pressure
2.2. Mechanical State of Equlibrium
2.3. Thermal State of Equlibrium
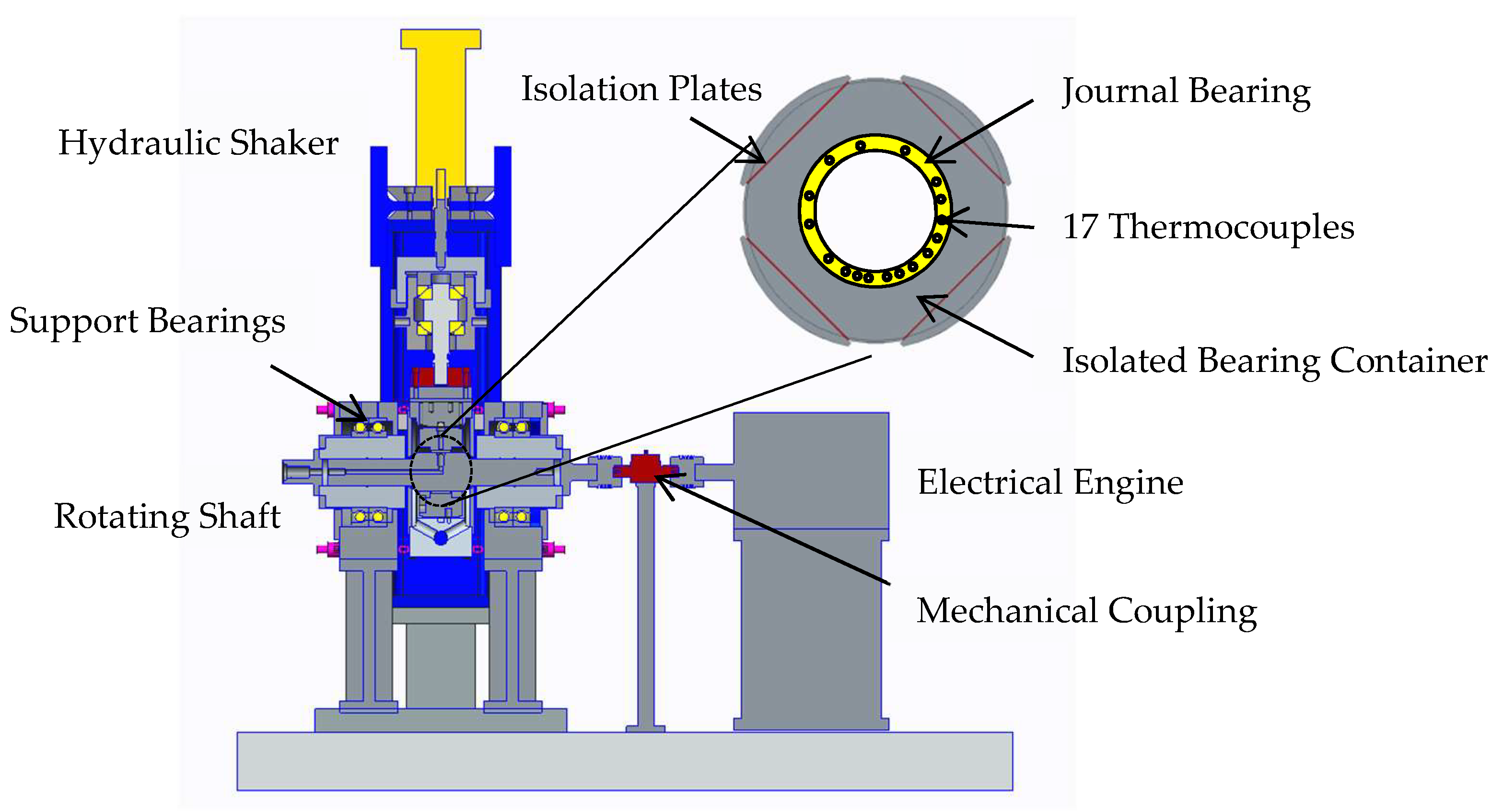
3. Experimental Setup
3.1. Test Bearing and Test Rig
3.2. Test Conditions
4. Results
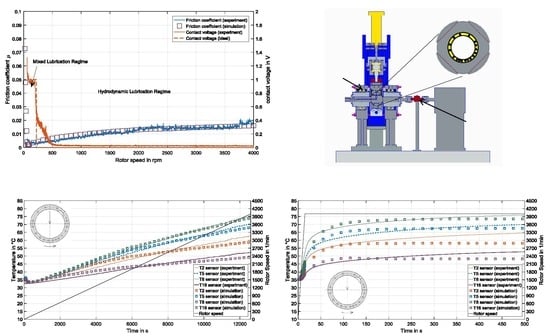
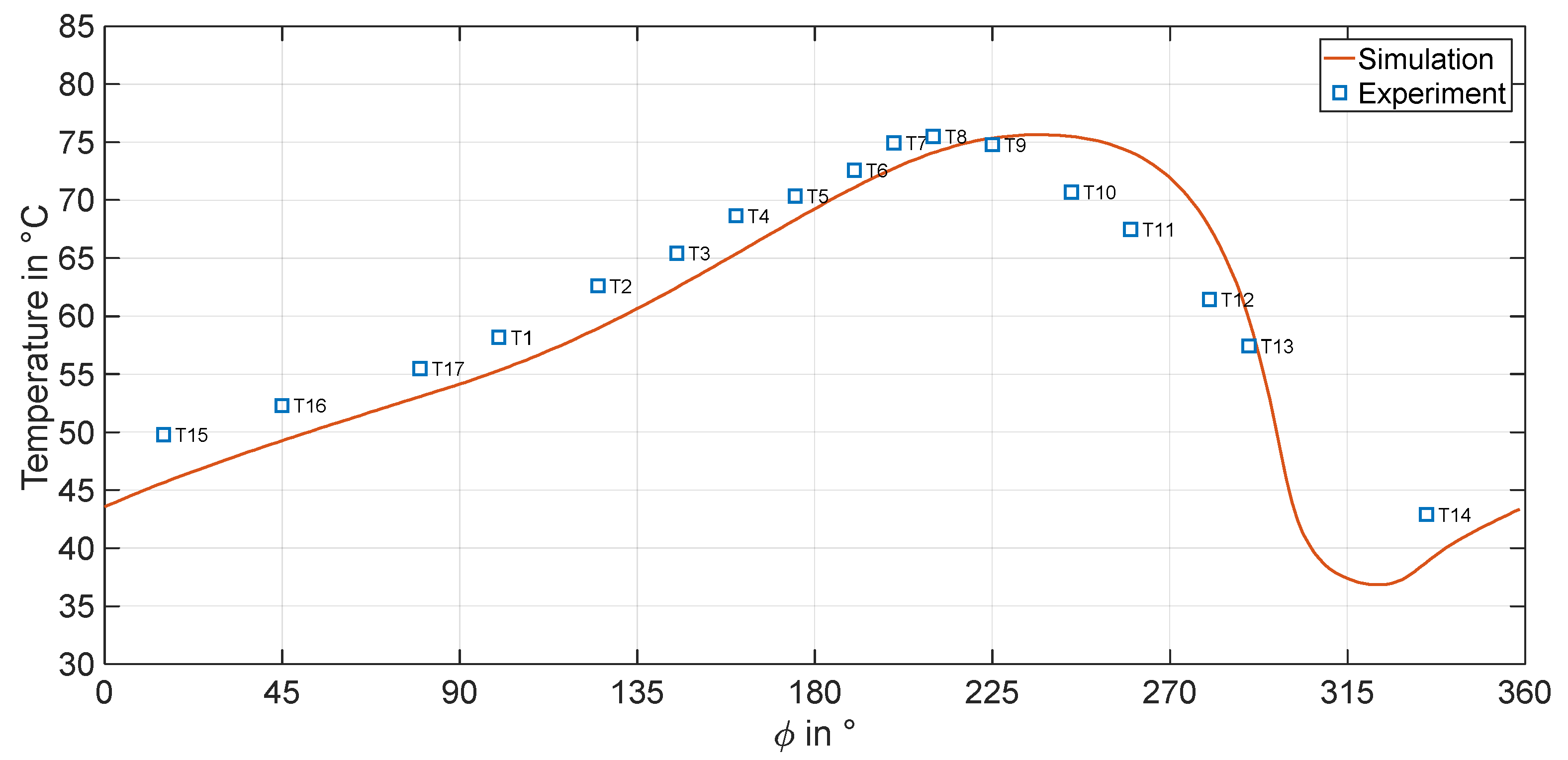
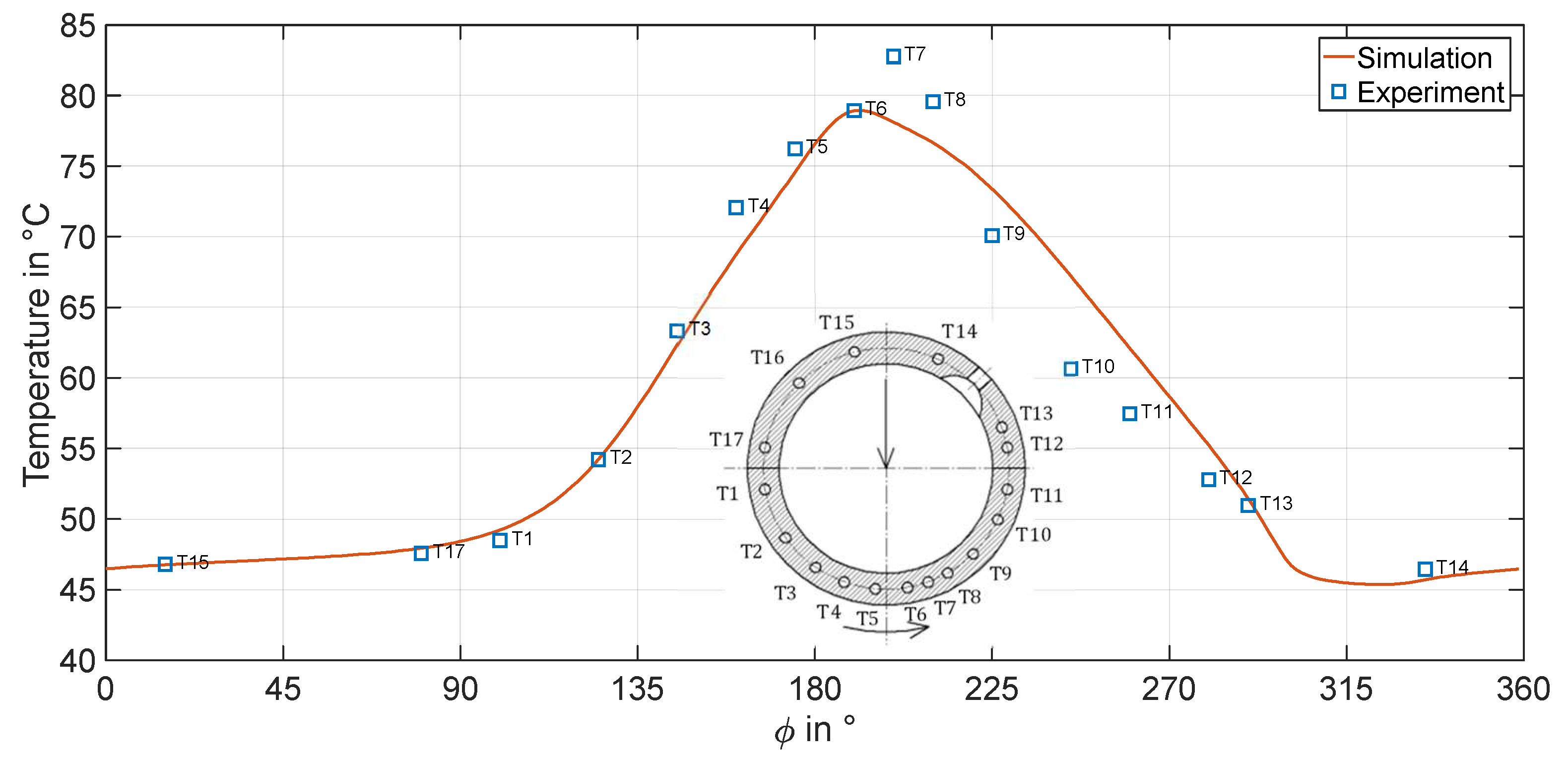
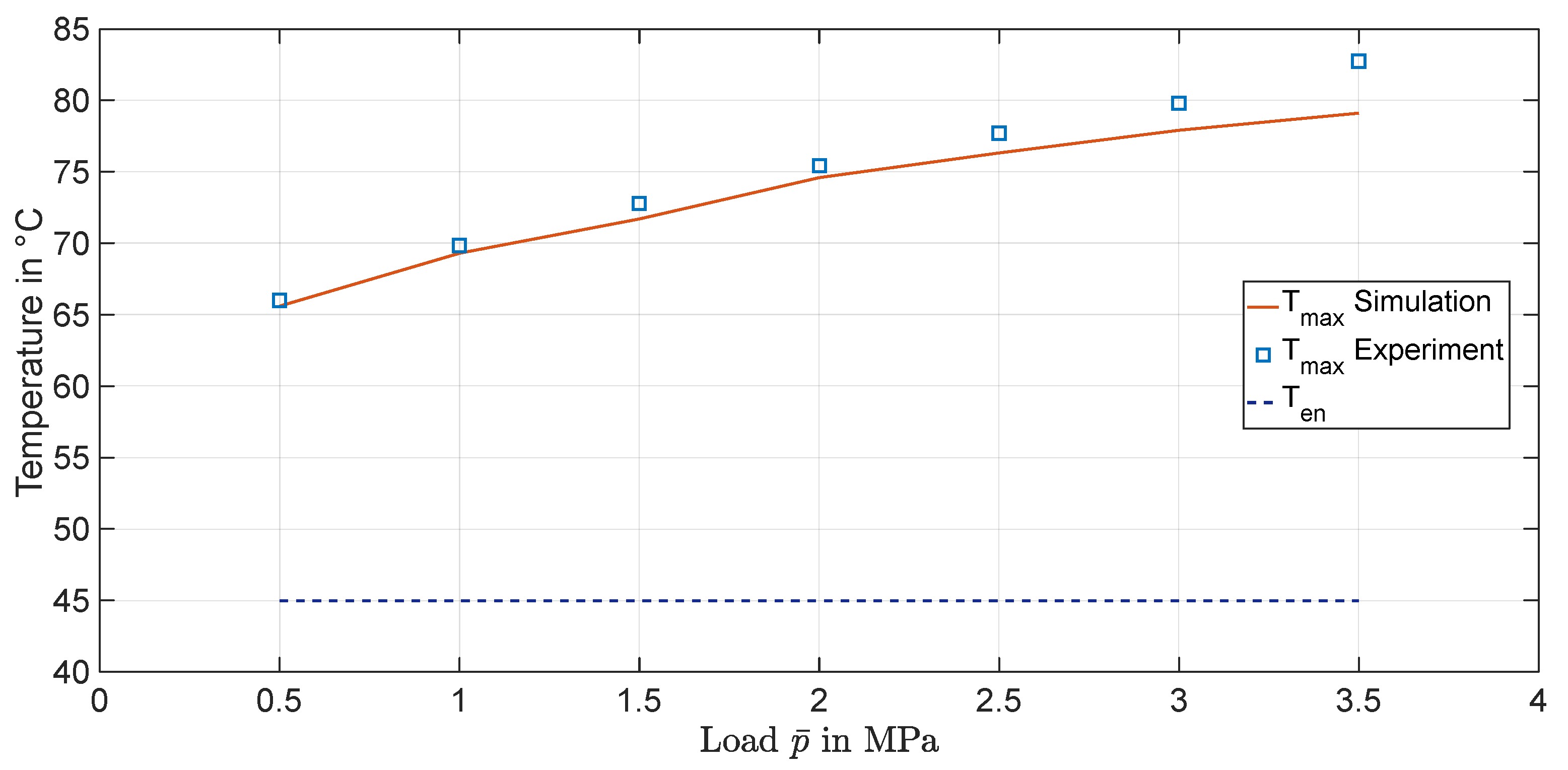
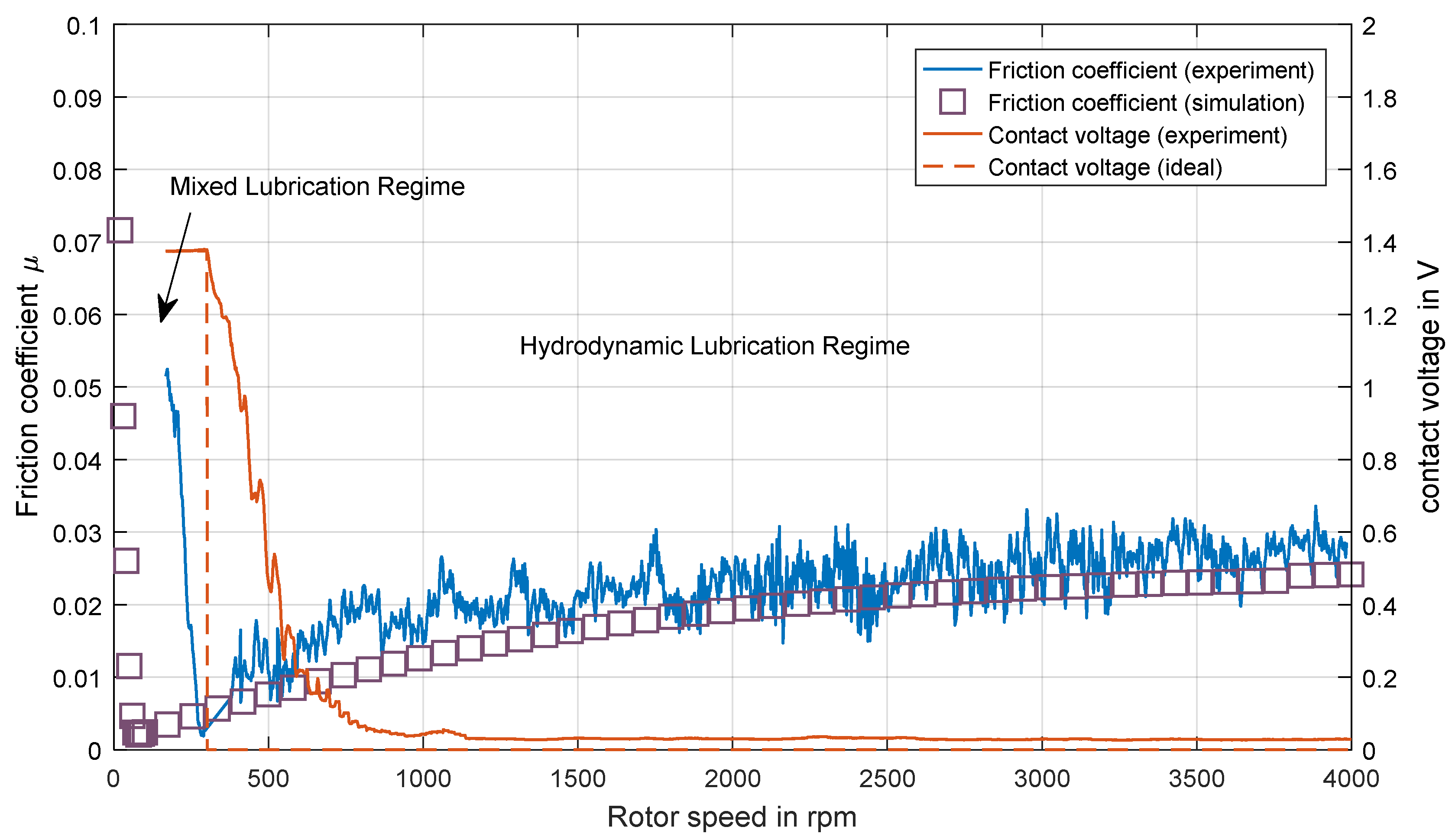
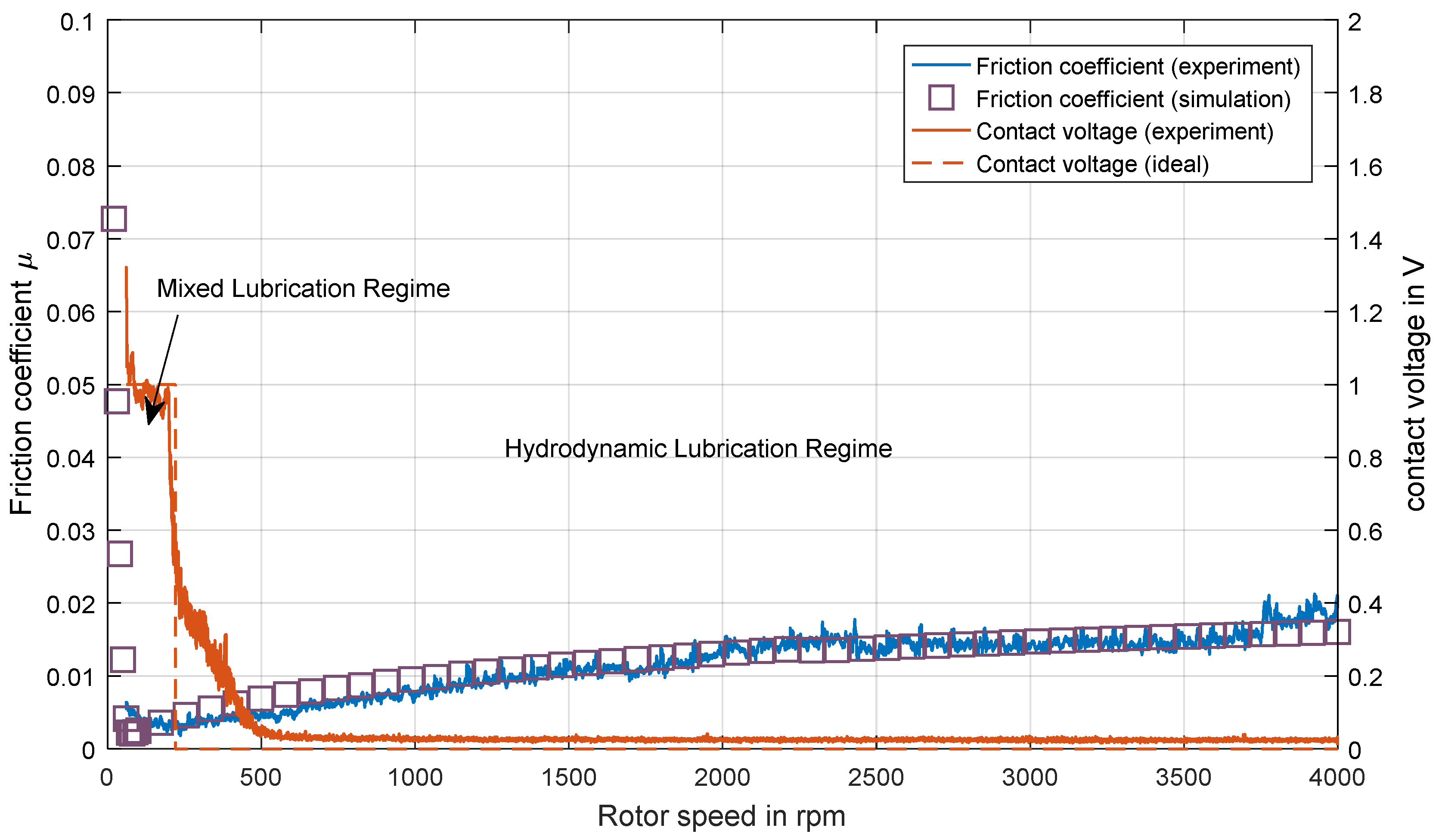
4.1. Validation for Operation in Hydrodynamic Lubrication Regime
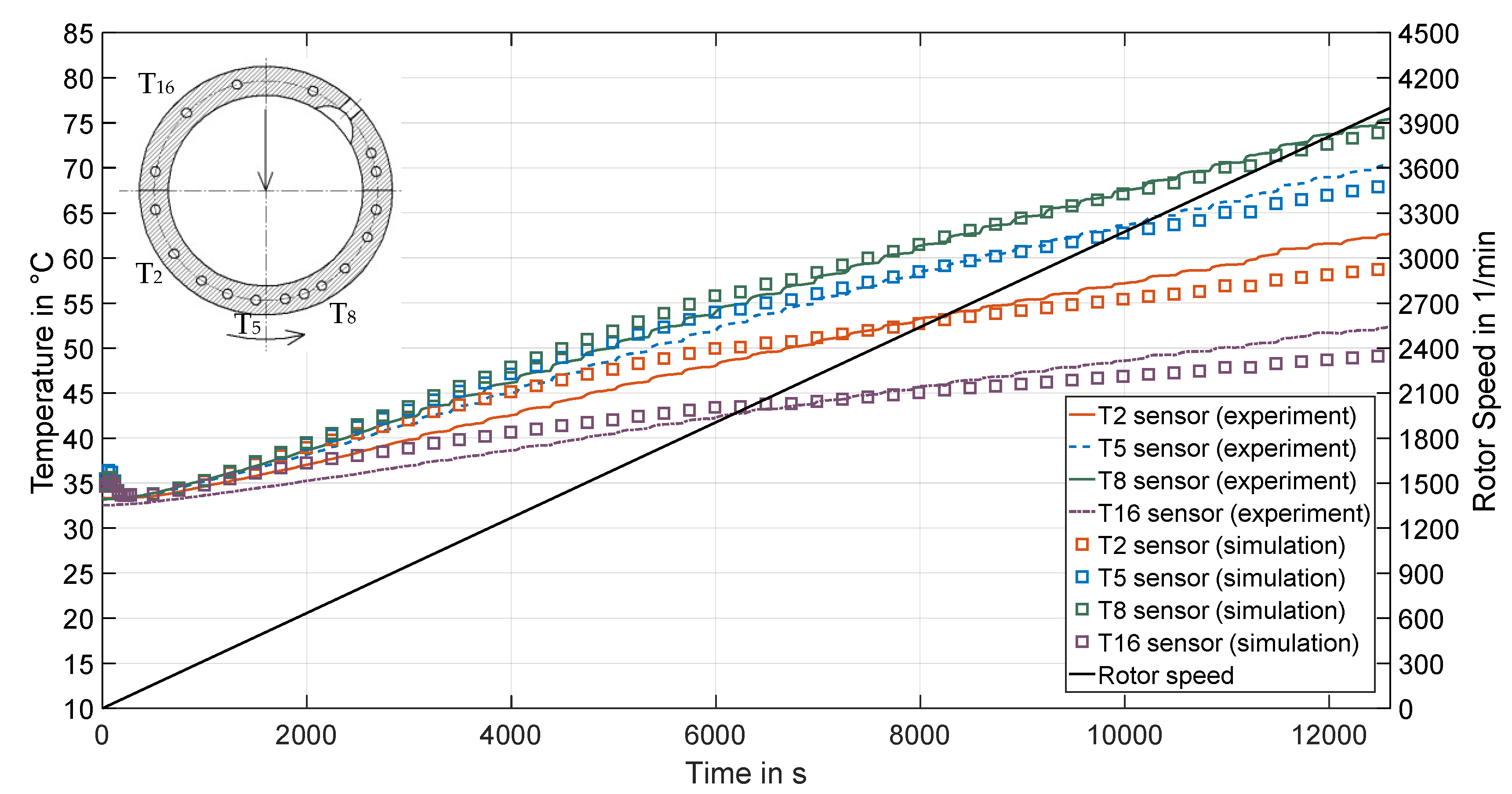
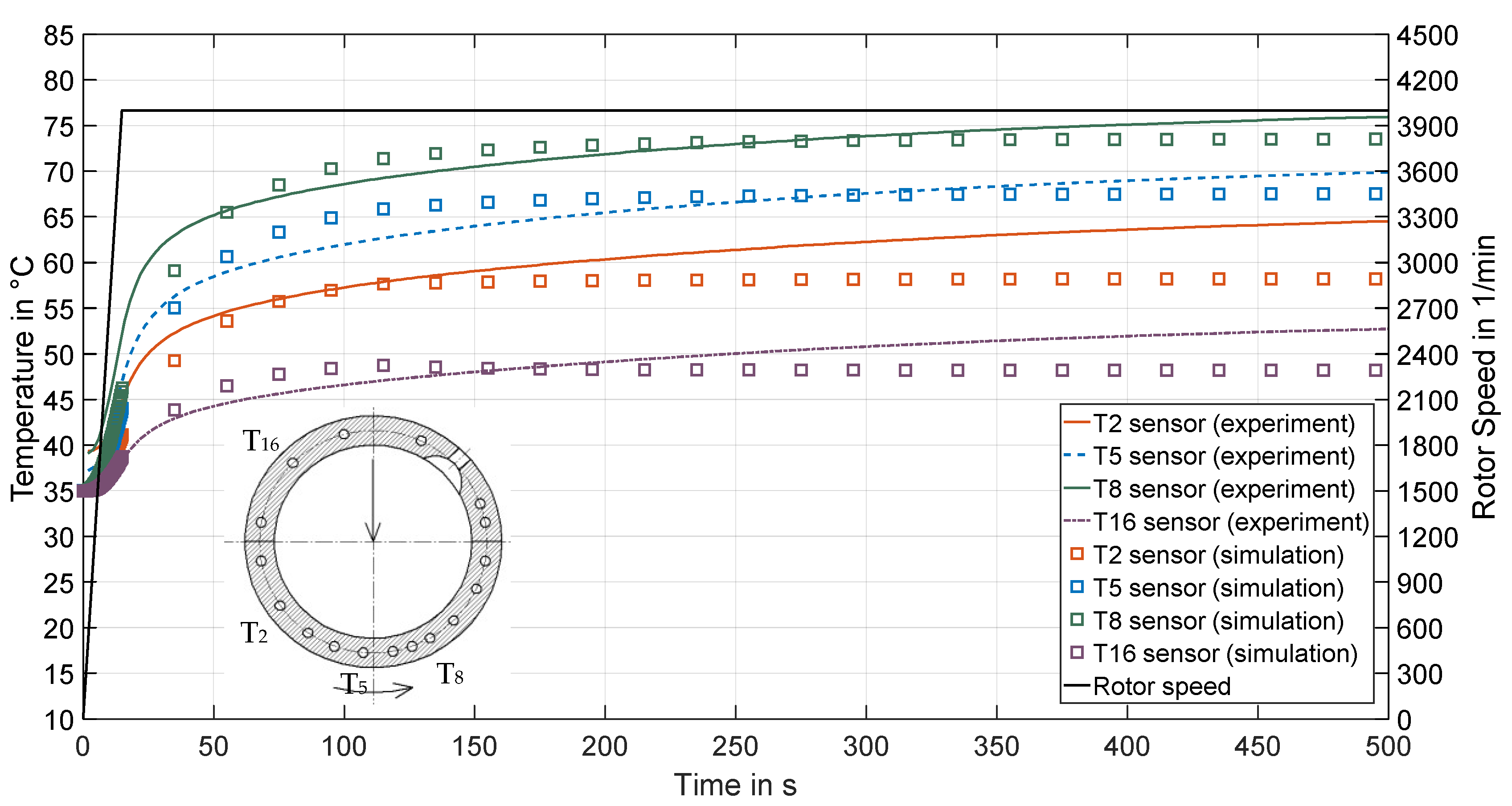
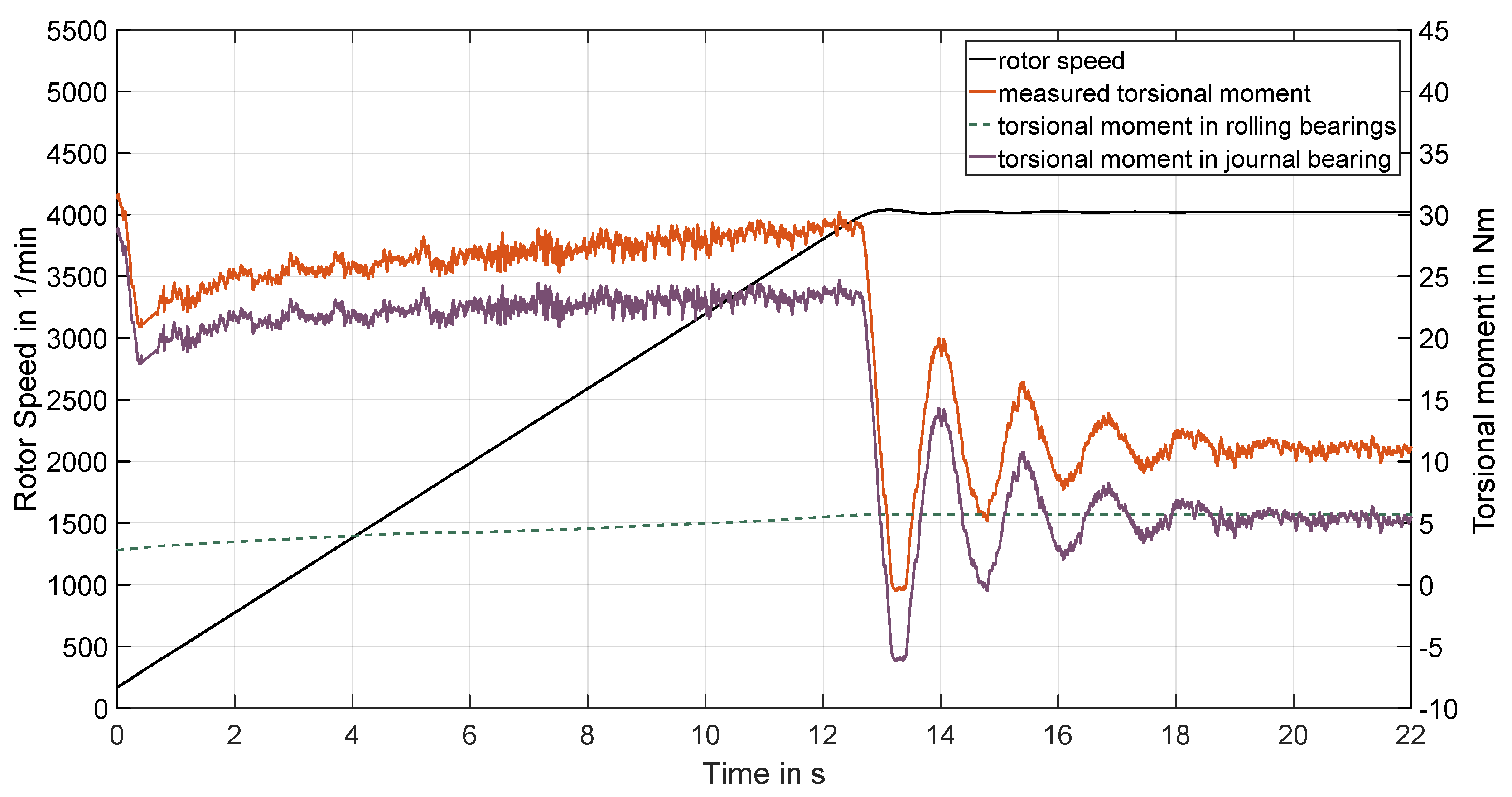
4.2. Effects of Transient Run-Ups
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| c | Specific heat capacity (J/(kg K)) |
| cc | Stiffness of asperities in contact (N/mm) |
| chyd | Stiffness of fluid film (N/mm) |
| ctot | Aggregate stiffness (N/mm) |
| dJ | Diameter of journal (mm) |
| h | Film thickness (μm) |
| hcr | Critical film thickness (μm) |
| Ered | Combined Young’s modulus (GPa) |
| F | External load (kN) |
| F0 | Correction Factor (m/(Pa s) |
| F1, | Correction Factor (m2/(Pa s) |
| F2 | Viscosity Correction Factor (m3/(Pa s) |
| FR | Friction force (N) |
| FN | Normal force (N) |
| Kx, Kz | Turbulence correction factors |
| Msb | Torsional moment of support bearings (Nm) |
| Min | Inertia moment of drivetrain (Nm) |
| Mtot | Measured moment of drivetrain (Nm) |
| n | Rotational speed (rpm) |
| ncr | Critical rotational speed (rpm) |
| pc | Solid contact pressure (bar) |
| phyd | Hydrodynamic pressure (bar) |
| ptot | Aggregate Pressure (bar) |
| Conductive heat flow in bearing (W/m2) | |
| Convective heat flow in fluid (W/m2) | |
| Conductive heat flow in journal (W/m2) | |
| Dissipated energy of boundary friction (W/m2) | |
| Dissipated energy of fluid (W/m2) | |
| Rq | Root mean square roughness (μm) |
| t | Time (s) |
| T | Temperature (°C) |
| Ten | Entrance temperature (°C) |
| u | Relative velocity (m/s) |
| wel | Elastic deformation (μm) |
| Shear strain (1/s) | |
| η | Dynamic viscosity (Pa·s) |
| λ | Heat conductivity (W/(m K)) |
| μ | Friction Coefficient |
| ν | Poisson ratio |
| ρ | Density (kg/m3) |
| τhyd | Shear stress in fluid (Pa) |
| Φ | Dissipation (W/m3) |
| Pressure flow factor x-direction | |
| Pressure flow factor z-direction | |
| Shear flow factor x-direction |
References
- Khonsari, M.M.; Wang, S.H. Notes on transient THD effects in a lubricating film. Tribol. Trans. 1992, 35, 177–183. [Google Scholar] [CrossRef]
- Paranjpe, R.S.; Han, T. A Study of the Thermohydrodynamic Performance of Steadily Loaded Journal Bearings. Tribol. Trans. 1994, 37, 679–690. [Google Scholar] [CrossRef]
- Kucinschi, B.R.; Fillon, M.; Frene, J.; Pascovici, M.D. A transient thermoelastohydrodynamic study of steadily loaded plain journal bearings using finite element method analysis. J. Tribol. 2000, 122, 219–226. [Google Scholar] [CrossRef]
- Akbarzadeh, S.; Khonsari, M.M. Effect of surface pattern on stribeck curve. Tribol. Lett. 2010, 37, 477–486. [Google Scholar] [CrossRef]
- Adatepe, H.; Bıyıklıoglu, A.; Sofuoglu, H. An experimental investigation on frictional behavior of statically loaded micro-grooved journal bearing. Tribol. Int. 2011, 44, 1942–1948. [Google Scholar] [CrossRef]
- Boussinesq, J. Application des potentiels à l’étude de l’équilibre et du mouvement des solides élastiques: Principalement au calcul des déformations et des pressions que produisent, dans ces solides, des efforts quelconques exercés sur une petite partie de leur surface ou de leur intérieur: Mémoire suivi de notes étendues sur divers points de physique, mathematique et d’analyse; Gauthier-Villars: Paris, France, 1885; Volume 4. [Google Scholar]
- Greenwood, J.A.; Williamson, J.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. A 1966, 295, 300–319. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Tripp, J.H. The contact of two nominally flat rough surfaces. Proc. Inst. Mech. Eng. 1970, 185, 625–633. [Google Scholar] [CrossRef]
- Hu, Y.; Cheng, H.S.; Arai, T.; Kobayashi, Y.; Aoyama, S. Numerical simulation of piston ring in mixed lubrication—A nonaxisymmetrical analysis. J. Tribol. 1994, 116, 470–478. [Google Scholar] [CrossRef]
- Panayi, A.P.; Schock, H.J. Approximation of the integral of the asperity height distribution for the Greenwood—Tripp asperity contact model. Proc. Inst. Mech. Eng. 2008, 222, 165–169. [Google Scholar] [CrossRef]
- Teodorescu, M.; Taraza, D.; Henein, N.A.; Bryzik, W. Simplified Elasto-Hydrodynamic Friction Model of the Cam-Tappet Contact; SAE Technical Paper No. 2003-01-0985; SAE International: Warrendale, PA, USA, 2003. [Google Scholar]
- Pogačnik, A.; Kalin, M. How to determine the number of asperity peaks, their radii and their heights for engineering surfaces: A critical appraisal. Wear 2013, 300, 143–154. [Google Scholar] [CrossRef]
- Choi, J.; Kim, S.S.; Rhim, S.S.; Choi, J.H. Numerical modeling of journal bearing considering both elastohydrodynamic lubrication and multi-flexible-body dynamics. Int. J. Automot. Technol. 2012, 13, 255–261. [Google Scholar] [CrossRef]
- Offner, G. Modelling of condensed flexible bodies considering non-linear inertia effects resulting from gross motions. Proc. Inst. Mech. Eng. 2011, 225, 204–219. [Google Scholar] [CrossRef]
- Cubillo, A.; Uriondo, A.; Perinpanayagam, S. Computational Mixed TEHL Model and Stribeck Curve of a Journal Bearing. Tribol. Trans. 2017, 60, 1053–1062. [Google Scholar] [CrossRef]
- Lu, X.; Khonsari, M.M.; Gelinck, E.R. The Stribeck curve: Experimental results and theoretical prediction. J. Tribol. 2006, 128, 789–794. [Google Scholar] [CrossRef]
- Sander, D.E.; Allmaier, H.; Priebsch, H.H.; Witt, M.; Skiadas, A. Simulation of journal bearing friction in severe mixed lubrication–Validation and effect of surface smoothing due to running-in. Tribol. Int. 2016, 96, 173–183. [Google Scholar] [CrossRef]
- Patankar, S. Numerical Heat Transfer and Fluid Flow; Taylor & Francis: Boca Raton, FL, USA, 1980; ISBN 978-0-89116-522-4. [Google Scholar]
- Hagemann, T.; Schwarze, H. A model for oil flow and fluid temperature inlet mixing in hydrodynamic journal bearings. ASME J. Tribol. 2019, 141, 021701. [Google Scholar] [CrossRef]
- Hagemann, T. Ölzuführungseinfluss bei Schnell Laufenden und Hoch Belasteten Radial-Gleitlagern unter Berücksichtigung des Lagerdeformationsverhaltens. Ph.D. Thesis, TU Clausthal, Lower Saxony, Germany, 2011. [Google Scholar]
- Hagemann, T.; Kukla, S.; Schwarze, H. Measurement and prediction of the static operating conditions of a large turbine tilting-pad bearing under high circumferential speeds and heavy loads. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013. ASME Paper No. GT2013-95004. [Google Scholar]
- Patir, N.; Cheng, H.S. An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Application of average flow model to lubrication between rough sliding surfaces. J. Lubr. Technol. 1979, 101, 220–229. [Google Scholar] [CrossRef]
- Dowson, D. A Generalized Reynolds Equation for Fluid Film Lubrication. Int. J. Mech. Sci. 1962, 4, 159–170. [Google Scholar] [CrossRef]
- Constantinescu, V.N.; Galetuse, S.; Kennedy, F. On the comparison between lubricant theory, including turbulence and inertia forces, and some existing experimental data. ASME J. Lubr. Technol. 1975, 97, 439–449. [Google Scholar] [CrossRef]
- Elrod, H.G. A cavitation algorithm. J. Lubr. Technol. 1981, 103, 350–354. [Google Scholar] [CrossRef]
- McCool, J.I. Comparison of models for the contact of rough surfaces. Wear 1986, 107, 37–60. [Google Scholar] [CrossRef]
- Rempke, A. Numerische Optimierung Eines Deterministischen Kontaktmodells zur Berech-nung Reibungsbehafteter Festkörperkontakte auf großen Berechnungsgittern unter Einsatz der DC-FFT Technik. Bachelor Thesis, TU-Clausthal, Lower Saxony, Germany, 2008. [Google Scholar]
- Mittwollen, N. Betriebsverhalten von Radialgleitlagern bei hohen Umfangsgeschwindigkei-ten und hohen Thermischen Belastungen—Theoretische Untersuchungen; VDI Series 1, No. 187; VDI-Verlag: Dusseldorf, Germany, 1990. [Google Scholar]
- Hagemann, T.; Schwarze, H. Theoretical and experimental analyses of directly lubricated tilting-pad journal bearings with leading edge groove. ASME J. Eng. Gas Turb. Power 2018. [Google Scholar] [CrossRef]
- Hagemann, T.; Zeh, C.; Prölß, M.; Schwarze, H. The impact of convective fluid inertia forces on operation of tilting-pad journal bearings. Int. J. Rotat. Mach. 2017, 2017. [Google Scholar] [CrossRef]
| Bearing | Case A | Case B | Schematic Drawing |
|---|---|---|---|
| Shaft diameter | 100 mm | 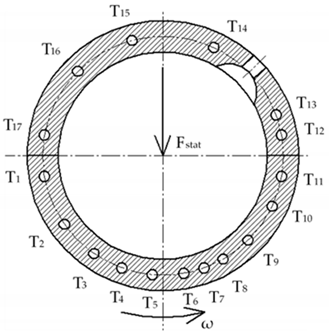 | |
| Bearing outer diameter | 130 mm | ||
| Relative radial clearance | 1.6‰ | 3.2‰ | |
| Bearing width | 50 mm | ||
| Supply groove width | 40 mm | ||
| Supply groove length | 26 mm | ||
| Supply temperature | 30 °C | 45 °C | |
| Supply pressure | 2 bar | ||
| Speed range | 0–4000 rpm | ||
| Load | 4 kN | 5–17.5 kN | |
| Property | Lubricant | Bearing | Journal | Container |
|---|---|---|---|---|
| Material | ISOVG 32 | CuSn7Zn4Pb7 | 42CrMo4 | 42CrMo4 |
| Density | 853 kg/m3 | 8830 kg/m3 | 7720 kg/m3 | 7720 kg/m3 |
| Specific heat capacity | 2090 J/(kg·K)−1 | 380 J/(kg·K)−1 | 470 J/(kg·K)−1 | 470 J/(kg·K)−1 |
| Heat conductivity | 0.134 W/(m·K) | 68 W/(m·K) | 42.6 W/(m·K) | 42.6 W/(m·K) |
| Thermal expansion coefficient | - | 18 × 10−6 K−1 | 11 × 10−6 K−1 | 11 × 10−6 K−1 |
| Elasticity modulus | - | 101 GPa | 210 GPa | 210 GPa |
| Rapid Run-Up | Slow Run-Up | |||
|---|---|---|---|---|
| Simulation | Experiment | Simulation | Experiment | |
| Transition speed | 103 rpm | ~300 rpm | 94 rpm | ~220 rpm |
| Final friction coefficient | 0.024 | 0.028 | 0.016 | 0.018 |
| Speed of minimum friction coefficient | 95 rpm | 205 rpm | 90 rpm | 173 rpm |
| Minimum friction coefficient | 0.0021 | 0.0015 | 0.0024 | 0.0036 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prölß, M.; Schwarze, H.; Hagemann, T.; Zemella, P.; Winking, P. Theoretical and Experimental Investigations on Transient Run-Up Procedures of Journal Bearings Including Mixed Friction Conditions. Lubricants 2018, 6, 105. https://doi.org/10.3390/lubricants6040105
Prölß M, Schwarze H, Hagemann T, Zemella P, Winking P. Theoretical and Experimental Investigations on Transient Run-Up Procedures of Journal Bearings Including Mixed Friction Conditions. Lubricants. 2018; 6(4):105. https://doi.org/10.3390/lubricants6040105
Chicago/Turabian StylePrölß, Maximilian, Hubert Schwarze, Thomas Hagemann, Philipp Zemella, and Philipp Winking. 2018. "Theoretical and Experimental Investigations on Transient Run-Up Procedures of Journal Bearings Including Mixed Friction Conditions" Lubricants 6, no. 4: 105. https://doi.org/10.3390/lubricants6040105
APA StylePrölß, M., Schwarze, H., Hagemann, T., Zemella, P., & Winking, P. (2018). Theoretical and Experimental Investigations on Transient Run-Up Procedures of Journal Bearings Including Mixed Friction Conditions. Lubricants, 6(4), 105. https://doi.org/10.3390/lubricants6040105