Meta-Analysis Comparing Wettability Parameters and the Effect of Wettability on Friction Coefficient in Lubrication
Abstract
1. Introduction
2. Results and Discussion
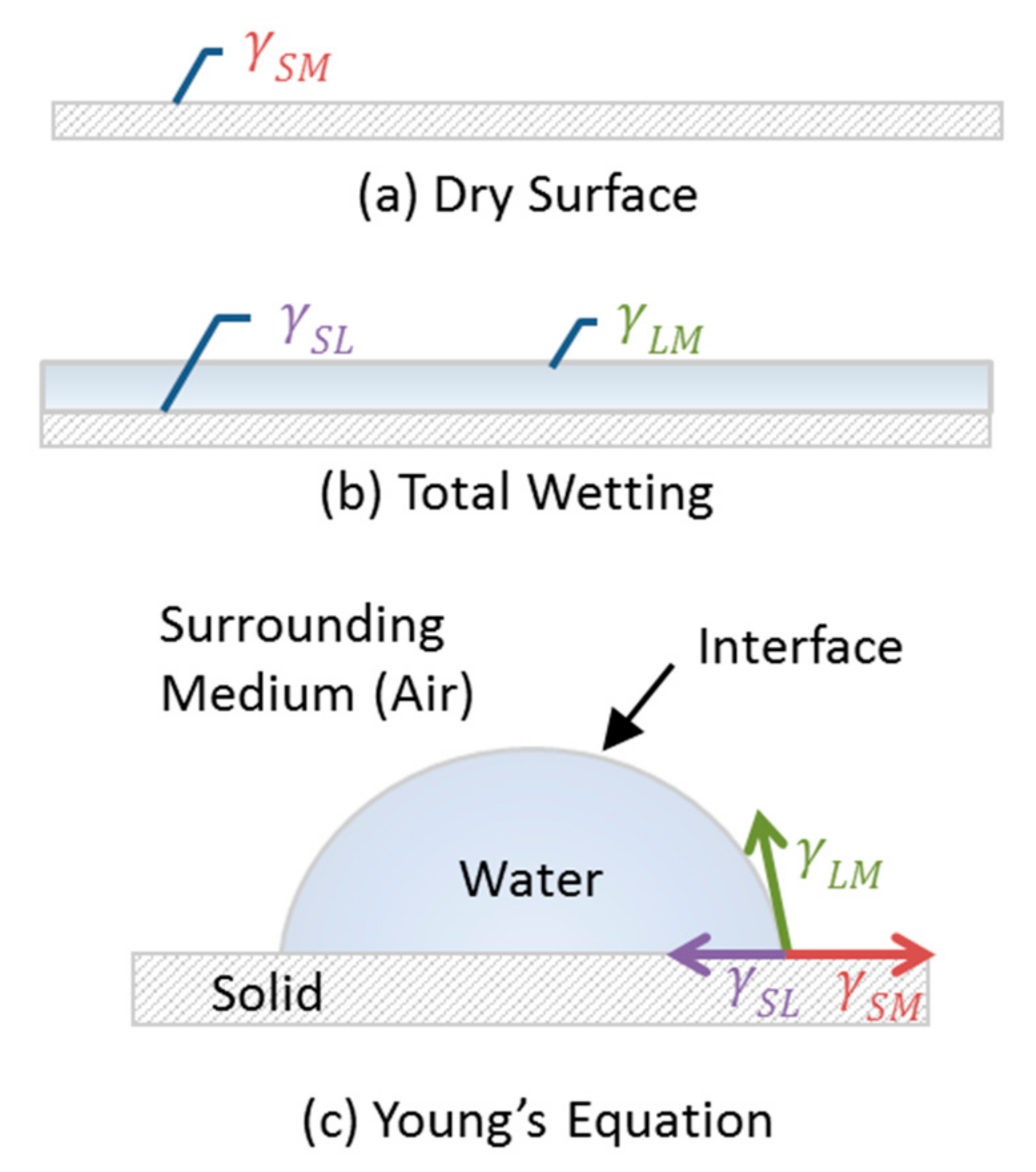
2.1. Defining Parameters to Characterize Wettability
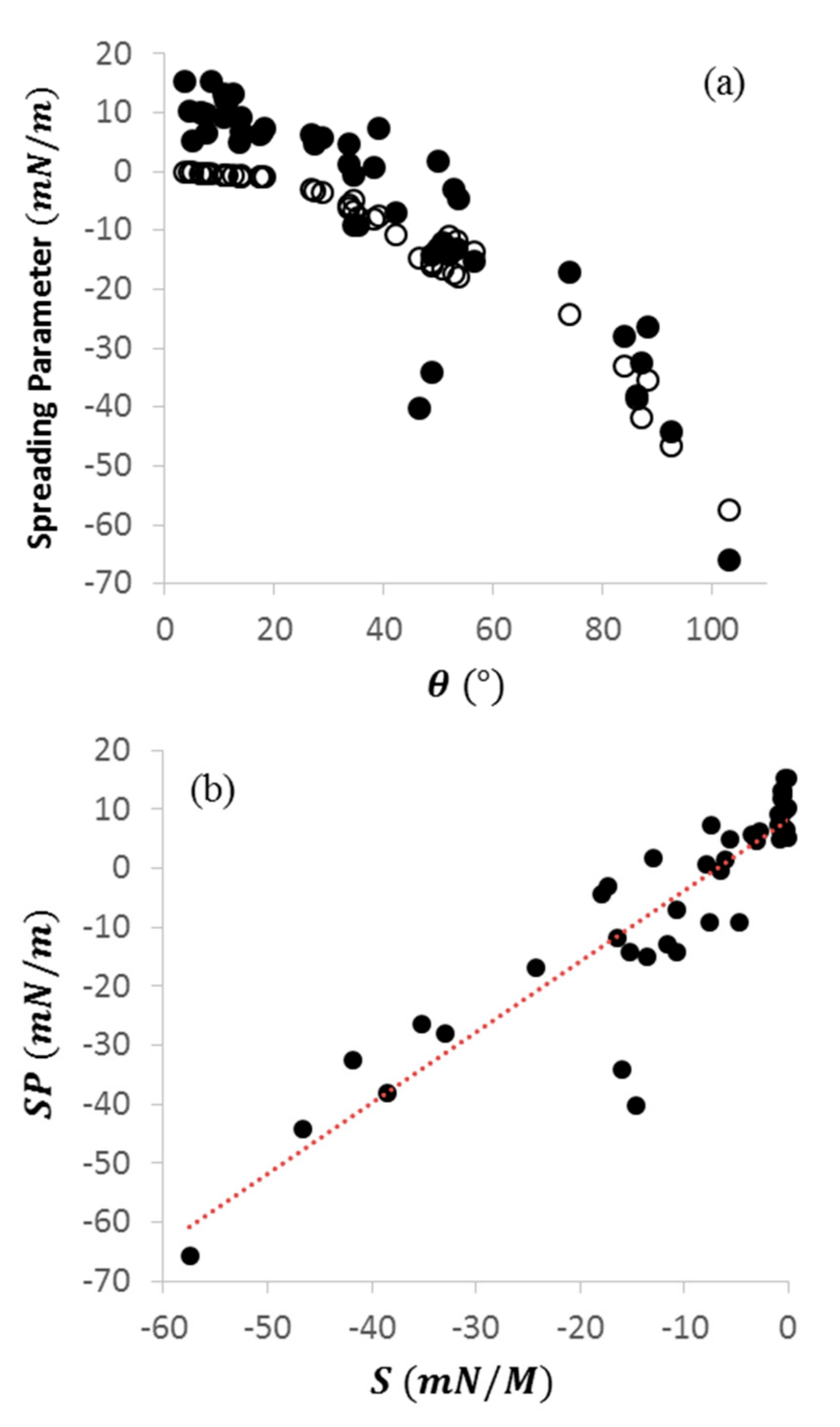
2.2. Comparing Characteristic Parameters for Wettability
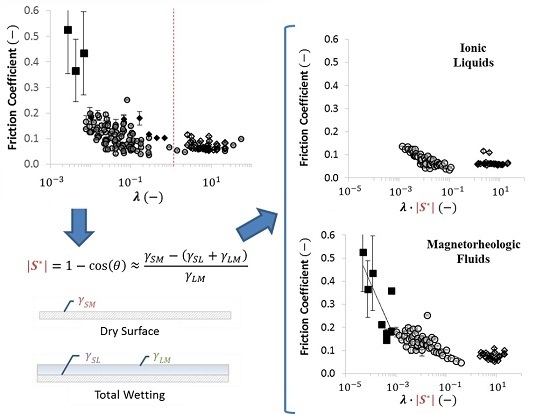
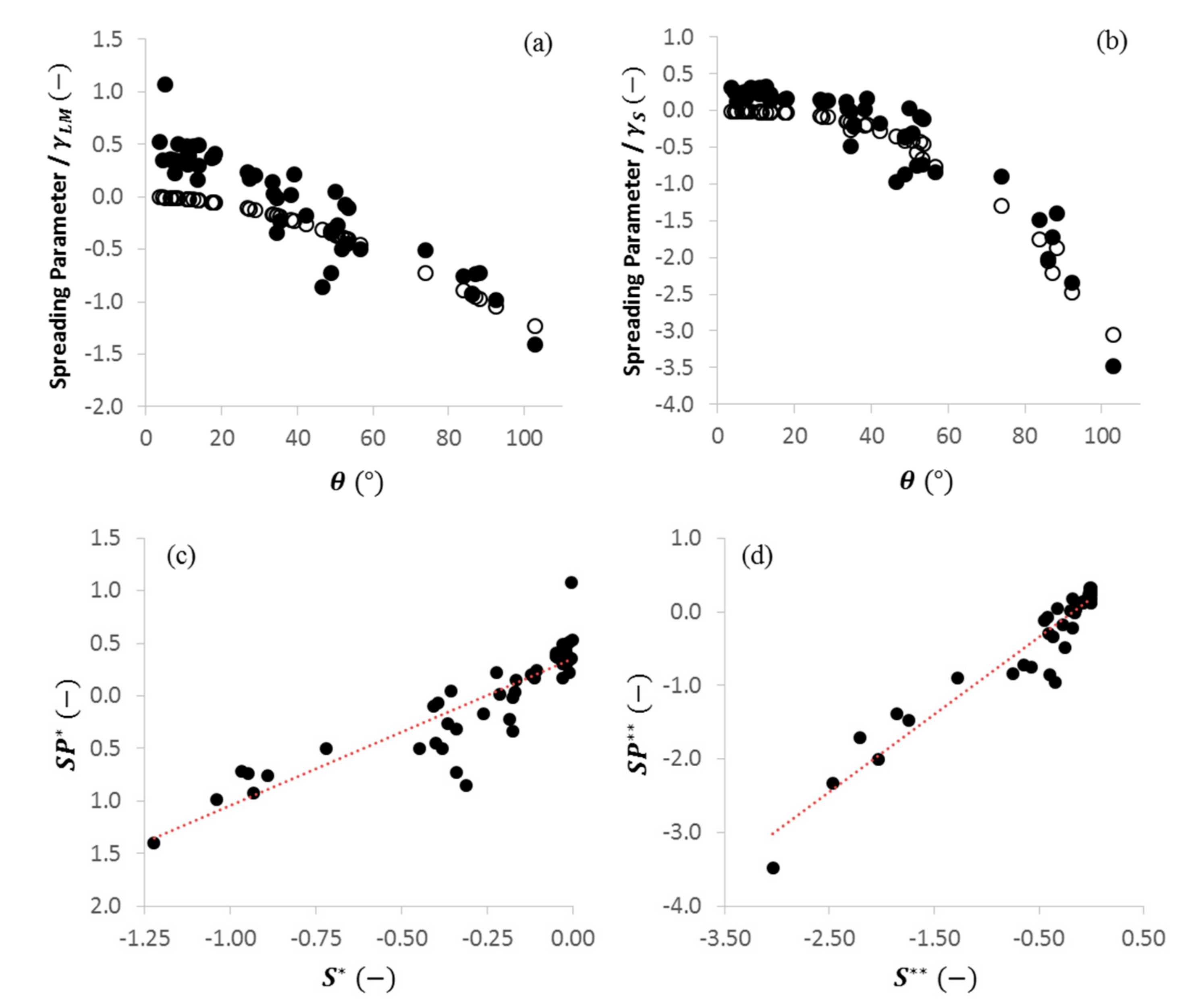
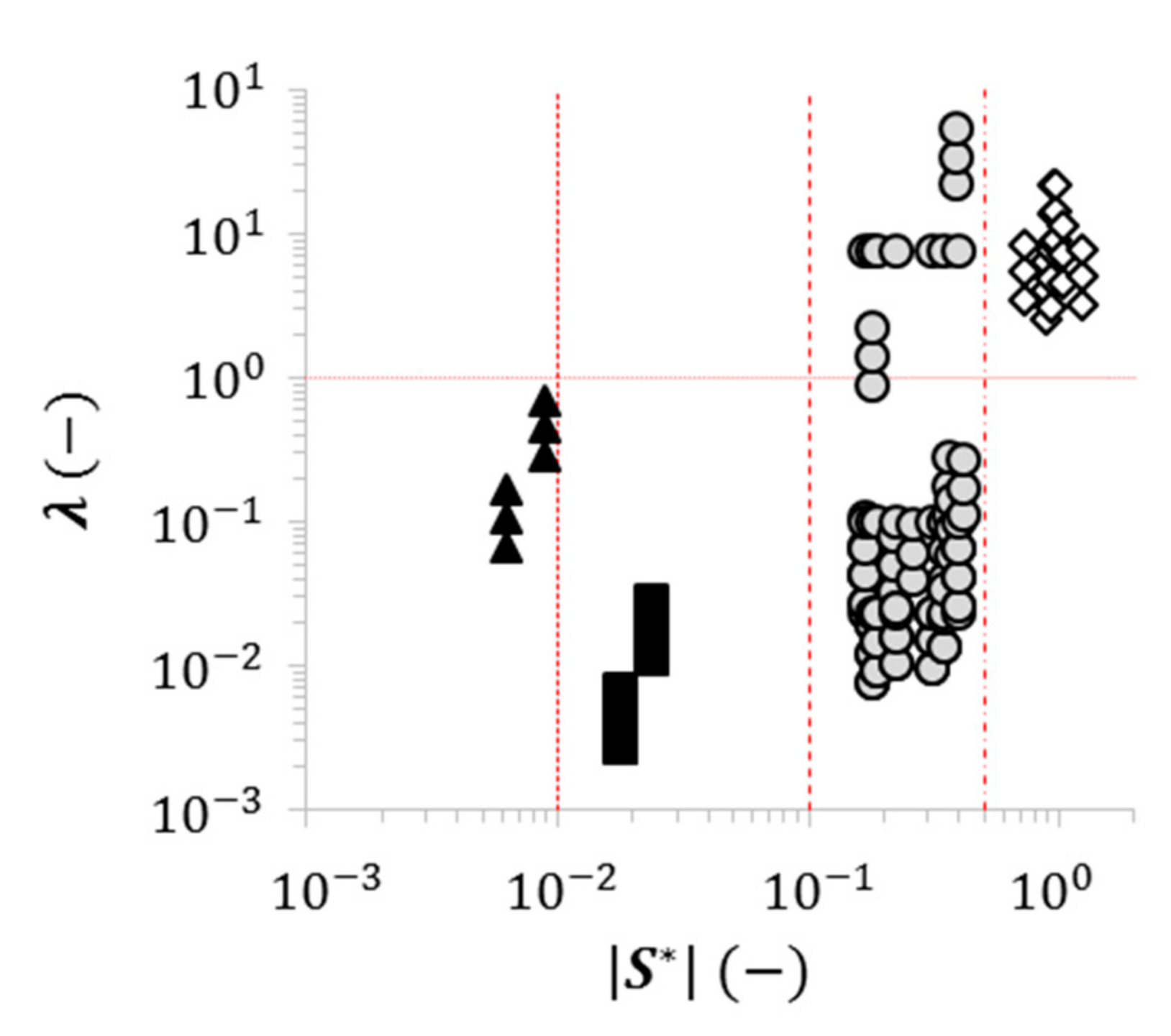
2.3. Dimensionless Wetting Parameters
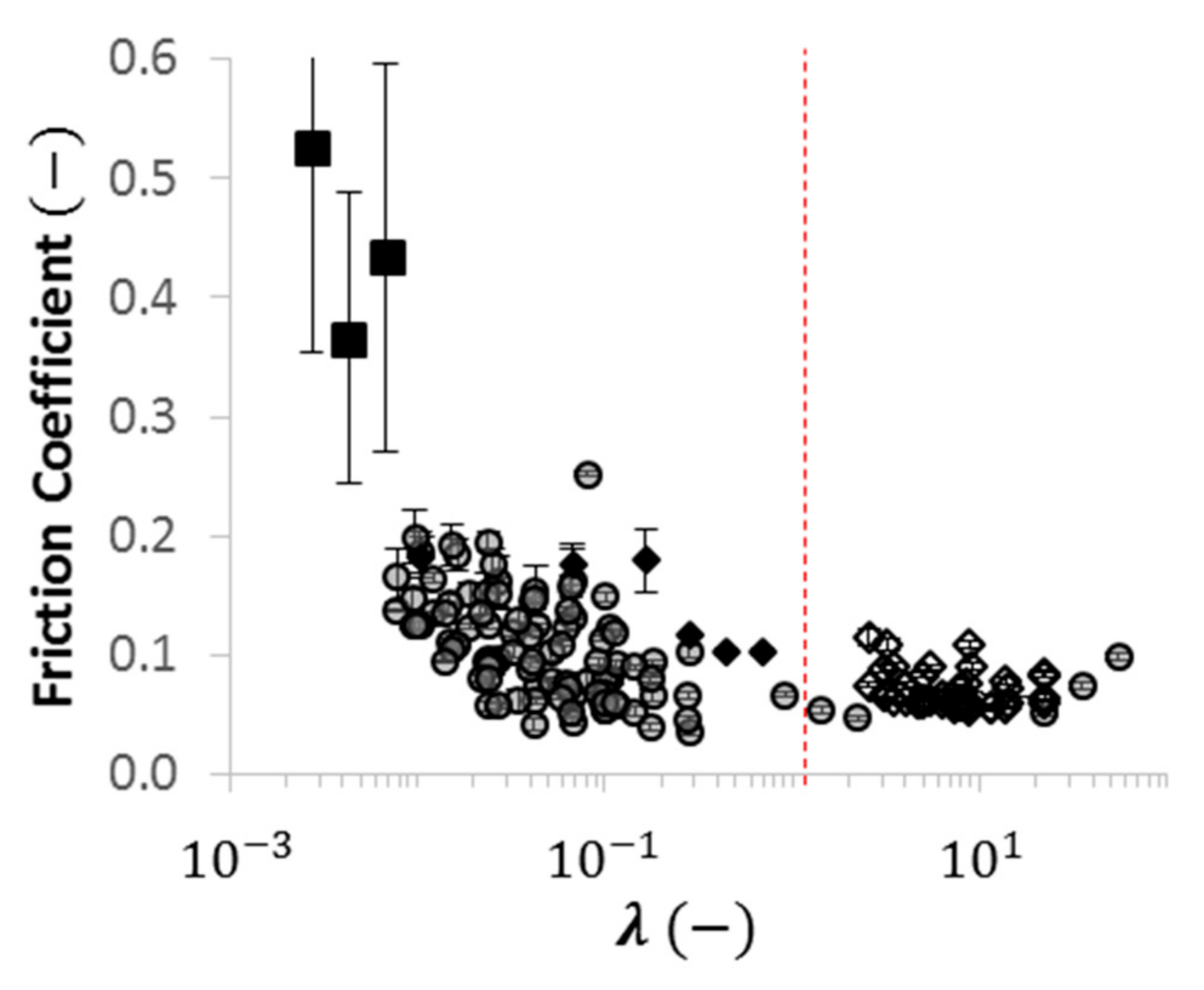
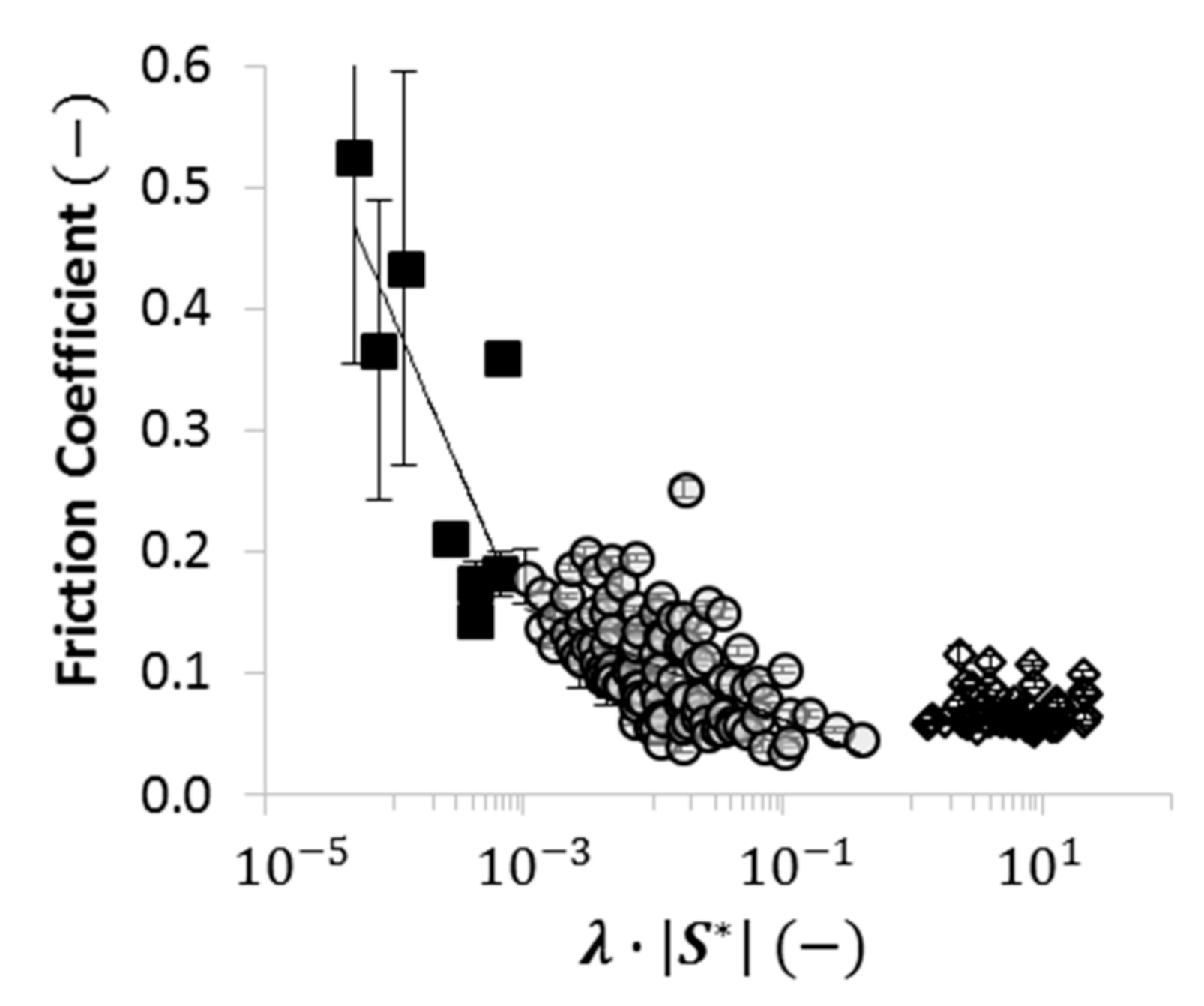
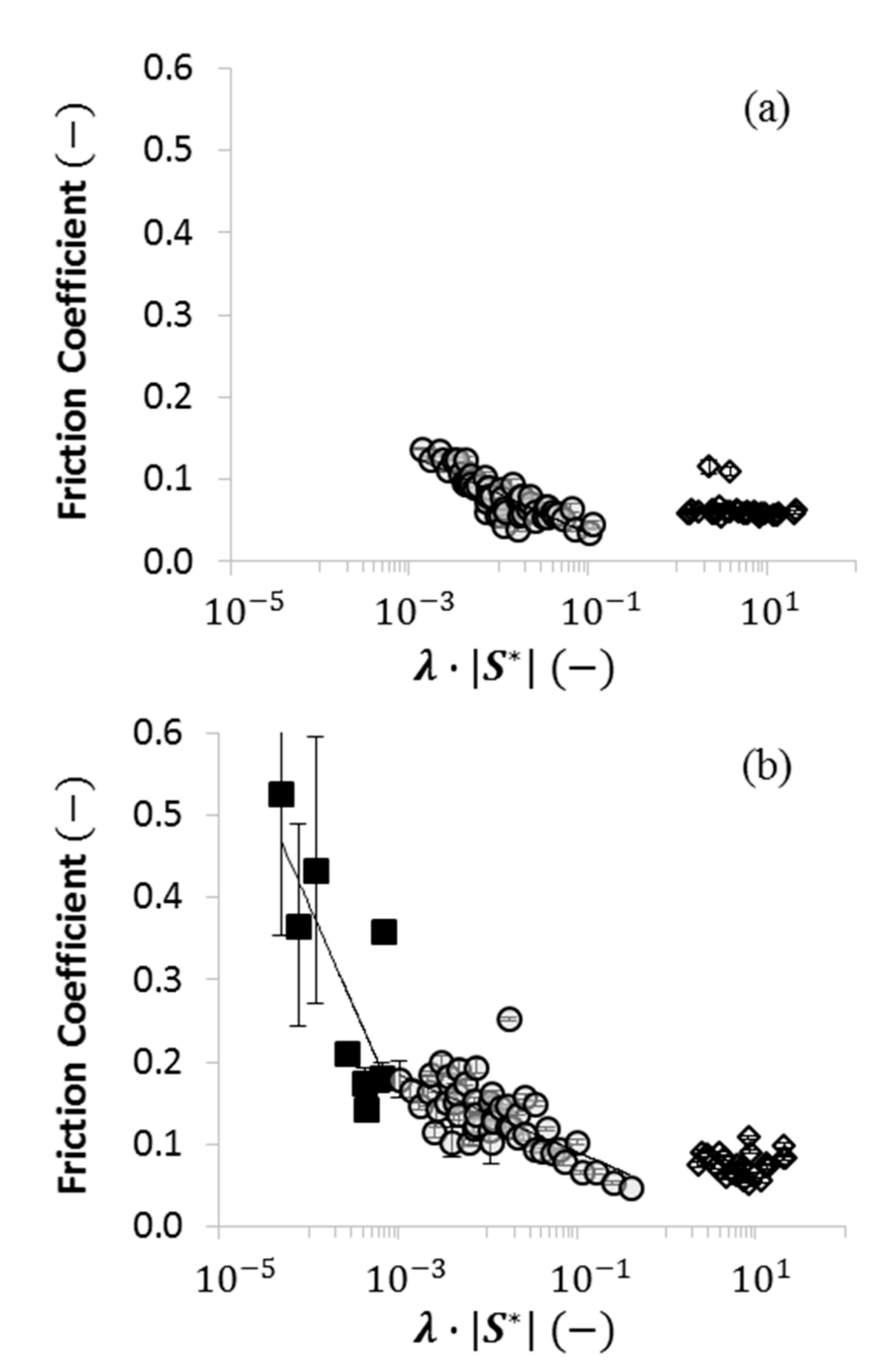
2.4. Using Wettability to Characterize Friction
- were low and consistent when was above approximately ;
- increased dramatically as decreased below approximately ; and
- increased moderately when .
3. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Parameter/Abbreviation | Description | Unit |
| Subscript for adhesion work per unit area | ||
| a-C:H | Hydrogenated amorphous diamond-like carbon | |
| [BMIM][SCN] | 1-Butyl-3-methylimidazolium thiocyanate | |
| [BMIM][NTF2] | 1-Butyl-3-methylimidazolium bis(trifluoromethanesulfonyl imige/“Triflimide” | |
| [BMIM][BF4] | 1-Butyl-3-methylimidazolium tetrafluoroborate | |
| [BMIM][PF6] | 1-Butyl-3-methylimidazolium hexafluorophosphate | |
| [BMIM][CH3COO] | 1-Butyl-3-methylimidazolium | |
| BL | Boundary lubrication regime | |
| Subscript for cohesion work per unit area | ||
| D | Superscript for disperse component of | |
| [EMIM][NTf2] | 1-Ethyl-3-methylimdazolium bis(trifluoromethanesulfonyl) imide/Triflimide” | |
| [EMIM][CF3SO3] | 1-Ethyl-3-methylimdazolium trifluoromethanesulfonate/“Triflate” | |
| F-DLC | Hydrogenated amorphous diamond-like carbon doped with silicon and fluorine | |
| Lubricant film thickness | ||
| HL | Hydrodynamic lubrication regime | |
| IL | Ionic liquid | |
| IL104 | Trihexyltetradecylphosphonium bis(2,4,4-trimethylpentyl) phosphinate (Cytec) | |
| LM | Subscript for the interface between the liquid and the surrounding medium | |
| ML | Mixed lubrication regime | |
| MR | Magnetorhelogical | |
| N-DLC | N-doped diamond-like carbon | |
| OWRK | Owens–Wendt–Tabel–Kaelble | |
| Superscript for polar component of | ||
| PAO | Polyalphaolefin oil | |
| PAO4 | Low-viscosity polyalphaolefin oil (Chevron Philips) | |
| PAO9 | High-viscosity polyalphaolefin oil (Chevron Philips) | |
| PDMS | Polydimethylsiloxane | |
| POM | Polyoxymethylene | |
| Spreading parameter | ||
| Si-DLC | Hydrogenated amophorous diamond-like carbon | |
| SL | Subscript for the interface between the surface and the liquid | |
| SM | Subscript for the interface between the surface and the surrounding medium | |
| Spreading parameter derived by Kalin and Polajnar | ||
| ta-C | Non-hydrogenated tetrahedral amorphous diamond-like carbon | |
| [THTDP][NTf2] | Trihexyltetradecyl phosphonium bis(trifluoromethylsulfonyl) amide | |
| [THTDA][NTf2] | Trihexyltetradecyl ammonium bis(trifluoromethylsulfonyl) | |
| Work per unit area | ||
| [1TD3HI][NTf2] | 1-Tetradecyl-3-hexyl imidazolium bis(trifluoromethylsulfonyl) amide | |
| Surface tension (and surface energy) | or | |
| Surface roughness (average or root mean square) roughness | ||
| Contact angle | ||
| Specific film thickness | ||
| Superscript for a dimensionless parameter |
References
- Tzanakis, I.; Hadfield, M.; Thomas, B.; Noya, S.M.; Henshaw, I.; Austen, S. Future perspectives on sustainable tribology. Renew. Sustain. Energy Rev. 2012, 16, 4126–4140. [Google Scholar] [CrossRef]
- Stern, D.I. Energy and economic growth in the USA. Energy Econ. 1993, 15, 137–150. [Google Scholar] [CrossRef]
- Hutchings, I.M. Tribology, Friction and Wear of Engineering Materials; Edward Arnold: London, UK, 1992; ISBN 034056184X. [Google Scholar]
- Maru, M.M.; Tanaka, D.K. Consideration of stribeck diagram parameters in the investigation on wear and friction behavior in lubricated sliding. J. Braz. Soc. Mech. Sci. Eng. 2007, 29, 55–62. [Google Scholar] [CrossRef]
- Xie, Z.; Rao, Z.; Ta-Na; Liu, L.; Chen, R. Theoretical and experimental research on the friction coefficient of water lubricated bearing with consideration of wall slip effects. Mech. Ind. 2016, 17, 106. [Google Scholar] [CrossRef]
- Bombard, A.J.F.; Gonçalves, F.R.; Shahrivar, K.; Ortiz, A.L.; de Vicente, J. Tribological behavior of ionic liquid-based magnetorheological fluids in steel and polymeric point contacts. Tribol. Int. 2015, 81, 309–320. [Google Scholar] [CrossRef]
- De Vicente, J.; Stokes, J.R.; Spikes, H.A. The frictional properties of Newtonian fluids in rolling—Sliding soft-EHL contact. Tribol. Lett. 2005, 20, 273–286. [Google Scholar] [CrossRef]
- Stachowiak, G.W.; Batchelor, A.W. Engineering Tribology; Elsevier Science & Technology Books: Amsterdam, The Netherlands, 2013; ISBN 9780123977762. [Google Scholar]
- Kalin, M.; Polajnar, M. The correlation between the surface energy, the contact angle and the spreading parameter, and their relevance for the wetting behaviour of DLC with lubricating oils. Tribol. Int. 2013, 66, 225–233. [Google Scholar] [CrossRef]
- Kalin, M.; Polajnar, M. The effect of wetting and surface energy on the friction and slip in oil-lubricated contacts. Tribol. Lett. 2013, 52, 185–194. [Google Scholar] [CrossRef]
- Kalin, M.; Polajnar, M. The wetting of steel, DLC coatings, ceramics and polymers with oils and water: The importance and correlations of surface energy, surface tension, contact angle and spreading. Appl. Surf. Sci. 2014, 293, 97–108. [Google Scholar] [CrossRef]
- Blanco, D.; Bartolomé, M.; Ramajo, B.; Viesca, J.L.; González, R.; Hernández Battez, A. Wetting Properties of Seven Phosphonium Cation-Based Ionic Liquids. Ind. Eng. Chem. Res. 2016, 55, 9594–9602. [Google Scholar] [CrossRef]
- Brochard, F. Motions of droplets on solid surfaces inducted by chemical or thermal gradients. Langmuir 1989, 5, 432–438. [Google Scholar] [CrossRef]
- Blanco, D.; Viesca, J.L.; Mallada, M.T.; Ramajo, B.; González, R.; Battez, A.H. Wettability and corrosion of [NTf 2] anion-based ionic liquids on steel and PVD (TiN, CrN, ZrN) coatings. Surf. Coat. Technol. 2016, 302, 24–32. [Google Scholar] [CrossRef]
- Matczak, L.; Johanning, C.; Gil, E.; Smith, T.W.; Schertzer, M.J.; Iglesias Victoria, P. Effect of cation nature on the lubricating and physicochemical properties of three ionic liquids. Tribol. Int. 2018, 124, 23–33. [Google Scholar] [CrossRef]
- Chen, W.; Foster, A.S.; Alava, M.J.; Laurson, L. Stick-Slip Control in Nanoscale Boundary Lubrication by Surface Wettability. Phys. Rev. Lett. 2015, 114, 95502. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Li, K.; Zhang, S.; Amann, T.; Zhang, C. Anti-spreading behavior of 1,3-diketone lubricating oil on steel surfaces. Tribol. Int. 2018, 121, 108–113. [Google Scholar] [CrossRef]
- Lawes, S.D.; Hainsworth, S.V.; Blake, P.; Ryder, K.S.; Abbott, A.P. Lubrication of steel/steel contacts by choline chloride ionic liquids. Tribol. Lett. 2010, 37, 103–110. [Google Scholar] [CrossRef]
- Qu, J.; Bansal, D.G.; Yu, B.; Howe, J.Y.; Luo, H.; Dai, S.; Li, H.; Blau, P.J.; Bunting, B.G.; Mordukhovich, G.; et al. Antiwear performance and mechanism of an oil-miscible ionic liquid as a lubricant additive. ACS Appl. Mater. Interfaces 2012, 4, 997–1002. [Google Scholar] [CrossRef] [PubMed]
- Bonaccurso, E.; Kappl, M.; Butt, H.-J. Hydrodynamic force measurements: Boundary slip of water on hydrophilic surfaces and electrokinetic effects. Phys. Rev. Lett. 2002, 88, 76103–76104. [Google Scholar] [CrossRef] [PubMed]
- Pit, R.; Hervet, H.; Leger, L. Direct experimental evidence of slip in hexadecane: Solid interface. Phys. Rev. Lett. 2000, 85, 980–983. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, K.; Udagawa, Y.; Udagawa, H. Drag reduction of Newtonian fluid in a circular pipe with a highly water-repellent wall. J. Fluid Mech. 1999, 381, 225–238. [Google Scholar] [CrossRef]
- Maali, A.; Bhushan, B. Nanorheology and boundary slip in confined liquids using atomic force microscopy. J. Phys. Condens. Matter 2008, 20, 315201. [Google Scholar] [CrossRef]
- Raj, R.; Enright, R.; Zhu, Y.; Adera, S.; Wang, E.N. Unified Model for Contact Angle Hysteresis on Heterogeneous and Superhydrophobic Surfaces. Langmuir 2012, 28, 15777–15788. [Google Scholar] [CrossRef] [PubMed]
- Kozbial, A.; Trouba, C.; Liu, H.; Li, L. Characterization of the Intrinsic Water Wettability of Graphite Using Contact Angle Measurements: Effect of Defects on Static and Dynamic Contact Angles. Langmuir 2017, 33, 959–967. [Google Scholar] [CrossRef] [PubMed]
- Extrand, C.; Kumagai, Y. An experimental study of contact angle hysteresis. J. Colloid Interface Sci. 1997, 191, 378–383. [Google Scholar] [CrossRef] [PubMed]
- Lam, C.; Wu, R.; Li, D.; Hair, M.; Neumann, A. Study of the advancing and receding contact angles: Liquid sorption as a cause of contact angle hysteresis. Adv. Colloid Interface Sci. 2002, 96, 169–191. [Google Scholar] [CrossRef]
- Bormashenko, E. Wetting of real solid surfaces: New glance on well-known problems. Colloid Polym. Sci. 2013, 291, 339–342. [Google Scholar] [CrossRef]
- Bermudez, M.; Jimenez, A. Surface interactions in lubrication of titanium, aluminium, and titanium-aluminium alloys with the ionic liquid [C(2)mim]Tf2N under increasing temperature. Proc. Inst. Mech. Eng. Part J. 2012, 226, 977–990. [Google Scholar] [CrossRef]
- Minami, I. Ionic liquids in tribology. Molecules 2009, 14, 2286–2305. [Google Scholar] [CrossRef] [PubMed]
- Mahrova, M.; Conte, M.; Roman, E.; Nevshupa, R. Critical Insight into Mechanochemical and Thermal Degradation of Imidazolium-Based Ionic Liquids with Alkyl and Monomethoxypoly(ethylene glycol) Side Chains. J. Phys. Chem. C 2014, 118, 22544–22552. [Google Scholar] [CrossRef]
- Jiménez, A.E.; Bermúdez, M.D.; Iglesias, P. Lubrication of Inconel 600 with ionic liquids at high temperature. Tribol. Int. 2009, 42, 1744–1751. [Google Scholar] [CrossRef]
- Iglesias, P.; Bermudez, M.; Carrion, F.; Martinez-Nicolas, G. Friction and wear of aluminium–steel contacts lubricated with ordered fluids-neutral and ionic liquid crystals as oil additives. Wear 2004, 256, 386–392. [Google Scholar] [CrossRef]
- Lee, S.J.; Hong, J.; Kang, K.H.; Kang, I.S.; Lee, S.J. Electrowetting-induced droplet detachment from hydrophobic surfaces. Langmuir 2014, 30, 1805–1811. [Google Scholar] [CrossRef] [PubMed]
- Owens, D.K.; Wendt, R.C. Estimation of the surface free energy of polymers. J. Appl. Polym. Sci. 1969, 13, 1741–1747. [Google Scholar]
- Burkhart, C.T.; Maki, K.L.; Schertzer, M.J. Effects of Interface Velocity, Diffusion Rate, and Radial Velocity on Colloidal Deposition Patterns Left by Evaporating Droplets. ASME J. Heat Transf. 2017, 139, 111505. [Google Scholar] [CrossRef]
- Kudtarkar, K.; Johnson, M.; Iglesias, P.; Smith, T.W.; Schertzer, M.J. Effects of chemicla composition on the electromechanical properties of microfluidically synthesized hydrogel beads. ASME J. Fluids Eng. 2018, 140, 101103. [Google Scholar] [CrossRef]
| Source | Surface | Lubricant | Temp. | θ (°) | S | SP | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Polar | Disperse | Total | Polar | Disperse | Total | (°C) | (mN/m) | (mN/m) | ||||
| [10] | Steel | PAO4 | 4.8 | 24.2 | 29.0 | 12.1 | 31.4 | 43.5 | 11.1 | −0.02 | 12.34 | |
| [10] | Steel | PAO9 | 6.5 | 23.7 | 30.2 | 12.1 | 31.4 | 43.5 | 11.3 | −0.02 | 11.86 | |
| [10] | ta-C | PAO4 | 4.8 | 24.2 | 29.0 | 16.5 | 31.9 | 48.4 | 3.5 | 0.00 | 15.38 | |
| [10] | ta-C | PAO9 | 6.5 | 23.7 | 30.2 | 16.5 | 31.9 | 48.4 | 8.5 | −0.01 | 15.31 | |
| [10] | Si-DLC | PAO4 | 4.8 | 24.2 | 29.0 | 8.6 | 31.8 | 40.4 | 4.3 | 0.00 | 10.32 | |
| [10] | Si-DLC | PAO9 | 6.5 | 23.7 | 30.2 | 8.6 | 31.8 | 40.4 | 10.9 | −0.02 | 9.44 | |
| [10] | N-DLC | PAO4 | 4.8 | 24.2 | 29.0 | 7.8 | 32.5 | 40.2 | 6.8 | −0.01 | 10.24 | |
| [10] | N-DLC | PAO9 | 6.5 | 23.7 | 30.2 | 7.8 | 32.5 | 40.2 | 13.8 | −0.03 | 9.25 | |
| [10] | a-C:H | PAO4 | 4.8 | 24.2 | 29.0 | 4.3 | 31.8 | 36.1 | 7.6 | −0.01 | 6.55 | |
| [10] | a-C:H | PAO9 | 6.5 | 23.7 | 30.2 | 4.3 | 31.8 | 36.1 | 13.6 | −0.03 | 5.06 | |
| [10] | F-DLC | PAO4 | 4.8 | 24.2 | 29.0 | 1.2 | 16.8 | 18.0 | 53.2 | −0.40 | −12.96 | |
| [10] | F-DLC | PAO9 | 6.5 | 23.7 | 30.2 | 1.2 | 16.8 | 18.0 | 56.5 | −0.45 | −14.99 | |
| [7] | Steel | PAO | 0.0 | 27.0 | 27.0 | 2.2 | 39.6 | 41.8 | 10.8 | −0.02 | 13.20 | |
| [7] | Steel | [EMIM][NTf2] | 11.4 | 25.6 | 37.0 | 2.2 | 39.6 | 41.8 | 34.5 | −0.18 | −0.46 | |
| [7] | Steel | [EMIM][CF3SO3] | 17.8 | 23.5 | 41.3 | 2.2 | 39.6 | 41.8 | 35.3 | −0.18 | −9.10 | |
| [7] | Steel | [BMIM][SCN] | 39.2 | 7.8 | 47.0 | 2.2 | 39.6 | 41.8 | 46.4 | −0.31 | −40.15 | |
| [7] | Steel | [BMIM][NTF2] | 0.9 | 32.7 | 33.6 | 2.2 | 39.6 | 41.8 | 38.9 | −0.22 | 7.44 | |
| [7] | Steel | [BMIM][BF4] | 20.7 | 24.1 | 44.8 | 2.2 | 39.6 | 41.8 | 48.8 | −0.34 | −14.12 | |
| [7] | Steel | [BMIM][PF6] | 5.2 | 38.9 | 44.1 | 2.2 | 39.6 | 41.8 | 52.6 | −0.39 | −3.02 | |
| [7] | Steel | [BMIM][CH3COO] | 9.9 | 26.5 | 36.4 | 2.2 | 39.6 | 41.8 | 33.6 | −0.17 | 1.36 | |
| [7] | Steel | IL I04 | 6.0 | 22.3 | 28.3 | 2.2 | 39.6 | 41.8 | 6.4 | −0.01 | 10.21 | |
| [7] | POM | PAO | 0.0 | 27.0 | 27.0 | 4.5 | 35.4 | 39.9 | 12.4 | −0.02 | 13.20 | |
| [7] | POM | [EMIM][NTf2] | 11.4 | 25.6 | 37.0 | 4.5 | 35.4 | 39.9 | 38.2 | −0.21 | 0.72 | |
| [7] | POM | [EMIM][CF3SO3] | 17.8 | 23.5 | 41.3 | 4.5 | 35.4 | 39.9 | 42.2 | −0.26 | −6.97 | |
| [7] | POM | [BMIM][SCN] | 39.2 | 7.8 | 47.0 | 4.5 | 35.4 | 39.9 | 48.8 | −0.34 | −34.07 | |
| [7] | POM | [BMIM][NTF2] | 0.9 | 32.7 | 33.6 | 4.5 | 35.4 | 39.9 | 33.4 | −0.17 | 4.88 | |
| [7] | POM | [BMIM][BF4] | 20.7 | 24.1 | 44.8 | 4.5 | 35.4 | 39.9 | 50.6 | −0.37 | −11.88 | |
| [7] | POM | [BMIM][PF6] | 5.2 | 38.9 | 44.1 | 4.5 | 35.4 | 39.9 | 53.5 | −0.41 | −4.41 | |
| [7] | POM | [BMIM][CH3COO] | 9.9 | 26.5 | 36.4 | 4.5 | 35.4 | 39.9 | 49.9 | −0.36 | 1.78 | |
| [7] | POM | IL I04 | 6.0 | 22.3 | 28.3 | 4.5 | 35.4 | 39.9 | 7.7 | −0.01 | 9.89 | |
| [7] | PDMS | PAO | 0.0 | 27.0 | 27.0 | 0.1 | 18.8 | 18.9 | 34.5 | −0.18 | −9.10 | |
| [7] | PDMS | [EMIM][NTf2] | 11.4 | 25.6 | 37.0 | 0.1 | 18.8 | 18.9 | 83.7 | −0.89 | −27.99 | |
| [7] | PDMS | [EMIM][CF3SO3] | 17.8 | 23.5 | 41.3 | 0.1 | 18.8 | 18.9 | 86.1 | −0.93 | −38.02 | |
| [7] | PDMS | [BMIM][SCN] | 39.2 | 7.8 | 47.0 | 0.1 | 18.8 | 18.9 | 102.9 | −1.22 | −65.76 | |
| [7] | PDMS | [BMIM][NTF2] | 0.9 | 32.7 | 33.6 | 0.1 | 18.8 | 18.9 | 73.8 | −0.72 | −16.89 | |
| [7] | PDMS | [BMIM][BF4] | 20.7 | 24.1 | 44.8 | 0.1 | 18.8 | 18.9 | 92.3 | −1.04 | −44.10 | |
| [7] | PDMS | [BMIM][PF6] | 5.2 | 38.9 | 44.1 | 0.1 | 18.8 | 18.9 | 87.0 | −0.95 | −32.47 | |
| [7] | PDMS | [BMIM][CH3COO] | 9.9 | 26.5 | 36.4 | 0.1 | 18.8 | 18.9 | 88.1 | −0.97 | −26.28 | |
| [7] | PDMS | IL I04 | 6.0 | 22.3 | 28.3 | 0.1 | 18.8 | 18.9 | 51.7 | −0.38 | −14.12 | |
| [16] | Steel | [THTDA][NTf2] | 11.0 | 15.6 | 26.6 | 2.2 | 39.6 | 41.8 | 25 | 26.6 | −0.11 | 6.34 |
| [16] | Steel | [THTDA][NTf2] | 10.6 | 18.1 | 28.7 | 2.2 | 39.6 | 41.8 | 40 | 28.7 | −0.12 | 5.87 |
| [16] | Steel | [THTDA][NTf2] | 10.9 | 7.2 | 18.0 | 2.2 | 39.6 | 41.8 | 100 | 18.0 | −0.05 | 7.41 |
| [16] | Steel | [THTDP][NTf2] | 9.8 | 4.0 | 13.8 | 2.2 | 39.6 | 41.8 | 25 | 13.8 | −0.03 | 6.81 |
| [16] | Steel | [THTDP][NTf2] | 11.1 | 6.5 | 17.7 | 2.2 | 39.6 | 41.8 | 40 | 17.7 | −0.05 | 6.72 |
| [16] | Steel | [THTDP][NTf2] | 11.1 | 6.5 | 17.7 | 2.2 | 39.6 | 41.8 | 100 | 17.7 | −0.05 | 6.72 |
| [16] | Steel | [1TD3HI][NTf2] | 4.4 | 0.5 | 4.9 | 2.2 | 39.6 | 41.8 | 25 | 4.9 | 0.00 | 5.23 |
| [16] | Steel | [1TD3HI][NTf2] | 11.2 | 6.1 | 17.3 | 2.2 | 39.6 | 41.8 | 40 | 17.3 | −0.05 | 6.43 |
| [16] | Steel | [1TD3HI][NTf2] | 12.1 | 15.3 | 27.4 | 2.2 | 39.6 | 41.8 | 100 | 27.4 | −0.11 | 4.79 |
| Source | Surface | Lubricant | Type | Friction Coefficient at | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.05 (m/s) | 0.10 (m/s) | 0.20 (m/s) | 0.05 (m/s) | 0.10 (m/s) | 0.20 (m/s) | |||||
| [7] | Steel | PAO | MR | 0.018 | 0.52 | 0.36 | 0.43 | 0.003 | 0.004 | 0.007 |
| [7] | Steel | [EMIM][NTf2] | MR | 0.176 | 0.17 | 0.17 | 0.15 | 0.008 | 0.012 | 0.019 |
| [7] | Steel | [EMIM][CF3SO3] | MR | 0.183 | 0.15 | 0.15 | 0.15 | 0.009 | 0.015 | 0.023 |
| [7] | Steel | [BMIM][SCN] | MR | 0.310 | 0.20 | 0.19 | 0.19 | 0.010 | 0.015 | 0.024 |
| [7] | Steel | [BMIM][NTF2] | MR | 0.222 | 0.19 | 0.18 | 0.18 | 0.010 | 0.016 | 0.026 |
| [7] | Steel | [BMIM][BF4] | MR | 0.341 | 0.14 | 0.14 | 0.13 | 0.014 | 0.022 | 0.034 |
| [7] | Steel | [BMIM][PF6] | MR | 0.393 | 0.15 | 0.15 | 0.16 | 0.027 | 0.042 | 0.066 |
| [7] | Steel | [BMIM][CH3COO] | MR | 0.167 | 0.16 | 0.16 | 0.16 | 0.027 | 0.043 | 0.067 |
| [7] | Steel | IL I04 | MR | 0.006 | 0.18 | 0.18 | 0.18 | 0.068 | 0.106 | 0.166 |
| [7] | POM | PAO | MR | 0.023 | 0.21 | 0.14 | 0.36 | 0.012 | 0.018 | 0.029 |
| [7] | POM | [EMIM][NTf2] | MR | 0.214 | 0.12 | 0.11 | 0.26 | 0.033 | 0.051 | 0.081 |
| [7] | POM | [EMIM][CF3SO3] | MR | 0.259 | 0.12 | 0.12 | 0.12 | 0.040 | 0.062 | 0.098 |
| [7] | POM | [BMIM][SCN] | MR | 0.341 | 0.14 | 0.14 | 0.15 | 0.041 | 0.064 | 0.101 |
| [7] | POM | [BMIM][NTF2] | MR | 0.165 | 0.12 | 0.13 | 0.13 | 0.044 | 0.069 | 0.108 |
| [7] | POM | [BMIM][BF4] | MR | 0.365 | 0.11 | 0.10 | 0.09 | 0.059 | 0.092 | 0.145 |
| [7] | POM | [BMIM][PF6] | MR | 0.406 | 0.12 | 0.08 | 0.07 | 0.113 | 0.177 | 0.277 |
| [7] | POM | [BMIM][CH3COO] | MR | 0.356 | 0.09 | 0.10 | 0.10 | 0.115 | 0.180 | 0.283 |
| [7] | POM | IL I04 | MR | 0.009 | 0.12 | 0.10 | 0.10 | 0.284 | 0.446 | 0.699 |
| [7] | PDMS | PAO | MR | 0.176 | 0.07 | 0.06 | 0.05 | 0.911 | 1.430 | 2.243 |
| [7] | PDMS | [EMIM][NTf2] | MR | 0.890 | 0.08 | 0.08 | 0.07 | 2.576 | 4.043 | 6.344 |
| [7] | PDMS | [EMIM][CF3SO3] | MR | 0.931 | 0.09 | 0.08 | 0.08 | 3.125 | 4.903 | 7.694 |
| [7] | PDMS | [BMIM][SCN] | MR | 1.223 | 0.07 | 0.06 | 0.06 | 3.213 | 5.041 | 7.911 |
| [7] | PDMS | [BMIM][NTF2] | MR | 0.721 | 0.09 | 0.09 | 0.08 | 3.448 | 5.410 | 8.489 |
| [7] | PDMS | [BMIM][BF4] | MR | 1.040 | 0.06 | 0.06 | 0.06 | 4.614 | 7.240 | 11.361 |
| [7] | PDMS | [BMIM][PF6] | MR | 0.947 | 0.11 | 0.08 | 0.09 | 8.841 | 13.873 | 21.768 |
| [7] | PDMS | [BMIM][CH3COO] | MR | 0.966 | 0.09 | 0.07 | 0.09 | 9.027 | 14.165 | 22.228 |
| [7] | PDMS | IL I04 | MR | 0.380 | 0.06 | 0.07 | 0.10 | 22.308 | 35.005 | 54.929 |
| Source | Surface | Lubricant | Type | Speed (−) | λ (−) | |S*| (−) | Friction Coefficient (−) |
|---|---|---|---|---|---|---|---|
| [7] | PDMS | [EMIM][NTf2] | IL | 7.900 | 0.176 | 0.060 | |
| [7] | POM | [EMIM][NTf2] | IL | 0.101 | 0.176 | 0.079 | |
| [7] | Steel | [EMIM][NTf2] | IL | 0.024 | 0.176 | 0.124 | |
| [7] | PDMS | [EMIM][CF3SO3] | IL | 7.900 | 0.183 | 0.062 | |
| [7] | POM | [EMIM][CF3SO3] | IL | 0.101 | 0.183 | 0.060 | |
| [7] | Steel | [EMIM][CF3SO3] | IL | 0.024 | 0.183 | 0.095 | |
| [7] | PDMS | [BMIM][SCN] | IL | 7.900 | 0.310 | 0.060 | |
| [7] | POM | [BMIM][SCN] | IL | 0.101 | 0.310 | 0.054 | |
| [7] | Steel | [BMIM][SCN] | IL | 0.024 | 0.310 | 0.090 | |
| [7] | PDMS | [BMIM][NTF2] | IL | 7.900 | 0.222 | 0.060 | |
| [7] | POM | [BMIM][NTF2] | IL | 0.101 | 0.222 | 0.080 | |
| [7] | Steel | [BMIM][NTF2] | IL | 0.024 | 0.222 | 0.092 | |
| [7] | PDMS | [BMIM][BF4] | IL | 7.900 | 0.341 | 0.059 | |
| [7] | POM | [BMIM][BF4] | IL | 0.101 | 0.341 | 0.067 | |
| [7] | Steel | [BMIM][BF4] | IL | 0.024 | 0.341 | 0.080 | |
| [7] | PDMS | [BMIM][PF6] | IL | 7.900 | 0.393 | 0.055 | |
| [7] | POM | [BMIM][PF6] | IL | 0.101 | 0.393 | 0.060 | |
| [7] | Steel | [BMIM][PF6] | IL | 0.024 | 0.393 | 0.057 | |
| [7] | PDMS | [BMIM][CH3COO] | IL | 7.900 | 0.167 | 0.059 | |
| [7] | POM | [BMIM][CH3COO] | IL | 0.101 | 0.167 | 0.056 | |
| [7] | Steel | [BMIM][CH3COO] | IL | 0.024 | 0.167 | 0.097 |
| Source | Surface | Lubricant | Type | Friction Coefficient at | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.05 (m/s) | 0.10 (m/s) | 0.50 (m/s) | 0.05 (m/s) | 0.10 (m/s) | 0.20 (m/s) | |||||
| [7] | Steel | [EMIM][NTf2] | IL | 0.176 | 0.14 | 0.13 | 0.12 | 0.008 | 0.012 | 0.019 |
| [7] | Steel | [EMIM][CF3SO3] | IL | 0.183 | 0.12 | 0.11 | 0.10 | 0.009 | 0.015 | 0.023 |
| [7] | Steel | [BMIM][SCN] | IL | 0.310 | 0.12 | 0.10 | 0.09 | 0.010 | 0.015 | 0.024 |
| [7] | Steel | [BMIM][NTF2] | IL | 0.222 | 0.12 | 0.10 | 0.09 | 0.010 | 0.016 | 0.026 |
| [7] | Steel | [BMIM][BF4] | IL | 0.341 | 0.09 | 0.08 | 0.06 | 0.014 | 0.022 | 0.034 |
| [7] | Steel | [BMIM][PF6] | IL | 0.393 | 0.06 | 0.04 | 0.05 | 0.027 | 0.042 | 0.066 |
| [7] | Steel | [BMIM][CH3COO] | IL | 0.167 | 0.10 | 0.06 | 0.04 | 0.027 | 0.043 | 0.067 |
| [7] | POM | [EMIM][NTf2] | IL | 0.214 | 0.10 | 0.08 | 0.08 | 0.033 | 0.051 | 0.081 |
| [7] | POM | [EMIM][CF3SO3] | IL | 0.259 | 0.09 | 0.08 | 0.06 | 0.040 | 0.062 | 0.098 |
| [7] | POM | [BMIM][SCN] | IL | 0.341 | 0.10 | 0.07 | 0.05 | 0.041 | 0.064 | 0.101 |
| [7] | POM | [BMIM][NTF2] | IL | 0.165 | 0.08 | 0.07 | 0.08 | 0.044 | 0.069 | 0.108 |
| [7] | POM | [BMIM][BF4] | IL | 0.365 | 0.06 | 0.07 | 0.05 | 0.059 | 0.092 | 0.145 |
| [7] | POM | [BMIM][PF6] | IL | 0.406 | 0.06 | 0.04 | 0.05 | 0.113 | 0.177 | 0.277 |
| [7] | POM | [BMIM][CH3COO] | IL | 0.356 | 0.06 | 0.07 | 0.03 | 0.115 | 0.180 | 0.283 |
| [7] | PDMS | [EMIM][NTf2] | IL | 0.890 | 0.12 | 0.06 | 0.06 | 2.576 | 4.043 | 6.344 |
| [7] | PDMS | [EMIM][CF3SO3] | IL | 0.931 | 0.07 | 0.06 | 0.06 | 3.125 | 4.903 | 7.694 |
| [7] | PDMS | [BMIM][SCN] | IL | 1.223 | 0.11 | 0.06 | 0.06 | 3.213 | 5.041 | 7.911 |
| [7] | PDMS | [BMIM][NTF2] | IL | 0.721 | 0.06 | 0.06 | 0.06 | 3.448 | 5.410 | 8.489 |
| [7] | PDMS | [BMIM][BF4] | IL | 1.040 | 0.06 | 0.06 | 0.06 | 4.614 | 7.240 | 11.361 |
| [7] | PDMS | [BMIM][PF6] | IL | 0.947 | 0.05 | 0.06 | 0.06 | 8.841 | 13.873 | 21.768 |
| [7] | PDMS | [BMIM][CH3COO] | IL | 0.966 | 0.06 | 0.06 | 0.06 | 9.027 | 14.165 | 22.228 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schertzer, M.J.; Iglesias, P. Meta-Analysis Comparing Wettability Parameters and the Effect of Wettability on Friction Coefficient in Lubrication. Lubricants 2018, 6, 70. https://doi.org/10.3390/lubricants6030070
Schertzer MJ, Iglesias P. Meta-Analysis Comparing Wettability Parameters and the Effect of Wettability on Friction Coefficient in Lubrication. Lubricants. 2018; 6(3):70. https://doi.org/10.3390/lubricants6030070
Chicago/Turabian StyleSchertzer, Michael J., and Patricia Iglesias. 2018. "Meta-Analysis Comparing Wettability Parameters and the Effect of Wettability on Friction Coefficient in Lubrication" Lubricants 6, no. 3: 70. https://doi.org/10.3390/lubricants6030070
APA StyleSchertzer, M. J., & Iglesias, P. (2018). Meta-Analysis Comparing Wettability Parameters and the Effect of Wettability on Friction Coefficient in Lubrication. Lubricants, 6(3), 70. https://doi.org/10.3390/lubricants6030070