Vibration Technologies for Friction Reduction to Overcome Weight Transfer Challenge in Horizontal Wells Using a Multiscale Friction Model
Abstract
:1. Introduction
2. Overview of Friction Reduction through Vibration
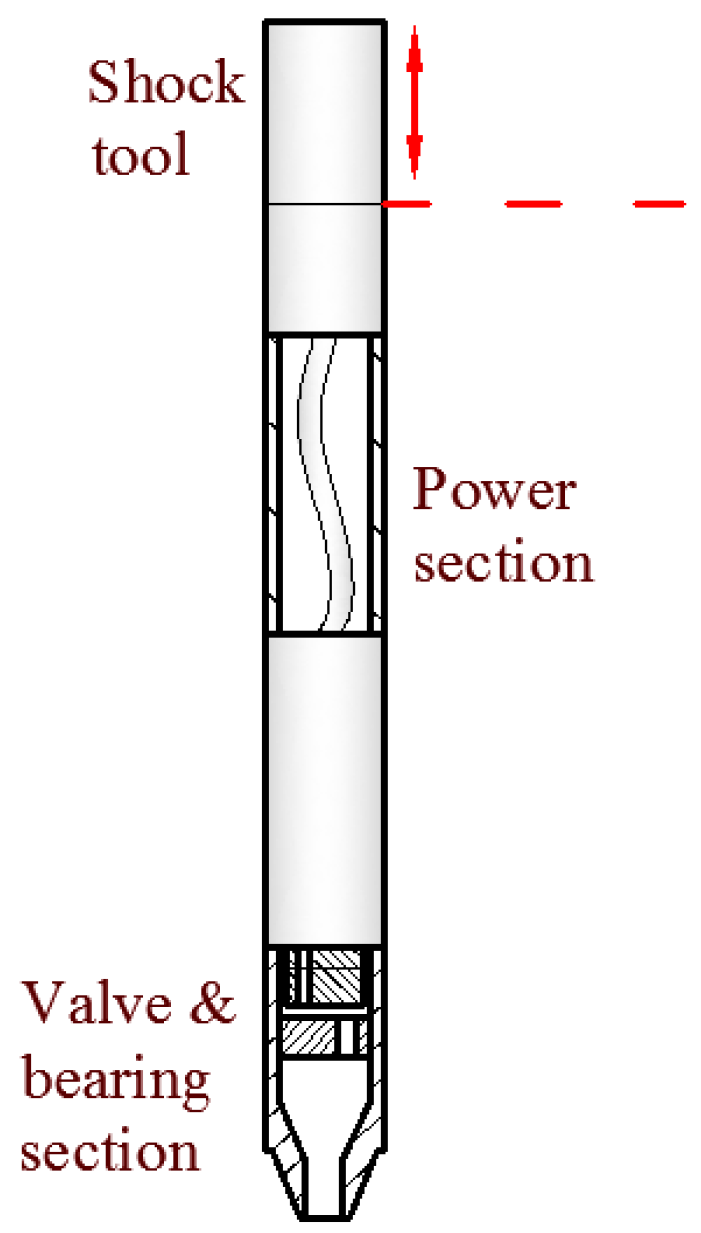
2.1. Drilling Agitator System (DAS)
2.1.1. NOV Hydraulic Oscillation System
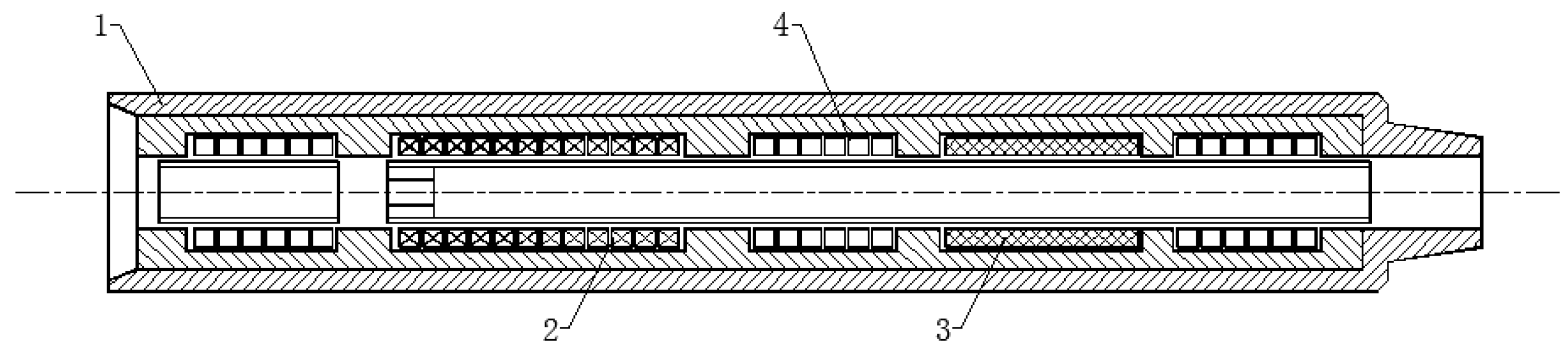
2.1.2. Three-Dimensional (3D) Hydraulic Oscillation System
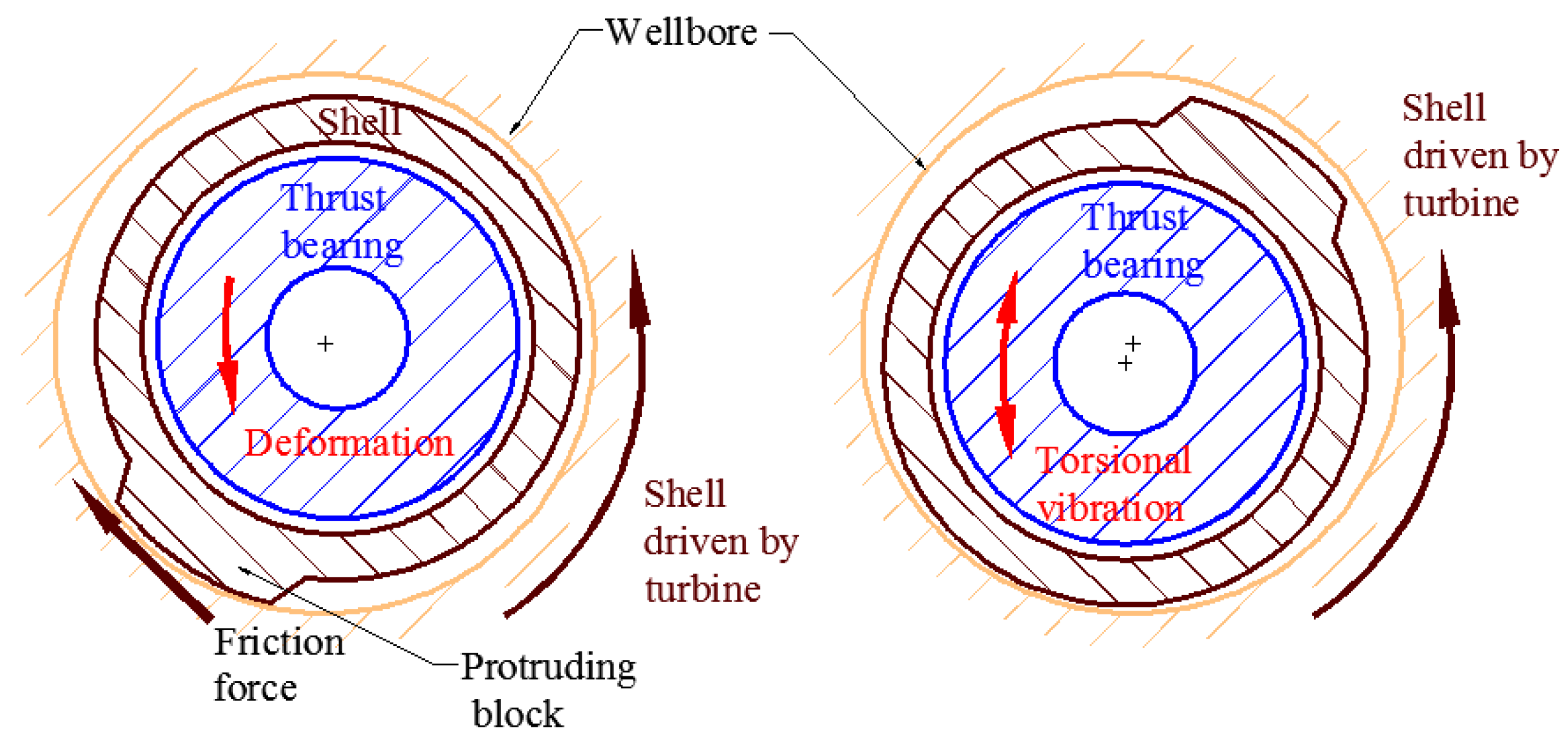
2.1.3. Radial Hydraulic Oscillator
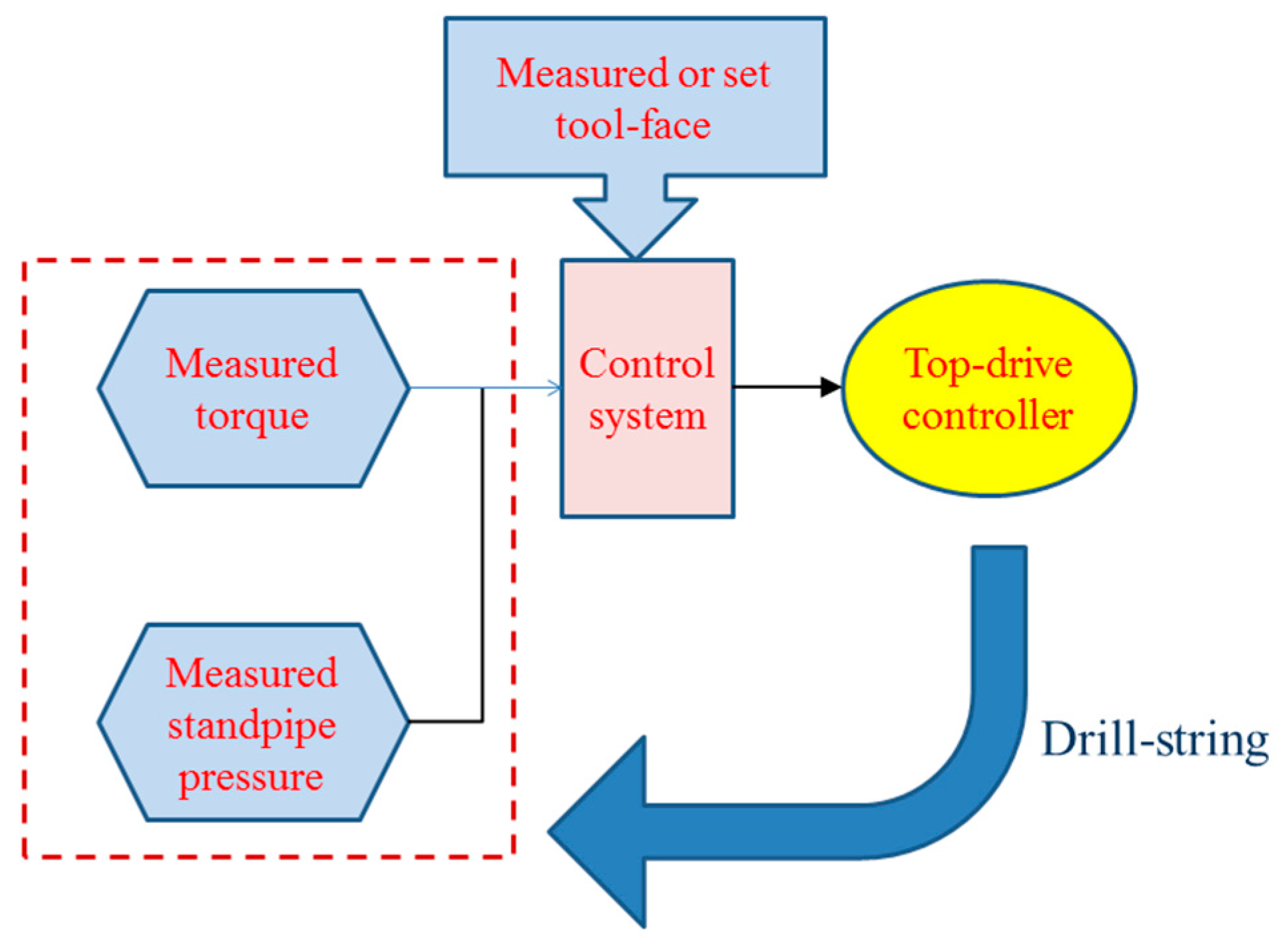
2.2. Slider Drilling Technology
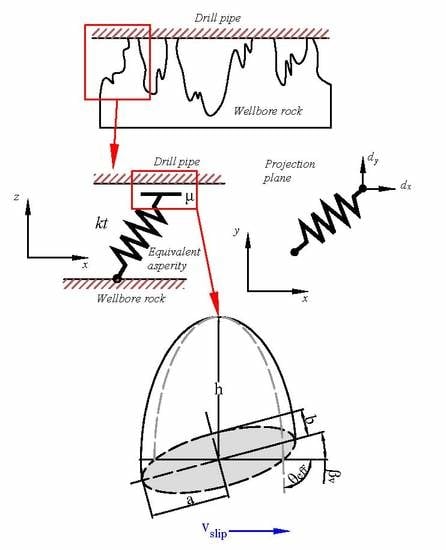
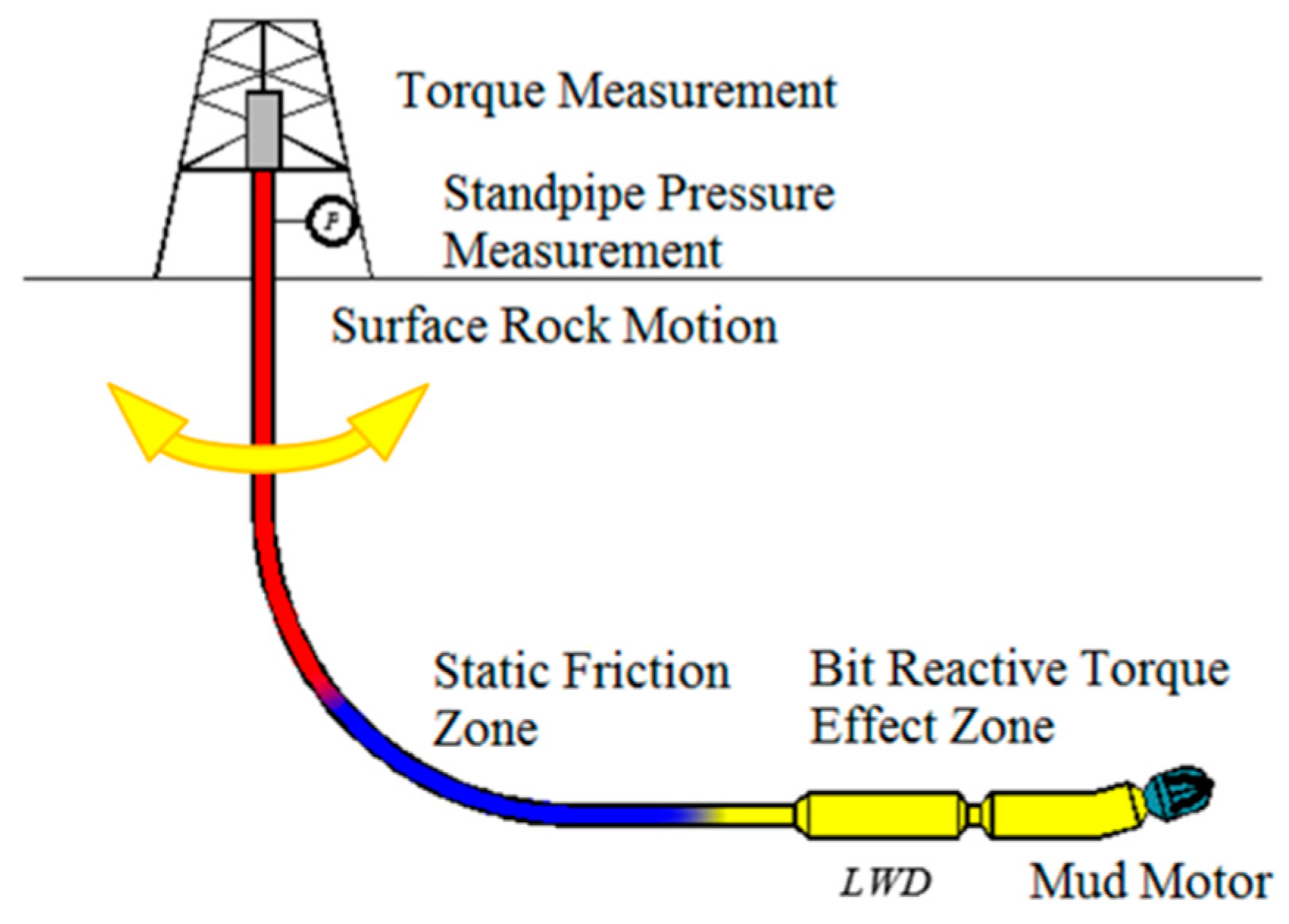
3. Friction Model between Tools and Drill String
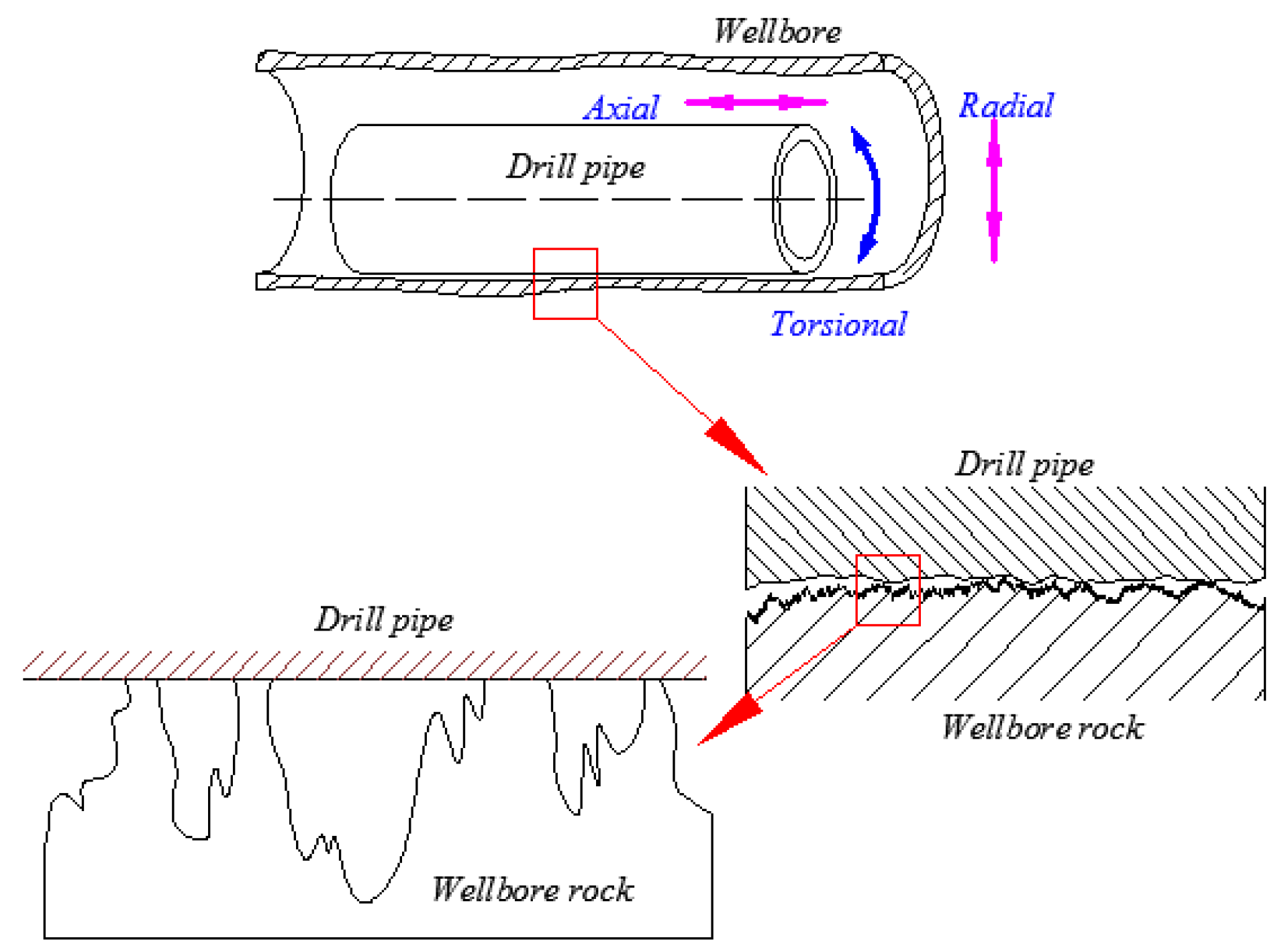
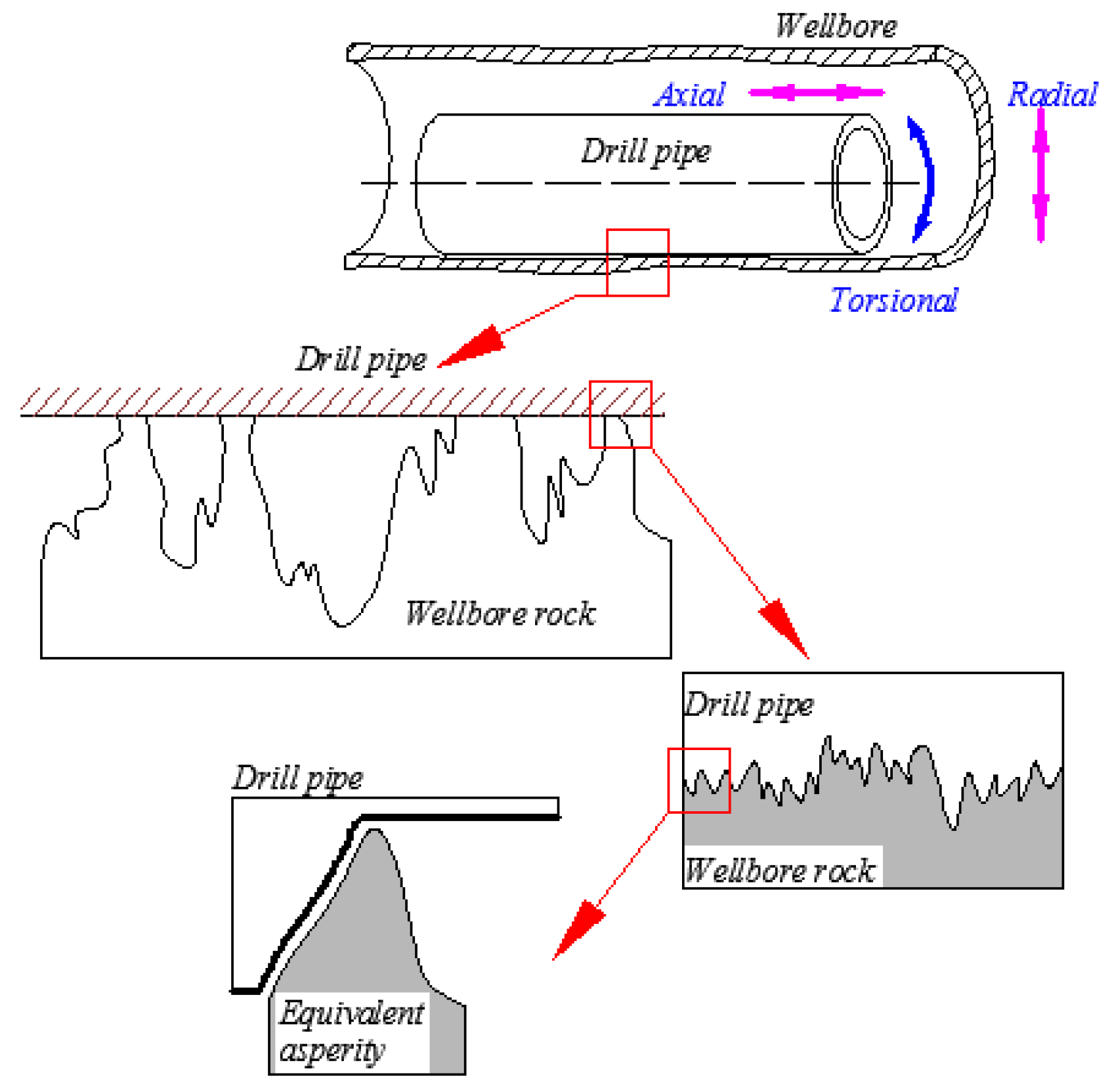
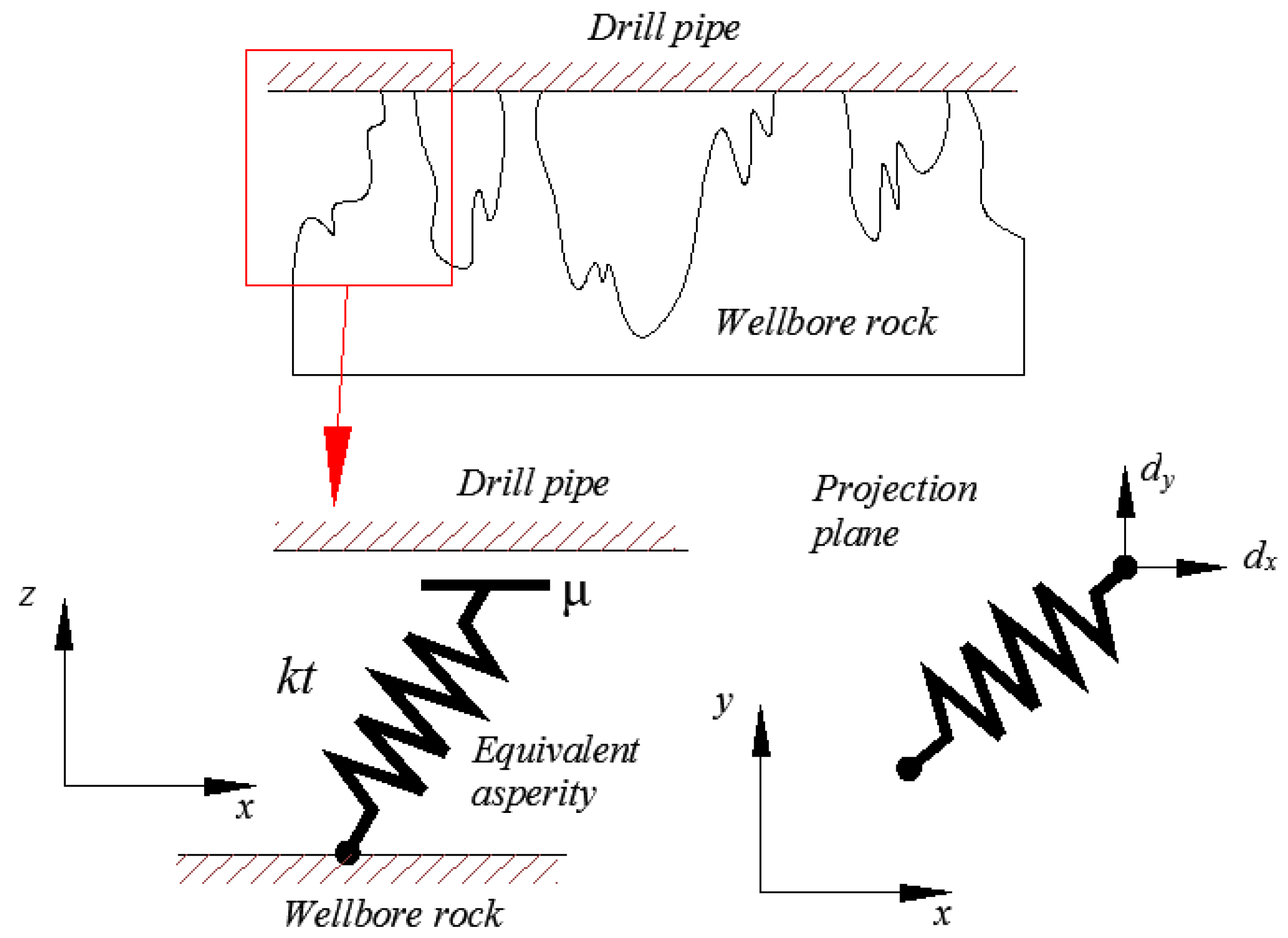
3.1. Surface and Contacts Forms
3.2. Basic Assumptions
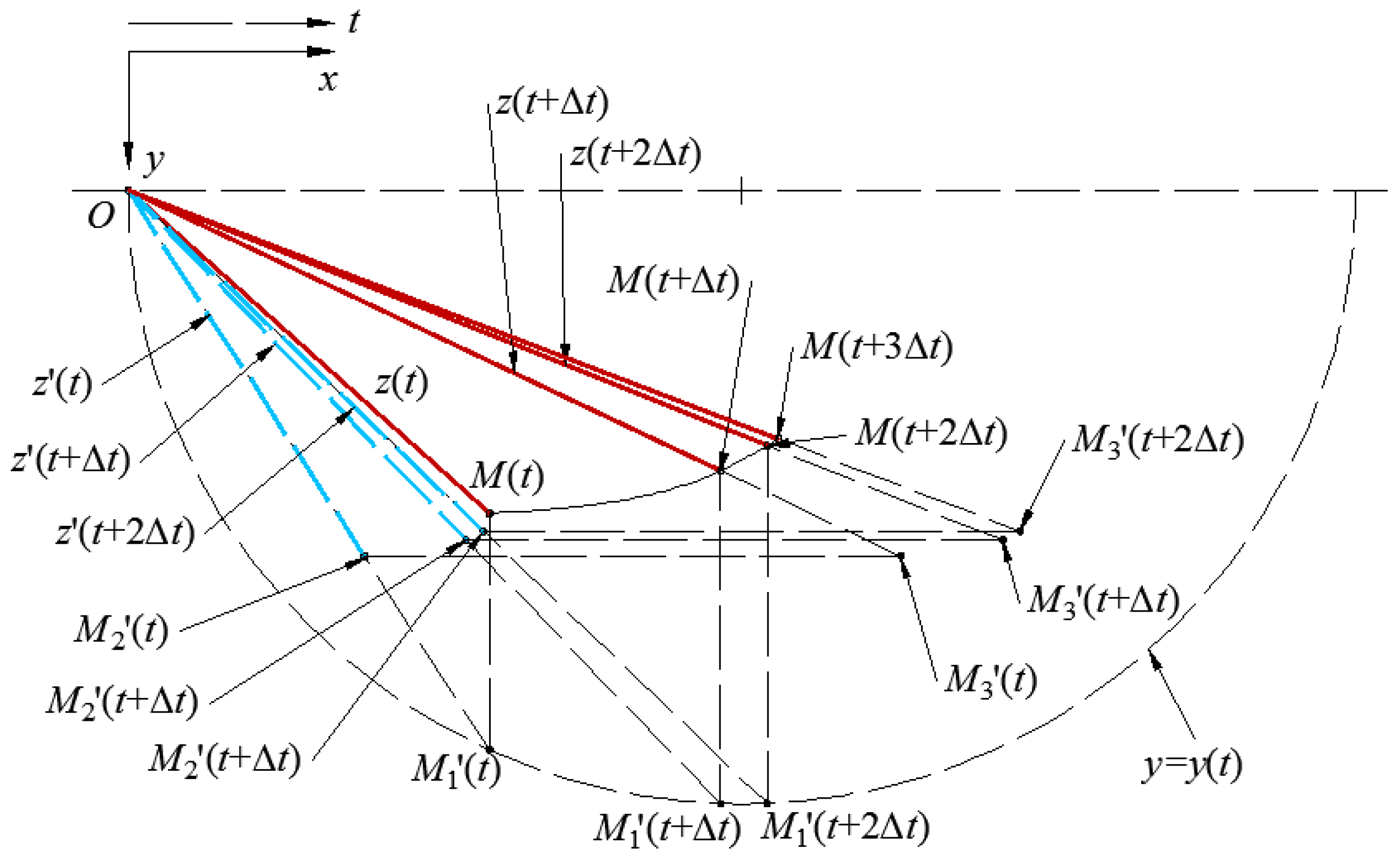
3.3. Multiscale Friction Model
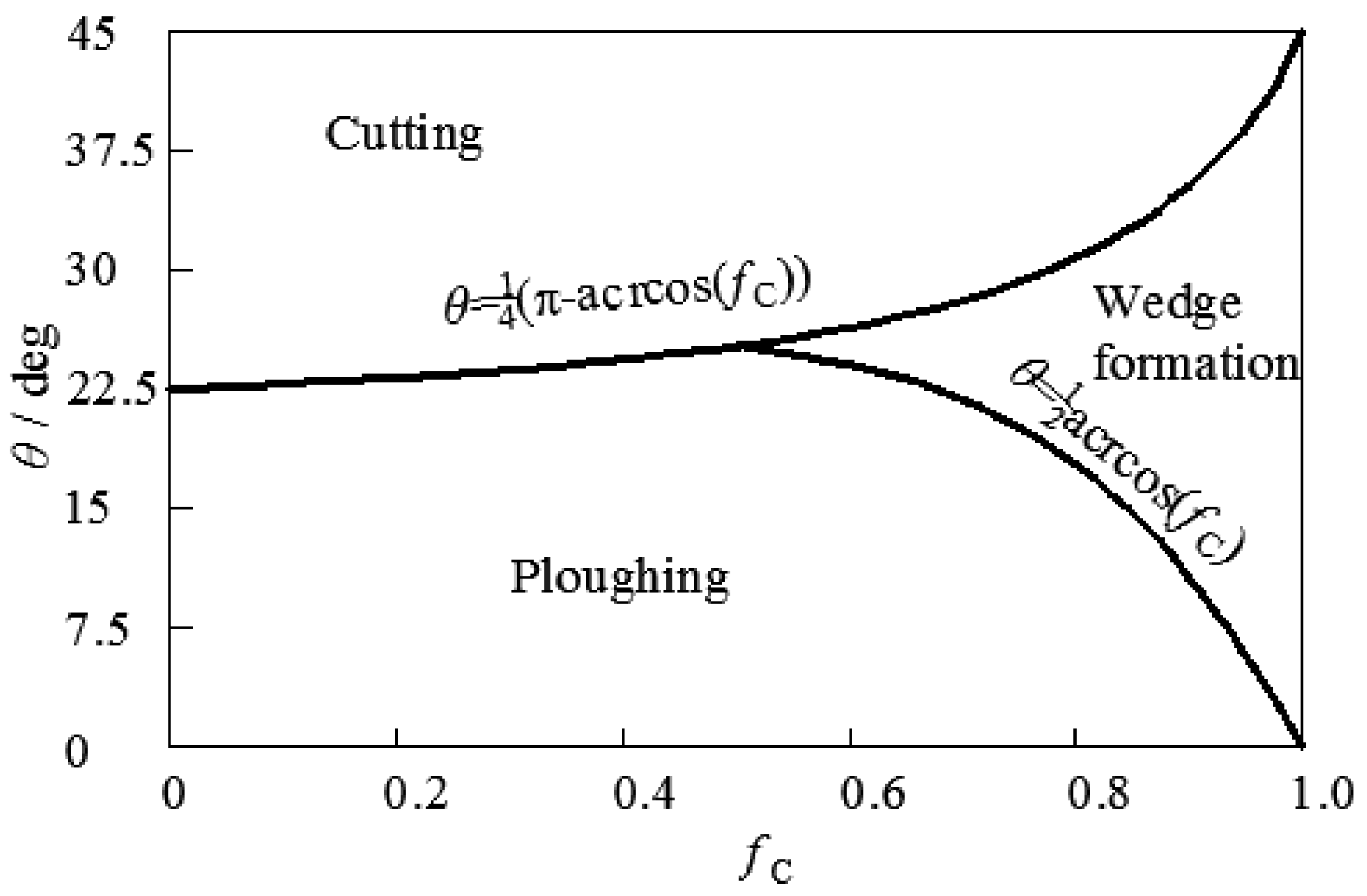
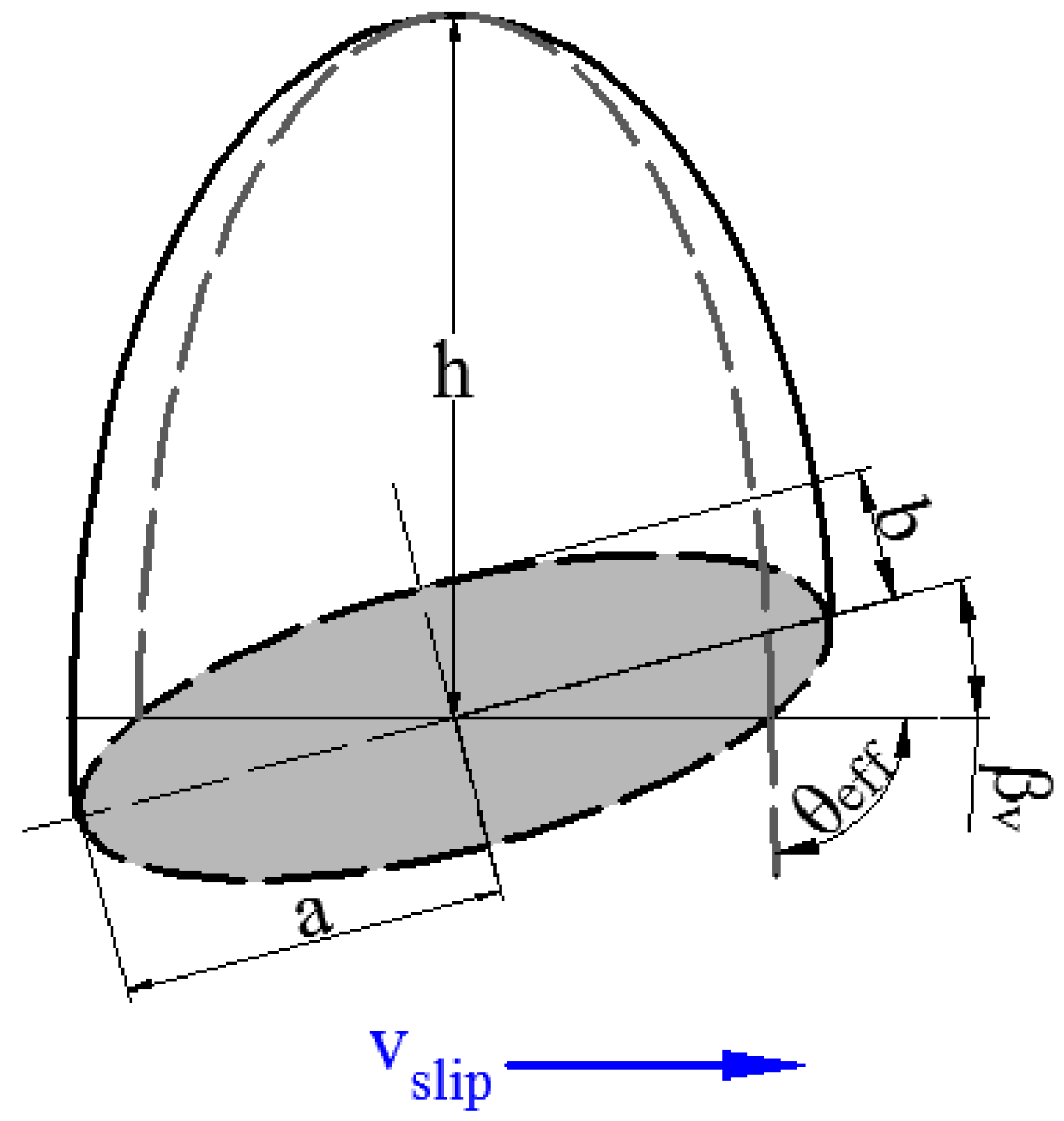
3.3.1. Asperity Friction Model
3.3.2. Asperity Deformation
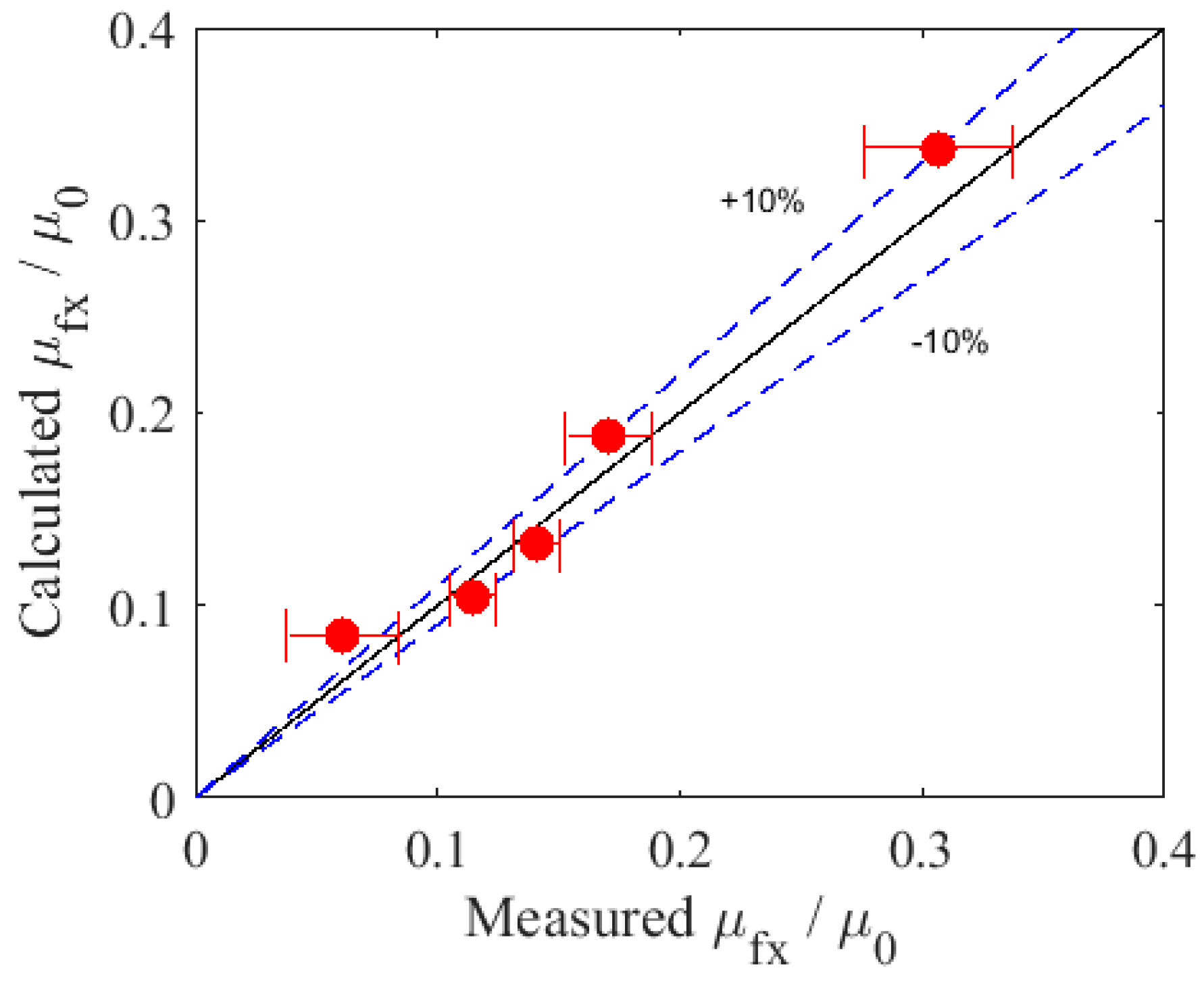
4. Model Verification
5. Mechanism of Friction Reduction Tools
5.1. Computational Parameters
5.2. Friction Characteristic of the DAS
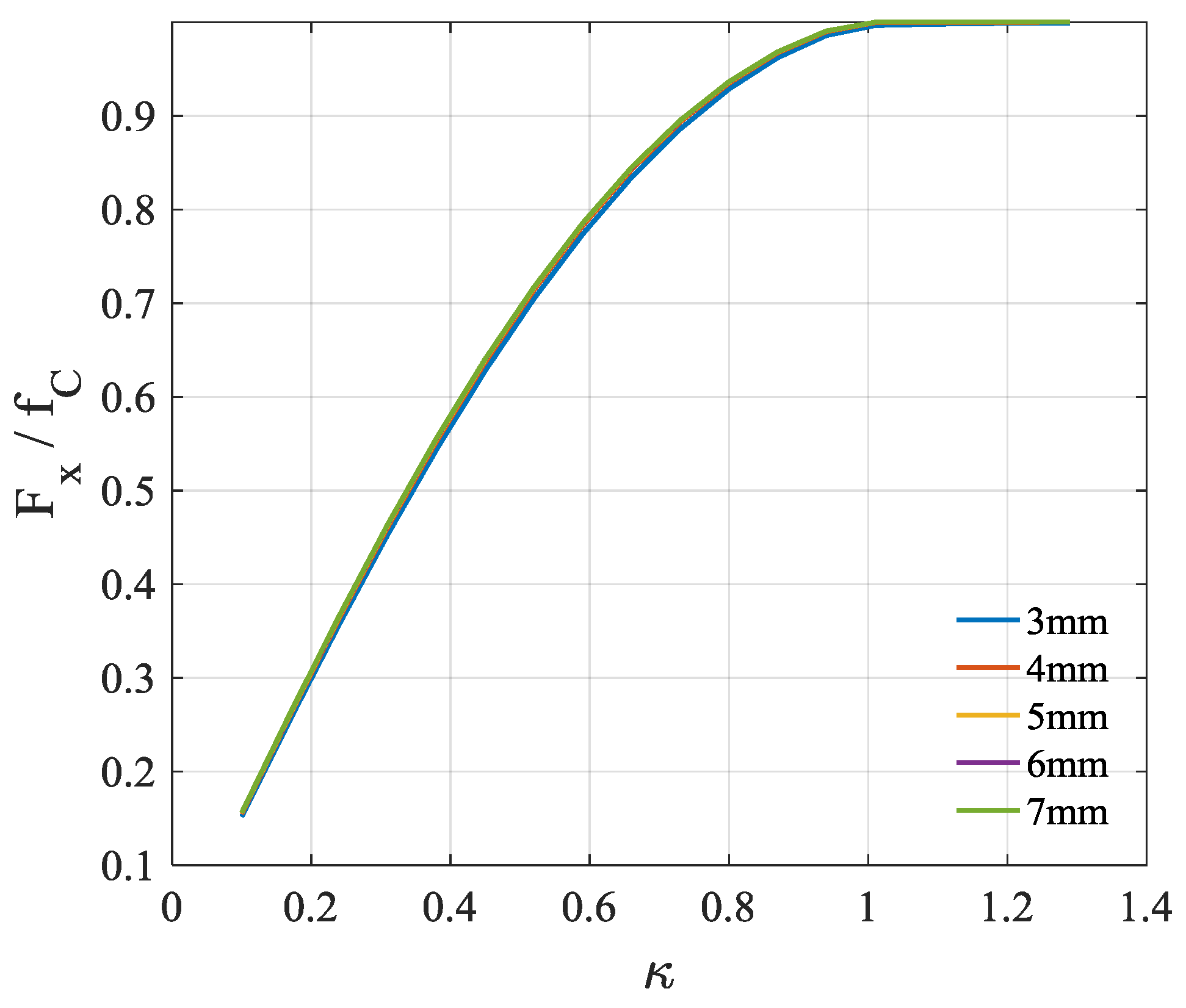
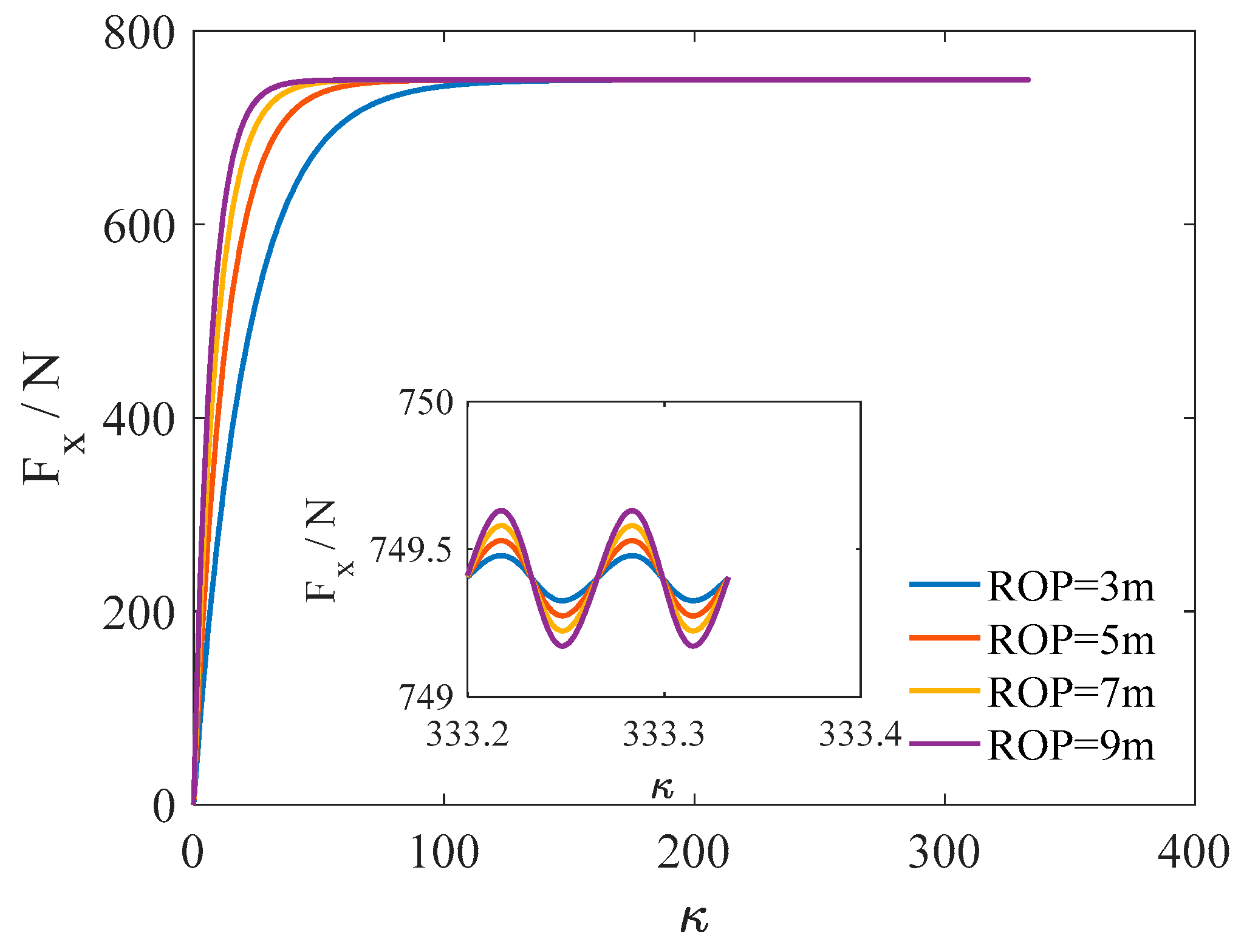
5.2.1. Longitudinal Oscillation
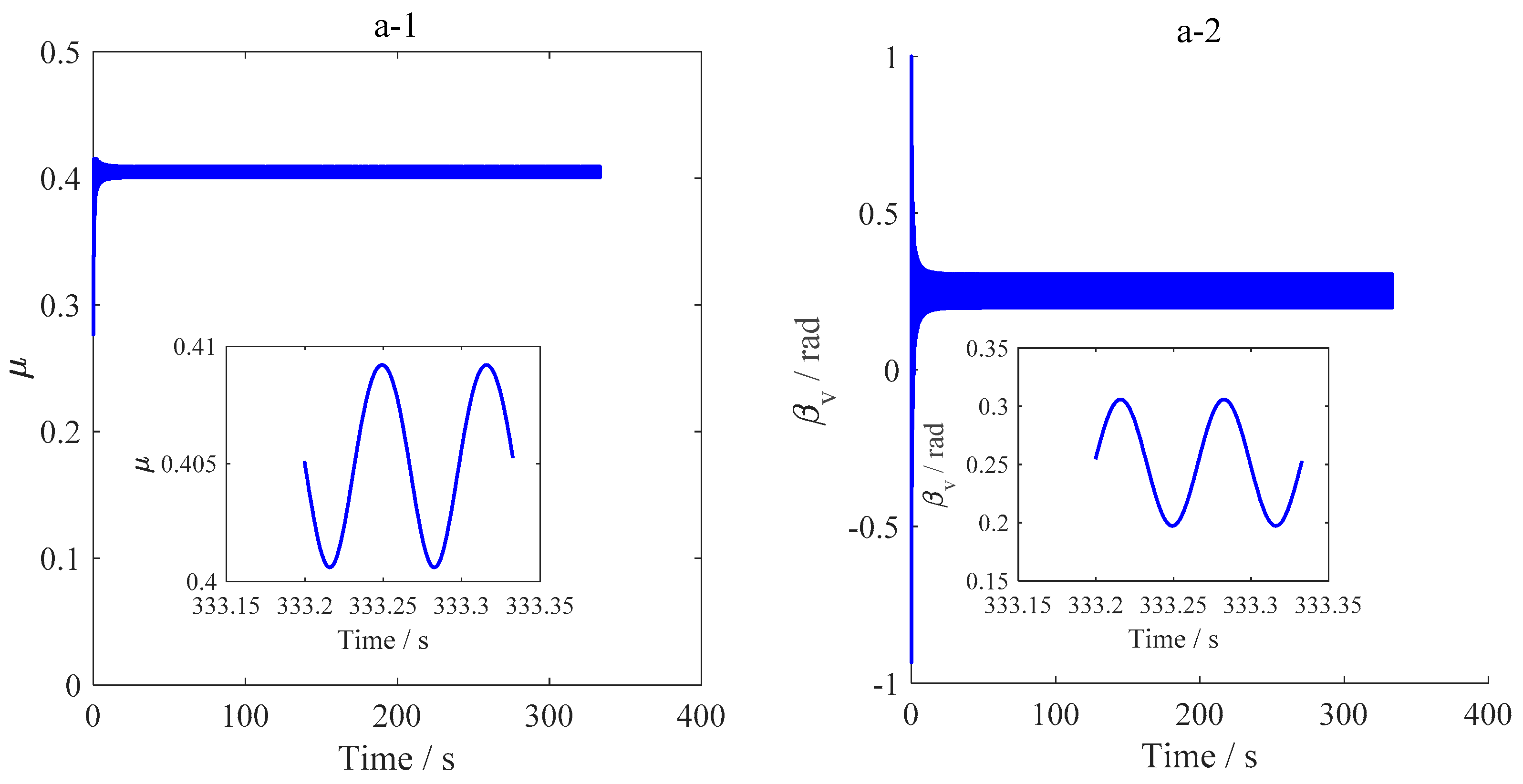
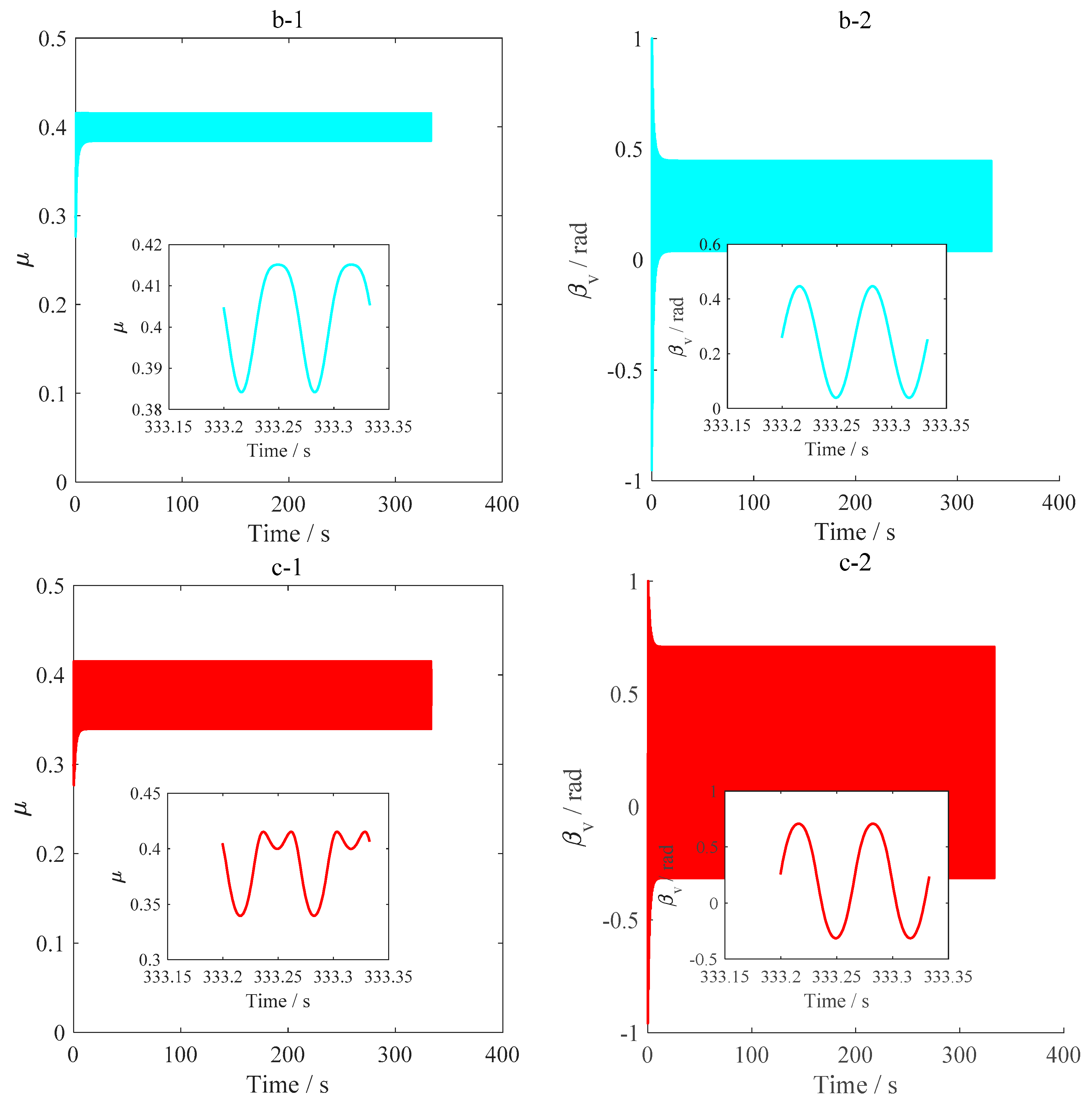
5.2.2. Radial Oscillation
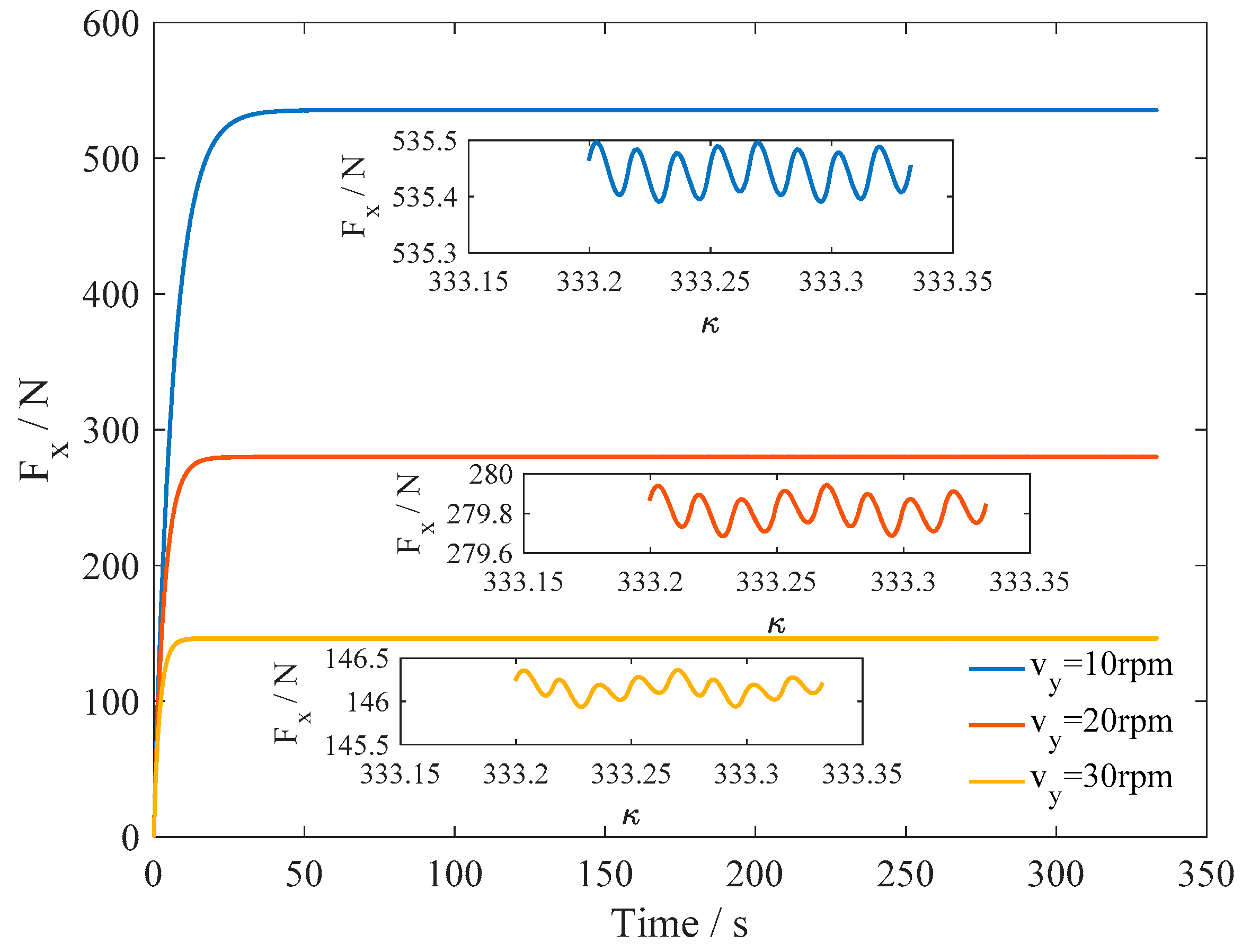
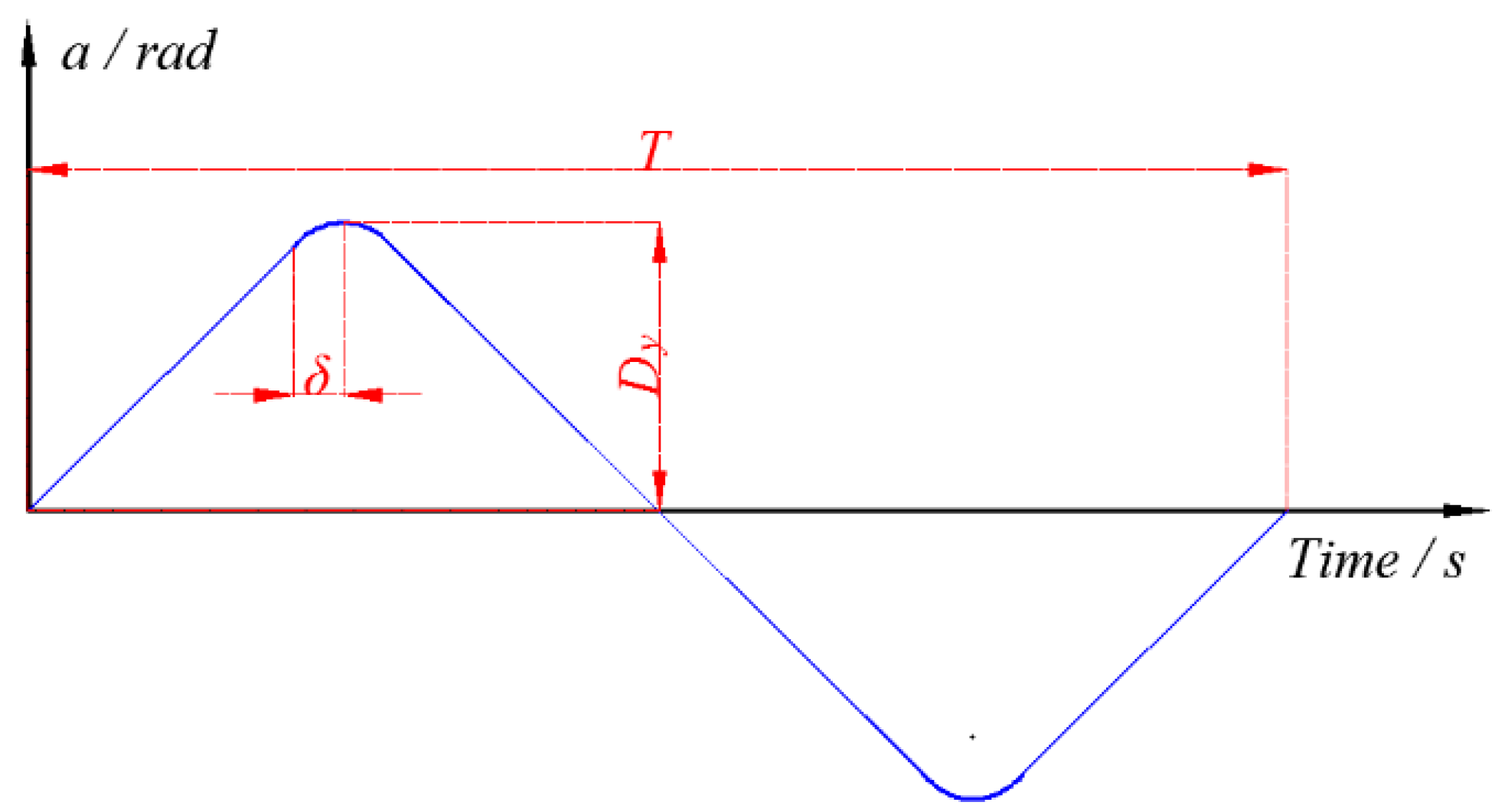
5.2.3. Torsional Oscillation
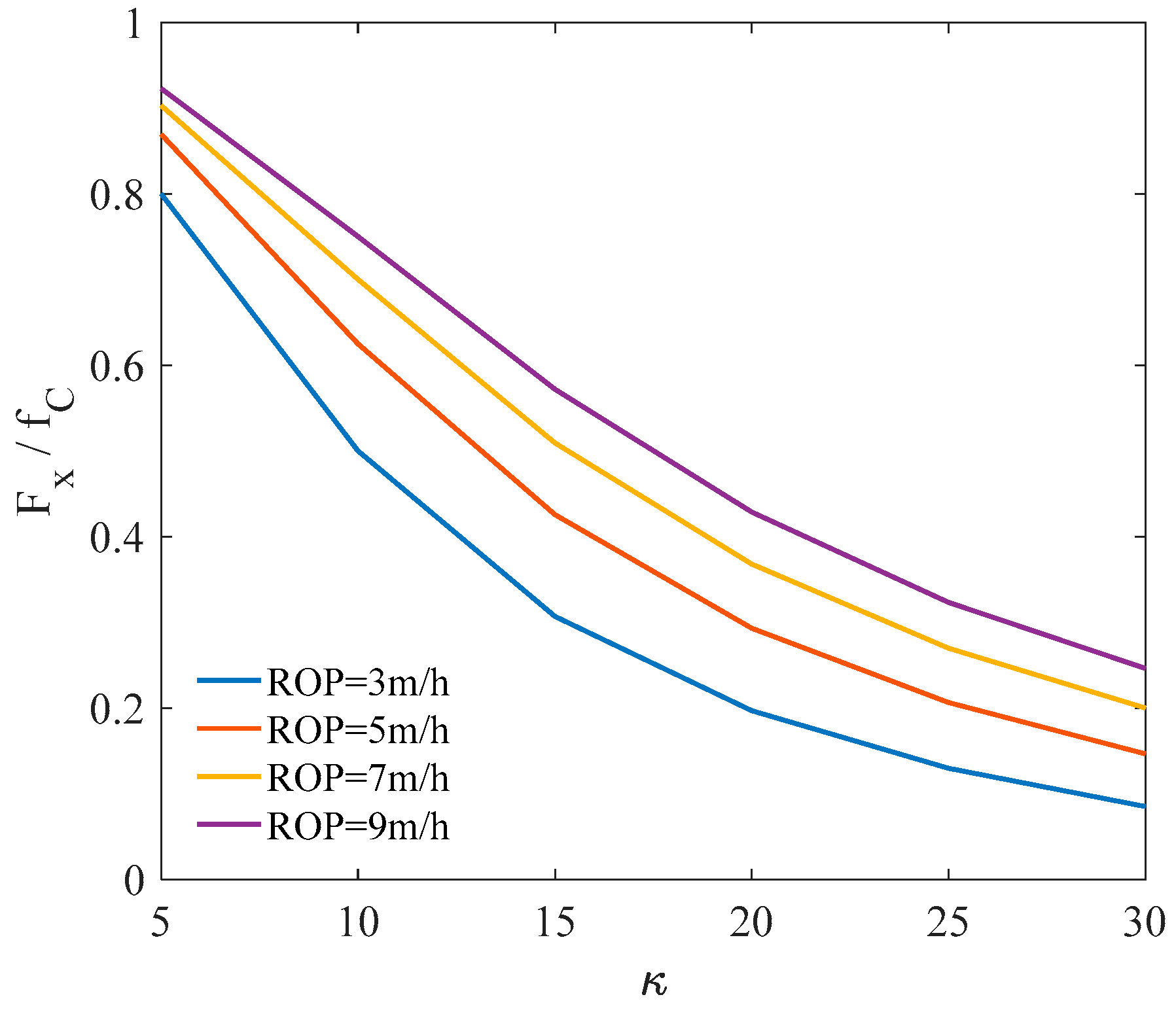
5.3. Friction Characteristic of Slider Drilling Technology
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| θ | attack angle of wedge-shaped asperity |
| fC | shear factor |
| μcutting | friction coefficient in the cutting regime |
| μploughing | friction coefficient in the ploughing regime |
| μwear | friction coefficient in the wedge formation regime |
| A1, A2 | coefficient |
| a | minor axis of asperity |
| b | major axis of asperity |
| h | height of asperity |
| dx | drill string displacement in the X direction |
| dy | drill string displacement in the Y direction |
| e1 | unit vector of the axial direction |
| e2 | unit vector of the tangential direction |
| e3 | unit vector of the principle axis of asperity |
| z | projection of the length of asperity |
| z′ | virtual projection of the length of asperity |
| kt | stiffness of asperity |
| vr | relative velocity |
| FN | normal force |
| i | index of the Dahl model |
| M | projection point |
| M′ | virtual projection point |
| O | fixed point of asperity |
| α, β | angle between the direction of asperity projection and the axial of the wellbore |
| βv | angle between the drill string motion direction and the principal axis of asperity |
| Fc | Coulomb friction |
| Ff | friction force of the multiscale friction model |
| Fx | average axial friction force |
| fx | axial friction force |
| My | average axial friction torque |
| my | tangential friction torque |
| R0 | outer diameter of the drill string |
| κ | ratio between the amplitude of the vibration velocity and the slip velocity |
| χ | ratio between the amplitude of the vibration force and the gravity of the drill string |
References
- Rui, Z.; Guo, T.; Feng, Q.; Qu, Z.; Qi, N.; Gong, F. Influence of gravel on the propagation pattern of hydraulic fracture in the glutenite reservoir. J. Pet. Sci. Eng. 2018, 165, 627–639. [Google Scholar] [CrossRef]
- Rui, Z.; Wang, X.; Zhang, Z.; Lu, J.; Chen, G.; Zhou, X.; Patil, S. A realistic and integrated model for evaluating oil sands development with Steam Assisted Gravity Drainage technology in Canada. Appl. Energy 2018, 213, 76–91. [Google Scholar] [CrossRef]
- Thomas, R.L.; Mckeever, S.O.; Hartwig, D.D.; Egedahl, D.B.; Patton, J.; Holtzman, K.; Smith, L. Overcoming Weight Transfer Challenges in Complex, Shallow, Extended Reach Wells on Alaska’s North Slope. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–8 May 2008. (OTC-19550-MS). [Google Scholar]
- Stuart, D.; Hamer, C.D.; Henderson, C.; Gaynor, T.; Chen, D.C.-K. New Drilling Technology Reduces Torque and Drag by Drilling a Smooth and Straight Wellbore. In Proceedings of the SPE/IADC Drilling Conference, Amsterdam, The Netherlands, 19–21 February 2003. (SPE-79919-MS). [Google Scholar]
- Mccormick, J.E.; Chiu, T.F. The Practice and Evolution of Torque and Drag Reduction: Theory and Field Results. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 30 October–2 November 2012. (SPE-147100-MS). [Google Scholar]
- Maehs, J.; Renne, S.; Logan, B.; Diaz, N. Proven Methods and Techniques to Reduce Torque and Drag in the Pre- Planning and Drilling Execution of Oil and Gas Wells. In Proceedings of the IADC/SPE Drilling Conference and Exhibition, New Orleans, LA, USA, 2–4 February 2010. (IDAC/SPE128329). [Google Scholar]
- Schuh, F.J.; Coragliotti, A.; Dicicco, C.D.; Nagatani, R.A.; Rea, A.; Carlton, T.; Johnson, P.; Noble, R. Characterization of Encapsulated Oil as an Additive to Water-Based Drilling Fluids: Operational Improvements in Lubricity, Drag, and ROP. In Proceedings of the SPE Western North American and Rocky Mountain Joint Meeting, Denver, CO, USA, 17–18 April 2014. (SPE-169547-MS). [Google Scholar]
- Livescu, S.; Craig, S.H.; Watkins, T. Challenging the Industry’s Understanding of the Mechanical Friction Reduction for Coiled Tubing Operations. In Proceedings of the SPE Annual Technical Conference and Exhibition, Amsterdam, The Netherlands, 27–29 October 2014. (SPE-170635-MS). [Google Scholar]
- Patel, A.; Zhang, H.J.; Ke, M.; Panamarathupalayam, B. Lubricants and Drag Reducers for Oilfield Applications—Chemistry Performance and Environmental Impact. In Proceedings of the SPE International Symposium on Oilfield Chemistry, The Woodlands, TX, USA, 8–10 April 2013. (SPE-164049-MS). [Google Scholar]
- Wang, X.; Chen, P.; Rui, Z.; Jin, F. Modeling Friction Performance of Drill String Torsional Oscillation Using Dynamic Friction Model. Shock Vib. 2017, 2017, 4051541. [Google Scholar] [CrossRef]
- Wang, X.; Chen, P.; Ma, T.; Liu, Y. Modeling and experimental investigations on the drag reduction performance of an axial oscillation tool. J. Nat. Gas Sci. Eng. 2017, 39, 118–132. [Google Scholar] [CrossRef]
- Herrington, D.; Mercer, S. Fully Mechanical 3D Rotary Steering Technology Provides Economical Alternative to Conventional Rotary Steerable Tools. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 30 September–2 October 2013. (SPE-166517-MS). [Google Scholar]
- Gillan, C.; Kostiuk, G.; Schlembach, C.; Pinto, J.; LeBlanc, M. Applying Precision Drill Pipe Rotation and Oscillation to Slide Drilling Problems. In Proceedings of the SPE/IADC Drilling Conference and Exhibition, Amsterdam, The Netherlands, 17–19 March 2009. (SPE/IADC-118656). [Google Scholar]
- Heisig, G.; Macpherson, J.D.; Mounzer, F.; Linke, C.; Jenkins, M.A. Bending Tool Face Measurement While Drilling Delivers New Directional Information, Improved Directional Control. In Proceedings of the IADC/SPE Drilling Conference and Exhibition, New Orleans, LA, USA, 2–4 February 2010. (SPE-128789-MS). [Google Scholar]
- Barton, S.P.; Baez, F.; Alali, A. Drilling Performance Improvements in Gas Shale Plays using a Novel Drilling Agitator Device. In Proceedings of the North American Unconventional Gas Conference and Exhibition, The Woodlands, TX, USA, 14–16 June 2011. (SPE-144416-MS). [Google Scholar]
- Clausen, J.R.; Schen, A.E.; Forster, I.; Prill, J.; Gee, R. Drilling With Induced Vibrations Improves ROP and Mitigates Stick/Slip in Vertical and Directional Wells. In Proceedings of the IADC/SPE Drilling Conference and Exhibition, Fort Worth, TX, USA, 4–6 March 2014. (SPE-168034-MS). [Google Scholar]
- Martinez, J.; Carson, C.R.; Canuel, L.A.P.; Burnett, T.G.; Gee, R. New Technology Enables Rigs With Limited Pump Pressure Capacity to Utilize the Latest Friction Reduction Technology. In Proceedings of the SPE Eastern Regional Meeting, Pittsburgh, PA, USA, 20–22 August 2013. (SPE-165700-MS). [Google Scholar]
- Lv, J.; Liu, X.; Qian, L.; Xia, C.; Liu, F.; Hua, Y.; Li, M. Study on the Influence Factors of Performance of the 3D Hydraulic Oscillator. China Pet. Mach. 2016, 44, 27–30. [Google Scholar]
- Hess, D.P.; Soom, A. Normal Vibrations and Friction under Harmonic Loads: Part I—Hertzian Contacts. J. Tribol. 1991, 113, 87–92. [Google Scholar] [CrossRef]
- Zhang, H.; Guan, Z.; Liu, Y.; Dou, Y. Development of drilling string excitation drag reduction tool based on rotary excitation. China Pet. Mach. 2015, 43, 9–12. [Google Scholar]
- Maidla, E.; Haci, M.; Jones, S.; Cluchey, M.; Alexander, M.; Warren, T. Field Proof of the New Sliding Technology for Directional Drilling. In Proceedings of the SPE/IADC Drilling Conference, Amsterdam, The Netherlands, 23–25 February 2005. (SPE-92558-MS). [Google Scholar]
- Maidla, E.E.; Wojtanowicz, A.K. Laboratory Study of Borehole Friction Factor with a Dynamic-Filtration Apparatus. SPE Drill. Eng. 1990, 5, 247–255. [Google Scholar] [CrossRef]
- Gillan, C.; Boone, S.; Leblanc, M.; Picard, R.P.; Fox, R.T. Applying Computer Based Precision Drill Pipe Rotation and Oscillation to Automate Slide Drilling Steering Control. In Proceedings of the Canadian Unconventional Resources Conference, Calgary, AB, Canada, 15–17 November 2011. (SPE-148192-MS). [Google Scholar]
- Maidla, E.E.; Haci, M.; Wright, D. Case History Summary: Horizontal Drilling Performance Improvement Due to Torque Rocking on 800 Horizontal Land Wells Drilled for Unconventional Gas Resources. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 4–7 October 2009. (SPE-123161-MS). [Google Scholar]
- Maidla, E.; Haci, M. Understanding Torque: The Key to Slide-Drilling Directional Wells. In Proceedings of the IADC/SPE Drilling Conference, Dallas, TX, USA, 2–4 March 2004. (SPE-87162-MS). [Google Scholar]
- Kragjcek, R.H.T.; Al-Dossary, A.; Kotb, W.; Al Gamal, A. Automated Technology Improved the Efficiency of Directional Drilling in Extended Reach Wells in Saudi Arabia. In Proceedings of the SPE/DGS Saudi Arabia Section Technical Symposium and Exhibition, Al-Khobar, Saudi Arabia, 15–18 May 2011. (SPE-149108-MS). [Google Scholar]
- Urbakh, M.; Klafter, J.; Gourdon, D.; Israelachvili, J. The nonlinear nature of friction. Nature 2004, 430, 525–528. [Google Scholar] [CrossRef] [PubMed]
- Dougherty, P.S.M.; Pudjoprawoto, R.; Iii, C.F.H. Bit cutter-on-rock tribometry: Analyzing friction and rate-of-penetration for deep well drilling substrates. Tribol. Int. 2014, 77, 178–185. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1966, 295, 300–319. [Google Scholar] [CrossRef]
- Majumdar, A.; Bhushan, B. Fractal model of elastic-plastic contact between rough surfaces. J. Tribol. 1991, 113, 1–11. [Google Scholar] [CrossRef]
- Challen, J.M.; Oxley, P.L.B. An explanation of the different regimes of friction and wear using asperity deformation models. Wear 1979, 53, 229–243. [Google Scholar] [CrossRef]
- Challen, J.M.; Oxley, P.L.B. Slip-line fields for explaining the mechanics of polishing and related processes. Int. J. Mech. Sci. 1984, 26, 403–418. [Google Scholar] [CrossRef]
- Hol, J. Multi-Scale Friction Modeling for Sheet Metal Forming; University of Twente: Enschede, The Netherlands, 2013. [Google Scholar]
- Westeneng, J.D. Modelling of Contact and Friction in Deep Drawing Processes; University of Twente: Enschede, The Netherlands, 2001. [Google Scholar]
- Ma, X.; Rooij, M.D.; Schipper, D. A load dependent friction model for fully plastic contact conditions. Wear 2010, 269, 790–796. [Google Scholar] [CrossRef]
- Dahl, P.R. A Solid Friction Model; Aerospace Corp: El Segundo, CA, USA, 1968. [Google Scholar]
- Dahl, P.R. Measurement of Solid Friction Parameters of Ball Bearings; Aerospace Corp El Segundo CA Engineering Science Operations: El Segundo, CA, USA, 1977. [Google Scholar]
- Piatkowski, T. Dahl and LuGre dynamic friction models—The analysis of selected properties. Mech. Mach. Theory 2004, 73, 91–100. [Google Scholar] [CrossRef]
- Olsson, H.; Åström, K.J.; Wit, C.C.D.; Lischinsky, P. Friction Models and Friction Compensation. Eur. J. Control 1998, 4, 5517–5522. [Google Scholar] [CrossRef]
- Tsai, C.C.; Tseng, C.H. The effect of friction reduction in the presence of in plane vibrations. Arch. Appl. Mech. 2006, 75, 164–176. [Google Scholar] [CrossRef]
- Gutowski, P.; Leus, M. The effect of longitudinal tangential vibrations on friction and driving forces in sliding motion. Tribol. Int. 2012, 55, 108–118. [Google Scholar] [CrossRef]
- Wang, P.; Ni, H.; Wang, R.; Liu, W.; Lu, S. Research on the Mechanism of In-Plane Vibration on Friction Reduction. Materials 2017, 10, 1015. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Ni, H.; Wang, R.; Li, Z.; Wang, Y. Experimental investigation of the effect of in-plane vibrations on friction for different materials. Tribol. Int. 2016, 99, 237–247. [Google Scholar] [CrossRef]
- Wang, P.; Ni, H.; Li, Z.; Wang, R. A Modified Model for Friction Reduction by Vibrating Drill-String Longitudinally. Appl. Mech. Mater. 2014, 535, 597–601. [Google Scholar] [CrossRef]
- Wang, P.; Ni, H.; Wang, X.; Wang, R.; Lu, S. Research on the characteristics of earthworm-like vibration drilling. J. Pet. Sci. Eng. 2017, 160, 60–71. [Google Scholar] [CrossRef]
- Wang, X.; Ni, H.; Wang, R.; Liu, T.; Xu, J. Modeling and analyzing the movement of drill string while being rocked on the ground. J. Nat. Gas Sci. Eng. 2017, 39, 28–43. [Google Scholar] [CrossRef]




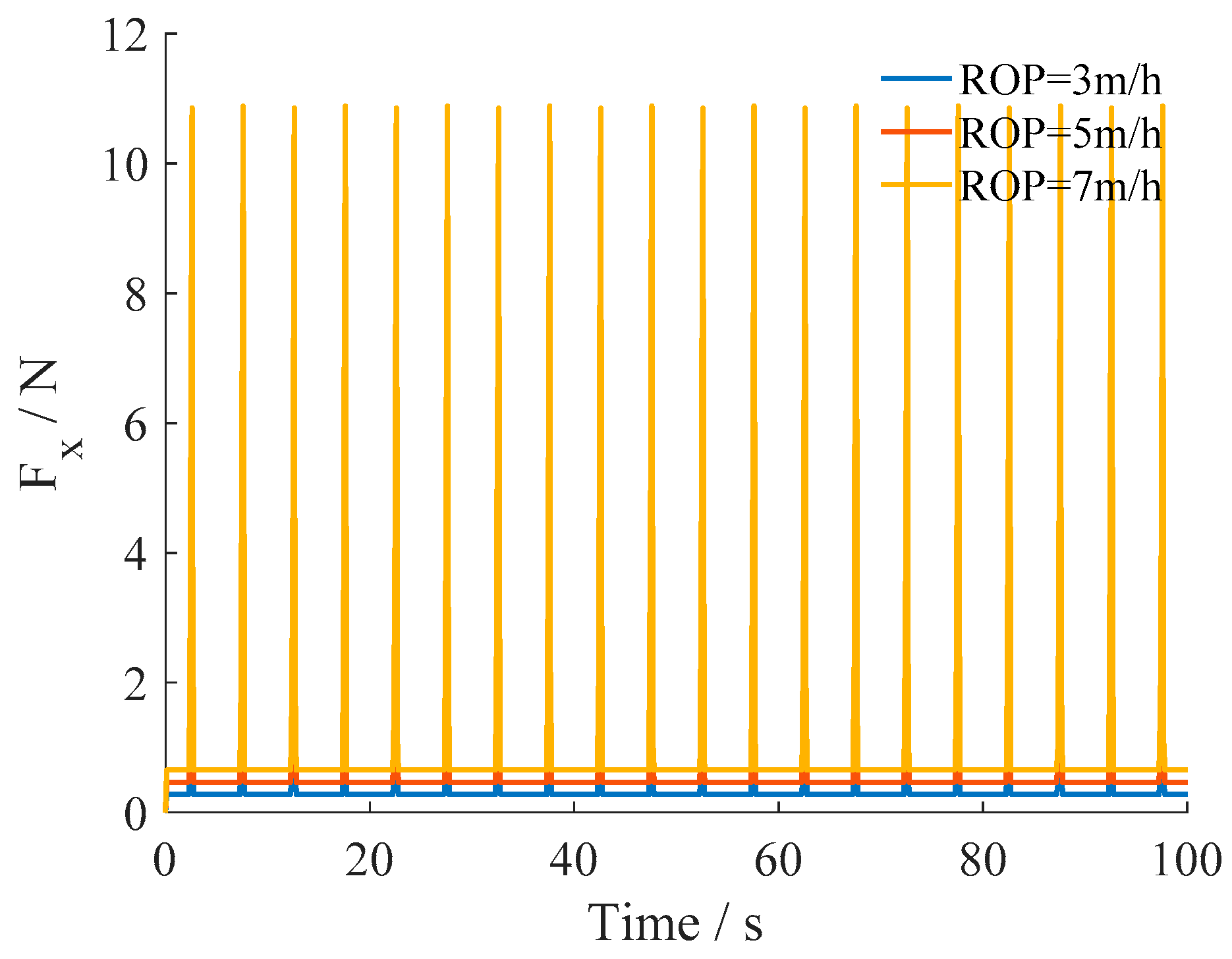


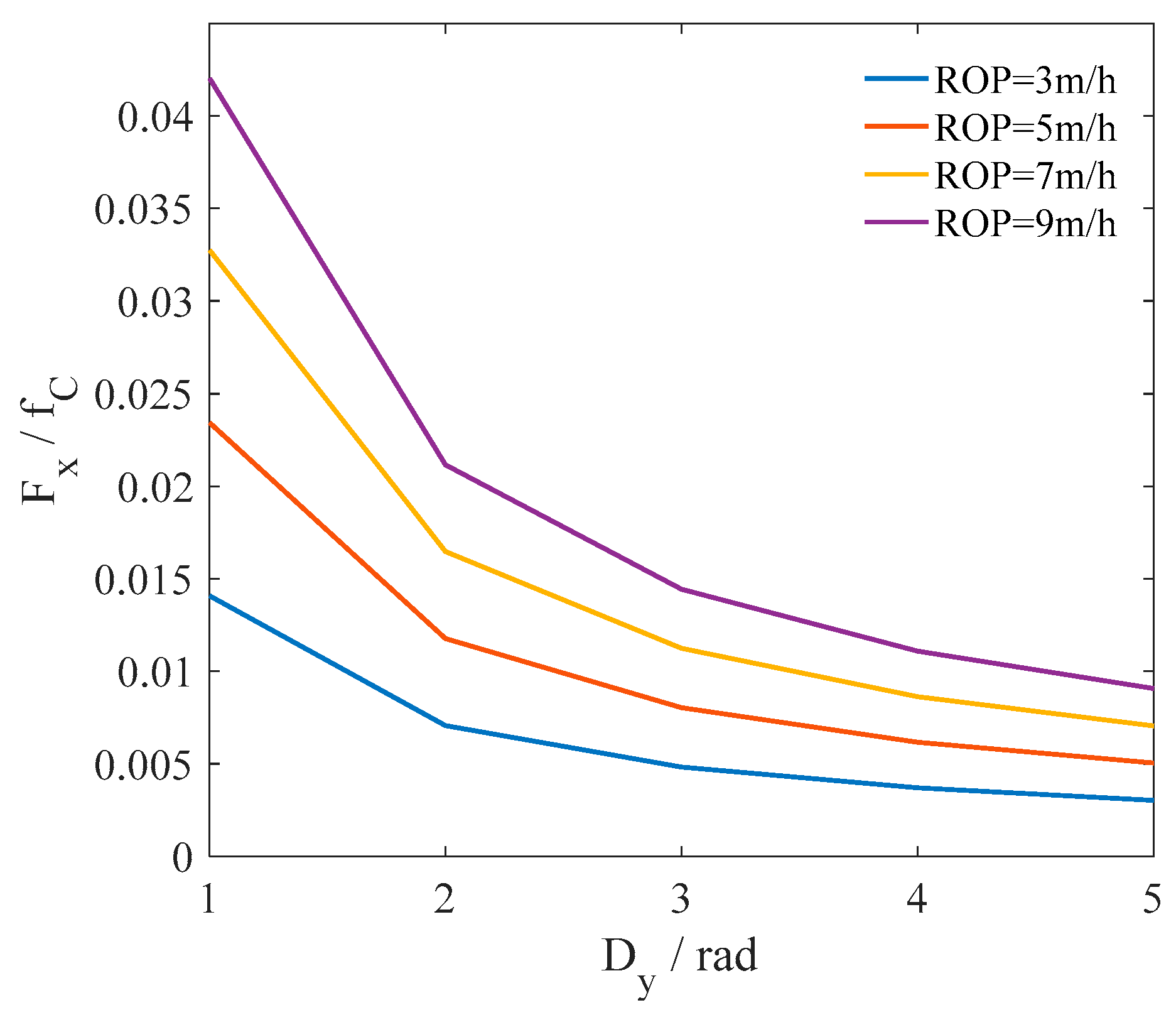
| No. | Parameter (Unit) | Value |
|---|---|---|
| 1 | Length of the drill string (m) | 10 |
| 2 | Outer diameter of the drill string (m) | 0.127 |
| 3 | Inner diameter of the drill string (m) | 0.1086 |
| 4 | Hole diameter (m) | 0.2156 |
| 5 | Density of drill pipe (kg/m3) | 7850 |
| 6 | Density of drilling fluid (kg/m3) | 2200 |
| 7 | Inclination of the wellbore (°) | 90 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.-M.; Yao, X.-M. Vibration Technologies for Friction Reduction to Overcome Weight Transfer Challenge in Horizontal Wells Using a Multiscale Friction Model. Lubricants 2018, 6, 53. https://doi.org/10.3390/lubricants6020053
Wang X-M, Yao X-M. Vibration Technologies for Friction Reduction to Overcome Weight Transfer Challenge in Horizontal Wells Using a Multiscale Friction Model. Lubricants. 2018; 6(2):53. https://doi.org/10.3390/lubricants6020053
Chicago/Turabian StyleWang, Xing-Ming, and Xing-Miao Yao. 2018. "Vibration Technologies for Friction Reduction to Overcome Weight Transfer Challenge in Horizontal Wells Using a Multiscale Friction Model" Lubricants 6, no. 2: 53. https://doi.org/10.3390/lubricants6020053
APA StyleWang, X.-M., & Yao, X.-M. (2018). Vibration Technologies for Friction Reduction to Overcome Weight Transfer Challenge in Horizontal Wells Using a Multiscale Friction Model. Lubricants, 6(2), 53. https://doi.org/10.3390/lubricants6020053