Abstract
Laser surface texturing is an efficient way to control the friction and wear properties of materials. Although described in many papers, most previous work relates to a pure topographic view of laser-textured surfaces. As lasers are heat sources, their thermal impact during treatment can be high enough to modify the material’s microstructure or surface chemistry and affect tribological properties as well. This research took a closer look at the microstructure of laser-textured TiAl multilayers, besides topographic aspects. Direct laser interference patterning was used to create well-defined line-like surface textures in TiAl multilayers with differing lateral feature sizes in the micron range. High-resolution techniques such as TEM and XRD highlighted the effect of this method on microstructure, and in particular, the phase situation of the TiAl multilayer. Thermal simulations demonstrated that the maximum achievable temperatures were around 2000 K, thus being high enough to melt Ti and Al. Cooling rates on the order of 109 K/s depended on the lateral feature size, potentially leading to metastable microstructures. Finally, ball-on-disk tests on as-textured TiAl specimens showed a reduction in wear under dry conditions depending on the periodicity of the line-like textures used.
1. Introduction
Laser surface texturing (LST) to improve friction and wear under dry and lubricated conditions is not a new idea. Hamilton et al. showed in the late 60s that well-defined surface textures under hydrodynamic conditions can produce additional pressure [1], leading to further separation of the involved surfaces. Since then, numerous manuscripts appeared addressing improvements under hydrodynamic, elasto-hydrodynamic, mixed and even boundary lubrication [2]. In the absence of lubricants, i.e., oils or greases, surface textures can trap wear debris, thus reducing the abrasive component of the coefficient of friction (COF). Additionally, surface texturing leads to a reduction of the real area of contact, reducing friction and potentially causing wear [3]. As far as their efficiency for applications is concerned, Etsion et al., amongst others, has published a number of manuscripts, for example regarding the LST used in hydrostatic mechanical seals [4] or parallel thrust bearings [5].
However, most of these articles are mainly focused on the formation of well-defined surface topographies, such as dimples, grooves or chevrons, with varying geometrical dimensions or area densities [2] and neglect the influence of the respective texturing method on the materials’ microstructure, i.e., grain size, the formation of intermetallic phases, and defect situations, such as dislocation density. In this context, it is well known that material properties are strongly influenced by their microstructural properties, such as grain size and the grain size distribution (see Hall–Petch effect). Hence, it is essential to study microstructural influences besides topographical aspects of the respective texturing technique and subsequently its effect on friction and wear. Laser sources used for LST deposit a significant amount of energy over a short period into materials, with heating and cooling rates of approximately 109 K/s, thus inducing metallurgical effects such as melting, recrystallization and the formation of intermetallic phases [6]. In order to study the possible effects of laser surface texturing on resulting microstructures, well described model material systems with technological relevance are needed. In this work, TiAl has been selected as the system of interest, since titanium aluminides are attractive due to their high melting point, low density, as well as good corrosion resistance, and thus, their intrinsic potential for high temperature applications in the aircraft industry [7,8]. In this study, the material was not used in bulk shape but as alternating multilayers of titanium and aluminum, which was deposited onto Si substrates by magnetron sputtering. The advantage of multilayers is based on short diffusion paths and high interface density, increasing the possibility of elucidating the interacting mechanisms between the stored thermal energy from the laser process and the linked microstructural, as well as topographical changes. For LST, Direct Laser Interference Texturing (DLIP), which enables the surface texturing of different materials in a well-defined way on macroscopic areas in one shot, was used. The laser beam was split into secondary beams using suitable optical elements. Subsequently, these sub-beams interfered with each other on the sample’s surface, resulting in an interference pattern with positions of constructive and destructive interference. The resulting surface textures can be line-like in the case of two interfering beams (n = 2) or even dimple-like for three interfering beams (n = 3). More information on the technique and details of the experimental setup have already been published elsewhere [6]. The laser textured TiAl multilayer films were analyzed by high-resolution electron microscopy with regard to microstructural modifications but also X-ray diffraction concerning phase formation. Thermal simulations were used to demonstrate the heat impact of the laser on the material regarding spatial/temporal temperature distributions, the maximum achievable temperatures and cooling rate, as a function of the used periodicities. Finally, ball-on-disk sliding tests were performed to record the COF and to evaluate wear behavior depending on the periodicity of the laser textures.
2. Material and Methods
2.1. Deposition of TiAl Multilayer Thin Films
TiAl multilayers were produced by magnetron sputtering (von Ardenne, LS 730 C(Dresden, Germany) on double side polished, (100)-oriented p–type silicon wafers. In order to facilitate the sample’s handling, the wafer was diced into specimens of 2 × 2 cm2. The metallic film, with a total thickness of around 300 nm, consisted of 14 Ti and Al layers with individual layer thicknesses of 17 and 5 nm, respectively. Due to its good adhesion to silicon, Ti was chosen as the first layer. In addition, a 30 nm thick Ti layer was added as a top layer since the material with the higher melting point needs to be on top to avoid pronounced topographic texturing. The deposition process was carried out in an argon atmosphere, with a power of 300 W, a pressure of 3 × 10−3 mbar and a gas flow of 80 sccm.
2.2. Direct Laser Interference Texturing (DLIP)
A pulsed solid state Nd:YAG laser (Spectra Physics, Quanta Ray Pro 290, Darmstadt, Germany was used for LST. The fundamental wavelength of the laser was 1064 nm, from which shorter wavelengths (532, 355 and 266 nm) could be produced by harmonic generation. Due to the absorption characteristics of the selected materials, the third harmonic at 355 nm was used for DLIP. The repetition rate of the laser was 10 Hz, with a pulse duration of 10 ns. Moreover, all the experiments were performed under ambient conditions, at 21 °C and about 45% relative humidity. The primary laser beam was split into two sub-beams by suitable beam splitters and then guided by coated mirrors to interfere with each other on the sample’s surface resulting in a line-like pattern. Further information about DLIP and the experimental set-up can be found in [6]. The laser fluence was varied between 50 and 500 mJ/cm2. The periodicity of the line-like pattern (distance between the adjacent topographic maxima or minima) was set to be 2, 4, 8 and 12 µm. In this context, a periodicity of 2 µm represents the lower limit for DLIP, since lateral thermal diffusivity restricts smaller periodicities for metals. A periodicity larger than 12 µm results in additional topographic double-maxima and inhomogeneous patterns.
2.3. Sample Characterization
2.3.1. Scanning Electron Microscopy and Focused Ion Beam Microscopy
All specimens were studied by high-resolution scanning electron microscopy (SEM) equipped with a field emission gun (FEI, Helios Nanolab (Frankfurt, Germany) at an acceleration voltage of 5 kV. In addition, focused ion beam microscopy (FIB) was used for cross-sections of the as-patterned specimens and a detailed characterization of the wear tracks after tribological experiments. Moreover, FIB was used to prepare thin foils for a subsequent localized cross-sectional study using transmission electron microscopy (TEM) (JEOL 2010, Freising, Germany).
2.3.2. White Light Interferometry
The white light interferometer (WLI) used was a Zygo New View 7300 (AMETEK, Weiterstadt, Germany) with a vertical resolution of about 0.1 nm and an objective-dependent lateral resolution ranging between 0.36 and 9.5 µm.
2.3.3. Transmission Electron Microscopy
Transmission electron microscopy (TEM) studies were carried out using a JEOL 2010 facility at an operating voltage of 200 kV. Both direct imaging scrutinizing the microstructural aspects and the selected area diffraction (SAD) were applied to the specimens.
2.3.4. X-ray Diffraction
X-ray diffraction (XRD) phase analysis measurements, using grazing incidence geometry (GI-XRD), were performed to achieve statistically relevant phase data. For this purpose, a seven-axis diffractometer (Panalytical, X’pert MRD HR (Kassel, Germany) with a copper X-ray tube (λ = 0.154056 nm) was used.
2.3.5. Tribometry
The tribological tests were performed using a ball-on-disk tribometer in linear reciprocating sliding mode (NTR1, Anton Paar; formerly CSM Instruments (Graz, Austria). The tribometer is based on a stiff cantilever, which acts as a frictionless force transducer in both vertical and horizontal directions. The cantilever used for the experiments had a normal and tangential stiffness of 0.7624 and 1.1447 mN/µm, respectively. The static partner was loaded onto the substrate with a precisely known force using piezo-actuation. The normal load and friction force were determined during the experiment by measuring the deflection of this elastic spring in both horizontal and vertical planes with two high precision fiber optical displacement sensors. Through a PID control, the piezo-actuation maintained the normal load independent of any surface irregularities. The normal force was kept constant at 1 mN for all sliding experiments. The linear sliding speed was set to 0.1 cm/s for 1000 cycles. Deviation from the nominal normal load was less than 10% related to the reference value in the experiments. The counter-body was a 100Cr6 bearing steel ball with a radius of 1.5 mm and a Rq value of around 3 nm measured by WLI. The stroke length was 0.3 mm. After each tribological test, the balls were cleaned by isopropanol and analyzed by WLI with regard to geometrical size accuracy, that is, possible deviations from the sphericity. Temperature and relative humidity were kept constant at 21 °C and 45%, respectively.
3. Results and Discussion
3.1. Topographic and Microstructural Analysis of TiAl Multi-Layered Thin Films
First, the microstructure of the as-deposited multilayers was studied by TEM. Figure 1a shows a TEM image of the as-deposited TiAl multilayers.

Figure 1.
(a) TEM analysis of an as-deposited 300 nm thick TiAl multilayer. The bright layers correspond to Al and the darker ones to Ti; (b) SAD pattern of the as-deposited multilayer. The normal vector of the sample surface is represented by np.
Slight differences in nominal thickness can be explained by uncertainties in the respective sputter rates (Ti: 0.18 nm/s, Al: 0.23 nm/s). TEM foils were prepared by FIB and analyzed by SAD using TEM (Figure 1b). The diffraction spots were blurred because of overlapping reflections coming from the Al–{111} and Ti–{0001} planes and due to the waviness of the near-surface layers. Despite this, with the Ti–{0001} and Al–{111} planes being parallel to the sample’s surface, a fiber-texture could be identified. Analysis of the topography after magnetron sputtering by WLI revealed a smooth surface, with Rq roughness of about 1 nm.
During DLIP, three fluence regimes, independent of the periodicity adjustment, could be identified by performing a fluence series. The resulting surface topography and morphology is displayed in Figure 2, for a periodicity of 8 µm.

Figure 2.
SEM micrographs of different fluence regimes (regime A (~50 mJ/cm2), regime B (~170 mJ/cm2) and regime C (~476 mJ/cm2)) in TiAl for a fixed periodicity of around 8 µm.
Figure 2 shows SEM images of samples fabricated at distinct laser fluences for a fixed periodicity of 8 µm. In Figure 2a, the laser patterns are only slightly visible and the topography is very shallow (regime A). The laser fluence in this example was set to 50 mJ/cm2. In regime B (Figure 2b), the fluence was increased to 170 mJ/cm2. The brighter topographic maxima could be clearly seen and the surface patterns appeared homogeneous. Additionally, the melting and mixing of layers started to occur. A further increase in laser fluence (regime C for fluence values of around 476 mJ/cm2) resulted in bubble-like structures inside the multilayer and ablated areas due to the high energy density (Figure 2c). The most homogeneous laser patterns were found for fluence values of around 170 mJ/cm2.
Figure 3 shows a comparison of the resulting XRD-patterns measured for an unpatterned and as-deposited reference sample, as well as specimens irradiated by laser fluences of 170 and 476 mJ/cm2.
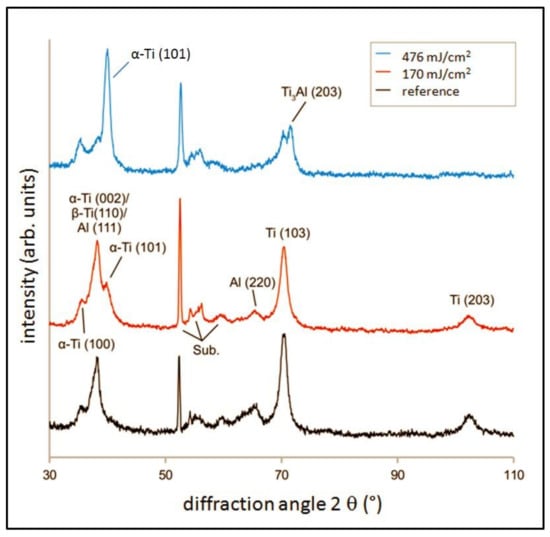
Figure 3.
GI-XRD measurement of laser-patterned specimens at ~170 mJ/cm2 (regime B) and ~476 mJ/cm2 (regime C), compared to the as-deposited reference.
Direct comparison of the XRD-patterns of the reference and specimen B did not reveal considerable differences. At a higher level of laser fluence (regime C at around 476 mJ/cm2), an α–Ti (101) peak was clearly visible. Additionally, a Ti3Al (203) peak appeared, and at 38.4°, a reduction of the overlapping peak could be observed. The unambiguous identification of the phases in this overlapping peak was hindered due to several reflections, such as α–Ti (002), Al (111) and β–Ti (110). The indexing was further complicated by peak shifts due to the formation of a solid solution and residual stresses. In addition, the presence of textures and peak broadening due to small grain size were additional aspects that need to be considered.
Figure 4 shows the respective TEM dark field image, as well as the related SAD zone-axis pattern for the specimen from regime B.
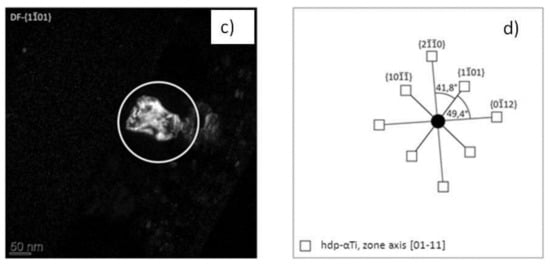
Figure 4.
TEM analysis of a laser-patterned multilayer (fluence: ~170 mJ/cm2). The position of maximum laser intensity is displayed in (a); (b) SAD pattern of zone-axis; (c) dark field image of the encircled grain; and (d) schematic drawing of the pattern.
In Figure 4a, it can be seen that the lamellar structure of the multilayer in the top area disappeared after DLIP. However, it is worth emphasizing that the reaction did not spread over the entire film thickness. Some layers of the as-deposited state close to the substrate were still visible. The SAD pattern in the reaction zone (Figure 4b) indicated the presence of hdp α-Ti. A schematic drawing of the diffraction pattern in Figure 4d considering the respective angles and planes clearly confirms the presence of hdp α–Ti with a (01–11) zone-axis. The findings refer to the diffraction volume of the encircled grain in the top left image of Figure 4c.
In contrast, TEM analysis of an adjacent grain in the same specimen indicated the existence of bcc β–Ti (see Figure 5a–c). The determination of diffracting planes and the calculation of the respective angles revealed the existence of bcc β–Ti with a (–111) zone-axis (Figure 5d).
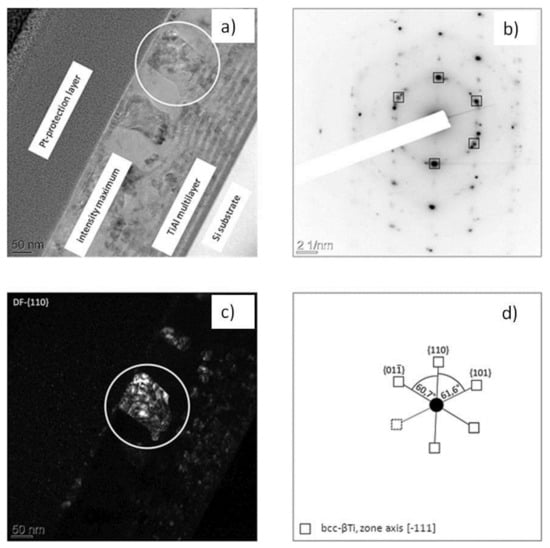
Figure 5.
TEM images of a laser-irradiated multilayer (fluence: 170 mJ/cm2). The position of maximum laser intensity is displayed in (a); (b) SAD pattern of zone-axis; (c) dark field image of the encircled grain; and (d) schematic drawing of the pattern. The indexing revealed the presence of bcc β–Ti with a (–111) zone-axis.
As a first conclusion, it is worth emphasizing that no complete reaction of the TiAl multilayer specimen over the entire film thickness was observed at a laser fluence of around 170 mJ/cm2 (regime B). Apart from hdp α–Ti, the metastable β–Ti phase was detected, which could be attributed to high cooling rates on the order of 109 K/s [6]. A deeper discussion about the formation of intermetallic phases in the system TiAl due to DLIP can be found in [9] for a similar multilayer stack with slightly different laser parameters and SiN as substrate material.
3.2. Thermal Simulation of the DLIP Process
In order to gain a better understanding of the observed microstructural phenomena after DLIP, simulations with COMSOL Multiphysics, based upon the approach in [10] solving the classical heat diffusion equation with symmetrical boundary conditions, were performed. The heat diffusion equation is given by:
where p denotes density in (g/cm3), Cp the specific heat capacity in (J/kgK), λ the thermal conductivity in (W/mK), and Q the laser heat source (further details can be found in [10])
The following assumptions were made [9]:
- No radiation loss from the surface.
- Convection above the surface can be neglected.
- No convection occurs due to gravitational or electromagnetic effects during melting.
- The laser energy is considered as a sinusoidal function with a Gaussian distribution in time.
- The heat conduction includes solid/liquid and liquid/vapor transitions, considering the latent heat required to melt and vaporize metals.
First, it was necessary to determine the maximum depth up to which heat could be absorbed. Using Lambert–Beer’s law and the respective absorption coefficients at 355 nm laser wavelength (αAl = 153 µm−1 and αTi = 71.3 µm−1 [11]), the skin depth for Al and Ti was estimated to be 6.6 and 14 nm, respectively. Consequently, most of the laser-induced heat was absorbed in the topmost layers.
The thermal diffusion length for Al and Ti could be calculated using Equation (2):
where τ is the pulse duration of the laser source (here 10 ns) and κ the thermal diffusivity according to (3):
Table 1 shows the values used for density, specific heat capacity and thermal conductivity for Al, Ti and Si [11]:

Table 1.
Density, specific heat capacity and thermal conductivity for the elements Al, Ti and Si. These values were used for calculating thermal diffusion lengths according to Equations (2) and (3).
According to Equation (2), the thermal diffusion lengths for Al and Ti were lD,Al ≈ 2 µm and lD,Ti ≈ 0.61 µm, respectively. A schematic representation of the used model is illustrated in Figure 6.
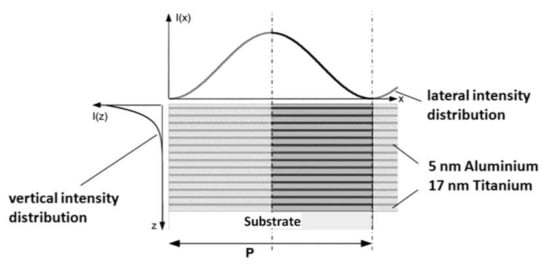
Figure 6.
Schematic overview of the model used for thermal simulation. Due to symmetric boundary conditions, only half of the model is considered.
Figure 7 shows the spatial (Figure 7a–c) and temporal temperature distributions Figure 7d after t = 33.5 ns (moment of maximum laser intensity, which corresponds to a maximum temperature of 1936 K (Figure 7d)) for a fixed pattern periodicity of 8 µm. A comparison of the spatial temperature distribution at the top and bottom layer is given in Figure 7b. The spatial temperature distribution at the laser intensity minimum and maximum, as a function of the depth, is depicted in Figure 7c.
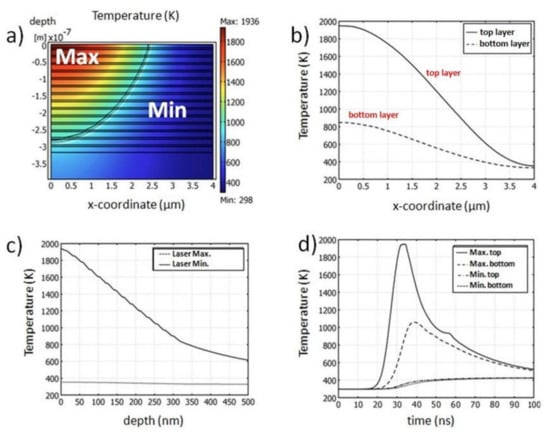
Figure 7.
Simulated temperature distributions for a periodicity of 8 µm and a laser fluence of ~170 mJ/cm2. (a) Spatial temperature distribution at t = 33.5 ns; (b) spatial temperature distribution for cross-sections parallel to the surface; (c) spatial temperature distributions for cross-sections perpendicular to the surface; and (d) temporal distribution of temperature.
As can be seen in Figure 7d, the maximum temperature for the bottom layer was reached after 38 ns. As far as the minimum laser intensity was concerned, the temperature only gradually increased, finally reaching the maximum temperature at around 60 ns. As can be seen in the temperature curve after laser impact, only Al with a melting point of 934 K was molten, whereas Ti (melting point of 1941 K) remained solid [11]. Furthermore, it was observed that the temperature in the intensity minimum never exceeded 400 K. Therefore, no significant microstructural influence was expected in these areas for none of the elements. The resolution in the temporal temperature distribution in Figure 7d was high enough to even reveal the latent heat being released in the temperature distribution of the top layer in the position of maximum laser intensity. There was a pronounced deviation from the continuous cooling taking place between 900 and 1000 K, indicating the solidification point of Al.
Further characteristic aspects of the thermal simulation were the maximum achievable temperatures, molten fractions, cooling rates and melting durations. The maximum achievable temperatures, as a function of periodicity, are represented in Figure 8. Tmax,o and Tmax,u are the maximum temperatures directly at the surface and the interface TiAl multilayer/substrate for the positions of maximum laser intensity. Tmin,o/Tmin,u denote the maximum temperatures for the laser intensity minima positions, respectively.
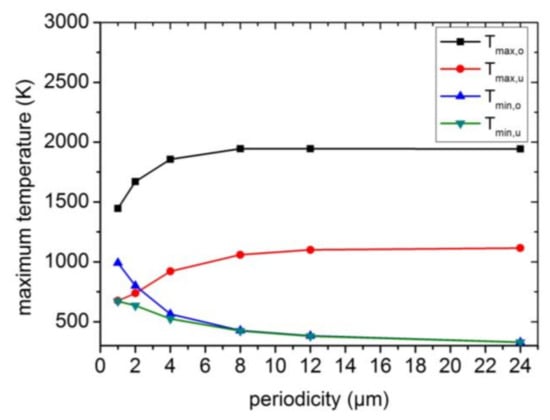
Figure 8.
Maximum achievable temperatures depending on periodicity, for a fixed fluence of ~170 mJ/cm2. Tmax,o and Tmax,u denote the maximum temperatures at the surface and the multilayer-substrate interface for the laser intensity maximum position. Tmin,o and Tmin,u represent the respective maximum temperaturesatthesurfaceandthemultilayer-substrateinterfaceforthelaserintensityminimumposition.
As can be seen in Figure 8, the maximum temperatures for Tmax,o and Tmax,u were reached at approximately 8 µm and remained almost constant, even for larger periodicities. The maximum temperature for a periodicity of 8 µm was attributed to the fact that for smaller periodicities, the heat is directly carried away due to a larger specific laser patterned area, whereas for larger periodicities, the laser-induced gain in surface by the texturing is smaller and the distances between adjacent intensity minima and maxima larger. Therefore, the material remains molten for a longer time.
Finally, the respective cooling rate as a function of the periodicity is displayed in Figure 9.
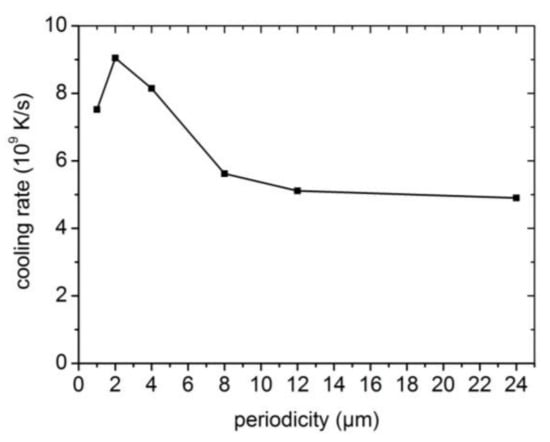
Figure 9.
Simulated cooling rates as a function of periodicity for TiAl after DLIP using a laser fluence of ~170 mJ/cm2.
In this context, the time needed for cooling from 1800 to 1000 K was used to determine the maximum cooling rate. With the exception of one periodicity (1 µm), the cooling rate decreased with increasing periodicities. This can be traced back to higher maximum temperatures and melting durations for larger periodicities. The determined cooling rates, typically on the order of 109 K/s, were much higher than in the case of other solidification processes. Hence, the formation of metastable phases was possible. In most cases, a high cooling rate leads to a more fine-grained microstructure and complicates diffusion-controlled phase transitions. Moreover, the formation of an ultra-fine grained or even nanocrystalline microstructure has immediate implications on the tribo-mechanical properties by Hall–Petch strengthening. Therefore, it is important to take microstructural effects due to surface texturing methods into consideration.
3.3. Tribological Properties
Figure 10 summarizes the results of the tribological experiments dependent on the orientation of the line-like surface topography (parallel or perpendicular to the laser patterns) and the patterns’ periodicity.
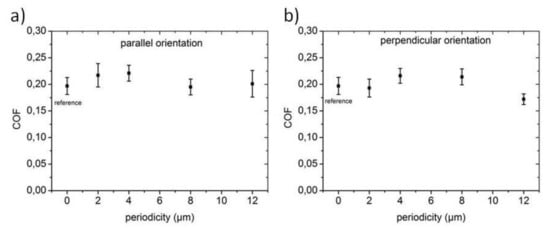
Figure 10.
Measured COF vs. periodicity for an orientation parallel (a) and perpendicular to the line-like patterns (b). The point 0 µm represents the unpatterned reference sample. Each data point in the graphs represent an averaged value of ten individual sliding experiments, with the corresponding standard deviation.
As can be seen, there was no significant difference between the specimens, regarding neither the periodicity nor the orientation. This may be attributed to the nearly vanishing topography after DLIP with typical structural depths of about 10–20 nm at a given laser fluence of 170 mJ/cm2. In this context, Lasagni et al. demonstrated that the structural depth of laser interference patterned surfaces increases with larger periodicities for a given laser fluence [12]. Only the specimen with the largest periodicity of 12 µm demonstrated a slightly lower COF in the case of perpendicular sliding. In fact, this was the specimen with a slightly larger structural depth of approximately 20 nm.
Apart from the COF, the resulting wear volume was determined for each sample by measuring the resulting wear tracks by WLI and considering the ASTM G99 [13]. The results are shown in Figure 11 for parallel and perpendicular alignments.
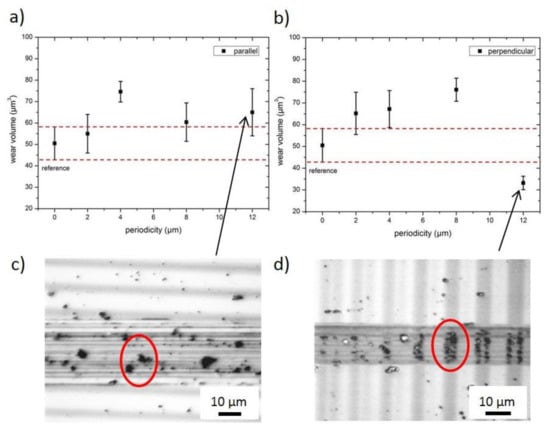
Figure 11.
Wear volume vs. periodicity for parallel (a) and perpendicular (b) orientation; (c) light microscopic image of the wear scar observed for a patterned surface with a periodicity of 12 µm under parallel sliding; and (d) with perpendicular alignment for 12 µm. The red ellipses show exemplarily wear particles within the wear track in (c) for parallel sliding and wear debris accumulation in the recessions of the laser surface textures for the largest periodicity and in (d) for the perpendicular case.
A direct comparison between parallel and perpendicular sliding showed a significant difference (see Figure 11a,b). Under parallel sliding conditions, wear debris shifted back and forth during the linear reciprocal movement, thus always contributing to abrasion in the wear scar (see Figure 11c). The textured samples scattered more or less around the error range of the reference sample (the only exception was sample at 4 µm periodicity). On the other hand, perpendicular sliding likely ensured the effective trapping of wear debris in respective recessions if these were deep enough (Figure 11d). The wear volume of the reference sample was lower than for the textured specimens at 2, 4, and 8 µm because the wear particles were still freely moveable on the surface. It can be noticed that the wear volume slowly increased to 8 µm periodicity as debris was trapped in the topographic valleys but not completely covered, thus still contributing to abrasive behavior. Therefore, topographic recessions can act as debris traps if they are sufficiently deep. Otherwise, the recessions reduce the mobility of the wear particles by blocking them. Therefore, it can be assumed that the abrasive effect of the wear particles is only minimized if the recessions efficiently store the debris, thus resulting in a lower wear volume, as can be seen for the sample with 12 µm periodicity and the largest structural depth. The direct comparison of both wear tracks additionally revealed that the laser texture could not be identified anymore in the parallel case because the abrasive wear particles ploughed through the entire pattern, thus destroying it. In contrast, the line-like pattern was still visible for the perpendicular alignment. These findings are also in good correlation with the recorded COF in Figure 10. Here, the COF for 12 µm periodicity and perpendicular orientation was slightly lower compared to other periodicities and orientations because of the reduced abrasive component of the COF.
4. Conclusions
This research work focused on laser surface texturing of TiAl multilayer films and the effects of the microstructure and topography of these films on friction and wear. The following main conclusions could be drawn:
- Laser as a heat source allows for microstructural modifications, such as the formation of intermetallic phases, variations in grain sizes or increased defect densities. Consideration of microstructural changes is important as it is related to the friction and wear properties of materials, in addition to topography effects depending on the texturing method used. In the case of laser processing, in particular for direct laser interference patterning DLIP, the heating and cooling rates are extremely high, in the range of 109 K/s, therefore non-equilibrium phases may be induced. Heat is localized in positions of constructive interference of the superimposing laser beams.
- Well-defined and long-range ordered topographies can be created with lateral feature sizes in the micron range. These so-fabricated textures can be successfully used to reduce contact area or to store formed wear debris to reduce wear.
Acknowledgments
Andreas Rosenkranz gratefully acknowledges the Alexander von Humboldt foundation for the financial support of his Postdoctoral Fellowship (Feodor Lynen Research Fellowship).
Author Contributions
Carsten Gachot wrote the paper and designed most experiments; Andreas Rosenkranz interpreted data and supported experiments; Philipp Grützmacher discussed results, recommended improvements of data interpretation and wrote conclusions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hamilton, B.; Walowit, J.A.; Allen, C.M. A theory of lubrication by micro-irregularities. J. Basic Eng. 1966, 88, 177–185. [Google Scholar] [CrossRef]
- Gachot, C.; Rosenkranz, A.; Hsu, S.M.; Costa, H.L. A critical assessment of surface texturing for friction and wear improvement. Wear 2017, 372, 21–41. [Google Scholar] [CrossRef]
- Gachot, C.; Rosenkranz, A.; Reinert, L.; Ramos-Moore, E.; Souza, N.; Müser, M.H.; Mücklich, F. Dry friction between laser-patterned surfaces: role of alignment, structural wavelength and surface chemistry. Tribol. Lett. 2013, 49, 193–202. [Google Scholar] [CrossRef]
- Etsion, I.; Halperin, G. A laser surface textured hydrostatic mechanical seal. Tribol. Trans. 2002, 45, 430–434. [Google Scholar] [CrossRef]
- Etsion, I.; Halperin, G.; Brizmer, V.; Kligerman, Y. Experimental investigation of laser surface textured parallel thrust bearings. Tribol. Lett. 2004, 17, 295–300. [Google Scholar] [CrossRef]
- Mücklich, F.; Lasagni, A.; Daniel, C. Laser Interference Metallurgy–using interference as a tool for micro/nano structuring. Zeitschrift für Metallkunde 2006, 97, 1337–1344. [Google Scholar] [CrossRef]
- Cao, J.; Feng, J.C.; Li, Z.R. Joining of TiAl intermetallic by self-propagating high-temperature synthesis. J. Mater. Sci. 2006, 41, 4720–4724. [Google Scholar] [CrossRef]
- Senkov, O.N.; Uchic, M.D. Microstructure evolution during annealing of an amorphous TiAl sheet. Mater. Sci. Eng. A 2003, 340, 216–224. [Google Scholar] [CrossRef]
- Detemple, E.; Leibenguth, P.; Gachot, C.; Mücklich, F. Large-area patterned formation of intermetallic phases on Ti/Al multilayer systems by laser interference metallurgy. Thin Solid Films 2010, 519, 736–741. [Google Scholar] [CrossRef]
- Lasagni, A.; Mücklich, F. FEM simulation of periodical local heating caused by Laser Interference Metallurgy. J. Mater. Process. Technol. 2009, 209, 202–209. [Google Scholar] [CrossRef]
- Haynes, W.M.; Lyde, D.R. A Ready-reference Book of Chemical and Physical Data. In Crc Handbook of Chemistry and Physics; CRC Press: Florida, LA, USA, 2010. [Google Scholar]
- Lasagni, A.F. Advanced Design of Periodical Structures by Laser Interference Metallurgy in the Micro/Nano Scale on Macroscopic Areas. Ph.D. Thesis, Universität des Saarlandes, Saarbrücken, German, 2006. [Google Scholar]
- Peterson, M.B.; Winer, W.O. Wear Control Handbook; ASME: New York, NY, USA, 1980. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).