Water Pool Behaviors of Water Lubricating for Glass/Steel Point Contact
Abstract
:1. Introduction
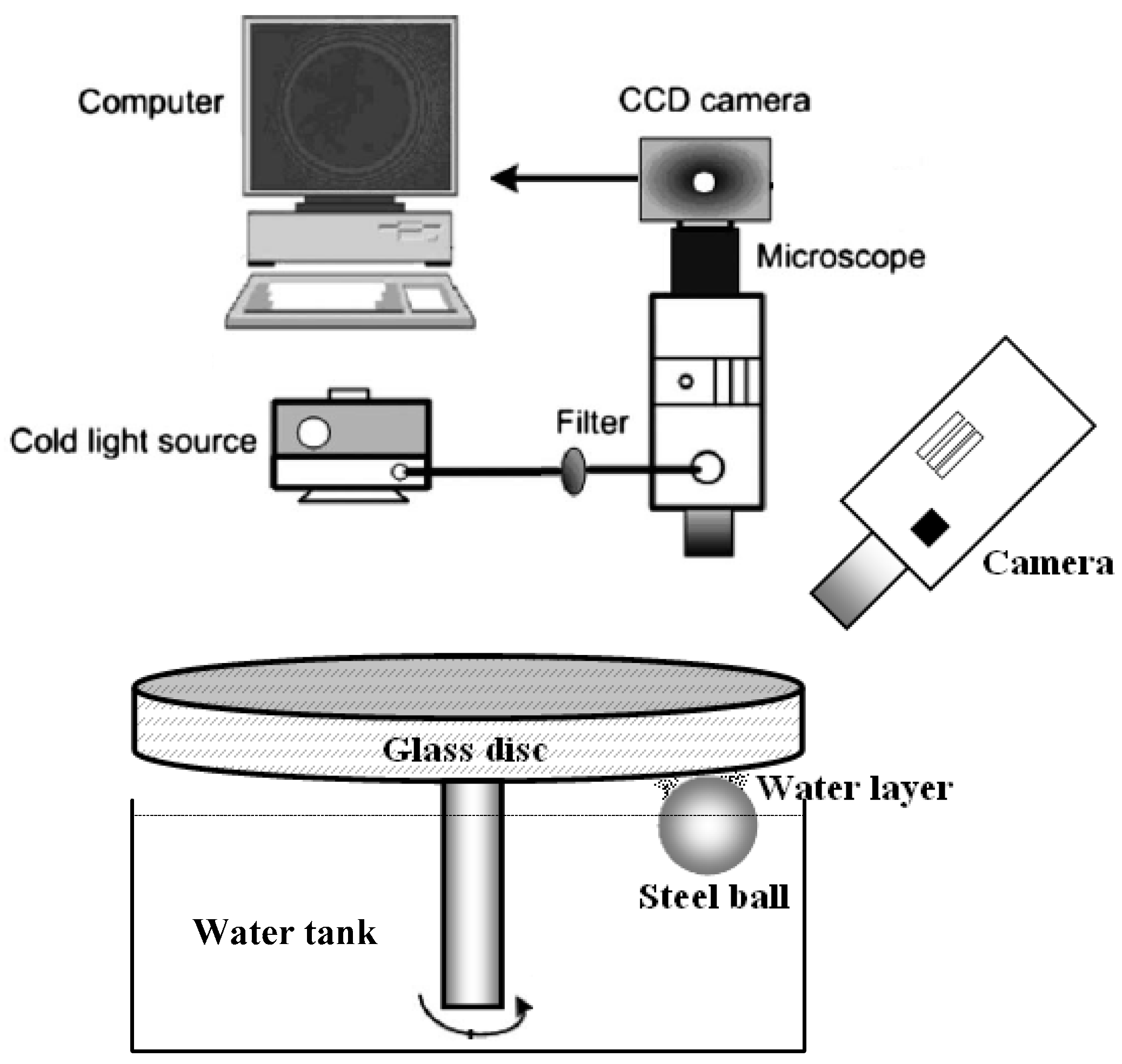
2. Experimental Conditions
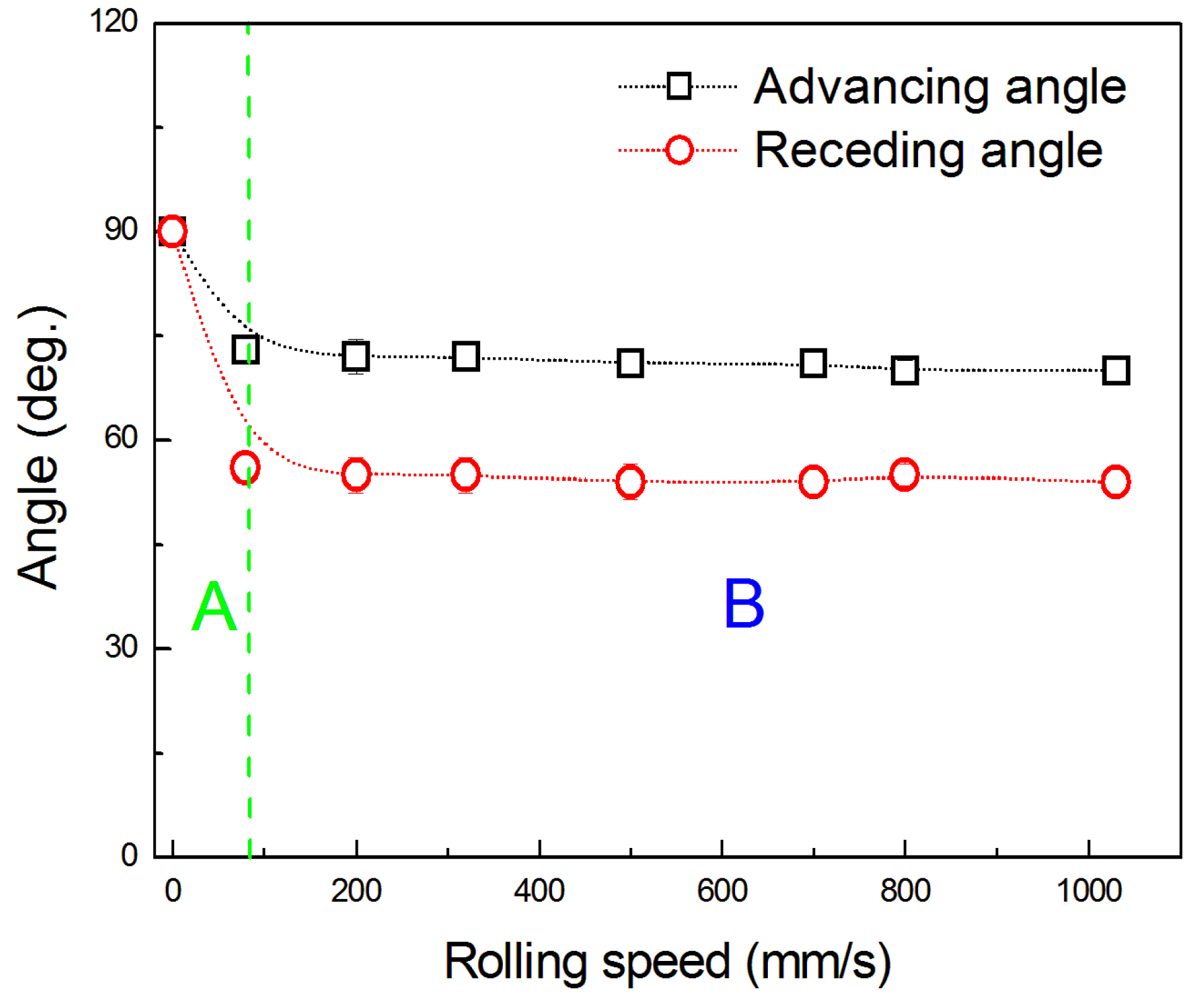
3. Results and Discussion
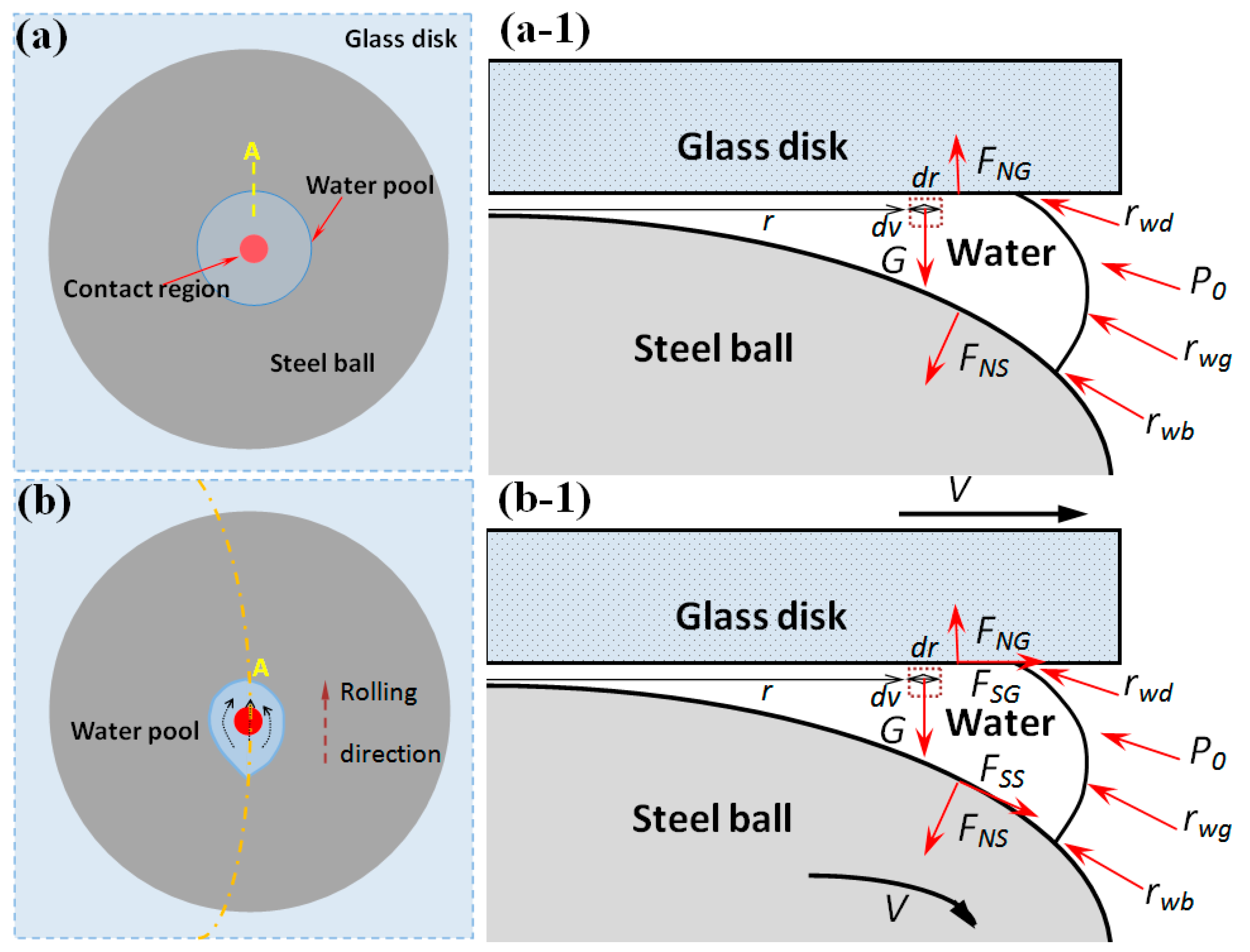
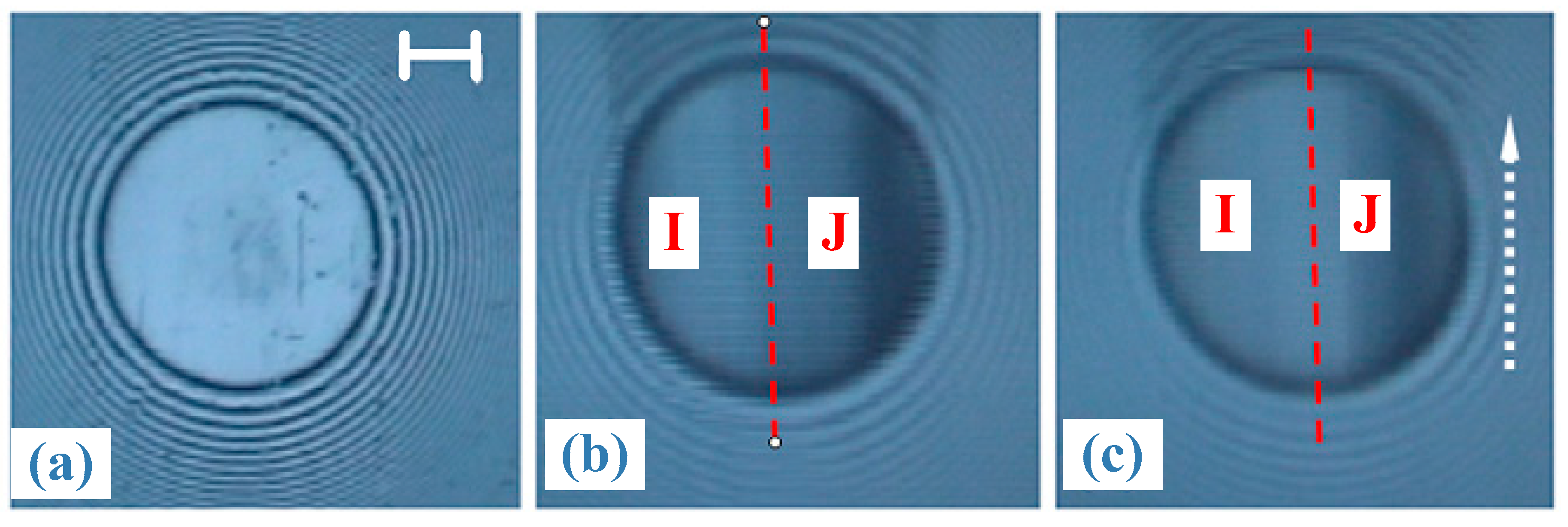
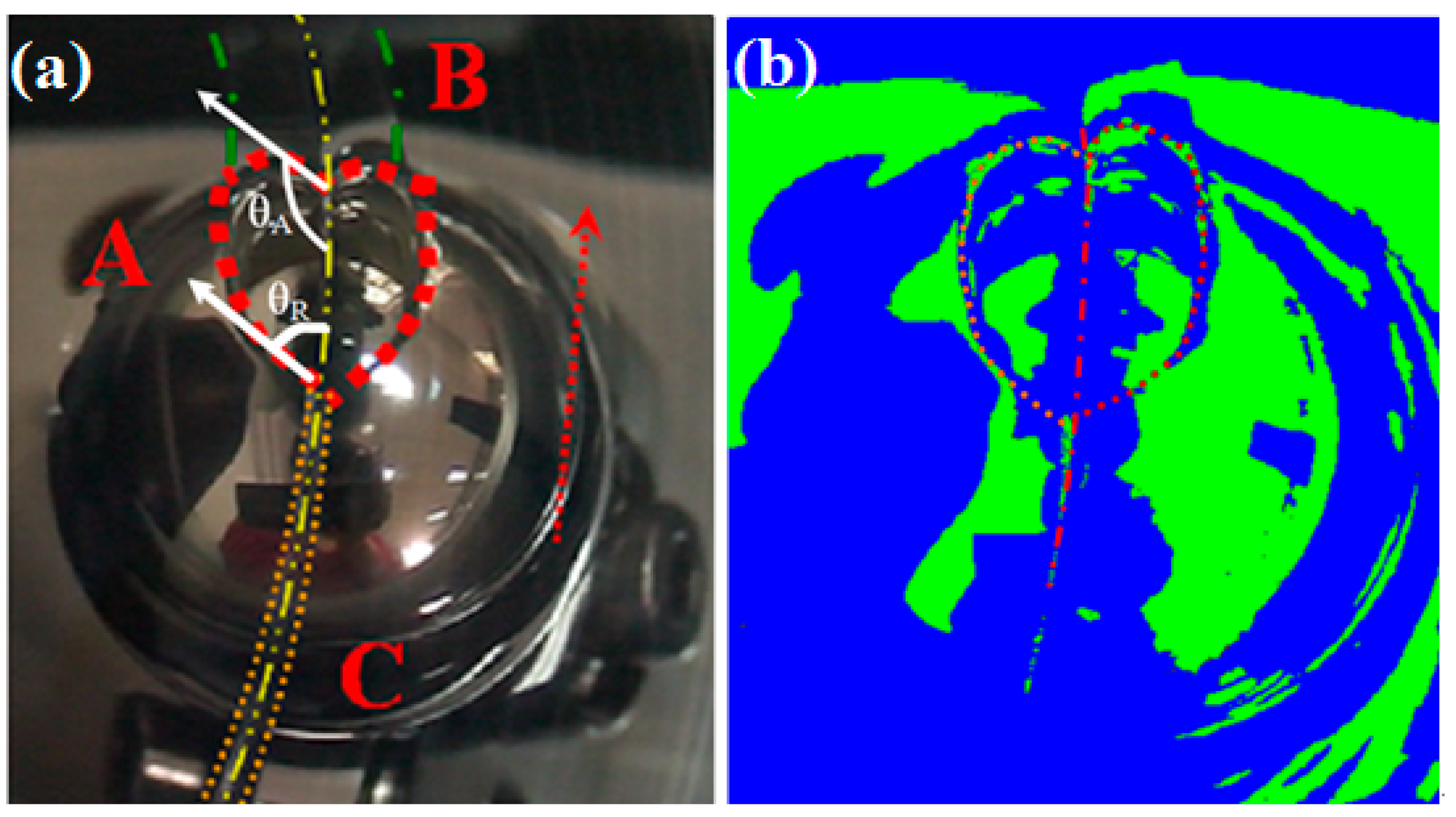
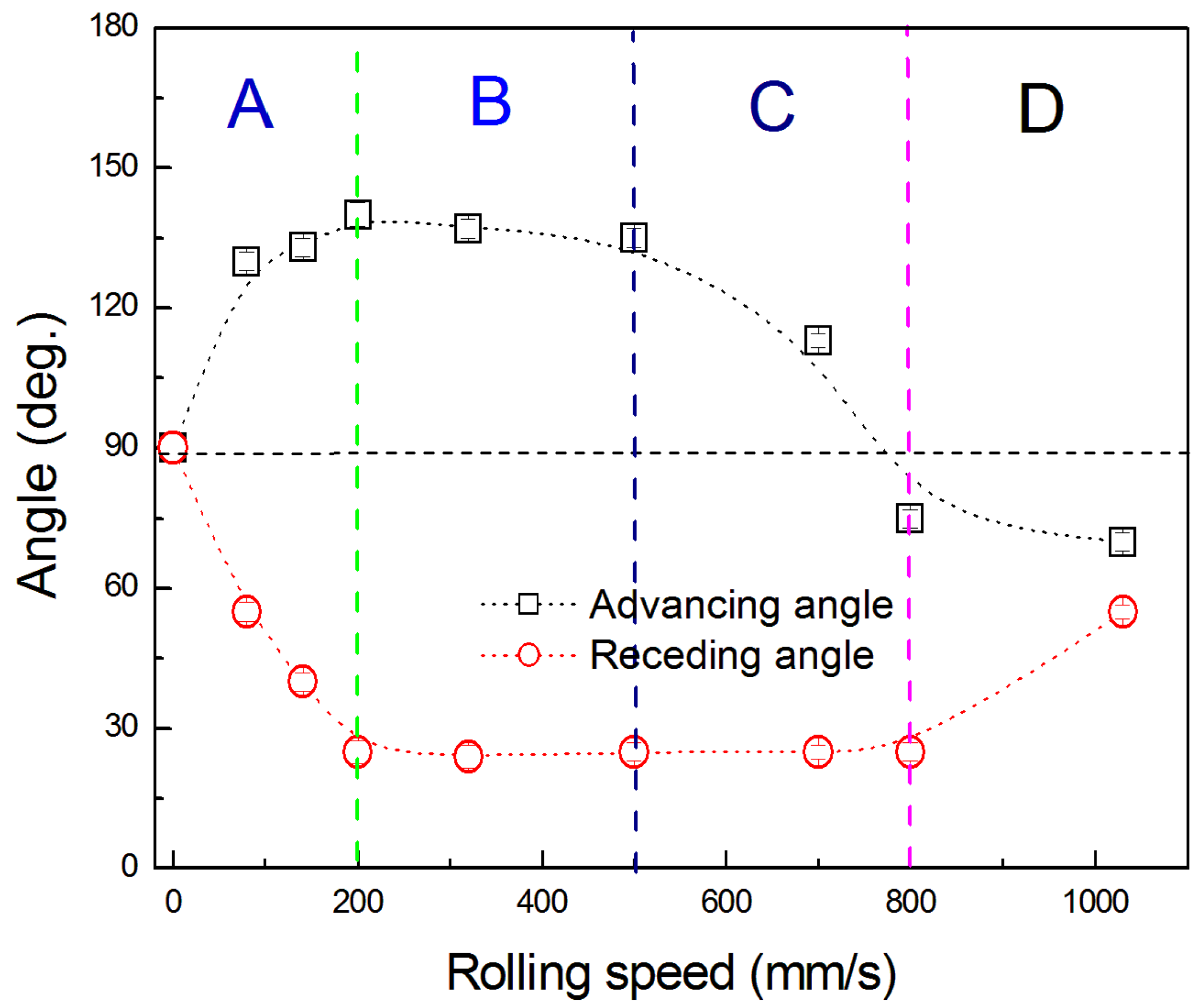
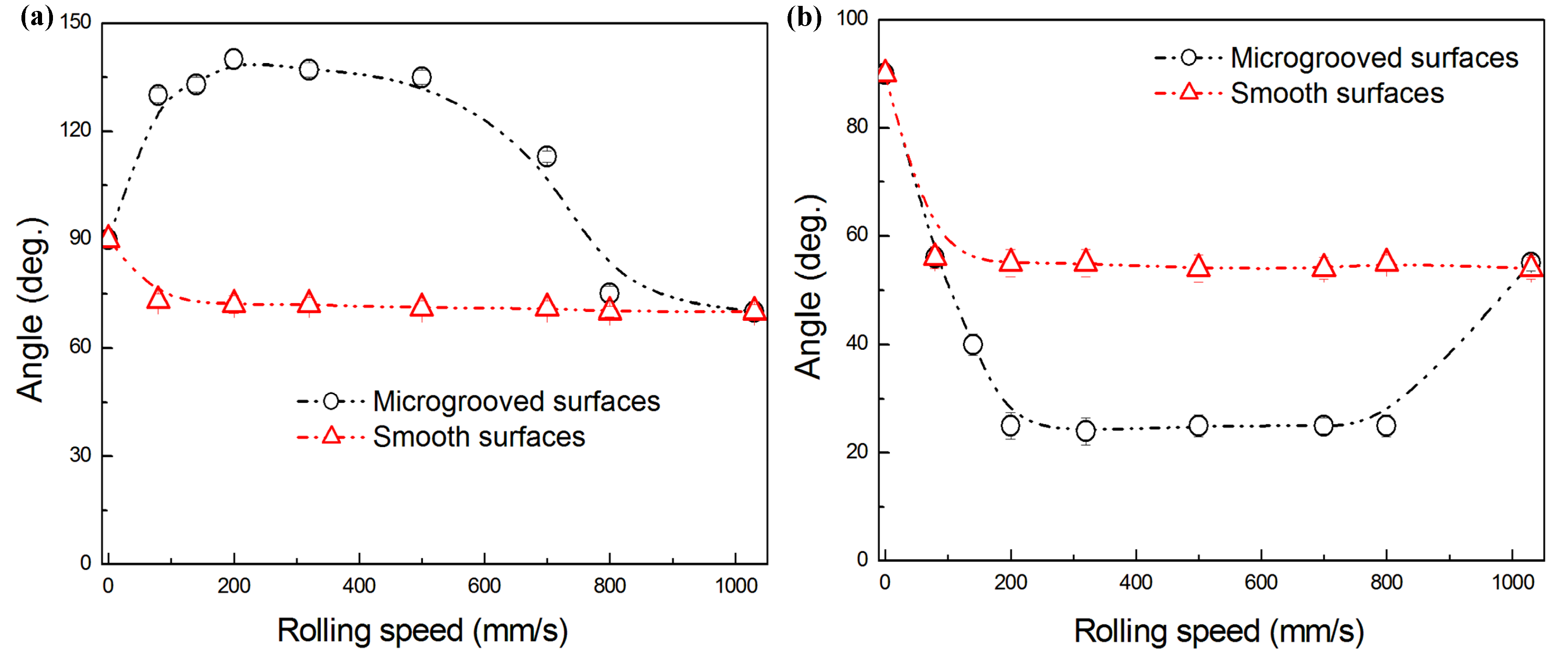
3.1. Observation on Water Flow between Smooth Surfaces
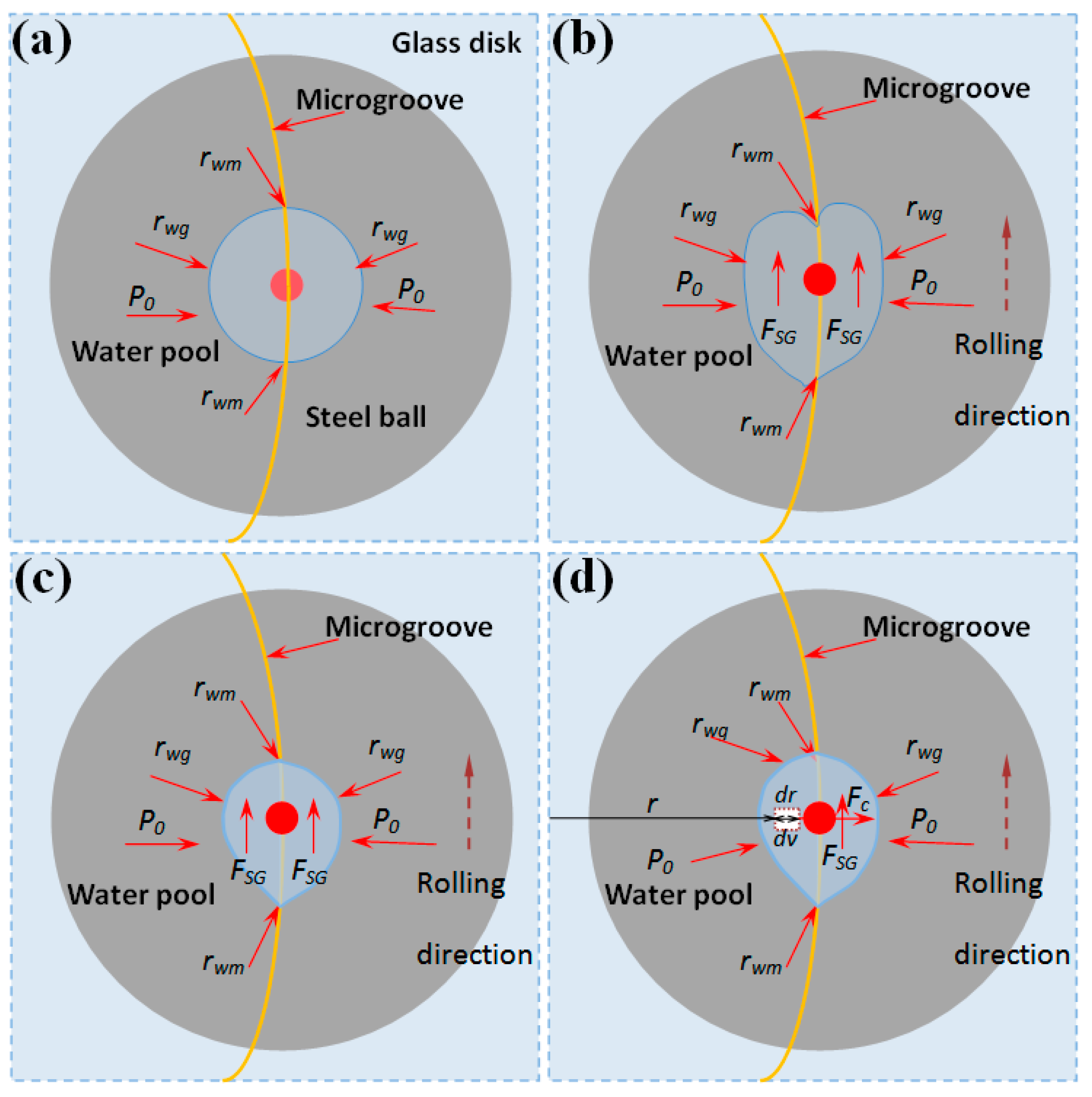
3.2. Observation on Water Flow between Microgrooved Surfaces
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dowson, D. History of Tribology; Longman: London, UK, 1979. [Google Scholar]
- Özmen, Y. Si3N4 as a biomaterial and its tribo-characterization under water lubrication. Lubr. Sci. 2016, 28, 243–254. [Google Scholar] [CrossRef]
- Cyriac, F.; Lugt, P.M.; Bosman, R. Impact of water on the rheology of lubricating greases. Tribol. Trans. 2016, 59, 679–689. [Google Scholar] [CrossRef]
- Huang, W.; Cao, X.; Wen, Z. A Subscale Experimental Investigation on the Influence of Sanding on Adhesion and Rolling Contact Fatigue of Wheel/Rail Under Water Condition. J. Tribol. 2017, 139, 011401. [Google Scholar] [CrossRef]
- Lei, X.; Shen, B.; Chen, S. Tribological behavior between micro-and nano-crystalline diamond films under dry sliding and water lubrication. Tribol. Int. 2014, 69, 118–127. [Google Scholar] [CrossRef]
- Gao, C.P.; Guo, G.F.; Zhao, F.Y. Tribological behaviors of epoxy composites under water lubrication conditions. Tribol. Int. 2016, 95, 333–341. [Google Scholar] [CrossRef]
- Dong, C.; Shi, L.; Li, L.; Bai, X.; Yuan, C.; Tian, Y. Stick-slip behaviours of water lubrication polymer materials under low speed conditions. Tribol. Int. 2017, 106, 55–61. [Google Scholar] [CrossRef]
- Ma, Q.; Zhou, F.; Gao, S. Influence of boron content on the microstructure and tribological properties of Cr-BN coatings in water lubrication. Appl. Surf. Sci. 2016, 377, 394–405. [Google Scholar] [CrossRef]
- Niu, Q.L.; Zheng, X.H.; Ming, W.W. Friction and wear performance of titanium alloys against tungsten carbide under dry sliding and water lubrication. Tribol. Trans. 2013, 56, 101–108. [Google Scholar] [CrossRef]
- Mamada, K.; Kosukegawa, H.; Fridrici, V. Friction properties of PVA-H/steel ball contact under water lubrication conditions. Tribol. Int. 2011, 44, 757–763. [Google Scholar] [CrossRef]
- Wang, J.; Yan, F.; Xue, Q. Friction and wear behavior of ultra-high molecular weight polyethylene sliding against GCr15 steel and electroless Ni–P alloy coating under the lubrication of seawater. Tribol. Lett. 2009, 35, 85–95. [Google Scholar] [CrossRef]
- Chen, B.; Wang, J.; Yan, F. Friction and wear behaviors of several polymers sliding against GCr15 and 316 steel under the lubrication of sea water. Tribol. Lett. 2011, 42, 17–25. [Google Scholar] [CrossRef]
- Chen, B.; Wang, J.; Yan, F. Comparative investigation on the tribological behaviors of CF/PEEK composites under sea water lubrication. Tribol. Int. 2012, 52, 170–177. [Google Scholar] [CrossRef]
- Liu, S.H.; Luo, J.B.; Li, G.; Zhang, C.H.; Lu, X.C. Effect of surface physicochemical properties on the lubricating properties of water film. Appl. Surf. Sci. 2008, 254, 7137–7142. [Google Scholar] [CrossRef]
- Liu, S.H.; Luo, J.B.; Xie, G.X.; Guo, D. Effect of surface charge on water film nanoconfined between hydrophilic solid surfaces. J. Appl. Phys. 2009, 105, 124301. [Google Scholar] [CrossRef]
- Liu, S.H.; Guo, D.; Xie, G.X. Water film confined in a nanoscale gap: Surface polarity and hydration effects. J. Appl. Phys. 2010, 108, 084315. [Google Scholar] [CrossRef]
- Jahanmir, S.; Ozmen, Y.; Ives, L.K. Water lubrication of silicon nitride in sliding. Tribol. Lett. 2004, 17, 409–417. [Google Scholar] [CrossRef]
- Briscoe, W.H.; Titmuss, S.; Tiberg, F. Boundary lubrication under water. Nature 2006, 444, 191–194. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Xiao, X.D.; Ogletree, D.F. Imaging the condensation and evaporation of molecularly thin films of water with nanometer resolution. Science 1995, 268, 267–269. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Szoszkiewicz, R.; Landman, U. Structured and viscous water in subnanometer gaps. Phys. Rev. B 2007, 75, 115415. [Google Scholar]
- Major, R.C.; Houston, J.E.; McGrath, M.J. Viscous water meniscus under nanoconfinement. Phys. Rev. Lett. 2006, 96, 177803. [Google Scholar] [CrossRef] [PubMed]
- Goertz, M.P.; Houston, J.E.; Zhu, X.Y. Hydrophilicity and the viscosity of interfacial water. Langmuir 2007, 23, 5491–5497. [Google Scholar] [CrossRef] [PubMed]
- Wong, P.L.; Huang, P.; Meng, Y. The effect of the electric double layer on a very thin water lubricating film. Tribol. Lett. 2003, 14, 197–203. [Google Scholar] [CrossRef]
- Leng, Y.; Cummings, P.T. Fluidity of hydration layers nanoconfined between mica surfaces. Phys. Rev. Lett. 2005, 94, 026101. [Google Scholar] [CrossRef] [PubMed]
- Lane, J.M.D.; Chandross, M.; Stevens, M.J. Water in nanoconfinement between hydrophilic self-assembled monolayers. Langmuir 2008, 24, 5209–5212. [Google Scholar] [CrossRef] [PubMed]




© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Liu, S.-H.; Xiao, H.-P. Water Pool Behaviors of Water Lubricating for Glass/Steel Point Contact. Lubricants 2017, 5, 36. https://doi.org/10.3390/lubricants5030036
Zhang H, Liu S-H, Xiao H-P. Water Pool Behaviors of Water Lubricating for Glass/Steel Point Contact. Lubricants. 2017; 5(3):36. https://doi.org/10.3390/lubricants5030036
Chicago/Turabian StyleZhang, Hang, Shu-Hai Liu, and Hua-Ping Xiao. 2017. "Water Pool Behaviors of Water Lubricating for Glass/Steel Point Contact" Lubricants 5, no. 3: 36. https://doi.org/10.3390/lubricants5030036
APA StyleZhang, H., Liu, S.-H., & Xiao, H.-P. (2017). Water Pool Behaviors of Water Lubricating for Glass/Steel Point Contact. Lubricants, 5(3), 36. https://doi.org/10.3390/lubricants5030036



