Numerical Treatments of Slipping/No-Slip Zones in Cold Rolling of Thin Sheets with Heavy Roll Deformation
Abstract
:1. Introduction on Strip Rolling Models, Roll Deformation and the Role of the Friction Stress
1.1. Elastic Roll Deformation Modeling
- First the Influence Function Method initiated by Jortner et al. [6] and its numerous variants, still in use today.
1.2. Plastic Strip Deformation Modeling and Coupling with Roll Deformation
1.3. The role of Friction: Regularization
1.4. Purpose and Organization of the Paper
2. Models Description
2.1. Slab Method-Based Model
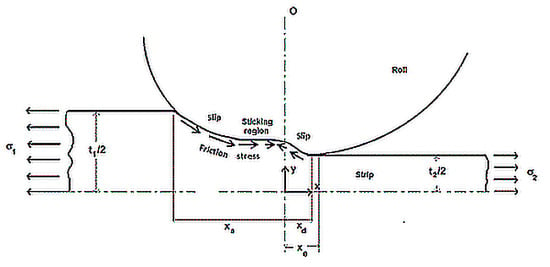
2.1.1. Stress Field in the Strip
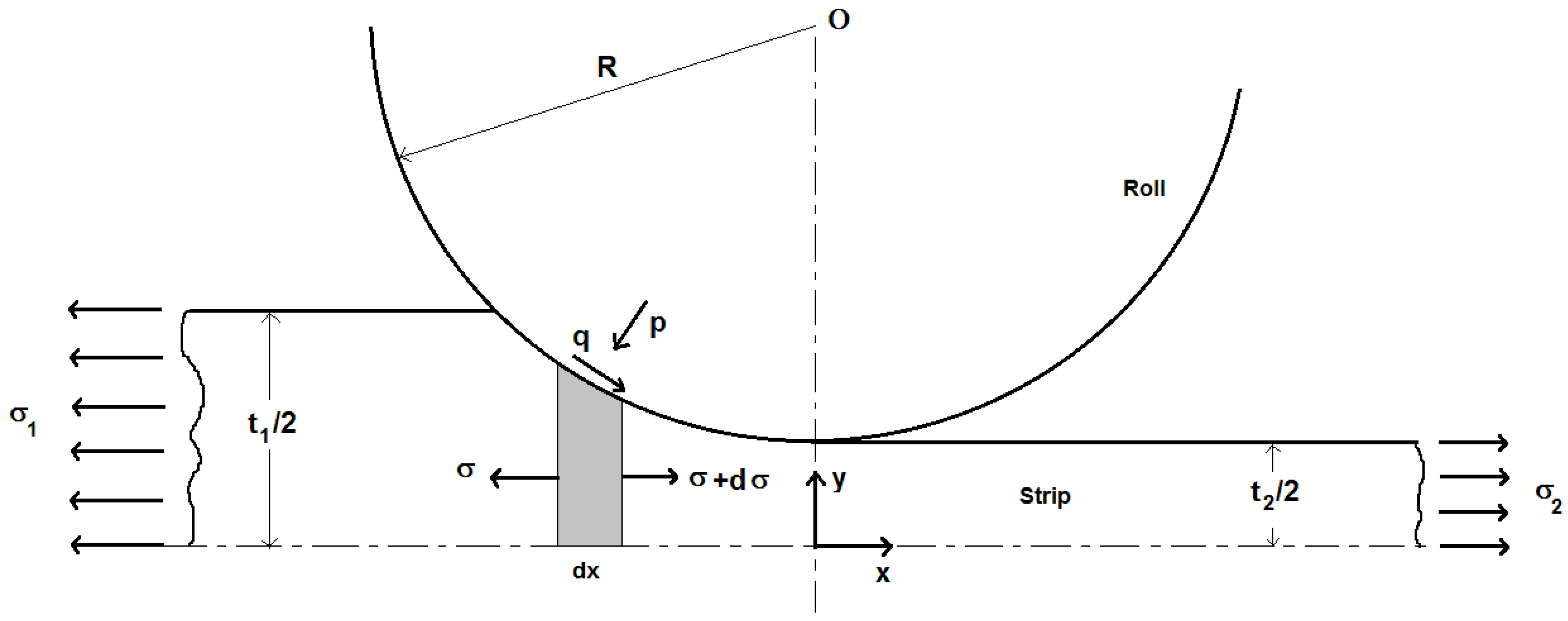
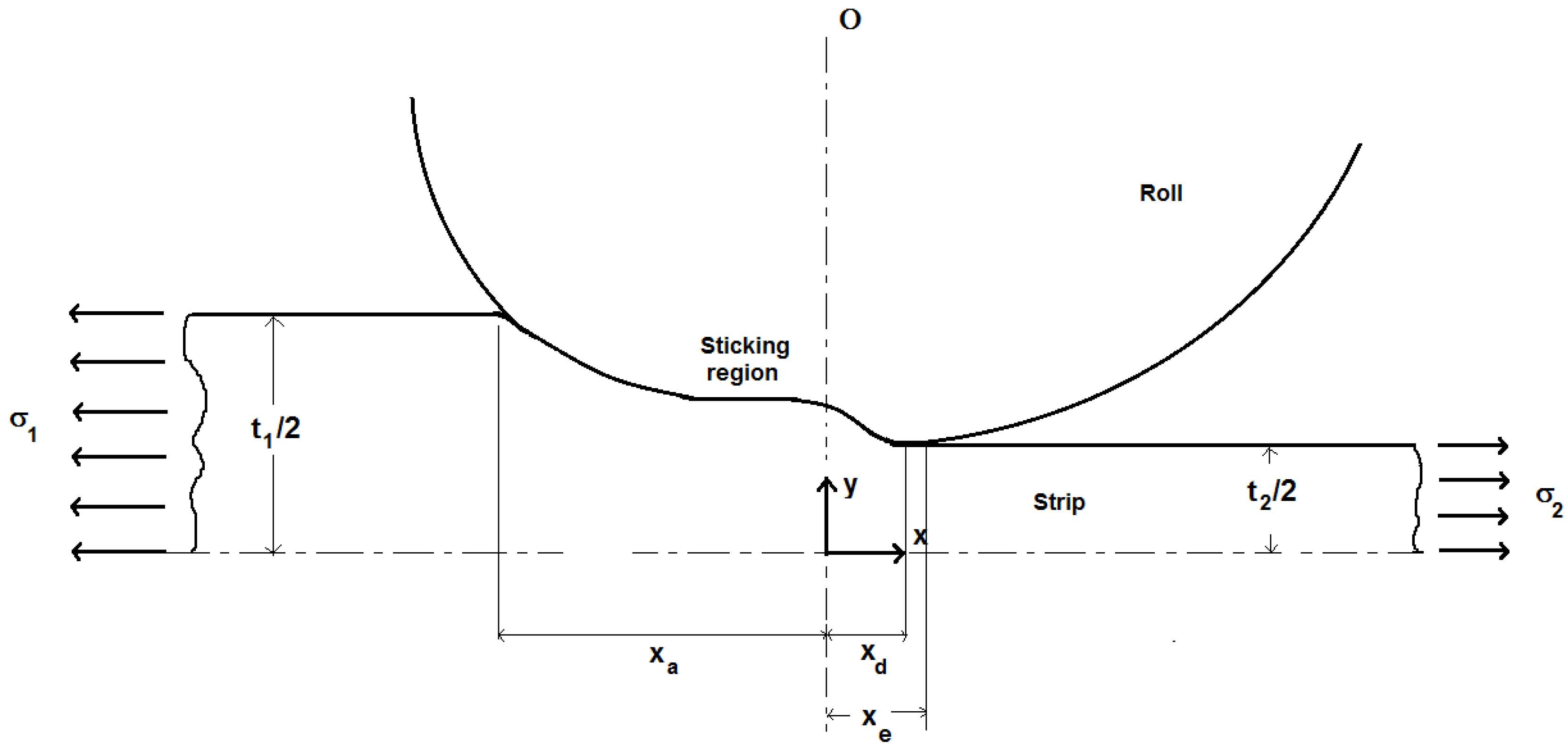
- (a)
- In the plastic slip region, the equilibrium Equation (5) is solved together with the elastic-plastic constitutive model. A Tresca yield criterion is assumed: p + σ = Ys (Ys is the plane strain yield stress of the strip), giving, once reported into Equation (5):
- (b)
- In the elastic zones at entry and exit of the roll bite, where slip necessarily takes place, the elastic constitutive equations and the equilibrium equation are reprocessed according to Le and Sutcliffe [17]:
- (c)
- In the contained plastic zone (CPZ), the pressure gradient and shear stress for roll and strip are calculated by imposing the no-slip condition, giving, instead of Equations (5) and (8):
2.1.2. Work Roll Deformation Equations
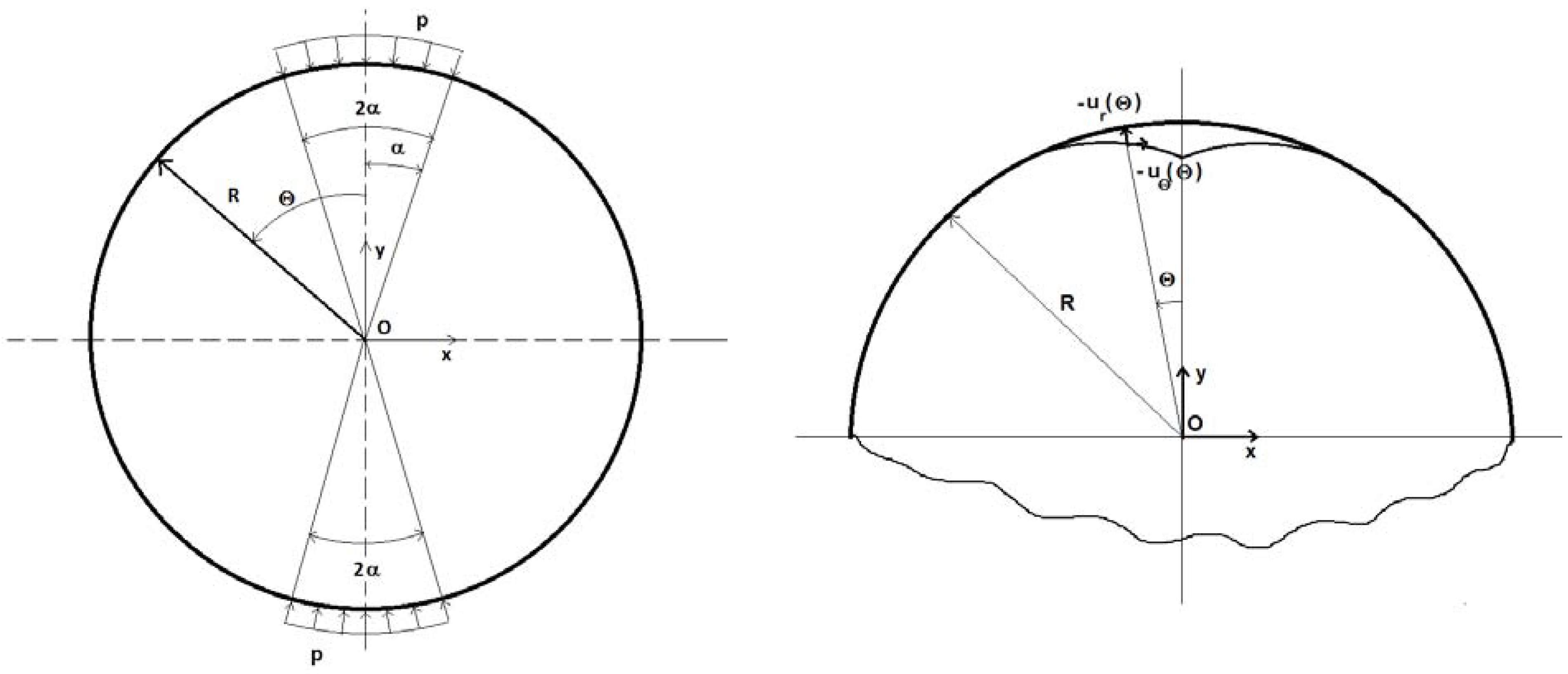
- (i.e., outside the load area)
2.1.3. Numerical Implementation
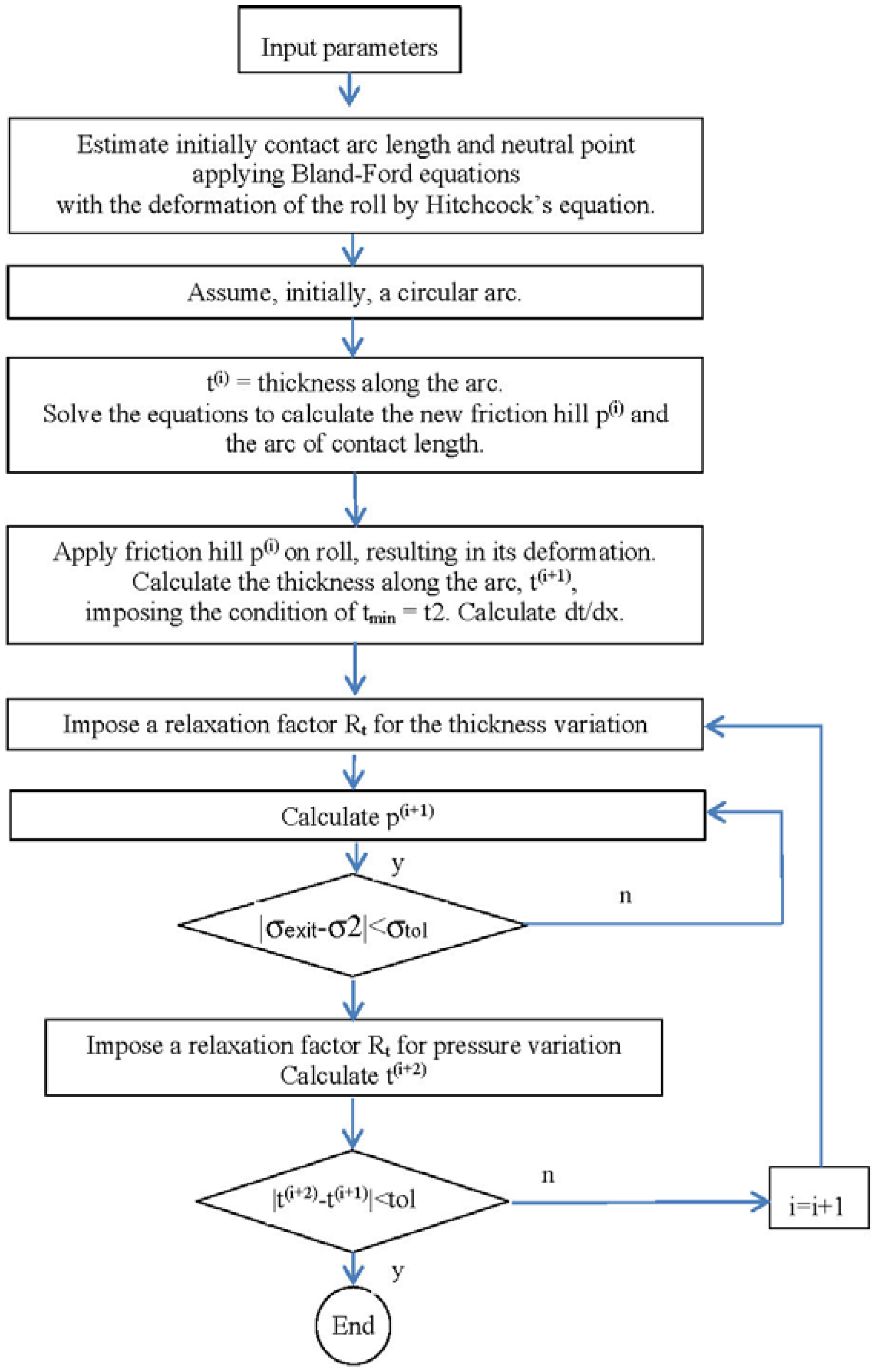
2.2. FEM-Based Model
- -
- A 3D implicit FEM software called Lam3, fully described by Hacquin [19,20]. It is used here in its steady state option based on streamlines. The integration of the elastic-plastic constitutive model uses the radial return technique; the compatibility with steady state modeling and the streamline method is ensured through the ELDTH formulation (Eulerian-Lagrangian with Heterogeneous Time step). The software uses 8-node hexahedra with reduced pressure integration. Steady state allows adapted refinement in critical locations (bite entry and exit). Thermo-mechanical coupling is not activated here.
- -
- A 3D semi-analytical elastic roll deformation model called Tec3, fully described in Hacquin et al. [21]. It combines roll bending based on Timoshenko’s beam model, roll flattening based on Boussinesq equations for a semi-infinite solid arbitrarily loaded on its surface, Hertz contact theory for the work roll/back-up roll contact. End effects for the complex geometry and boundary conditions of the roll barrel edge have been corrected by analytical expressions derived from extensive FEM comparisons. All equations are discretized by a 3D influence function method. Due to the unknown work roll/back-up roll contact areas, the resulting equations are non-linear and are solved using a Newton-Raphson scheme.
3. Influence of the Regularization Parameter on Rolling Process Mechanics
| Variable | Value |
|---|---|
| Inlet/exit thickness, t1/t2 | 0.355 mm/0.252 mm |
| Work roll diameter | 555 mm |
| Work roll velocity | 20.482 m·s−1 |
| Back/front tension stress, σ1/σ2 | 170 MPa/100 MPa |
| Young’s modulus (roll and strip) | 210 GPa |
| Poisson’s ratio (roll and strip) | 0.3 |
| Flow curve | (MPa) |
| Accumulated strain (prior to the pass investigated) | 2.05 |
| μ | 0.02; 0.04 |
| Kreg (Slab Method) | 10−2; 3.16 × 10−3; 10−3 |
| Kreg (FEM) | 10−1; 10−2; 3.16 10−3; 10−3 |
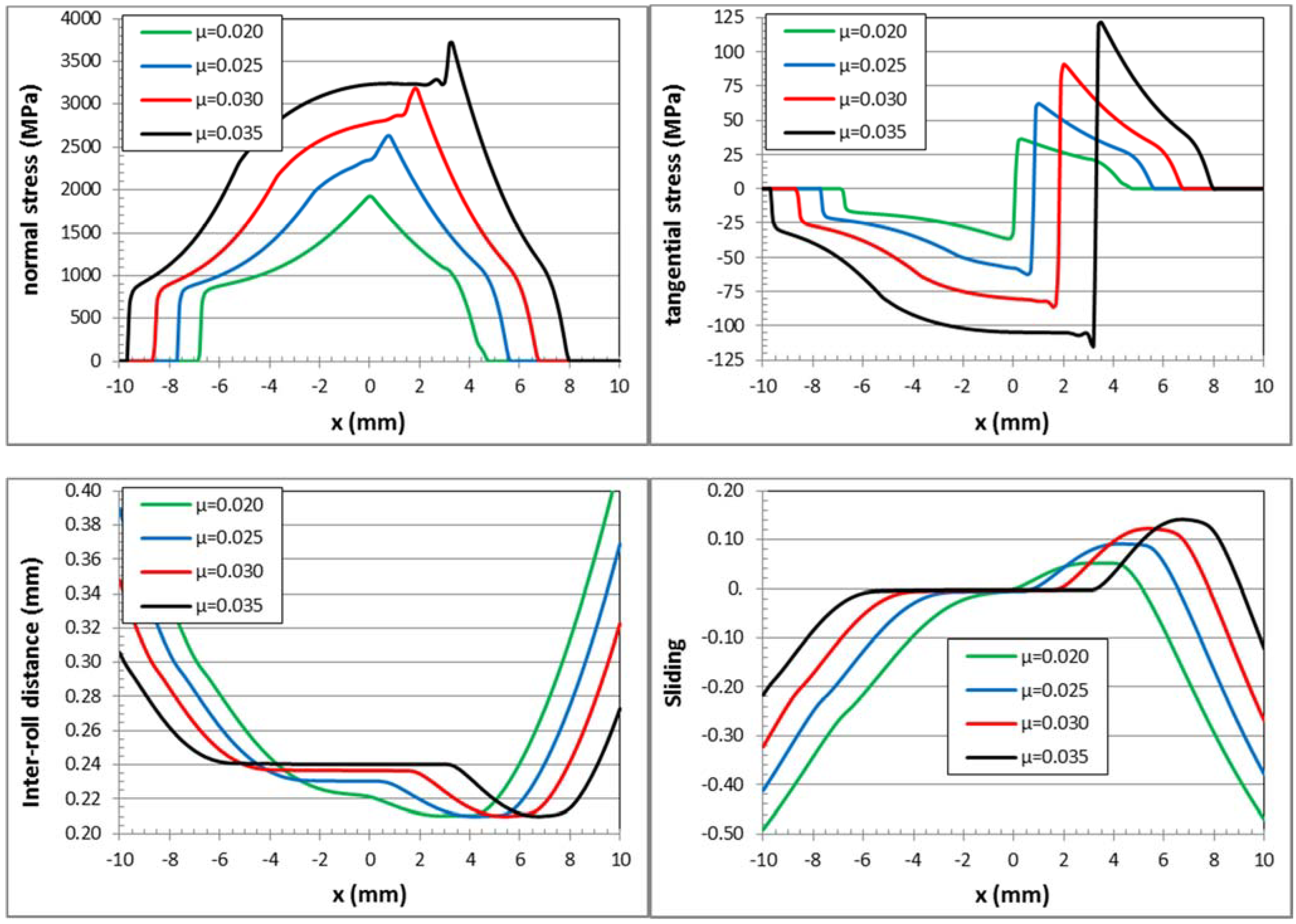
3.1. Impact of Friction Regularization: FEM
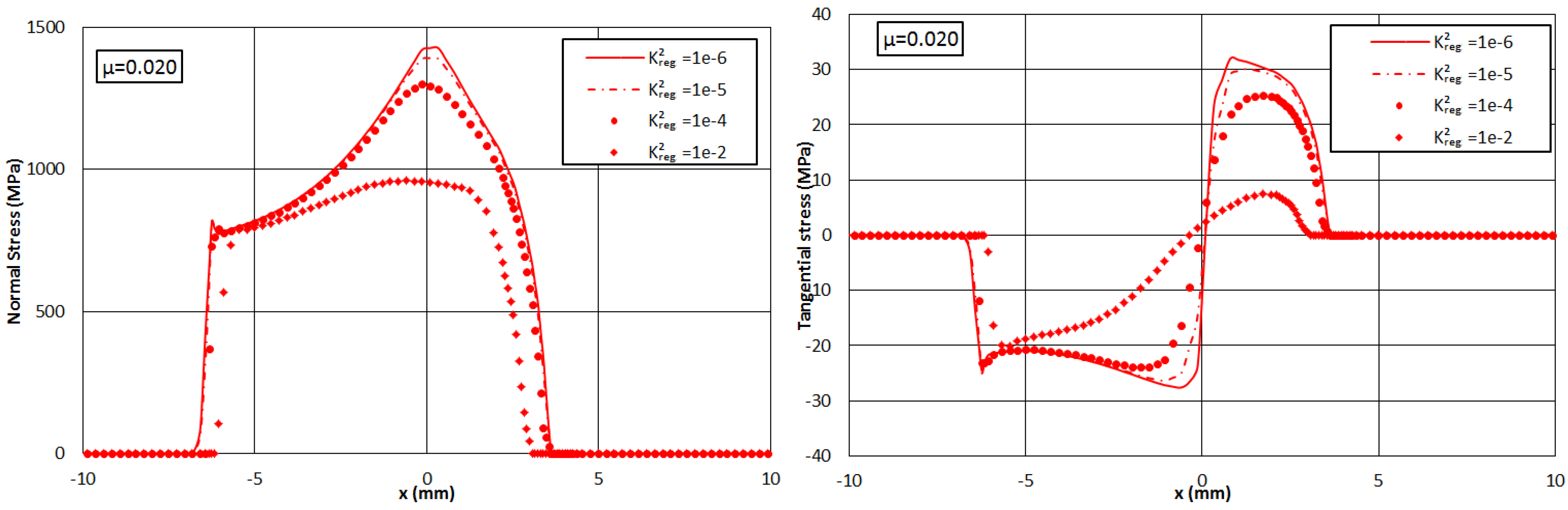
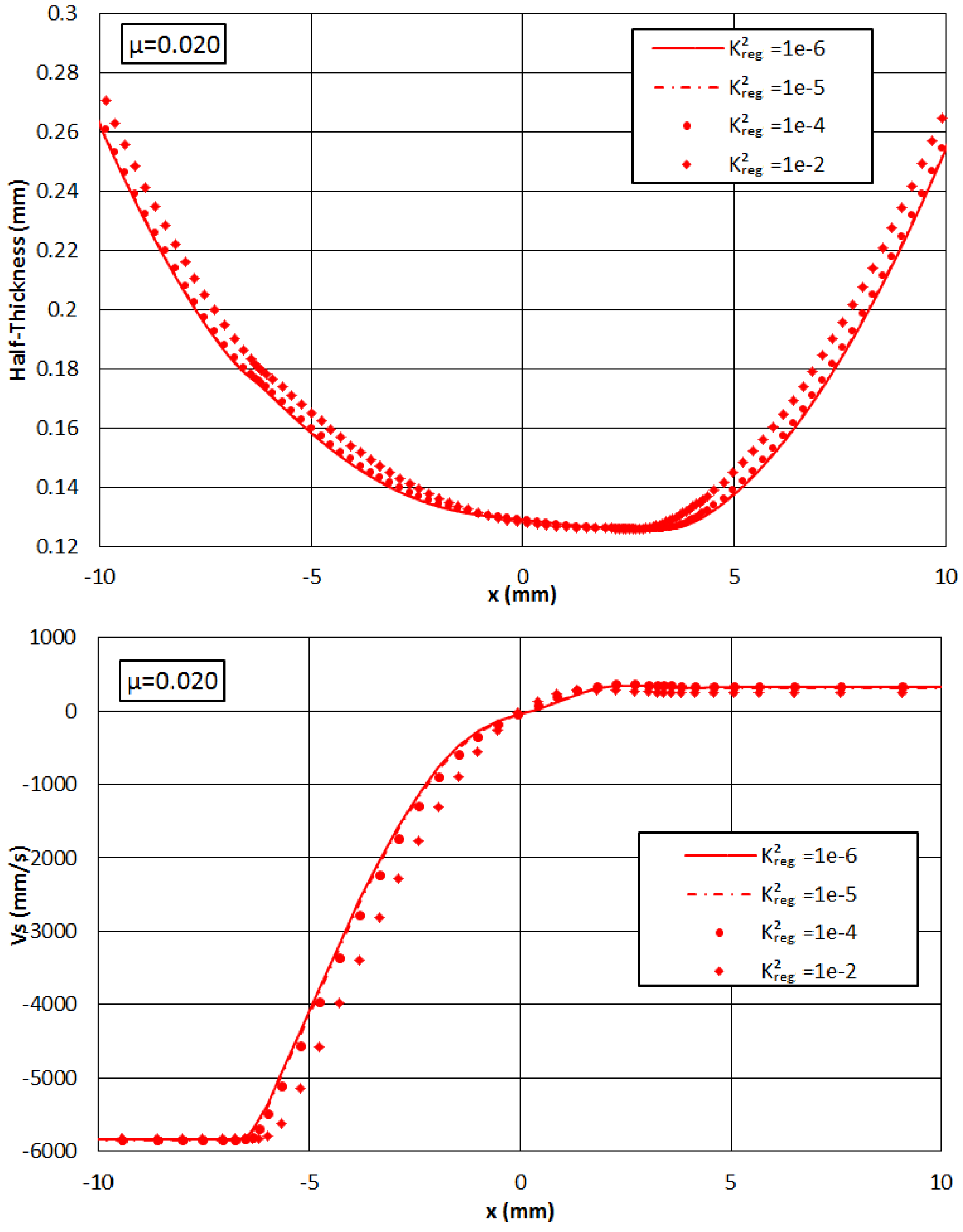
3.2. Impact of Friction Regularization: Slab Method
4. Discussions
4.1. Importance of Friction Regularization and Choice of Kreg

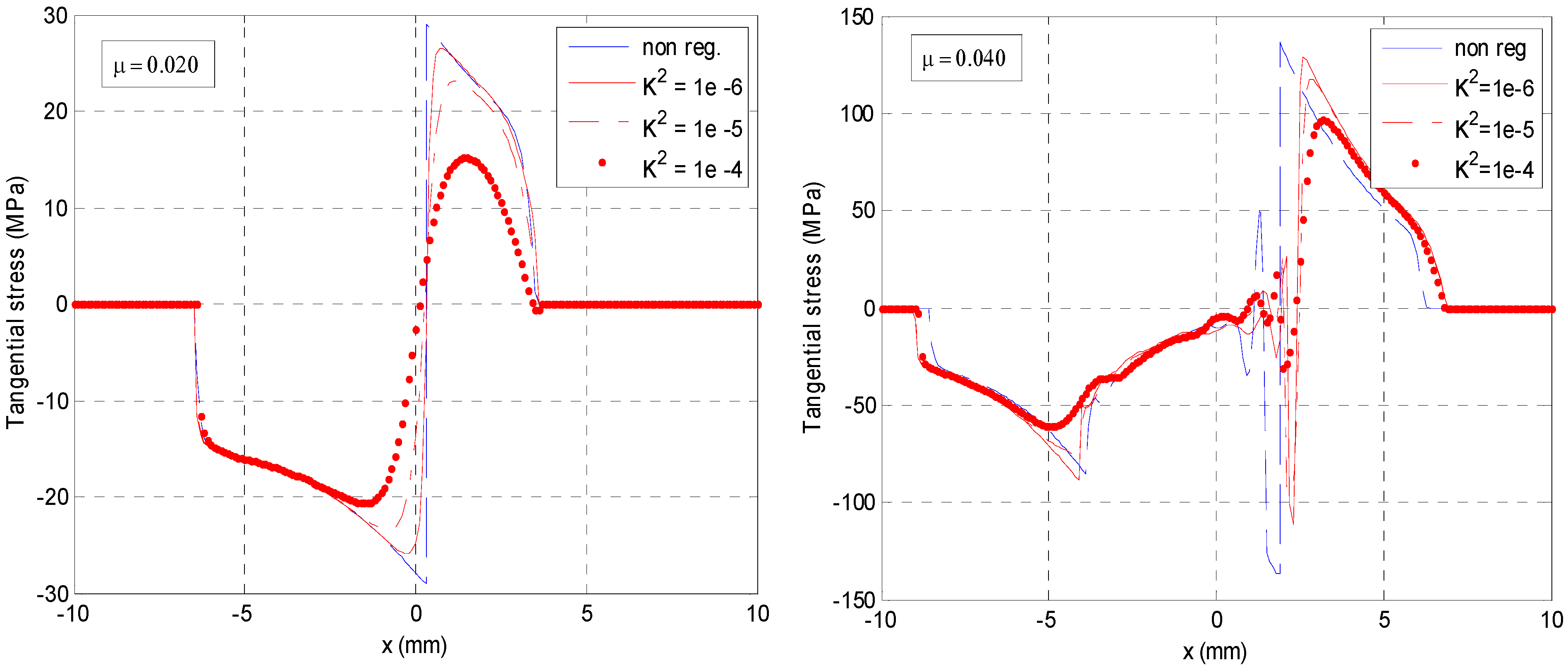
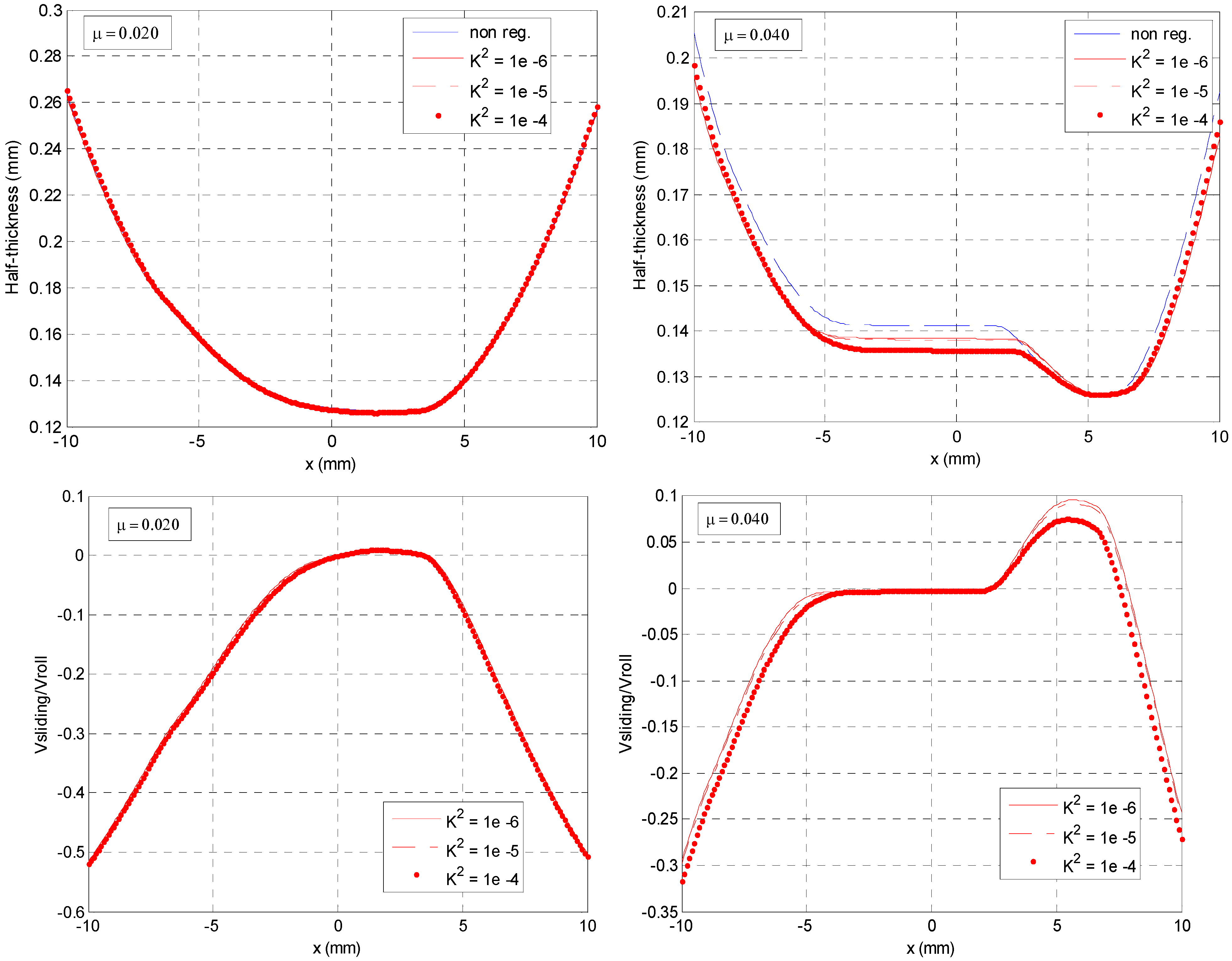
| Kreg | Force (MN/m), FEM, µ = 0.02 | Force (MN/m), SM, µ = 0.02 | Force (MN/m), SM, µ = 0.04 | Lstick (mm) SM, µ = 0.04 |
|---|---|---|---|---|
| 10−1 | 7.47 MN/m | - | - | - |
| 10−2 | 9.59 MN/m | 9.68 MN/m | 31.6 MN/m | 5.5 mm |
| 3.16 10−3 | 10.1 MN/m | 10.1 MN/m | 33.1 MN/m | 6.2 mm |
| 10−3 | 10.2 MN/m | 10.1 MN/m | 33.4 MN/m | 6.4 mm |
| Non-regularized | - | 10.1 MN/m | 29.9 MN/m | 5.5 mm |
4.2. Generality of the Approach
4.3. Coupling Regularization with the Static/Dynamic Friction Concept
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Roberts, W.L. Flat Processing of Steel; Marcel Dekker: New York, NY, USA, 1988. [Google Scholar]
- Johnson, K.L. Contact Mechanics, 1st ed.; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Hitchcock, J.H. Roll neck bearings. Report ASME Res. Comm. 1935. [Google Scholar]
- Bland, D.R.; Ford, H. The calculation of roll force and torque in cold strip rolling with tensions. Proc. Inst. Mech. Eng. 1948, 159, 144–153. [Google Scholar] [CrossRef]
- Montmitonnet, P.; Wey, E.; Delamare, F.; Chenot, J.-L.; Fromholz, C.; de Vathaire, M. A mechanical model of cold rolling. Influence of the friction law on roll flattening calculated by a Finite Element Method. In Proceedings of the 4th International Steel Rolling Conference, Deauville, France, 1–3 June, 1987.
- Jortner, D.; Osterle, J.F.; Zorowski, C.F. An analysis of cold strip rolling. Int. J. Mech. Sci. 1960, 2, 179–194. [Google Scholar] [CrossRef]
- Atreya, A.; Lenard, J.G. A study of cold strip rolling. J. Eng. Mater. Technol. (Trans. ASME) 1979, 101, 129–134. [Google Scholar] [CrossRef]
- Kim, T.H.; Lee, W.H.; Hwang, S.M. An integrated FE process model for the prediction of strip profile in flat rolling. ISIJ Int. 2003, 43, 1947–1956. [Google Scholar] [CrossRef]
- Orowan, E. The calculation of roll pressure in hot and cold flat rolling. Proc. Inst. Mech. Eng. 1943, 150, 140–167. [Google Scholar] [CrossRef]
- Grimble, M.J.; Fuller, M.A.; Bryant, G.F. A non-circular arc force model for cold rolling. Int. J. Numer. Methods Eng. 1978, 12, 643–663. [Google Scholar] [CrossRef]
- Gratacos, P.; Montmitonnet, P.; Fromholz, C.; Chenot, J.-L. A plane strain elastoplastic finite element model for cold rolling of thin strip. Int. J. Mech. Sci. 1992, 34, 195–210. [Google Scholar] [CrossRef]
- Matsumoto, H. Elastic-Plastic Theory of Cold and Temper Rolling. In Proceedings of the 8th International Conference on Technology of Plasticity, Verona, Italy, 9–13 October, 2005.
- Legrand, N.; Ngo, T.; Suzuki, Y.; Takahama, Y.; Dbouk, T.; Montmitonnet, P.; Matsumoto, H. Advanced Roll Bite Models for Cold and Temper Rolling Processes. In Proceedings of the Rolling 2013 Conference, Venice, Italy, 10–12 June 2013.
- Krimpelstätter, K. Non circular arc temper rolling model considering radial and circumferential displacements. Ph.D. Thesis, Linz University, Linz, Austria, 2005. [Google Scholar]
- Fleck, N.A.; Johnson, K.L. Towards a new theory of cold rolling thin foil. Int. J. Mech. Sci. 1987, 29, 507–524. [Google Scholar] [CrossRef]
- Sutcliffe, M.P.F.; Montmitonnet, P. Numerical modelling of lubricated foil rolling. Rev. Met. SGM 2001, 98, 435–442. [Google Scholar] [CrossRef]
- Le, H.R.; Sutcliffe, M.P.F. A robust model for rolling of thin strip and foil. Int. J. Mech. Sci. 2001, 43, 1405–1419. [Google Scholar] [CrossRef]
- Meindl, W. Roll flattening with consideration of shear contact stress. Ph.D. Thesis, Linz University, Linz, Austria, 2001. [Google Scholar]
- Hacquin, A. Modélisation Thermomécanique Tridimensionnelle du Laminage: Couplage Bande—Cylindres (3D Thermomechanical Modelling of Rolling Processes: Coupling Strip and Rolls). Ph.D. Dissertation, MINES ParisTech, Paris, France, 1996. [Google Scholar]
- Hacquin, A.; Montmitonnet, P.; Guillerault, J.P. A steady state thermo-elastoviscoplastic finite element model of rolling with coupled thermo-elastic roll deformation. J. Mat. Proc. Tech. 1996, 60, 109–116. [Google Scholar] [CrossRef]
- Hacquin, A.; Montmitonnet, P.; Guillerault, J.P. A 3D semi-analytical model of rolling stand deformation with finite element validation. Eur. J. Mech. A (Solids) 1998, 17, 79–106. [Google Scholar] [CrossRef]
- Van der Lugt, J. A FEM for the Simulation of Thermomechanical Contact Problems in Forming Processes. Ph.D. Dissertation, Twente University, The Netherlands, 1988. [Google Scholar]
- Li, G.J.; Kobayashi, S. Rigid plastic finite element analysis of plane strain rolling. Trans. ASME J. Eng. Mat. Technol. 1982, 104, 55–64. [Google Scholar] [CrossRef]
- Ogawa, S.; Hamauzu, S.; Matsumoto, H.; Kawanami, T. Prediction of flatness of fine gauge strip rolled by 12-high Cluster Mill. ISIJ Int. 1991, 31, 599–606. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shigaki, Y.; Nakhoul, R.; Montmitonnet, P. Numerical Treatments of Slipping/No-Slip Zones in Cold Rolling of Thin Sheets with Heavy Roll Deformation. Lubricants 2015, 3, 113-131. https://doi.org/10.3390/lubricants3020113
Shigaki Y, Nakhoul R, Montmitonnet P. Numerical Treatments of Slipping/No-Slip Zones in Cold Rolling of Thin Sheets with Heavy Roll Deformation. Lubricants. 2015; 3(2):113-131. https://doi.org/10.3390/lubricants3020113
Chicago/Turabian StyleShigaki, Yukio, Rebecca Nakhoul, and Pierre Montmitonnet. 2015. "Numerical Treatments of Slipping/No-Slip Zones in Cold Rolling of Thin Sheets with Heavy Roll Deformation" Lubricants 3, no. 2: 113-131. https://doi.org/10.3390/lubricants3020113
APA StyleShigaki, Y., Nakhoul, R., & Montmitonnet, P. (2015). Numerical Treatments of Slipping/No-Slip Zones in Cold Rolling of Thin Sheets with Heavy Roll Deformation. Lubricants, 3(2), 113-131. https://doi.org/10.3390/lubricants3020113