On the Characteristics of Misaligned Journal Bearings
Abstract
:1. Introduction
- Asymmetric bearing loading;
- Elastic deflection of the shaft, under an imposed under load or its own weight;
- Thermal distortion of the shaft;
- Distortions caused by bearing housing supports;
- Manufacturing tolerances (due to inaccurate machining, casting and forging); and
- Errors due to installation and assembly defects.
1.1. Types of Misalignment and Coupling Effects
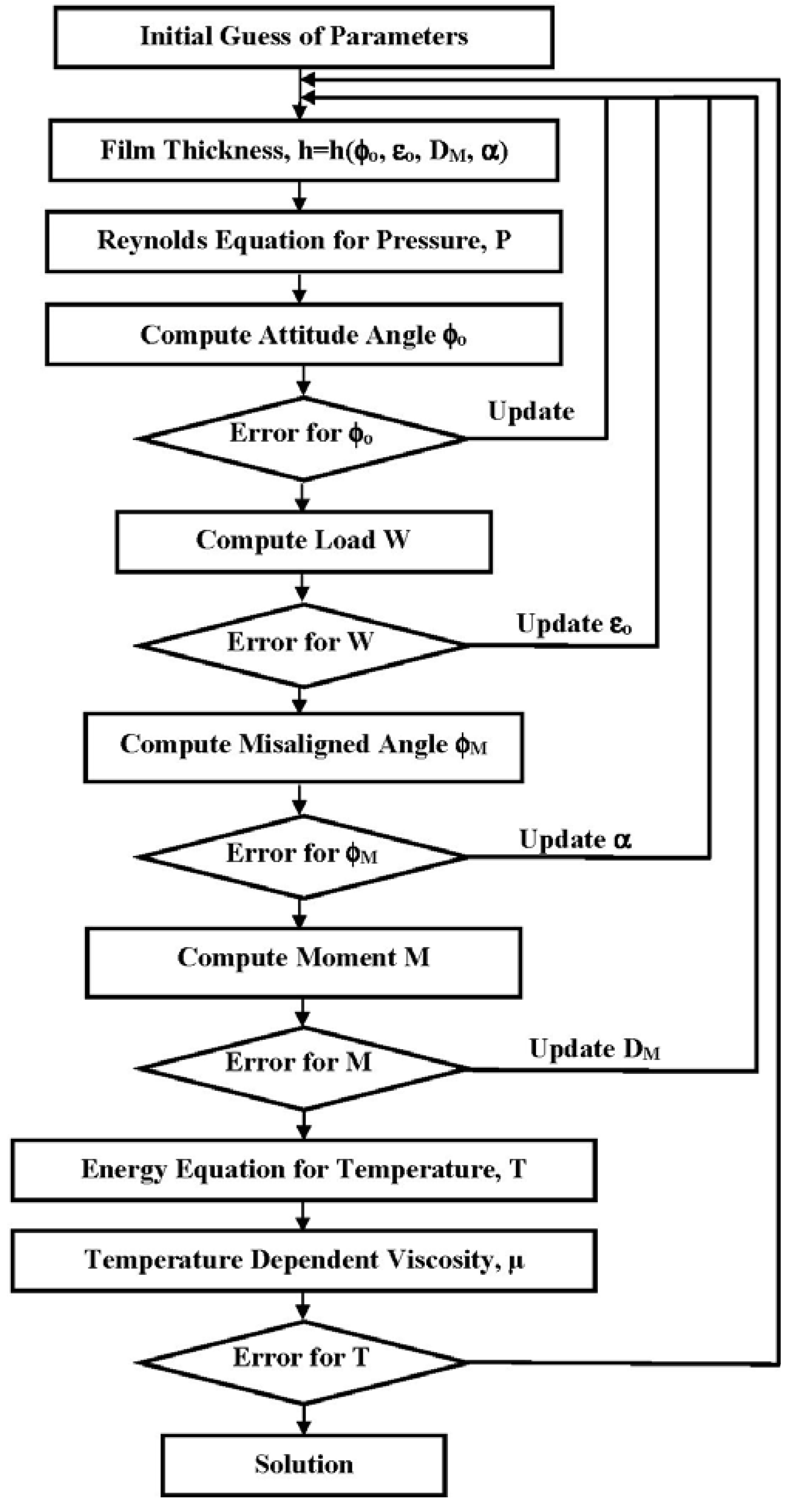
1.2. Film Thickness
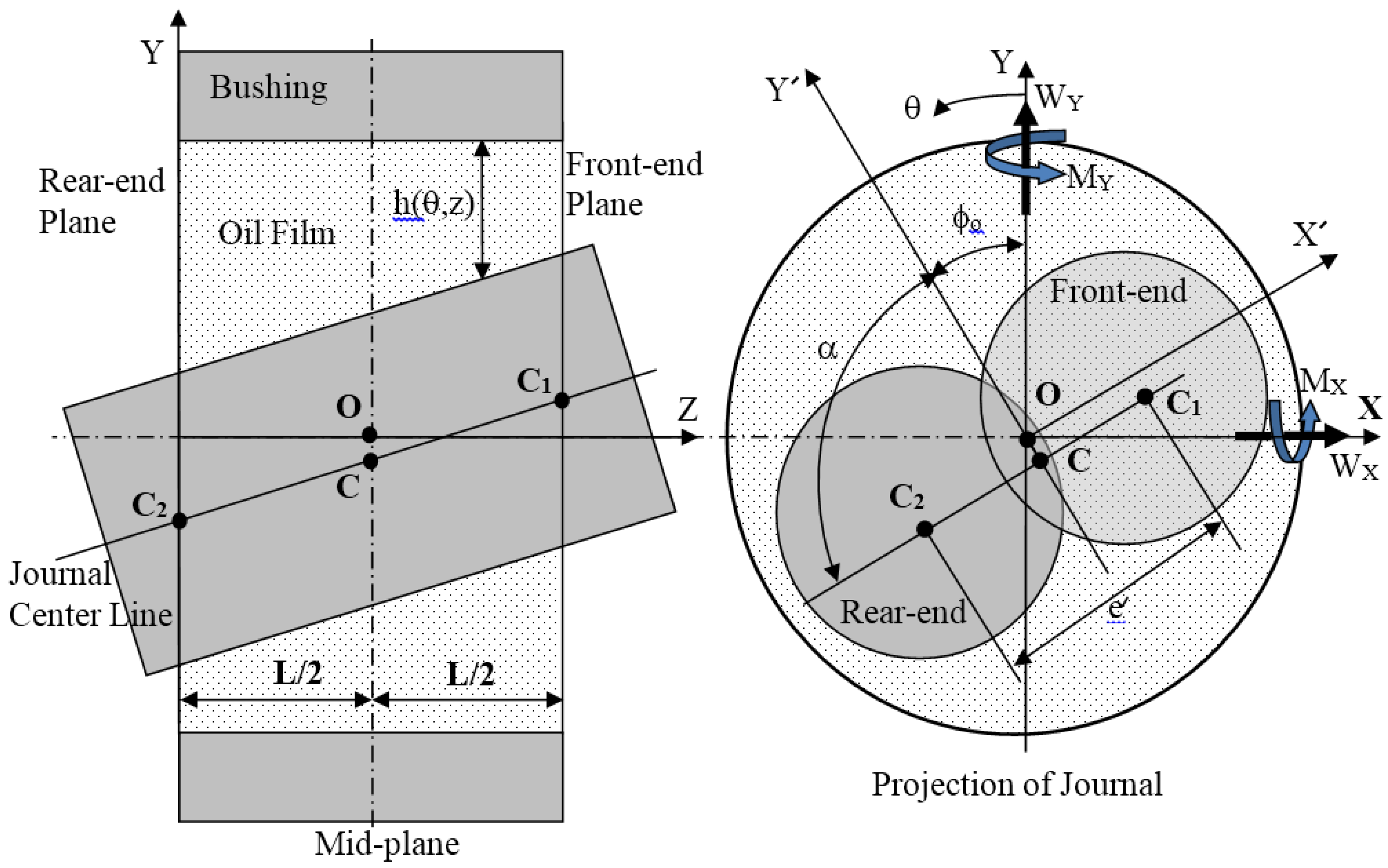
1.3. Pressure Field
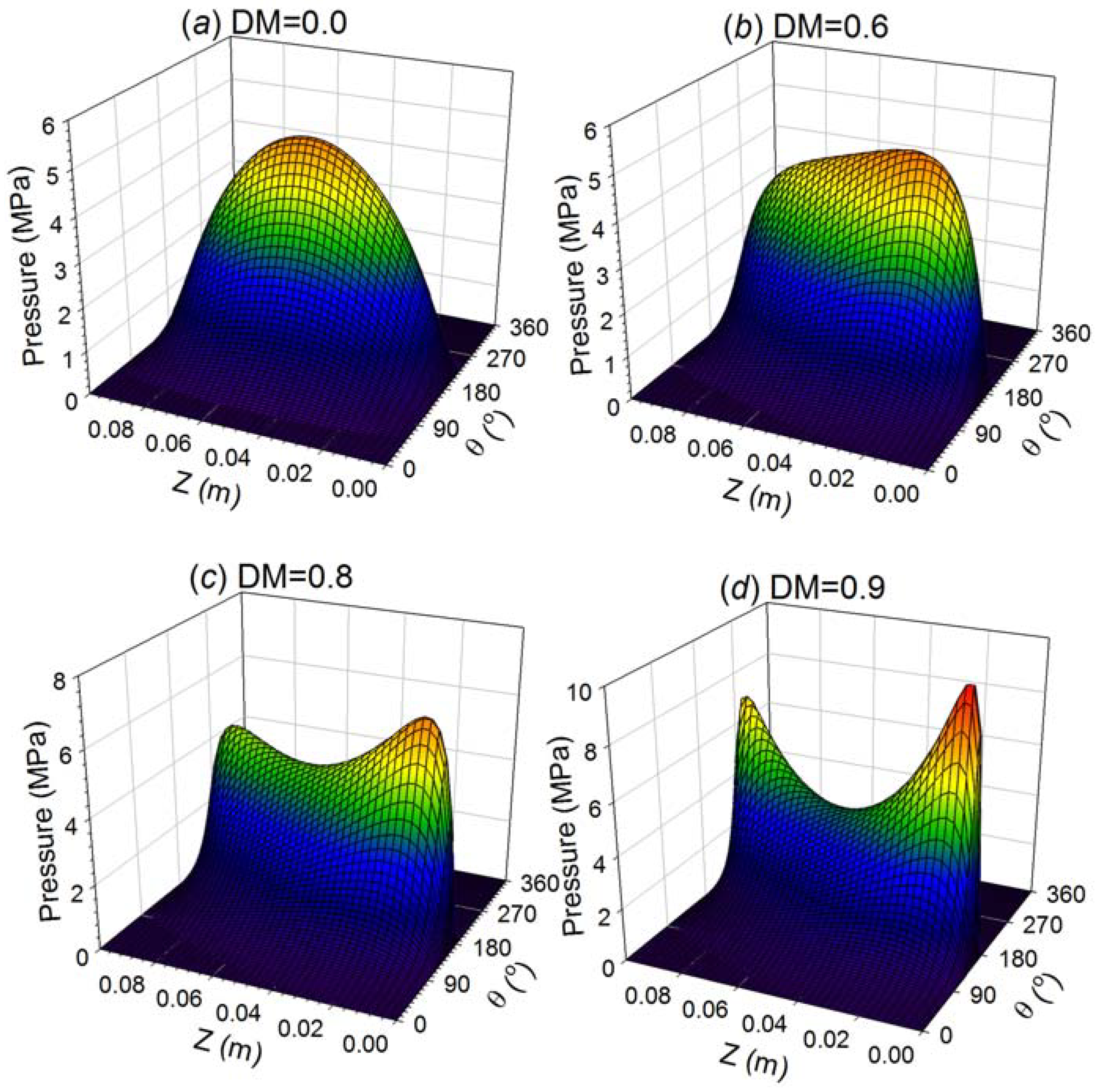
1.4. Temperature Field
2. Literature Review
2.1. General Effects
2.2. Early Discoveries
2.3. Application to Different Types of Bearings
2.4. Consideration of Cavitation Effects
2.5. Dynamic Characteristics
2.6. Experimental Tests
2.7. Surface Roughness
2.8. Structural Effects
2.9. Thermal Effects
2.10. Thermally-Induced Bearing Failure
2.11. Tilting-Pad Journal Bearings
2.13. Turbulent Effects
2.14. Dynamic Loading and Engine Bearings
2.15. Wear Effects
2.16. Hydrostatic Bearings
2.17. Porosity Effects
2.18. Variable Axial Profile
| Bearing Category | References |
|---|---|
| Adiabatic Solution | [46,83,97] |
| THD/TEHD Analysis | [4,12,15,19,20,23,25,27,28,29,31,51,72,82,84,85,86,104,106] |
| Transient Condition | [27,28,76,86,107,108,109,110,111] |
| Roughness | [69,70,71,72,73,117] |
| Turbulence | [101,102,103,104,105,106,120,121] |
| Non-Newtonian | [14,15,53,79,81,96,97,98,99,100,104] |
| Gas Bearing | [37,38,40,49] |
| Wear or Defect | [25,105,113,116,118,119,120] |
| Dynamic Characteristics | [52,53,54,58,77,98,106,122] |
| Experiment | [16,17,18,49,51,55,56,57,59,60,61,75,76,115] |
| Three-Lobe Journal Bearing | [59] |
| Tilting-Pad Journal Bearing | [20,27,28] |
| Hole-Entry Hybrid Journal Bearing | [71,105,120] |
| Axial and Spiral Oil Inlet | [45,46] |
| Circumferential Groove | [47,108] |
| Axial Groove | [1,22,25,29,44,50,51,56,77,104,111,125] |
3. Conclusions
Acknowledgments
Author contributions
Conflicts of Interest
References
- Vijayaraghavan, D.; Keith, T.G. Effect of Cavitation on the Performance of a Grooved Misaligned Journal Bearing. Wear 1989, 134, 377–397. [Google Scholar] [CrossRef]
- Elod, H.G. A Cavitation Algorithm. ASME J. Lubr. Tech. 1981, 103, 350–354. [Google Scholar] [CrossRef]
- Elrod, H.G.; Adams, M. A Computer Program for Cavitation and Starvation Problems. In Proceedings of the 1st Leeds-Lyon Symposium on Cavitation and Related Phenomena in Lubrication, Leeds, UK, September 1974; pp. 37–41.
- Booser, E.R.; Ryna, F.D. Linkinhoker, Maximum Temperature for Hydrodynamic Bearings under Steady Load. Lubr. Eng. 1970, 26, 226–235. [Google Scholar]
- Khonsari, M.M.; Booser, E.R. Applied Tribology: Bearing Design and Lubrication, 2nd ed.; John Wiley & Sons: West Sussex, UK, 2008. [Google Scholar]
- Khonsari, M.M.; Wang, S.H. On the Maximum Temperature in Double-Layered Journal Bearings. ASME J. Tribol. 1991, 113, 464–469. [Google Scholar] [CrossRef]
- Khonsari, M.M.; Wang, S. On the Role of Particulate Contamination in Scuffing Failure. Wear 1990, 137, 51–62. [Google Scholar] [CrossRef]
- Khonsari, M.M.; Jang, J.Y.; Fillon, M. On the Generalization of Thermohydrodynamic Analyses for Journal Bearings. ASME J. Tribol. 1996, 118, 571–579. [Google Scholar] [CrossRef]
- Jang, J.Y.; Khonsari, M.M. Design of Bearings on the Basis of Thermohydrodynamic Analysis. J. Eng. Tribol. 2004, 218, 355–363. [Google Scholar]
- Dyson, A.; Wilson, A.R. Film Thickness in Elastohydrodynamic Lubrication by Silicone Fluids. J. Multi Body Dyn. 1966, 180, 97–105. [Google Scholar]
- Khonsari, M.M.; Beaman, J.J. Thermohydrodynamic Analysis of Laminar Incompressible Journal Bearing. ASLE Trans. 1986, 29, 141–150. [Google Scholar] [CrossRef]
- Khonsari, M.M.; Wang, S.H. On the Fluid-Solid Interaction in Reference to Thermoelastohydrodynamic Analysis of Journal Bearings. ASME J. Tribol. 1991, 113, 398–404. [Google Scholar] [CrossRef]
- Keogh, P.; Gomiciaga, R.; Khonsari, M.M. CFD Based Design Techniques for Thermal Prediction in a Generic Two-axial Groove Hydrodynamic Journal Bearing. ASME J. Tribol. 1997, 119, 426–436. [Google Scholar]
- Jang, J.Y.; Khonsari, M.M. Performance Analysis of Grease-Lubricated Journal Bearings Including Thermal Effects. ASME J. Tribol. 1997, 119, 859–868. [Google Scholar] [CrossRef]
- Jang, J.Y.; Khonsari, M.M. Thermohydrodynamic Analysis of Journal Bearings Lubricated with Multigrade Oils. Comput. Model. Eng. Sci. 2002, 3, 455–464. [Google Scholar]
- Dowson, D.; Hudson, J.D.; Hunter, B.; March, C.N. An Experimental Investigation of the Thermal Equilibrium of Steadily Loaded Journal Bearings. Proc. Inst. Mech. Eng. 1966, 131, 70–80. [Google Scholar]
- Mitsui, J. A Study of Thermohydrodynamic Lubrication in a Circular Journal Bearing. Tribol. Int. 1987, 20, 331–341. [Google Scholar] [CrossRef]
- Ferron, J.; Frene, J.; Boncompain, R. A Study of Thermohydrodynamic Performance of a Plain Journal Bearing Comparison between Theory and Experiments. ASME J. Tribol. 1983, 105, 422–428. [Google Scholar]
- Jang, J.Y.; Khonsari, M.M. Thermohydrodynamic Design Charts for Slider Bearings. ASME J. Tribol. 1997, 119, 733–740. [Google Scholar] [CrossRef]
- Fillon, M.; Khonsari, M.M. Thermohydrodynamic Design Charts for Tilting-Pad Journal Bearings. ASME J. Tribol. 1996, 118, 232–238. [Google Scholar] [CrossRef]
- Allmaier, H.; Priestner, C.; Reich, F.M.; Priebsch, H.H.; Novotny-Farkas, F. Predicting Friction Reliably and Accurately in Journal Bearings—Extending the EHD Simulation Model to TEHD. Tribol. Int. 2013, 58, 20–28. [Google Scholar] [CrossRef]
- Jang, J.Y.; Khonsari, M.M. On the Behavior of Misaligned Journal Bearings Based on Mass-Conservative Thermohydrodynamic Analysis. ASME J. Tribol. 2010, 132, 011702. [Google Scholar] [CrossRef]
- Medwell, J.O.; Gethin, D.T. Synthesis of Thermal Effects in Misaligned Hydrodynamic Journal Bearings. Int. J. Num. Method Fluids 1986, 6, 445–458. [Google Scholar] [CrossRef]
- Boncompain, R.; Fillon, M.; Frene, J. Analysis of Thermal Effects in Hydrodynamic Bearings. ASME J. Tribol. 1986, 108, 219–224. [Google Scholar] [CrossRef]
- Bouyer, J.; Fillon, M. Improvement of the THD Performance of a Misaligned Plain Journal Bearing. ASME J. Tribol. 2003, 125, 334–342. [Google Scholar] [CrossRef]
- Kucinschi, B.; Fillon, M.; Pascovici, M.; Frene, J. A Transient Thermoelastohydrodynamic Study of Steadily Loaded Plain Journal Bearings using Finite Element Method Analysis. ASME J. Tribol. 2000, 122, 219–226. [Google Scholar] [CrossRef]
- Monmousseau, P.; Fillon, M. Analysis of Static and Dynamic Misaligned Tilting-Pad Journal Bearings. Proc. Inst. Mech. Eng. 1999, 213, 253–261. [Google Scholar] [CrossRef]
- El-Butch, A.M.; Ashour, N.M. Transient Analysis of Misaligned Elastic Tilting-Pad Journal Bearing. Tribol. Int. 2005, 38, 41–48. [Google Scholar] [CrossRef]
- Thomsen, K.; Klit, P. Improvement of Journal Bearing Operation at Heavy Misalignment Using Bearing Flexibility and Compliant Liners. J. Eng. Tribol. 2012, 226, 651–660. [Google Scholar]
- Tieu, A.K; Qiu, Z.L. Stability of Finite Journal Bearings—From Linear and Nonlinear Bearing Forces. STLE Tribol. Trans. 1995, 38, 627–635. [Google Scholar] [CrossRef]
- Banwait, S.S.; Chandrawat, H.N.; Adithan, M. Thermohydrodynamic Analysis of Misaligned Plain Journal Bearing. In Proceedings of the 1st Asia International Conference on Tribology, Beijing, China, 12–15 October, 1998; pp. 35–40.
- Safar, Z.S. Energy Loss due to Misalignment of the Journal Bearings. Tribol. Int. 1984, 17, 107–109. [Google Scholar] [CrossRef]
- McKee, S.A.; McKee, T.R. Pressure Distribution in Oil Films of Journal Bearings. Trans. ASME 1932, 5, 149–165. [Google Scholar]
- Cowlin, F.J. The Lubrication of Steam-Turbine Driven Electric Generator. J. Eng. Tribol. 1940, 143, 83–100. [Google Scholar]
- Pigott, R.J.S. Bearings and Lubrication—Bearing Troubles Traceable to Design Can Be Avoided by Engineering Study. Mech. Eng. 1942, 64, 259–269. [Google Scholar]
- DuBois, G.B.; Mabie, H.H.; Ocvirk, F.W. Experimental Investigation of Oil Film Pressure Distribution for Misaligned Plain Bearings. National Advisory Committee for Aeronautics: Kitty Hawk, NC, USA, 1951. [Google Scholar]
- DuBois, G.B.; Ocvirk, F.W.; Wehe, R.L. Properties of Misaligned Journal Bearings. ASME J. Basic Eng. 1957, 79, 1205–1212. [Google Scholar]
- Ausman, J.S. Torque produced by Misalignment of Hydrodynamic Gas-Lubricated Journal Bearings. ASME J. Fluids Eng. 1960, 82, 335–340. [Google Scholar]
- Galletti-Manacorda, L.; Capriz, G. Torque Produced by Misalignment in Short Lubricated Bearings. ASME J. Fluids Eng. 1965, 87, 847–849. [Google Scholar]
- Rice, J.R. Misalignment Torques of Hydrodynamic Gas-Lubricated Journal Bearings. ASME J. Fluids Eng. 1965, 87, 193–198. [Google Scholar]
- Smalley, A.J.; McCallion, H. The Effect of Journal Misalignment on the Performance of a Journal Bearing under Steady Running Conditions. Proc. Inst. Mech. Eng. 1966, 181, 45–54. [Google Scholar]
- Ocvirk, F.W. Measured Oil Film Distribution in Misaligned Plain Bearings. J. Lubr. Eng. 1954, 10, 262–265. [Google Scholar]
- Stockley, J.R.; Donaldson, R.R. Misalignment Effects in 180° Partial Journal Bearings. ASLE Trans. 1969, 12, 216–226. [Google Scholar] [CrossRef]
- Pinkus, O.; Bupara, S.S. Analysis of Misaligned Grooved Journal Bearings. ASME J. Tribol. 1979, 101, 503–509. [Google Scholar]
- Mokhtar, M.O.A.; Rahman, M.A.A.; Safar, Z.S. An Analysis of Misaligned Journal Bearings with Axial and Spiral Feedings. Wear 1983, 85, 331–337. [Google Scholar] [CrossRef]
- Safar, Z.S.; Mokhtar, M.O.A.; Peekent, H.J. Thermal Characteristics of Misaligned Finite Journal Bearings. Tribol. Int. 1985, 18, 13–16. [Google Scholar] [CrossRef]
- Ikeuchi, K.; Katsuse, S.; Hamamura, K.; Mori, H. Effects of Misalignment in Full Journal Bearing with Circumferential Oil Groove. In Proceedings of the JSLE International Tribology Conference, Tokyo, Japan, 8–10 July, 1985; pp. 67–72.
- Wang, Y.; Wang, Q.J.; Lin, C. A Mixed-EHL Analysis of Effects of Misalignment and Elastic Deformations on the Performance of a Coupled Journal-Thrust System. Tribol. Int. 2006, 39, 281–289. [Google Scholar] [CrossRef]
- Howard, S.A. Misalignment in Gas Foil Journal Bearings: An Experimental Study. ASME J. Eng. Gas Turb. Power 2009, 131. [Google Scholar] [CrossRef]
- Vijayaraghavan, D.; Keith, T.G. Analysis of a Finite Grooved Misaligned Journal Bearing Considering Cavitation and Starvation Effects. ASME J. Tribol. 1990, 112, 60–67. [Google Scholar] [CrossRef]
- Pierre, I.; Bouyer, J.; Fillon, M. Thermohydrodynamic Behavior of Misaligned Plain Journal Bearings: Theoretical and Experimental Approaches. STLE Tribol. Trans. 2004, 47, 594–604. [Google Scholar] [CrossRef]
- Singh, D.V.; Sinhasan, R. Performance Characteristics of an Ungrooved Big-End Bearing with Misalignment. STLE Tribol. Trans. 1989, 32, 234–238. [Google Scholar] [CrossRef]
- Choy, F.K.; Braun, M.J.; Hu, Y. Analytical and Numerical Study of a Misaligned Cavitating Hydrodynamic Cryogenic Journal Bearing. Tribol. Int. 1992, 25, 3–15. [Google Scholar] [CrossRef]
- Nikolakopoulos, P.G.; Papadopoulos, C.A. Non-Linearities in Misaligned Journal Bearings. Tribol. Int. 1994, 27, 243–257. [Google Scholar] [CrossRef]
- Asanabe, S.; Akahoshi, M.; Asai, R. Theoretical and Experimental Investigation of Misaligned Journal Bearing Performance. Tribol. Conv. Inst. Mech. Eng. 1972, 1–8. [Google Scholar]
- Nicolas, D.; Frene, J. Tilting Torque Permissible in Plain Bearings. Theory, Experimental Results and Application to Machine Design. In Proceedings of the First European Tribology Congress, London, UK, 25–27 September, 1973; pp. 353–360.
- Tieu, A.K.; Qiu, Z.L. Experimental Study of Freely Alignable Journal Bearings—Part I: Static Characteristics. ASME J. Tribol. 1996, 118, 498–502. [Google Scholar] [CrossRef]
- Qiu, Z.L.; Tieu, A.K. Experimental Study of Freely Alignable Journal Bearings—Part II: Dynamic Characteristics. ASME J. Tribol. 1996, 118, 503–508. [Google Scholar] [CrossRef]
- Arumugam, P.; Swarnamani, S.; Prabhu, B.S. Effects of Journal Misalignment on the Performance Characteristics of Three-lobe Bearings. Wear 1997, 206, 122–129. [Google Scholar] [CrossRef]
- Huber, M.; Strzelecki, S.; Steinhilper, W. Theoretical and Experimental Determination of the Performances of Misaligned and Statically Loaded Cylindrical Journal Bearings. Austrib Congress 1998, 243–248. [Google Scholar]
- Bouyer, J.; Fillon, M. An Experimental Analysis of Misalignment Effects on Hydrodynamic Plain Journal Bearing Performances. ASME J. Tribol. 2002, 124, 313–319. [Google Scholar] [CrossRef]
- Christensen, H. Stochastic Models for Hydrodynamic Lubrication of Rough Surfaces. Proc. Inst. Mech. Eng. 1969, 184, 1013–1026. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. ASME J. Tribol. 1978, 100, 12–17. [Google Scholar]
- Patir, N.; Cheng, H.S. Application of Average Flow Model to Lubrication between Rough Sliding Surfaces. ASME J. Tribol. 1979, 100, 12–17. [Google Scholar]
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally Flat Surfaces. Proc. R. Soc. Lond. 1966, A295, 300–319. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Tripp, J.H. The Contact of Two Nominally Flat Rough Surfaces. Proc. Inst. Mech. Eng. 1970–1971, 185, 625–633. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. Elastic-Plastic Contact Analysis of a Sphere and a Rigid Flat. ASME J. Appl. Mech. 2002, 69, 657–662. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. A Finite Element Based Elastic-Plastic Model for the Contact of Rough Surfaces. Tribol. Trans. 2003, 46, 383–390. [Google Scholar] [CrossRef]
- Abdel-Latif, L.A.; Mokhtar, M.O.A. Misalignment Effects on Hydrodynamically Lubricated Journal Bearings with Rough Surfaces. Wear 1988, 128, 225–237. [Google Scholar] [CrossRef]
- Guha, S.K. Analysis of Steady-state Characteristics of Misaligned Hydrodynamic Journal Bearings with Isotropic Roughness Effect. Tribol. Int. 2000, 33, 1–12. [Google Scholar] [CrossRef]
- Sharma, S.C.; Jain, S.C.; Nagaraju, T. Combined Influence of Journal Misalignment and Surface Roughness on the Performance of an Orifice Compensated Non-Recessed Hybrid Journal Bearing. STLE Tribol. Trans. 2002, 45, 457–463. [Google Scholar] [CrossRef]
- Sun, J.; Deng, M.; Fu, Y.; Gui, C. Thermohydrodynamic Lubrication Analysis of Misaligned Plain Journal Bearing with Rough Surface. ASME J. Tribol. 2010, 132. [Google Scholar] [CrossRef]
- Sun, J.; Zhu, X.; Zhang, L.; Wang, X.; Wang, C.; Wang, H.; Zhao, X. Effect of Surface Roughness, Viscosity-Pressure Relationship and Elastic Deformation on Lubrication Performance of Misaligned Journal Bearings. Ind. Lubr. Tribol. 2014, 66, 337–345. [Google Scholar] [CrossRef]
- Sun, J.; Gui, C. Hydrodynamic Lubrication Analysis of Journal Bearing Considering Misalignment Caused by Shaft Deformation. Tribol. Int. 2004, 37, 841–848. [Google Scholar] [CrossRef]
- Sun, J.; Gui, C.; Li, Z. An Experimental Study of Journal Bearing Lubrication Effected by Journal Misalignment as a Result of Shaft Deformation under Load. ASME J. Tribol. 2005, 127, 813–819. [Google Scholar] [CrossRef]
- Sun, J.; Gui, C.; Li, Z.; Li, Z. Influence of Journal Misalignment Caused by Shaft Deformation under Rotational Load on Performance of Journal Bearing. J. Eng. Tribol. 2005, 219, 275–283. [Google Scholar]
- Ebrat, O.; Mourelatos, Z.P.; Vlahopoulos, N.; Vaidyanathan, K. Calculation of Journal Bearing Dynamic Characteristics Including Journal Misalignment and Bearing Structural Deformation. STLE Tribol. Trans. 2004, 47, 94–102. [Google Scholar] [CrossRef]
- Allmaier, H.; Priestner, C.; Reich, F.M.; Priebsch, H.H.; Forstner, C.; Novotny-Farkas, F. Predicting Friction Reliably and Accurately in Journal Bearings—The Importance of Extensive Oil-Models. Tribol. Int. 2012, 48, 93–101. [Google Scholar] [CrossRef]
- Jang, J.Y.; Khonsari, M.M.; Bair, S. On the Elastohydrodynamic Analysis of Shear-Thinning Fluids. Proc. R. Soc. Lond. Ser. A 2007, 463, 3271–3290. [Google Scholar] [CrossRef]
- Kumar, P.; Khonsari, M.M. Combined Effects of Shear Thinning and Viscous Heating on EHL Characteristics of Rolling/Sliding Line Contacts. ASME J. Tribol. 2008, 130. [Google Scholar] [CrossRef]
- Kumar, P.; Khonsari, M.M.; Bair, S. Full EHL Simulations using the Actual Ree-Eyring Model for Shear Thinning Lubricants. ASME J. Tribol. 2009, 131. [Google Scholar] [CrossRef]
- Kumar, P.; Khonsari, M.M. Traction in EHL Line Contacts Using Free Volume Pressure-Viscosity Relationship with Thermal and Shear Thinning Effects. ASME J. Tribol. 2009, 131. [Google Scholar] [CrossRef]
- Mokhtar, M.O.A.; Safar, Z.S.; Abd-Ei-Rahman, M.A.M. An Adiabatic Solution of Misalignment Journal Bearings. ASME J. Tribol. 1985, 107, 263–267. [Google Scholar] [CrossRef]
- Pierre, I.; Fillon, M.; Bouyer, J. Thermohydrodynamic Study of Misaligned Plain Journal Bearings—Comparison between Experimental Data and Theoretical Results. Int. J. Appl. Mech. Eng. 2002, 7, 949–960. [Google Scholar]
- He, Z.P.; Xie, W.; Zhang, J.H.; Xie, W.S.; Li, Z.Y.; Zhang, G.C. Misalignment Analysis of Journal Bearing Influenced by Asymmetric Deflection, Based on a Simple Stepped Shaft Model. J. Zheijang Univ. Sci. A Appl. Phys. Eng. 2012, 13, 647–664. [Google Scholar] [CrossRef]
- Khonsari, M.; Kim, H. On Thermally Induced Seizure in Journal Bearings. ASME J. Tribol. 1989, 111, 661–667. [Google Scholar] [CrossRef]
- Wang, Q. Seizure Failure of Journal-Bearing Conformal Contacts. Wear 1997, 210, 8–16. [Google Scholar] [CrossRef]
- Dufrane, K.F.; Kannel, J.W. Thermally Induced Seizure of Journal Bearings. ASME J. Tribol. 1989, 111, 288–292. [Google Scholar] [CrossRef]
- Hazlett, T.L.; Khonsari, M.M. Finite Element Model of Journal Bearings Undergoing Rapid Thermally Induced Seizure. Tribol. Int. 1992, 25, 177–182. [Google Scholar] [CrossRef]
- Hazlett, T.L.; Khonsari, M.M. Thermoelastic Behaviors of Journal Bearings Undergoing Seizure. Tribol. Int. 1992, 25, 183–187. [Google Scholar] [CrossRef]
- Krishivasan, R.; Khonsari, M.M. Thermally Induced Seizure in Journal Bearings during Start up and Transient Flow Disturbance. ASME J. Tribol. 2003, 125, 833–841. [Google Scholar] [CrossRef]
- Krishivasan, R.; Khonsari, M.M. Thermomechanical Analysis of Oscillatory Pin-Bushing Performance. Rev. Eur. Élém. Finis 2005, 14, 255–269. [Google Scholar] [CrossRef]
- Pascovici, M.; Khonsari, M.M.; Jang, J.Y. On the Modeling of a Thermomechanical Seizure. ASME J. Tribol. 1995, 117, 744–747. [Google Scholar] [CrossRef]
- Jang, J.Y.; Khonsari, M.M.; Pascovici, M. Thermohydrodynamic Seizure: Experimental and Theoretical Evaluation. ASME J. Tribol. 1998, 120, 8–15. [Google Scholar] [CrossRef]
- Jang, J.Y.; Khonsari, M.M.; Pascovici, M. Modeling Aspect of a Rate-controlled Seizure in an Unloaded Journal Bearing. STLE Tribol. Trans. 1998, 41, 481–488. [Google Scholar] [CrossRef]
- Buckholz, R.H.; Lin, J.F. The Effect of Journal Bearing Misalignment on Load and Cavitation for non-Newtonian Lubricants. ASME J. Tribol. 1986, 108, 645–654. [Google Scholar] [CrossRef]
- Jang, J.Y.; Chang, C.C. Adiabatic Solution for a Misaligned Journal Bearing with Non-Newtonian Lubricants. Tribol. Int. 1987, 20, 267–275. [Google Scholar] [CrossRef]
- Boucherit, H.; Lahmar, M.; Bou-Said, B. Misalignment Effects on Steady-State and Dynamic Behavior of Compliant Journal Bearings Lubricated with Couple Stress Fluids. Lubr. Sci. 2008, 20, 241–268. [Google Scholar] [CrossRef]
- Osman, T.A. Misalignment Effect on the Static Characteristics of Magnetized Journal Bearing Lubricated with Ferrofluid. Tribol. Lett. 2001, 11, 195–203. [Google Scholar] [CrossRef]
- Das, S.; Guha, S.K.; Chattopadhyay, A.K. On the Steady-State Performance of Misaligned Hydrodynamic Journal Bearings Lubricated with Micropolar Fluids. Tribol. Int. 2002, 35, 201–210. [Google Scholar] [CrossRef]
- Safar, Z.S.; Riad, M.S.M. Prediction of the Coefficient of Friction of a Misaligned Turbulent Flow Journal Bearings. Tribol. Int. 1988, 21, 15–19. [Google Scholar] [CrossRef]
- Safar, Z.S.; El-Kotb, M.M.; Mokhtar, D.M. Analysis of Misaligned Journal Bearings Operating in Turbulent Regime. ASME J. Tribol. 1989, 111, 215–219. [Google Scholar] [CrossRef]
- Shenoy, S.B.; Pai, R. Theoretical Investigations on the Performance of an Externally Adjustable Fluid-film Bearing Including Misalignment and Turbulence Effects. Tribol. Int. 2009, 42, 1088–1100. [Google Scholar] [CrossRef]
- Abass, B.A.; Sahib, M.M. Effect of Bearing Compliance on Thermo-hydrodynamic Lubrication of High Speed Misaligned Journal Bearing Lubricated with Bubbly Oil. Ind. Eng. Lett. 2013, 3, 48–60. [Google Scholar]
- Ram, N.; Sharma, S.C. Influence of Wear on the Performance of Hole-Entry Hybrid Misaligned Journal Bearing in Turbulent Regime. Ind. Lubr. Tribol. 2014, 66, 509–519. [Google Scholar] [CrossRef]
- Xu, G.; Zhou, J.; Geng, H.; Lu, M.; Yang, L.; Yu, L. Research on the Static and Dynamic Characteristics of Misaligned Journal Bearing Considering the Turbulent and Thermo-hydrodynamic Effects. J. Tribol. 2015, 137. [Google Scholar] [CrossRef]
- Goenka, P.K. Dynamically Loaded Journal Bearings: Finite Element Method Analysis. ASME J. Tribol. 1984, 106, 429–437. [Google Scholar] [CrossRef]
- Lahmar, M.; Frihi, D.; Nicolas, D. The Effect of Misalignment on Performance Characteristics of Engine Main Crankshaft Bearings. Eur. J. Mech. A 2002, 21, 703–714. [Google Scholar] [CrossRef]
- Booker, J.F. Dynamically Loaded Journal Bearings: Numerical Application of the Mobility Method. ASME J. Tribol. 1971, 93, 168–174. [Google Scholar]
- Boedo, S.; Booker, J.F. Classic Bearing Misalignment and Edge Loading: A Numerical Study of Limiting Cases. ASME J. Tribol. 2004, 126, 535–541. [Google Scholar] [CrossRef]
- Li, Q.; Liu, S.L.; Pan, X.H.; Zheng, S.Y. A New Method for Studying the 3D Transient Flow of Misaligned Journal Bearings in Flexible Rotor-Bearing System. J. Zhejiang Univ. Sci. A Appl. Phys. Eng. 2012, 13, 293–310. [Google Scholar] [CrossRef]
- Landheer, D.; Faessen, J.P.M.; de Gee, A.W.J. A Transition Diagram for Plain Journal Bearings. Tribol. Trans. 1990, 33, 418–424. [Google Scholar] [CrossRef]
- Ligterink, D.J.; de Gee, A.W.J. Measurements of Wear in Radial Journal Bearings. Tribotest J. 1996, 3, 45–54. [Google Scholar] [CrossRef]
- Lu, X.; Khonsari, M.M. On the Lift-off Speed in Journal Bearings. Tribol. Lett. 2005, 20, 299–305. [Google Scholar] [CrossRef]
- Lu, X.; Khonsari, M.M.; Gelnick, E.R.M. The Stribeck Curve: Experimental Results and Theoretical Prediction. ASME J. Tribol. 2006, 128, 789–794. [Google Scholar] [CrossRef]
- Akbarzadeh, S.; Khonsari, M.M. Prediction of Steady State Adhesive Wear in Spur Gears Using the EHL Load Sharing Concept. ASME J. Tribol. 2009, 131. [Google Scholar] [CrossRef]
- Akbarzadeh, S.; Khonsari, M.M. Performance of Spur Gears Considering Surface Roughness and Shear Thinning Lubricant. ASME J. Tribol. 2008, 130. [Google Scholar] [CrossRef]
- Priestner, C.; Allmaier, H.; Priebsch, H.H.; Forstner, C. Refined Simulation of Friction Power Loss in Crank Shaft Slider Bearings Considering Wear in the Mixed Lubrication Regime. Tribol. Int. 2012, 46, 200–207. [Google Scholar] [CrossRef]
- Nikolakopoulos, P.G.; Papadopoulos, C.A. A Study of Friction in Worn Misaligned Journal Bearings under Severe Hydrodynamic Lubrication. Tribol. Int. 2008, 41, 461–472. [Google Scholar] [CrossRef]
- Ram, N.; Sharma, S. A Study of Misaligned Hole-Entry Worn Journal Bearing Operating in Turbulent Regime. Ind. Lubr. Tribol. 2013, 65, 108–118. [Google Scholar] [CrossRef]
- Andres, L.S. The Effect of Journal Misalignment on the Operation of a Turbulent Flow Hydrostatic Bearing. ASME J. Tribol. 1993, 115, 355–363. [Google Scholar] [CrossRef]
- Jain, S.C.; Sharma, S.C.; Nagaraju, T. Misaligned Journal Effects in Liquid Hydrostatic Non-Recessed Journal Bearings. Wear 1997, 210, 67–75. [Google Scholar] [CrossRef]
- Elsharkawy, A.A. Effects of Misalignment on the Performance of Flexible Porous Journal Bearings. STLE Tribol. Trans. 2003, 46, 119–127. [Google Scholar] [CrossRef]
- Gulwadi, S.D.; Shrimpling, G. Journal Bearing Analysis in Engines Using Simulation Techniques. In Society of Automotives Engineers Technical Paper Series; Society of Automotive Engineers: Warrendale, PA, USA, 2003. [Google Scholar]
- Strzelecki, S. Operating Characteristics of Heavy Loaded Cylindrical Journal Bearing with Variable Axial Profile. Mater. Res. 2005, 8, 481–486. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, J.Y.; Khonsari, M.M. On the Characteristics of Misaligned Journal Bearings. Lubricants 2015, 3, 27-53. https://doi.org/10.3390/lubricants3010027
Jang JY, Khonsari MM. On the Characteristics of Misaligned Journal Bearings. Lubricants. 2015; 3(1):27-53. https://doi.org/10.3390/lubricants3010027
Chicago/Turabian StyleJang, Joon Young, and Michael M. Khonsari. 2015. "On the Characteristics of Misaligned Journal Bearings" Lubricants 3, no. 1: 27-53. https://doi.org/10.3390/lubricants3010027
APA StyleJang, J. Y., & Khonsari, M. M. (2015). On the Characteristics of Misaligned Journal Bearings. Lubricants, 3(1), 27-53. https://doi.org/10.3390/lubricants3010027






