Study on the Nonlinear Dynamic Behavior and Bifurcation of the Double-Rotor System Under the Coupling of Rubbing and Oil-Film Force
Abstract
1. Introduction
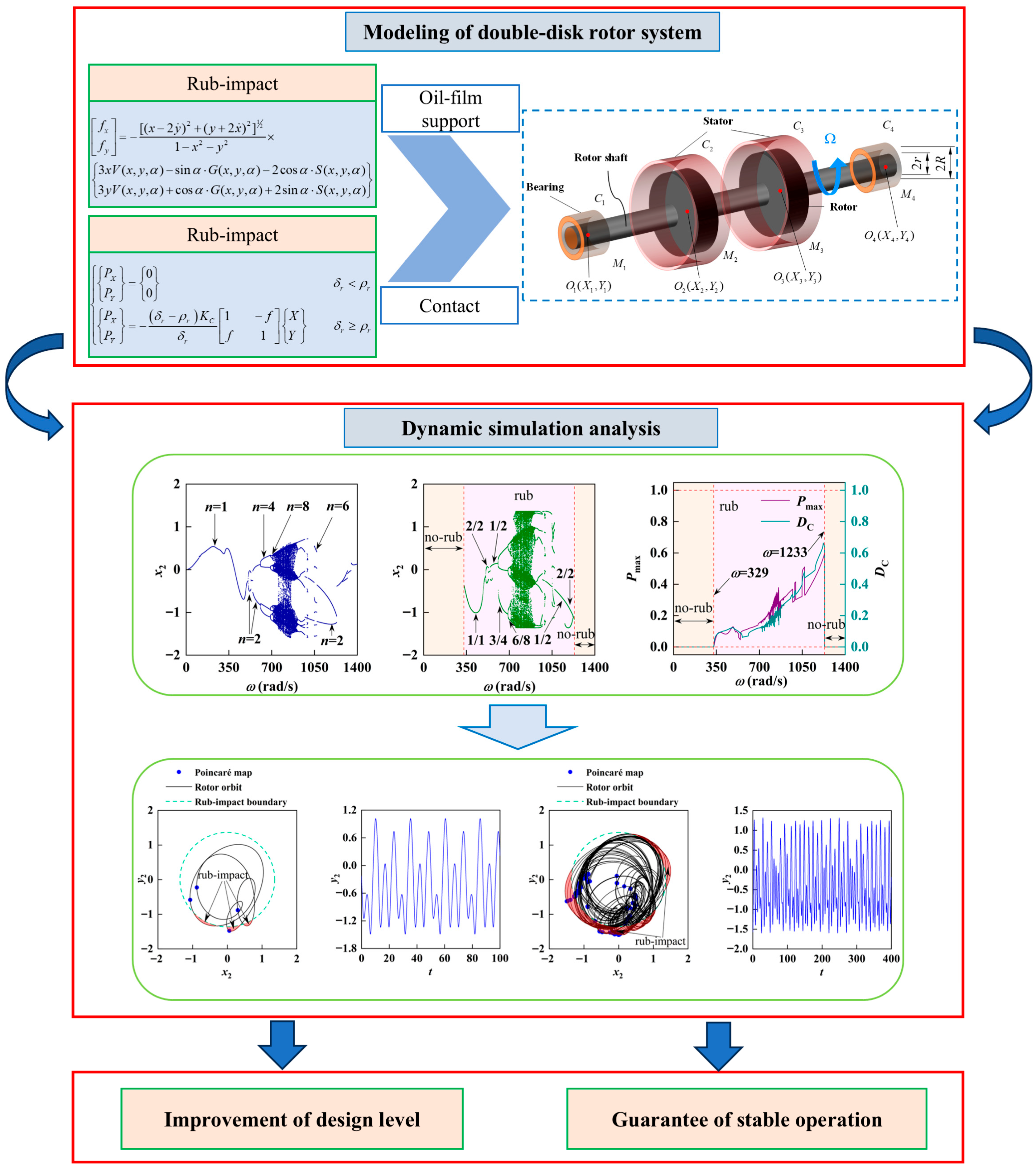
2. Mathematical Model
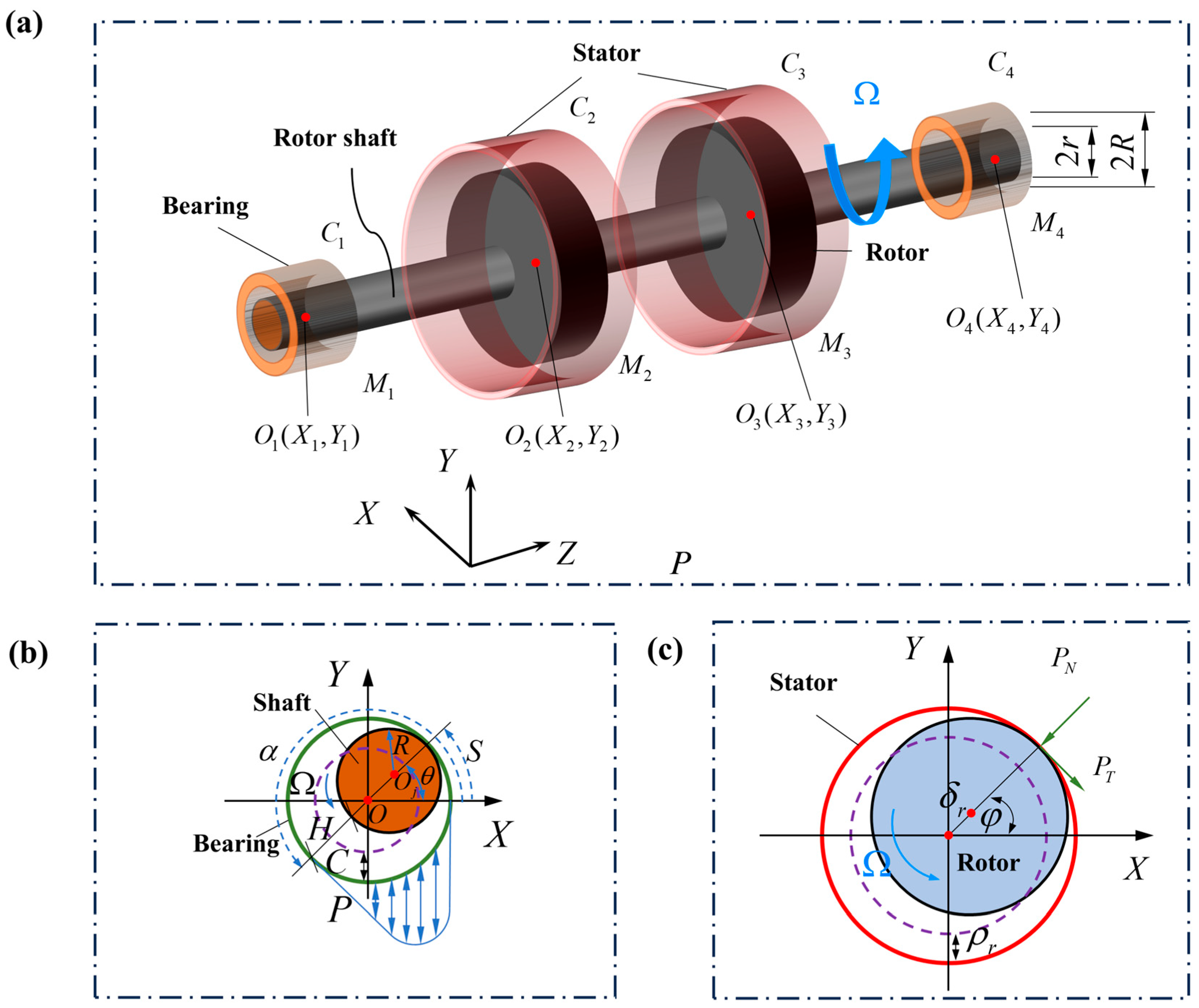
2.1. Model of Rotor-Bearing System
2.2. Model of Oil Film Forces
2.3. Rub-Impact Forces
2.4. Differential Equation of System Motion
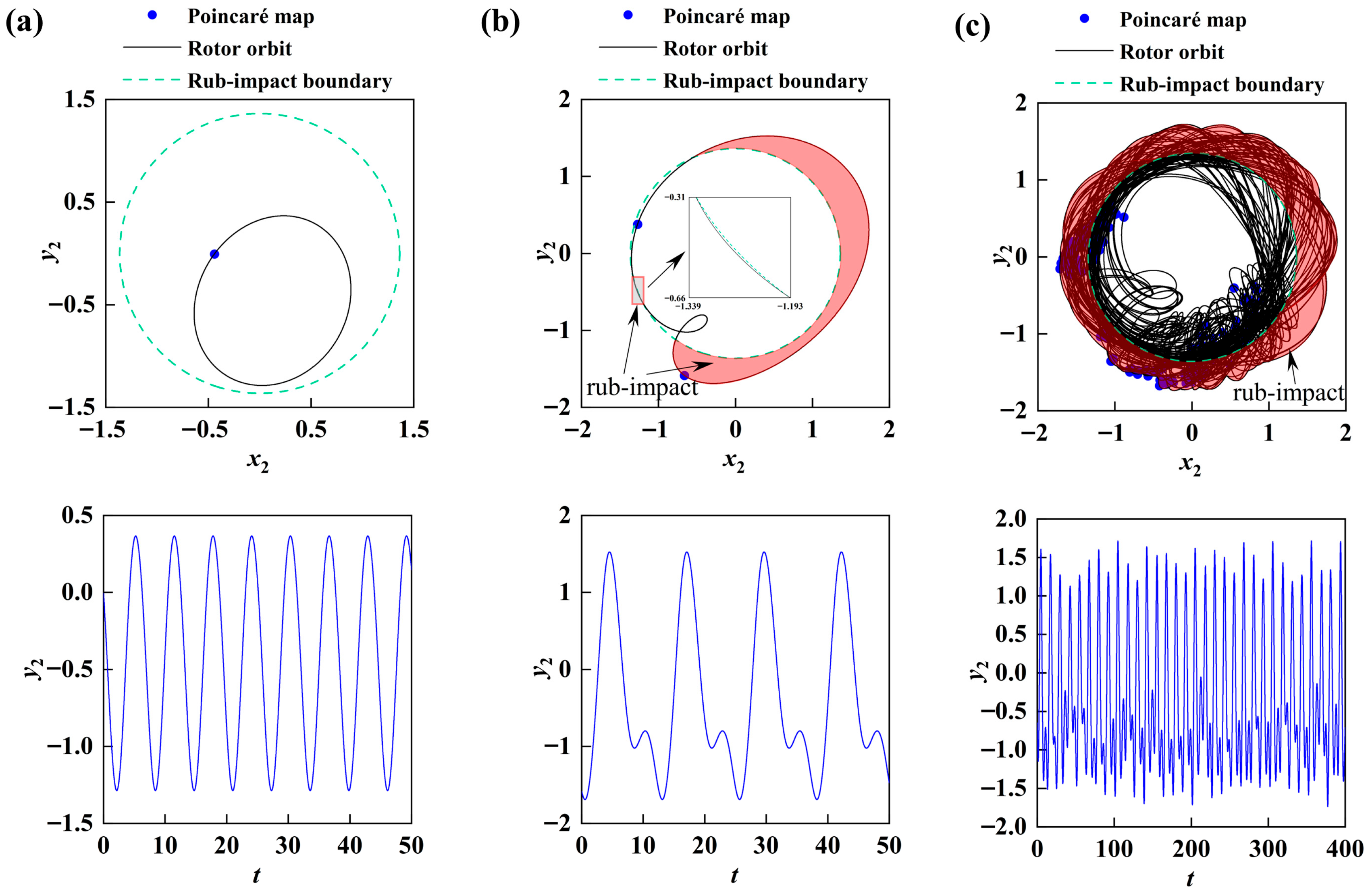
3. Defining the Poincaré Map, Rub-Impact Force, and Duty Cycle
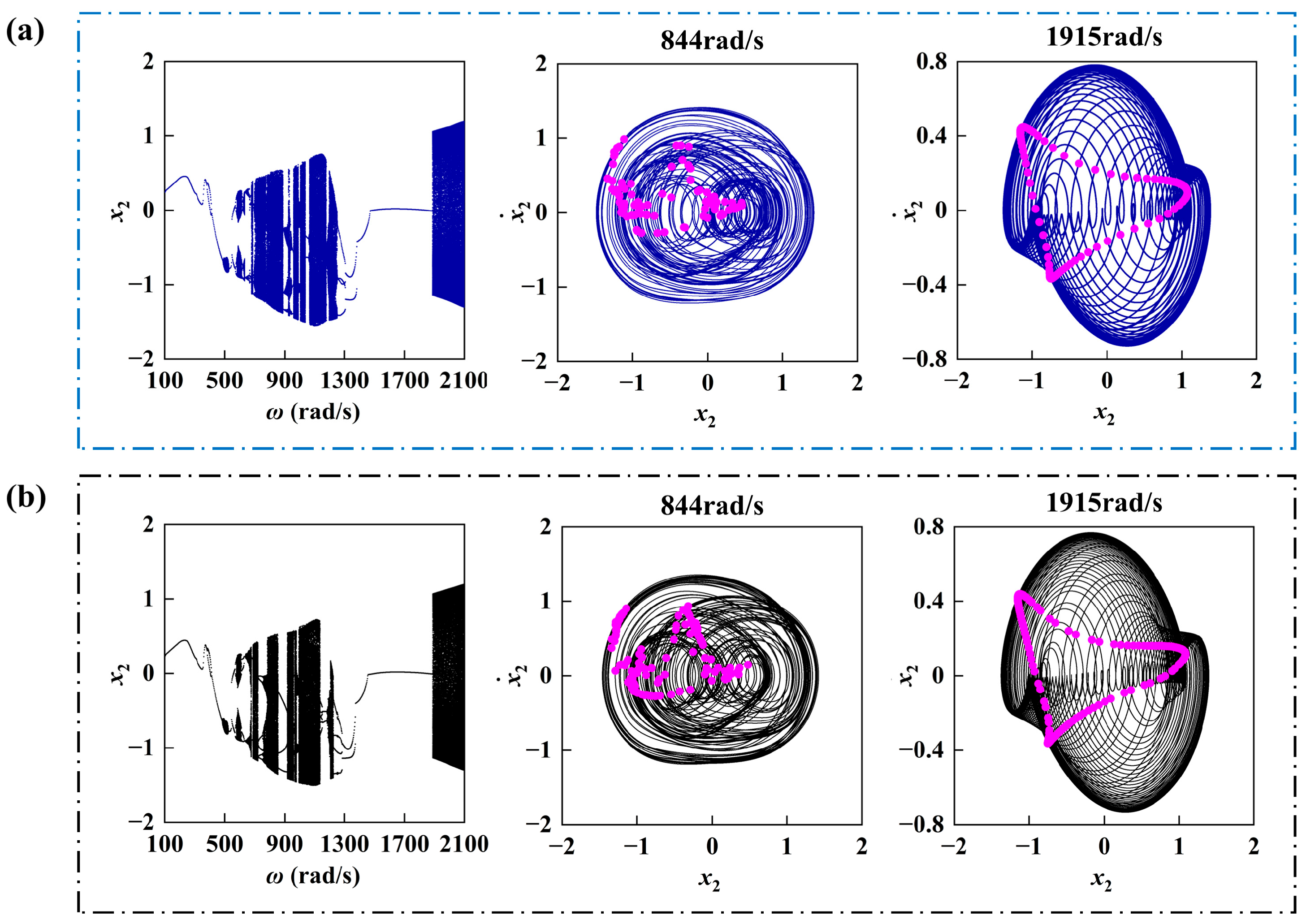
4. Model Validation
5. Nonlinear Dynamic Analysis
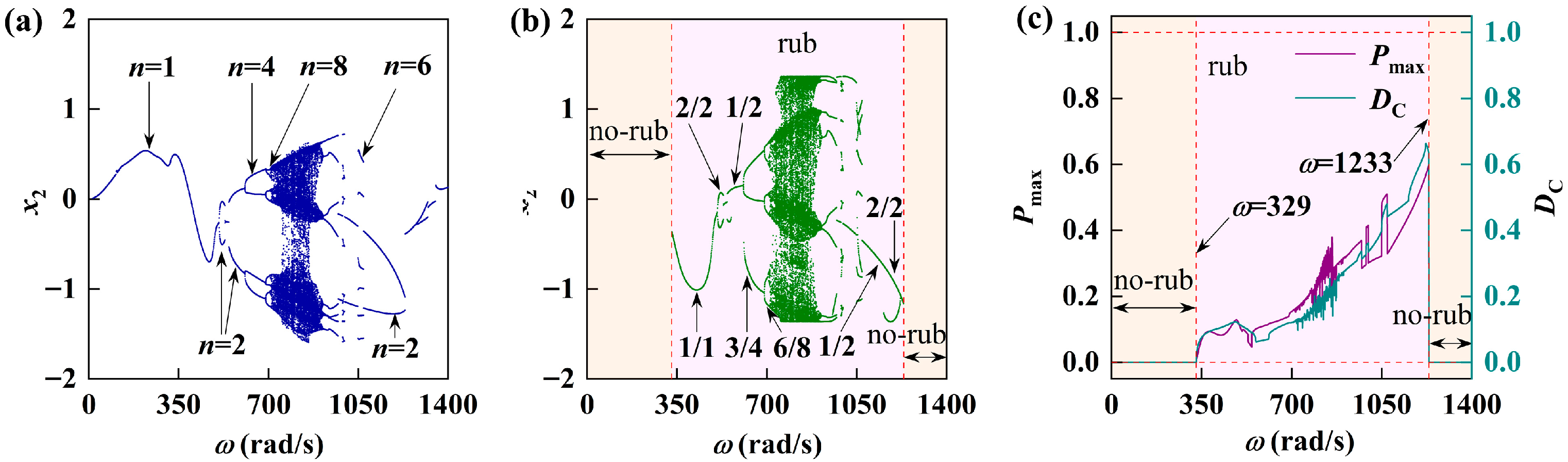
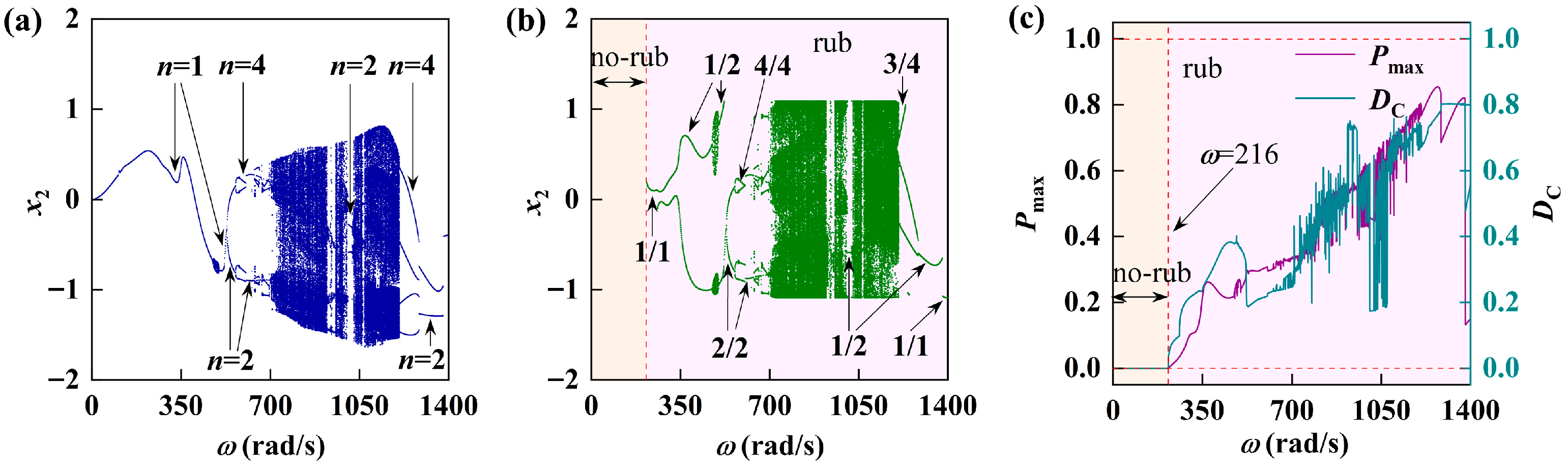
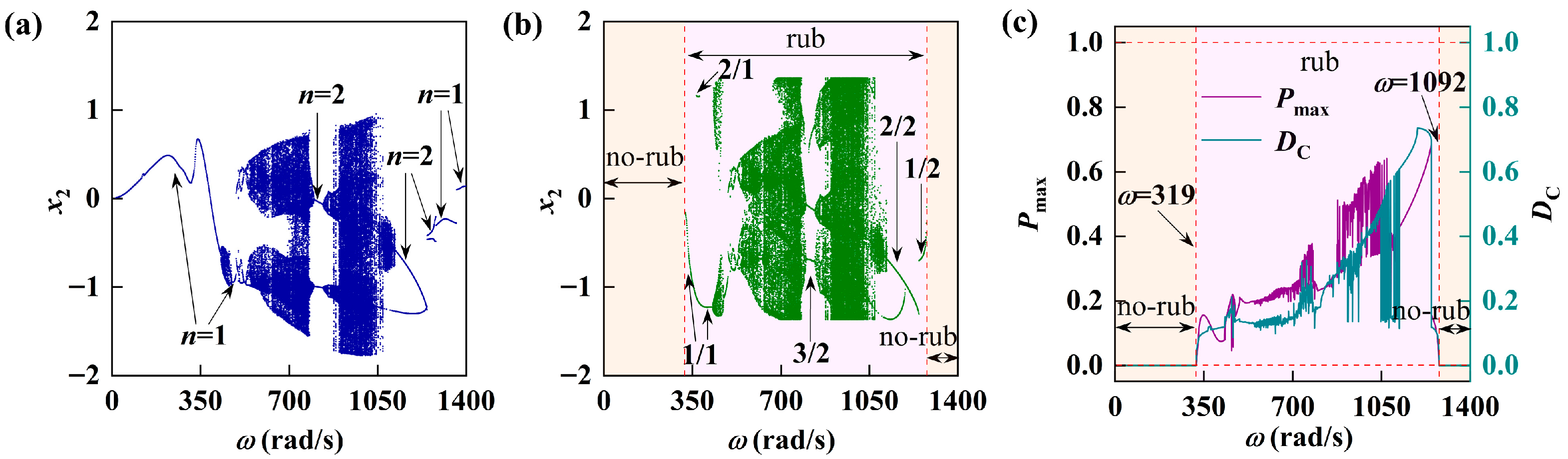
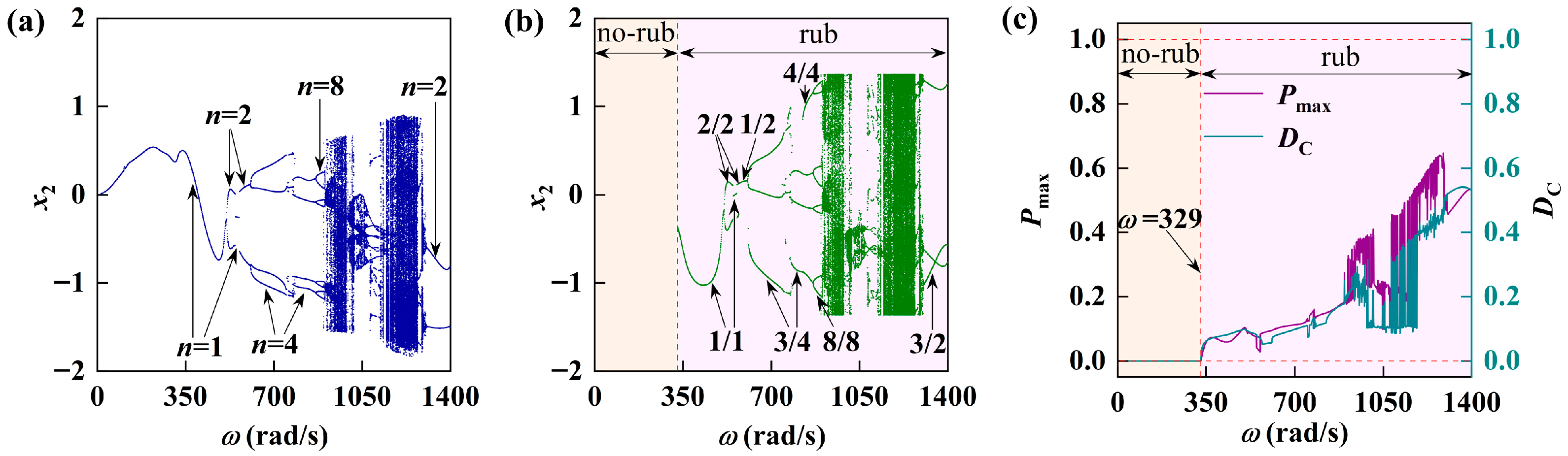
5.1. Response of Rotor-Bearing System with Varying Rotating Speed
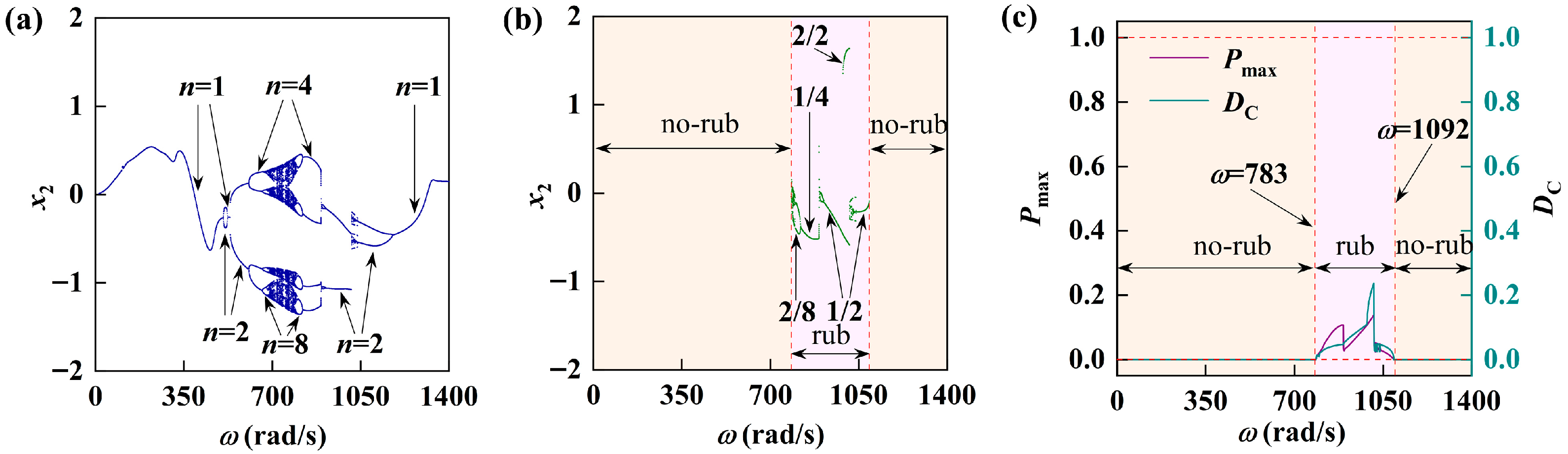
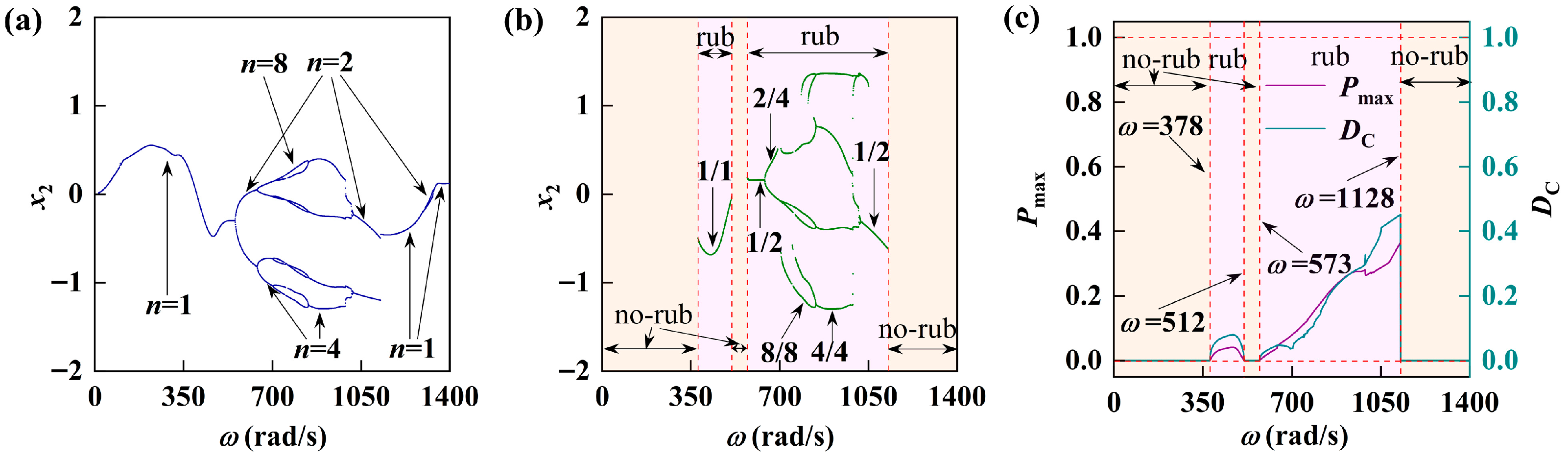
5.2. Influence of Different Rotor–Stator Clearances
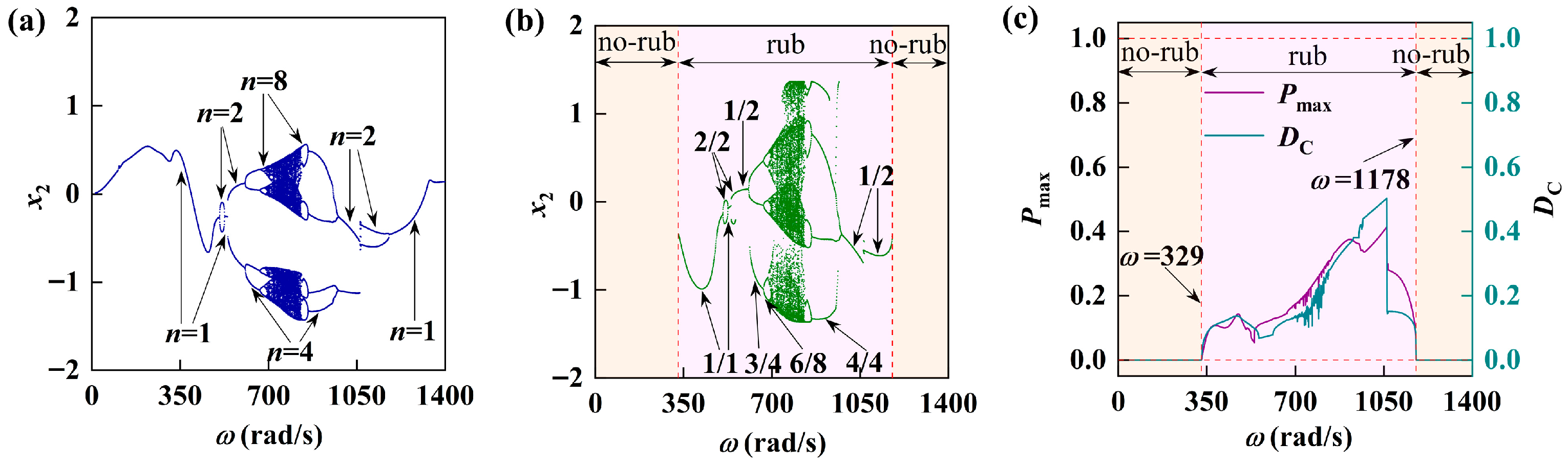
5.3. Influence of Different Lubricating Oil Viscosity
5.4. Influence of Different Stator Stiffness
5.5. Analysis of Some Typical Phenomena of the System
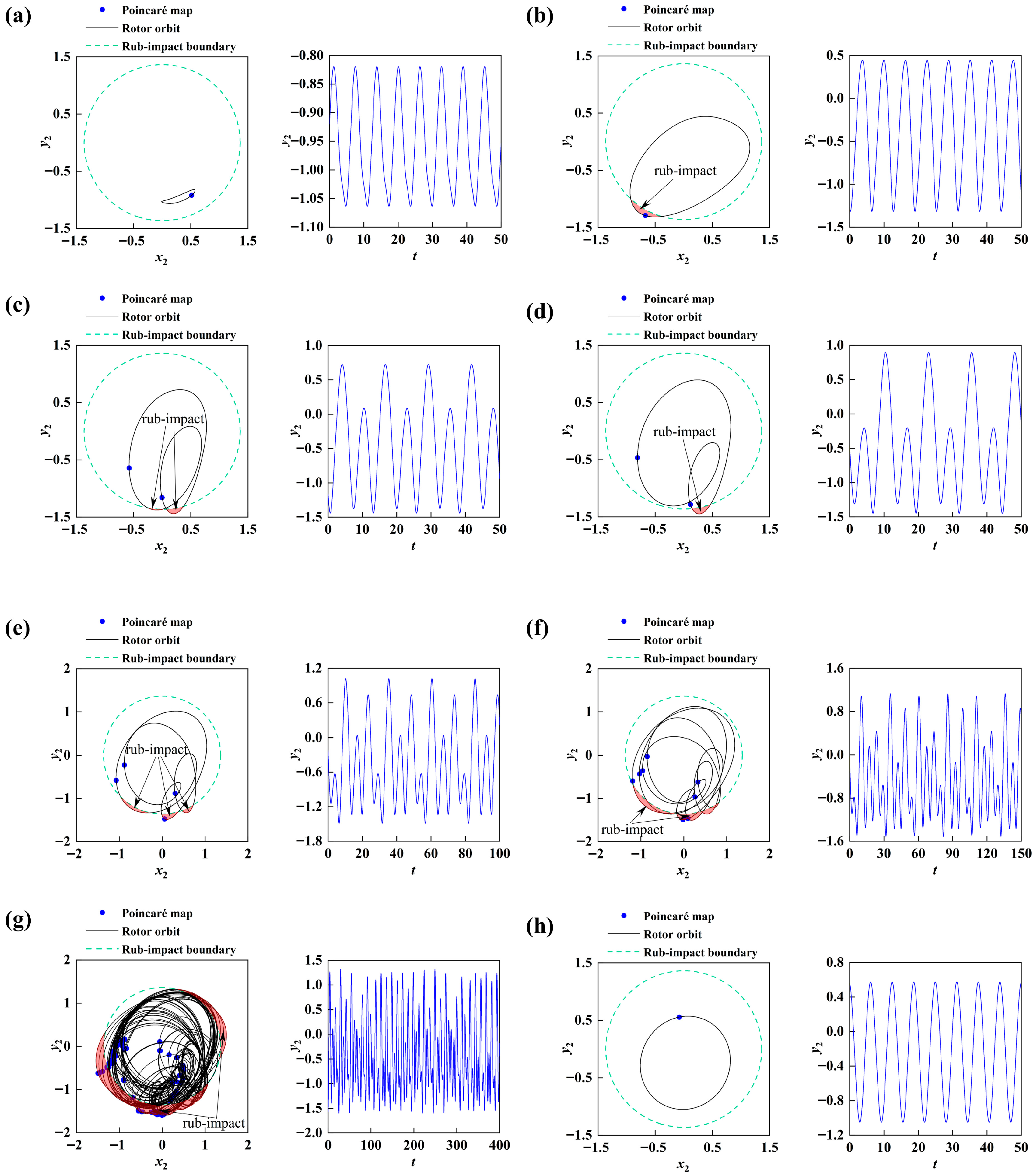
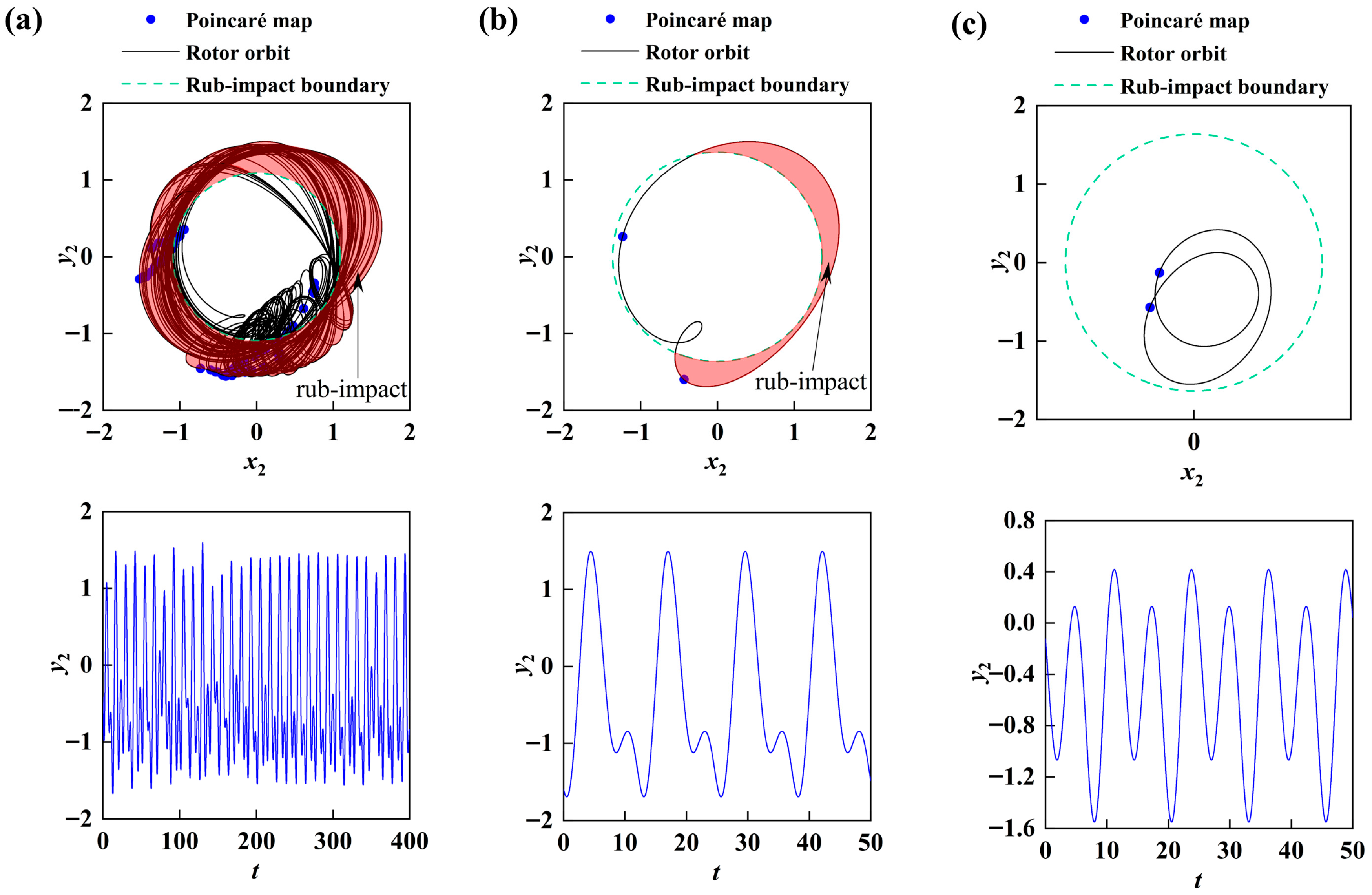
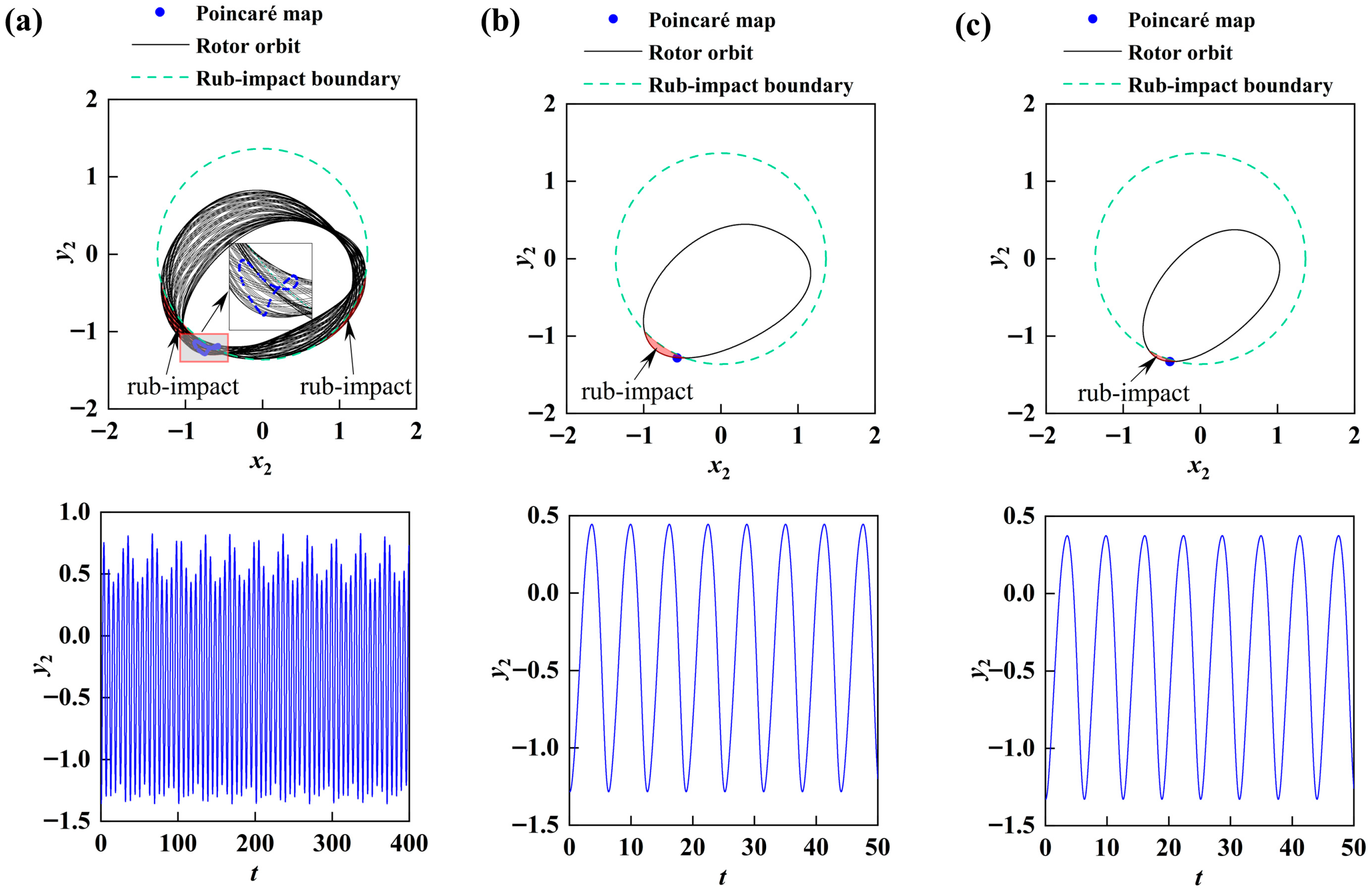
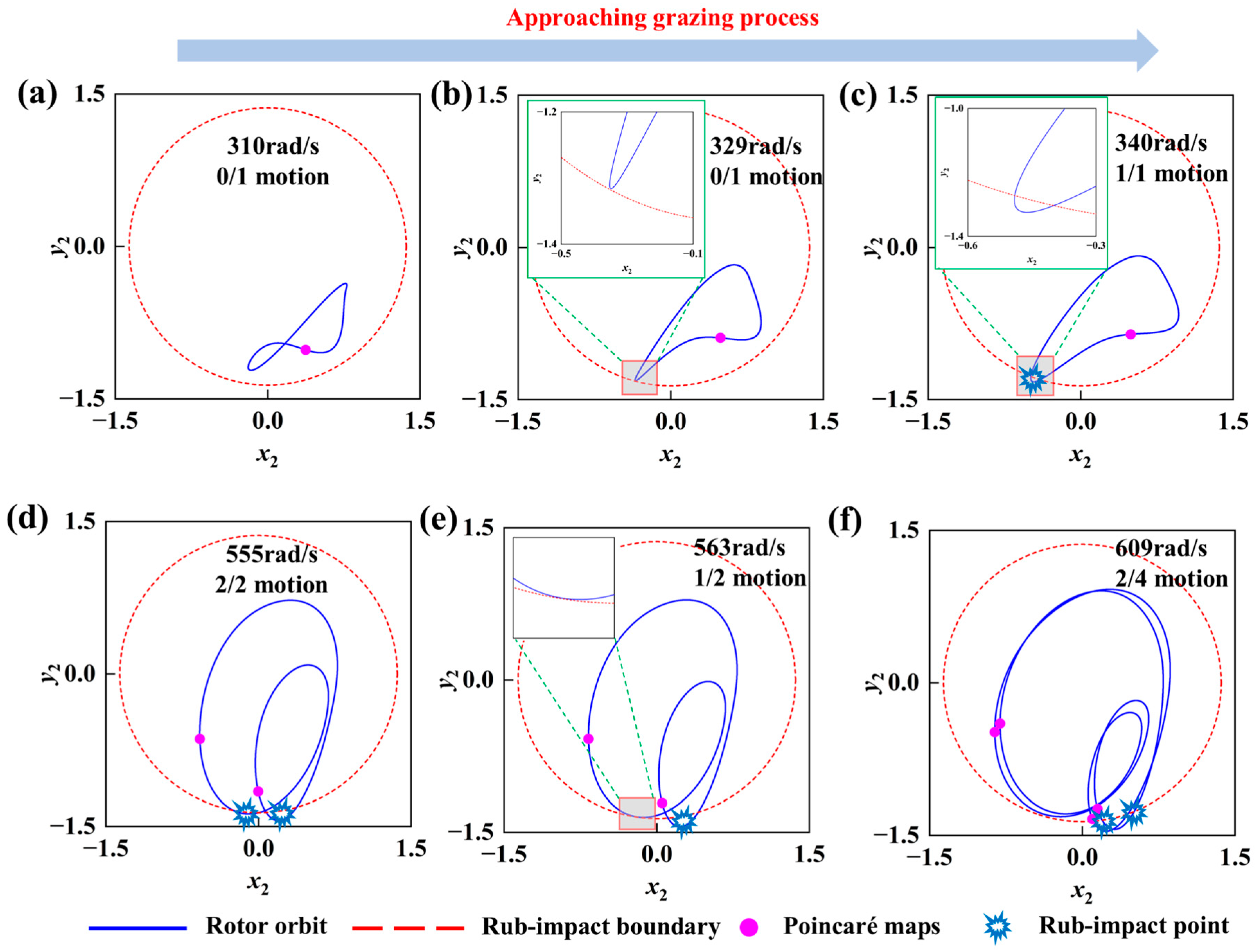
5.5.1. Grazing Phenomenon
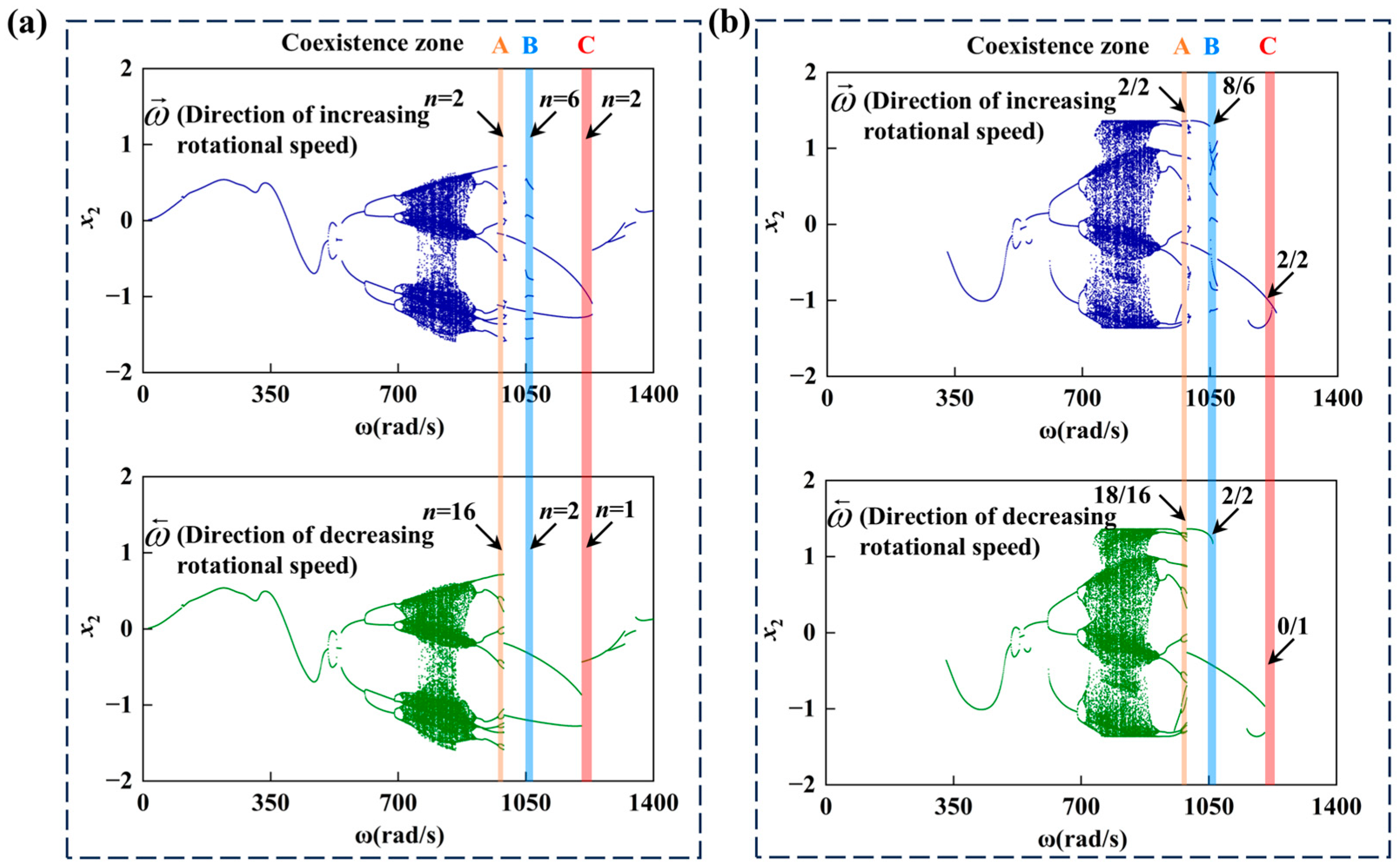
5.5.2. The Coexistence Phenomenon of System Periodic Rubbing Vibration
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Nomenclature | |
| C | Bearing radial clearance (mm) |
| Ci | Damping coefficient (N·s/m) |
| f | Friction coefficient |
| FX, FY | Dimensional components of fluid film force (N) |
| PX, PY | Dimensional components of rub-impact force (N) |
| K | Shaft stiffness (N/m) |
| Kc | Stator stiffness (N/m) |
| L | Length of bearing (mm) |
| R | Bearing radius (mm) |
| μ | Lubricating oil viscosity (Pa·s) |
| σ | Somerfield revision number |
| g | Acceleration of gravity (m/s2) |
| M1/M4 | Mass of bearings (kg) |
| M2/M3 | Mass of disks (kg) |
| O1/O4 | Geometric center of bearing |
| O2/O3 | Geometric center of disks |
| X, Y | Vibration displacement in the X and Y directions (m) |
| x, y | Dimensionless vibration displacements of the X and Y directions |
| δj | Mass eccentricity of the j-th disk (mm) |
| δr | Radial displacement of the rotor (mm) |
| ρr | Clearance between rotor and stator (mm) |
| p/n | A method for representing a motion state (number of collisions/number of cycles) |
| Pmax | Dimensionless maximum friction force |
| DC | Friction duty cycle |
References
- Shaw, A.D.; Champneys, A.R.; Friswell, M.I. Asynchronous partial contact motion due to internal resonance in multiple de-gree-of-freedom rotor dynamics. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20160303. [Google Scholar]
- Chang-Jian, C.W.; Chen, C.K. Bifurcation and chaos analysis of a flexible rotor supported by turbulent long journal bearings. Chaos Solitons Fractals 2007, 34, 1160–1179. [Google Scholar] [CrossRef]
- Xiang, L.; Gao, X.; Hu, A. Nonlinear dynamics of an asymmetric rotor-bearing system with coupling faults of crack and rub-impact under oil-film forces. Nonlinear Dyn. 2016, 86, 1057–1067. [Google Scholar] [CrossRef]
- Vlajic, N.; Champneys, A.R.; Balachandran, B. Nonlinear dynamics of a Jeffcott rotor with torsional deformations and rotor-stator contact. Int. J. Non-Linear Mech. 2017, 92, 102–110. [Google Scholar] [CrossRef]
- Ma, H.; Li, H.; Zhao, X.; Niu, H.; Wen, B. Effects of eccentric phase difference between two discs on oil-film instability in a rotor–bearing system. Mech. Syst. Signal Process. 2013, 41, 526–545. [Google Scholar] [CrossRef]
- Phadatare, H.P.; Pratiher, B. Large deflection model for rub-impact analysis in high-speed rotor-bearing system with mass unbalance. Int. J. Non-Linear Mech. 2021, 132, 103702. [Google Scholar] [CrossRef]
- Zhou, W.J.; Wei, X.S.; Wei, X.Z.; Wang, L.Q. Numerical analysis of a nonlinear double disc rotor-seal system. J. Zhejiang Univ.—Sci. A Appl. Phys. Eng. 2014, 15, 39–52. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, W.; Wei, D.; Wang, G.; Xu, J.; Liu, K. Unbalance Response and Stability Analysis of a High-speed Turbocharger Bearing-Rotor System. Tribology 2021, 41, 620–631. [Google Scholar]
- Xiang, L.; Hu, A.; Hou, L.; Xiong, Y.; Xing, J. Nonlinear coupled dynamics of an asymmetric double-disc rotor-bearing system under rub-impact and oil-film forces. Appl. Math. Model. 2016, 40, 4505–4523. [Google Scholar] [CrossRef]
- Hu, A.; Hou, L.; Xiang, L. Dynamic simulation and experimental study of an asymmetric double-disk rotor-bearing system with rub-impact and oil-film instability. Nonlinear Dyn. 2016, 84, 641–659. [Google Scholar] [CrossRef]
- Zeng, X. Nonlinear dynamic response analysis of dual-disk rub-impact rotor-rolling bearing system. Mod. Manuf. Eng. 2020, 479, 141–146. [Google Scholar]
- Liu, J.; Zhang, L.; Yin, F.; Qin, Z. Nonlinear response analysis of double disk rubbing rotor—oil film bearing system. J. Mech. Strength 2020, 42, 1310–1315. [Google Scholar]
- Qin, Z.-F.; Shi, H.-R.; Shi, Y.-Q. Dynamic behavior of a double-disc rotor system considering oil film force-impact force coupling. J. Lanzhou Jiaotong Univ. 2020, 39, 95–100. [Google Scholar]
- Zhang, L.-Y.; Li, L.; He, X.-Y. Influence of Rotary Disc eccentricity on Dynamic Response of Misaligned and anti-friction Rotor. Mach. Tools Hydraul. 2024, 52, 117–123. [Google Scholar]
- Yin, F.; Wang, X.; Wang, X. Rub-impact vibration characteristics of double-disc rotor system with magnetic bearings. J. Railw. Sci. Eng. 2024, 21, 299–313. [Google Scholar]
- Cao, L.; Li, D.; Yu, M.; Si, H.; Zhang, Z. Influence of Seal Structure on the Motion Characteristics and Stability of a Steam Turbine Rotor. Machines 2024, 12, 670. [Google Scholar] [CrossRef]
- Gao, J.; Qin, W.; Liang, X.; Yang, Y.-F.; Wang, Z. Stochastic bifurcation and chaos analysis of a rub-impact rotor-bearing system. J. Vib. Shock. 2013, 32, 161–164. [Google Scholar]
- Zhou, Z.; Huang, J. Study of RCS characteristics of Tilt-rotor aircraft based on dynamic calculation approach. Chin. J. Aeronaut. 2022, 35, 426–437. [Google Scholar] [CrossRef]
- Huang, J.; Zhou, Z. V-shaped deformation quadrotor radar cross-section analysis. Proc. Inst. Mech. Eng. 2025, 239, 1276–1290. [Google Scholar]
- Jin, H.; Wang, Y.; Wang, X.; Zhang, X.; Wang, K.; Li, G. Nonlinear vibrations of a dual-rotor system with aerodynamic excitation. Int. J. Mech. Sci. 2025, 305, 110738. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, Y.; Deng, W.; Zhao, S.; Zhu, Q.; Ma, H.; Han, Q.; Qin, Z.; Liu, W. Vibration energy analysis of rub-impact rotor system: Nonlinear fault-induced energy response and transfer state. Mech. Syst. Signal Process. 2025, 236, 113035. [Google Scholar] [CrossRef]
- Liu, Y.; Yan, C.; Shi, J.; Kang, J.; Liu, B.; Wu, L. Nonlinear dynamic analysis of supporting bearing in rotor-bearing system considering vibration interaction. Nonlinear Dyn. 2025, 113, 22435–22458. [Google Scholar] [CrossRef]
- Fasihi, A.; Shahgholi, M.; Kudra, G.; GhandchiTehrani, M.; Awrejcewicz, J. The influence of rotor-stator contact on the nonlinear vibration of an asymmetrical rotor. Nonlinear Dyn. 2025, 113, 27435–27457. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, Z.; Zhang, K.; Deng, Z.; Wu, D.; Su, Z.; Huang, X.; Song, M.; Cao, Y.; Sui, J. Nonlinear Dynamic Analysis of Gas Bearing-Rotor System by the Hybrid Method Which Combines Finite Difference Method and Differential Transform Method. Lubricants 2022, 10, 302. [Google Scholar] [CrossRef]
- Capone, G. Descrizione analitica del campo di forze fluidodinamico nei cuscinetti cilindrici lubrificati. Energ. Elettr. 1991, 68, 105–110. [Google Scholar]
- Adiletta, G.; Guido, A.R.; Rossi, C. Chaotic motions of a rigid rotor in short journal bearings. Nonlinear Dyn. 1996, 10, 251–269. [Google Scholar] [CrossRef]
- Sun, W.; Yan, Z.; Tan, T.; Zhao, D.; Luo, X. Nonlinear characterization of the rotor-bearing system with the oil-film and unbalance forces considering the effect of the oil-film temperature. Nonlinear Dyn. 2018, 92, 1119–1145. [Google Scholar] [CrossRef]
- Luo, G.W. Hopf-flip bifurcations of vibratory systems with im-pacts. Nonlinear Anal. Real World Appl. 2006, 7, 1029–1041. [Google Scholar] [CrossRef]
| Parameters | Units | Values |
|---|---|---|
| 4, 32, 34, 4 | ||
| 1100, 2100, 2200, 1100 | ||
| , | ||
| 25, 12, 0.11, 0.04, 0.06, 0.15 | ||
| 0.018 | ||
| dimensionless | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Liu, J.; Wang, J.; Zhang, L.; Wang, T.; Liu, M.; Zhao, G. Study on the Nonlinear Dynamic Behavior and Bifurcation of the Double-Rotor System Under the Coupling of Rubbing and Oil-Film Force. Lubricants 2026, 14, 32. https://doi.org/10.3390/lubricants14010032
Liu J, Wang J, Zhang L, Wang T, Liu M, Zhao G. Study on the Nonlinear Dynamic Behavior and Bifurcation of the Double-Rotor System Under the Coupling of Rubbing and Oil-Film Force. Lubricants. 2026; 14(1):32. https://doi.org/10.3390/lubricants14010032
Chicago/Turabian StyleLiu, Junjie, Jingxin Wang, Lingyun Zhang, Tongrui Wang, Manchang Liu, and Guorui Zhao. 2026. "Study on the Nonlinear Dynamic Behavior and Bifurcation of the Double-Rotor System Under the Coupling of Rubbing and Oil-Film Force" Lubricants 14, no. 1: 32. https://doi.org/10.3390/lubricants14010032
APA StyleLiu, J., Wang, J., Zhang, L., Wang, T., Liu, M., & Zhao, G. (2026). Study on the Nonlinear Dynamic Behavior and Bifurcation of the Double-Rotor System Under the Coupling of Rubbing and Oil-Film Force. Lubricants, 14(1), 32. https://doi.org/10.3390/lubricants14010032





