Modeling of Oil-Film Traction Behavior and Lubricant Selection for Aeroengine Mainshaft Ball Bearings

Abstract

The traction behavior of lubricant films forms the foundation of dynamic modeling for aeroengine mainshaft ball bearings. Its accuracy directly determines the reliability of predicted dynamic responses and the available design safety margins. Existing traction models produce artificial friction in the zero slip region and exhibit strong sensitivity to ball size effects, which leads to significant deviations from experimental observations. These limitations make them unsuitable for high-fidelity analyses of aeroengine mainshaft bearings. In this study, a self-developed high-speed traction test rig was used to systematically measure the traction–slip responses of three aviation lubricants, including the newly developed 4102 (7 cSt) and the inservice 4050 (5 cSt) and 4010 (3 cSt). The tests covered a wide range of operating conditions, including maximum Hertzian pressures of 1.0 to 1.5 GPa, oil supply temperatures of 25 to 120 °C, entrainment speeds of 25 to 40 m/s, and slide–roll ratios (SRR) of 0 to 0.3. The evolution of lubricant traction characteristics was examined in detail. Based on the experimental data, a four-parameter and three-coefficient traction model was proposed. This model eliminates the non-physical traction outputs at zero slip observed in previous formulations. When embedded into the bearing dynamic simulations, the maximum deviation between the predicted friction torque and the measured values is only 3.79%. On the basis of typical operating conditions of aeroengine bearings, lubricant selection guidelines were established. Under combined high-speed, light-load, and high-temperature conditions, the high-viscosity lubricant 4102 is preferred because it suppresses cage sliding and enhances film stiffness. When the cage slip ratio is below 15% and lubrication is sufficient, the low-viscosity lubricant 4010 is recommended, followed by 4050, in order to reduce frictional heating. This study provides a theoretical basis for high-accuracy dynamic design and lubricant selection for aeroengine ball bearings.

1. Introduction

The performance of lubricating oils is crucial to the service life and operational reliability of aeroengine mainshaft ball bearings. Under high-speed, high-temperature, and heavy-load conditions, the bearing’s frictional and thermal responses directly govern the reliability and efficiency of the entire engine. With the continuous increase in aeroengine performance demands, accurately modeling the frictional behavior of lubricants with varying viscosities under complex operating conditions has emerged as a central challenge in bearing dynamics research.

In the development of lubrication theory, film thickness models have reached a relatively mature stage. The minimum film thickness equation proposed by Dowson et al. [1], derived from experimental observations and theoretical analysis, has been extensively validated and widely applied in engineering practice. In contrast, the field of friction and traction still lacks a complete quantitative theory that can be directly applied to engineering prediction [2]. This challenge has persisted in the tribology community since the mid-20th century. Early studies demonstrated that the assumption of a Newtonian fluid and consideration of thermal effects alone could not account for the nonlinear friction coefficients observed experimentally. Smith [3] and Crook [4] were the first to recognize this limitation, attributing it to non-Newtonian rheological behavior. Later, Smith [5] introduced the concept of limiting shear strength, suggesting that once the traction coefficient reaches a critical threshold, the lubricant exhibits solid-like yielding behavior, resulting in an upper bound for the friction coefficient. Building on Smith’s insight, researchers began developing viscosity–shear relationship models by fitting experimental data. Cross, Bingham, Carreau, and Eyring [6,7,8,9] successively proposed various rheological formulations. Among them, the Eyring and Carreau–Yasuda models gained wide acceptance, as they were able to reproduce the nonlinear features observed in elastohydrodynamic lubrication (EHL) experiments. Johnson et al. [10,11] further addressed the complex response of lubricants under high pressure and proposed a constitutive equation coupling the Eyring and Maxwell models to describe isothermal shear behavior. Subsequently, Higashitani et al. [12] developed a fully coupled finite-element EHL line-contact model that accounts for both shear behavior and thermal effects of lubricants, thereby providing a more rational theoretical basis for improving conventional heat distribution calculations.

However, as research has progressed, although the aforementioned models have provided important insights into lubricant traction behavior, no consensus has yet been reached regarding the selection of an appropriate constitutive traction model [13,14,15]. One group of researchers, represented by Bair et al. [16,17], tends to favor Carreau-type shear-thinning models. Their main advantage lies in the ability to describe the transition of lubricants from the Newtonian regime to the power-law regime in a continuous and smooth manner, offering relatively stable numerical implementation. As a result, such models have been widely adopted in recent thermo-elastohydrodynamic lubrication (TEHL) analyses. In contrast, another group of researchers, including Neupert et al. [18,19], argues that Eyring-type models exhibit greater physical consistency in describing traction and shear behavior. Under a single set of parameters, the Eyring model is capable of more consistently reproducing both experimentally observed traction levels and molecular-scale shear responses, whereas Carreau-type models tend to overestimate viscosity in low-temperature, high-viscosity regimes. Gao et al. [20], based on molecular dynamics simulations combined with comparative analyses of multiple rheological models, demonstrated that even for linear alkane systems with relatively simple molecular structures, the choice of shear-thinning model can introduce substantial discrepancies in high-shear predictions. This finding indicates that, even at the level of base lubricants, the selection and calibration of rheological constitutive relations exert a non-negligible influence on numerical results. Furthermore, MacLaren et al. [21,22] conducted high-speed EHL experiments with simultaneous measurements of oil-film thickness and traction response, clearly demonstrating that thermal effects play a dominant role in traction behavior under high rotational speeds. Taylor, Cordier, and Liu et al. [23,24,25] separately investigated the influence of contact boundary conditions, surface roughness, and contact geometry on friction coefficients, revealing that even the same lubricant may exhibit markedly different traction characteristics depending on the contact configuration. These findings have led to the recognition that directly equating traction curves with rheological flow curves may involve conceptual oversimplifications [26]. Overall, as understanding has deepened, research on friction and traction characteristics has gradually shifted from comparisons of individual rheological models toward a more systematic characterization of multi-physical coupling mechanisms [27]. Recent experimental and numerical studies consistently indicate that lubricant friction and traction behavior is jointly governed by pressure viscosity relationships, temperature rise, shear-rate distributions, and the thermal properties of contact materials. Consequently, due to inherent assumptions and limited applicability, models based solely on lubricant rheology struggle to accurately predict experimental traction coefficients under realistic operating conditions [28].

To address the requirements of bearing engineering calculations, many researchers have adopted ball–disk test methods to replicate realistic operating conditions and investigate the traction behavior of lubricating films. Wang et al. [29] and Deng et al. [30] conducted systematic experiments using ball–disk tribometers under varying loads, speeds, and temperatures. They developed corresponding rheological equations and a five-parameter empirical model, which provided key parameters for bearing dynamic analysis. However, this model employs load as the fitting variable rather than directly reflecting contact stress, thereby limiting its general applicability. In addition, the five-parameter, four-coefficient formulation for the traction coefficient yields a nonzero value at zero slip ratio, introducing inconsistencies in bearing dynamic analysis. Nevertheless, this class of models has been widely applied in studies of bearing frictional power loss, cage dynamics, thermal response, and vibration [31,32,33,34,35,36,37,38,39,40], thereby confirming the profound impact of lubricant properties on the dynamic performance of rolling bearings.

In summary, as the demand for higher accuracy and reliability in the simulation of advanced bearing systems continues to increase, traditional modeling approaches based on rheological constitutive equations remain a matter of considerable debate. On the one hand, there is still no consensus within the research community on whether traction curves can be considered equivalent to rheological flow curves, and the applicability of models such as the Eyring and Carreau formulations remains controversial. Although TEHL methods can comprehensively account for temperature rise and thermo-coupling effects, their engineering application is often restricted by low computational efficiency, poor numerical convergence, and the difficulty of obtaining accurate material parameters [41]. On the other hand, while existing empirical models still exhibit certain limitations in representing contact stress and predicting the zero slip boundary, they have demonstrated substantial engineering practicality in bearing dynamic simulations and have contributed to advancing the understanding of underlying mechanisms. To address the above issues, this study employs a self-developed ball–disk traction test rig to systematically investigate the oil-film traction characteristics of three aviation lubricants with representative viscosity levels. These include the newly developed 4102 oil (7 cSt) from Sinopec Yiping Chemical Plant, the inservice 4050 oil (5 cSt) from the same manufacturer, and the inservice 4010 oil (3 cSt) from Sinopec Great Wall Lubricant Company. Although the three lubricants differ in kinematic viscosity, they all contain a high proportion of polar polyol ester functional groups within their molecular chains, enabling the formation of stable adsorption films on M50 material surfaces. This contributes to their excellent load-carrying capacity and anti-scuffing performance under high-temperature conditions. Experiments were conducted over a wide range of loads, speeds, and temperatures to comprehensively characterize their traction behavior. Based on the experimentally measured traction force data, a semi-empirical, data-driven traction coefficient model for rolling bearings is proposed. The model possesses clear physical relevance and provides a reliable basis for high-fidelity dynamic simulations of rolling bearings, as well as for lubricant selection in aeroengine applications.

2. Traction Characteristics Tests of Lubricant Oil Films

2.1. Experimental Principle

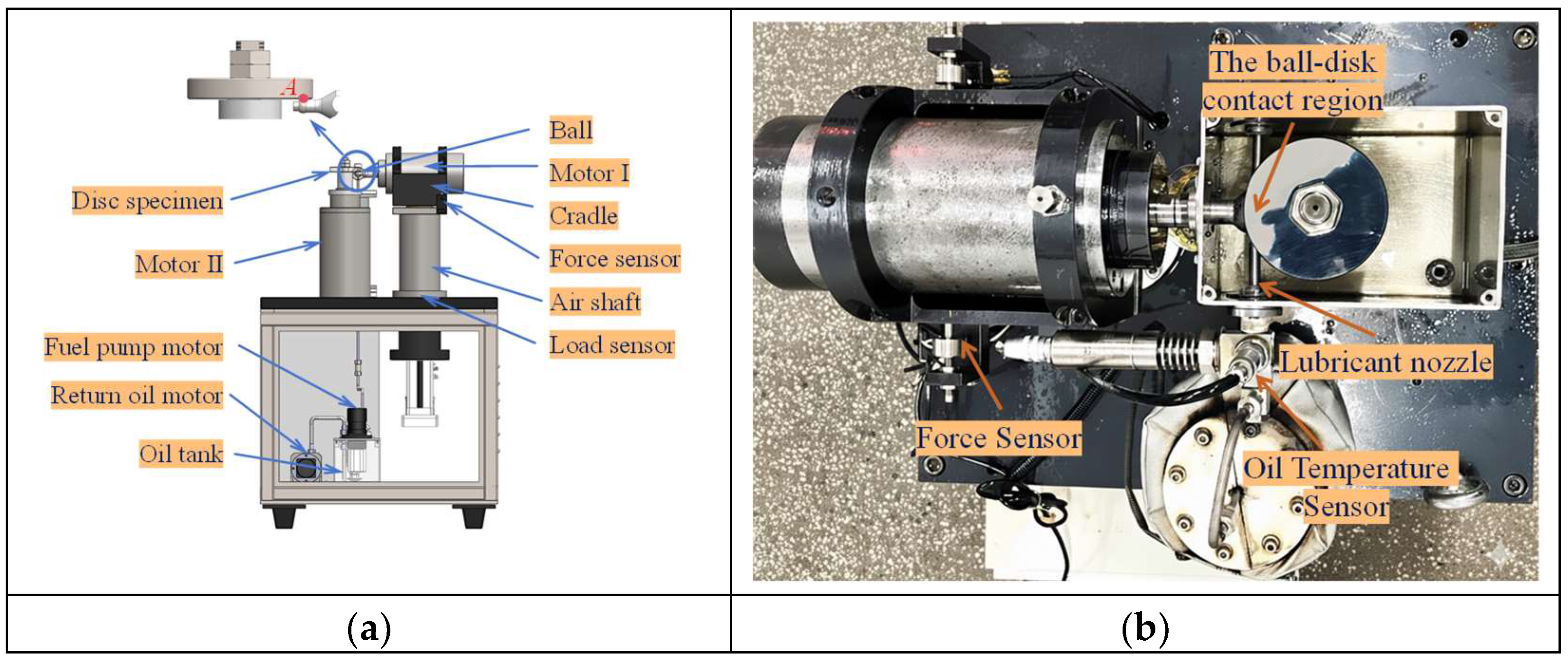
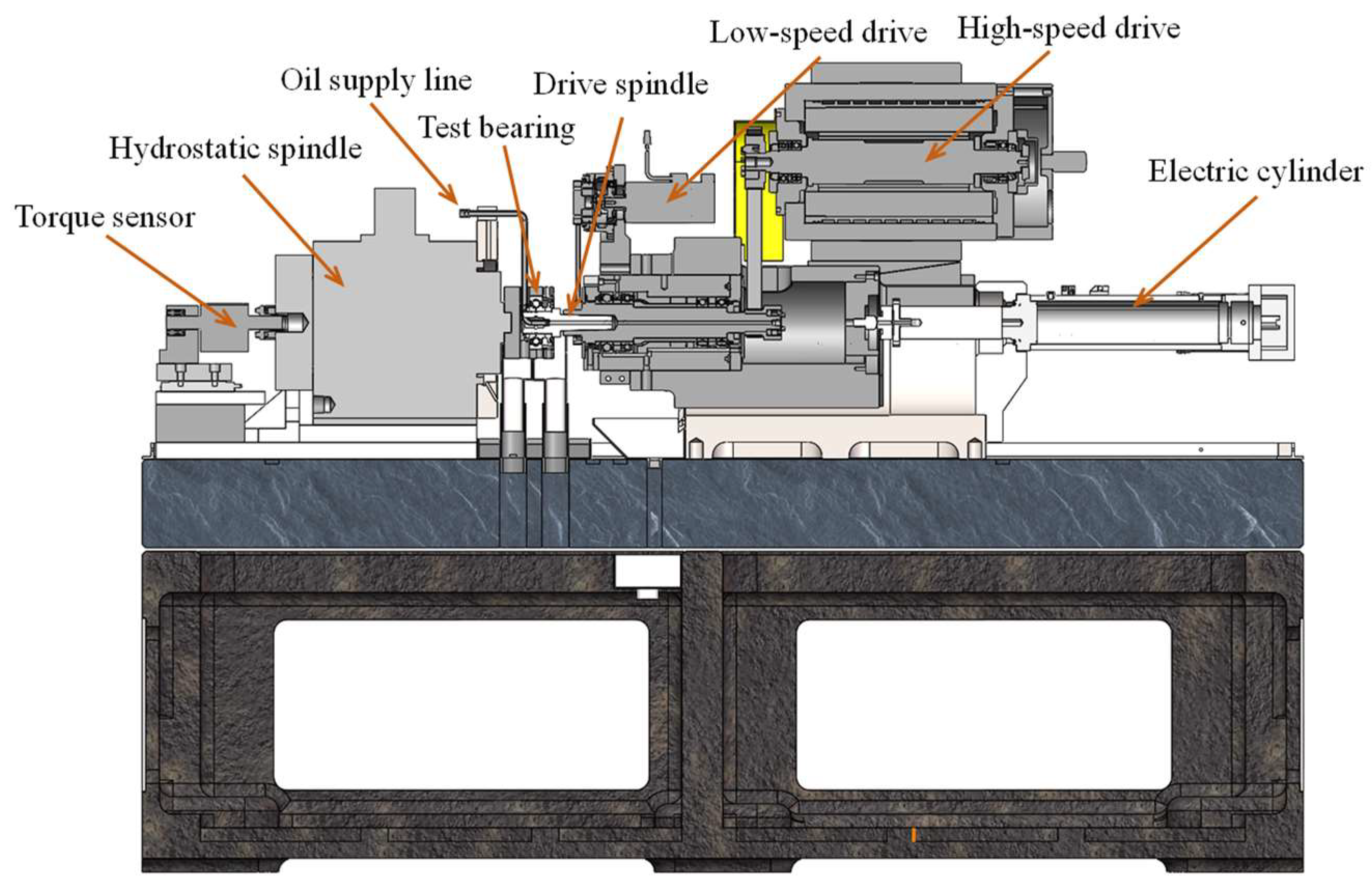
In this study, a self-developed oil-film traction test rig was employed to measure the oil-film traction coefficients of aviation lubricants. The test apparatus adopts a ball–disk configuration (see Figure 1). Figure 1a illustrates the overall structure of the system, while Figure 1b presents the schematic diagram of the test head. In this setup, the ball specimen represents the rolling element of a ball bearing, and the circular disk specimen simulates the bearing raceway. Both the ball and disk specimens are manufactured from M50 material, with a surface hardness of HRC 60–64. The diameters of the ball and disk are 20 mm and 90 mm, respectively. The surface roughness values (Ra) of the ball and disk are less than or equal to 0.014 μm and 0.01 μm, resulting in a composite surface roughness below 0.017 μm. Since the lubricant film thickness exceeds 0.1 μm, fully developed EHL conditions are ensured. The face runout of the ball–disk pair is controlled below 1 μm, guaranteeing high rotational accuracy. A gas-lubricated air spindle is used to minimize rotational resistance. Owing to its extremely low friction—several orders of magnitude smaller than the traction coefficient of the tested lubricants—the air spindle introduces negligible interference to the measurement accuracy of the traction coefficient. All sensors used in the test rig are high-precision sensors with an accuracy of 0.1%. The load and traction force sensors (Model 102A, BEDELL Electronic Technology Co., Ltd., Shanghai, China) were calibrated using standard weights to ensure the linearity and accuracy of the normal load and traction force measurements. The rolling speed at the ball–disk contact can be continuously adjusted up to 50 m/s. The SRR can be precisely controlled within the range of 0 to 0.3. The maximum Hertzian contact pressure between the ball and disk is adjustable up to 3.0 GPa, and the lubricant inlet temperature can be regulated from ambient conditions to 150 °C. The normal load is applied using a servo electric actuator, the temperature is controlled through a PID regulator, and the rotational speeds are monitored and adjusted via Hall-effect sensors. These components represent high-precision instrumentation commonly used in advanced tribological testing, thereby ensuring high measurement accuracy of the traction tests.

The ball specimen is affixed to a horizontally oriented electric spindle (Spindle I). Spindle I is secured to a cradle, which permits free rotation in the horizontal plane about an air-lubricated vertical axis. Precise positioning of the ball specimen at the designated contact point A on the disk is achieved by adjusting the horizontal location of Spindle I on the cradle. Conversely, the disk specimen is installed on a vertically oriented electric spindle (Spindle II), which is rigidly mounted on the machine frame. The axes of the two spindles are configured orthogonally. The vertical position of Spindle I can be precisely adjusted via the air spindle, thereby enabling the upward movement of the ball specimen to establish contact with the disk and apply the load. The applied load W is measured by a force sensor located at the base of the air spindle. Upon application of the load, elastic deformation is induced at the ball–disk interface, causing the initial point contact to expand into a circular contact zone of very small radius. The maximum Hertzian contact stress between the ball and disk is determined using Hertzian elastic contact theory. During high-speed operation under fully flooded lubrication-where lubricant is continuously directed through an oil nozzle onto the contact region-an EHL film of finite thickness develops between the ball and the disk. The presence of relative sliding between the two contacting surfaces induces shear within the lubricant film, which in turn generates traction forces at the interface.

Under the action of the EHL traction force, the ball specimen, motorized spindle I, and its supporting cradle undergo a slight angular deflection about the axis of the aerostatic vertical spindle. This deflection presses against the traction force sensor mounted on the machine frame, enabling the measurement of the pure oil-film traction force F, free from rolling-resistance components. When a rolling–sliding velocity difference exists between the ball and the disk, elastic compliance between the air spindle and the cradle generates a tangential traction force. This tangential force further induces a small rotation of the ball specimen, motorized spindle I, and the cradle around the vertical air-spindle axis, allowing the traction force sensor to accurately capture the magnitude of the EHL oil-film traction force.

2.2. Experimental Procedure

The test begins by setting the entrainment speed U. After loading, the ball and disk specimens come into point contact at position A. Assuming pure rolling at A, the linear speeds of the ball and disk at this point are equal, i.e., U₁ = U₂. The entrainment speed is defined as:

$$U=0.5(U_1+U_2)$$

(1)

Thus, the rotational speeds of Spindle I and Spindle II are determined as:

$$n_1=30U/(\pi R_1)$$

(2)

$$n_2=30U/(\pi R_2)$$

(3)

where R₁ and R₂ are the radii from each spindle axis to the contact point on the ball and disk, respectively.

Under fully flooded lubrication, the surfaces near the contact region form a continuous lubricant film. When Spindle I and Spindle II rotate at n₁ and n₂, respectively, the ball and the disk achieve pure rolling at point A, with no relative sliding. In this state, the lubrication film at the interface produces only a normal hydrodynamic supporting force and no traction force. Consequently, the ball, together with Spindle I, does not experience lateral deflection, and the traction force sensor outputs zero. To eliminate the influence of residual friction in the system on the subsequent traction measurements, the zero output under pure rolling conditions is set as the reference baseline for the traction force acquisition system.

With the load W, entrainment speed U and temperature T held constant, a specified SRR is produced by decreasing the rotational speed of the ball specimen while simultaneously increasing the rotational speed of the disk specimen. This adjustment yields a targeted sliding velocity ΔU at the contact. The rotational speeds of the ball and disk are then given by:

$$n_1=30(U-\Delta U/2)/(\pi R_1)$$

(4)

$$n_2=30(U-\Delta U/2)/(\pi R_2)$$

(5)

The resulting SRR is defined as S = ΔU/U. The elastohydrodynamic traction force drives the ball, Spindle I, and the cradle to deflect as a unit about the vertical axis. This lateral deflection compresses the traction force sensor mounted on the frame, and the acquisition system records the traction force F generated by the lubricant film. The traction coefficient is then calculated as:

$$\mu =F/W$$

(6)

By repeating the procedure at successive values of ΔU, the μ–S curve is obtained to characterize the lubricant’s traction behavior.

2.3. Test Lubricants

The characteristic parameters of the three representative lubricants, including density, kinematic viscosity, thermal conductivity, and specific heat capacity, are evaluated at 100 °C and summarized in

Table 1. Physical properties of lubricating oils.

Lubricants	Density: $\mathit{\rho }\mathbf{(}kg/m^3\mathbf{)}$	Kinematic Viscosity: $\mathit{\nu }\mathbf{(}m{m}^2/s\mathbf{)}$	Thermal Conductivity: $\mathit{\lambda }\mathbf{(}W/m\cdot k\mathbf{)}$	Specific Heat: $\mathit{C}\mathbf{(}J/kg·k\mathbf{)}$	Viscosity Index	Operating Temperature Range (°C)
4010	900.8	3.311	0.1328	2136	120	−51~200 °C
4050	917.2	5.141	0.1335	2016	136	−40~204 °C
4102	922.6	7.357	0.1415	1677	139	−40~240 °C

.

2.4. Experimental Results

The traction tests of the lubricant film were conducted entirely within the EHL regime. The test conditions were determined based on theoretical calculations to ensure a film thickness ratio of λ > 3 in the ball–disk contact zone, thereby guaranteeing full-film lubrication. The corresponding test parameters for the lubricant traction measurements are listed in

Table 2. Test parameters for lubricating oil-film traction characteristics.

Operating Conditions	Values
Oil supply temperature T (°C)	25, 70, 120
Entrainment speed U (m/s)	25, 30, 35, 40
Maximum contact stress P (GPa)	1.0, 1.1, 1.2, 1.3, 1.4, 1.5
Slide-to-roll ratio S	SRR range: 0–0.3; step size 0.01

.

Traction tests were carried out under the combinations of inlet temperature, entrainment speed, and maximum Hertzian stress listed in Table 2. For each lubricant, 72 sets of traction-coefficient–SRR curves were obtained based on the operating conditions specified in Table 2, providing a sufficiently comprehensive experimental database for the subsequent development of the lubricant traction model.

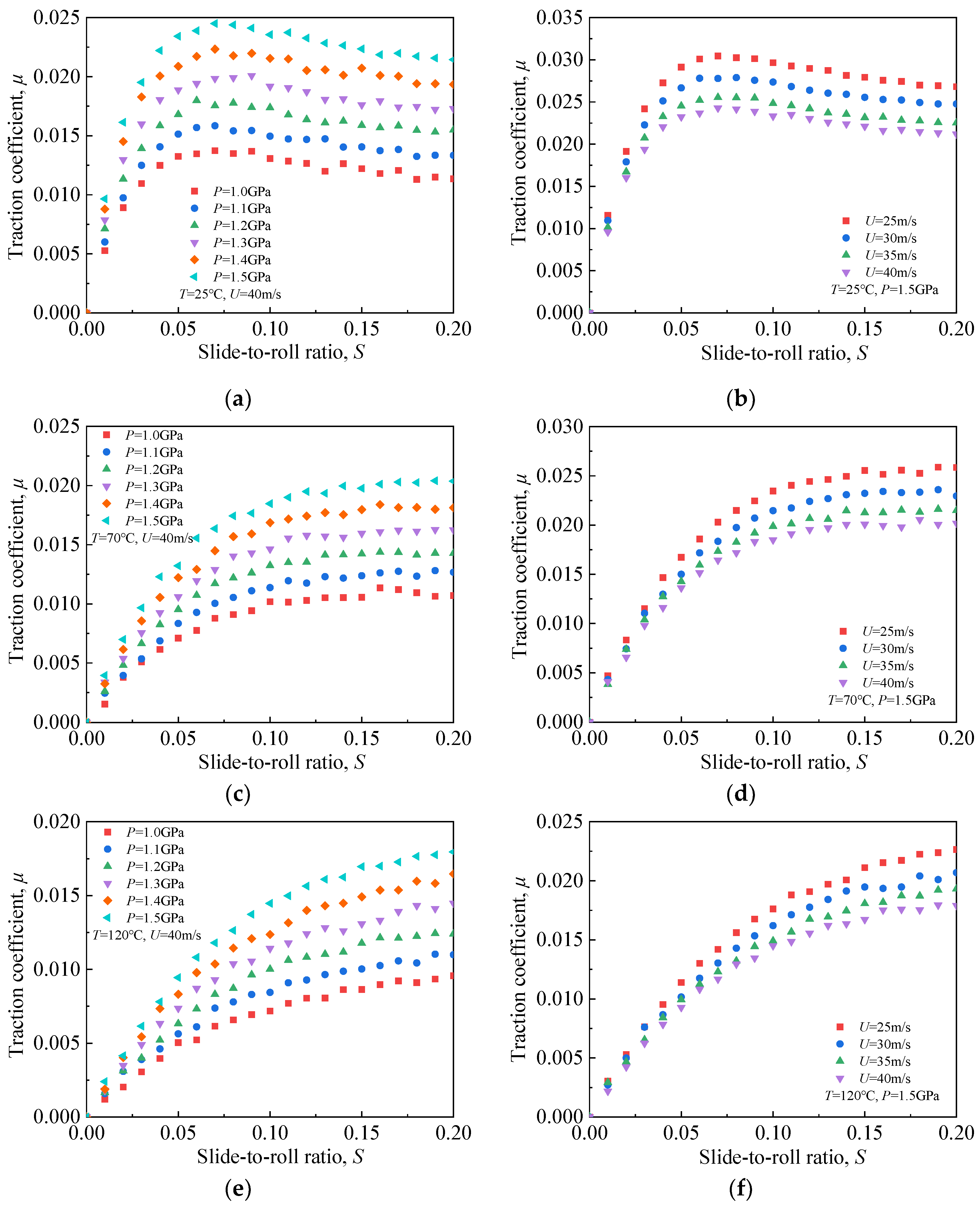
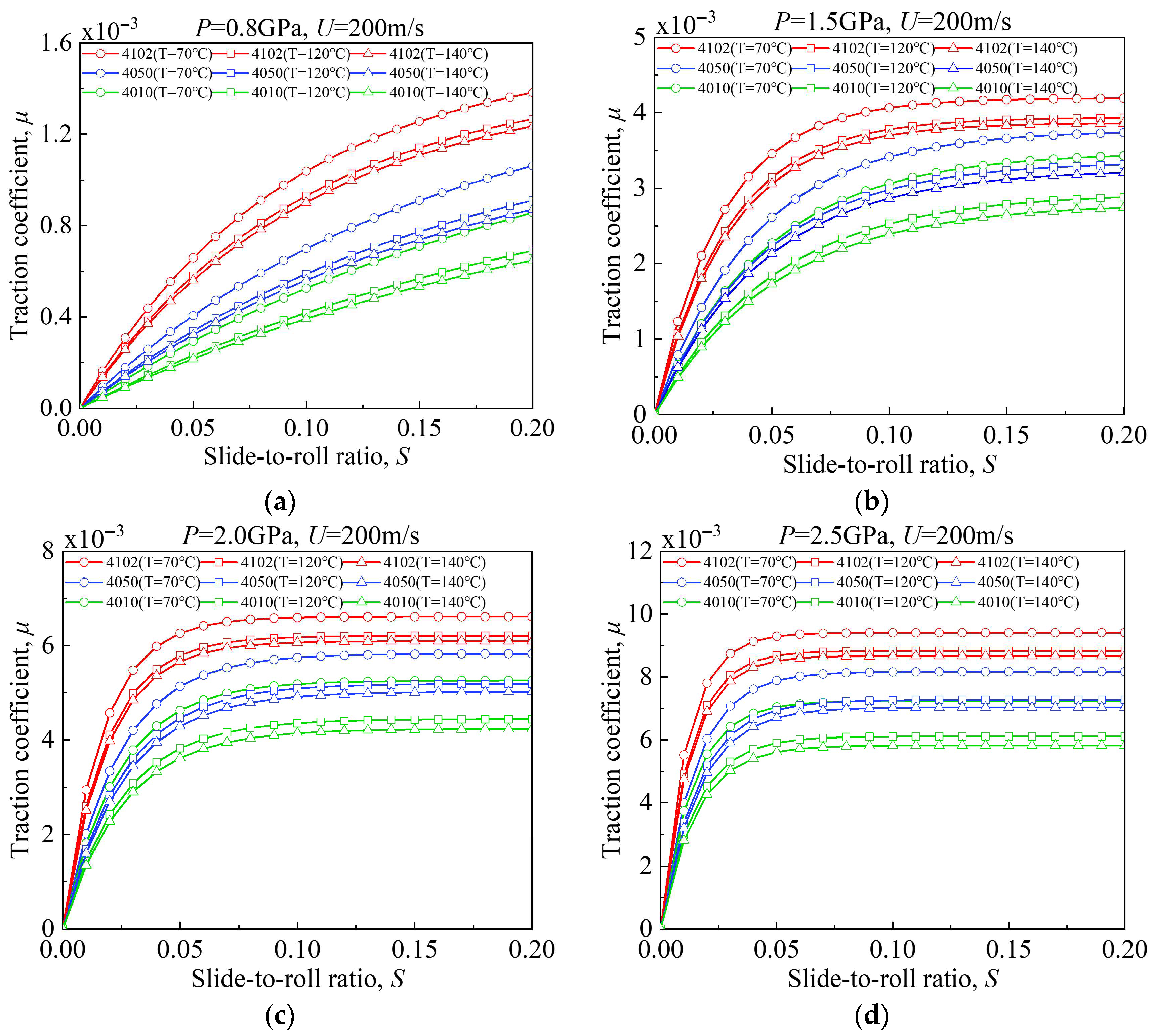
Taking lubricant 4102 as an example, Figure 2 presents representative traction-coefficient curves under several typical operating conditions. As shown in Figure 2, when the inlet temperature, entrainment speed, and maximum contact stress are held constant, the traction coefficient initially increases almost linearly with increasing SRR. In this region, the lubricant exhibits typical Newtonian behavior, where shear stress is proportional to shear rate. When the SRR exceeds a certain threshold, the rate of increase in traction coefficient gradually slows, and a pronounced nonlinear relationship emerges between the traction coefficient and SRR, indicating clear non-Newtonian behavior. As the SRR continues to increase, the traction coefficient eventually reaches a maximum value. Beyond this point, further increases in SRR cause a slight decline in the traction coefficient. The experimental traction curves in Figure 2 demonstrate that the lubricant undergoes a transition from viscoelastic to plastic behavior. The shear stress increases with shear strain rate, and under conditions of high pressure and high shear rate, the lubricant approaches its limiting shear stress.

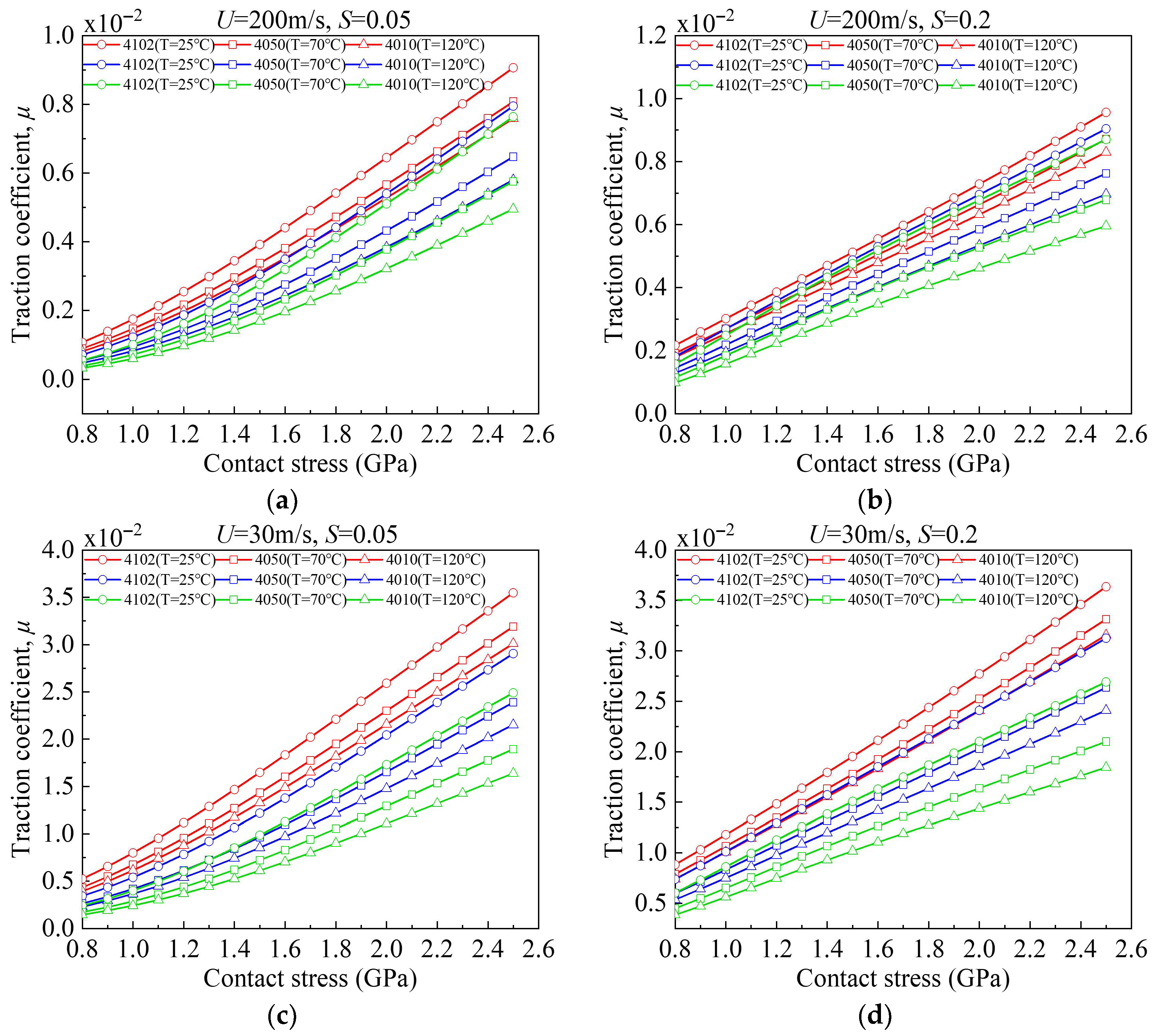
In addition, the oil-film traction coefficient exhibits an overall decreasing trend with increasing oil supply temperature. This behavior is primarily attributed to the temperature-induced reduction in the lubricant’s base viscosity, pressure–viscosity coefficient, and limiting shear stress. At high entrainment speeds, this effect is further amplified by shear heating, which weakens the effective shear load-carrying capacity of the lubricant film. As a result, the overall traction level shifts downward and enters the saturation regime at lower SRR values.

3. Development of the Traction Model

Based on the data from the oil-film traction tests, a mathematical model was con-structed. The primary challenge lies in capturing the potential functional structure among the variables. By integrating the measured curve trends of three types of aviation lubricants under various working conditions and combining with professional experience, the mapping relationship between the oil-film traction coefficient μ and the SRR S can be described using the exponential saturation function in Equation (7). Equation (7) satisfies the physical boundary condition μ = 0 at zero SRR. With increasing SRR, the exponential term decays monotonically, and the traction coefficient asymptotically approaches a finite saturation level governed by the fitted parameter A, which is consistent with the experimentally observed traction behavior under EHL conditions.

$$\mu =\left(A+BS\right)e^{-CS}-A$$

(7)

where S represents the SRR, while A, B, and C are the condition-sensitive coefficients, whose values depend on the maximum contact stress, the supply oil temperature, and the entrainment speed. These values can be uniquely determined through the least squares fitting of the experimental data. During the regression process, sign constraints are imposed on the model parameters, with parameter A required to be negative and parameters B and C positive. These constraints ensure that the predicted traction coefficient remains non-negative under all operating conditions and effectively eliminate non-physical negative values. Based on this formulation, a traction calculation model characterized by four governing parameters and three fitted coefficients is established.

To establish a general traction coefficient model applicable over a wide range of load, speed, and temperature conditions, a nonlinear multivariate regression framework based on dimensionless variables is adopted. Reference values are selected as P₀ = 1 (GPa), U₀ = 20 (m/s), and T₀ = 20 (°C). Accordingly, the maximum contact stress P, entrainment speed U, and inlet temperature T are nondimensionalized as:

$$\begin{array}{l}\overline{P}=P/P_0\\ \overline{U}=U/U_0\\ \overline{T}=T/T_0\end{array}$$

(8)

Since the coefficients A, B, and C are dependent on the maximum contact stress, entrainment speed, and inlet temperature, they can be expressed as functions of these parameters.

$$\left\{\begin{array}{l}A=A_0{\overline{P}}^{A_1}{\overline{U}}^{A_2}{\overline{T}}^{A_3}\\ B=B_0{\overline{P}}^{B_1}{\overline{U}}^{B_2}{\overline{T}}^{B_3}\\ C=C_0{\overline{P}}^{C_1}{\overline{U}}^{C_2}{\overline{T}}^{C_3}\end{array}\right.$$

(9)

where A₀~A₃, B₀~B₃, and C₀~C₃ are constants that can be determined from the results of the oil-film traction characteristic tests.

By substituting Equation (9) into Equation (7), once the contact stress, entrainment speed, and lubricant inlet temperature are specified in the traction test, the traction coefficient of the lubricant becomes a function of the twelve constants A₀~A₃, B₀~B₃, and C₀~C₃. Accordingly, the theoretical traction coefficient can be expressed as μ = f (A₀, A₁, A₂, A₃, B₀, B₁, B₂, B₃ C₀, C₁, C₂, C₃) For each lubricant, 72 traction tests were conducted, yielding 72 traction coefficient–SRR curves. To determine the twelve constants, the optimization objective was defined as the sum of squared error between the theoretical traction coefficient μ and the experimental values μ_test across all operating conditions and SRR data. Letting Ω denote the dataset consisting of all test conditions and SRR values, the objective function is expressed as:

$$\mathrm{y}=\min {\displaystyle \sum _{\mathsf{\Omega }}{\left(\mu -{\mu }_{\mathrm{test}}\right)}^2}$$

(10)

where A₀~A₃, B₀~B₃, and C₀~C₃ are treated as optimization variables, and the constraint condition is that the traction coefficient µ must be greater than or equal to zero.

A genetic algorithm was employed to optimize the objective function, and the optimal solutions for the twelve constant parameters were obtained. Based on these results, the specific forms of Equation (9) corresponding to each lubricant can be determined.

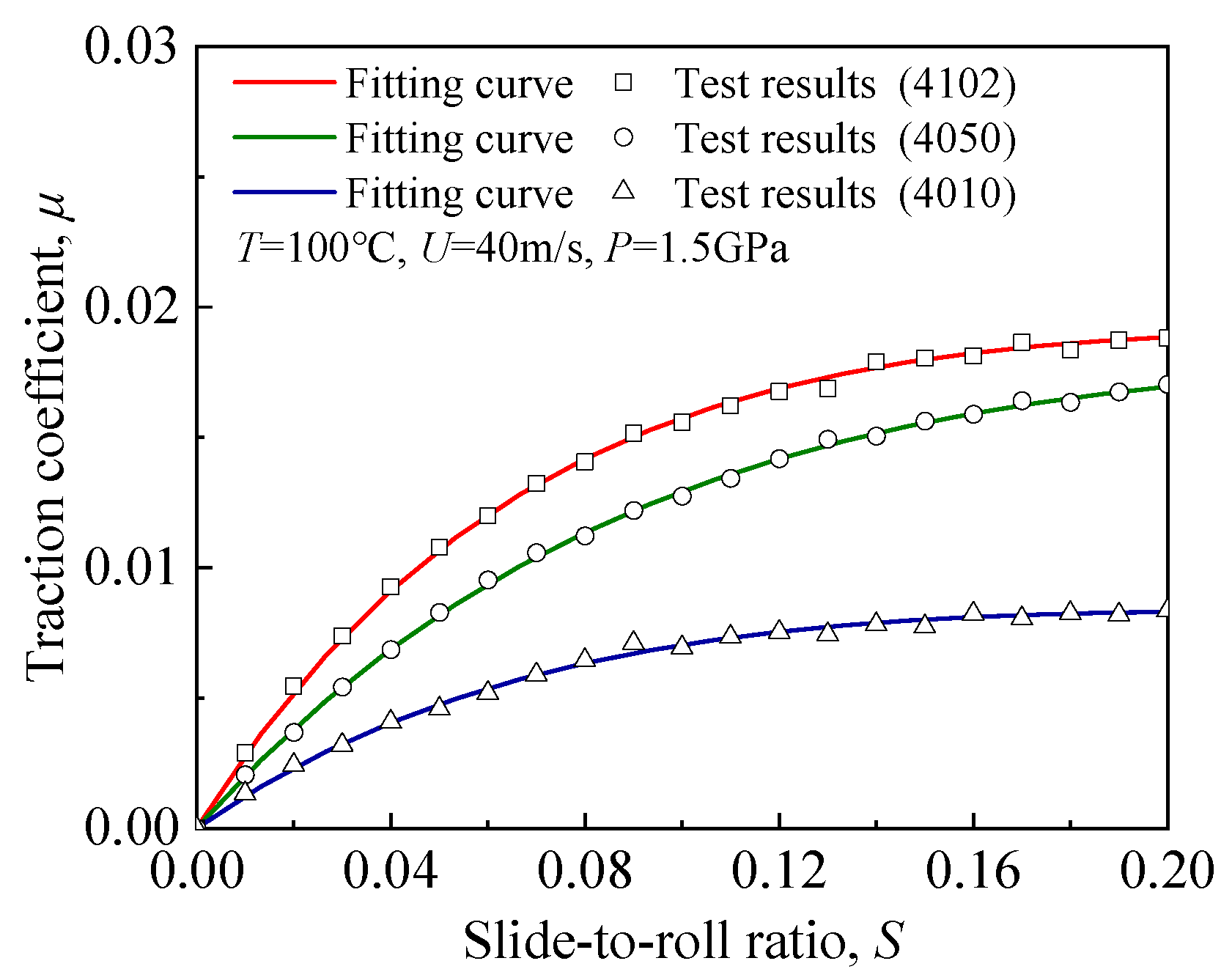
Based on the traction test results of lubricants 4102, 4050, and 4010, data regression yielded the following expressions for the coefficients A, B, and C in the traction coefficient model:

For lubricant 4102 (7 cSt):

$$\left\{\begin{array}{l}\overline{P}=P/P_0\\ \overline{U}=U/U_0\\ \overline{T}=T/T_0\\ A=-0.01567792{\overline{P}}^{1.6654}{\overline{U}}^{-0.5014}{\overline{T}}^{-0.1065}\\ B=0.63482685{\overline{P}}^{1.2727}{\overline{U}}^{-0.4139}{\overline{T}}^{-1.2181}\\ C=24.43483717{\overline{P}}^{0.3964}{\overline{U}}^{0.1591}{\overline{T}}^{-0.7121}\end{array}\right.$$

(11)

For lubricant 4050 (5 cSt):

$$\left\{\begin{array}{l}\overline{P}=P/P_0\\ \overline{U}=U/U_0\\ \overline{T}=T/T_0\\ A=-0.03064724{\overline{P}}^{0.4336}{\overline{U}}^{-0.4682}{\overline{T}}^{-0.2778}\\ B=0.51366989{\overline{P}}^{1.8006}{\overline{U}}^{-0.5817}{\overline{T}}^{-1.3051}\\ C=22.59058876{\overline{P}}^{0.6871}{\overline{U}}^{0.0022}{\overline{T}}^{-0.8711}\end{array}\right.$$

(12)

For lubricant 4010 (3 cSt):

$$\left\{\begin{array}{l}\overline{P}=P/P_0\\ \overline{U}=U/U_0\\ \overline{T}=T/T_0\\ A=-0.0082654{\overline{P}}^{3.1164}{\overline{U}}^{-0.5335}{\overline{T}}^{-0.1233}\\ B=2.21517466{\overline{P}}^{2.0131}{\overline{U}}^{-0.0285}{\overline{T}}^{-2.3707}\\ C=49.8739777{\overline{P}}^{0.4731}{\overline{U}}^{0.0843}{\overline{T}}^{-0.9377}\end{array}\right.$$

(13)

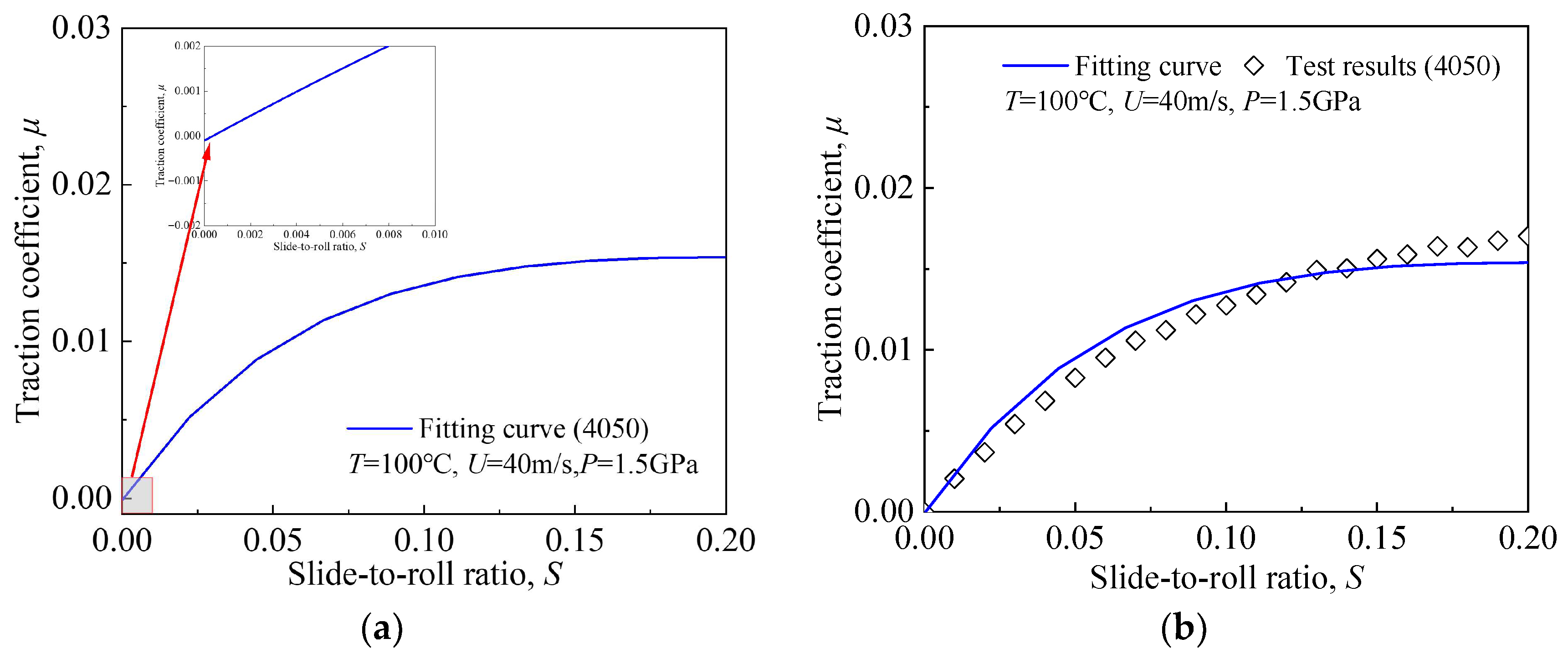
By substituting Equations (11)–(13) into Equation (7), the theoretical traction-coefficient formulations for each lubricant are obtained. These formulations can be directly applied in rolling bearing dynamic analyses.

4. Discussion

4.1. Analysis of Different Traction Models

To verify the accuracy of the lubricant traction model described by Equations (7)–(13), Figure 3 presents a comparison between the experimental traction coefficient data and the fitted results for the three aviation lubricants at 100 °C. The results indicate that the proposed model not only maintains a high level of predictive accuracy but also captures the traction behavior of lubricants under various operating conditions with good fidelity. Therefore, it demonstrates excellent engineering applicability and meets the requirements for dynamic analysis of aeroengine ball bearings.

This study proposes a four-parameter, three-coefficient model for calculating the traction coefficient of lubricating oil films. Compared with the five-parameter (dynamic viscosity, elastic modulus, viscosity–temperature coefficient, thermal conductivity, and SRR) and four-coefficient (A, B, C, D) model of Wang and Deng, the present model ensures that the traction coefficient is zero when the SRR is zero, thereby satisfying the physical boundary condition. In contrast, the Wang–Deng model predicts a non-zero traction coefficient at zero slip (Figure 4a). It is worth emphasizing that properties such as dynamic viscosity, viscosity–temperature coefficient, and thermal conductivity are already fully reflected in the experimentally measured traction data; therefore, these parameters do not need to be explicitly introduced for normalization during curve fitting. This simplification effectively avoids the problem of overfitting caused by parameter redundancy and coupling in the Wang–Deng model (Figure 4b), while significantly improving both the accuracy and efficiency of traction coefficient calculations.

4.2. Application and Validation of the Traction Model in Bearing Dynamic Analysis

The traction model that uses the maximum Hertzian contact stress as the independent variable and the model that uses the applied load as the independent variable are, respectively, incorporated into the bearing dynamic equations. Dynamic simulations of the ball bearing are then performed to quantitatively assess the different influences of these two types of oil-film traction models on the bearing friction characteristics. Subsequently, the theoretical predictions are validated on a dedicated test rig. The main parameters of the test ball bearing are listed in

Table 3. Main bearing parameters.

Parameters	Values
Inner diameter/(mm)	33
Outer diameter/(mm)	78
Bearing width/(mm)	20
Diameter of ball/(mm)	12.7
Contact angle/°	35
Number of balls	11
Lubricant grade	4050
Lubrication method	oil supply under the ring
Oil supply temperature/(°C)	100
Bearing speed/(rpm)	10,000

, and its friction torque is evaluated by comparing the theoretical and measured values. The experimental setup is illustrated in Figure 5. In the experiments, the bearing is subjected to pure axial loading, and the friction torque is measured in real time using a high-precision torque sensor (model: UTMII-50NM). The inner ring of the test bearing is interference-fitted onto the drive shaft. The drive shaft is equipped with high-speed and low-speed drive modes that are mechanically interlocked and mounted as a whole on a movable loading carriage. An electric cylinder located at the rear of the assembly applies axial load through a force sensor (model: CL-YB-14YA), and the load is transmitted through the drive shaft to the test bearing. The reaction force is balanced by a hydrostatic spindle with nearly zero friction. The outer ring of the bearing is fixed inside the loading housing and clamped by an end cap. The loading housing is connected coaxially to the front end of the hydrostatic spindle, and the rear end of the hydrostatic spindle is directly coupled to the high-precision torque sensor. The bearing is lubricated using an under-race oil supply configuration. The lubricant is delivered through an oil supply pipe directly to the inner-ring oil holes to ensure sufficient lubrication of the bearing. All temperature measurements in the test rig are performed using PT100 temperature sensors.

When an axial load is applied to the inner ring, the inner ring rotates at high speed and drives the rolling elements. Through oil-film traction, the rolling elements in turn drive the outer ring. The output torque of the outer ring is transmitted to the rear end of the hydrostatic spindle and recorded in real time by the torque sensor. In this manner, the bearing friction torque under different loads, rotational speeds, and lubrication conditions can be obtained. The traction coefficient at the raceway interface is then determined by inversion, allowing the accuracy of the oil-film traction model to be validated.

Figure 6 presents the comparison between the theoretical and experimental friction torques of the ball bearing obtained using the two types of oil-film traction models. The overall computational framework for predicting the bearing friction torque follows the method described in Ref. [42], and the only difference lies in the traction model itself. Figure 6 shows that the new traction model, which uses the maximum Hertzian contact stress as the independent variable, agrees very well with the experimental measurements. The maximum relative error is only 3.79%, demonstrating both high accuracy and strong physical consistency. In contrast, the models in Refs. [29,30], which use the applied load as the independent variable, exhibit pronounced systematic deviations, and the maximum relative error increases to 249%, indicating that the model has lost engineering applicability.

The underlying reason is that the contact stress directly characterizes the local elastoplastic and viscoelastic responses, as well as the thermo-mechanical coupling effects, at the ball–raceway interface. The applied load, on the other hand, is only a macroscopic nominal quantity and fails to capture the variations in friction coefficient induced by scale effects. Therefore, the traction coefficient model formulated with contact stress as the primary variable demonstrates superior numerical robustness and physical consistency in bearing dynamic simulations.

Overall, the results shown in Figure 6 confirm that the traction model developed in this study offers significant advantages over the conventional five-parameter model and is more suitable for dynamic analysis of high-speed angular contact ball bearings used in aeroengine applications.

4.3. Influence of Operating Parameters on Traction Characteristics

For aeroengine mainshaft ball bearings, the bearing speed parameter d_mn has now approached 4.0 × 10⁶ mm·r/min, corresponding to a rolling speed in the ball–raceway contact region of nearly 200 m/s. The lubricant supply temperature is typically maintained between 70 °C and 140 °C. Given the complex and highly fluctuating load spectrum of aeroengine mainshaft bearings, the design guidelines explicitly stipulate that the maximum contact stress must not exceed 2 GPa under long-term operating loads and 2.5 GPa under short-term peak loads. At high-speed and light-load conditions, special attention must be paid to controlling the cage slip ratio to prevent slip-induced failure. The cage slip phenomenon represents the collective sliding motion of all rolling elements relative to the raceways, and the ball SRR can be approximately regarded as equivalent to the cage slip ratio. In this study, systematic comparative traction tests were conducted for the newly developed aviation lubricant 4102 and the inservice lubricants 4050 and 4010 under typical aeroengine operating conditions. These measurements provide essential experimental support for lubricant selection and high-fidelity dynamic modeling of aeroengine mainshaft ball bearings. In addition to the results obtained within the experimental range, part of the traction analysis under higher stress and higher speed conditions was obtained through extrapolative predictions of the oil-film traction model, which had been calibrated and validated using the test data. This approach enables the simulation of operating conditions that more closely approximate the actual aeroengine environment.

4.3.1. Comparative Analysis of the Effect of SRR on Lubricant Traction Behavior

Figure 7 illustrates the variation in the oil-film traction coefficient with SRR under different operating conditions. As shown in the figure, when the SRR is small, the traction coefficient increases almost linearly with SRR, indicating that the lubricants exhibit Newtonian-like behavior in the low-shear regime. With increasing SRR, shear heating within the EHL contact becomes more pronounced, leading to a reduction in effective viscosity; consequently, the slope of the traction curve gradually decreases and the lubricants transition into a non-Newtonian shear-thinning regime. When the SRR exceeds a critical value, the traction coefficient approaches a plateau, suggesting that the lubricant has reached its limiting shear stress. Across all loads and temperatures, the three aviation lubricants demonstrate a consistent trend: the traction level of lubricant 4102 is the highest, followed by 4050, while 4010 exhibits the lowest traction response. This behavior reflects the superior film-carrying capacity and resistance to shear deformation associated with higher-viscosity lubricants.

In Figure 7a, at a contact pressure of 0.8 GPa, the overall traction levels remain low, and the curves shift markedly downward at elevated oil temperatures, indicating insufficient traction capacity under light-load and high-speed conditions. This implies a greater tendency for microslip or macroscopic sliding, suggesting that higher-viscosity lubricants are preferable in such regimes to ensure adequate traction. When the load increases to 1.5 GPa, as shown in Figure 7b, the traction curves shift upward, and the onset of nonlinearity occurs at a smaller SRR. This observation indicates that higher load enhances traction generation and helps suppress sliding; however, increased temperature still significantly weakens the lubricant’s traction performance. For the higher load cases shown in Figure 7c,d, corresponding to 2.0 GPa and 2.5 GPa, the traction curves rise further and reach the plateau region at relatively low SRR values, demonstrating stronger traction capability and earlier attainment of the limiting shear stress under heavy load. Even so, the detrimental influence of high temperature remains evident, consistently reducing the traction coefficient.

Overall, the results indicate that under heavy-load and high-speed conditions, low-viscosity lubricants may be employed to reduce frictional heating when sliding is well controlled and sufficient film thickness is maintained. Conversely, when the risk of sliding or insufficient film thickness is present, high-viscosity lubricants should be selected to provide higher traction output and ensure lubrication stability.

4.3.2. Comparative Analysis of the Effect of Entrainment Speed on Lubricant Film Traction Behavior

Figure 8 presents the variation in the oil-film traction coefficient with entrainment speed for three aviation lubricants of different viscosities under constant contact stress and various SRR. The results show that the traction coefficient decreases markedly and nonlinearly with increasing entrainment speed. Even at a high SRR of 0.20, the traction coefficient continues to decline as the entrainment speed increases from 20 m/s to 200 m/s.

A comparison of Figure 8a–d indicates that the overall traction level gradually increases as the SRR rises from 0.05 to 0.20, demonstrating that SRR strongly amplifies the absolute magnitude of traction. Nevertheless, all curves exhibit a clear plateau at high entrainment speeds, reflecting a saturation phenomenon. This behavior is primarily attributed to the pronounced shear heating and the rapid viscosity reduction induced at high entrainment speeds, which diminish the effective traction capacity of the lubricant. Among the three lubricants, lubricant 4102 consistently exhibits the highest traction coefficient, followed by 4050, while 4010 shows the lowest traction response. In addition, increasing the inlet oil temperature leads to a further reduction in the overall traction level for all lubricants.

For high-speed bearing applications, an increase in entrainment speed not only directly weakens the traction capacity but also indirectly intensifies frictional heating and oil-film thinning. Based on engineering experience with aeroengine ball bearings, when the cage slip ratio remains below approximately 15%, its influence on bearing performance is generally considered limited. Under such conditions, and provided that lubrication is sufficient, the use of a low-viscosity lubricant such as 4010 is preferred to minimize frictional heating. However, when the cage slip ratio exceeds 15%, a lubricant with higher traction capability should be selected to suppress severe sliding and prevent potential failure. In such cases, lubricant 4050 is recommended, and if necessary, lubricant 4102 may be adopted to provide even greater traction support.

4.3.3. Comparative Analysis of the Effect of Load on Lubricant Film Traction Behavior

Figure 9 shows the variation in the oil-film traction coefficient with maximum Hertzian contact stress for the three lubricants of different viscosities under constant entrainment speed and SRR. Overall, the traction coefficient exhibits an approximately linear increase with the maximum contact stress. Both the slope and intercept of the linear relationship shift noticeably with changes in speed and SRR, indicating strong coupling between load effects and operating dynamics.

Figure 9a,b show that under high-speed conditions (200 m/s), the overall traction level is comparatively low. However, as the contact stress increases from 0.8 GPa to 2.5 GPa, the curves rise progressively, and the increase is more pronounced at a high SRR of 0.20. This indicates that although traction is limited at high speed, increasing the load intensifies the pressure–viscosity effect within the film, thereby improving traction. At the same time, elevated temperature shifts the curves downward, indicating that the weakening effect of temperature can partly offset the traction enhancement induced by load. Figure 9c,d show that under low-speed conditions (30 m/s), the traction coefficient is substantially higher than at high speed. In particular, at large SRR values, the increase in traction coefficient with load is especially pronounced. This suggests that at low speeds, the longer residence time of the lubricant in the contact zone amplifies the viscous shear effect, leading to greater load sensitivity. Among the three lubricants, 4102 consistently exhibits the highest traction coefficient, while 4010 consistently shows the lowest, confirming that high-viscosity lubricants provide more stable traction reserves under heavy loads. Although increasing temperature reduces the overall level, the linear trend is preserved.

Under light-load conditions (<1.0 GPa), the traction coefficient remains low and the traction capacity insufficient, making the cage prone to slip. In this case, higher-viscosity lubricants such as 4102 are recommended to compensate for traction. In contrast, under heavy-load conditions (≥2.0 GPa), lubricants inherently provide an adequately high traction level, and the risk of slip is substantially reduced. Here, the design focus should shift toward controlling frictional power loss and ensuring adequate film thickness. When the load-carrying capacity of the film is sufficient, a low-viscosity lubricant such as 4010 may be prioritized to reduce frictional heating; if the film thickness is inadequate, 4050 or 4102 are recommended.

4.3.4. Comparative Analysis of the Effect of Temperature on Lubricant Film Traction Behavior

Figure 10 illustrates the relationship between the oil-film traction coefficient and supply temperature for three lubricants of different viscosities under constant entrainment speed and load. Overall, the traction coefficients of all lubricants decrease markedly in a nonlinear manner with increasing temperature and gradually approach a plateau. In the low-temperature range (approximately 20–60 °C), the decrease is more pronounced, whereas in the high-temperature range (>100 °C), the curves flatten progressively. This behavior results from the combined effects of reduced base viscosity and pressure–viscosity coefficient, along with the temperature-induced decrease in limiting shear stress, which together weaken the average shear stress in the contact zone and thereby reduce the effective traction capacity.

Specifically, the low-speed cases, shown in Figure 10b,d, exhibit higher traction coefficients with greater sensitivity to temperature, showing a rapid decline as temperature increases. This indicates that at low speeds, traction is primarily governed by viscous effects, and elevated temperature leads to substantial reductions in inlet viscosity and film thickness, thereby degrading traction performance. In contrast, the high-speed cases, illustrated in Figure 10a,c, show lower traction levels with reduced sensitivity to temperature. The curves reach saturation earlier in the high-temperature range, suggesting that shear heating and thermal thinning of viscosity dominate at high speeds, while further temperature rise has a progressively smaller effect on traction reduction. Increasing the load from 0.8 GPa to 2.0 GPa increases the absolute traction level but does not alter the underlying trend of decreasing traction with temperature followed by a plateau.

The comparison among the three lubricants reveals a consistent and distinct separation of traction coefficients, with 4102 being the highest, followed by 4050, and 4010 the lowest. This indicates that a higher viscosity grade offers greater traction capacity under a given SRR. Notably, in the high-temperature region, the three curves gradually converge, reflecting a “high-temperature equivalence” phenomenon: when the base viscosity and pressure–viscosity coefficient decrease to low levels, the influence of viscosity grade on traction characteristics is progressively diminished. Nevertheless, because high-viscosity lubricants still maintain higher absolute traction levels across the entire temperature range, the use of 4102 or 4050 remains a more reliable strategy under elevated-temperature conditions.

4.3.5. Lubricant Selection Criteria and Engineering Implications

In summary, load, speed, temperature, and cage slip ratio are the key factors jointly determining the selection of lubricants for aeroengine bearings. Under light-load or high-temperature and high-speed conditions, where the traction capability is insufficient and slip is likely to occur, high-viscosity lubricants such as 4102 or 4050 should be prioritized to compensate for the loss of traction. Under heavy-load conditions, the lubricant itself can provide a sufficiently high traction level; thus, when the oil-film thickness is adequate, the low-viscosity lubricant 4010 can be preferred to reduce frictional power loss.

At medium-to-low speeds and temperatures, the traction margin becomes larger, allowing flexible use of low-viscosity lubricants 4010 to minimize frictional heating. Meanwhile, the cage slip ratio is an equally important constraint. When it remains below 15% and the lubrication state is good, using a low-viscosity lubricant 4010 helps reduce frictional heat generation. Conversely, when the slip ratio exceeds 15%, a lubricant with higher viscosity 4050 or 4102 should be selected to enhance traction and prevent slip-induced failure.

5. Conclusions

In this study, comprehensive traction data were obtained on a ball–disk test rig for three aviation lubricants, including the newly developed 4102 (7 cSt) and the inservice grades 4050 (5 cSt) and 4010 (3 cSt), across the full range of operating conditions. The experimental results clarified the dominant influence of viscosity on oil-film traction behavior. Based on these findings, a four-parameter and three-coefficient engineering model was developed by using the maximum Hertzian contact stress as the independent variable. This formulation eliminates the non-physical paradox of nonzero traction at zero slip and the overfitting problem reported for the five-parameter and four-coefficient model proposed by Wang and Deng. It also avoids the abnormal traction behavior observed in traditional load-based models, which arises from geometric scaling effects of the ball specimen. The traction model proposed in this work exhibits excellent extrapolation capability and prediction accuracy. It can be directly integrated into aeroengine mainshaft bearing dynamic simulation frameworks, enabling rapid lubricant selection and reliable bearing performance evaluation. The main conclusions are as follows:

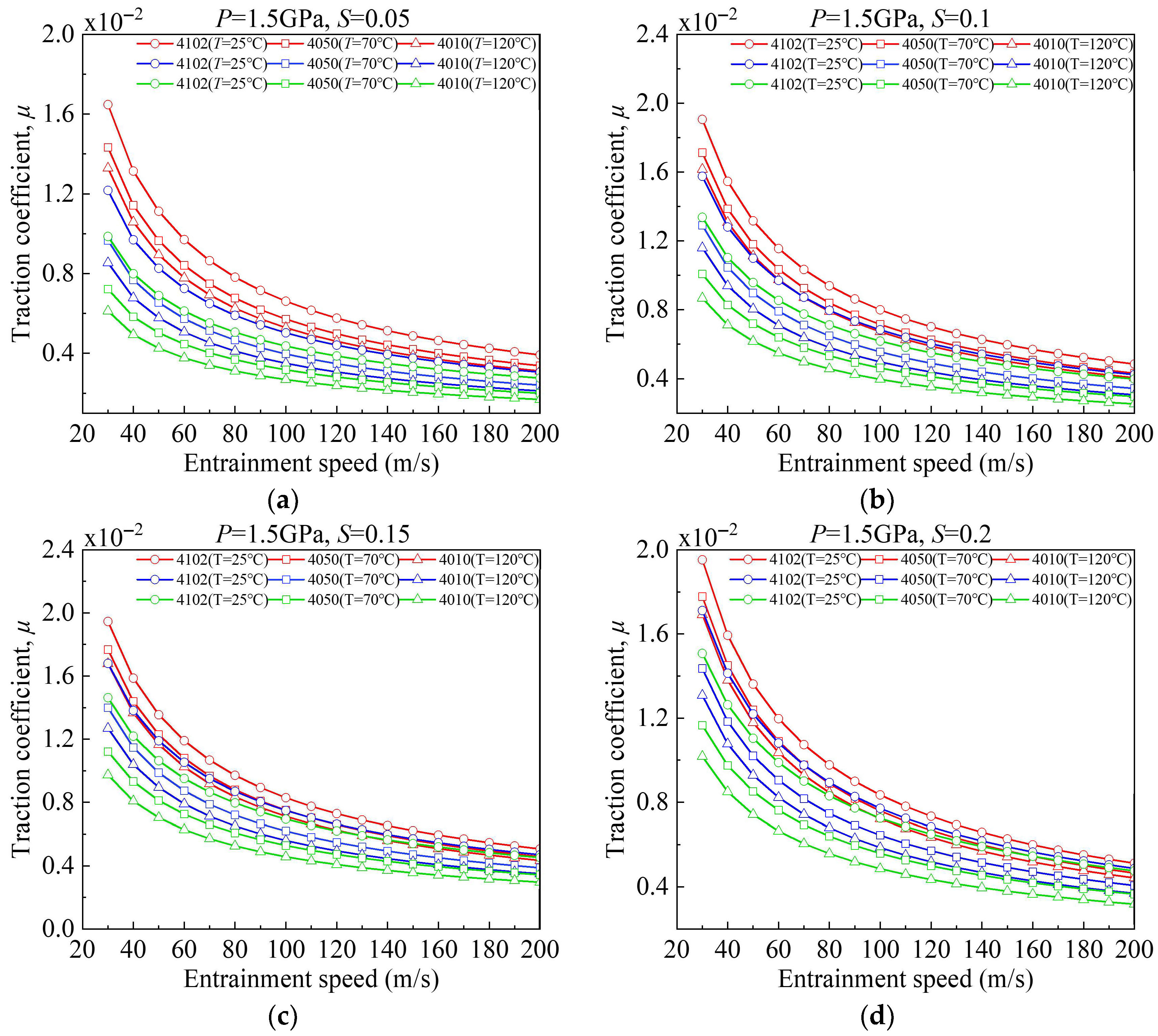
(1) Lubricant viscosity exerts a significant influence on the oil-film traction coefficient. Higher viscosity consistently leads to higher traction. Under identical operating conditions, lubricant 4102 exhibits the highest traction coefficient, followed by 4050, whereas 4010 shows the lowest traction response.

(2) The oil-film traction coefficient increases significantly with increasing load. In contrast, higher temperature and higher entrainment speed both lead to a reduction in traction, and the weakening effect induced by entrainment speed is particularly pronounced.

(3) The SRR governs the transition of lubricant flow behavior. At low SRR, the oil-film traction coefficient increases linearly with SRR, indicating Newtonian fluid behavior. After the SRR exceeds a critical value, the rate of increase in traction slows, and the lubricant exhibits non-Newtonian shear-thinning behavior. With further increases in SRR, the traction coefficient approaches a stable plateau, and the three lubricants display a similar limiting trend.

(4) The guideline for selecting lubricants for aeroengine ball bearings is as follows. Under high-speed, light-load and high-temperature conditions in which the cage slip ratio exceeds 15 percent, the high-viscosity lubricant 4102 should be prioritized to compensate for insufficient traction and to suppress sliding. When the cage slip ratio does not exceed 15 percent and adequate lubrication is ensured, the low-viscosity lubricant 4010 is preferred in order to reduce frictional heating, with 4050 as the secondary option.