Using the Principle of Newton’s Rings to Monitor Oil Film Thickness in CNC Machine Tool Feed Systems
Abstract
1. Introduction
2. Principle and Methodology
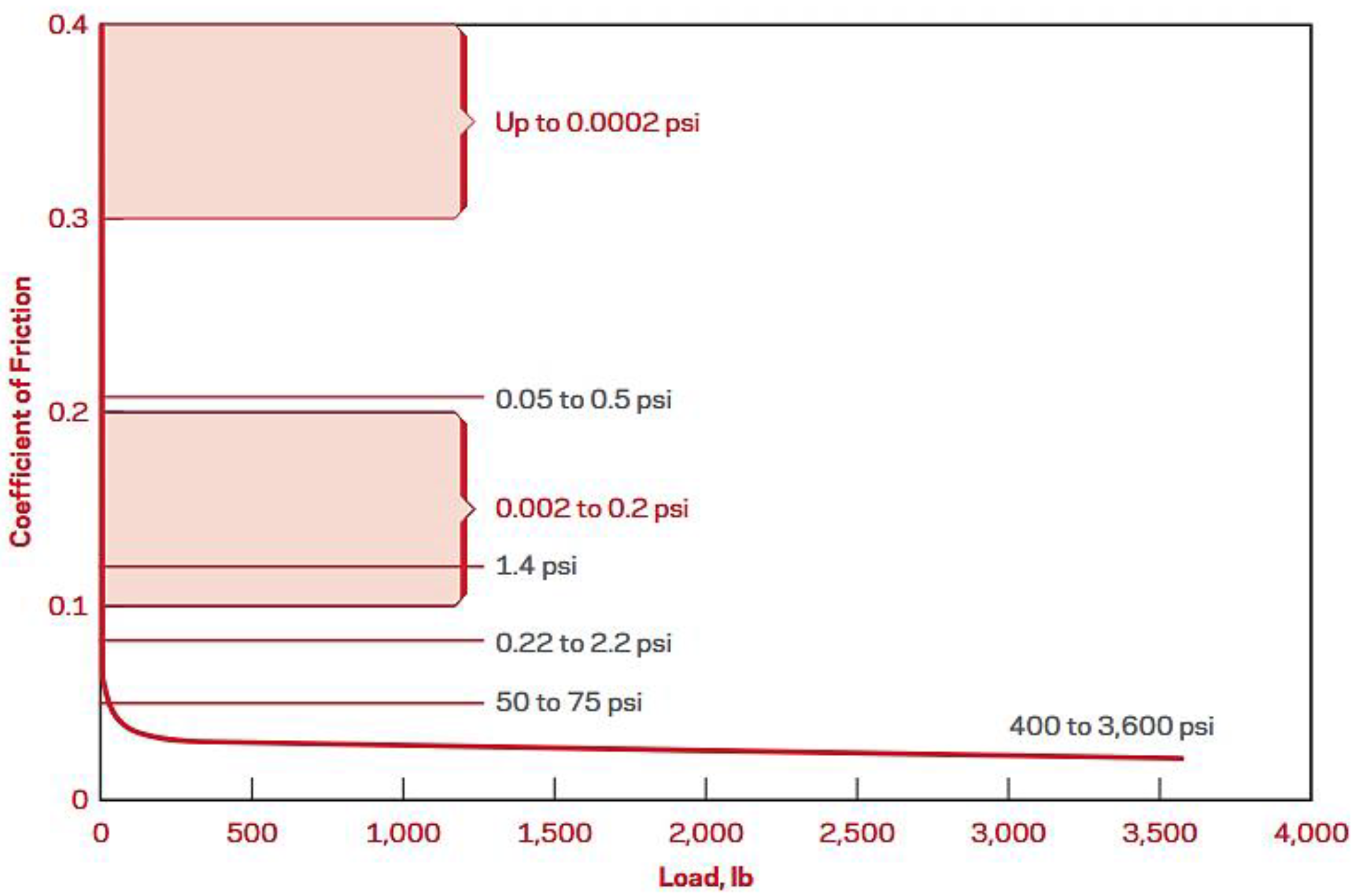
2.1. Principle of Feed System Lubrication
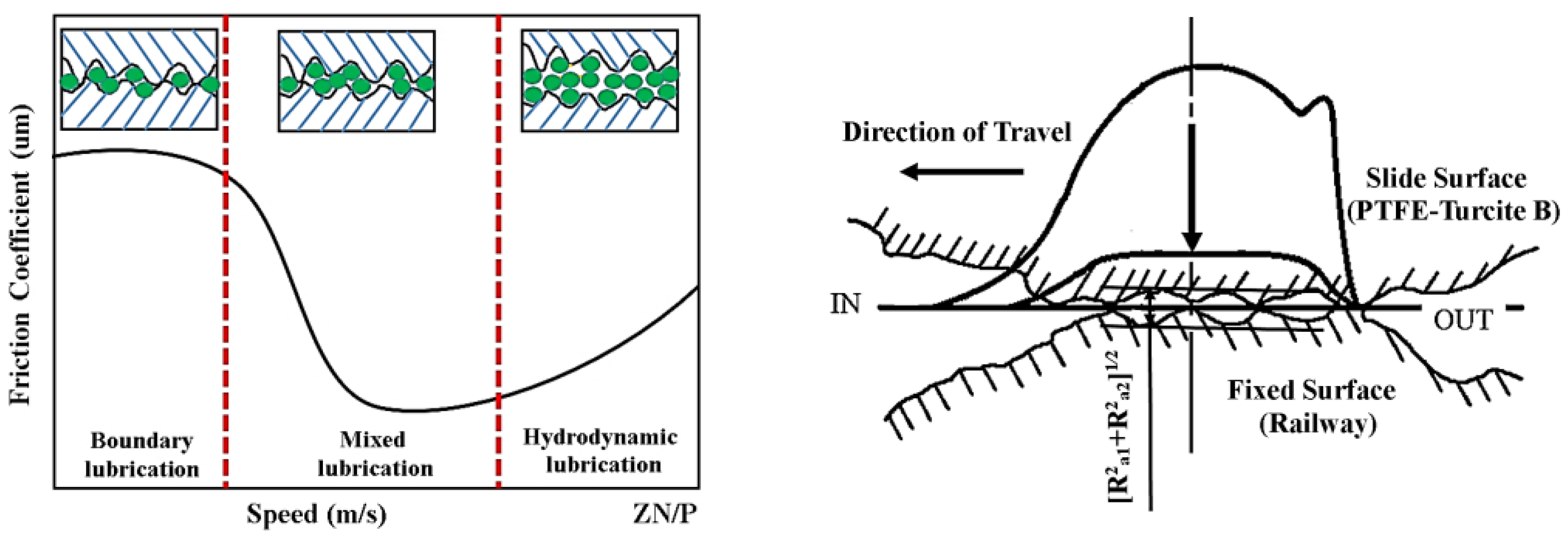
2.2. Principle of Lubrication
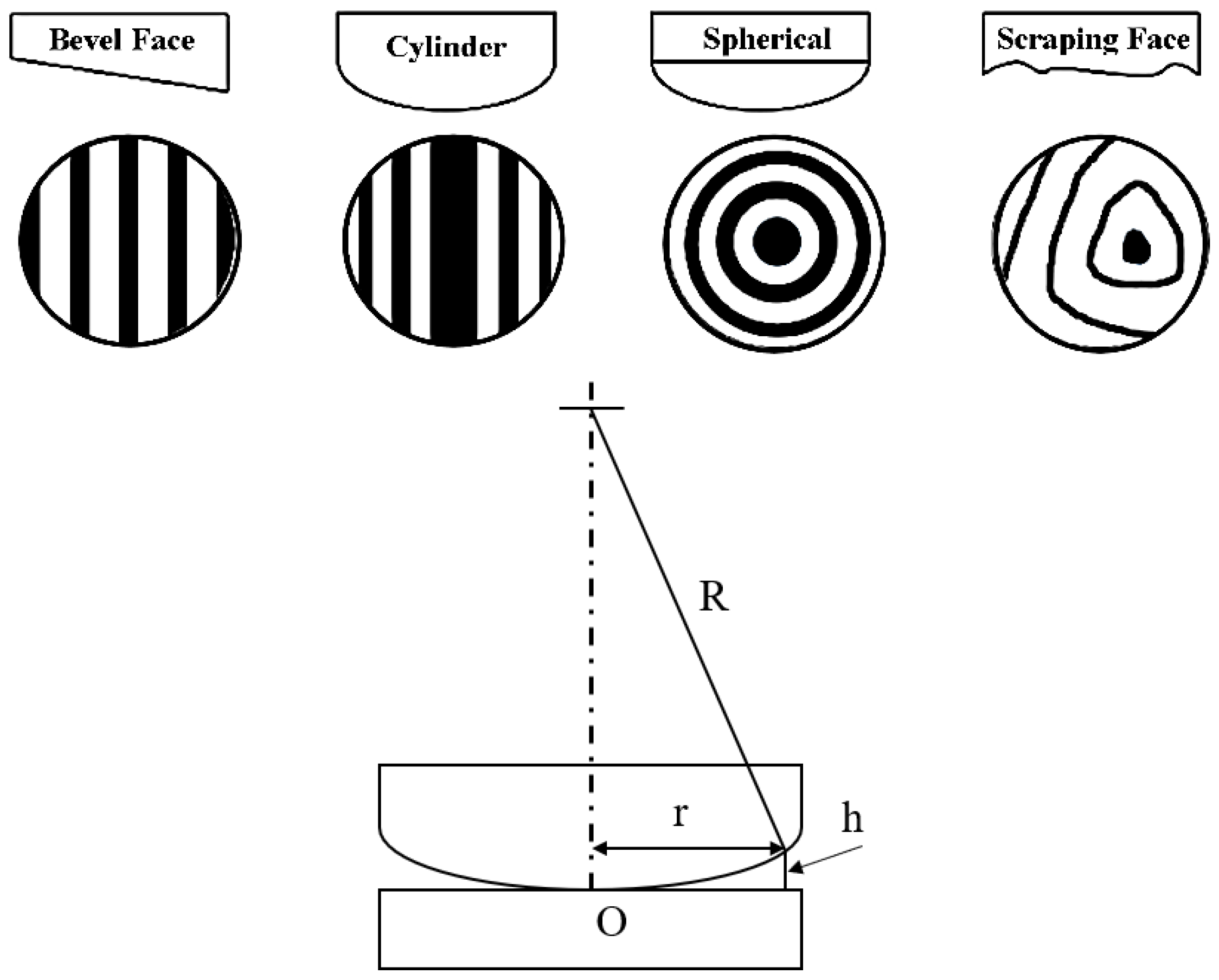
2.3. Principle of Newton’s Rings
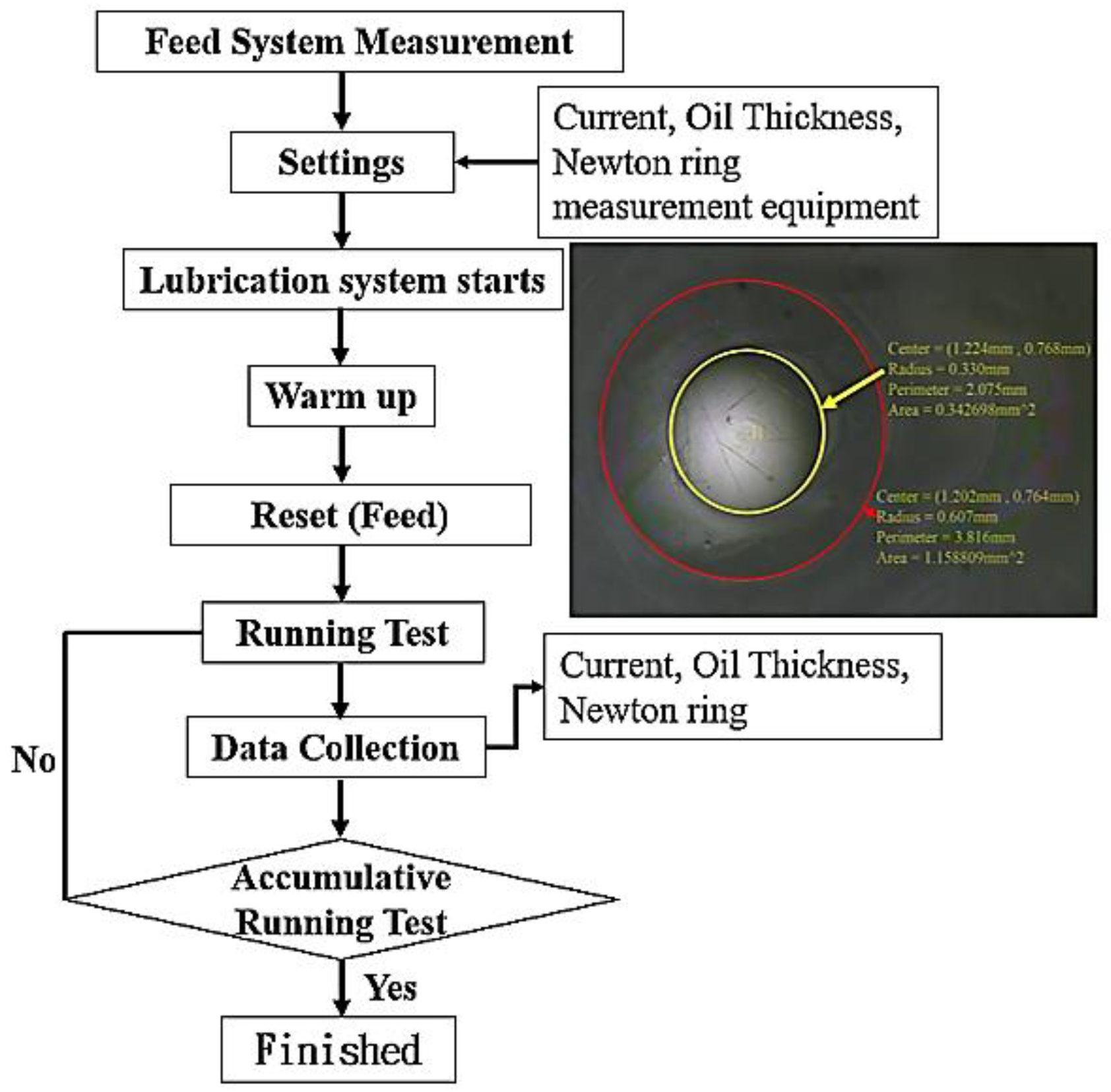
3. Experimental Equipment Development and Process
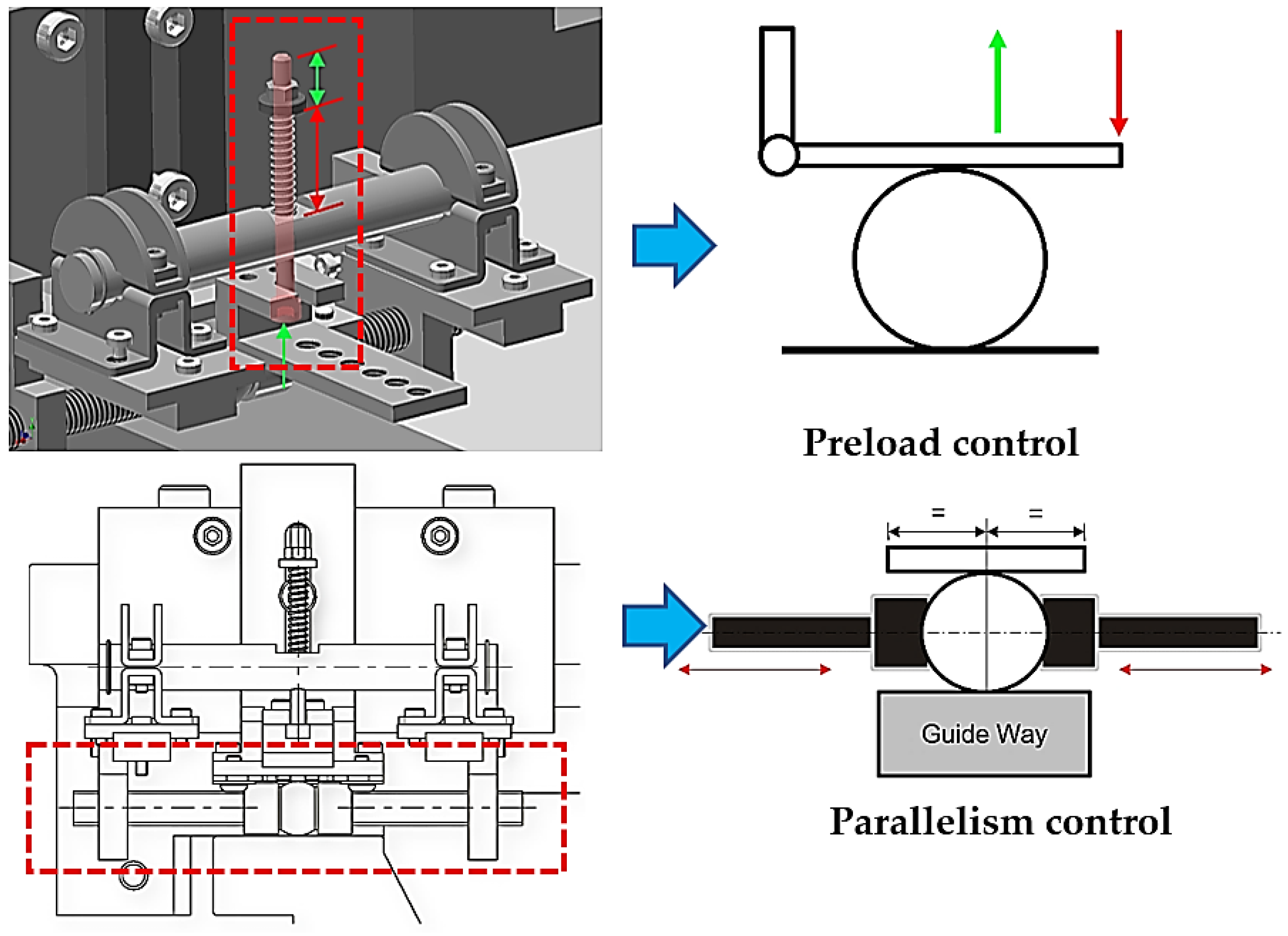
3.1. Newton’s Rings Image Measurement System
3.2. Experimental Design and Method
4. Results and Discussion
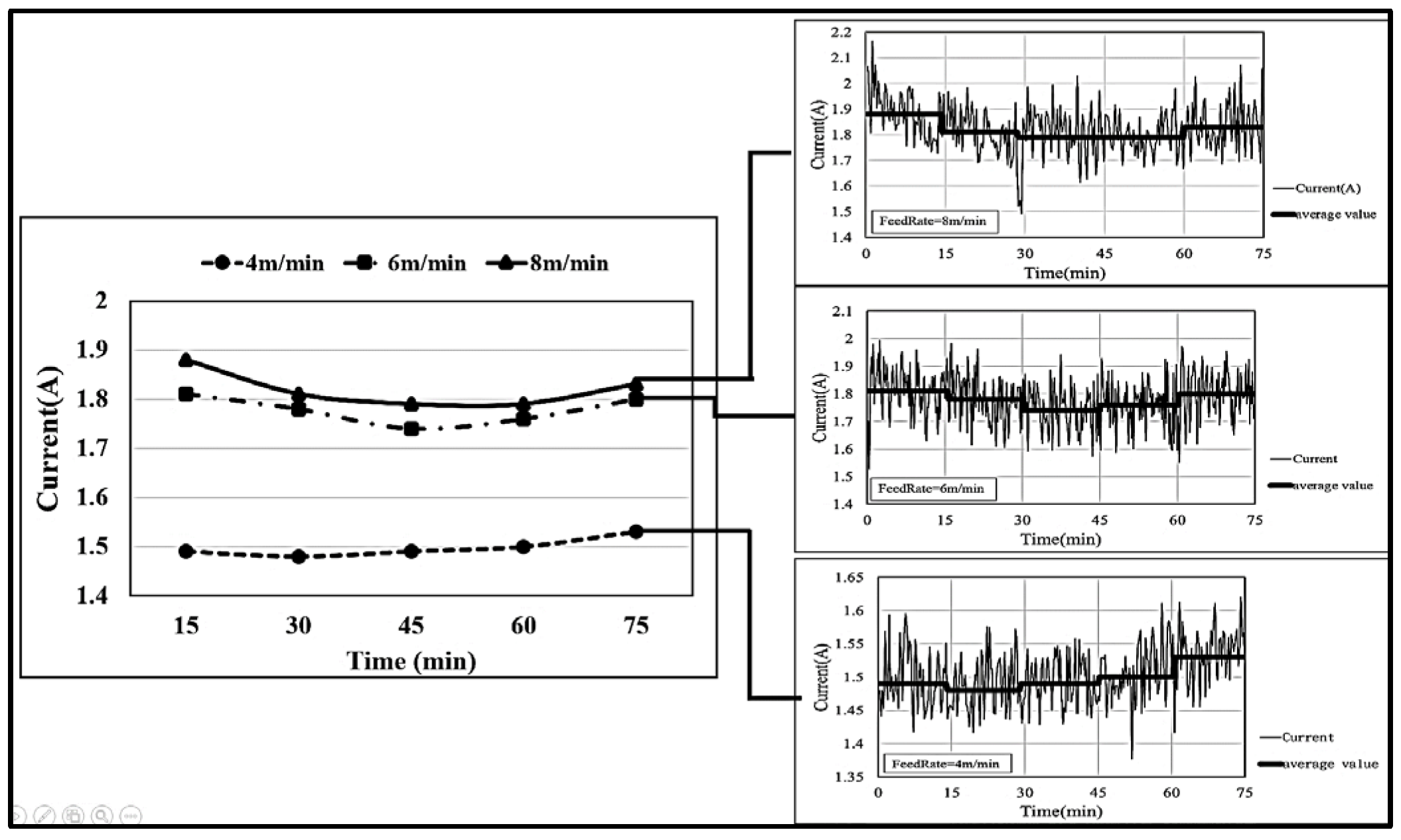
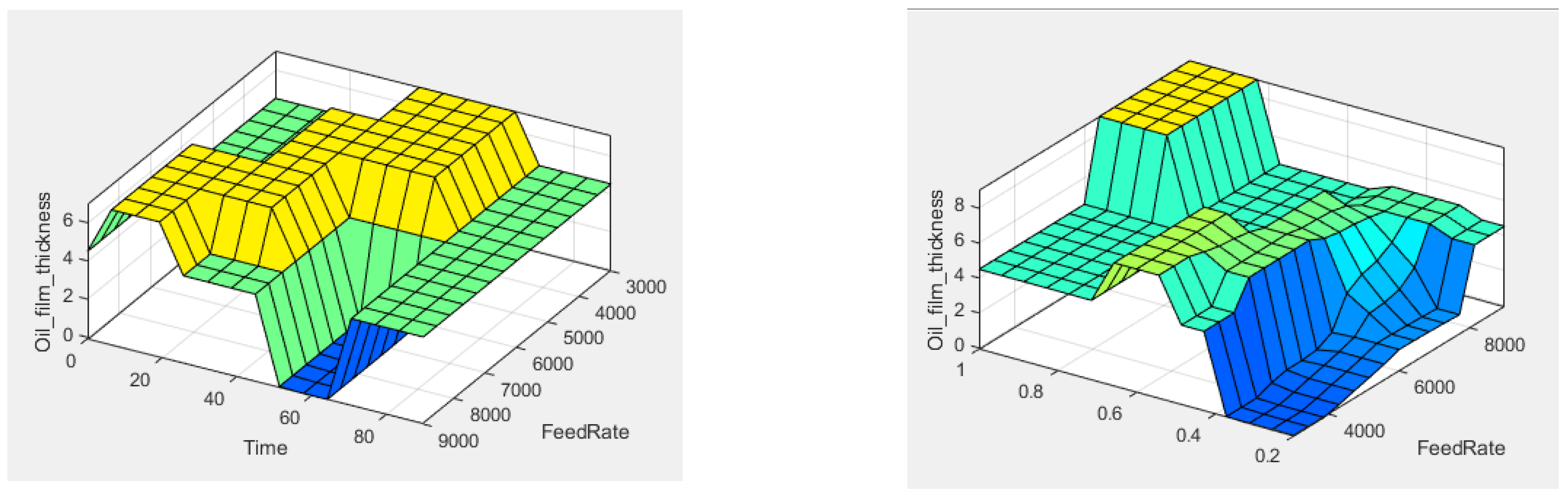
4.1. Effect of Different Feed Rates on Oil Film Thickness
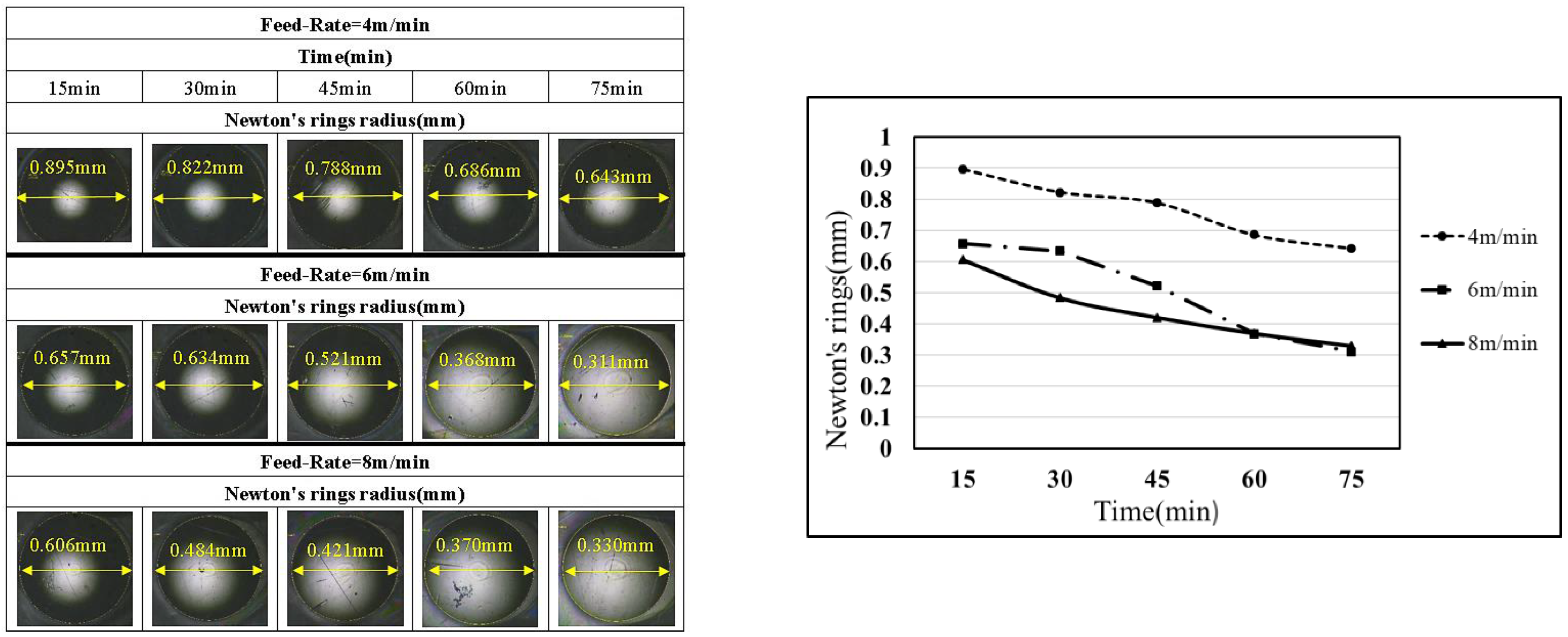
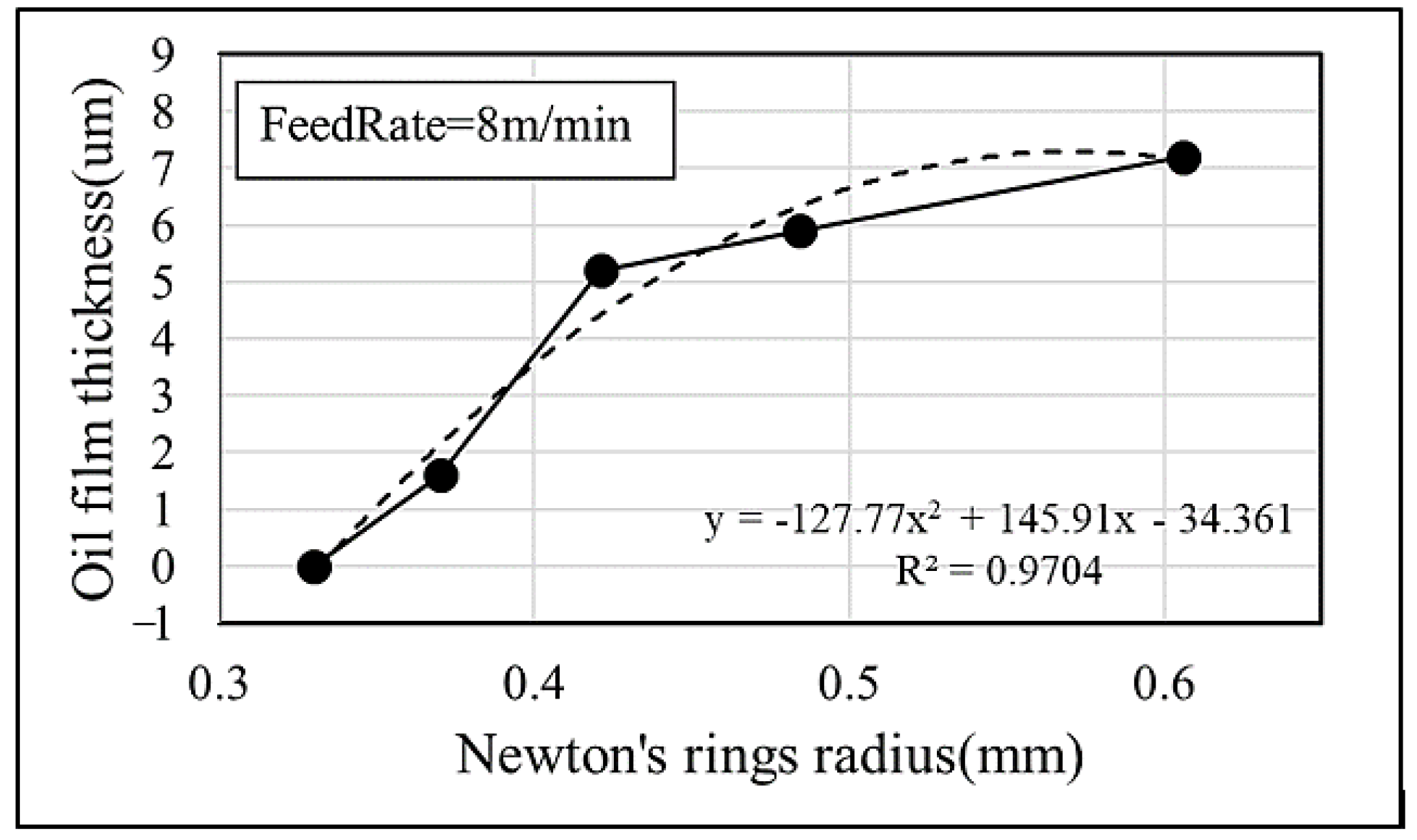
4.2. Relationship Between the Radius of Newton’s Rings and Oil Film Thickness
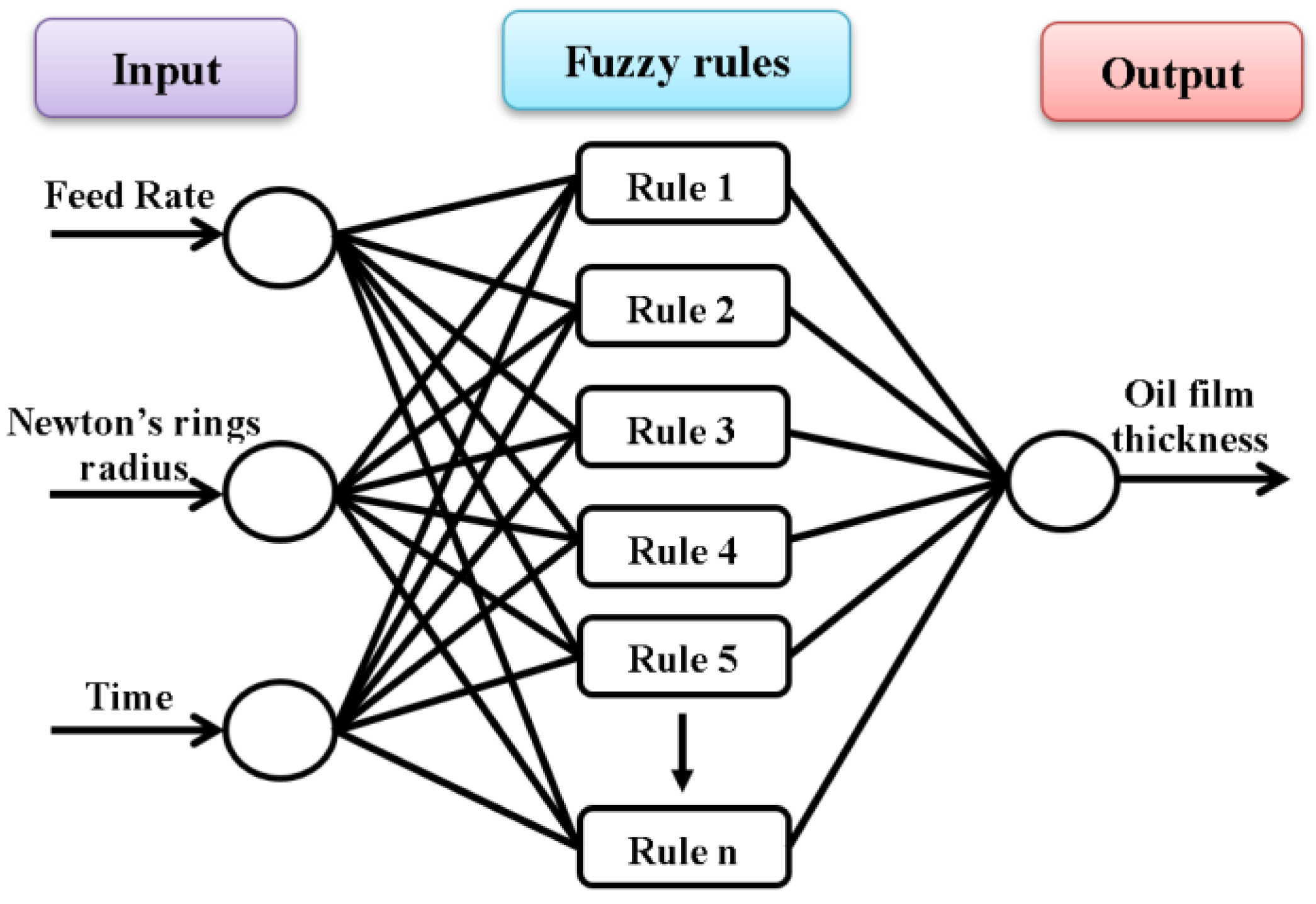
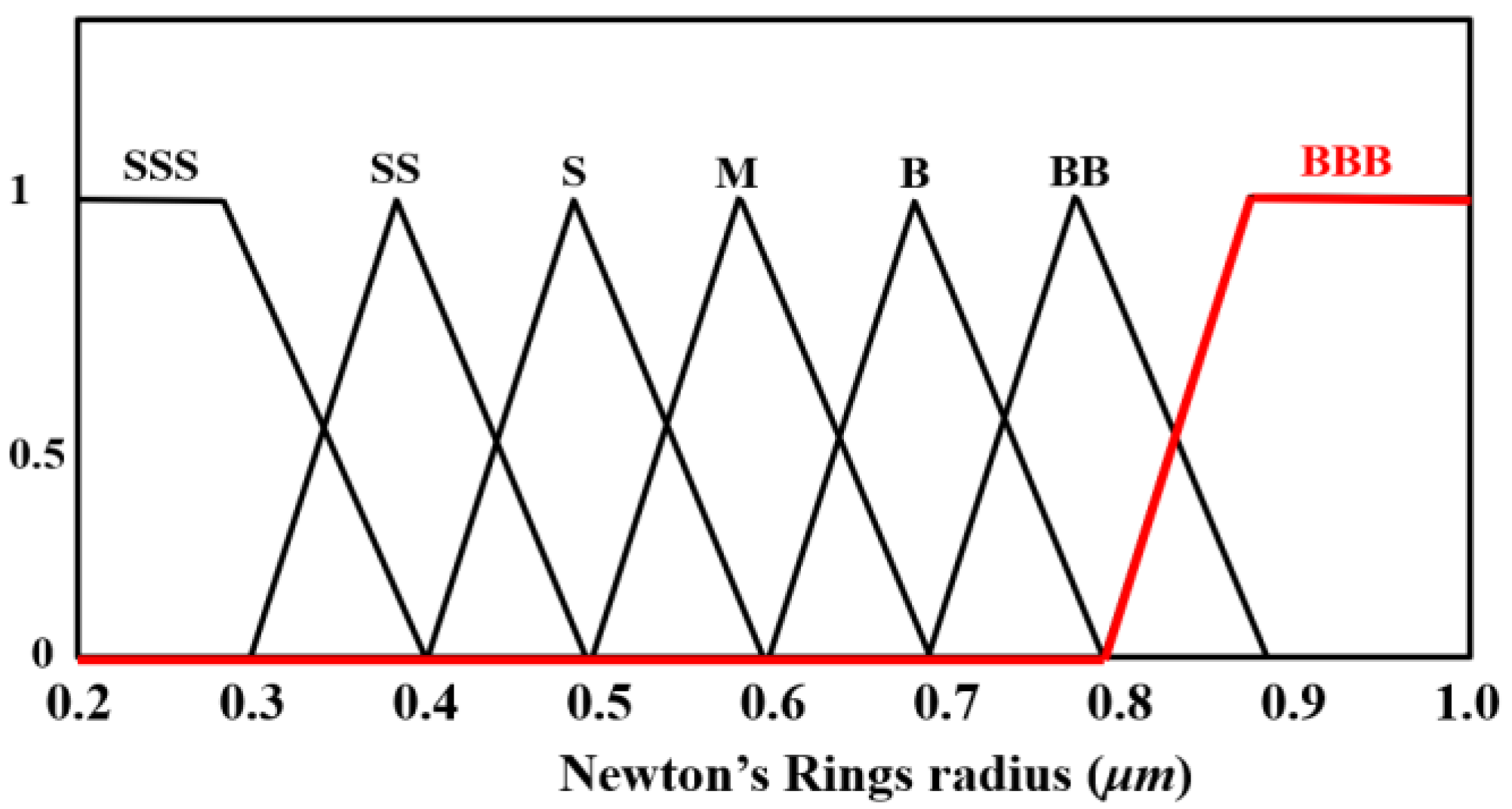
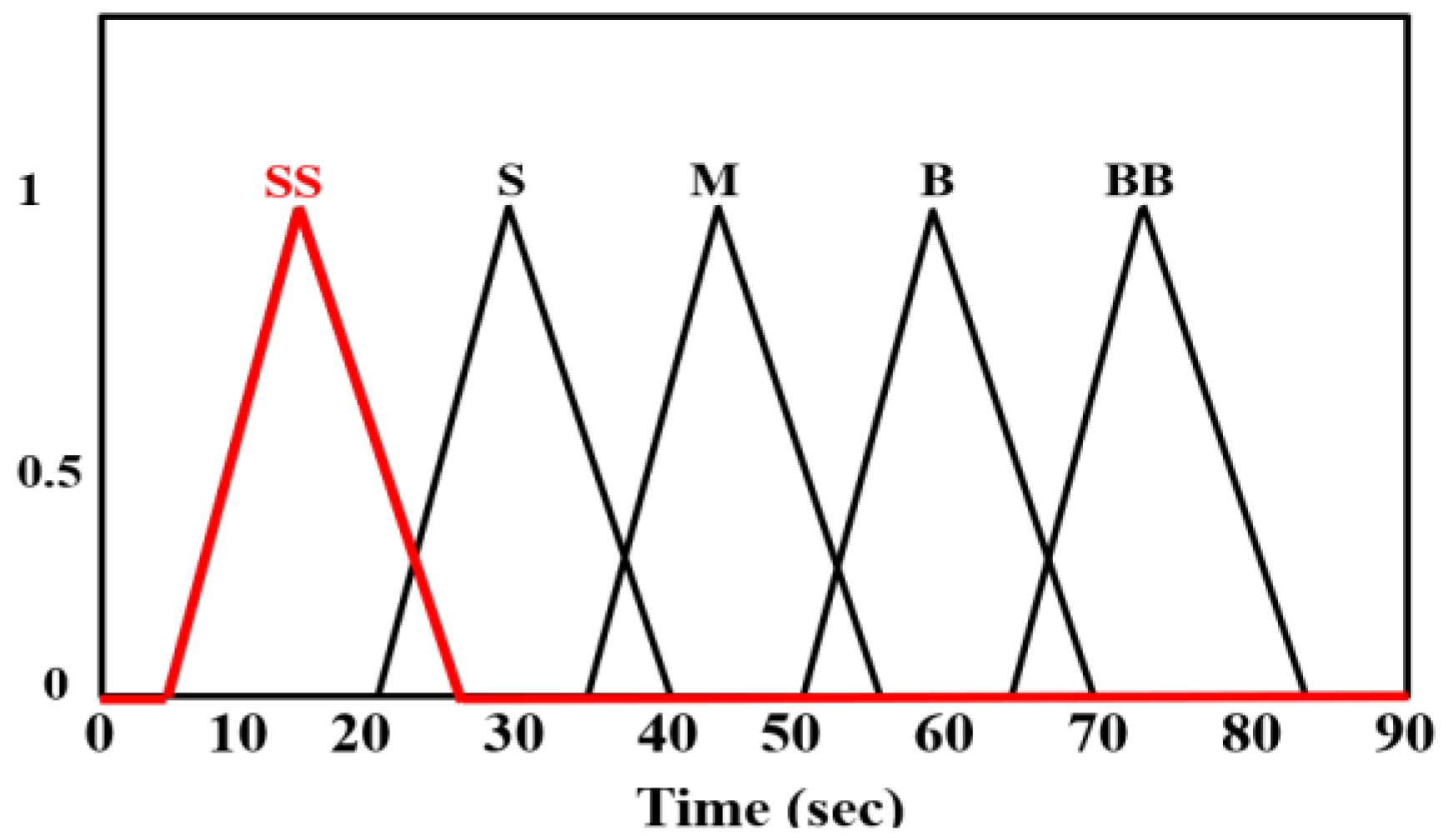
4.3. Using Fuzzy Theory to Predict Oil Supply Timing and Oil Film Thickness
5. Conclusions
- An increase in feed rate from 4 m/min to 6 m/min led to an 18% rise in current. Further increasing the feed rate to 8 m/min resulted in a 21% increase in current. There are two main reasons for this observation: (1) the smaller the feed rate, the lower the mechanical power and the smaller the relative current; (2) the feed rate is proportional to the viscosity coefficient of the lubricating oil.
- The variation trend in the radius of Newton’s rings is consistent with the trend of the oil film thickness value. The radius of Newton’s rings and oil film thickness were measured at different feed rates, and linear regression shows that the R2 ranges from 0.87 to 0.94, surpassing the threshold of 0.7 for a high correlation. The average error is 6.5%.
- Oil film consumption is proportional to the feed rate, as shown in Formula 10. An increase in feed rate from 4 m/min to 6 m/min resulted in a 219% increase in oil film consumption, while a further increase to 8 m/min led to a 300% increase.
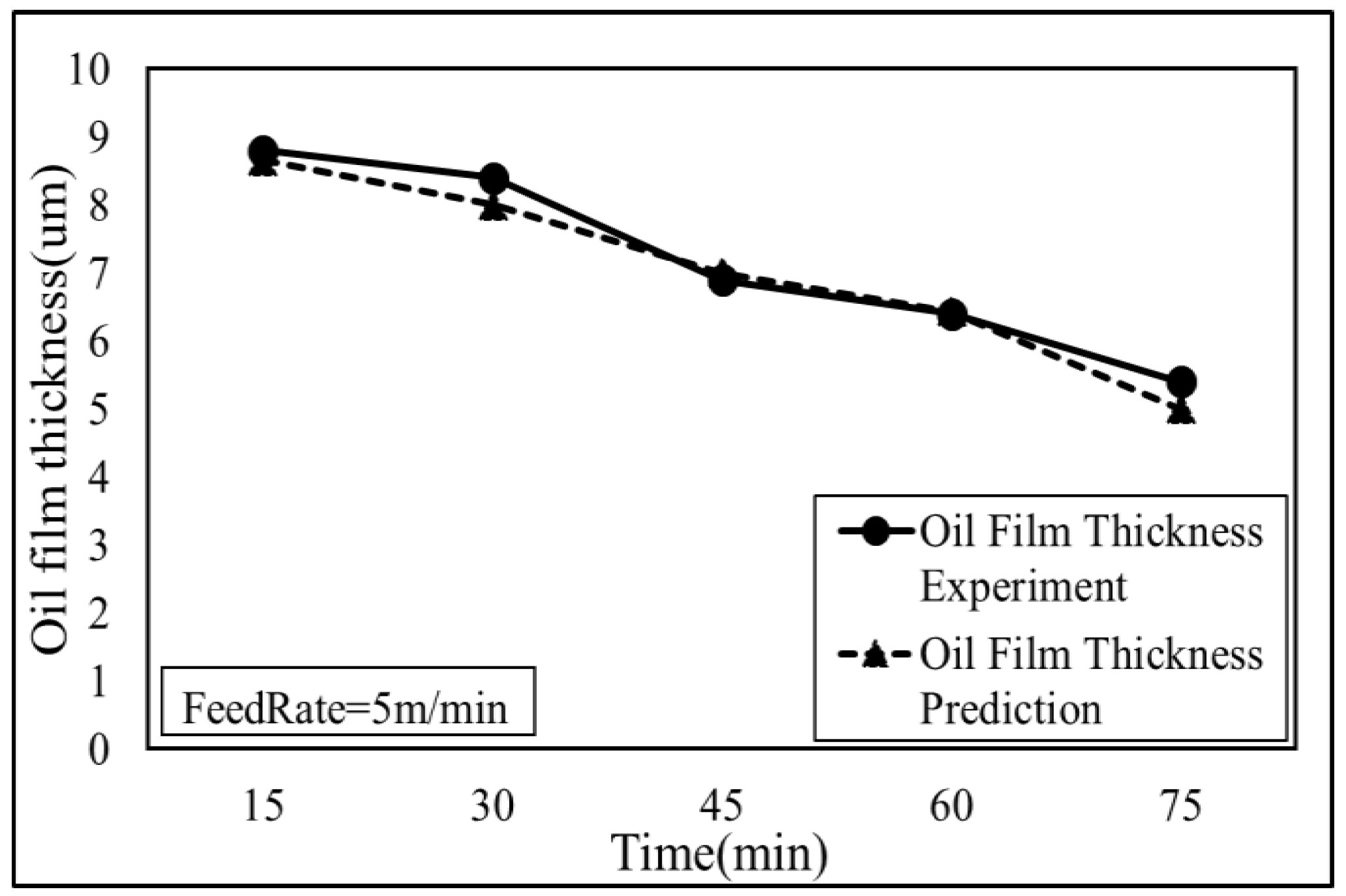
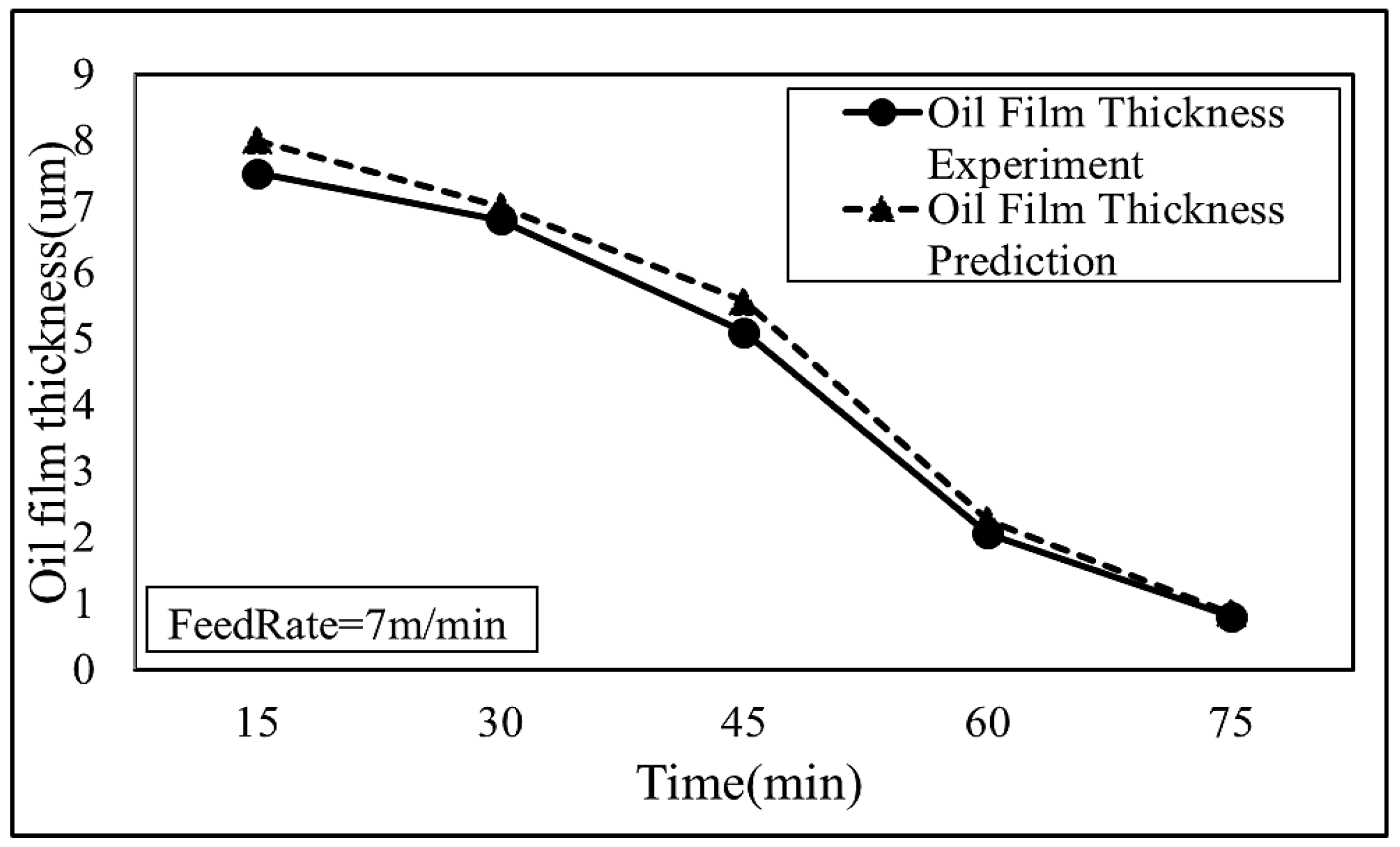
- This study uses fuzzy theory with three different feed rates to predict the oil supply timing and oil film thickness. It is verified that the experimental results are consistent with the predicted results, with errors less than 10%. The regression analysis method is used to illustrate that the trends in oil film thickness and the radius of Newton’s rings are consistent, a result that can be used to identify the rail lubrication state.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Z | Absolute viscosity of lubricant |
| N | Feed speed (mm/min) |
| P | Load per unit area (N) |
| Ra1, Ra2 | Contact surfaces |
| Λ | Boundary lubrication |
| F | Friction (N) |
| η | Viscosity coefficient of lubricating oil |
| A | Contact area (um2) |
| N | Feeding system platform reciprocating feed rate |
| H | Displacement-meter-measured rail oil film thickness value (um) |
| Composite surface roughness (um) | |
| Ra track | Hard rail surface roughness (um) |
| Ra Turcite | Wear plate surface roughness (um) |
| r | Radius of ring (um) |
| R | Radius of curvature of lens (um) |
| I1, I2 | Light intensity (CD) |
References
- Lo, S.W.; Yang, T.S. A New Mechanism of Asperity Flattening in Sliding Contact—The Role of Tool Elastic Micro-wedge. ASME Trans. J. Tribol. 2003, 125, 713–719. [Google Scholar] [CrossRef]
- Maurya, A.; Kumar, A.; Punia, A.D. CFD and Frictional Torque Analysis of Hydrodynamic Journal Bearing. IJERT 2019, 8, 959–968. [Google Scholar]
- Meng, Y.; Xu, J.; Jin, Z.; Prakash, B.; Hu, Y. A review of recent advances in tribology. Friction 2020, 8, 221–300. [Google Scholar] [CrossRef]
- Zapletal, T.; Sperka, P.; Krupka, I.; Hartl, M. The effect of surface grooves on transition to mixed lubrication. Tribol. Int. 2017, 114, 409–417. [Google Scholar] [CrossRef]
- Nordhagen, E.M.; Sveinsson, H.A.; Malthe-Sørenssen, A. Diffusion-Driven Frictional Aging in Silicon Carbide. Tribol. Lett. 2023, 71, 95. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, B.; Cai, L.; Wang, W.; Liang, T.; Lei, M. High-Temperature and High-Pressure Tribological Properties of Siliconized Graphite for Water-Lubricated Thrust Bearing Application in Main Coolant Pump. Lubricants 2024, 12, 159. [Google Scholar] [CrossRef]
- Qi, B.; Zhao, J.; Chen, C.; Song, X.; Jiang, H. Accuracy decay mechanism of ball screw in CNC machine tools for mixed sliding-rolling motion un-der non-constant operating conditions. Int. J. Adv. Manuf. Technol. 2023, 124, 4349–4363. [Google Scholar] [CrossRef]
- Parameswaran, G.; Jayaram, V.; Kailas, S.V. Frictional Characteristic Curves of Ground Surfaces in Lubricated Sliding. Lubricants 2023, 11, 354. [Google Scholar] [CrossRef]
- Li, C.; Xu, M.; Song, W.; Zhang, H. A review of static and dynamic analysis of ball screw feed drives, recirculating linear guideway, and ball screw. Int. J. Mach. Tools Manuf. 2023, 188, 104021. [Google Scholar] [CrossRef]
- Verma, K.; Belokar, R.M. Experimental investigations of ball screws over static and accelerating torque-based lead factor in CNC machining centre. J. Eng. 2018, 2018, 17–21. [Google Scholar] [CrossRef]
- Chen, S.H.; Lin, M.Y. Development and design of intelligent lubricating equipment for feed systems. Heliyon 2024, 10, e26124. [Google Scholar] [CrossRef] [PubMed]
- Rigacci, M.; Sato, R.; Shirase, K. Experimental evaluation of mechanical and electrical power consumption of feed drive systems driven by a ball-screw. Precis. Eng. 2020, 64, 280–287. [Google Scholar] [CrossRef]
- Yu, H.; Luan, X.; Zheng, G.; Hao, G.; Liu, Y.; Xing, H.; Liu, Y.; Fu, X.; Liu, Z. Analysis and Experiment of Thermal Field Distribution and Thermal Deformation of Nut Rotary Ball Screw Transmission Mechanism. Appl. Sci. 2024, 14, 5790. [Google Scholar] [CrossRef]
- Cui, P.; Hou, Z.; He, L.; Zheng, H.; He, Y.; Fan, Y.; An, L.; Huang, Y. Experimental Study on In Situ Storage of Grease-Lubricated Ball Screws. Appl. Sci. 2024, 14, 2734. [Google Scholar] [CrossRef]
- Goncalves, D.; Graca, B.; Campos, A.V.; Seabra, J. Film thickness and friction behaviour of thermally aged lubricating greases. Tribol. Int. 2016, 100, 231–241. [Google Scholar] [CrossRef]
- Grebe, M.; Ruland, M. Influence of Mechanical, Thermal, Oxidative and Catalytic Processes on Thickener Structure and Thus on the Service Life of Rolling Bearings. Lubricants 2022, 10, 77. [Google Scholar] [CrossRef]
- Wen, S.; Huang, P. Principles of Tribology; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Luo, J. Thin Film Lubrication. In Encyclopedia of Tribology; Wang, Q.J., Chung, Y.W., Eds.; Springer: Boston, MA, USA, 2013. [Google Scholar] [CrossRef]
- Ramadan, W.A.; Wahba, H.H.; El-Tawargy, A.S. Enhanced short temporal coherence length measurement using Newton’s rings interference. Opt. Laser Technol. 2020, 127, 106192. [Google Scholar] [CrossRef]
- Chu, H.M.; Lee, R.T.; Chiou, Y.C.; Huang, B.W. EHL Optical interferometry Inverse approach Viscosity. Bull. Yung-Ta Inst. Technol. Commer. 2005, 6, 53–63. Available online: http://catalog.digitalarchives.tw/item/00/4c/40/e2.html (accessed on 30 June 2025).
- Tofighi-Niaki, E.; Safizadeh, M.S. Dynamic of a Flexible Rotor-Bearing System Supported by Worn Tilting Journal Bearings Experiencing Rub-Impact. Lubricants 2023, 11, 212. [Google Scholar] [CrossRef]
- Tošić, M.; Larsson, R.; Lohner, T. Thermal Effects in Slender EHL Contacts. Lubricants 2022, 10, 89. [Google Scholar] [CrossRef]
- Zhu, J.; Li, X.; Beamish, S.; Dwyer-Joyce, R.S. An ultrasonic method for measurement of oil films in reciprocating rubber O-ring seals. Tribol. Int. 2022, 167, 107407. [Google Scholar] [CrossRef]
- Qin, W.; Wang, M.; Sun, W.; Shipway, P.; Li, X. Modeling the effectiveness of oil lubrication in reducing both friction and wear in a fretting contact. Wear 2019, 426, 770–777. [Google Scholar] [CrossRef]
- Khare, H.S.; Moore, A.C.; Haidar, D.R.; Gong, L.; Ye, J.; Rabolt, J.F.; Burris, D.L. Interrelated effects of temperature and environment on wear and tribochemistry of an ultralow wear PTFE composite. J. Phys. Chem. C 2015, 119, 16518–16527. [Google Scholar] [CrossRef]
- Chen, S.-H.; Haung, Z.-J. A study of using back-propagation neural model in automatic lubrication installation for the feeding system of computer numerical control machine tool. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2022, 236, 1219–1231. [Google Scholar] [CrossRef]
- Teflon PTFE. Properties Handbook. 2020. Available online: http://www.rjchase.com/ptfe_handbook.pdf (accessed on 30 June 2025).
- Sheng, L.R. Lubrication; Quan-Hua Science and Technology Book Co., Ltd.: Taipei, Taiwan, 1994; ISBN 9789571410067. [Google Scholar]
- Tsai, C.-H.; Tien, K.-C.; Chen, M.-C.; Chang, K.-M.; Lin, M.-S.; Cheng, H.C.; Lin, Y.-H.; Chang, H.-W.; Lin, H.-W.; Lin, C.-L.; et al. Characterizing coherence lengths of organic light-emitting devices using Newton’s rings apparatus. Org. Electron. 2010, 11, 439–444. [Google Scholar] [CrossRef]
- Beamish, S.; Reddyhoff, T.; Hunter, A.; Dwyer-Joyce, R.S. A method to determine acoustic properties of solids and its application to measuring oil film thickness in bearing shells of unknown composition. Measurement 2022, 195, 111176. [Google Scholar] [CrossRef]
- Yang, S.W.; Lin, C.S.; Fu, S.H.; Yeh, M.S.; Tsou, C.; Lai, T.H. Lens sag measurement of microlens array using optical interferometric microscope. Opt. Commun. 2012, 285, 1066–1074. [Google Scholar] [CrossRef]
- Guo, S.D. Optical Testing Technology; Beijing Institute of Technology Press: Beijing, China, 2010; ISBN 9787564025649. [Google Scholar]
- Lee, K.-T. Lubrication; Gaoli Books Co., Ltd.: Taipei, Taiwan, 2019; ISBN 9789575840617. [Google Scholar]






| Feed Rate | R2 | F | Formula |
|---|---|---|---|
| 4 m/min | 0.87 | 19.68 | = 1.9604x2 + 5.0079x + 2.6109 |
| 6 m/min | 0.94 | 25.37 | = −45.395x2 + 60.094x − 12.319 |
| 8 m/min | 0.97 | 14.68 | = −127.77x2 + 145.91x − 34.361 |
| Feed Rate (m/min) | Time (min) | Newton’s Rings (mm) | Predicted Thickness (mm) | Actual Thickness (mm) | Error Value |
|---|---|---|---|---|---|
| 4 | 15 | 0.9 | 8.7 | 8.6 | 1% |
| 75 | 0.6 | 6.3 | 5.5 | 15% | |
| 6 | 30 | 0.8 | 6.7 | 6.9 | 3% |
| 75 | 0.3 | 1.6 | 1.5 | 8% | |
| 8 | 30 | 0.5 | 6.6 | 6.2 | 7% |
| 45 | 0.4 | 3.5 | 3.4 | 5% | |
| Average error | 6.5% | ||||
| Time (min) | Newton’s Rings Radius (mm) | Oil Film Thickness (um) | Relative Error e% | ||
|---|---|---|---|---|---|
| Actual Value | Figure | Actual | Predict | ||
| 15 | 0.87 |  | 8.8 | 8.65 | 2% |
| 30 | 0.86 |  | 8.4 | 8 | 5% |
| 45 | 0.66 |  | 6.9 | 7 | 1% |
| 60 | 0.53 |  | 6.4 | 6.43 | 0% |
| 75 | 0.51 |  | 5.4 | 8 | 7% |
| Time (min) | Newton’s Rings Radius (mm) | Oil Film Thickness (um) | Relative Error e% | ||
|---|---|---|---|---|---|
| Actual Value | Figure | Actual | Predict | ||
| 15 | 0.73 |  | 7.5 | 8 | 7% |
| 30 | 0.62 |  | 6.8 | 7 | 3% |
| 45 | 0.46 |  | 5.1 | 5.56 | 9% |
| 60 | 0.37 | 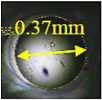 | 2.05 | 2.25 | 10% |
| 75 | 0.3 |  | 0.85 | 0.8 | 7% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.-H.; Haung, L.-Y. Using the Principle of Newton’s Rings to Monitor Oil Film Thickness in CNC Machine Tool Feed Systems. Lubricants 2025, 13, 371. https://doi.org/10.3390/lubricants13080371
Chen S-H, Haung L-Y. Using the Principle of Newton’s Rings to Monitor Oil Film Thickness in CNC Machine Tool Feed Systems. Lubricants. 2025; 13(8):371. https://doi.org/10.3390/lubricants13080371
Chicago/Turabian StyleChen, Shao-Hsien, and Li-Yu Haung. 2025. "Using the Principle of Newton’s Rings to Monitor Oil Film Thickness in CNC Machine Tool Feed Systems" Lubricants 13, no. 8: 371. https://doi.org/10.3390/lubricants13080371
APA StyleChen, S.-H., & Haung, L.-Y. (2025). Using the Principle of Newton’s Rings to Monitor Oil Film Thickness in CNC Machine Tool Feed Systems. Lubricants, 13(8), 371. https://doi.org/10.3390/lubricants13080371





