Theoretical Modeling and Numerical Simulation of Current-Carrying Friction and Wear: State of the Art and Challenges

Abstract

Current-carrying friction and wear in contact components are key issues in modern electromechanical systems such as slip rings, electrical connectors, motors, and pantographs, directly influencing their efficiency, reliability, and lifespan. Due to the limitations of experimental methods under some extreme conditions, computational simulations have become essential for studying current-carrying friction and wear in such scenarios. This paper presents a comprehensive review of theoretical modeling and numerical simulation methods for current-carrying friction and wear. It begins with discussions of approaches to solve the electrical contact resistance (ECR), a critical parameter that governs current-carrying friction and wear behaviors. Then, it delves into various modeling strategies for current-carrying friction, with an emphasis on the coupled effects of thermal, mechanical, electrical, and magnetic fields. Finally, the review addresses modeling techniques for current-carrying wear, encompassing mechanical wear and arc erosion. By summarizing existing research, this paper identifies key advancements, highlights existing challenges, and outlines future directions, advocating for the development of efficient, universal, and industry-oriented tools that can seamlessly bridge the gap between theoretical modeling and practical applications.

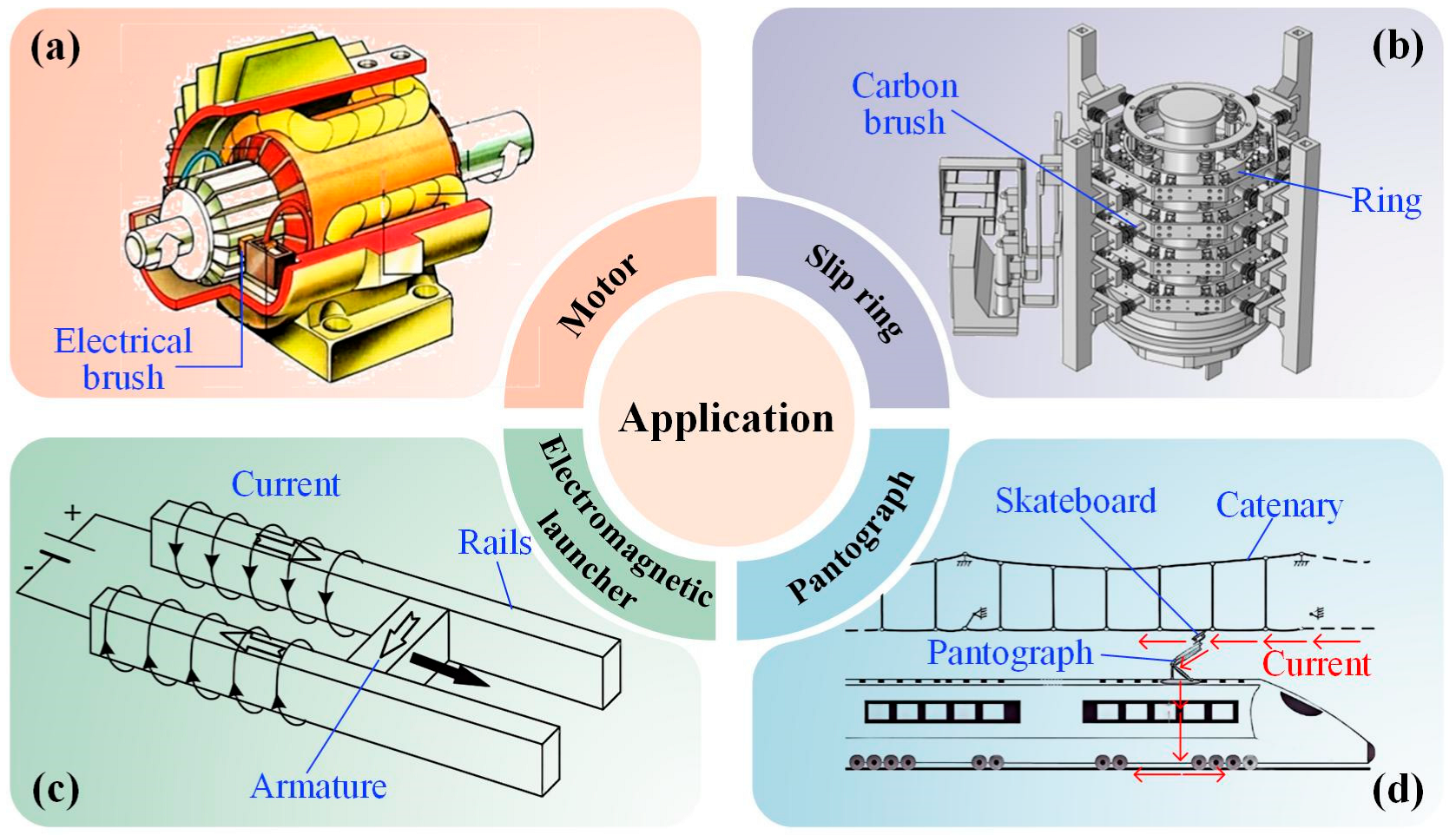
1. Introduction

Current-carrying friction pairs play a critical role in transmitting power or signals between moving components and are widely used in electromechanical systems, including motors [1], slip rings [2], electromagnetic launchers [3], and pantograph-catenary systems [4], as shown in Figure 1. As key components in these devices, the friction and wear failures of current-carrying friction pairs severely affect the performance and service life of the entire system. For instance, in wind turbines, wear of pitch slip rings not only reduces power generation efficiency but also causes equipment failure [5,6]. In electric ships, pod slip rings undergo severe wear and arc erosion under high-power loads, directly affecting propulsion efficiency [2,7]. During electromagnetic railgun launches, the local current density between the rail and armature can reach up to 10⁹ A/m², causing dramatic temperature rises and even material melting, which shortens rail lifespan [8,9]. Therefore, understanding the mechanisms of current-carrying friction and wear, particularly under extreme conditions, is crucial for evaluating their effects on system performance and for guiding the design and optimization of related equipment.

Compared to conventional friction and wear, the mechanisms of current-carrying friction and wear are more intricate, involving the coupling of thermal-mechanical-electrical-magnetic fields [10,11,12] (Figure 2a). Under mechanical load, friction heat raises the temperature, leading to thermal expansion that alters the material deformation and contact state [13]. This represents a classic thermo-mechanical coupling process, where mechanical friction is the primary driver of wear [14]. When electrical load is introduced, Joule or arc heat causes a significant temperature rise, potentially softening the material and modifying the contact interface [15,16]. On one hand, the elevated temperature alters the material’s resistivity [17] and exacerbates surface oxidation [18]; on the other hand, the altered contact state affects current constriction. Both factors significantly influence the electrical contact resistance (ECR), which in turn affects the temperature of the current-carrying friction pair. In this coupled scenario, wear is driven by both mechanical friction and electrical sparking [19,20]. Additionally, the magnetic field generated by fluctuating current can interfere with signal transmission [21] and alter the contact state through electromagnetic force [22].

In addition to the complex mechanisms, current-carrying friction and wear are influenced by various factors, including operating conditions, material properties, surface characteristics, and harsh environments (Figure 2b). Numerous studies have shown that current, force, and sliding speed are the key parameters affecting current-carrying friction and wear [23,24,25]. The wear rate increases significantly as the current increases [26], while it exhibits a characteristic “U-shaped” trend with the increase of mechanical force [14]. The effect of sliding speed is more complex, with different trends observed at different speed ranges [27,28]. Material properties and surface characteristics also play critical roles [29,30]. Friction pairs with high thermal and electrical conductivity exhibit low ECR and high heat dissipation, thereby enhancing electrical contact performance. Harder surfaces provide better wear resistance, while greater surface roughness causes an increase in localized contact pressure and current density. Environmental factors, such as humidity [31] and oxygen concentration [32], also exert a significant influence. In humid environments, a water film may form to lubricate the surface, but moisture also promotes electrochemical reactions that accelerate corrosion. Elevated oxygen levels accelerate oxidation, further degrading frictional performance.

Although numerous experimental studies have explored the effects of various factors on current-carrying friction and wear, the underlying mechanisms and the interactions among these factors remain poorly understood [10,12]. Moreover, experiments conducted under extreme operating conditions are often influenced by multiple unidentified factors, making it difficult to isolate and characterize the individual contributions of each. As such, numerical simulation becomes essential for gaining deeper insights into the mechanisms of friction and wear under diverse conditions and further optimizing the design of current-carrying friction pairs. This paper presents a comprehensive review of theoretical modeling and numerical simulation related to current-carrying friction and wear. First, methods for determining ECR, a key parameter influencing current-carrying friction and wear, are discussed. Next, modeling approaches for current-carrying frictional contact considering multi-field coupling are examined, followed by analyses of modeling current-carrying wear. Finally, the present achievements and existing challenges in this field are summarized, and future research directions are envisaged to guide further investigation and support practical applications.

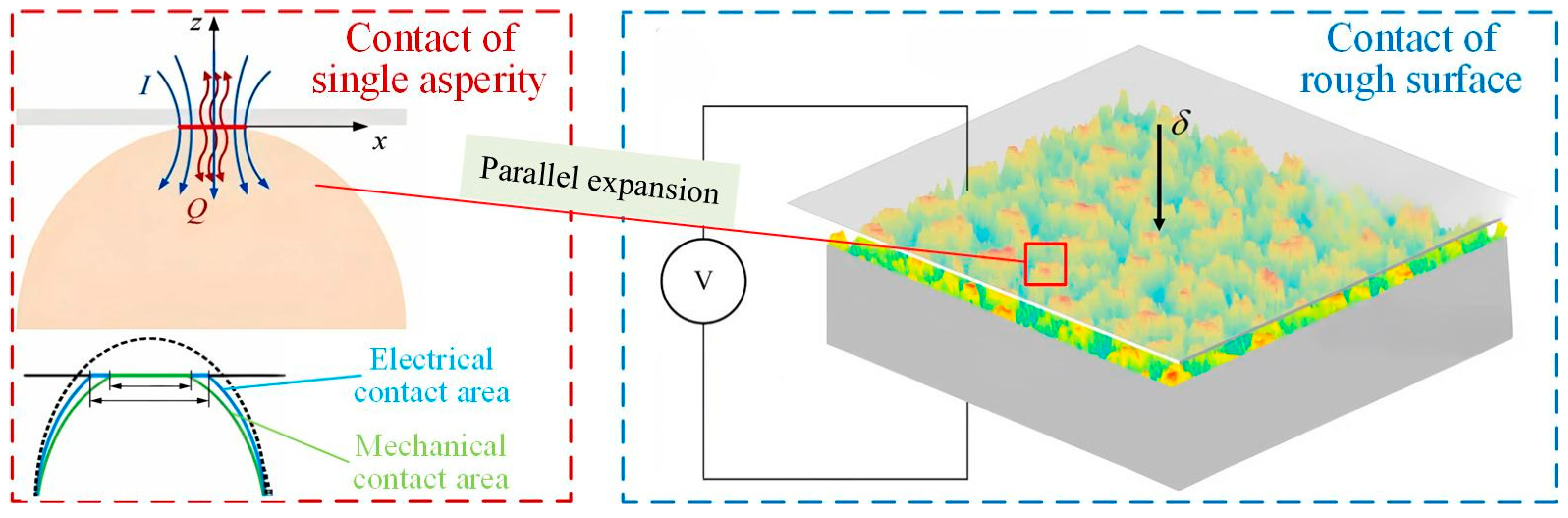
2. Solving Electrical Contact Resistance (ECR)

The ECR plays a pivotal role in current-carrying friction, as it not only reflects the contact state but also directly influences current conduction and heat distribution within the friction pair. Accordingly, theoretical modeling and numerical simulation of ECR are essential for accurately characterizing current-carrying friction behavior and optimizing the design of frictional interfaces. The ECR R comprises constriction resistance R_c and film resistance R_f, which can be expressed as follows:

$$R=R_{\mathrm{c}}+R_{\mathrm{f}}$$

(1)

where R_c is caused by the constriction of current as it flows through the contact interface, and R_f results from surface oxide layers, adsorbed films, or other contaminants.

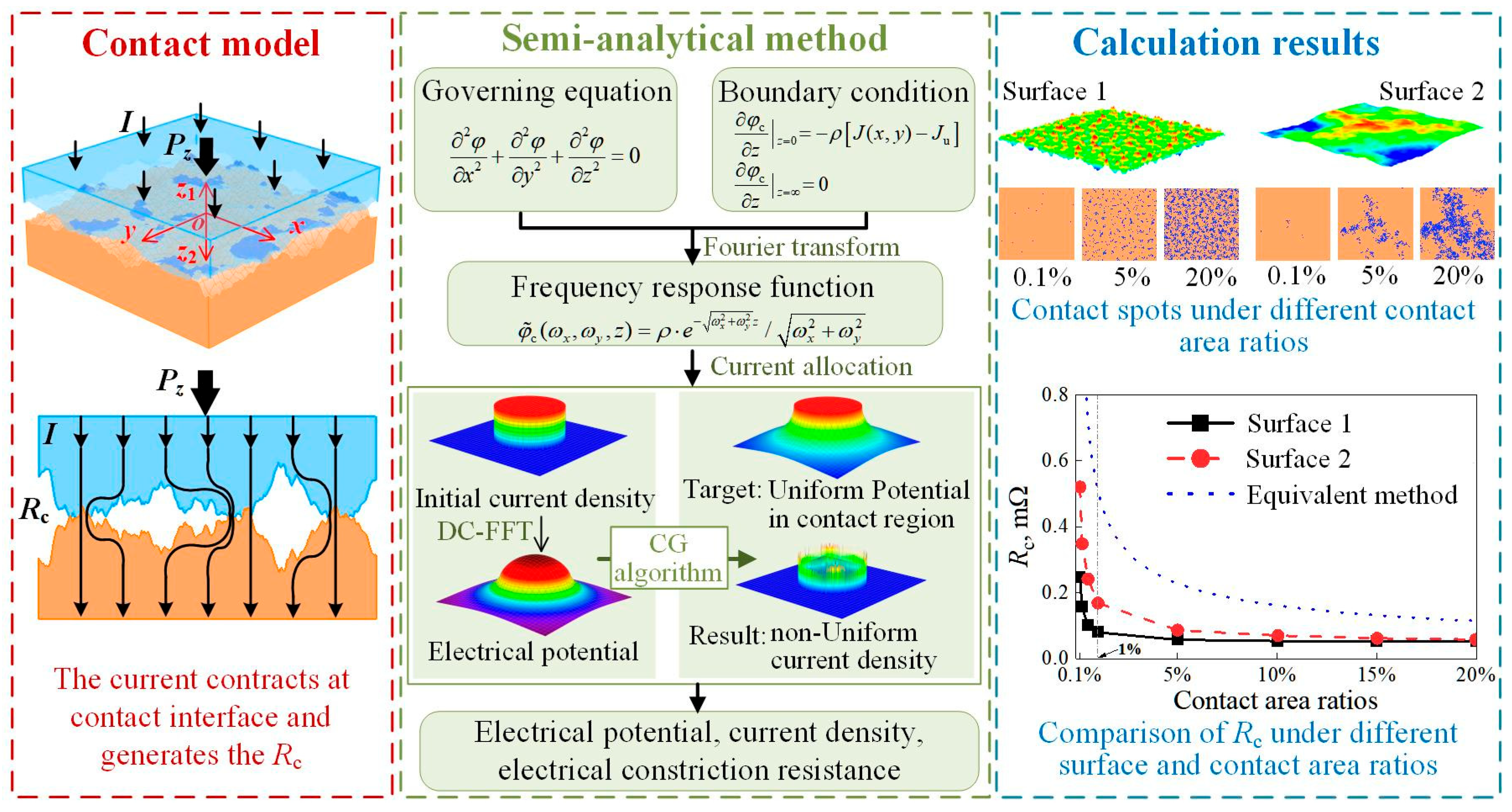
2.1. Constriction Resistance R_c

Holm derived the R_c for a single circular contact spot [33]:

$$R_{\mathrm{c}}=({\rho }_1+{\rho }_2)/2a$$

(2)

where ρ₁ and ρ₂ denote the resistivity of the two contact parts, and a is the radius of the circular contact spot. Although Equation (2) has been widely used to date, its assumption that the contact spot is perfectly circular and much smaller than the contact parts may introduce significant errors. Timsit further considered the contact parts with finite size and derived detailed expressions [34,35]:

$$R_{\mathrm{c}}={\displaystyle \frac{({\rho }_1+{\rho }_2)}{2a}}\left[1-1.41581({\displaystyle \frac{a}{b}})+0.06322{({\displaystyle \frac{a}{b}})}^2+0.15261{({\displaystyle \frac{a}{b}})}^3+0.19998{({\displaystyle \frac{a}{b}})}^4\right]$$

(3)

where a/b is the ratio of spot radius to contact part size. To simulate the contact of rough surfaces that contain multiple contact spots, Greenwood derived the R_c of multiple circular spots [36]:

$$R_{\mathrm{c}}={\displaystyle \frac{{\rho }_1+{\rho }_2}{4{\displaystyle \sum a_i}}}+{\displaystyle \frac{{\rho }_1+{\rho }_2}{2\pi }}({\displaystyle \sum _{i\ne j}\frac{a_i{a}_j}{d_{ij}}})/{({\displaystyle \sum a_i})}^2$$

(4)

where d_ij represents the center-to-center distance between any two circular spots. In Equation (4), both the parallel resistance of all spots and the interaction resistance between each pair of spots are considered. However, this approach still imposes limitations when modeling real, irregular contact spots.

All the aforementioned studies assume a predefined shape or distribution of contact spots without directly addressing the actual contact behavior of rough surfaces. In 2003, Barber [37] proposed that R_c is proportional to contact stiffness, establishing a quantitative link between R_c and mechanical contact. Currently, the equivalent method and the parallel method are two representative approaches for estimating the R_c of rough surface contact (Figure 3). The equivalent method, which is widely used in engineering applications, approximates multiple contact spots as a single circular contact spot with the same total area (Figure 3b), allowing the use of Equation (2) to calculate R_c. The parallel method refers to obtaining R_c by paralleling the resistance of each contact spot (Figure 3c) and has been applied to a variety of contact configurations due to its computational simplicity [38,39,40,41,42]. However, both methods introduce some errors due to neglecting the actual spot geometry or the interaction between contact spots.

With advances in computational technology, various numerical methods have been applied to solve R_c. Nakamura et al. [43] employed the Monte Carlo method to simulate randomly distributed contact spots, followed by the finite element method (FEM) to obtain R_c. FEM naturally considers the irregular shapes of contact spots and their mutual interactions; however, achieving high accuracy requires extremely fine meshes and substantial computational resources. As a result, FEM is typically applied to relatively simple contact scenarios, such as point or line contact on smooth surfaces [44,45,46,47]. Recently, Sui et al. [48] proposed a semi-analytical model to solve R_c for the contact of rough surfaces, as shown in Figure 4. The general solution (i.e., the frequency response function) for electrical potential φ_c was obtained by solving a partial differential equation (PDE) in the frequency domain (i.e., the governing equation in Figure 4), where ρ is the material resistivity, and ω_x and ω_y are coordinate variables in the frequency domain corresponding to the x and y directions. A conjugate gradient (CG) algorithm was then proposed to determine the non-uniform current density at the contact interface, fully considering the interaction among contact spots. The discrete convolution-fast Fourier transform (DC-FFT) was employed to accelerate the calculation, which allows using very precise grids to simulate irregular shapes of contact spots and reduces computation time by at least one order of magnitude compared with FEM.

2.2. Film Resistance R_f

It is generally assumed that current flows uniformly through the oxide film; thus, the film resistance R_f of a single contact spot can be expressed as [33,49,50]:

$$R_{\mathrm{f}}={\rho }_{\mathrm{f}}{l}_{\mathrm{f}}/A$$

(5)

where ρ_f and l_f are the resistivity and thickness of the oxide film, and A is the area of the contact spot. The electron tunneling theory proposed by Simmons [51], which models electron transport through insulating films, offers another approach for calculating R_f [52,53]:

$$R_{\mathrm{f}}={\displaystyle \frac{\Delta S\exp (1.025\Delta S{\phi }_L^{1/2})}{3.16\times {10}^{10}{\phi }_L^{1/2}}}{\displaystyle \frac{1}{A}}$$

(6)

where ∆S = S₂ − S₁, S₁ = 6/(Kφ₀) and S₂ = l_f − 6/(Kφ₀) are the limits of barrier at Fermi level, K is the dielectric constant, φ_L = φ₀ − [5.75/(K∆S)]·ln[S₂(l_f − S₁)/S₁/(l_f − S₂)], φ₀ is the energy height above the Fermi level of conductive surface. Both these methods require prior knowledge of the film’s thickness and contact area. However, during current-carrying friction, especially under high-speed or high-current conditions, the oxide film undergoes dynamic evolution, which significantly influences both R_f and the overall tribological performance [54]. Kondo et al. [55] used FEM to simulate the decrease of R_f with increasing loading due to the fracture of the oxide film. Currently, there remains a lack of simulation methods capable of capturing the growth and evolution of oxide films during current-carrying friction, and the resulting changes in R_f require further investigation.

The phase-field method (PFM) is a numerical technique that has recently gained widespread attention for its ability to address physical problems involving complex interfaces or phase transformation processes. PFM offers several distinct advantages in predicting the evolution of oxide films: it inherently incorporates time-dependent behavior, naturally describes interface evolution without requiring explicit interface tracking, and readily accounts for multi-field coupling effects. Yang et al. [56] developed a 2D phase-field model to simulate the growth of oxide film and investigate its effects on the surface roughness. Recently, Wang et al. [57] applied PFM to investigate the oxidation of alloy surfaces under high-temperature conditions, providing a valuable foundation for modeling surface oxidation in extreme environments. The existing phase-field models are mostly limited to 2D, whereas 3D characteristics of oxide films are essential for accurately determining R_f. Therefore, it is imperative to establish a 3D phase-field model for simulating the evolution of the oxide film and further investigating the dynamic variation of R_f under different conditions.

2.3. Total ECR

Although various methods have been developed to solve R_c and R_f, most are based solely on contact or oxidation conditions of the surfaces and fail to reveal the relationship between ECR and key engineering parameters such as working conditions, material properties, and surface roughness. How to establish this relationship is currently a primary concern in practical applications. Guo et al. [58] experimentally investigated the relationship between surface characteristics and working conditions and then derived an empirical formula of ECR based on experimental data and the GW contact model. With the development of artificial intelligence, data-driven machine learning (ML) offers strong potential for analyzing experimental data and predicting ECR across a wide range of scenarios. For instance, Cai et al. [59] conducted experiments to measure ECR under varying conditions, including load, sliding speed, current, sliding distance, and surface roughness. And then, ECR under different conditions can be obtained with high accuracy by using these experimental data and ML algorithms, as shown in Figure 5.

The above review indicates that practical methods for accurately determining ECR in engineering applications remain limited. The primary challenge lies in capturing the dynamic evolution of ECR and establishing a direct link between ECR and engineering parameters. Although data-driven ML can establish this link, its outcomes depend on the quantity and quality of experimental data. In the future, integrating physical principles into artificial intelligence may be an approach to revealing the relationship between ECR and engineering parameters with both efficiency and universality.

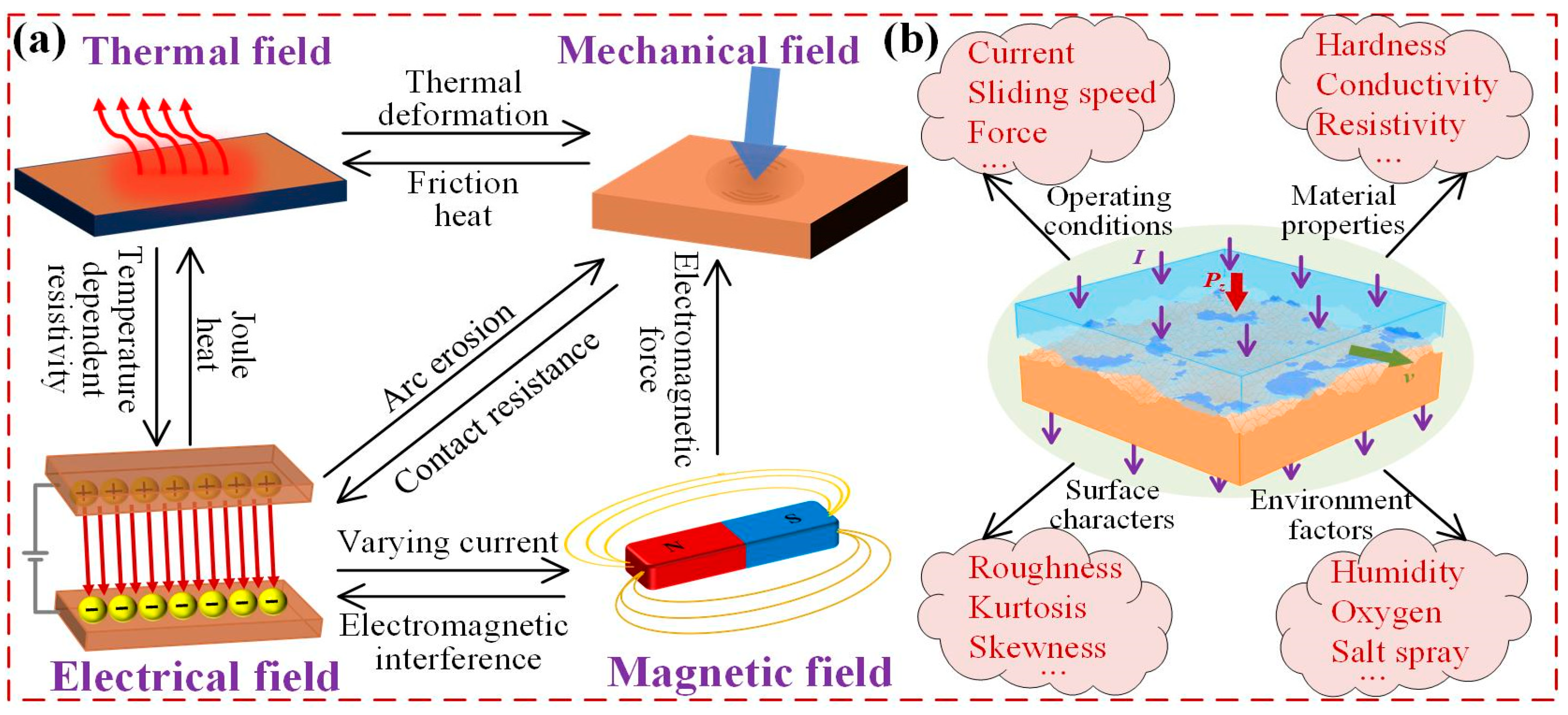
3. Modeling Current-Carrying Friction

ECR, as well as other critical parameters in current-carrying friction, such as temperature rise, contact pressure, and stress, are influenced by multi-field coupled effects. Consequently, multi-field coupled modeling is essential not only for revealing the underlying mechanisms of current-carrying friction but also for predicting equipment performance and preventing its failure.

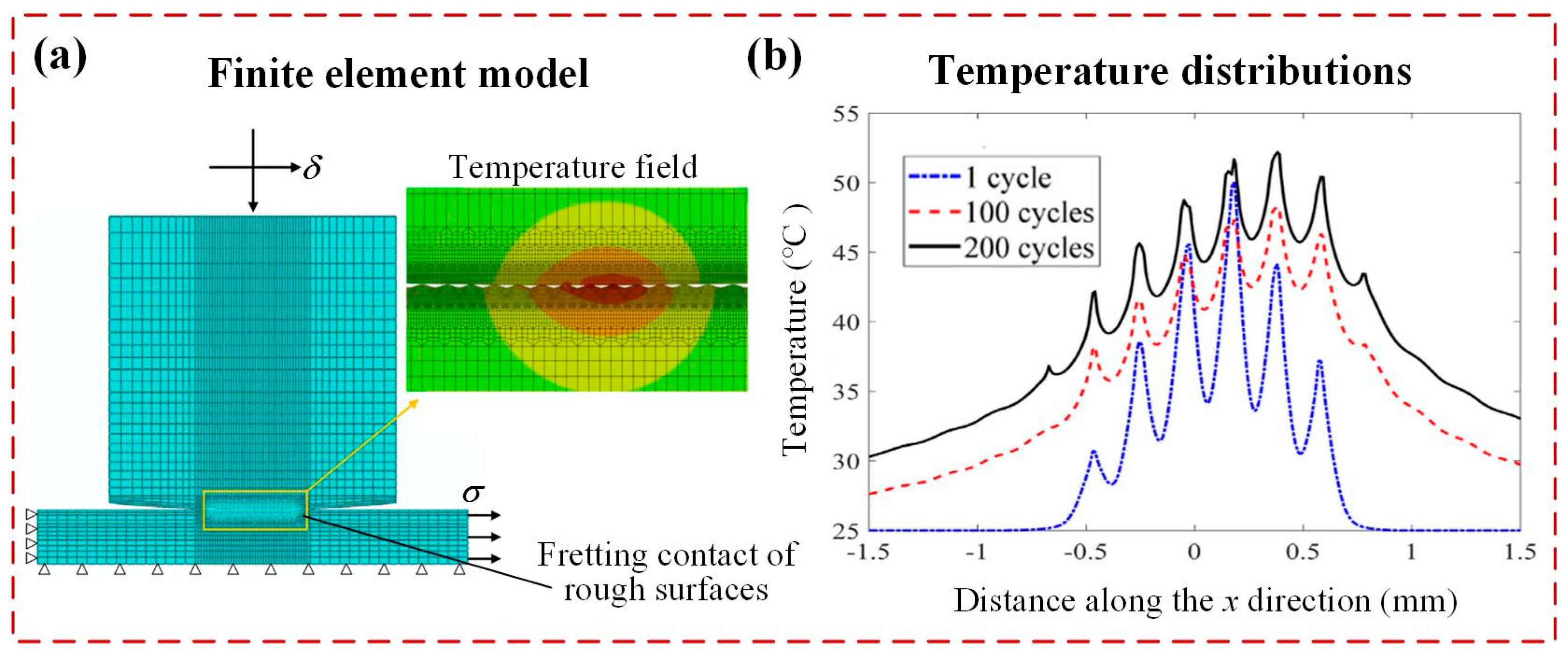
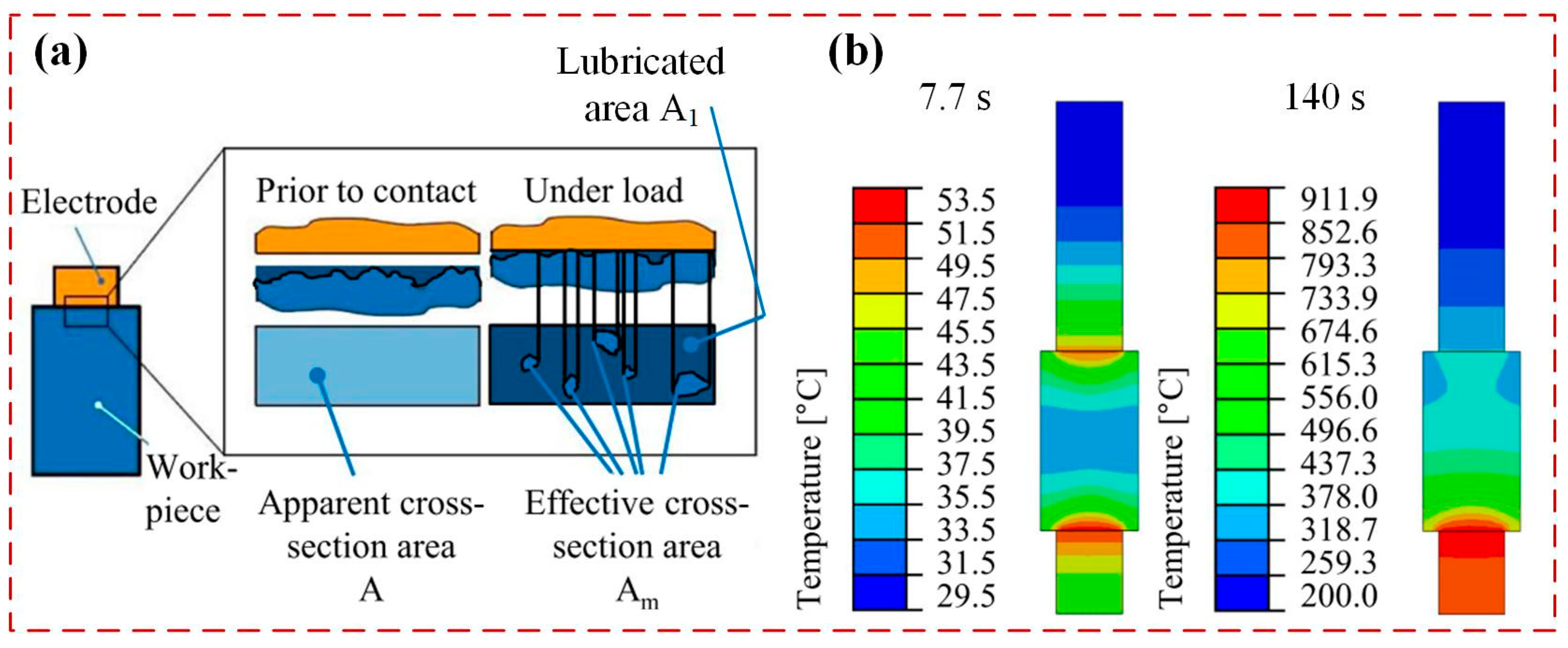
3.1. Thermal Field

Thermal effects in current-carrying friction, mainly including friction heat and Joule heat, have attracted widespread attention due to their significant effect on the performance of friction pairs. Both the semi-analytical method (SAM) and FEM are effective approaches for simulating the temperature rise and thermal stress induced by friction. For instance, Wang et al. used SAM to model both steady-state [60] and transient [61] thermoelastic contact problems, and then obtained the distribution of frictional temperature rise and thermal displacement. Zhang et al. [13] applied SAM to solve the thermoelastic contact problem, enabling convenient analysis of temperature and stress in multi-layered materials with arbitrary designs. Shen et al. [62] employed FEM to analyze the temperature distribution and evolution during fretting friction, considering the plastic deformation, surface roughness, and wear, as shown in Figure 6.

Regarding Joule heat, Greenwood [63] theoretically derived the temperature rise of a single circular contact spot as early as 1958, establishing a foundational link between the electrical field and thermal field:

$$U^2=8{\displaystyle {\int }_0^{{\theta }_m}\lambda (\theta )\rho (\theta )}\mathrm{d}\theta$$

(7)

where U and θ are the contact voltage drop and temperature, λ and ρ are the thermal conductivity and electrical resistivity, and θ_m is the maximum temperature rise. Nituca [64] developed a static thermal analysis model to calculate Joule heat in pantographs, accounting for temperature-dependent resistivity. Plesca [65] further incorporated the combined effects of Joule heat and friction heat generated during pantograph sliding. The FEM is also a feasible method to investigate the thermal effects of Joule heat. Terhorst et al. [66] developed an FE model for electrical contact of rough surfaces and then investigated the effects of Joule heat on temperature rise in electromechanical systems (Figure 7). Guo et al. [67] applied FEM to analyze the influence of rough surface characteristics on temperature rise under different operating conditions.

In addition to friction heat and Joule heat, arc heat generated by electrical sparking also significantly affects current-carrying friction behaviors, particularly under high-power or high-speed conditions. However, existing studies on arc heat remain limited and often neglect the coupling between arc-induced thermal effects and the contact mechanics [68,69,70].

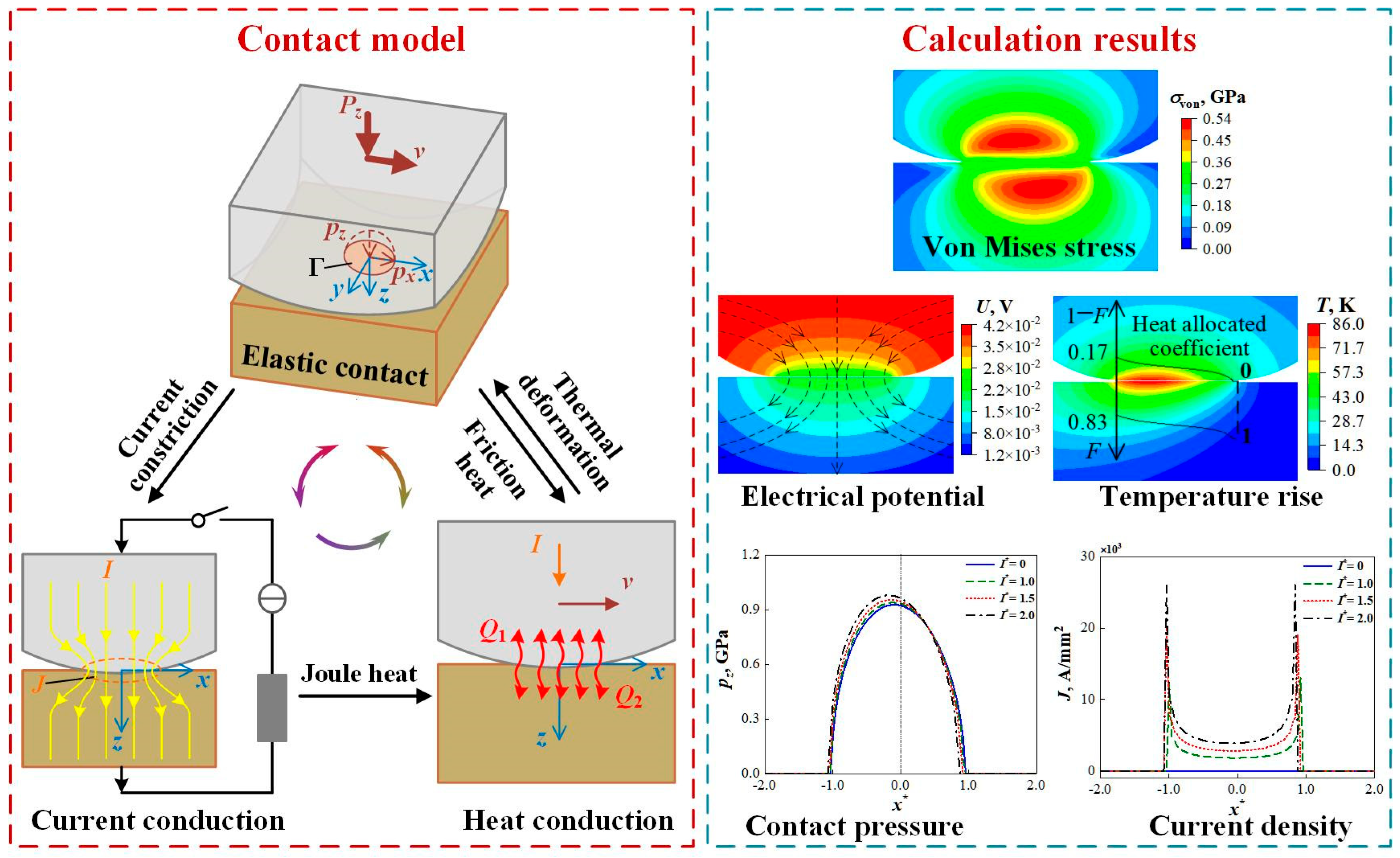
3.2. Thermal-Mechanical-Electrical Coupling

To comprehensively predict current-carrying friction performance, modeling of thermal-mechanical-electric field coupling has become a central focus in recent years. Komvopoulos [71] applied fractal theory to address sliding current-carrying contact of rough surfaces, accounting for elastoplastic contact, friction heat, and ECR but neglecting Joule heat. In addition to analytical approaches, numerical methods such as FEM and the boundary element method (BEM) have been widely used to model the current-carrying contact by solving heat-transfer, elastic mechanics, and potential equilibrium equations. Michopoulos et al. [72] proposed a multi-scale model to solve the current-carrying contact problem, where the macroscopic scale is solved by FEM, while the mesoscopic and microscopic scales are solved by the analytical method. The comparison of ECR histories between the model and experimental values was also conducted, showing that theoretical results are in good agreement with the experimental data, with only slightly higher values in the initial stage. Ke et al. analytically solved the thermo-mechanical-electrical coupled contact problem of a single asperity [50] and further analyzed rough surface contact using the parallel method, where the distribution of contact spots was solved via BEM [73,74], as shown in Figure 8. More recently, Ke et al. [75] developed a new BEM-based model that accounts for interactions between contact spots by directly solving the Laplace equation for electric potential and has higher accuracy than the parallel method.

Both models proposed by Michopoulos and Ke mainly focus on static contact conditions and therefore do not involve the friction heat. More recently, Sui et al. [76] developed a semi-analytical model that fully couples the thermal-mechanical-electrical field to solve the 3D sliding current-carrying frictional contact problem, as shown in Figure 9. This model incorporates the combined effects of friction heat and Joule heat, as well as non-uniform allocation of the heat flow towards two contact surfaces—an aspect particularly important when the contact materials are dissimilar. Based on this framework, the current-carrying friction performance under various operating conditions can be efficiently predicted, as illustrated in Figure 9.

Although numerous models have been proposed to analyze current-carrying friction, several challenges remain, particularly for extreme operating conditions such as high-power and high-speed. The existing models often assume constant material properties, neglecting the temperature-dependent variations in elastic modulus and electrical resistivity at elevated temperatures. In addition, the present models are still limited to steady-state analysis, lacking the ability to capture the dynamic evolution of current-carrying friction performance.

3.3. Thermal-Mechanical-Electrical-Magnetic Coupling

In current-carrying friction, the magnetic field generated by varying current can significantly affect the performance of friction pairs. The electromagnetic force, which arises from the interaction between current and magnetic field, directly alters the contact pressure and affects the contact behavior. Additionally, electromagnetic radiation and interference caused by the magnetic field or electrical arc may disrupt signal transmission in current-carrying friction systems. At present, the effects of the magnetic field on current-carrying friction are primarily investigated through experiments. For example, He et al. [22] introduced permanent magnets to simulate a magnetic environment and examine the influence of magnetic field intensity on the friction coefficient. The results indicate that as the magnetic induction intensity increases, the friction coefficient initially decreases slightly and then increases sharply. The turning point occurs at a magnetic induction intensity of 0.1 T, beyond which the friction-increasing effect of the magnetic field (crack initiation) outweighs its friction-reducing effect (oxide film formation). Guo et al. [21] investigated the distribution characteristics and influencing factors of electromagnetic noise in pantograph-catenary systems by experiments, providing a basis for further theoretical research for electromagnetic noise suppression methods.

Zhao et al. [77] developed a theoretical model to investigate the effects of the surrounding magnetic field on the contact performance of high-speed train pantograph-catenary systems whose structure is the same as Figure 1d. The study demonstrates that the traction current in the pantograph generates a significant electromagnetic force, accounting for 30% to 50% of the contact pressure and seriously affecting the dynamic behavior of pantograph-catenary systems, including both tribology performance and power transmission capability. Liu et al. [78] theoretically investigated the velocity skin effect of the current in pantographs and found it to be strongly influenced by the magnetic field, resulting in an uneven distribution and aggregation toward the trailing edge of the skateboard. Therefore, regulating the velocity skin effect via the magnetic field can improve current-carrying performance and mitigate local temperature rise on the skateboard surface. Existing models primarily concern the effects of the magnetic field on the contact state and current distribution, while the theoretical modeling and numerical simulation studies on the coupled effects of thermal-mechanical-electrical-magnetic field remain scarce and underexplored.

The above review indicates that although FEM is a versatile approach to model current-carrying friction, it remains limited in addressing the fully coupled effects of thermal-mechanical-electrical-magnetic field in rough surface contact due to the huge computational burden. By combining SAM with DC-FFT, computational efficiency can be significantly improved, enabling comprehensive consideration of multi-field coupling effects and rough surface contact while maintaining high accuracy. However, SAM still faces limitations in addressing certain problems under extreme conditions, such as considering the temperature-dependent material properties. This problem is actually solving a set of coupled PDEs in which the material properties are functions of temperature. The physical information neural network (PINN) [79] that integrates physical laws into ML algorithms has huge potential to address PDEs and has been used in contact problems under simple cases [80,81,82,83,84]. Therefore, integrating PINN with SAM or FEM to model current-carrying friction under extreme conditions for more comprehensive analysis is a promising direction for future research.

4. Modeling Current-Carrying Wear

Contact inevitably leads to material wear, and current-carrying wear is a primary cause of failure in electrical contact systems. Studies on the wear evolution of current-carrying friction pairs are of great significance for predicting the service life of related equipment. Numerous experimental studies denote that the mechanism of current-carrying wear primarily includes mechanical wear and arc erosion [10,12]. Therefore, theoretical modeling of current-carrying wear must account for both mechanical wear and arc erosion, as well as their coupled interactions.

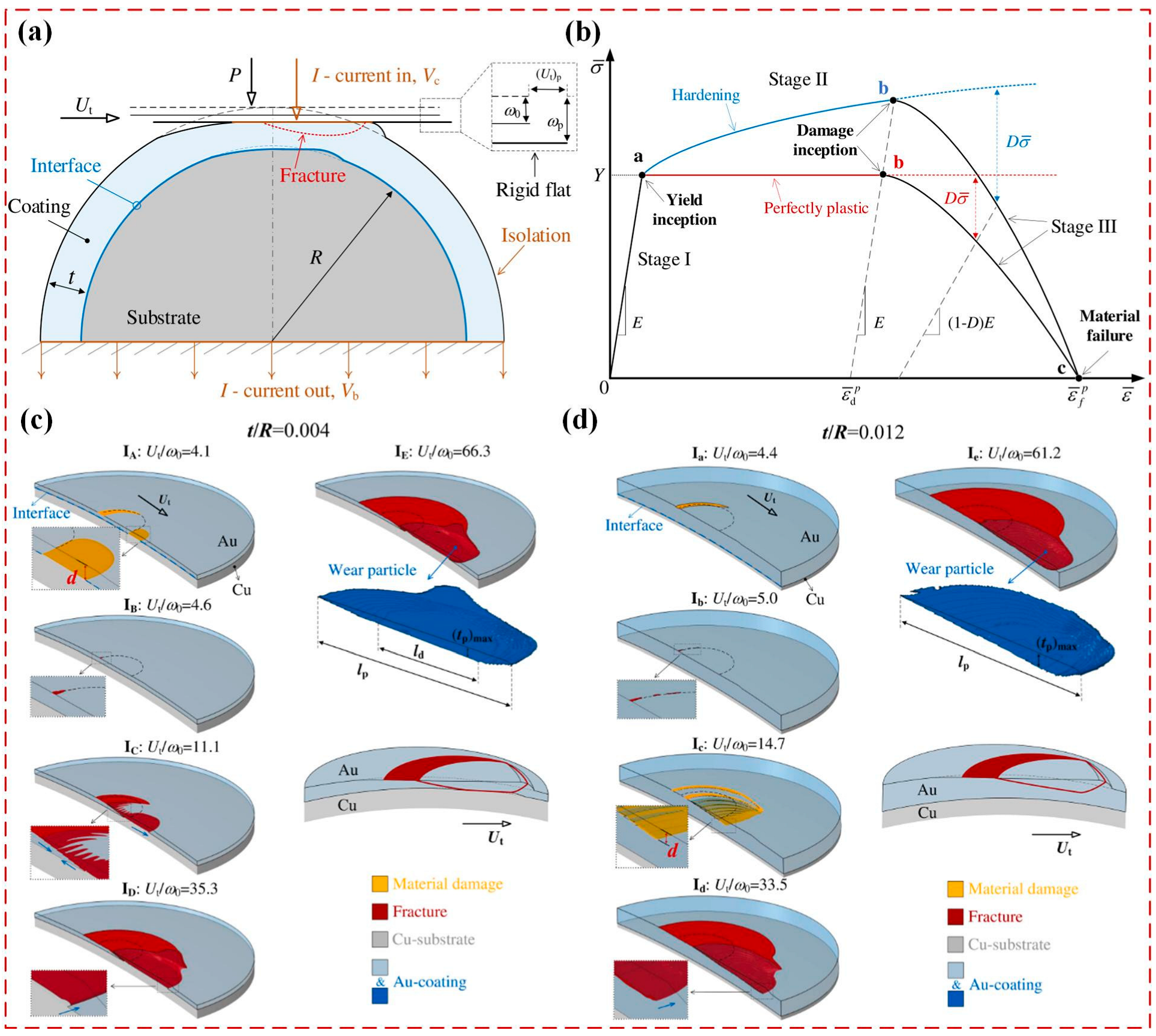
4.1. Mechanical Wear

The mechanical wear of materials is one of the most fundamental yet critical issues in engineering. In 1953, Archard [85] proposed an adhesive wear model, now known as the “Archard model”. In this model, the radius of a hemispherical wear particle is assumed to be the radius of the contact zone when the asperity undergoes complete plastic deformation, and the wear rate is proportional to the applied load. Therefore, the wear volume can be expressed as follows [86]:

$$V=K{\displaystyle \frac{P}{H}}s$$

(8)

where V, s, P, and H are the wear volume, sliding distance, applied load, and hardness of worn material, respectively. K is the wear coefficient, an empirical parameter determined by experiments, interpreted by Archard as the probability of wear particle formation. Although the Archard model lacks a deep understanding of the physical laws governing material wear and requires empirical determination of wear coefficients, it has still been widely used in engineering for decades due to its simple form and reliance only on working conditions and surface hardness. In 1958, Rabinowicz [87] discovered that when the contact width exceeds a certain critical size, the accumulated frictional energy surpasses the adhesion energy of the material, leading to the generation of wear particles. This critical size can be expressed as follows:

$$d_{\mathrm{c}}=30EW/{\sigma }_Y^2$$

(9)

where d_c, E, W, and σ_Y represent the critical size, elastic modulus, the work of adhesion per unit area, and yield stress, respectively. Rabinowicz’s theory laid the foundation for modeling wear from an energy-based perspective and continues to inspire the development of wear models across diverse engineering applications [88,89,90,91]. The above studies primarily focus on wear induced by mechanical forces, without accounting for the effects of current and heat.

Under current-carrying conditions, the effects of electrical and thermal factors become significant, necessitating the consideration of multi-field coupling. The FEM has proven effective in addressing this complex problem [92,93,94,95,96]. Weißenfels and Wriggers [92] used FEM to develop a constitutive model for thermal-mechanical-electrical coupling based on the dissipation of friction and Joule heat at the contact interface, and simulate the temperature, electrical potential, and wear amount in current-carrying conditions. The results show that when the current is constant, total wear initially decreases and then increases with applied pressure, and the electrical effect dominates under low pressure, whereas the mechanical effect becomes predominant at higher pressure, aligning well with experimental results [14]. Recently, Zhang et al. [96] proposed a wear model of metallic coating systems under current-carrying conditions based on FEM (Figure 10a). The ductile failure is used to model the wear process, and the uniaxial stress–strain behavior of the investigated metal is illustrated in Figure 10b. Using this model, the effects of coating thickness on wear performance were analyzed, and the fracture evolutions with the increase of tangential displacement for different coating thicknesses t/R are shown in Figure 10c,d. As tangential displacement increases, flake-like wear particles gradually form, and the damage occurs on both the surface and interface for thin coating and only on the coating surface for thick coating.

Although FEM has been widely applied to model the mechanical wear under current-carrying conditions, the predicted wear morphology and volume do not yet accurately match experimental tests [93,94,95]. Furthermore, its computational inefficiency remains a major challenge, particularly in simulating long-duration or large-distance wear of rough surfaces. In 2000, Doelling et al. [97] experimentally demonstrated a strong correlation between wear volume and system entropy increase. This finding later evolved into the widely accepted energy dissipation theory, which posits that wear volume is proportional to energy dissipation, itself dependent on applied multi-physical loads [98]. Consequently, modeling wear volume as a function of multi-physical loads using energy dissipation theory is both feasible and promising. Existing models primarily focus on predicting total wear volume; however, a key future direction lies in capturing the evolution of surface morphology by linking energy dissipation to contact pressure, current density, and heat flux density.

4.2. Modeling Arc Erosion

Under high-speed or high-power conditions, frequent arc discharges occur at the contact interface, and arc erosion becomes a critical contributor to current-carrying wear [99]. In a recent study, Xu et al. [100] emphasized that neglecting arc discharge leads to an overestimation of ECR, resulting in a singular current density distribution and impairing the accurate evaluation of current-carrying performance. Existing methods for predicting current-carrying wear involving arc erosion primarily rely on experimental data to construct heuristic models [101,102]. As shown in Figure 11, Bucca et al. [101] conducted current-carrying wear tests to analyze the effects of various factors, and subsequently proposed an approximate formula to predict the wear volume NWR:

$$\begin{array}{cc}\hfill NWR=& k_1{[{\displaystyle \frac{1}{2}}\cdot (1+{\displaystyle \frac{I_{\mathrm{c}}}{I_0}})]}^{-\alpha }\cdot {({\displaystyle \frac{F_{\mathrm{m}}}{F_0}})}^{\beta }\cdot {\displaystyle \frac{F_{\mathrm{m}}}{H}}\hfill \\ & +k_2{\displaystyle \frac{R_{\mathrm{c}}(F_{\mathrm{m}})\cdot I_{\mathrm{c}}^2}{H\cdot V}}(1-u)+k_3\cdot u{\displaystyle \frac{V_{\mathrm{a}}\cdot I_{\mathrm{c}}}{V\cdot H_{\mathrm{m}}\cdot \rho }}\hfill \end{array}$$

(10)

where three terms represent the contributions of friction, Joule heat and arc erosion, respectively; F_m, I_c, V, R_c and V_a are the contact force, current, sliding speed, ECR and electrical arc potential; H, H_m, and ρ are the material hardness, latent heat of fusion, and resistivity; other parameters are reference values or unknown coefficients that need to be determined experimentally. These models effectively incorporate the combined effects of mechanical wear and arc erosion and show good agreement with the experimental results in terms of wear volume or wear rate, but they are often complex and require numerous empirically determined coefficients, limiting their general applicability [101,102]. Moreover, although arc-induced wear is included, the models typically overlook the underlying mechanisms of arc initiation and their impact on surface morphology, which is essential for understanding the full behavior of current-carrying wear.

In 2015, Mesyats et al. [103] developed a 2D fluid dynamics model based on the heat conduction and Navier-Stokes equations, simplifying the arc erosion process as the combined effects of arc-induced heat flux and pressure on the electrode. This model effectively simulates the formation of the molten metal pool under arc erosion and the initial splashing of liquid metal. Benilov et al. [104] employed FEM to construct a 2D arc erosion model, successfully capturing the morphological evolution of arc-induced damage. Wang et al. [105] developed an axisymmetric model to simulate the initiation and evolution of arc erosion by solving hydrodynamic and heat-transfer equations in a 2D rectangular coordinate system:

$$\left\{\begin{array}{cc}\begin{array}{c}{\displaystyle \frac{𝜕\rho }{𝜕t}}+\nabla \cdot (\rho \stackrel{\rightharpoonup }{u})=0\\ {\displaystyle \frac{𝜕}{𝜕t}}(\rho \stackrel{\rightharpoonup }{u})+\nabla \cdot (\rho \stackrel{\rightharpoonup }{u}\stackrel{\rightharpoonup }{u})=-\nabla \rho +\nabla \cdot \stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{\tau }}+\rho g\end{array}& \begin{array}{cc}\mathrm{hydrodynamic}& \mathrm{equations}\end{array}\\ c\rho ({\displaystyle \frac{𝜕T}{𝜕t}}+\stackrel{\rightharpoonup }{V}\nabla T)=\nabla (\lambda \nabla T)+{\displaystyle \frac{j^2}{\sigma }}& \begin{array}{cc}\text{heat-transfer}& \mathrm{equation}\end{array}\end{array}\right.$$

(11)

where ρ, t, u, τ, g, c, T, V, λ, j, and σ are the fluid density, time, fluid velocity vector, viscous stress tensor, gravitational acceleration, specific heat capacity, temperature, heat source speed, thermal conductivity, current density, and electrical conductivity, respectively. And Equation (11) satisfies the following boundary conditions:

$$\left\{\begin{array}{l}{-\lambda \nabla |}_S=q-q_{ev}\\ \begin{array}{cc}{{\displaystyle \frac{𝜕T}{𝜕r}}|}_{r=0}=0,& {T|}_{r=r_{\mathrm{m}}}=T_0\\ {T|}_{z=z_{\mathrm{m}}}=T_0,& T|{T|}_{z=-z_{\mathrm{m}}}=T_0\end{array}\end{array}\right.$$

(12)

where q, q_ev, and T₀ are the energy flux density, energy flux loss, and initial temperature. Through this model, detailed insights into the geometry and temperature distribution of erosion pits were obtained.

The above review indicates that numerical methods are feasible for simulating local arc erosion characteristics. However, existing models are limited to 2D or axisymmetric form, which cannot accurately capture the 3D erosion morphology of rough surfaces. Moreover, the interaction between mechanical wear and arc erosion significantly influences current-carrying wear, yet its underlying mechanisms remain unclear. Developing comprehensive models that incorporate both mechanical wear and arc erosion, while fully accounting for their coupled effects, remains a critical scientific challenge in the study of current-carrying wear.

5. Conclusions and Perspectives

Current-carrying friction and wear play a pivotal role in the reliability and performance of modern electromechanical systems. Accurate modeling and simulation of these phenomena are essential for elucidating underlying mechanisms, predicting performance degradation, and guiding the design of advanced systems. This review systematically summarizes the theoretical modeling and numerical simulation of current-carrying friction and wear, with an emphasis on methods for solving ECR and predicting contact and wear performance under multi-field coupling effects (

Table 1. Summary of methods for solving ECR and predicting contact and wear performance.

	Methods	Efficiency	Accuracy	Coupling Degree	Scale (Spatial, Temporal)
ECR	Theoretical formulas	+++	+	+	Regular spots, static
	FEM	+	+++	++	Simple case, static
	SAM	+++	+++	+++	Rough surfaces, static
	ML	++	++	++	Rough surfaces, static
Friction	Fractal theory	+++	+	+	Fractal surfaces, steady
	FEM	+	+++	++	Rough surfaces, transient
	BEM	++	++	++	Rough surfaces, steady
	SAM	+++	+++	+++	Rough surfaces, steady
Wear	FEM	+	+	+	Asperity level, short time
	Energy dissipation theory	+++	++	++	Rough surfaces, long time

The number of the symbol “+” represents the level of how much larger or higher it is.

).

The key findings are as follows:

(1)

Theoretical formulas, FEM, and SAM are widely used in solving ECR. Among them, theoretical formulas are typically restricted to idealized scenarios, such as contact spots with regular shapes, resulting in low accuracy; FEM offers high accuracy but consumes a lot of computation time; SAM effectively balances precision and efficiency, making it better suited for more realistic rough surface contacts. Currently, research on the dynamic evolution of ECR during current-carrying friction remains limited. The primary challenge lies in capturing the evolution of the 3D geometry of the oxide film and subsequently determining the time-dependent behavior of film resistance. Modeling the evolution of 3D oxide film morphology via PFM, in combination with electron tunneling theory for film resistance prediction, presents a promising direction.

(2)

FEM, BEM, and SAM have proven effective in addressing multi-field coupling problems in current-carrying friction with high accuracy. FEM offers strong geometric adaptability and modeling flexibility but is limited due to high computational cost. BEM and SAM are more efficient; however, BEM struggles to obtain fundamental solutions under multi-field coupling, and SAM poorly accommodates the actual geometry of contact parts. Furthermore, their adaptability remains limited under complex conditions such as high-power, high-speed, and alternating current. The primary challenges lie in incorporating temperature-dependent material properties and modeling the effects of magnetic fields induced by alternating currents at the contact interface. To address these limitations, future efforts could focus on two aspects: capturing the spatial variability of material properties to account for temperature dependence; coupling magnetic field effects with thermal-mechanical-electrical fields. Additionally, to enhance the applicability of models across diverse operating environments, external factors such as humidity must also be integrated into the modeling framework.

(3)

FEM is widely employed to model current-carrying wear at the microscale, while energy dissipation principles provide an effective means to simulate macro wear amount. Effective methods for simulating long-distance surface wear evolution remain lacking. The main challenges include the absence of models capable of characterizing the 3D morphology of arc erosion and the low computational efficiency of existing approaches in capturing surface evolution. A key future research direction is developing an integrated model that couples the 3D arc erosion with mechanical wear under multi-field conditions. Such a model is essential for accurately identifying arc initiation criteria and predicting current-carrying wear by capturing the synergistic effects of mechanical and electrical degradation. Additionally, incorporating energy dissipation principles into wear models could enable efficient simulation of surface morphology evolution over extended wear durations.

(4)

The advances in artificial intelligence have made the application of ML to current-carrying friction and wear a central focus of future research. For instance, employ PINN to solve complex partial differential equations in multi-field coupling problems, establish quantitative relationships between wear characteristics and engineering parameters for friction pair design, and predict the remaining service life of components based on wear evolution. In the future, the primary challenge will be to integrate physical principles with ML techniques for multi-scale modeling, spanning contact damage analysis at the asperity level to wear evolution simulation at the rough-surface level, enabling real-time prediction of component performance and remaining service life.

In summary, developing efficient and universal industry-oriented tools that bridge the gap between theoretical modeling and real-world applications is the main exploration direction in the future. The application of computer technology to current-carrying friction and wear not only enhances the theoretical understanding of its potential mechanisms but also contributes to the design and optimization of advanced electromechanical systems, ensuring their reliability and efficiency under increasingly demanding operating conditions.