A Comprehensive Review of Safety Tire Research
Abstract
1. Introduction
2. Classification of Safety Tires
2.1. Structural Design of RFTs
2.1.1. Structural Design of ISRFTs
2.1.2. Structural Design of SSRFT
2.2. Structural Design of NPT
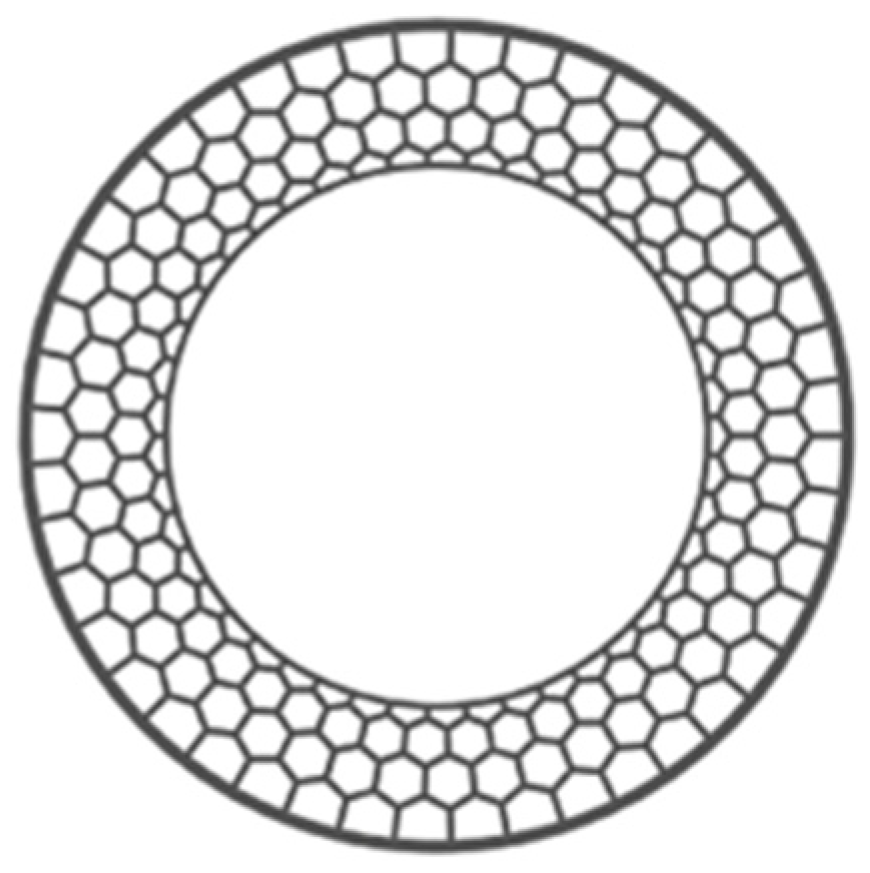
2.2.1. Structural Design of Porous-Structure NPT
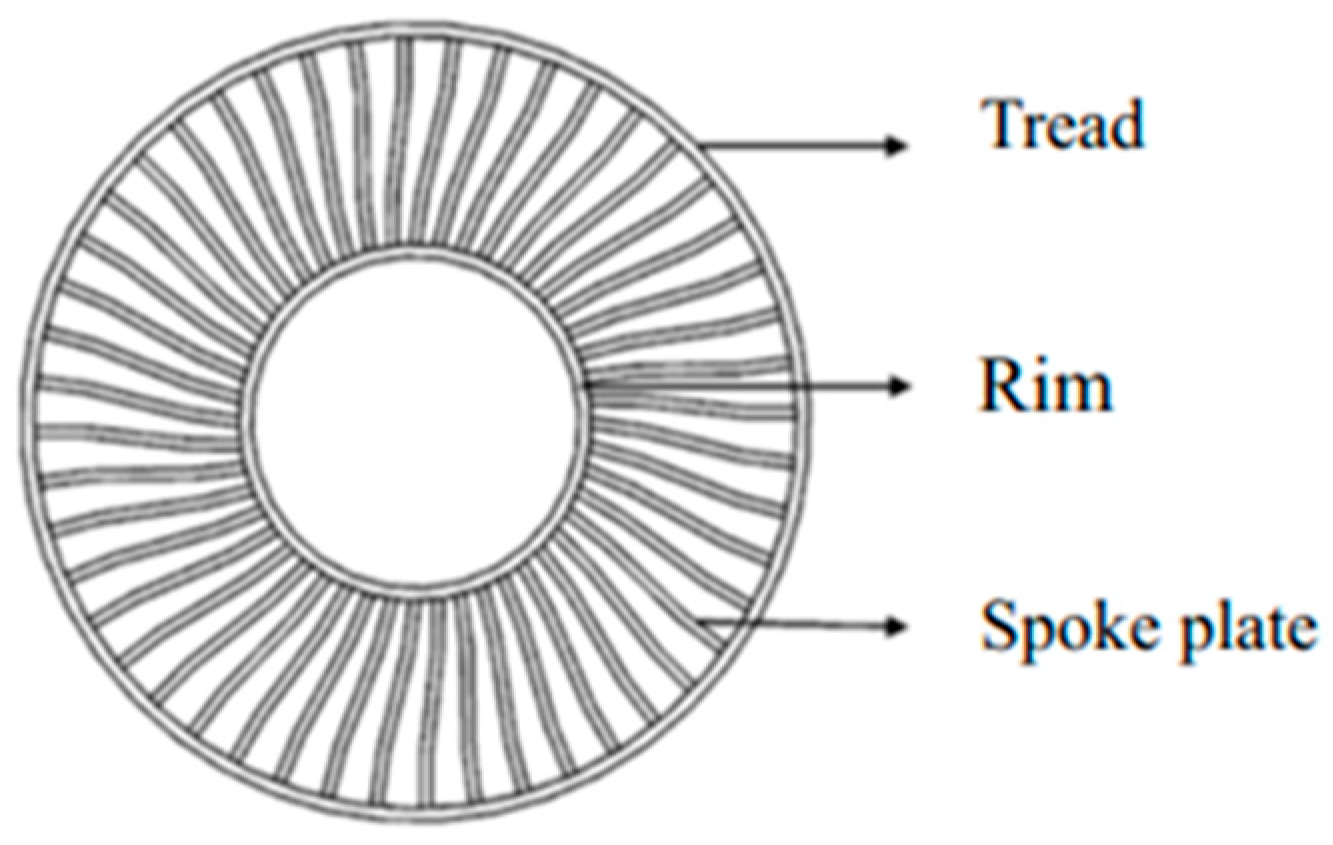
2.2.2. Structural Design of Spoke-Structure NPT
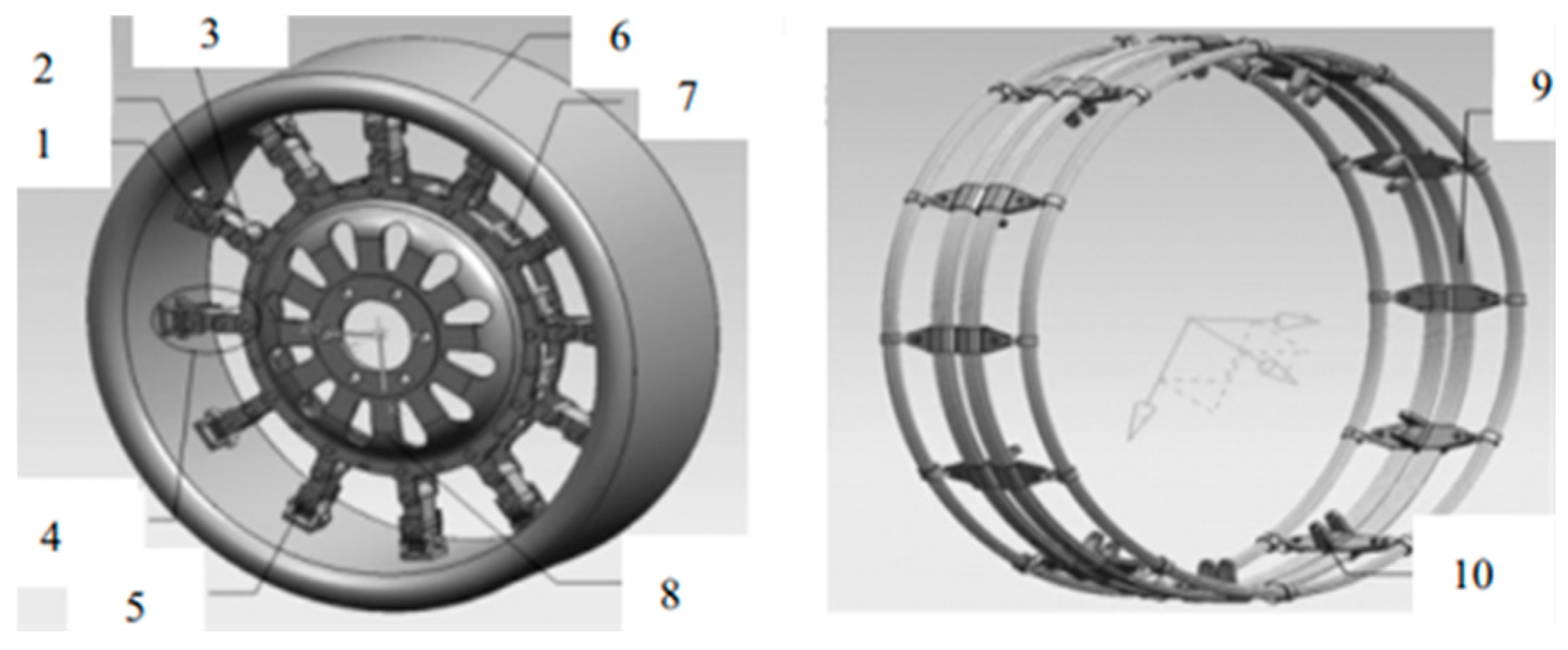
2.2.3. Structural Design of ME Wheel
3. Material Design of Safety Tires
3.1. Materials for RFTs
3.1.1. Materials for Inserts Body
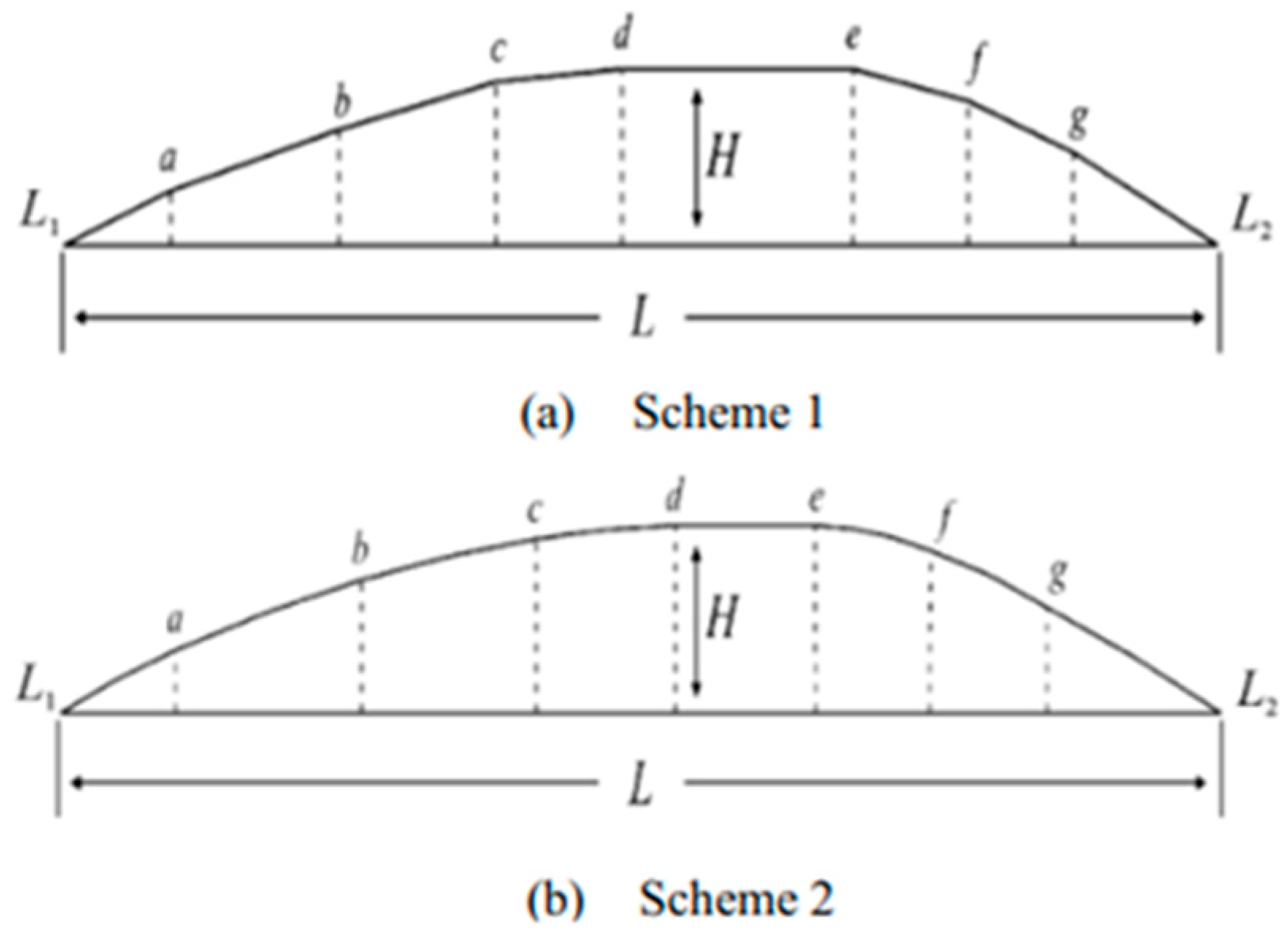
3.1.2. Materials for Sidewall Insert Rubbers
3.2. Materials for NPTs
3.2.1. Material for Elastic Support
3.2.2. Multi-Material and Manufacturing Process Integration
4. Study on Mechanical Characteristics of Safety Tires
4.1. Mechanical Characteristics of RFTs
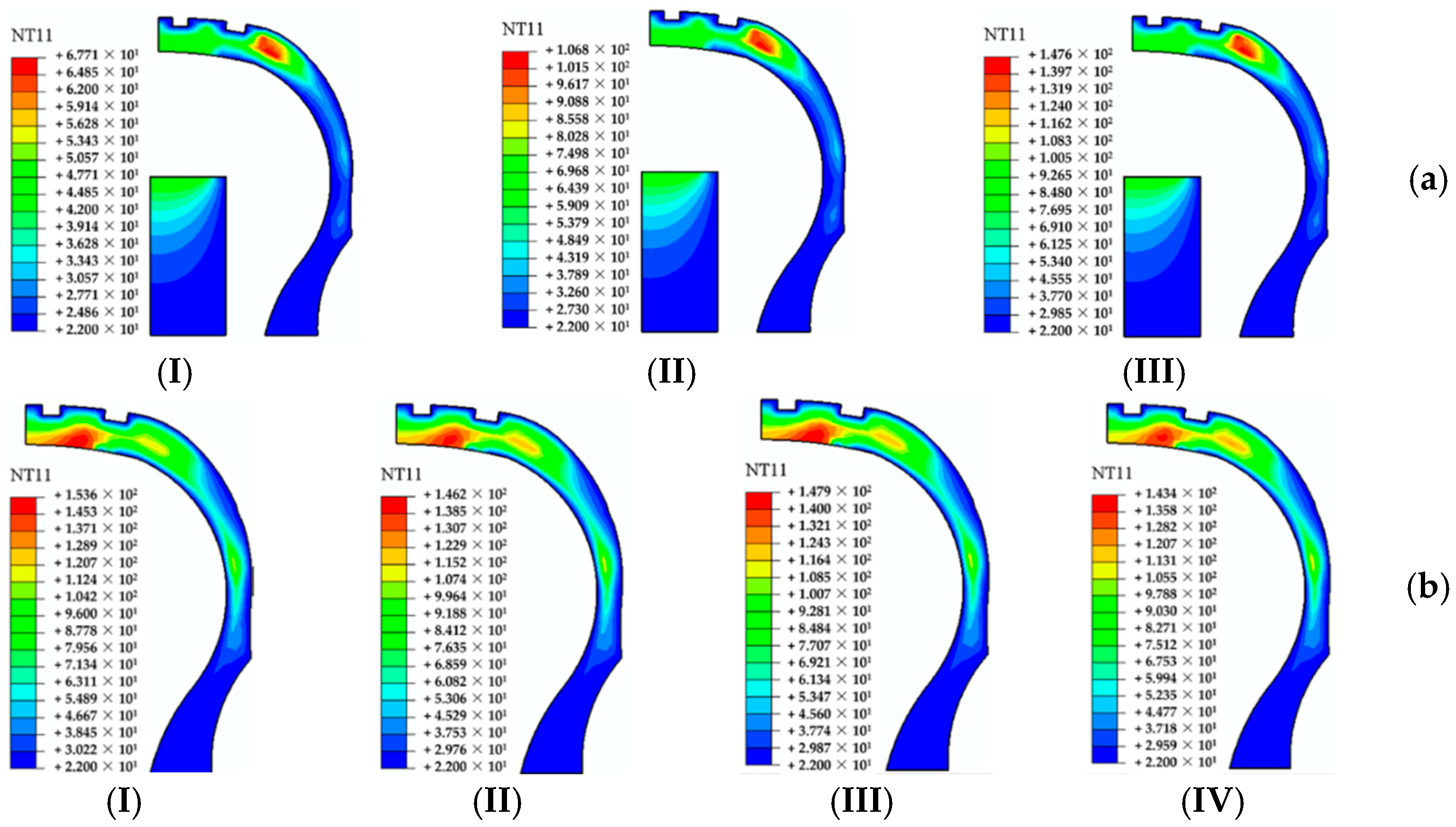
4.1.1. Mechanical Characteristics Under Pressure Relief Condition
4.1.2. Mechanical Characteristics Under Zero-Pressure Conditions
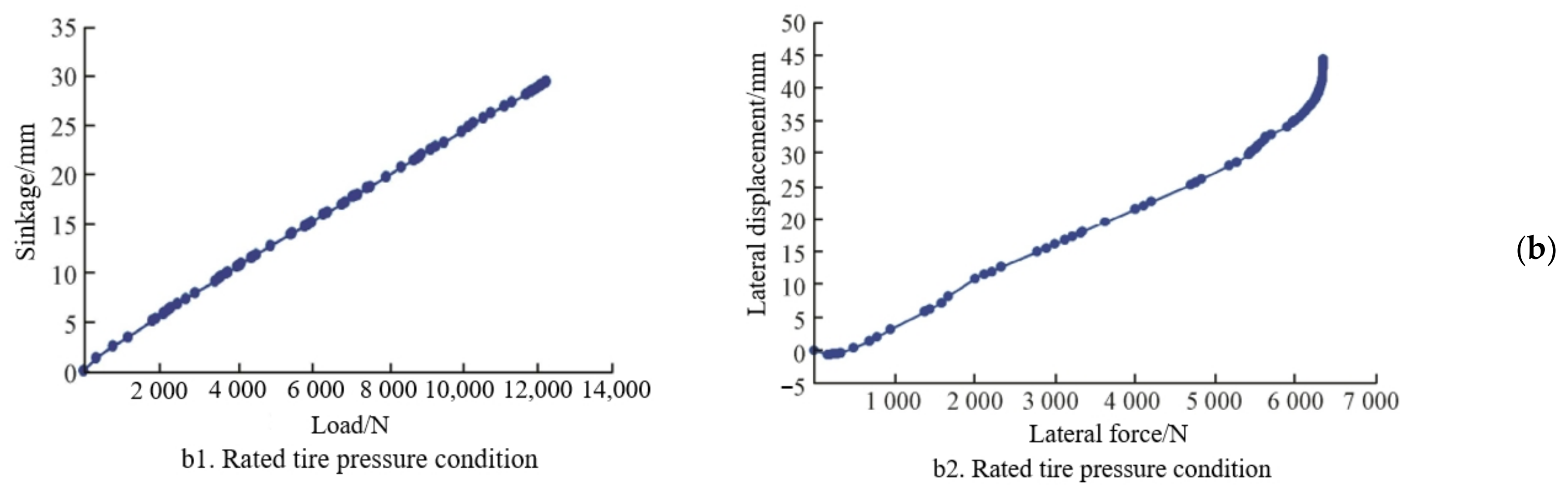
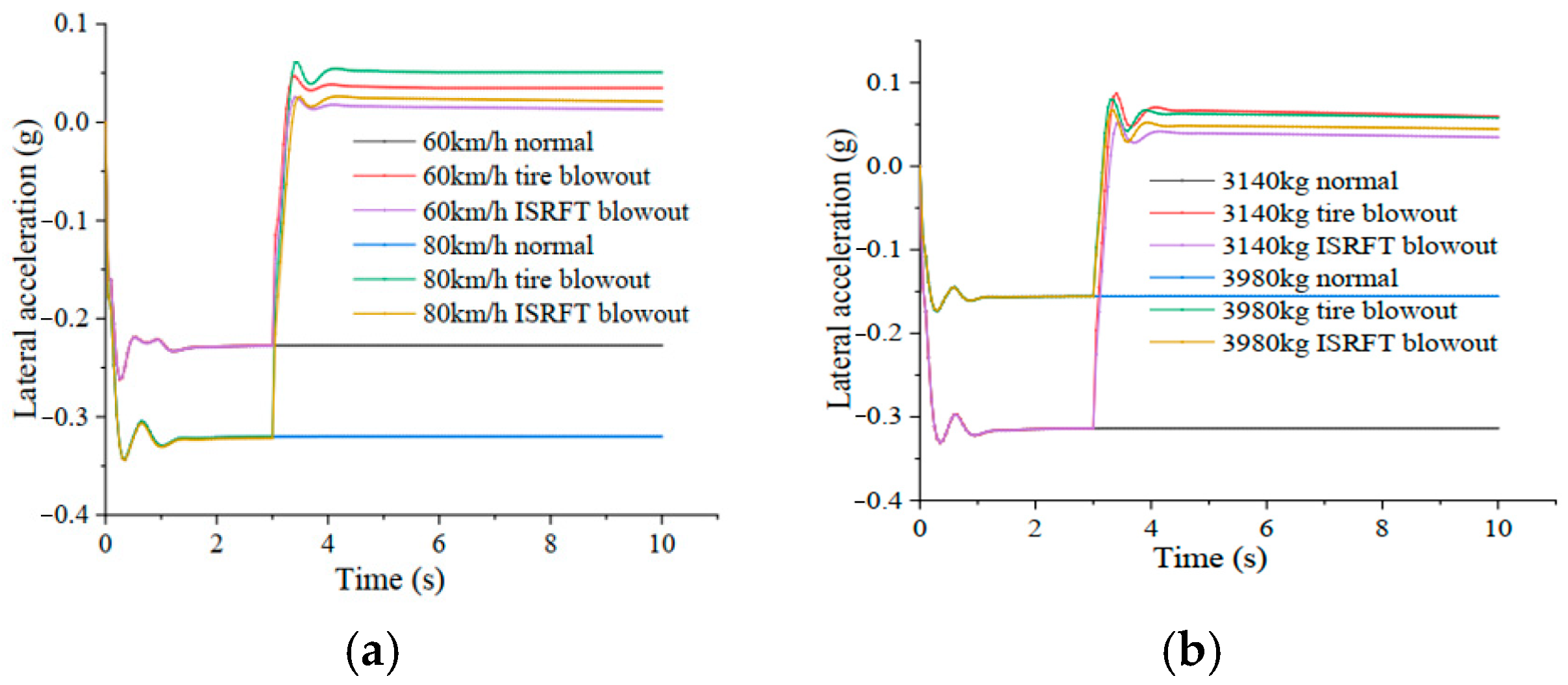
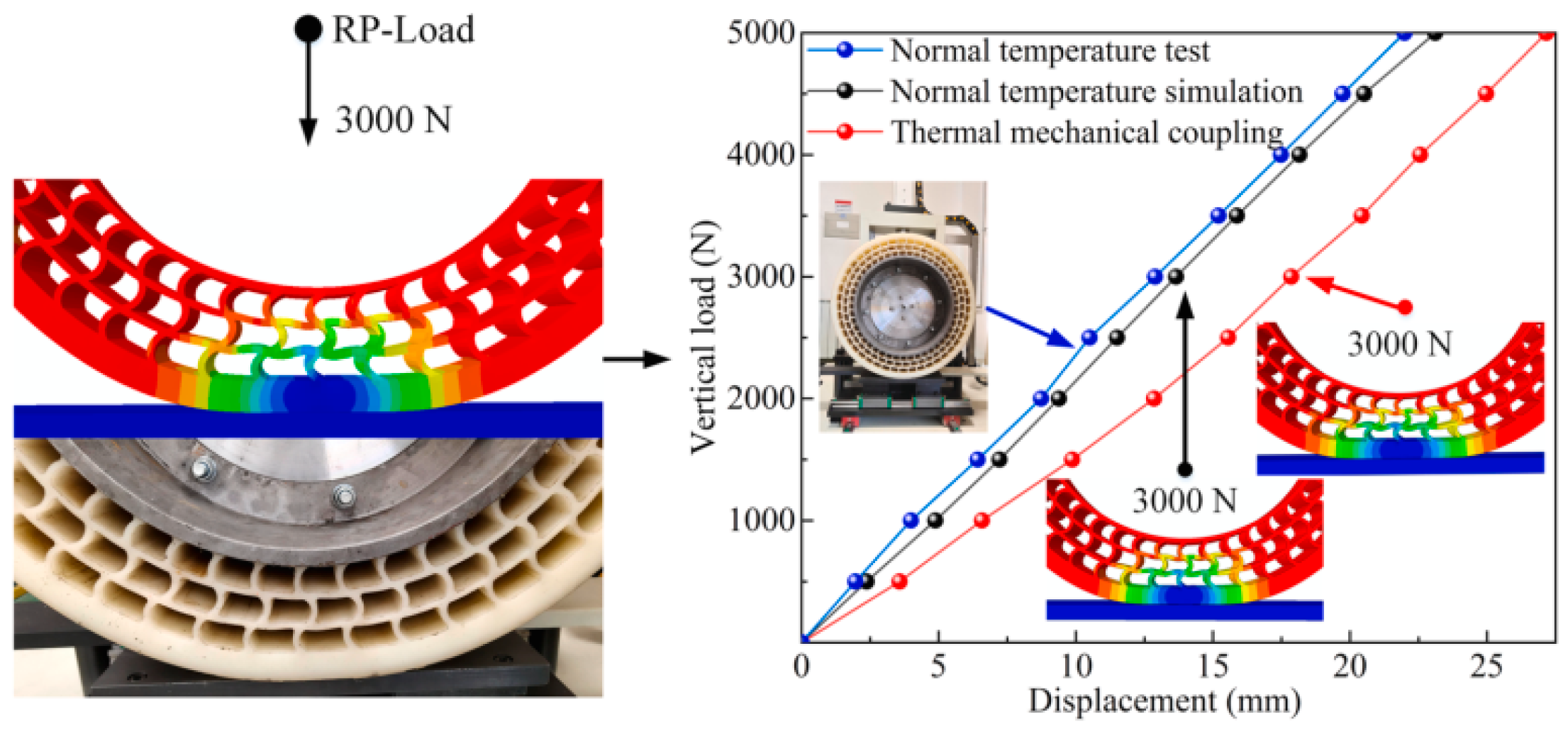
4.1.3. Mechanical Characteristics Under Typical Working Conditions
4.2. Mechanical Characteristics of NPTs
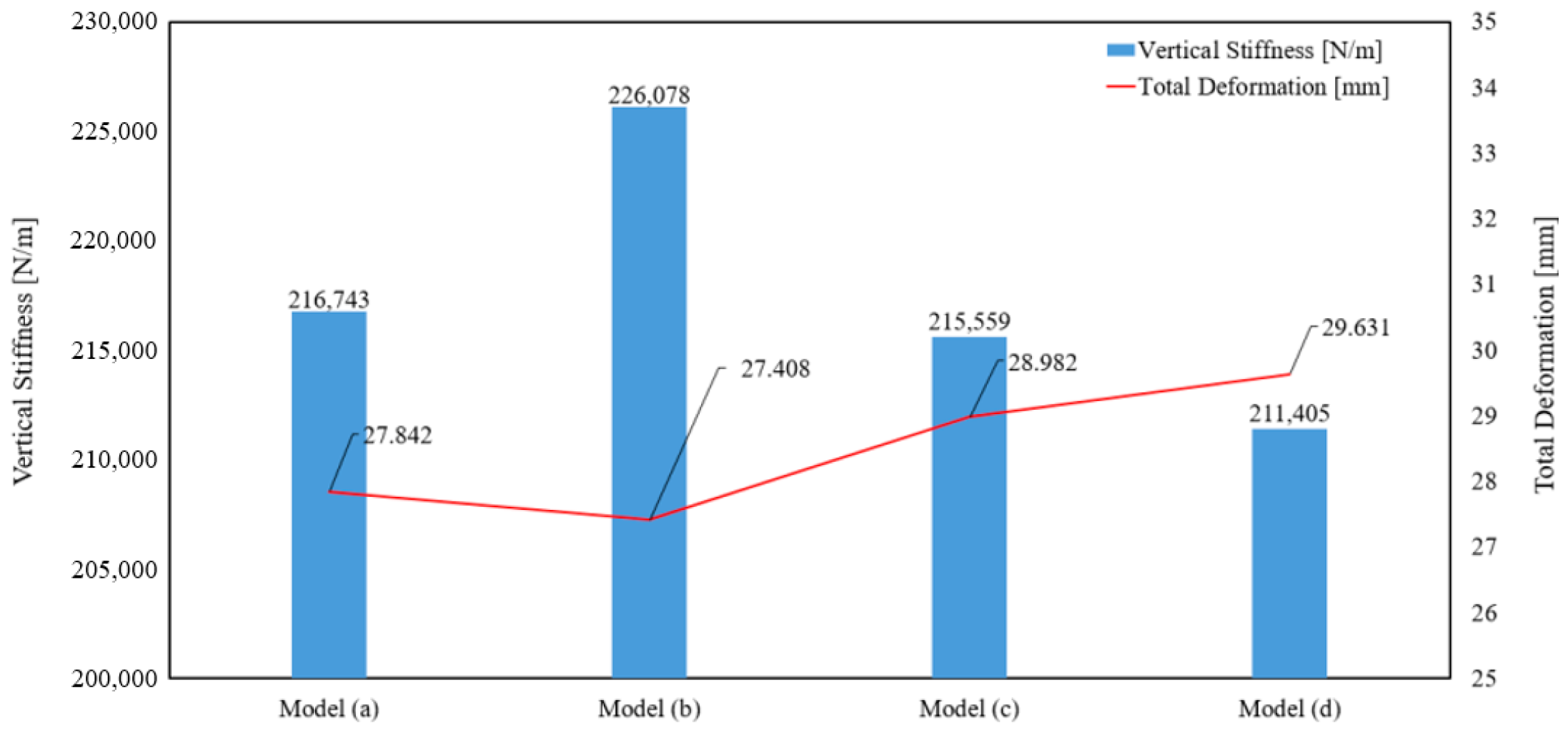
4.2.1. Static Mechanical Characteristics
- Vertical stiffness
- Radial stiffness
- Grounding characteristics
4.2.2. Dynamic Mechanical Response
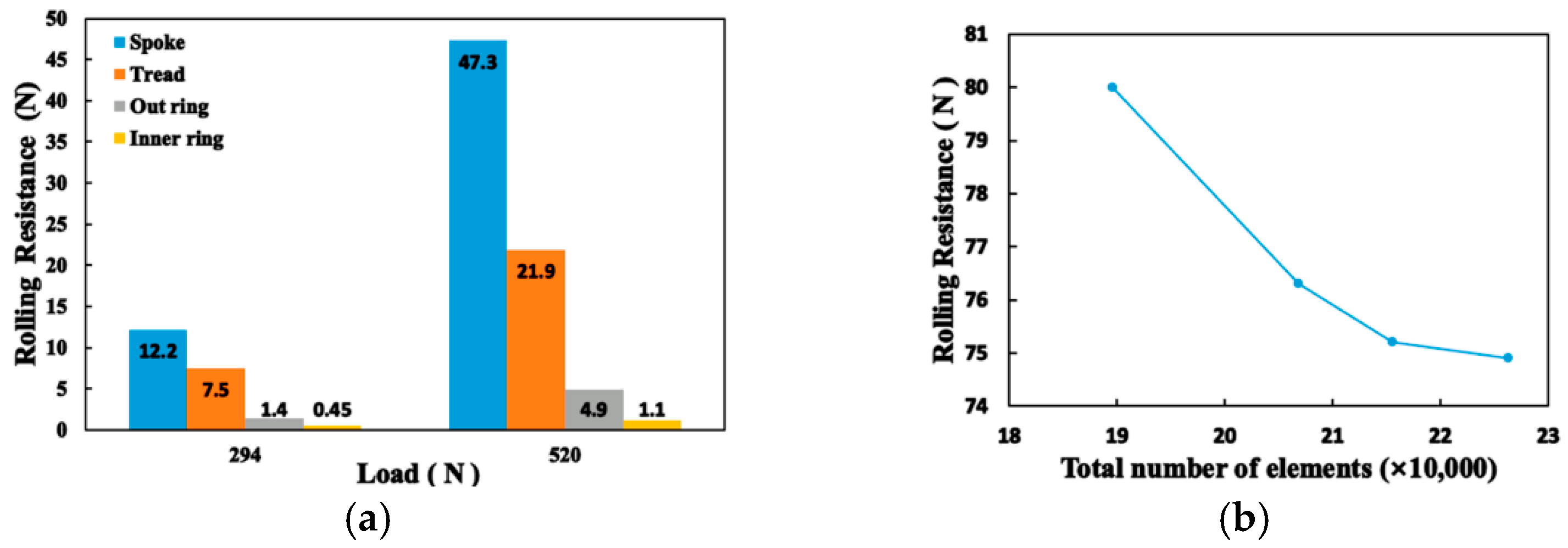
- Rolling resistance
- Vibration and shock
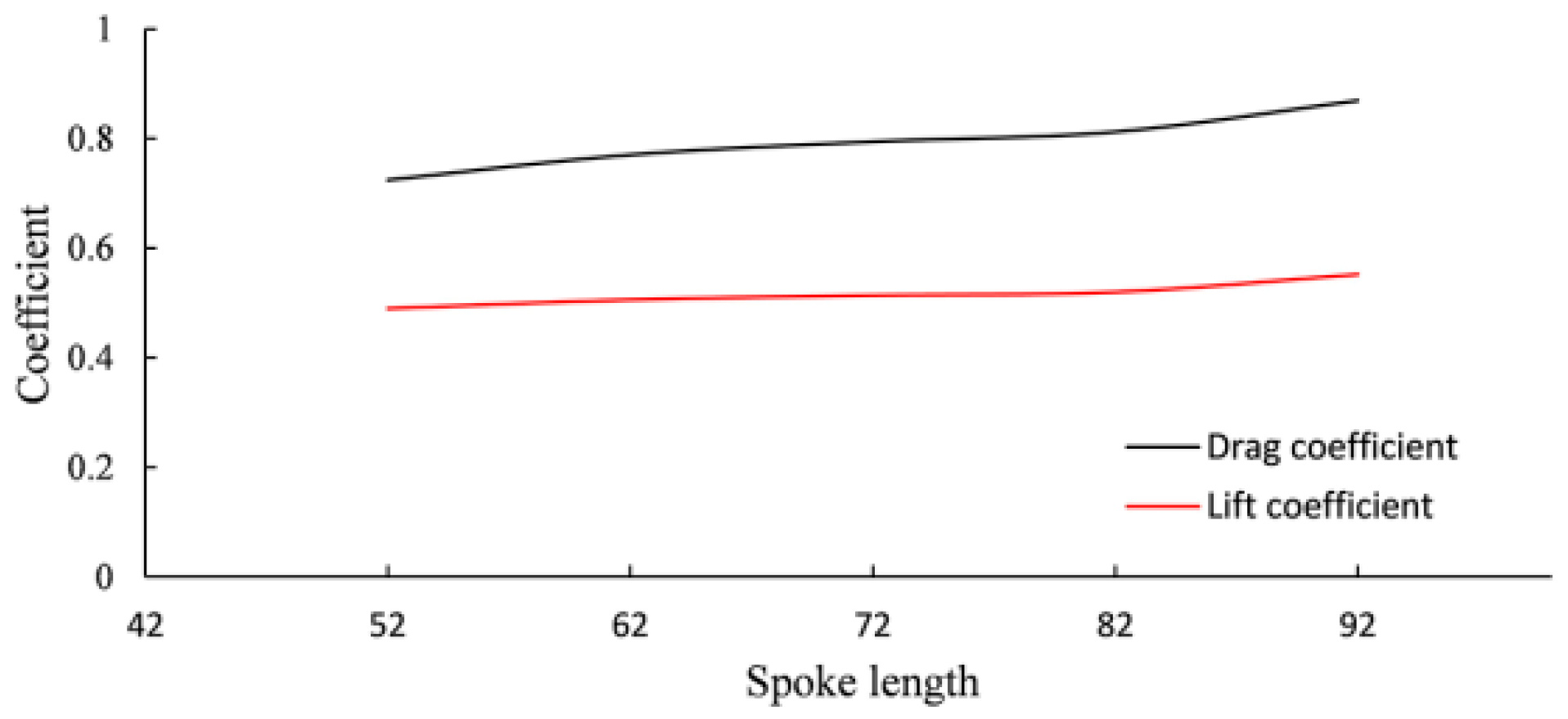
- Aerodynamic characteristics
4.2.3. Mechanical Characteristics Under Complex Conditions
5. Conclusions and Prospects
5.1. Conclusions
- (1)
- Structural designAll three tires exhibit their unique structural characteristics. The ISRFT relies on optimizing its internal support structure, which can achieve lightweight and improve heat dissipation. The SSRFT enhances load-bearing capacity under zero-pressure conditions by increasing the stiffness of the SIR. For NPTs, the optimized design of porous structures and spoke structures can reduce stress concentration and improve load-carrying capacity. The structural characteristics of the ME wheel enable it to adapt to complex road conditions.
- (2)
- Material designThe goal of material research for RFTs is to enhance support performance under zero-pressure conditions. The inserts body of ISRFT focuses on screening the mechanical characteristics of engineering materials. For the SIR of SSRFT, it involves various rubber systems, new alternative rubbers and fiber reinforcements. NFTs mostly combine composite materials with advanced manufacturing processes. This combination optimizes tire heat resistance, lightweight characteristics and load-carrying capacity, while also resolving the contradictions in the performance of single materials.
- (3)
- Mechanical characteristicsThe research on the mechanical characteristics of RFTs under different conditions is reviewed. Under pressure relief and zero-pressure conditions, the tire exhibits nonlinear mutations such as increased radial stiffness, expanded ground pressure and increased rolling resistance. Meanwhile, thermal-mechanical coupling intensifies. Optimization improves local performance but fails to balance overall uniformity. Under tire blowout conditions, the tire shows advantages in stability but struggles to balance emergency safety and normal handling. For NPTs, static performance is centered on spoke topology optimization, with spoke parameters adjusted to balance stiffness and grounding characteristics; rolling resistance mainly depends on spoke structure; vibration and impact are influenced by structure, material and dynamic load; and aerodynamic performance is determined by the overall structure. Under complex conditions, the influence of complex loads, special road surfaces and thermal-mechanical coupling on the mechanical characteristics of NPTs is mainly studied.
5.2. Prospects
- (1)
- Integrate structural design with interdisciplinary approaches. By incorporating bionics, replace traditional hexagonal honeycombs with adaptive irregular honeycomb structures featuring lightweight thermal management integration. Construct a multi-physics-coupled topology optimization model to simultaneously address heat dissipation, structural stiffness, and lightweight requirements.
- (2)
- Synergize materials and manufacturing processes. Develop novel materials featuring enhanced strength, superior thermal dissipation, lightweight properties and environmental sustainability. Implement advanced noise-reduction technologies and cushioning materials to improve driving comfort. Achieve optimal balance between performance and lightweight through multi-material integrated manufacturing. Leverage smart manufacturing and 3D printing technologies to propel performance enhancement and sustainable development of safety tires.
- (3)
- Expand special-scenario applications. Develop high-temperature-resistant, puncture-resistant composite-structure tires for extreme environments, concurrently optimizing heat dissipation and self-healing capabilities to ensure long-term reliable operation under complex working conditions. Drive synergistic advancement between safety tire technology, autonomous driving, and intelligent connected vehicle (ICV) technologies.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| L | total length of sidewall inserts rubber of SSRFT, mm |
| H | maximum thickness of sidewall inserts rubber of SSRFT, mm |
| U | strain energy of elastic body, J |
| σ | stress elastic body, Pa |
| ε | strain elastic body |
| Ft | rolling resistance force of tires, N |
| b | width of the contact trace between the tread and the ground, m |
| A | area of the contact trace between the tire and the ground, m2 |
| zk | wheel normal load, N |
| uz | radial deflection of tires, m |
| h | lag coefficient of tires |
| pk | inflation pressure of tires, kPa |
| fr | rolling resistance coefficient of tires |
| Fx0 | tangential force of tires, N |
| Fy0 | lateral force of tires, N |
| Mz0 | aligning moment of tires, Nm |
| b1 | width of the inserts body, mm |
| l1 | length of the wrap angle arc of the inserts body, mm |
| s0 | zero-pressure towing distance of RFT, mm |
| V | velocity of different conditions, km/h |
| N | the number of honeycombs |
References
- Tong, J.; Yang, X.; Zhang, F.; Zhang, S.J.; Chen, B.C. Development of run flat tire technology. Trans. Chin. Soc. Agric. Mach. 2007, 38, 182–187. [Google Scholar] [CrossRef]
- Drozd, K.; Tarkowski, S.; Caban, J.; Nieoczym, A.; Vrábel, J.; Krzysiak, Z. Analysis of truck tractor tire damage in the context of the study of road accident causes. Appl. Sci. 2022, 12, 12333. [Google Scholar] [CrossRef]
- Jilek, P. Vehicle wheel positioning innovation on a machine for measuring the contact parameters between a tyre and the road. Arch. Automot. Eng.-Arch. Mot. 2023, 100, 31–43. [Google Scholar] [CrossRef]
- Shi, H.X. A Century of Tire Evolution: Tracing the Developmental Journey. Automob. Parts 2005, 44, 2. [Google Scholar]
- Gao, S.X.; He, J.Q.; Jie, L.Q. Run-Flat tires and their applications in military vehicles. Tire Ind. 2009, 29, 259–263. [Google Scholar] [CrossRef]
- Zhao, Y.Q. Research progress on a non-pneumatic mechanical elastic safety wheel. Chin. J. Mech. Eng. 2019, 55, 105–116. [Google Scholar]
- Zhang, X.; Zhao, H.R.; Cao, Y.; Li, L.W.; Cui, W.W.; Cui, J.J.; Feng, Z.B.; Li, S.Y.; Hao, G.Q.; He, D.F. Theoretical Study on Inner Support of Run-Flat Tire. Adv. Mater. Res. 2012, 479–481, 2033–2036. [Google Scholar] [CrossRef]
- Zhou, H.C.; Jiang, Z.; Yang, J.; Zhai, H.H.; Wang, G.L. Numerical Investigation of Aerodynamic Noise Reduction of Nonpneumatic Tire Using Nonsmooth Riblet Surface. Appl. Bionics Biomech. 2020, 2020, 4345723. [Google Scholar] [CrossRef]
- Wu, T.Y.; Li, M.X.; Zhu, X.L.; Lu, X.F. Research on non-pneumatic tire with gradient Anti-tetrachiral structures. Mech. Adv. Mater. Struct. 2021, 28, 2351–2359. [Google Scholar] [CrossRef]
- Deng, Y.J.; Wang, Z.Y.; Shen, H.; Gong, J.J.; Xiao, Z. A comprehensive review on non-pneumatic tyre research. Mater. Des. 2023, 227, 111742. [Google Scholar] [CrossRef]
- Sun, M.; Zhong, H.L.; Qin, K.P.; Xu, T.; Yang, W.A.; Zhang, Y.; Lu, L. The Development of Processing Methods and Materials Used for Non-Pneumatic Tires: A Review. Materials 2024, 17, 5660. [Google Scholar] [CrossRef] [PubMed]
- Sardinha, M.; Vaz, M.F.; Reis, L. Design, properties, and applications of non-pneumatic tires: A review. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2023, 237, 2677–2697. [Google Scholar] [CrossRef]
- Yang, X.; Tong, J.; Zhang, F.; Zhang, S.J. Application of self-adaptive virtual design to run flat tire insertion. J. Jilin Univ. Eng. Techn. Ed. 2006, 36, 705–709. [Google Scholar] [CrossRef]
- Yang, X.; Tong, J.; Chen, D.H.; Zhang, S.J.; Chen, B.C. Finite element static analysis and improved design of the inner-supported 3-D structure of RFT. Chin. Soc. Agric. Mach. 2008, 39, 10–13. [Google Scholar]
- Zang, L.G.; Yin, R.D.; Zhao, Y.Q.; Peng, Z.X.; Zhao, Z.D.; Pei, Y.X. Design and simulation of combined inserts supporting a run-flat tire. J. Harbin Eng. Univ. 2019, 40, 1517–1523. [Google Scholar] [CrossRef]
- Zang, L.G.; Lv, T.; Li, Y.W.; Wang, X.Y. Topology optimization of inserts structure of run-flat tire under zero-pressure driving condition. Int. J. Automot. Technol. 2024, 24, 311–321. [Google Scholar] [CrossRef]
- Liu, H.Q.; Pan, Y.R.; Bian, H.G.; Wang, C.S. Optimize design of run-flat tires by simulation and experimental research. Materials 2021, 14, 474. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Xu, S.C.; Tong, J.; Huan, J. Analysis of the zero-pressure walking mechanism of the inner-supported RFT. J. Tsinghua Univ. (Sci. Technol.) 2014, 54, 871–876. [Google Scholar] [CrossRef]
- Cho, J.R.; Lee, J.H.; Jeong, K.M. Optimum design of run-flat tire insert rubber by genetic algorithm. Finite Elem. Anal. Des. 2012, 52, 60–70. [Google Scholar] [CrossRef]
- Lv, T.; Zang, L.G.; Li, Y.W.; Xue, C.; Jiao, J. Mechanical characteristics of self-supporting run-flat tires with different sidewall support rubber structures. J. Chongqing Univ. (Nat. Sci.) 2022, 36, 42–49. [Google Scholar] [CrossRef]
- Lv, T.; Zang, L.G.; Xue, C.; Li, Y.W.; Mao, Y.L.; Wang, X.Y. Study on the effect of different design parameters of sidewall insert rubber on the mechanical characteristics of self-supporting run-flat tires. Lubricants 2023, 11, 458. [Google Scholar] [CrossRef]
- Mao, R.; Sun, P.F.; Zhou, S.T.; Chen, L.W.; Meng, J.L.; Yang, W.Q.; Yang, C.Y.; Luo, K.J. Optimization of tire-ground performance through meshed belt layer structure. J. Ind. Text. 2024, 54, 15280837241275137. [Google Scholar] [CrossRef]
- Gipser, M. FTire–the tire simulation model for all applications related to vehicle dynamics. Veh. Syst. Dyn. 2007, 45, 139–151. [Google Scholar] [CrossRef]
- Mavros, G.; Rahnejat, H.; King, P. Analysis of the transient handling properties of a tyre, based on the coupling of a flexible carcass—Belt model with a separate tread incorporating transient viscoelastic frictional properties. Veh. Syst. Dyn. 2005, 43, 199–208. [Google Scholar] [CrossRef]
- Yamashita, H.; Jayakumar, P.; Sugiyama, H. Physics-based flexible tire model integrated with LuGre tire friction for transient braking and cornering analysis. J. Comput. Nonlinear Dyn. 2016, 11, 031017. [Google Scholar] [CrossRef]
- Hankin, H.; Gagen, J.; Peters, W.; Crann, A.; Chen, Y.; Fares, S.; Sareh, P. Airless tires: Structural concepts, mechanical design, and application prospects. Mater. Des. 2025, 235, 113933. [Google Scholar] [CrossRef]
- Jin, X.C.; Hou, C.; Fan, X.L.; Sun, Y.L.; Lv, J.A.; Lu, C.S. Investigation on the static and dynamic behaviors of non-pneumatic tires with honeycomb spokes. Compos. Struct. 2018, 187, 27–35. [Google Scholar] [CrossRef]
- Ganniari-Papageorgiou, E.; Chatzistergos, P.; Wang, X.X. The influence of the honeycomb design parameters on the mechanical behavior of non-pneumatic tires. Int. J. Appl. Mech. 2020, 12, 2050024. [Google Scholar] [CrossRef]
- Zheng, Z.; Rakheja, S.; Sedaghati, R. Multi-axis stiffness and road contact characteristics of honeycomb wheels: A parametric analysis using Taguchi method. Compos. Struct. 2021, 279, 114735. [Google Scholar] [CrossRef]
- Zhao, Y.; Song, S.; Li, J.C.; Yang, H.T. Design and performance analysis of a novel negative poisson’s ratio non-pneumatic tire support structure. J. Nanjing Univ. Sci. Technol. 2021, 45, 751–760. [Google Scholar] [CrossRef]
- Zang, L.G.; Peng, X.L.; Sun, J.; Cui, S.; Bai, Y.X. Investigation on structural design and grounding characteristics of two-dimensional double-U honeycomb non-pneumatic tires. Eur. J. Mech. A-Solids 2025, 111, 105599. [Google Scholar] [CrossRef]
- Yang, J.; Zhou, H.F.; Zhou, H.C.; Zheng, Z.; Wang, G.L. Comparative study of static and dynamic characteristics of non-pneumatic tires with gradient honeycomb structure. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 366. [Google Scholar] [CrossRef]
- Rugsaj, R.; Suvanjumrat, C. Development of a novel spoke structure of non-pneumatic tires for skid-steer loaders using finite element analysis. Mech. Based Des. Struct. Mach. 2023, 51, 6905–6927. [Google Scholar] [CrossRef]
- Rugsaj, R.; Suvanjumrat, C. Study of geometric effects on nonpneumatic tire spoke structures using finite element method. Mech. Based Des. Struct. Mach. 2022, 50, 2379–2399. [Google Scholar] [CrossRef]
- Fu, H.X.; Liang, X.M.; Wang, Y.; Ku, L.Y.; Xiao, Z. Thermal mechanical coupling analysis of a flexible spoke non-pneumatic tire. Stroj. Vestn.-J. Mech. Eng. 2022, 68, 143–154. [Google Scholar] [CrossRef]
- Fu, H.X.; Chen, X.X.; Zhao, Q.; Xiao, Z.; Liang, X.M. Fatigue life prediction and influencing factors analysis of mesh flexible spoke non-pneumatic tire. Adv. Mech. Eng. 2021, 13, 16878140211052454. [Google Scholar] [CrossRef]
- Ku, L.Y.; Fu, H.X.; Chen, K.; Zhang, J.Y.; Bi, S.Y.; Zhou, L. Numerical analysis of steady-state mechanical characteristics of the flexible spoke non-pneumatic tire under multiple working conditions. J. Terramech. 2023, 106, 35–45. [Google Scholar] [CrossRef]
- Zhang, Z.F.; Fu, H.X.; Zhao, Q.; Tan, D.; Yang, K. Pattern design and performance analysis of a flexible spoke bionic non-pneumatic tire. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 41. [Google Scholar] [CrossRef]
- Shuai, Z.B.; Gao, S.C.; Yu, Y.; Zhao, X.Z.; Yang, W.M.; Song, Z.C.; Zheng, Y.J.; Yuan, J.M.; Jiao, Z.W. Characteristic study and design factor analysis of a novel non-pneumatic tyre with V-shaped spokes. Mater. Des. 2024, 238, 112681. [Google Scholar] [CrossRef]
- Rugsaj, R.; Suvanjumrat, C. Revolutionizing tire engineering: Finite element analysis and design of an X-shaped spoke structure for non-pneumatic military tires. Alexandria Eng. J. 2024, 99, 303–318. [Google Scholar] [CrossRef]
- Liu, X.Y.; Xu, T.; Zhu, L.L.; Gao, F. Multi-Objective Optimization of the geometry of a non-pneumatic tire for three-dimensional stiffness adaptation. Machines 2023, 10, 1183. [Google Scholar] [CrossRef]
- Sun, M.Y.; Liu, W.D.; Zhang, Q.S.; Chen, Y.X.; Jiang, J.S.; Liu, X.T. Study on the load-bearing characteristics analysis model of non-pneumatic tire with composite spokes. Machines 2024, 12, 358. [Google Scholar] [CrossRef]
- Ni, S.Q.; Fu, H.X.; Li, X.L.; Chen, K.; Zhang, J.Y. Design and simulation of a new type of composite flexible-spoke non-pneumatic tire. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 310. [Google Scholar] [CrossRef]
- Zhou, H.C.; Ren, H.Z.; Zhou, H.F.; Xu, T.; Wang, G.L. Investigation of the spoke lateral thickness effects on non-pneumatic tire radial and lateral stiffness. Mater. Recycl. 2025, 26, 505–523. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, Y.Q.; Huang, C.; Jiang, C. Modeling and off-road performance study of the novel mechanical elastic wheel. Chin. Mech. Eng. 2013, 24, 724–729. [Google Scholar] [CrossRef]
- Yan, L.L.; Zhao, Y.Q.; Fu, H.X.; Wang, Q. Structure parameterized design for a new mechanical elastic wheel. Chin. Mech. Eng. 2016, 27, 1251–1256. [Google Scholar] [CrossRef]
- Feng, Z.L.; Zhao, Y.Q.; Zhang, C.X. Lightweight analysis of mechanical elastic wheel based on topology optimization. J. Jiangsu Univ. (Nat. Sci. Ed.) 2023, 44, 511–516. [Google Scholar] [CrossRef]
- Jiang, C.; Zhao, Y.Q.; Ruan, M.Q.; Wang, W. Structure optimization of the mechanical elastic wheel based on the sequential quadratic programming algorithm. Mech. Sci. Technol. Aerosp. Eng. 2014, 33, 423–427. [Google Scholar] [CrossRef]
- Li, H.Q.; Zhao, Y.Q. Impact of mechanical elastic wheel structural parameters on automotive rollover stability. Chin. Mech. Eng. 2019, 30, 1519–1527. [Google Scholar] [CrossRef]
- Li, X.L.; Zhao, Y.Q.; Liu, Y.J. Hydraulic Composite Wheel. China Patent 201310236856.4, 11 September 2013. [Google Scholar]
- Zhao, Y.Q.; Li, X.L.; Li, B. Segmented Elastic Wheel. China Patent 201310431410.7, 1 January 2014. [Google Scholar]
- Xue, Z.C.; He, J.Y.; Ding, Y.M.; Yang, W.M.; Jiao, Z.W. Research on mechanical properties of airless plastic tires with wheel spokes under static load. China Plast. 2014, 28, 91–95. [Google Scholar] [CrossRef]
- Huang, Z.G.; Li, C.Y.; Wang, Y.C.; Yong, Z.F. Design and simulation analysis of supercritically foamed polyurethane run-flat tire. Chin. Elastomer 2019, 29, 12–16. [Google Scholar] [CrossRef]
- Yu, M.; Hong, H.; Hao, C. Study on the Properties of NR/NdBR Blends. Rubber Ind. 2010, 57, 606–608. [Google Scholar] [CrossRef]
- Ni, H.C.; Chen, J.J.; Xue, B.B.; Zhang, M. Application of high-cis polybutadiene composite rubber VCR617 in sidewall support compounds of run-flat tires. Tire Ind. 2021, 41, 299–302. [Google Scholar] [CrossRef]
- Ren, F.J.; Chen, Q.M.; Wang, D.L.; Huang, D.Y. Application of carbon black-modified low-cis polybutadiene rubber in run-flat tire support compounds. Tire Ind. 2018, 38, 601–604. [Google Scholar] [CrossRef]
- Park, N.; Seo, J.; Kim, K.; Sim, J.; Kang, Y.; Han, M.; Kim, W. Sidewall-insert compound based on ZnO-treated aramid pulp fibers for run-flat tires. Compos. Interfaces 2016, 23, 781–796. [Google Scholar] [CrossRef]
- Hu, S.K.; Shou, T.; Guo, M.M.; Wang, R.G.; Wang, J.; Tian, H.C.; Qin, X.; Zhao, X.Y.; Zhang, L.Q. Fabrication of new thermoplastic polyurethane elastomers with high heat resistance for 3D printing derived from 3,3-dimethyl-4, 40-diphenyl diisocyanate. Ind. Eng. Chem. Res. 2020, 59, 10476–10482. [Google Scholar] [CrossRef]
- Priyankkumar, D.; Soumyadipta, M.; Beena, R. Effect of spoke design and material nonlinearity on non-pneumatic tire stiffness and durability performance. SAE Int. J. Passeng. Cars-Mech. Syst. 2021, 14, 20213610851096. [Google Scholar] [CrossRef]
- Wang, J.; Yang, B.; Lin, X.; Gao, L.; Liu, T.; Lu, Y.L.; Wang, R.G. Research of TPU materials for 3D printing aiming at Non-Pneumatic Tires by FDM method. Polymer 2020, 12, 2492. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.W.; He, P.; Geng, Q.Q.; Huang, H.; Sang, L.; Yao, Z.Q. Investigation of additive-manufactured carbon fiber-reinforced polyethylene terephthalate honeycomb for application as non-pneumatic tire support structure. Polymer 2024, 16, 1091. [Google Scholar] [CrossRef]
- Andrae, J.; Lisboa, T.D.; Spickenheuer, A. The development of a non-pneumatic tire concept based on a fiber-reinforced epoxy composite. Polymers 2025, 17, 505. [Google Scholar] [CrossRef]
- Zastrow, M. 3D printing gets bigger, faster and stronger. Nature 2020, 578, 20–23. [Google Scholar] [CrossRef] [PubMed]
- Tan, L.J.; Zhu, W.; Zhou, K. Recent progress on polymer materials for additive manufacturing. Adv. Funct. Mater. 2020, 30, 2003062. [Google Scholar] [CrossRef]
- Dezianian, S.; Azadi, M. Multi-Material metamaterial topology optimization to minimize the compliance and the constraint of weight: Application of non-pneumatic tire additive-manufactured with PLA/TPU polymers. Polymers 2023, 15, 1927. [Google Scholar] [CrossRef]
- Suvanjumrat, C.; Rugsaj, R. Study of 3D printing for forming spoke of non-pneumatic tire using finite element method. MSE 2021, 1137, 012020. [Google Scholar] [CrossRef]
- Rugsaj, R.; Suvanjumrat, C. Finite element analysis of hyperelastic material model for non-pneumatic tire. Key Eng. Mater. 2018, 775, 554–559. [Google Scholar] [CrossRef]
- Rugsaj, R.; Suvanjumrat, C. Determination of material property for non-pneumatic tire spokes by inverse method. Key Eng. Mater. 2018, 777, 411–415. [Google Scholar] [CrossRef]
- Bae, J.J.; You, Y.; Suh, J.B.; Kang, N. Calculation of the structural stiffness of run-flat and regular tires by considering strain energy. Int. J. Automot. Technol. 2019, 20, 979–987. [Google Scholar] [CrossRef]
- Wang, X.Y.; Zang, L.G.; Wang, Z.; Zhao, Z.D.; Lin, F.; Teng, F. Analysis of mechanical characteristics of inserts supporting run-flat tire during pressure relief. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 235. [Google Scholar] [CrossRef]
- Zang, L.G.; Xue, C.; Peng, X.L.; Jiao, J.; Feng, Y.X.; Mao, Y.L. Investigation on dynamic characteristics of inserts supporting run-flat tyre based on the modified non-linear ground pressure distribution. Int. J. Non-Linear Mech. 2024, 167, 104916. [Google Scholar] [CrossRef]
- Pacejka, H.B.; Bakker, E. The magic formula tyre model. Veh. Syst. Dyn. 1992, 21, 1–18. [Google Scholar] [CrossRef]
- Pacejka, H.B.; Besselink, I. Magic formula tyre model with transient properties. Veh. Syst. Dyn. 1997, 27, 234–249. [Google Scholar] [CrossRef]
- Zang, L.G.; Lv, T.; Xue, C.; Wei, F.Q.; Zhao, W.Q.; Teng, F. Investigation on mechanical and temperature characteristics of self-supporting run-flat tire during pressure relief. Int. J. Automot. Technol. 2024, 26, 857–876. [Google Scholar] [CrossRef]
- Kim, S.J.; Savkoor, A.R. The contact problem of in-plane rolling of tires on a flat road. Veh. Syst. Dyn. 1997, 27, 189–206. [Google Scholar] [CrossRef]
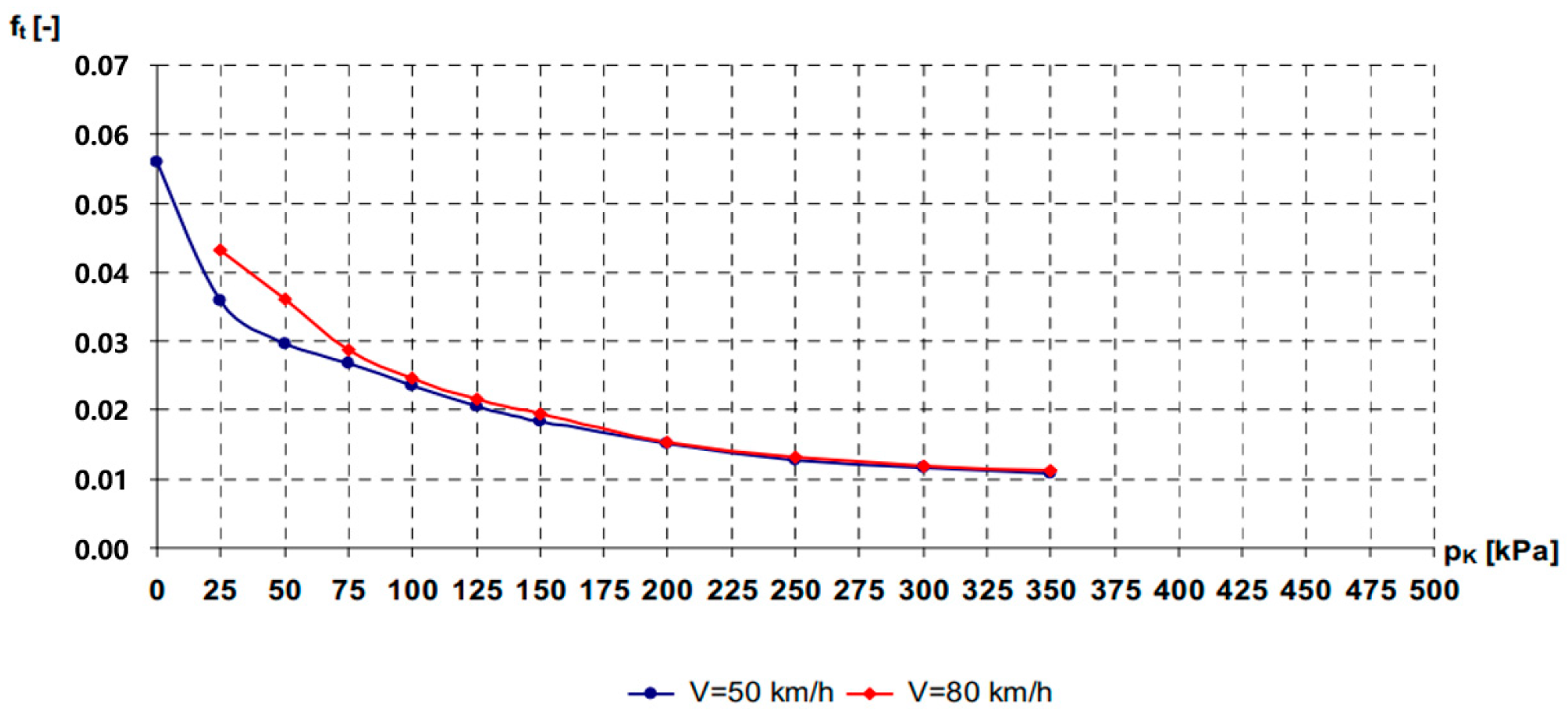
- Ejsmont, J.; Jackowski, J.; Luty, W.; Motrycz, G.; Stryjek, P.; Świeczko-Żurek, B. Analysis of rolling resistance of tires with run flat insert. Key Eng. Mater. 2014, 597, 1165–1170. [Google Scholar] [CrossRef]
- Pasterkamp, W.R.; Pacejka, H.B. The tyre as a sensor to estimate friction. Veh. Syst. Dyn. 1997, 27, 409–422. [Google Scholar] [CrossRef]
- Guo, K.H.; Wu, H.D.; Lu, D. Brush model for steady-state side-slip of tire on icy road. J. Jilin Univ. Eng. Techn. Ed. 2007, 37, 253–258. [Google Scholar] [CrossRef]
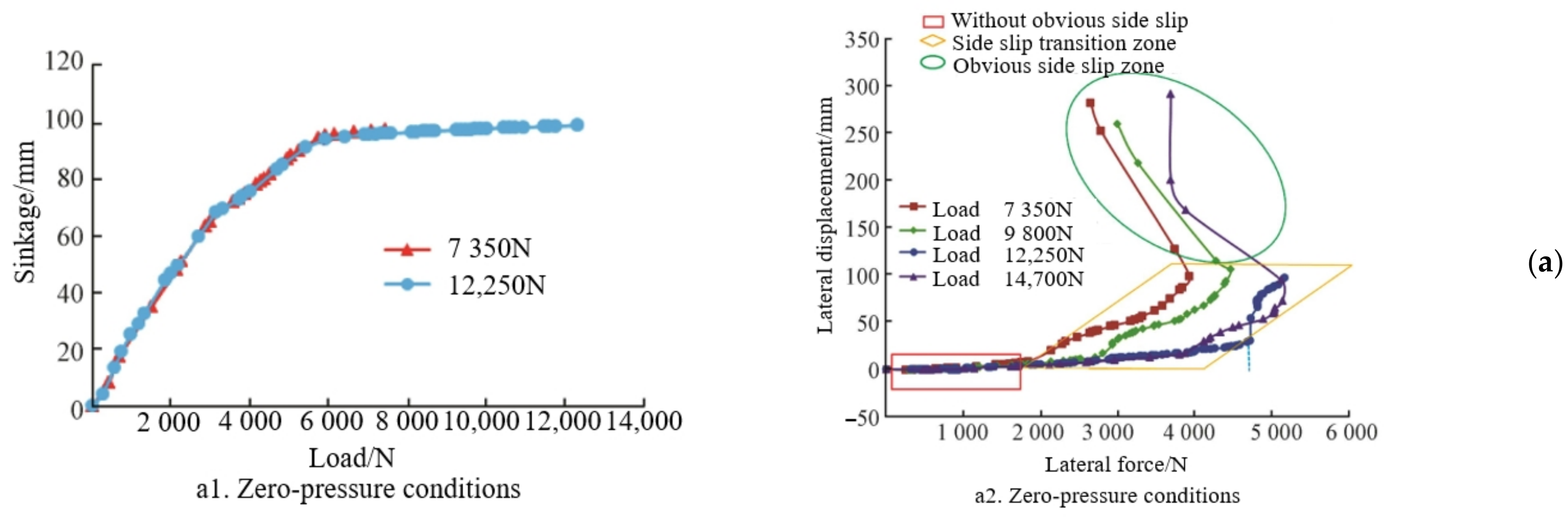
- Zang, L.G.; Wang, X.Y.; Zhao, Y.Q.; Yin, R.D.; Lin, F.; Zhao, Z.D. Mechanical characteristics of inserts supporting run-flat tire under zero-pressure conditions. Trans. Chin. Soc. Agric. Mach. 2020, 36, 80–86. [Google Scholar] [CrossRef]
- Zang, L.G.; Wang, X.Y.; Wu, C.Y.; Teng, F.; Yang, S.Q. Analysis of load characteristic and contact patch characteristic of support insert run-flat tire under zero-pressure condition. Int. J. Automot. Technol. 2021, 1, 11. [Google Scholar] [CrossRef]
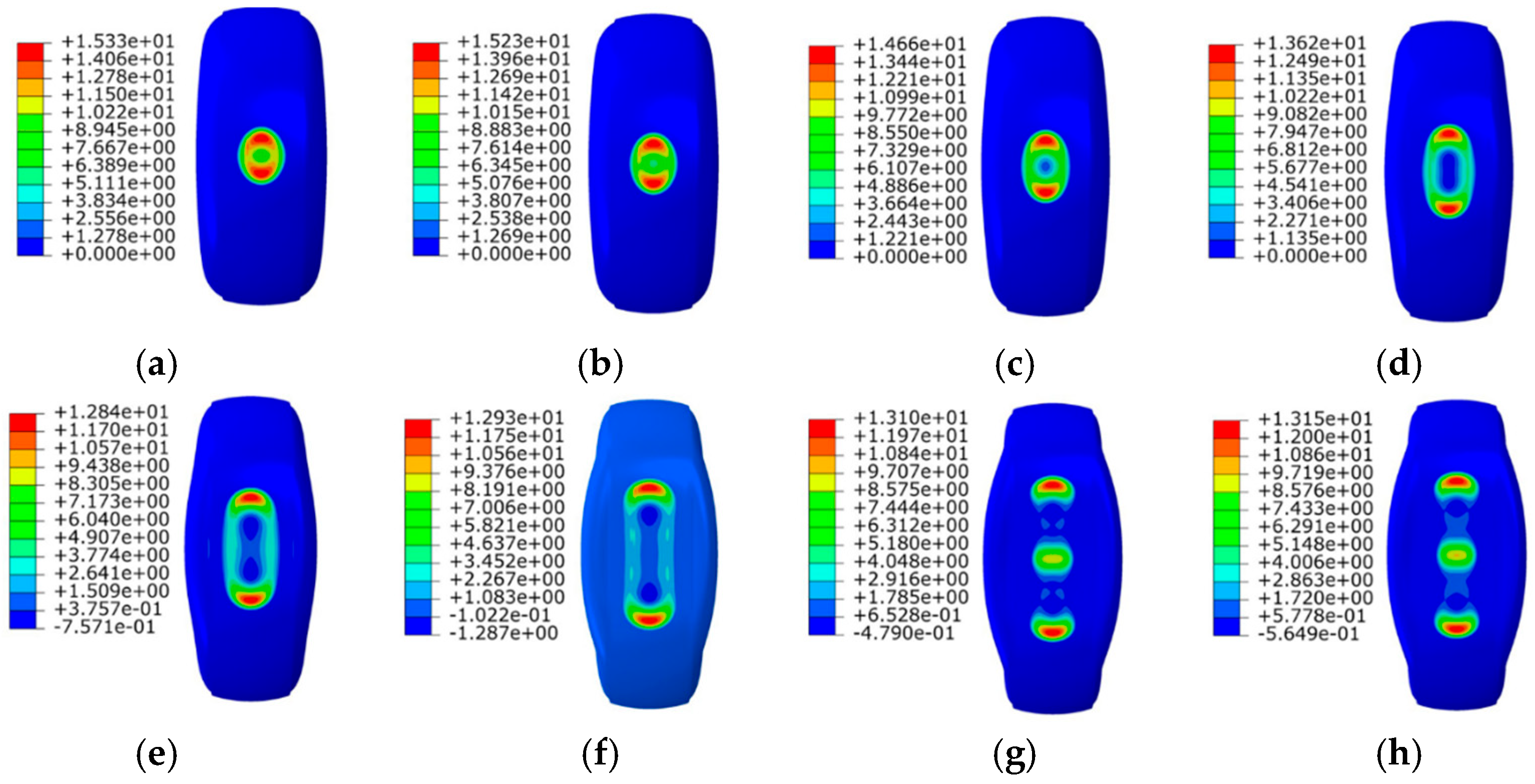
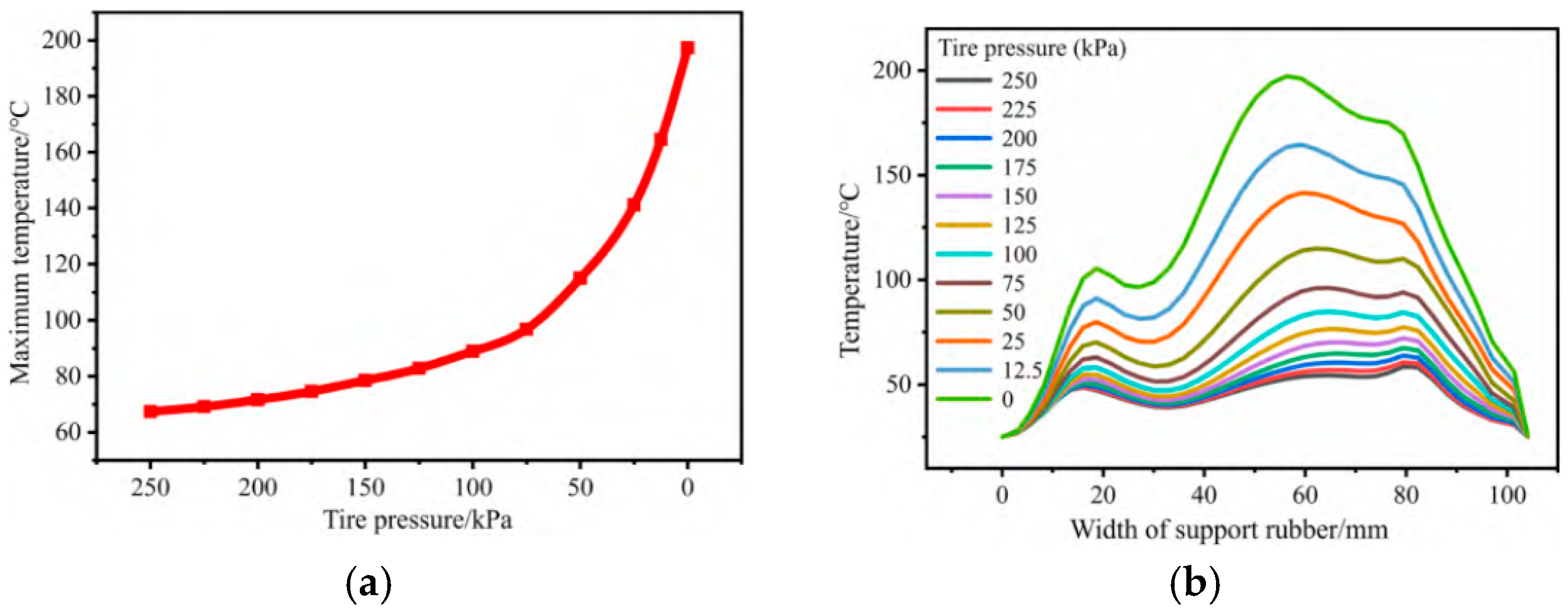
- Xue, C.; Zang, L.G.; Wei, F.Q.; Feng, Y.X.; Zhou, C.; Lv, T. Thermo-Mechanical coupling analysis of inserts supporting run-flat tires under zero-pressure conditions. Machines 2024, 12, 578. [Google Scholar] [CrossRef]
- Xie, L.Q.; Gao, S.X.; Zhao, M.; Wan, Y.Q.; He, J.Q. Road test comparison of self- sealing safety tire and ordinary tire. Automot. Technol. 2007, 8, 52–54. [Google Scholar] [CrossRef]
- Zhou, H.C.; Wang, G.L.; Ding, Y.M.; Yang, J.; Liang, C.; Fu, J. Effect of friction model and tire maneuvering on tire-pavement contact stress. Adv. Mater. Sci. Eng. 2015, 2015, 632647. [Google Scholar] [CrossRef]
- Wang, X.Y.; Zang, L.G.; Li, Y.W.; Wang, Z.; Lv, T. Study on tire blowout characteristics of insert supporting run-flat tire. In Proceedings of the 2021 5th CAA International Conference on Vehicular Control and Intelligence (CVCI), Tianjin, China, 29–31 October 2021. [Google Scholar] [CrossRef]
- Guo, K.H. UniTire unified tire model. Chin. J. Mech. Eng. 2016, 52, 90–99. [Google Scholar] [CrossRef]
- Wang, X.Y.; Zang, L.G.; Lv, T.; Li, Y.W. Dynamic characteristics of ISRFT blowout considering camber angle under typical driving conditions. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2025, 239, 568–602. [Google Scholar] [CrossRef]
- Rugsaj, R.; Suvanjumrat, C. Proper radial spokes of non-pneumatic tire for vertical load supporting by finite element analysis. Int. J. Automot. Technol. 2019, 20, 801–812. [Google Scholar] [CrossRef]
- Sim, J.; Hong, J.; Cho, I.; Lee, J. Analysis of vertical stiffness characteristics based on spoke shape of non-pneumatic tire. Appl. Sci. 2021, 11, 2369. [Google Scholar] [CrossRef]
- Phromjan, J.; Suvanjumrat, C. Effects on spoke structure of non-pneumatic tires by finite element analysis. Int. J. Automot. Technol. 2022, 23, 1437–1450. [Google Scholar] [CrossRef]
- Seong, J.Y.; Ji, S.M.; Choi, D.H.; Lee, S.J.; Lee, S. Optimizing generative adversarial network (GAN) models for non-pneumatic tire design. Appl. Sci. 2023, 13, 10664. [Google Scholar] [CrossRef]
- Zhao, C.X.; Zhao, Y.Q.; Feng, S.L.; Zheng, X.; Xu, H. Stiffness analysis of new type non-pneumatic tires based on pseudo-rigid-flexible body coupling model. Chin. J. Mech. Eng. 2021, 32, 1051–1060. [Google Scholar] [CrossRef]
- Du, X.B.; Zhao, Y.Q.; Ma, Y.J.; Fu, H.X. Influence of hinge length and distribution number on the camber and cornering properties of a non-pneumatic tire. Adv. Mech. Eng. 2020, 12, 1687814020984687. [Google Scholar] [CrossRef]
- Furlan, M.; Mavros, G. On the relationship between tyre cornering stiffness and road surface roughness. Veh. Syst. Dyn. 2025, 1–33. [Google Scholar]
- Liang, C.; Wei, W.; Mousavi, H.; Chen, K.; Asafo-Duho, B.; Wang, G. Investigation on static grounding analysis model of nonpneumatic tire with nonlinear spokes. AIP Adv. 2021, 11, 015303. [Google Scholar] [CrossRef]
- Liang, X.M.; Fu, H.X.; Wang, Y.; Ku, L.Y.; Qiao, H.B.; Li, N. Study of composite load-bearing characteristics of the Uptis non-pneumatic tyre. Int. J. Veh. Syst. Model. Test. 2022, 16, 79–93. [Google Scholar] [CrossRef]
- Lu, D.; Wang, X.F.; Wu, H.D.; Chen, N.S.; Zhang, Z.W. Performance decoupling and optimization of non-pneumatic tires based on structured modeling. Lect. Notes Electr. Eng. 2024, 1151, 1520–1535. [Google Scholar] [CrossRef]
- Guo, S.; Zhao, Y.Q.; Lin, F.; Xu, T.; Li, D.Y. Steady-state rolling resistance prediction model of non-pneumatic tyres considering tread temperature: Theory and experiment. Veh. Syst. Dyn. 2025, 5, 876–896. [Google Scholar] [CrossRef]
- Liu, S.; Liu, W.; Zhou, S.; Li, X.; Zhang, Q. Steady-State temperature field and rolling resistance characteristics of low-speed and low-load capacity non-pneumatic tires. Lubricants 2023, 11, 402. [Google Scholar] [CrossRef]
- Sidhu, C.S.; El-sayegh, Z.; Ly, A. Non-pneumatic tire-mars soil interaction using advanced computational techniques. SAE Int. J. Adv. Curr. Pract. Mobil. 2023, 6, 729–735. [Google Scholar] [CrossRef]
- Li, H.Y.; Zhou, H.C.; Yang, J.; Ge, J.H.; Wang, G.L.; Xu, T. Study of the dynamic performance of rolling non-pneumatic tires using finite element method. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 289. [Google Scholar] [CrossRef]
- Chen, K.; Fu, H.X.; Xiao, Z.; Yang, B.W.; Ni, S.Q.; Huo, R.J. Key dynamic performance analysis of flexible spoke non-pneumatic tire for matched unmanned ground vehicles. Proc. Inst. Mech. Eng. D J. Automob. Eng. 2025, 239, 1419–1431. [Google Scholar] [CrossRef]
- Zhou, X.H.; Liu, X.Y.; Xu, T.; Hu, X.J.; Pan, Y.; Leng, J. Numerical investigation and comparison of the aerodynamic characteristics of non-pneumatic tire and pneumatic tire. J. Wind Eng. Ind. Aerodyn. 2024, 250, 105766. [Google Scholar] [CrossRef]
- Li, H.; Xu, Y.L.; Si, C.L.; Yang, Y. A Research on aerodynamic characteristics of non-pneumatic tire. Mech. Ind. 2021, 22, 27. [Google Scholar] [CrossRef]
- Sidhu, C.S.; El-Sayegh, Z. Comparative analysis of non-pneumatic tire spoke designs for on-road applications: A traction force perspective. In Proceedings of the ASME 2024 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Washington, DC, USA, 25–28 August 2024. [Google Scholar] [CrossRef]
- Sharaf, A.M.; Mavros, G.; Rahnejat, H.; King, P.D.; Mohan, S.K. Optimisation of AWD off-road vehicle performance using visco-lock devices. Int. J. Heavy Veh. Syst. 2008, 15, 89–106. [Google Scholar] [CrossRef]
- Sharaf, A.M.; Rahnejat, H.; King, P.D. Analysis of handling characteristics of all-wheel-drive off-road vehicles. Int. J. Heavy Veh. Syst. 2008, 15, 188–207. [Google Scholar] [CrossRef]
- Jackowski, J.; Zmuda, M.; Wieczorek, M.; Zuska, A. Quasi-Static research of ATV/UTV non-pneumatic tire. Energies 2021, 14, 6557. [Google Scholar] [CrossRef]
- Zang, L.G.; Wang, X.Y.; Chen, Y.; Li, Y.W.; Jin, H.J.; Yang, G.Q. Investigation on mechanical characteristics of non-pneumatic tire with rhombus structure under complex pavement conditions. Simul. Model. Pract. Theory 2022, 116, 102494. [Google Scholar] [CrossRef]
- Fu, H.X.; Liang, X.M.; Chen, K.; Wang, Y.; Xiao, Z. Study on key mechanical properties of the flexible spoke non-pneumatic tire considering thermo-mechanical coupling. Adv. Eng. Softw. 2022, 173, 103281. [Google Scholar] [CrossRef]
- Yuan, X.H.; Zhai, B.Q.; Su, C.Q.; Liu, X.; Wang, Y.P. Flow field analysis and aerodynamic drag optimization of non-pneumatic tires. Phys. Fluids 2024, 36, 085184. [Google Scholar] [CrossRef]















Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zang, L.; Sun, J.; Peng, X.; Lin, F.; Deng, Y.; Bai, Y. A Comprehensive Review of Safety Tire Research. Lubricants 2025, 13, 357. https://doi.org/10.3390/lubricants13080357
Zang L, Sun J, Peng X, Lin F, Deng Y, Bai Y. A Comprehensive Review of Safety Tire Research. Lubricants. 2025; 13(8):357. https://doi.org/10.3390/lubricants13080357
Chicago/Turabian StyleZang, Liguo, Jing Sun, Xinlei Peng, Fen Lin, Yaoji Deng, and Yuxing Bai. 2025. "A Comprehensive Review of Safety Tire Research" Lubricants 13, no. 8: 357. https://doi.org/10.3390/lubricants13080357
APA StyleZang, L., Sun, J., Peng, X., Lin, F., Deng, Y., & Bai, Y. (2025). A Comprehensive Review of Safety Tire Research. Lubricants, 13(8), 357. https://doi.org/10.3390/lubricants13080357






