Numerical and Experimental Investigations of Oil Return Efficiency in Tapered Roller Bearings Under Oil Jet Lubrication
Abstract
1. Introduction
2. Numerical Simulation Modeling
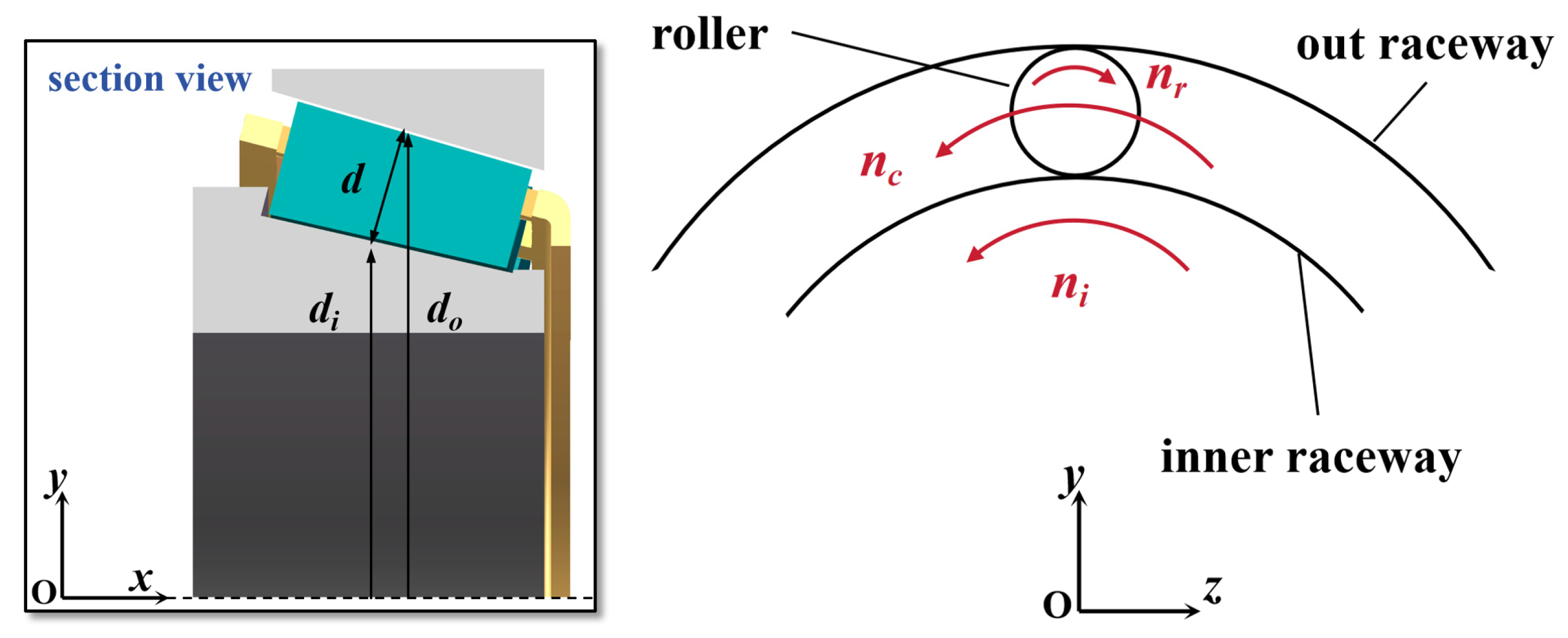
2.1. Oil and Air Two-Phase Flow Model
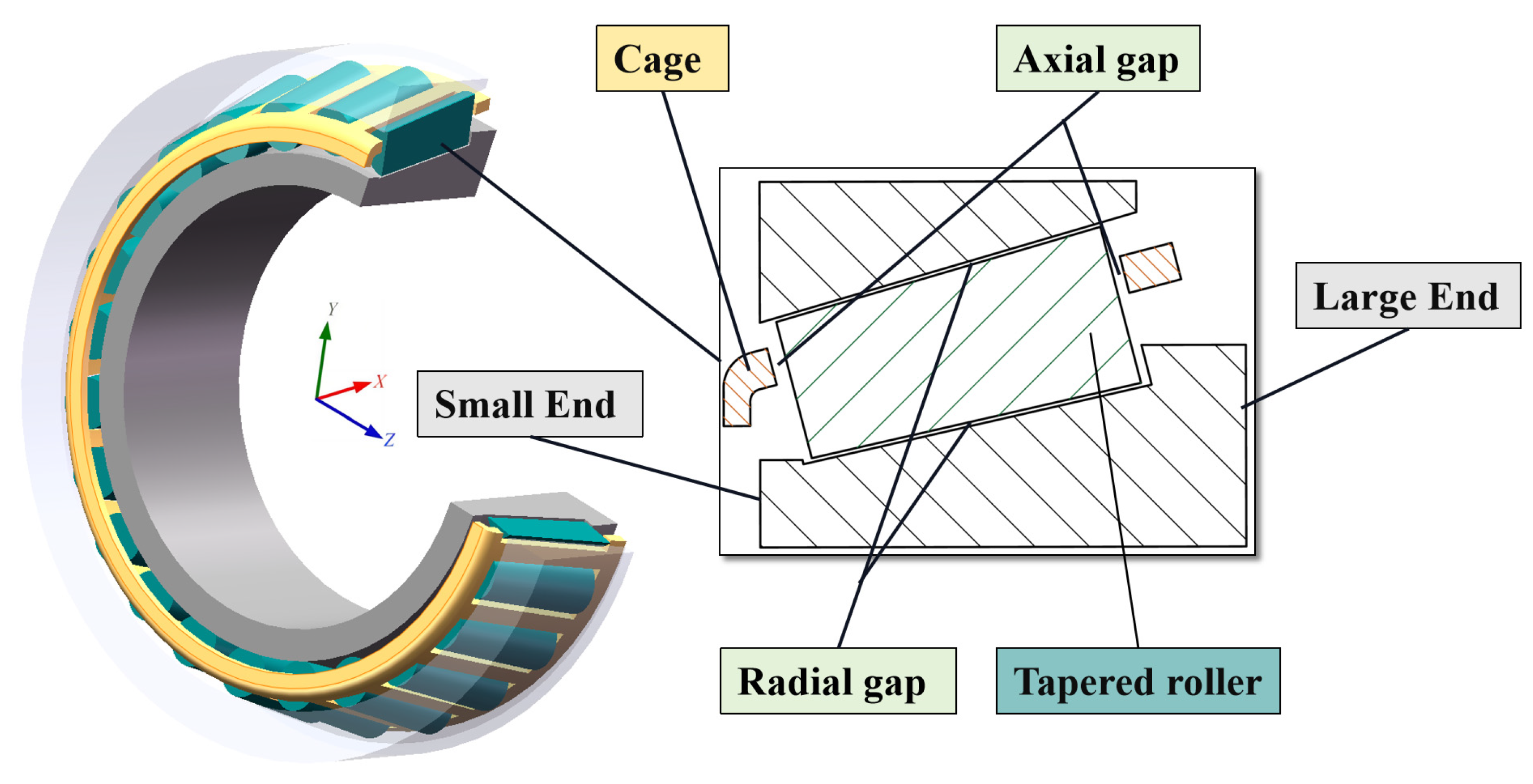
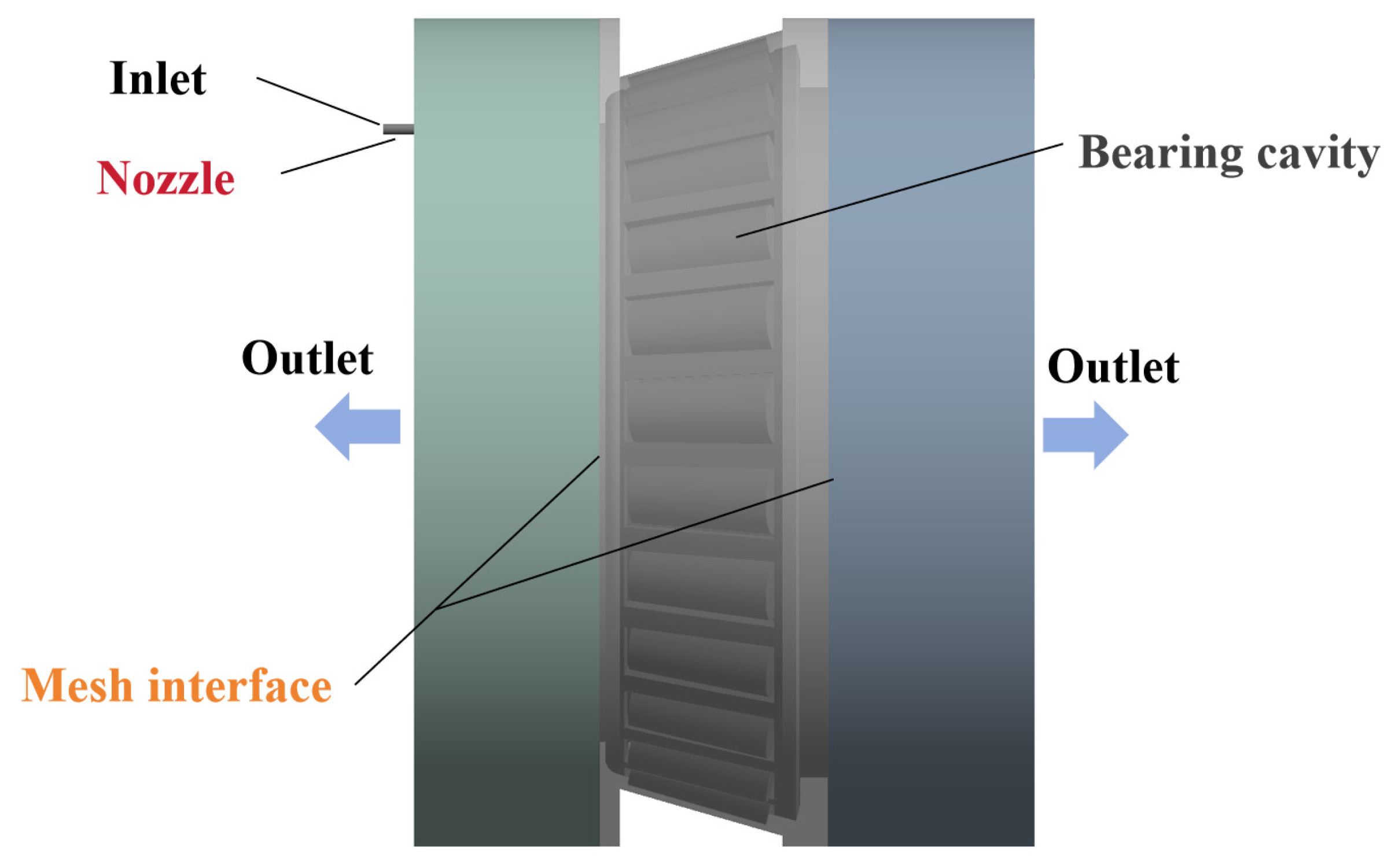
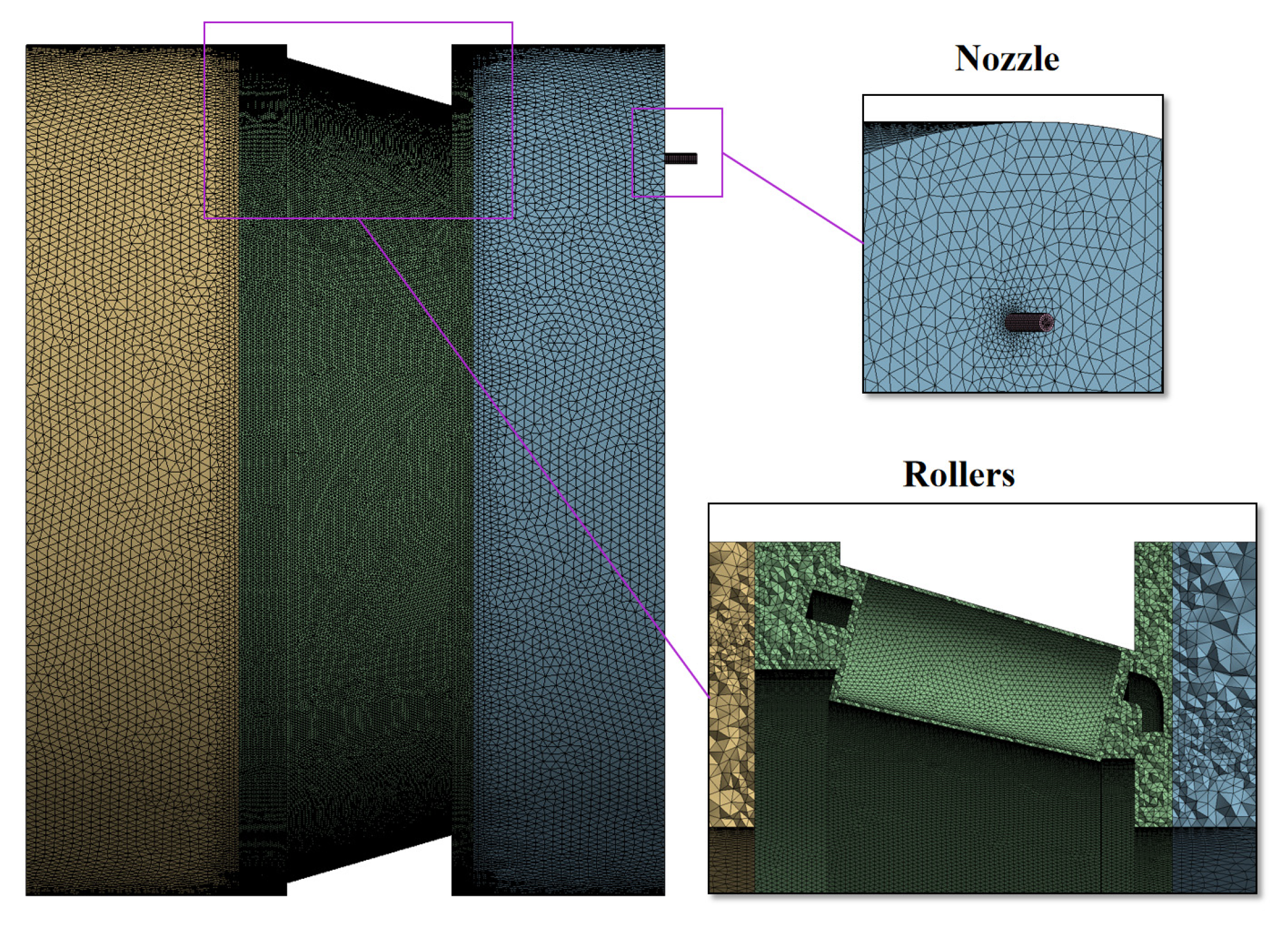
2.2. Geometric Modeling and Fluid Domain Meshing
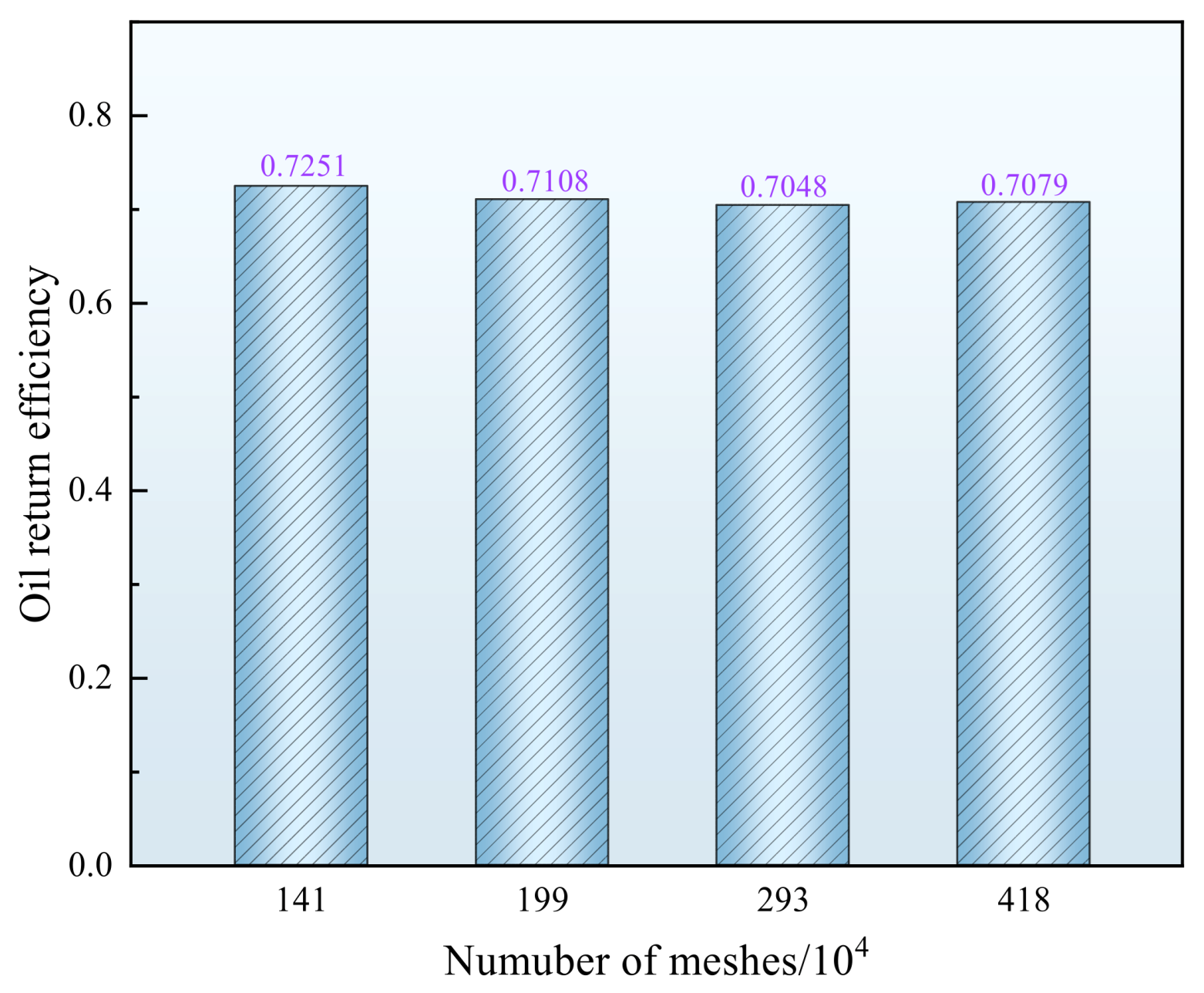
2.3. Boundary Conditions and Mesh Independence Tests
3. Oil Return Efficiency Principle Test Verification
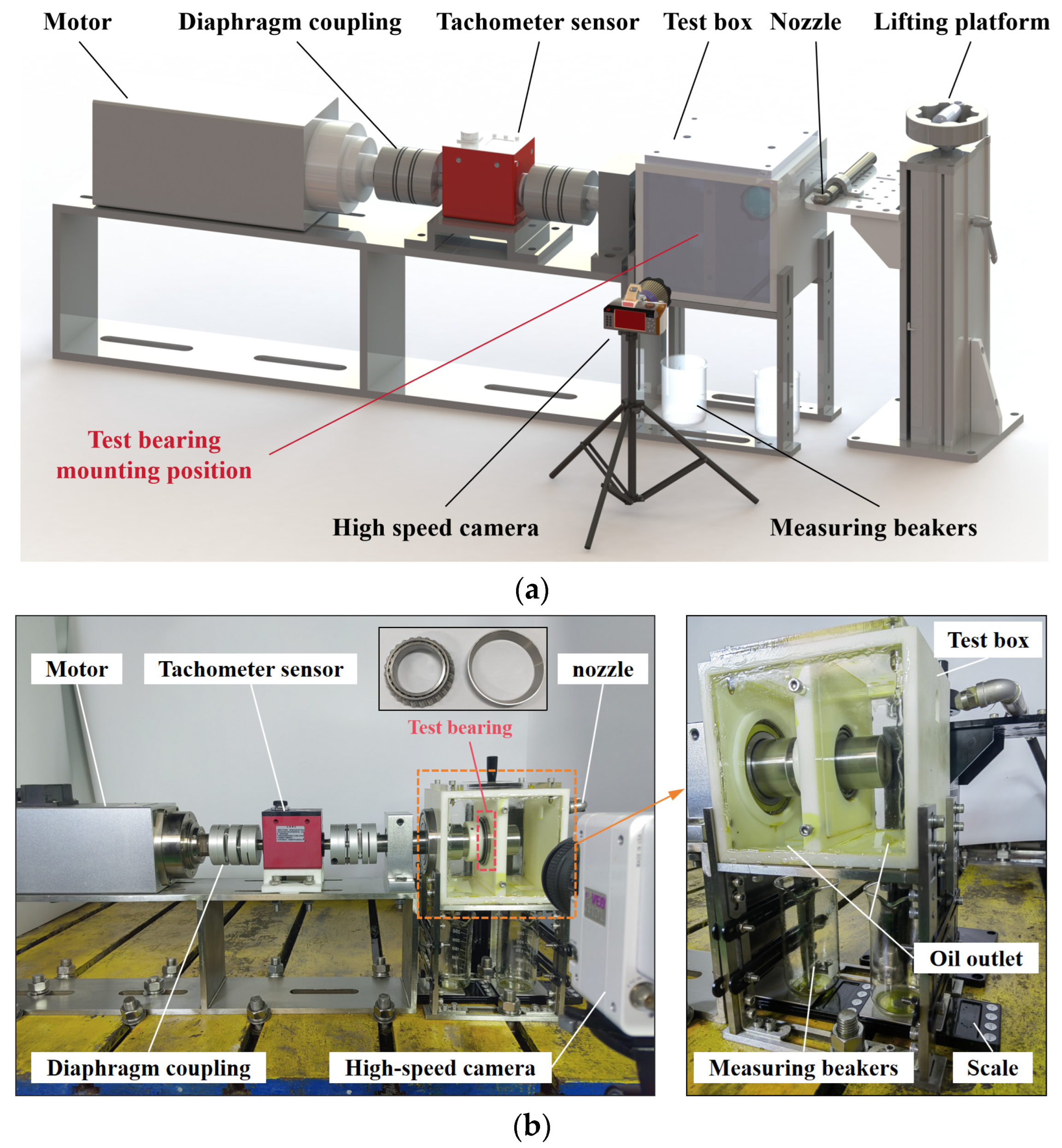
3.1. Tapered Roller Bearing Jet Lubrication Test Rig
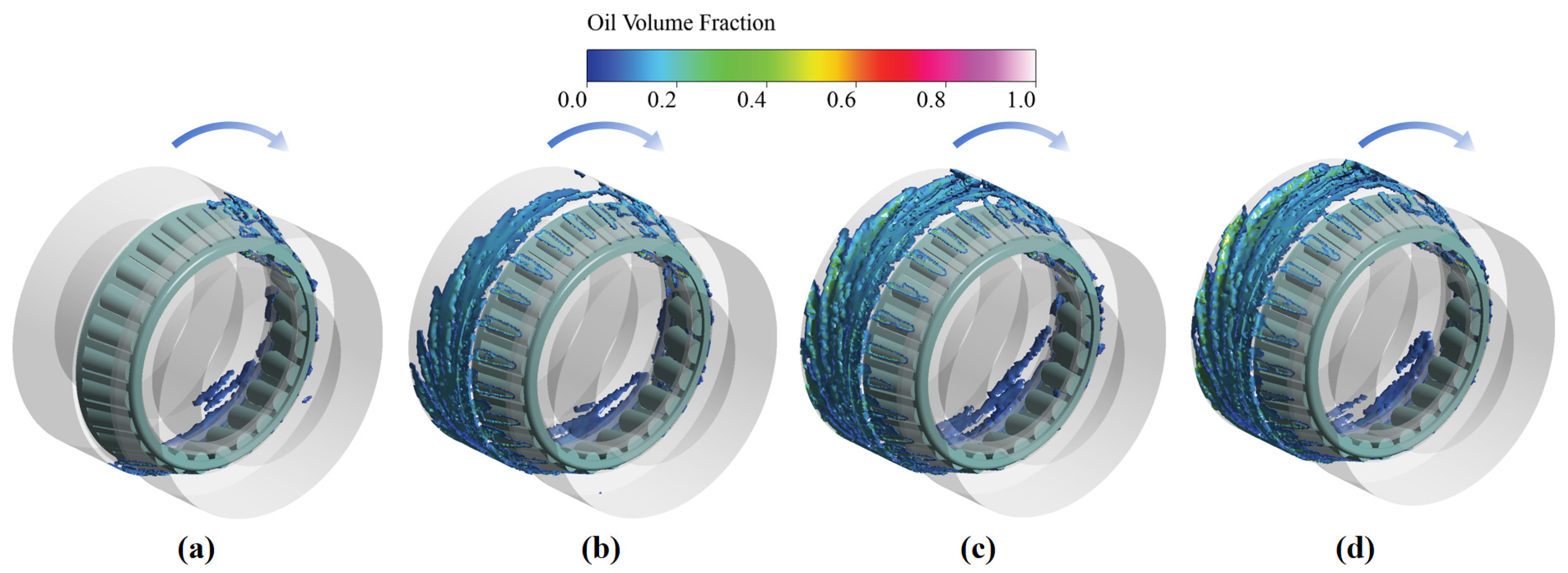
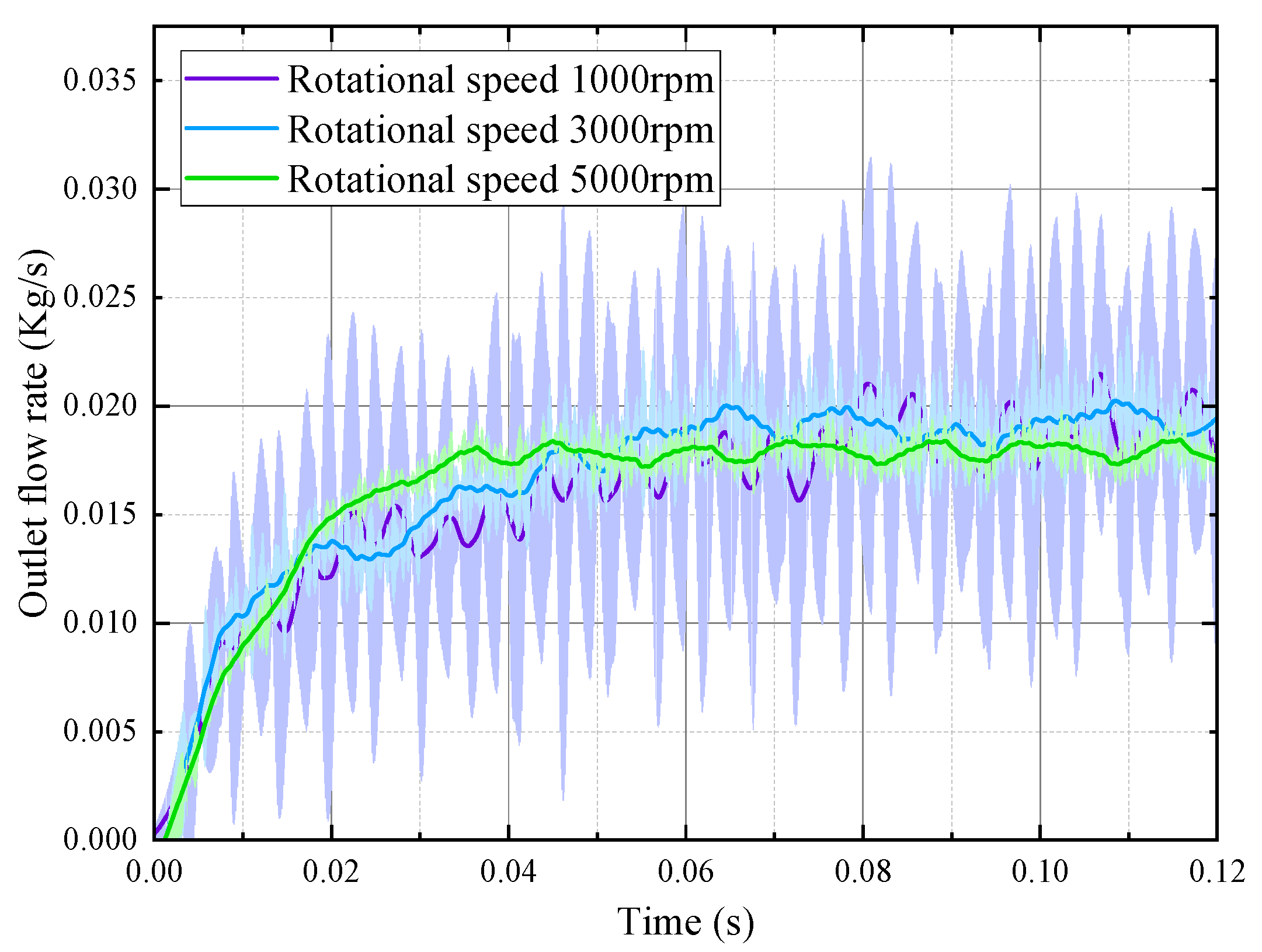
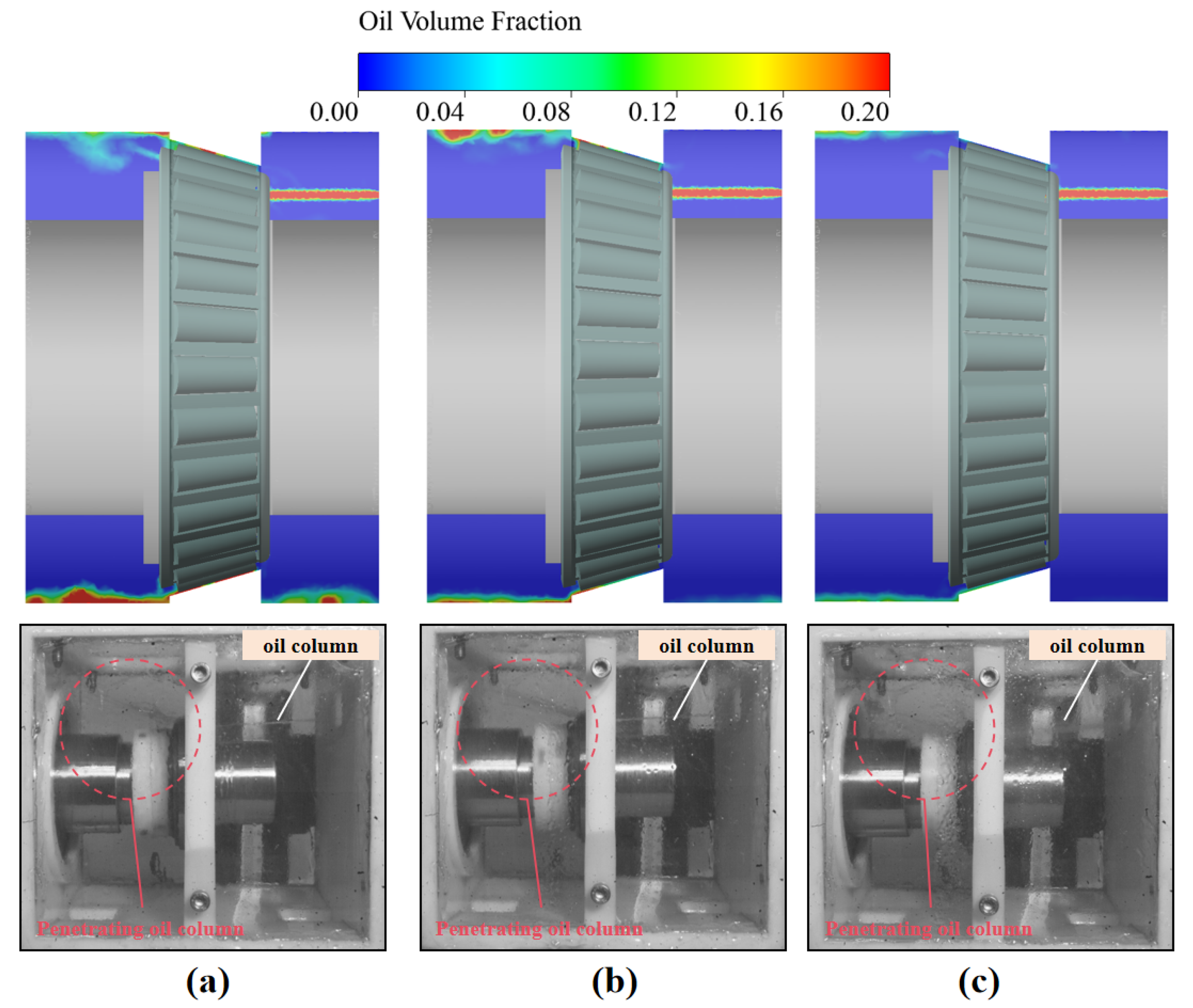
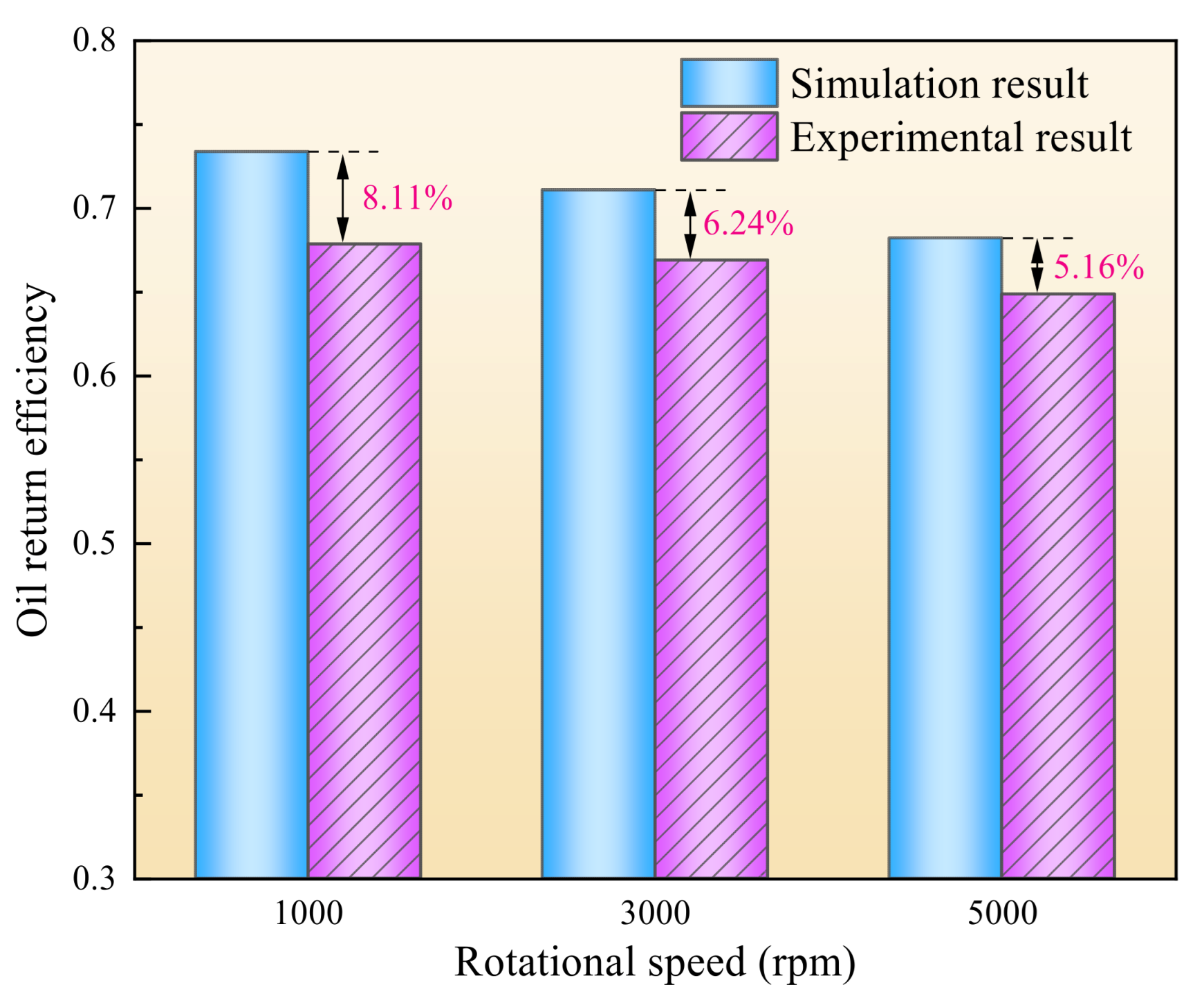
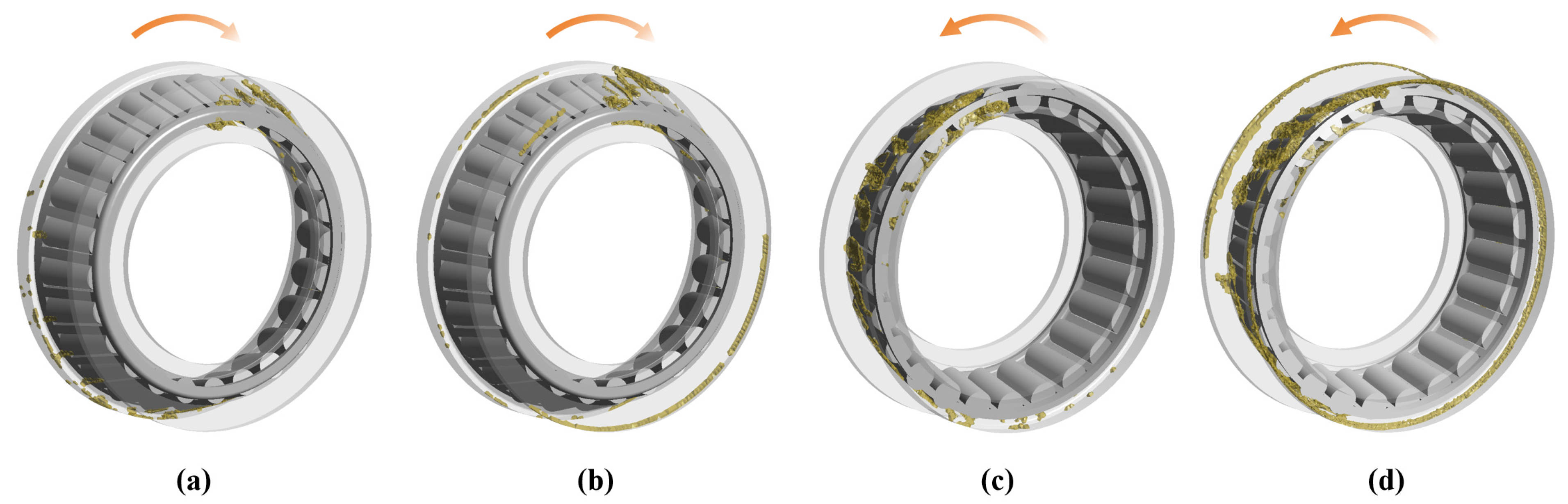
3.2. Comparison of Experimental and Numerical Results
4. Analysis and Verification
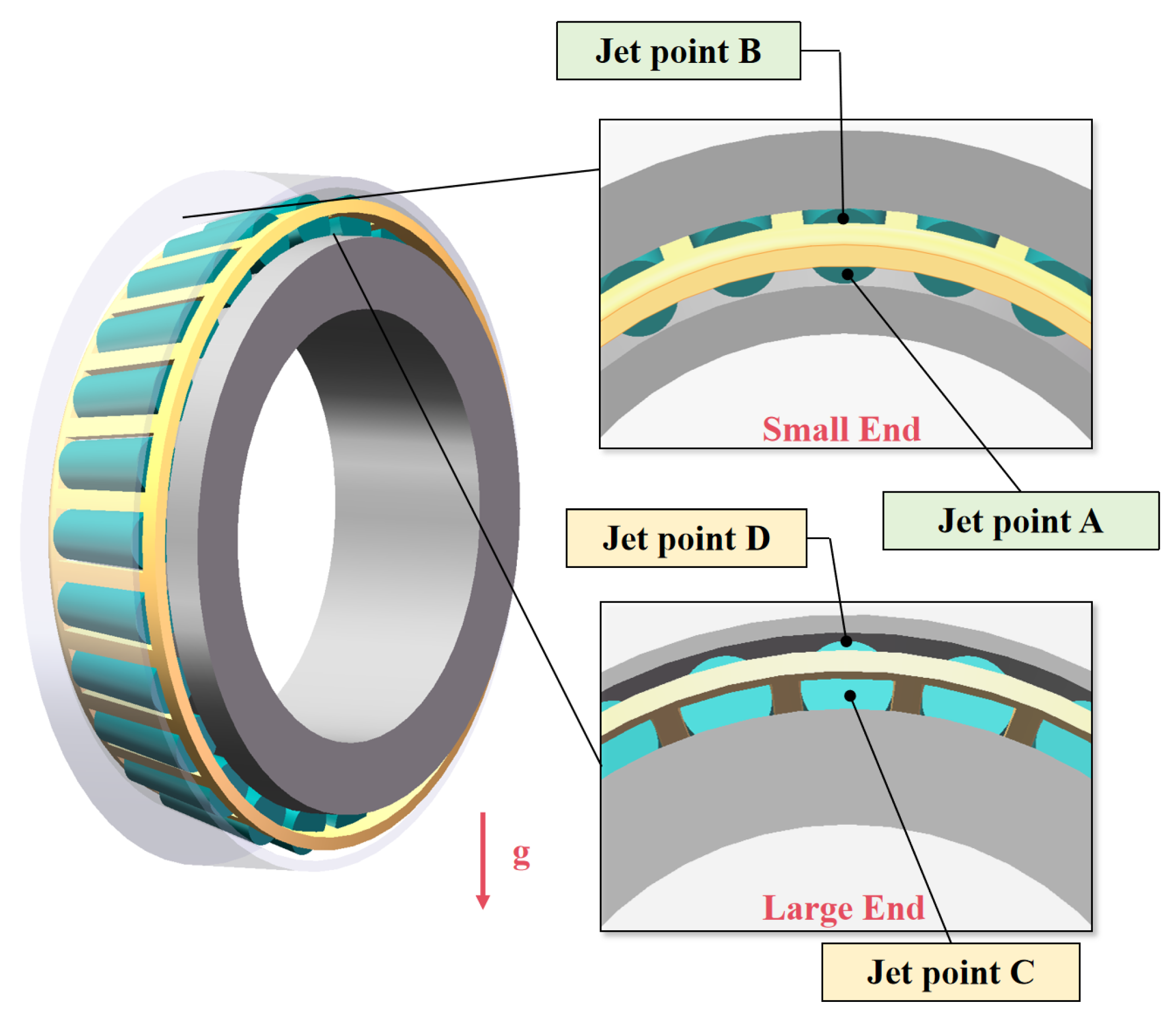
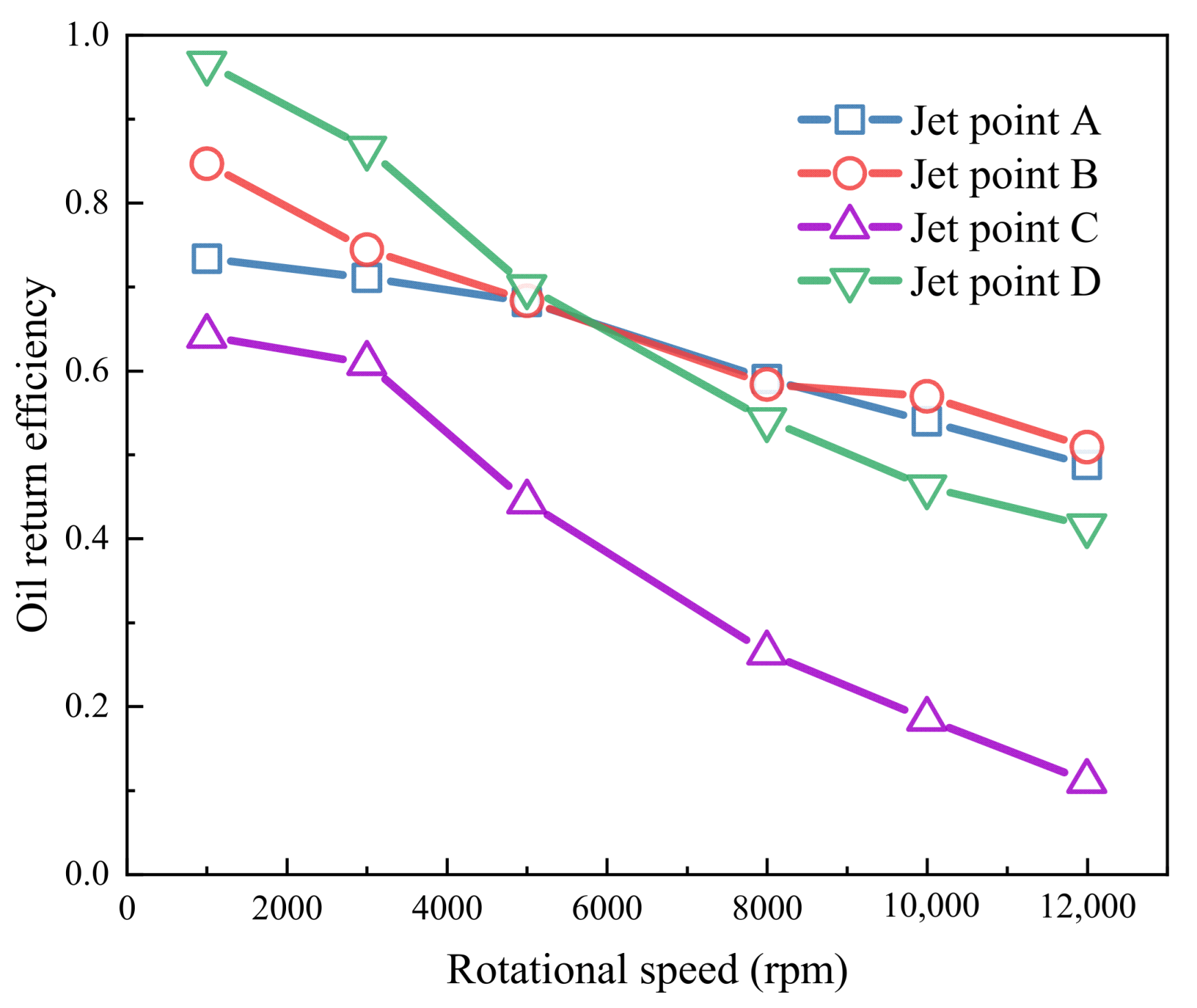
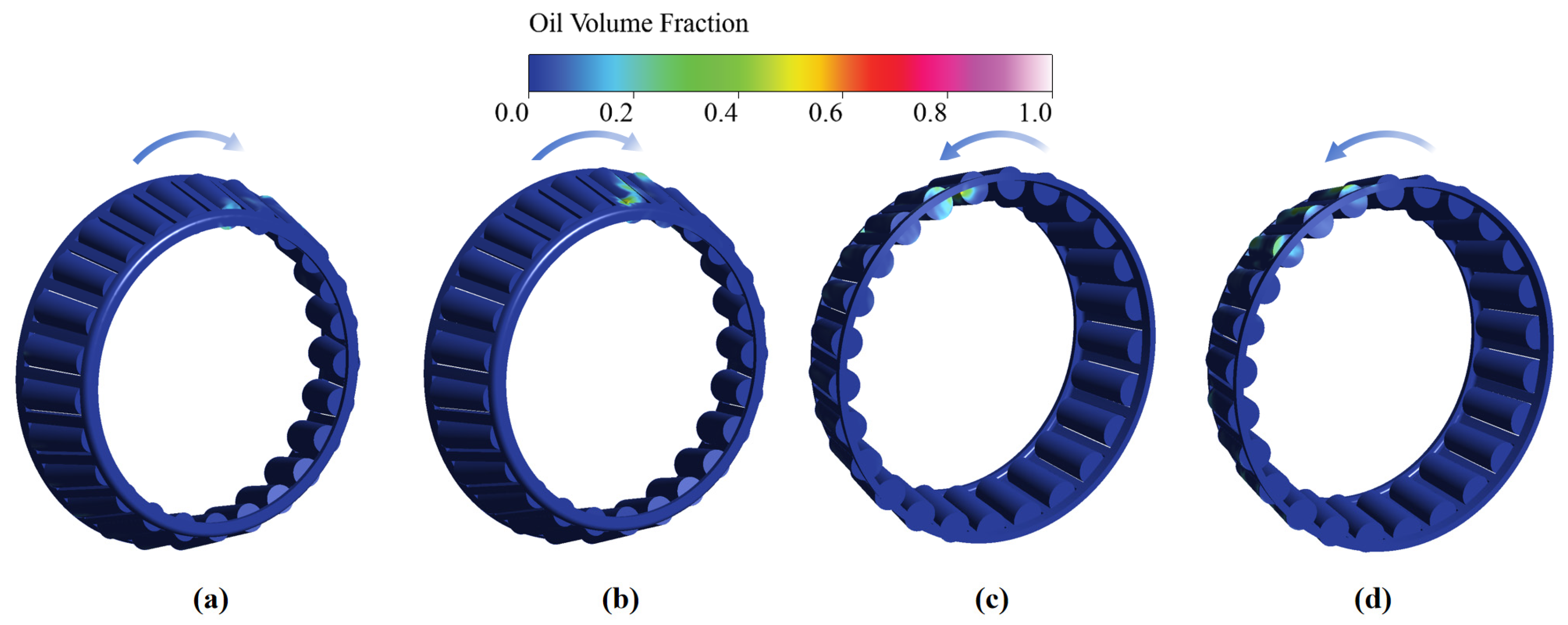
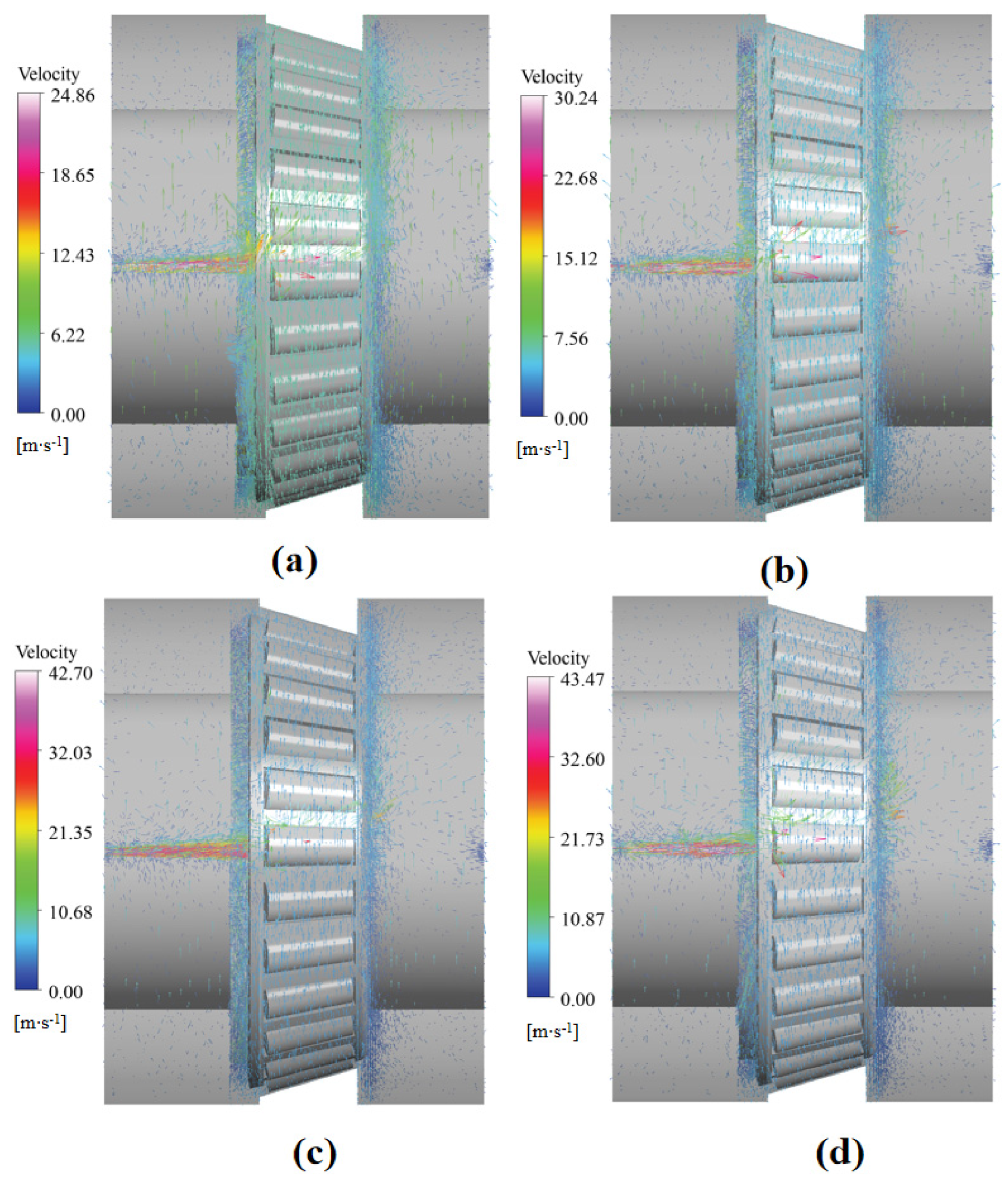
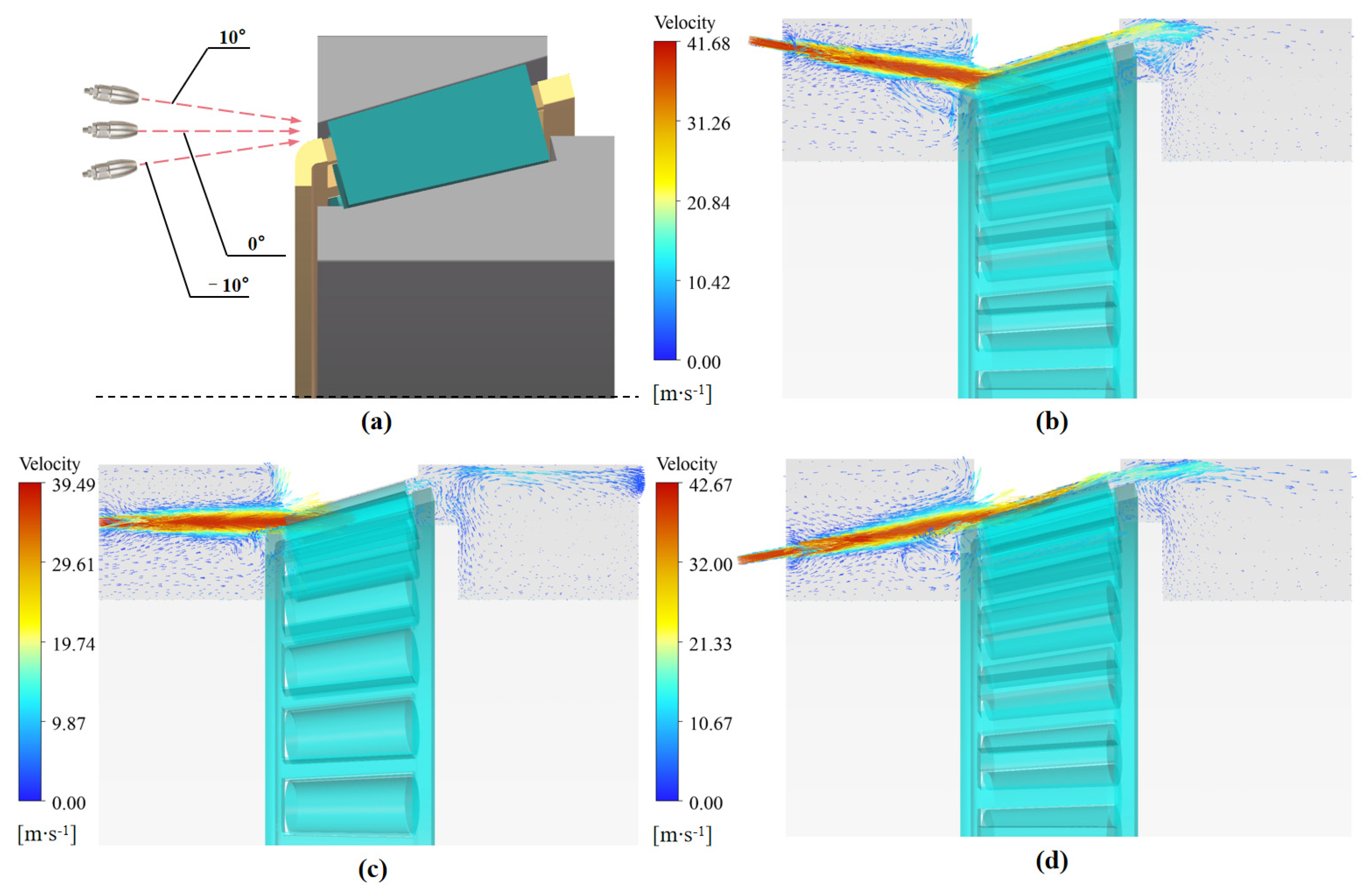
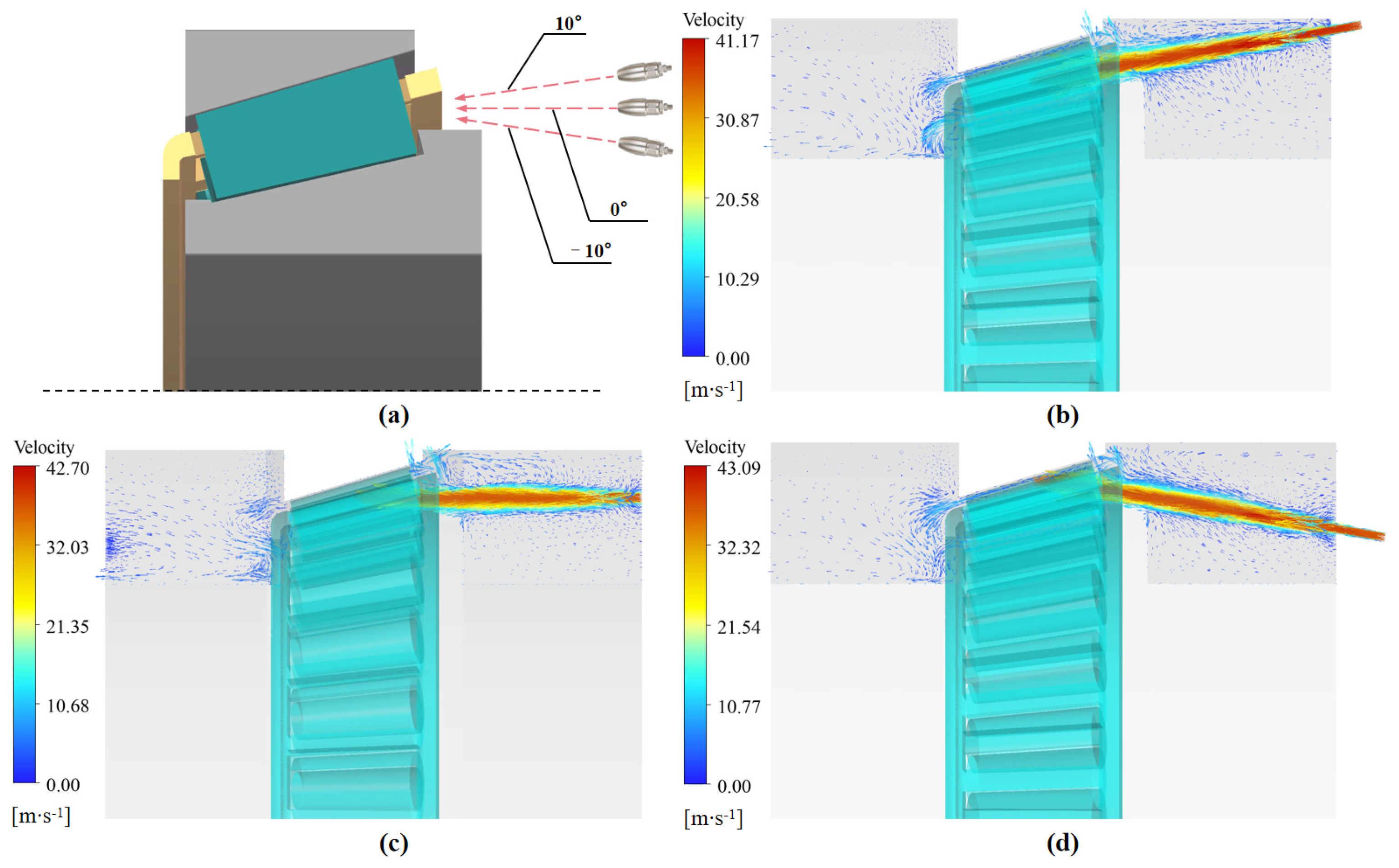
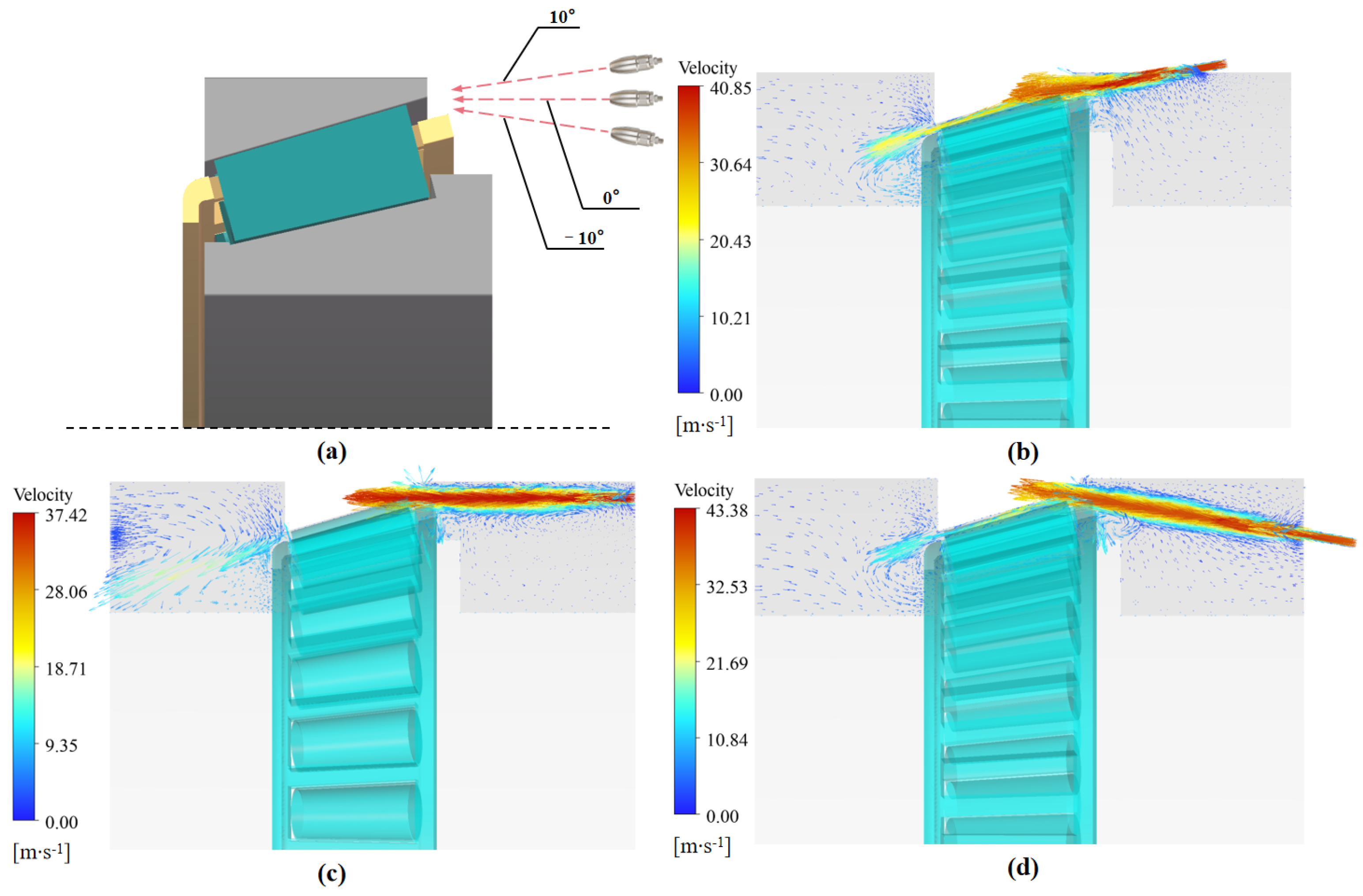
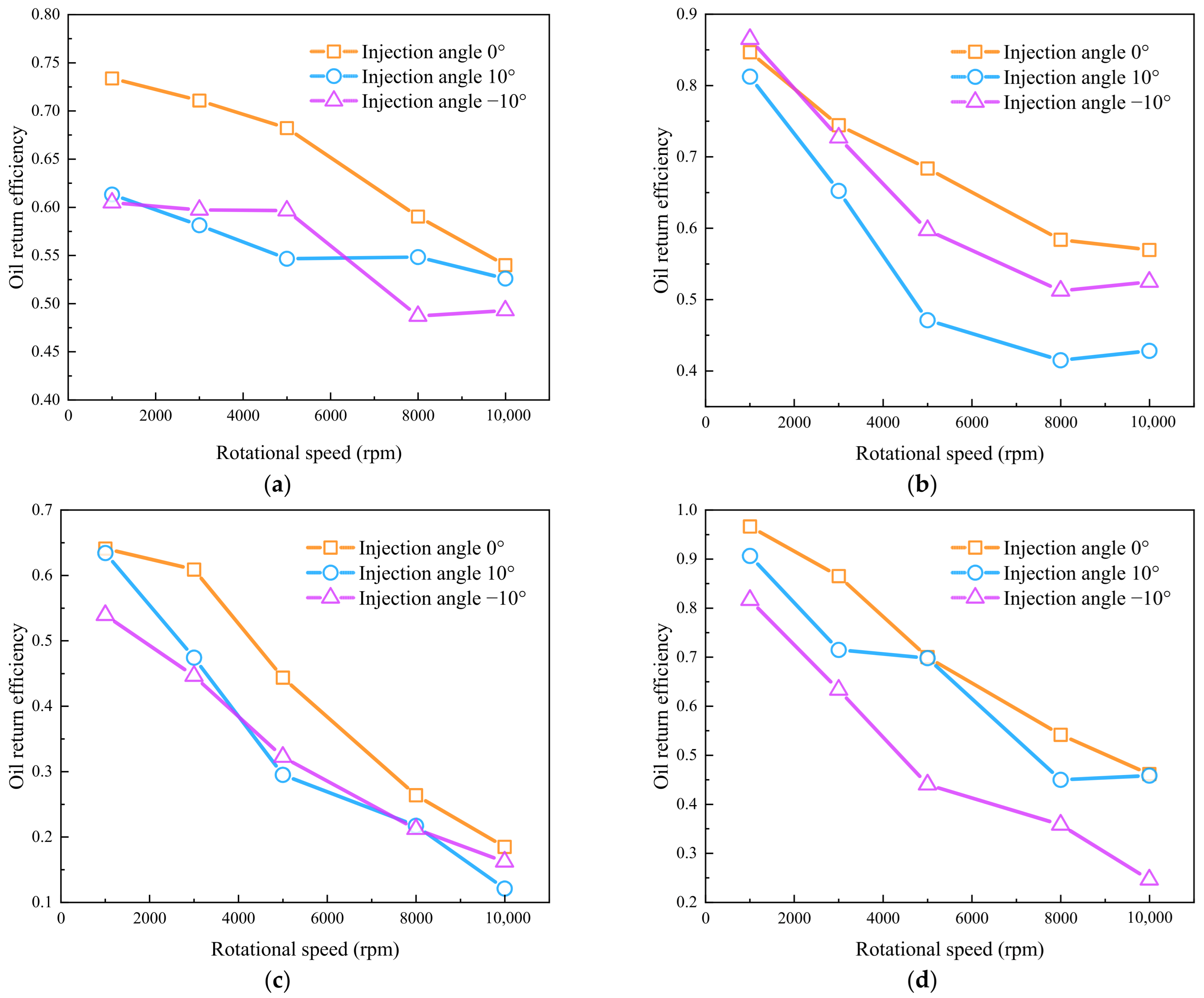
4.1. Effects of Jet Lubrication Position
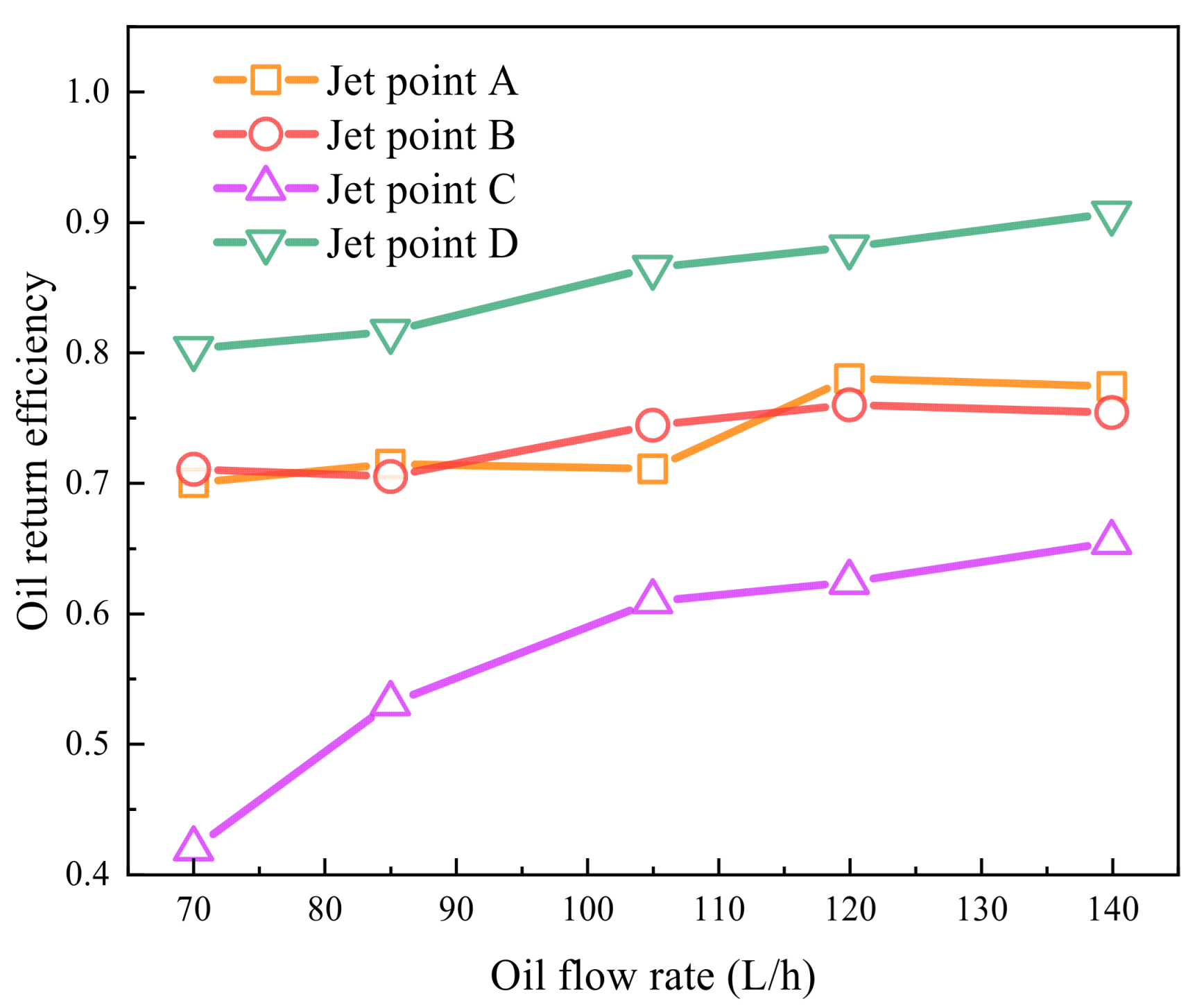
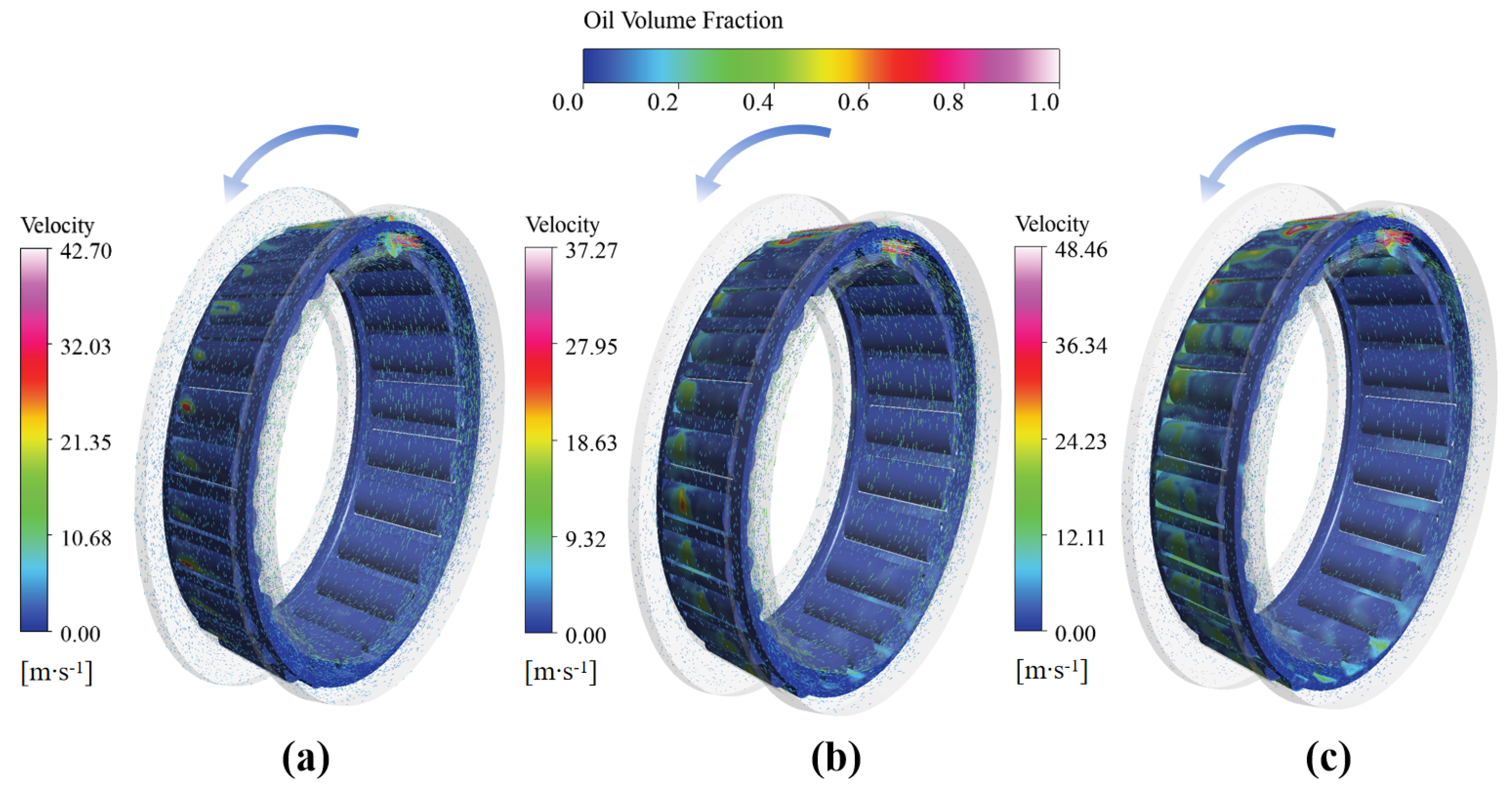
4.2. Effects of Jet Lubrication Flow Rate
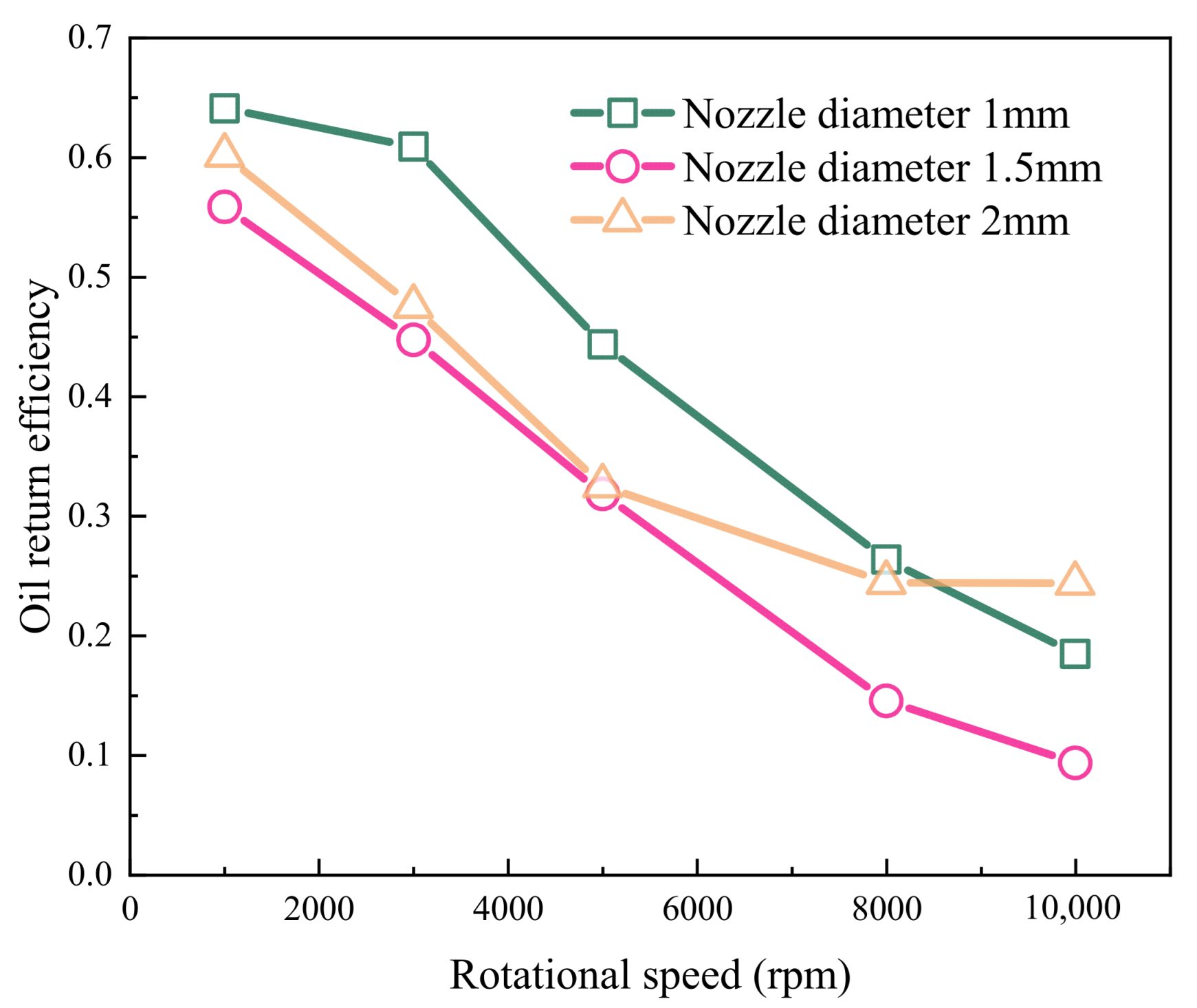
4.3. Effects of the Nozzle Diameter
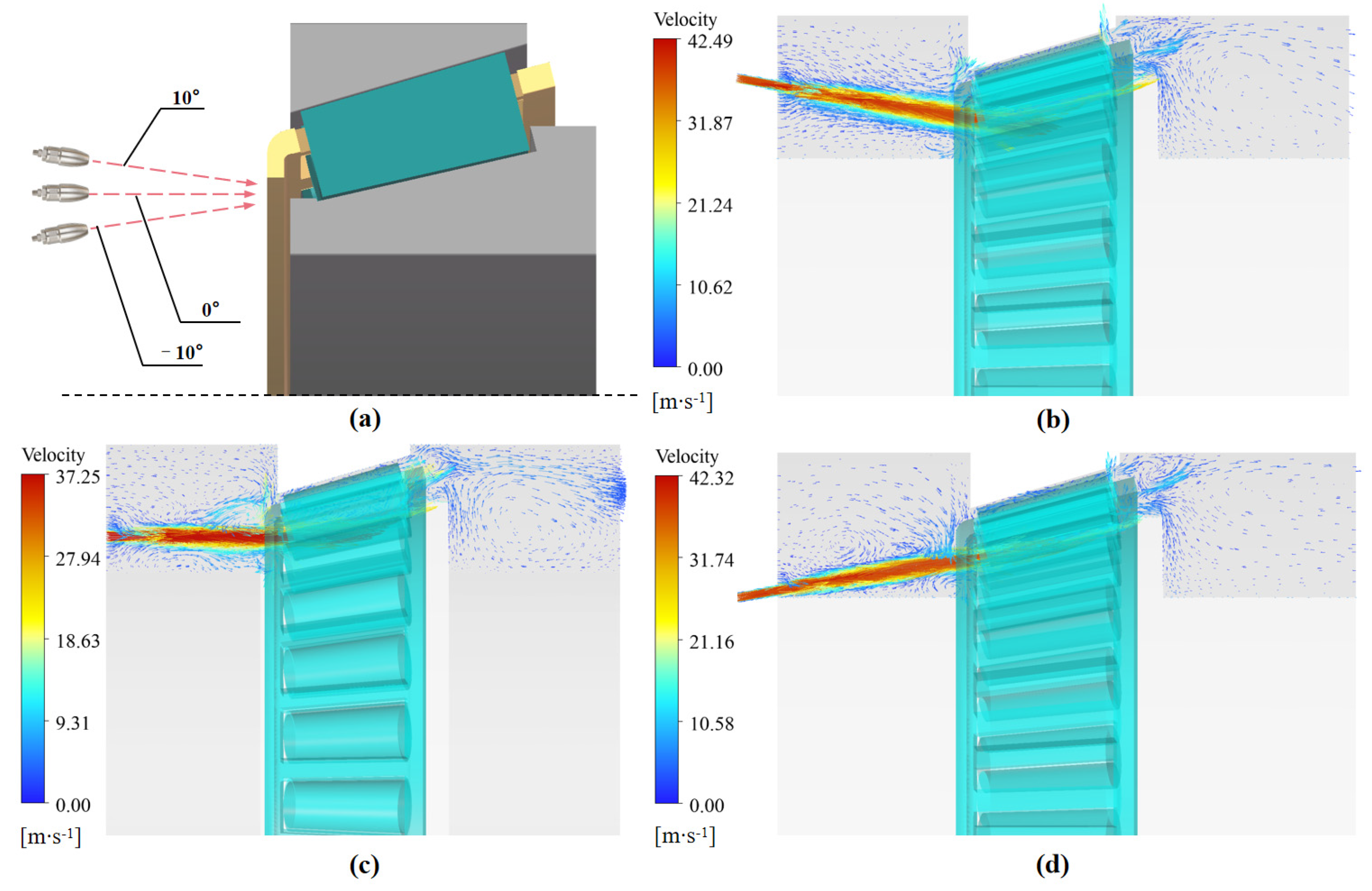
4.4. Effects of the Injection Angle
5. Conclusions
- The simulation model demonstrated high accuracy, with predicted oil return efficiency values deviating by less than 10% from experimental measurements.
- The oil injection position significantly affects lubrication performance. At higher bearing speeds, injecting oil from the small end yields superior oil return efficiency compared to the large end, suggesting the practical prioritization of small-end injection when designing bearing components.
- While increasing the oil jet flow rate improves lubrication, enlarging the nozzle diameter (despite boosting efficiency) causes oil accumulation in the bearing cavity, increasing torque loss. An optimal nozzle diameter-to-angle ratio of 1 mm/0° was identified to balance these effects.
- The influence of the incidence angle depends on the injection location, with the strongest impact observed at the small end of the inner ring. Positive-angle oil jets consistently delivered the highest oil return efficiency and lubrication performance.
- In summary, directing the oil jet toward the smaller end of the bearing, appropriately increasing the nozzle flow rate, and utilizing positive jetting can significantly improve the lubrication performance of tapered roller bearings.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| the equivalent volumetric force vector, N | |
| the volume of oil collected at the return port, Kg/s | |
| the total oil volume, Kg/s | |
| the mass source terms of air | |
| the mass source terms of lubricant | |
| roller inner diameter, mm | |
| roller internal rotating diameter, mm | |
| roller outer rotating diameter, mm | |
| the gravitational acceleration vector, m/s2 | |
| the oil return efficiency | |
| the speed of revolution of the rollers, rpm | |
| the cage speed, rpm | |
| the inner ring speed, rpm | |
| the rollers’ speed of rotation, rpm | |
| the velocity vector, m/s | |
| the air velocity vectors, m/s | |
| the lubricant velocity vectors, m/s | |
| the lubricant and air mixing viscosity, Pa.s | |
| the viscosity of air, Pa.s | |
| the viscosity of the lubricant, Pa.s | |
| the lubricant and air mixing density, Kg/m3 | |
| the densities of air, Kg/m3 | |
| the densities of lubricant, Kg/m3 | |
| the volume fraction of air | |
| the volume fraction of lubricant |
References
- Zhu, W.; Zhu, R.; Tang, X.; Lu, F.; Bai, X.; Wu, X.; Li, F. CFD-based analysis of oil and gas two-phase flow characteristics in double-row tapered roller bearings with different rib structures. Appl. Sci. 2022, 12, 1156. [Google Scholar] [CrossRef]
- Tong, V.C.; Hong, S.W. Study on the stiffness and fatigue life of tapered roller bearings with roller diameter error. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2017, 231, 176–188. [Google Scholar] [CrossRef]
- Maruyama, T.; Saitoh, T.; Yokouchi, A. Differences in mechanisms for fretting wear reduction between oil and grease lubrication. Tribol. Trans. 2017, 60, 497–505. [Google Scholar] [CrossRef]
- Aidarinis, J.; Missirlis, D.; Yakinthos, K.; Goulas, A. CFD modeling and LDA measurements for the air-flow in an aero engine front bearing chamber. J. Eng. Gas Turbines Power 2011, 133, 082504. [Google Scholar] [CrossRef]
- Pinel, S.I.; Signer, H.R.; Zaretsky, E.V. Comparison between oil-mist and oil-jet lubrication of high-speed, small-bore, angular-contact ball bearing. Tribol. Lubr. Technol. 2011, 67, 32. [Google Scholar] [CrossRef]
- Hager, C.H., Jr.; Doll, G.L.; Evans, R.D.; Shiller, P.J. Minimum quantity lubrication of M50/M50 and M50/Si3N4 tribological interfaces. Wear 2011, 271, 1761–1771. [Google Scholar] [CrossRef]
- Hannon, W.M. Rolling-element bearing heat transfer—Part I: Analytic model. J. Tribol. 2015, 137, 031102. [Google Scholar] [CrossRef]
- Adeniyi, A.A.; Morvan, H.P.; Simmons, K.A. A multiphase computational study of oil-air flow within the bearing sector of aeroengines. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2015; Volume 56734, p. V05CT15A024. [Google Scholar]
- Adeniyi, A.A.; Morvan, H.; Simmons, K. A computational fluid dynamics simulation of oil–air flow between the cage and inner race of an aero-engine bearing. J. Eng. Gas Turbines Power 2017, 139, 012506. [Google Scholar] [CrossRef]
- Zhu, D.; Chen, G.; Li, Y.; Zhang, C.; Wang, L. A 3D CFD simulation of oil spray-collection and delivery process in an aeroengine inter-shaft bearing. Chin. J. Aeronaut. 2022, 35, 366–378. [Google Scholar] [CrossRef]
- Li, M.; Wang, Y.; Chen, W.; Zhu, R. Temperature rise characteristics for angular-contact ball bearings with oil-air lubrication based on fluid-solid conjugate heat transfer. Adv. Mech. Eng. 2021, 13, 1687814021990927. [Google Scholar] [CrossRef]
- Gao, F.; Jia, W.; Li, Y.; Zhang, D.; Wang, Z. Analysis and experimental research on the fluid–solid coupled heat transfer of high-speed motorized spindle bearing under oil–air lubrication. J. Tribol. 2021, 143, 071801. [Google Scholar] [CrossRef]
- Bhat, J.A.; Harmain, G.A.; Wani, M.F.; Sehgal, R.K.; Najar, F.A. Performance enhancement of hydrodynamic thrust bearings: Investigating cooling strategies, deep recesses, and textured surfaces. Tribol. Int. 2025, 110877. [Google Scholar] [CrossRef]
- Jin, X.; Wang, Y.; Bai, Q.; Li, X.; Jiang, H.; Guo, F.; Poll, G. Cage parameters on friction within cage-pockets contacts and lubrication behaviors in ball-raceway contacts. Tribol. Int. 2025, 110747. [Google Scholar] [CrossRef]
- Wu, W.; Hu, C.; Hu, J.; Yuan, S. Jet cooling for rolling bearings: Flow visualization and temperature distribution. Appl. Therm. Eng. 2016, 105, 217–224. [Google Scholar] [CrossRef]
- Zi, X.; Chen, K.; Bai, Q.; Li, X.; Jin, X.; Wang, X.; Guo, F. The enhancement of oil delivery and bearing performance via a guiding-structured nozzle under oil–air lubrication. Lubricants 2024, 12, 60. [Google Scholar] [CrossRef]
- Hu, J.; Wu, W.; Wu, M.; Yuan, S. Numerical investigation of the air–oil two-phase flow inside an oil-jet lubricated ball bearing. Int. J. Heat Mass Transf. 2014, 68, 85–93. [Google Scholar] [CrossRef]
- Zhang, J.J.; Lu, L.M.; Zheng, Z.Y.; Gan, L.; Lv, Z.Y. Visual comparative analysis for the oil-air two-phase flow of an oil-jet lubricated roller-sliding bearing. J. Appl. Fluid Mech. 2022, 16, 179–191. [Google Scholar] [CrossRef]
- Concli, F.; Mastrone, M.N. Advanced lubrication simulations of an entire test rig: Optimization of the nozzle orientation to maximize the lubrication capability. Lubricants 2023, 11, 300. [Google Scholar] [CrossRef]
- Li, R.; Zhu, P.; Yuan, H.; Liang, H.; Wang, W. Dynamics of oil droplet impacting oil film in bearing chamber. Int. J. Mech. Sci. 2025, 302, 110555. [Google Scholar] [CrossRef]
- Kim, D.; Kim, M.; Park, J. Analytical study about effects of kerosene lubrication on slip, heat, and temperature of a cylindrical roller bearing. J. Mech. Sci. Technol. 2023, 37, 4671–4679. [Google Scholar] [CrossRef]
- Ishaq Khan, M.; Maccioni, L.; Concli, F. Trends in lubrication research on tapered roller bearings: A review by bearing type and size, lubricant, and study approach. Lubricants 2025, 13, 204. [Google Scholar] [CrossRef]
- Maccioni, L.; Chernoray, V.G.; Concli, F. Investigating lubricant behavior in a partially flooded tapered roller bearing: Validation of a multiphase CFD solver for aerated oil sump via particle image velocimetry studies and high-speed camera acquisitions. Tribol. Int. 2025, 201, 110274. [Google Scholar] [CrossRef]
- Brennen, C.E. Fundamentals of Multiphase Flow; Cambridge Ltd.: Cambridge, UK, 2005. [Google Scholar]
- Da Riva, E.; Del Col, D. Numerical simulation of laminar liquid film condensation in a horizontal circular minichannel. J. Heat Transfer 2012, 134, 051019. [Google Scholar] [CrossRef]
- Xiao, J.; Zhu, E.; Wang, G. Numerical simulation of emergency shutdown process of ring gate in hydraulic turbine runaway. J. Fluids Eng. 2012, 134, 124501. [Google Scholar] [CrossRef]
- Hu, S.; Gong, W.; Xu, X.; Liu, X. Modeling of ball bearing churning losses. Phys. Fluids 2024, 36, 083305. [Google Scholar] [CrossRef]
- Liu, J.; Ni, H.; Zhou, R.; Li, X.; Xing, Q.; Pan, G. A simulation analysis of ball bearing lubrication characteristics considering the cage clearance. J. Tribol. 2023, 145, 044301. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, F.; Duan, H.; Wang, W.; Guo, R.; Yu, Q. Numerical investigation of oil–air flow inside tapered roller bearings with oil bath lubrication. J. Appl. Fluid Mech. 2023, 17, 273–283. [Google Scholar] [CrossRef]
- Dai, Y.; Tang, R.; Yu, C.; Yang, C.; Yang, D.; Zhu, X. Air–oil two-phase flow and oil penetration characteristics of angular contact ball bearing under oil jet lubrication: Numerical and experimental investigations. Phys. Fluids 2025, 37, 047133. [Google Scholar] [CrossRef]
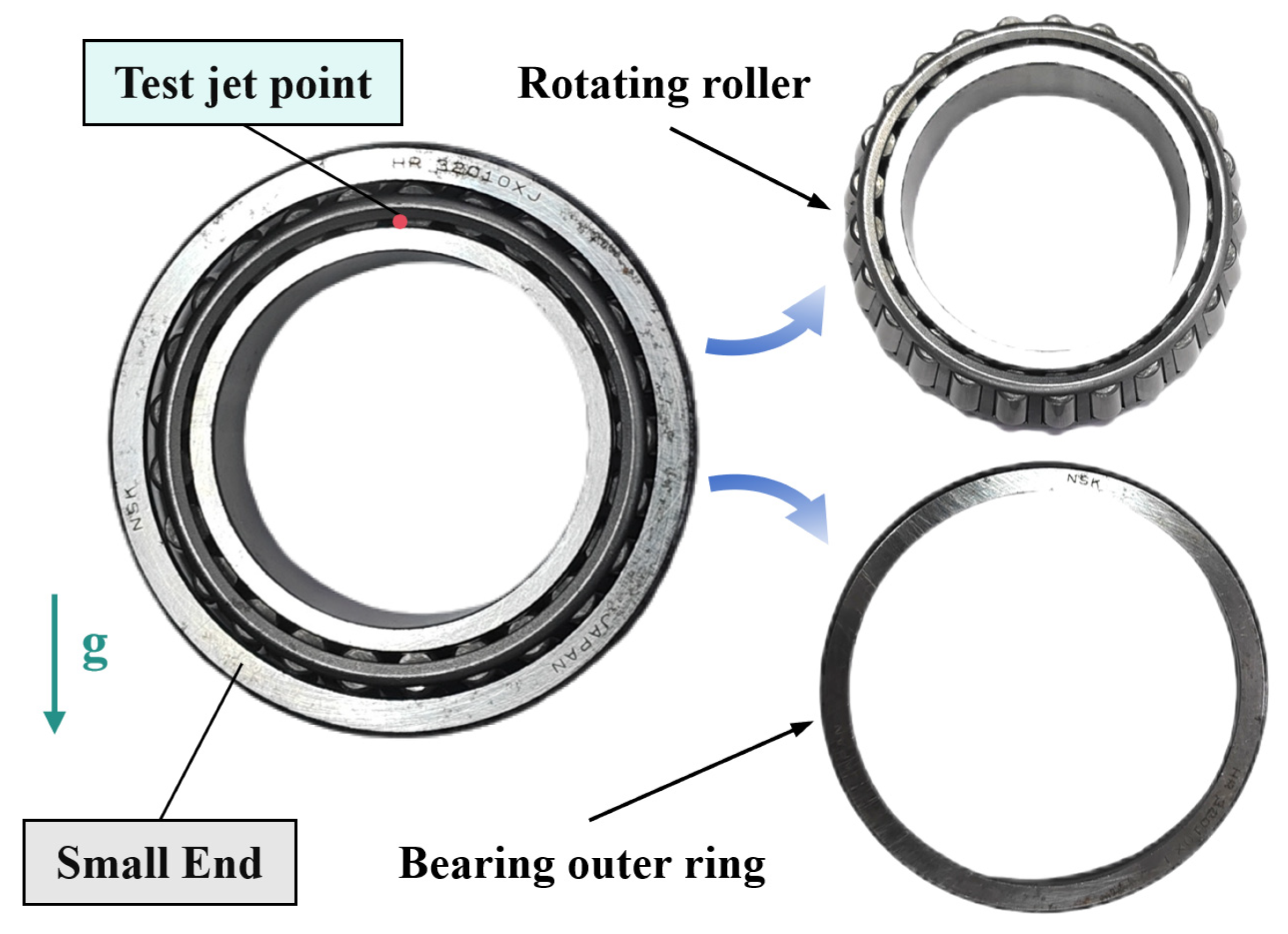


| Parameters | Value |
|---|---|
| Bearing type | NSK HR32010XJ |
| Inside diameter d (mm) | 50 |
| Outside diameter D (mm) | 80 |
| Overall width T (mm) | 20 |
| Inner ring width B (mm) | 20 |
| Outer ring width C (mm) | 15.5 |
| Contact angle | 13°20′ |
| Rolling diameter (mm) | 6.32 (Large end face) |
| Roll length (mm) | 13.8 |
| Half cone angle of rolling elements | 1°7′10″ |
| Number of rolling elements | 25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, Y.; Yu, C.; Wu, H.; Zhong, J.; Zhu, X.; Wang, G. Numerical and Experimental Investigations of Oil Return Efficiency in Tapered Roller Bearings Under Oil Jet Lubrication. Lubricants 2025, 13, 333. https://doi.org/10.3390/lubricants13080333
Dai Y, Yu C, Wu H, Zhong J, Zhu X, Wang G. Numerical and Experimental Investigations of Oil Return Efficiency in Tapered Roller Bearings Under Oil Jet Lubrication. Lubricants. 2025; 13(8):333. https://doi.org/10.3390/lubricants13080333
Chicago/Turabian StyleDai, Yu, Cheng Yu, Hongmei Wu, Jianfeng Zhong, Xiang Zhu, and Gang Wang. 2025. "Numerical and Experimental Investigations of Oil Return Efficiency in Tapered Roller Bearings Under Oil Jet Lubrication" Lubricants 13, no. 8: 333. https://doi.org/10.3390/lubricants13080333
APA StyleDai, Y., Yu, C., Wu, H., Zhong, J., Zhu, X., & Wang, G. (2025). Numerical and Experimental Investigations of Oil Return Efficiency in Tapered Roller Bearings Under Oil Jet Lubrication. Lubricants, 13(8), 333. https://doi.org/10.3390/lubricants13080333







