Simulation Study of the Effect of Oil Injection Speed on the Air Curtain of High-Speed Bearings
Abstract
1. Introduction
2. Numerical Simulation Model and Boundary Conditions
2.1. Mathematical Models
2.1.1. VOF Model
2.1.2. RNG k-ε Turbulence Model
2.2. Geometric and Mesh Models
2.3. Boundary Conditions and Solution Setup
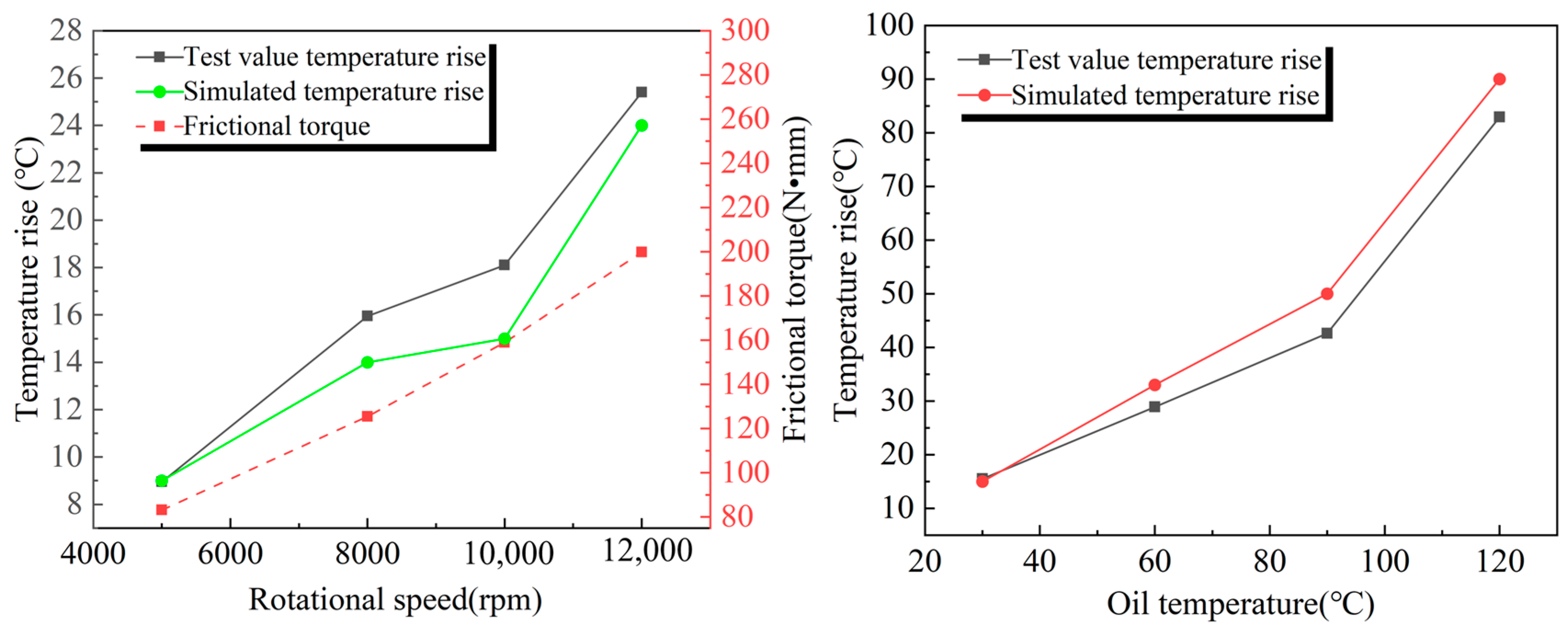
2.4. Model Validation
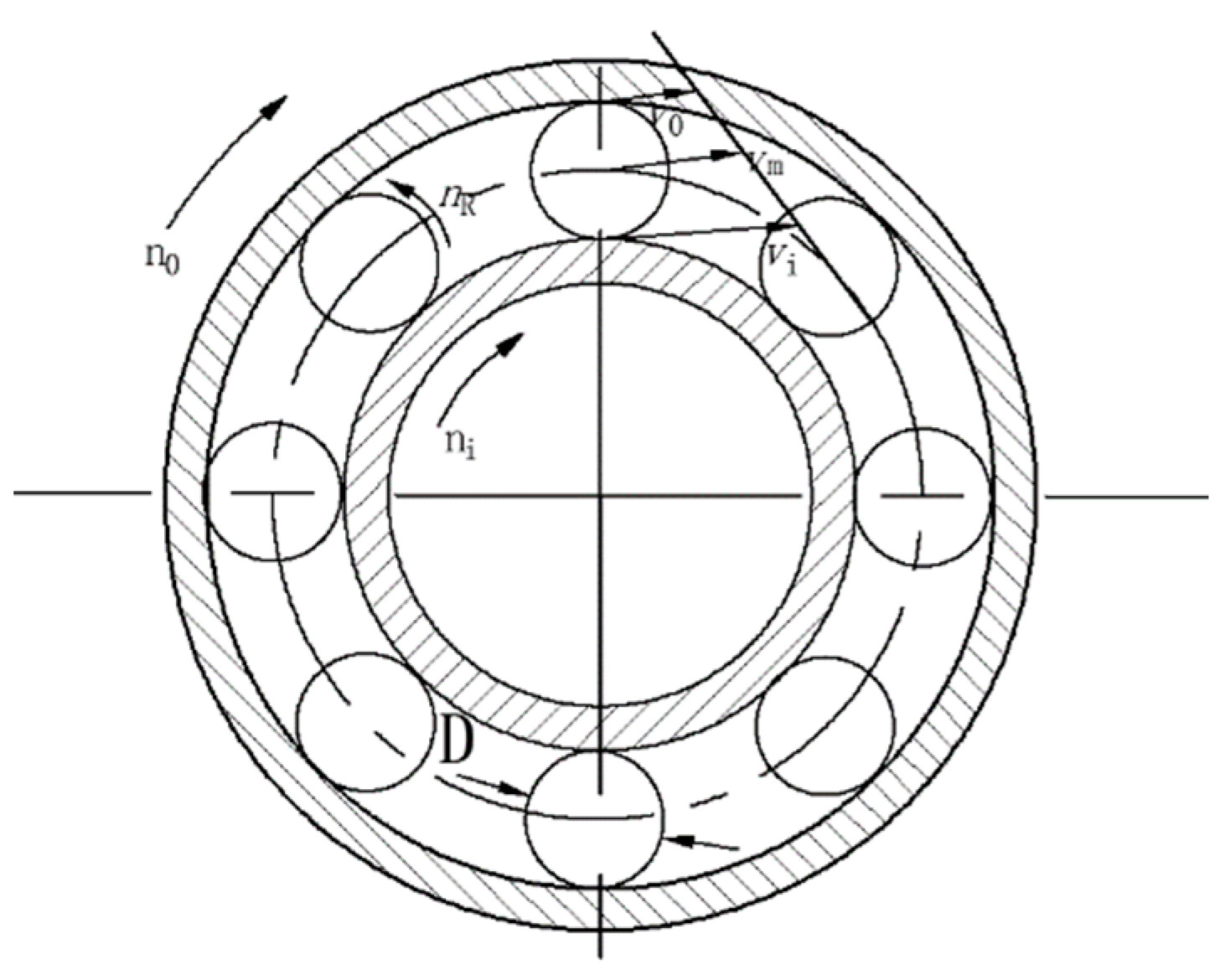
2.5. Rotation Axis and Geometric Centers
3. Simulation Results Analysis
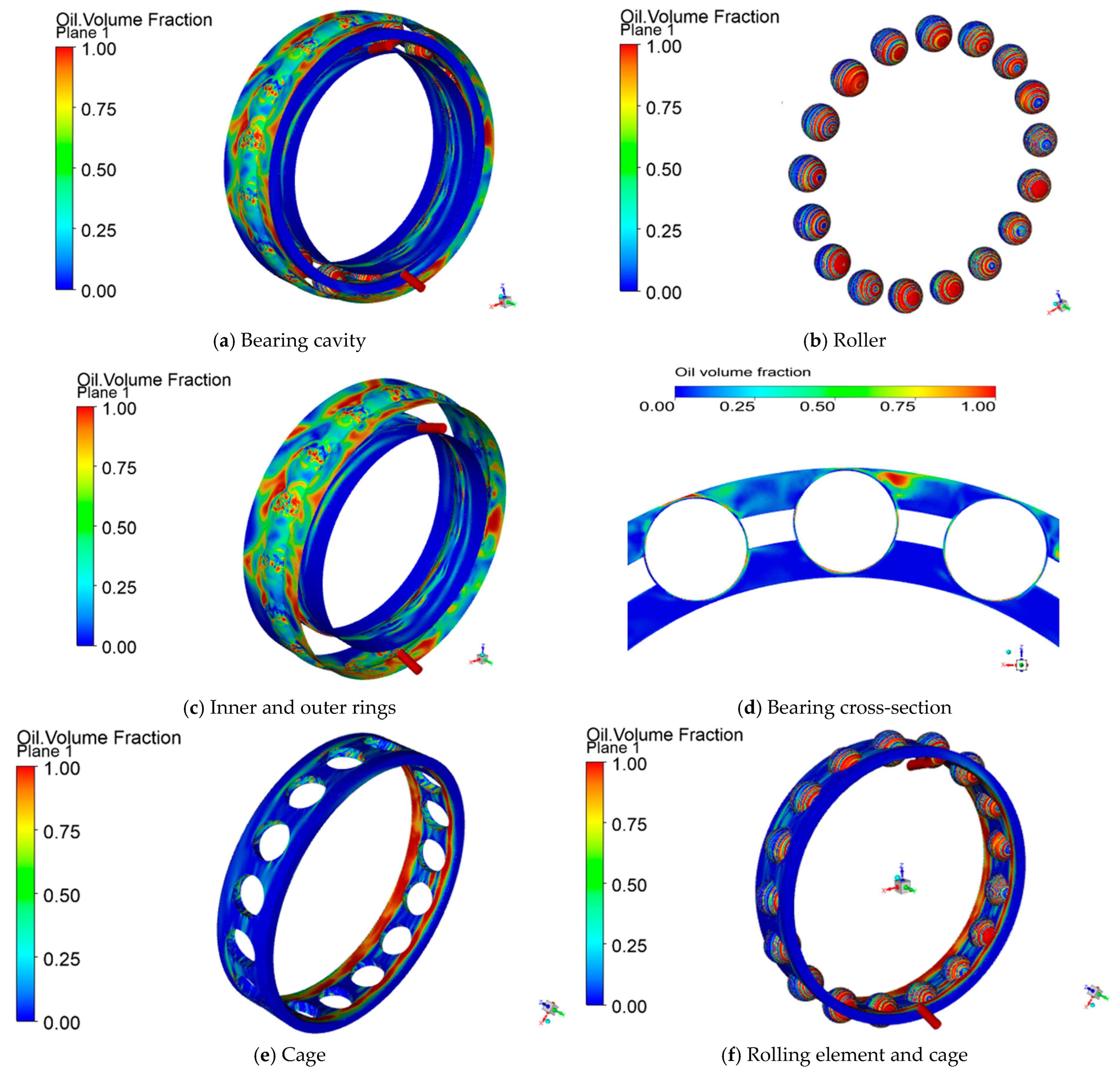
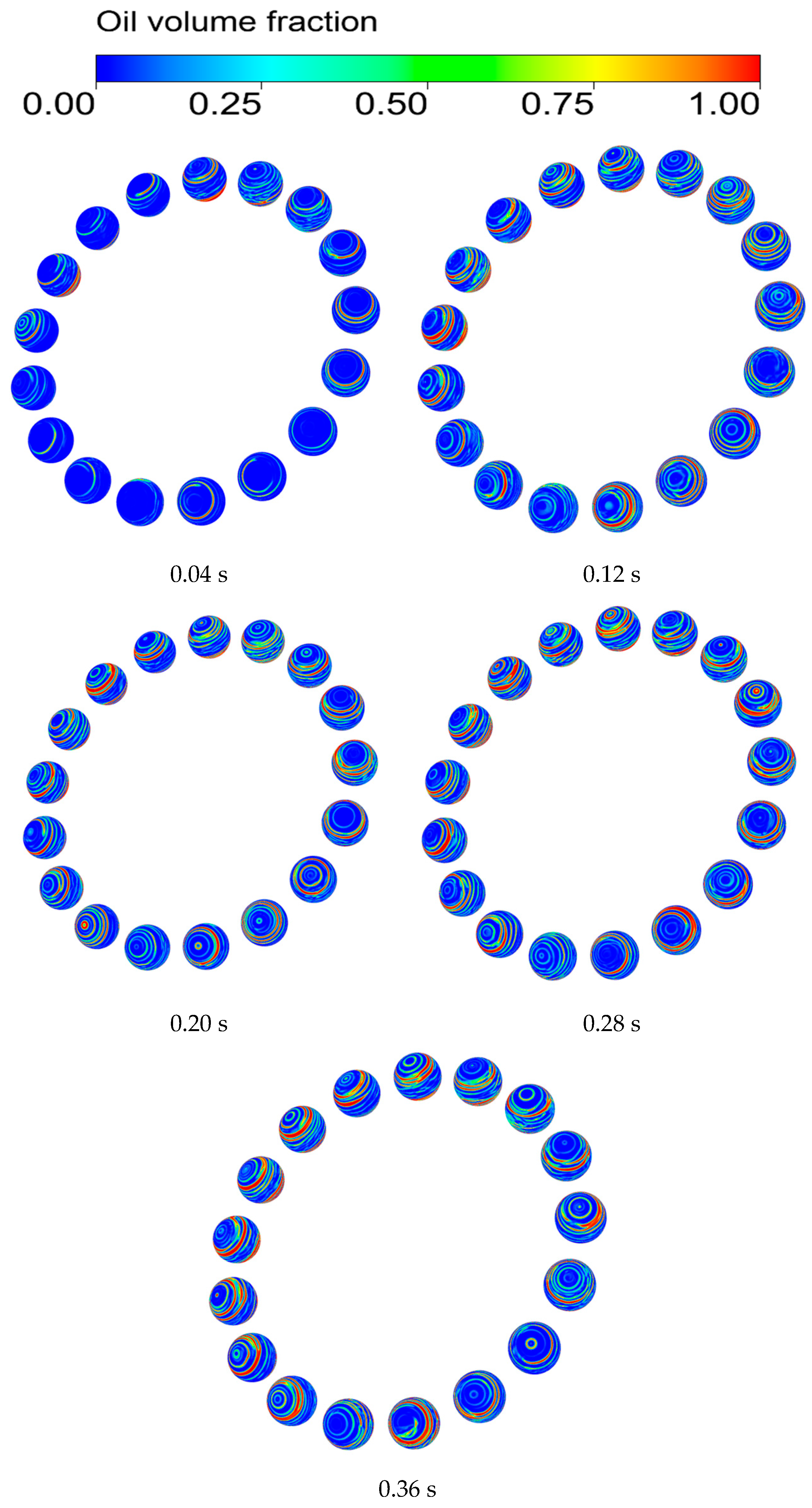
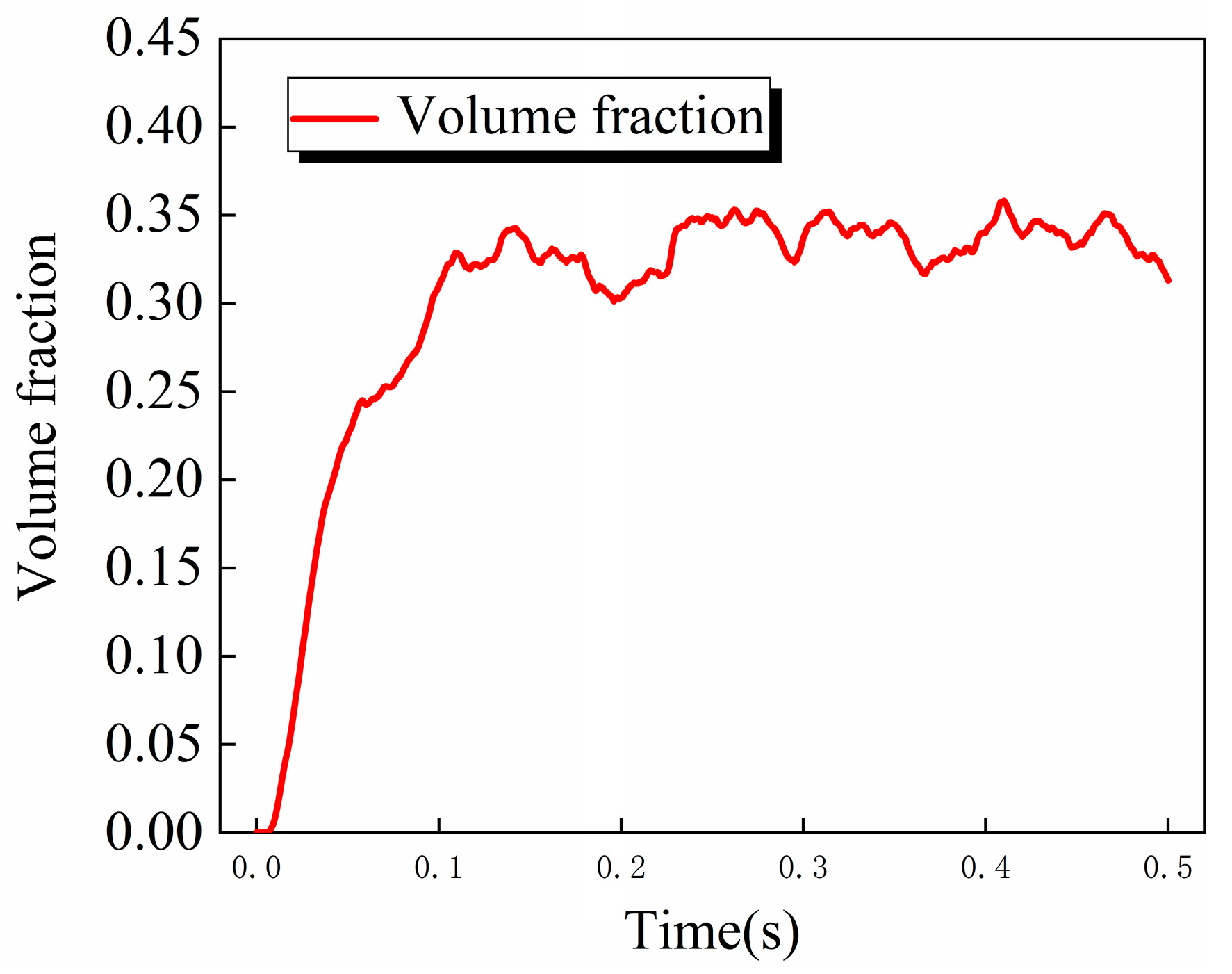
3.1. Lubricant Distribution Status
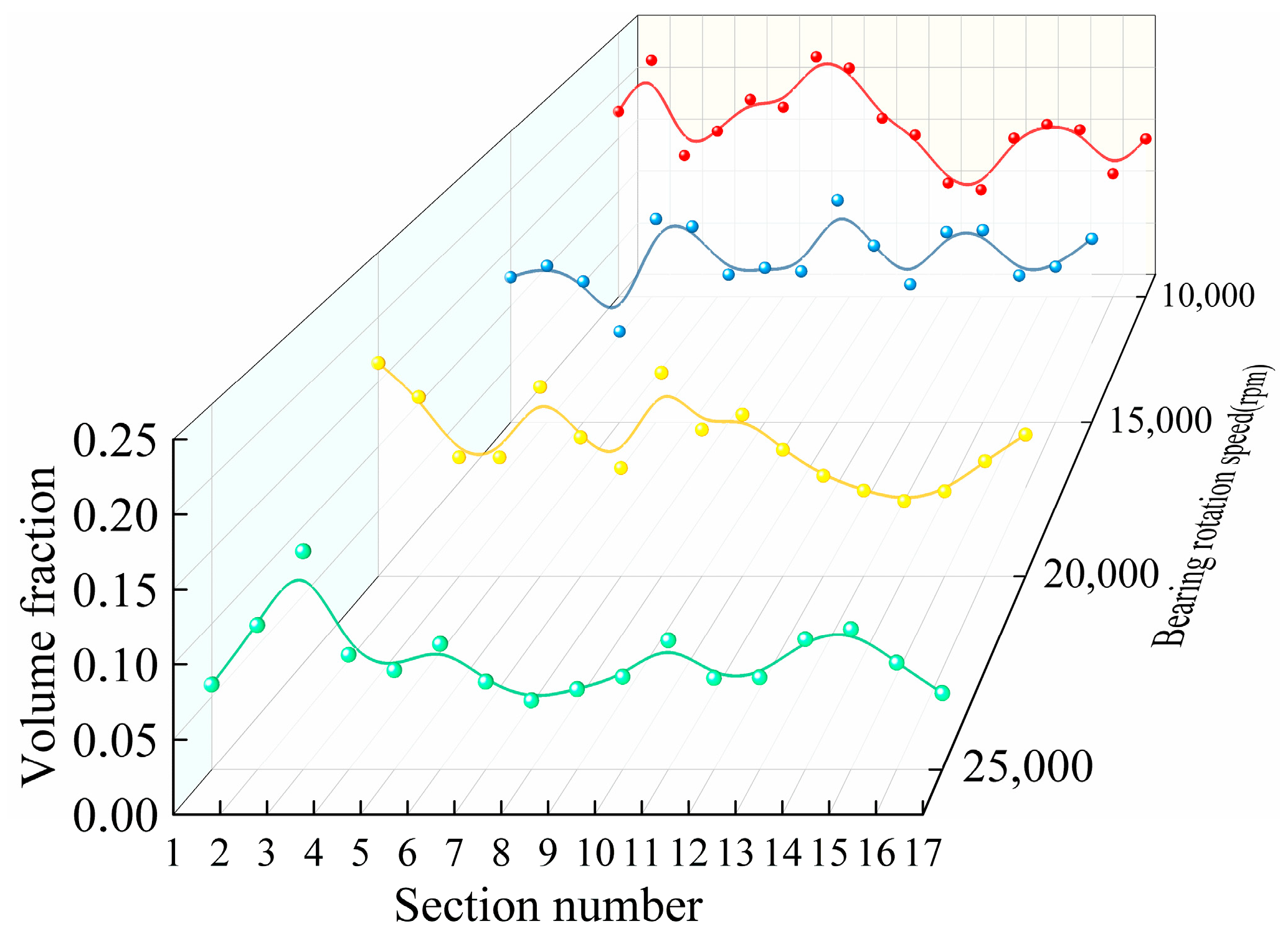
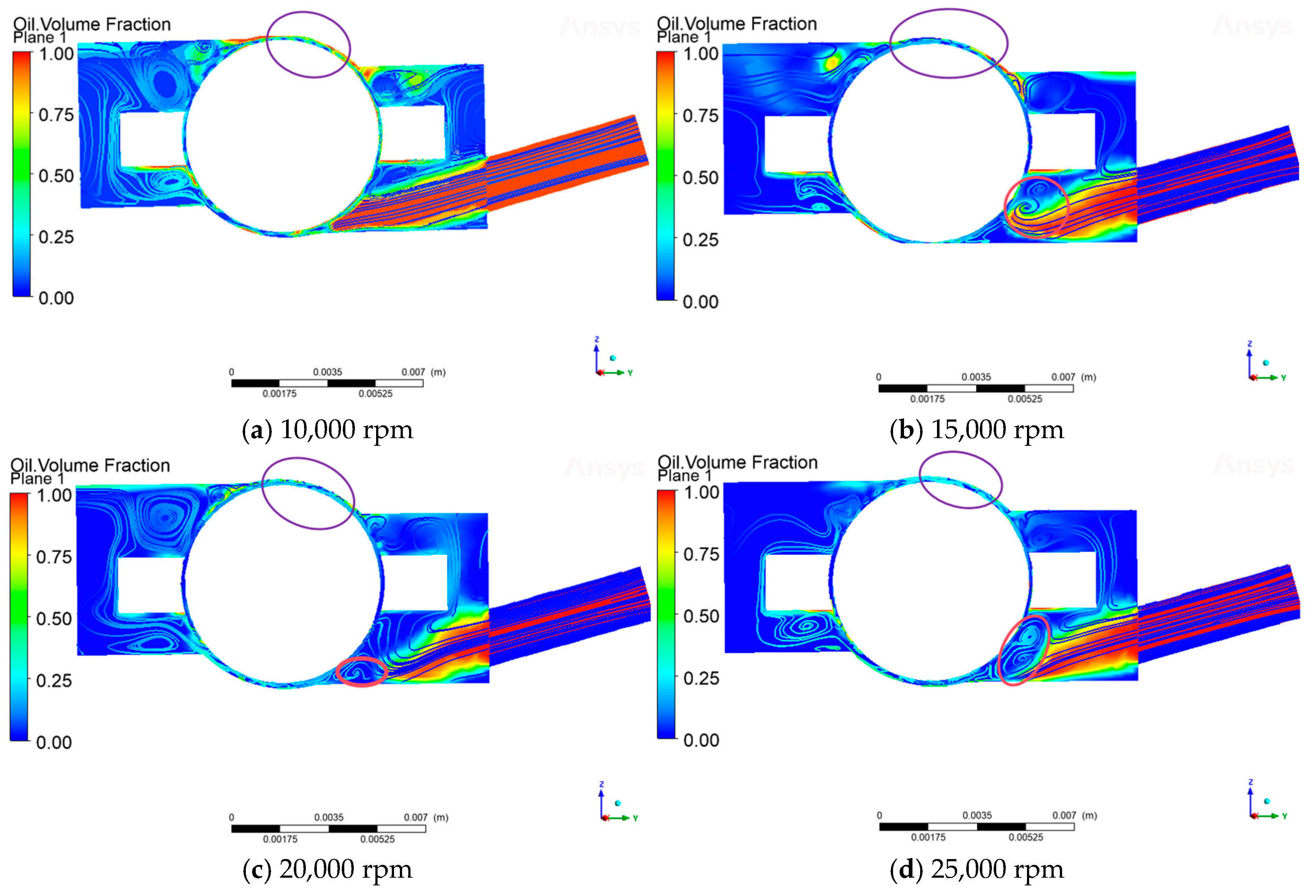
3.2. Effect of Rotational Speed on the Volume Fraction of Oil on the Surface of Steel Balls
3.3. Air Curtain Effect in the Bearing Cavity
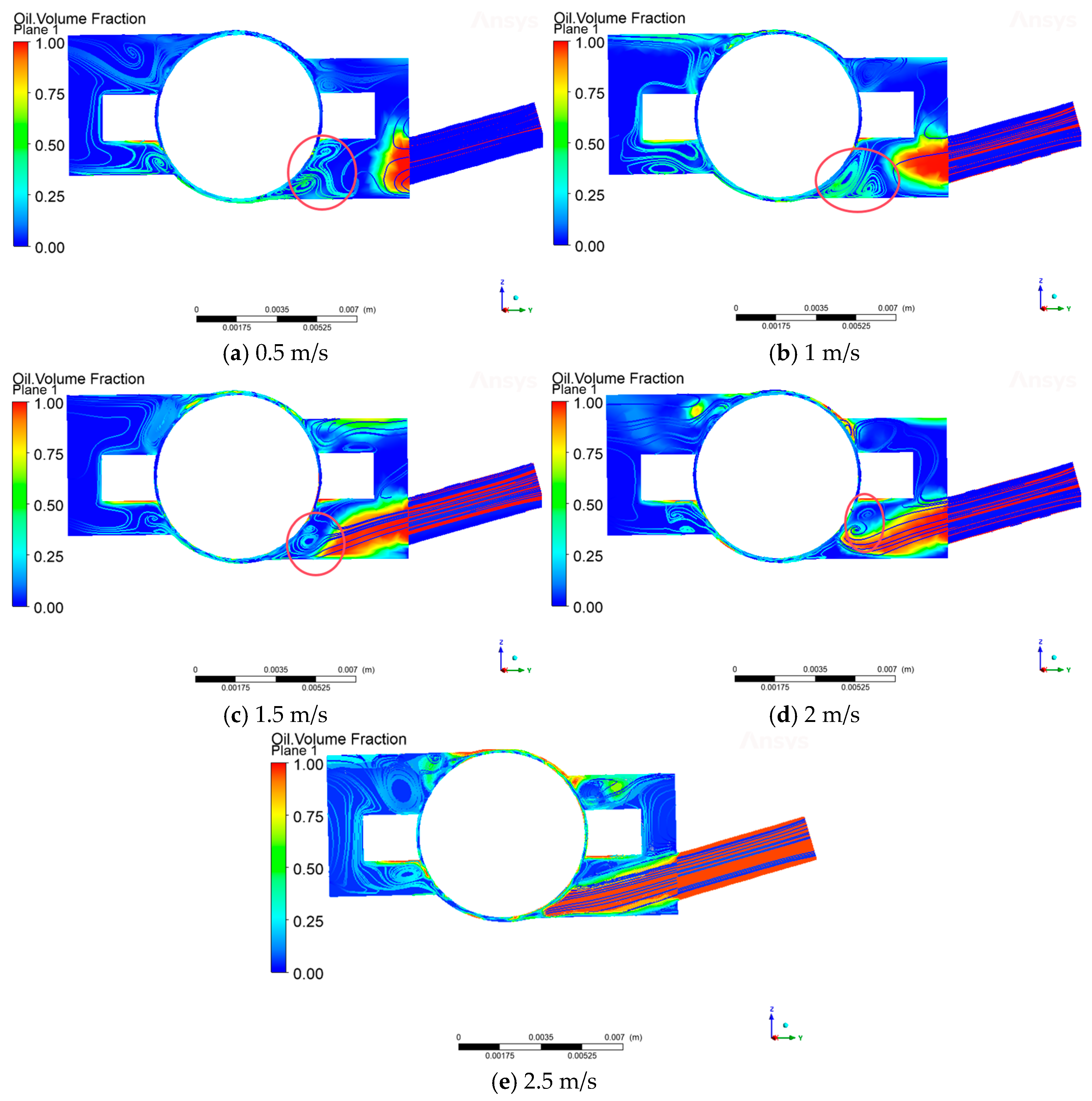
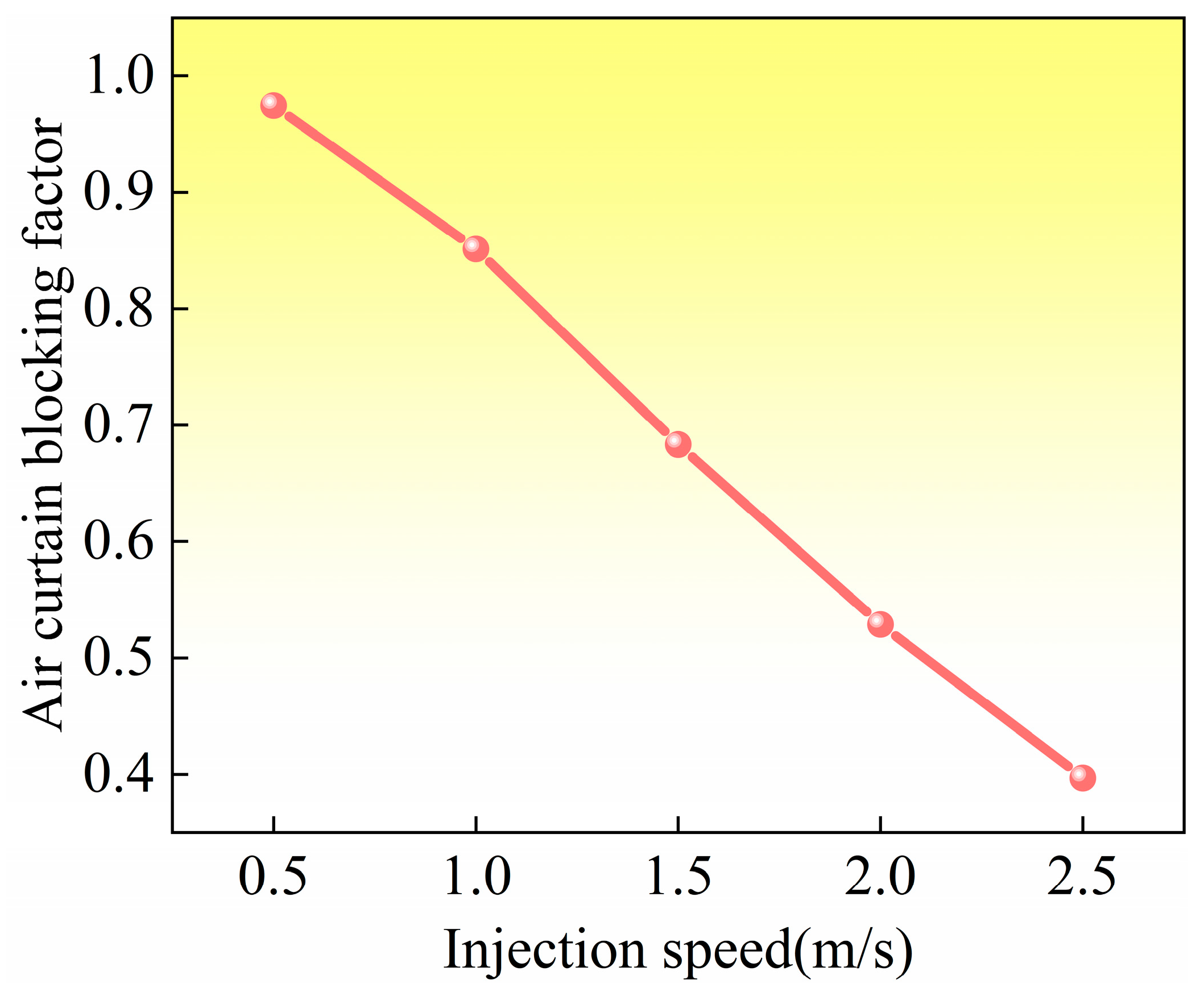
3.3.1. Influence of Oil Jet Velocity on Air Curtain Effect in Bearing Cavity
3.3.2. Influence of Rotational Speed on the Air Curtain Effect in the Bearing Cavity
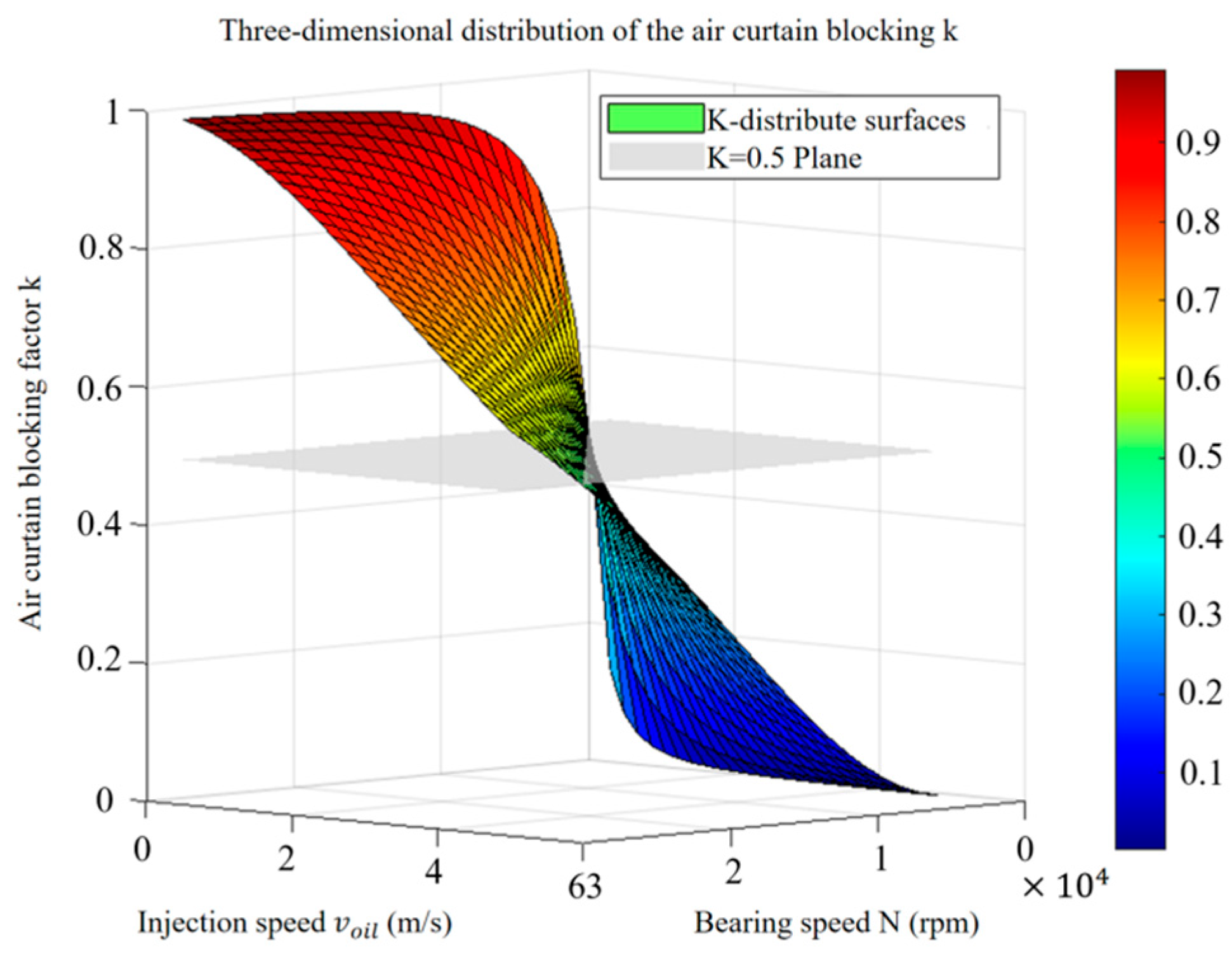
3.3.3. Establishment of Air Curtain Blocking Factor K
4. Conclusions
- The lubricant is affected by centrifugal force and contact pressure, etc., in the high-speed rotating bearings, and it spreads from the vicinity of the nozzle to both sides of the steel ball, gradually forming a stable oil film. The contact area results in less oil due to high pressure distribution.
- The intensity of the air curtain effect increases with the increase in rotational speed, which produces shear and other disturbances in the lubricant path. Under the influence of the air curtain effect, the end of the lubricant will produce the phenomenon of “warping”, resulting in a decrease in the lubrication effect.
- Increasing the injection speed can effectively weaken the air curtain effect, and the air curtain blocking coefficient K is established; when K is reduced to below 0.4, the lubricant can penetrate the air curtain smoothly. Under different rotational speeds, reasonable adjustment of the oil injection speed can improve the lubrication effect under different working conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wen, B.; Li, Y.; Li, Y.; Wang, M.; Zhai, J. Influence and Optimization of Nozzle Position on Lubricant Distribution in an Angular Contact Ball Bearing Cavity. Lubricants 2024, 12, 419. [Google Scholar] [CrossRef]
- Wu, M.; Wu, W.; Yuan, S.; Hu, J. Study of multiple-point oil-jet lubrication of high-speed ball bearings. Power Transm. Eng. 2014, 6, 44–46. [Google Scholar]
- Hu, J.; Wu, W.; Wu, M.; Yuan, S. Numerical investigation of the air–oil two-phase flow inside an oil-jet lubricated ball bearing. Int. J. Heat Mass Transf. 2014, 68, 85–93. [Google Scholar] [CrossRef]
- Zhang, R.; Wei, C.; Wu, W.; Yuan, S. CFD investigation on the influence of jet velocity of oil-jet lubricated ball bearing on the characteristics of lubrication flow field. In Proceedings of the 2015 International Conference on Fluid Power and Mechatronics (FPM), Harbin, China, 5–7 August 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1324–1328. [Google Scholar]
- Lu, P.; Ye, Q.; Fang, L.; Yang, P.; Yang, Q. Research on the air–oil two-phase flow regime in an aeroengine bearing chamber based on Hilbert–Huang transform. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2022, 236, 24–32. [Google Scholar] [CrossRef]
- Bao, H.; Hou, X.; Lu, F. Analysis of oil-air two-phase flow characteristics inside a ball bearing with under-race lubrication. Processes 2020, 8, 1223. [Google Scholar] [CrossRef]
- Gao, W.; Li, C.; Li, Y.; Liu, Z.; Lyu, Y. Oil–air two-phase flow distribution characteristics inside cylindrical roller bearing with under-race lubrication. Lubricants 2024, 12, 133. [Google Scholar] [CrossRef]
- Lu, F.; Wang, T.; Zhao, Z. Thermal characteristics for bearing combined EHL theory with CFD method. J. Aerosp. Power 2020, 35, 1204–1210. [Google Scholar]
- Liu, J.; Ni, H.; Zhou, R.; Li, X.; Xing, Q.; Pan, G. A simulation analysis of ball bearing lubrication characteristics considering the cage clearance. J. Tribol. 2023, 145, 044301. [Google Scholar] [CrossRef]
- Zhang, J.J.; Lu, L.M.; Zheng, Z.Y.; Gan, L.; Lv, Z.Y. Visual comparative analysis for the oil-air two-phase flow of an oil-jet lubricated roller-sliding bearing. J. Appl. Fluid Mech. 2022, 16, 179–191. [Google Scholar]
- Bei, Y.; Lei, D.; Ke, Y. Effects of oil-air lubrication methods on the internal fluid flow and heat dissipation of high-speed ball bearings. Mechnical Syst. Signal Process. 2021, 151, 107409. [Google Scholar]
- Jiang, L.; Lyu, Y.; Gao, W.; Zhu, P.; Liu, Z. Numerical investigation of the oil–air distribution inside ball bearings with under-race lubrication. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2022, 236, 499–513. [Google Scholar] [CrossRef]
- Gao, S.; Hou, X.; Ma, C.; Yang, Y.; Li, Z.; Yin, R.; Zhu, R. Transient simulation analysis of needle roller bearing in oil jet lubrication and planetary gearbox lubrication conditions based on computational fluid dynamics. Lubricants 2024, 12, 39. [Google Scholar] [CrossRef]
- Ge, L.; Yan, K.; Wang, C.; Zhu, Y.; Hong, J. A novel method for bearing lubrication enhancement via the inner ring groove structure. J. Phys. Conf. Ser. 2021, 1820, 012092. [Google Scholar] [CrossRef]
- Liu, J.; Ni, H.; Xu, Z.; Pan, G. A simulation analysis for lubricating characteristics of an oil-jet lubricated ball bearing. Simul. Model. Pract. Theory 2021, 113, 102371. [Google Scholar] [CrossRef]
- Zhu, W.; Zhu, R.; Tang, X.; Lu, F.; Bai, X.; Wu, X.; Li, F. CFD-based analysis of oil and gas two-phase flow characteristics in double-row tapered roller bearings with different rib structures. Appl. Sci. 2022, 12, 1156. [Google Scholar] [CrossRef]
- Gong, P.; Liu, Z.; Yu, Q.; Chen, F. Research on internal two-phase flow in the local micro-clearance design of a high-speed ball bearing with under-race lubrication. Lubr. Sci. 2024, 36, 216–230. [Google Scholar] [CrossRef]
- Ramdin, M.; Henkes, R. Computational fluid dynamics modeling of Benjamin and Taylor bubbles in two-phase flow in pipes. J. Fluids Eng. 2012, 134, 041303. [Google Scholar] [CrossRef]
- Banerjee, R.; Isaac, K.M.; Oliver, L.; Breig, W. Features of automotive gas tank filler pipe two-phase flow: Experiments and computational fluid dynamics simulations. J. Eng. Gas Turbines Power 2002, 124, 412–420. [Google Scholar] [CrossRef]
- Xiao, J.; Zhu, E.; Wang, G. Numerical simulation of emergency shutdown process of ring gate in hydraulic turbine runaway. J. Fluids Eng. 2012, 134, 124501. [Google Scholar] [CrossRef]
- Lyu, Y.; Li, Y.; Li, C.; Jiang, L.; Liu, Z. Oil-air distribution prediction inside ball bearing with under-race lubrication based on numerical simulation. Appl. Sci. 2024, 14, 3770. [Google Scholar] [CrossRef]
- Shan, W.; Chen, Y.; Huang, J.; Wang, X.; Han, Z.; Wu, K. A multiphase flow study for lubrication characteristics on the internal flow pattern of ball bearing. Results Eng. 2023, 20, 101429. [Google Scholar] [CrossRef]
- Adeniyi, A.A.; Morvan, H.P.; Simmons, K.A. A multiphase computational study of oil-air flow within the bearing sector of aeroengines. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015; American Society of Mechanical Engineers: New York, NY, USA, 2015; Volume 56734, p. V05CT15A024. [Google Scholar]
- Foord, C.A. High-speed ball bearing analysis. Proceedings of the Institution of Mechanical Engineers. Part G J. Aerosp. Eng. 2006, 220, 537–544. [Google Scholar]
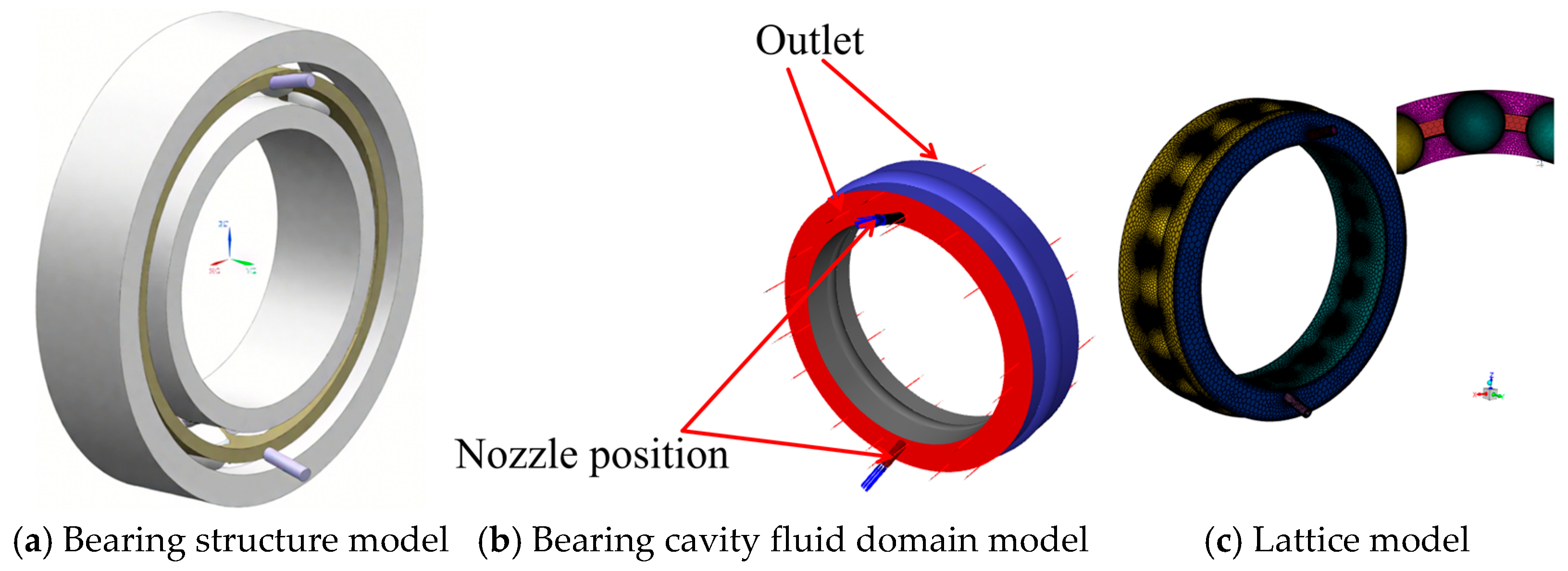


| Parameters | Numerical Value |
|---|---|
| Rolling body diameter/mm | 7.144 |
| Number of scrollers | 17 |
| Initial contact angle/° | 15 |
| Radius of curvature of inner ring groove/mm | 4 |
| Radius of curvature of outer ring groove/mm | 3.79 |
| Pitch circle diameter/mm | 54 |
| Parameters | Air | 4050 Aviation Lubricant | GCr15 |
|---|---|---|---|
| Density (kg/m3) | 1.255 | 878 | 7810 |
| Dynamic viscosity (kg/m·s) | 1.7894 × 10−5 | 0.026 | --- |
| Ball Number | Steel Ball Center Coordinates | Axis of Rotation |
|---|---|---|
| 1 | (0.027 m * sin(0 * 2 * PI/17), 0, 0.027 m * cos(0 * 2 * PI/17)) | (0, −cos(PI/12), sin(PI/12)) |
| 2 | (0.027 m * sin(1 * 2 * PI/17), 0, 0.027 m * cos(1 * 2 * PI/17)) | (sin(PI/12) * sin(1 * 2 * PI/17), −cos(PI/12), sin(PI/12) * cos(1 * 2 * PI/17)) |
| 3 | (0.027 m * sin(2 * 2 * PI/17), 0, 0.027 m * cos(2 * 2 * PI/17)) | (sin(PI/12) * sin(2 * 2 * PI/17), −cos(PI/12), sin(PI/12) * cos(2 * 2 * PI/17)) |
| 4 | (0.027 m * sin(3 * 2 * PI/17), 0, 0.027 m * cos(3 * 2 * PI/17)) | (sin(PI/12) * sin(3 * 2 * PI/17), −cos(PI/12), sin(PI/12) * cos(3 * 2 * PI/17)) |
| 5 | (0.027 m * sin(4 * 2 * PI/17), 0, 0.027 m * cos(4 * 2 * PI/17)) | (sin(PI/12) * sin(4 * 2 * PI/17), −cos(PI/12), sin(PI/12) * cos(4 * 2 * PI/17)) |
| 6 | (0.027 m * sin(5 * 2 * PI/17), 0, 0.027 m * cos(5 * 2 * PI/17)) | (sin(PI/12) * sin(5 * 2 * PI/17), −cos(PI/12), sin(PI/12) * cos(5 * 2 * PI/17)) |
| 7 | (0.027 m * sin(6 * 2 * PI/17), 0, 0.027 m * cos(6 * 2 * PI/17)) | (sin(PI/12) * sin(6 * 2 * PI/17), −cos(PI/12), sin(PI/12) * cos(6 * 2 * PI/17)) |
| 8 | (0.027 m * sin(7 * 2 * PI/17), 0, 0.027 m * cos(7 * 2 * PI/17)) | (sin(PI/12) * sin(7 * 2 * PI/17), −cos(PI/12), sin(PI/12) * cos(7 * 2 * PI/17)) |
| 9 | (0.027 m * sin(8 * 2 * PI/17), 0, 0.027 m * cos(8 * 2 * PI/17)) | (sin(PI/12) * sin(8 * 2 * PI/17), −cos(PI/12), sin(PI/12) * cos(8 * 2 * PI/17)) |
| 10 | (0.027 m * sin(9 * 2 * PI/17), 0, 0.027 m * cos(9 * 2 * PI/17)) | (sin(PI/12) * sin(9 * 2 * PI/17), −cos(PI/12), sin(PI/12) * cos(9 * 2 * PI/17)) |
| 11 | (0.027 m * sin(10 * 2 * PI/17), 0, 0.027 m * cos(10 * 2 * PI/17)) | (sin(PI/12) * sin(10 * 2 * PI/17), −cos(PI/12), sin(PI/12) * cos(10 * 2 * PI/17)) |
| 12 | (0.027 m * sin(11 * 2 * PI/17), 0, 0.027 m * cos(11 * 2 * PI/17)) | (sin(PI/12) * sin(11 * 2 * PI/17), −cos(PI/12), sin(PI/12) * cos(11 * 2 * PI/17)) |
| 13 | (0.027 m * sin(12 * 2 * PI/17), 0, 0.027 m * cos(12 * 2 * PI/17)) | (sin(PI/12) * sin(12 * 2 * PI/17), −cos(PI/12), sin(PI/12) * cos(12 * 2 * PI/17)) |
| 14 | (0.027 m * sin(13 * 2 * PI/17), 0, 0.027 m * cos(13 * 2 * PI/17)) | (sin(PI/12) * sin(13 * 2 * PI/17), −cos(PI/12), sin(PI/12) * cos(13 * 2 * PI/17)) |
| 15 | (0.027 m * sin(14 * 2 * PI/17), 0, 0.027 m * cos(14 * 2 * PI/17)) | (sin(PI/12) * sin(14 * 2 * PI/17), −cos(PI/12), sin(PI/12) * cos(14 * 2 * PI/17)) |
| 16 | (0.027 m * sin(15 * 2 * PI/17), 0, 0.027 m * cos(15 * 2 * PI/17)) | (sin(PI/12) * sin(15 * 2 * PI/17), −cos(PI/12), sin(PI/12) * cos(15 * 2 * PI/17)) |
| 17 | (0.027 m * sin(16 * 2 * PI/17), 0, 0.027 m * cos(16 * 2 * PI/17)) | (sin(PI/12) * sin(16 * 2 * PI/17), −cos(PI/12), sin(PI/12) * cos(16 * 2 * PI/17)) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Y.; Ye, B.; Yan, Z.; Zhang, H.; Yu, W.; Sun, J.; Zhou, W. Simulation Study of the Effect of Oil Injection Speed on the Air Curtain of High-Speed Bearings. Lubricants 2025, 13, 334. https://doi.org/10.3390/lubricants13080334
Dong Y, Ye B, Yan Z, Zhang H, Yu W, Sun J, Zhou W. Simulation Study of the Effect of Oil Injection Speed on the Air Curtain of High-Speed Bearings. Lubricants. 2025; 13(8):334. https://doi.org/10.3390/lubricants13080334
Chicago/Turabian StyleDong, Yanfang, Botao Ye, Zibo Yan, Hai Zhang, Wei Yu, Jianyong Sun, and Wenbo Zhou. 2025. "Simulation Study of the Effect of Oil Injection Speed on the Air Curtain of High-Speed Bearings" Lubricants 13, no. 8: 334. https://doi.org/10.3390/lubricants13080334
APA StyleDong, Y., Ye, B., Yan, Z., Zhang, H., Yu, W., Sun, J., & Zhou, W. (2025). Simulation Study of the Effect of Oil Injection Speed on the Air Curtain of High-Speed Bearings. Lubricants, 13(8), 334. https://doi.org/10.3390/lubricants13080334





