Analysis of the Impact of Frog Wear on the Wheel–Rail Dynamic Performance in Turnout Zones of Urban Rail Transit Lines

Abstract

To investigate how severe wear at No. 12 turnout frogs in an urban rail transit line operating at speeds over 120 km/h on the dynamic performance of the vehicle, a vehicle–frog coupled dynamic model was established by employing the 2021 version of SIMPACK software. Profiles of No. 12 alloy steel frogs and metro wheel rims were measured to simulate wheel–rail interactions as the vehicle traverses the turnout, using both brand-new and worn frog conditions. The experimental results indicate that increased service life deepens frog wear, raises equivalent conicity, and intensifies wheel–rail forces. When a vehicle passes through the frog serviced for over 17 months at the speed of 120 km/h, the maximum derailment coefficient, lateral acceleration of the car body, and lateral and vertical wheel–rail forces increased by 0.14, 0.17 m/s², 9.52 kN, and 105.76 kN, respectively. The maximum contact patch area grew by 35.73%, while peak contact pressure rose by 236 MPa. To prevent dynamic indicators from exceeding safety thresholds and ensure train operational safety, it is recommended that the frog maintenance cycle be limited to 12 to 16 months.

1. Introduction

As a vital component of urban rail transit, the subway system plays a crucial role in safeguarding public safety and national assets through safe, reliable, and efficient operation. Unlike mainline tracks, turnout zones feature non-uniform rail profiles. The variation in rail contours within switch areas intensifies wheel–rail interactions as metro vehicles pass through, leading to significantly harsher service conditions. Consequently, rail wear in these regions presents a critical and challenging issue in subway operation and maintenance.

Frog wear and its associated issues have drawn significant attention from researchers in recent years. Nielsen et al. [1] investigated rolling contact fatigue and wear in switch rails by analyzing cumulative rail damage in turnout zones. The contact stress distribution, adhesion, and slip zones were obtained by employing the FASTSIM in their research. Sun et al. [2] established a vehicle–turnout dynamic model in VAMPIRE and evaluated frog wear using a wear index model. And the train speed was highlighted as a significant factor that affects wheel and rail wear when the train passes through the frog rail. Ignesti et al. [3] enhanced a multi-point contact model to improve wheel–rail contact calculations. A wear prediction model that correlated the wear volume with the frictional work was proposed and validated based on field tests. Wen et al. [4] simulated the rolling contact in a finite element model by applying normal and tangential stresses in the dynamic simulation. Zhao et al. [5] constructed a 3D wheel–rail rolling contact model using FE analysis to compute contact stresses and investigate the wear mechanism.

The dynamic performance of a train passing through turnout zones has also been a significant focus of research due to its direct effects on the running safety and ride comfort of the train. Kim et al. [6] investigated the influence of the frog rail geometry and the wing rail length on running safety for a specific European turnout design. Sala et al. [7] optimized the design of a swing-nose to reduce wheel–rail impact forces when the train passed through the turnout zone. Eugène et al. [8] developed a 3D coupled vehicle–track model, incorporating flexible rail and wheelset deformations, and revealed derailment mechanisms in turnouts. Braghin et al. [9] conducted tests on a BU300 roller rig to evaluate creep rates under different wear ratios and proposed an algorithm to calculate wear depth. Their results indicated that wear depth increases with the wear coefficient, vehicle speed, and the duration of wheel passage through a given cell, while it decreases with higher material density. Moreover, they categorized the wear coefficient into three regions based on the wear ratio. Seo et al. [10] performed twin-disk rolling tests to investigate the contact fatigue and wear behavior of UIC60 and KS60 rails. They found that material ductility and fracture toughness are critical factors influencing wear and contact fatigue. The UIC60 rail, which exhibits better ductility and fracture toughness, demonstrated superior resistance to contact fatigue but inferior wear resistance. Cremona et al. [11] applied uncertainty analysis methods to improve the Archard coefficient, reconstructing the wear coefficient map and providing more rational theoretical guidance for wear prediction. Xin et al. [12] employed an explicit finite element method to calculate the stress–strain behavior of the turnout and used the Jiang–Sehitoglu model based on the critical plane method to predict fatigue damage and crack initiation life. Based on previous experimental results, Jendel [13] divided the wear coefficient in the Archard wear model into four regions according to the creep velocity and normal stress between two contacting bodies and provided the corresponding coefficient ranges for each region. Pearce and Sherratt [14] proposed that material loss is proportional to the dissipated energy within the wheel–rail contact patch and used this wear model to calculate the long-term wear of P8 and P11 wheels operating on a typical railway line. Zobory [15], in 1997, pointed out that material loss is related to the energy dissipation flux density, and based on this theory, proposed a fast computation model that does not require solving the tangential contact conditions, as well as a precise model that does. Markine et al. [16], through field measurements, analyzed the locations and influencing factors of turnout damage, and proposed that increasing track elasticity can reduce wheel–rail impact. Aniolek et al. [17] developed a vehicle–turnout dynamic model to calculate the wheel–rail normal force and further employed finite element analysis to determine surface contact stress. Ishak et al. [18] reviewed and classified the typical types of track failures occurring in turnout zones and proposed a comprehensive turnout maintenance methodology. Zhou et al. [19] analyzed the influence of the transition curve in turnouts under braking conditions on vehicle running safety and suggested that flange lubrication can effectively reduce the dynamic wheel–rail interaction when trains pass through turnouts.

Given the limited number of operational metro express lines with speeds of 120 km/h or higher, research and data on related turnout components remain scarce. This study addresses this gap by analyzing the wear progression of a type 12 alloy steel combined frog from a metro express line. Using measured rail profiles and cross-sectional data collected at various wear stages, the study examines frog wear dynamics. A coupled vehicle–frog dynamics model was developed in the multi-body dynamics software SIMPACK to investigate vehicle responses and wheel–rail interactions at different wear stages in both straight and reverse directions. The primary objective is to clarify the impact of frog wear and damage on wheel–rail dynamic performance, contributing to a deeper understanding of wear mechanisms and their implications for operational safety and efficiency in high-speed metro systems.

The main contributions of this paper can be drawn as follows:

• Conducted dimensional testing on frog profiles and wheel tread geometries across different service cycles, quantitatively analyzing the wear distribution characteristics and their evolution patterns with accumulated operational duration.
• Developed vehicle–frog coupled dynamics models reflecting varying wear severity levels by incorporating measured frog profiles from distinct service phases into multi-body dynamics simulations.
• Systematically evaluated the evolution trends of safety performance metrics, ride stability indices, and wheel–rail contact stresses relative to service cycles through dynamics modeling and parametric studies.

2. Investigation and Analysis of Frog Wear

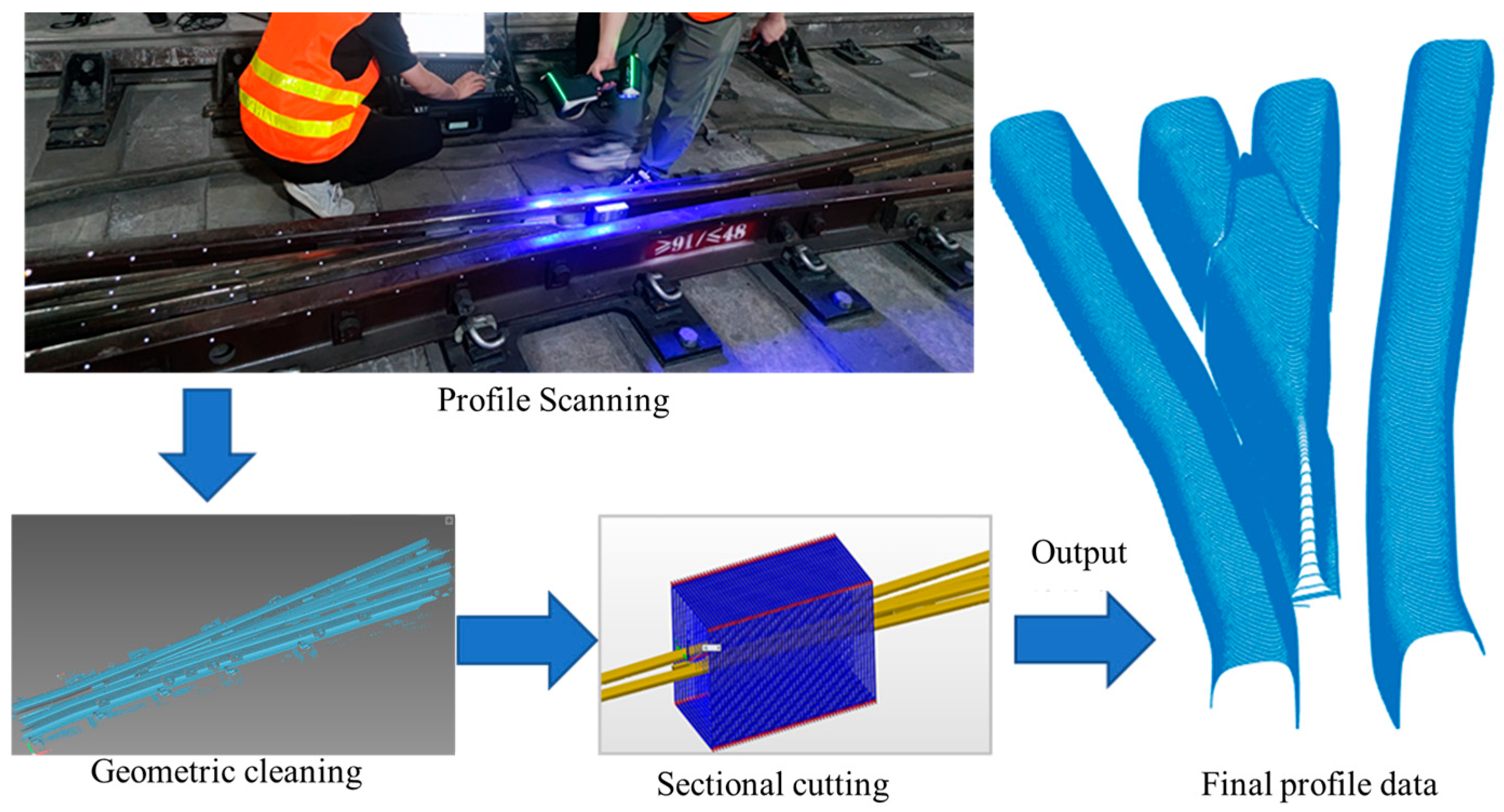
2.1. Investigation of the Defect

The investigated metro line in Chengdu operates at a maximum speed of 140 km/h on the mainline and 120 km/h through turnouts. Following the initial detection of defects in manganese frogs in January 2021, the metro track maintenance department promptly conducted a comprehensive inspection across the entire line. Concurrently, maintenance measures such as turnout surface grinding and repairs were implemented. As of 10 March 2021, defects in the frog were identified in 23 out of 100 manganese turnouts. These defects, including cracks and spalling, were observed regardless of train speed, direction (facing or trailing), or turnout type (No. 9 or No. 12), as shown in Figure 1.

Research indicates that the wheel–rail interaction in the frog zone is the primary contributor to the abnormal frog defect. The severe wheel–rail impacts accelerate the generation of transverse cracks under high wheel–rail contact stresses, which leads to localized spalling and material loss. Moreover, the deterioration is also likely to result in the fracture of the frog, posing potential safety risks and property losses. Focusing on experimental testing and field investigations, this study aims to analyze patterns of the frog wear, simulate dynamic behaviors of the vehicle passing through turnout zones, reveal characteristics of the wheel–rail contact, and evaluate the vehicle–turnout dynamic performance affected by the frog wear.

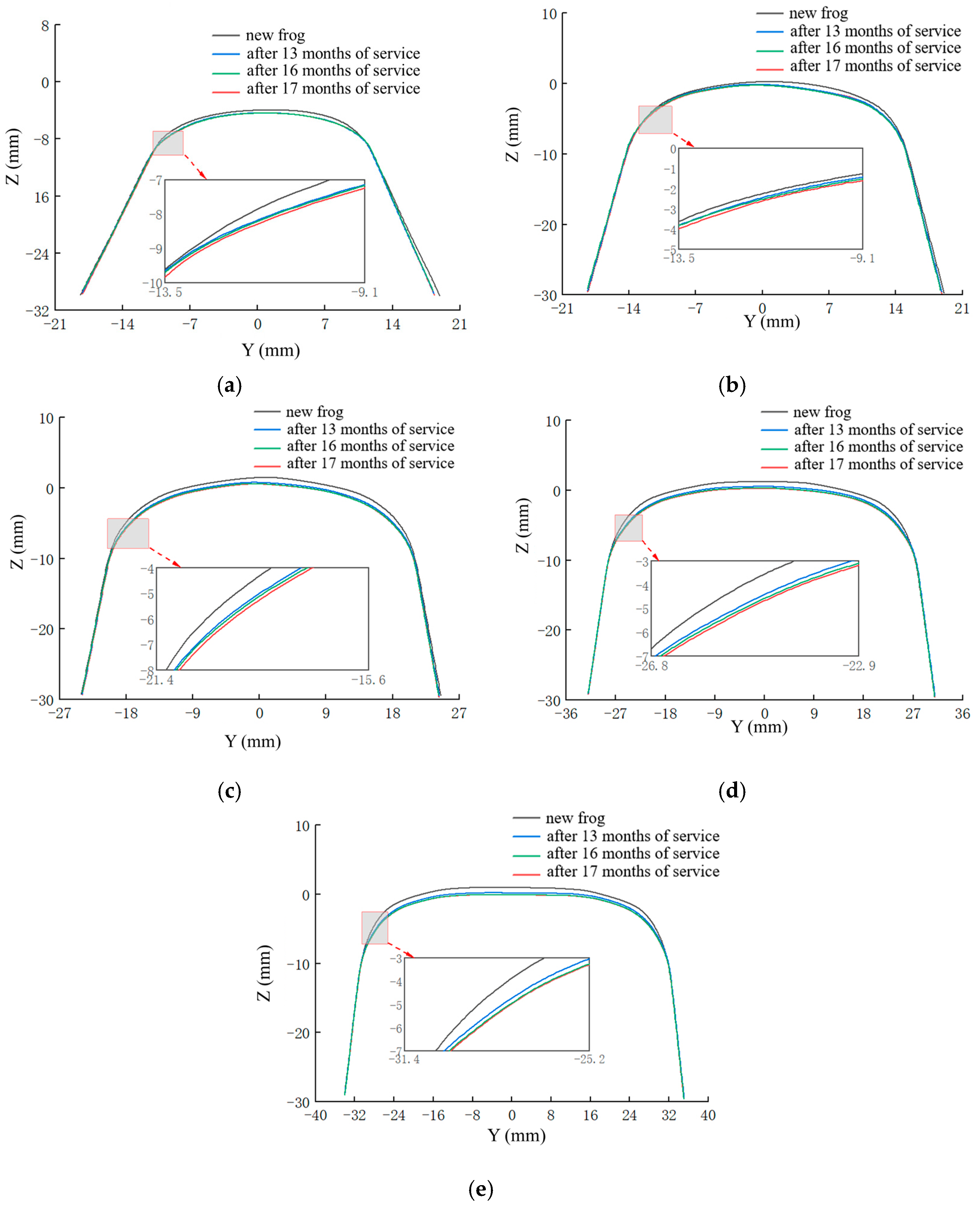
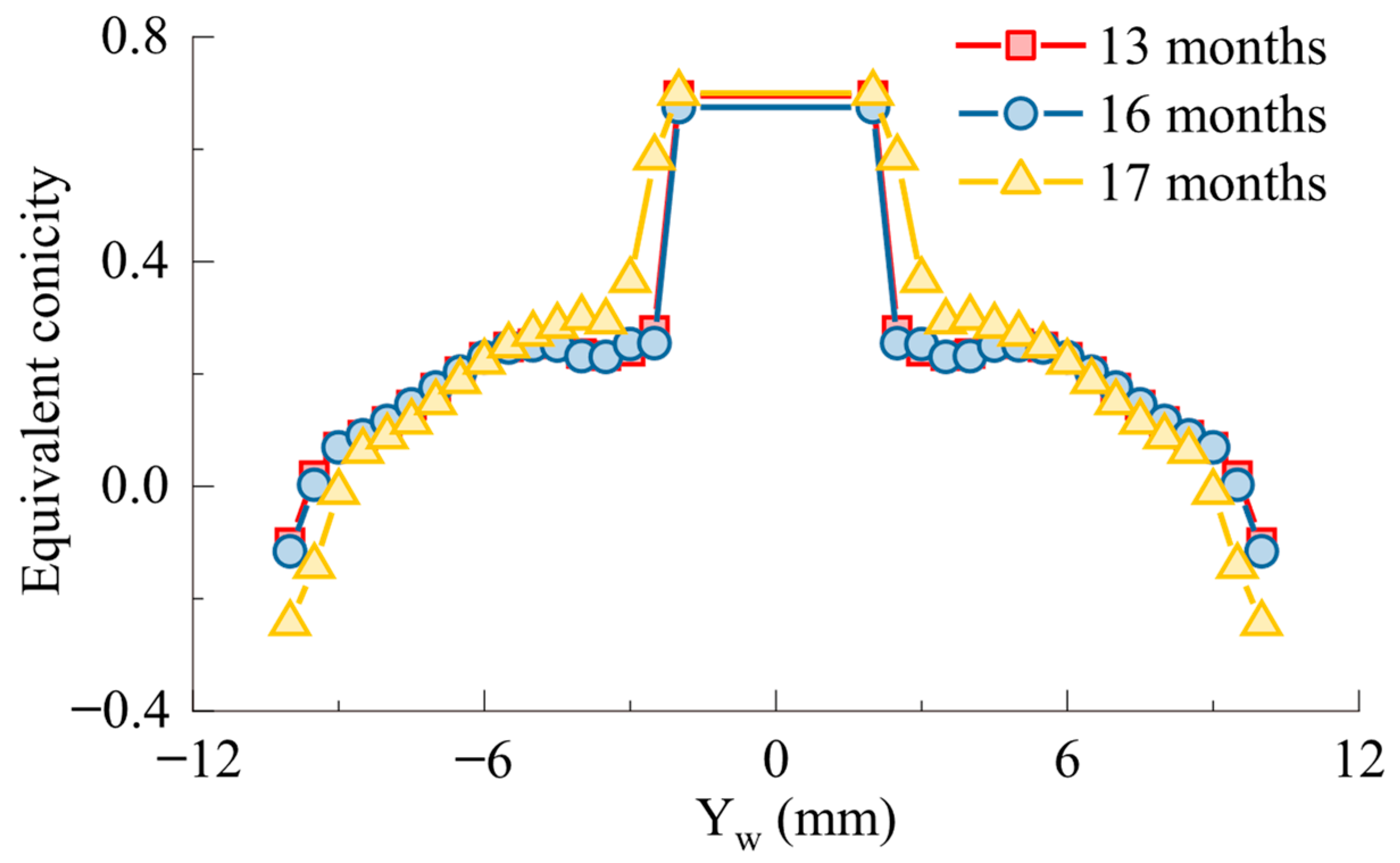
2.2. Influence of the Frog Wear on the Wheel and Rail Profiles

A brand-new frog, along with the same frog after 13, 16, and 17 months of service, was measured using a laser scanning device (3D laser scanner with a maximum accuracy of 0.01 mm) according to the zones illustrated in Figure 2. Figure 3 presents the measurement procedure and the results obtained from one of the tests.

Additionally, profiles of wheels at the in-service vehicle were collected using the Miniprof instrument, as shown in Figure 4.

Figure 5 shows the cross-sectional profiles of the frog at progressive wear stages, measured at 200 mm intervals (from 200 to 1000 mm) along the trailing direction, with the frog center serving as the longitudinal origin (x = 0). As shown in Figure 5, the wear depth of the frog nose is relatively small at the cross-section 200 mm from the center of the frog. However, as the distance from the center increases, the wear on the frog’s nose exhibits a significant growth trend.

Furthermore, the characteristics of frog wear were analyzed based on the test results by calculating wear at each cross-section. Figure 6a shows the wear distribution on the frog after 13 months of service. Figure 6b illustrates the relationship between wear depth and frog service time. The results indicate that wear depth increases consistently with service time. On average, the wear depth increased by 0.11 mm as the service time extended from 13 to 17 months. Additionally, a higher frequency of train passages accelerates wear progression and enlarges the wear-affected zone. The primary wear region was identified approximately 500 mm from the frog center.

3. Dynamics Model

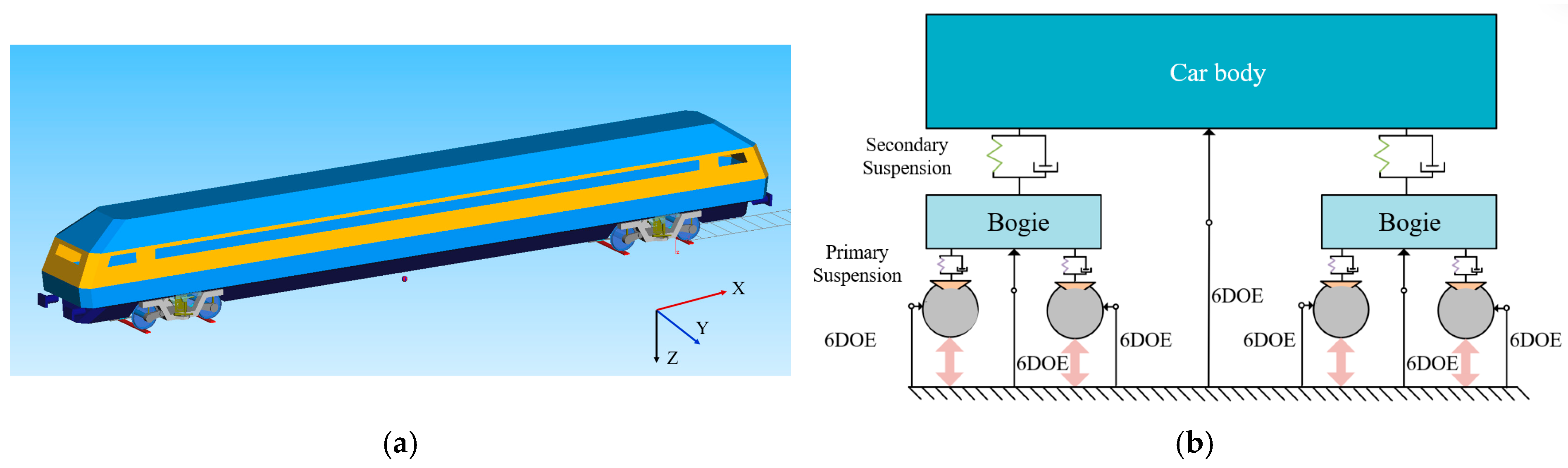
3.1. Vehicle–Turnout Coupled Dynamic Model

To investigate the influence of frog wear on the dynamic performance of the vehicle, a vehicle–turnout coupled dynamics model was established based on the SIMPACK software. The vehicle dynamics model consists of 15 rigid bodies, including 1 car body, 2 bogie frames, 4 wheelsets, and 8 axle boxes. The car body, bogie frames, and wheelsets each possess six degrees of freedom (DOFs), while the axle boxes retain only the pitch DOF, resulting in a total of 50 DOFs for the entire system. The bogie system incorporates primary suspension components such as steel coil springs, vertical dampers, swing-arm axle boxes, and vertical end stops, along with secondary suspension elements including air springs, vertical and lateral dampers, lateral end stops, dual traction rods, and an anti-roll torsion bar. The key parameters are provided in

Table 1. Key parameters of the vehicle.

Parameter	Value
Car Body Length/m	22
Car Body Width/m	3
Floor Height Above Rail/m	1.13
Vehicle Wheelbase/m	15.7
Axle Load/t	17
Track Gauge/m	1.435
Bogie Wheelbase/m	2.5
Wheelset Back-to-Back Distance/m	1.353
Wheel Diameter/m	0.86

. The topology and force transmission relationships of the vehicle dynamics model are illustrated in Figure 7.

The measured frog profiles at different positions were utilized to construct the frog model. In this study, the frog profile section extends 3000 mm, ranging from −1000 mm to 2000 mm relative to the center. The profile data locations and sampling intervals are detailed in

Table 2. Frog profile data measurement locations and intervals.

Profile Location (mm)	Interval (mm)
−1000 to 0	100
0 to 200	50
200 to 1000	100
1000 to 2000	20

. The stock rail conforms to the 60 kg/m rail standard, with the frog zone beginning at 28.2 m along the track. Figure 8 illustrates the frog profile configuration and modeling approach.

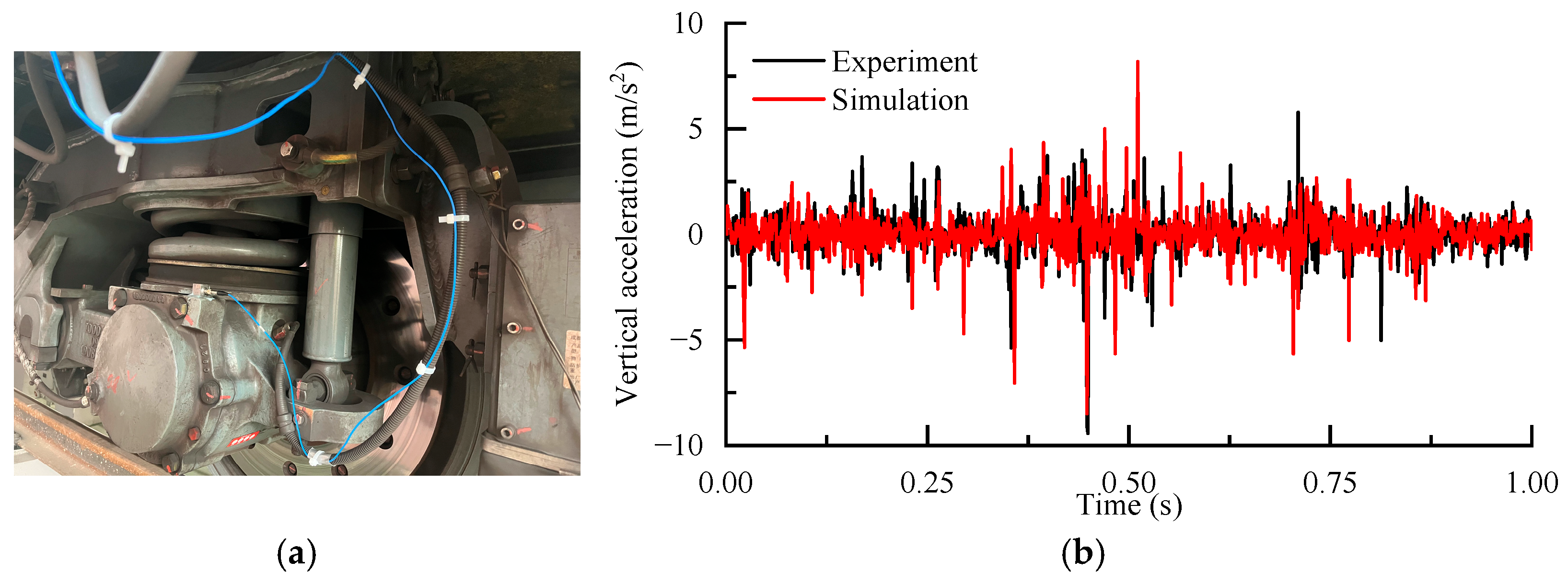
3.2. Model Validation

To validate the model’s accuracy, vibration accelerometers were installed on the metro vehicle’s axle boxes to measure their vibration acceleration. The test results from a straight track section were compared with the simulation model, as shown in Figure 9. The test results demonstrate excellent agreement between the simulation and measurement data. The standard deviation is 1.3 m/s², and the peak error is 0.92 m/s², representing a maximum error of approximately 9.75%. The measured maximum acceleration was 9.42 m/s², while the simulated maximum was 8.50 m/s².

4. Simulation Analysis

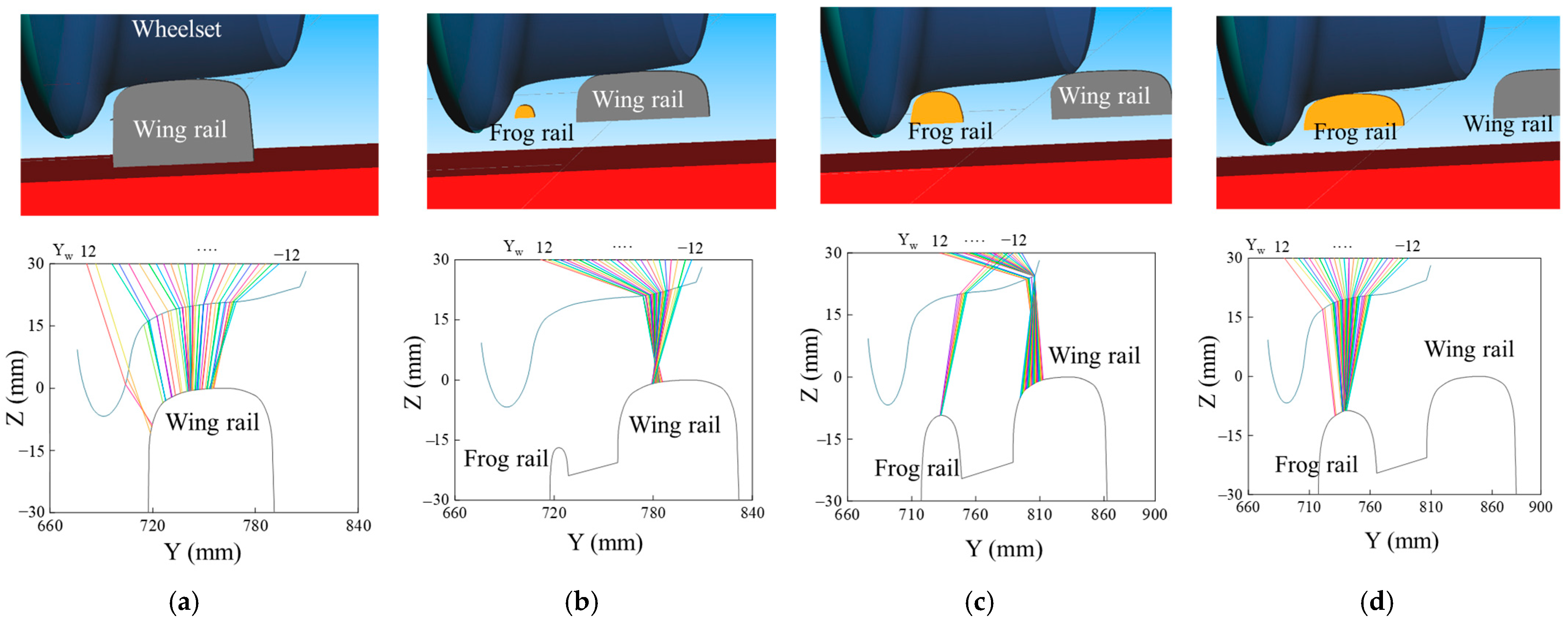
4.1. Wheel–Rail Contact Analysis

The wheel–rail interaction was simulated when the vehicle passed through the turnout zone with the brand-new frog. Figure 10 shows the relative position of the right wheel and rail when the vehicle passes through the frog area. As shown in Figure 10, within the range of d = −1000~0 mm, the wheel–rail contact occurs between the wheelset and the wing rail; within the range of d = 0~400 mm, the right wheel transitions from the wing rail to the frog center and passes through the harmful space. At approximately d = 400 mm, there is a possibility of multi-point contact between the wheel and rail depending on the lateral displacement of the wheelset. At around d = 800 mm, the right wheel has separated from the wing rail. And the right wheel is in contact solely with the frog rail, with the contact point concentrated near the center of the wheel tread.

As the frog wear increases, the equivalent conicity of the wheel tread changes during its transit through the frog area. Figure 11 illustrates the equivalent conicity under different frog wear conditions. Since wheel load transition in a fixed frog typically occurred within the frog nose section—approximately between d = 20 mm and d = 50 mm—the relationship between the equivalent conicity and the frog wear at d = 30 mm was focused on. As shown in Figure 11, the equivalent conicity of the wheel tread increases with the progression of frog rail wear.

4.2. Influence of the Frog Wear on Vehicle Dynamic Performance

A brand-new frog, along with the same frog after 13, 16, and 17 months of service, were used to investigate the influence of the frog wear on the dynamic performance of the vehicle passing through the frog area. In simulation, the LMA tread was adopted as the wheel profile, the loading condition of the vehicle was empty, and the speed was set as 120 km/h.

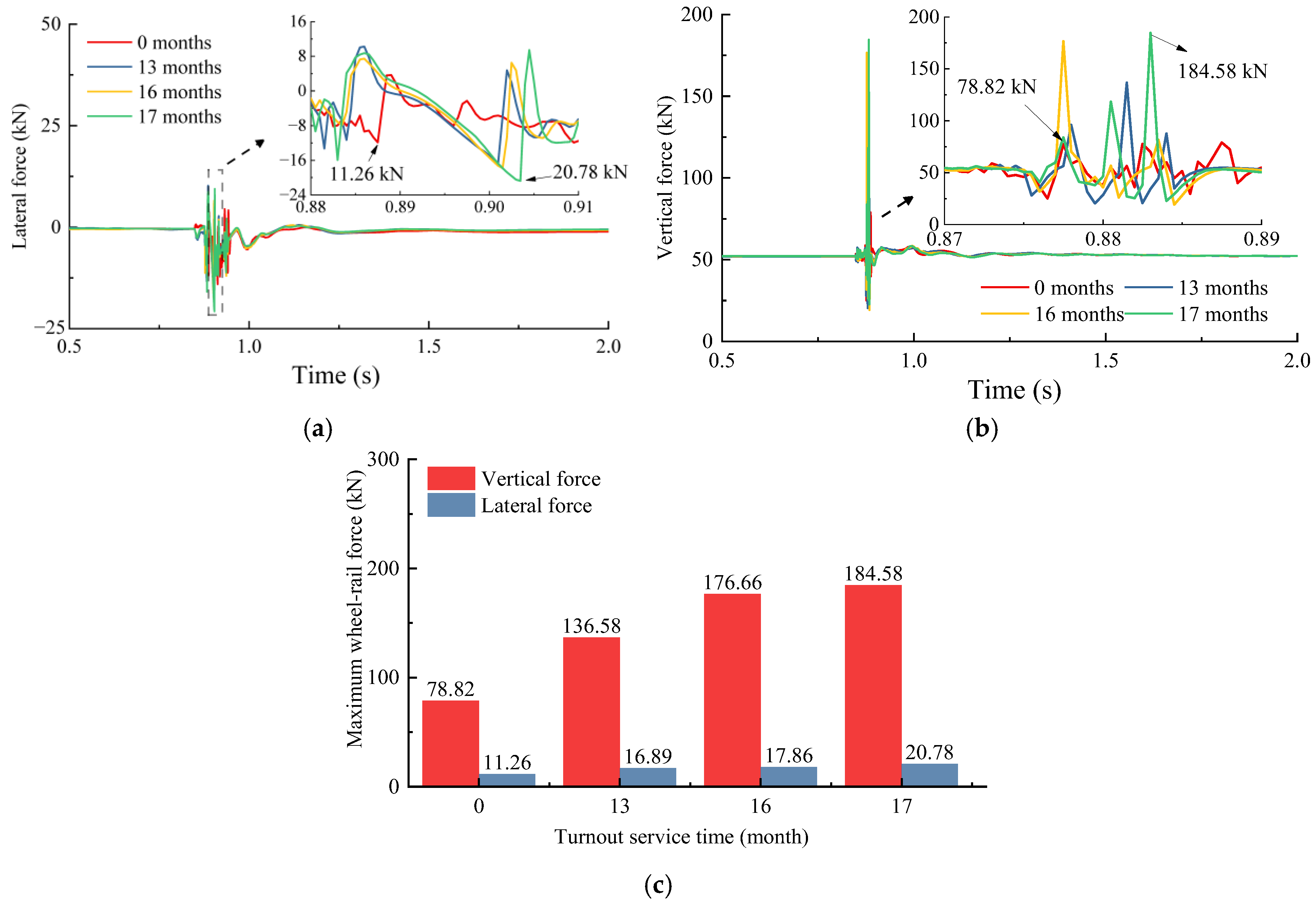
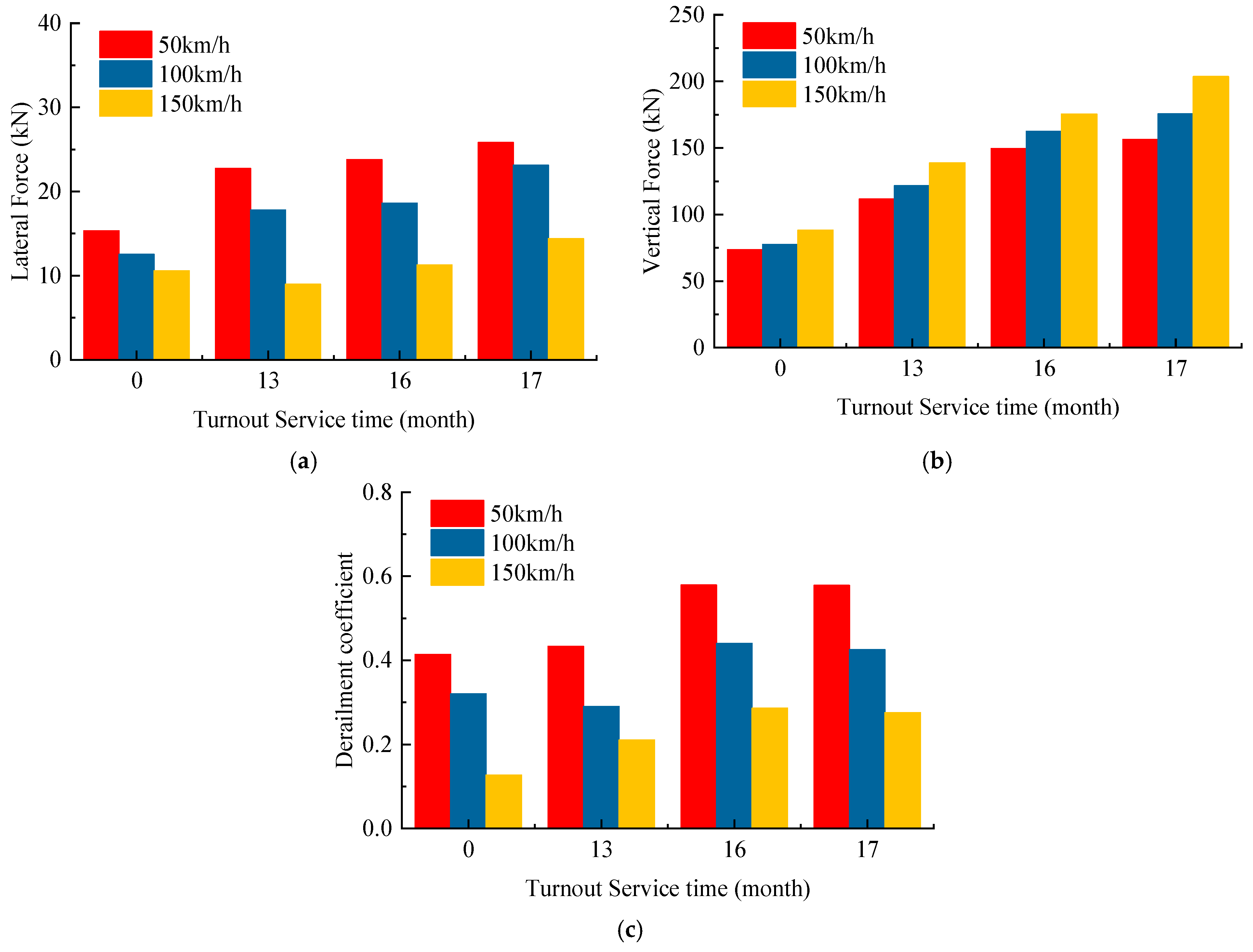
4.2.1. Wheel–Rail Forces

Figure 12 presents wheel–rail forces in the time domain when a vehicle passes through frogs with varying wear levels at 120 km/h. As shown in Figure 12a, the maximum lateral wheel–rail force reaches 20.78 kN when the vehicle passes through the frog worn for 17 months, representing an increase of 9.52 kN over the unworn condition. The trend of wheel–rail forces across different wear stages is summarized in Figure 12c, revealing that both lateral and vertical forces escalate significantly with the increasing service time of the frog.

4.2.2. Dynamic Performance of the Vehicle

Figure 13 shows accelerations of key components of the vehicle. As shown in Figure 13a, the maximum lateral acceleration of the frame when the vehicle passed through the frog area was 1.63 m/s², representing an increase of 0.17 m/s² compared to the brand-new frog condition. Figure 13b,c present the lateral and vertical accelerations of the car body, respectively. Two significant fluctuations were observed on both the lateral and vertical accelerations, corresponding to the moments when the front and trailing bogies passed through the frog area, respectively. The changes in car body accelerations are similar under different conditions, suggesting that frog wear has a limited effect on car body vibrations. Figure 13d presents the derailment coefficient of the vehicle in the time domain. The peak values of derailment coefficients show an overall upward trend accompanied by more pronounced fluctuations as the frog wear progresses. The maximum derailment safety index reached 0.39 when the vehicle passed through the frog that had served for 17 months, representing an increase of 0.14 compared to the brand-new frog condition.

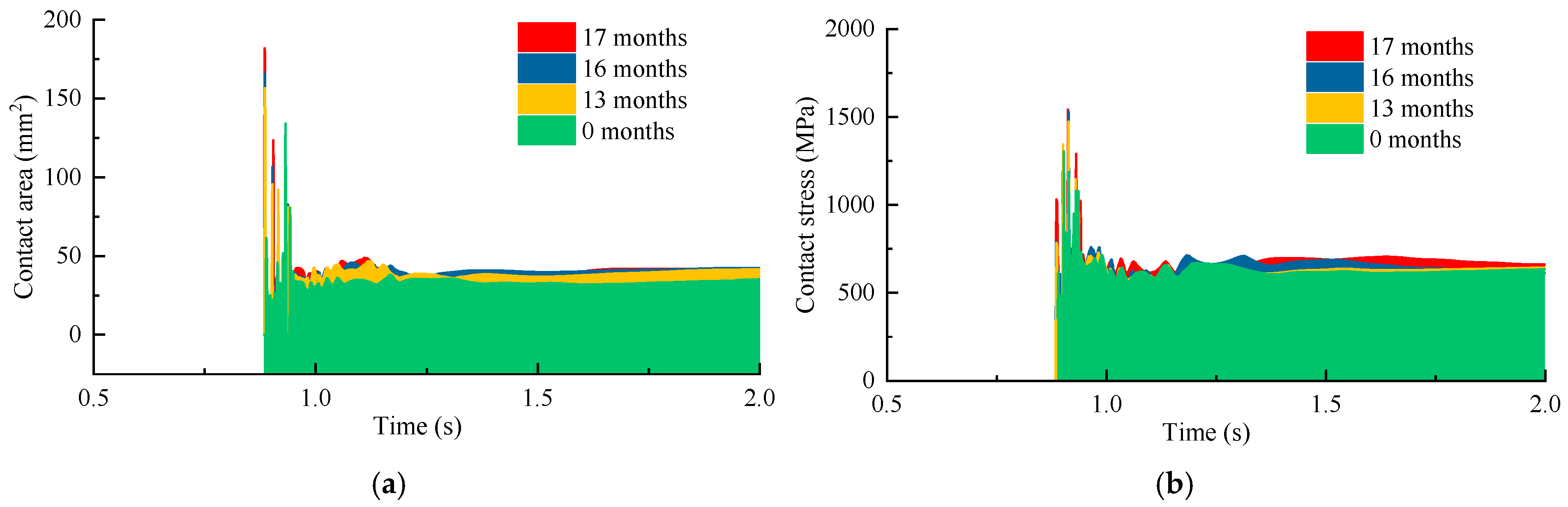
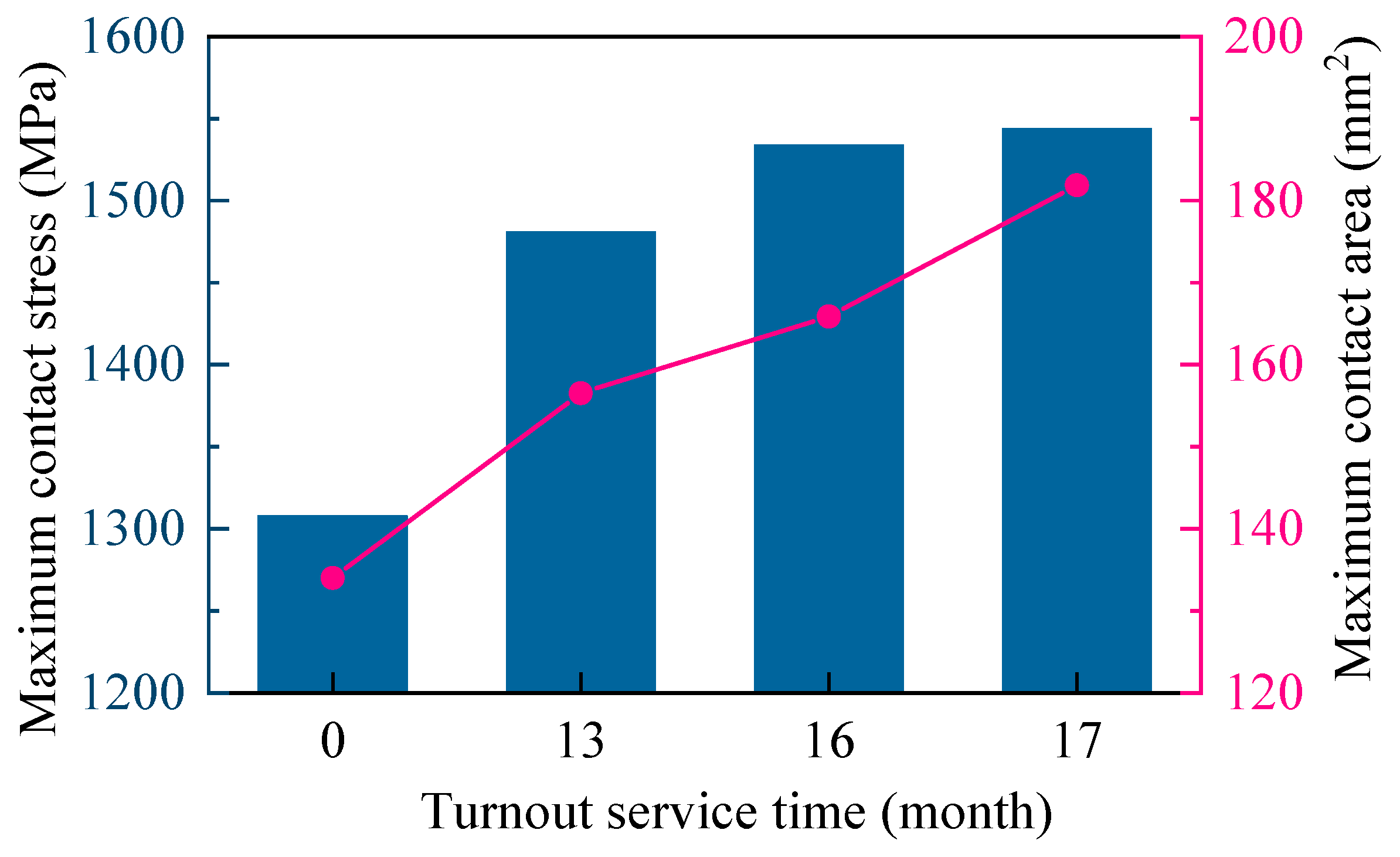
4.2.3. Contact Stress

The variations in contact patches and contact pressure on the frog rail in the time domain when the vehicle traversed the brand-new frog in the reverse direction at a speed of 120 km/h are shown in Figure 14a,b, respectively. The results indicate that the maximum contact patches and contact stresses occur at the wheel load transition zone, and the elevated contact stress is the primary factor contributing to the increasing frog wear.

Figure 15 presents the contact stress distributions within the contact patches under different conditions. The peak contact pressures in the wheel load transition zone were 1308 MPa, 1481 MPa, 1534 MPa, and 1544 MPa, respectively.

Figure 16 demonstrates the trends in the maximum contact pressure and the maximum contact patch area with increasing service duration. Both parameters exhibit an upward trend as wear progresses. After 17 months of operation, compared to the brand-new frog condition, the maximum contact stress increased by 18%, while the contact patch area expanded by 35.73%.

4.3. Influence of Frog Wear on Dynamic Performance of Vehicles Under Different Operating States

To comprehensively analyze the impact of frog wear on the dynamic performance of metro vehicles, simulations were conducted to evaluate dynamic indicators under varying operating speeds and loading conditions. The metro system studied is a high-speed type with a maximum permissible operating speed of 180 km/h. To encompass lower speeds, three operating speeds were selected: low speed, high speed, and ultra-high speed, corresponding to 50 km/h, 100 km/h, and 150 km/h, respectively. Under no-load conditions, the vehicle body mass is approximately 26 t. Under full-load conditions, the loaded vehicle mass is approximately 52 t. Consequently, three loading conditions were considered: empty, medium, and heavy, with corresponding vehicle body masses of 26 t, 39 t, and 52 t. When analyzing the effect of speed, the vehicle mass was held constant at the empty condition. When analyzing the effect of loading, the operating speed was held constant at 100 km/h.

4.3.1. Vehicle Passing Speed

Figure 17 presents the calculated vehicle dynamic performance results under different speeds. Across all speeds, the dynamic indicators increase with greater frog wear. At 50 km/h, after 17 months of frog service, compared to a new frog, the lateral force, vertical force, and derailment coefficient increase from 15.33 kN, 73.68 kN, and 0.41 to 25.82 kN, 156.46 kN, and 0.58, respectively. This represents increases of 10.49 kN (68%), 82.78 kN (112%), and 0.16 (34%). When the speed increases to 150 km/h, the increases in vehicle dynamic indicators for a frog after 17 months of service, compared to a new frog, are 3.81 kN (36%) for lateral force, 115.28 kN (130%) for vertical force, and 0.15 (116%) for derailment coefficient. Evidently, as speed increases, the increase in lateral force diminishes, while the increase in vertical force and derailment coefficient become more pronounced. Additionally, notably, with increasing speed, the maximum lateral force decreases significantly, while the vertical force gradually increases. This leads to a significant reduction in the maximum derailment coefficient. This occurs because higher vehicle speeds make it easier for wheels to traverse the gap at the frog throat (harmful gap). However, the increased speed also intensifies the vertical wheel–rail interaction.

4.3.2. Vehicle Loading Conditions

Figure 18 presents the calculated vehicle dynamic performance results under different loading conditions. Across all the loading conditions, the dynamic indicators increase with greater frog wear. Under empty conditions, after 17 months of frog service, compared to a new frog, the lateral force, vertical force, and derailment coefficient increase from 12.53 kN, 77.52 kN, and 0.32 to 23.12 kN, 175.65 kN, and 0.43, respectively. This represents increases of 10.59 kN (84%), 98.13 kN (126%), and 0.11 (32%). When the vehicle is fully loaded (heavy), the increases in vehicle dynamic indicators for a frog after 17 months of service, compared to a new frog, are 7.39 kN (25%) for lateral force, 128.34 kN (90%) for vertical force, and 0.19 (54%) for derailment coefficient. Evidently, as frog wear increases, heavier vehicle loads correspond to reduced percentage increases in dynamic indicators such as lateral and vertical wheel–rail forces. Conversely, the percentage increase in the derailment coefficient becomes larger. Additionally, higher vehicle loads cause all the dynamic indicators to increase substantially. For a frog after 17 months of service, the vertical force for a fully loaded vehicle increases from 141.47 kN to 269.82 kN, exceeding the safety standard limit of 250 kN. Therefore, for a metro operating speed of 100 km/h, the inspection and maintenance cycle for metro turnouts must not exceed 16 months. For higher operating speeds, the maintenance cycle needs to be further shortened. Consequently, it is recommended that turnouts undergo inspection and maintenance every 12 to 16 months.

5. Conclusions

This study investigates the influence of frog wear on the dynamic performance of the vehicle based on measured wheel/rail profiles. A vehicle–turnout coupled dynamics model was developed using the multibody dynamics software SIMPACK to analyze the dynamic responses and wheel–rail interaction when trains traverse turnouts with varying degrees of wear. The key findings are summarized as follows:

• With increased service time, the wear of the frog gradually deepens. After 13 months of service, the wear reaches 1.31 mm, and after 17 months, it increases by an additional 0.11 mm. The primary wear occurs in the region located 500 mm behind the frog point.
• The wheel–rail contact state undergoes significant variation as the vehicle enters the frog area. Initially, the wheel contacts the wing rail at the mid-region of the tread. Within the flangeway gap, both the tread and flange back of the wheel interact with the gauge corner and inner face of the wing rail, respectively. After passing over the frog point, the wheel contacts both the frog and the right rail simultaneously, leading to a high-stress concentration at the primary contact location, which is prone to frog damage. Subsequently, the wheel is fully supported by the railhead, and the contact state improves.
• When a vehicle passes over a frog with 17 months of wear at 120 km/h, compared to a new frog, the maximum lateral wheel–rail force increases by 9.52 kN, the maximum vertical force increases by 105.76 kN, the derailment coefficient increases by up to 0.14, the peak lateral acceleration of the car body rises by 0.17 m/s², the maximum contact pressure increases by 236 MPa, and the contact patch area expands by 35.73%. As speed increases, the magnitude of the increase in lateral force diminishes, while the magnitudes of the increases in vertical force and derailment coefficient become more pronounced. Additionally, with increasing speed, the maximum lateral force itself decreases significantly, while the vertical force gradually increases. This results in a significant reduction in the maximum derailment coefficient.
• Under different vehicle loading conditions, all dynamic indicators increase with greater frog wear. As frog wear increases, heavier vehicle loads correspond to reduced percentage increases in dynamic indicators such as lateral and vertical wheel–rail forces. Conversely, the percentage increase in the derailment coefficient becomes larger. Furthermore, higher vehicle loads cause substantial increases in all dynamic indicators. After 17 months of turnout service, the vertical force for a fully loaded vehicle increases from 141.47 kN to 269.82 kN, exceeding the safety standard limit. For high-speed metro systems, it is recommended that turnouts undergo inspection and maintenance every 12 to 16 months.