Study on the Characteristics of CO2 Displacing Non-Newtonian Fluids
Abstract
1. Introduction
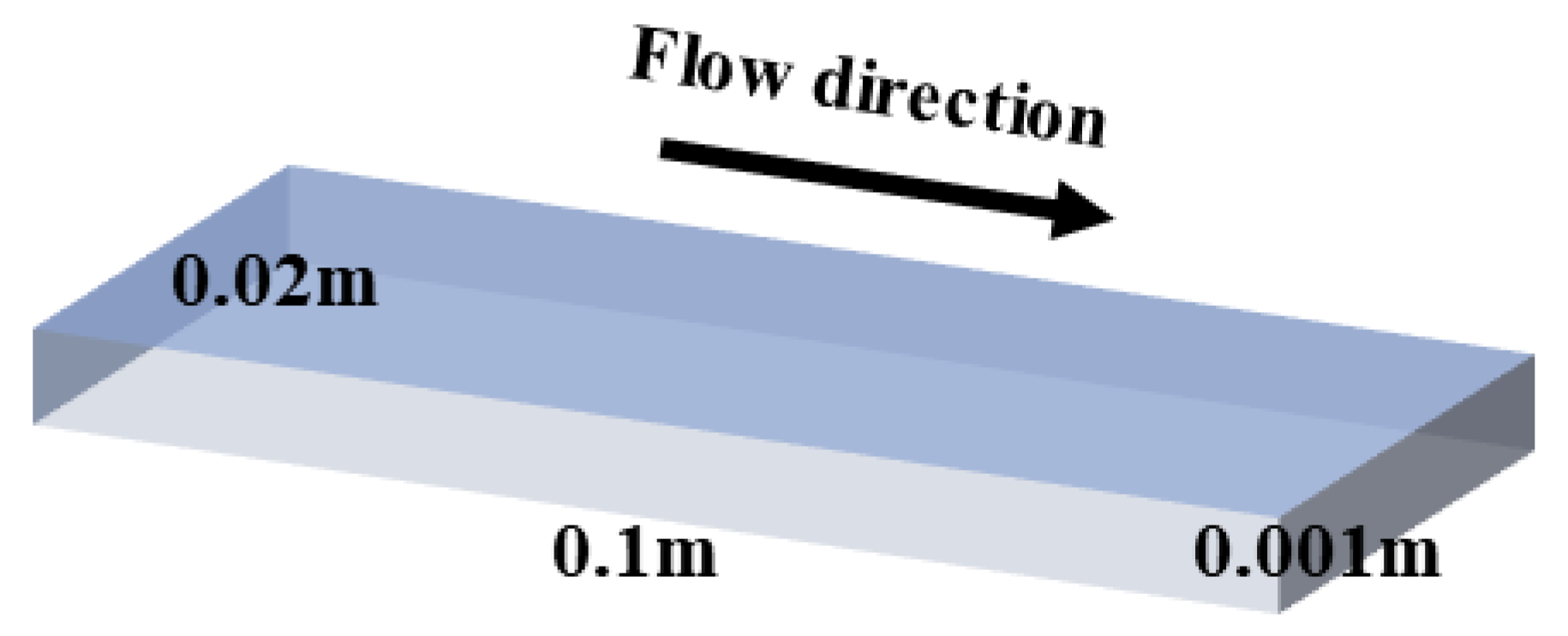
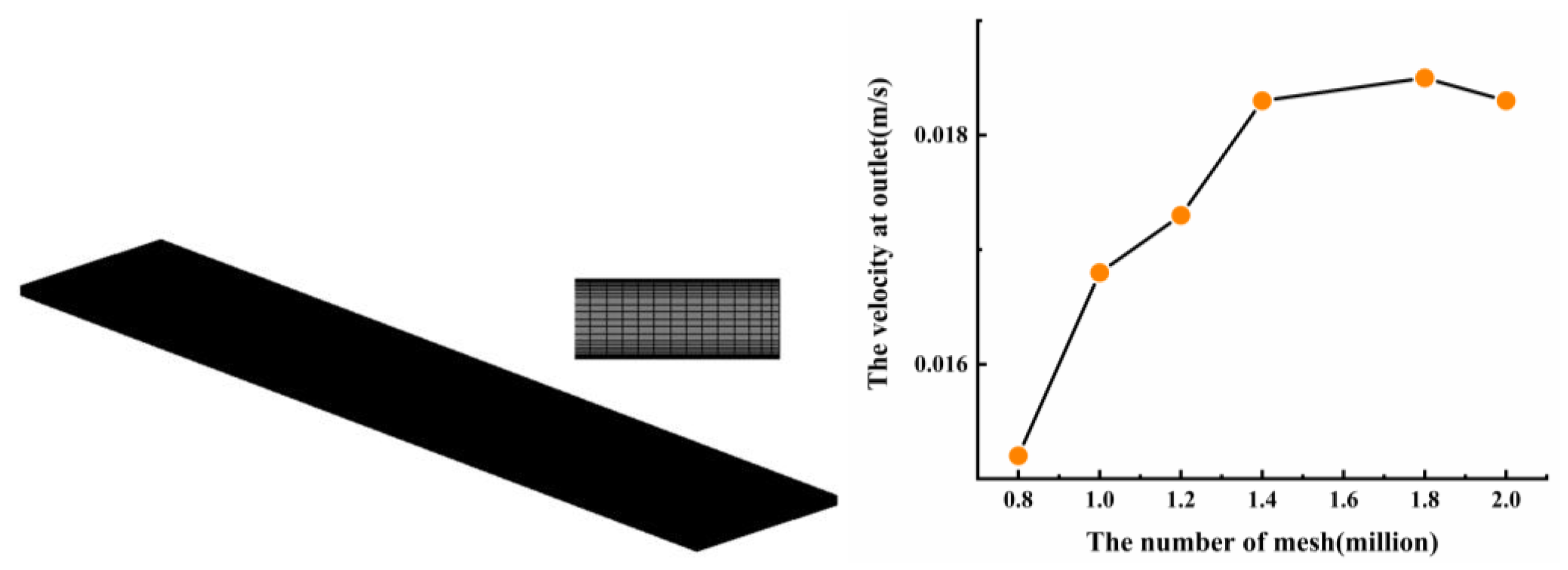
2. Numerical Method
3. Comparative Analysis of Air and CO2 Displacing Non-Newtonian Fluids
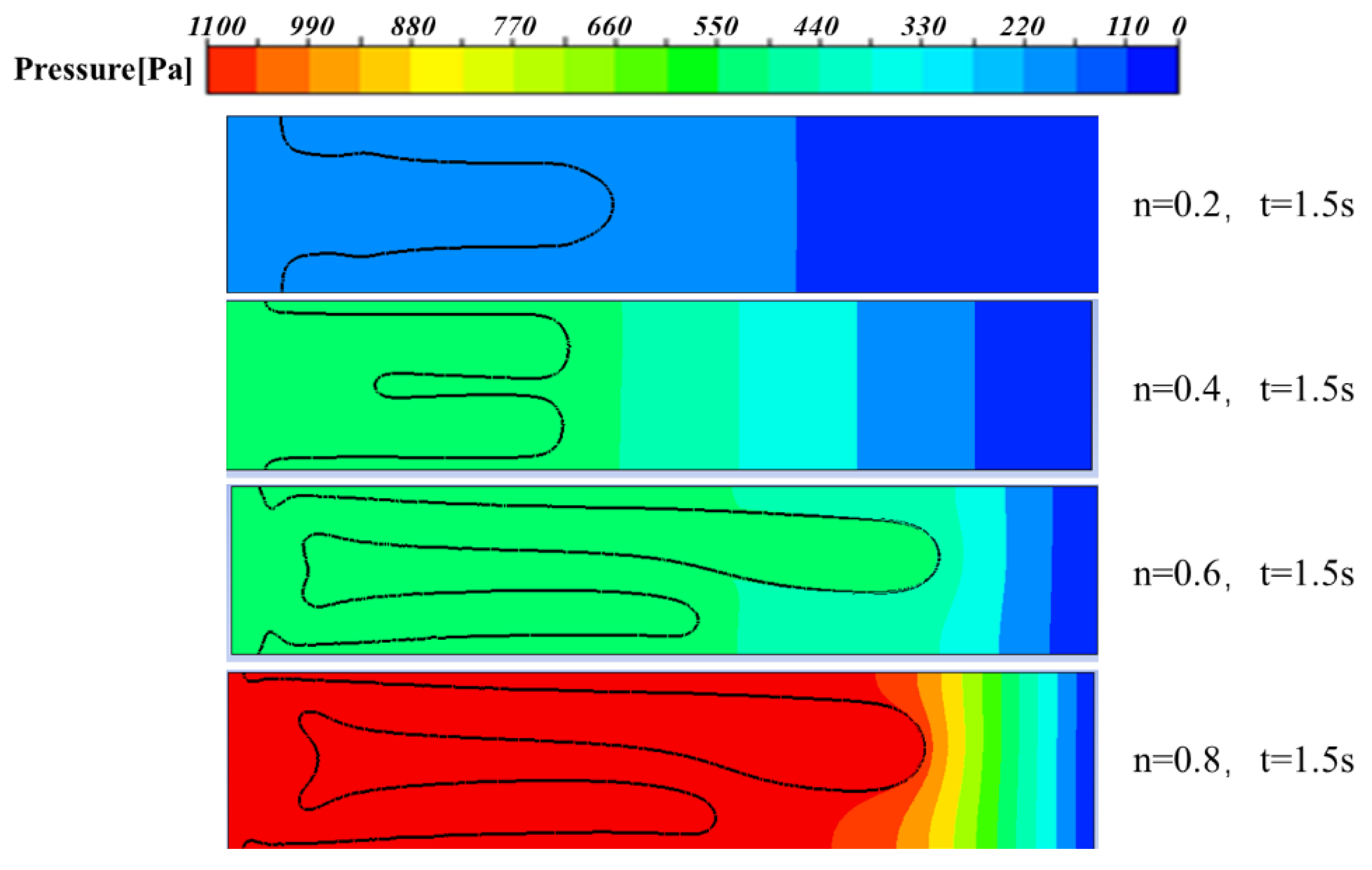
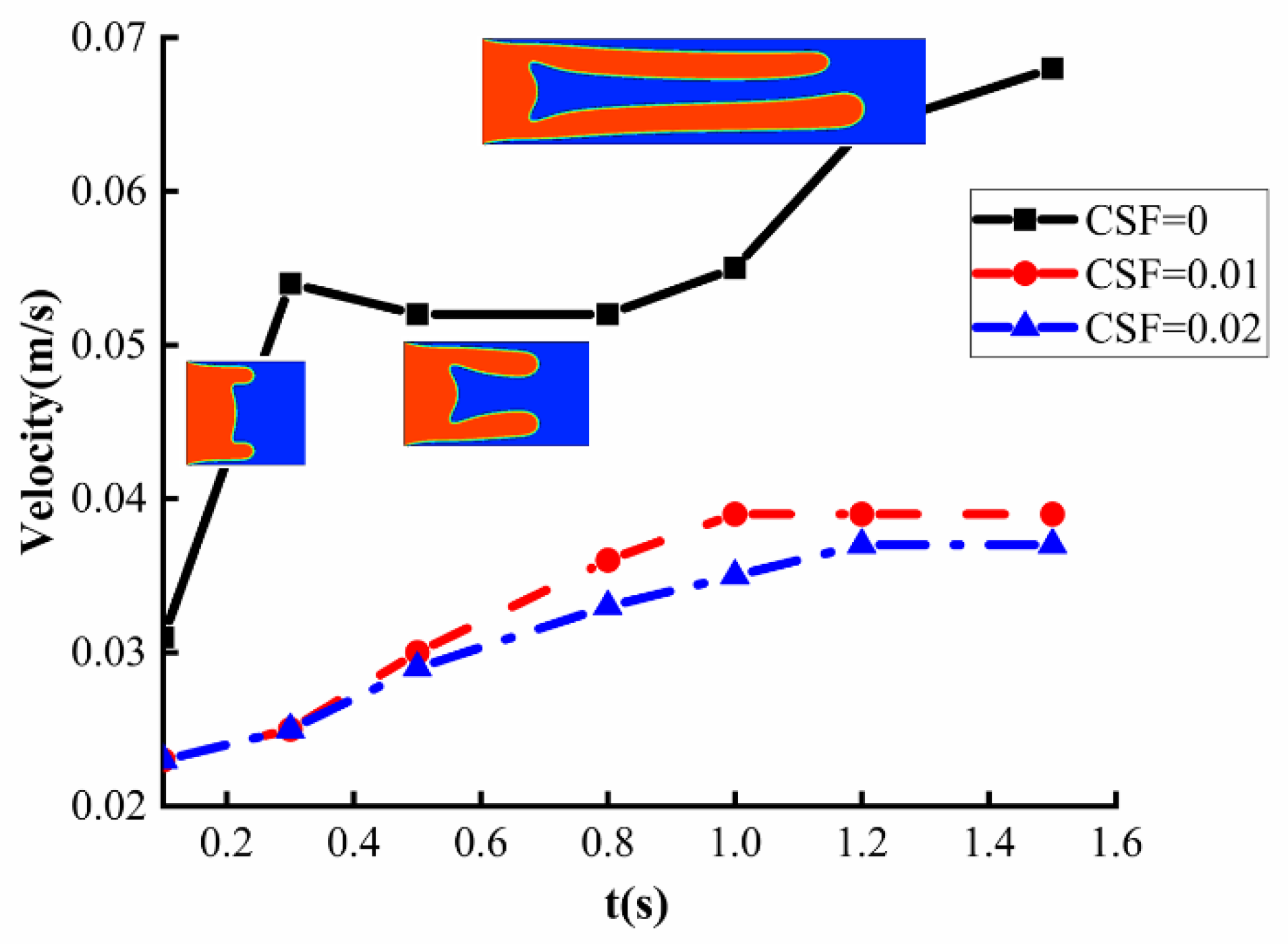
4. CO2 Displaces Shear-Thinning Fluids with Different Properties
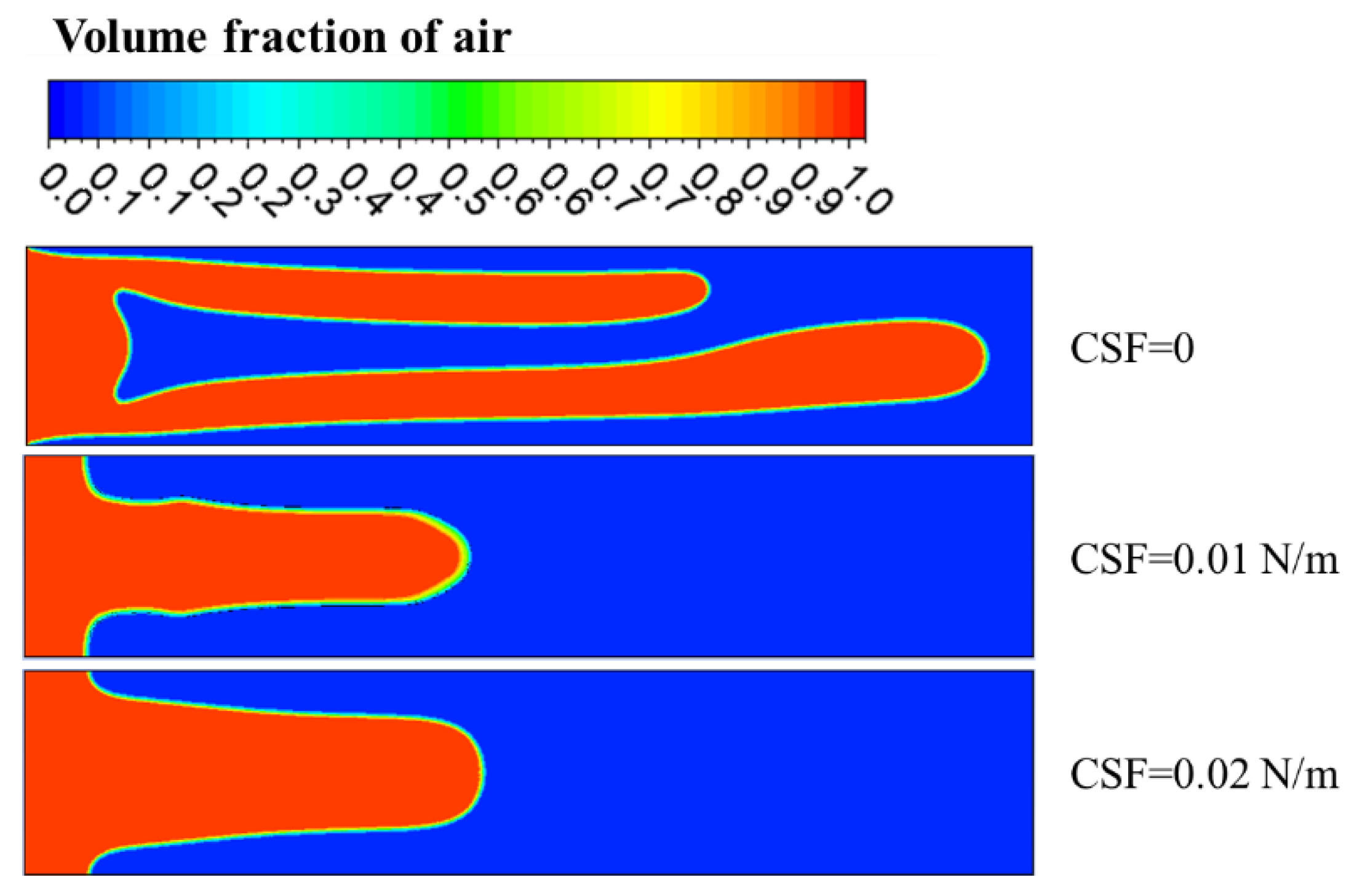
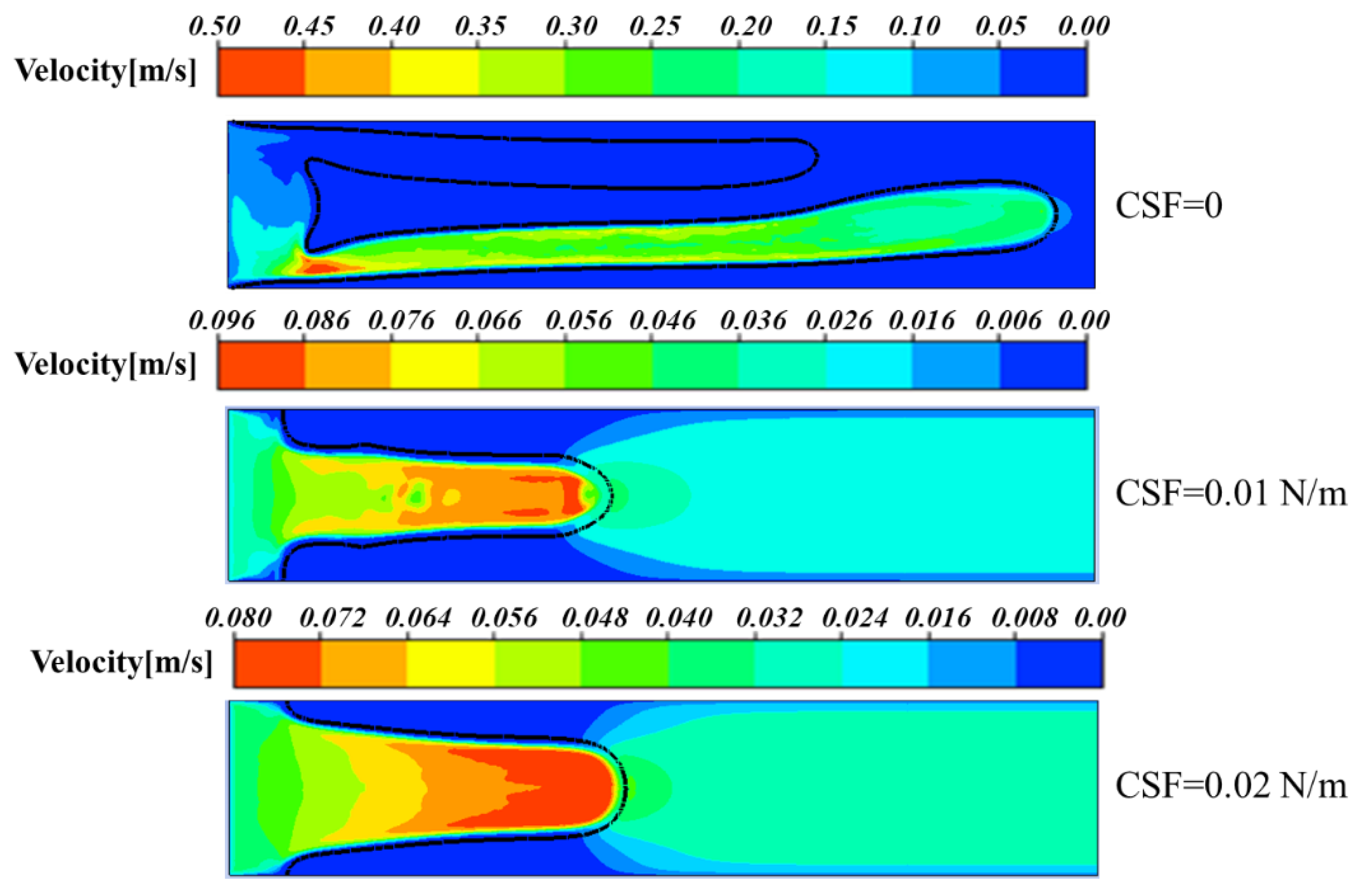
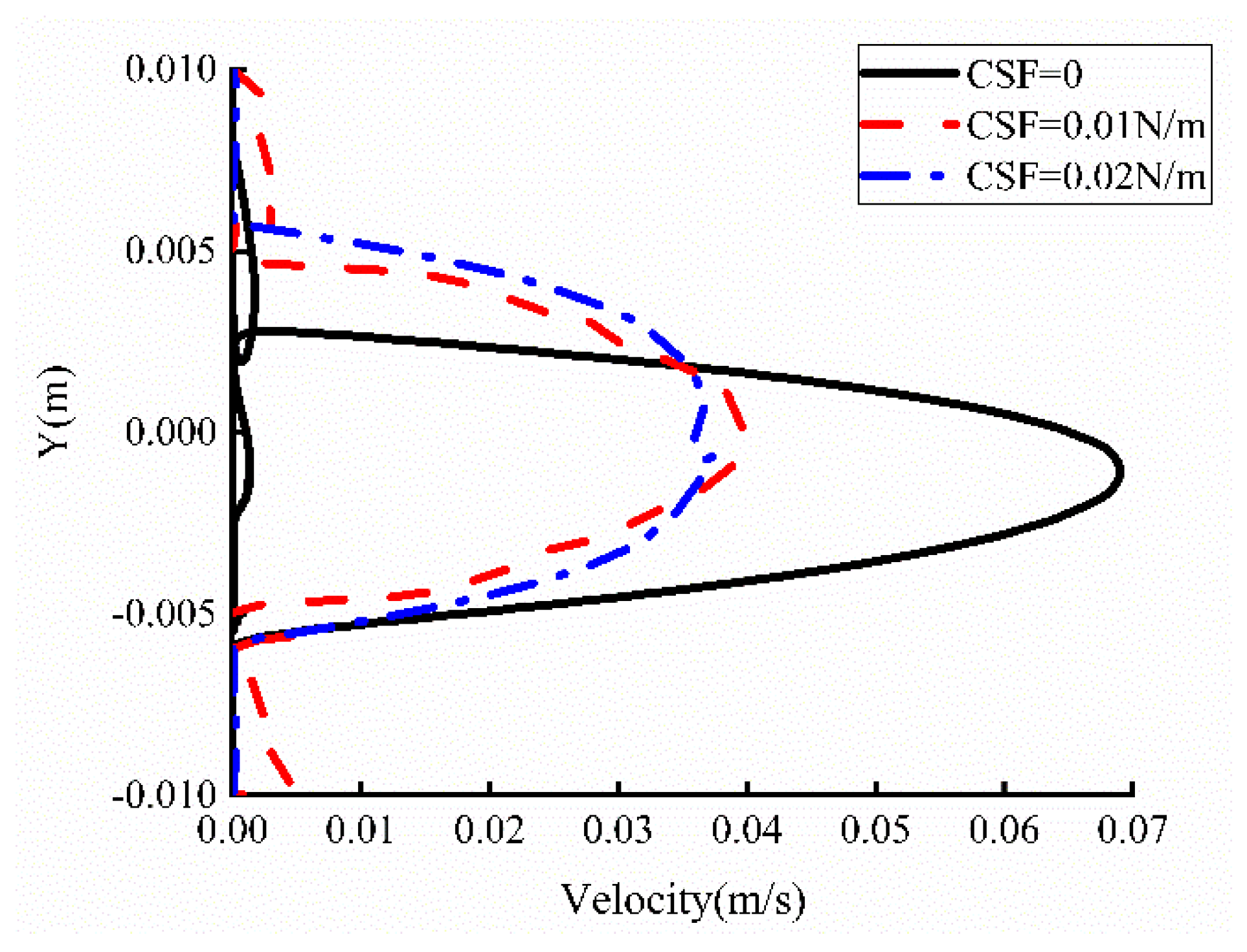
5. Properties of Shear-Thinning Fluids Displaced by CO2 Under Different Interfacial Tensions
6. Conclusions
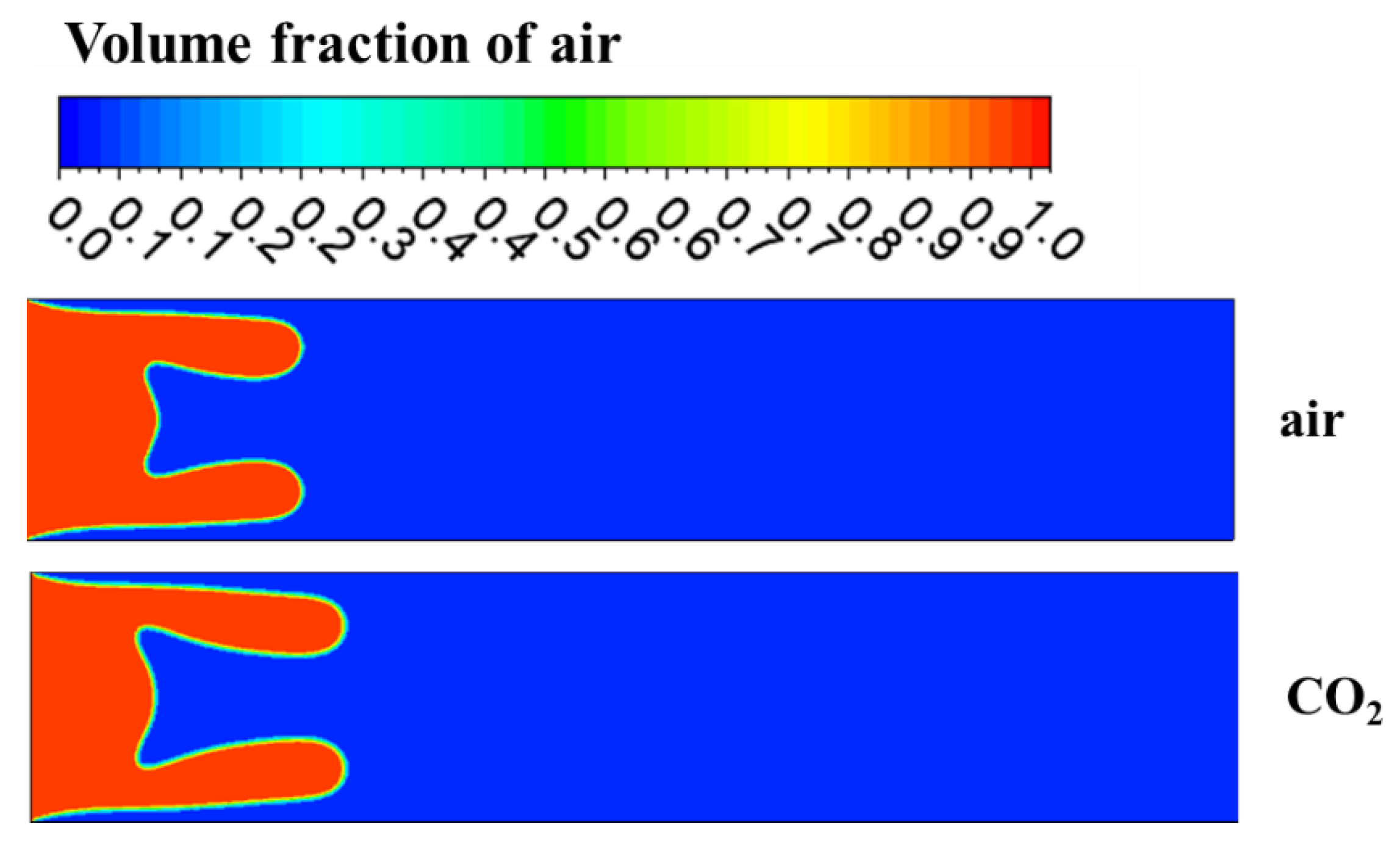
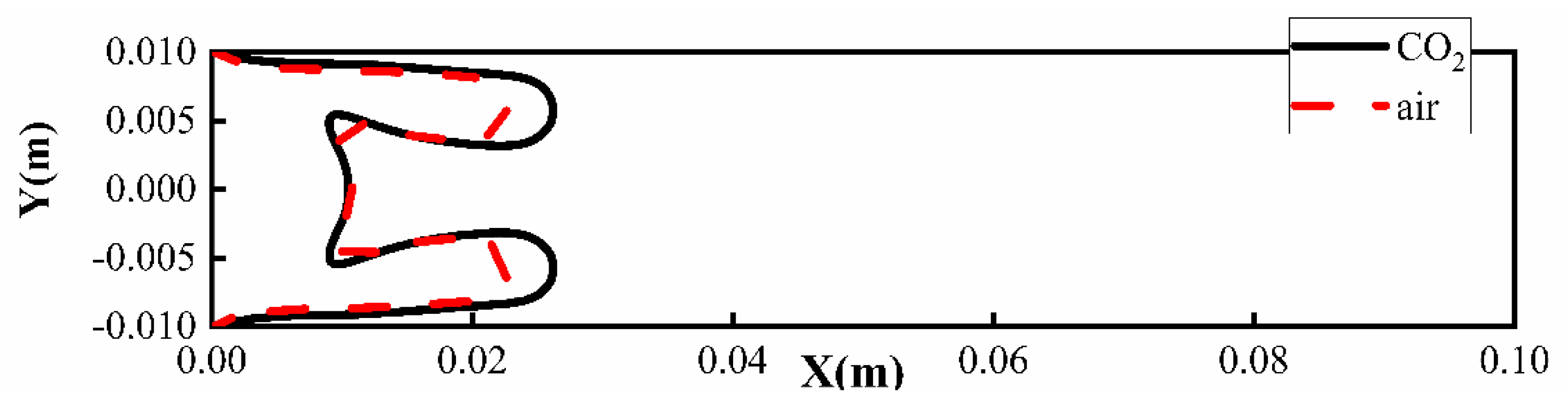
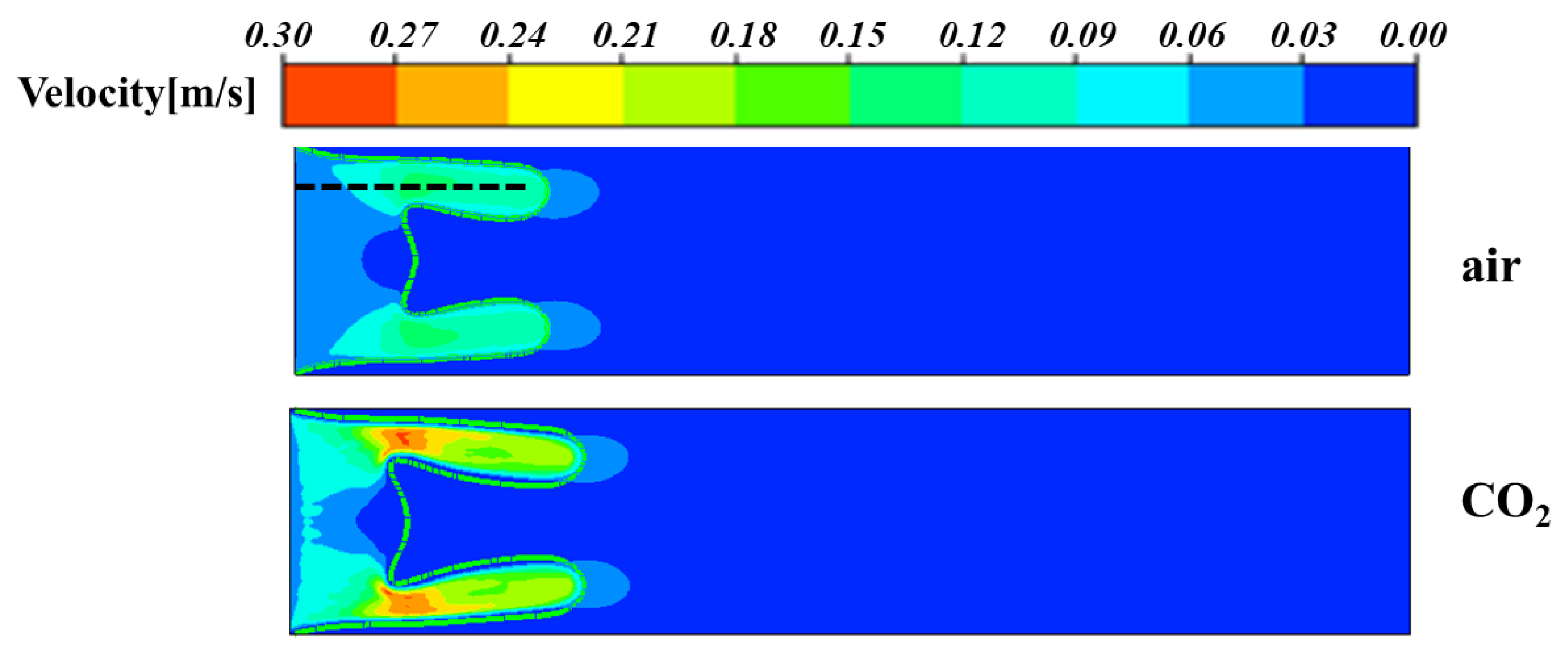
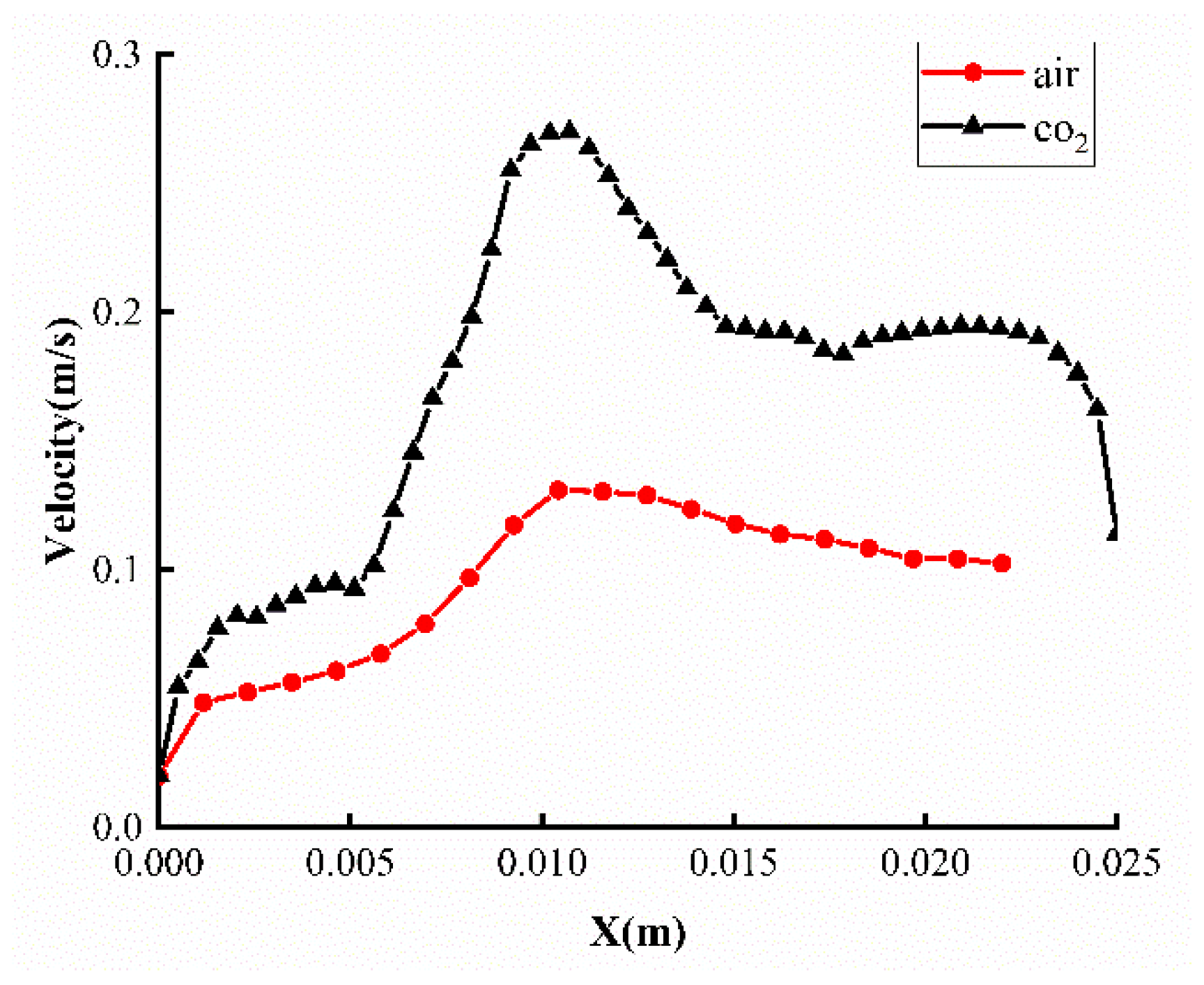
- For both air and CO2 as displacing fluids, branching occurs during displacement, forming symmetrical upper and lower fingers. Throughout the fingering structures, velocities under CO2 displacement exceed those under air displacement. This is attributed to CO2’s ability to significantly reduce crude oil viscosity through dissolution and swelling effects. The shear-thinning effect further diminishes flow resistance in high-velocity channels, enhancing flow velocity. Consequently, viscous fingering under CO2 displacement propagates farther, achieving higher displacement efficiency compared to air displacement.
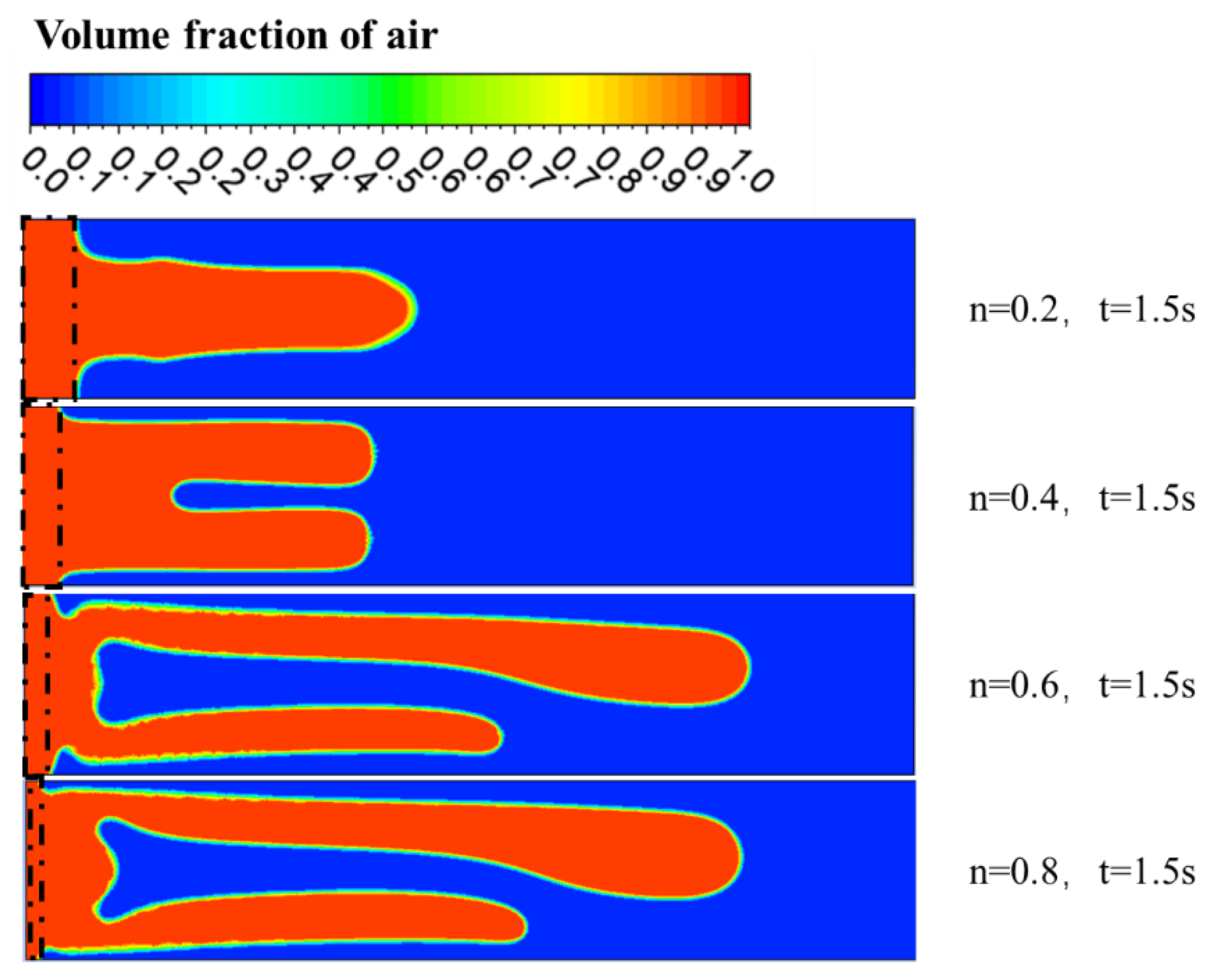
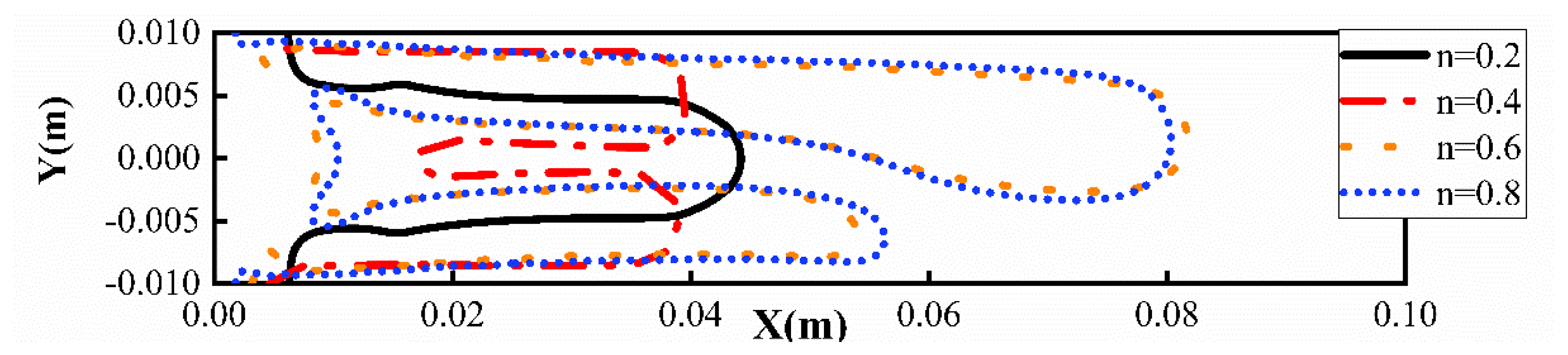
- The shear-thinning behavior of non-Newtonian fluids significantly impacts CO2 displacement processes. Enhanced shear-thinning behavior improves interface stability and weakens viscous fingering instability. Concurrently, fingering root thickness increases with shear-thinning intensity, peaking at , which minimizes residual displaced fluid in the displacement zone. This arises from amplified viscosity heterogeneity and elevated viscosity ratios under lower n, which intensify fingering prominence.
- For varying interfacial tensions, it is observed that increasing interfacial tension enhances interface stability. When interfacial tension is a minimum, which is , viscous fingering becomes highly pronounced, with two elongated fingers displacing fluid near the upper and lower plates. In contrast, at N/m, a single, smooth coherent finger forms without bifurcation tendencies. This demonstrates that interfacial tension effectively suppresses short-wavelength perturbations through curvature-driven restoring forces, high-wavenumber dependencies in the dispersion relation, and energy dissipation mechanisms.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Homsy, G.M. Viscous Fingering in Porous Media. Annu. Rev. Fluid Mech. 1987, 19, 271–311. [Google Scholar] [CrossRef]
- Wooding, R.A.; Morel-Seytoux, H.J. Multiphase fluid flow through porous media. Annu. Rev. Fluid Mech. 1976, 8, 233–274. [Google Scholar] [CrossRef]
- Bensimon, D.; Kadanoff, L.P.; Liang, S.; Shraiman, B.I.; Tang, C. Viscous flows in two dimensions. Rev. Mod. Phys. 1986, 58, 977–999. [Google Scholar] [CrossRef]
- Chen, X.L.; Li, Y.Q.; Liao, G.Z.; Zhang, C.M.; Xu, S.Z.; Qi, H.; Tang, X. Experimental investigation on stable displacement mechanism and oil recovery enhancement of oxygen-reduced air assisted gravity drainage. Pet. Explor. Dev. 2020, 47, 836–845. [Google Scholar] [CrossRef]
- Tsai, M.C.; Wei, S.Y.; Fang, L.; Chen, Y.-C. Viscous fingering as a rapid 3D Pattering Technique for Engineering Cell-Laden Vascular-Like Constructs. Adv. Healthc. Mater. 2022, 11, e2101392. [Google Scholar] [CrossRef]
- Grotberg, J.; Jensen, O. Biofluid mechanics in flexible tubes. Annu. Rev. Fluid Mech. 2004, 36, 121–147. [Google Scholar] [CrossRef]
- Huh, D.; Fujioka, H.; Tung, Y.-C.; Futai, N.; Paine, R.; Grotberg, J.B.; Takayama, S. Acoustically detectable cellular-level lung injury induced by fluid mechanical stresses in microfluidic airway systems. Proc. Natl. Acad. Sci. USA 2007, 104, 18886–18891. [Google Scholar] [CrossRef]
- Nadirah, L.; Abdurahman, H.; Rizauddin, D. Rheological study of petroleum fluid and oil-in-water emulsion. Int. J. Eng. Sci. Res. Technol. 2014, 3, 129–134. [Google Scholar]
- Gorell, S.B.; Homsy, G.M. A Theory of the Optimal Policy of Oil Recovery by Secondary Displacement Processes. SIAM J. Appl. Math. 1983, 43, 79–98. [Google Scholar] [CrossRef]
- Orr, F.M.; Taber, J.J. Use of Carbon Dioxide in Enhanced Oil Recovery. Science 1984, 224, 563–569. [Google Scholar] [CrossRef]
- Jha, B.; Cueto-Felgueroso, L.; Juanes, R. Fluid Mixing from Viscous Fingering. Phys. Rev. Lett. 2011, 106, 194502. [Google Scholar] [CrossRef] [PubMed]
- Saffman, P.G.; Taylor, G.I. The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1958, 245, 312–329. [Google Scholar]
- Dong, B.; Yan, Y.Y.; Li, W.; Song, Y. Lattice Boltzmann simulation of viscous fingering phenomenon of immiscible fluids displacement in a channel. Comput. Fluids 2010, 39, 768–779. [Google Scholar] [CrossRef]
- He, A.; Belmonte, A. Inertial effects on viscous fingering in the complex plane. J. Fluid Mech. 2011, 668, 436–445. [Google Scholar] [CrossRef]
- Al-Housseiny, T.T.; Tsai, P.A.; Stone, H.A. Control of interfacial instabilities using flow geometry. Nat. Phys. 2012, 8, 747–750. [Google Scholar] [CrossRef]
- Kang, Q.; Zhang, D.; Chen, S. Immiscible displacement in a channel: Simulations of fingering in two dimensions. Adv. Water Resour. 2004, 27, 13–22. [Google Scholar] [CrossRef]
- Shi, Y.; Tang, G.H. Simulation of Newtonian and non-Newtonian rheology behavior of viscous fingering in channels by the lattice Boltzmann method. Comput. Math. Appl. 2014, 68, 1279–1291. [Google Scholar] [CrossRef]
- Rabbani, H.S.; Or, D.; Liu, Y.; Lai, C.-Y.; Lu, N.B.; Datta, S.S.; Stone, H.A.; Shokri, N. Suppressing viscous fingering in structured porous media. Proc. Natl. Acad. Sci. USA 2018, 115, 4833–4838. [Google Scholar] [CrossRef] [PubMed]
- Zhao, B.; Mohanty, K.K. Effect of wettability on immiscible viscous fingering in porous media. J. Pet. Sci. Eng. 2019, 174, 738–746. [Google Scholar] [CrossRef]
- Zhang, J.H.; Luo, J.; Qu, S.X.; Liu, Z.H. Experimental Simulation and Multifractal Investigation of Viscous Fingering Phenomena. Bull. Sci. Technol. 1998, 8–13. [Google Scholar]
- Redapangu, P.R.; Vanka, S.P.; Sahu, K.C. Multiphase lattice Boltzmann simulations of buoyancy-induced flow of two immiscible fluids with different viscosities. Eur. J. Mech. B Fluids 2012, 34, 105–114. [Google Scholar] [CrossRef]
- Bakharev, F.; Campoli, L.; Enin, A.; Matveenko, S.; Petrova, Y.; Tikhomirov, S.; Yakovlev, A. Numerical Investigation of Viscous Fingering Phenomenon for Raw Field Data. Transp. Porous Media 2020, 132, 443–464. [Google Scholar] [CrossRef]
- Azaiez, J.; Singh, B. Stability of Miscible Displacements of Shear-Thinning Fluids in a Hele-Shaw Cell. Phys. Fluids 2002, 14, 1557–1571. [Google Scholar] [CrossRef]
- Logvinov, O.A. Viscous fingering in poorly miscible power-law fluids. Phys. Fluids 2022, 34, 063105. [Google Scholar] [CrossRef]
- Qin, Z.; Wu, Y.T.; Ma, C.; Lyu, S.K. Effect of power law on viscous fingering behavior of shear-thinning fluid in a lifted hele-shaw cell. J. Mech. Sci. Technol. 2023, 37, 3555–3562. [Google Scholar] [CrossRef]
- Mafi, M.; Qin, Z.; Wu, Y.; Lyu, S.K.; Ma, C. Research on the Interfacial Instability of Non-Newtonian Fluid Displacement Using Flow Geometry. Coatings 2023, 13, 1848. [Google Scholar] [CrossRef]
- Yang, X.; Tang, Y.; Li, M.; Li, C.; Wang, M.; Li, X.; Zhao, J. Effect of shear-thinning of non-Newtonian fluid on the crossover from capillary fingering to viscous fingering in porous media. Phys. Lett. A 2022, 449, 128364. [Google Scholar] [CrossRef]
- Singh, A.; Pandey, K.M.; Singh, Y. CFD analysis of viscous fingering in hele-shaw cell for air-glycerin system. Mater. Today Proc. 2021, 45, 6381–6385. [Google Scholar] [CrossRef]
- Wu, Y.T.; Qin, Z.; Ma, H.; Lyu, S.K. Numerical study on the characteristics of viscous fingering during the displacement process of non-Newtonian fluid. PLoS ONE 2024, 19, e0309176. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.-T.; Lyu, S.-K.; Qin, Z.; Qin, Y.; Qiao, H.; Li, B. Study on the Characteristics of CO2 Displacing Non-Newtonian Fluids. Lubricants 2025, 13, 300. https://doi.org/10.3390/lubricants13070300
Wu Y-T, Lyu S-K, Qin Z, Qin Y, Qiao H, Li B. Study on the Characteristics of CO2 Displacing Non-Newtonian Fluids. Lubricants. 2025; 13(7):300. https://doi.org/10.3390/lubricants13070300
Chicago/Turabian StyleWu, Yu-Ting, Sung-Ki Lyu, Zhen Qin, Yanjun Qin, Hua Qiao, and Bing Li. 2025. "Study on the Characteristics of CO2 Displacing Non-Newtonian Fluids" Lubricants 13, no. 7: 300. https://doi.org/10.3390/lubricants13070300
APA StyleWu, Y.-T., Lyu, S.-K., Qin, Z., Qin, Y., Qiao, H., & Li, B. (2025). Study on the Characteristics of CO2 Displacing Non-Newtonian Fluids. Lubricants, 13(7), 300. https://doi.org/10.3390/lubricants13070300




