Single-Step Drilling Using Novel Modified Drill Bits Under Dry, Water, and Kerosene Conditions and Optimization of Process Parameters via MOGA-ANN and RSM
Abstract
1. Introduction
2. Materials and Methods
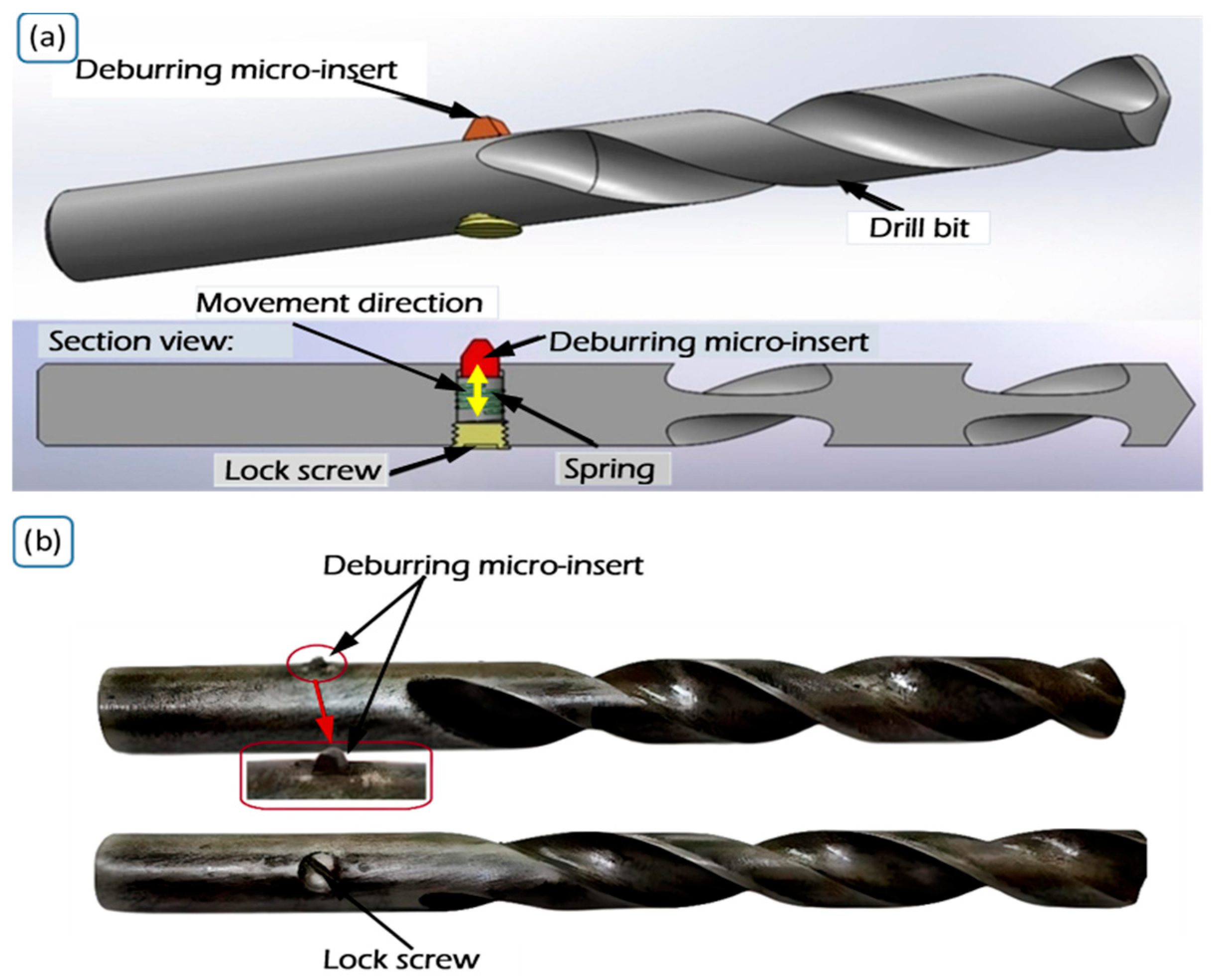
2.1. Modified-1: With a Deburring Micro-Insert Fitted Inside the Twist Drill Bit
Working Principle of Modified-1 Drill Bit with Deburring Micro-Insert
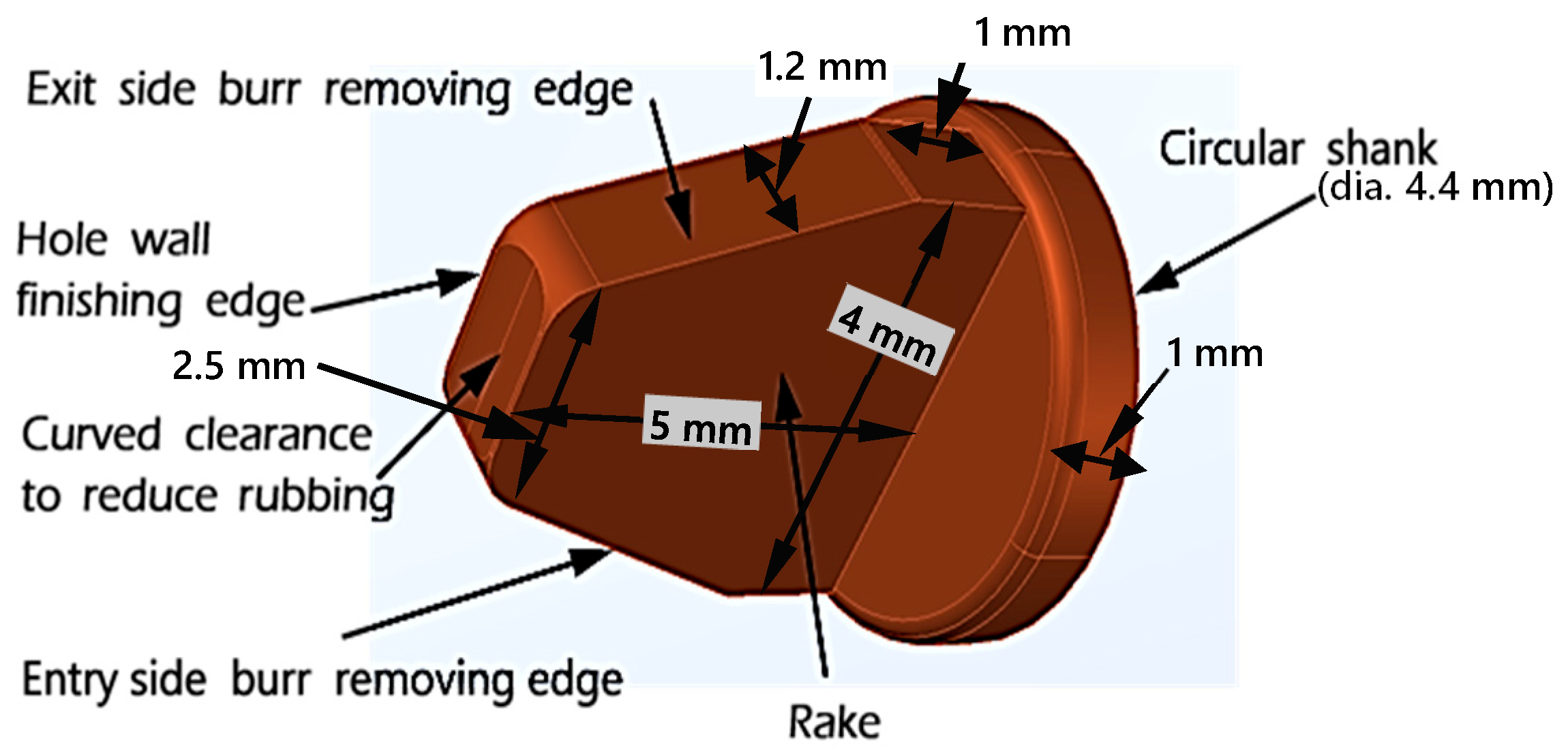
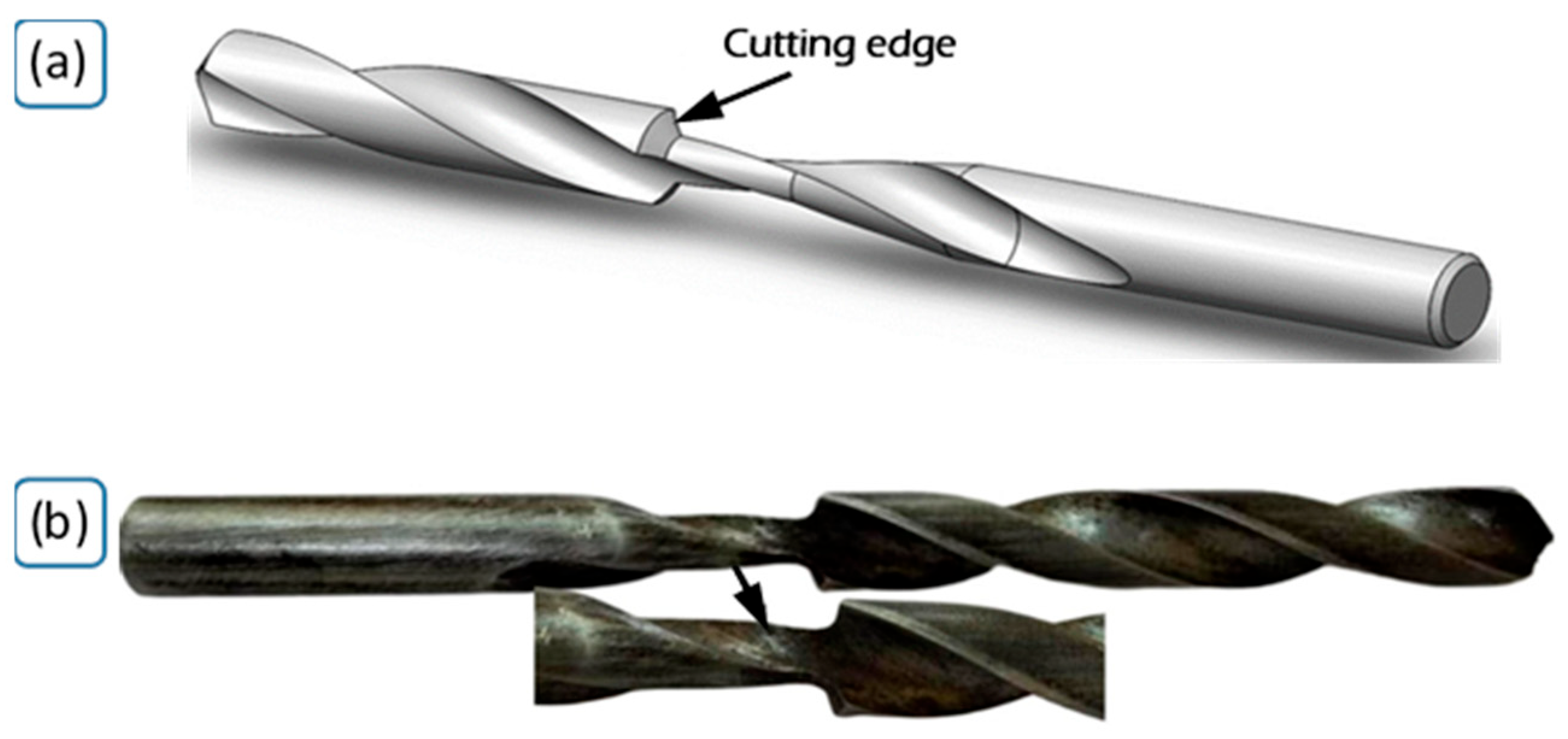
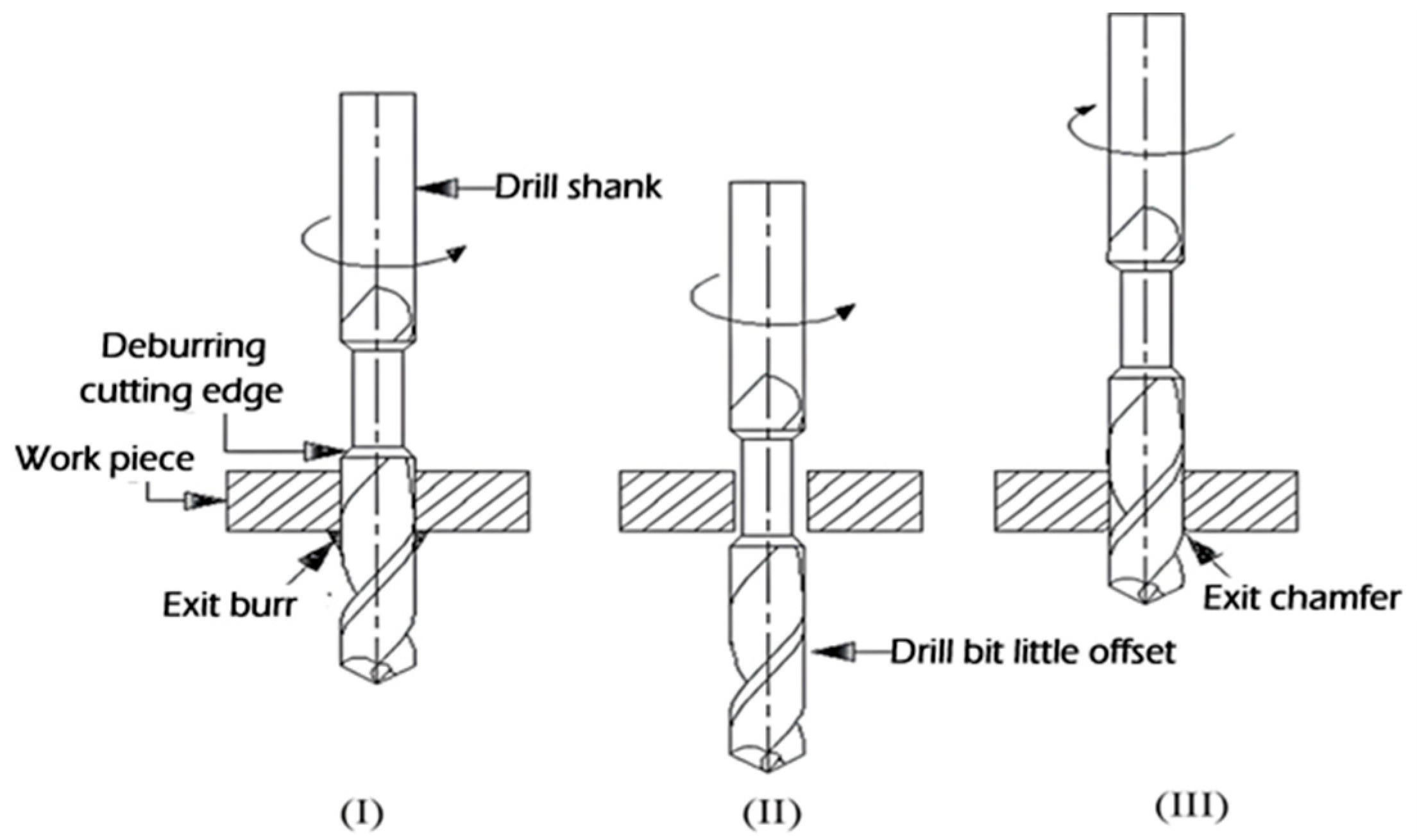
2.2. Modified-2: Drill Bit with Additional Cutting Edge
Working Principle of Modified-2 Drill Bit
2.3. Experimental Details
2.3.1. Design Parameters with Their Levels
2.3.2. Measurement Methods
2.4. Multi-Response Optimization
2.4.1. Response Surface Methodology
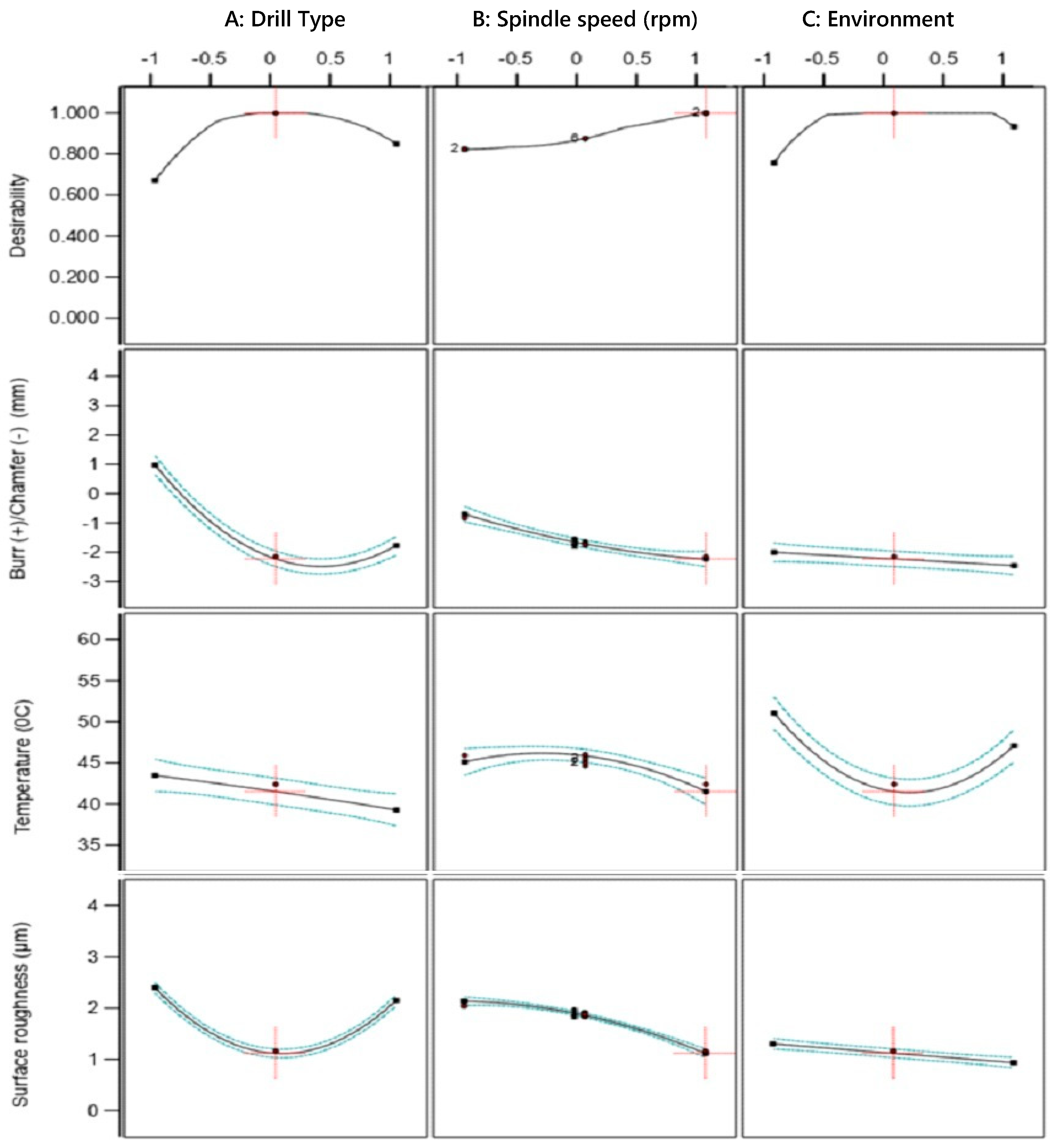
2.4.2. Desirability Function Analysis
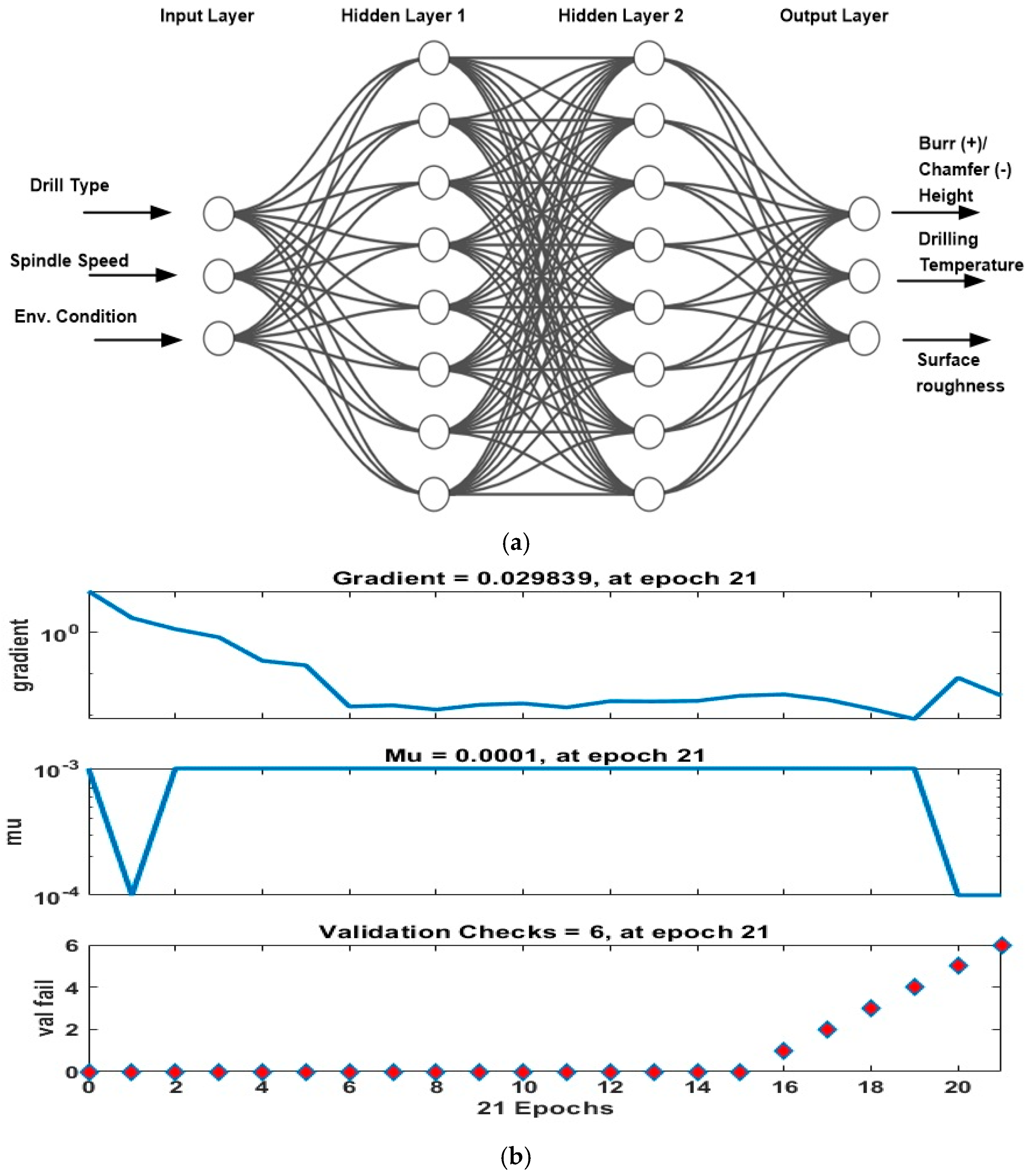
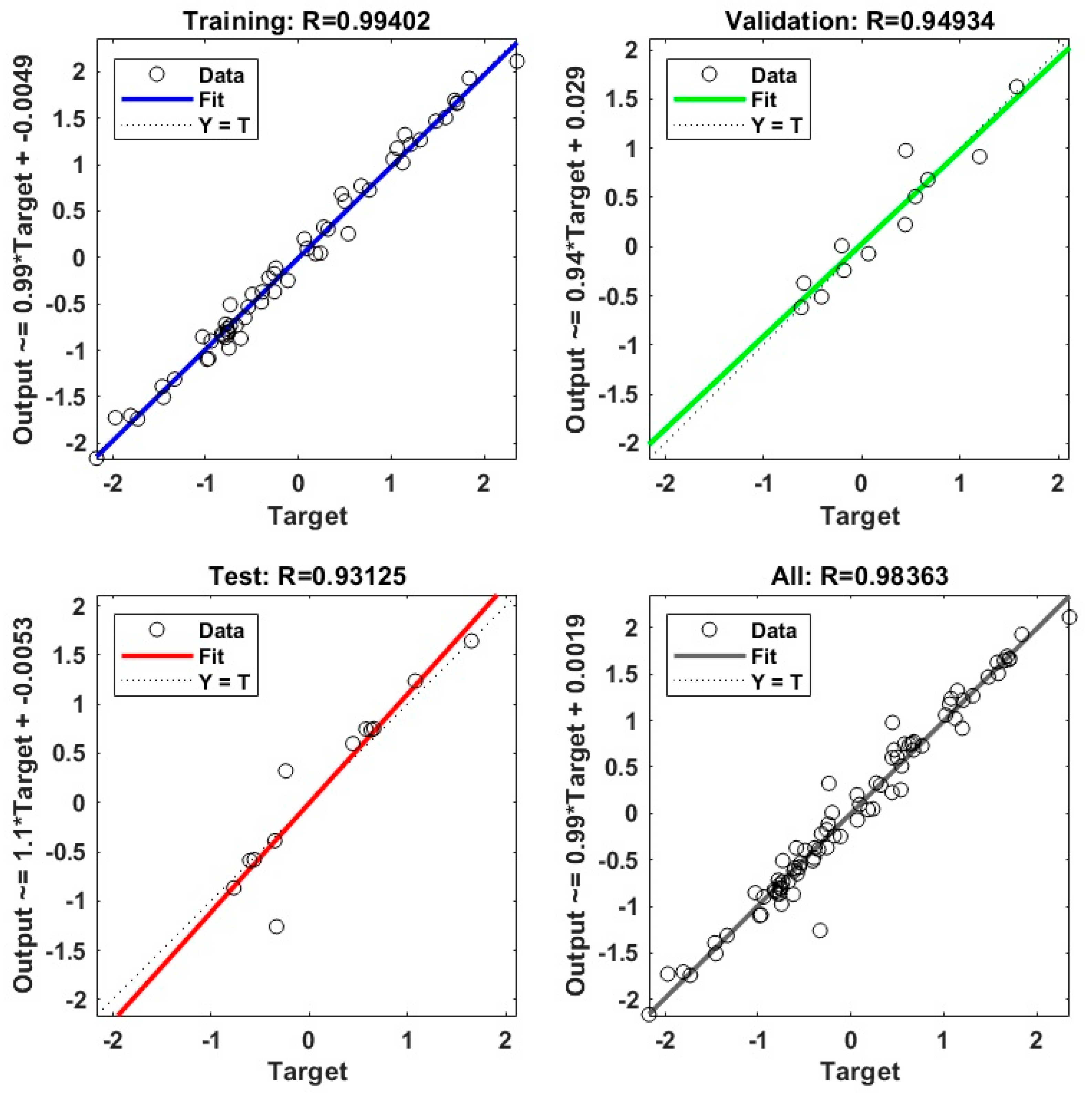
2.4.3. Artificial Neural Networks
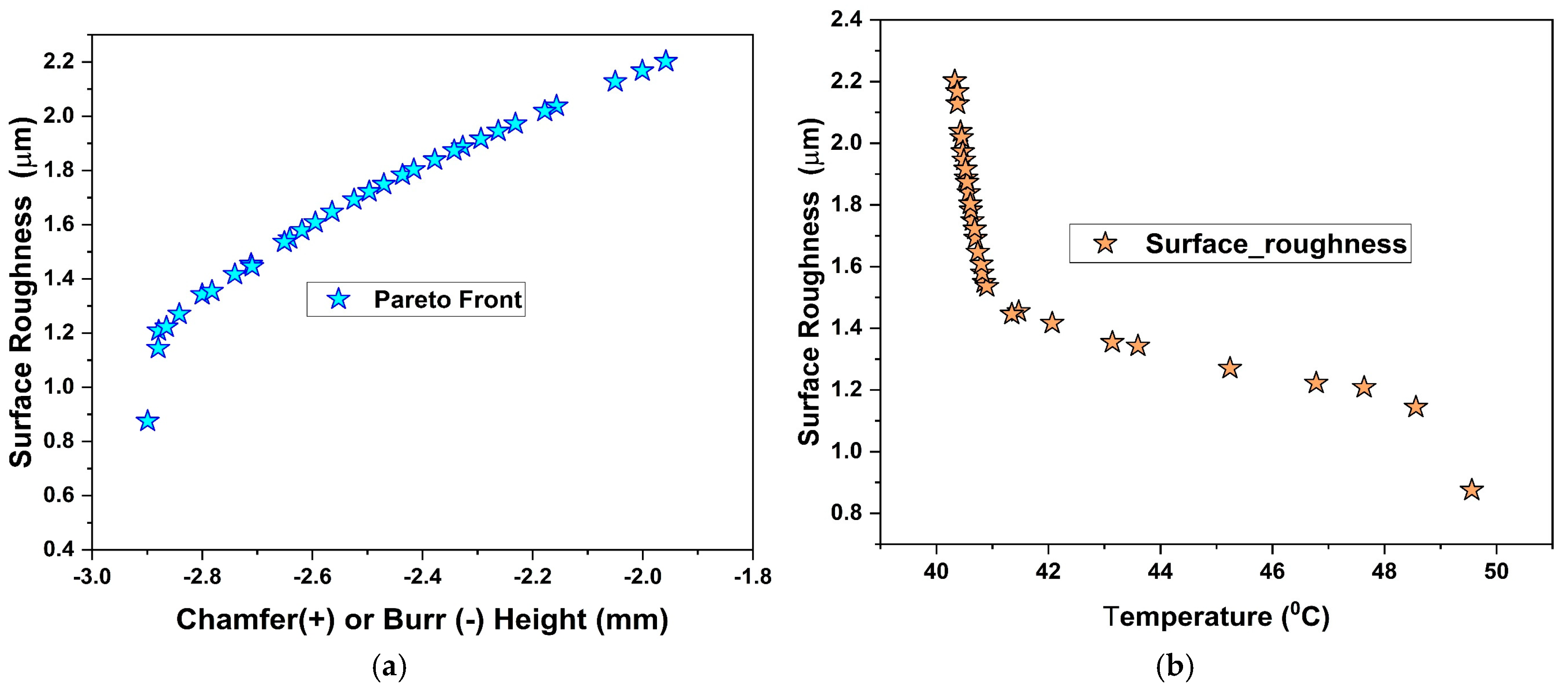
2.4.4. MOGA Analysis
- z1 = min (burr height (positive)/chamfer height (negative));
- z2 = min (drilling temperature);
- z3 = min (surface roughness).
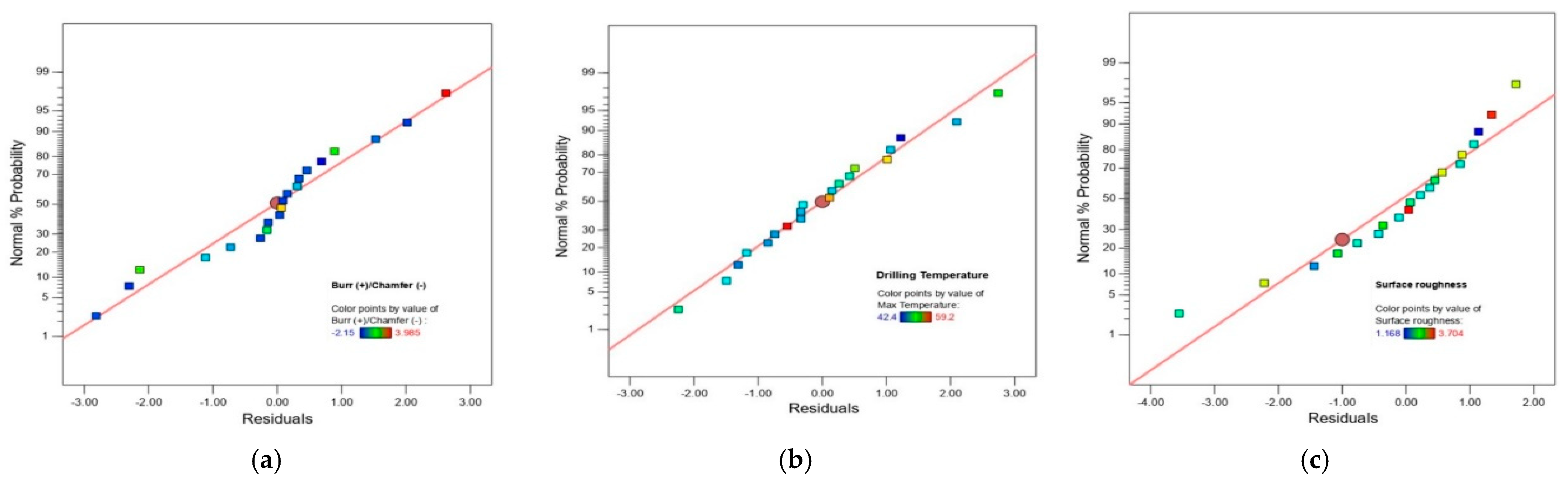
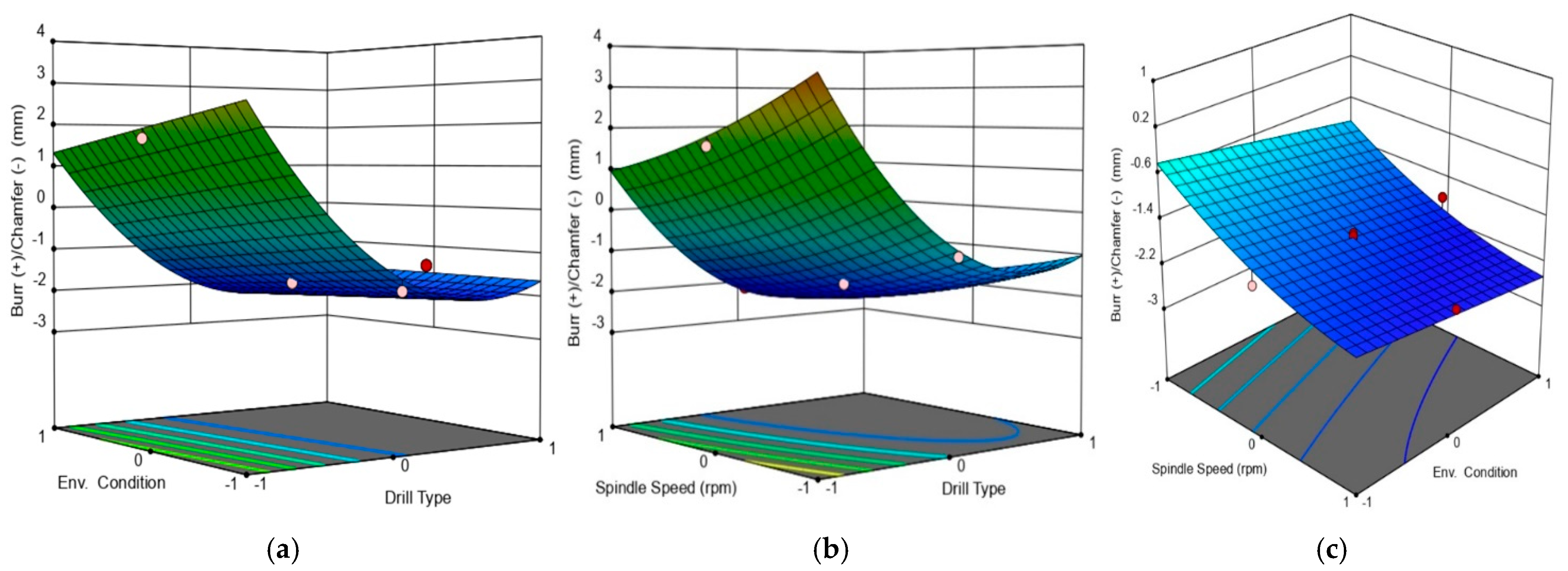
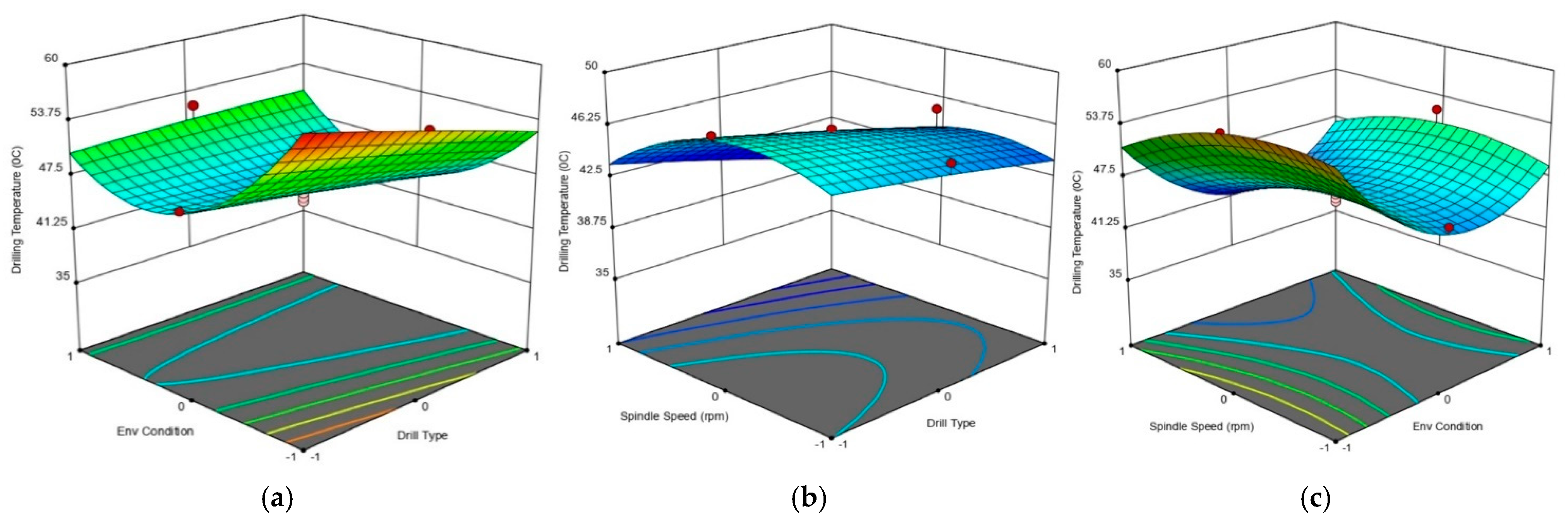
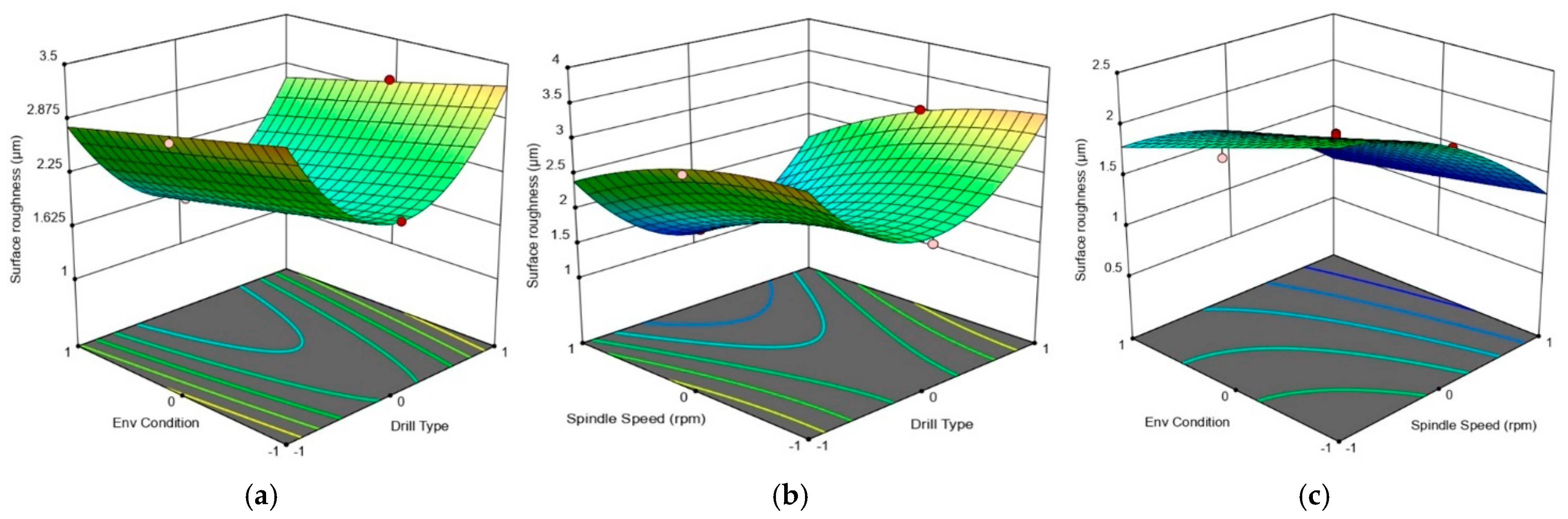
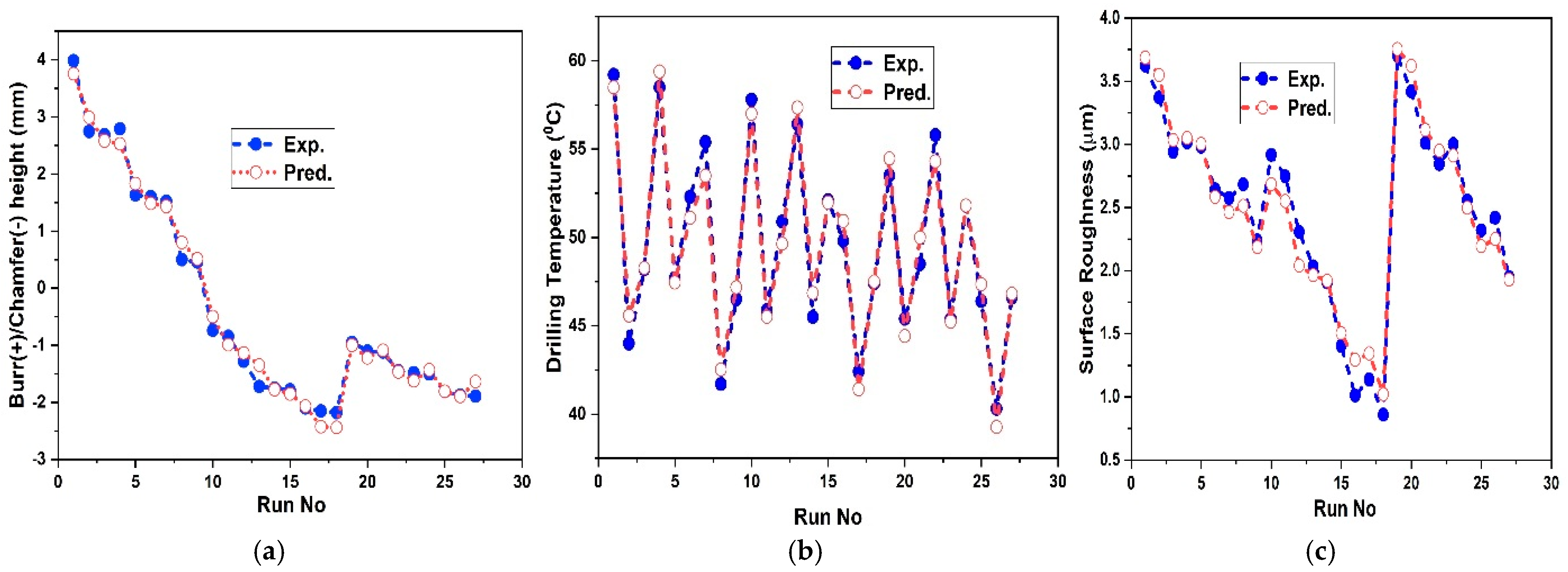
3. Results and Discussion
4. Conclusions
- Two modified drill bits were developed for single-pass burr-free drilling, with Modified-1 showing superior burr removal and chamfering performance.
- The RSM and MOGA-ANN effectively modeled and optimized the drilling process, offering reliable predictions of multiple responses.
- Optimal parameters were identified as the use of Modified-1, 3000 rpm, and a water environment, achieving minimal chamfer heights (−2.066 mm), low drilling temperatures (42.19 °C), and an excellent surface finish (1.514 µm).
- Typically, a superior surface finish with roughness as low as 0.016 µm can be achieved under a kerosene-based environment as compared to dry and wet conditions.
- The experimental results matched the MOGA-ANN predictions, with deviations under 6%, validating the model’s accuracy.
- This approach demonstrates the novel integration of tool design and AI optimization, enhancing productivity, reducing post-processing, and improving drilling quality.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dey, B.; Mondal, N.; Mondal, S. Experimental Study to Minimize The Burr Formation in Drilling Process With Artifical Neural Networks (ANN) Analysis. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 377, p. 012120. [Google Scholar]
- Gillespie, L.K. Deburring precision miniature parts. Precis. Eng. 1979, 1, 189–198. [Google Scholar] [CrossRef]
- Blotter, P.T.; Gillespie, L.K. The formation and properties of machining burrs. J. Manuf. Sci. Eng. 1976, 98, 66–74. [Google Scholar]
- Kim, J.; Min, S.; Dornfeld, D.A. Optimization and control of drilling burr formation of AISI 304L and AISI 4118 based on drilling burr control charts. Int. J. Mach. Tools Manuf. 2001, 41, 923–936. [Google Scholar] [CrossRef]
- Min, S.; Dornfeld, D.A.; Kim, J.; Shyu, B. Finite element modeling of burr formation in metal cutting. Mach. Sci. Technol. 2001, 5, 307–322. [Google Scholar] [CrossRef]
- Mondal, N.; Mandal, M.C.; Dey, B.; Das, S. Genetic algorithm-based drilling burr minimization using adaptive neuro-fuzzy inference system and support vector regression. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2020, 234, 956–968. [Google Scholar] [CrossRef]
- Mondal, N.; Mandal, S.; Mandal, M.C. FPA based optimization of drilling burr using regression analysis and ANN model. Measurement 2020, 152, 107327. [Google Scholar] [CrossRef]
- Biermann, D.; Hartmann, H. Reduction of burr formation in drilling using cryogenic process cooling. Procedia CIRP 2012, 3, 85–90. [Google Scholar] [CrossRef]
- Davim, J.P.; António, C.A.C. Optimisation of cutting conditions in machining of aluminium matrix composites using a numerical and experimental model. J. Mater. Process. Technol. 2001, 12, 78–82. [Google Scholar] [CrossRef]
- Davim, J.P. Statistical and Computational Techniques in Manufacturing; Springer: Berlin/Heidelberg Germany, 2014. [Google Scholar] [CrossRef]
- Davim, J.P.; António, C.A.C. Optimal drilling of particulate metal matrix composites based on experimental and numerical procedures. Int. J. Mach. Tools Manuf. 2001, 41, 21–31. [Google Scholar] [CrossRef]
- Mondal, N.; Mandal, S.; Mandal, C.M.; Das, S.; Haldar, B. ANN-FPA based modelling and optimization of drilling burrs using RSM and GA. In Advance in Manufacturing Process, Intelligent Methods and System in Production Engineering, Proceedings of the GCMM 2021, Liverpool, UK, 7–9 June 2021; Springer: Cham, Switzerland, 2022; pp. 180–195. [Google Scholar] [CrossRef]
- Gaitonde, N.V.; Karnik, R.S. Minimizing burr size in drilling using artificial neural network (ANN)-particle swarm optimization (PSO) approach. Int. J. Adv. Manuf. Technol. 2012, 23, 1783–1793. [Google Scholar] [CrossRef]
- Suresh, S.; Rao, P.V.; Prasad, B. Optimization of drilling parameters for burr minimization in aluminum alloys using RSM. J. Manuf. Sci. Eng. 2016, 138, 051005. [Google Scholar]
- Kumar, S.; Gupta, M.; Sharma, R. Analysis of drilling burr formation using response surface method-ology. Mater. Manuf. Process. 2018, 33, 678–689. [Google Scholar]
- Saha, S.; Mondal, A.K.; Čep, R.; Joardar, H.; Haldar, B.; Kumar, A.; Alsalah, N.A.; Ataya, S. Multi-response optimization of electrochemical machining parameters for Inconel 718 via RSM and MOGA-ANN. Machines 2024, 12, 335. [Google Scholar] [CrossRef]
- Kumar, L.; Kumar, K.; Chhabra, D. Experimental investigations of electrical discharge micro-drilling for Mg-alloy and multi-response optimization using MOGA-ANN. CIRP-J. Manuf. Sci. Technol. 2022, 38, 774–786. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Mohanty, R.R.; Routara, B.C. Hybrid MOGA-ANN approach for tool wear and burr height optimization in drilling. Procedia CIRP 2019, 84, 415–420. [Google Scholar]
- Singh, H.; Nayak, D.; Ghosh, S. Multi-objective optimization of drilling force and burr formation in composites using MOGA-ANN. Mater. Today Proc. 2020, 45, 2135–2143. [Google Scholar]
- Dornfeld, D.A.; Kim, J.S.; Dechow, H.; Hewson, J.; Chen, L.J. Drilling burr formation in titanium alloy, Ti-6AI-4V. CIRP Ann. 1999, 48, 73–76. [Google Scholar] [CrossRef]
- Murthy, K.S.; Rajendran, I.G. Prediction and analysis of multiple quality characteristics in drilling under minimum quantity lubrication. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2012, 226, 1061–1070. [Google Scholar] [CrossRef]
- Pramanik, A.; Basak, A.K.; Prakash, C.; Shankar, S.; Chattopadhyaya, S. Sustainability in drilling of aluminum alloy. Clean. Mater. 2022, 3, 100048. [Google Scholar] [CrossRef]
- Heisel, U.; Schaal, M. Burr formation in short hole drilling with minimum quantity lubrication. Prod. Eng. 2009, 3, 157–163. [Google Scholar] [CrossRef]
- Agrawal, S.M.; Patil, N.G. Effects of Cryogenic Cooling on Burr Height in Drilling of Ceramic Rein-forced Aluminium Matrix Composites. Int. J. Adv. Res. Eng. Technol. 2020, 11, 851–856. [Google Scholar]
- Govindaraju, N.; Ahmed, L.S.; Kumar, M.P. Experimental investigations on cryogenic cooling in the drilling of AISI 1045 steel. Mater. Manuf. Process. 2014, 29, 1417–1421. [Google Scholar] [CrossRef]
- Zhu, Z.; Sun, X.; Guo, K.; Sun, J.; Li, J. Recent Advances in Drilling Tool Temperature: A State-of-the-Art Review. Chin. J. Mech. Eng. 2022, 35, 148. [Google Scholar] [CrossRef]
- Hussein, R.; Sadek, A.; Elbestawi, M.A.; Attia, M.H. Elimination of delamination and burr formation using high-frequency vibration-assisted drilling of hybrid CFRP/Ti6Al4V stacked material. Int. J. Adv. Manuf. Technol. 2019, 105, 859–873. [Google Scholar] [CrossRef]
- Franczyk, E.; Ślusarczyk, Ł.; Zębala, W. Drilling Burr minimization by changing drill geometry. Materials 2020, 13, 3207. [Google Scholar] [CrossRef]
- Ko, S.L.; Lee, J.K. Analysis of burr formation in drilling with a new-concept drill. J. Mater. Process. Technol. 2001, 113, 392–398. [Google Scholar] [CrossRef]
- HuaNa Tools. All You Need to Know About HSS Drill Bits. Available online: https://huanatools.com/introduction-of-high-performance-drill-bits/ (accessed on 11 January 2023).
- Quality Tools. A-Z guide for Drilling Aluminium. 11 January 2023. Available online: https://qlt.tools/blogs/insights/drilling-aluminium-guide?srsltid=AfmBOoorMDJmBe7syZrGJ7EQ433eRZcyNhW5jxlynuEE-32svZArOjRv (accessed on 11 January 2024).
- Ramesh, B.; Elayaperumal, A.; Venkatesh, R.; Madhav, S.; Jain, K. Determination of optimum parameter levels for multi-performance characteristics in conventional milling of beryllium copper alloy by using response surface methodology. Int. J. Innov. Res. Sci. Eng. Technol. 2014, 3, 10916–10923. [Google Scholar]
- Kim, K.H.; Cho, C.H.; Jeon, S.Y.; Lee, K.; Dornfeld, D.A. Drilling and deburring in a single process. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2003, 217, 1327–1331. [Google Scholar] [CrossRef]
- Kim, K.H.; Park, N.J. A new deburring for intersecting holes. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2005, 219, 865–870. [Google Scholar] [CrossRef]





| Element | Mg | Si | Fe | Cu | Cr | Zn | Ti | Mn | Others | Al |
|---|---|---|---|---|---|---|---|---|---|---|
| Amount (% wt) | 0.80–1.20 | 0.40–0.80 | 0.0–0.70 | 0.15–0.40 | 0.04–0.35 | 0.0–0.25 | 0.0–0.15 | 0.0–0.15 | 0.0–0.15 | Balance |
| Property | Density | Modulus of Elasticity | Poisson’s Ratio | Melting Point | Thermal Conductivity | Thermal Expansion Coefficient | Proof Stress | Tensile Strength | Shear Strength | Brinell Hardness |
|---|---|---|---|---|---|---|---|---|---|---|
| Value | 2.70 g/cm3 | 70 GPa | 0.33 | 650 °C | 166 W/m.K | 23.6 × 10−6/K | 240 MPa | 260 MPa | 180 MPa | 95 |
| Level | |||
|---|---|---|---|
| Parameters | −1 | 0 | +1 |
| Speed (rpm) | 1000 | 2000 | 3000 |
| Drill type | Normal twist drill | Modified-1 | Modified-2 |
| Environmental condition | Dry | Water | Kerosene |
| Parameter | Measuring Instrument | Specifications |
|---|---|---|
| Burr Height | Vision Measuring Machine | Maker: Mitutoyo Model: Quick Scope—l2010Z/AFC XYZ measuring volume: 200 × 100 × 150 mm Resolution: 0.1 pm |
| Temperature | Infrared thermometer | Model no.: HTC MTX-1 Temperature range: −50 °C to 500 °C Accuracy: −20 °C to 0 °C/−4 °F |
| Spindle Speed | Digital tachometer | Model no.: DT—2235B Speed range: 5 to 19,999 RPM |
| Surface Roughness | Taly Surf | Mitutoyo SurfTest SJ-210, Kawasaki, Japan |
| SL No. | Drill Type | Spindle Speed (rpm) | Environmental Condition | Burr (+)/Chamfer (−) Height (mm) (Z1) | Drilling Temperature (°C) (Z2) | Surface Roughness (µm) (Z3) |
|---|---|---|---|---|---|---|
| 1 | Normal | 1000 | Dry | 3.985 | 59.2 | 3.624 |
| 2 | Normal | 1000 | Water | 2.745 | 44 | 3.218 |
| 3 | Normal | 1000 | Kerosene | 2.685 | 48.2 | 2.941 |
| 4 | Normal | 2000 | Dry | 2.790 | 58.5 | 3.015 |
| 5 | Normal | 2000 | Water | 1.630 | 47.7 | 2.981 |
| 6 | Normal | 2000 | Kerosene | 1.600 | 52.3 | 2.644 |
| 7 | Normal | 3000 | Dry | 1.520 | 55.4 | 2.575 |
| 8 | Normal | 3000 | Water | 0.497 | 41.7 | 2.683 |
| 9 | Normal | 3000 | Kerosene | 0.456 | 46.5 | 2.240 |
| 10 | Modified-1 | 1000 | Dry | −1.250 | 57.8 | 0.917 |
| 11 | Modified-1 | 1000 | Water | −1.260 | 45.9 | 0.746 |
| 12 | Modified-1 | 1000 | Kerosene | −1.280 | 50.9 | 0.106 |
| 13 | Modified-1 | 2000 | Dry | −1.720 | 56.4 | 0.734 |
| 14 | Modified-1 | 2000 | Water | −1.750 | 45.5 | 0.506 |
| 15 | Modified-1 | 2000 | Kerosene | −1.780 | 52.1 | 0.084 |
| 16 | Modified-1 | 3000 | Dry | −2.100 | 49.8 | 0.512 |
| 17 | Modified-1 | 3000 | Water | −2.150 | 42.4 | 0.338 |
| 18 | Modified-1 | 3000 | Kerosene | −2.180 | 47.4 | 0.082 |
| 19 | Modified-2 | 1000 | Dry | −0.950 | 53.5 | 3.704 |
| 20 | Modified-2 | 1000 | Water | −1.100 | 45.4 | 3.418 |
| 21 | Modified-2 | 1000 | Kerosene | −1.120 | 48.5 | 3.013 |
| 22 | Modified-2 | 2000 | Dry | −1.450 | 55.8 | 2.843 |
| 23 | Modified-2 | 2000 | Water | −1.480 | 45.4 | 3.002 |
| 24 | Modified-2 | 2000 | Kerosene | −1.500 | 51.8 | 2.753 |
| 25 | Modified-2 | 3000 | Dry | −1.810 | 46.4 | 2.319 |
| 26 | Modified-2 | 3000 | Water | −1.870 | 40.3 | 2.219 |
| 27 | Modified-2 | 3000 | Kerosene | −1.890 | 46.6 | 1.948 |
| Source | Burr (+)/Chamfer (−) Height | Drilling Temperature | Surface Roughness | |||
|---|---|---|---|---|---|---|
| F-Value | p-Value | F-Value | p-Value | F-Value | p-Value | |
| Linear vs. Mean | 9.12 | 0.0009 | 3.11 | 0.0560 | 3.21 | 0.0514 |
| 2FI vs. Linear | 0.3772 | 0.7710 | 0.7554 | 0.5387 | 0.0944 | 0.9618 |
| Quadratic vs. 2FI | 229.63 | <0.0001 | 61.00 | <0.0001 | 599.59 | <0.0001 |
| Cubic vs. Quadratic | 25.52 | 0.0007 | 0.6406 | 0.6530 | 2.92 | 0.1166 |
| Source | Burr (+)/Chamfer (−) Height | Drilling Temperature | Surface Roughness | |||
|---|---|---|---|---|---|---|
| F-Value | p-Value | F-Value | p-Value | F-Value | p-Value | |
| Model | 227.58 | <0.0001 | 38.75 | <0.0001 | 327.70 | <0.0001 |
| A—Drill Type | 1070.56 | <0.0001 | 25.27 | 0.0005 | 34.73 | 0.0048 |
| B—Spindle Speed | 203.01 | <0.0001 | 29.71 | 0.0003 | 866.75 | <0.0001 |
| C—Environmental Condition | 24.92 | 0.0005 | 77.11 | <0.0001 | 239.62 | <0.0001 |
| AB | 40.90 | <0.0001 | 1.40 | 0.2635 | 20.59 | 0.0011 |
| AC | 19.47 | 0.0013 | 26.13 | 0.0005 | 0.0813 | 0.7813 |
| BC | 0.4630 | 0.5117 | 6.11 | 0.0330 | 18.75 | 0.0015 |
| A2 | 319.29 | <0.0001 | 0.0438 | 0.8384 | 1232.53 | <0.0001 |
| B2 | 6.19 | 0.0321 | 16.16 | 0.0024 | 48.80 | <0.0001 |
| C2 | 3.168 × 10−6 | 0.9986 | 144.42 | <0.0001 | 0.0046 | 0.9473 |
| Lack of Fit | 4.51 | 0.2303 | 5.08 | 0.6581 | 2.84 | 0.1221 |
| Not significant | Not significant | Not significant | ||||
| R2 | 0.9951 | 0.9721 | 0.9966 | |||
| Adj R2 | 0.9908 | 0.9470 | 0.9936 | |||
| SL No. | Input Parameter | Output | ||||
|---|---|---|---|---|---|---|
| Drill Type | Spindle Speed (rpm) | Environmental Condition | Burr (+)/Chamfer (−) Height (mm) | Drilling Temperature (°C) | Surface Roughness (µm) | |
| 1 | Modified-1 | 3000 | Kerosene | −2.252 | 47.88 | 0.081 |
| 2 | Modified-1 | 3000 | Water | −2.611 | 40.76 | 0.187 |
| 3 | Modified-2 | 3000 | Water | −1.916 | 40.28 | 2.236 |
| 4 | Modified-2 | 3000 | Water | −2.001 | 40.34 | 2.131 |
| 5 | Modified-1 | 3000 | Water | −2.673 | 40.88 | 0.291 |
| 6 | Modified-1 | 3000 | Water | −2.012 | 42.25 | 0.113 |
| 7 | Modified-2 | 3000 | Water | −2.268 | 40.47 | 1.939 |
| 8 | Modified-1 | 3000 | Kerosene | −2.829 | 45.77 | 0.182 |
| 9 | Modified-1 | 3000 | Water | −2.339 | 40.51 | 0.374 |
| 10 | Modified-1 | 3000 | Water | −2.448 | 40.59 | 0.270 |
| 11 | Modified-1 | 3000 | Kerosene | −2.809 | 44.94 | 0.122 |
| 12 | Modified-1 | 3000 | Water | −2.510 | 40.66 | 0.096 |
| 13 | Modified-2 | 3000 | Water | −2.001 | 40.34 | 2.131 |
| 14 | Modified-1 | 3000 | Kerosene | −2.816 | 43.95 | 0.015 |
| 15 | Modified-2 | 3000 | Water | −2.321 | 40.50 | 1.891 |
| 16 | Modified-2 | 3000 | Water | −1.977 | 40.31 | 2.188 |
| 17 | Modified-1 | 3000 | Kerosene | −1.910 | 46.66 | 0.311 |
| 18 | Modified-1 | 3000 | Water | −2.540 | 40.68 | 0.173 |
| SL No. | Input Parameter | Output | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Drill Type | Spindle Speed (rpm) | Environmental Condition | Burr (+)/Chamfer (−) Height (mm) | Drilling Temperature (°C) | Surface Roughness (µm) | |||||||
| MOGA-ANN | Experimental | % Variation | MOGA-ANN | Experimental | % Variation | MOGA-ANN | Experimental | % Variation | ||||
| 1 | Modified-1 | 3000 | Kerosene | −2.252 | −2.18 | <3% | 47.88 | 47.4 | <1% | 0.081 | 0.079 | <2% |
| 2 | Modified-1 | 3000 | Water | −2.611 | −2.55 | <3% | 40.76 | 42.4 | <4% | 0.187 | 0.179 | <4% |
| 3 | Modified-2 | 3000 | Water | −1.916 | −1.87 | <2.5% | 40.28 | 40.3 | <1% | 2.236 | 2.2 | <2% |
| 4 | Modified-2 | 3000 | Water | −2.001 | −1.89 | <6% | 40.34 | 42.6 | <5% | 2.131 | 2.031 | <5% |
| 5 | Modified-1 | 3000 | Water | −2.673 | −2.521 | <4% | 40.88 | 41.88 | <2% | 0.291 | 0.281 | <3.5% |
| 6 | Modified-1 | 3000 | Water | −2.012 | −2 | <1% | 42.25 | 43.45 | <3% | 0.113 | 0.116 | <2% |
| 7 | Modified-2 | 3000 | Water | −2.268 | −2.168 | <5% | 40.47 | 43 | <5% | 1.939 | 1.9 | <2% |
| 8 | Modified-1 | 3000 | Kerosene | −2.829 | −2.67 | <6% | 45.77 | 44.54 | <3% | 0.182 | 0.185 | <2% |
| 9 | Modified-1 | 3000 | Water | −2.339 | −2.39 | <2% | 40.51 | 42.01 | <3% | 0.374 | 0.37 | <2% |
| 10 | Modified-1 | 3000 | Water | −2.448 | −2.65 | <7% | 40.59 | 42.9 | <5% | 0.27 | 0.276 | <1% |
| 11 | Modified-1 | 3000 | Kerosene | −2.809 | −2.81 | <1% | 44.94 | 43.74 | <3% | 0.122 | 0.124 | <2% |
| 12 | Modified-1 | 3000 | Water | −2.51 | −2.42 | <4% | 40.66 | 41.95 | <3% | 0.096 | 0.093 | <2% |
| 13 | Modified-2 | 3000 | Water | −2.001 | −2.1 | <4% | 40.34 | 40.94 | <1% | 2.131 | 2.1 | <3% |
| 14 | Modified-1 | 3000 | Kerosene | −2.816 | −2.844 | <1% | 43.95 | 42.75 | <2% | 0.015 | 0.016 | <1% |
| 15 | Modified-2 | 3000 | Water | −2.321 | −2.301 | <1% | 40.5 | 40.35 | <2% | 1.891 | 1.88 | <1% |
| 16 | Modified-2 | 3000 | Water | −1.977 | −1.99 | <1% | 40.31 | 41.01 | <2% | 2.188 | 2.19 | <1% |
| 17 | Modified-1 | 3000 | Kerosene | −1.91 | −1.87 | <2% | 46.66 | 45.06 | <3% | 0.311 | 0.309 | <1% |
| 18 | Modified-1 | 3000 | Water | −2.54 | −2.643 | <4% | 40.68 | 42.01 | <3% | 0.173 | 0.175 | <1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paul, S.; Haldar, B.; Joardar, H.; Mondal, N.; Alsaleh, N.A.; Akhtar, M. Single-Step Drilling Using Novel Modified Drill Bits Under Dry, Water, and Kerosene Conditions and Optimization of Process Parameters via MOGA-ANN and RSM. Lubricants 2025, 13, 273. https://doi.org/10.3390/lubricants13060273
Paul S, Haldar B, Joardar H, Mondal N, Alsaleh NA, Akhtar M. Single-Step Drilling Using Novel Modified Drill Bits Under Dry, Water, and Kerosene Conditions and Optimization of Process Parameters via MOGA-ANN and RSM. Lubricants. 2025; 13(6):273. https://doi.org/10.3390/lubricants13060273
Chicago/Turabian StylePaul, Sumitava, Barun Haldar, Hillol Joardar, Nripen Mondal, Naser A. Alsaleh, and Maaz Akhtar. 2025. "Single-Step Drilling Using Novel Modified Drill Bits Under Dry, Water, and Kerosene Conditions and Optimization of Process Parameters via MOGA-ANN and RSM" Lubricants 13, no. 6: 273. https://doi.org/10.3390/lubricants13060273
APA StylePaul, S., Haldar, B., Joardar, H., Mondal, N., Alsaleh, N. A., & Akhtar, M. (2025). Single-Step Drilling Using Novel Modified Drill Bits Under Dry, Water, and Kerosene Conditions and Optimization of Process Parameters via MOGA-ANN and RSM. Lubricants, 13(6), 273. https://doi.org/10.3390/lubricants13060273






