Abstract
Wet multi-disc clutches in transmission systems suffer from the incomplete separation of the friction components, which raises the drag torque and results in power loss and heightened fuel consumption. This incomplete separation arises from the force imbalance between resistance forces, such as the oil viscosity force, and the lack of an axial separating force. Therefore, providing an axial separating force is a potential solution to this problem. In this investigation, small-angle conical separate plates were designed which can provide the elastic restoring force during the separation process. Based on its structural properties, a model describing the clutch engagement and separation process was established. Through bench tests, the feasibility of the model was verified. The influence of the conical plate on the dynamics of the clutch was studied, including the influence of the separation gap, uniformity, and drag torque. Though the transmitted torque was reduced by 10.31% in the low-piston-pressure condition and by less than 2% in the high-piston-pressure condition, the problem of incomplete separation was successfully resolved. The results show that when applying the conical plates, the separation time was reduced by 18.78%, with a 25.31% increase in the uniformity of the gaps. Accordingly, the drag torque was reduced by 37.73%.
1. Introduction
Wet multi-disc clutches find widespread usage in various types of facilities, including in ocean-going ships, helicopters, heavy vehicles, and construction machinery, due to their compact structure, large transmission torque, and notable wear resistance [1,2]. In these clutches, power shifting and torque regulation are realized by the engagement and separation of friction components [3,4]. The working process of a wet clutch determines its stability and reliability, and thus is of great importance [5]. The engagement process takes place under high pressure and high speed difference conditions. During the separation process, the friction components are released when the piston pressure is reduced. Under the action of the oil film and rotating friction components, drag torque is generated. In ideal conditions, the friction components should move back to their original positions before engagement. However, in practice, the friction components may not completely separate, meaning that the drag torque is much higher than calculated. Accordingly, jamming and shift delay may occur [6].
The typical phenomenon of incomplete separation involves all the friction components sticking together after the separation process. As shown in Figure 1, though the piston can be pulled back by the return spring, there is no axial force to help the friction components move away from each other. Under the action of the oil viscosity force [7,8], the adsorption force caused by surface tension [9], and atmospheric pressure, the friction components stick together. Therefore, the narrowed gaps and oil film between friction pairs may increase the drag torque and power loss [10,11]. Robert [12] studied the influence of the pack clearance, oil flow and level, and clutch on the power loss from the drag torque. Lukas et al. [13] also used an experimental method to investigate the drag loss of a clutch. Leister et al. pointed out that the drag torque under separation status is a major source of energy loss [14]. Thomas et al. [15] warned that the significant loss in power that occurs under separation status should be given more serious consideration. Since the wet clutch is under separation status for most of the operating duration, the energy consumption and exhaust emissions generated by the drag torque under separation status make up a large proportion of all energy consumed. Furthermore, Hilpert et al. [16] indicated that if friction components cannot fully separate, rough contact may occasionally occur. Hou et al. [17] suggested that the mechanical contact caused by the oscillating motion was the reason for the sharp increase in torque.
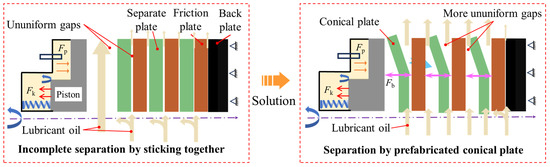
Figure 1.
Schematic diagram of incomplete separation and the solution.
The solution to the incomplete separation is to provide an external force to forcibly separate the separate plate from the friction plate. Yu et al. [18] introduced and analyzed a waveform-separating spring, which can provide extra force to help pull apart the friction components, emphasizing the influence of the wavenumber on the load–deformation relationship. Erfanian-Naziftoosi et al. [19] verified that waveform-separating springs can retain their stiffness even after millions of load cycles. Li et al. [20] then analyzed multiple parameters of the separating spring, indicating that the radial deformation is related mostly to the wave height and width of the spring. Yan et al. [21] investigated the non-linear influence of the wave-shaped cushion plate and the deformed diaphragm spring on the engagement and disengagement characteristics in pull-type diaphragm spring clutches. Wang et al. [22] investigated the influence of the wavenumber and thickness of the separating spring on the engagement process. Unfortunately, the results showed that a pressure loss during engagement leads to a transfer torque loss, which was unexpected. Furthermore, additional components may cause the system to become more complex and undermine the compactness of the clutch. Wu et al. [23] studied a cone-shape friction plate and realized that the engaging time increased significantly. Zhao et al. [24] demonstrated that a conical buckled plate has a special property, in that it can provide a normal force in the axial direction. To utilize the elastic restoring force, the influence of the conical plate on the engagement and separation characteristics should be investigated.
Herein, in order to help separate the friction components and reduce the drag torque without adding extra elements, a conical plate was introduced. Based on the structural properties, a dynamic model featuring a conical plate rather than the traditional flat plate was established. The engagement and separation properties of the clutch system were analyzed via a numerical method and verified in an experiment. The influences of the cone angle on the separation time, gaps, and drag torque were studied, and the optimal layout of the conical plate is presented.
2. Numerical Model
2.1. Conical Separate Plate Design
Inspired by the buckling deformation of the separate plate [24], a conical separate plate was designed, as shown in Figure 2. The plate was circumferential uniform with deformation in the radial direction, presenting as a conical (saucer) shape. The initial deformation was w0. The force was applied along the z direction, as shown by the red arrows in Figure 2. The structural parameters were as follows:
where α is the cone angle, indicating the conical degree; d and D are the inner and outer diameter of the conical plate, respectively; and Ri = 0.086 m and Ro = 0.125 m are the inner and outer radius of the flat plate, respectively. The number and size of male splines were the same as those of the flat plate. The material of the plate was 30CrMnSi stainless steel with a high elastic modulus of 216 GPa and a Poisson’s ratio of 0.3. Its density was 7750 kg/m3.
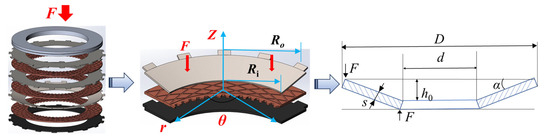
Figure 2.
Conical separate plate.
The most notable difference between the flat separate plate and the conical separate plate was that the conical plate could provide axial force Fb (elastic restoring force) [24]:
where KF is the stiffness of the conical plate; E is the elastic modulus; s = 0.002 m is the thickness; υ is the Poison’s ratio; and w and w0 are the deflection and initial deflection, respectively.
Since stiffness is a quadratic function of deflection w, the discriminant deciding the monotonicity of the plate was obtained as:
From Equation (4), if the condition w0/s < (2/a0)0.5 is satisfied, the stiffness is positive during the deformation process. Otherwise, there will be negative stiffness. Because the conical plate should provide enough force during the whole separation process, the force should be monotone increasing. Thus, the cone angle should satisfy the moderate size requirement.
2.2. Dynamic Model
The structure of a wet multi-disc clutch is illustrated in Figure 3. For a N pair wet clutch, there were N/2 separate plates, N/2 friction plates, one back plate, and one piston involved in the movement. Using two-dimensional coordinates, with the origin located on the left side of the back plate, the location of each component was 0 to N. The subscripts p, s, and f denote the piston, separate plate, and friction plate, respectively. The force governing equations along the axial direction is:
where x, its derivative, and its second derivative denote the displacement, speed, and acceleration; m is the mass; subscripts p, s, and f denote the piston, separate plate, and friction plate, respectively; Fk is the force of the return springs; FR is the resistance force which prevents friction components from fully separation; Fb is the elastic restoring force; Fp is the hydraulic force provided by the piston, which tightly compresses the friction components; Fd is the damping force; Fimp is the impact contact force; Fcen is the centrifugal oil force, mainly acting when separation occurs; Fc is the asperity rough contact force; Fv is the viscus force; and Fs is the spline friction force. They could be calculated as:
where kspr is the stiffness of the return spring, l is the initial compression length of the return spring, and x0 and X0 are the axial and maximum axial displacement of the piston, respectively; ξ is the impact compression and equals X0 − x0; c0 is the damping between the piston and the cylinder liner; ρ and ω are the density and rotational speed of the lubrication oil, respectively, R0 to R4 are the geometric parameters of the piston (Figure 3b); K0 is the impact stiffness; and Rs, αs, and μs are the pitch circle radius, the pressure angle of the spline, and the spline friction coefficient, respectively.
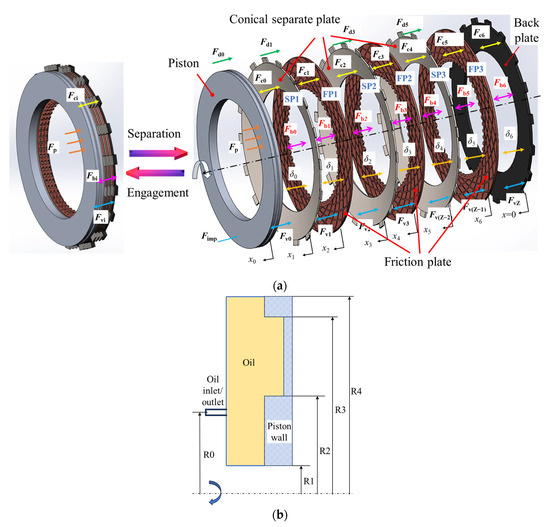
Figure 3.
A schematic of the clutch system. (a) The dynamics of the clutch; (b) the structure of the piston.
After pressure relief, the elastic restoring force pushed the adjacent components away. However, resistance force tried to make the friction components stay together:
where Fd is the disengagement resistance force calculated by the thin-layer fluid separation model [13]; Fcap is the adsorption force caused by surface tension [25]; η is the viscosity of the oil; v is the separating velocity; h is the thickness of the oil film; Rlb is the radius of the liquid bridge between the friction and separate plate; γ is the surface tension coefficient of oil; and θ is the contact angle between the oil and the solid surface.
In response to the displacement change, the gaps between each pair were as follows:
where si is the thickness of the separate plate or the friction plate.
2.3. Contact and Lubrication Model
As is shown in Figure 4, the actual contact area Ac only took up a small proportion of the nominal contact area An of the surface and can be expressed as follows [26]:
where F2(H) is the distribution function of asperities.

Figure 4.
A sketch of the contact model.
In general, part of the asperities experienced plastic deformation, while other parts experienced elastic deformation. Index κ can represent the degree and 1 ≤ κ ≤ 2. K could be used to calculate the elastic–plastic deformation status:
where E’ is the equivalent elastic modulus of the two contact surfaces, while E1 and E2 denote the elastic modulus of the two surfaces, respectively; υ1 and υ2 are the Poisson’s ratio of the two surfaces, respectively; HB is the Brinell hardness; and β, σ, and N are the radius, height, and the density of asperities, respectively.
The distribution of the asperities can be regarded as the Gaussian surface assumption [27]:
Thus:
The contact pressure of the asperities can be calculated by the GT model [28]:
where H is the film-thickness ratio H = h/σ; h is the film thickness; and the contact index K′ can be calculated as:
The contact ratio C can be expressed as:
The rough contact force is:
where Ag is the ratio of the non-grooved area.
The Reynolds equation, considering the inertial force of the oil film, was established as follows [29]:
where p is the oil-film pressure and ω is the rotational speed of the oil, which could be calculated as follows based on the laminar flow assumption due to the small Reynolds number:
The boundary conditions were as follows:
Substituting, the velocity components could be calculated as
The average oil film pressure between the friction pairs was
where ϕr is the pressure flow factor:
The average oil-film pressure was integrated into the fluid lubrication area, and the viscus force between the friction pairs was deduced as:
2.4. Torque Model
According to Newton’s law of internal friction, the viscous torque is expressed as [30]:
Further, it could be calculated as:
where ϕf and ϕs are the shear stress coefficients.
The rough contact torque is expressed as [31]:
The total friction torque is the sum of the viscous and rough contact torque:
3. Experiments
3.1. Apparatus
To verify the feasibility of the numerical method and obtain more detailed torque information, the long-time-sliding experiment was arranged. As is shown in Figure 5, the test bench was composed of a control system, a data acquisition system, a clutch pack, a torque sensor, etc. The clutch pack contained the piston, back plate, friction plates, and separate plates. In the six-pair system, N = 6, meaning that there were three separate plates and three friction plates. The torque transducer could record the torque data during the sliding and separation.

Figure 5.
Experimental apparatus. (a) Test bench; (b) conical plate.
To guarantee the compactness of the clutch, the total reserved clearance of the clutch was 3.5 mm. In every case, all three separate plates were replaced with the conical plate, except for the original design. Since the total deformation of all the plates had to be smaller than the reserved clearance, a cone angle of 0.5°, 1°, or 1.5° was chosen to represent slight, moderate, or large conical degrees, respectively, with corresponding total initial deformations of 1.02 mm, 2.04 mm, and 3.06 mm, respectively. The arrangement of the friction components is shown in Figure 6. The cases are referred to as 0°, 0.5°, 1°, and 1.5°, respectively.
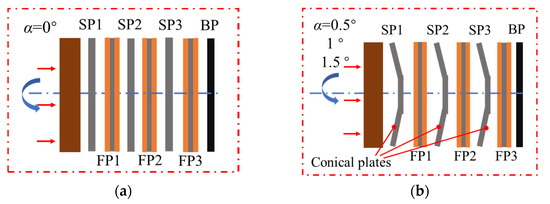
Figure 6.
Experiment and simulation conditions. (a) C-0; (b) C-1 to C-3.
3.2. Methods
The simulation and experiment conditions are shown in Table 1 and Figure 6. For each cycle, the total time was 60 s. The piston pressure increased linearly at the beginning until reaching t = 0.5 s and was then maintained. Then, the piston pressure was revoked from t = 15 s. Controlled by the piston pressure, the working process of the clutch can be divided into three main stages: the engagement and stable sliding process (E), the separation process (S), and the separation status (R). Under the separation status, the piston pressure was reduced to zero; the rotational speed of the friction plates remained unchanged and was equal to the rotational speed of the motor.

Table 1.
Conditions of the numerical method.
A numerical simulation was carried out using Matlab/Simulink 2022b, and the modules were programmed based on the models established in Section 2.1, Section 2.2, Section 2.3 and Section 2.4. Based on the characteristics of the clutch engagement–separation process and the coupling of multiple variables, the ode23s solver was used in the simulation, the relative-tolerance error limit of which is smaller than 10−3.
To verify the feasibility of the established model, the friction torque during sliding (abbreviated as the sliding torque) and under the separation status (drag torque) were obtained from the torque sensor and compared with the simulation results. To further verify the model, the performances under different values of piston pressure and rotational speed were simulated and tested. The influence of the cone angle was mainly analyzed under the conditions of 0.3 MPa and 400 r/min.
4. Results and Discussion
4.1. Model Verification
Figure 7 shows the comparison results of the friction torque between tests and simulations under 0.3 MPa 400 r/min. The red line indicates the experiment result and the black line indicates the simulation result. Figure 7 indicates that the larger the angle, the lower the friction torque during sliding (sliding torque). After the sharp increase and decrease caused by the overshoot of the motor, the sliding torque became basically stable in each case. The average sliding torque of the original design was 172.74 Nm, while the sliding torques for 0.5°, 1°, and 1.5° were 170.41 Nm, 160.34 Nm, and 155.22 Nm, respectively. The decrease came from the attenuative effect of the counterforce provided by the conical plate, which was comparable to when the piston pressure was as low as 0.3 MPa. The maximum difference between the simulation and experiments was 1.64%.
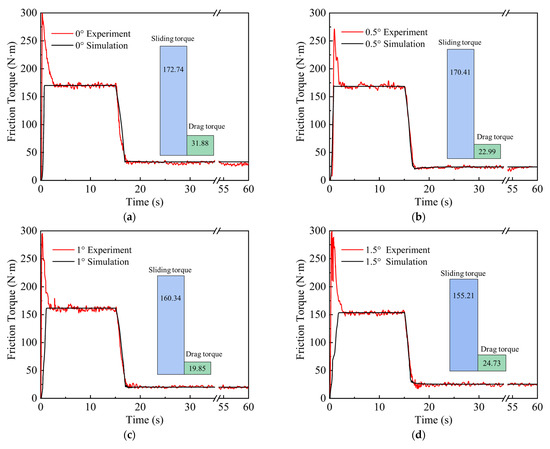
Figure 7.
The torque results. (a) 0°; (b) 0.5°; (c) 1°; (d) 1.5°.
Figure 7 demonstrates that the larger the angle, the higher the drag torque. The average drag torque of the 0° case was 31.88 Nm, since the friction components stuck together even if the piston returned to its original position. The drag torques for 0.5°, 1°, and 1.5° were 22.99 Nm, 19.85 Nm, and 24.73 Nm, respectively. Because the oil films between pairs were rendered ineffective with the expansion of the conical plate, the drag torque was reduced. The maximum difference between the simulation and experiments was 4.50%.
To further verify the feasibility of the established model, the difference between simulations and experiments was obtained under different values of piston pressure and rotational speed (Figure 8). The maximum relative error of the sliding torque between experiments and simulations was 1.68%, while that of the drag torque was 6.76%, present at 0.35 MPa 400 r/min. Because of the force of the return springs, when an increase of 0.05 MPa from 0.25 MPa to 0.3 MPa and from 0.3 MPa to 0.35 MPa took place, the increased sliding torque was different. The drag torque had little influence over the piston pressure, while it was obviously affected by the rotational speed. The reason for this is that, when separated, the piston pressure was reduced to zero while the rotational speed of friction components was kept constant; the higher the speed, the larger the viscous force between each pair and the larger the drag torque. However, the sliding torque was minimally affected, mostly due to the difference in the friction coefficient.
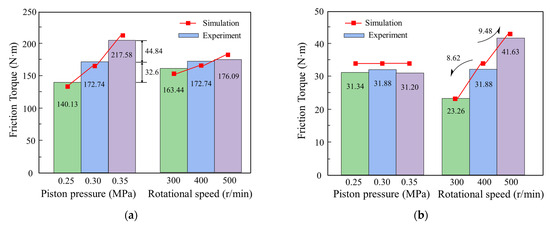
Figure 8.
Further verification of the established model. (a) Sliding torque; (b) drag torque.
Since the relative error between the simulation and experiment was small and the trend of the simulation was close to that of the experiment, the viability of the numerical model was verified by the experiments.
4.2. Gap Characteristics
Based on the established model, the dynamic characteristics of the conical separate plate are discussed. The most notable differences when applying the conical plate were the width and uniformity of the gaps, which affected the lubrication and drag torque. Therefore, the difference in the gaps was studied. In addition, the engagement and separation time is discussed. The gaps between the plates underwent a cycle of narrowing–eliminating–expanding during the whole process. During the engagement process, the friction components moved axially and the speed difference narrowed to zero. During the separation process, the friction components separated and the gaps increased.
To quantitative analyze the influence on the dynamic characteristics, the coefficient of gap nonuniformity δu was defined as:
where δ* = 0.5 mm is the ideal gap. A larger δu indicates higher nonuniformity.
The influence of the cone angle on the engagement and separation is obvious. As the angle increased from 0° to 1.5°, the engagement time increased from 0.79 s to 1.87 s. It was 137% longer for the 1.5° case (Table 2). The piston pressure needed to firstly overcome the elastic restoring force of the conical plates and then narrow the clearance. The restoring force is comparable with the piston force under low-pressure conditions and accordingly, the piston was slowed down. This is consistent with Wu’s [23] results, in which a conical friction plate was found to delay the engagement.

Table 2.
Time needed for engagement and separation.
Figure 9 illustrates the gaps during the engagement process. The gaps experienced a sharp drop when the applied force exceeded the force of the return springs. Meanwhile, the contact ratio of each pair grew exponentially. When the resultant force was stable, the gaps were nearly unchanged. In the original design α = 0°, after t = 0.79 s, the gaps of all pairs were narrowed in order from S0 to S6 to an average of 10.55 μm. The average gap was narrowed from 9.65 μm to 9.18 μm with the increasing angle. This difference results from the structure of the conical plate. Although in macrography the plates were flattened when sliding, deformation occurred [24]. Therefore, deformation squeezed and narrowed the oil films between the contact pairs. The lubrication status was boundary lubrication due to the thin oil film.
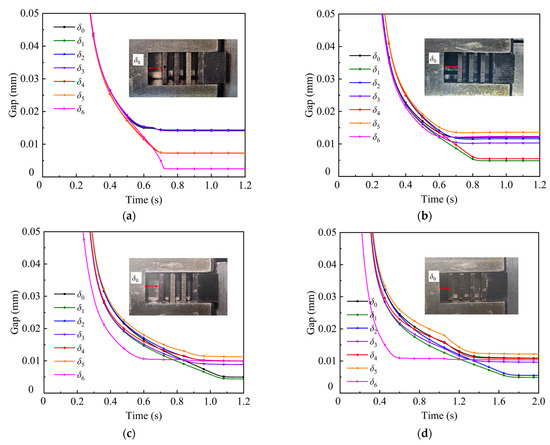
Figure 9.
The influence of the conical plate on the engagement. (a) α = 0°; (b) α = 0.5°; (c) α = 1°; (d) α = 1.5°.
Figure 10 demonstrates the gaps during separation. The position of each plate is shown in Figure 10 as SP1, SP2, and SP3. The gaps are also illustrated. Since the applied pressure was revoked, the gaps gradually reverted to their initial positions. The time needed for separation decreased from 2.29 s to 1.86 s, i.e., 18.78% shorter on account of the external elastic restoring force. The reason for the minimal difference was that the elastic restoring force was small compared with the piston force, so the length of the separation time was mostly due to the withdrawal of the piston. The elastic restoring force was much larger than the disengagement resistance force and the adsorption force; thus, the larger the angle, the larger the elastic restoring force, and the shorter the time needed for separation. However, when the angle exceeded 1°, the separation time was extended, because recovering from deformation also required time.
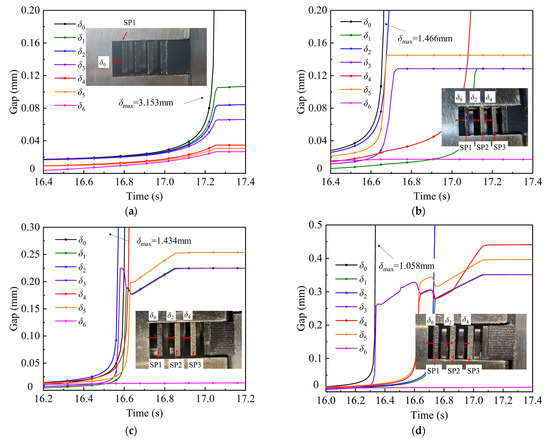
Figure 10.
The influence of the conical plate on the separation. (a) α = 0°; (b) α = 0.5°; (c) α = 1°; (d) α = 1.5°.
Unlike the engagement process, the time needed for separation varied from pair to pair. When α = 0°, though, the separation times were close, because the time needed was fully dictated by the action of the piston, while that of the conical plates was decided by both the action of the piston and the conical plates themselves. Taking α = 1°as an example, the times needed to reach stable gaps were t = 16.72 s, 17.07 s, 16.86 s, 17.08 s, 16.88 s, 16.88 s and 16.54 s. It was clear that the restoring side of the plate needed more time to become stable.
When there was no conical plate, δ0 occupied most of the clearance, while δ1 to δ6 decreased in turn, with a smaller clearance (Figure 10a). Since the return spring was connected to the piston directly, when the piston pressure was revoked, the piston was pulled back to the original position. However, there was no external force impacting the rest of plates, so they could only separate through the centrifugal effect and could not move further. The lubrication statuses were mixture lubrication for all pairs except S0.
When introducing the elastic restoring force, δ0, δ2, δ4 became the largest. For example, the gaps for α = 1° were 1.434 mm, 0.225 mm, 0.701 mm, 0.224 mm, 0.647 mm, 0.254 mm, and 0.014 mm (Figure 10c). The elastic restoring force provided by the conical separate plate forced the separate plates and friction plates to move axially rather than only relying on the centrifugal force. However, the gap δ6 was still as small as in the original design due to the lack of the elastic restoring force for FP3 or the back plate. The nonuniformity of gaps also decreased with the increasing angle until α = 1.5°. The more uniform gaps enabled the lubricating oil to be allocated to each pair. The lubrication status was hydrodynamic lubrication for all pairs except S6, since gap δ6 was too small.
4.3. Torque Characteristics
Figure 11 demonstrates the influence of conical plates on the friction torque during engagement and sliding (E). The influence of the cone angle on the sliding torque and drag torque is illustrated. After the piston chamber had been filled with oil, the friction torque increased quickly during the E1 stage. At stage E2, the viscous torque decreased to nearly 0, while the rough contact torque grew to its maximum, which can be referred to as the sliding torque. Since te, the sliding between separate plate and friction plates became stable. Figure 11 illustrates that the larger the cone angle, the smaller the sliding torque. The difference arose from the elastic restoring force provided by the conical plate. When the piston pressure was as small as 0.3 MPa, the counterforce between cases was not negligible. Specifically, the difference between the 0° and 1.5° cases was about 17.53 N·m, 10.31%. When the piston pressure was high, the difference was negligible. For example, when p = 1.2 MPa, the difference between the 0° and 1.5° cases was less than 2%. A high piston pressure is extensively employed in heavy-duty vehicles and facilities, and the clutch continues to increase the piston pressure and rotational speed to increase the energy density. Therefore, the advantages of the conical plate can outweigh the disadvantages, especially in high-piston-pressure conditions now and in the future.
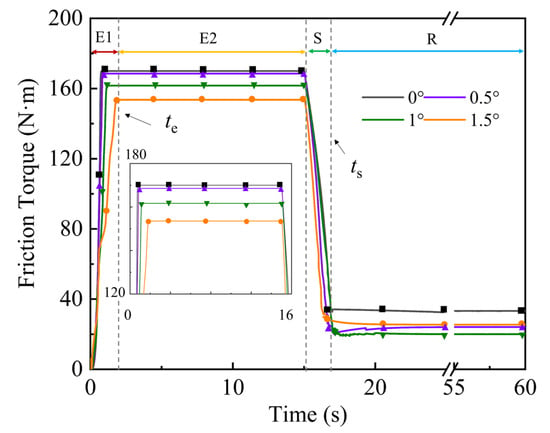
Figure 11.
The friction torque during the cycle.
Then, during the separation process (S), the rough contact torque quickly declined while the viscous torque took effect. Under the separation status (R), the viscous torque increased a little and became stable; this can be referred to as the drag torque. Figure 12b demonstrates the influence of the cone angle on the drag torque. In the original design (α = 0°), the friction components were stuck together, so that the drag torque was the highest among cases.
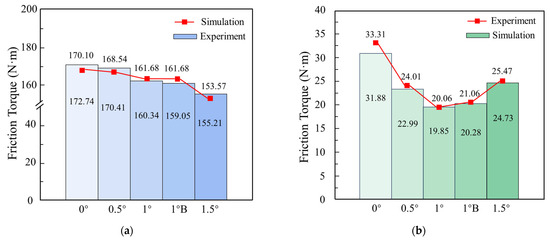
Figure 12.
The influence of the conical plate on the sliding torque and drag torque. (a) Sliding torque; (b) drag torque.
With the increasing cone angle, the gaps were enlarged by the conical plate so that the drag torque decreased. The smallest drag torque was 19.85 Nm, 37.73% smaller than the 0° group, present in the 1° case. The reason for this is that the thick oil film between the friction pairs was rendered ineffective, so the viscous nature of the oil was partly reduced. When the angle increased to 1.5°, since the reserved clearance was occupied mostly by the conical plates, the gaps at the outermost edge and innermost edge between the friction plates and separate plates decreased again. Accordingly, the oil film became thick and strong, and the drag torque increased again, i.e., higher than the 1° and 0.5° cases. In addition, though the 1° case displayed the smallest drag torque, the drag torque of 0.5° and 1.5° was obviously smaller than the original design. On occasions where the reserved clearance is too small to contain the 1° plates, the 0.5° plates may help. In applications where the lubricating oil has a higher viscosity, 1.5° plates are an alternative option, as they can provide a larger elastic restoring force.
Clutches are under separation status most of the time and thus, reducing the drag torque can conserve a large proportion of power and energy. Though the cost of the conical plate is higher and processing is more complicated, the cost and time needed for manufacturing are less than 10% more than those required for the flat plate. In mass production, the time and cost will be further decreased. In contrast, the effect of reducing the drag torque is clear. Therefore, by applying the conical plate, the drag torque is reduced significantly and much of the power can be saved.
5. Conclusions
To solve the incomplete separation problem and reduce the drag loss in wet multi-disc clutches, conical separate plates were designed. A numerical model, which evaluated the dynamic characteristics during the engagement and separation process, was verified via bench tests. No extra components are required, maintaining the compactness of the clutch. This investigation provides a theoretical basis for further studies on conical plates, clutch dynamics, and failure prevention. The results show that the advantages outweigh the disadvantages, especially in high-piston-pressure conditions. The main conclusions are as follows:
- (1)
- The conical plate can provide elastic restoring force during the separation process to assist separation, reducing the separation time by 18.78%. The uniformity of the gaps is increased by 25.31%, resulting in a change in the lubrication status from the mixture lubrication to the hydrodynamic lubrication.
- (2)
- The established numerical model can effectively describe the clutch engagement and separation characteristics, and its feasibility is verified by experiments. As evidenced by the simulations and experiments, the best layout is the 1° conical plates.
- (3)
- By avoiding the sticking of the friction components, 37.73% of the drag torque is reduced and the transmitted torque is reduced by 10.31%. Since the separation status occupies most of the operating time, the trade-off is acceptable. In addition, under higher-piston-pressure conditions, the influence on the transmitted torque, but not the drag torque, can be reduced.
Author Contributions
Conceptualization, B.M. and C.X.; methodology, S.Y.; software, B.F.; validation, L.Y. and S.Y.; formal analysis, Q.Z.; investigation, Q.Z.; resources, B.M.; data curation, B.F.; writing—original draft preparation, Q.Z.; writing—review and editing, L.Y.; visualization, Q.Z.; supervision, C.X.; project administration, B.M.; funding acquisition, B.M., C.X., L.Y. and S.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant numbers 52205047, 52175037, and 51805289; the Frontier Cross Project of Beijing Institute of Technology, grant number 2024CX11006; and Shandong Provincial Natural Science Foundation, grant number ZR2024QE531. The APC was funded by the National Natural Science Foundation of China, grant number 51805289.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Shufa Yan was employed by the company Automotive Research Institute, China National Heavy Duty Truck Group. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Šabík, V.; Futáš, P.; Pribulová, A. Failure analysis of a clutch wheel for wind turbines with the use of casting process simulation. Eng. Fail. Anal. 2022, 135, 106159. [Google Scholar] [CrossRef]
- Zhang, Z.; Mu, Z.; Yu, X. Mechanistic Study of Groove Parameters on the Thermoelastic Instability of Wet Clutch. Lubricants 2025, 13, 150. [Google Scholar] [CrossRef]
- Wu, J.; Wang, L.; Li, L.; Shu, Y.; Yang, L.; Lei, T.J.M. Sliding State Analysis of Fractal Rough Interface Based on the Finite Element Method. Materials 2021, 14, 2121. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Liu, Y.; Chen, H.; Chen, Y.; Xie, D. An investigation into the failure mechanism of severe abrasion of high-speed train brake discs on snowy days. Eng. Fail. Anal. 2019, 101, 121–134. [Google Scholar] [CrossRef]
- Zhang, Z.; Zou, L.; Liu, H.; Feng, J.; Chen, Z. Response Characteristics of Dynamic Torque for Wet Clutch Engagement: A Numerical and Experimental Study. Shock Vib. 2021, 2021, 5522998. [Google Scholar] [CrossRef]
- Pointner-Gabriel, L.; Schermer, E.; Schneider, T.; Stahl, K. Experimental analysis of oil flow and drag torque generation in disengaged wet clutches. Sci. Rep. 2023, 13, 17193. [Google Scholar] [CrossRef]
- Falade, A.; Brenner, H. First-order wall curvature effects upon the Stokes resistance of a spherical particle moving in close proximity to a solid wall. J. Fluid Mech. 1988, 193, 533–568. [Google Scholar] [CrossRef]
- Yuan, Y.; Liu, E.A.; Hill, J.; Zou, Q. An Improved Hydrodynamic Model for Open Wet Transmission Clutches. J. Fluids Eng. 2006, 129, 333–337. [Google Scholar] [CrossRef]
- Jakubov, T.S.; Mainwaring, D.E. The surface tension of a solid at the solid–vacuum interface, an evaluation from adsorption and wall potential calculations. J. Colloid Interface Sci. 2007, 307, 477–480. [Google Scholar] [CrossRef]
- Pointner-Gabriel, L.; Flamm, S.; Menzel, M.; Voelkel, K.; Stahl, K. Experimental investigation of drag loss and plate separation behavior of wet clutches under external forces. Results Eng. 2024, 24, 102918. [Google Scholar] [CrossRef]
- Mahmud, S.F.; Pahlovy, S.A.; Kubota, M.; Ogawa, M.; Takakura, N. Multi-Phase Simulation for Studying the Effect of Different Groove Profiles on the Drag Torque Characteristics of Transmission Wet Clutch; 2016-01-1144; SAE International: Warrendale, PA, USA, 2016. [Google Scholar]
- Fish, R.L. Using the SAE #2 Machine to Evaluate Wet Clutch Drag Losses. SAE Trans. 1991, 100, 1041–1054. [Google Scholar]
- Pointner-Gabriel, L.; Menzel, M.; Voelkel, K.; Schneider, T.; Stahl, K. Experimental investigation of drag loss behavior of dip-lubricated wet clutches for building a data-driven prediction model. Sci. Rep. 2024, 14, 9241. [Google Scholar] [CrossRef] [PubMed]
- Leister, R.; Najafi, A.F.; Gatti, D.; Kriegseis, J.; Frohnapfel, B. Non-dimensional characteristics of open wet clutches for advanced drag torque and aeration predictions. Tribol. Int. 2020, 152, 106442. [Google Scholar] [CrossRef]
- Neupert, T.; Bartel, D. Evaluation of Various Shear-Thinning Models for Squalane Using Traction Measurements, TEHD and NEMD Simulations. Lubricants 2023, 11, 178. [Google Scholar] [CrossRef]
- Hilpert, C.R. Gyroscopically Induced Failure in Multiple Disc Clutches, Its Causes, Its Characteristics and Its Cures. SAE Trans. 1969, 78, 354–371. [Google Scholar]
- Hou, S.; Hu, J.; Peng, Z. Experimental Investigation on Unstable Vibration Characteristics of Plates and Drag Torque in Open Multiplate Wet Clutch at High Circumferential Speed. J. Fluids Eng. 2017, 139, 111103. [Google Scholar] [CrossRef]
- Yu, Y.; Peng, Y.; Lan, S.; Zhou, P. Finite Element Analysis for Wave Spring of Multi-Disc Wet Clutch Based on ANSYS. Appl. Mech. Mater. 2013, 419, 203–208. [Google Scholar] [CrossRef]
- Erfanian-Naziftoosi, H.R.; Shams, S.S.; Elhajjar, R. Composite wave springs: Theory and design. Mater. Des. 2016, 95, 48–53. [Google Scholar] [CrossRef]
- Li, S.-X.; Liao, H.-R.; Li, S.-C.; Chen, L.; Li, Q.-Z.; Cheng, T.-F.; Chen, K.-Y. Effect of structural parameters on the bearing characteristics of wave spring. J. Mach. Des. 2020, 37, 22–27. [Google Scholar] [CrossRef]
- Yan, Z.; Wu, B.; Gao, X.; Bai, X. Engagement/Disengagement Characteristics of Pull-Type Diaphragm Spring Clutch for Heavy-Duty Commercial Vehicles. Chin. J. Mech. Eng. 2024, 37, 124. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, C.; Yang, X.; Niu, Y.; Bao, H.; Zhu, R. Study on the engagement characteristics of wet multi-plate friction clutch based on separating spring. Forsch. Im Ingenieurwesen 2024, 88, 3. [Google Scholar] [CrossRef]
- Wu, J.; Cui, J.; Shu, W.; Wang, L.; Li, H. Coupling mechanism and data-driven approaches for high power wet clutch torque modeling and analysis. Tribol. Int. 2024, 191, 109166. [Google Scholar] [CrossRef]
- Zhao, Q.; Ma, B.; Yu, L.; Zhang, Y.; Dong, Y.; Zhou, R. Numerical and experimental studies on the thermodynamic characteristics of post-buckling separate plate in the clutch. Tribol. Int. 2024, 195, 109607. [Google Scholar] [CrossRef]
- Matsuoka, T. Study on Effect of Oiliness Agents in the Presence of Detergents on Friction Characteristics of Paper-Based Friction Materials Under Low Sliding Velocity. Jpn. J. Tribol. 2002, 47, 488–497. [Google Scholar]
- Greenwood, J.; Williamson, J. Contact of Nominally Flat Surfaces. Proc. R. Soc. Lond. 1966, 295, 300–319. [Google Scholar] [CrossRef]
- Jung, W.; Hyeon, J.; Doh, N. Robust Cuboid Modeling from Noisy and Incomplete 3D Point Clouds Using Gaussian Mixture Model. Remote Sens. 2022, 14, 5035. [Google Scholar] [CrossRef]
- Bao, H.; Xu, T.; Jin, G.; Huang, W. Analysis of Dynamic Engaged Characteristics of Wet Clutch in Variable Speed Transmission of a Helicopter. Processes 2020, 8, 1474. [Google Scholar] [CrossRef]
- Zheng, L.; Ma, B.; Chen, M.; Yu, L.; Xue, J. Numerical studies on the dynamic characteristics of a wet multi-disc clutch during the disengaging process. J. Mech. Sci. Technol. 2022, 36, 3277–3289. [Google Scholar] [CrossRef]
- Shutin, D.; Kazakov, Y. Theoretical and Numerical Investigation of Reduction of Viscous Friction in Circular and Non-Circular Journal Bearings Using Active Lubrication. Lubricants 2023, 11, 218. [Google Scholar] [CrossRef]
- Yu, L.; Ma, B.; Chen, M.; Li, H.; Liu, J.; Li, M. Investigation on the failure mechanism and safety mechanical-thermal boundary of a multi-disc clutch. Eng. Fail. Anal. 2019, 103, 319–334. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).