Research on Ground Contact Characteristics and Influencing Factors of Tires with Complex Tread Patterns Based on Inverse Modeling
Abstract
1. Introduction
2. Tire Finite Element Modeling
2.1. Finite Element Model of a Tire with Complex Tread Patterns
2.2. Material Characteristics
3. Experimental Verification
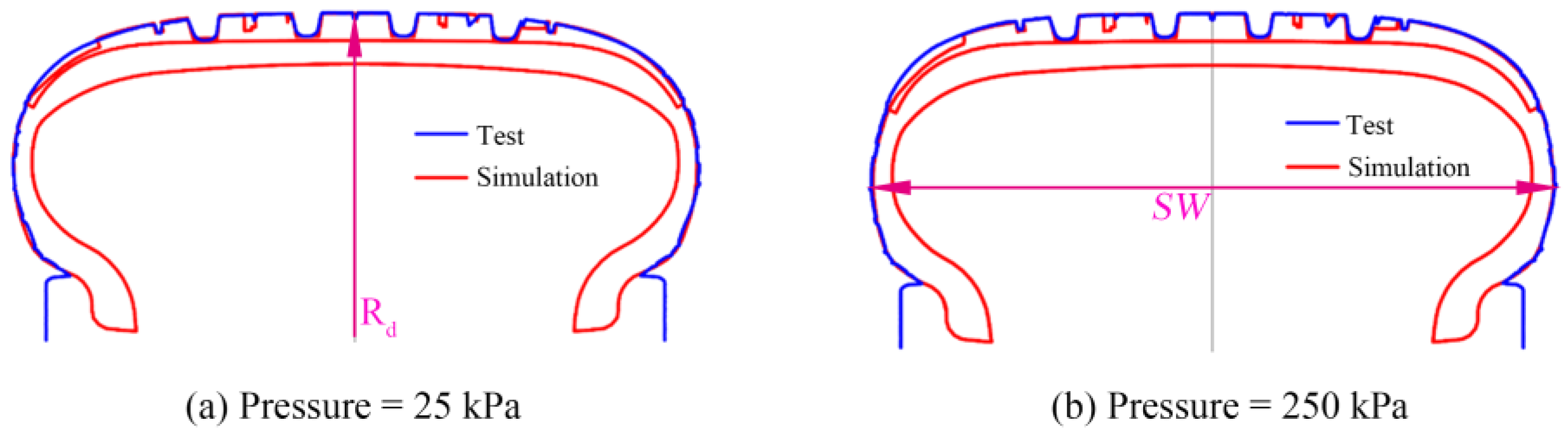
3.1. Tire Inflation Contour Scanning Test
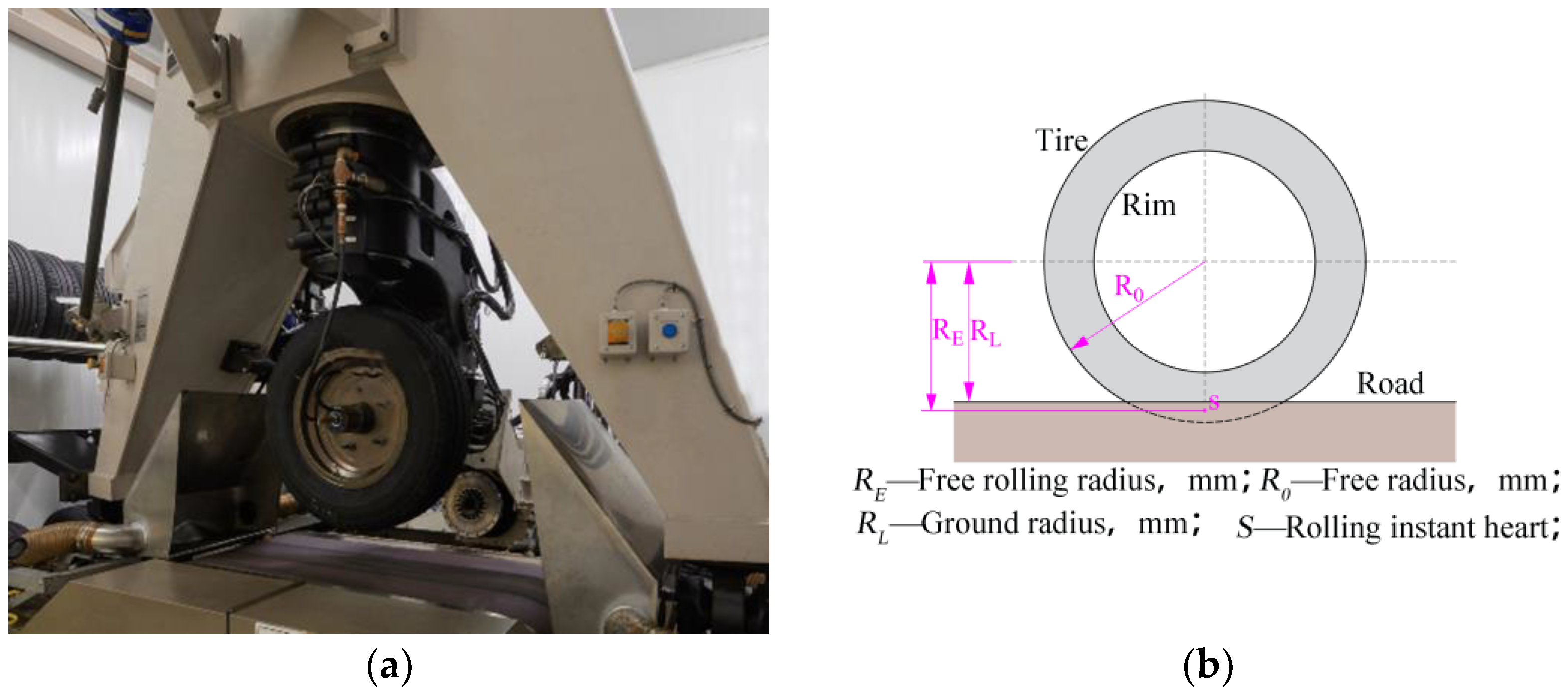
3.2. Tire Free-Rolling Test
4. Results and Discussion
4.1. Definition and Influencing Factors of Tire–Road Contact Geometric Characteristics
4.2. Inflation Pressure
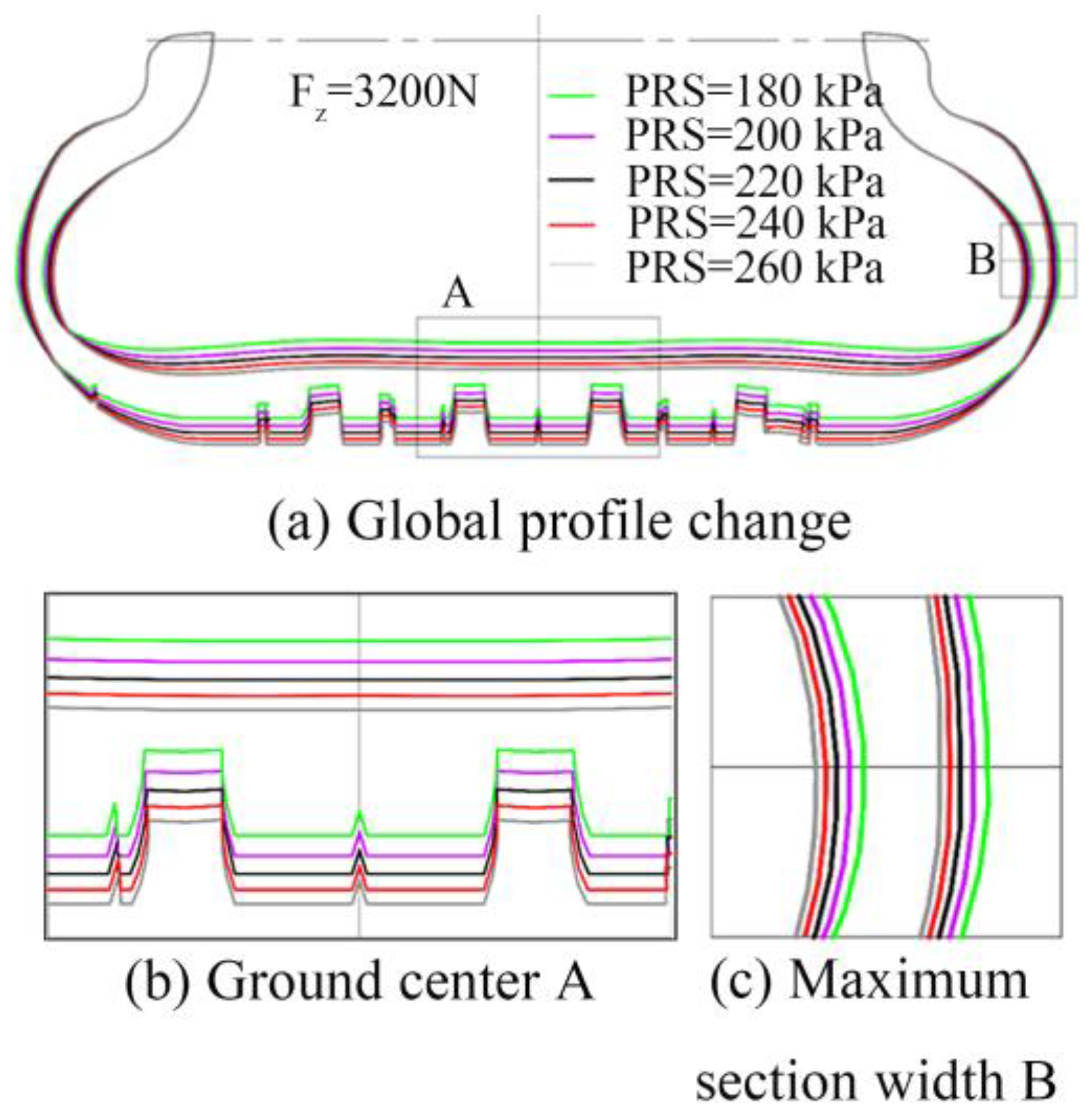
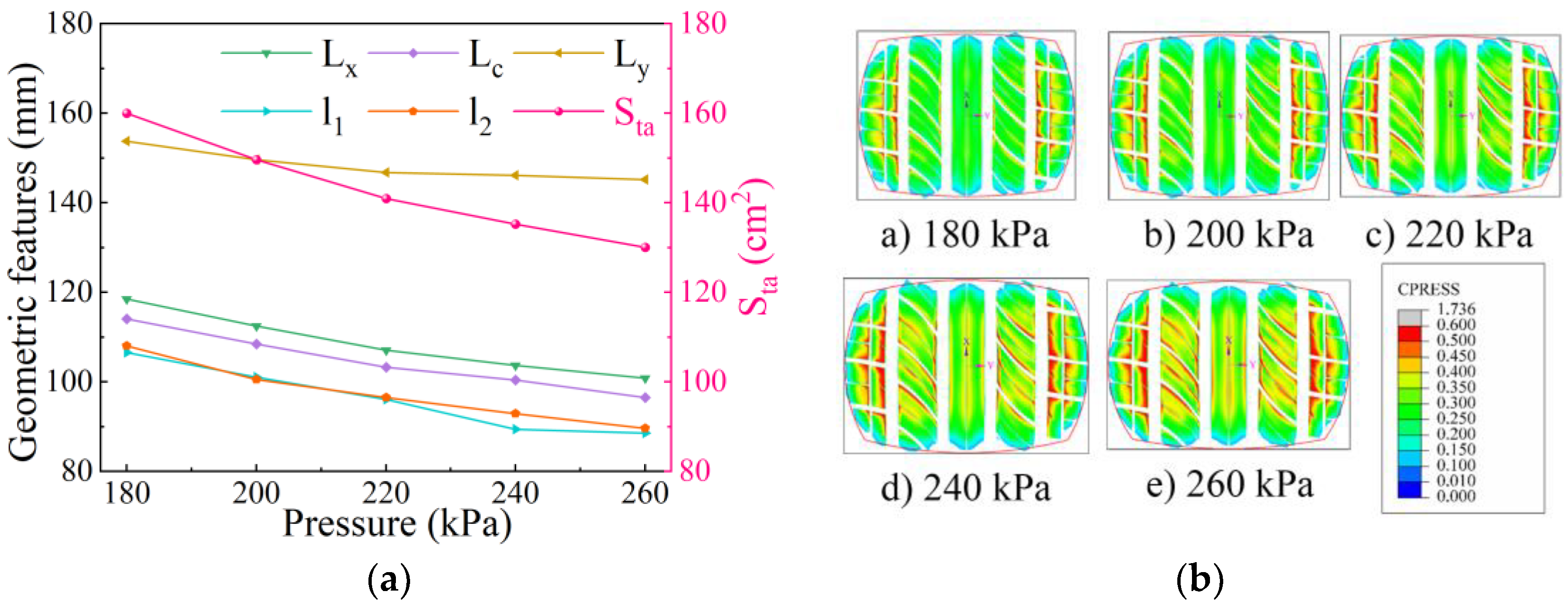
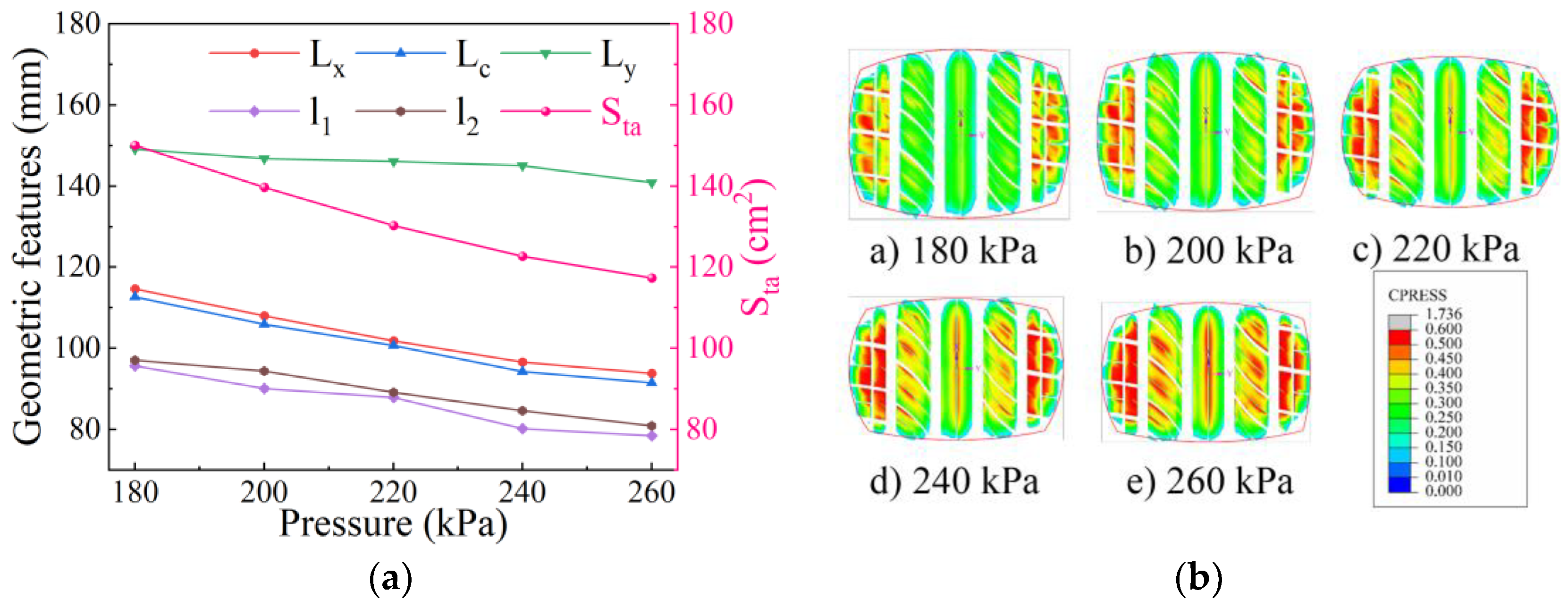
4.2.1. Influence of Inflation Pressure on Static Contact Characteristics
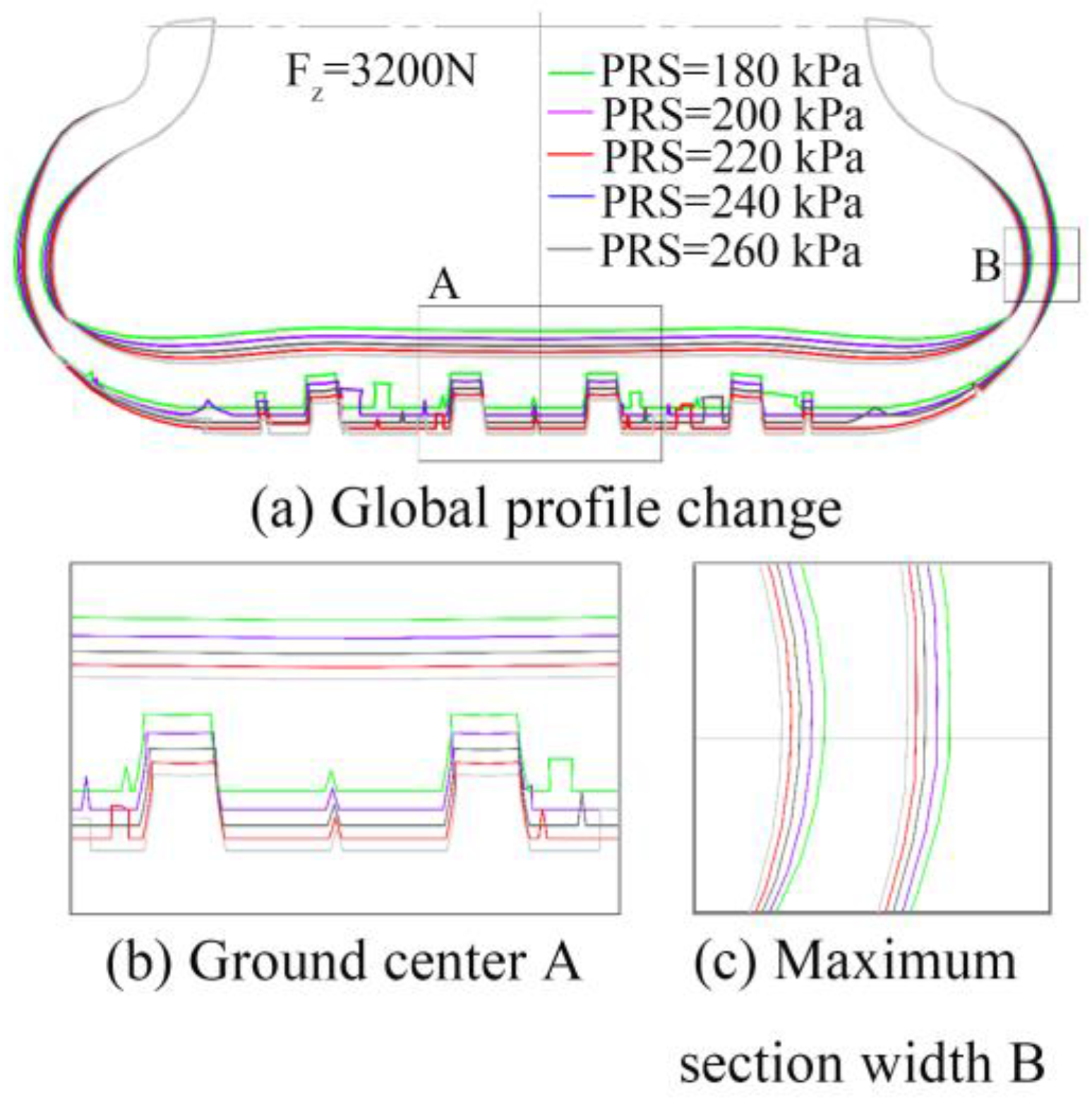
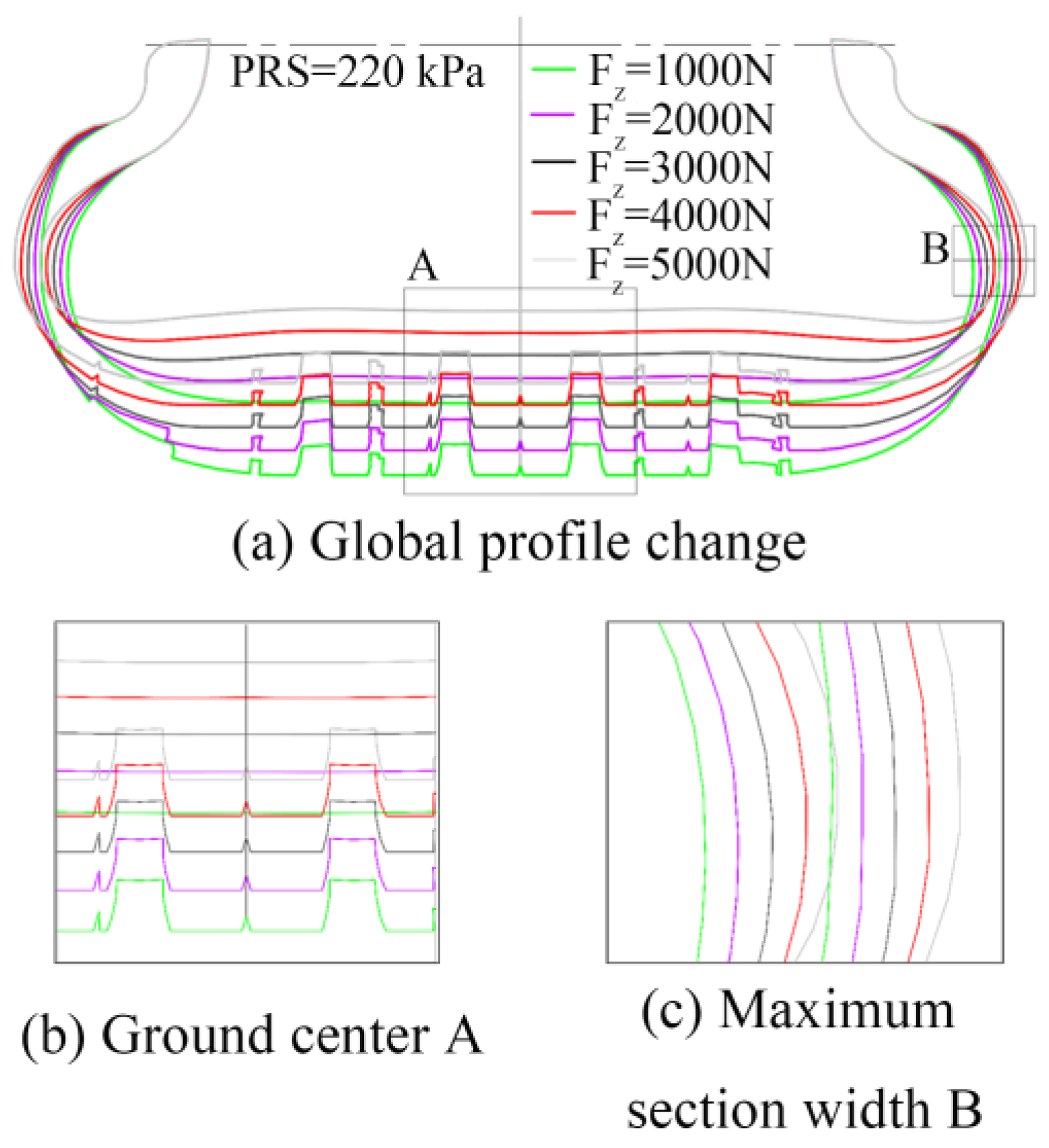
4.2.2. Influence of Inflation Pressure on Contact Characteristics of Free-Rolling Tires
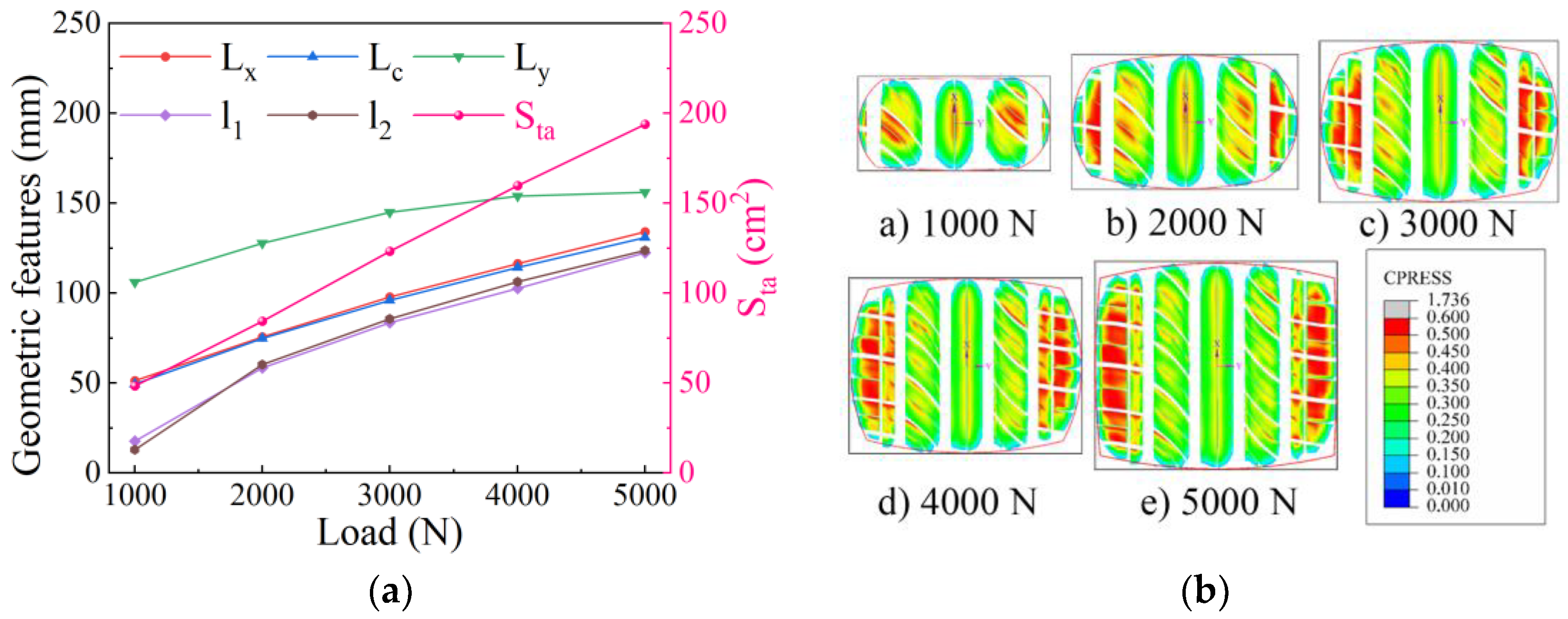
4.3. Radial Load
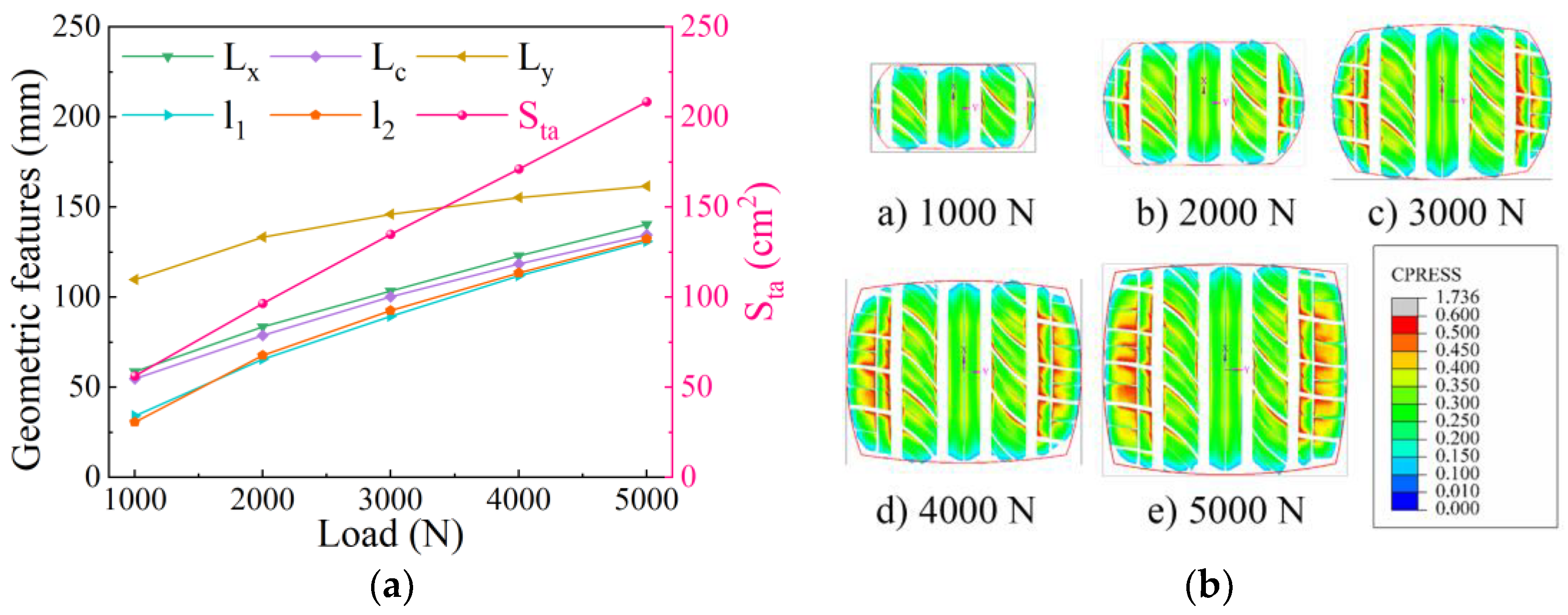
4.3.1. Influence of Radial Load on Static Contact Characteristics
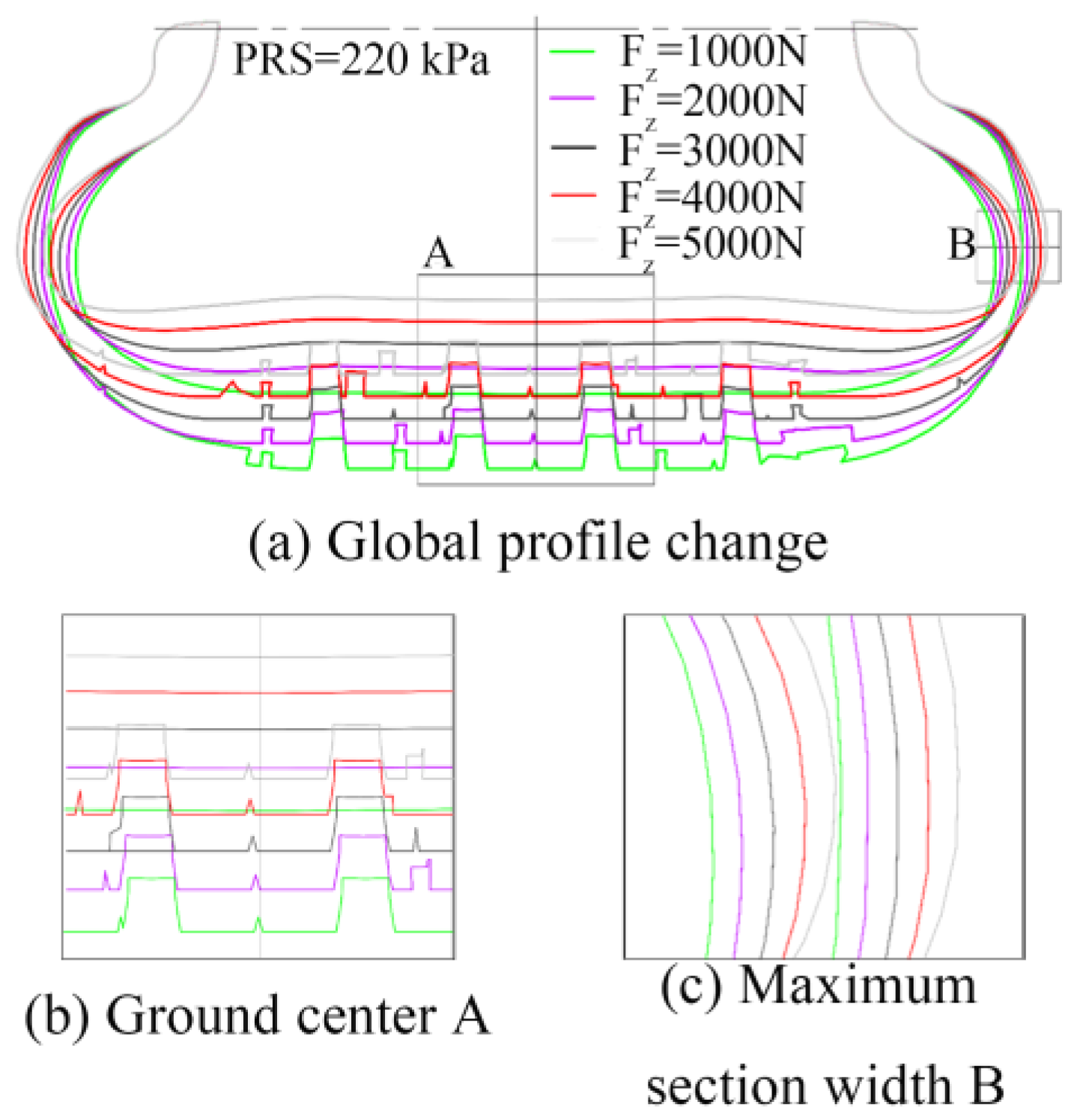
4.3.2. Influence of Radial Load on Contact Characteristics of Free-Rolling Tires
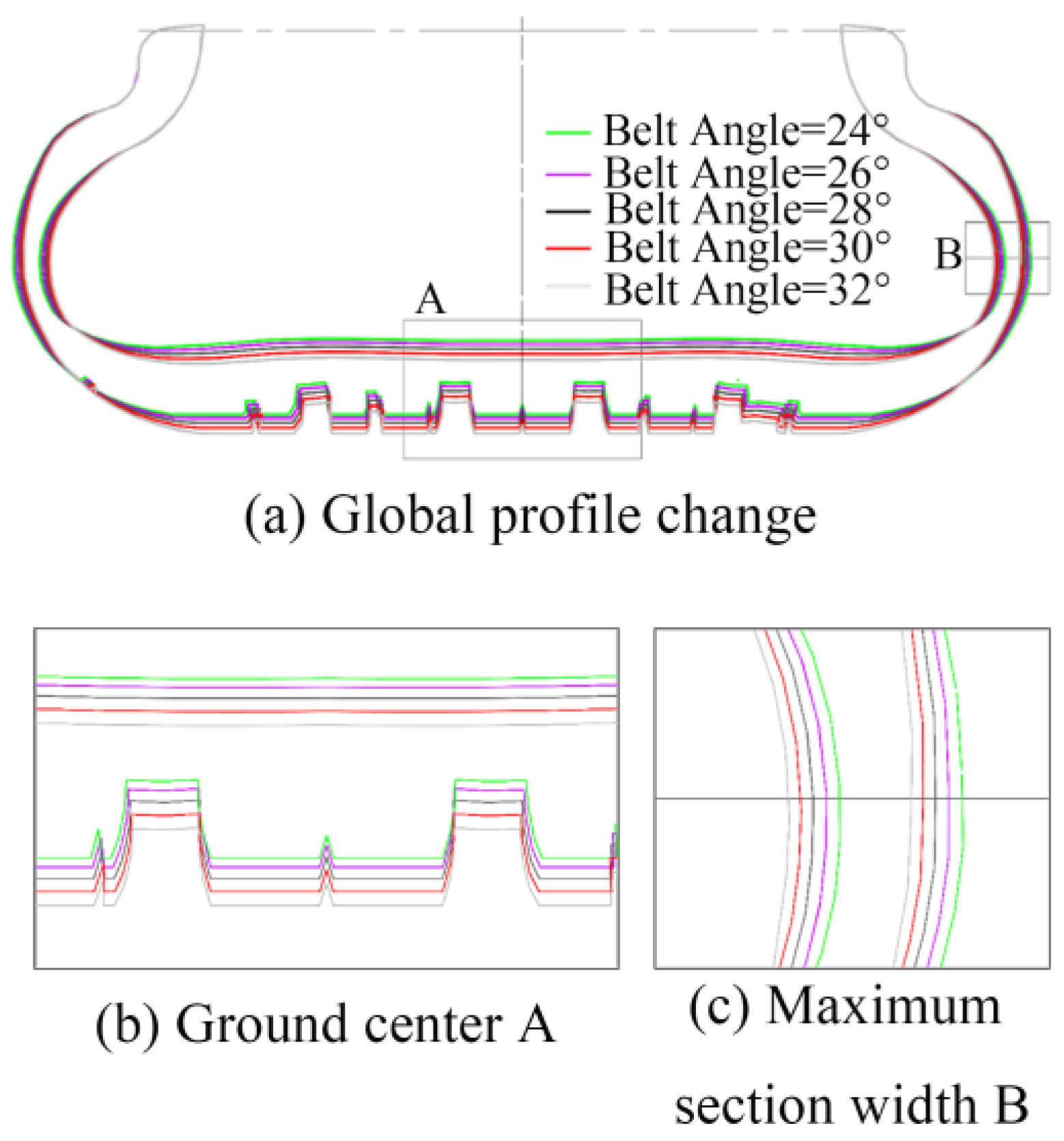
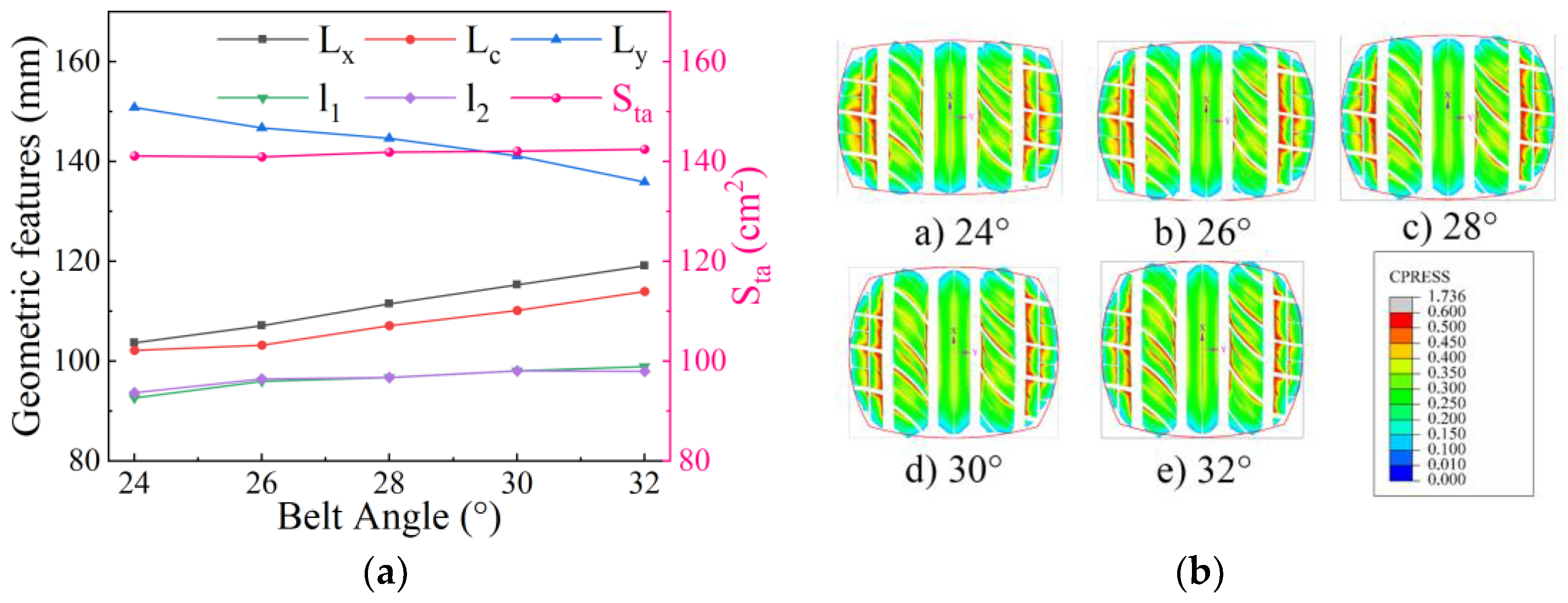
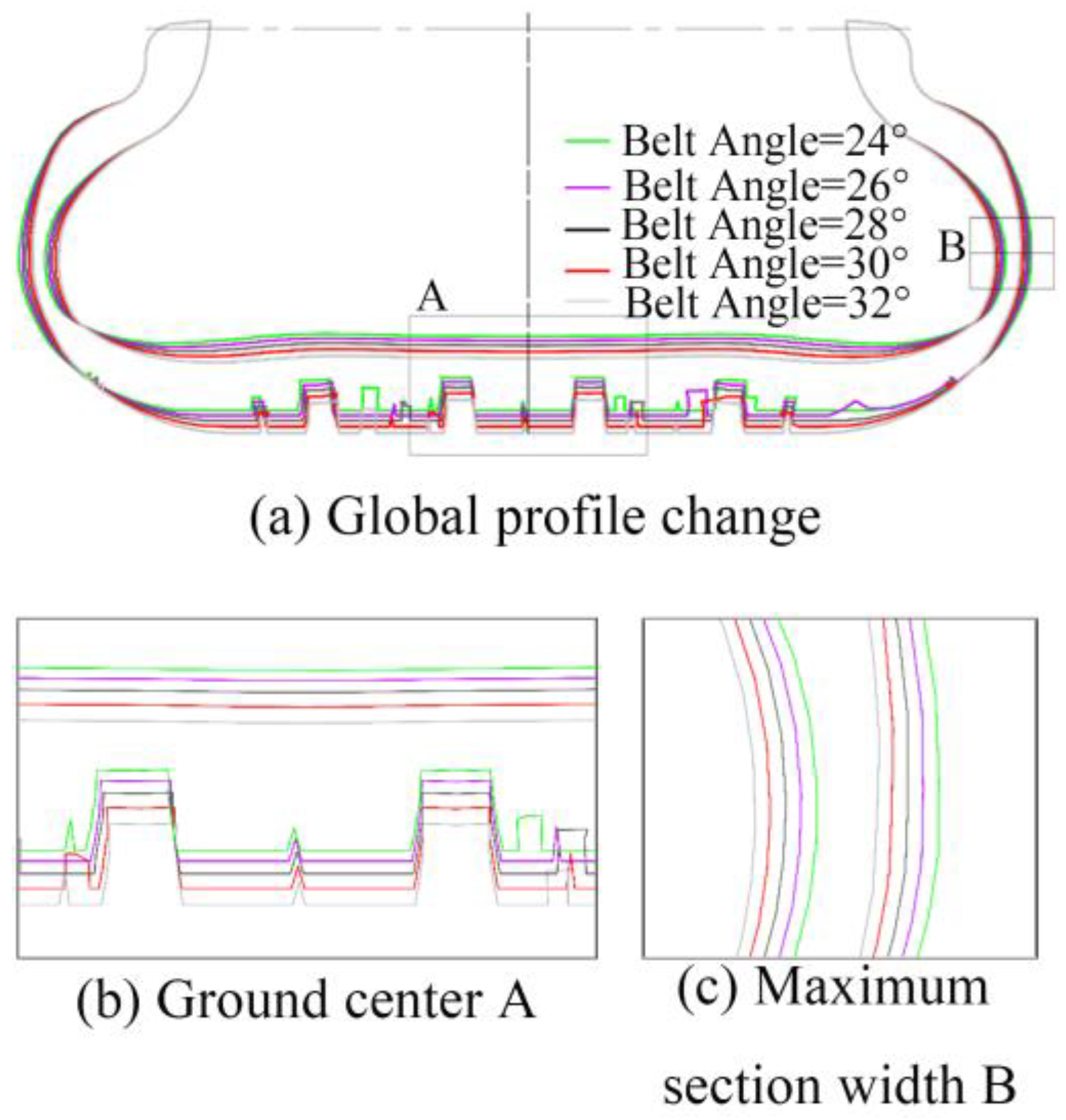
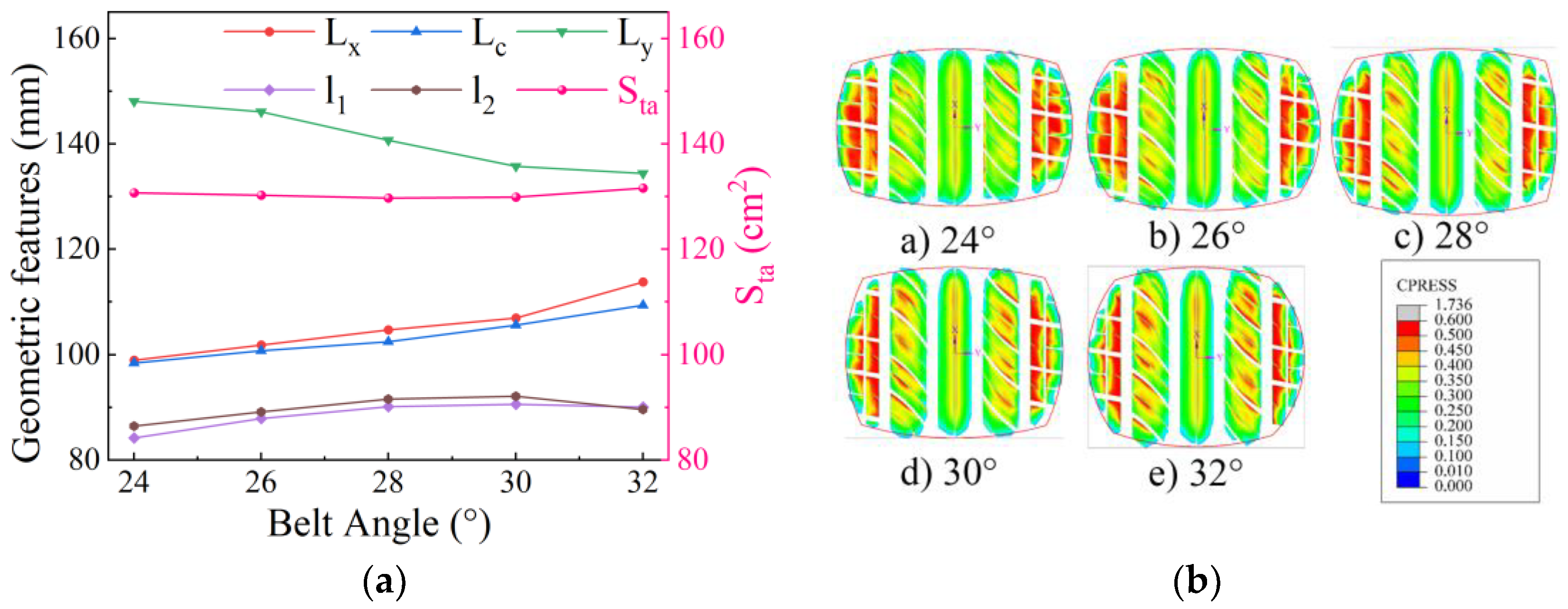
4.4. Belt Angle
4.4.1. Influence of Belt Angle on Static Contact Characteristics
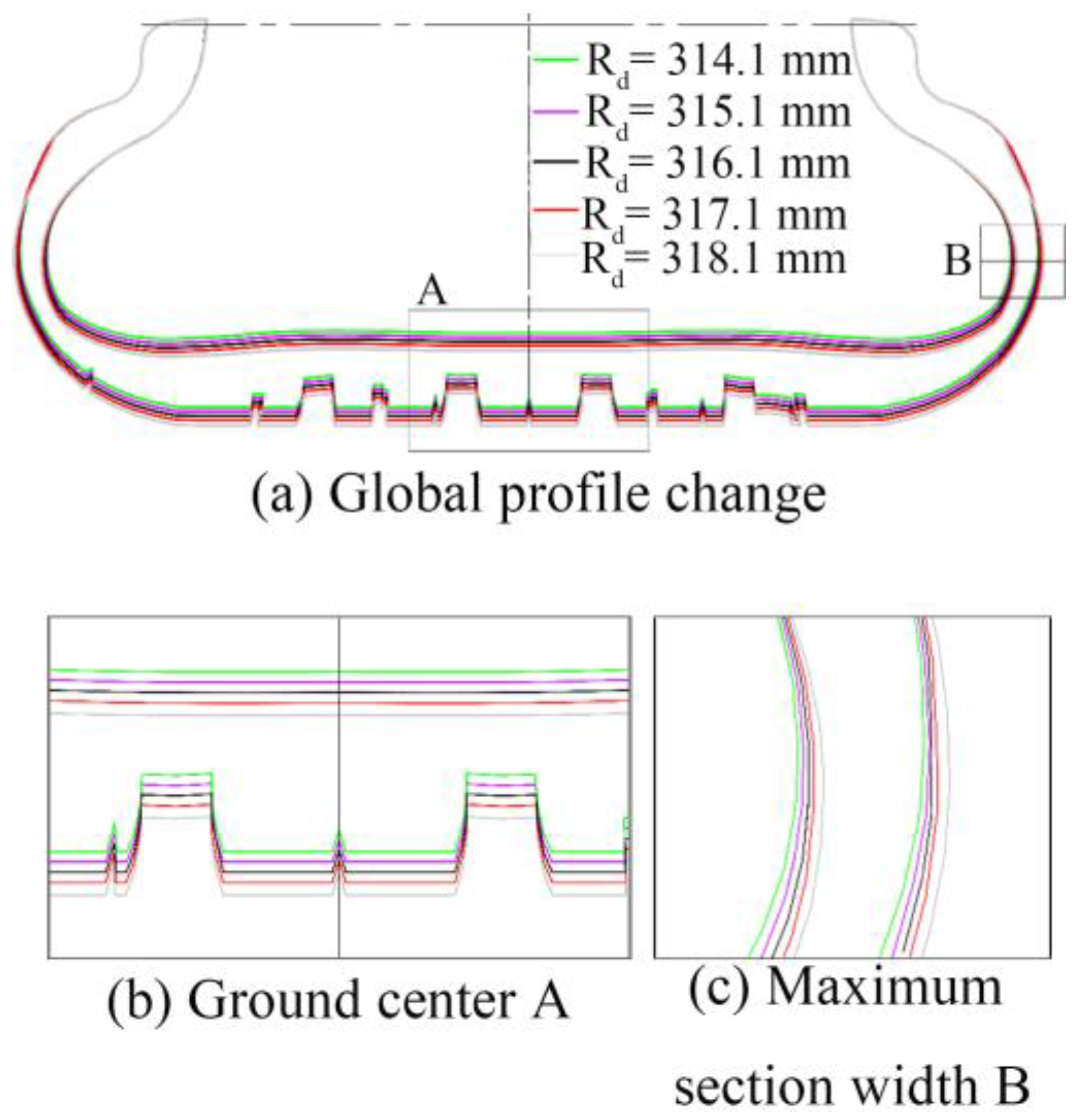
4.4.2. Influence of Belt Angle on Contact Characteristics of Free-Rolling Tires
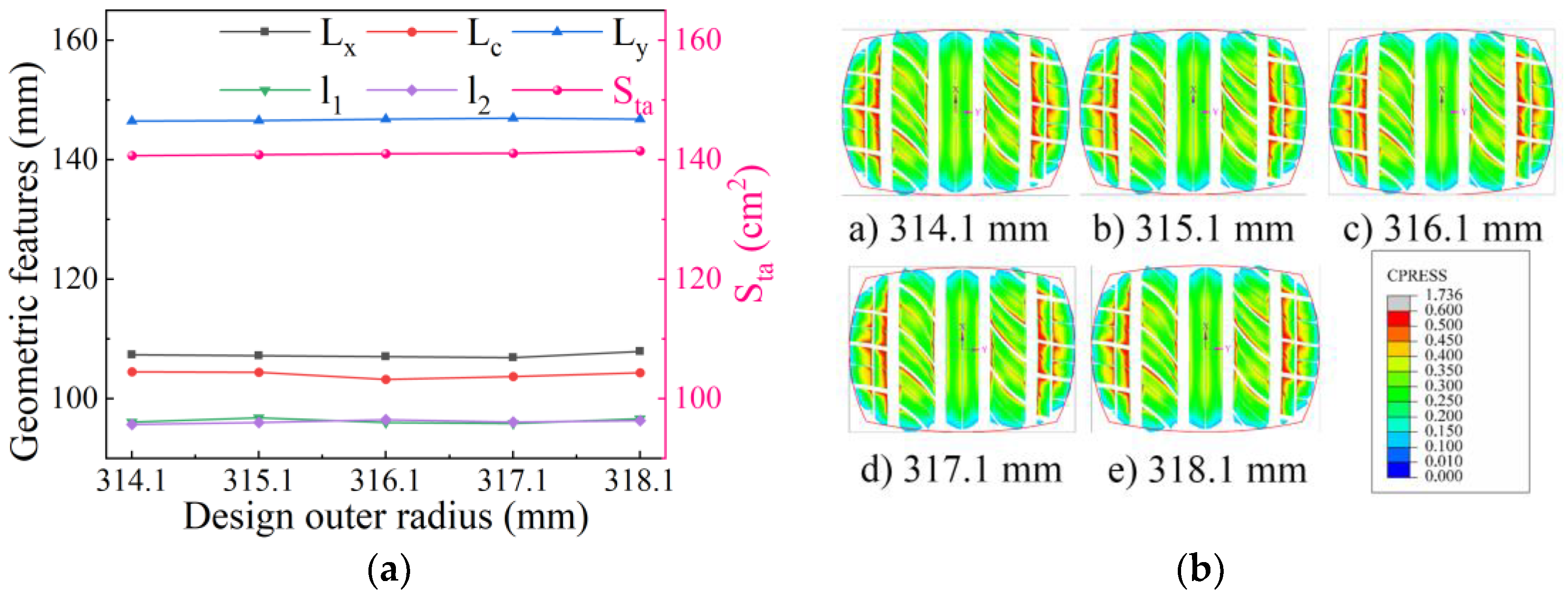
4.5. Design Outer Radius
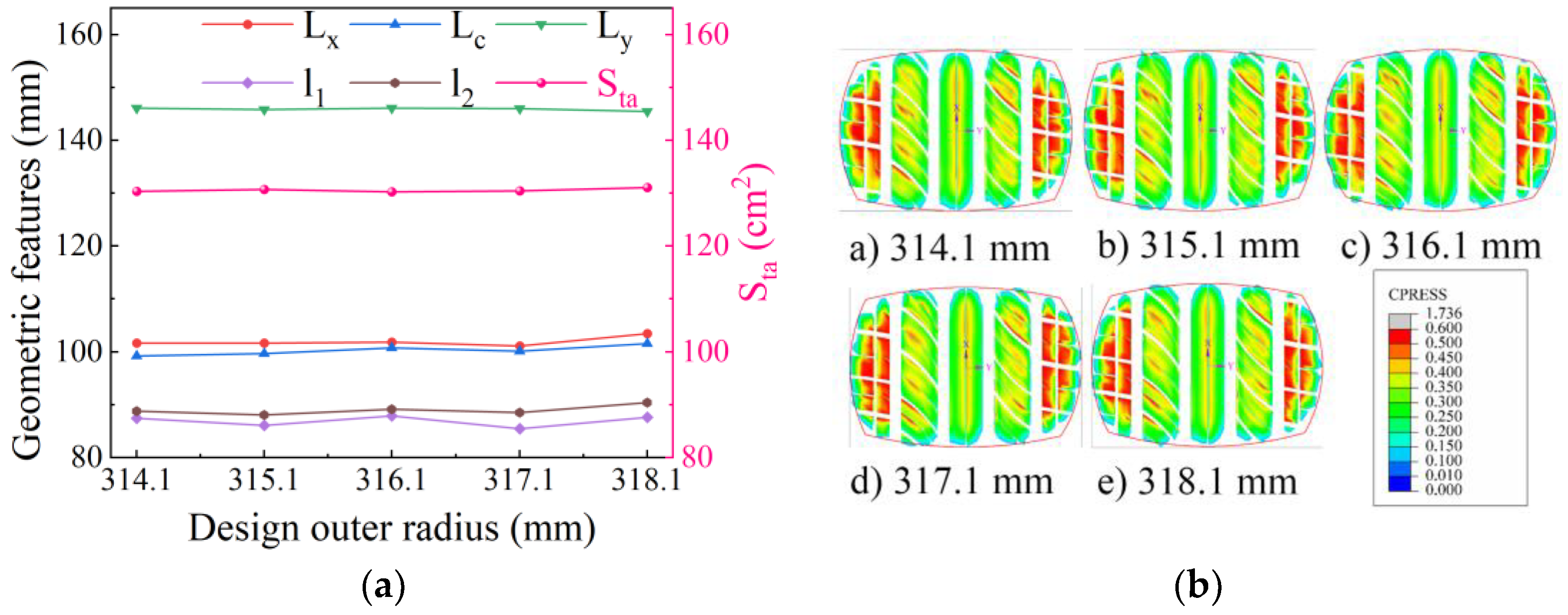
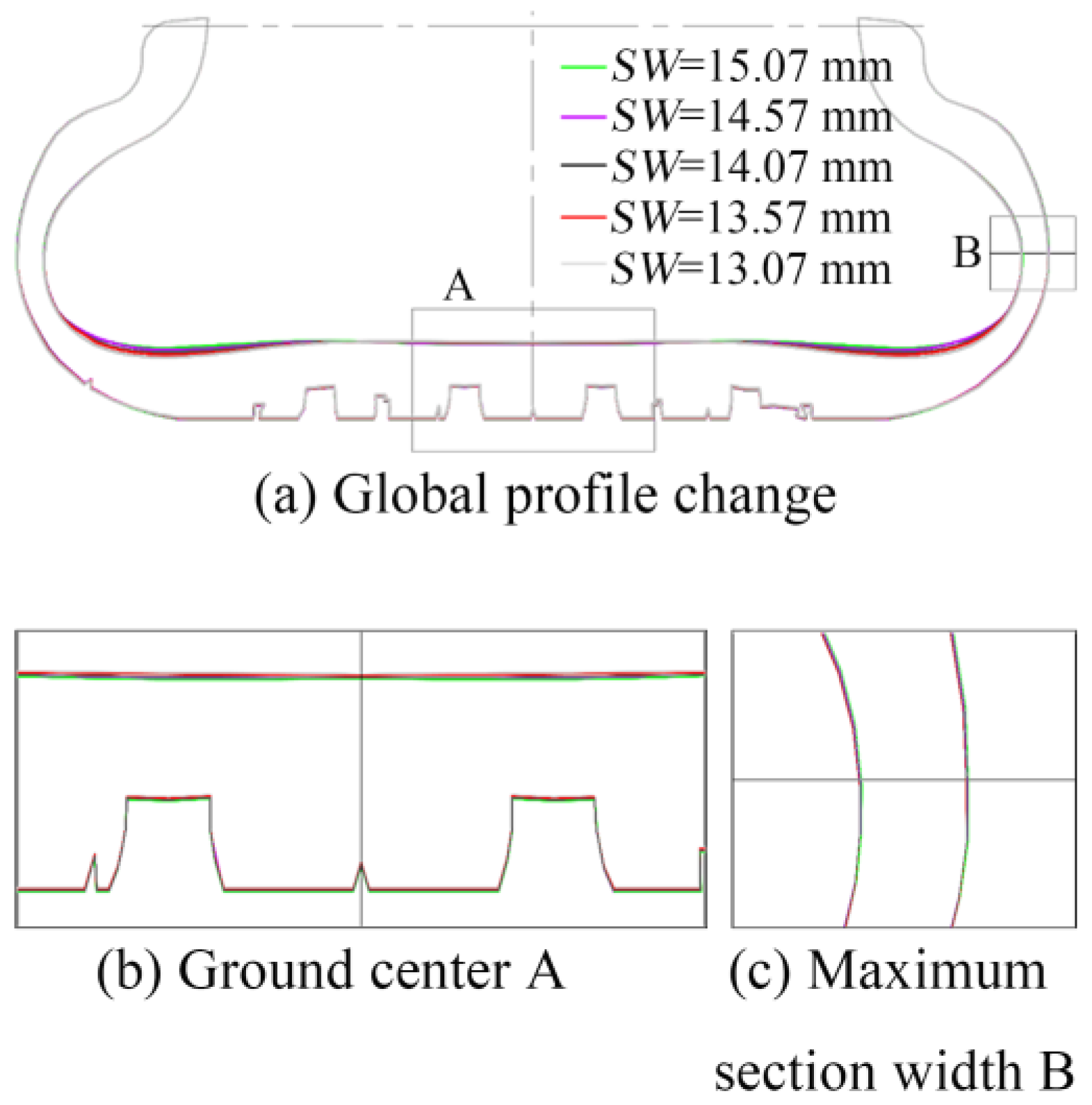
4.5.1. Influence of Design Outer Radius on Static Contact Characteristics
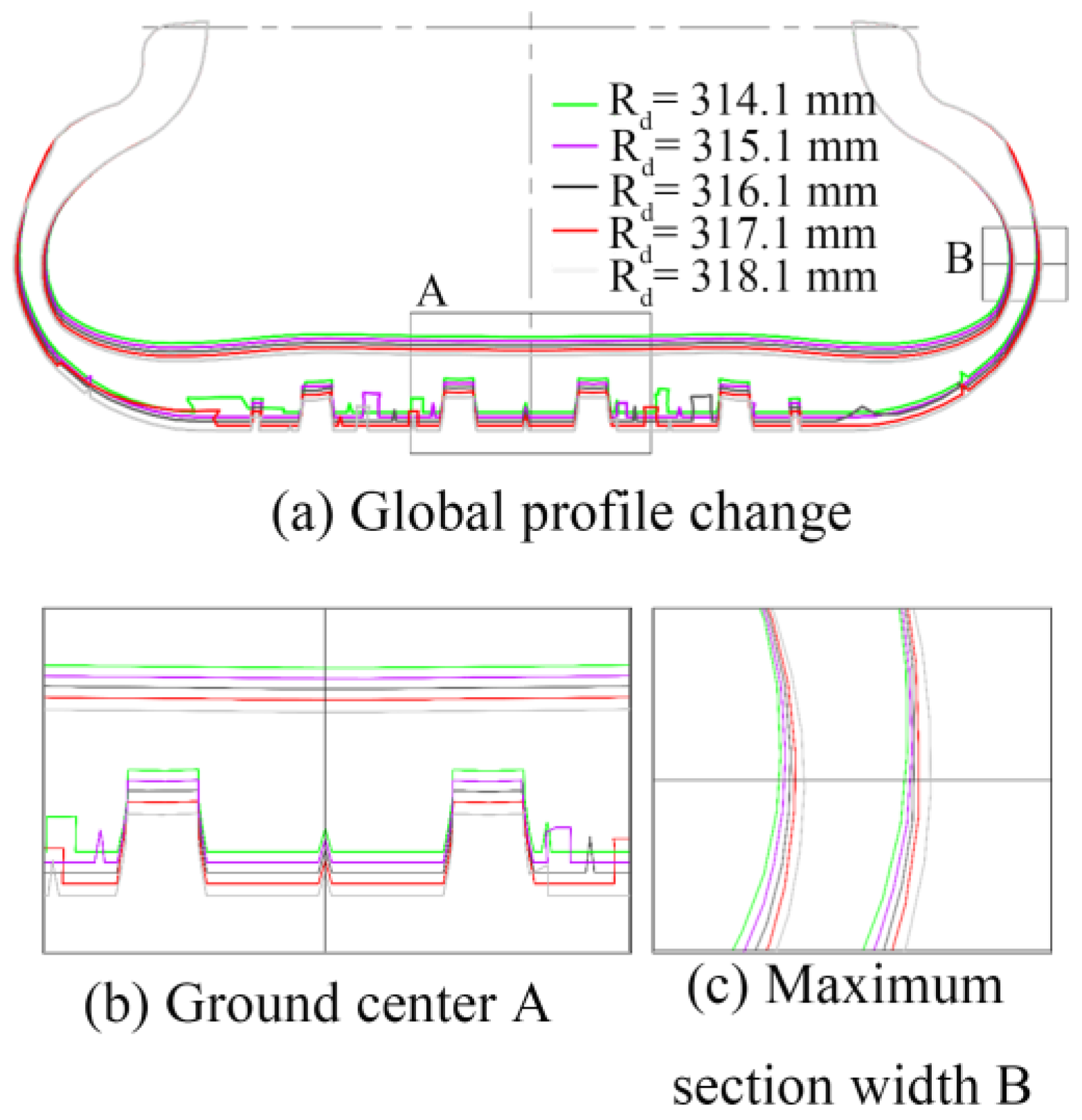
4.5.2. Influence of Design Outer Radius on Contact Characteristics of Free-Rolling Tires
4.6. Shoulder Thickness
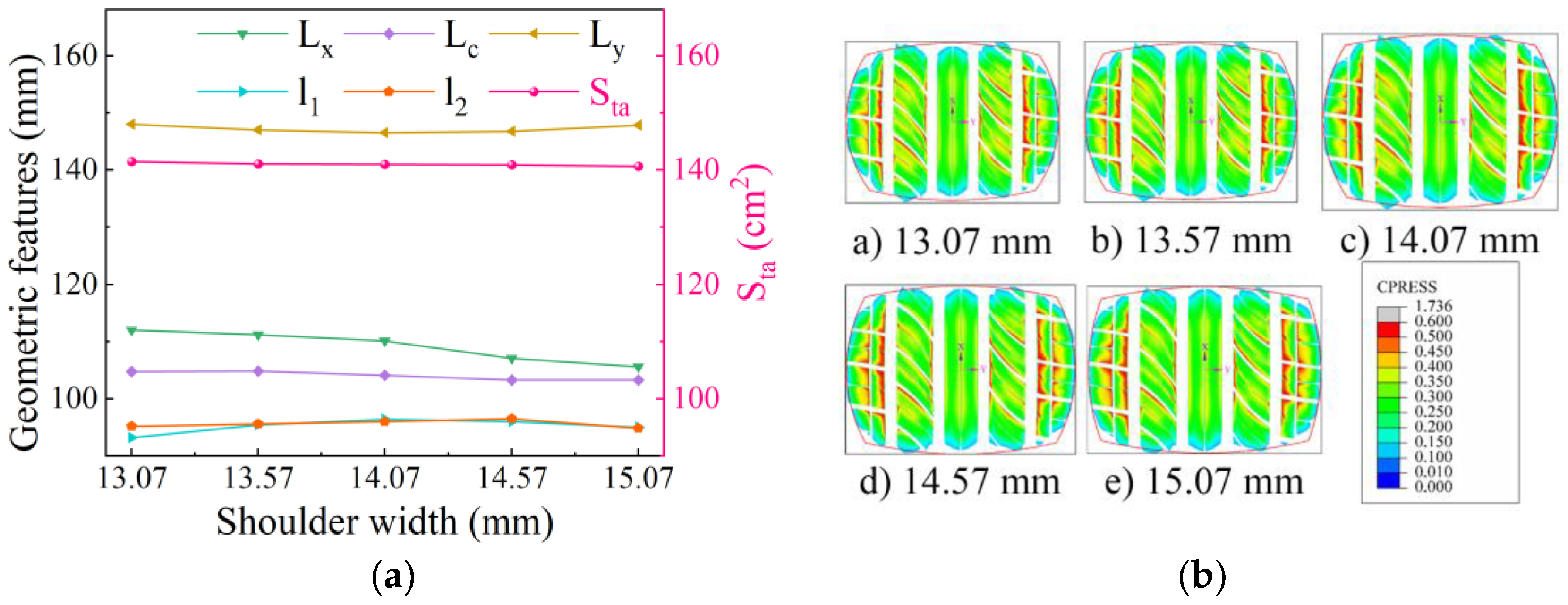
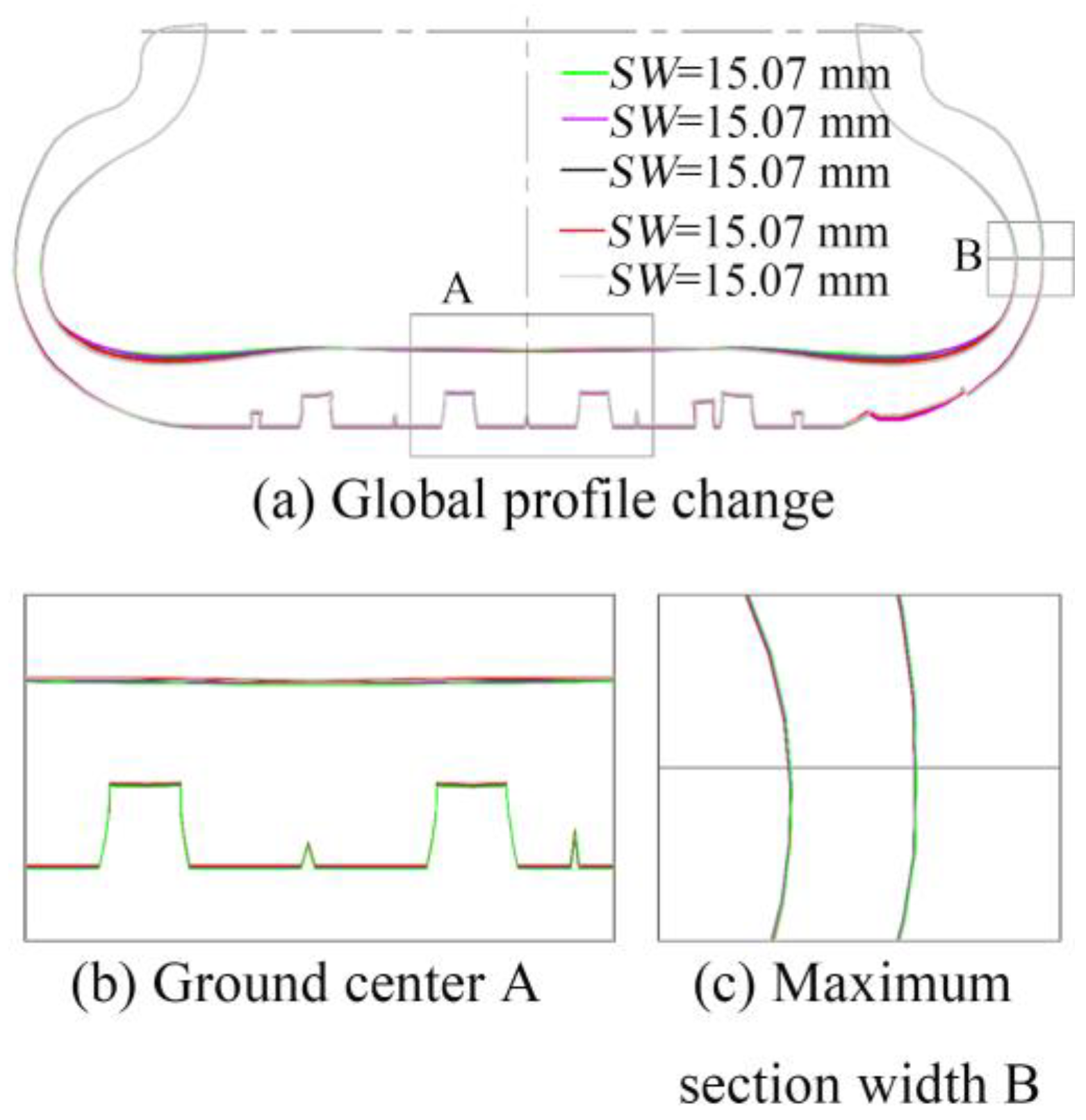
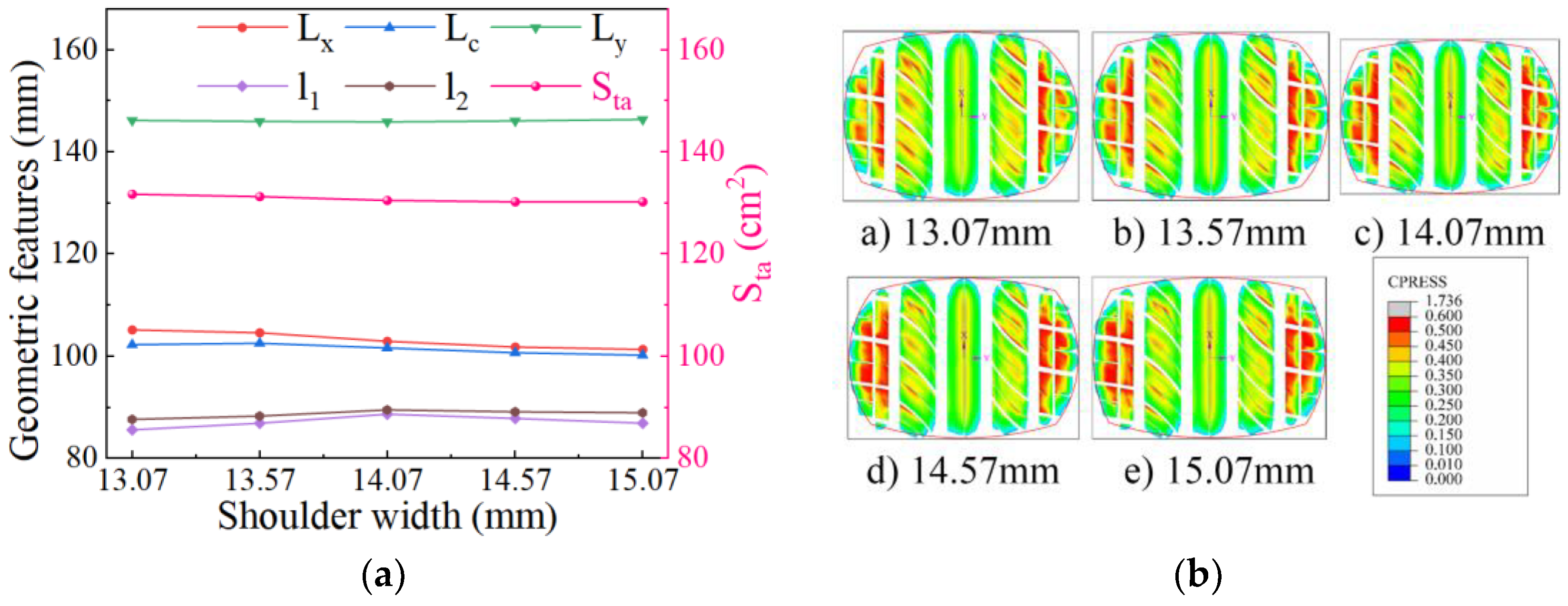
4.6.1. Influence of Shoulder Thickness on Static Contact Characteristics
4.6.2. Influence of Shoulder Thickness on Contact Characteristics of Free-Rolling Tires
5. Conclusions
- (1)
- Elevated inflation pressure systematically induces three static effects: crown curvature expansion, contact area linear contraction, and groove-wall stress concentration peaks. Concurrently in free rolling, pressure amplification exacerbates contact stress heterogeneity, ultimately inducing accelerated localized fatigue wear cyclic deterioration.
- (2)
- The radial load is positively correlated with the maximum section width and deformation of the lower tire sidewall, but negatively correlated with the ground contact radius. As the radial load increases, the ground contact shape progressively transforms from an elliptical shape to a rectangular form, and the asymmetry of the ground contact pressure distribution increases; the ground contact pressure of the shoulder pattern block increases more than that of the middle pattern block, and finally forms a saddle shape with high shoulders and a low middle.
- (3)
- Under fixed operating conditions, an increase in the belt angle weakens the belt’s reinforcing effect on the tire, while the bending effect of the upper sidewall intensifies, leading to crown buckling under bending stress. Compared to static contact characteristics, the tire’s effective ground contact area decreases in the rolling state, causing stress concentration at the tread groove edges.
- (4)
- An increase in the tire’s designed outer radius has a greater impact on the crown portion above the maximum section width, contributing to improved vehicle handling stability and driving economy through controlled outer radius design. In the free-rolling state, an increase in the designed outer radius alters the symmetry of the contact length in the shoulder area, reduces the effective contact area, and intensifies stress concentration.
- (5)
- Adjustments in shoulder design thickness at 85% of the tire’s tread width show the same trend for dynamic and static contact characteristics. However, the asymmetry of the ground contact footprint length is more pronounced in rolling conditions, and the ground contact pressure is significantly higher than in static conditions. Within the adjustment range, the ground contact length of the right tread block exhibits significant variation between static and free-rolling conditions due to asymmetric ground contact.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Baranowski, P.; Malachowski, J.; Mazurkiewicz, L. Local blast wave interaction with tire structure. Def. Technol. 2020, 16, 520–529. [Google Scholar] [CrossRef]
- Zang, L.; Peng, X.; Sun, J.; Cui, S.; Bai, Y. Investigation on structural design and grounding characteristics of two dimensional double-u honeycomb non-pneumatic tires. Eur. J. Mech. A Solids 2025, 111, 105599. [Google Scholar] [CrossRef]
- Sim, J.; Hong, J.; Cho, I.; Lee, J. Analysis of vertical stiffness characteristics based on spoke shape of non-pneumatic tire. Appl. Sci. 2021, 11, 2369. [Google Scholar] [CrossRef]
- Zhou, H.; Li, H.; Liang, C.; Zhang, L.; Wang, G. Relationship between tire ground characteristics and vibration noise. Strojniski Vestn. J. Mech. Eng. 2021, 67, 11–26. [Google Scholar] [CrossRef]
- Aguilar, J.J.C.; Carrillo, J.A.C.; Fernández, A.J.G.; Pozo, P.S. Optimization of an optical test bench for tire properties measurement and tread defects characterization. Sensors 2017, 17, 707. [Google Scholar] [CrossRef]
- Xia, K.; Yang, Y. Three-dimensional finite element modeling of tire/ground interaction. Int. J. Numer. Anal. Methods Geomech. 2012, 36, 498–516. [Google Scholar] [CrossRef]
- Fathi, H.; El-Sayegh, Z.; Ren, J.; El-Gindy, M. Analysis of Tire-Road interaction: A literature review. Machines 2024, 12, 812. [Google Scholar] [CrossRef]
- Farhadi, P.; Golmohammadi, A.; Sharifi, A.; Shahgholi, G. Potential of three-dimensional footprint mold in investigating the effect of tractor tire contact volume changes on rolling resistance. J. Terramech. 2018, 78, 63–72. [Google Scholar] [CrossRef]
- Schjønning, P.; Stettler, M.; Keller, T.; Lassen, P.; Lamandé, M. Predicted tyre–soil interface area and vertical stress distribution based on loading characteristics. Soil Tillage Res. 2015, 152, 52–66. [Google Scholar] [CrossRef]
- Pacejka, H.B.; Bakker, E. The magic formula tyre model. Vehicle Syst. Dyn. 1992, 21, 1–18. [Google Scholar] [CrossRef]
- Mavros, G.; Rahnejat, H.; King, P.D. Transient analysis of tyre friction generation using a brush model with interconnected viscoelastic bristles. Proc. Inst. Mech. Eng. Pt. K J. Multi-Body Dyn. 2005, 219, 275–283. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Y.; Gao, Q. In-Plane flexible ring modeling and a nonlinear stiffness solution for heavy-load radial tires. Mech. Syst. Signal Proc. 2022, 171, 108956. [Google Scholar] [CrossRef]
- Zang, L.; Wang, X.; Chen, Y.; Li, Y.; Jin, H.; Yang, G. Investigation on mechanical characteristics of non-pneumatic tire with rhombus structure under complex pavement conditions. Simul. Model. Pract. Theory 2022, 116, 102494. [Google Scholar] [CrossRef]
- Wang, H.; Al-Qadi, I.L.; Stanciulescu, I. Simulation of tyre–pavement interaction for predicting contact stresses at static and various rolling conditions. Int. J. Pavement Eng. 2012, 13, 310–321. [Google Scholar] [CrossRef]
- Chen, B.; Ding, P.; Wei, G.; Xiong, C.; Wang, F.; Yu, J.; Yu, H.; Zou, Y. A Study on the contact characteristics of tires–roads based on pressure-sensitive film technology. Materials 2023, 16, 6323. [Google Scholar] [CrossRef]
- Kang, D.; Lee, M.C.; Cho, S.; Shin, Y. Experimental study on mobility of a vehicle with ctis in soft soil. Int. J. Automot. Technol. 2014, 15, 71–77. [Google Scholar] [CrossRef]
- Shakiba, M.; Gamez, A.; Al-Qadi, I.L.; Little, D.N. Introducing realistic tire–pavement contact stresses into Pavement Analysis Using Nonlinear Damage Approach (PANDA). Int. J. Pavement Eng. 2017, 18, 1027–1038. [Google Scholar] [CrossRef]
- Guo, J.; Ding, P.; Gao, J.; Huang, Z.; Guo, Q.; Yang, X. Numerical simulation of grounding characteristics and temperature field of mine tires under multiple working conditions. Adv. Polym. Technol. 2022, 2022, 3830961. [Google Scholar] [CrossRef]
- Kong, X.; Zhang, J.; Wang, T.; Deng, L.; Cai, C.S. Non-contact vehicle weighing method based on tire-road contact model and computer vision techniques. Mech. Syst. Signal Proc. 2022, 174, 109093. [Google Scholar] [CrossRef]
- Tian, L.; Wang, D.; Su, P.; Wei, Q. A study on the viscoelastic behaviors of tire cords using dynamic mechanical analysis. J. Eng. Fibers Fabr. 2020, 15, 1558925020915195. [Google Scholar] [CrossRef]
- Xie, M.; Tang, H.; Yao, H. Failure Analysis of tire separation in two-sized tires on airbus planes. Eng. Fail. Anal. 2016, 61, 21–27. [Google Scholar] [CrossRef]
- Gipser, M. FTire—The tire simulation model for all applications related to vehicle dynamics. Vehicle Syst. Dyn. 2007, 45, 139–151. [Google Scholar] [CrossRef]
- Mavros, G.; Rahnejat, H.; King, P. Analysis of the transient handling properties of a tyre, based on the coupling of a flexible Carcass—Belt Model with a separate tread incorporating transient viscoelastic frictional properties. Vehicle Syst. Dyn. 2005, 43, 199–208. [Google Scholar] [CrossRef]
- Chen, L.; Sun, P.; Zhou, S.; Meng, J.; Qian, C.; Sun, X. Analysis of cord stress during tire dynamic longitudinal slip. J. Ind. Text. 2023, 53, 15280837231214465. [Google Scholar] [CrossRef]
- Namjoo, M.; Golbakhshi, H. An efficient design tool based on fem for evaluating effects of components properties and operating conditions on interaction of tire with rigid road. J. Cent. S. Univ. 2015, 22, 189–195. [Google Scholar] [CrossRef]
- Mao, R.; Sun, P.; Zhou, S.; Chen, L.; Meng, J.; Yang, W.; Yang, C.; Luo, K. Optimization of tire-ground performance through meshed belt layer structure. J. Ind. Text. 2024, 54, 15280837241275137. [Google Scholar] [CrossRef]
- Meng, J.L.; Sun, P.F.; Zhou, S.T.; Li, Y.; Chen, L.-W.; Mao, R. Study on the influence of belt angle on tire grounding characteristics under longitudinal slip conditions. J. Eng. Fibers Fabr. 2024, 19, 15589250241252633. [Google Scholar] [CrossRef]
- Yunta, J.; Garcia-Pozuelo, D.; Diaz, V.; Olatunbosun, O. Influence of camber angle on tire tread behavior by an on-board strain-based system for intelligent tires. Measurement 2019, 145, 631–639. [Google Scholar] [CrossRef]
- Liu, Q.; Pei, J.; Wang, Z.; Hu, D.; Huang, G.; Meng, Y.; Lyu, L.; Zheng, F. Analysis of tire-pavement interaction modeling and rolling energy consumption based on finite element simulation. Constr. Build. Mater. 2024, 425, 136101. [Google Scholar] [CrossRef]
- Liang, C.; Shan, M.; Wang, G.; Zhu, D.; Chen, X. A method for tire wet grip performance evaluation based on grounding characteristics. Proc. Inst. Mech. Eng. D J. Automob. Eng. 2022, 236, 109–117. [Google Scholar] [CrossRef]
- Oubahdou, Y.; Wallace, E.-R.; Reynaud, P.; Picoux, B.; Dopeux, J.; Petit, C.; Nélias, D. Effect of the tire—Pavement contact at the surface layer when the tire is tilted in bend. Constr. Build. Mater. 2021, 305, 124765. [Google Scholar] [CrossRef]
- Du, X.; Zhao, Y.; Wang, Q.; Fu, H.; Lin, F. Grounding characteristics of a non-pneumatic mechanical elastic tire in a rolling state with a camber angle. Strojniski Vestn. J. Mech. Eng. 2019, 65, 287–296. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, Z.; Liu, T.; Liang, W.; Shen, H.; Xiao, Z. Static and dynamic mechanical characteristics of honeycomb non-pneumatic tire under structural damage condition. Eur. J. Mech. A Solids 2023, 102, 105120. [Google Scholar] [CrossRef]
- Yu, L.; Hu, J.; Li, R.; Yang, Q.; Guo, F.; Pei, J. Tire-pavement contact pressure distribution analysis based on ABAQUS simulation. Arab. J. Sci. Eng. 2022, 47, 4119–4132. [Google Scholar] [CrossRef]
- Liang, C.; Wang, G.; An, D.; Ma, Y. Tread wear and footprint geometrical characters of truck bus radial tires. Chin. J. Mech. Eng. 2013, 26, 506–511. [Google Scholar] [CrossRef]
- Bonet, J.; Wood, R.D. Nonlinear Continuum Mechanics for Finite Element Analysis, 2nd Ed; Cambridge University Press: Cambridge, UK, 2008; pp. 140–180. [Google Scholar]
- Wang, Y.; Lu, Y.J.; Si, C.D. Tire-pavement coupling dynamic simulation under tire high-speed-rolling condition. Int. J. Simul. Model. 2016, 15, 236–248. [Google Scholar] [CrossRef]
- Conradie, J.M.; Els, P.S.; Heyns, P.S. Finite element modelling of off-road tyres for radial tyre model parameterization. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2016, 230, 564–578. [Google Scholar] [CrossRef]
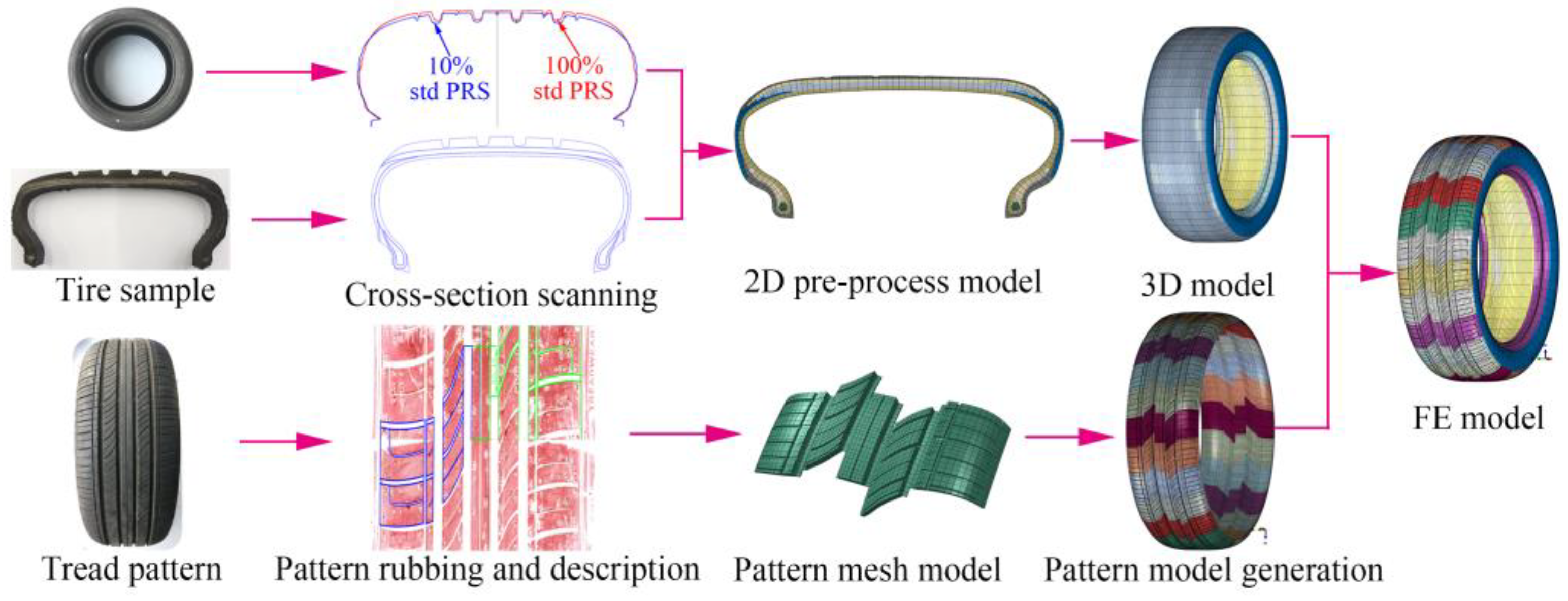
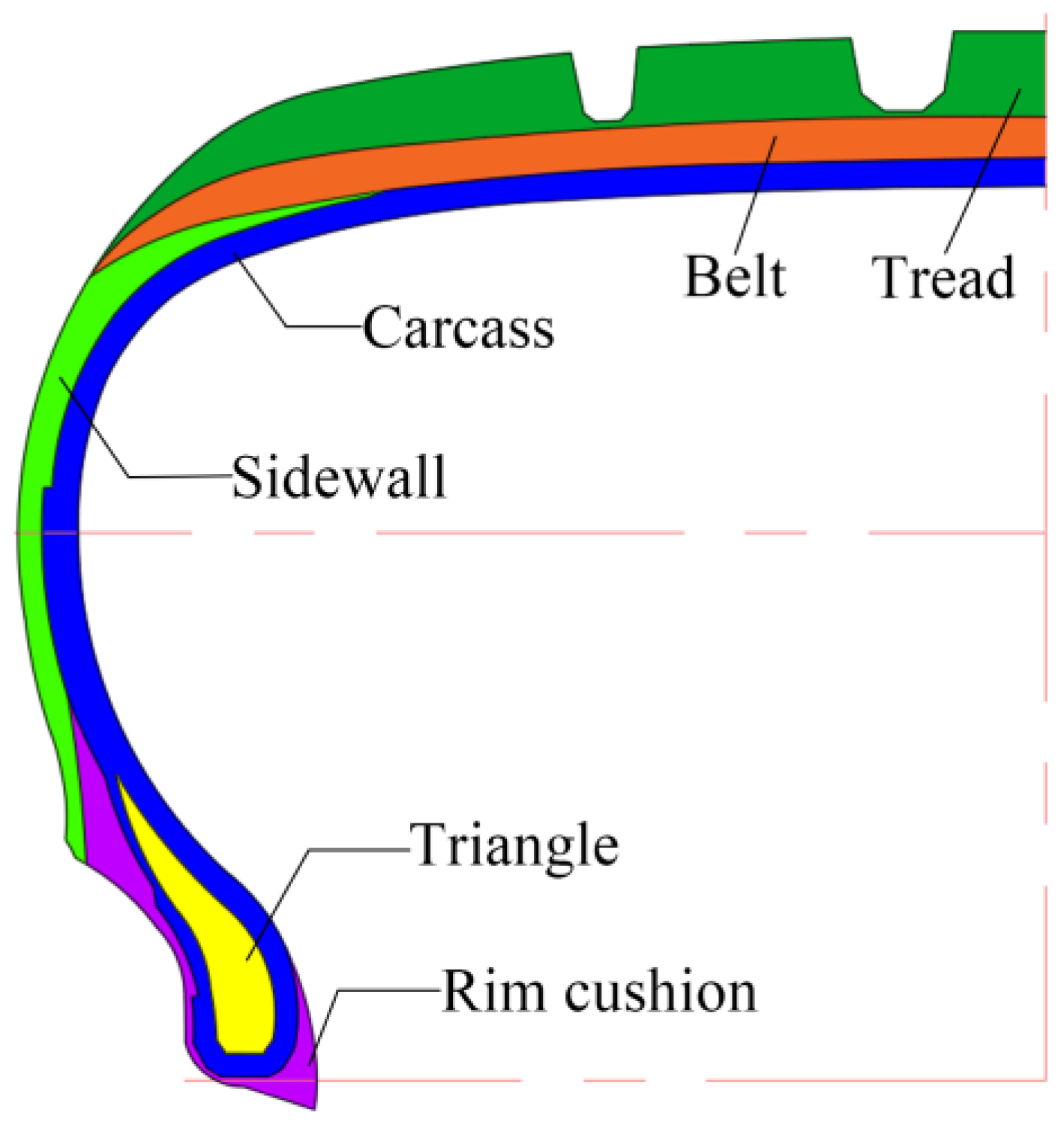


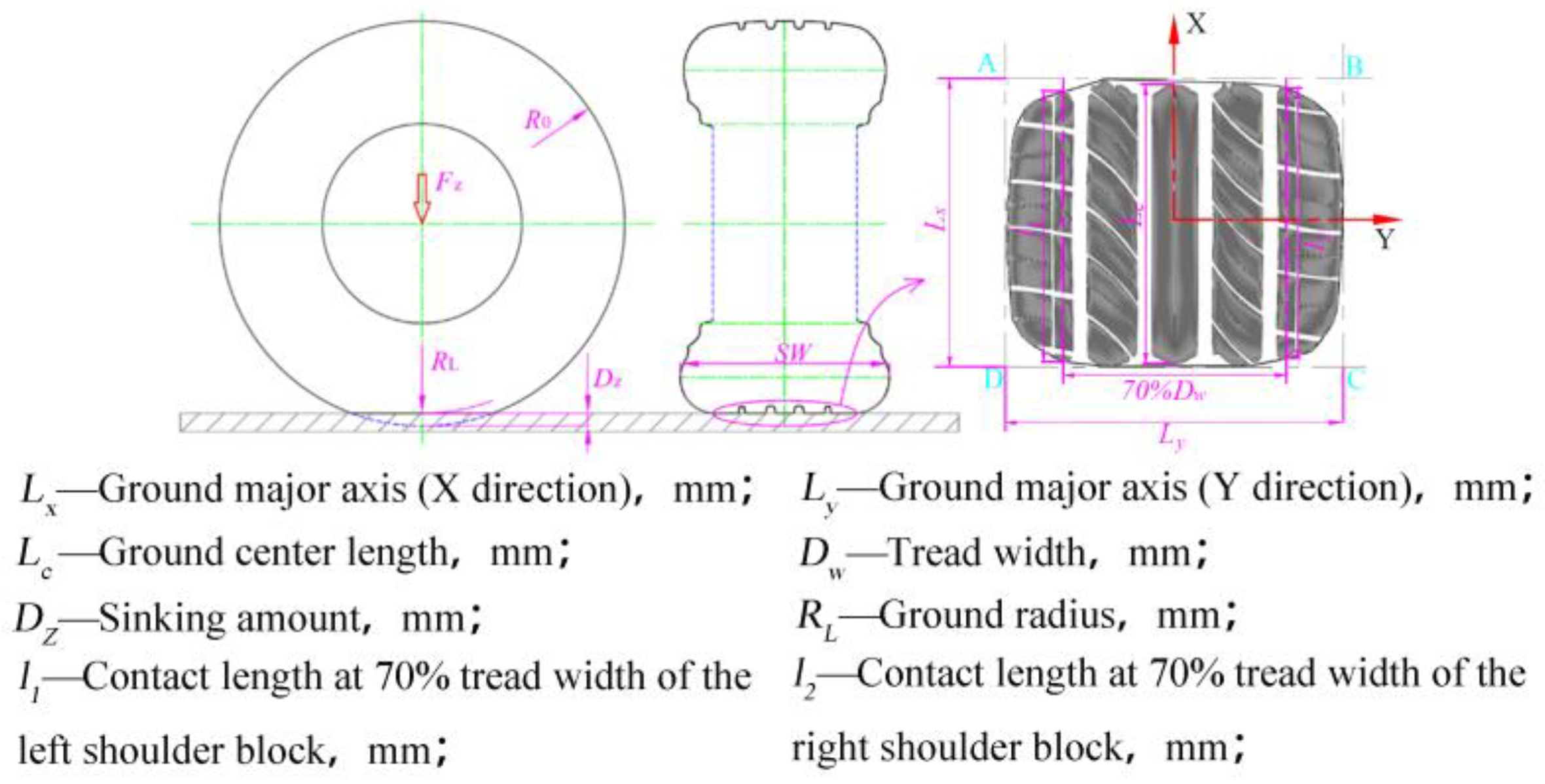
| Component | Tread | Belt | Carcass | Sidewall | Triangle | Rim Cushion |
|---|---|---|---|---|---|---|
| C10 | 0.5933 | 1.0965 | 0.5591 | 0.4126 | 2.4029 | 1.1238 |
| Component | Steel Belt | Carcass Ply | Bead Wire |
|---|---|---|---|
| Elastic modulus (GPa) | 110.9 | 9.36 | 210 |
| Poisson’s ratio | 0.29 | 0.4 | 0.3 |
| Inflation Pressure/kPa | Tire Outer Radius Rd/mm | Inflated Section Width SW/mm | ||||||
|---|---|---|---|---|---|---|---|---|
| Test1 | Test2 | Simulation | Error | Test1 | Test2 | Simulation | Error | |
| 25 | 316.35 | 316.1 | 316.476 | −0.08% | 213.858 | 214.186 | 213.481 | 0.25% |
| 250 | 319.95 | 319.85 | 319.535 | 0.11% | 212.016 | 211.198 | 210.965 | 0.30% |
| Type | Project | Analysis Conditions | ||||
|---|---|---|---|---|---|---|
| Operating conditions | Inflation pressure IP/kPa | 180 | 200 | 220 | 240 | 260 |
| Radial load Fz/N | 1000 | 2000 | 3000 | 4000 | 5000 | |
| Design parameters | Belt angle ABT/° | 24 | 26 | 28 | 30 | 32 |
| Design outer radius Rd/mm | 314.1 | 315.1 | 316.1 | 317.1 | 318.1 | |
| 85% shoulder thickness S85/mm | 15.07 | 14.57 | 14.07 | 13.57 | 13.07 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, X.; Li, H.; Xu, M.; Ge, Y. Research on Ground Contact Characteristics and Influencing Factors of Tires with Complex Tread Patterns Based on Inverse Modeling. Lubricants 2025, 13, 261. https://doi.org/10.3390/lubricants13060261
Du X, Li H, Xu M, Ge Y. Research on Ground Contact Characteristics and Influencing Factors of Tires with Complex Tread Patterns Based on Inverse Modeling. Lubricants. 2025; 13(6):261. https://doi.org/10.3390/lubricants13060261
Chicago/Turabian StyleDu, Xianbin, Haoyu Li, Mengdi Xu, and Yunfei Ge. 2025. "Research on Ground Contact Characteristics and Influencing Factors of Tires with Complex Tread Patterns Based on Inverse Modeling" Lubricants 13, no. 6: 261. https://doi.org/10.3390/lubricants13060261
APA StyleDu, X., Li, H., Xu, M., & Ge, Y. (2025). Research on Ground Contact Characteristics and Influencing Factors of Tires with Complex Tread Patterns Based on Inverse Modeling. Lubricants, 13(6), 261. https://doi.org/10.3390/lubricants13060261




