Analytical Method for Predicting Wear Life of Angular Contact Ball Bearings Under Variable Loading Based on Mixed Lubrication
Abstract
:1. Introduction
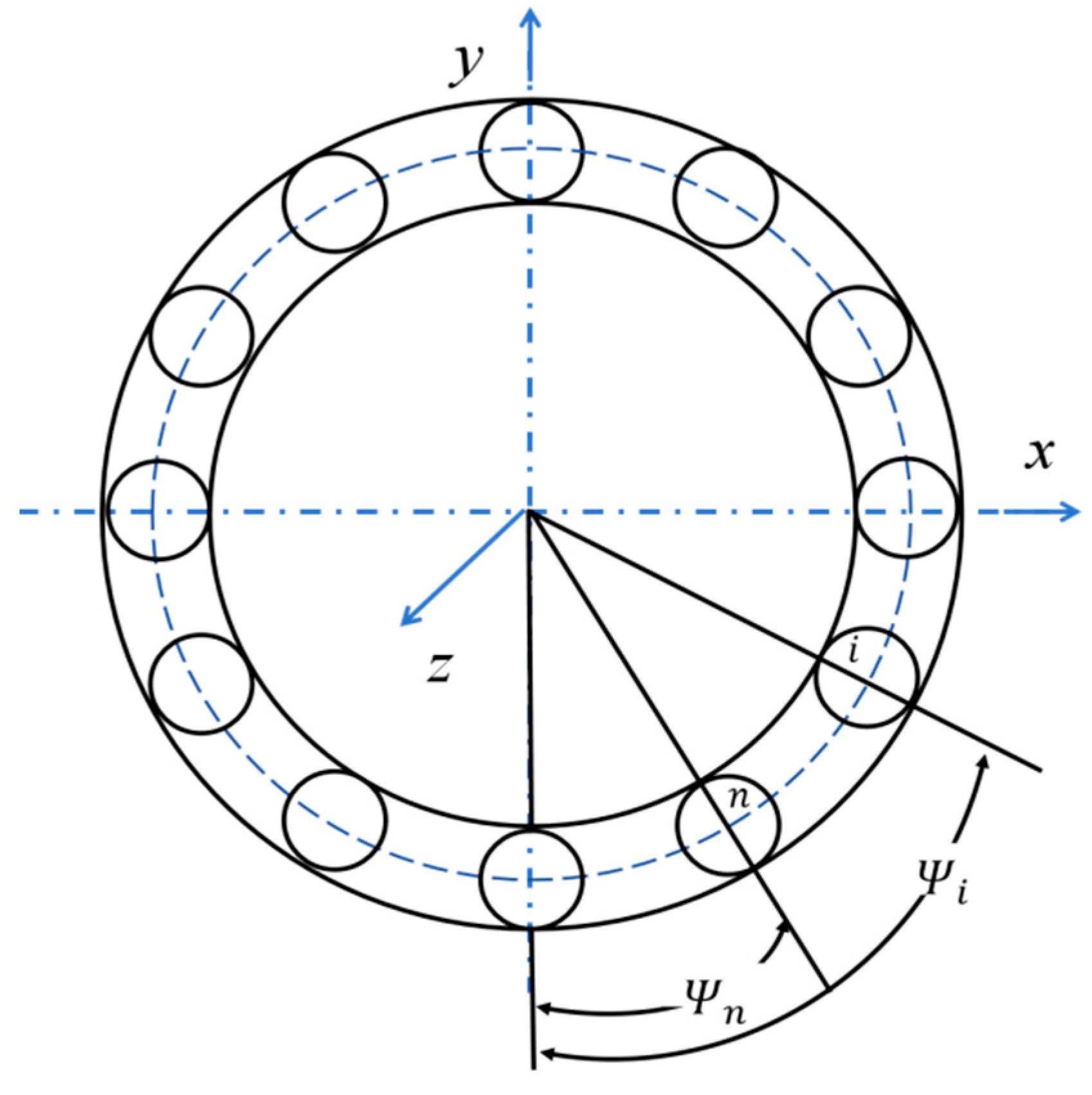
2. Optimized Dynamic Load Distribution Calculation Method
3. A Calculation Method of Wear Based on the Dynamic Load Distribution and Archard Model Considering Mixed Lubrication
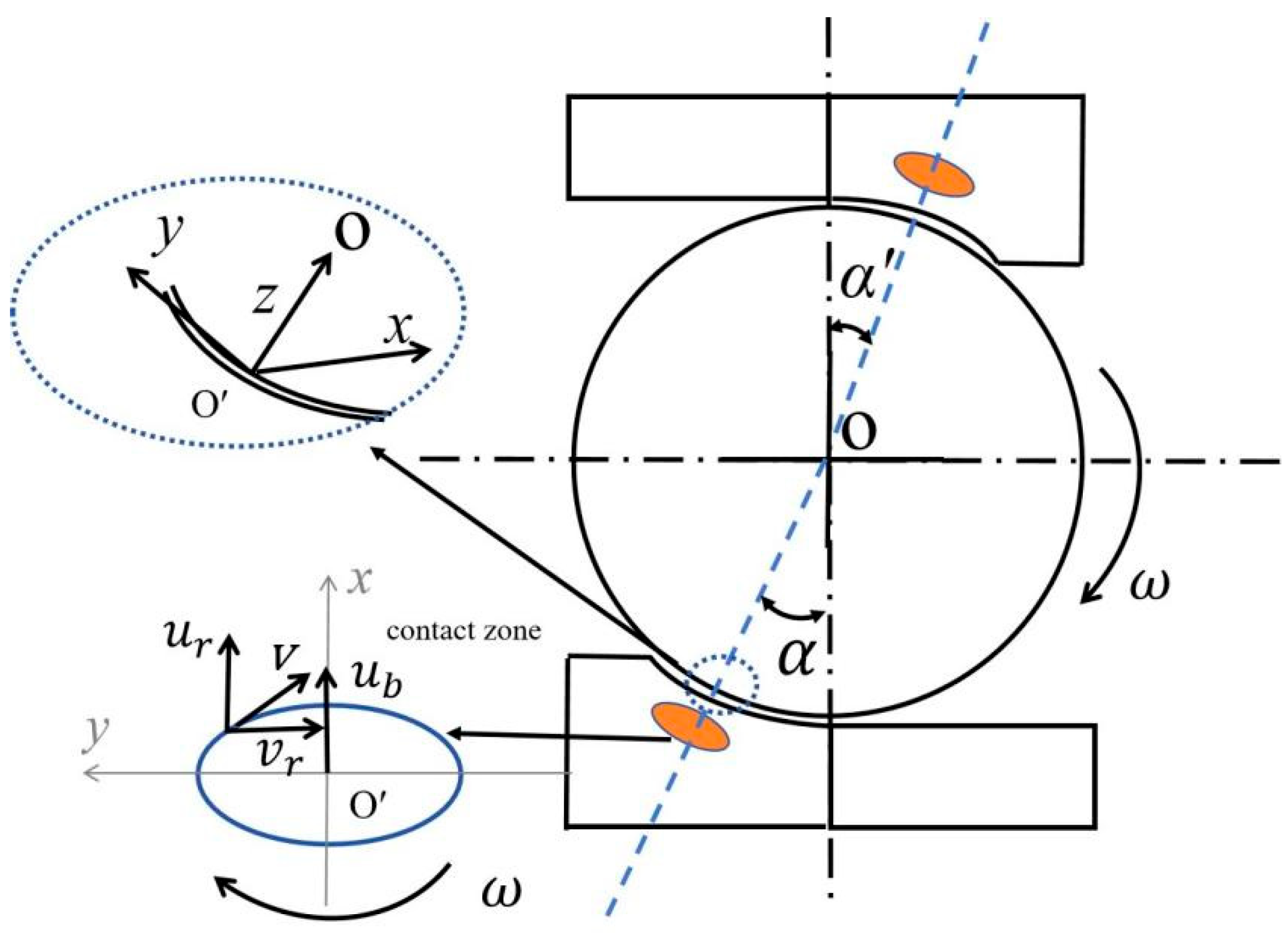
3.1. Contact Stress Distribution Model
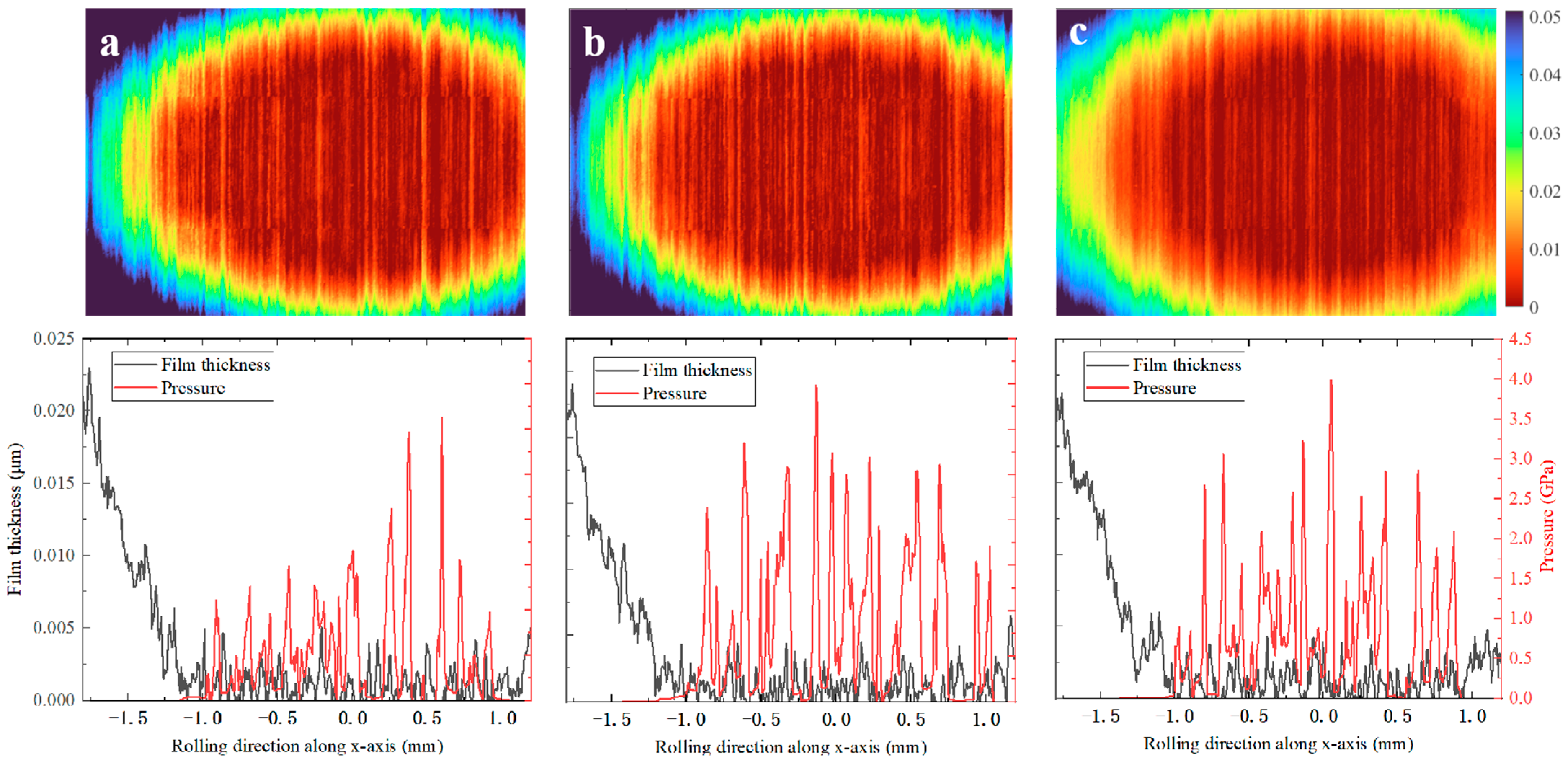
3.2. Wear Depth Calculation Model Under Mixed Lubrication State
3.3. Vibration Equation Considering Wear
4. Calculation Results and Analysis
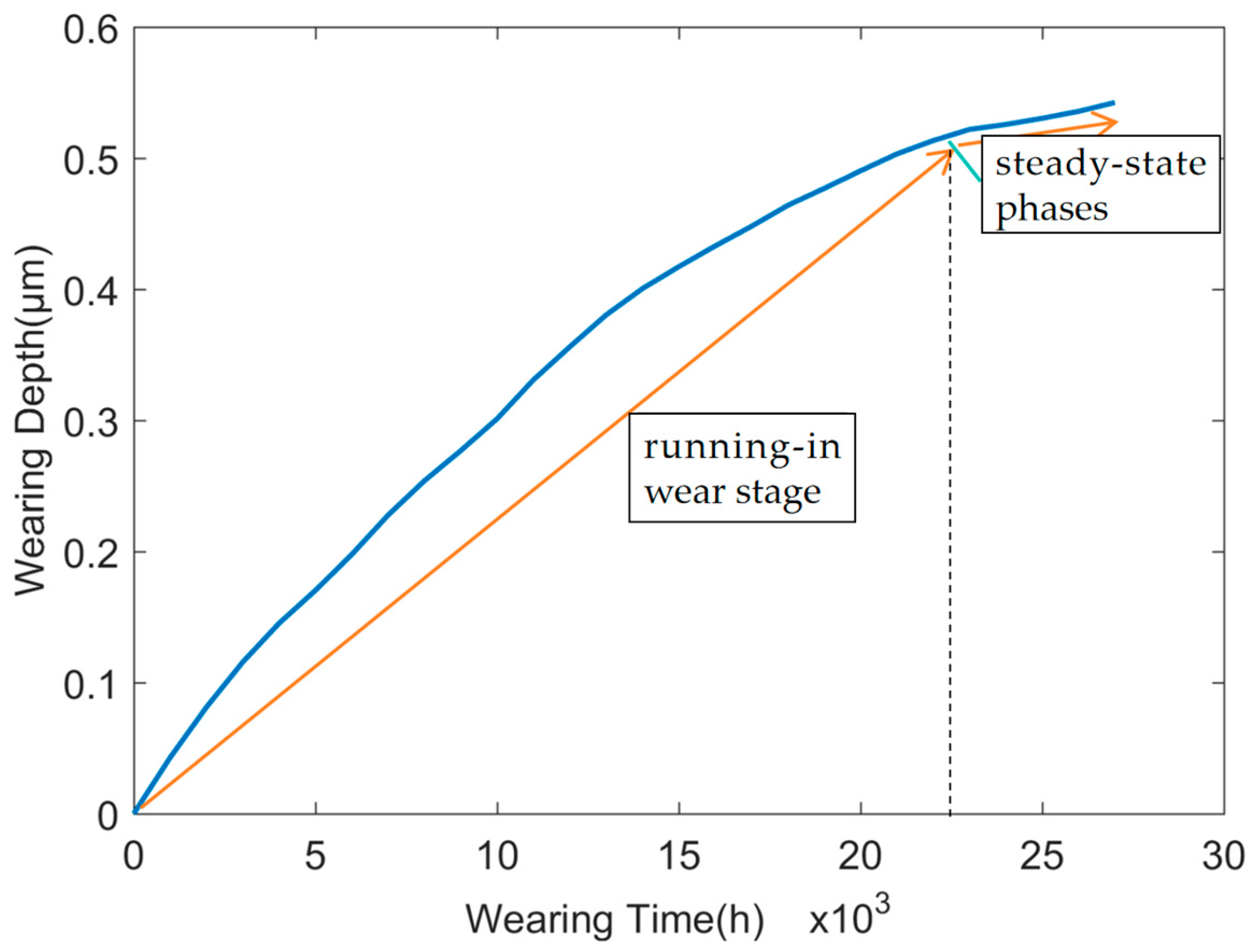
4.1. Wear Analysis of Angular Contact Ball Bearings
4.2. Spectral Analysis of Acceleration of Bearings
4.3. Analysis of Vibration Signal
4.4. Vibration Signal Testing
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Liu, Q.; Guo, Y. Dynamic model of faulty rolling element bearing on double impact phenomenon. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015; pp. 2017–2021. [Google Scholar]
- Lundberg, G.; Palmgren, A. Dynamic Capacity of Rolling Bearings. J. Appl. Mech. 1949, 16, 165–172. [Google Scholar] [CrossRef]
- Ioannides, E.; Harris, T.A. A New Fatigue Life Model for Rolling Bearings. J. Tribol. 1985, 107, 367–377. [Google Scholar] [CrossRef]
- Zaretsky, E.V. Fatigue criterion to system design, life, and reliability. J. Propuls. Power 1987, 3, 76–83. [Google Scholar] [CrossRef]
- Deolalikar, N.; Sadeghi, F. Fatigue Life Reduction in Mixed Lubricated Elliptical Contacts. Tribol. Lett. 2007, 27, 197–209. [Google Scholar] [CrossRef]
- Morales-Espejel, G.E.; Gabelli, A. A model for rolling bearing life with surface and subsurface survival: Surface thermal effects. Wear 2020, 461, 124–137. [Google Scholar] [CrossRef]
- Ghaffari, M.A.; Zhang, Y.; Xiao, S.H.P. Multiscale modeling and simulation of rolling contact fatigue. Int. J. Fatigue 2018, 108, 9–17. [Google Scholar] [CrossRef]
- Sesana, R.; Ossola, E.; Pagliassotto, S.; Rizzo, S.; Brusa, E. Influence of microinclusion in life of rolling elements: Experimental, microstructural, analytical and numerical investigation. Int. J. Fatigue 2020, 139, 345–353. [Google Scholar] [CrossRef]
- Shi, X.J.; Wang, L.Q.; Qin, F.Q. Relative fatigue life prediction of high-speed and heavy-load ball bearing based on surface texture. Tribol. Int. 2016, 101, 364–374. [Google Scholar] [CrossRef]
- Lin, F.H.; Wang, L.Q.; Li, Z.H.; Wu, J.Q.; Wei, S.S.; Su, K.; Liu, Y.B. Fatigue damage evolution and failure of G13Cr4Mo4Ni4V bearing steel under heavy load rolling contact. Tribology 2024, 44, 1–11. (In Chinese) [Google Scholar]
- Zhao, J.X.; Jiang, C.; Li, W.M.; Liu, H.M.; Li, X.M. Micro-pitting: Research progress and prospects. Tribology 2024, 44, 715–728. (In Chinese) [Google Scholar]
- Ardah, S.; Profito, F.J.; Dini, D. An integrated finite volume framework for thermal elasto-hydrodynamic lubrication. Tribol. Int. 2022, 177, 107935. [Google Scholar] [CrossRef]
- Chen, Q.; Yang, P.; Jiang, N.; Li, X.M.; Guo, F.; Yang, P.R. Experimental observation and numerical simulation of rheological properties of lubricating films under different sliding-rolling ratios. Tribol 2020, 40, 158–165. (In Chinese) [Google Scholar]
- Wu, J.; Wang, L.; He, T.; Gu, L.; Zhang, C.; Lu, Y. Investigation on the angular contact ball bearings under low speed and heavy load with coupled mixed lubrication and quasi-dynamic analysis. Lubr. Sci. 2020, 32, 108–120. [Google Scholar] [CrossRef]
- Wen, B.; Li, Y.; Wang, M.; Yang, Y. Measurement for Lubricant Distribution in an Angular Contact Ball Bearing and Its Influence Investigation. Lubricants 2023, 11, 63. [Google Scholar] [CrossRef]
- Wen, B.; Li, Y.; Li, Y.; Wang, M.; Zhai, J. Influence and Optimization of Nozzle Position on Lubricant Distribution in an Angular Contact Ball Bearing Cavity. Lubricants 2024, 12, 419. [Google Scholar] [CrossRef]
- Chen, G.; Wang, L.Q.; Gu, L.; Zhen, D. Heating analysis of the high speed ball bearing. J. Aerosp. Power 2007, 22, 165–168. [Google Scholar]
- Xie, Z.; Wang, Y.; Wu, R.; Yin, J.; Yu, D.; Liu, J.Q.; Cheng, T.H. A high-speed and long-life triboclectric sensor with charge supplement for monitoring the speed and skidding of rollingbearing. Nano Energy 2022, 92, 106747. [Google Scholar] [CrossRef]
- Park, D.; Kolivand, M.; Kahraman, A. An approximate method to predict surface wear of hypoid gears using surface interpolation. Mech. Mach. Theory 2014, 71, 64–78. [Google Scholar] [CrossRef]
- Lai, X.M.; Han, J.C.; Gao, P.; Qu, J.J.; Li, Y.; Tan, C.L.; Jiang, J. Research on wear mechanism of solid lubrication bearing in vacuum environment. Appl. Mech. Mater. 2015, 798, 424–429. [Google Scholar] [CrossRef]
- Jamari, J. Wear predication using GIWM (global incremental wear model) method. Rotasi 2012, 11, 1–4. [Google Scholar] [CrossRef]
- Cura, F.; Waqar, Q.; Andrea, M. A methodological approach for incremental fretting wear formulation. Tribol. Lett. 2016, 64, 1–10. [Google Scholar] [CrossRef]
- Cubillas, D.; Olave, M.; Llavori, I.; Ulacia, I.; Larranaga, J.; Zurutuza, A.; Lopez, A. Semi-analytical methodology to predict fretting damage areas in angular contact ball bearing raceways under variable loading. Wear 2022, 508–509, 204477. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, X.; Gu, J.; Wang, Z. Influences of preload on the friction and wear properties of high-speed instrument angular contact ball bearings. Chin. J. Aeronaut. 2018, 31, 597–607. [Google Scholar] [CrossRef]
- Gu, J.; Zhang, Y.; Liu, H. Influences of wear on dynamic characteristics of angular contact ball bearings. Meccanica 2019, 54, 945–965. [Google Scholar] [CrossRef]
- Jang, J.Y.; Khonsari, M.M. On the wear of dynamically-loaded engine bearings with provision for misalignment and surface roughness. Tribol. Int. 2020, 141, 105919. [Google Scholar] [CrossRef]
- Wang, J.; Xu, H. Load sequence and life analysis of deep groove ball bearing. J. Mech. Eng. 2017, 53, 131–140. [Google Scholar] [CrossRef]
- Liu, Z.J.; He, S.Q.; Liu, H. Application of Rolling Bearing; China Machine Press: Beijing, China, 2007. [Google Scholar]
- Luo, J.W. Elastic Contact Problems of Rolling Bearing and Their Numerical Methods; Tsinghua University: Beijing, China, 1989. [Google Scholar]
- Ning, F.P.; Yao, J.T.; An, J.T.; Zhao, Y. Effect of assembly situation variation on wear of space precision bearings. J. Mech. Eng. 2017, 53, 68–74. [Google Scholar] [CrossRef]
- Wu, Z.G.; Lu, G.J. Analysis of angular-contact ball bearings under different conditions. Chin. J. Constr. Mach. 2013, 11, 107–111. [Google Scholar]
- Zhang, X.N.; Han, Q.K.; Chu, F.L. Contact angle of ball bearings based on a simplified Jones-Harris method. J. Vib. Shock 2013, 32, 170–175. [Google Scholar]
- Harris, T.A. Rolling Bearing Analysis; John Whey and Sons: Hoboken, NJ, USA, 1984. [Google Scholar]
- Luo, J.; Zhu, M.; Wang, Y.; Zheng, J.; Mo, J. Study on rotational fretting wear of bonded MoS2 solid lubricant coating prepared on medium carbon steel. Tribol. Int. 2011, 44, 1565–1570. [Google Scholar] [CrossRef]
- Li, Z. Wheel-Rail Rolling Contact and Its Application to Wear Simulation; TU Delft, Delft University of Technology: Delft, The Netherlands, 2002. [Google Scholar]
- Hu, Y.-Z.; Zhu, D. A Full Numerical Solution to the Mixed Lubrication in Point Contacts. J. Tribol. 1999, 122, 1–9. [Google Scholar] [CrossRef]


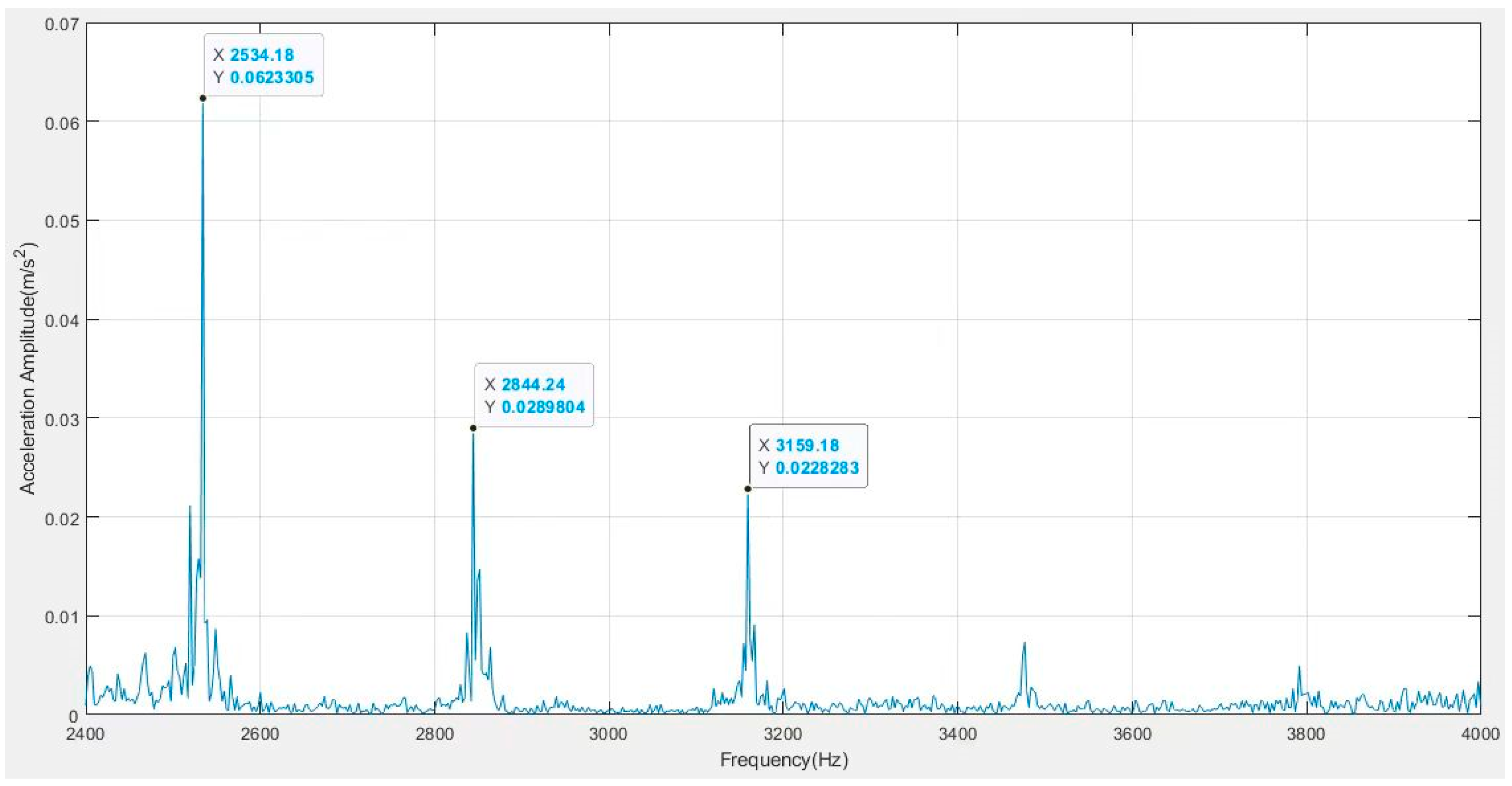
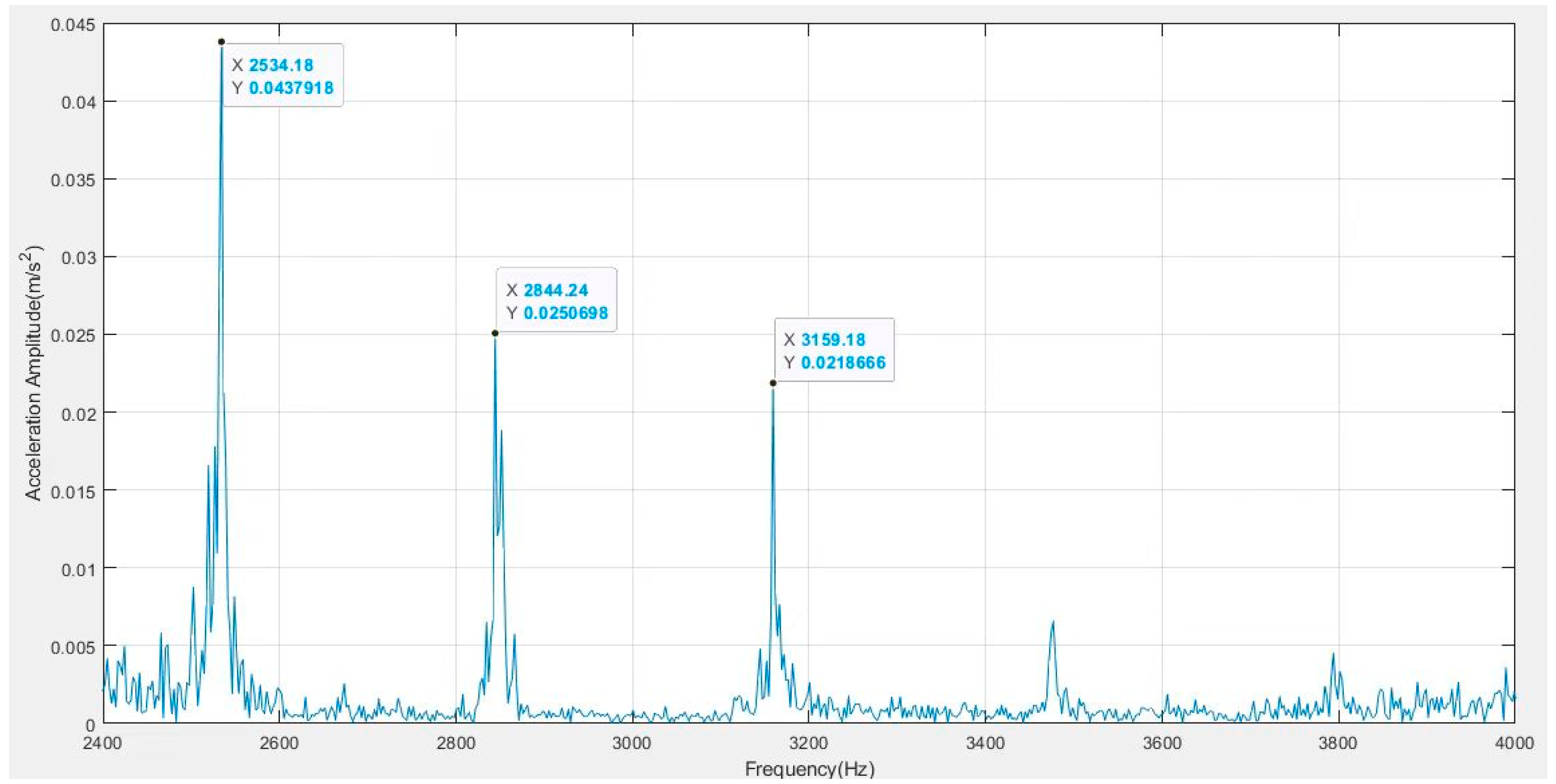
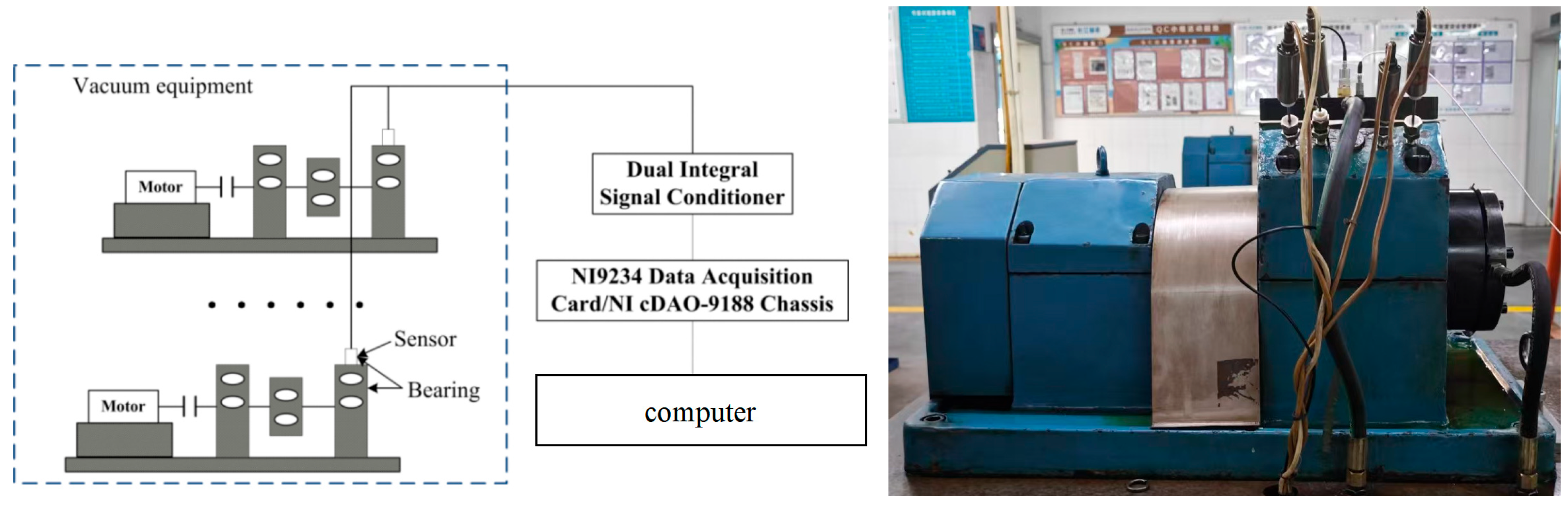

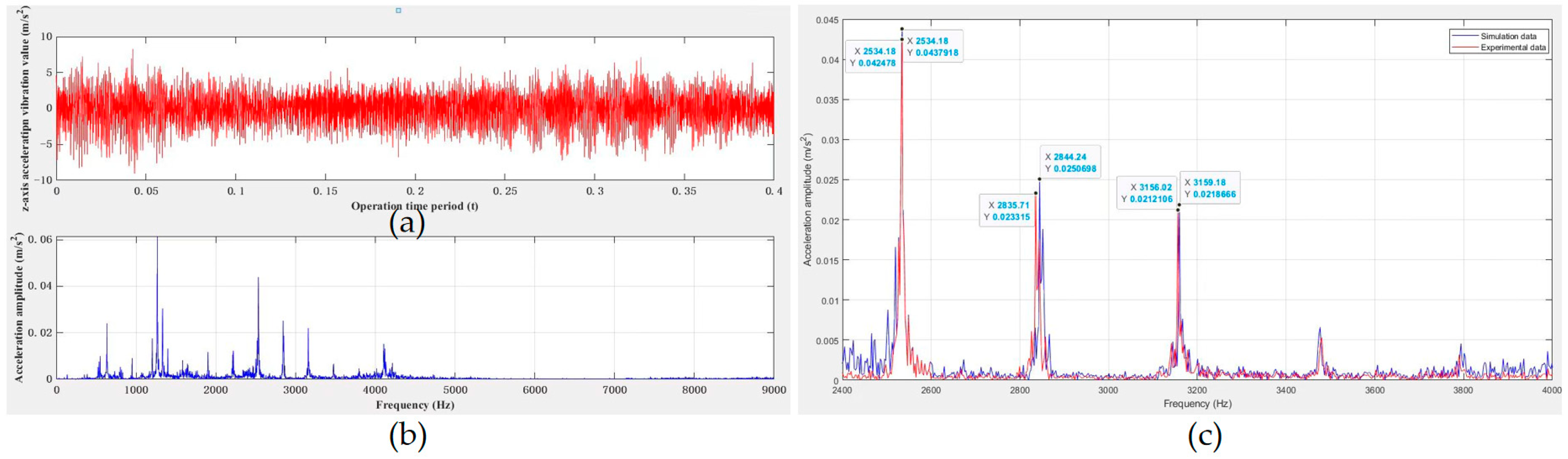
| Number of Balls | Ball Diameter mm | Pitch Diameter mm | Groove Curvature Radius mm | Initial Contact Angle Degree | Outer Raceway Diameter mm | Inner Raceway Diameter mm |
|---|---|---|---|---|---|---|
| 16 | 22.225 | 125.2601 | 11.6281 | 40 | 147.7264 | 102.7938 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, X.; Cheng, G.; Dong, S.; Yi, L.; Liu, H. Analytical Method for Predicting Wear Life of Angular Contact Ball Bearings Under Variable Loading Based on Mixed Lubrication. Lubricants 2025, 13, 212. https://doi.org/10.3390/lubricants13050212
Mu X, Cheng G, Dong S, Yi L, Liu H. Analytical Method for Predicting Wear Life of Angular Contact Ball Bearings Under Variable Loading Based on Mixed Lubrication. Lubricants. 2025; 13(5):212. https://doi.org/10.3390/lubricants13050212
Chicago/Turabian StyleMu, Xiaoyan, Gong Cheng, Shaojiang Dong, Liang Yi, and Hongliang Liu. 2025. "Analytical Method for Predicting Wear Life of Angular Contact Ball Bearings Under Variable Loading Based on Mixed Lubrication" Lubricants 13, no. 5: 212. https://doi.org/10.3390/lubricants13050212
APA StyleMu, X., Cheng, G., Dong, S., Yi, L., & Liu, H. (2025). Analytical Method for Predicting Wear Life of Angular Contact Ball Bearings Under Variable Loading Based on Mixed Lubrication. Lubricants, 13(5), 212. https://doi.org/10.3390/lubricants13050212





