Effects of Contact Characteristics on Dynamic Response of Planar Mechanical Systems with Lubricated Revolute Joint
Abstract
:1. Introduction
2. Dynamic Modeling of Revolute Clearance Joint Considering Lubrication
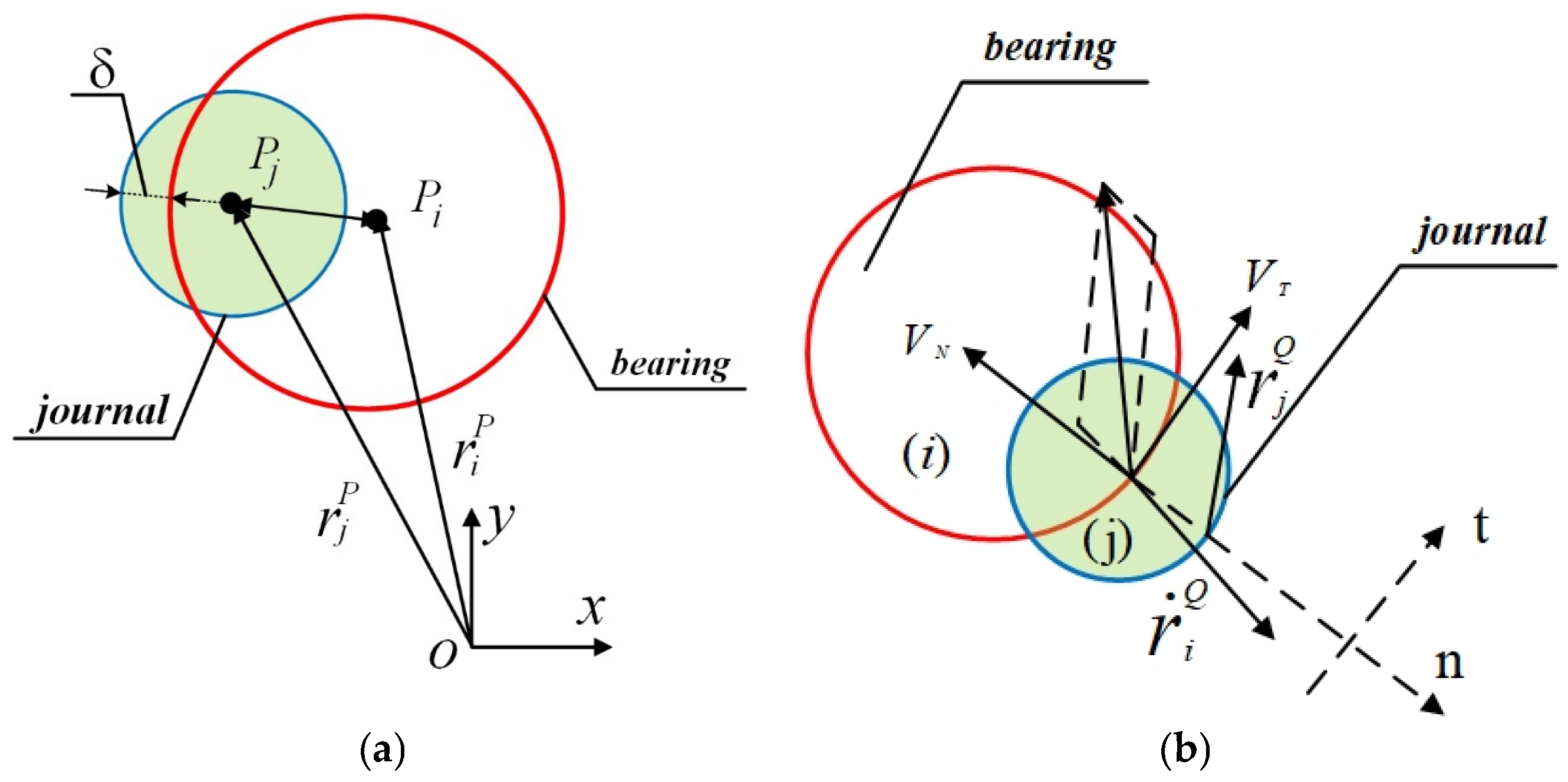
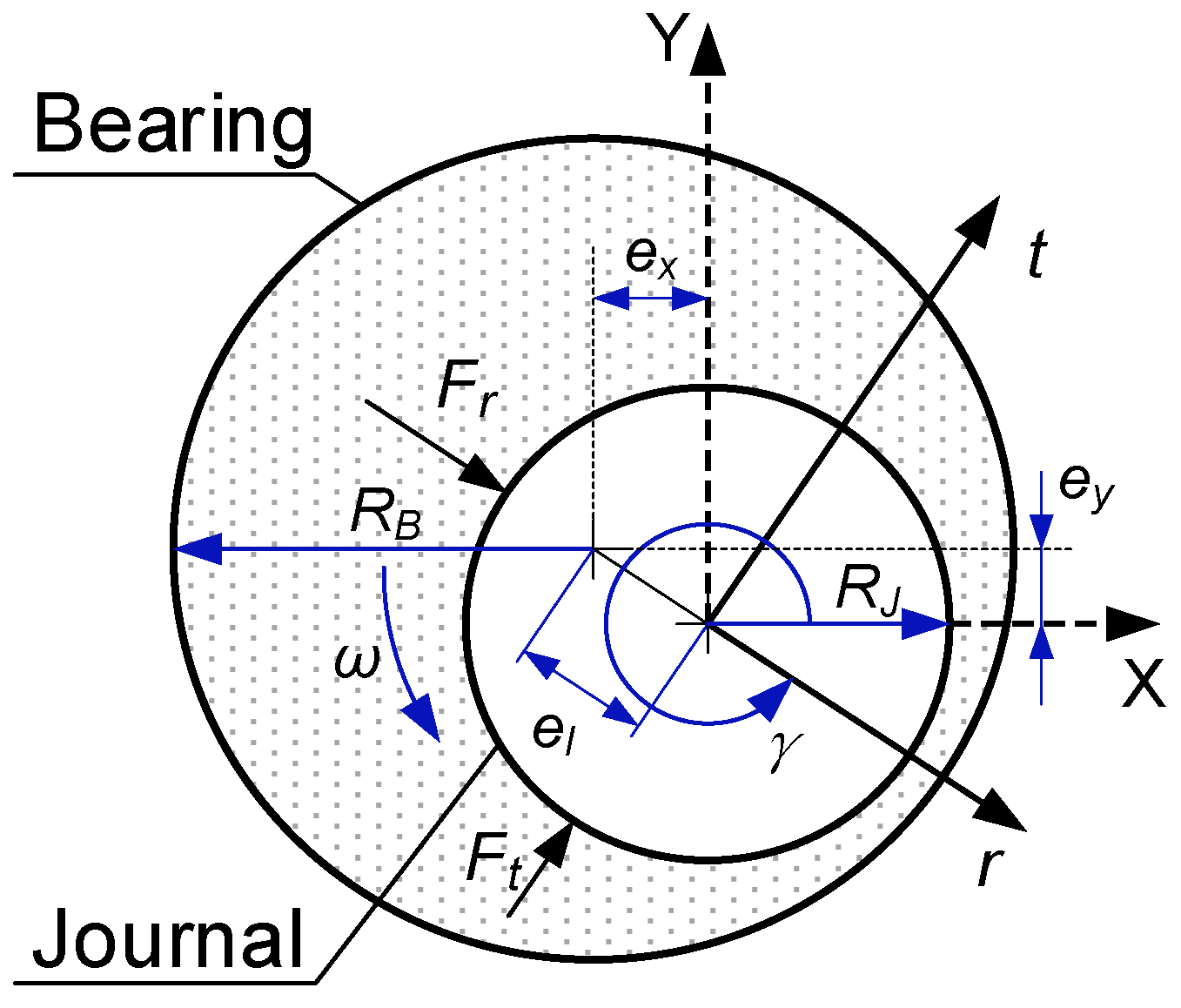
2.1. Modeling of Revolute Clearance Joint
2.2. Modeling of Contact and Friction Characteristics
2.3. Modeling of Lubrication Force
3. Dynamic Equation of Mechanical System with Clearance Joint
4. Case Study
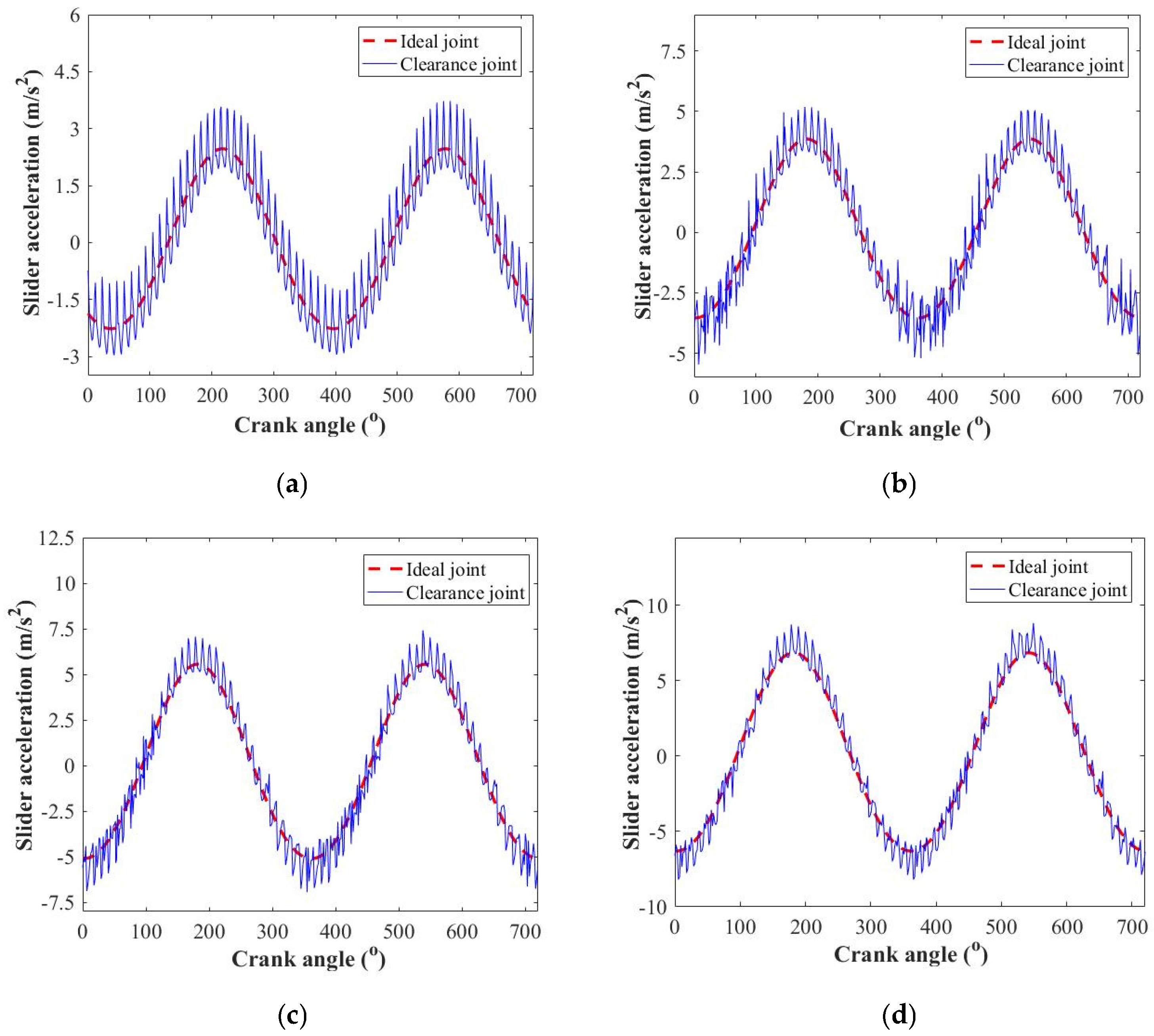
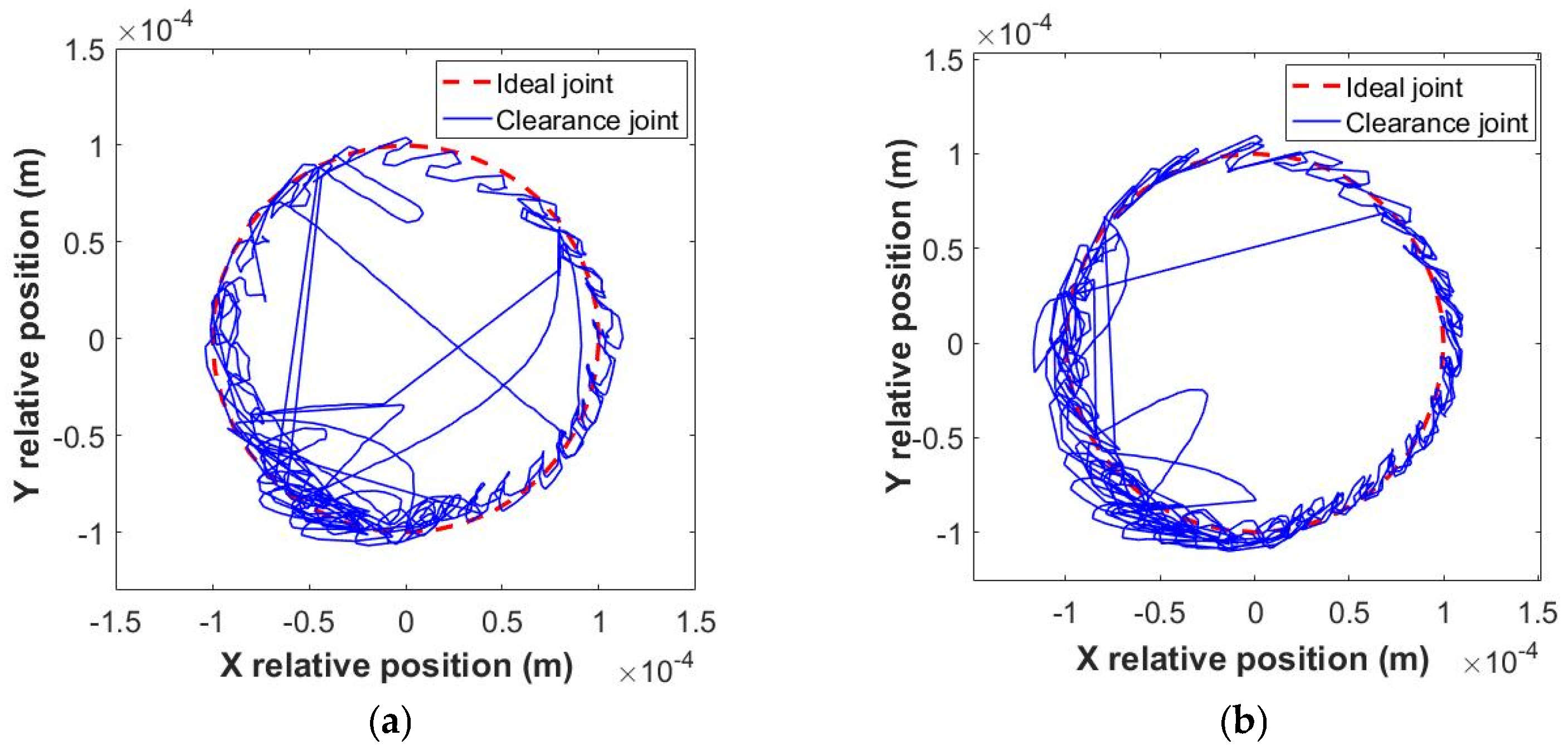
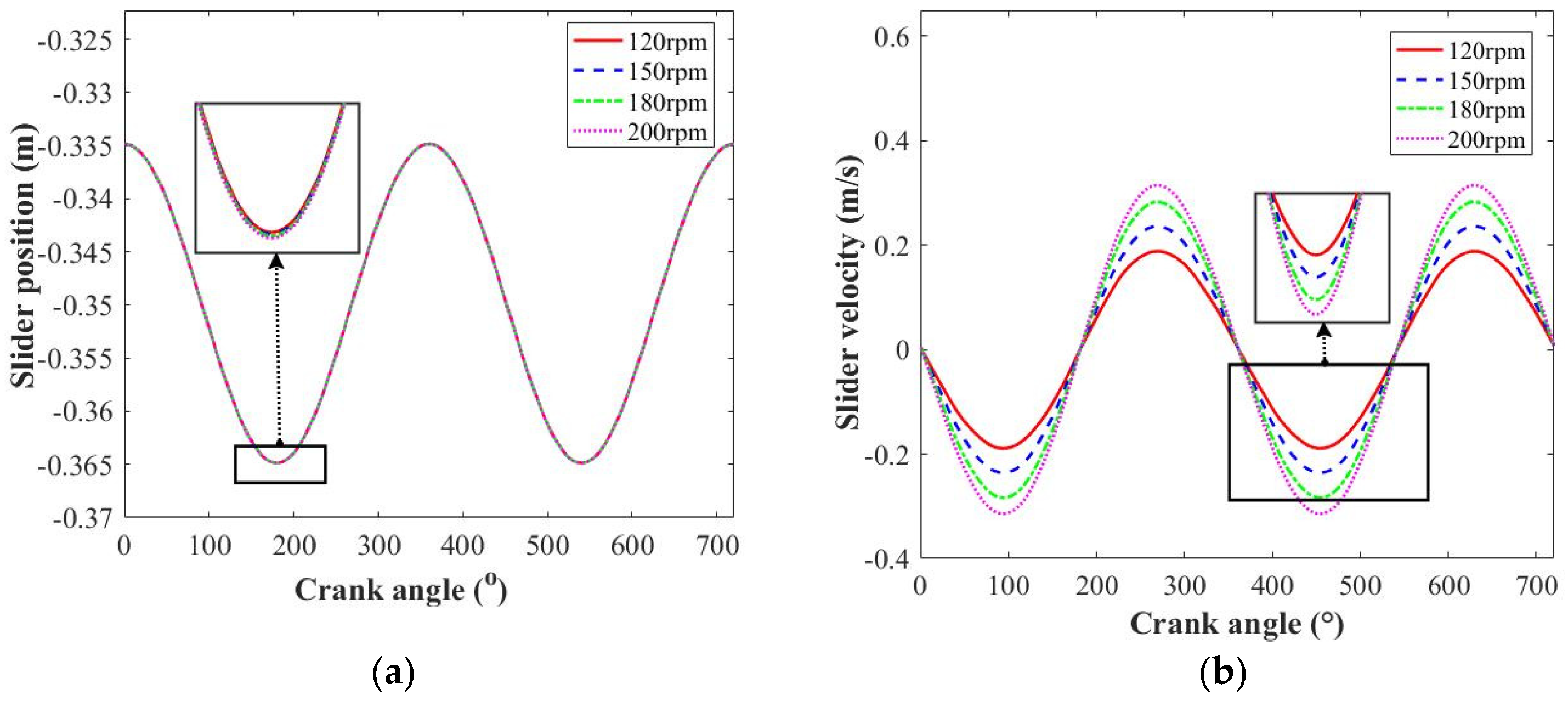
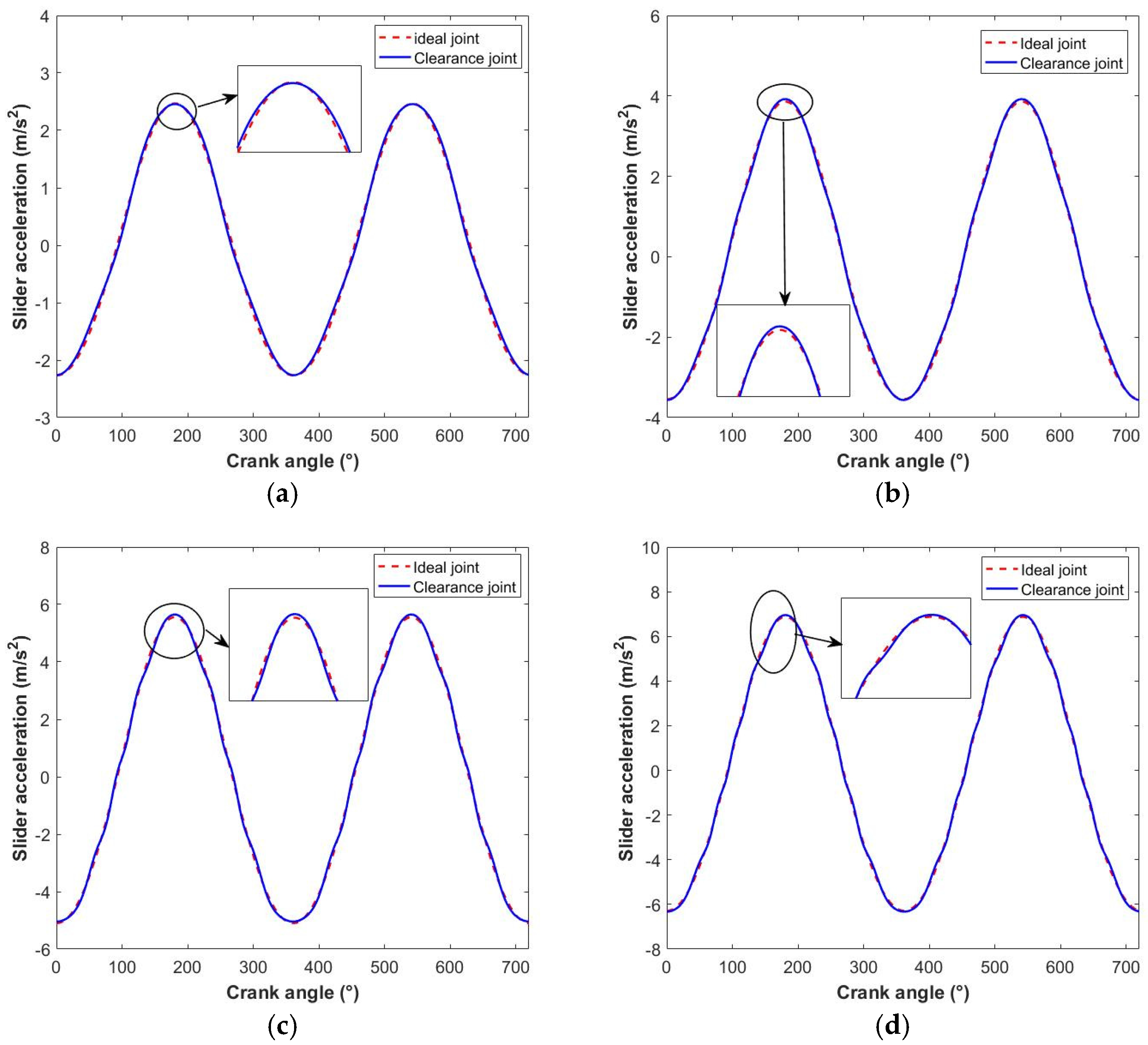
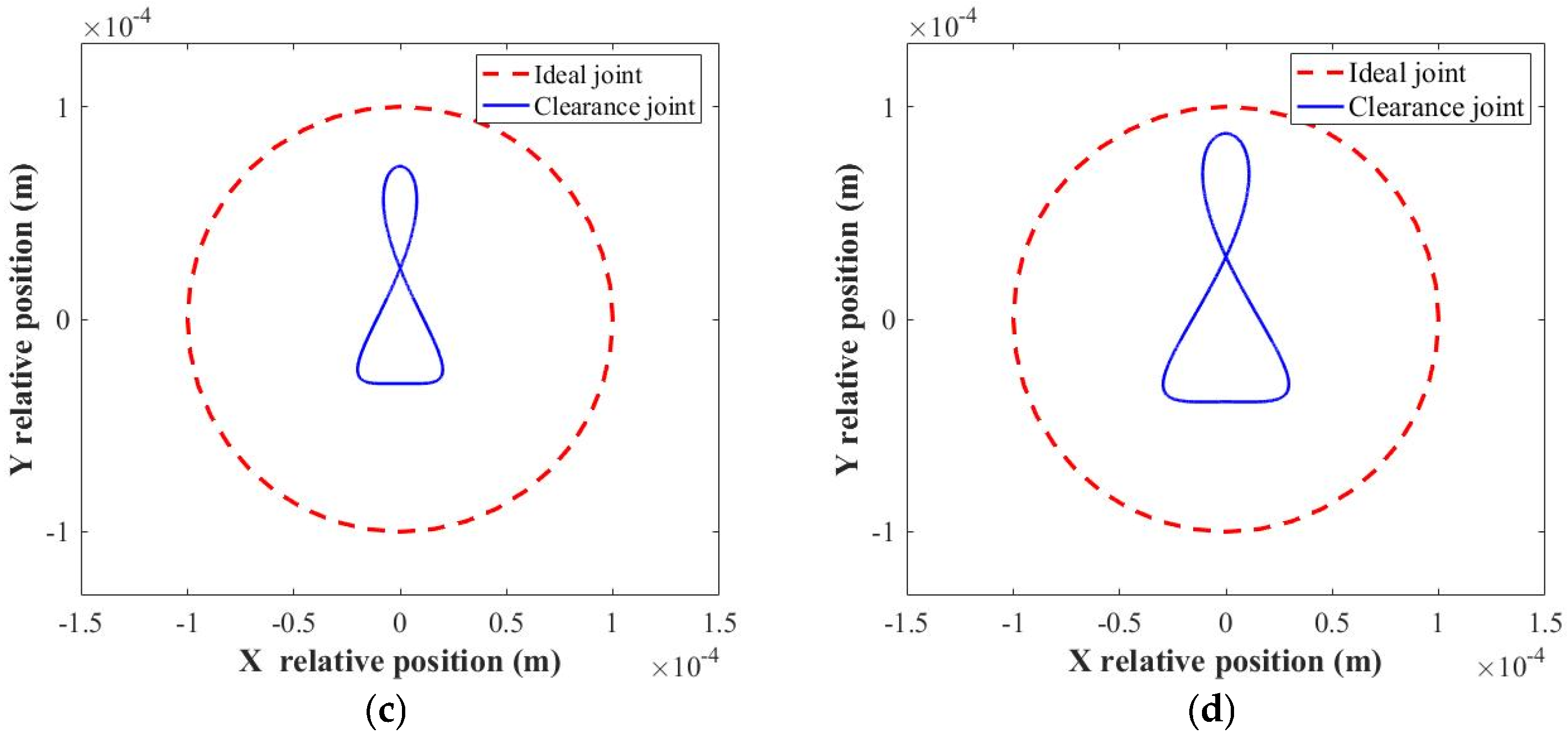
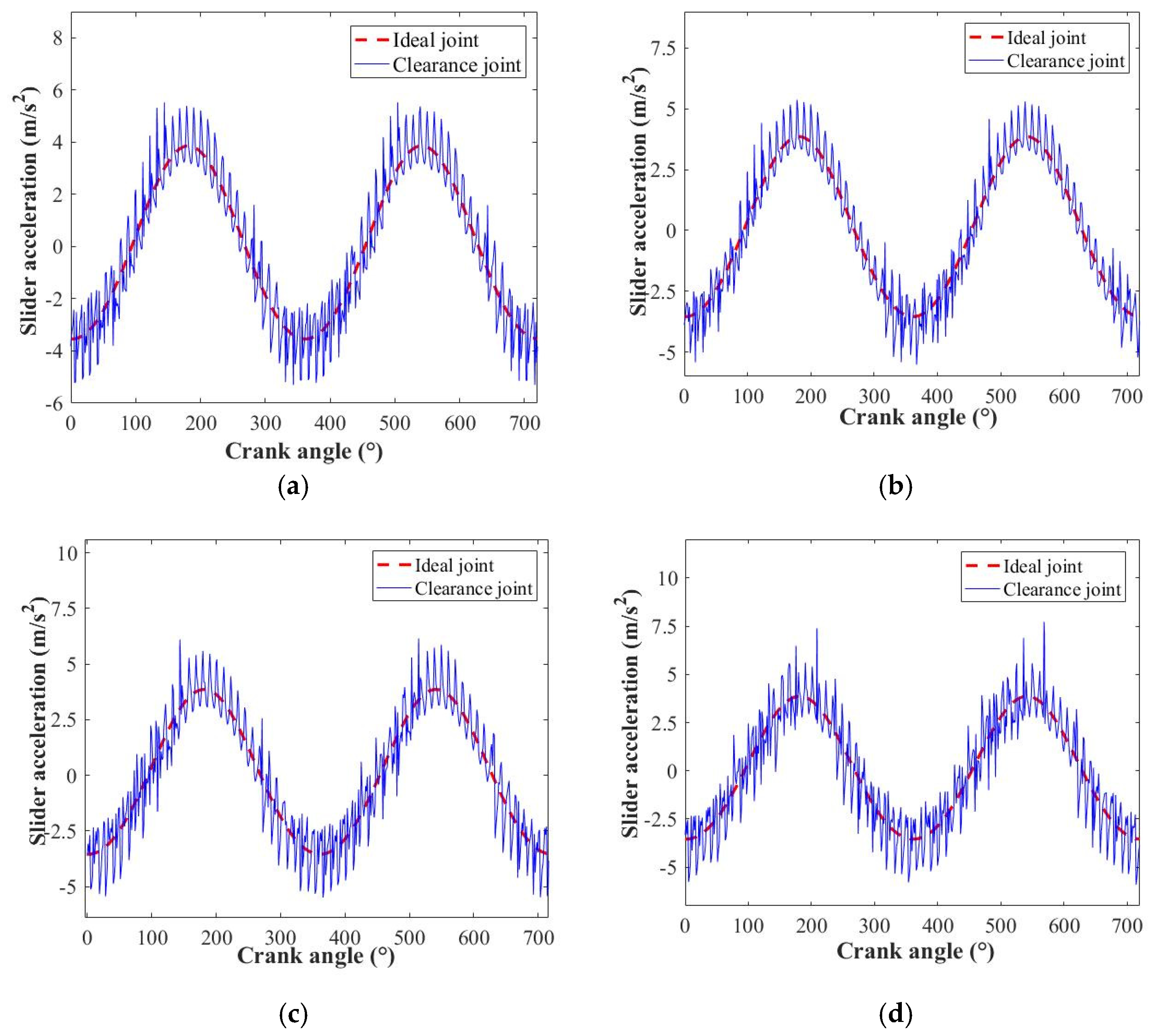
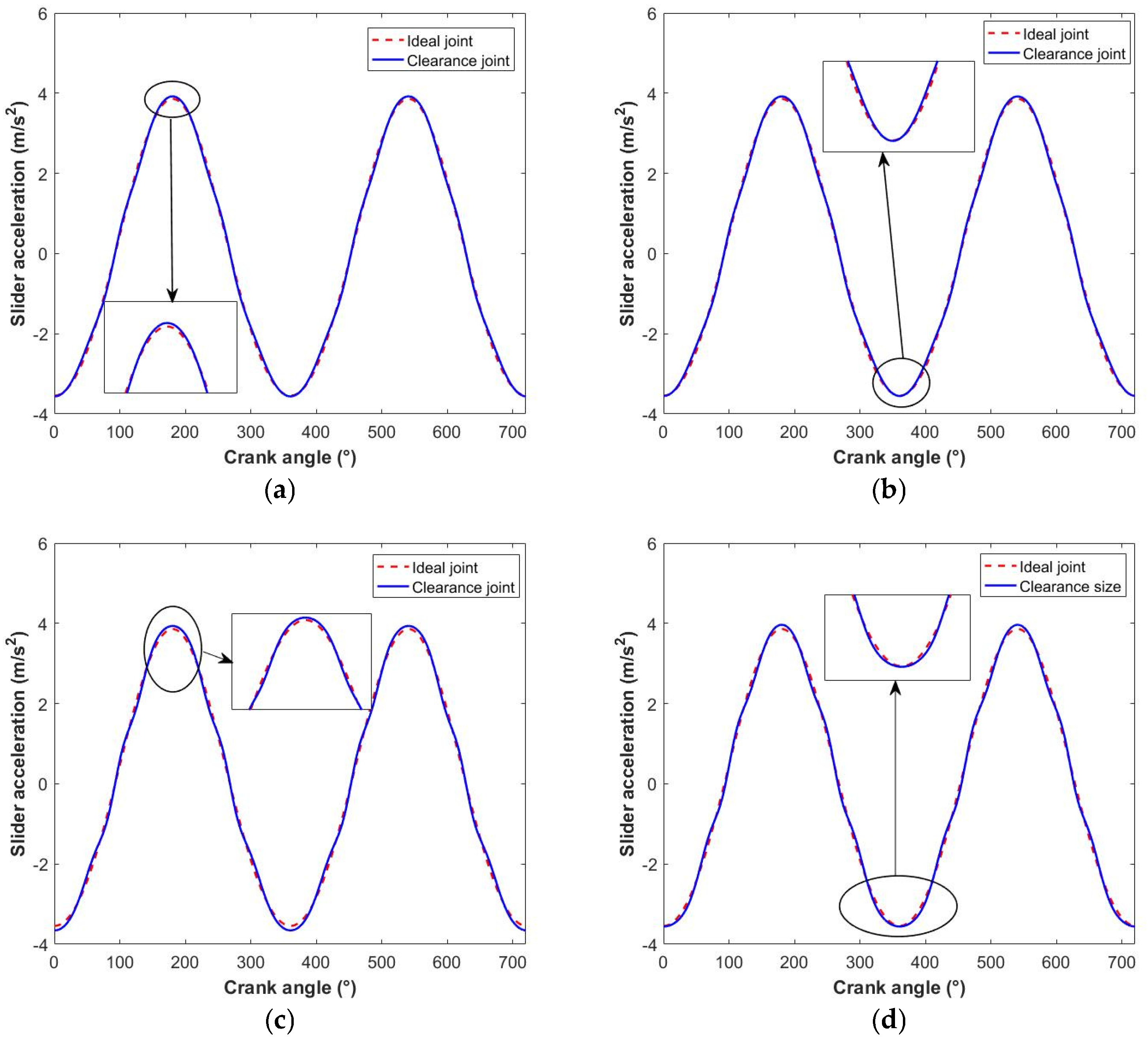
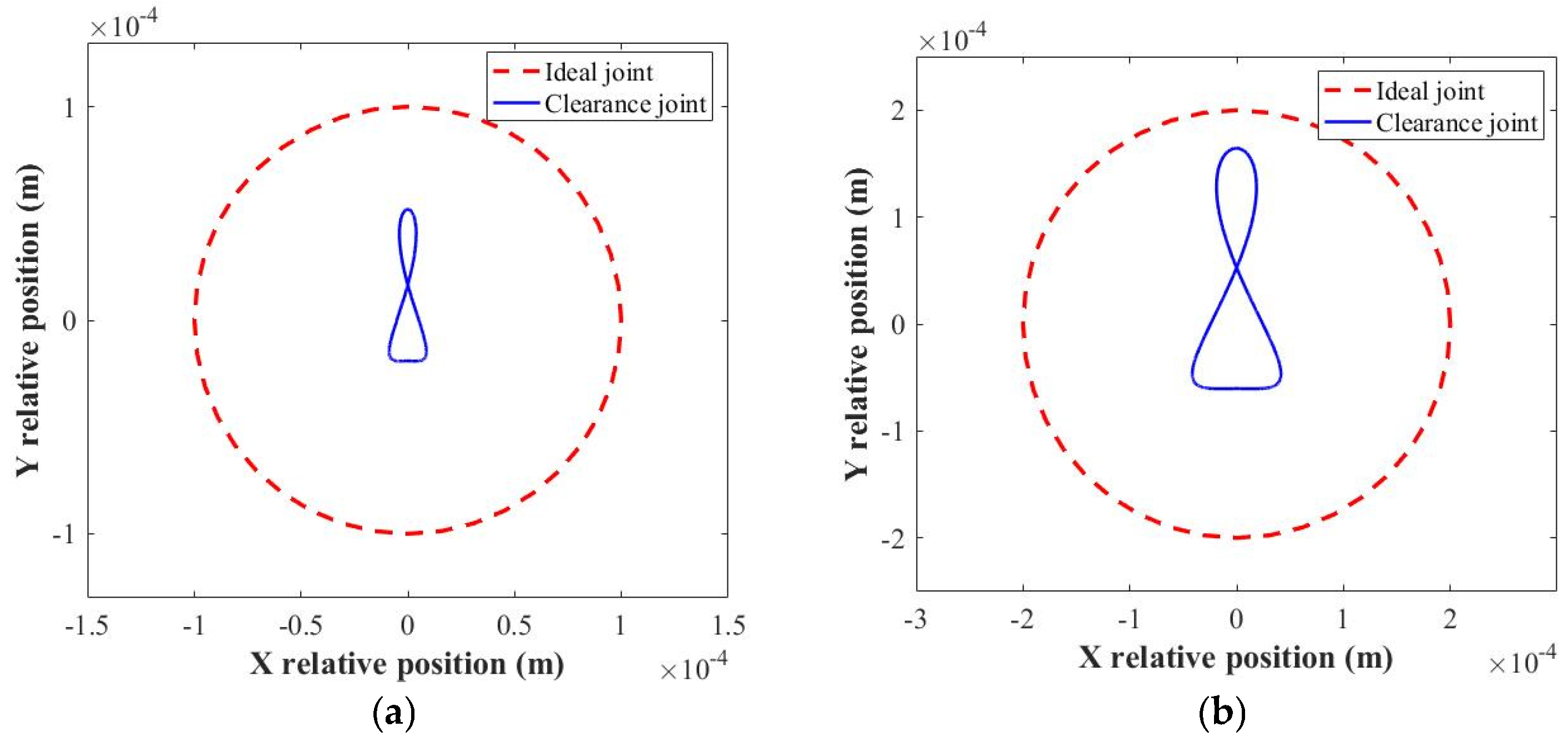
4.1. Influence of Rotation Speed
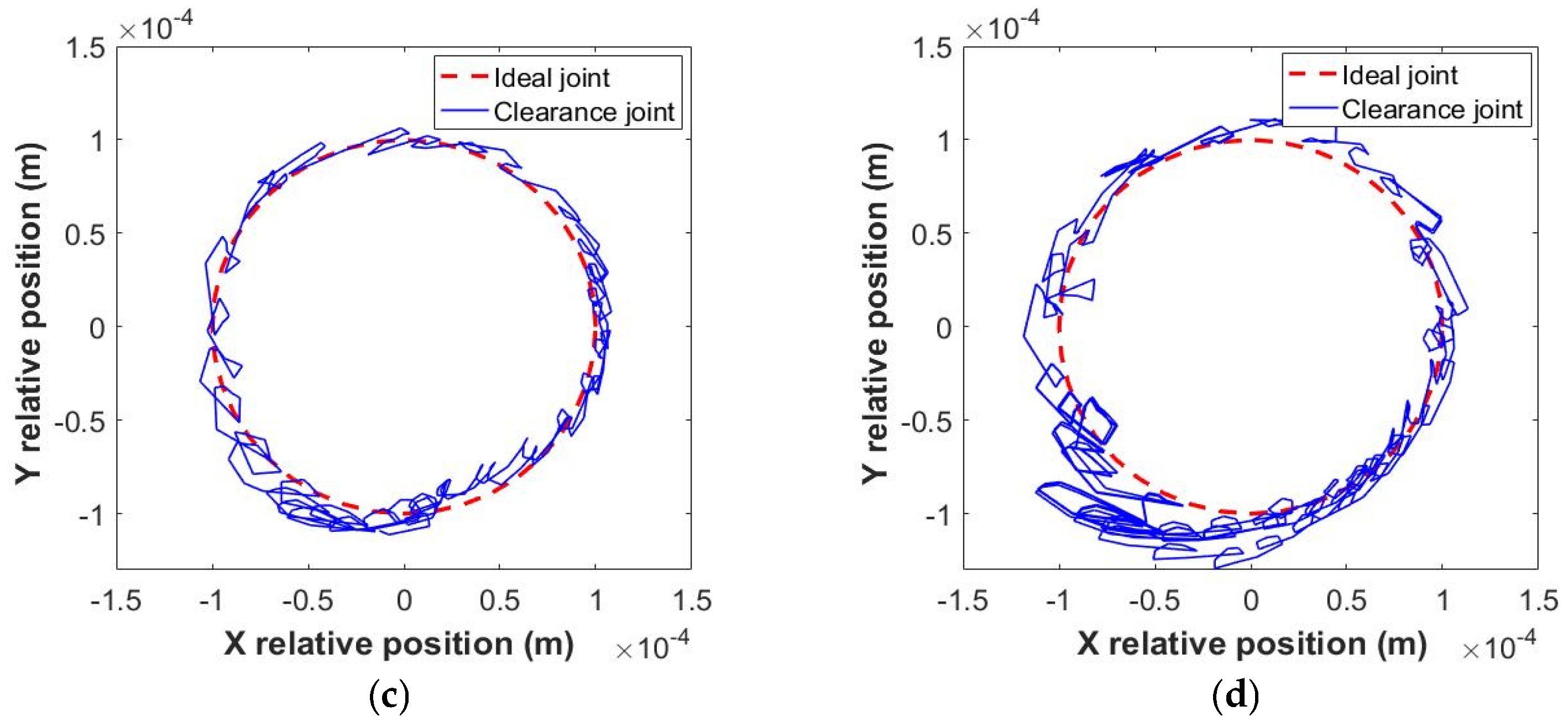
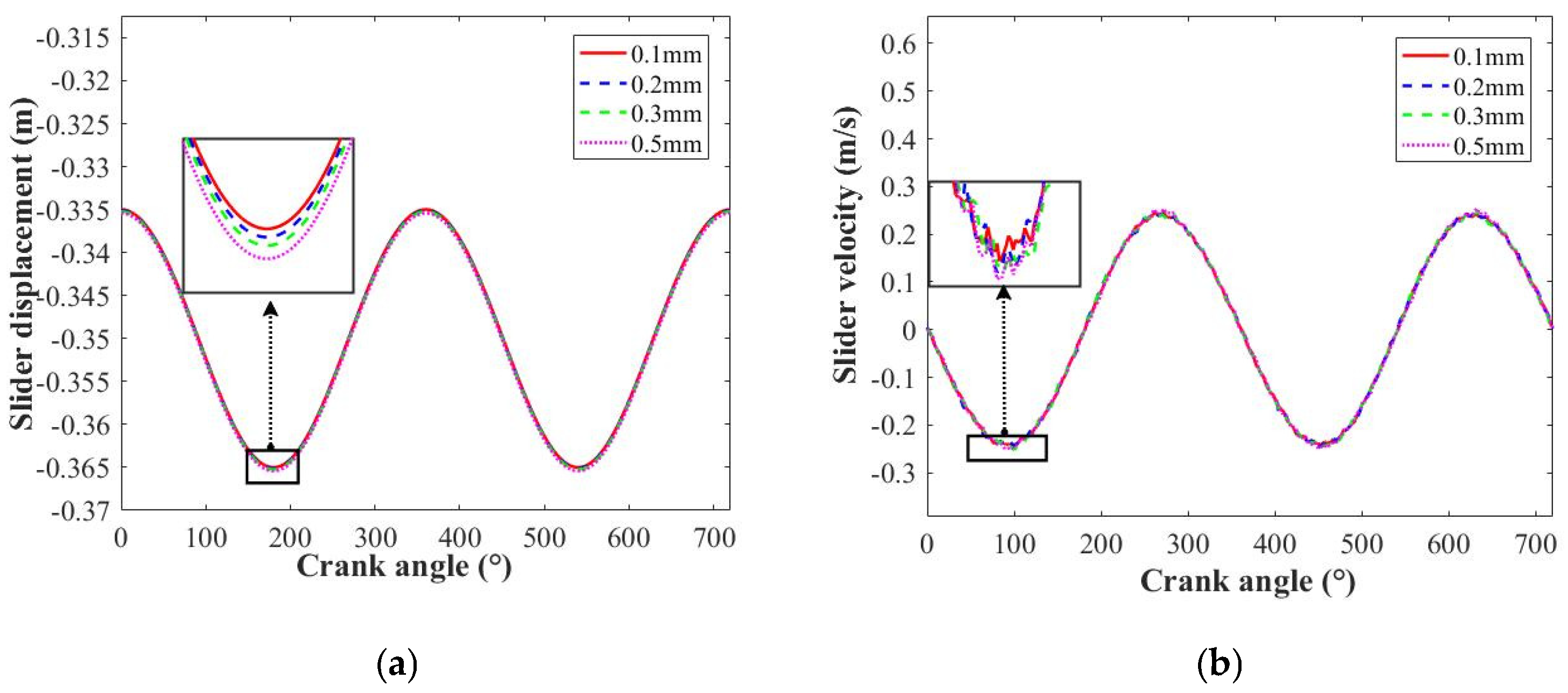
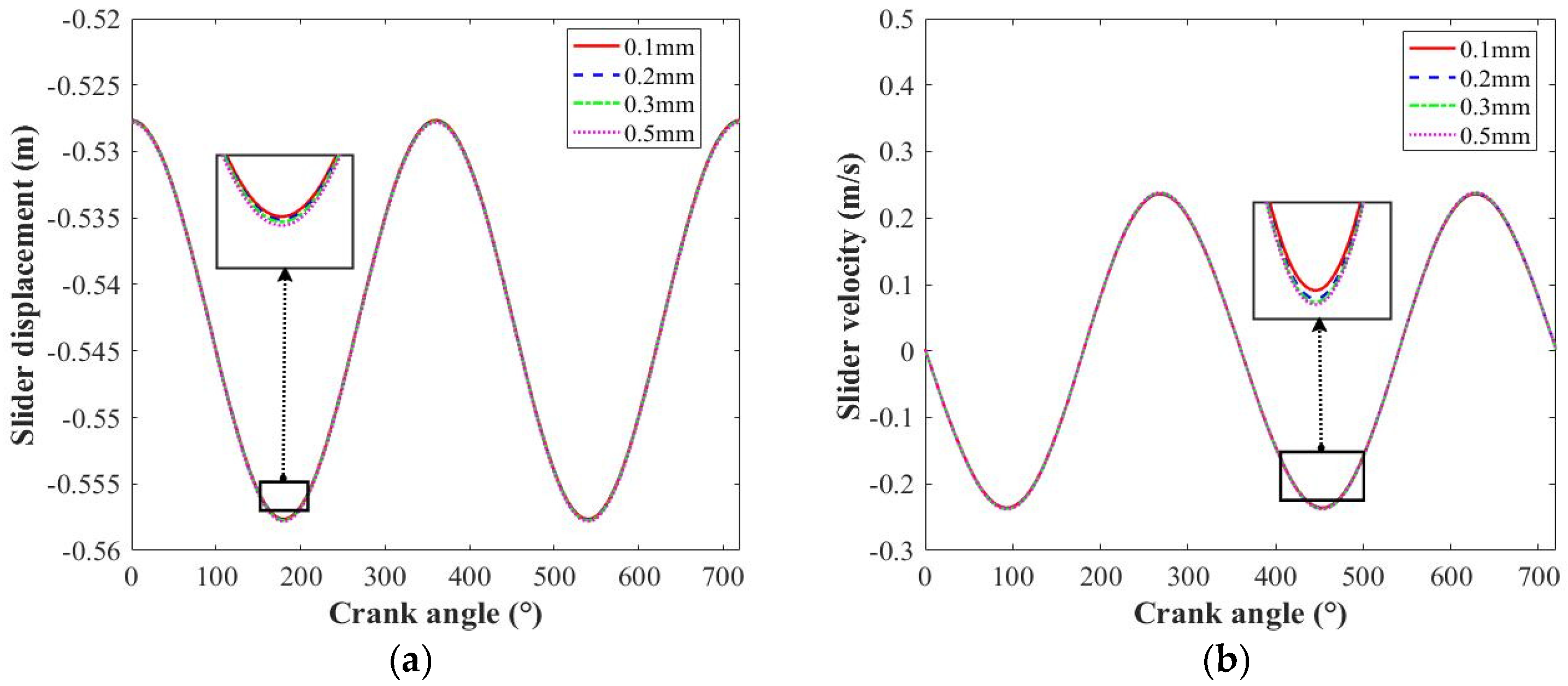
4.2. Influence of Clearance Size
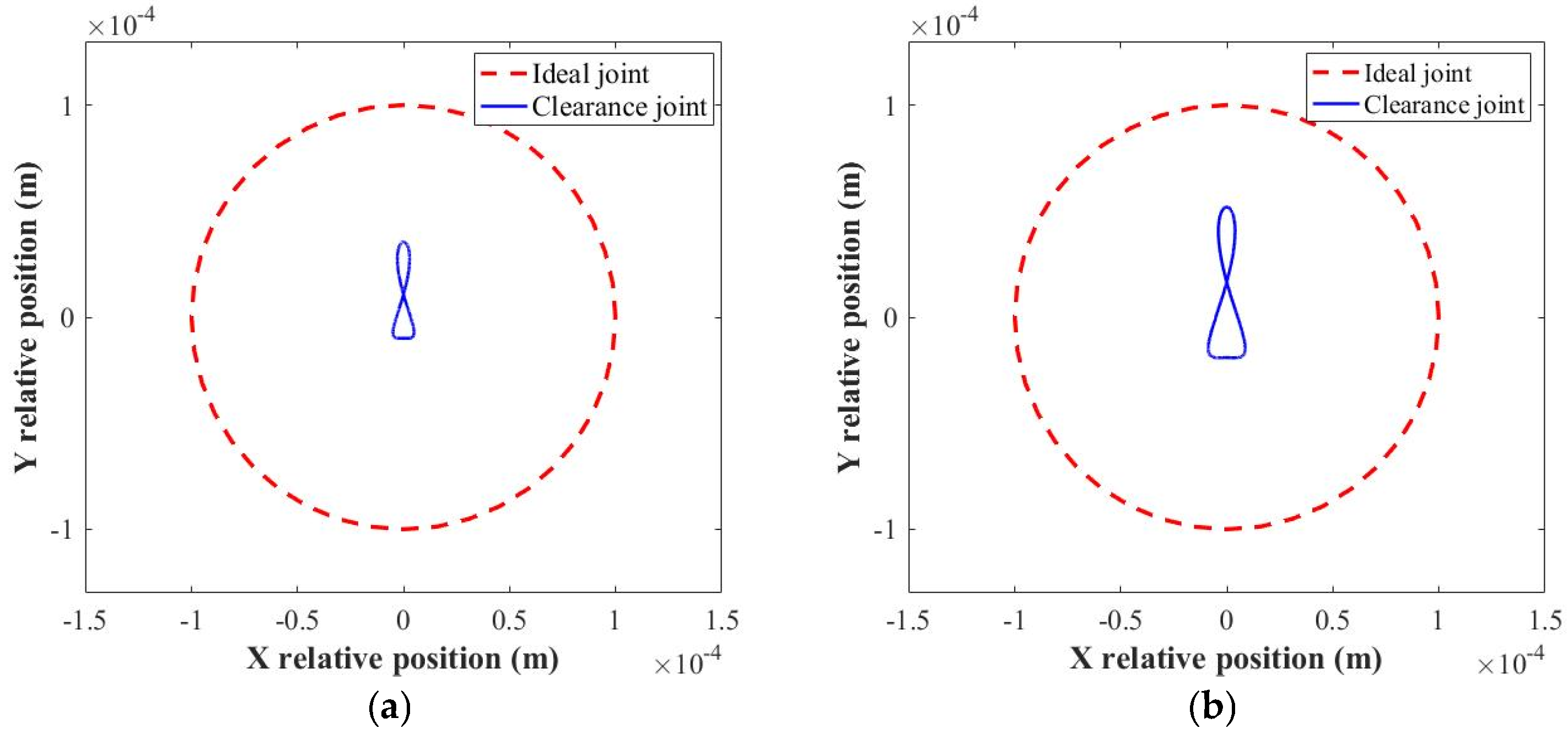
5. Experimental Test
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yan, S.Z.; Guo, P. Kinematic accuracy analysis of flexiblemechanisms with uncertain link lengths and joint clearances. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 225, 1973–1983. [Google Scholar] [CrossRef]
- Muvengei, O.; Kihiu, J.; Ikua, B. Dynamic analysis of planar multi-body systems with LuGre friction at differently located revolute clearance joints. Multibody Syst. Dyn. 2012, 28, 369–393. [Google Scholar] [CrossRef]
- Farahan, S.B.; Ghazavi, M.R.; Rahmanian, S. Bifurcation in a planar four-bar mechanism with revolute clearance joint. Nonlinear Dyn. 2017, 87, 955–973. [Google Scholar] [CrossRef]
- Lai, X.M.; Lai, Q.F.; Huang, H. New approach to assess and rank the impact of revolute joint wear on the kinematic accuracy in the low-velocity planar mechanism. Adv. Eng. Softw. 2016, 102, 71–82. [Google Scholar] [CrossRef]
- Farahanchi, F.; Shaw, S.W. Chaotic and periodic dynamics of a slider-crank mechanism with slider clearance. J. Sound Vib. 1994, 177, 307–324. [Google Scholar] [CrossRef]
- Skrinjar, L.; Slavic, J.; Boltezar, M. A validated model for a pin-slot clearance joint. Nonlinear Dyn. 2017, 88, 131–143. [Google Scholar] [CrossRef]
- Sun, J.L.; Tian, Q.; Hu, H.Y. Topology optimization based on level set for a flexible multibody system modeled via ANCF. Struct. Multidiscip. Opt. 2017, 55, 1159–1177. [Google Scholar] [CrossRef]
- Zheng, E.L.; Fan, Y.D.; Zhu, R.; Zhu, Y. Prediction of the vibration characteristics for wheeled tractor with suspended driver seat including air spring and MR damper. J. Mech. Sci. Technol. 2016, 30, 4143–4156. [Google Scholar] [CrossRef]
- Zhao, Q.Q.; Guo, J.K.; Hong, J. Analysis of angular errors of the planar multi-closed-loop deployable mechanism with link deviations and revolute joint clearances. Aerosp. Sci. Technol. 2019, 87, 25–36. [Google Scholar] [CrossRef]
- Guo, H.N.; He, P.; Liu, Z.S. Investigation of an improved planar revolute joint contact model with rough surface. Tribol. Int. 2019, 134, 385–393. [Google Scholar] [CrossRef]
- Erkaya, S. Trajectory optimization of a walking mechanism having revolute joints with clearance using ANFIS approach. Nonlinear Dyn. 2013, 71, 75–91. [Google Scholar] [CrossRef]
- Bai, Z.F.; Zhao, Y. A hybrid contact force model of revolute joint with clearance for planar. Int. J. Nonlinear Mech. 2013, 48, 15–36. [Google Scholar] [CrossRef]
- Bai, Z.F.; Sun, Y. A study on dynamics of planar multibody mechanical systems with multiple revolute clearance joints. Eur. J. Mech. A/Solid 2016, 60, 95–111. [Google Scholar] [CrossRef]
- Zheng, X.D.; Zhang, F.; Wang, Q. Modeling and simulation of planar multibody systems with revolute clearance joints considering stiction based on an LCP method. Mech. Mach. Theory 2018, 130, 184–202. [Google Scholar] [CrossRef]
- Li, X.; Ding, X.L.; Chirikjian, G.S. Analysis of angular-error uncertainty in planar multiple-loop structures with joint clearances. Mech. Mach. Theory 2015, 91, 69–85. [Google Scholar] [CrossRef]
- Muvengei, M.; Kihiu, J.; Ikua, B. Effects of clearance size on the dynamic response of planar multi-body systems with differently located frictionless revolute clearance joints. J. Energy Technol. Policy 2012, 2, 7–18. [Google Scholar]
- Rahmanian, S.; Ghazavi, M.R. Bifurcation in planar slider-crank mechanism with revolute clearance joint. Mech. Mach. Theory 2015, 91, 86–101. [Google Scholar] [CrossRef]
- Li, Y.Y.; Wang, C.; Huang, W.H. Dynamics analysis of planar rigid-flexible coupling deployable solar array system with multiple revolute clearance joints. Mech. Syst. Signal Process. 2019, 117, 188–209. [Google Scholar] [CrossRef]
- Li, Y.Y.; Wang, Z.; Wang, C. Effects of torque spring, CCL and latch mechanism on dynamic response of planar solar arrays with multiple clearance joints. Acta Astronaut. 2017, 132, 243–255. [Google Scholar] [CrossRef]
- Flores, P.; Leine, R.; Glocker, C. Modeling and analysis of planar rigid multibody systems with translational clearance joints based on the non-smooth dynamics approach. Multibody Syst. Dyn. 2010, 23, 165–190. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, Z.N.; Fang, C.C.; Dai, X.D.; Xie, Y.B. Modeling and analysis of planar multibody system with mixed lubricated revolute joint. Tribol. Int. 2016, 98, 229–241. [Google Scholar] [CrossRef]
- Zhao, B.; Zhou, K.; Xie, Y.B. A new numerical method for planar multibody system with mixed lubricated revolute joint. Int. J. Mech. Sci. 2016, 113, 105–119. [Google Scholar] [CrossRef]
- Flores, P.; Lankarani, H.M. Dynamic response of multibody systems with multiple clearance joints. J. Comput. Nonlinear Dyn. 2012, 7, 031003. [Google Scholar] [CrossRef]
- Daniel, G.B.; Cavalca, K.L. Analysis of the dynamics of a slider–crank mechanism with hydrodynamic lubrication in the connecting rod–slider joint clearance. Mech. Mach. Theory 2011, 46, 1434–1452. [Google Scholar] [CrossRef]
- Chen, X.L.; Jia, Y.T. Dynamic modeling and responses investigation of spatial parallel robot considering lubricated spherical joint. Eur. J. Mech. A/Solid 2022, 92, 104458. [Google Scholar] [CrossRef]
- Jin, G.G.; Wang, Z.M.; Liang, D. Modeling and dynamics characteristics analysis of six-bar rocking feeding mechanism with lubricated clearance joint. Arch. Appl. Mech. 2023, 93, 2831–2854. [Google Scholar] [CrossRef]
- Song, N.N.; Peng, H.J.; Kan, Z.Y. Nonsmooth strategy for rigid-flexible multibody system considering different types of clearance joints and lubrication. Multibody Syst. Dyn. 2022, 55, 341–374. [Google Scholar] [CrossRef]
- Li, Y.Y.; Yang, Y.; Li, M. Dynamics analysis and wear prediction of rigid-flexible coupling deployable solar array system with clearance joints considering solid lubrication. Mech. Syst. Signal Process. 2022, 162, 108059. [Google Scholar] [CrossRef]
- Xu, L.X.; Yang, Y.H. Modeling a non-ideal rolling ball bearing joint with localized defects in planar multibody systems. Multibody Syst. Dyn. 2015, 35, 409–426. [Google Scholar] [CrossRef]
- Ping, T.; Zhang, Y.Q. Simulation of planar mechanisms with revolute clearance joints using the multipatch based isogeometric analysis. Comput. Methods Appl. Mech. Energy 2019, 343, 453–489. [Google Scholar]
- Zhao, Y.; Bai, Z.F. Dynamics analysis of space robot manipulator with joint clearance. Acta Astronaut. 2011, 68, 1147–1155. [Google Scholar] [CrossRef]
- Li, H.G.; Meng, G.; Meng, Z.Q.; Wen, B.C. Effects of boundary conditions on a self-excited vibration system with clearance. Int. J. Nonlinear Sci. Numer. Simul. 2007, 8, 571–580. [Google Scholar] [CrossRef]
- Bai, Z.F.; Chen, J.; Sun, Y. Effects of contact force model on dynamics characteristics of mechanical system with revolute clearance joints. Iran. J. Sci. Technol. Trans. Mech. Eng. 2014, 38, 375–388. [Google Scholar]
- Harsha, S.P.; Nataraj, C. Nonlinear dynamic response of high speed ball bearings due to surface waviness and unbalanced rotor. Int. J. Nonlinear Sci. Numer. 2006, 7, 163–166. [Google Scholar] [CrossRef]
- Xu, L.X.; Li, Y.G. Investigation of joint clearance effects on the dynamic performance of a planar 2-DOF pick-and-place parallel manipulator. Robot. Comput. Integr. Manuf. 2014, 301, 62–73. [Google Scholar]
- Wang, J.Y.; Wang, H.T.; Wang, H.; Guo, L.X. Influence of random system parameters on the nonlinear dynamic characteristics of gear transmission system. Int. J. Nonlinear Sci. Numer. 2017, 18, 619–630. [Google Scholar] [CrossRef]
- Lankarani, H.M.; Nikravesh, P.E. A contact force model with hysteresis damping for impact analysis of multibody systems. J. Mech. Des. 1990, 112, 369–376. [Google Scholar] [CrossRef]
- Pérez-González, A.; Fenollosa-Esteve, C.; Sancho-Bru, J.L. A modified elastic foundation contact model for application in 3D models of the prosthetic knee. Med. Eng. Phys. 2008, 30, 387–398. [Google Scholar] [CrossRef]
- Zhuang, F.F.; Wang, Q. Modeling and analysis of rigid multibody systems with driving constraints and frictional translation joints. Acta Mech. Sin. 2014, 30, 437–446. [Google Scholar] [CrossRef]
- Tian, Q.; Sun, Y.; Liu, C.; Hu, H.Y.; Flores, P. Elastohydrodynamic lubricated cylindrical joints for rigid–flexible multibody dynamics. Comput. Struct. 2013, 114, 106–120. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, X.; Zhu, H.; Guo, Y.; Wu, X.; Chen, Y. Effects of Contact Characteristics on Dynamic Response of Planar Mechanical Systems with Lubricated Revolute Joint. Lubricants 2025, 13, 124. https://doi.org/10.3390/lubricants13030124
Peng X, Zhu H, Guo Y, Wu X, Chen Y. Effects of Contact Characteristics on Dynamic Response of Planar Mechanical Systems with Lubricated Revolute Joint. Lubricants. 2025; 13(3):124. https://doi.org/10.3390/lubricants13030124
Chicago/Turabian StylePeng, Xu, Haoran Zhu, Yang Guo, Xuze Wu, and Yu Chen. 2025. "Effects of Contact Characteristics on Dynamic Response of Planar Mechanical Systems with Lubricated Revolute Joint" Lubricants 13, no. 3: 124. https://doi.org/10.3390/lubricants13030124
APA StylePeng, X., Zhu, H., Guo, Y., Wu, X., & Chen, Y. (2025). Effects of Contact Characteristics on Dynamic Response of Planar Mechanical Systems with Lubricated Revolute Joint. Lubricants, 13(3), 124. https://doi.org/10.3390/lubricants13030124



