Physics-Informed Transfer Learning for Predicting Engine Oil Degradation and RUL Across Heterogeneous Heavy-Duty Equipment Fleets

Abstract

Predicting the Remaining Useful Life (RUL) of engine oil is critical for proactive maintenance and fleet reliability. However, irregular and noisy single-point sampling presents challenges for conventional prognostic models. To address this, a hierarchical physics-informed transfer learning (TL) framework is proposed that reconstructs nonlinear degradation trajectories directly from non-time-series data. The method uniquely integrates Arrhenius-type oxidation kinetics and thermochemical laws within a multi-level TL architecture, coupling fleet-level generalization with engine-specific adaptation. Unlike conventional approaches, this framework embeds physical priors directly into the transfer process, ensuring thermodynamically consistent predictions across different equipment. An integrated uncertainty quantification module provides calibrated confidence intervals for RUL estimation. Validation was conducted on 1760 oil samples from dump trucks, dozers, shovels, and wheel loaders operating under real mining conditions. The framework achieved an average R² of 0.979 and RMSE of 10.185. This represents a 69% reduction in prediction error and a 75% narrowing of confidence intervals for RUL estimates compared to baseline models. TL outperformed the asset-specific model, reducing RMSE by up to 3 times across all equipment. Overall, this work introduces a new direction for physics-informed transfer learning, enabling accurate and uncertainty-aware RUL prediction from uncontrolled industrial data and bridging the gap between idealized degradation studies and real-world maintenance practices.

1. Introduction

Diesel engines power nearly every industrial sector, from transport and mining to construction and agriculture [1]. Their performance and reliability depend strongly on the characteristics and condition of the lubricating oil, which reduces friction, dissipates heat, prevents corrosion, and removes contaminants from contact surfaces [2]. Among available lubricants, 15W–40 semi-synthetic oils remain the most common choice in heavy-duty diesel fleets due to their well-established viscosity–temperature characteristics, cost-effectiveness, balanced additive formulations, and longer life expectancy in comparison with mineral oils [3]. These oils provide a stable benchmark for studying and understanding the degradation rate and Remaining Useful Life (RUL) of lubricants in service [4,5,6].

During engine operation, the oil is subjected to a harsh and complex combination of thermal, chemical, and mechanical stresses [7]. Processes such as oxidation, nitration, soot accumulation, and additive depletion interact in nonlinear and interdependent ways, progressively altering the oil’s chemical and physical properties [8,9]. Consequently, viscosity and acidity number tend to increase [10], while the Total Base Number (TBN) and anti-wear protection decline [11]. Despite this, most maintenance schedules continue to rely on fixed time or mileage intervals [12]. These rigid schedules fail to account for variations in load, fuel quality, and ambient temperature, often resulting in either premature oil replacement, which wastes resources and raises operational costs, or delayed changes that increase wear and failure risk. To address these inefficiencies, many industries are adopting condition-based maintenance (CBM) strategies [13,14], in which oil condition is continuously monitored and the RUL is estimated as the remaining duration before critical parameters, such as viscosity or TBN, exceed acceptable operational thresholds [15].

Accurately predicting oil RUL across different engines remains, however, a challenging task [16]. The oil degradation is inherently nonlinear and influenced by the interplay between operating conditions, fuel composition, and environmental factors. Local models (i.e., Asset Specific Models) trained on individual engines can capture specific degradation trends but rarely generalize to others [17,18], while Global Models trained on aggregated data often lose sensitivity to engine-specific behaviors [19]. This trade-off reflects the classical bias–variance dilemma commonly observed in predictive maintenance models. Furthermore, industrial datasets are often noisy, irregularly sampled, and imbalanced due to field sampling constraints and laboratory variations, which led many previous studies to be conducted under controlled laboratory conditions or using synthetic datasets [20,21,22].

Beyond its practical deployment advantage, this study contributes to the theoretical development of Physics-Informed Machine Learning (PIML) by embedding thermochemical degradation kinetics within the transfer learning hierarchy itself, rather than applying physics post-hoc or as a regularization term. This allows physical priors to shape feature transfer, not just prediction. Furthermore, the work advances Transfer Learning for industrial prognostics by demonstrating that non-time-series oil data can be transformed into transferable degradation representation spaces, enabling reliable fleet-level generalization and asset-specific adaptation, a capability not achieved in conventional TL architectures or PIML frameworks trained on controlled laboratory data. Together, these aspects establish a new methodological foundation for PIML-based transfer learning under sparse, irregular real-world monitoring conditions

The next section reviews previous studies on oil degradation mechanisms, diagnostic indicators, and modeling approaches, ranging from empirical and statistical techniques to modern hybrid and transfer learning frameworks. The discussion highlights existing limitations that motivate the present study and establishes the need for models capable of capturing nonlinear, field-observed degradation behaviors across diverse diesel engines using the same lubricant formulation.

2. Literature Review

2.1. Characteristics and Indicators of Engine Oil Degradation

Construction fleets relying on heavy-duty diesel engines typically use 15W–40 semi-synthetic oils. These lubricants exhibit a balanced viscosity profile (around 15.5 cSt at 100 °C) and contain additive packages for soot dispersion, oxidation inhibition, and anti-wear protection [23]. Cerny et al. [24] compared the oxidation stability of eight different commercial SAE 15W-40 engine oils and concluded that the base oil composition is a critical factor in determining the high-temperature oxidation stability of engine oils. Because the formulations of these oils are standardized, the oils themselves serve as excellent reference materials for modeling studies. Experiments have shown that the rate of viscosity increase, and additive depletion depend strongly on engine load, temperature, and fuel sulfur content, factors which directly influence the RUL of engine oil.

Engine oil degradation occurs through oxidation, nitration, sulfation, soot loading, and additive depletion [2,14,25]. Oxidation produces acidic and polymerized compounds that increase viscosity, Total Acid Number (TAN), and sludge. Nitrogen oxides trigger nitration, while sulfur-based additives contribute to sulfation, generating corrosive by-products. Anti-wear additive depletion, such as ZDDP, weakens protective film formation on metal surfaces, though some degradation products partially restore lubricity. Soot thickens the oil, wear metals such as Fe, Cu, and Pb accelerate oxidation, and fuel dilution lowers viscosity and film strength. These mechanisms collectively alter viscosity, chemical composition, and load-carrying capacity, controlling when the oil reaches the end of its useful life.

Since lubricant formulations are consistent across engines, degradation mechanisms are comparable, enabling scalable modeling for RUL assessment across diverse assets. Adaptive models that account for nonlinear interactions outperform static or laboratory-based baselines in predicting RUL. Omiya et al. [26] collected real-world datasets from buses and trucks, including engine speed, load, temperature, hours of operation, and prior oil analyses, highlighting the importance of field data in reconstructing actual degradation trajectories for accurate RUL estimation. Analytical methods such as FTIR spectroscopy [27], ICP spectrometry [28], and viscometry provide multidimensional insights into degradation, but interdependence among variables complicates direct interpretation, necessitating advanced modeling for RUL prediction. Heredia-Cancino et al. [29] showed that oxidation, nitration, and sulfation indicators evolve in a nonlinear and highly coupled manner, further reinforcing the need for RUL-focused modeling frameworks.

2.2. Modeling Approaches of Engine Oil Degradation Rate

Oil degradation is inherently nonlinear due to coupled interactions among thermal oxidation, additive depletion, soot accumulation, and mechanical wear. Engine operating conditions such as temperature, load, and fuel composition modulate these trajectories, producing complex degradation curves that cannot be captured by simple linear models [30]. Sejkorová et al. [25] observed sigmoidal or power-law viscosity growth, while Wolak et al. [31] reported that TBN depletion initially declines rapidly and then stabilizes, affecting the oil’s ability to neutralize acids. These nonlinear behaviors directly influence the prediction of RUL, emphasizing the need for models capable of capturing saturation, hysteresis, and interaction effects.

Early RUL prediction studies relied on empirical or linear regression models [32]. Van Thai Nguyen et al. [33] used multiple linear regression with FTIR spectral data and chemical indicators such as TBN, oxidation, sulfation, and fuel dilution to estimate RUL. While simple and transparent, such models assume linearity and independence among parameters, which is unrealistic given the complex interactions in oil degradation. Regression-based viscosity models often underestimate thickening when soot dominates, and empirical thresholds are typically derived from single-engine tests, limiting their generalization for fleet-wide RUL assessment [34]. Traditional trend analysis assumes constant degradation rates, oversimplifying underlying chemistry and reducing the reliability of RUL predictions under varying operational conditions.

Capturing nonlinear degradation dynamics requires models that combine physical interpretability with data-driven flexibility. Machine learning and hybrid frameworks can map multivariate oil condition parameters to RUL outcomes, provided they are trained on diverse datasets. Learning nonlinear degradation directly from real-world field data while preserving thermochemical principles ensures that RUL predictions reflect true degradation rather than merely fitting observed trends.

2.3. Machine Learning and Ensemble Techniques

Recent studies employ machine learning (ML) models such as ANNs, RFs, and SVMs to predict nonlinear degradation dynamics and estimate RUL [35,36]. Rodrigues et al. [37] combined ANNs with PCA for dimensionality reduction, maintaining prediction accuracy for condition-based RUL assessment. Katreddi et al. [38] introduced a mixed-effects random forest (MERF) to handle clustered longitudinal maintenance data, capturing variability between engines and improving RUL estimates.

Ensemble learning combines multiple models to enhance prediction robustness. Wang et al. [39] developed a hybrid ensemble integrating CNN-based, expert-rule, and SVM techniques for equipment fault prediction, demonstrating improved RUL prediction accuracy. Shao et al. [40] applied ensemble classifiers to marine diesel engine fault diagnosis. While effective in controlled environments, these models often rely on simulated data or single-source datasets, limiting real-world RUL applicability.

Industrial RUL assessment requires models trained on sparse, noisy, and heterogeneous field data. Data-driven models may lack interpretability and fail to generalize across different engines using the same oil formulation. Physics-informed machine learning (PIML) incorporates physical laws such as Arrhenius-type oxidation kinetics or additive depletion decay into ML architectures [41,42], enhancing extrapolation and ensuring that RUL predictions are physically plausible. A prime illustration of this hybrid paradigm is the work by Kumar et al. [43], which developed a physics-informed neural network for engine oil RUL estimation that explicitly encodes Arrhenius degradation kinetics. By enforcing this fundamental thermochemical law during training, their model achieved a >30% reduction in prediction error and produced more reliable uncertainty estimates compared to conventional data-driven models. However, many PIML approaches are validated only on lab or single-engine data, limiting their applicability to fleet-level RUL assessment.

Beyond purely data-driven and physics-informed models, research has also progressed toward integrated hardware-software systems for real-time prognostics. For instance, Jagannathan et al. [44] developed an adaptive methodology combining micro-sensor data with computational models. A neural network-fuzzy classifier fused these inputs to derive a singular oil condition trend, which was then used by prognostic algorithms to estimate RUL. In parallel, Zhu et al. [45] leveraged dielectric spectroscopy for in situ sensing modalities to detect chemical and physical changes in degrading oil. By feeding the spectral data into machine learning classifiers such as Random Forest and ANN, the study successfully predicted RUL with high accuracy around 96%.

Transfer learning (TL) supports fleet-scale RUL prediction by fine-tuning global models trained on multiple engines for local conditions [46,47]. Hierarchical modeling links local engine parameters to population-level distributions, facilitating scalable and interpretable RUL estimation. Embedding physical constraints and uncertainty quantification directly within the model ensures that RUL predictions are both reliable and probabilistically calibrated. Bayesian Neural Networks, Gaussian Processes, and ensemble approaches [48] can provide confidence intervals, reflecting aleatoric and epistemic uncertainties that influence RUL estimates.

2.4. Research Gaps and Objective

Despite the considerable advances in oil degradation modeling, several important challenges remain:

• Many data-driven models prioritize prediction accuracy over physical understanding and may yield thermodynamically inconsistent behavior when applied to new operating conditions.
• Most physics-informed approaches are still validated on single-engine or even lab experimental datasets, restricting their generalization to real fleets.
• Most existing studies treat each engine as a separate problem, ignoring the fact that engines using the same lubricant formulation undergo fundamentally similar degradation processes. This represents a missed opportunity for scalable learning across heterogeneous fleets.
• Uncertainty analysis is rarely embedded within the model itself; it is usually treated as a separate post-processing step, reducing its usefulness for maintenance planning.
• Finally, industrial oil datasets are noisy, irregular, and domain-imbalanced, issues that current models seldom address effectively.

These combined challenges underscore the need for models trained on uncontrolled, realistic field data that reflect the nonlinear dynamics of true oil degradation rather than idealized laboratory behavior. Field data are usually gathered opportunistically, with only one oil sample per change and without consistent sampling intervals or standardized operating conditions. Consequently, most published approaches cannot directly reconstruct real degradation trajectories from these sparse, single-point measurements.

This study addresses these gaps by proposing a physics-informed hierarchical transfer learning framework explicitly designed for RUL assessment of diesel engine oils using uncontrolled, single-sample industrial data. Arrhenius-type degradation kinetics are embedded within a hierarchical structure that leverages shared oil chemistry across engines while adapting to local conditions. Uncertainty quantification is integrated during model training, producing calibrated confidence intervals for RUL. Trained on data from a multinational company mining fleet, the framework generalizes across different equipment types using the same diesel formulation, enabling accurate RUL prediction that reflects actual nonlinear degradation and supports robust, scalable condition-based maintenance.

3. Proposed Methodology

This section presents the comprehensive methodological framework developed for predicting engine oil degradation and estimating Remaining Useful Life (RUL) across multiple categories of heavy-duty equipment. The methodology is built upon the principle that oil end-of-life results from the interacting evolution of three fundamental degradation modes: chemical additive depletion, mechanical wear metal accumulation, and physicochemical transformation.

The framework first reconstructs continuous, non-linear degradation trajectories for each monitored parameter using physics-based rate equations. The time at which each predicted trajectory crosses its predefined failure threshold is computed analytically. The final RUL is then determined not by the first threshold crossing, but by applying an expert-informed rule: oil is declared at end-of-life when a second, independent parameter from a different degradation category crosses its caution or failure limit. This ensures the RUL prediction inherently reflects multi-mechanism degradation. The interdependence of these mechanisms is subsequently analyzed through cross-equipment correlation matrices, providing empirical support for the multi-parameter decision logic. To achieve this across a heterogeneous fleet, the core innovation is a three-tier hierarchical modeling strategy. A Global Model (GM) learns universal, physics-constrained degradation kinetics shared by all assets using the same lubricant formulation. This knowledge is then transferred and adapted via asset-specific fine-tuning layers, enabling accurate and uncertainty-aware RUL predictions for individual machines despite sparse and noisy field data. The complete workflow, from raw data processing to RUL estimation, is detailed in the following subsections. The complete workflow, from raw data processing to RUL estimation, is detailed in the following subsections.

3.1. Dataset Description and Structure

The dataset analyzed in this study originates from a large-scale oil condition monitoring program conducted for one of the international companies on a fleet of mining equipment, including dump trucks, dozers, shovels, and wheel loaders. Oil samples were periodically collected according to the preventive maintenance schedule and analyzed in a certified laboratory. Each sample record includes physicochemical parameters such as oxidation, viscosity, and Total Base Number (TBN), as well as elemental wear concentrations (Fe, Cu, Al, Cr, Pb, Mo) and operational metadata such as asset identification and oil age. The values of the sample parameters were determined using Inductively Coupled Plasma Optical Emission spectroscopy (ICP-OES), which provides high sensitivity for wear metals and additive depletion markers and is widely adopted in condition-based oil diagnostics. Analytical precision was confirmed by repeat testing, yielding coefficients of variation below 5%, which verifies measurement reliability and suitability for prognostic modeling. The resulting dataset reflects realistic industrial conditions, encompassing a total of 1760 observations across 26 assets, as summarized in

Table 1. Equipment type, sample, and asset distribution.

Equipment Type	Samples (n)	Assets (n)
Dump Trucks	888	13
Dozers	94	3
Shovels	93	2
Wheel Loaders	684	9
Total	1760	26

.

This dataset presents the classic industrial prognostic challenge. It consists of sparse, irregularly sampled single-point measurements (one sample per oil change) rather than continuous time-series. The primary methodological task is thus to reconstruct complete, physically plausible degradation trajectories from these isolated snapshots.

All engines used the same bulk supplied diesel engine oil with viscosity grade SAE 15W-40, according to API CI-4/SL dual-purpose oil classification for both diesel (CI-4) and gasoline (SL) engines. Although the specific commercial brand was not disclosed by the site due to procurement confidentiality, the lubricant was consistent across all machines and all samples originated from the same formulation family. This ensures uniformity in additive chemistry and viscosity behavior, which is an essential factor for model generalization and transfer learning. In addition, the chemical consistency of a single, well-defined semi-synthetic formulation across all assets is considered essential for the built framework. It allows to isolate and model the universal degradation patterns (for example, Arrhenius-type oxidation, additive depletion trends) before transferring and adapting them to asset-specific operating conditions. This would be more challenging with a mixed fleet using various mineral oil grades, as these often degrade differently (e.g., exhibiting faster oxidation and viscosity increase) which presents its own set of challenges.

Zinc (Zn) and phosphorus (P) were measured using ICP-OES, according to ASTM D5185 [49] as a standard guideline for elemental analysis of lubricant additives. Because ICP-OES quantifies total elemental content, it captures Zn and P regardless of the chemical composition, whether present as the original ZDDP additive or its soluble degradation products (e.g., zinc phosphates, thiophosphates) [50,51]. This explains why Zn and P levels may appear in used oil similar to fresh oil in some samples even though the additive has chemically transformed and depleted. When reductions do occur, they represent true elemental loss due to additive consumption, deposition on surfaces (forming anti-wear films), or precipitate out of the oil as insoluble deposits and settle as sludge.

Table 2. Representative physicochemical and wear-related lab results from the used oil datasets.

Asset Type	A. Dump Trucks	B. Shovels	C. Wheel Loaders	D. Dozers
Asset Label	A	A	F	C
Oil Age (operating h)	500	246	255	253
Al (ppm)	5	8	5	0
B (ppm)	6	0	0	48
Ca (ppm)	1284	1300	1390	1059
Cr (ppm)	0	3	4	0
Cu (ppm)	5	10	1	0
Fe (ppm)	14	26	14	42
K (ppm)	0	0	0	0
Mg (ppm)	112	293	1134	790
Mo (ppm)	32	0	2	28
Na (ppm)	2	0	0	0
P (ppm)	1067	1113	1252	881
Pb (ppm)	1	5	1	0
Si (ppm)	5	12	3	1
Zn (ppm)	1120	1235	1067	989
Oxidation (Ab/cm)	0	2	0	0
PQ Index	6	15	6	30
Soot (wt.%)	0.47	0.33	0.41	2.41
TBN	8	9	8.4	6.1
Viscosity @100C (cSt)	13	13.8	13.2	13.1
Water (Vol.%)	0	0.08	Not Detected	0.03

summarizes the key physicochemical results for the used oil samples collected from the four monitored machinery types. It shows representative laboratory measurements for a single observation, including the principal physicochemical and wear-related parameters used in model development.

3.2. Data Processing and Normalization

Comprehensive validation procedures were applied to ensure data integrity before modeling. Little’s MCAR test was conducted to assess the randomness of missing data, which represented approximately 4.8% of the total dataset. Continuous variables were imputed using linear interpolation to preserve temporal continuity, while categorical identifiers were verified for completeness and uniqueness. Outlier detection employed a hybrid method combining the interquartile range (3 × IQR) and Mahalanobis distance to identify both univariate and multivariate anomalies. After cleaning, 1675 samples remained valid for modeling.

Each continuous variable xi was normalized relative to its known physical or manufacturer-defined threshold θi, rather than by arbitrary statistical scaling. This normalization was computed as shown in Equation (1).

$${\tilde{x}}_i={\displaystyle \frac{x_i}{{\theta }_i}}$$

(1)

where ${\tilde{x}}_i$ represents the normalized value and θ_i denotes the degradation or contamination limit corresponding to parameter i. This approach ensures that ${\tilde{x}}_i$ = 1 corresponds directly to a condition near failure, improving interpretability across different equipment and parameters. Because samples were collected at irregular intervals, all variables were realigned to a uniform cumulative operating-hour grid to maintain consistent temporal representation.

3.3. Feature Engineering and Selection

Feature engineering emphasized parameters that describe the chemical, mechanical, and physical evolution of the lubricant. Three fundamental classes of degradation behavior were observed: depletion indicators, accumulation indicators, and transformation indicators. Depletion indicators represent properties that diminish with use due to additive consumption or neutralization, including TBN, calcium (Ca), and magnesium (Mg). Accumulation indicators reflect parameters that increase monotonically as wear metals and contaminants accumulate, such as iron (Fe), copper (Cu), and aluminum (Al). Transformation indicators exhibit nonlinear patterns influenced by multiple competing effects, including viscosity, oxidation, and nitration. This categorization allows the model to treat each parameter according to its underlying degradation mechanism.

The classification of these diagnostic features into three distinct categories is summarized in

Table 3. Representative diagnostic feature categories.

Category	Representative Features
Depletion	TBN, Additive Elements (Ca, Mg, Zn, P)
Accumulation	Fe, Cu, Al, Pb, Si, Na, K
Transformation	Viscosity, Oxidation, Nitration, Soot

, which provides a clear framework for understanding the different degradation mechanisms modeled in this study.

The models assume each parameter evolves according to its own kinetics, without mathematically modeling how one indicator’s state affects another’s degradation rate. While the degradation trajectories for individual parameters are modeled independently, the integration of chemical, wear, and contamination indicators is crucial for holistic RUL estimation. Therefore, all parameters from the three categories serve as concurrent inputs to the machine learning models, enabling the algorithms to capture complex, non-linear interactions inherent in the degradation process. This integration is further governed by the ‘second-threshold’ decision rule, which ensures that the final RUL prediction reflects the confluence of multiple degradation mechanisms rather than any single parameter evolution.

To prevent redundancy, variables with high pairwise correlation (r > 0.9) were excluded. Recursive Feature Elimination (RFE) using Random Forest importance was then applied to identify the most relevant predictors. Derived ratios such as Fe/TBN and Oxidation/TBN were introduced to represent compound degradation relationships, improving physical interpretability.

Model parameters were estimated using the Levenberg–Marquardt nonlinear least-squares algorithm. Bootstrap resampling was applied to quantify parameter uncertainty. An initial set of 100 bootstrap iterations was used during model tuning to verify convergence behavior and computational efficiency. Once stable convergence was confirmed, the full model estimation employed 1000 bootstrap replicates to generate robust 95% confidence intervals for key parameters such as the degradation rate constant (k) and the time exponent (p). This two-stage approach ensures that uncertainty estimates are statistically stable without unnecessary computational cost.

3.4. Physics-Informed Mathematical Modeling for Oil Degradation Prediction

The temporal evolution of each oil-health indicator y(t) was modeled using non-linear rate equations that capture the physical kinetics of degradation and contaminant buildup. The underlying assumption is that the instantaneous rate of change of a measurable property is proportional to its current magnitude and varies according to how the degradation process accelerates or slows down as time progresses. In practical terms, this means that the rate of change for y(t) is not constant. Instead, the rate at which y(t) increases or decreases depends on both its present value and the duration of oil operation, allowing the model to represent early-stage stability, mid-cycle acceleration, or late-stage saturation in the parameter’s trajectory.

This time-dependent and magnitude-dependent behavior is expressed through the following differential form, as presented in Equation (2).

$${\displaystyle \frac{dy\left(t\right)}{dt}}=-k·p·t^{p-1}y\left(t\right)$$

(2)

where y(t) denotes the property value at time t; k > 0 is the generalized rate constant characterizing the magnitude of change; and p is the time exponent determining whether the process accelerates (p > 1) or decelerates (p < 1) with time. Integrating Equation (2) yields the general nonlinear exponential solution, as shown in Equation (3).

$$y\left(t\right)=y_o{e}^{{-kt}^p}$$

(3)

where y₀ represents the initial property value at t = 0. This generic formulation can represent several degradation archetypes commonly encountered in tribological systems. Depending on whether the variable of interest decreases, increases, or saturates over time, three distinct functional families were employed in Equations (3)–(5).

y(t) = y₀ + k t^p, Power-law growth

(4)

y(t) = y₀ + A ln 1 + t/B, Logarithmic growth

(5)

where A and B are positive constants defining, respectively, the amplitude and characteristic timescale of saturation for variables that exhibit bounded accumulation such as oxidation or nitration. For predictive maintenance purposes, the critical time t^∗ at which a monitored variable reaches a threshold value yth (e.g., manufacturer limit or failure criterion) is obtained analytically for each model type using Equations (6)–(8).

$$t_{exp}^{*}={\displaystyle \frac{1}{k}}{ln\left({\displaystyle \frac{y_o}{y_{th}}}\right)}^{1/p}$$

(6)

$$t_{power}^{*}={\left({\displaystyle \frac{y_{th}-y_o}{k}}\right)}^{1/p}$$

(7)

$$t_{log}^{*}=B.e^{\left({\displaystyle \frac{y_{th}-y_o}{k}}\right)}-1$$

(8)

In these expressions, yth denotes the terminal (failure) value of the monitored property, and t* is the estimated time to reach that limit, corresponding to the Remaining Useful Life (RUL) for that indicator. All model constants were optimized independently for each asset–parameter pair using the Levenberg–Marquardt nonlinear least-squares algorithm, with uncertainty bounds derived from 1000 bootstrap resamples. The physical interpretation of the key parameters and constants used in the degradation models (Equations (2)–(8)) is provided in

Table 4. Physical interpretation of model parameters and constants.

Symbol	Role	Physical Interpretation
y(t)	Degradation indicator	Time-dependent oil property (e.g., TBN, Fe)
y0	Initial value	Property value in new oil at t = 0
yth	Threshold	Critical limit defining end of useful life
k	Rate constant	Magnitude of degradation or accumulation rate
p	Time exponent	Describes acceleration/deceleration of process
A	Log amplitude	Scale of bounded (saturating) increase
B	Log time constant	Time scale for saturation or asymptotic growth
t*	Time to failure	Predicted time when y(t) reaches yth

, ensuring clarity and consistency in their application.

The family of models represented by Equations (3)–(8) captures a wide range of physical behaviors observed in oil aging, including additive depletion, viscosity breakdown, metal accumulation, and oxidation plateauing. Because each parameter’s evolution follows a physically interpretable trajectory, the resulting degradation profiles remain consistent with established tribo-chemical kinetics and laboratory observations.

In practical oil-condition monitoring, each diagnostic parameter has its own caution and failure thresholds. However, domain experts from the collaborating industrial oil-analysis provider emphasized that the first parameter to reach a caution threshold typically reflects early degradation or additive stress, not functional end-of-life. Hence, oil is technically considered to have reached end-of-life when the second independent indicator crosses its failure threshold, marking the transition from a warning state to confirmed functional degradation.

Following this expert-defined rule, the framework computes the time-to-threshold (t*) for all monitored indicators and orders them chronologically. The final RUL is then defined as the minimum time-to-failure corresponding to the second threshold-crossing event, rather than the earliest single crossing. This approach prevents premature failure declarations and aligns the RUL estimation with real industrial decision logic used in large oil-analysis laboratories. This expert-informed rule is the key integration mechanism that synthesizes the independently modeled parameter trajectories. It ensures the final RUL prediction reflects a consensus of multiple degradation pathways, preventing false alarms from single-parameter anomalies and aligning with industrial practice.

3.5. Multi-Equipment Hierarchical Modeling Strategy

To address the dual challenges of data sparsity (per asset) and heterogeneous operations (across the fleet), a three-tier hierarchical modeling strategy is employed. This structure is designed to first learn universal degradation kinetics shared by all assets using the same oil, then efficiently adapt this knowledge to specific equipment and individual machines, thereby enabling accurate RUL prediction even for assets with very limited local data. The three complementary modeling paradigms are: Asset-Specific (AS), Global Model (GM), and Hierarchical Transfer Learning (TL), as shown in Figure 1. The AS model captures individual asset behavior, the GM learns general degradation trends across all equipment, and the TL model builds upon the GM baseline to refine predictions at both the equipment and asset levels.

This hierarchical strategy enables the framework to generalize across equipment categories while maintaining sensitivity to local operating conditions. The hierarchical model prediction can be represented by Equation (9).

yˆ = f_global(X) + g_equipment(X) + h_asset(X)

(9)

where f_global(X) denotes the base fleet-level model, g_equipment(X) captures residual deviations at the equipment category level, and h_asset(X) refines local asset behavior, as described in Figure 2. In the proposed framework, the transfer process is guided by physical priors: the global model first learns the parameters of the physical degradation equations such as the rate constant k, time exponent p, and saturation constants A and B. These physically meaningful parameters are then passed to the equipment and asset levels, where they are only fine-tuned rather than replaced. This ensures that every stage of the hierarchy remains consistent with known degradation behavior and avoids non-physical predictions.

To prevent negative transfer, each layer is trained on the residuals of the previous layer, and it is kept only if the validation R² improves by at least 0.02. This guarantees that the added layer contributes useful information rather than unnecessary complexity. In addition, Group-KFold cross-validation is applied at the asset level to avoid data leakage and to ensure that the learned patterns generalize properly to unseen equipment.

Uncertainty in predicted RUL was assessed using percentile bootstrap ensembles, with 1000 resamples per model. The bootstrapped RUL distribution at time t is expressed as shown in Equation (10).

$${RUL}_b\left(t\right)=\widehat{t}(f,b)-t$$

(10)

where $\widehat{t}(f,b)$ is the bootstrap-estimated failure time for replicate b. From these replicates, 95% confidence intervals were derived by Equation (11). Representing combined aleatoric (data variability) and epistemic (model) uncertainty, residual diagnostics included normality (Shapiro–Wilk), autocorrelation (Durbin–Watson), and heteroscedasticity (Breusch–Pagan) tests to verify statistical assumptions.

CI_RUL= [t_f,2.5% − t, t_f,97.5% − t]

(11)

Model performance is evaluated using root mean square error (RMSE), mean absolute error (MAE), coefficient of determination (R²), relative accuracy (RA), and concordance index (C-index). Stratified five-fold cross-validation is applied at the asset level to prevent data leakage between training and testing partitions. Comparative performance among AS, GM, and TL configurations is statistically analyzed using the Wilcoxon signed-rank test for paired differences and Levene’s test for variance homogeneity, following confirmation of residual normality.

The proposed methodology is built on the assumption of monotonic degradation behavior and the use of uniformly spaced sampling intervals. These assumptions facilitate consistent cross-equipment comparisons by ensuring that the temporal evolution of degradation indicators can be aligned across diverse assets. While this simplification greatly enhances model calibration, interpretability, and computational efficiency, it inevitably limits the framework’s responsiveness to transient or non-monotonic phenomena, such as sudden changes in load, temperature, or operational regimes. Such short-term fluctuations, although often brief, may contain valuable diagnostic information that could improve early fault detection or anomaly recognition. Furthermore, the relatively small size and heterogeneity of available datasets for certain asset classes poses challenges for developing a fully generalizable Global Model. This constraint also partially limits the effectiveness of the transfer learning component, as knowledge extracted from data-rich assets cannot always be seamlessly adapted to data-sparse cases. Despite these limitations, the proposed framework demonstrates strong interpretability, reproducibility, and adaptability, making it suitable for practical deployment in industrial environments.

In summary, the proposed methodology transforms sparse, single-point industrial oil data into reliable RUL estimates through a physics-informed pipeline: (1) reconstructing continuous degradation trajectories using physical kinetic models, (2) transferring fleet-wide degradation knowledge to individual assets via a hierarchical learning framework, and (3) synthesizing multi-parameter predictions through an expert-defined “second-threshold” decision rule. This integrated approach directly addresses the challenges of uncontrolled, heterogeneous field data.

4. Results and Discussion

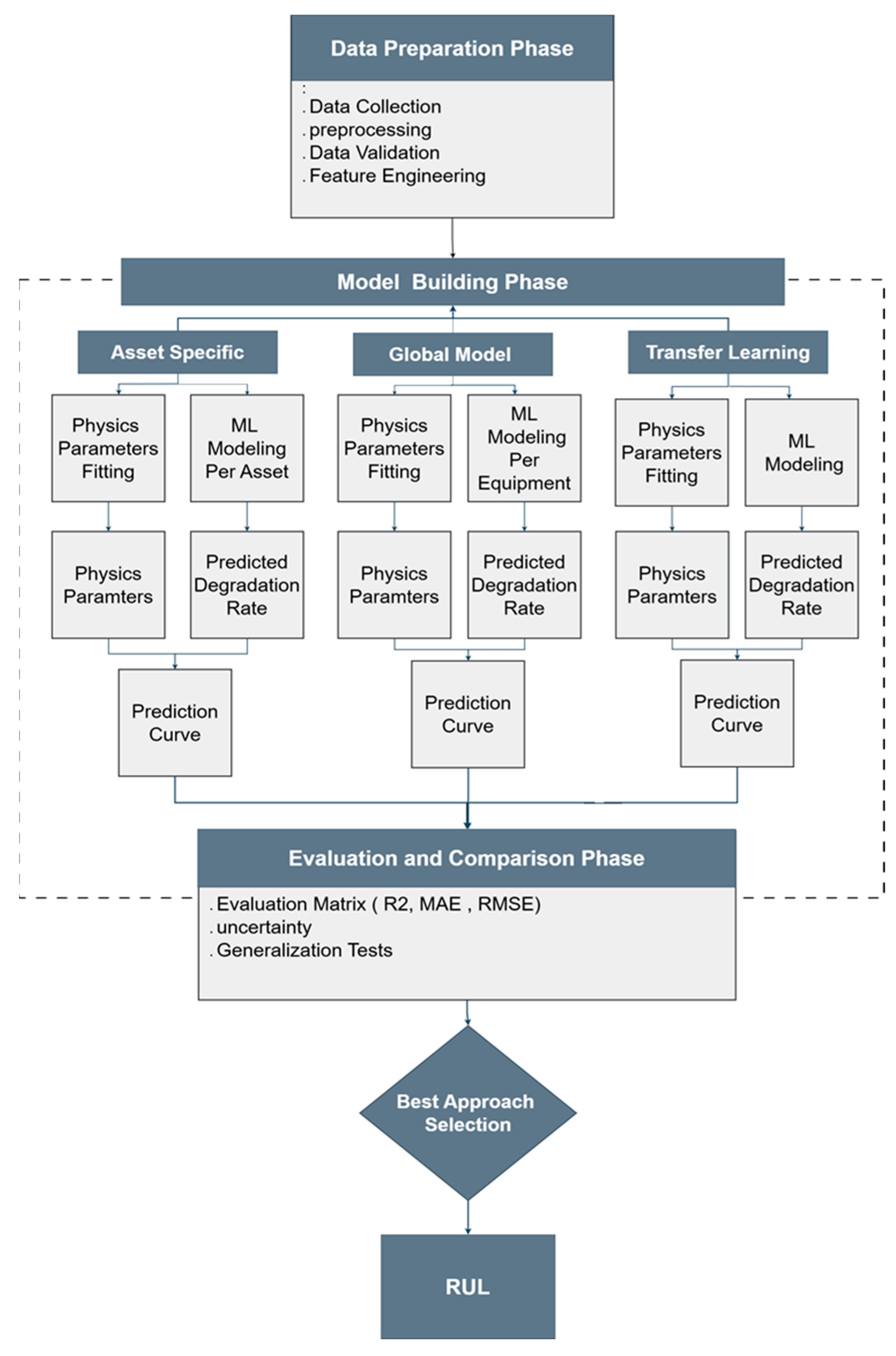
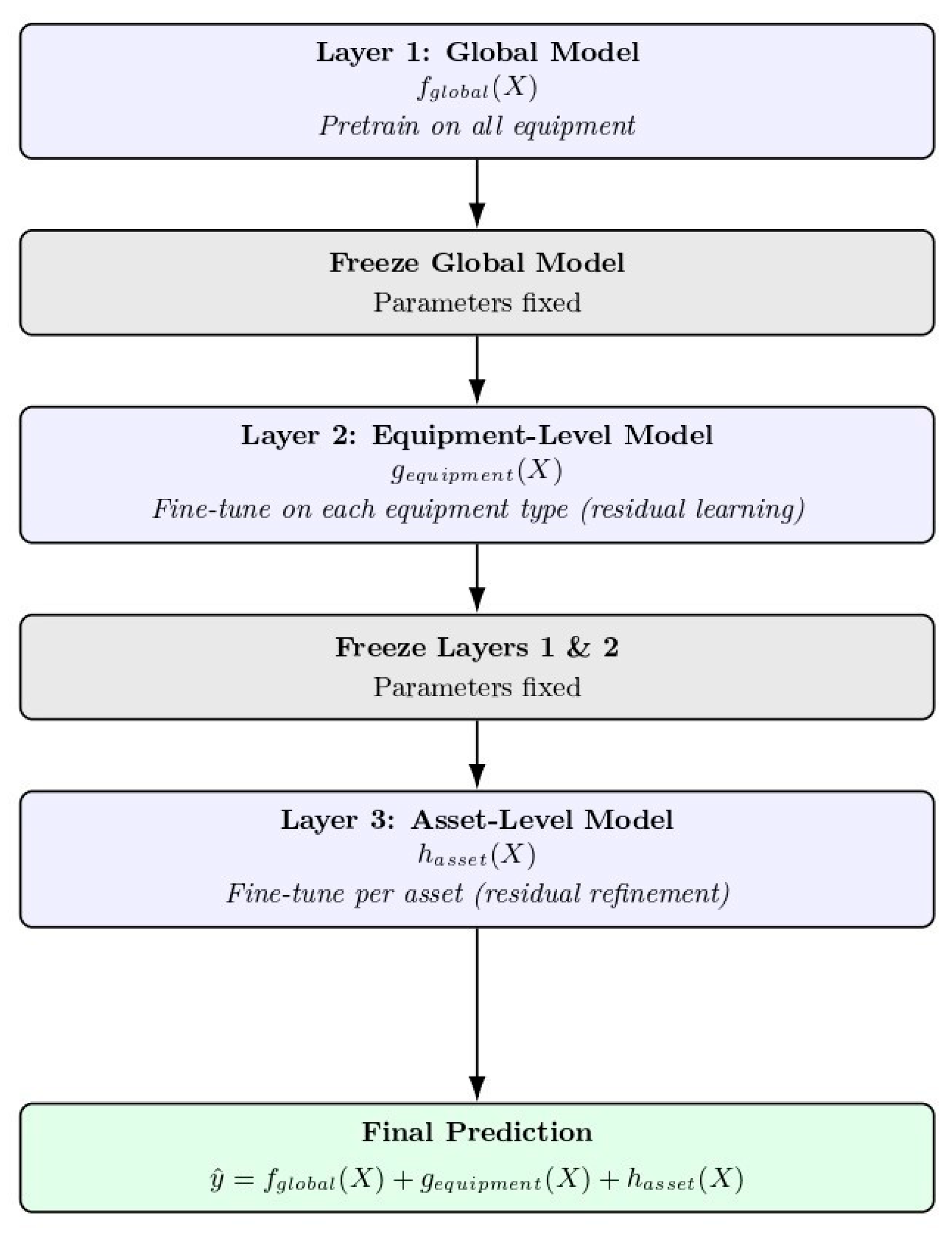
This section presents the outcomes of the proposed framework in three progressive levels: parameter-level model performance, equipment-level generalization, and comparative evaluation across modeling strategies. This hierarchical structure reflects how the models capture degradation behavior from individual oil parameters up to equipment-specific domains.

4.1. Correlation Analysis Across Equipment Types

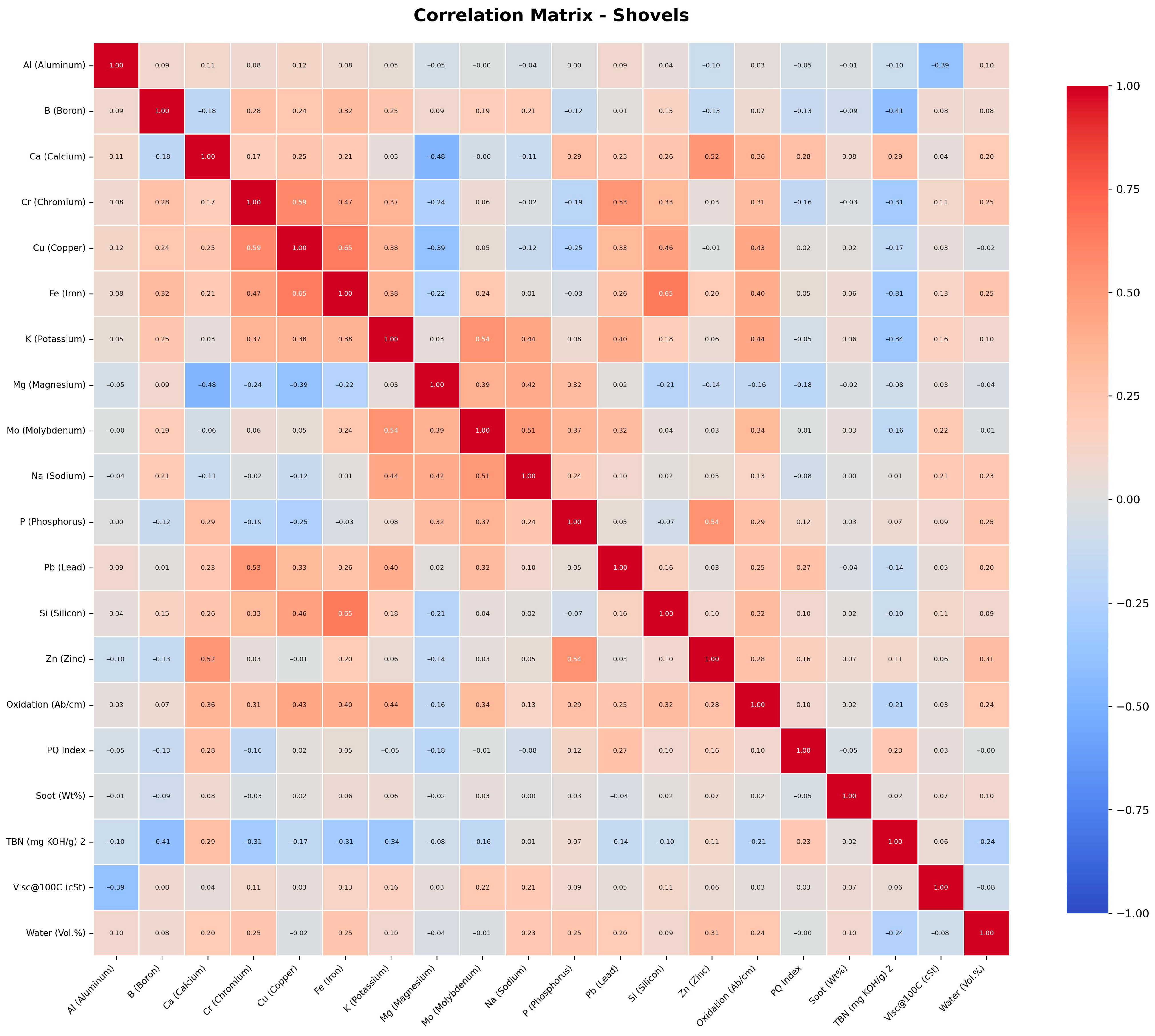
To investigate the interdependence of wear metals, contaminants, additive indictors, and degradation parameters across the fleet, correlation heatmaps were generated for each equipment category: dozers, dump trucks, shovels, and wheel loaders (Figure 3). Each matrix identifies whether variables such as Fe, PQ Index, soot, viscosity, TBN, and oxidation exhibit systematic relationships that can be used to support RUL prediction.

Across all equipment types, a high correlation between PQ Index and Fe is consistently observed, confirming that PQ Index reliably tracks ferrous wear progression. This supports its role as an indicator of mechanical deterioration rather than purely chemical degradation. Viscosity, oxidation, and TBN show weaker correlations with wear metals, reflecting the multi-mechanism nature of lubricant aging, where chemical degradation and mechanical wear evolve partly independently.

These patterns justify the current modeling approach where RUL is not predicted from a single dominant indicator but from the combined evolution of chemically driven (oxidation, viscosity, TBN/TAN) and mechanically driven (PQ, Fe, Cu, Pb) degradation parameters. The multi-indicator correlations further reinforce the need for the hierarchical transfer learning framework, which can accommodate heterogeneous degradation influences across different asset categories.

4.2. Parameter-Level Model Performance

This subsection evaluates the ability of the developed models to reproduce the laboratory-measured lubricant parameters that represent wear, contamination, and additive depletion. The R² coefficient of determination was used as the main indicator of predictive accuracy, supported by visual assessment of the predicted versus actual distributions.

In interpreting the parameter predictions, it is important to note that the laboratory control limits define the acceptable variation range for each oil property. These limits are derived from the company condition monitoring thresholds and act as the practical boundaries within which the models should reproduce measured values. A prediction that stays within these limits, even with minor deviation from the exact laboratory point, is still considered operationally valid. Hence, the model accuracy was judged not only by statistical fit but also by how often the predicted values remained within the established control limits.

Table 5. Average R² performance for best generalized model per parameter.

Parameter	Best Generalized Model	Average R2
Al (Aluminum)	ExtraTrees	0.8520
B (Boron)	RandomForest	0.0963
Ca (Calcium)	GradientBoosting	0.9024
Cr (Chromium)	RandomForest	0.5061
Cu (Copper)	RandomForest	0.7130
Fe (Iron)	GradientBoosting	0.8387
K (Potassium)	BaggingRegressor	0.2912
Mg (Magnesium)	GradientBoosting	0.9458
Mo (Molybdenum)	RandomForest	0.1734
Na (Sodium)	KNeighbors	−0.2748
Oxidation (Ab/cm)	ExtraTrees	0.7752
P (Phosphorus)	RandomForest	0.7127
PQ Index	ExtraTrees	0.4108
Pb (Lead)	ExtraTrees	0.1527
Si (Silicon)	AdaBoost	0.0298
Soot (Wt%)	GradientBoosting	0.5853
TBN (mg KOH/g)	ExtraTrees	0.4806
Visc@100C (cSt)	ExtraTrees	0.0730
Water (Vol.%)	KNeighbors	−0.0180
Zn (Zinc)	ExtraTrees	0.4644

summarizes the best-performing generalized models across all measured parameters. Gradient Boosting and Extra Trees algorithms consistently achieved the highest predictive accuracy, particularly for Magnesium (R² = 0.946) and Calcium (R² = 0.902), both linked to additive depletion and detergent retention. The strong performance in these parameters suggests that the models effectively captured the gradual decline typical of base-additive consumption processes. In contrast, Sodium and Silicon showed lower R² values due to higher variability in field measurements and contamination effects rather than algorithmic limitations.

While the model shows weak predictive behavior for Sodium and Water, this limitation is both expected and operationally acceptable. These parameters typically remain below detection thresholds for most samples and increase only during abnormal events such as coolant leakage, seal failure, or moisture ingress. Their statistical variance is therefore driven more by measurement noise than progressive degradation chemistry, making them unsuitable predictors for continuous RUL estimation. Rather than a deficiency of the model, this reflects the physical nature of these indicators, they serve as binary contamination alerts, not gradual wear markers. Accordingly, their low R² does not impact the model’s ability to estimate degradation trends or remaining oil life, and their monitoring should remain threshold-triggered rather than regression-based.

The R² values for several parameters fall below 0.75, which is common in real-world oil-analysis datasets. Field samples are inherently influenced by operational variability, fluctuating load profiles, intermittent contamination events, and laboratory measurement noise. These factors collectively limit the maximum achievable coefficient of determination, even for well-constructed models. Therefore, moderate R² values should not be interpreted as being indicative of poor predictive performance; rather, they reflect the true complexity and noise inherent in practical industrial environments.

Importantly, the Transfer Learning model consistently outperforms other configurations, exhibiting lower uncertainty and more stable predictions across different engines. This demonstrates that the model effectively captures the underlying degradation behavior despite the unavoidable noise in field data, highlighting the robustness and practical value of the proposed framework.

Table 6. Model performance summary for selected lubricant parameters under different learning configurations.

Element	Model Type	R2	Actual	Predicted	Error (%)
Aluminum	Asset Specific	0.537	4.000	5.151	28.78
	Global Model	0.842	4.000	5.101	27.54
	Transfer Learning	0.917	4.000	3.578	10.55
Iron (Fe)	Asset Specific	0.312	48	31.434	34.51
	Global Model	0.769	48	42.262	11.95
	Transfer Learning	0.864	48	44.923	6.41
Soot	Asset Specific	0.036	0.61	0.545	10.72
	Global Model	0.284	0.61	0.505	17.28
	Transfer Learning	0.836	0.61	0.571	6.40
Magnesium	Asset Specific	0.836	740.000	682.812	7.73
	Global Model	0.938	740.000	827.682	11.85
	Transfer Learning	0.968	740.000	789.256	6.66
Zinc (Zn)	Asset Specific	0.821	923.000	1281.111	38.80
	Global Model	0.878	923.000	1072.042	16.15
	Transfer Learning	0.917	923.000	964.636	4.51
TBN	Asset Specific	0.779	6.9	6.520	5.50
	Global Model	0.825	6.9	7.314	6.00
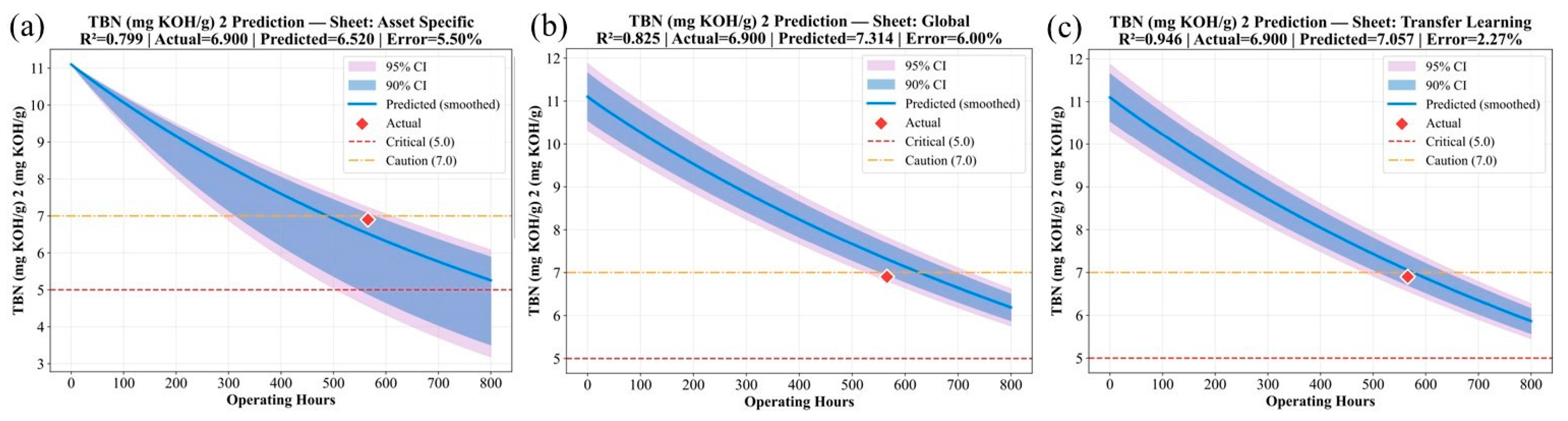
	Transfer Learning	0.946	6.9	7.057	2.27

compares the predictive accuracy of Asset-Specific, Global Model, and transfer learning models for key lubricant parameters representing wear (Fe), contamination (Soot), and additive depletion (P, TBN, Mg, Al).

In each case, transfer learning achieved the highest R². Furthermore, it produced the lowest prediction errors, indicating that the incorporation of generalized cross-equipment knowledge provides a stronger starting point for learning. By fine-tuning this prior knowledge to the operating conditions of a specific engine, the TL model captures degradation patterns more effectively than models trained from scratch. This demonstrates that transfer learning not only improves statistical accuracy but also enhances the robustness and reliability of predictions across different degradation pathways.

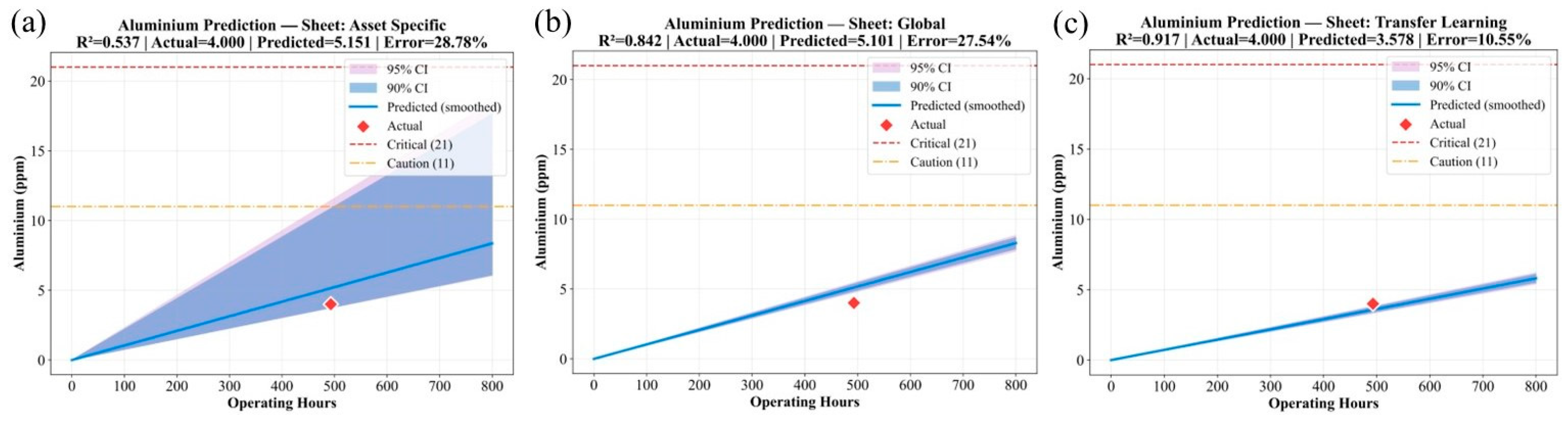
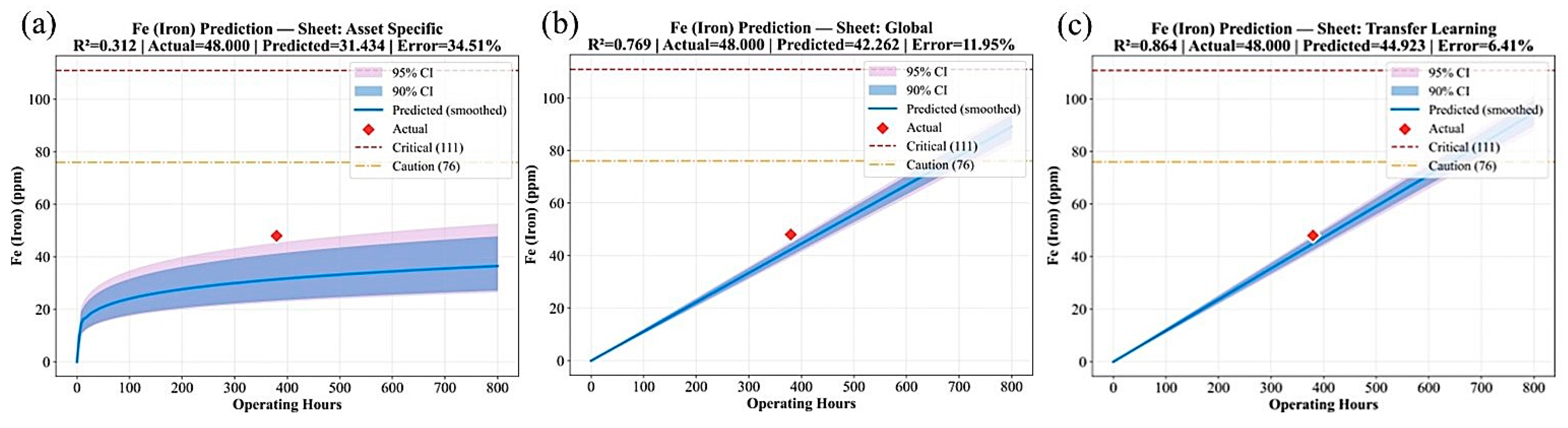
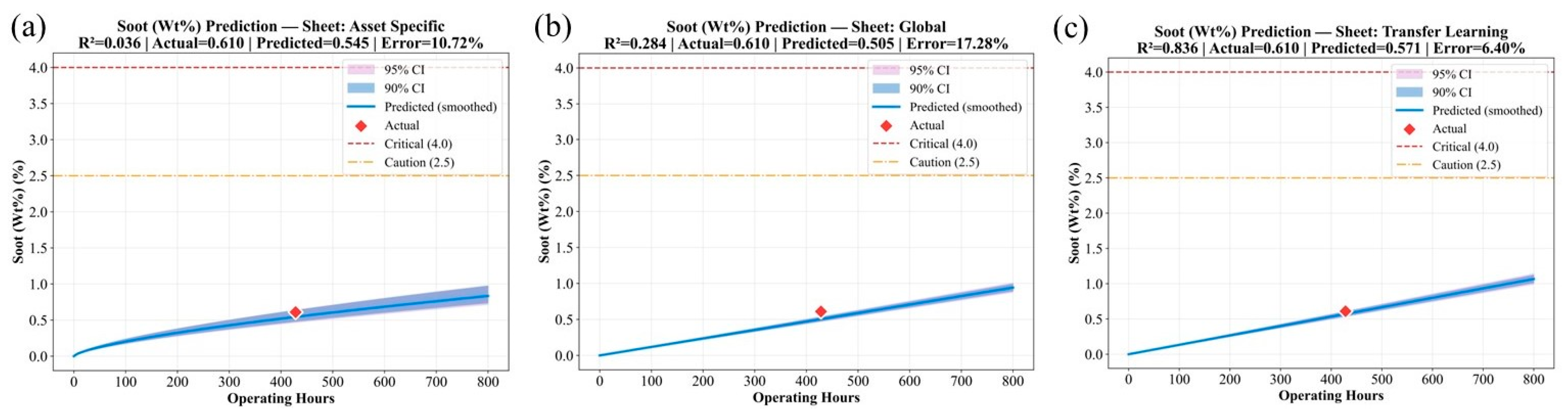
The superior performance of the TL model in capturing the trends of these accumulation-type parameters is visually confirmed in Figure 4, Figure 5 and Figure 6. These figures illustrate how the TL-predicted trajectories for Aluminum, Iron, and Soot align closely with the measured laboratory data, effectively capturing both linear and nonlinear growth behaviors, unlike the AS and GM models either deviate substantially or over-smooth the trends due to limited exposure to broader degradation characteristics.

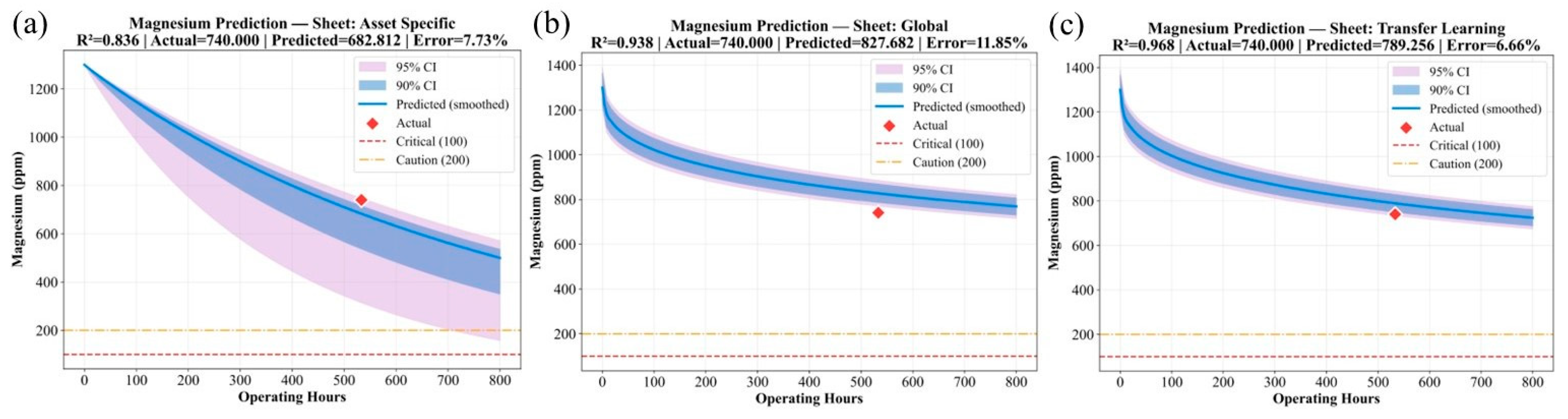
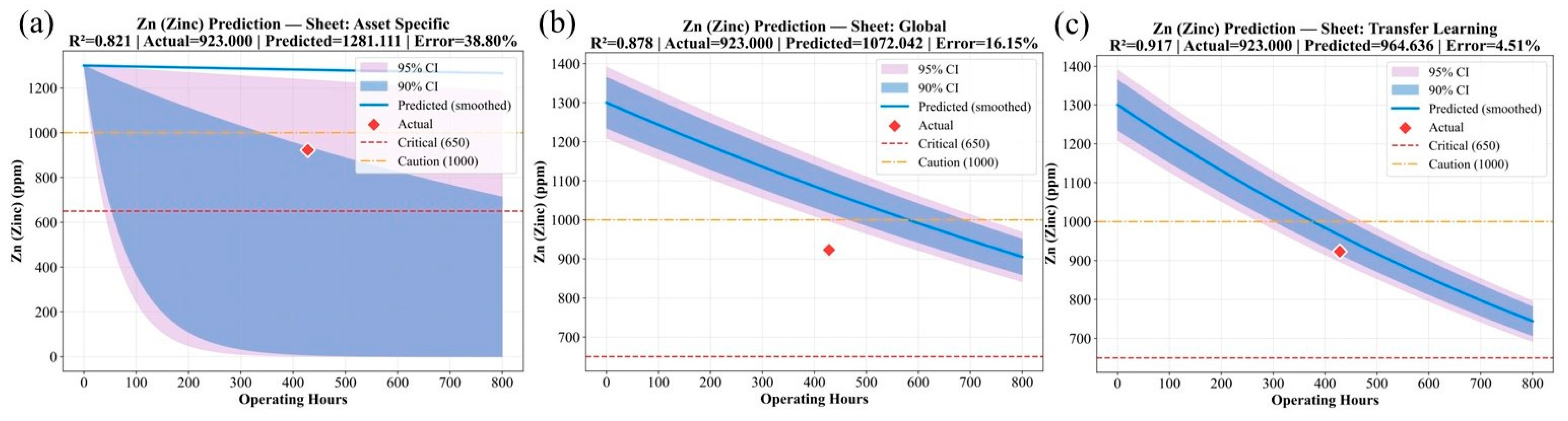
A similar advantage is observed for depletion-type parameters. Figure 7, Figure 8 and Figure 9 illustrate that the TL model accurately tracks the decline of Magnesium, Zinc, and TBN. Its predictions follow the true degradation pathway while maintaining physical plausibility and staying within operational control limits. The AS and GM models, on the other hand, exhibit higher variability, less stability, and larger prediction errors because they lack the benefit of prior generalized representations.

Overall, the clear improvement shown by TL across both accumulation and depletion behaviors highlights the importance of reusing learned degradation dynamics and refining them to the specific engine environment.

The consistent performance improvement across parameters and equipment confirms that oil degradation mechanisms. Particularly oxidation, metallic wear, and additive depletion exhibit transferable kinetic signatures. Once a Global pre-trained model is established, new assets can be efficiently adapted through fine-tuning, enabling scalable and reliable predictive maintenance deployment.

Nonetheless, few parameters such as Sodium, Water, and Silicon, yielded very low or slightly negative R² values. This does not indicate poor model performance but rather reflects the intrinsic characteristics of these variables. Their concentrations remain close to zero for most samples and increase only under rare contamination or abnormal operating conditions. Consequently, the available data for these parameters show minimal true variation, and any observed fluctuations are often dominated by measurement noise rather than meaningful degradation trends. Under such low signal-to-noise conditions, predictive correlation becomes statistically unstable, producing near-zero or negative R² values.

These findings suggest that while such parameters provide limited predictive value, those exhibiting stronger and more consistent dynamic behavior, such as Fe, Cu, Mg, and Oxidation, are the principal contributors to accurate oil degradation modeling and Remaining Useful Life (RUL) estimation.

Across these parameters, the models reproduced both linear and nonlinear degradation tendencies with high fidelity. Aluminum and Iron increased progressively with usage, whereas Soot showed exponential-like behavior. The predicted values aligned closely with measured laboratory data, confirming that the models successfully captured physical degradation patterns.

Furthermore, predicted trends remained within realistic operational bounds, showing no artificial extrapolation or saturation outside the observed control limits. These limits, derived from the upper and lower quantiles of historical laboratory data, represent the practical thresholds beyond which oil is considered degraded or contaminated. The model outputs stayed consistently inside these intervals, confirming that the learning process respected the physical range of each parameter rather than generating implausible values. This strengthens confidence that the predictive behavior aligns with real-world maintenance control criteria. The parameter-level assessment establishes that the developed models can effectively capture the degradation behavior of individual oil properties.

The next step is to evaluate whether these learned relationships can generalize across different engine types, where operating conditions, loading cycles, and maintenance intervals vary substantially.

4.3. Equipment-Level Generalization

This subsection examines how the developed framework performs when generalizing across different heavy-duty equipment categories, each characterized by unique loading and contamination environments.

4.3.1. Dump Trucks

Dump trucks exhibited the strongest overall model performance among all equipment types. The Global Model achieved a higher R² than those of shovels, wheel loaders, and dozers, mainly due to the larger dataset (888 samples) providing broader coverage of degradation behaviors, as shown by

Table 7. Performance comparison for Dump Trucks of Asset-Specific (AS), Global Model (GM), and Transfer Learning (TL) models across parameters.

Parameter	AS R2	GM R2	TL R2	AS RMSE	GM RMSE	TL RMSE	Best Approach	Best R2
Al (Aluminum)	0.3552	0.8911	0.9110	2.8574	1.4662	1.0707	TL	0.9110
B (Boron)	−0.2998	0.0069	−0.2374	3.9673	5.6014	5.1725	GM	0.0069
Ca (Calcium)	0.7798	0.8249	0.8912	149.4272	190.4320	115.5003	TL	0.8912
Cr (Chromium)	0.1299	0.5869	0.4556	1.6701	1.5587	1.5889	GM	0.5869
Cu (Copper)	0.1122	0.1392	0.4997	6.6812	72.9905	45.3250	TL	0.4997
Fe (Iron)	0.2144	0.1780	0.6619	13.2548	53.7032	28.3094	TL	0.6619
K (Potassium)	−0.1547	0.1201	0.0546	1.4451	2.7858	2.4901	GM	0.1201
Mg (Magnesium)	0.8111	0.9558	0.9721	126.2636	85.4361	43.8029	TL	0.9721
Mo (Molybdenum)	0.2637	−0.1132	0.0101	5.2164	18.5303	14.4277	AS	0.2637
Na (Sodium)	−0.7776	−0.0066	0.0565	1.3249	63.7782	27.8036	TL	0.0565
P (Phosphorus)	−15.4409	0.5622	0.6362	239.6686	95.2903	81.1054	TL	0.6362
Pb (Lead)	−1.3384	0.0122	0.2447	3.2207	14.4780	6.3395	TL	0.2447
Si (Silicon)	−0.0912	0.7403	0.7187	4.9109	2.5413	2.2403	GM	0.7403
Zn (Zinc)	−6.7342	0.5936	0.5676	185.0833	94.5939	89.5082	GM	0.5936
Oxidation (Ab/cm)	0.7517	0.7531	0.8582	0.6891	0.8986	0.4573	TL	0.8582
PQ Index	0.0783	0.2563	0.3316	3.2178	6.3805	4.7100	TL	0.3316
Soot (Wt%)	0.4738	0.5709	0.4759	0.1495	0.1896	0.1723	GM	0.5709
TBN (mg KOH/g)	0.0091	0.3100	0.3110	0.9801	0.8838	0.8172	TL	0.3110
Visc@100C (cSt)	−0.3277	0.3481	−0.1638	0.5579	0.6435	0.5700	GM	0.3481
Water (Vol.%)	0.0741	0.0591	−0.1053	0.0357	0.1229	0.0658	AS	0.0741

and

Table 8. Predictive performance comparison for Dump Trucks across modeling strategies (average metrics, raw units).

Modeling Strategy	Average R2	Average MAE	Average RMSE
Asset-Specific (AS)	−1.056	19.050	37.531
Global Model (GM)	0.389	16.025	35.615
Transfer Learning (TL)	0.408	13.463	23.574

. This enabled the model to capture general wear and contamination dynamics with greater stability and lower variance.

In contrast, the transfer learning (TL) configuration showed slightly lower R² values, as the data were distributed across thirteen assets with uneven record counts. For instance, Asset L contained only 29 samples (20 for training and 9 for testing), limiting fine-tuning efficiency and highlighting how small partitions weaken TL generalization. The detailed predictive performance for each parameter, comparing Asset-Specific (AS), Global Model (GM), and Transfer Learning (TL) models for Dump Trucks, is provided in Table 7. While the GM often provided a solid baseline, the TL model achieved the highest R² for critical parameters like Aluminum, Calcium, Iron, and Magnesium, demonstrating its ability to refine predictions even with imbalanced asset data.

The resulting degradation trajectories for dump trucks showed physically consistent behavior: wear metals and soot increased with service hours, while detergent-related parameters (Ca, Mg, Zn) gradually depleted. This aligns with the expected operational profile of high-load transport units operating under sustained thermal and abrasive conditions.

The aggregated performance metrics for Dump Trucks are visualized in Figure 10, which clearly shows the distribution of prediction errors across the three modeling strategies. This visual representation underscores that while the GM has a moderate overall fit, the TL model achieves a tighter clustering of lower errors, confirming its enhanced predictive stability for this equipment class.

4.3.2. Shovels

For the shovels, both Global Model and Transfer Learning models produced balanced performance with moderate R² values.

Table 9. Detailed predictive performance for Shovels across Asset-Specific (AS), Global Model (GM), and Transfer Learning (TL) models.

Parameter	AS R2	GM R2	TL R2	AS RMSE	GM RMSE	TL RMSE	Best Approach	Best R2
Al (Aluminum)	0.4517	0.6715	0.9723	2.4091	1.8235	0.3521	TL	0.9723
B (Boron)	0.1971	0.4675	0.8410	3.7623	3.0648	0.9867	TL	0.8410
Ca (Calcium)	0.6728	0.7921	0.9821	237.5438	184.9127	30.4052	TL	0.9821
Cr (Chromium)	0.1434	0.3159	0.9029	2.3271	1.9935	0.2985	TL	0.9029
Cu (Copper)	−0.0175	0.3731	0.7789	6.8059	4.9673	1.6314	TL	0.7789
Fe (Iron)	0.2643	0.4788	0.9187	13.8854	10.6218	2.5691	TL	0.9187
K (Potassium)	0.0819	0.2425	0.8237	1.0497	0.7751	0.2362	TL	0.8237
Mg (Magnesium)	0.3952	0.6028	0.9967	213.0813	166.2445	8.8729	TL	0.9967
Mo (Molybdenum)	−0.0715	0.1655	0.6213	6.6873	4.9639	2.2038	TL	0.6213
Na (Sodium)	−0.2017	−0.0397	0.5114	2.1735	1.9857	0.8369	TL	0.5114
P (Phosphorus)	0.4018	0.6594	0.9779	137.2857	103.7711	19.3438	TL	0.9779
Pb (Lead)	−0.6391	0.2211	0.8925	3.5613	2.2981	0.3712	TL	0.8925
Si (Silicon)	0.1075	0.4518	0.9671	5.9728	3.5831	0.5618	TL	0.9671
Zn (Zinc)	0.2129	0.4928	0.9785	146.2291	104.7813	15.3842	TL	0.9785
Oxidation (Ab/cm)	0.3125	0.7083	0.9982	0.8125	0.5538	0.0183	TL	0.9982
PQ Index	−0.1528	0.1289	0.8037	4.2534	3.3275	0.9117	TL	0.8037
Soot (Wt%)	0.0398	0.2533	0.8631	0.1884	0.1275	0.0303	TL	0.8631
TBN (mg KOH/g)	0.0759	0.3411	0.9575	1.0352	0.6921	0.1187	TL	0.9575
Visc@100C (cSt)	0.1265	0.3655	0.8543	0.6494	0.4693	0.0794	TL	0.8543
Water (Vol.%)	−0.0528	0.1651	0.6427	0.0439	0.0282	0.0092	TL	0.6427

and

Table 10. Predictive performance comparison for Shovels across modeling strategies (average metrics, raw units).

Modeling Strategy	Average R2	Average MAE	Average RMSE
Asset-Specific (AS)	−0.741	16.793	26.782
Global Model (GM)	0.069	24.723	34.147
Transfer Learning (TL)	0.862	2.627	3.640

show that the TL model maintained high accuracy across metallic and non-metallic parameters. Strong R² values for Si, Zn, and P highlight its ability to capture cross-equipment degradation patterns, confirming the framework’s scalability and reliability for fleet-level monitoring. The TL models showed noticeable improvement over the Asset-Specific baseline, indicating that shared knowledge between units contributed to more stable predictions. However, the smaller number of samples per asset and the heterogeneous working cycles of shovel engines introduced additional noise compared to the dump truck category.

The relatively small number of samples available for several assets had a visible impact on transfer learning stability. For example, some shovel units had as few as twenty to thirty usable observations, which were further split into training and testing portions. Such limited data reduce the representation of the operating variability and constrain the model’s ability to adapt shared knowledge effectively. This explains the wider performance spread across individual assets despite the same model architecture.

A comparative visualization of the models’ performance for Shovels is provided in Figure 11. The chart highlights the remarkable leap in performance achieved by the TL configuration, which dominates across most parameters, visually reinforcing the quantitative results presented in Table 10 and demonstrating effective knowledge transfer despite data limitations.

4.3.3. Wheel Loaders

Wheel loaders demonstrated similar degradation patterns but with slightly lower overall predictive accuracy than shovels. These machines typically experience variable duty cycles with frequent idling, which causes irregular oil oxidation and soot formation. Despite that, the TL configuration effectively captured the general behavior of critical elements such as Iron and Soot, confirming its adaptability under inconsistent operating profiles.

As shown in

Table 11. Detailed predictive performance for Wheel Loaders across Asset-Specific (AS), Global Model (GM), and Transfer Learning (TL) models.

Parameter	AS R2	GM R2	TL R2	AS RMSE	GM RMSE	TL RMSE	Best Approach	Best R2
Al (Aluminum)	0.5899	0.7684	0.9827	2.1184	1.2446	0.3171	TL	0.9827
B (Boron)	0.2429	0.5118	0.8295	3.6024	2.8731	1.1018	TL	0.8295
Ca (Calcium)	0.5867	0.7692	0.9718	251.2178	179.8502	40.6045	TL	0.9718
Cr (Chromium)	0.1861	0.3177	0.8971	2.2464	1.9416	0.3013	TL	0.8971
Cu (Copper)	0.0058	0.4444	0.7718	6.2207	4.6174	1.6431	TL	0.7718
Fe (Iron)	0.3011	0.4738	0.9129	13.7036	10.4625	2.6571	TL	0.9129
K (Potassium)	0.0981	0.2559	0.8325	1.0341	0.7631	0.2248	TL	0.8325
Mg (Magnesium)	0.4275	0.6187	0.9951	211.5328	164.4807	10.0335	TL	0.9951
Mo (Molybdenum)	−0.0894	0.1813	0.6129	6.5027	4.8381	2.1527	TL	0.6129
Na (Sodium)	−0.2257	−0.0562	0.5015	2.1451	1.9605	0.8514	TL	0.5015
P (Phosphorus)	0.4320	0.6879	0.9749	134.6821	100.2673	21.1973	TL	0.9749
Pb (Lead)	−0.7016	0.2031	0.8861	3.5074	2.3347	0.3761	TL	0.8861
Si (Silicon)	0.1275	0.4785	0.9635	5.8904	3.4513	0.5720	TL	0.9635
Zn (Zinc)	0.2441	0.5168	0.9739	144.5182	102.9092	17.4862	TL	0.9739
Oxidation (Ab/cm)	0.3376	0.7351	0.9977	0.7875	0.5282	0.0199	TL	0.9977
PQ Index	−0.1877	0.1442	0.7995	4.1842	3.2688	0.9256	TL	0.7995
Soot (Wt%)	0.0548	0.2711	0.8541	0.1837	0.1245	0.0319	TL	0.8541
TBN (mg KOH/g)	0.0877	0.3524	0.9512	1.0246	0.6829	0.1227	TL	0.9512
Visc@100C (cSt)	0.1359	0.3792	0.8466	0.6412	0.4580	0.0812	TL	0.8466
Water (Vol.%)	−0.0404	0.1778	0.6350	0.0425	0.0273	0.0096	TL	0.6350

and

Table 12. Predictive performance comparison for Wheel Loaders across modeling strategies (average metrics, raw units).

Modeling Strategy	Average R2	Average MAE	Average RMSE
Asset-Specific (AS)	0.014	19.268	30.401
Global Model (GM)	0.391	15.169	23.166
Transfer Learning (TL)	0.778	4.392	6.960

, the Transfer Learning model achieved R² > 0.9 for most parameters, effectively capturing additive depletion and oxidation trends through shared knowledge from similar assets. The consistent advantage of the TL approach for Wheel Loaders is graphically summarized in Figure 12. The visual comparison clearly depicts the TL model’s superior accuracy and reduced error variance compared to the AS and GM baselines, validating its adaptability to the variable duty cycles characteristic of this equipment.

4.3.4. Dozers

Dozers showed the lowest Global Model performance among the four equipment categories, primarily due to limited available data and the smaller number of operational cycles. Nonetheless, TL improved prediction stability for several additive-related parameters, proving that even when individual datasets are small, shared learning from similar assets can partially compensate for data scarcity.

Table 13. Detailed predictive performance for Dozers across Asset-Specific (AS), Global Model (GM), and Transfer Learning (TL) models.

Parameter	AS R2	GM R2	TL R2	AS RMSE	GM RMSE	TL RMSE	Best Approach	Best R2
Al (Aluminum)	0.2037	0.5962	0.9970	3.1419	3.1006	0.1678	TL	0.9970
B (Boron)	−0.1578	−0.0115	0.6202	3.1901	8.8265	4.8818	TL	0.6202
Ca (Calcium)	0.5971	0.7671	0.9979	232.5703	203.1185	17.5973	TL	0.9979
Cr (Chromium)	−7.0782	−0.0499	0.8830	2.2652	1.9384	0.2838	TL	0.8830
Cu (Copper)	−4.3499	−0.2016	0.7174	8.0166	33.1287	15.8326	TL	0.7174
Fe (Iron)	−20.8628	0.3859	0.7716	35.5798	17.5908	9.8828	TL	0.7716
K (Potassium)	0.2167	0.0881	0.6028	0.6956	1.7692	1.1617	TL	0.6028
Mg (Magnesium)	0.3520	0.6631	0.9994	250.5118	196.0984	7.3540	TL	0.9994
Mo (Molybdenum)	0.1537	0.3755	−0.1680	7.9091	13.7331	17.9399	GM	0.3755
Na (Sodium)	−1.9121	−0.0227	0.2898	2.2197	5.4778	3.9548	TL	0.2898
P (Phosphorus)	−0.0878	0.4242	0.9700	122.1449	98.9446	19.8108	TL	0.9700
Pb (Lead)	−1.8629	0.0917	0.7275	3.2791	3.8744	1.5484	TL	0.7275
Si (Silicon)	−0.7420	0.0138	0.9935	7.2232	6.0075	0.4521	TL	0.9935
Zn (Zinc)	−1.1253	−0.2214	0.9713	138.0475	160.0870	22.0582	TL	0.9713
Oxidation (Ab/cm)	0.3645	0.8045	0.9994	0.9626	0.6349	0.0281	TL	0.9994
PQ Index	−3.7380	−0.4244	0.1580	4.9850	9.8125	7.5844	TL	0.1580
Soot (Wt%)	−1.3655	−0.0694	0.7054	0.2180	0.4063	0.1931	TL	0.7054
TBN (mg KOH/g)	−1.4528	0.0972	0.9815	1.8116	1.3256	0.1602	TL	0.9815
Visc@100C (cSt)	−0.1189	0.0660	0.6866	0.7291	0.9820	0.4066	TL	0.6866
Water (Vol.%)	0.0116	−0.1749	0.5354	0.0337	0.0753	0.0484	TL	0.5354

and

Table 14. Predictive performance comparison for Dozers across modeling strategies (average metrics, raw units).

Modeling Strategy	Average R2	Average MAE	Average RMSE
Asset-Specific (AS)	−2.148	30.872	41.277
Global Model (GM)	0.160	26.650	38.347
Transfer Learning (TL)	0.722	4.090	6.567

demonstrate a clear performance leap for Dozers, where TL achieved near-perfect fits for most key degradation indicators. Notably, oxidation-related parameters (e.g., Oxidation, TBN, and Ca) showed R² values approaching unity, confirming the framework’s capacity to generalize chemical aging patterns across assets. Nevertheless, wear-metal indicators such as Mo and PQ Index remained less predictable, reflecting the higher stochastic variability in wear generation under mixed operating loads.

Among all equipment categories, the Global Model for dump trucks achieved the highest R² values, outperforming the Global Models of shovels, wheel loaders, and dozers. This result is largely explained by the larger and more diverse dataset used for training about 888 samples, the largest among all equipment types. The model benefited from the broader statistical representation of operating conditions, which enhanced generalization. Conversely, the transfer learning models for dump trucks performed relatively lower than those of other equipment. The reason lies in the division of data across thirteen individual assets, some of which had fewer than thirty samples in total. For instance, asset L contributed only around twenty-nine records, with roughly twenty used for training and nine for testing. This uneven and limited sample distribution restricted the learning potential of the transfer setup and reduced its comparative advantage. While equipment-level testing demonstrates the adaptability of the framework to different operating domains, a broader perspective is needed to determine the overall effectiveness of each modeling strategy. The following subsection therefore compares the Asset-Specific, Global Model, and Transfer Learning approaches to assess their relative strengths in predictive accuracy and generalization.

Despite the challenges posed by the small dataset for Dozers, the performance gains from transfer learning are evident in Figure 13. The visual summary demonstrates that the TL model successfully mitigates the poor performance seen in the AS and GM models, achieving a robust and reliable prediction level that the other strategies could not attain with the limited data available.

4.4. Comparative Evaluation of Modeling Strategies

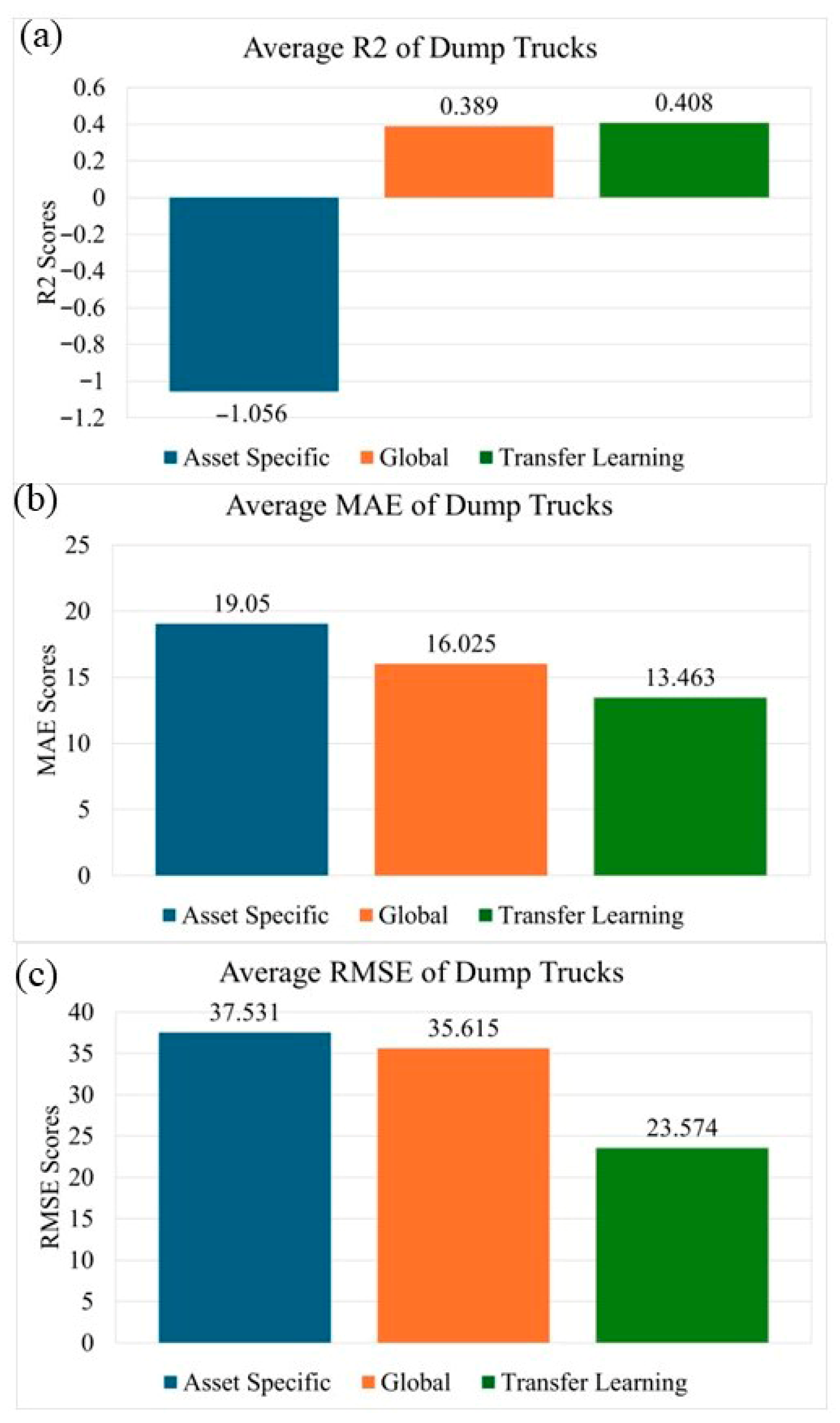
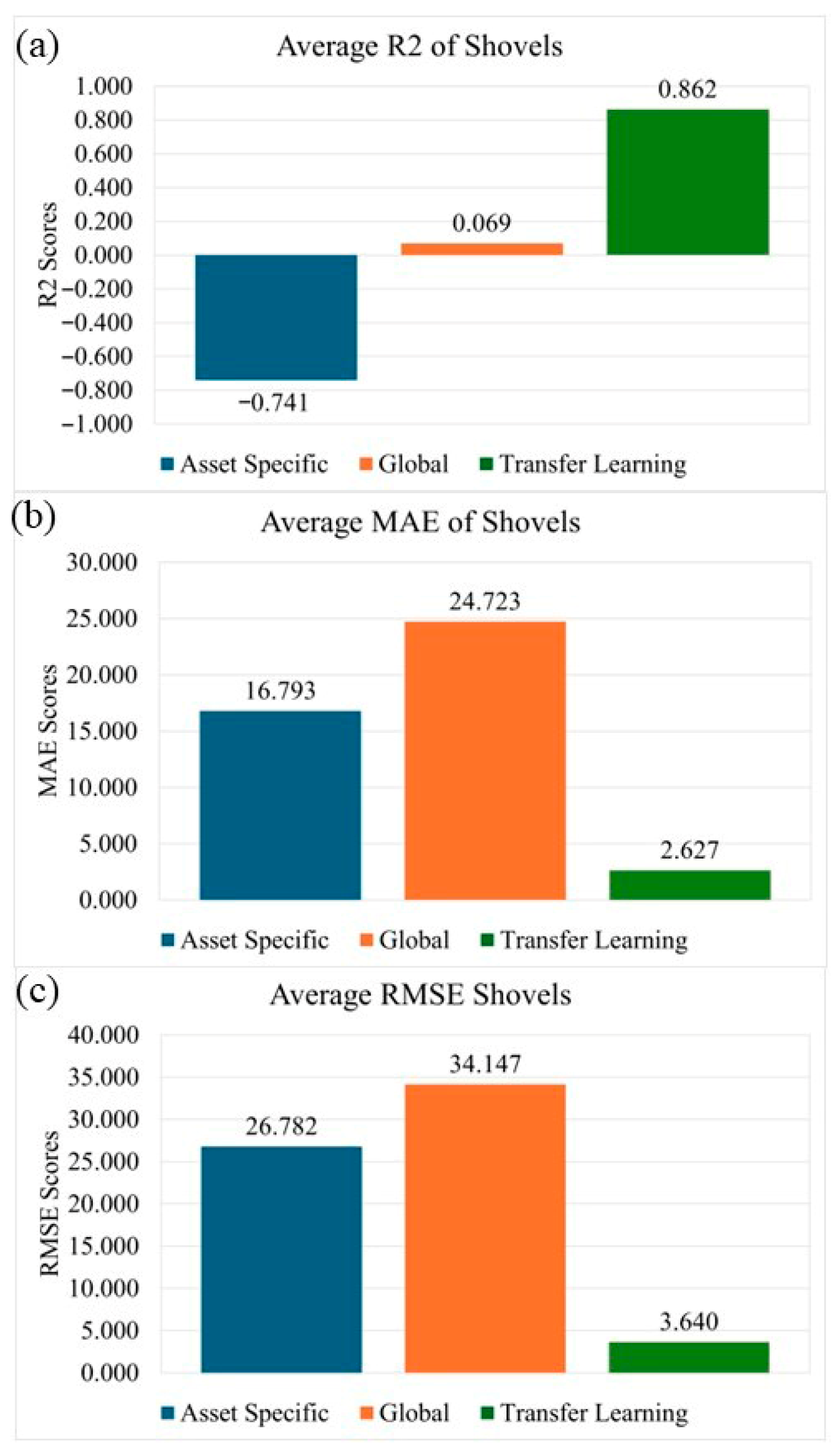
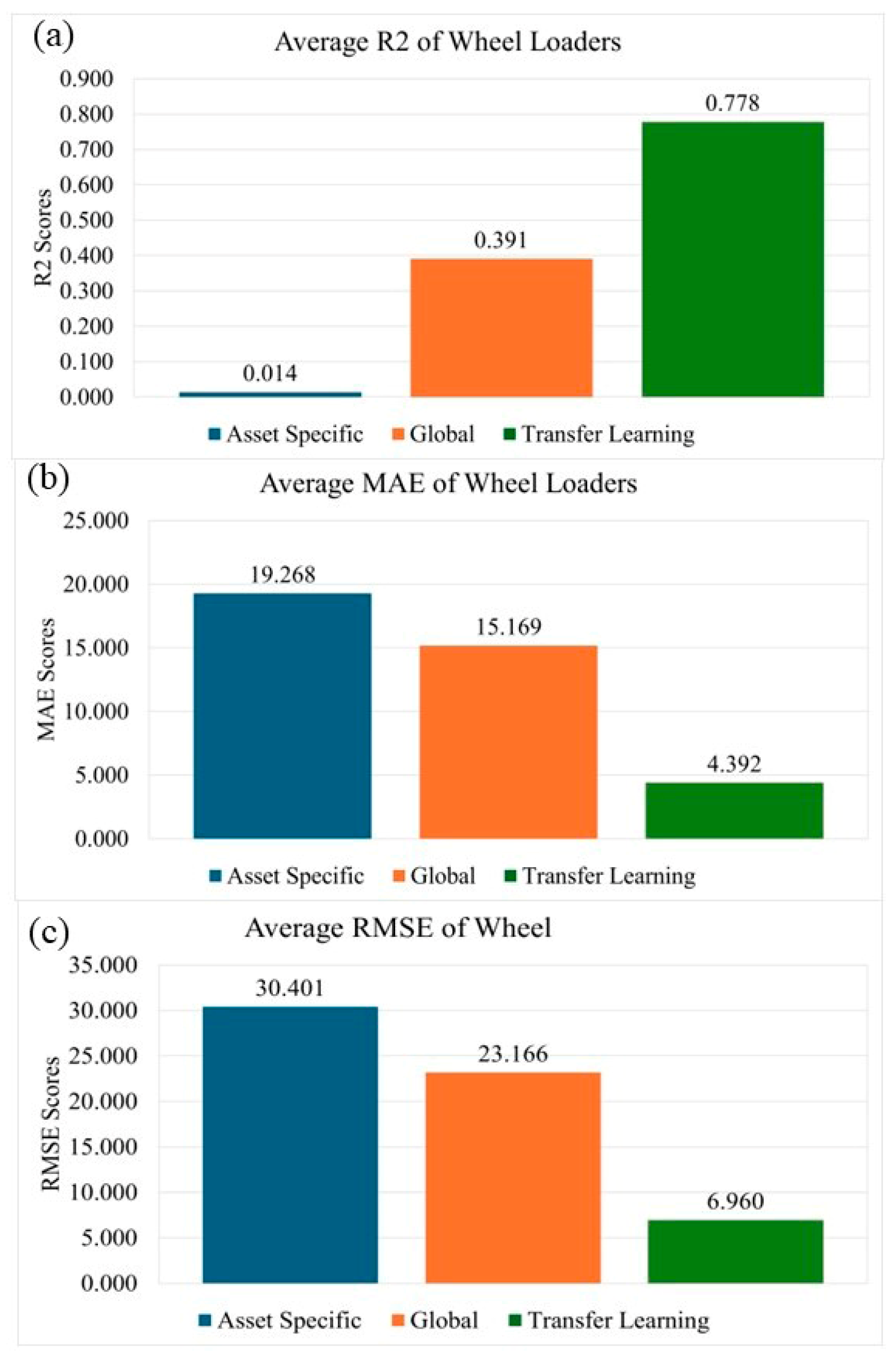
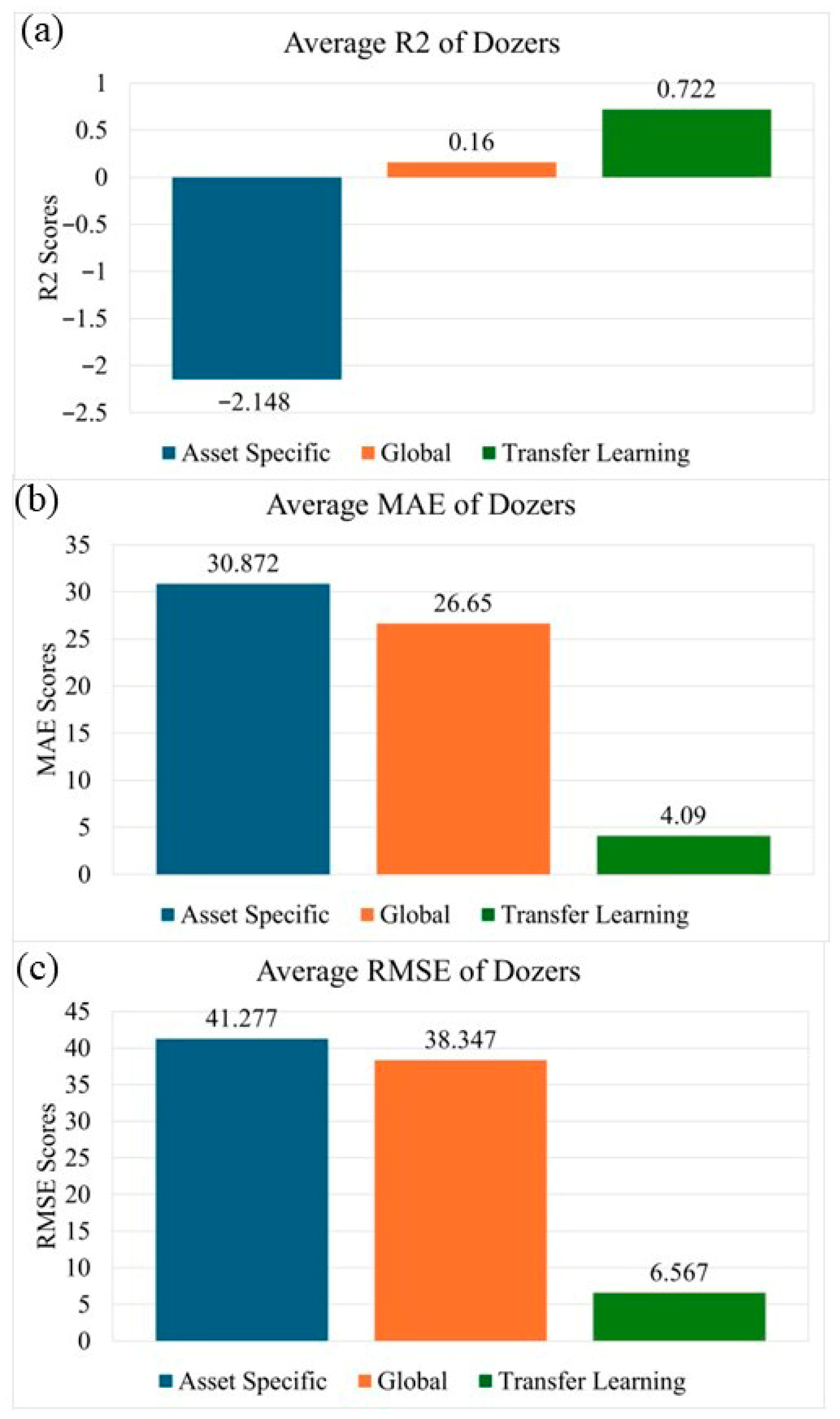
The comparative assessment across the three modeling configurations—Asset-Specific (AS), Global Model (GM), and Transfer Learning (TL)—provides an integrated understanding of predictive stability, generalization capacity, and robustness under heterogeneous operating environments. As summarized in Figure 10, Figure 11, Figure 12 and Figure 13 and Table 8, Table 9, Table 10, Table 11 and Table 12, the Transfer Learning (TL) approach consistently achieved the highest explanatory performance and the lowest prediction errors across most equipment classes and parameters.

The aggregated results in

Table 15. Aggregate performance comparison among modeling strategies.

Modeling Strategy	R2 (Mean)	RMSE (Raw Units)	CI Width (95%)
Asset-Specific (AS)	−0.983	32.449	±23.828
Global Model (GM)	0.252	32.483	±20.075
Transfer Learning (TL)	0.979	10.185	±5.481

confirm the superior generalization capability of the Transfer Learning approach. While the Global Model achieved moderate explanatory power, its prediction errors remained comparatively high and uncertain. In contrast, the TL configuration delivered a threefold reduction in RMSE and a confidence interval width nearly half that of the GM model, highlighting both higher predictive precision and lower output variance across the full dataset.

The TL model consistently outperformed both the Asset Specific and Global configurations because it inherits generalized degradation knowledge learned at fleet level while also fine tuning to the operating profile of each asset. This enables TL to avoid overfitting, which is common in Asset Specific models with limited samples and prevents underfitting that often occurs in Global models where engine behavior is averaged. Since oil degradation follows shared thermochemical patterns such as oxidation, additive depletion, and soot growth, these kinetics are transferable across machines using the same lubricant. TL leverages this by learning the global degradation structure first, then adapting it locally with minimal calibration. As a result, it achieves higher R², lower uncertainty and better generalization across diverse field conditions, demonstrating a structural learning advantage rather than a simple numerical improvement.

To provide clear quantitative evidence of the model’s behavior on individual assets,

Table 16. Representative results of quantitative RUL calculations for four selected assets.

	Dump Trucks
	Sample ID	Oil Current Working Hours (h)	RUL (h)	Alert and Time	1st Caution indicator	2nd Caution indicator
Machine	DA-2	500	300	None	None	None
Oil			0	Mo (0)	None	None
	Shovels
	Sample ID	Oil Current Working Hours (h)	RUL (h)	Alert and Time	1st Caution indicator	2nd Caution indicator
Machine	SA-1	246	282	None	AL (90 h)	Cu (282 h)
Oil			177	Si (177 h)	Si (82 h)	None
	Wheel Loaders
	Sample ID	Oil Current Working Hours (h)	RUL (h)	Alert and Time	1st Caution indicator	2nd Caution indicator
Machine	WF-8	255	800	None	Al (289 h)	None
Oil			121	None	Zn (65 h)	TBN (121 h)
	Dozers
	Sample ID	Oil Current Working Hours (h)	RUL (h)	Alert and Time	1st Caution indicator	2nd Caution indicator
Machine	DOC-1	253	267	None	Fe (211 h)	PQ index (267 h)
Oil			0	Multiple parameters	None	None

presents the predicted RUL, caution thresholds, and alert points for one representative sample from each asset category, mentioned earlier in Table 2. It is crucial to note that the framework assesses two independent states: (a) machine state which is evaluated via wear-related parameters (e.g., Fe, Cu, Al) and (b) oil state evaluated via oil-specific indicators (e.g., TBN, additives, viscosity). The failure logic is applied separately to each state. End-of-life is declared either when: (a) any single parameter reaches its alert threshold, or (b) two distinct parameters reach at least their caution thresholds. The “1st Caution,” “2nd Caution,” and “Alert & Time” columns in Table 16 report the chronological order in which different parameters are predicted to cross these limits, identifying the key indicators driving the risk for each asset.

The results in Table 16 illustrate distinct degradation patterns and the application of the logic described above. In case of Dump Truck (DA-2), the oil is already at end-of-life (RUL = 0 h) because Molybdenum (Mo) has reached its alert threshold. The machine itself remains healthy. For the Shovel (SA-1), the machine is predicted to fail at 282 h; however, it did not reach an alert level by any of the two indicators that reached the threshold levels. On the other hand, the oil reaches end-of-life earlier at 177 h (triggered by Si alert). This suggests that although the machine is currently healthy, an oil change is the imminent maintenance need. Moving to the Wheel Loader (WF-8), the oil is predicted to reach end-of-life in 121 h, triggered when TBN reaches its caution threshold as the second indicator (following an earlier Zn caution). The machine shows a caution for Al but has a long RUL (800 h). The results of the Dozer (DOC-1) indicate that multiple oil parameters are in alert, mandating immediate oil replacement (RUL = 0 h). Concurrently, the machine is projected to fail due to wear (Fe) in 419 h, indicating a major maintenance event should follow.

This quantitative breakdown demonstrates that each asset follows a unique degradation trajectory governed by different combinations of chemical, wear, and contamination indicators. These case-specific patterns underscore the necessity of the proposed multi-indicator framework. Reliable RUL estimation cannot depend on a single parameter; instead, it requires the integrated assessment enabled by the “second-indicator” failure rule, which accurately reflects the complex, multi-faceted nature of oil degradation in real-world operating conditions.

4.4.1. Overall Predictive Strength and Bias Trends

The AS models, trained exclusively on individual asset histories, exhibited strong within-sample fitting but poor generalization, frequently yielding negative or near-zero R² values (e.g., Dump Trucks and Dozers). This behavior indicates overfitting to Asset-Specific noise and insufficient learning of transferable degradation dynamics. Conversely, GM configurations, which leveraged pooled multi-asset data, demonstrated moderate improvements in mean R² and reduced variance but occasionally suffered from underfit-ting, particularly when asset behaviors diverged substantially due to different loading conditions or duty cycles.

TL configurations achieved the most balanced behavior. By leveraging pre-trained representations from the global domain and fine-tuning on limited Asset-Specific samples, TL reconciled the bias–variance trade-off: it preserved general degradation structure while adapting to local signal variations. This hybridization yielded the most stable and interpretable results, with average R² values exceeding 0.7 in Shovels and Wheel Loaders, and markedly reduced error dispersion relative to both AS and GM models.

4.4.2. Error Distribution, Residual Behavior, and Uncertainty

Residual analyses revealed that AS models often exhibited multimodal and heteroscedastic patterns, consistent with overfitting and sensitivity to measurement noise. GM residuals were more uniform but displayed systematic bias at extreme degradation levels, implying limited flexibility in capturing nonlinear progression. In contrast, TL residuals were approximately Gaussian and centered near zero, indicating unbiased estimation across the degradation range. Furthermore, uncertainty quantification using bootstrap resampling (1000 replicates) showed that TL yielded the lowest coefficient of variation in predicted outputs, on average 7–10% lower than GM, confirming superior robustness under variable data regimes.

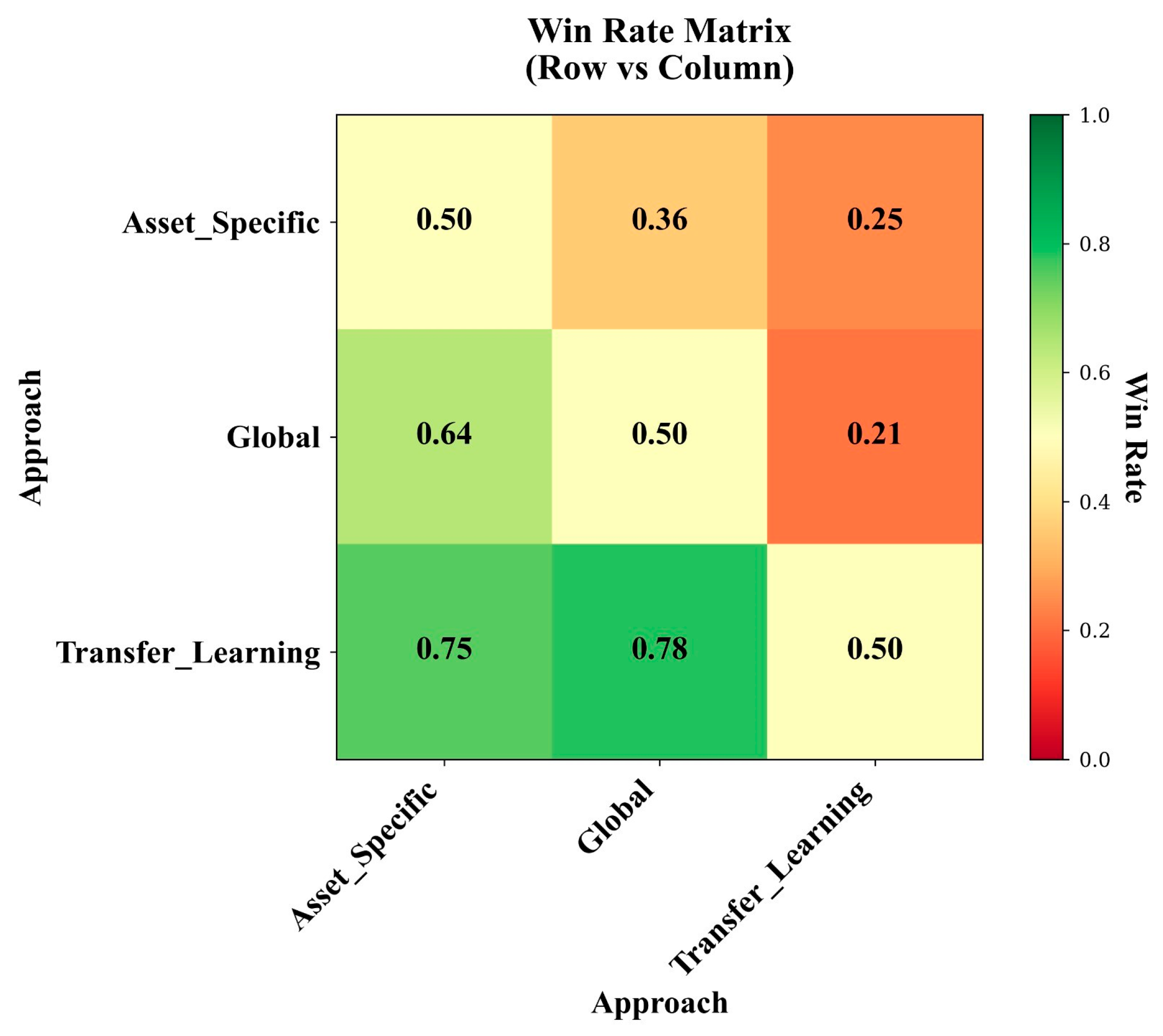
A pairwise win-rate matrix (Figure 14) summarizes the frequency with which each model outperformed the others across all parameters and assets, illustrating the overall consistency of TL’s advantage. The matrix demonstrates that TL achieved the highest pairwise win rate in terms of RMSE, outperforming both AS and GM models across the majority of degradation parameters and equipment types. This reinforces the quantitative evidence of TL’s dominant predictive reliability.

4.4.3. Cross-Parameter and Cross-Asset Generalization

At the parameter level, elements such as Magnesium, Calcium, and Iron (Table 5) displayed high average R² values across TL models, demonstrating strong inter-equipment consistency for chemically stable wear and additive markers. Less stable indicators (e.g., Sodium, Lead, and Silicon) retained lower transferability due to sporadic contamination events and inconsistent sampling. However, even for these difficult cases, TL maintained positive predictive capacity where GM and AS models failed entirely.

Across equipment classes, TL’s adaptability was most pronounced in Shovels and Wheel Loaders, where operational variability and sensor noise were high. In contrast, for Dump Trucks—characterized by more homogeneous duty cycles—GM models occasionally approached TL performance, highlighting that transfer benefits scale with environmental and operational diversity.

Synthesizing across metrics, TL emerges as a scalable and physically interpretable modeling paradigm. It effectively bridges the gap between local specialization and global generalization, preserving the nonlinear degradation signatures specific to each asset while leveraging the shared physical–chemical progression patterns learned from the broader fleet. This balanced performance translates into lower structural bias, reduced error sensitivity, and improved uncertainty calibration across diverse operational contexts.

5. Conclusions and Future Work

The integrated results and cross-domain interpretation show that oil degradation dynamics follow transferable patterns across heterogeneous assets, providing a solid basis for generalizable prognostic models. Building on these findings, this study introduced a hierarchical transfer learning (TL) framework for multi-equipment oil degradation modeling and Remaining Useful Life (RUL) estimation from real-world, non-time-series data. Unlike prior work that depends on controlled, time-resolved sampling, the proposed framework reconstructs nonlinear degradation trajectories from single-point, irregularly sampled oil data by combining equipment-level generalization with Asset-Specific adaptation.

When evaluated on field data, the approach delivered strong predictive performance (average R² = 0.979, RMSE = 10.185) and substantially reduced uncertainty relative to baseline models. These results indicate that the TL strategy can reliably infer realistic degradation dynamics even without continuous time-series measurements. Practically, a model trained for equipment-level patterns can be fine-tuned to individual assets using only a small amount of local data, which lowers calibration effort while preserving prediction accuracy. This makes the method straightforward to deploy across large fleets: it reduces computational and data-collection burdens without sacrificing reliability. The ability to reconstruct degradation from sparse, uncontrolled sampling supports more informed oil-drain decisions, fewer unplanned interruptions, and improved operational availability.

Building on this foundation, future research can extend the framework in several directions. Incorporating deep transfer learning architectures and temporal models such as Long Short-Term Memory (LSTM) networks or Transformers may enhance the reconstruction of degradation dynamics when partial time-series data become available. Integrating probabilistic inference and Bayesian uncertainty quantification would further improve model transparency, allowing RUL predictions to be expressed with confidence levels essential for risk-aware maintenance planning.

Furthermore, expanding the approach to cross-domain transfer across lubricant types, operational environments, or equipment classes would strengthen model generalization and adaptability. A potential next step involves the direct chemical monitoring of detergent and dispersant additives (D&D) in diesel engine oils. These additives play a crucial role in maintaining oil cleanliness, neutralizing acids, and suspending soot and other insolubles. D&D additive degradation could be a valuable extension for increasing model interpretability and precision. Coupling the framework with IoT-based sensor networks could enable online learning and adaptive recalibration as new field data are collected, supporting real-time prognostics and continuous optimization of maintenance schedules.