Assessing Impact of Wheel–Rail Force on Insufficient Displacement of Switch Rail in High-Speed Railway
Abstract
1. Introduction
- •
- A switch rail–slide plate coupling model is developed which, for the first time, enables dynamic wheel–rail force assessment of insufficient displacement of a switch rail in a No. 18 high-speed turnout.
- •
- By examining the influence of wheel–rail forces under different slide plate friction coefficients, the modelling approach is extended to a wider range of operating scenarios, thereby establishing design criteria for surface treatment and lubrication strategies.
- •
- The finite-element model is validated at multiple scales using both static and dynamic inspection data, together with on-site verification.
2. Methodology
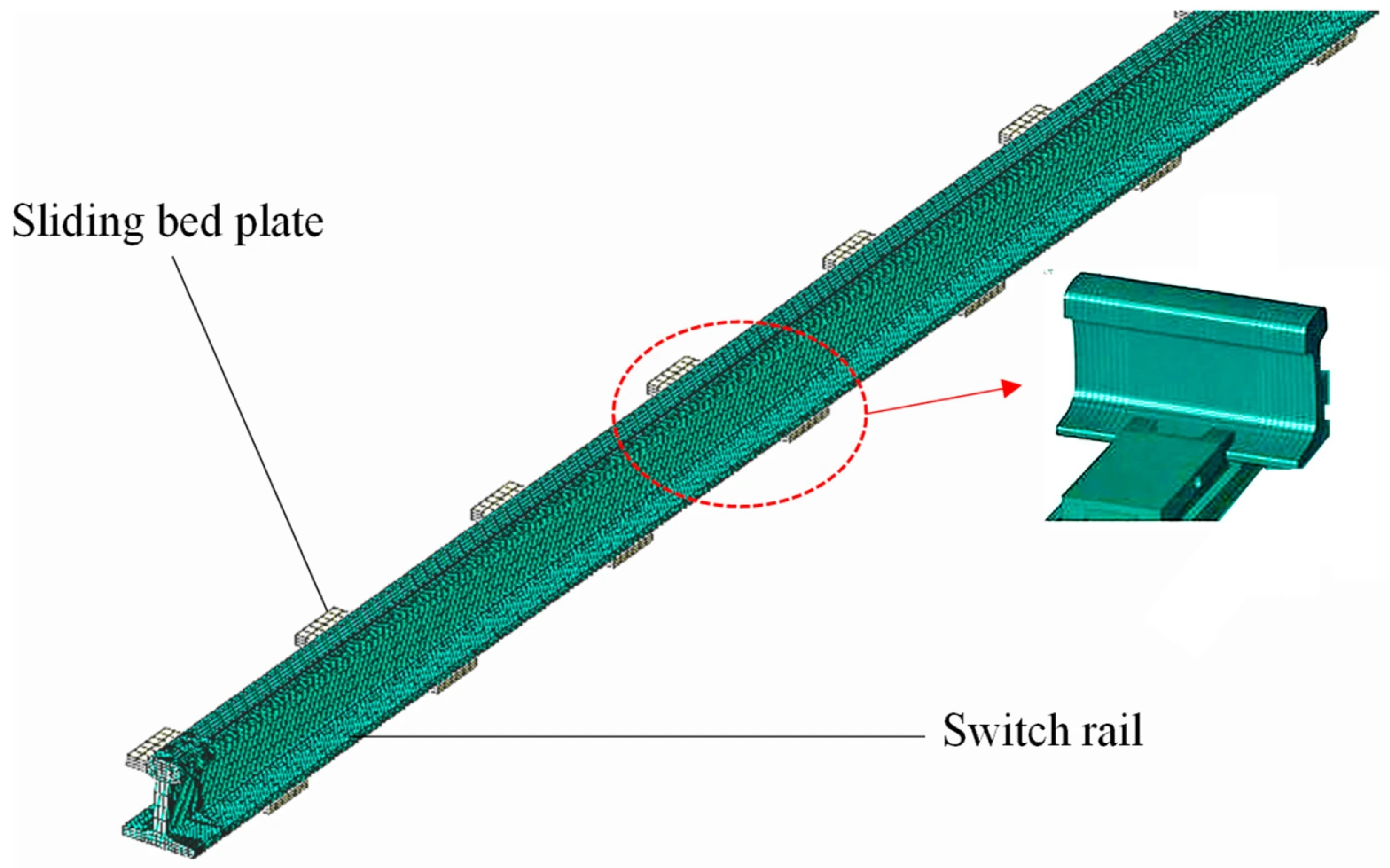
2.1. Switch Rail–Slide Plate Coupling Model
2.2. Calculation Method
- •
- The direction of the slide plate’s friction force is opposite to the direction of the movement of the switch rail, and its value is proportional to the weight of the rail above the slide plate, which does not change with the change in the rail displacement.
- •
- The centre of the third tractive point of the switch rail is the free-moving end, and the interval iron of the heel end is assumed to be the rigidly fixed end.
- •
- In the initial state, the switch and basic rails are in a close state. By moving the free-moving end, the switch rail changes from the close state to the repulsive state and then moves from the repulsive state to the free-moving end. Due to the influence of friction, the gap between the switch and stock rails is caused by insufficient displacement of the switch rail.
3. Results and Discussion
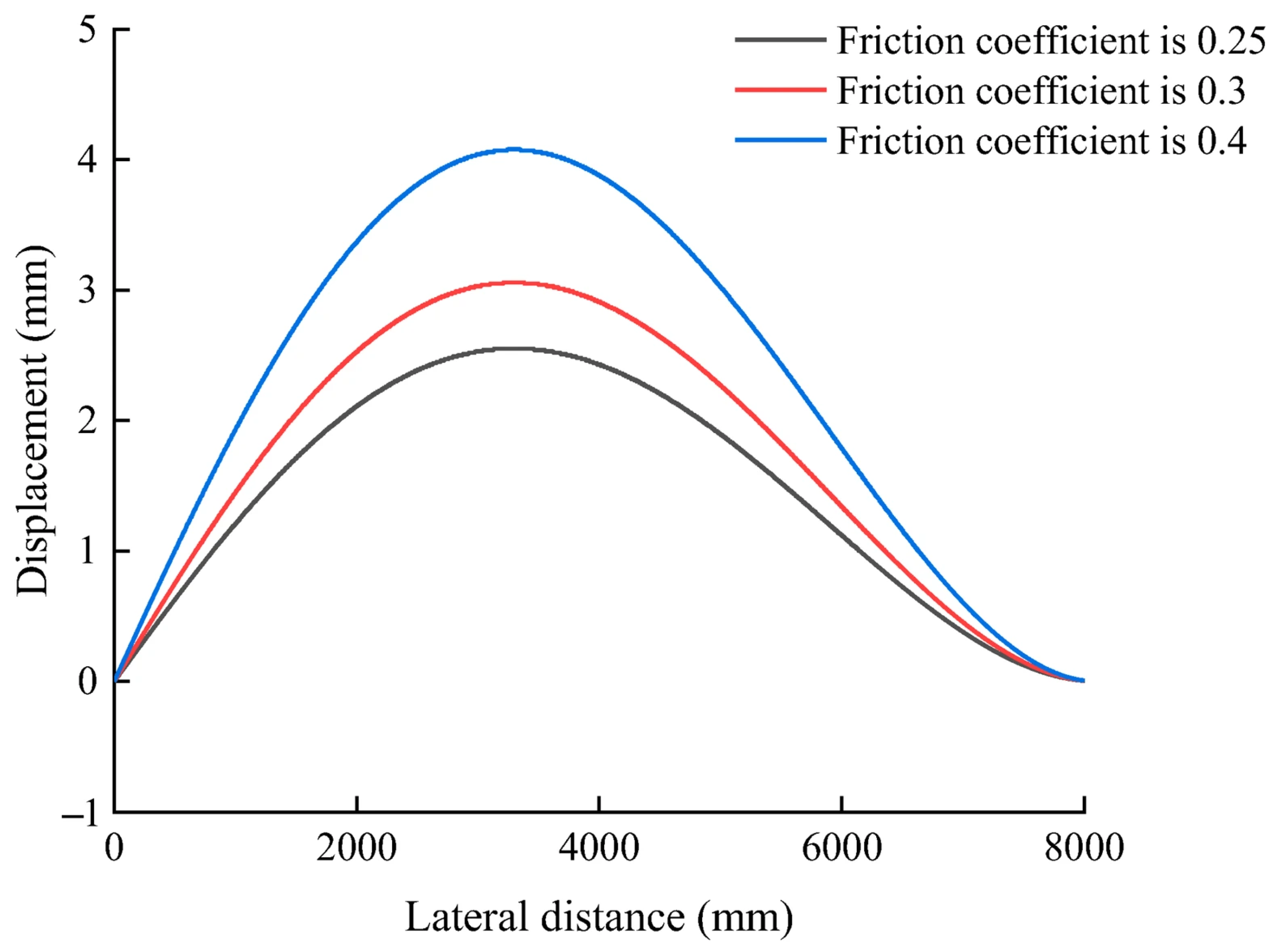
3.1. Analysis of Insufficient Displacement of Switch Rail Under Different Friction Coefficients
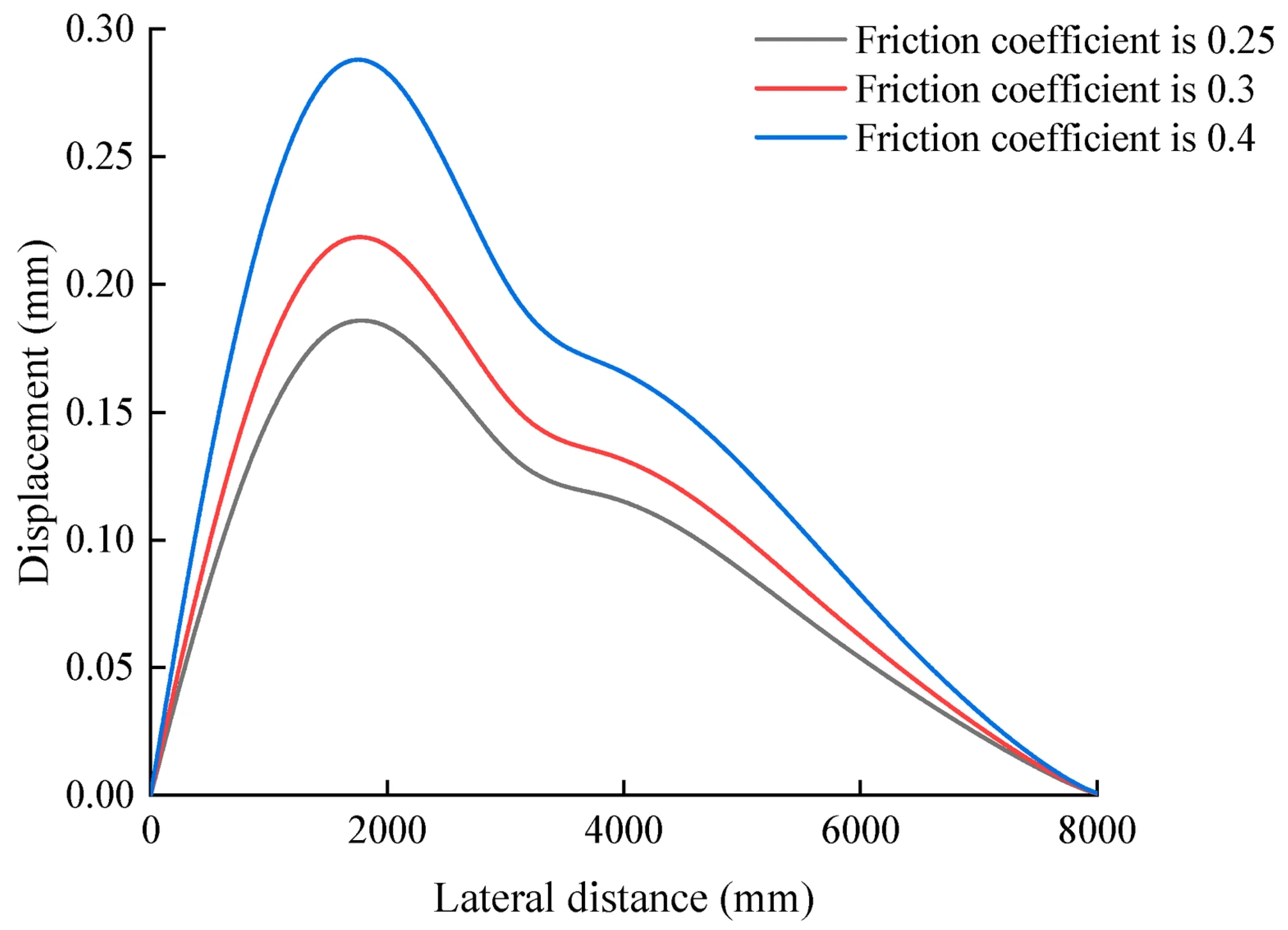
3.2. Analysis of Insufficient Displacement of Switch Rail Under Wheel–Rail Force
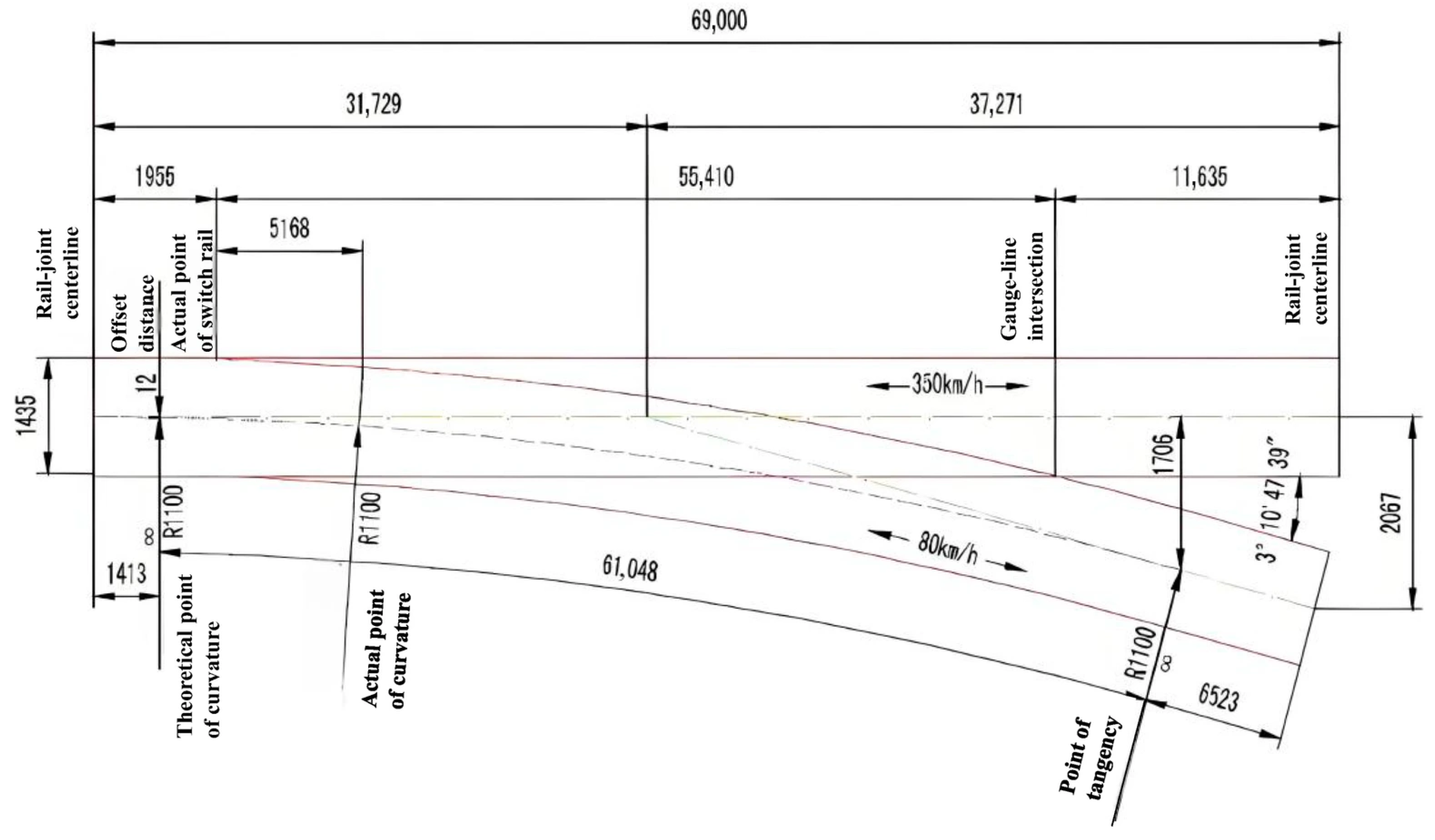
4. Case Study
4.1. Evaluation Standard for Improvement
4.2. Comparison of Static and Dynamic Inspection Results
4.3. On-Site Verification
5. Conclusions
- •
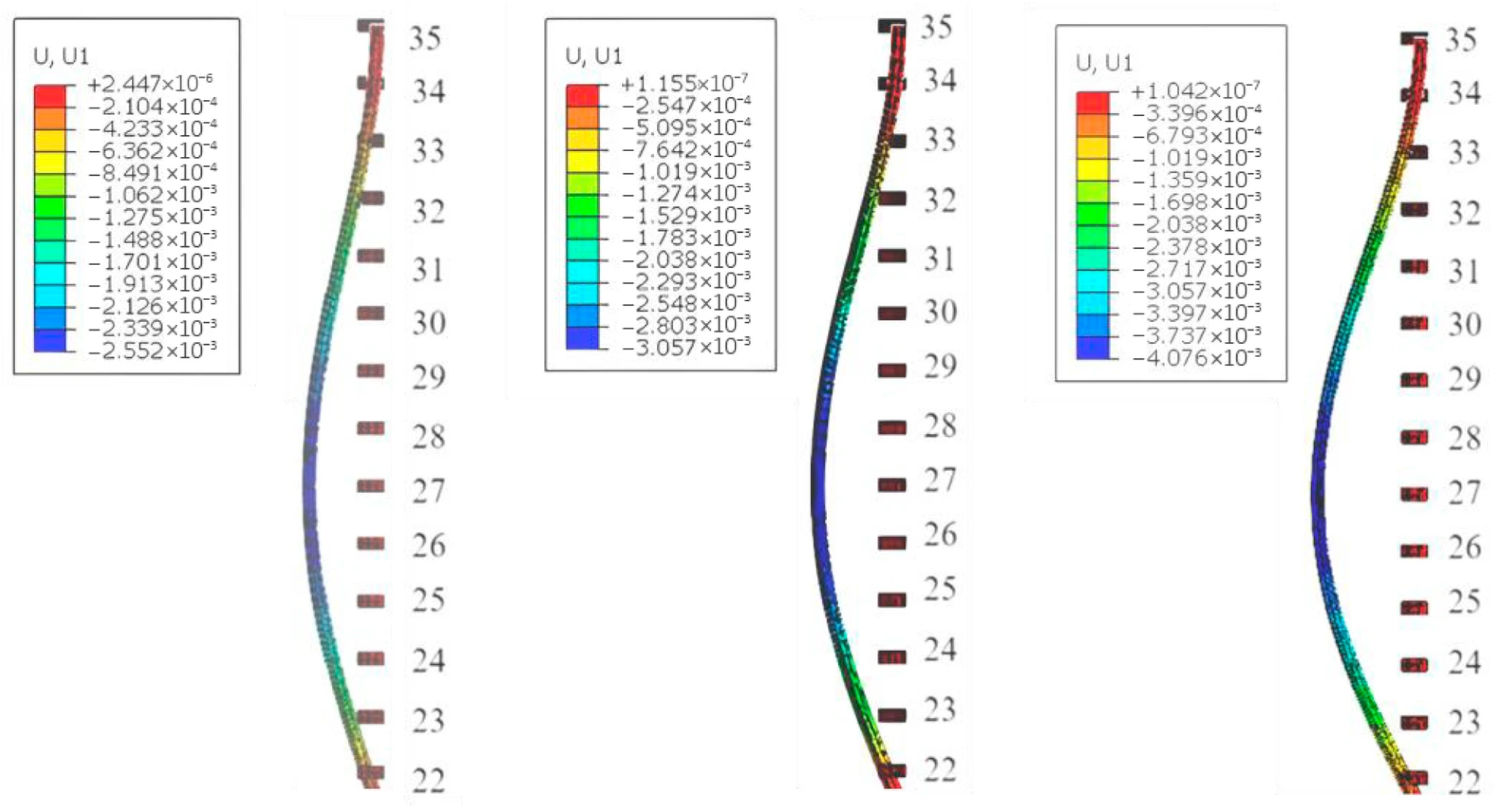
- Without considering the force of the iron block, the maximum insufficient displacement of the switch rail appears correspondingly at sleeper No. 27. The deformation of the switch rail first increases and then decreases laterally. The maximum insufficient displacement of the switch rail increases linearly with the increase in friction coefficient, with a regression coefficient of 1.02.
- •
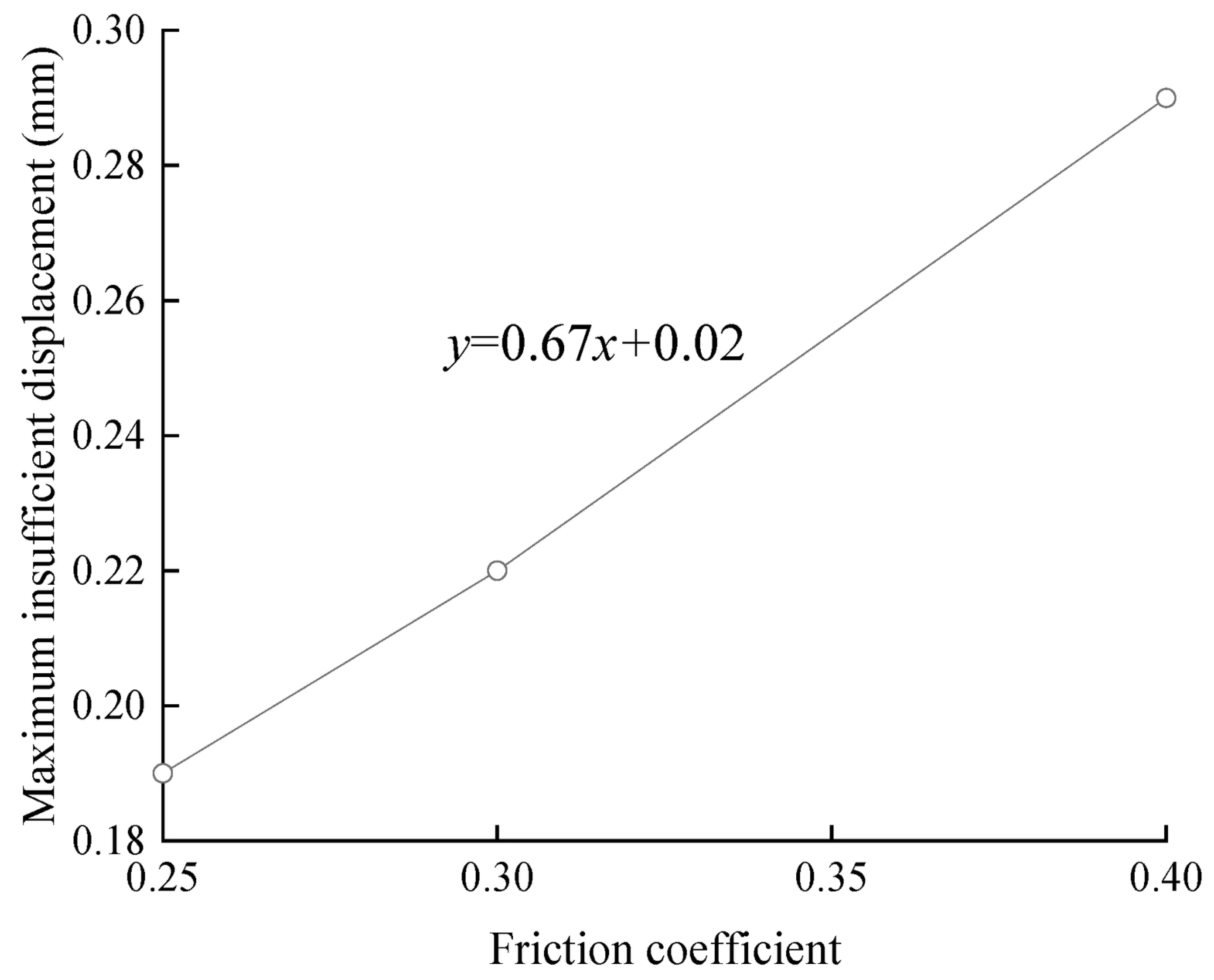
- Under the influence of lateral wheel–rail force, the insufficient displacement of the switch rail is partially offset. The maximum insufficient displacement of the switch rail is transferred correspondingly from sleeper No. 27 to sleeper No. 25. The maximum insufficient displacement of the switch rail increases linearly with the increase in friction coefficient, with a regression coefficient of 0.67 after the offset.
- •
- Comparing the data measured using the dynamic track inspection car and the track inspection instrument, insufficient displacement of the switch rail exceeding 2 mm is found to improve under the influence of the train’s wheel–rail force, with the improvement ratio reaching more than 90%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jing, G.; Siahkouhi, M.; Qian, K.; Wang, S. Development of a field condition monitoring system in high speed railway turnout. Measurement 2021, 169, 108358. [Google Scholar] [CrossRef]
- Cai, X.; Tang, X.; Yang, F.; Wang, T.; Sun, J. Estimation of turnout irregularities using vehicle responses with improved BiLSTM and Gaussian process regression. Measurement 2023, 221, 113513. [Google Scholar] [CrossRef]
- Wang, F.; Wang, A.; Tang, T.; Shi, J. SGL-PCA: Health Index Construction with Sensor Sparsity and Temporal Monotonicity for Mixed High-Dimensional Signals. IEEE Trans. Autom. Sci. Eng. 2023, 20, 372–384. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, Z.; Ma, J.; Wang, S. Study on the optimization of high-speed turnout crossing structures based on actual elastic deformation of point and splice rails. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2023, 238, 141–151. [Google Scholar] [CrossRef]
- Wang, P.; Chen, R.; Xu, H. Conversion and its deviation control of electric switch machine of high speed railway turnout. J. Vibroeng. 2013, 15, 1513–1525. [Google Scholar]
- Xu, J.; Zhu, X.; Wang, X.; Chen, R.; Wang, P.; Liu, B.; Luo, Y. Fatigue damage analysis of the straight switch rail considering complex random loads. Veh. Syst. Dyn. 2023, 61, 2394–2414. [Google Scholar] [CrossRef]
- Wang, P.; Chen, R.; Chen, X. Key technologies in high-speed railway turnout design. China Railw. 2022, 8, 1–7. [Google Scholar] [CrossRef]
- Wang, P.; Wang, S.G.; Wang, M.; Zhao, Z.H.; Si, D.L.; Ma, S.Y.; Sun, Z.L. Number selection and structural optimization of 400 km/h high-speed turnout. J. Traffic Transp. Eng. 2023, 23, 114–126. [Google Scholar] [CrossRef]
- Wang, P. Computation and analysis of the switchingpower by multipoint traction. Railw. Stand. Des. 2002, 46, 23–25. [Google Scholar]
- Cai, X.; Li, C. Study on controlling the switching force and scant displacement of the point rail of the high speed turnout. J. China Railw. Soc. 2008, 30, 48–51. [Google Scholar]
- Cai, X. A Study on the Switching and Its Controlling of the Switch and Nose Rails in High Speed Turnout. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2008. [Google Scholar]
- Chen, M.; Liu, C.; Wang, P. Finite element analysis of switch rail conversion for no.6 turnout in the streetcar line. Railw. Eng. 2017, 58, 135–137. [Google Scholar]
- Wang, B.; Wang, P.; Xie, K.; Wang, L.; Quan, S. Analysis of Influence Factors of Switching Force and Inadequate Displacement of Switch Rail of NO.9 Turnout. Appl. Mech. Mater. 2012, 226–228, 872–876. [Google Scholar] [CrossRef]
- Zeng, R.; Wang, S.; Wang, P.; Yang, L. FEM Simulation Analysis About Influence of Rail Bottom Slicing on Switch Rail Transformation. Railw. Eng. 2019, 59, 140–142+146. [Google Scholar]
- Si, D.; Zhao, Z.; Wang, S. Study on switching characteristics of switch rail for No.9 turnout of new 50 kg·m−1 rail. China Railw. Sci. 2021, 42, 27–33. [Google Scholar]
- Ma, H.; Wang, C. Experimental analysis and control of inadequate displacement of turnout switch rail. Railw. Qual. Control 2017, 45, 41–45. [Google Scholar]
- Jing, G. Analysis of No.18 Moveable-Turnoutinsufficient Displacement. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2006. [Google Scholar]
- Jing, G. ANSYS simulation analysis of No.18 moveableturnout insufficient displacement. Railw. Eng. 2007, 47, 108–110. [Google Scholar]
- Su, X. Analysis of Insufficient Switch Rail Displacement of High-Speed Turnout. Master’s Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2013. [Google Scholar]
- Wang, F.; Sun, S.; Cao, Y.; Pei, Y.; Tang, T. Optimal Design of Tractive Layout for Minimizing the Insufficient Displacement of Railway Turnout. IEEE Trans. Intell. Transp. Syst. 2023, 24, 12597–12613. [Google Scholar] [CrossRef]
- Zhang, Y.; Cheng, Y.; Xu, T.; Wang, G.; Chen, C.; Yang, T. Fault Prediction of Railway Turnout Systems Based on Improved Sparse Auto Encoder and Gated Recurrent Unit Network. IEEE Trans. Intell. Transp. Syst. 2021, 23, 12711–12723. [Google Scholar] [CrossRef]
- Li, C.; Zhao, L. A Railway Turnout Closeness Monitoring Method Based on Switch Gap Images. IEEE Intell. Transp. Syst. Mag. 2022, 14, 214–229. [Google Scholar] [CrossRef]
- Dutta, S.; Harrison, T.; Ward, C.P.; Dixon, R.; Scott, T. A new approach to railway track switch actuation: Dynamic simulation and control of a self-adjusting switch. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2019, 234, 779–790. [Google Scholar] [CrossRef]
- Wang, P.; Ma, X.-C.; Wang, J.; Xu, J.-M. Effect on the scant displacement of switch rail of high-speed turnout by the differential motion device. J. Railw. Eng. Soc. 2015, 32, 43–48. [Google Scholar]
- Yan, Q.; Sun, X.; Yang, S.; Zhang, L. Study of Spring Transfer Drive Device for Scant Displacement of Switch Rail. Railw. Signal. Commun. 2017, 53, 28–31. [Google Scholar]
- Kraśkiewicz, C.; Anysz, H.; Zbiciak, A.; Płudowska-Zagrajek, M.; Al Sabouni-Zawadzka, A. Artificial neural networks as a tool for selecting the parameters of prototypical under sleeper pads produced from recycled rubber granulate. J. Clean. Prod. 2023, 405, 136975. [Google Scholar] [CrossRef]
- Chen, L. Research on Failure Mechanism and Damage Recognition Algorithm of Turnout Slide Plate in Alpine Region. Master’s Thesis, Lanzhoou Jiaotong University, Lanzhou, China, 2023. [Google Scholar]
- Luo, Y.; Xu, Y. Investigation of Dry Bearings in Railway Switch Slide Baseplate. J. Shanghai Tiedao Univ. (Nat. Sci. Ed.) 1998, 10, 41–46. [Google Scholar]

| Working Condition | Friction Coefficient | Wheel–Rail Force Applied |
|---|---|---|
| 1 | 0.25 | No |
| 2 | 0.3 | No |
| 3 | 0.4 | No |
| 4 | 0.25 | Yes |
| 5 | 0.3 | Yes |
| 6 | 0.4 | Yes |
| Friction Coefficient | Maximum Insufficient Displacement/mm | Mean/mm | Standard Deviation/mm | Coefficient of Variation/% | ||||
|---|---|---|---|---|---|---|---|---|
| Test 1 | Test 2 | Test 3 | Test 4 | Test 5 | ||||
| 0.25 | 2.48 | 2.56 | 2.54 | 2.57 | 2.60 | 2.55 | 0.045 | 1.8 |
| 0.30 | 3.00 | 3.08 | 3.05 | 3.10 | 3.07 | 3.06 | 0.038 | 1.2 |
| 0.40 | 4.02 | 4.05 | 4.09 | 4.11 | 4.12 | 4.08 | 0.042 | 1.0 |
| Friction Coefficient | Maximum Insufficient Displacement Without Wheel–Rail Force/mm | Maximum Insufficient Displacement with Wheel–Rail Force/mm | Displacement Reduction/mm | Percentage Reduction in Displacement/% |
|---|---|---|---|---|
| 0.25 | 2.55 | 0.19 | 2.36 | 92.55 |
| 0.30 | 3.06 | 0.22 | 2.84 | 92.81 |
| 0.40 | 4.08 | 0.29 | 3.79 | 92.89 |
| Friction Coefficient | Maximum Insufficient Displacement/mm | Mean/mm | Standard Deviation/mm | Coefficient of Variation/% | ||||
|---|---|---|---|---|---|---|---|---|
| Test 1 | Test 2 | Test 3 | Test 4 | Test 5 | ||||
| 0.25 | 0.189 | 0.190 | 0.190 | 0.190 | 0.191 | 0.190 | 0.00071 | 0.37 |
| 0.30 | 0.220 | 0.220 | 0.220 | 0.221 | 0.220 | 0.220 | 0.00045 | 0.20 |
| 0.40 | 0.290 | 0.290 | 0.291 | 0.290 | 0.290 | 0.290 | 0.00045 | 0.15 |
| Turnout | No Improvement | Improvement | Obvious Improvement | Total Number | Improvement Proportion |
|---|---|---|---|---|---|
| A | 2 | 7 | 16 | 25 | 92.0% |
| B | 1 | 1 | 11 | 13 | 92.3% |
| Sleeper Number | Results of Track Inspection Instrument Before Conversion/mm | Results of Track Inspection Instrument After Conversion/mm | Difference Between Results of Two Track Inspection Instruments/mm | Results of Dynamic Track Inspection Car/mm | Difference Between Static and Dynamic Measurement Result/mm |
|---|---|---|---|---|---|
| D23 | −1.8 | 0.7 | 2.5 | 0.2 | 2.0 |
| D24 | −3.0 | 0.8 | 3.7 | 0.3 | 3.3 |
| D25 | −4.2 | 0.7 | 4.9 | 0.5 | 4.7 |
| D26 | −5.4 | 0.3 | 5.7 | 0.2 | 5.6 |
| D27 | −6.4 | −0.3 | 6.1 | −0.5 | 5.9 |
| D28 | −7.0 | −0.9 | 6.1 | −1.2 | 5.8 |
| D29 | −6.9 | −1.4 | 5.5 | −1.8 | 5.1 |
| D30 | −6.2 | −1.9 | 4.3 | −1.4 | 4.8 |
| D31 | −5.0 | −2.5 | 2.5 | −1.6 | 3.4 |
| D32 | −3.7 | −2.5 | 1.2 | −1.1 | 2.6 |
| D33 | −2.4 | −1.8 | 0.6 | −0.3 | 2.1 |
| D34 | −0.8 | −0.3 | 0.5 | 0.7 | 1.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Han, L.; Wei, X.; Yang, D.; Si, D.; Zhang, M.; Wang, S.; Jing, G. Assessing Impact of Wheel–Rail Force on Insufficient Displacement of Switch Rail in High-Speed Railway. Lubricants 2025, 13, 497. https://doi.org/10.3390/lubricants13110497
Wang P, Han L, Wei X, Yang D, Si D, Zhang M, Wang S, Jing G. Assessing Impact of Wheel–Rail Force on Insufficient Displacement of Switch Rail in High-Speed Railway. Lubricants. 2025; 13(11):497. https://doi.org/10.3390/lubricants13110497
Chicago/Turabian StyleWang, Pu, Lei Han, Xiaohua Wei, Dongsheng Yang, Daolin Si, Moyan Zhang, Shuguo Wang, and Guoqing Jing. 2025. "Assessing Impact of Wheel–Rail Force on Insufficient Displacement of Switch Rail in High-Speed Railway" Lubricants 13, no. 11: 497. https://doi.org/10.3390/lubricants13110497
APA StyleWang, P., Han, L., Wei, X., Yang, D., Si, D., Zhang, M., Wang, S., & Jing, G. (2025). Assessing Impact of Wheel–Rail Force on Insufficient Displacement of Switch Rail in High-Speed Railway. Lubricants, 13(11), 497. https://doi.org/10.3390/lubricants13110497






