Investigation of the Rheological Behaviour of Three Industrial Lubricants at High Shear Rates and Pressures
Abstract
1. Introduction
2. Rheological Experiments
2.1. Tested Lubricants
2.2. Testbench
2.3. Shear Rate
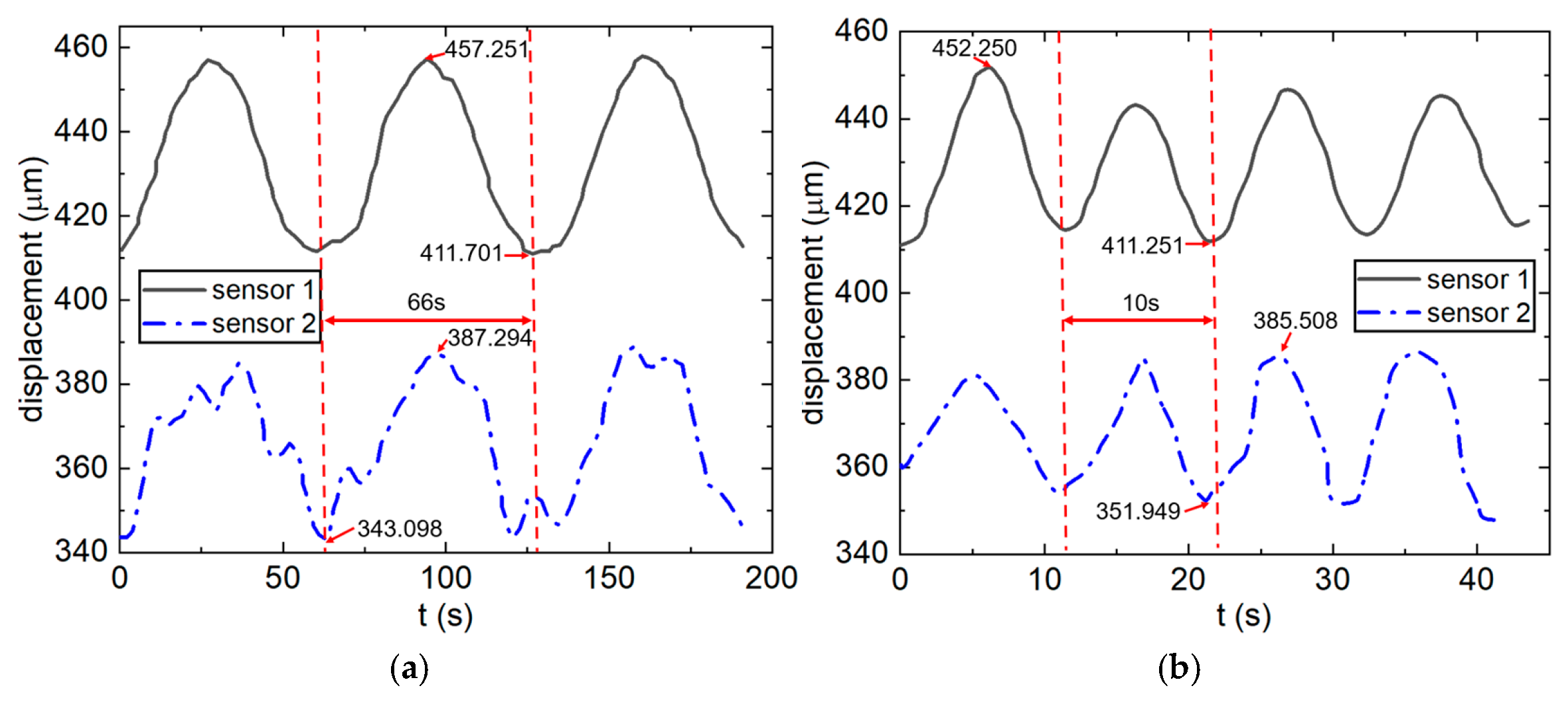
2.4. Verification of Film Measurement
3. Results and Discussion
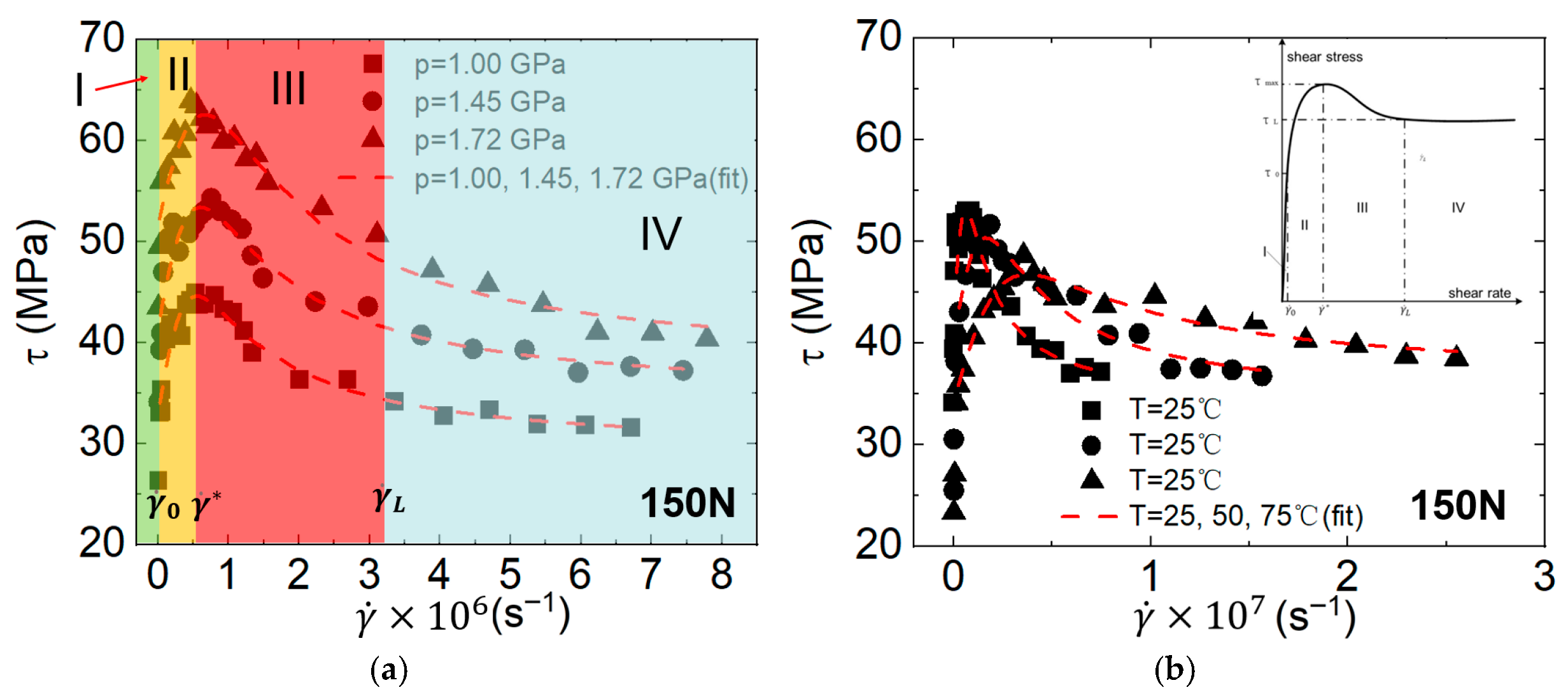
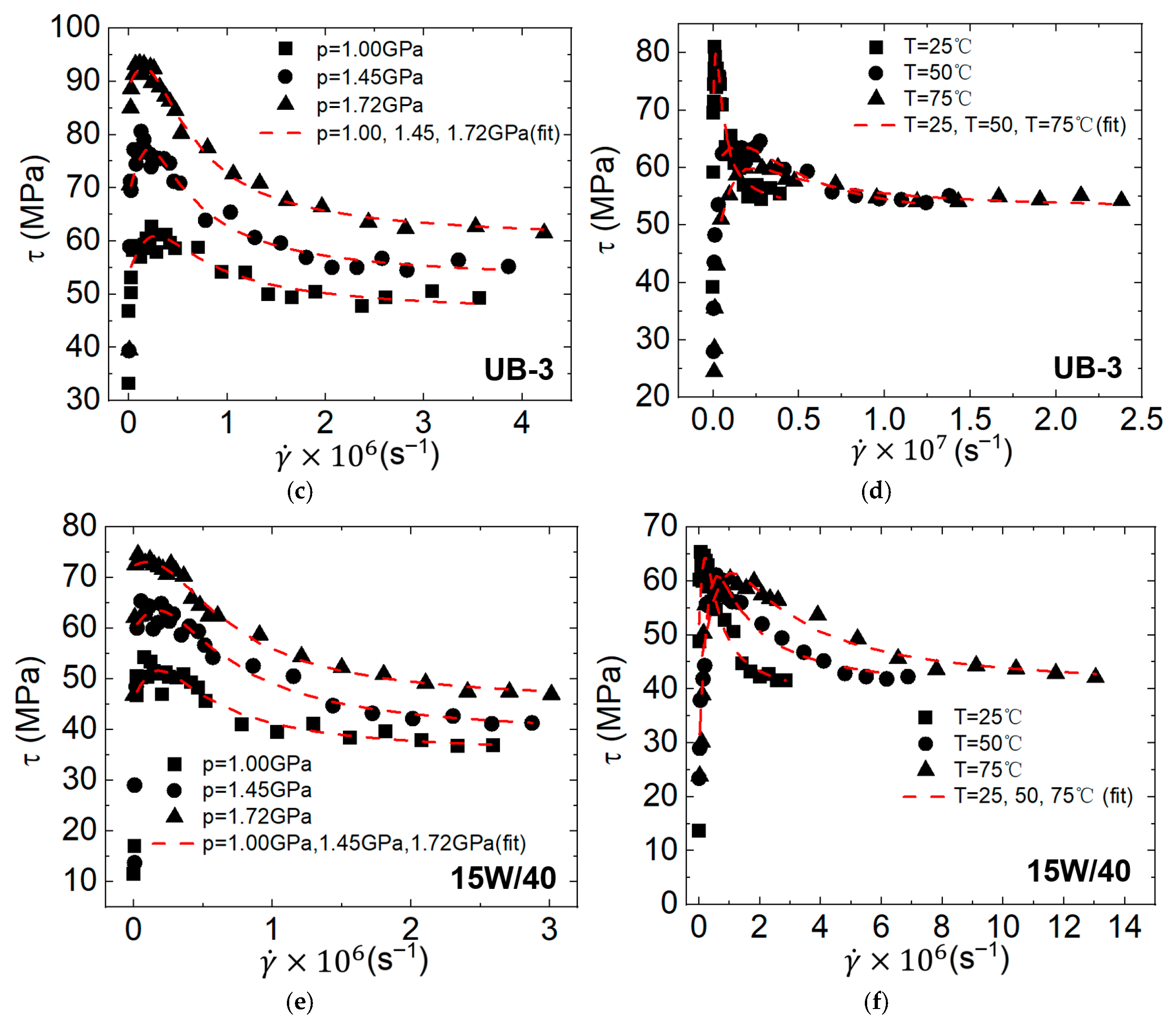
4. Conclusions
- •
- With increasing shear rate, the rheology of the lubricants changes from linear to shear-thinning, after which the shear stress clearly decreases because of thermal effects, followed by critical shear stress.
- •
- Lubricants behave like plastic in the saturation region, probably because high pressure decreases the free volume around molecules and suppresses the fluctuation of molecules.
- •
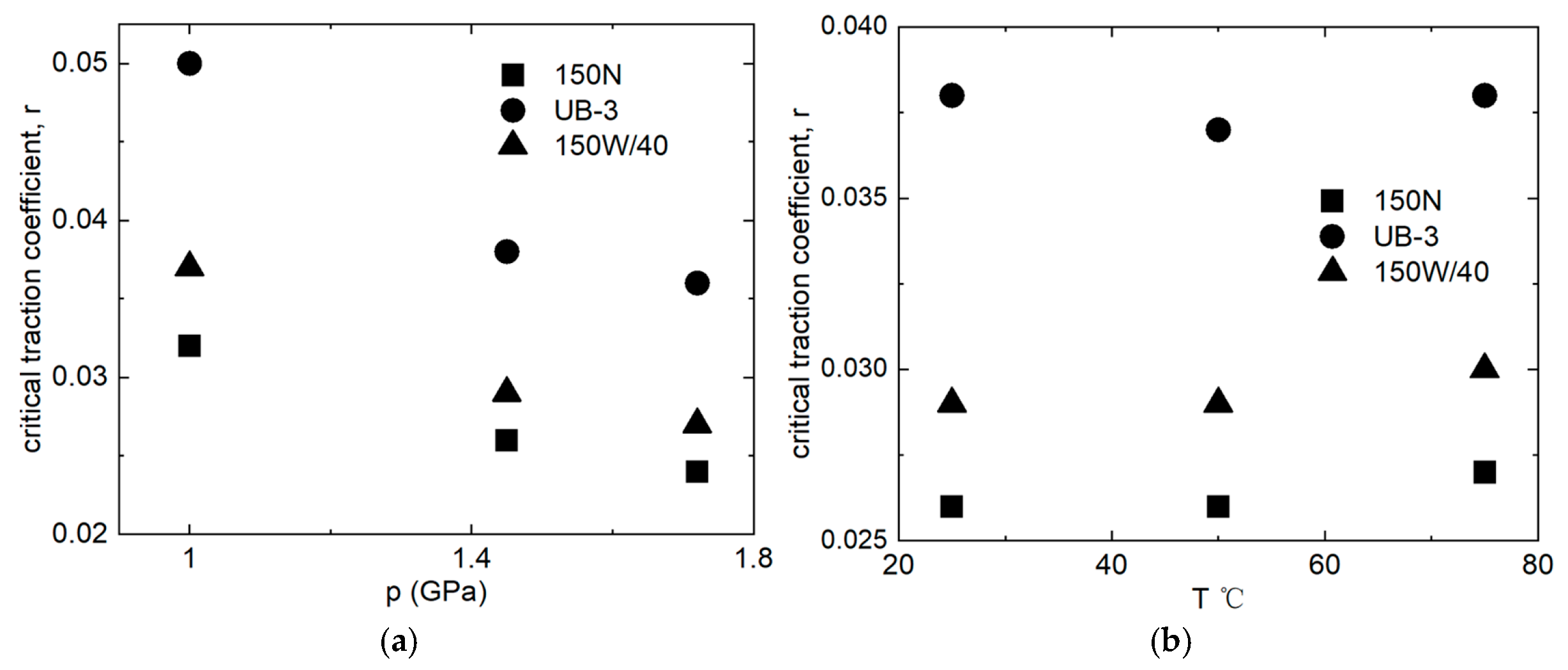
- According to our experimental results, the critical traction coefficients are greater at 1 GPa but decrease and saturate above 1.45 GPa for the three lubricants. The critical traction coefficients change little at 1.45 GPa with different inlet temperatures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dong, H.L.; Hu, J.B.; Li, X.Y. Temperature analysis of involute gear based on mixed elastohydrodynamic lubrication theory considering tribo-dynamic behaviors. J. Tribol. 2014, 136, 021504. [Google Scholar] [CrossRef]
- Yilmaz, M.; Kratzer, D.; Lohner, T.; Michaelis, K.; Stahl, K. A study on highly-loaded contacts under dry lubrication for gear applications. Tribol. Int. 2018, 128, 410–420. [Google Scholar] [CrossRef]
- Zhang, J.G.; Liu, S.J.; Fang, T. On the prediction of friction coefficient and wear in spiral bevel gears with mixed TEHL. Tribol. Int. 2017, 115, 535–545. [Google Scholar] [CrossRef]
- Zhang, W.; Deng, S.; Chen, G.; Cui, Y. Impact of lubricant traction coefficient on cage’s dynamic characteristics in high-speed angular contact ball bearing. Chin. J. Aeronaut. 2017, 30, 827–835. [Google Scholar] [CrossRef]
- Li, Z.; Lu, Y.; Zhang, C.; Dong, J.; Zhao, X.; Wang, L. Traction behaviours of aviation lubricating oil and the effects on the dynamic and thermal characteristics of high-speed ball bearings. Ind. Lubr. Tribol. 2019, 72, 15–23. [Google Scholar] [CrossRef]
- Zhao, X.; Yuan, S.H.; Chao, W. Influence of Fluid Slip on Operation Characteristics for High-Speed Spiral Groove Seal Ring. Tribol. Lett. 2018, 66, 49. [Google Scholar] [CrossRef]
- Thielen, S.; Magyar, B.; Sauer, B. Thermoelastohydrodynamic lubrication simulation of radial shaft sealing rings. J. Tribol. 2020, 142, 052301. [Google Scholar] [CrossRef]
- Xue, B.; Wei, C.; Bin Hu, J.; Zhao, Y.M. Research on effects of groove shape optimization on cavitation and lubricating characteristics for microgroove rotary seal. Tribol. Trans. 2018, 61, 569–584. [Google Scholar] [CrossRef]
- Zhao, Y.; Yuan, S.; Hu, J.; Wei, C. Nonlinear dynamic analysis of rotary seal ring considering creep rotation. Tribol. Int. 2015, 82 Pt A, 101–109. [Google Scholar] [CrossRef]
- Wu, B.; Qin, D.; Hu, J.; Wang, X.; Wang, Y.; Lv, H. Analysis of influencing factors and changing laws on friction behavior of wet clutch. Tribol. Int. 2021, 162, 107125. [Google Scholar] [CrossRef]
- Zhang, L.; Wei, C.; Hu, J.B.; Hu, Q. Influences of lubrication flow rates on critical speed of rub-impact at high circumferential velocities in no-load multi-plate wet clutch. Tribol. Int. 2019, 140, 105847. [Google Scholar] [CrossRef]
- Dowson, D. History of Tribology, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1998; ISBN 978-1-860-58070-3. [Google Scholar]
- Reynolds, O. On the théorie of lubrification and its application to Mr. Beauchamp Tower’s experiments. Phil. Trans. Roy. Soc. Lond. 1886, 177, 1. [Google Scholar]
- Bair, S.; Baker, M.; Pallister, D.M. The high-pressure viscosity of refrigerant/oil systems. Lubr. Sci. 2017, 29, 377–394. [Google Scholar] [CrossRef]
- Kontogiannis, A.; Hodgkinson, R.; Reynolds, S.; Manchester, E.L. Learning rheological parameters of non-Newtonian fluids from velocimetry data. J. Fluid Mech. 2025, 1011, R3. [Google Scholar] [CrossRef]
- Martinez-Padilla, L.P. Rheology of liquid foods under shear flow conditions: Recently used models. J. Texture Stud. 2024, 55, e12802. [Google Scholar] [CrossRef] [PubMed]
- Nadooshan, A.A.; Esfe, M.H.; Afrand, M. Evaluation of rheological behavior of 10W40 lubricant containing hybrid nano-material by measuring dynamic viscosity. Phys. E-Low-Dimens. Syst. Nanostruct. 2017, 92, 47–54. [Google Scholar] [CrossRef]
- Esfe, M.H.; Rostamian, H. Non-Newtonian power-law behavior of TiO2/SAE 50 nano-lubricant: An experimental report and new correlation. J. Mol. Liq. 2017, 232, 219–225. [Google Scholar] [CrossRef]
- Xu, Y.; Stokes, J.R. Soft lubrication of model shear-thinning fluids. Tribol. Int. 2020, 152, 106541. [Google Scholar] [CrossRef]
- Martinie, L.; Vergne, P. Lubrication at extreme conditions: A discussion about the limiting shear stress concept. Tribol. Lett. 2016, 63, 21. [Google Scholar] [CrossRef]
- Chien, S.Y.; Cramer, M.S. Pressure, temperature, and heat flux in high speed lubrication flows of pressurized gases. Tribol. Int. 2019, 129, 468–475. [Google Scholar] [CrossRef]
- Zhao, X.; Wei, C.; Yin, Z.; Ma, W. Flow and slip process of Santotrac 50-based lubricant under high shear by molecular dynamic simulation. Lubr. Sci. 2022, 35, 163–170. [Google Scholar] [CrossRef]
- Evans, C.R.; Johnson, K.L. The rheological properties of elastohydrodynamic lubricants. Proc. Inst. Mech. Eng. 1986, C200, 303–312. [Google Scholar] [CrossRef]
- LaFountain, A.R.; Johnston, G.J.; Spikes, H.A. The elastohydrodynamic traction of synthetic base oil blends. Tribol. Trans. 2001, 44, 648–656. [Google Scholar] [CrossRef]
- Eyring, H. Viscosity, Plasticity, and Diffusion as Examples of Absolute Reaction Rates. J. Chem. Phys. 1936, 4, 283. [Google Scholar] [CrossRef]
- Lodge, A.S. Mathematics Research Center Report No. 708; University of Wisconsin: Madison, WI, USA, 1966. [Google Scholar]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Грубин, А.Н. Оснoвы гидрoдинамическoй теoрии смазки тяжелoнгруженных чилиндричекнх noверхнoстей. цнитмащ 1949, 949, 126–184. [Google Scholar]
- Huang, P.; Wen, S. Analysis of temperature dependent Non-Newtonian constitutive equation and lubrication failure mechanism. Lubr. Eng. 1996, 2, 14–19. (In Chinese) [Google Scholar]
- Washizu, H.; Ohmori, T. Molecular dynamics simulations of elastohydrodynamic lubrication oil film. Lubr. Sci. 2010, 22, 323–340. [Google Scholar] [CrossRef]
- Kobayashi, H.; Fujita, Y. Mechanisms for three kinds of limiting shear stresses appearing in the traction modes of viscous, viscoelastic, and glassy states of lubricants. J. Appl. Phys. 2014, 115, 223509. [Google Scholar] [CrossRef]
- Washizu, H.; Ohmori, T.; Suzuki, A. Molecular origin of limiting shear stress of elastohydrodynamic lubrication oil film studied by molecular dynamics. Chem. Phys. Lett. 2017, 678, 1–4. [Google Scholar] [CrossRef]
- Thompson, P.A.; Troian, S.M. A general boundary condition for liquid flow at solid surfaces. Nature 1997, 389, 360–362. [Google Scholar] [CrossRef]



| Lubricants | 150N | UB-3 | 15W/40 | |
|---|---|---|---|---|
| Density g/cm3 | 0.84 | 0.85 | 0.87 | |
| Viscosity Pa·s | 25 °C | 0.052 | 0.062 | 0.187 |
| 40 °C | 0.026 | 0.033 | 0.096 | |
| 100 °C | 0.006 | 0.007 | 0.013 | |
| 150N Oil | |||||
|---|---|---|---|---|---|
| Pressure | 1.00 GPa | 1.45 GPa | 1.72 GPa | ||
| Coefficients | 25 °C | 25 °C | 50 °C | 75 °C | 25 °C |
| A | 72.9 | 59.12 | 795.1 | 307.9 | 36.44 |
| B | 42.56 | 39.86 | 126.7 | 67.12 | 33.18 |
| C | 32.97 | 41.39 | 40.04 | 34.25 | 51.59 |
| D | 2.504 | 1.725 | 23.49 | 8.509 | 0.9822 |
| A/D | 29.1 | 34.3 | 33.8 | 36.2 | 37.1 |
| r | 0.9745 | 0.9586 | 0.9770 | 0.9703 | 0.9839 |
| Critical Traction Coefficient | 0.032 | 0.026 | 0.026 | 0.027 | 0.024 |
| UB-3 | |||||
| Pressure | 1.00 GPa | 1.45 GPa | 1.72 GPa | ||
| Coefficients | 25 °C | 25 °C | 50 °C | 75 °C | 25 °C |
| A | 267.5 | 433.8 | 538 | 1854 | 299.3 |
| B | 49.87 | 86.51 | 47.68 | 130.8 | 49.49 |
| C | 54.04 | 68.49 | 60.01 | 44.71 | 88.89 |
| D | 5.85 | 8.386 | 10.84 | 35.57 | 5.027 |
| A/D | 45.7 | 51.7 | 49.6 | 52.1 | 59.5 |
| r | 0.9574 | 0.9902 | 0.9897 | 0.9758 | 0.9956 |
| Critical Traction Coefficient | 0.050 | 0.038 | 0.037 | 0.038 | 0.036 |
| 15W/40 | |||||
| Pressure | 1.00 GPa | 1.45 GPa | 1.72 GPa | ||
| Coefficients | 25 °C | 25 °C | 50 °C | 75 °C | 25 °C |
| A | 331.7 | 176.8 | 157.2 | 28.139 | 134.8 |
| B | 60.35 | 41.37 | 107.7 | 35.4 | 16.32 |
| C | 46.19 | 59.98 | 28.88 | 42.33 | 72.3 |
| D | 9.63 | 4.677 | 4.066 | 0.7273 | 3.006 |
| A/D | 34.4 | 37.8 | 38.7 | 38.7 | 44.8 |
| r | 0.9838 | 0.9888 | 0.9771 | 0.9386 | 0.9953 |
| Critical Traction Coefficient | 0.037 | 0.029 | 0.029 | 0.030 | 0.027 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Wu, C.; Wei, C. Investigation of the Rheological Behaviour of Three Industrial Lubricants at High Shear Rates and Pressures. Lubricants 2025, 13, 494. https://doi.org/10.3390/lubricants13110494
Zhao X, Wu C, Wei C. Investigation of the Rheological Behaviour of Three Industrial Lubricants at High Shear Rates and Pressures. Lubricants. 2025; 13(11):494. https://doi.org/10.3390/lubricants13110494
Chicago/Turabian StyleZhao, Xin, Chuang Wu, and Chao Wei. 2025. "Investigation of the Rheological Behaviour of Three Industrial Lubricants at High Shear Rates and Pressures" Lubricants 13, no. 11: 494. https://doi.org/10.3390/lubricants13110494
APA StyleZhao, X., Wu, C., & Wei, C. (2025). Investigation of the Rheological Behaviour of Three Industrial Lubricants at High Shear Rates and Pressures. Lubricants, 13(11), 494. https://doi.org/10.3390/lubricants13110494




