Abstract
Optimising the friction coefficient helps reduce friction losses and improve the efficiency of mechanical systems. The purpose of this study is to experimentally investigate the impact of roughness orientation on the friction coefficient in elastohydrodynamic (EHD) contact. Tests were carried out on a twin-disc machine. Three pairs of discs of identical material (nitrided steel) and geometry were tested: a smooth pair (the root mean square surface roughness Sq = 0.07 µm), a pair with transverse roughness and another with longitudinal roughness. The two rough pairs have similar roughness amplitudes (Sq = 0.5 µm). A comparison of the friction generated by these different pairs was carried out to highlight the effect of the roughness orientation under different operating conditions (oil injection temperature from 60 to 80 °C, Hertzian pressure from 1.2 to 1.5 GPa and mean rolling speed from 5 to 30 m/s). Throughout all the tests conducted in this study, longitudinal roughness resulted in higher friction than transverse, with an increase of up to 30%. Moreover, longitudinal roughness is more sensitive to variations in operating conditions. Finally, in all tests, the asperities of longitudinal roughness were found to influence the friction behaviour, unlike transverse roughness.
1. Introduction
One of the main objectives of engineering in the future is to reduce energy consumption. This is a key factor in improving the efficiency of mechanical systems and limiting their environmental impact. Among the various sources of energy loss, friction in mechanical contacts plays a major role. It occurs particularly in mechanical transmissions, where friction is mainly generated in gear teeth and bearings (between rolling elements and rings) [1]. Instantaneous friction power losses depend on three parameters: the sliding speed, the applied load and the friction coefficient [2]. Reducing these losses improves the efficiency of transmissions and increases their durability [3]. Numerous studies have led to significant progress in research. This includes optimising the geometry of parts [4], selecting appropriate materials [5], enhancing surface finish [6,7,8], improving heat treatments and developing more effective lubricants [9]. Among these avenues, the influence of roughness orientation on the friction coefficient remains an under-explored area.
It is important to note that there is a difference between the surface finish of gears and that of rolling element bearings (REBs). In general, tooth roughness is transverse to sliding [10], with a typical value for the root mean square surface roughness Sq ≈ 0.5 µm. On the other hand, in REBs, the roughness of the raceways is aligned with the direction of rolling (longitudinal), with Sq ≈ 0.2 µm [11,12]. As for the rolling elements, they generally have a super finite isotropic roughness, with Sq of less than 0.08 µm. Setting aside manufacturing-related constraints, one can consider whether there is any advantage, in terms of friction performance, to use surfaces with longitudinal rather than transverse roughness, or vice versa.
Previous studies focus on a single surface condition, whether for a gear or REB, without any real comparison between different roughness orientations. In addition, a large difference in roughness values leads to difficulty in comparing available results. In 1986, Hamrock and Jeng [13] studied theoretically the influence of roughness orientation on friction. They concluded that the friction is higher for longitudinal roughness compared to transverse. A few years later, Makino et al. [14] predicted (theoretically) that the friction is lower for longitudinal roughness than that for transverse. It appears that there is no consensus on the issue.
Some other studies can be found which have primarily investigated the relationship between lubricant film thickness (which plays a key role in friction) and surface roughness. In 1993, Kaneta et al. [15] numerically showed that increasing roughness leads to a decrease in film thickness. As with the coefficient of friction, many studies have only considered a single roughness orientation [16]. However, some numerical studies report conflicting results. For example, Hook et al. [17] found that transverse roughness causes a local thinning of the oil film, while Venner and Lubrecht [18] predicted the opposite effect. According to Zhu and Wang [19], the outcome depends on the value of the ellipticity ratio k: in some cases, longitudinal roughness results in a thicker film than transverse roughness, and in others, the reverse is true.
As with friction behaviour, the influence of roughness orientation on film thickness remains a debated topic. Moreover, most existing studies are numerical (although a few experimental investigations exist).
In this context, experimentally analysing the effect of roughness orientation may lead to new prospects for optimising the performance of mechanical transmissions.
To analyse the coefficient of friction, most of the experimental tests are carried out using a ball-on-disc machine [20,21] or a twin-disc machine [22,23]. The twin-disc machine seems to have a major advantage over the ball-on-disc one. This is due to its configuration, which is more representative for real operating conditions [24], being applicable both to tooth and to rolling element–ring contact frictions [25].
The present work exposes the influence of roughness orientation on the coefficient of friction, thanks to tests carried out using a twin-disc machine. The aim is to evaluate the impact of longitudinal and transverse roughness on the coefficient of friction. First, the test rig, lubricant and specimens are presented. Then, the operating procedure is explained. Finally, the experimental results are compared and discussed.
2. Materials and Methods
2.1. Materials
2.1.1. Test Rig
The friction coefficients presented in this article were measured using a twin-disc test rig. A complete description of the test rig can be found in [25,26]. Only the most relevant information is given hereafter. The test rig is equipped with two independently driven motors. Each motor drives a rotating shaft, onto which a disc is mounted. These discs are designed in a way to be in contact under a controlled applied load, using a pneumatic actuator. Lubrication is provided by an injection system (Figure 1). The temperatures of the oil and discs (bulk) are measured with an accuracy of ±2 °C. Friction data are recorded during the tests. The relative error on this value is 0.3%.
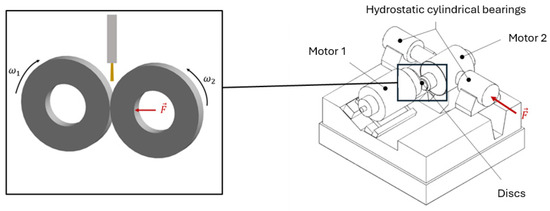
Figure 1.
Test rig.
2.1.2. Lubricant
The tests were conducted using a mineral gear transmission oil (NATO-0155). Table 1 gives oil properties.

Table 1.
Mineral oil properties.
2.1.3. Specimens
The parameter used in this study to describe the surface roughness is the root mean square (RMS) surface roughness, Sq. Additional information on surface roughness is provided in Appendix B. There are various methods to measure roughness, depending on the parameter selected and the characteristics of the surface being analysed [27,28,29]. In this study, the roughness was measured using a Sensofar Plu neox optical profiler (×50) coupled to MountainMap 10.
To evaluate the equivalent surface roughness of a profile, i.e., of the two surfaces, it is useful to introduce the parameter . It can be estimated for an equivalent contact between two anisotropic surfaces, 1 and 2, using the following equation:
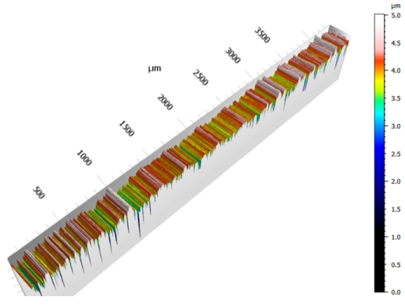
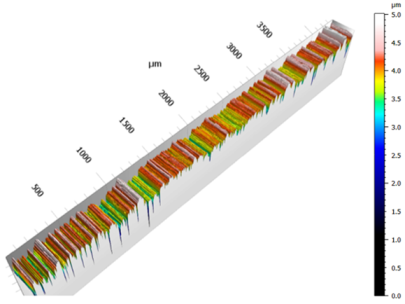
For this study, three pairs of discs were used: one smooth pair (Sq ≈ 0.07 µm), corresponding to superfinished surfaces, and two rough pairs with controlled surface finishes exhibiting similar roughness levels (Sq ≈ 0.5 µm), but differing in roughness orientation, one transverse and one aligned with the sliding direction (Figure 2).

Figure 2.
Disc pairs.
The disc pairs mounted on the shafts consist of a cylindrical disc and a crown disc. The contact surface between the two discs is elliptical. Both discs are made of nitrided steel 32CrMoV13 and have the same geometries (Table 2). There are several nitriding processes, including gas nitriding (which is the method used for the material in this study), plasma nitriding [30] or liquid nitriding [31]. The formulas for calculating the semi-minor and semi-major widths and the ellipticity ratio, or to determine the Hertzian pressure, are presented in Appendix A. The ellipticity ratio (k), which depends solely on the geometry of the discs (constant), is not investigated in this study.

Table 2.
Material and geometry data of specimens.
Detailed roughnesses of the discs are shown in Table 3. For the two smooth discs, Sq values are low (less than 0.085 µm). Sq values of the transverse discs are of the same order of magnitude as those of the longitudinal discs, allowing a comparison between these two pairs.

Table 3.
RMS surface roughness of the discs.
Table 4 presents the values for these pairs. It shows that, although the roughness values of the longitudinal and transverse surfaces are close, the values of of the transverse/transverse and longitudinal/longitudinal pairs are not identical. To assess the influence of roughness orientation on friction, surface pairings were arranged to create smooth/longitudinal and smooth/transverse combinations, with the smooth discs corresponding to the crown elements and the rough ones to the cylindrical elements.

Table 4.
Pair .
2.2. Methods
Traction tests were carried out on the three pairs of discs for a fixed Hertz pressure, injection temperature and mean rolling speed. A traction test involves varying the slide-to-roll-ratio (SRR) between two values and measuring the coefficient of friction.
Figure 3 shows the evolution of the friction coefficient (in blue) and the average temperature of the two tested discs (in red) as a function of the SRR for both smooth/smooth and longitudinal/longitudinal pairs (Operating conditions: Tinj = 60 °C; p0 = 1.5 GPa; Ve = 20 m/s). The measurement procedure of disc bulk temperatures was described by Isaac [24]. A traction curve consists of three distinct regions [32]:
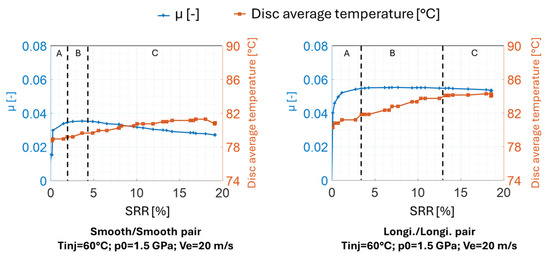
Figure 3.
Evolution of the friction coefficient and the disc average temperature as a function of the SRR for both smooth/smooth and longitudinal/longitudinal pairs (Operating conditions: Tinj = 60 °C; p0 = 1.5 GPa; Ve = 20 m/s).
- The linear region (region A from Figure 3). The lubricant behaves as a Newtonian fluid. The slope of the curve is governed by viscosity and piezoviscosity.
- The nonlinear region (region B from Figure 3). The lubricant exhibits non-Newtonian behaviour.
- The thermal region (region C from Figure 3). Increasing the SRR leads to higher power losses. This raises the disc bulk temperature and thus, the temperature of the oil at the contact. The oil film thickness decreases, resulting in a lower fluid shearing. The friction coefficient decreases. In our study, this phenomenon will be defined as the thermal effects. Additionally, it is noted that the higher the mean rolling speed, the greater the thermal effects. The more the fluid governs the friction, the more significant the thermal effects become (as evidenced by the greater decrease in friction observed in region C for the smooth/smooth pair compared to the longitudinal/longitudinal pair).
Each test is performed at least two times to ensure its repeatability. For example, Figure 4 shows the three performed tests with the smooth/smooth pair under the following operating conditions: Tinj = 60 °C, p0 = 1.5 GPa, Ve = 30 m/s. For these tests, the mean absolute deviation on the friction coefficient is , while the maximum absolute deviation is .
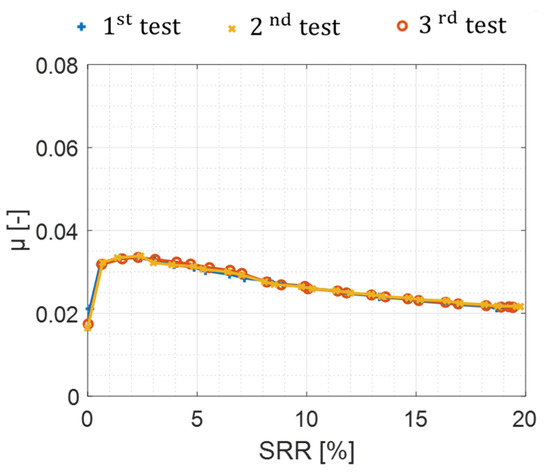
Figure 4.
Test repeatability. Operating conditions: Tinj = 60 °C, p0 = 1.5 GPa, Ve = 30 m/s for the smooth/smooth pair.
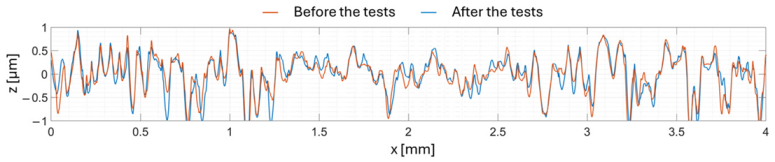
The surface roughness is measured before and after the tests to ensure that there is no significant alteration in the surface topography (no running-in or wear). The relative deviation between the different measurements ranges from 0% to 1.3%. For example, Table 5 shows the evolution of the longitudinal roughness of the crowned disc before and after all the tests. The difference between the Sq values, as well as the comparison of the 2D profiles, clearly show that there was no change in roughness.

Table 5.
Roughness evolution for the crown longitudinal disc.
Once the surface topography is characterised, the lubrication regime must be analysed. Based on experiments on hydrodynamic bearings, Stribeck [33] demonstrated that different lubrication regimes exist. The Stribeck curve describes the evolution of the friction coefficient as a function of the Sommerfeld number (the product of viscosity and speed divided by the load). Following the Stribeck curve, 3 lubrication regimes can be described:
- Full-film lubrication: The surfaces are fully separated by the oil film. The load is solely supported by the fluid. The friction coefficient does not depend on the surface roughness.
- Mixed lubrication: The load is supported partly by the oil film and partly by surface asperities.
- Boundary lubrication: A significant proportion of the load is supported by the asperities.
Tallian [34,35] also characterises lubrication regimes, but replaces the Sommerfeld number with a parameter Λ. However, studies do not all agree on the boundaries between the different lubrication regimes. Thus, according Tallian, the transition from full-film to mixed lubrication and from the mixed to the boundary regime occurs at around Λ = 3 and Λ = 1, respectively. Zhu and Wang [36] suggested, on the basis of their numerical modelling, to separate the full-film and mixed regimes at Λ = 1 and the mixed and boundary regimes at Λ = 0.05. Further studies showed different ways of estimating Λ from other roughness parameters such as [27] or (reduced peak height) [37]. Recently, Hansen et al. have sought to adapt the parameter Λ as a function of roughness orientation [37]. To avoid these inconsistencies, this study focuses on calculating the central oil film thicknesses associated with the smooth/smooth pair. For elliptical contacts (which correspond to the contact between the two studied discs), the central oil film thickness is estimated using the formula provided by Hamrock and Dowson [38,39]. Table 6 shows the calculated film thicknesses for the different configurations, under the assumption of pure rolling (the disc temperature is equal to the injection temperature, since there are no power losses). The film thicknesses are sufficiently large compared to the surface roughness of the smooth discs, which likely indicates that the lubrication regime during these tests is full-film. Thus, for identical operating conditions (configuration), if the friction generated by a pair with one or both rough surfaces is identical to that obtained with a pair with smooth surfaces, it could be concluded that the rough pair is in full film.

Table 6.
Calculated central oil film thickness (6 configurations) for the smooth/smooth pair (pure rolling).
Three series of tests were conducted to assess the influence of surface roughness orientation on friction behaviour, under varying operating conditions:
- For minimum oil film thickness (configuration 1):
- ▪
- Conditions: oil injection temperature, Tinj = 60 °C; maximal Hertz pressure, p0 = 1.5 GPa; and mean rolling speed, Ve = 5 m/s;
- ▪
- Surface pairs tested: smooth/smooth, transverse/transverse, longitudinal/longitudinal, smooth/transverse, smooth/longitudinal.
- For maximum oil film thickness (configuration 6):
- ▪
- Conditions: Tinj = 60 °C, p0 = 1.2 GPa, Ve = 30 m/s;
- ▪
- Surface pairs tested: smooth/smooth, transverse/transverse, longitudinal/longitudinal.
- For intermediate oil film thickness (to explore the role of individual parameters):
- ▪
- Tests conducted on smooth/smooth, transverse/transverse, and longitudinal/longitudinal pairs;
- ▪
- Parameters varied: oil injection temperature (Configurations 2 and 3), Hertzian pressure (Configurations 3 and 4), and mean rolling speed (Configurations 3 and 5).
These configurations span the full range of values used in the study, allowing the investigation of the influence of surface roughness on friction.
3. Results
3.1. Lowest : Maximising the Influence of Asperities
Figure 5 shows the friction coefficients measured for the first series of experiments. According to Table 6, the smooth/smooth contact operates under the full-film lubrication regime. The other pairs exhibiting higher friction coefficients are likely operating under different lubrication regimes.
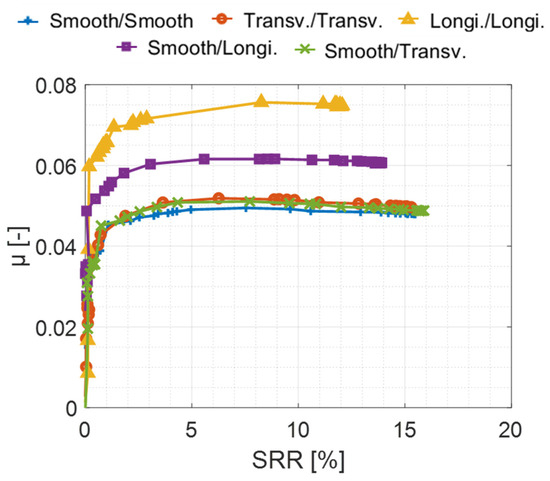
Figure 5.
Experimental traction curves obtain for different combined pairs. Operating conditions: Tinj = 60 °C, p0 = 1.5 GPa, Ve = 5 m/s.
The friction coefficient of the longitudinal/longitudinal pair is significantly higher than that of the transverse/transverse pair (with a difference of 0.025 for an SRR of 10%), even though both pairs show similar ranges of values (Table 7). The smooth/transverse pair produces less friction than the smooth/longitudinal one, which supports the observations reported by Jeng [40]. Furthermore, the friction coefficient of the smooth/longitudinal combination exceeds that of the transverse/transverse pair, despite its being lower. These findings suggest that, for a given roughness level, longitudinal roughness tends to generate more friction than transverse.

Table 7.
at SRR = 10% for all tested pairs (p0 = 1.5 GPa; Ve = 5 m/s: Tinj = 60 °C).
3.2. Highest : Minimising the Influence of Asperities
Figure 6 (second experimental series) shows the friction coefficients under operating conditions where the value is expected to be highest, i.e., at high mean rolling speed, low load.
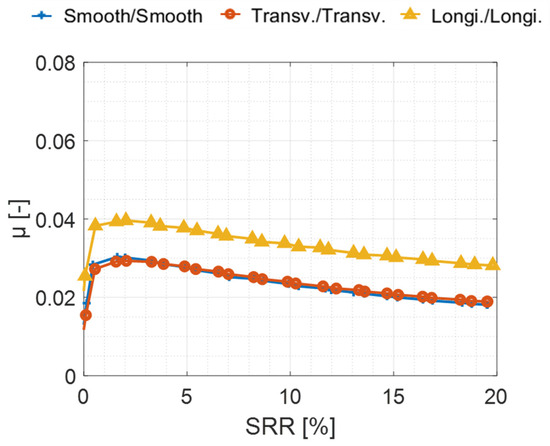
Figure 6.
Experimental traction curves obtained for smooth/smooth, longitudinal/longitudinal and transverse/transverse pairs. Operating conditions: Tinj = 60 °C, p0 = 1.2 GPa, Ve = 30 m/s.
For all three pairs of discs, a rapid increase in friction up to a peak around an SRR of 2% is observed, followed by a continuous decrease. The results also indicate that the friction coefficients for smooth/smooth and transverse/transverse roughness pairs are identical, implying that a full-film lubrication regime is likely achieved.
In contrast, the longitudinal/longitudinal pair exhibits significantly higher friction (by approximately 0.01) across all data points compared to the other two cases (Table 8). This substantial difference indicates that, for this pair of discs, friction is no longer solely governed by the fluid but also involves asperity contacts. Nevertheless, the presence of thermal effects confirms that the fluid still contributes to the overall friction.

Table 8.
at SRR = 10% for all tested pairs (p0 = 1.2 GPa; Ve = 30 m/s: Tinj = 60 °C).
3.3. Intermediate Values: Influence of Operating Conditions
In the following section, the impact of operating conditions will be analysed based on the experiments that have been conducted.
3.3.1. Influence of the Mean Rolling Speed
Figure 7 illustrates the effect of mean rolling speed on the friction coefficient for the three surface pairings: smooth/smooth, transverse/transverse and longitudinal/longitudinal. For all three pairs, increasing the mean rolling speed from 10 to 30 m/s reduces the friction coefficient by approximately 30% for an SRR of 10%. In the smooth/smooth and transverse/transverse cases, this reduction remains constant up to an SRR of 20%. At 30 m/s, friction coefficients for the smooth/smooth and transverse/transverse pairs are identical, indicating a probably full-film lubrication regime. However, at 10 m/s, the results are no longer the same. In contrast, the longitudinal/longitudinal pair exhibits consistently higher friction at both speeds (Table 9).
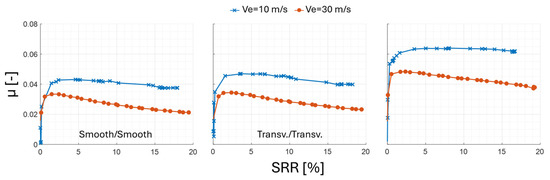
Figure 7.
Experimental traction curves obtained for smooth, longitudinal and transverse pairs. Operating conditions: Tinj = 60 °C, p0 = 1.5 GPa, Ve = 10 and 30 m/s.

Table 9.
Experimental results for two mean rolling speeds (p0 = 1.5 GPa; Tinj = 60 °C).
3.3.2. Influence of the Hertzian Pressure
Figure 8 shows the influence of Hertzian pressure on friction for the three pairs of discs. For the smooth/smooth pair, increasing the Hertzian pressure from 1.2 to 1.5 GPa slightly increases the coefficient of friction. The smooth/smooth curves converge towards the same value at higher SRRs. The transverse/transverse curves also show a slight increase in friction between 1.2 and 1.5 GPa. This difference seems to disappear for an SRR of 15%. For both operating conditions, the friction generated by the longitudinal/longitudinal pair is greater than that of the two other pairs. At 1.2 GPa, the friction generated by the longitudinal/longitudinal pair is 37% higher than that generated by the transverse/transverse pair (Table 10). Increasing the Hertzian pressure from 1.2 to 1.5 GPa leads to an increase in the friction coefficient for both longitudinal/longitudinal (15% at an SRR of 15%) and transverse/transverse (5% at an SRR of 15%).
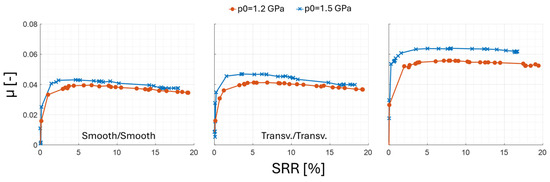
Figure 8.
Experimental traction curves obtained for smooth, longitudinal and transverse pairs. Operating conditions: Tinj = 60 °C, p0 = 1.2 and 1.5 GPa, Ve = 10 m/s.

Table 10.
Experimental results for two Hertzian pressures (Ve = 10 m/s; Tinj = 60 °C).
3.3.3. Influence of the Oil Injection Temperature
Figure 9 shows the influence of the oil injection temperature on friction for the three pairs of discs. Increasing the oil injection temperature from 60 to 80 °C slightly modifies the friction associated to the smooth/smooth and transverse/transverse pairs:
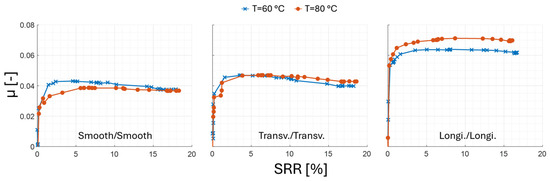
Figure 9.
Experimental traction curves obtained for smooth/smooth, longitudinal/longitudinal and transverse/transverse pairs. Operating conditions: Tinj = 60 and 80 °C, p0 = 1.5 GPa, Ve = 10 m/s.
- The friction observed at 60 °C is higher than that at 80 °C for the smooth/smooth pair.
- The two transverse/transverse curves are identical up to an SRR of 10%. Then, at 60 °C, the friction decreases. However, at 80 °C, the friction remains constant. The decrease in the first curve (60 °C) is attributed to thermal effects.
For both operating conditions, the friction generated by the longitudinal/longitudinal pair is greater than the other two. For the longitudinal/longitudinal pair, increasing the oil injection temperature increases the coefficient of friction for an SRR of 10% by 10% (Table 11). Beyond a 10% SRR, the gap between the two curves remains constant. There is less thermal effect noticed in either case.

Table 11.
Experimental results for two injection temperatures (p0 = 1.5 Gpa; Ve = 10 m/s).
4. Discussion
The tests showed that for all operating conditions, the friction corresponding to the longitudinal/longitudinal pair is much greater than that of the transverse/transverse pair, even though values of these two pairs are close.
For rough pairs, friction is higher for higher injection oil temperature, lower mean rolling speed, and higher Hertzian pressure. Also, the variation in friction due to changing the operating conditions for longitudinal roughness is more significant than that for transverse, as indicated in Table 10, Table 11 and Table 12. For all tested conditions, the friction generated by the longitudinal/longitudinal pair is not identical to that of the smooth/smooth pair. Table 12 summarises the results obtained for an SRR of 10%. In this table, the disc bulk temperatures measured during the test are used to determine oil properties, which are then applied in central oil film thickness equation.

Table 12.
Summarised results of the tested configuration (friction coefficient for SRR = 10% for the three pairs, calculated central oil film thickness of the smooth/smooth pair).
These experimental results suggest that the roughness behaviour within the contact varies with roughness orientation, indicating that the oil film thickness that separates the surfaces is influenced by the direction of the surface roughness. These findings indicate that surfaces exhibiting longitudinal roughness tend to form thinner lubricant films compared to those with transverse roughness. These findings support the conclusions drawn by Venner and Lubrecht [18], who demonstrated numerically that the oil film thickness in a smooth/longitudinal contact reaches a minimum value lower than that in a smooth/transverse contact. The same conclusion is presented by Zhu and Wang [19] for a Hertzian contact ellipticity strictly greater than 2, which is the case in our study.
5. Conclusions
This study highlights the impact of roughness orientation on the friction coefficient in EHL contacts. Experiments were conducted on a twin-disc machine under different operating conditions (oil injection temperature from 60 to 80 °C, Hertzian pressure from 1.2 to 1.5 GPa and mean rolling speed from 5 to 30 m/s). For all the tested operating conditions, this study leads to the following conclusions:
- It has been shown that longitudinal roughness results in higher friction than transverse roughness.
- Variations in operating conditions have a greater influence on the friction associated to the longitudinal roughness compared to the transverse one.
- The friction generated by the longitudinal pair, unlike the transverse pair, is consistently different from that of the smooth pair.
- The lubricant film thickness between surfaces with longitudinal roughness seems to be lower than that between surfaces with transverse roughness.
- Without considering the limitation related to the manufacturing processes, the choice of a transverse roughness (Sq ≈ 0.5 µm) for the gear teeth is convenient.
- As for REBs, the influence of roughness is not considered in most cases due to their low roughness amplitude (Sq ≈ 0.2 µm). However, in certain critical situations, such as under marginal/starved lubrication conditions (limited oil supply), transverse roughness may be more beneficial than longitudinal roughness.
For future work, it would be interesting to conduct experiments on an EHL test rig in order to further analyse the oil film thickness. In addition, the development of a numerical friction law, considering the two roughness orientations, would improve the understanding and prediction of the tribological behaviour of lubricated contacts.
Author Contributions
Writing—original draft, M.C.; Writing—review and editing, Y.D., J.C., F.M., C.C. and F.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by ANRT, grant number [CIFRE n°2022/1074].
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Pa | Young modulus | |
| Pa | Reduced elastic modulus | |
| - | Complete elliptic integral of the second kind | |
| N | Normal load | |
| m | Central oil film thickness | |
| k | - | Ellipticity ratio |
| m | Width of the disc | |
| p0 | Pa | Maximum Hertz pressure |
| m | Curvature sum | |
| m | Quadratic roughness of surface i | |
| m | Quadratic roughness in the direction of rolling/sliding | |
| m | Quadratic roughness transverse to the rolling/sliding direction | |
| m | Radius in the rolling/sliding direction | |
| m | Radius transverse to the rolling/sliding direction (crown radius) | |
| m | Equivalent surface roughness | |
| Sq | m | Root mean square surface roughness |
| Tinj | °C | Oil injection temperature |
| Ve | m/s | Mean rolling speed |
| Pressure-viscosity (piezoviscosity) coefficient | ||
| - | Complete elliptic integral of the first kind | |
| - | Curvature difference | |
| - | Reduced film thickness | |
| - | Friction coefficient | |
| - | Poisson’s ratio | |
| Oil density |
Appendix A
For elliptical contact, the Hertzian pressure and the contact semi-axes are calculated based on [38,41].
with:
Appendix B

Table A1.
Quadratic roughness of the discs.
Table A1.
Quadratic roughness of the discs.
| Pair | [µm] | [µm] | |
|---|---|---|---|
| Smooth | Disc 1 | 0.075 | 0.020 |
| Disc 2 | 0.050 | 0.018 | |
| Transverse | Disc 1 | 0.029 | 0.374 |
| Disc 2 | 0.048 | 0.433 | |
| Longitudinal | Disc 1 | 0.380 | 0.037 |
| Disc 2 | 0.489 | 0.039 | |
References
- Holmberg, K.; Erdemir, A. The impact of tribology on energy use and CO2 emission globally and in combustion engine and electric cars. Tribol. Int. 2019, 135, 389–396. [Google Scholar] [CrossRef]
- ISO/TR 14179-2; Gears—Thermal Capacity. Part 2: Thermal Load-Carrying Capacity. International Organization for Standardization: Geneva, Switzerland, 2001.
- Zhu, M.; Lu, X.; Li, H.; Cao, H.; Wu, F. Applicability analysis of nickel steel plate friction coefficient model based on fractal theory. Coatings 2023, 13, 1096. [Google Scholar] [CrossRef]
- Walton, D.; Cropper, A.B.; Weale, D.J.; Klein Meuleman, P. The efficiency and friction of plastic cylindrical gears. Part 2: Influence of tooth geometry. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2002, 216, 93–104. [Google Scholar] [CrossRef]
- Liu, P.; Rui, Y.; Wang, Y. Study of the sliding friction coefficient of different-size elements in discrete element method based on an experimental method. Appl. Sci. 2024, 14, 8802. [Google Scholar] [CrossRef]
- Bisson, E.E. Friction, Wear, and the Influence of Surfaces; American Society of Tool and Manufacturing Engineers: Dearborn, MI, USA, 1968. [Google Scholar]
- Hu, Q.; Pei, Q.; Li, P. Reducing the friction coefficient of heavy-load spherical bearings in bridges using surface texturing—A numerical study. Lubricants 2025, 13, 180. [Google Scholar] [CrossRef]
- Trzepieciński, T.; Szwajka, K.; Szewczyk, M. Analysis of coefficient of friction of deep-drawing-quality steel sheets using multi-layer neural networks. Lubricants 2024, 12, 50. [Google Scholar] [CrossRef]
- Duran, B.; Cavoret, J.; Philippon, D.; Ville, F.; Ruellan, A.; Berens, F. Influence of a transmission oil degradation on physico-chemical properties and tribological performance. Tribol. Int. 2024, 191, 109084. [Google Scholar] [CrossRef]
- Grenet De Bechillon, N.; Touret, T.; Cavoret, J.; Changenet, C.; Ville, F.; Ghribi, D. A new experimental methodology to assess gear scuffing initiation. Surf. Interfaces 2022, 16, 245–255. [Google Scholar] [CrossRef]
- Perka, P.; Kupka, I.; Hartl, M. Experimental study of real roughness attenuation in concentrated contacts. Tribol. Int. 2010, 43, 1893–1901. [Google Scholar] [CrossRef]
- Thomas, T.R. Rough Surfaces, 2nd ed.; Imperial College Press: London, UK, 1998. [Google Scholar]
- Hamrock, B.J.; Jeng, Y.R. The effect of surface roughness on elastohydrodynamically lubricated point contact. ASLE Trans. 1986, 30, 531–538. [Google Scholar] [CrossRef]
- Makino, T.; Morohoshi, S.; Saki, K. The effect of roughness orientation on mixed friction. Tribol. Ser. 1999, 36, 355–365. [Google Scholar] [CrossRef]
- Kaneta, M.; Sakai, T.; Nishikawa, H. Effects of surface roughness on point contact EHL. Tribol. Trans. 1993, 36, 605–612. [Google Scholar] [CrossRef]
- Šperka, P.; Křupka, I.; Hartl, M. Experimental study of roughness effect in a rolling–sliding EHL contact. Part I: Roughness deformation. Tribol. Trans. 2016, 59, 267–276. [Google Scholar] [CrossRef]
- Hook, C.J. Surface roughness modification in EHL line contacts—The effect of roughness wavelength, orientation and operating conditions. Tribol. Ser. 1999, 36, 193–202. [Google Scholar] [CrossRef]
- Venner, C.H.; Lubrecht, A.A. Numerical analysis of the influence of waviness on the film thickness of a circular EHL contact. J. Tribol. 1996, 118, 153–161. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, Q.J. Effect of roughness orientation on the elastohydrodynamic lubrication film thickness. J. Tribol. 2013, 135, 031501. [Google Scholar] [CrossRef]
- Baumann, A.; Bertsche, B. Coefficient of friction behavior of gear oils and significance for the meshing process of spur gears: Lubrication for improved properties. Forsch. Ingenieurwes. 2022, 86, 795–805. [Google Scholar] [CrossRef]
- Morgado, P.; Otero, J.; Lejarraga, J.; Sanz, J.; Lantada, A.; Muñoz-Guijosa, J.; Yustos, H.; Wiña, P.; García, J. Models for predicting friction coefficient and parameters with influence in elastohydrodynamic lubrication. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2009, 223, 949–958. [Google Scholar] [CrossRef]
- Rovira, A.; Roda, A.; Lewis, R.; Marshall, M.B. Application of Fastsim with variable coefficient of friction using twin disc experimental measurements. Wear 2012, 274–275, 109–126. [Google Scholar] [CrossRef]
- Bergseth, E.; Zhu, Y.; Söderberg, A. Study of surface roughness on friction in rolling/sliding contacts: Ball-on-disc versus twin-disc. Tribol. Lett. 2020, 68, 69. [Google Scholar] [CrossRef]
- Isaac, G.; Changenet, C.; Ville, F.; Cavoret, J.; Becquerelle, S. Thermal analysis of twin-disc machine for traction tests and scuffing experiments. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2018, 232, 1548–1560. [Google Scholar] [CrossRef]
- Ville, F.; Nélias, D.; Tourlonias, G.; Flamand, L.; Sainsot, P. On the two-disc machine: A polyvalent and powerful tool to study fundamental and industrial problems related to elastohydrodynamic lubrication. Tribol. Ser. 2001, 39, 393–402. [Google Scholar] [CrossRef]
- Gupta, P.K.; Flamand, L.; Berthe, D.; Godet, M. On the traction behavior of several lubricants. J. Lubr. Technol. 1981, 103, 55–64. [Google Scholar] [CrossRef]
- Hansen, J.; Björling, M.; Larsson, R. Topography transformations due to running-in of rolling-sliding non-conformal contacts. Tribol. Int. 2020, 144, 106126. [Google Scholar] [CrossRef]
- Kohutiar, M.; Krbaťa, M.; Escherová, J.; Eckert, M.; Mikuš, P.; Jus, M.; Polášek, M.; Janík, R.; Dubec, A. The influence of the geometry of movement during the friction process on the change in the tribological properties of 30CrNiMo8 steel in contact with a G40 steel ball. Materials 2024, 17, 127. [Google Scholar] [CrossRef] [PubMed]
- Stelmakh, O.; Fu, H.; Kolienov, S.; Kanevskii, V.; Zhang, H.; Hu, C.; Grygoruk, V. Criteria for evaluating the tribological effectiveness of 3D roughness on friction surfaces. Lubricants 2024, 12, 209. [Google Scholar] [CrossRef]
- Krbaťa, M.; Majerík, J.; Barényi, I.; Mikušová, I.; Kusmič, D. Mechanical and tribological features of the 90MnCrV8 steel after plasma nitriding. Manuf. Technol. 2019, 19, 238–242. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Fan, H.; Pan, D. Erosion–corrosion resistance properties of 316L austenitic stainless steels after low-temperature liquid nitriding. Appl. Surf. Sci. 2018, 440, 755–762. [Google Scholar] [CrossRef]
- Johnson, K.; Tevaawerk, J.L. Shear behaviour of elastohydrodynamic oil films. Proc. R. Soc. Lond. A Math. Phys. Sci. 1977, 356, 215–236. [Google Scholar] [CrossRef]
- Stribeck, R. Die wesentlichen Eigenschaften der Gleit- und Rollenlager. Z. Vereines Dtsch. Ingenieure 1902, 46, 1341–1348. [Google Scholar]
- Cocks, M.; Tallian, T.E. Sliding contacts in rolling bearings. ASLE Trans. 1971, 14, 32–40. [Google Scholar] [CrossRef]
- Tallian, T. The theory of partial elastohydrodynamic contacts. Wear 1972, 21, 49–101. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, Q.J. On the λ ratio range of mixed lubrication. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2012, 226, 1010–1022. [Google Scholar] [CrossRef]
- Hansen, J.; Björling, M.; Larsson, R. A new film parameter for rough surface EHL contacts with anisotropic and isotropic structures. Tribol. Lett. 2021, 69, 37. [Google Scholar] [CrossRef]
- Brewe, D.E.; Hamrock, B.J. Simplified solution for elliptical-contact deformation between two elastic solids. J. Lubr. Technol. 1977, 99, 485–490. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Dowson, D. Isothermal elastohydrodynamic lubrication of point contacts. Part IV—Starvation results. J. Lubr. Technol. 1977, 99, 15–23. [Google Scholar] [CrossRef]
- Jeng, Y.R. Experimental study of the effects of surface roughness on friction. Tribol. Trans. 1990, 33, 402–409. [Google Scholar] [CrossRef]
- Hertz, H. Über die Berührung fester elastischer Körper. J. Reine Angew. Math. 1881, 92, 156–171. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).