A Multi-Parameter-Driven SC-ANFIS Framework for Predictive Modeling of Acid Number Variations in Lubricating Oils

Abstract

The acid number is widely recognized as one of the most essential and frequently used indicators for evaluating the degradation state of lubricants. Changes in acid number serve as a direct reflection of the oil’s oxidative deterioration. Conventional prediction methods, however, often neglect the coupling effects among multiple physical factors and lack sufficient dynamic adaptability. Therefore, this study proposes a method for predicting the variation trend of lubricating oil acid number by integrating an Adaptive Neuro-Fuzzy Inference System (ANFIS) with Subtractive Clustering (SC), establishing an SC-ANFIS-based predictive model. The subtractive clustering technique automatically determines the number of fuzzy rules and initial parameters directly from the dataset, thereby eliminating redundant rules and simplifying the model architecture. The SC-ANFIS model further optimizes the parameters of the fuzzy inference system through the self-learning ability of neural networks. Lubricant aging tests were conducted using a laboratory oxidation stability tester. Regular sampling was carried out to acquire comprehensive lubricant performance degradation data. The input variables of the model include the current acid number, carbonyl peak intensity, metal element concentrations (Fe and Cu), viscosity, and water content of the lubricating oil, while the output variable corresponds to the rate of change in the acid number of the lubricating oil relative to the previous time step. The proposed model demonstrates effective prediction of the lubricating oil acid number variation trend. Posterior difference tests confirmed its high predictive accuracy, with all three evaluation metrics—RMSE, MAE, and MAPE—outperforming those of the BP model.

1. Introduction

Lubricating oil plays an indispensable role in ensuring the stable operation of mechanical systems. It effectively reduces the friction coefficient between moving components, suppresses abnormal temperature rise, and adsorbs and removes contaminants and wear debris from surfaces, thereby extending service life [1]. With the rapid advancement of technology, continuous innovation in oil condition monitoring has led to the widespread application of related technical solutions across various industrial scenarios, making it a key support for equipment reliability [2]. Currently, the common practice of periodic oil changes often leads to resource waste if conducted prematurely. Moreover, the degradation pattern of lubricating oil not only varies among different machines but also changes over time due to aging even in the same machine [3,4]. Therefore, developing a scientific and rational methodology for lubricant life assessment is of significant importance for extending equipment lifespan, reducing maintenance costs, ensuring industrial safety, and promoting resource recycling and environmental protection.

In recent years, the rapid development of artificial intelligence has attracted increasing scholarly interest in intelligent algorithms. Du et al. [5] proposed a Hidden Markov Model (HMM)-based approach for parameter estimation and remaining useful life (RUL) prediction of lubricating oil, successfully forecasting the RUL from a “like-new” state to failure by studying the degradation process under healthy machine conditions. Sun et al. [6] introduced a grey theory and GM model-based combined forecasting method to predict lubricant life, addressing the issues of limited data and low accuracy in single oil-change cycles. Yue et al. [7] integrated domain shift and uncertainty (DSU) with long short-term memory (LSTM) networks, proposing a DSU-LSTM model to tackle challenges arising from insufficient oil samples.

Although the aforementioned studies contributed to predicting lubricant performance, they exhibit certain limitations. The aforementioned methods demonstrate limited robustness when dealing with multi-factor coupling interference. Lubricant performance degradation is influenced by the synergistic effects of multiple operational factors, including mechanical load, temperature, and contaminant concentration. However, the Hidden Markov Model (HMM) primarily addresses state transitions, while grey theory combined with GM modeling relies mainly on data trends. Although the DSU-LSTM method incorporates cross-scenario adaptation, it lacks explicit modeling of the interactions among multiple factors. Consequently, when both operational parameters (e.g., a sudden high load) and oil condition parameters (e.g., a rapid impurity surge) change simultaneously, all three methods are susceptible to significant prediction deviations.

In contrast, the proposed SC-ANFIS approach exhibits superior capability in handling such multi-factor coupling effects. Unlike existing methods that focus narrowly on either oil data analysis or scenario transfer, SC-ANFIS explicitly captures the coupled relationships among operational conditions, oil characteristics, and degradation processes. This enables the model to maintain robust prediction stability even under concurrent variations of multiple influencing factors.

In practice, hybrid approaches that combine multiple forecasting methods often yield more satisfactory results. Thus, this paper proposes an SC-ANFIS model. The Adaptive Neuro-Fuzzy Inference System (ANFIS) is a hybrid model integrating fuzzy logic and neural networks, which optimizes fuzzy system parameters through neural network learning, making it particularly suitable for nonlinear and uncertain problems [8,9]. Subtractive Clustering (SC) is an unsupervised clustering algorithm that automatically extracts the number of fuzzy rules and initial parameters from data. It effectively handles high-dimensional data, reduces subjectivity in rule selection, minimizes redundant rules, and simplifies model structure [10,11,12]. The SC-ANFIS model combines subtractive clustering with ANFIS, enhancing the efficiency and accuracy of fuzzy rule generation. It has been widely applied in complex nonlinear system modeling, prediction, and fault diagnosis.

The acid number has been recognized as one of the most common indicators for assessing lubricant degradation [13]. It is defined as the amount of potassium hydroxide (in milligrams) required to neutralize the acidic compounds in one gram of oil, expressed in mg KOH/g [14]. Once the acid number reaches a certain threshold, the lubricating oil must be replaced. Accurate determination of the acid number is crucial for fundamental tribological research and lubrication engineering [15,16]. In this study, lubricant aging tests were simulated using a laboratory oxidation stability tester. Samples were collected every six hours to obtain extensive performance degradation data. The model inputs include the current acid number, carbonyl peak intensity, metal element concentrations (Fe, Cu), viscosity, and water content. The output is the rate of change of the acid number relative to the previous time point, which is used to evaluate the remaining useful life of the lubricating oil. The model’s performance was evaluated from multiple perspectives using metrics such as root mean square error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE) to quantify the deviation between predicted and actual values, thereby demonstrating the superiority and effectiveness of the SC-ANFIS model in predicting lubricant life.

2. Adaptive Neuro-Fuzzy Inference System

ANFIS is a five-layer fuzzy inference system based on the Takagi–Sugeno (T–S) model. Through self-learning from extensive datasets, it achieves high-precision approximation of nonlinear functions and autonomously derives the system’s membership functions and fuzzy rules [17,18]. A typical ANFIS structure operates under rules such as the following:

• If x is $A_1$ and y is $B_1$ then $f_1$ = $a_1$x + $b_1$y + $c_1$
• If x is $A_2$ and y is $B_2$ then $f_2$ = $a_2$x + $b_2$y + $c_2$

The overall architecture of the system is illustrated in Figure 1.

In Figure 1, fixed nodes are represented by circles, while adaptive nodes are denoted by squares. The ANFIS architecture comprises a five-layer fuzzy inference system. The functional roles of each layer are outlined as follows.

Layer 1: Input Layer. Receives the original input variables and passes them to the next layer, preparing for fuzzification. Each neuron in this layer corresponds to an input variable. Each node i is a square node represented by a node function.

$$O_i^1={\mu }_{A_i}\left(x_1\right) i=1,2$$

(1)

$$O_j^1={\mu }_{B_j}\left(x_2\right) j=1,2$$

(2)

where $O_i^1$, $O_j^1$—Output of the i-th and j-th nodes in layer 1; $x_1$ or $x_2$—Input to node i or j; $A_i$, $B_j$—Linguistic labels associated with the node functions; ${\mu }_{A_i}$, ${\mu }_{B_j}$—Corresponding node functions (membership functions).

Layer 2: Fuzzification Layer. Performs fuzzification on the input variables, converting precise input values into membership degrees of fuzzy sets. Each neuron corresponds to the antecedent part of a fuzzy rule, i.e., a fuzzy subset of an input variable. The nodes in this layer multiply the input signals. The output formula is:

$$O_i^2={\omega }_i={\mu }_{A_i}(x_1)\times {\mu }_{B_j}\left(x_2\right) i=1,2$$

(3)

where $O_i^2$, ${\omega }_i$—Output of the i-th node in layer 2 (Firing strength of rule i).

Layer 3: Rule Layer. Implements fuzzy rule matching and triggering, calculating the firing strength of each rule. Each neuron represents a fuzzy rule. Its input is the membership degree from the corresponding fuzzy subset in layer 2, and its output is the firing strength of that rule. The i-th node calculates the ratio of the firing strength of the i-th rule (wᵢ) to the sum of all rules’ w values:

$$O_i^3= {\overline{\omega }}_i= {\displaystyle \frac{{\omega }_i}{{\omega }_1+{\omega }_2}} i=1,2$$

(4)

where $O_i^3$—Output of the i-th node in layer 3; ω₁, ω₂—Outputs from the first and second nodes calculating the first and second rule outputs, respectively; ${\overline{\omega }}_i$—Normalized firing strength.

Layer 4: Normalization Layer. Normalizes the firing strengths of each rule to obtain relative firing strengths. Each neuron’s output is the ratio of that rule’s firing strength to the sum of all rules’ firing strengths. Node i in this layer is an adaptive node, and the output is:

$$O_i^4= {\overline{\omega }}_i{f}_i= {\overline{\omega }}_i(p_i{x}_1+ q_i{x}_2+r_i) i=1,2$$

(5)

where $O_i^4$—Output of the i-th node in layer 4; p_i, q_i, r_i—Consequent parameters (the number of parameters depends on the number of inputs).

Layer 5: Output Layer. Integrates the outputs of all rules and obtains the final output result through weighted summation. Each neuron corresponds to an output variable of the model. Its input is the normalized firing strength from layer 4 and the linear combination of the consequent part of that rule. This layer’s node calculates the total output of all input signals:

$$O_i^5= {\displaystyle \sum {\overline{\omega }}_i}{f}_i={\displaystyle \frac{{\displaystyle \sum _i{\omega }_i{f}_i}}{{\displaystyle \sum _i{\omega }_i}}} i=1,2$$

(6)

where $O_i^5$—Output of the i-th node in layer 5 (Overall system output).

From the structure above, it can be seen that ANFIS implements the complete process of “input fuzzification → rule matching → strength normalization → weighted output” through its 5-layer structure. This structure combines the parameter optimization capability of neural networks with the uncertainty handling ability of fuzzy logic and is widely used in prediction, control, fault diagnosis, and other fields.

3. Subtractive Clustering Algorithm

Subtractive clustering is a density-based unsupervised clustering algorithm. It determines cluster centers by measuring the “density” of data points. The core idea of subtractive clustering is to gradually screen out cluster centers from the dataset through a “subtractive” process [19,20]. Assume there are n data points ($x_1$, $x_2$, …, $x_n$) in an N-dimensional space. The density at point $x_i$, considered as a potential cluster center, is:

$$D_i={\displaystyle \sum _{j=1}^n\exp }\left(-{\displaystyle \frac{{‖x_i-x_j‖}^2}{{\left(r_a/2\right)}^2}}\right)$$

(7)

where $r_a$ is the influence radius, controlling the sparsity of cluster centers. It determines the range within which a data point contributes to the density. A smaller $r_a$ results in more cluster centers. When the distance exceeds $r_a$, the density contribution can be neglected. Using the density correction formula below (8), the possibility of points surrounding the chosen center becoming the next cluster center is excluded

$$D_i=D_i-D_{c_k}{\displaystyle \sum _{j=1}^{n}e}xp\left(-{\displaystyle \frac{{‖x_i-x_{c_k}‖}^2}{{\left(r_b{/}_2\right)}^2}}\right)$$

(8)

where $r_b$ is the squash radius, suppressing points around already selected centers from becoming new centers. Usually, $r_b$ = 1.5 $r_a$. Repeat the density correction steps, selecting the point with the maximum density from the updated densities as the next cluster center, until the maximum density of the remaining data points falls below a termination threshold. These clusters are used as the nonlinear parameters for the fuzzy rules in the T-S fuzzy model. Through continuous learning and training of parameters, the trained rules become more accurate.

4. Lubricating Oil Acid Number Prediction Experiment and Simulation

4.1. Experimental Data

The experimental data in this study were obtained from laboratory-simulated lubricant aging tests. Samples were collected at 6 h intervals to acquire full-cycle degradation data of the lubricating oil. The aging process was designed to comprehensively incorporate the effects of soot, water, and metal particles, reflecting realistic application scenarios. A total of 720 sets of sample data were gathered throughout the experiment.

Soot, generated through incomplete combustion of diesel fuel under high-temperature and oxygen-deficient conditions, presents as black flocculent or particulate matter. It consists primarily of carbon and adsorbs trace amounts of other combustion-derived impurities, with particle sizes typically ranging from 10 to 100 nm [21,22]. Water represents the second most critical contaminant following soot. Although not an intrinsic component of lubricating oil, it infiltrates the system through various pathways [23,24]. Via mechanisms such as physical dilution, chemical catalysis, and metal corrosion, water accelerates lubricant degradation and may ultimately lead to engine failure [25,26,27]. Metal particles serve as typical catalysts in the “wear–contamination–aging” cycle. Not only are they direct byproducts of wear in moving engine components, but they also promote further degradation through abrasive action and chemical catalysis, establishing a self-perpetuating cycle: increased particles → accelerated lubricant aging → enhanced wear [28,29].

Due to the practical challenges associated with obtaining authentic combustion soot under well-controlled laboratory conditions, this study employed Mitsubishi MAF-100 (Tokyo, Japan) high-pigment carbon black powder as a representative surrogate. This material was selected on the basis of its well-defined primary particle size of approximately 24 nm—a characteristic that closely aligns with the morphological features typically observed in real diesel soot. A visual representation of the physical powder is provided in Figure 2 below. To accurately replicate the influence of metallic contaminants present in real engine environments, finely powdered iron (Fe) and copper (Cu) were introduced into the experimental system. These powders, with carefully controlled particle sizes ranging from 10 to 30 μm, were selected to simulate the typical morphological and dimensional characteristics of wear debris commonly generated by mechanical components under operational conditions. Furthermore, laboratory-grade high-purity water was employed throughout the contamination protocol to systematically eliminate potential interference originating from dissolved ions or organic impurities. This rigorous approach ensured that any observed degradation effects could be unequivocally and exclusively attributed to the presence of water itself, thereby enhancing the reliability and interpretability of the experimental outcomes.

The aging tests were conducted using an oxidation stability tester. Initial performance indicators of the M3S840 lubricating (Shell, Shanghai, China) oil were first measured. Then, 500 mL of oil was aliquoted into three sample tubes, labeled ①, ②, and ③. The entire experiment was conducted at a constant temperature of 150 °C with an oxygen flow rate of 150 mL·min⁻¹·L⁻¹. Soot, water, and an iron–copper mixture were added to each tube, respectively. After a specified interval, additional pollutant simulation factors were introduced into each tube. Detailed descriptions of the experimental conditions are provided in

Table 1. Simulated Pollutant Factors Added to Test Tube Experiments.

NO.	6 h	12 h	18 h	24 h	……
①	Soot	Soot + Water	Soot + Water + Fe, Cu particles	Soot + Water + Fe, Cu particles	Soot + Water + Fe, Cu particles
②	Water	Water + Fe, Cu particles	Soot + Water + Fe, Cu particles	Soot + Water + Fe, Cu particles	Soot + Water + Fe, Cu particles
③	Fe, Cu particles	Fe, Cu particles + Soot	Soot + Water + Fe, Cu particles	Soot + Water + Fe, Cu particles	Soot + Water + Fe, Cu particles

.

4.2. Acid Number Prediction Model Establishment

The output variable of the model is the rate of change of the acid number relative to the previous time point. Accordingly, input variables were selected based on their strong correlation with the acid number. Drawing on relevant literature, the input layer of the model was constructed using the following parameters: the current acid number, carbonyl peak intensity, concentrations of Fe and Cu, viscosity, and water content of the lubricating oil. The SC-ANFIS model, which integrates subtractive clustering into the Adaptive Neuro-Fuzzy Inference System (ANFIS), was implemented via the Fuzzy Logic Toolbox in MATLAB.

The dataset, comprising 720 samples, was partitioned into a training set (504 samples, 70%) and a prediction set (216 samples, 30%). The training data were loaded into the ANFIS toolbox under the “Load data” option by selecting “Training” as the data type and importing from the workspace (“worksp”). This process is illustrated in Figure 3 below.

Under the “Generate FIS” option, “Sub.clustering” was selected to conduct fuzzy clustering analysis on the dataset, which automatically determines the number of fuzzy rules required for the prediction model. The radius parameter for the subtractive clustering algorithm was set to 0.50. The maximum number of iterations for the ANFIS training process was configured as 200, with an error goal of 0.0001—specifically referring to the acceptable deviation in predicting the rate of change of the acid number relative to the preceding time point.

The antecedent and consequent parameters of the ANFIS model were optimized using the backpropagation (BP) algorithm and the linear least squares estimation method, respectively. The training process continued iteratively until either the predefined error threshold was achieved or the maximum iteration count was reached. The fully trained model was subsequently employed to predict the acid number change rate. Corresponding error values were computed, and the simulation results were graphically visualized.

4.3. Performance Evaluation

The accuracy of the acid number change rate prediction model is essential for achieving reliable acid number forecasting. To quantitatively evaluate the prediction performance, three widely recognized metrics were adopted: Root Mean Square Error (RMSE), Mean Absolute Error (MAE), and Mean Absolute Percentage Error (MAPE). These metrics provide a comprehensive assessment of the model’s predictive validity. Lower values of RMSE, MAE, and MAPE correspond to higher prediction accuracy, indicating better overall model performance [30,31].

5. Results and Analysis

The primary data for this investigation were obtained from laboratory-simulated lubricant aging tests. Representative acid number change rate data from these tests are provided in

Table 2. Selected Results of the Acid Number Change Rate.

Duration	Simulated Pollutant Factors	Acid Number Change Rate
6 h	Soot	0.018
	Water	0.009
	Fe, Cu particles	0.013
12 h	Soot + Water	0.022
	Water + Fe, Cu particles	0.028
	Fe, Cu particles + Soot	0.035
……
120 h	Soot + Water + Fe, Cu particles	0.809
	Soot + Water + Fe, Cu particles	0.812
	Soot + Water + Fe, Cu particles	0.813

.

As evidenced by the data in the preceding table, soot constitutes the most influential contamination factor on the lubricant’s acid value, followed by iron-copper wear particles, with water demonstrating the least effect. At the subsequent monitoring interval, the synergistic interaction between soot and iron-copper wear particles produces the most substantial acid value alteration, exceeding the combined effects of water with wear particles. The soot-water combination manifests the minimal synergistic impact. Furthermore, the acid value change rate asymptotically approaches stability with prolonged duration.

This study was conducted using MATLAB 2021a. Under identical simulation conditions and using the same dataset, predictions were also generated using a conventional backpropagation (BP) neural network for comparative purposes. To enhance the validity of the simulation experiment, ten sets of data were randomly selected for testing, enabling a direct comparison of performance metrics between the SC-ANFIS model and the traditional BP neural network. The actual values of the acid number change rate relative to the previous time point, along with the predicted values from both the SC-ANFIS model and the BP neural network, are presented in

Table 3. True Values and Model Prediction Results of Acid Number Change Rate for 10 Randomly Selected Data Sets.

NO.	1	2	3	4	5	6	7	8	9	10
True Value	0.022	0.038	0.085	0.252	0.581	0.825	0.790	0.832	0.773	0.812
SC-ANFIS Predicted Value	0.027	0.044	0.092	0.273	0.594	0.858	0.824	0.865	0.817	0.878
BP Network Predicted Value	0.033	0.051	0.101	0.294	0.610	0.872	0.852	0.891	0.853	0.925

below.

Based on the ten randomly selected datasets, the RMSE, MAE, and MAPE values for both models were computed using relevant functions in MATLAB. Comparative charts of these evaluation metrics are presented in Figure 4, Figure 5 and Figure 6.

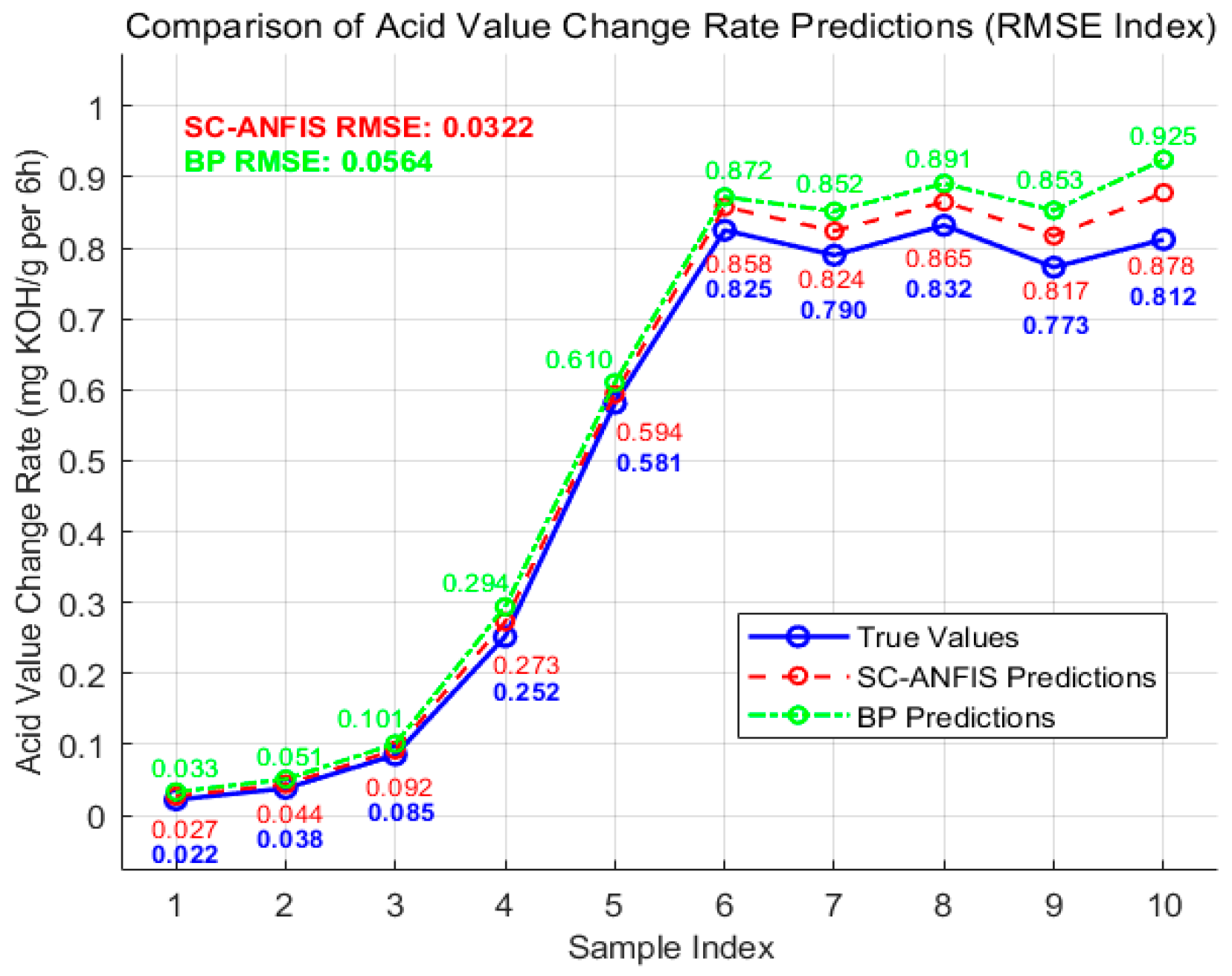
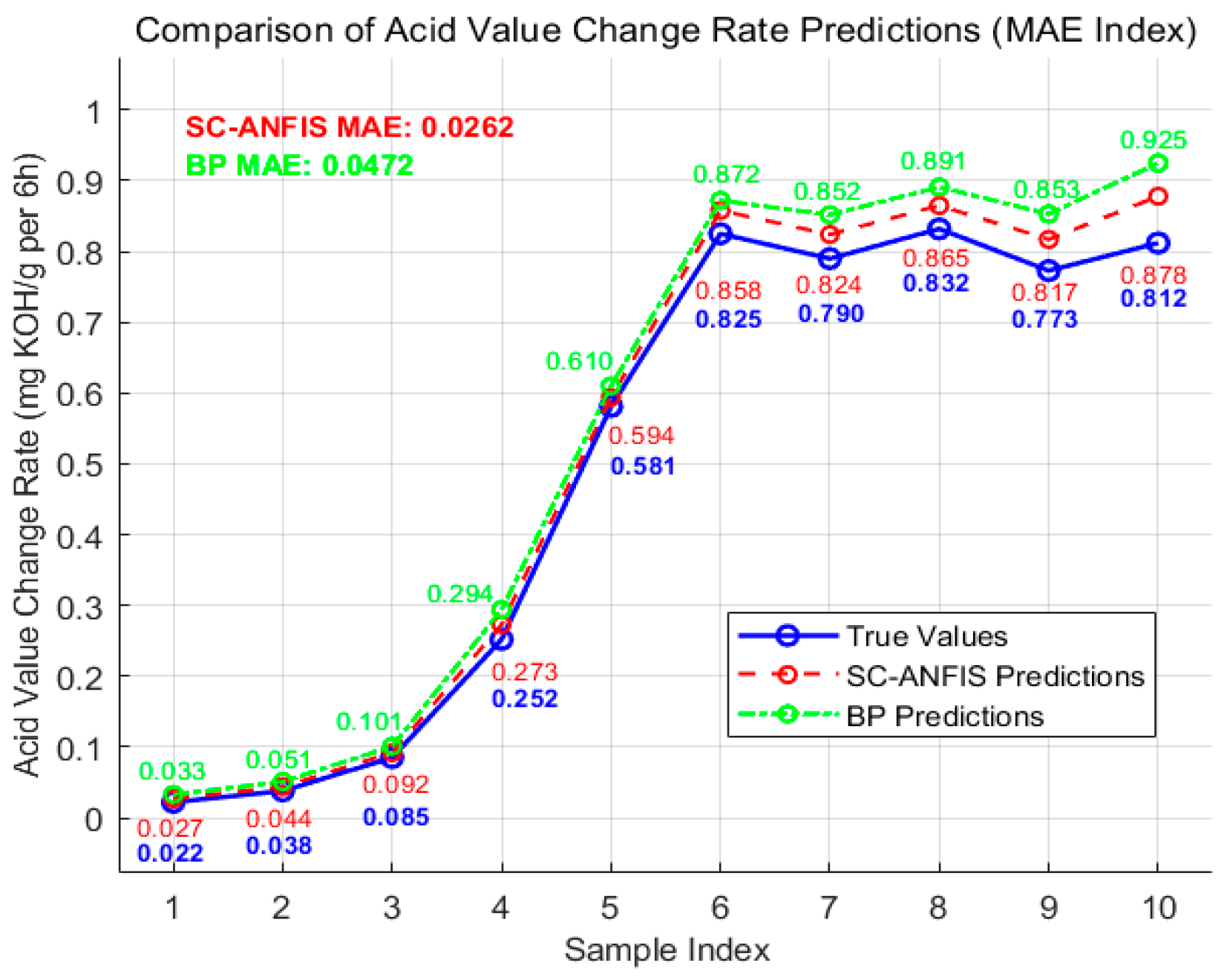
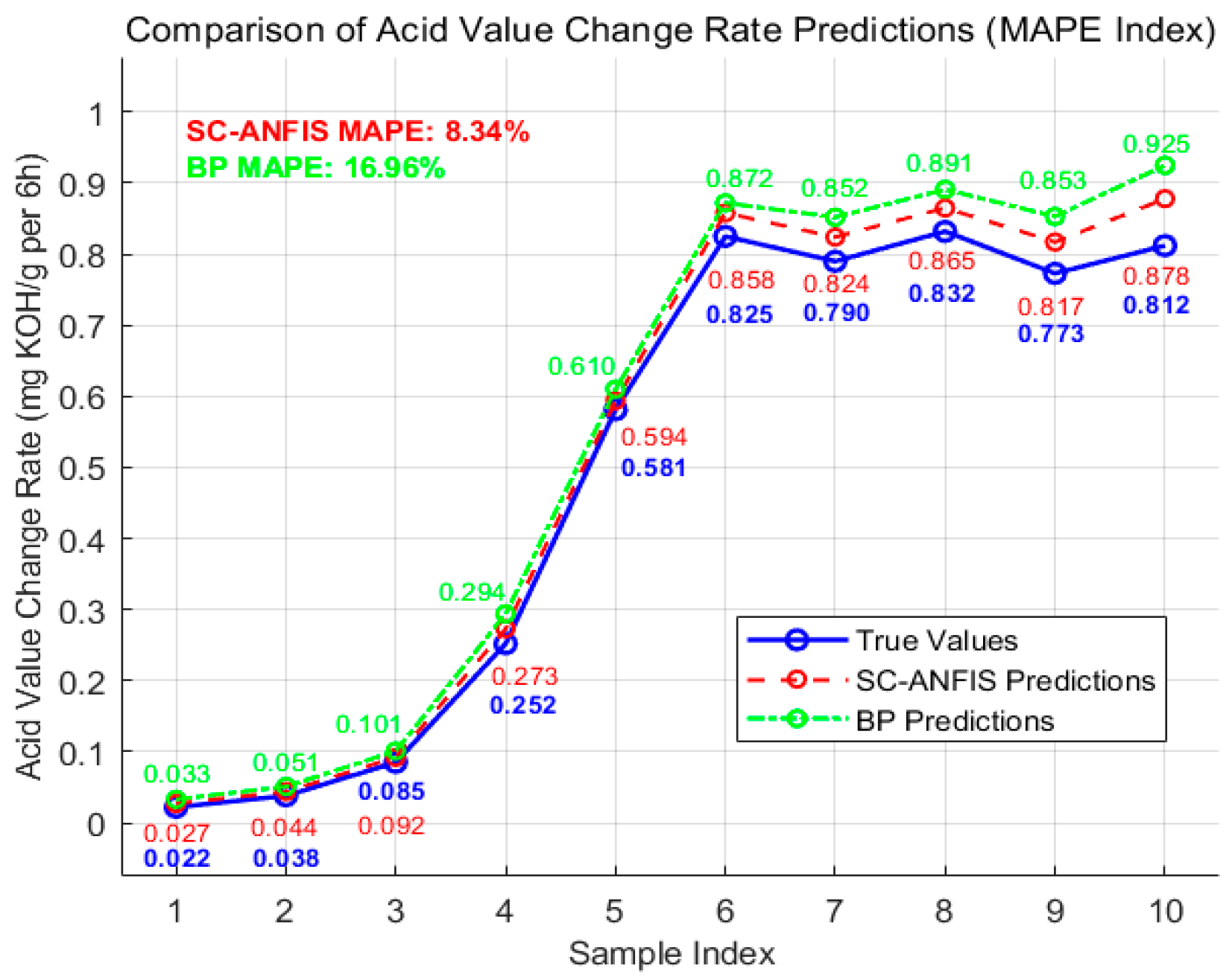
These three figures present comparative predictions of the acid number change rate, employing distinct evaluation metrics—RMSE, MAE, and MAPE—to assess the predictive performance of the SC-ANFIS and BP neural network models. In the graphs, the red dashed line represents predictions from the SC-ANFIS model, the green dashed line represents predictions from the BP model.

From a graphical perspective, the red dashed curve, which represents the predictions from the SC-ANFIS model, closely aligns with the blue solid curve indicating the true values across the entire sample index range. In contrast, the green dashed curve, corresponding to the BP neural network predictions, exhibits more pronounced deviations from the actual values. This discrepancy becomes especially evident beyond sample index 6, where the prediction error of the BP model increases substantially compared to that of the SC-ANFIS model.

To further quantitatively validate the superior predictive accuracy of the SC-ANFIS model over the conventional BP model, we systematically compiled and analyzed the prediction results of both approaches. The corresponding analytical results are summarized in

Table 4. Comparison of Prediction Results between SC-ANFIS and BP Models.

Model	RMSE	MAE	MAPE
SC-ANFIS Model	0.0322	0.0262	0.0834
BP Neural Network	0.0564	0.0472	0.1696

.

As shown in Table 3, the RMSE values obtained from the simulation tests are BP (0.0564) > SC-ANFIS (0.0322). RMSE, representing the square root of the average squared errors, emphasizes the effect of large prediction errors. The lower RMSE of the SC-ANFIS model indicates fewer instances of significant prediction deviations and enhanced stability in forecasting.

The MAE values from the simulation are BP (0.0472) > SC-ANFIS (0.0262). MAE measures the average absolute error between predicted and true values, with smaller values indicating higher accuracy. The reduced MAE of SC-ANFIS confirms its superior performance in minimizing average prediction error.

Similarly, the MAPE values are BP (0.1696) > SC-ANFIS (0.0834). MAPE expresses prediction error as a percentage, providing an intuitive measure of relative deviation. The lower MAPE value of the SC-ANFIS model suggests smaller relative errors and higher predictive accuracy compared to the BP model.

In summary, the SC-ANFIS model outperforms the BP model in predicting the acid number change rate, both in terms of adherence to the actual data trends and across all key error metrics including RMSE, MAE, and MAPE. These results demonstrate that the SC-ANFIS approach offers more accurate and reliable predictions for the acid number change rate.

6. Conclusions

This study addresses the prediction of the lubricating oil acid number trend by proposing an SC-ANFIS model that integrates Subtractive Clustering (SC) and the Adaptive Neuro-Fuzzy Inference System (ANFIS). The subtractive clustering algorithm automatically extracts the number of fuzzy rules and initial parameters in a data-driven manner, which helps eliminate redundant rules and simplifies the structure of the ANFIS model. Furthermore, the model leverages the self-learning capability of neural networks to enhance its ability to capture nonlinear and uncertain characteristics inherent in the lubricating oil aging process, thereby overcoming the limited prediction accuracy of traditional BP neural networks under complex operating conditions. Experimental and validation results demonstrate that the SC-ANFIS model exhibits significant advantages in predictive performance compared to the conventional BP neural network.

The current SC-ANFIS model is designed and optimized specifically for lubricating oil, without evaluation of its applicability to other oil types—such as hydraulic oil, gear oil, engine oil, or transformer oil—which clearly limits its scope of application. Moreover, the model training and validation in this study rely exclusively on lubricant data from specific brands and models of industrial lubricants, indicating insufficient sample diversity and scenario coverage. Since lubricating oils from different brands vary considerably in base oil composition and additive formulations—factors that critically affect oxidation aging rates and acid number evolution—the absence of such variant data in the current model leaves its predictive performance for acid number trends in untested brands and models unverified. Consequently, the generalizability of the model remains uncertain.

There remain several avenues for further development of this research. Future work could expand the variety of experimental samples by incorporating aging data from different brands and types of lubricating oils to improve the generalizability of the model. Additionally, integration with deep learning architectures such as LSTM and Transformer could be explored to enhance the model’s capacity for long-term trend prediction. Such improvements would contribute to more comprehensive solutions for intelligent management of industrial lubricant systems.