A Real-Time Dynamic Temperature Prediction Method for Double-Steel Plates in Wet Clutches
Abstract
1. Introduction
- The dynamic mechanisms of heat generation and heat dissipation in the friction pairs of wet clutches were elucidated, with particular focus on the real-time temperature evolution of separators under both high-slip-rate and low-slip-rate operating conditions.
- A novel real-time dynamic temperature prediction model for wet clutches was established, enabling analysis of the spatiotemporal temperature variation patterns of the friction pairs.
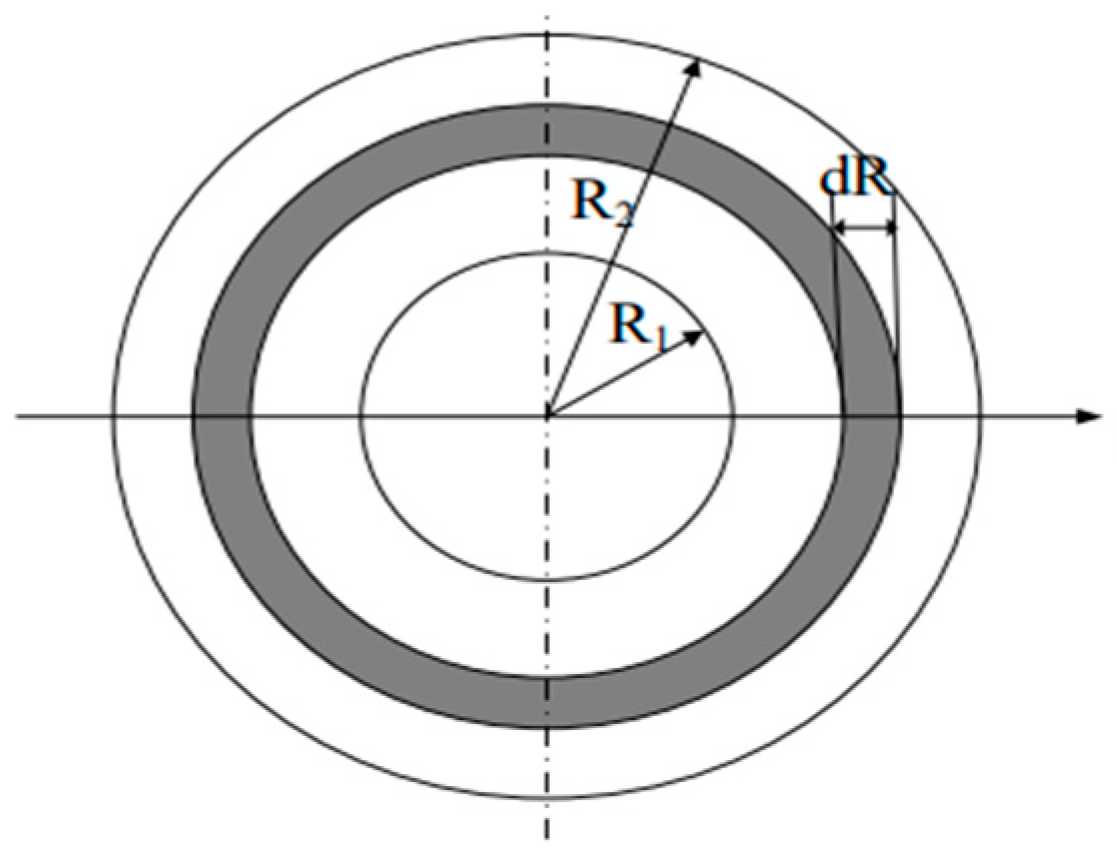
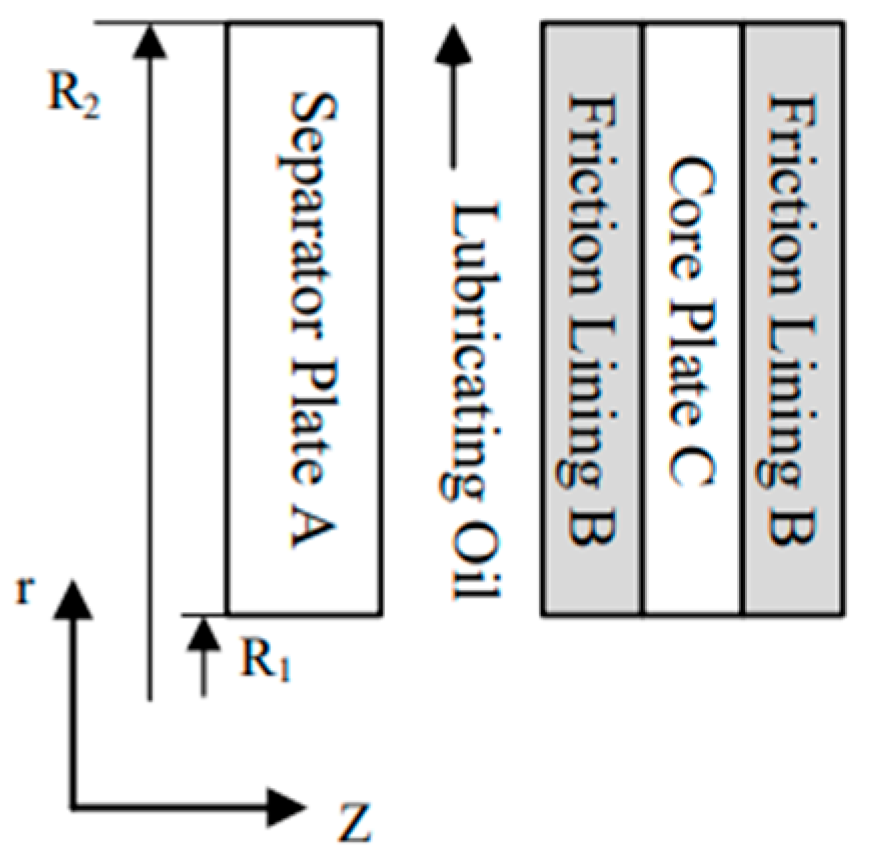
2. Wet Clutch Dynamic Heat Generation Mechanism
3. Heat Dissipation Mechanism of Wet Clutch
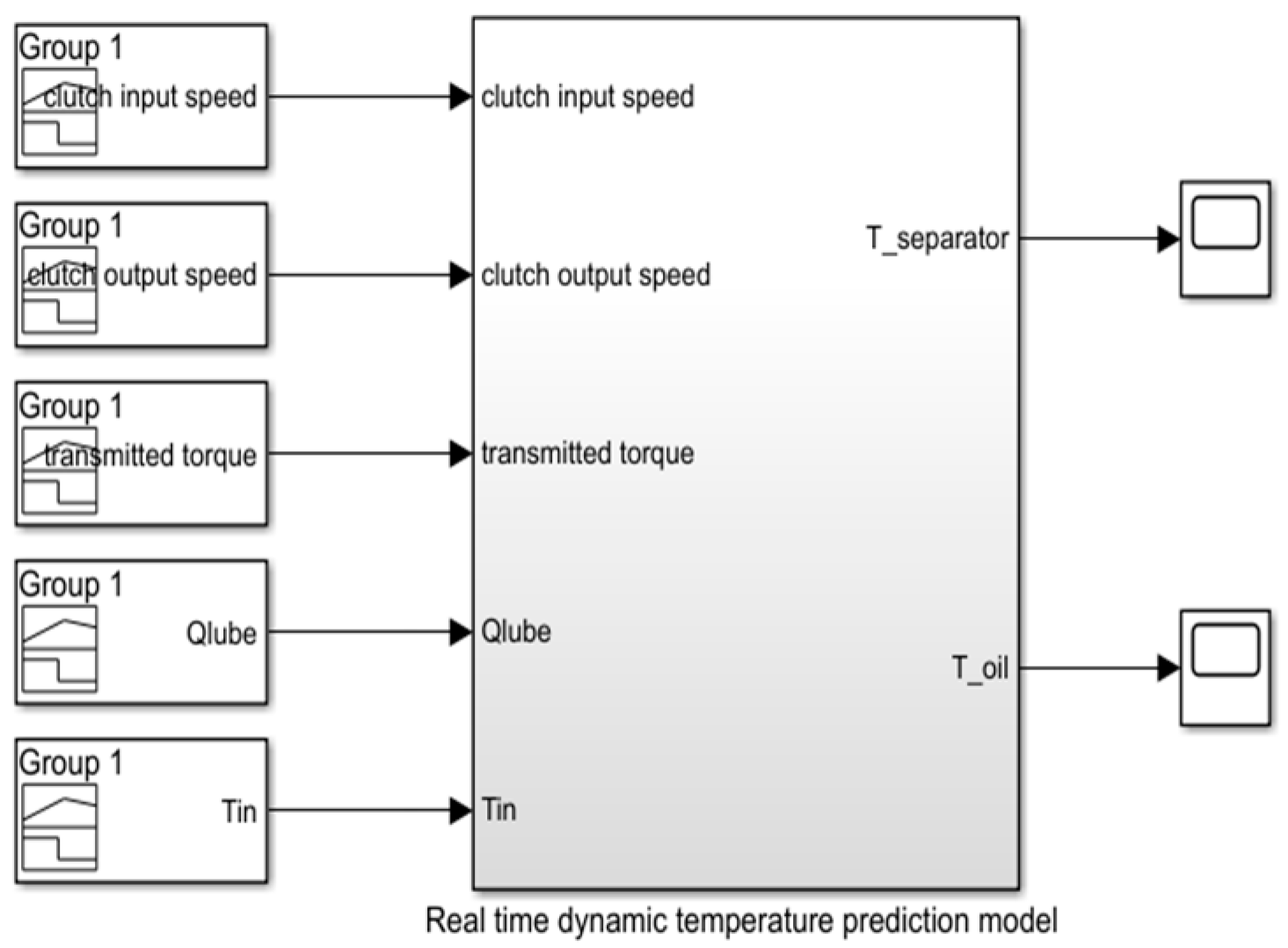
4. The Proposed Real-Time Dynamic Temperature Prediction Model
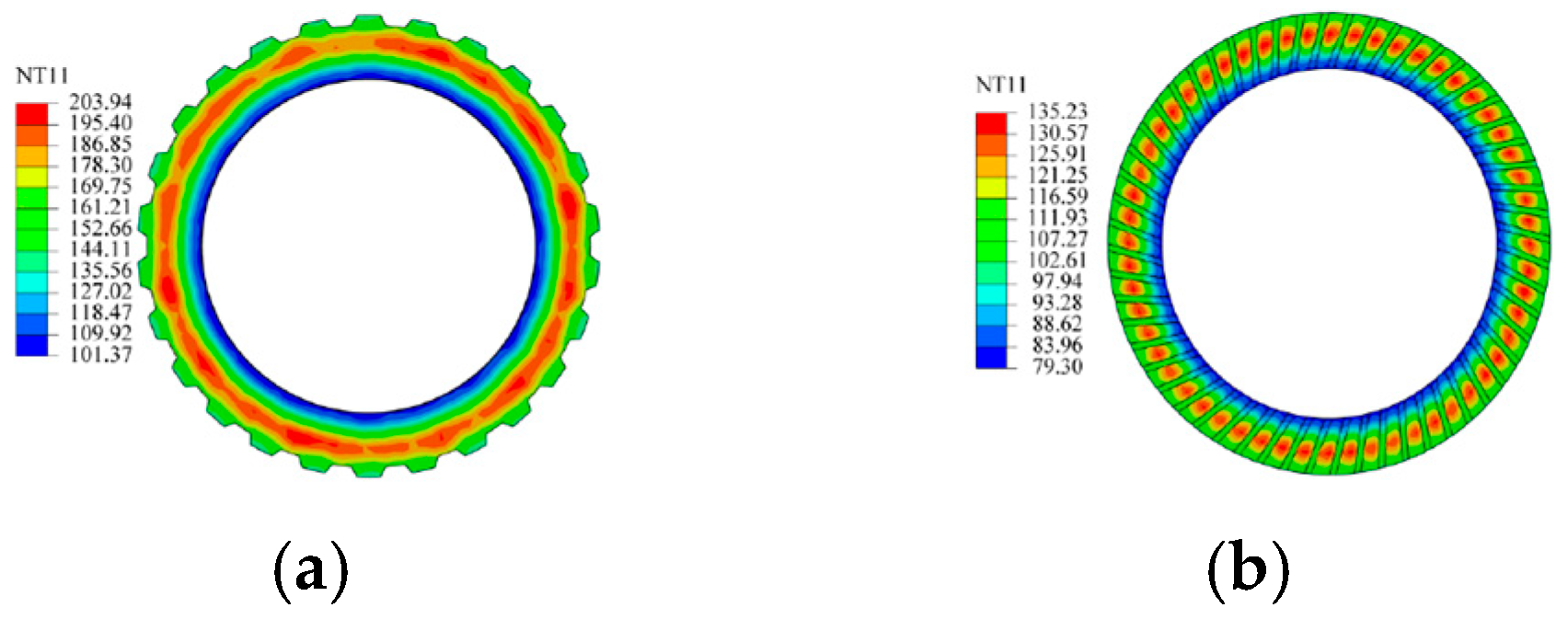
5. Test Verification
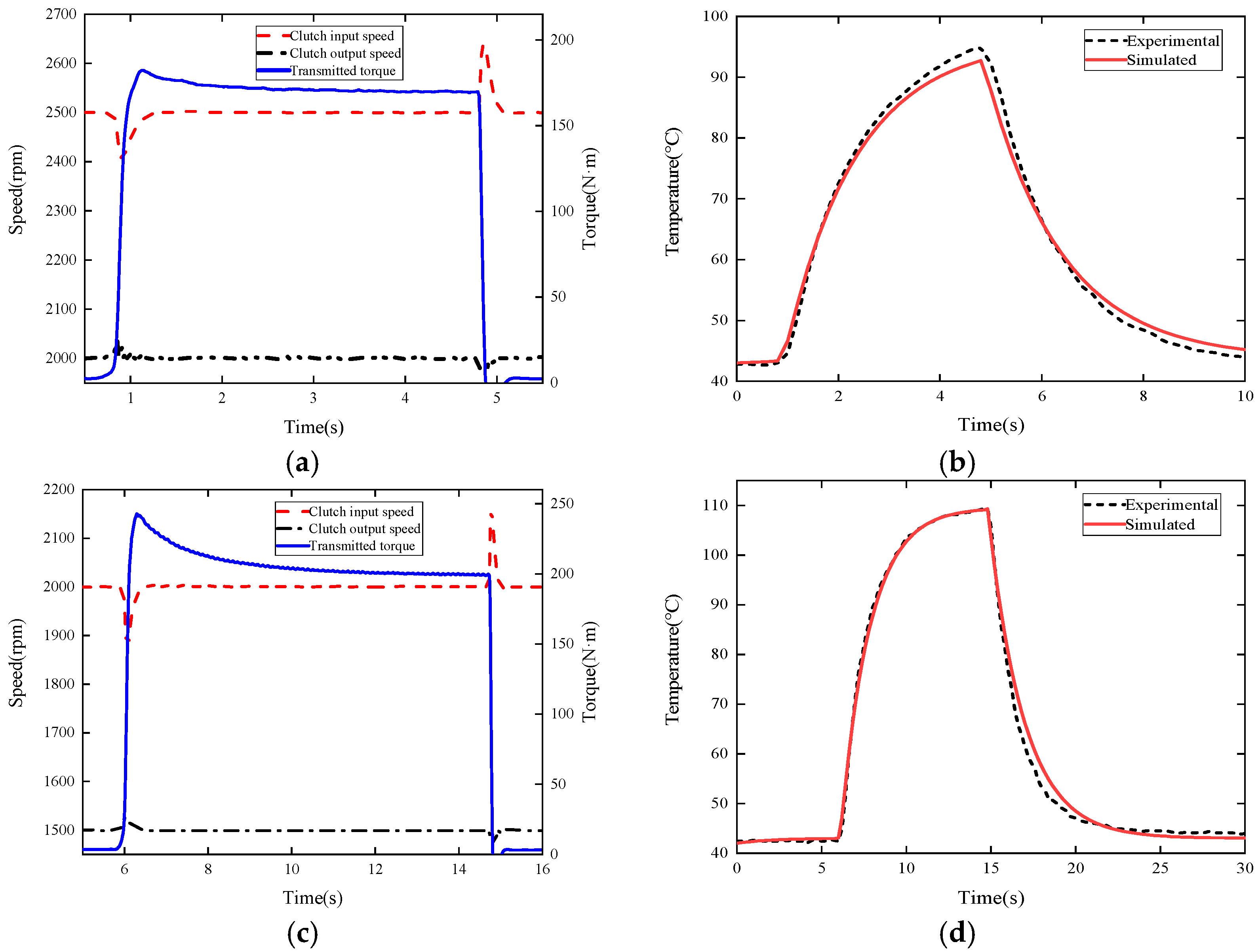
5.1. Comprehensive Performance Test of Wet Clutch
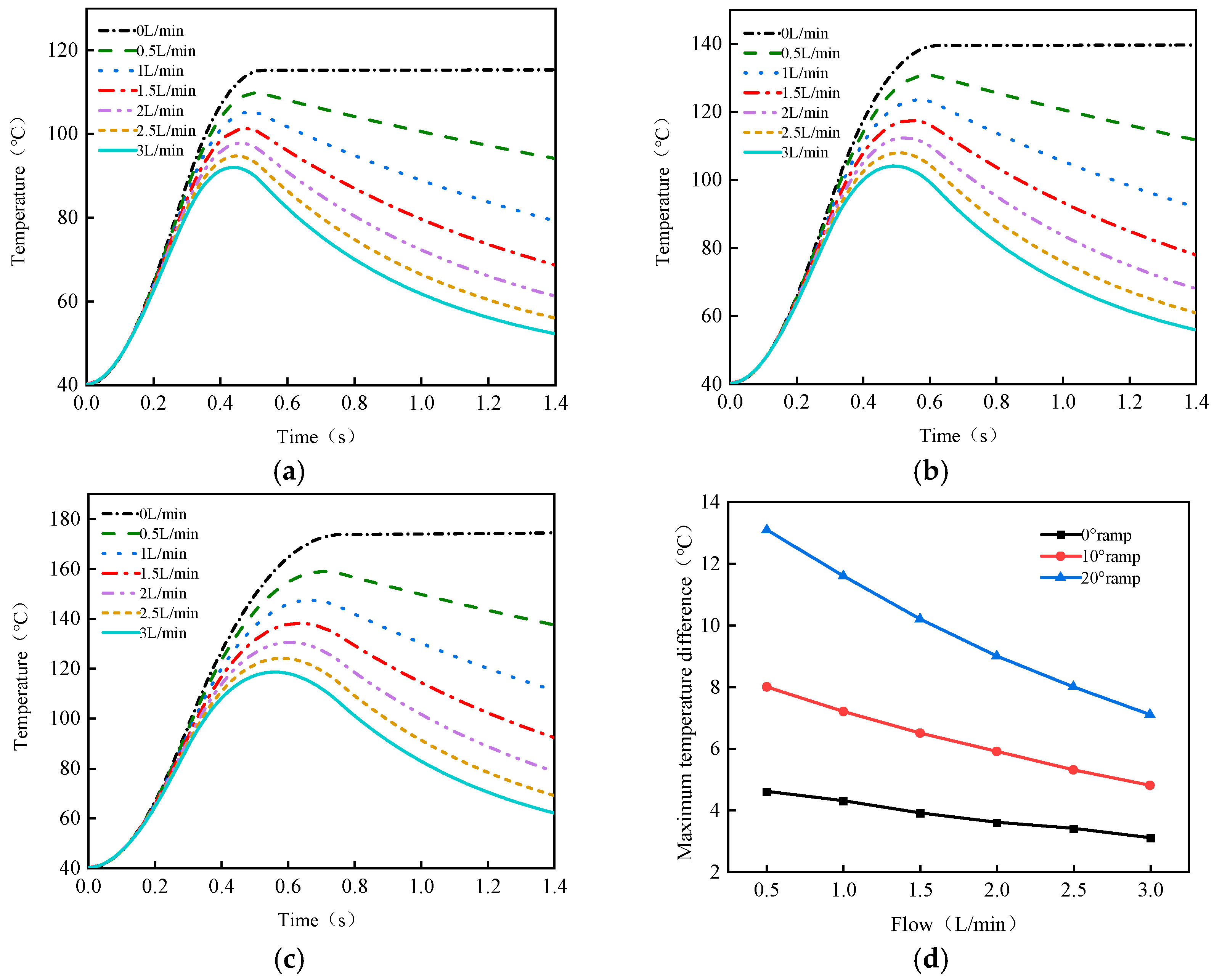
5.2. Model Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Name | Unit |
| A clutch transmits torque | ||
| Engine output torque | ||
| Coefficient of friction | -- | |
| Clutch clamping force | N | |
| N | Number of friction surfaces | -- |
| Effective friction radius | m | |
| Clutch drive end rotational speed | rad/s | |
| Speed of the clutch-driven end | rad/s | |
| Average normal pressure on the friction surface | Pa | |
| Inner diameter of the friction plate | m | |
| Friction plate outer diameter | m | |
| Effective friction radius | m | |
| Q | Sliding friction power | W |
| Heat flow distribution coefficient | -- | |
| Heat flux density of the paired steel sheets | ||
| Heat flux density of the friction plate | ||
| Thermal conductivity of the dual steel sheet | ||
| Thermal conductivity of the friction material | ||
| The density of the dual steel sheet | ||
| The density of the friction plate | ||
| Specific heat capacity of the dual steel sheet | ||
| Specific heat capacity of the friction disc | ||
| The temperature of the friction working surface of the baffle | °C | |
| Lubricating oil temperature | °C | |
| Friction working surface flow area |
References
- Pointner-Gabriel, L.; Flamm, S.; Menzel, M.; Voelkel, K.; Stahl, K. Experimental investigation of drag loss and plate separation behavior of wet clutches under external forces. Results Eng. 2024, 24, 102918. [Google Scholar] [CrossRef]
- Shin, S.; Choi, S.B. Control-oriented modeling of wet clutch friction considering thermal dynamics. Mechatronics 2024, 99, 103146. [Google Scholar] [CrossRef]
- Skulić, A.; Milojević, S.; Marić, D.; Ivanović, L.; Krstić, B.; Radojković, M.; Stojanović, B. The Impact of Lubricant Viscosity and Materials on Power Losses and Efficiency of Worm Gearbox. Teh. Vjesn.-Teh. Gaz. 2022, 29, 1853–1860. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, X.; Wang, D.; Cui, H.; Zhang, S.; Wang, J. Numerical simulation and experimental investigation on the thermal-fluid-solid multi-physical field coupling characteristics of wet friction pairs considering cavitation effect. Appl. Therm. Eng. 2025, 260, 124955. [Google Scholar] [CrossRef]
- Wu, J.; Yang, C.; Zhang, H.; Wang, L. The Cross-Scale Interactive Simulation and Artificial Neural Network Failure Prediction of Temperature Field on Wet Friction Interface. IEEE Trans. Instrum. Meas. 2025, 74, 2518012. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Y.; Wei, C.; Yan, Y. Optimization Design of Oil Groove Shape on the Surface of Friction Plate in High-Speed Wet Clutch Aimed at Minimizing Drag Torque. J. Tribol. 2024, 146, 034601. [Google Scholar] [CrossRef]
- Yang, X.; Bao, H.; Zhang, C.; Tan, W.; Zhu, R. Influence of Groove Type on Friction Coefficient of Wet Friction Clutch Pair. Int. J. Automot. Technol. 2024, 25, 119–129. [Google Scholar] [CrossRef]
- Li, J.; Jin, W.; Zhang, Z.; Lv, X.; Zhang, T. Analysis on effects of material parameters on thermoelastic instability of separate plate in wet clutch. J. Tribol. 2024, 146, 034103. [Google Scholar] [CrossRef]
- Ma, B.; Chen, X.; Zheng, C.; Yu, L.; Zhao, Q.; Lu, W. Study on Spline Stress of Separator Plates in a Wet Multi-Plate Clutch. Materials 2024, 17, 3039. [Google Scholar] [CrossRef]
- Wu, B. Friction Coefficient of Wet Clutches as a Function of Service Mileage. Lubricants 2024, 12, 147. [Google Scholar] [CrossRef]
- Li, A.; Qin, D.; Guo, Z. Adaptive torque control of wet dual clutch based on dynamic friction coefficient estimation. Mechatronics 2024, 100, 103175. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, H.; Zhang, P.; Wei, C.; Ma, N.; Yan, Y. Research on high-speed drag torque characteristics of wet clutches based on mechanism and data-driven approach. Nonlinear Dyn. 2024, 113, 6235–6252. [Google Scholar] [CrossRef]
- Zhou, W.; Su, H.; Liu, H.; Zhang, Y.; Qiu, N.; Gao, B. Leakage and Rotordynamic Performance of a Semi-Y Labyrinth Seal Structure for Centrifugal Pump Based on Multifrequency Whirl Method. ASME J. Eng. Gas Turbines Power 2025, 147, 101022. [Google Scholar] [CrossRef]
- Huang, Z.; Bao, H.; Xiao, Y.; Wei, Y. Transient thermal characteristic analysis and experimental validation of aviation wet friction clutch. J. Mech. Sci. Technol. 2025, 39, 2269–2283. [Google Scholar] [CrossRef]
- Pointner-Gabriel, L.; Flamm, S.; Schneider, T.; Stahl, K. A methodology for image-based measurement of plate movement in disengaged wet clutches. Sci. Rep. 2024, 14, 7631. [Google Scholar] [CrossRef]
- Feng, Y.; Zheng, C.; Yu, L.; Zhang, D.; Zhang, Y.; Zhou, R. A bivariate inverse Gaussian degradation process induced by a common random effect with RUL prediction for wet clutches. Measurement 2025, 251, 117284. [Google Scholar] [CrossRef]
- Bălășoiu, G.; Munteniță, C.; Amortila, V.T.; Titire, L. Optimisation of Clutch Disc Friction Material Using a Multi-Layer Perceptron Artificial Neural Network. Polymers 2024, 16, 3588. [Google Scholar] [CrossRef]
- Wang, B.; Wang, J.; Chen, L.; Ning, K.; Li, H. Effect of different sliding conditions on interface tribological behavior of friction torque limiter. Tribol. Int. 2025, 205, 110551. [Google Scholar] [CrossRef]
- Dong, Y.; Ma, B.; Xiong, C.; Zhao, Q.; Chen, H.; Zhang, Y.; Xie, G. Tribological and Wear Properties of Cu-Based Composite Reinforced by Core–Shell Structure in Multi-disk Clutch. Tribol. Lett. 2024, 72, 66. [Google Scholar] [CrossRef]
- Byeon, S.-J.; Kim, S.-J.; Park, J.-K.; Park, Y.-J.; Lee, J.-W. Parameter study for establishing a synchronizer control strategy in tractor dual-clutch transmission. Agriculture 2024, 14, 218. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, H.; Pan, W.; Cai, W.; Zhou, Y.; Zhai, B.; Ni, X. Nonlinear dynamic separation characteristics of friction pair and experimental analysis. Sci. Rep. 2024, 14, 8751. [Google Scholar] [CrossRef]
- Wu, B.; Qin, D.; Hu, J.; Wang, X.; Wang, Y.; Lv, H. Analysis of influencing factors and changing laws on friction behavior of wet clutch. Tribol. Int. 2021, 162, 107125. [Google Scholar] [CrossRef]
- Shan, L.; Wei, L.; Qiang, Y.; Cui, Y.; Zhan, P. Dynamic performance prediction and experimental analysis of wet clutch actuator considering thermal flow characteristics. Flow Meas. Instrum. 2024, 97, 102592. [Google Scholar] [CrossRef]
- Li, A.; Qin, D.; Guo, Z.; Xia, Y.; Lv, C. Wet clutch pressure hysteresis compensation control under variable oil temperatures for electro-hydraulic actuators. Control Eng. Pract. 2023, 141, 105723. [Google Scholar] [CrossRef]
- Rogkas, N.; Vasilopoulos, L.; Spitas, V. A hybrid transient/quasi-static model for wet clutch engagement. Int. J. Mech. Sci. 2023, 256, 108507. [Google Scholar] [CrossRef]
- Zhang, Z.; Mu, Z.; Yu, X. Mechanistic Study of Groove Parameters on the Thermoelastic Instability of Wet Clutch. Lubricants 2025, 13, 150. [Google Scholar] [CrossRef]



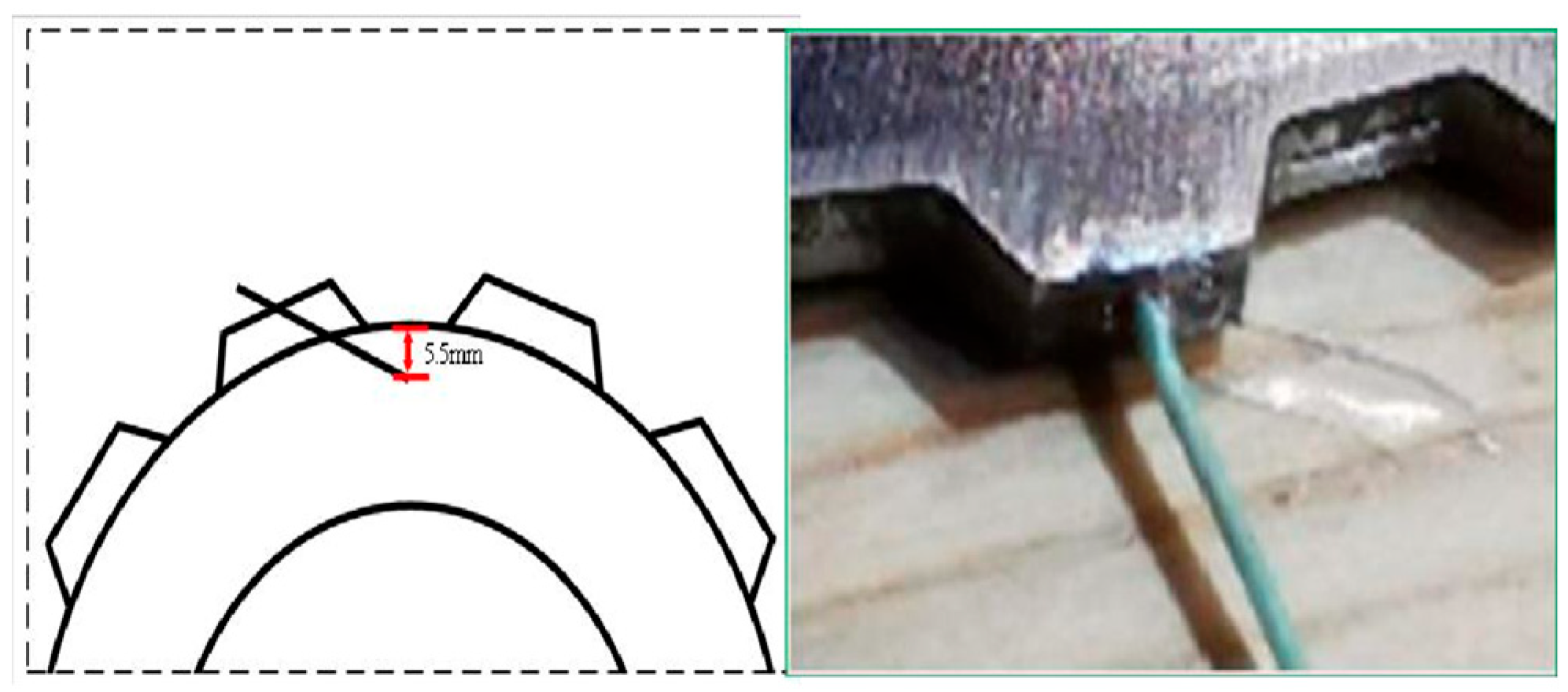


| Geometric Parameter | Counter Steel Plate | Friction Core Plate | Friction Lining |
|---|---|---|---|
| Inner Diameter/m | 0.106 | 0.106 | 0.106 |
| Outer Diameter/m | 0.138 | 0.138 | 0.138 |
| Tooth Height/m | 0.003 | 0.002 | -- |
| Number of Teeth/pc | 26 | 32 | -- |
| Thickness/m | 0.0018 | 0.0008 | 0.0005 |
| Groove Width/m | 0.002 | ||
| Groove Depth/m | 0.0005 | ||
| Number of Grooves/pc | 56 |
| Parameters | Separator Plate | Friction Plate |
|---|---|---|
| Thermal Conductivity (W·(m·°C)−1) | 44 | 54 |
| Elastic Modulus (Pa) | 2.1 × 1011 | 2.26 × 1010 |
| Poisson’s Ratio | 0.3 | 0.3 |
| Thermal Expansion Coefficient | 5.72 × 10−5 | 1.27 × 10−5 |
| Density (kg·m−3) | 7800 | 833 |
| Specific heat capacity (J·(kg·°C)−1) | 460 | 1740 |
| Parameters | Values |
|---|---|
| Density (kg·m−3) | 788.8 |
| Thermal Conductivity (W·(m·°C)−1) | 0.1322 |
| Specific Heat Capacity (J·(kg·°C)−1) | 2328.6 |
| Dynamic Viscosity (Pa·s) | 0.028891 |
| Prandtl Constant | 367.5 |
| Sensor Type | Measurement Range | Accuracy |
|---|---|---|
| Torque Sensor | ±500 N·m | ±0.1%F.S. |
| Speed Sensor | 0~12,000 rpm | 1 rpm |
| Pressure Sensor | 0~50 bar | ±0.1%F.S. |
| Temperature Sensor | −40~1000 °C | 1 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Liu, Y.; Yu, X. A Real-Time Dynamic Temperature Prediction Method for Double-Steel Plates in Wet Clutches. Lubricants 2025, 13, 425. https://doi.org/10.3390/lubricants13100425
Zhang Z, Liu Y, Yu X. A Real-Time Dynamic Temperature Prediction Method for Double-Steel Plates in Wet Clutches. Lubricants. 2025; 13(10):425. https://doi.org/10.3390/lubricants13100425
Chicago/Turabian StyleZhang, Zhigang, Yongle Liu, and Xiaoxia Yu. 2025. "A Real-Time Dynamic Temperature Prediction Method for Double-Steel Plates in Wet Clutches" Lubricants 13, no. 10: 425. https://doi.org/10.3390/lubricants13100425
APA StyleZhang, Z., Liu, Y., & Yu, X. (2025). A Real-Time Dynamic Temperature Prediction Method for Double-Steel Plates in Wet Clutches. Lubricants, 13(10), 425. https://doi.org/10.3390/lubricants13100425





