A Review of Numerical Techniques for Frictional Contact Analysis
Abstract
1. Introduction
1.1. The Importance of Frictional Contact Analysis in Engineering
1.2. Challenges in Modelling Frictional Contact Problems
- The complexity is further compounded by the frictional behavior at the contact interface. The coefficient of friction is often not a constant but may vary with factors, such as surface roughness, temperature, velocity, and pressure. Modelling these variations accurately can be challenging, requiring sophisticated constitutive models and potentially experimental data to calibrate parameters [26,39].
- Solving frictional contact problems often involves significant computational costs. The nonlinearity of the problem necessitates iterative solution procedures, which can be computationally expensive, especially for large-scale models with many degrees of freedom [40].
- The choice of material model significantly influences the accuracy and computational efficiency of the simulation. Realistic materials often exhibit complex constitutive behavior, including plasticity, viscoelasticity, and damage. Incorporating these effects into the contact model adds significant complexity and computational cost [41,42].
- Microslip’s localized nature demands extremely fine meshes, increasing computational cost. Macroslip introduces path dependence and nonlinearity, requiring robust solvers. Modeling fretting and sliding wear necessitates coupling contact mechanics with material removal, involving empirical parameters and uncertainties in surface roughness and material properties. Accurately predicting the transition between micro- and macroslip remains challenging [43,44].
- Coupled thermo-mechanical effects in contact problems pose significant challenges to numerical analysis. Heat generation due to friction alters material properties, influencing contact pressure and wear. Accurately modeling this feedback loop requires solving coupled heat transfer and mechanical equations, increasing computational complexity. Precise material models accounting for temperature-dependent properties and wear mechanisms are crucial but often lack experimental validation, introducing uncertainties into the analysis [45,46].
- Transient wear problems, involving time-dependent changes in surface geometry and contact conditions, require computationally expensive time-stepping schemes. Steady-state analyses, while simpler, may not be applicable for many wear scenarios, particularly those involving significant material removal or changing contact pressures. Accurately capturing the transition between transient and steady-state behaviors presents a major challenge. Model validation against experimental data is crucial [47,48,49].
1.3. Overview of Numerical Methods for Contact Analysis
1.4. Scope and Organization of the Review
2. Fundamentals of Frictional Contact Mechanics
2.1. Constitutive Laws for Friction
- Coulomb friction: Coulomb friction is a widely used model describing the frictional force between two surfaces in contact. It states that the frictional force is proportional to the normal force, with the proportionality constant being the coefficient of friction (μ) [54,55]. The frictional force opposes relative motion and its magnitude is less than or equal to μ times the normal force [56,57]. When the tangential force reaches this limit, a slip occurs. While simple, Coulomb friction neglects velocity dependence and the transition between static and kinetic friction, limiting its accuracy in certain scenarios.
- Rate-dependent friction models: Rate-dependent friction models acknowledge that frictional forces are not solely determined by the normal force but are also significantly influenced by the relative sliding velocity between contacting surfaces [58,59,60]. Unlike the simplistic velocity-independent Coulomb friction model, rate-dependent models incorporate velocity as a key variable. Common examples include viscous friction models, which add a velocity-proportional term, and the Stribeck curve, which empirically describes the friction coefficient’s decrease at low velocities before levelling off at higher velocities. These models enhance the realism of simulations, particularly when dealing with phenomena like stick-slip motion or high-speed contacts, offering more accurate predictions of dynamic behavior than Coulomb friction alone. However, they introduce additional parameters requiring careful calibration [61].
2.2. Contact Kinematics and Geometry
- Contact detection: This is the initial and often computationally demanding step in contact analysis. It involves identifying which parts of the body are in contact. The methods used depend heavily on the dimensionality (2D or 3D) and the complexity of the geometries involved. Common approaches include node-to-surface, surface-to-surface, bounding volume methods, and mesh-based methods [63].
- Penetration depth: Once contact is detected, the penetration depth needs to be determined. This represents the amount by which one body penetrates another. The accurate calculation of penetration depth is crucial for calculating contact forces. Different methods exist to calculate penetration depth, depending on the contact detection method used [64].
- Contact area: The contact area is the region where the bodies are in physical contact. It can range from a point contact to a large, extended area depending on the geometry, loading conditions, and material properties. For simple geometries, the contact area can be easily determined. However, for complex geometries, numerical methods are often necessary to calculate the contact area [65].
- Relative motion: Describing the relative motion between the contacting bodies is critical for determining whether contact is sticking or slipping. This involves calculating relative velocity and relative displacement [66].
- Geometric considerations: Several geometric factors such as curvature, surface roughness, and geometric nonlinearities significantly influence contact analysis [67].
3. Mathematical Formulation of Frictional Contact Problems
- Governing equations: The foundation lies in the equations of motion (for dynamic problems) or equilibrium (for static problems) for the bodies involved. For small deformations, these are typically expressed using linear elasticity. For larger deformations, nonlinear elasticity or plasticity models may be necessary. These equations can be represented in various forms, including strong form and weak form.
- Contact and friction conditions: The contact and friction conditions at the interface are expressed mathematically as constraints:
- Nonpenetration constraint: This constraint ensures that the bodies do not interpenetrate. It can be expressed using inequality conditions relating to the distance between the bodies at the contact interface.
- Friction constraint: Coulomb’s law of friction, or other friction models, defines the relationship between the tangential force and relative velocity at the contact interface. This introduces a nonsmooth and nonlinear relationship, further complicating the problem.
- Variational inequalities: The combination of the weak form of the governing equations and the contact and friction constraints leads to a variational inequality formulation. This is a powerful mathematical framework for expressing and solving frictional contact problems. The variational inequality formulation encapsulates the entire problem, including the governing equations and all constraints. It provides a rigorous mathematical framework for analyzing and solving frictional contact problems.
- Discretization: To obtain a numerical solution, the variational inequality is discretized. This typically involves using finite element methods (FEM), dividing the domain into a mesh of elements and approximating the displacement field using shape functions. The variational inequality then becomes a system of nonlinear equations or inequalities, which can be solved using iterative methods, such as Newton–Raphson or conjugate gradient methods.
- Solution techniques: The solution of the resulting system of equations is often challenging due to the nonlinearity and nonsmoothness arising from the friction constraints. Various numerical methods are employed to handle this complexity, including penalty methods, Lagrange multiplier methods, and augmented Lagrangian methods.
4. Different Numerical Techniques Used in Frictional Analysis
4.1. Penalty Method
4.2. Lagrange Multiplier Methods
4.3. Uzawa Algorithm
4.4. hp-Version of FEM
- h-version: This traditional approach refines the mesh by reducing the element size (h). Accuracy is improved by increasing the number of smaller elements.
- p-version: This approach keeps the mesh size constant but increases the polynomial degree (p) of the approximating functions within each element. Accuracy is improved by using higher-order polynomials to better represent the solution.
5. Computational Aspects and Efficiency
6. Applications and Case Studies
7. Challenges of the Numerical Techniques in Frictional Contact Analysis
8. Conclusions and Future Direction
9. Future Trends and Research Opportunities
- Advanced constitutive models: Current models often oversimplify frictional behavior. Future research should focus on developing more sophisticated constitutive models that incorporate factors, such as surface roughness, adhesion, temperature-dependent friction, and material anisotropy. This includes incorporating advanced experimental techniques to characterize frictional behavior at the micro- and nanoscale, informing the development of more realistic material models. Multiscale modelling approaches that bridge the gap between micro- and macroscale behavior will be crucial for accurately simulating complex contact scenarios.
- Enhanced computational efficiency: The computational cost of solving large-scale frictional contact problems remains a significant bottleneck. Future research should explore advanced numerical algorithms and parallel computing strategies to improve efficiency. This includes developing more efficient iterative solvers, preconditioning techniques, and adaptive mesh refinement strategies that dynamically adjust computational resources based on the problem’s complexity. The exploration of novel numerical methods, such as meshless methods or fast multipole methods, could also offer computational advantages for specific applications. The integration of machine learning techniques to accelerate convergence or even predict contact behavior directly represents a promising avenue for significant performance gains.
- Improved contact detection algorithms: Accurate and efficient contact detection is crucial for the success of frictional contact simulations. Future research should focus on developing more robust and efficient algorithms that can handle complex geometries and large deformations. This includes investigating advanced spatial data structures and algorithms that can quickly identify contacting elements, even in dynamic simulations with significant relative motion between bodies.
- Multibody dynamics and large deformations: Many real-world applications involve multiple interacting bodies undergoing large deformations. Future research needs to focus on developing robust numerical methods capable of handling these complex scenarios efficiently. This requires advancements in both contact detection and the solution of the governing equations of motion.
- Integration of experimental data and validation: The accuracy of numerical simulations depends heavily on the fidelity of input parameters and models. Future research should emphasize the integration of experimental data obtained from advanced experimental techniques, like digital image correlation (DIC) and micro-computed tomography (micro-CT), to validate and calibrate numerical models. This will lead to more accurate and reliable simulations.
- Coupling with other physical phenomena: Many real-world contact problems involve coupling with other physical phenomena, such as heat transfer, fluid flow, or wear. Future research should focus on developing multiphysics simulation capabilities that can accurately capture these coupled interactions.
- Application-specific methodologies: Developing specialized numerical techniques tailored to specific application domains (e.g., tire-road interaction, metal forming, biomechanics) is another important direction. This involves focusing on the specific challenges and complexities associated with each application, leading to more accurate and efficient simulations for those particular scenarios.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Laursen, T.A. Computational Contact and Impact Mechanics; Springer: Berlin/Heidelberg, Germany, 2003; ISBN 978-3-642-07685-5. [Google Scholar]
- Yin, Z.; Hu, Z.; Gao, H.; Lin, G. A FETI B-Differentiable Equation Method for Elastic Frictional Contact Problem with Nonconforming Mesh. Comput. Mech. 2024, 73, 1095–1124. [Google Scholar] [CrossRef]
- Ouakil, I.; Benabderrahmane, B.; Boukhatem, Y.; Feng, B. On a Dynamic Frictional Contact Problem with Normal Damped Response and Long-Term Memory. Math. Mech. Solids 2024, 29, 924–943. [Google Scholar] [CrossRef]
- Kwon, S.L.; Kim, S.; Ha, D.; Yun, G.J. A Fully Nonlinear Three-Dimensional Dynamic Frictional Contact Analysis Method under Large Deformation with the Area Regularization. Eng. Comput. 2024, 40, 399–421. [Google Scholar] [CrossRef]
- Wriggers, P. Computational Contact Mechanics, 2nd ed.; Springer: Berlin, Germany; New York, NY, USA, 2006; ISBN 978-3-540-32608-3. [Google Scholar]
- Konyukhov, A.; Schweizerhof, K. Computational Contact Mechanics: Geometrically Exact Theory for Arbitrary Shaped Bodies; Lecture Notes in Applied and Computational Mechanics; Springer: Berlin/Heidelberg, Germany, 2013; Volume 67, ISBN 978-3-642-31530-5. [Google Scholar]
- Hatanaka, S.; Ogawa, Y.; Okubo, H.; Hanzawa, K.; Kajiki, R.; Yamaguchi, K.; Nakano, K. Correlation between Friction and Wear of Rubber: An Experimental Approach Based on the Disconnections of Stribeck Curves. Wear 2025, 562–563, 205623. [Google Scholar] [CrossRef]
- Jackson, R.L. 12—Modeling Electrical Resistance of Lubricated Contacts. In Electric Vehicle Tribology; Farfan-Cabrera, L.I., Erdemir, A., Eds.; Elsevier Series on Tribology and Surface Engineering; Elsevier: Amsterdam, The Netherlands, 2024; pp. 207–224. ISBN 978-0-443-14074-7. [Google Scholar]
- Lei, B.; Yuan, T.; Liu, J.; Liu, C. Dynamic Modeling and Simulation for Pneumatic Landing Airbag System with Frictional Contact. Thin-Walled Struct. 2024, 195, 111417. [Google Scholar] [CrossRef]
- Chong, W.W.F.; Hamdan, S.H.; Wong, K.J.; Yusup, S. Modelling Transitions in Regimes of Lubrication for Rough Surface Contact. Lubricants 2019, 7, 77. [Google Scholar] [CrossRef]
- Zhang, Z.; Nie, X.; Cao, J. Variational Inequalities of Multilayer Viscoelastic Systems with Interlayer Tresca Friction: Existence and Uniqueness of Solution and Convergence of Numerical Solution. Math. Methods Appl. Sci. 2024, 47, 1170–1194. [Google Scholar] [CrossRef]
- Zheng, Y.; Cabboi, A.; Kuilen, J.-W. van de Identification of the Coefficient of Sliding Friction from an Apparent Non-Coulomb Behavior between Wood and Steel. Tribol. Int. 2024, 200, 110193. [Google Scholar] [CrossRef]
- Lu, Y.; Arakelian, V. A New Solution to Force Analysis Including Coulomb Friction in Mechanism Joints. Mech. Mach. Theory 2024, 202, 105776. [Google Scholar] [CrossRef]
- Ren, F.; Yang, Z.; Li, Z. An Efficient 3D Finite Element Procedure for Simulating Wheel–Rail Cyclic Contact and Ratcheting. Tribol. Int. 2024, 198, 109878. [Google Scholar] [CrossRef]
- Mani, H.; Taherizadeh, A.; Sadeghian, B.; Sadeghi, B.; Cavaliere, P. Thermal–Mechanical and Microstructural Simulation of Rotary Friction Welding Processes by Using Finite Element Method. Materials 2024, 17, 815. [Google Scholar] [CrossRef] [PubMed]
- Prajapati, D.K.; Prakash, C.; Saxena, K.; Gupta, M.; Mehta, J.S. Prediction of Contact Response Using Boundary Element Method (BEM) for Different Surface Topography. Int. J. Interact. Des. Manuf. 2024, 18, 2725–2732. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Duc, N.D. Frictional Contact Analysis between Two-Dimensional Deformable Anisotropic Magneto-Electro-Elastic Bodies via a Semi-Analytical Method. Eng. Anal. Bound. Elem. 2024, 166, 105858. [Google Scholar] [CrossRef]
- Das, S.K.; Gautam, S.S. A Comprehensive Isogeometric Analysis of Frictional Hertz Contact Problem. Tribol. Int. 2024, 200, 110078. [Google Scholar] [CrossRef]
- Zhang, R.; Tagliafierro, B.; Vanden Heuvel, C.; Sabarwal, S.; Bakke, L.; Yue, Y.; Wei, X.; Serban, R.; Negruţ, D. Chrono DEM-Engine: A Discrete Element Method Dual-GPU Simulator with Customizable Contact Forces and Element Shape. Comput. Phys. Commun. 2024, 300, 109196. [Google Scholar] [CrossRef]
- Huf, M.; Vallée, T.; Fricke, H. Numerical Modelling and Experimental Validation of Squeezing Flows in the Automobile Production. Int. J. Adhes. Adhes. 2024, 130, 103616. [Google Scholar] [CrossRef]
- Nath, D.; Ankit; Neog, D.R.; Gautam, S.S. Application of Machine Learning and Deep Learning in Finite Element Analysis: A Comprehensive Review. Arch. Comput. Methods Eng. 2024, 31, 2945–2984. [Google Scholar] [CrossRef]
- Olukoko, O.A.; Becker, A.A.; Fenner, R.T. A Review of Three Alternative Approaches to Modelling Frictional Contact Problems Using the Boundary Element Method. Proc. R. Soc. London. Ser. A: Math. Phys. Sci. 1994, 444, 37–51. [Google Scholar] [CrossRef]
- Klarbring, A. A Mathematical Programming Approach to Three-Dimensional Contact Problems with Friction. Comput. Methods Appl. Mech. Eng. 1986, 58, 175–200. [Google Scholar] [CrossRef]
- Mijar, A.R.; Arora, J.S. An Augmented Lagrangian Optimization Method for Contact Analysis Problems, 1: Formulation and Algorithm. Struct. Multidiscip. Optim. 2004, 28, 99–112. [Google Scholar] [CrossRef]
- De Lorenzis, L.; Wriggers, P.; Zavarise, G. A Mortar Formulation for 3D Large Deformation Contact Using NURBS-Based Isogeometric Analysis and the Augmented Lagrangian Method. Comput. Mech. 2012, 49, 1–20. [Google Scholar] [CrossRef]
- Fantetti, A.; Botto, D.; Zucca, S.; Schwingshackl, C. Guidelines to Use Input Contact Parameters for Nonlinear Dynamic Analysis of Jointed Structures: Results of a Round Robin Test. Tribol. Int. 2024, 191, 109158. [Google Scholar] [CrossRef]
- Fu, Y.; Wei, B. A Two-Dimensional Friction-Decoupling Method Based on Numerical Integration Method and Momentum Theorem. Eng. Struct. 2024, 301, 117323. [Google Scholar] [CrossRef]
- Singh, T. An Integrated Multicriteria Decision Making Framework for the Selection of Waste Cement Dust Filled Automotive Brake Friction Composites. Sci. Rep. 2024, 14, 6817. [Google Scholar] [CrossRef]
- Mishra, A.; Carrara, P.; Marfia, S.; Sacco, E.; De Lorenzis, L. Enhanced Transformation Field Analysis for Reduced-Order Modeling of Problems with Cohesive Interfaces. Comput. Methods Appl. Mech. Eng. 2024, 421, 116755. [Google Scholar] [CrossRef]
- Lamura, M.D.P.; Ammarullah, M.I.; Maula, M.I.; Hidayat, T.; Bayuseno, A.P.; Jamari, J. The Effect of Load, Diameter Ratio, and Friction Coefficient on Residual Stress in a Hemispherical Contact for Application in Biomedical Industry. J. Mater. Eng. Perform. 2024, 33, 7528–7536. [Google Scholar] [CrossRef]
- Escanciano, I.; Heras, I.; Macareno, L.M.; Aguirrebeitia, J. An Engineering Approach to Assess Friction Torque in Generally Loaded Four-Point Contact Slewing Bearings. Mech. Mach. Theory 2024, 192, 105542. [Google Scholar] [CrossRef]
- Man, K.W.; Aliabadi, M.H.; Rooke, D.P. BEM Frictional Contact Analysis: Modelling Considerations. Eng. Anal. Bound. Elem. 1993, 11, 77–85. [Google Scholar] [CrossRef]
- Gao, Q.; Fan, Y.; Wu, Y.G.; Li, L.; Zhang, D.Y. Insight into the Influence of Frictional Heat on the Modal Characteristics and Interface Temperature of Frictionally Damped Turbine Blades. J. Sound Vib. 2024, 581, 118410. [Google Scholar] [CrossRef]
- Natsiavas, S. Analytical Modeling of Discrete Mechanical Systems Involving Contact, Impact, and Friction. Appl. Mech. Rev. 2019, 71, 050802. [Google Scholar] [CrossRef]
- Millan, P.; Pagaimo, J.; Magalhães, H.; Antunes, P.; Ambrósio, J. Influence of the Friction Modelling Decisions on the Acceptance of the Running Behaviour of a Friction-Damped Locomotive. Veh. Syst. Dyn. 2024, 62, 719–738. [Google Scholar] [CrossRef]
- Gerosa, F.M.; Marsden, A.L. A Mechanically Consistent Unified Formulation for Fluid-Porous-Structure-Contact Interaction. Comput. Methods Appl. Mech. Eng. 2024, 425, 116942. [Google Scholar] [CrossRef] [PubMed]
- Lorez, F.; Pundir, M.; Kammer, D.S. Eulerian Framework for Contact between Solids Represented as Phase Fields. Comput. Methods Appl. Mech. Eng. 2024, 418, 116497. [Google Scholar] [CrossRef]
- Fang, H.; Yin, Z.-Y.; Zhang, D.; Cao, L. A Hydro-Mechanical Coupled Contact Method for Two-Phase Geotechnical Large Deformation Problems within the SNS-PFEM Framework. Comput. Methods Appl. Mech. Eng. 2024, 420, 116743. [Google Scholar] [CrossRef]
- Droniou, J.; Enchéry, G.; Faille, I.; Haidar, A.; Masson, R. A Bubble VEM-Fully Discrete Polytopal Scheme for Mixed-Dimensional Poromechanics with Frictional Contact at Matrix–Fracture Interfaces. Comput. Methods Appl. Mech. Eng. 2024, 422, 116838. [Google Scholar] [CrossRef]
- Koch, J.; Choi, W.; King, E.; Garcia, D.; Das, H.; Wang, T.; Ross, K.; Kappagantula, K. Neural Lumped Parameter Differential Equations with Application in Friction-Stir Processing. J. Intell. Manuf. 2024. [Google Scholar] [CrossRef]
- Huang, J.; Liu, J. Strength Constrained Topology Optimization of Hyperealstic Structures with Large Deformation-Induced Frictionless Contact. Appl. Math. Model. 2024, 126, 67–84. [Google Scholar] [CrossRef]
- Li, G.; Wang, K.; Tang, C.; Ye, J. Non-Break Modeling and Numerical Simulation for Non-Intact Rock Failure Process. Int. J. Rock Mech. Min. Sci. 2024, 176, 105725. [Google Scholar] [CrossRef]
- Han, Q.; Li, Y.; Lu, Y.; Wang, P. Effect of Faying Surface Treatments and Bolt Tightened Levels on Fretting Fatigue Performance of Slip Critical Connections with High Strength Bolts. Tribol. Int. 2025, 201, 110257. [Google Scholar] [CrossRef]
- Wang, Y.; Li, C.; Jia, T.; Pan, S. A Parameters Identification Method and Experimental Analysis of Contact Friction Interface in Thermal Environment. Mech. Based Des. Struct. Mach. 2024, 52, 9636–9654. [Google Scholar] [CrossRef]
- Li, Y.-H.; Shen, F.; Güler, M.A.; Ke, L.-L. An Efficient Method for Electro-Thermo-Mechanical Coupling Effect in Electrical Contact on Rough Surfaces. Int. J. Heat Mass Transf. 2024, 226, 125492. [Google Scholar] [CrossRef]
- Zhang, K.; Shen, R.; Hu, Z.; Tang, J.; Sun, Z.; Ning, A.; Yang, S. Dynamic Modeling and Analysis Considering Friction-Wear Coupling of Gear System. Int. J. Mech. Sci. 2024, 275, 109343. [Google Scholar] [CrossRef]
- Mróz, Z.; Páczelt, I. Analysis of Thermo-Elastic Wear Problems. J. Therm. Stress. 2011, 34, 569–606. [Google Scholar] [CrossRef]
- Chen, R.; Zhao, B.; He, T.; Tu, L.; Xie, Z.; Zhong, N.; Zou, D. Study on Coupling Transient Mixed Lubrication and Time-Varying Wear of Main Bearing in Actual Operation of Low-Speed Diesel Engine. Tribol. Int. 2024, 191, 109159. [Google Scholar] [CrossRef]
- Chen, R.; Zhao, B.; Xin, Q.; Niu, X.; Xie, Z.; Lu, X.; Zou, D. Analysis of Transient Lubrication and Wear Coupling Behaviors Considering Thermal Effect and Journal Misalignment for Main Bearings under Dynamic Load. Wear 2024, 554–555, 205478. [Google Scholar] [CrossRef]
- Babuška, I.; Suri, M. The h–p Version of the Finite Element Method with Quasiuniform Meshes. ESAIM Math. Model. Numer. Anal. 1987, 21, 199–238. [Google Scholar] [CrossRef]
- Lone, A.S.; Kanth, S.A.; Jameel, A.; Harmain, G.A. A State of Art Review on the Modeling of Contact Type Nonlinearities by Extended Finite Element Method. Mater. Today Proc. 2019, 18, 3462–3471. [Google Scholar] [CrossRef]
- Polonsky, I.A.; Keer, L.M. A Fast and Accurate Method for Numerical Analysis of Elastic Layered Contacts. J. Tribol. 1999, 122, 30–35. [Google Scholar] [CrossRef]
- Cheng, J.-H.; Kikuchi, N. An Incremental Constitutive Relation of Unilateral Contact Friction for Large Deformation Analysis. J. Appl. Mech. 1985, 52, 639–648. [Google Scholar] [CrossRef]
- Oktiovan, Y.P.; Messali, F.; Pulatsu, B.; Lemos, J.V.; Rots, J.G. A Contact-Based Constitutive Model for the Numerical Analysis of Masonry Structures Using the Distinct Element Method. Comput. Struct. 2024, 303, 107499. [Google Scholar] [CrossRef]
- Holey, H.; Sauer, F.; Ganta, P.B.; Mayrhofer, L.; Dienwiebel, M.; Schulze, V.; Moseler, M. Multiscale Parametrization Of a Friction Model For Metal Cutting Using Contact Mechanics, Atomistic Simulations, And Experiments. Tribol. Lett. 2024, 72, 113. [Google Scholar] [CrossRef]
- Schulze, V.; Bleicher, F.; Courbon, C.; Gerstenmeyer, M.; Meier, L.; Philipp, J.; Rech, J.; Schneider, J.; Segebade, E.; Steininger, A.; et al. Determination of Constitutive Friction Laws Appropriate for Simulation of Cutting Processes. CIRP J. Manuf. Sci. Technol. 2022, 38, 139–158. [Google Scholar] [CrossRef]
- Baek, S.; Baek, S. Influence of Contact Curvature on Frictional Energy Dissipation under Varying Tangential Loads. Friction 2024, 12, 363–374. [Google Scholar] [CrossRef]
- Gräser, C.; Kornhuber, R.; Podlesny, J. Numerical Simulation of Multiscale Fault Systems with Rate- and State-Dependent Friction. Comput. Geosci. 2024, 28, 1–21. [Google Scholar] [CrossRef]
- Yazdanparast, R.; Rafiee, R. A Rate-Dependent Crack Bridging Model for Dynamic Fracture of CNT-Reinforced Polymers. Eng. Fract. Mech. 2024, 311, 110535. [Google Scholar] [CrossRef]
- Guo, X.; Mao, N.; Kong, T.; Zhang, J.; Shen, J.; Wang, C.; Sun, C.; Li, P.; Xiong, Z. Strain Rate-Dependent Plastic Behavior of TWIP Steel Investigated by Crystal Plasticity Model. Mater. Sci. Eng. A 2024, 891, 145986. [Google Scholar] [CrossRef]
- Manzoli, O.L.; Tosati, M.; Rodrigues, E.A.; Bitencourt, L.A.G. Computational Modeling of 2D Frictional Contact Problems Based on the Use of Coupling Finite Elements and Combined Contact/Friction Damage Constitutive Model. Finite Elem. Anal. Des. 2022, 199, 103658. [Google Scholar] [CrossRef]
- da Silva, M.R.; Coelho, J.; Gonçalves, F.; Novais, F.; Flores, P. Multibody Dynamics in Robotics with Focus on Contact Events. Robotica 2024, 1–33. [Google Scholar] [CrossRef]
- Fan, Z.; Yang, K.; Yuan, B.; Mu, X.; Yin, K.; Sun, Q.; Sun, W. Analysis and Optimization of Repetitive Positioning Precision for Kinematic Couplings of Opto-Mechanical Components Considering Uncertainty. Precis. Eng. 2024, 89, 11–22. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Q.; Zhang, J.; Qin, X.; Sun, Y. A Knowledge-Based Fault Diagnosis Method for Rolling Bearings without Fault Sample Training. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 10253–10265. [Google Scholar] [CrossRef]
- Xing, M.; Zhang, B.; Deng, P.; Xu, J.; Cui, Y. A Comprehensive Analysis of Contact Kinematics for Planetary Roller Screw Mechanism. Tribol. Int. 2023, 179, 108127. [Google Scholar] [CrossRef]
- Lu, J. Isogeometric Contact Analysis: Geometric Basis and Formulation for Frictionless Contact. Comput. Methods Appl. Mech. Eng. 2011, 200, 726–741. [Google Scholar] [CrossRef]
- K, R.K.; Sen, D. Motion Space Analysis of Objects in Multiple Point Contacts with Applications to Form-Closure and Kinematic Pairs. Mech. Mach. Theory 2020, 153, 104001. [Google Scholar] [CrossRef]
- Hamad, F.; Giridharan, S.; Moormann, C. A Penalty Function Method for Modelling Frictional Contact in MPM. Procedia Eng. 2017, 175, 116–123. [Google Scholar] [CrossRef]
- Shimizu, T.; Sano, T. An Application of a Penalty Method Contact and Friction Algorithm to a 3-Dimensional Tool Surface Expressed by a B-Spline Patch. J. Mater. Process. Technol. 1995, 48, 207–213. [Google Scholar] [CrossRef]
- Liang, W.; Fang, H.; Yin, Z.-Y.; Zhao, J. A Mortar Segment-to-Segment Frictional Contact Approach in Material Point Method. Comput. Methods Appl. Mech. Eng. 2024, 431, 117294. [Google Scholar] [CrossRef]
- Ling, M.; Xiao, W.; Han, W. Numerical Analysis of a History-Dependent Mixed Hemivariational-Variational Inequality in Contact Problems. Comput. Math. Appl. 2024, 166, 65–76. [Google Scholar] [CrossRef]
- Sjövall, F.; Wallin, M.; Tortorelli, D.A. Shape Optimization of Hyperelastic Structures Subject to Frictionless Contact. Comput. Struct. 2024, 301, 107426. [Google Scholar] [CrossRef]
- Ouyang, Q.; Zhuang, X.; Rabczuk, T.; Ning, Y.; Kang, G.; Chen, P. Implementation of Three-Dimensional Contact Algorithm in Numerical Manifold Method for the Structural Impact Simulation. Int. J. Impact Eng. 2024, 193, 105040. [Google Scholar] [CrossRef]
- He, X.; Gu, F.; Ball, A. A Review of Numerical Analysis of Friction Stir Welding. Prog. Mater. Sci. 2014, 65, 1–66. [Google Scholar] [CrossRef]
- Lei, B.; Xu, H.; Tang, L.; Liu, J.; Liu, C. Modeling and Analysis for Landing Airbag–Lunar Soil Interaction Using a CPU–GPU-Based FMBD-DEM Computational Framework. Mech. Mach. Theory 2024, 198, 105668. [Google Scholar] [CrossRef]
- Mashayekhi, F.; Zucca, S. Modal Derivatives for Efficient Vibration Prediction of Geometrically Nonlinear Structures with Friction Contact. Appl. Sci. 2024, 14, 3936. [Google Scholar] [CrossRef]
- Nayak, S.S.; Iqbal, M.P.; Jain, R.; Pal, S.K.; Srirangam, P. A Computationally Efficient Multiphysics Model for Friction Stir Welding with Polygonal Pin Profiles. J. Adhes. Sci. Technol. 2024, 38, 654–686. [Google Scholar] [CrossRef]
- Lee, M.; Jang, Y.H.; Baek, S. Methodology for Predicting Optimal Friction Support Location to Attenuate Vibrational Energy in Piping Systems. Nucl. Eng. Technol. 2024, 56, 1627–1637. [Google Scholar] [CrossRef]
- Yuan, T.; Tang, L.; Liu, J. Dynamic Modeling and Analysis for Inflatable Mechanisms Considering Adhesion and Rolling Frictional Contact. Mech. Mach. Theory 2023, 184, 105295. [Google Scholar] [CrossRef]
- Cornejo, A.; Mataix, V.; Wriggers, P.; Barbu, L.G.; Oñate, E. A Numerical Framework for Modelling Tire Mechanics Accounting for Composite Materials, Large Strains and Frictional Contact. Comput. Mech. 2024, 73, 1–25. [Google Scholar] [CrossRef]
- Vadcard, T.; Thouverez, F.; Batailly, A. On the Detection of Nonlinear Normal Mode-Related Isolated Branches of Periodic Solutions for High-Dimensional Nonlinear Mechanical Systems with Frictionless Contact Interfaces. Comput. Methods Appl. Mech. Eng. 2024, 419, 116641. [Google Scholar] [CrossRef]
- Gismeros Moreno, R.; Marques, F.; Corral Abad, E.; Meneses Alonso, J.; Flores, P.; Castejon, C. Enhanced Modelling of Planar Radial-Loaded Deep Groove Ball Bearings with Smooth-Contact Formulation. Multibody Syst. Dyn. 2024, 60, 121–159. [Google Scholar] [CrossRef]
- Yang, F.; Liu, D.; Yin, W.; Yuan, C.; Hu, Y.; Xu, J.; Yang, Y.; Tang, J.; Chen, J. Three-Dimensional Finite Element Analysis of the Biomechanical Behaviour of Different Dental Implants under Immediate Loading during Three Masticatory Cycles. Heliyon 2024, 10, e32616. [Google Scholar] [CrossRef]
- Ramasubramanian, D.; Hernández-Verdejo, J.L.; López-Alonso, J.M. Influence of Contact Lens Parameters on Cornea: Biomechanical Analysis. Bioengineering 2024, 11, 966. [Google Scholar] [CrossRef]
- Ozlu, E.; Budak, E.; Molinari, A. Analytical and Experimental Investigation of Rake Contact and Friction Behavior in Metal Cutting. Int. J. Mach. Tools Manuf. 2009, 49, 865–875. [Google Scholar] [CrossRef]
- Das, A.; Choong, G.Y.H.; Dillard, D.A.; De Focatiis, D.S.A.; Bortner, M.J. Characterizing Friction for Fiber Reinforced Composites Manufacturing: Method Development and Effect of Process Parameters. Compos. Part B Eng. 2022, 236, 109777. [Google Scholar] [CrossRef]
- Tang, B.; Xiang, Z.Y.; Fan, Z.Y.; Zhang, Q.X.; Chen, W. Effect of the Perforated Structure of Friction Block on the Tribological Behavior of a High-Speed Train Brake Interface in Sandy Environments. Eng. Fail. Anal. 2024, 158, 108039. [Google Scholar] [CrossRef]
- Saurabh, A.; Verma, P.C.; Dhir, A.; Sikder, J.; Saravanan, P.; Tiwari, S.K.; Das, R. Enhanced Tribological Performance of MoS2 and hBN-Based Composite Friction Materials: Design of Tribo-Pair for Automotive Brake Pad-Disc Systems. Tribol. Int. 2024, 199, 110001. [Google Scholar] [CrossRef]
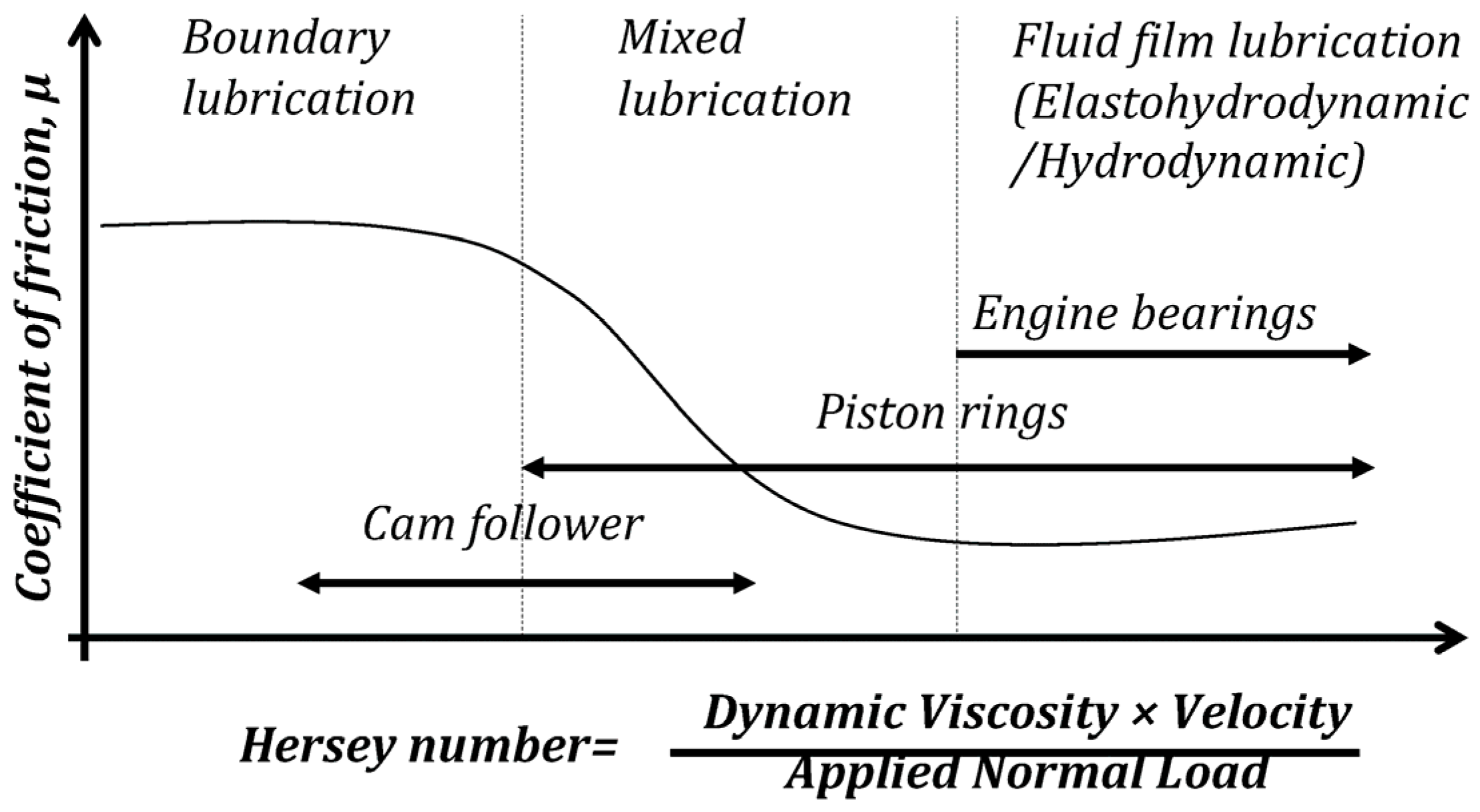

| Numerical Technique | Advantages | Disadvantages |
|---|---|---|
| Penalty Method | Relatively simple to implement; easily incorporated into existing FE codes. | Can lead to ill-conditioning for large penalty parameters; penetration may occur; parameter selection is crucial. |
| Lagrange Multiplier Method | Accurate constraint enforcement; no penetration; no penalty parameter needed. | More complex to implement; leads to larger systems of equations; and can suffer from instability. |
| Augmented Lagrangian Method | Combines advantages of penalty and Lagrange multiplier methods; improved stability. | More complex than the penalty method; requires careful parameter tuning. |
| Barrier Method | Handles inequality constraints effectively. | Can be computationally expensive; requires careful parameter selection to avoid ill-conditioning. |
| Nonlinear Complementarity Problem (NCP) Methods | Can be very accurate and efficient for certain problem classes. | Can be complex to implement; convergence can be sensitive to initial guess and problem parameters. |
| Node-to-Node Contact | Simple implementation; computationally efficient for small contact areas. | Can lead to inaccuracies in large deformation problems; may not accurately capture complex geometries. |
| Node-to-Segment Contact | More accurate than node-to-node for larger contact areas. | More computationally expensive than node-to-node. |
| Segment-to-Segment Contact | Most accurate representation of contact geometry. | Most computationally expensive; complex implementation. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vashishtha, G.; Chauhan, S.; Singh, R.; Singh, M.; Tejani, G.G. A Review of Numerical Techniques for Frictional Contact Analysis. Lubricants 2025, 13, 18. https://doi.org/10.3390/lubricants13010018
Vashishtha G, Chauhan S, Singh R, Singh M, Tejani GG. A Review of Numerical Techniques for Frictional Contact Analysis. Lubricants. 2025; 13(1):18. https://doi.org/10.3390/lubricants13010018
Chicago/Turabian StyleVashishtha, Govind, Sumika Chauhan, Riya Singh, Manpreet Singh, and Ghanshyam G. Tejani. 2025. "A Review of Numerical Techniques for Frictional Contact Analysis" Lubricants 13, no. 1: 18. https://doi.org/10.3390/lubricants13010018
APA StyleVashishtha, G., Chauhan, S., Singh, R., Singh, M., & Tejani, G. G. (2025). A Review of Numerical Techniques for Frictional Contact Analysis. Lubricants, 13(1), 18. https://doi.org/10.3390/lubricants13010018







