Impact of Oil Viscosity on Emissions and Fuel Efficiency at High Altitudes: A Response Surface Methodology Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of the Experimental Setup
2.2. Response Surface Methodology
3. Results
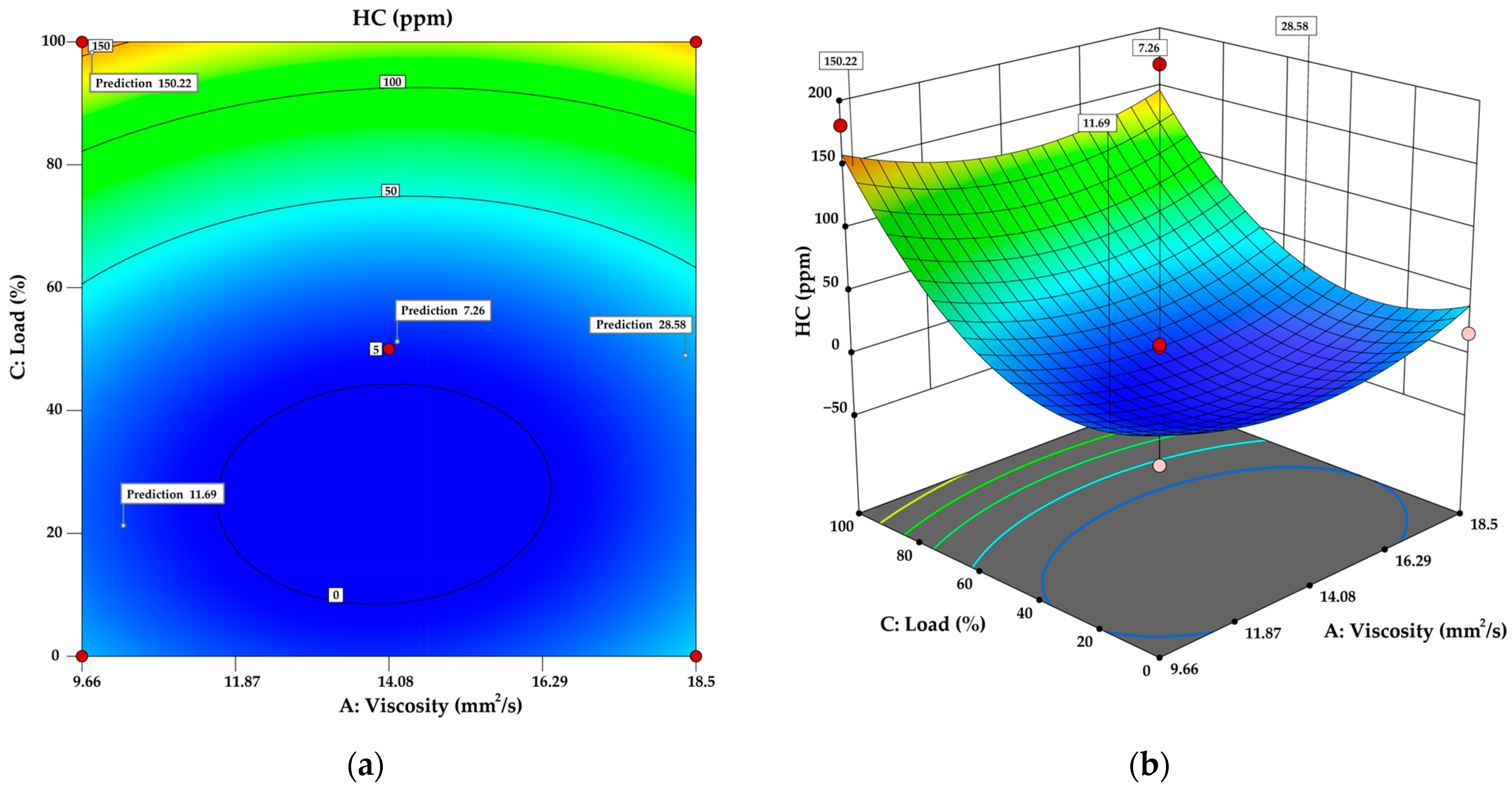
3.1. Model for HC
3.2. Model for CO2
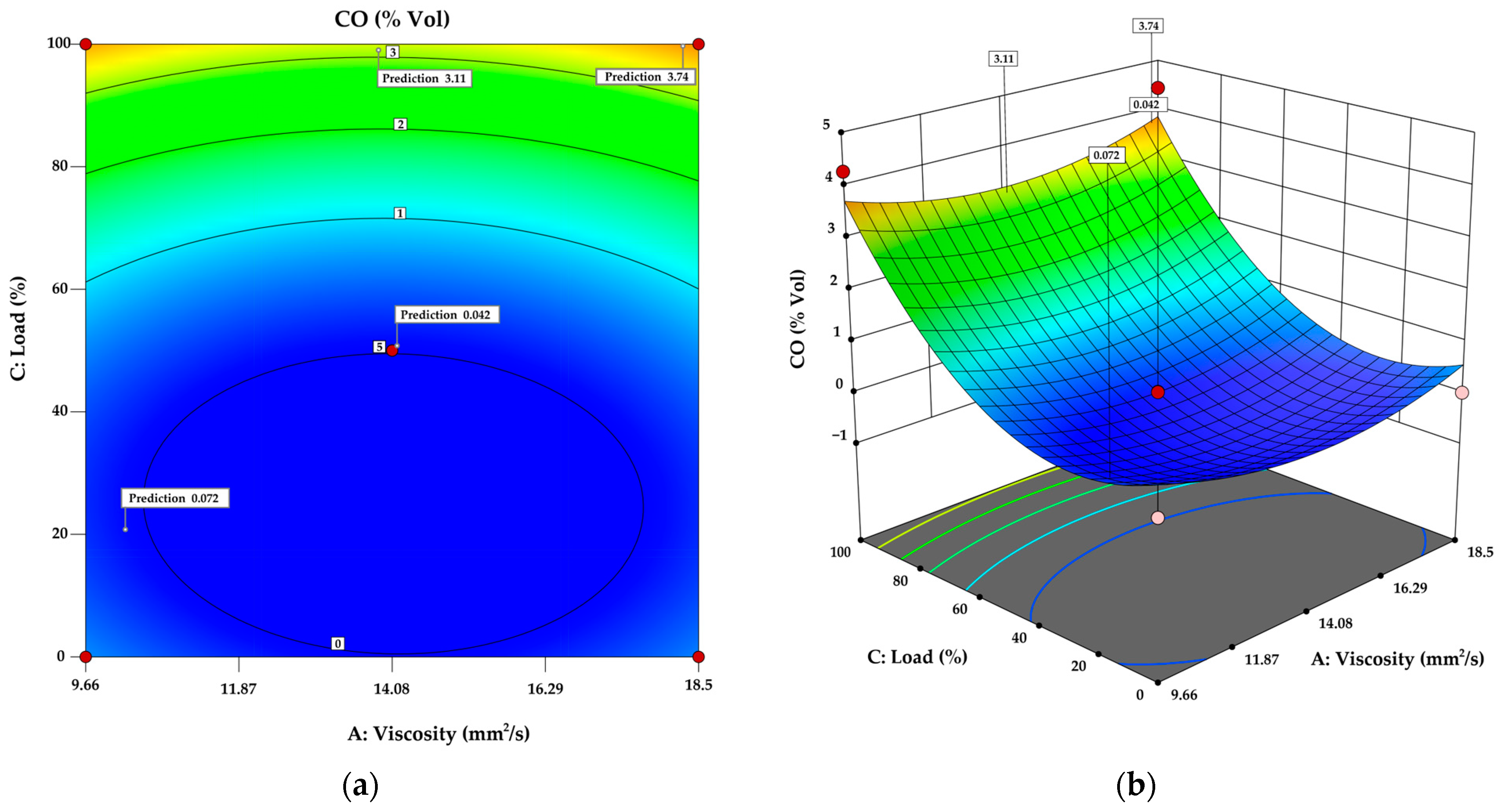
3.3. Model for CO
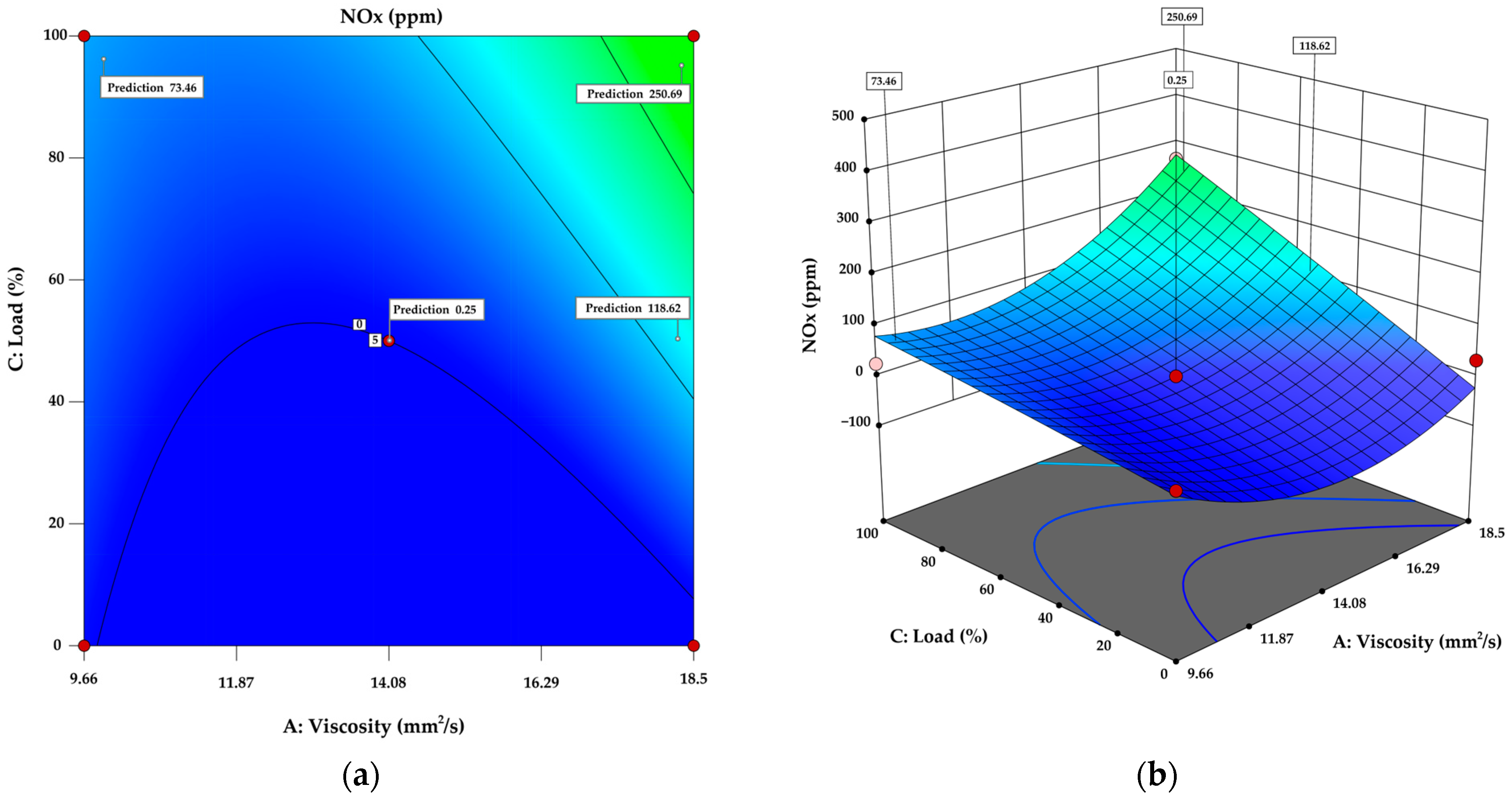
3.4. Model for NOx
3.5. Model for Consumption
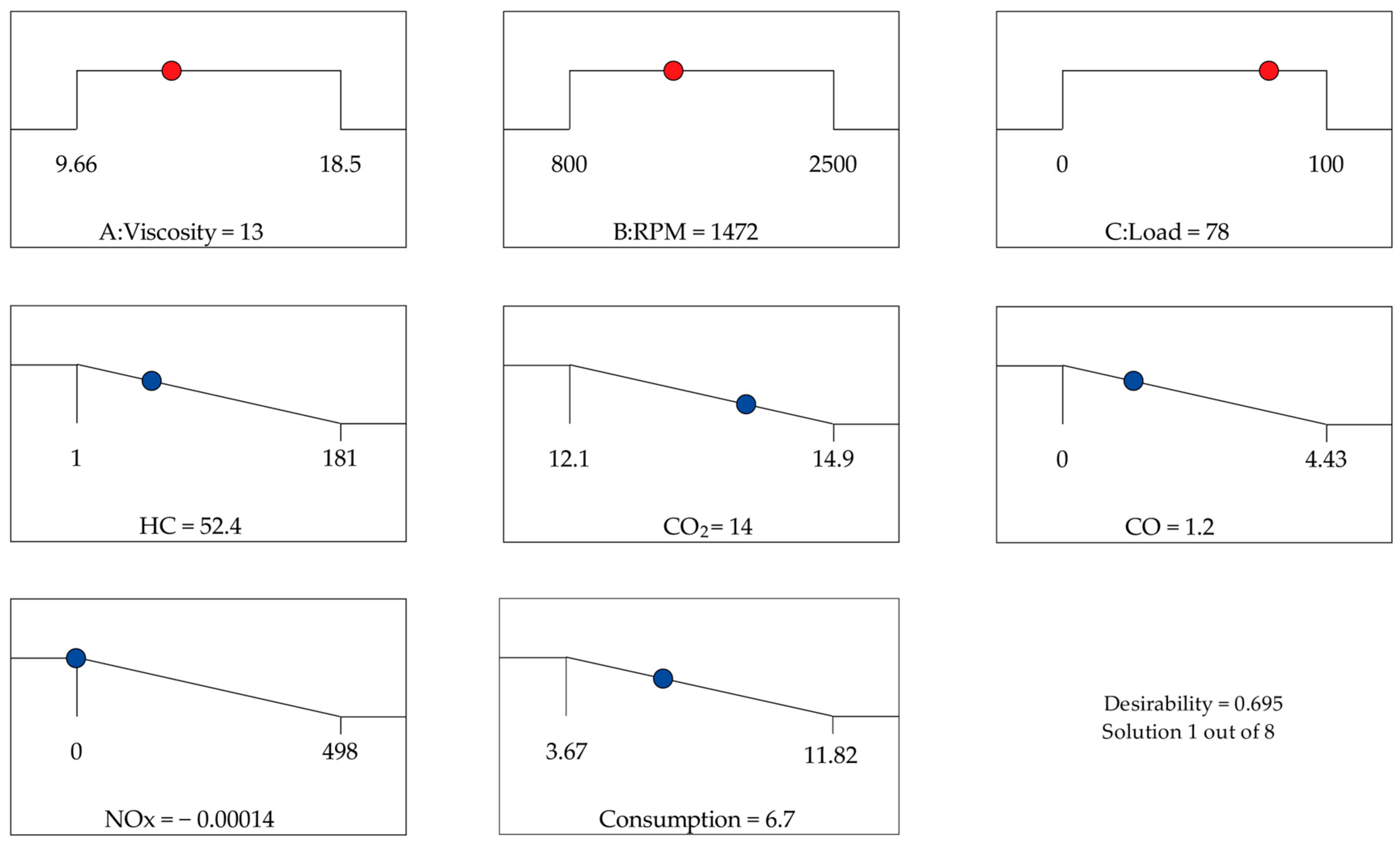
4. RSM-Based Optimization
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pischinger, S. Current and Future Challenges for Automotive Catalysis: Engine Technology Trends and Their Impact. Top. Catal. 2016, 59, 834–844. [Google Scholar] [CrossRef]
- Dargay, J. Road Vehicles: Future Growth in Developed and Developing Countries. Proc. Inst. Civ. Eng.-Munic. Eng. 2002, 151, 3–11. [Google Scholar] [CrossRef]
- 2030 Climate Targets-European Commission. Available online: https://climate.ec.europa.eu/eu-action/climate-strategies-targets/2030-climate-targets_en (accessed on 15 May 2024).
- Beles, H.; Tusinean, A.; Mitran, T.; Scurt, F.B. Research Regarding the Development of the Combustion Chamber of Internal Combustion Engines with Opposite Pistons. Machines 2023, 11, 309. [Google Scholar] [CrossRef]
- Khoa, N.X.; Lim, O. A Review of the External and Internal Residual Exhaust Gas in the Internal Combustion Engine. Energies 2022, 15, 1208. [Google Scholar] [CrossRef]
- Morgunov, B.; Chashchin, V.; Gudkov, A.; Chashchin, M.; Popova, O.; Nikanov, A.; Thomassen, Y. Health Risk Factors of Emissions from Internal Combustion Engine Vehicles: An Up-to-Date Status of the Problem. Здoрoвье Населения И Среда Обитания-ЗНиСО/Public Health Life Environ. 2022, 30, 7–14. [Google Scholar] [CrossRef]
- Van Basshuysen, R.; Schaefer, F. Internal Combustion Engine Handbook Basics, Components, Systems, and Perspectives; SAE International: Warrendale, PA, USA, 2004; ISBN 978-0-7680-1139-5. [Google Scholar]
- Payri González, F.; Desantes Fernández, J.M. Motores de Combustión Interna Alternativos; Editorial Universitat Politécnica de Valencia: Valencia, Spain, 2011; ISBN 8483637057. [Google Scholar]
- Posmyk, A. Influence of Material Properties on the Wear of Composite Coatings. Wear 2003, 254, 399–407. [Google Scholar] [CrossRef]
- Etsion, I.; Sher, E. Improving Fuel Efficiency with Laser Surface Textured Piston Rings. Tribol. Int. 2009, 42, 542–547. [Google Scholar] [CrossRef]
- Silva, C.; Ross, M.; Farias, T. Analysis and Simulation of “Low-Cost” Strategies to Reduce Fuel Consumption and Emissions in Conventional Gasoline Light-Duty Vehicles. Energy Convers. Manag. 2009, 50, 215–222. [Google Scholar] [CrossRef]
- Fontaras, G.; Vouitsis, E.; Samaras, Z. Experimental Evaluation of the Fuel Consumption and Emissions Reduction Potential of Low Viscosity Lubricants; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2009. [Google Scholar]
- Macián, V.; Tormos, B.; Bermúdez, V.; Ramírez, L. Assessment of the Effect of Low Viscosity Oils Usage on a Light Duty Diesel Engine Fuel Consumption in Stationary and Transient Conditions. Tribol. Int. 2014, 79, 132–139. [Google Scholar] [CrossRef]
- Murari, G.; Nahak, B.; Pratap, T. Hybrid Surface Modification for Improved Tribological Performance of IC Engine Components—A Review. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2023, 095440892211507. [Google Scholar] [CrossRef]
- Ha Hiep, N.; Cong Doan, N.; Quoc Quan, N.; Van Duong, N. Structural Modifications of the Inner Surface of Cylinder Liners for Decreasing Mechanical Losses in High-Speed Diesel Engines; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2023. [Google Scholar]
- Hazar, H. Effects of Biodiesel on a Low Heat Loss Diesel Engine. Renew. Energy 2009, 34, 1533–1537. [Google Scholar] [CrossRef]
- Balaji, M.; Sarfas, M.; Vishaal, G.S.B.; Madhusudhan, G.V.; Gupta, S.; Kanchan, S. Scope for Improving the Efficiency and Environmental Impact of Internal Combustion Engines Using Engine Downsizing Approach: A Comprehensive Case Study. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1116, 012070. [Google Scholar] [CrossRef]
- Menon, S.; Cadou, C. Scaling of Losses in Small IC Aero Engines with Engine Size. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, American Institute of Aeronautics and Astronautics, Reston, VA, USA, 5–8 January 2004. [Google Scholar]
- Leduc, P.; Dubar, B.; Ranini, A.; Monnier, G. Downsizing of Gasoline Engine: An Efficient Way to Reduce CO2 Emissions. Oil Gas Sci. Technol. 2003, 58, 115–127. [Google Scholar] [CrossRef]
- Podrigalo, M.; Tarasov, Y.; Kholodov, M.; Shein, V.; Tkachenko, A.; Kasianenko, O. Assessment of Increased Energy Efficiency of Vehicles with a Rational Reduction of Engine Capacity. Automob. Transp. 2022, 26–34. [Google Scholar] [CrossRef]
- Hernández-Comas, B.; Maestre-Cambronel, D.; Pardo-García, C.; Fonseca-Vigoya, M.D.S.; Pabón-León, J. Influence of Compression Rings on the Dynamic Characteristics and Sealing Capacity of the Combustion Chamber in Diesel Engines. Lubricants 2021, 9, 25. [Google Scholar] [CrossRef]
- Fan, Q.; Wang, Y.; Xiao, J.; Wang, Z.; Li, W.; Jia, T.; Zheng, B.; Taylor, R. Effect of Oil Viscosity and Driving Mode on Oil Dilution and Transient Emissions Including Particle Number in Plug-In Hybrid Electric Vehicle; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2020. [Google Scholar]
- Taylor, R.I.; Coy, R.C. Improved Fuel Efficiency by Lubricant Design: A Review. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2000, 214, 1–15. [Google Scholar] [CrossRef]
- Hei, D.; Zheng, M.; Liu, C.; Jiang, L.; Zhang, Y.; Zhao, X. Study on the Frictional Properties of the Top Ring-Liner Conjunction for Different-Viscosity Lubricant. Adv. Mech. Eng. 2023, 15, 168781322311550. [Google Scholar] [CrossRef]
- Macián, V.; Tormos, B.; Ramírez, L.; Pérez, T.; Martínez, J. CO2 Emissions Reduction by Using Low Viscosity Oils in Public Urban Bus Fleets. WIT Trans. Built Environ. 2015, 14, 255–266. [Google Scholar]
- Hawley, J.G.; Bannister, C.D.; Brace, C.J.; Akehurst, S.; Pegg, I.; Avery, M.R. The Effect of Engine and Transmission Oil Viscometrics on Vehicle Fuel Consumption. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2010, 224, 1213–1228. [Google Scholar] [CrossRef]
- Ishizaki, K.; Nakano, M. Reduction of CO2 Emissions and Cost Analysis of Ultra-Low Viscosity Engine Oil. Lubricants 2018, 6, 102. [Google Scholar] [CrossRef]
- Minami, I.; Murakami, H.; Nanao, H.; Mori, S. Additive Effect for Environmental Lubricants—Decreased Phosphorus Contents in Low Viscosity Base Oils for Antiwear Performance. J. Jpn. Pet. Inst. 2006, 49, 268–273. [Google Scholar] [CrossRef]
- Taylor, C.M. Engine Tribology; Elsevier: Amsterdam, The Netherlands, 1993; Volume 26, ISBN 0080875904. [Google Scholar]
- Ceballos, J.J.; Melgar, A.; Tinaut, F.V. Influence of Environmental Changes Due to Altitude on Performance, Fuel Consumption and Emissions of a Naturally Aspirated Diesel Engine. Energies 2021, 14, 5346. [Google Scholar] [CrossRef]
- Qi, Z.; Gu, M.; Cao, J.; Zhang, Z.; You, C.; Zhan, Y.; Ma, Z.; Huang, W. The Effects of Varying Altitudes on the Rates of Emissions from Diesel and Gasoline Vehicles Using a Portable Emission Measurement System. Atmosphere 2023, 14, 1739. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J. Investigation of the Effect of Simulated Atmospheric Conditions at Different Altitudes on the Combustion Process in a Heavy-Duty Diesel Engine Based on Zero-Dimensional Modeling. J. Eng. Gas Turbines Power 2022, 144, 061013. [Google Scholar] [CrossRef]
- Wan, M.; Huang, F.; Shen, L.; Lei, J. Experimental Investigation on Effects of Fuel Injection and Intake Parameters on Combustion and Performance of a Turbocharged Diesel Engine at Different Altitudes. Front. Energy Res. 2023, 10, 1090948. [Google Scholar] [CrossRef]
- He, C.; Ge, Y.; Ma, C.; Tan, J.; Liu, Z.; Wang, C.; Yu, L.; Ding, Y. Emission Characteristics of a Heavy-Duty Diesel Engine at Simulated High Altitudes. Sci. Total Environ. 2011, 409, 3138–3143. [Google Scholar] [CrossRef]
- Zheng, Y.M.; Xie, L.B.; Liu, D.Y.; Ji, J.L.; Li, S.F.; Zhao, L.L.; Zen, X.H. Emission Characteristics of Heavy-Duty Vehicle Diesel Engines at High Altitudes. J. Appl. Fluid Mech. 2023, 16, 2329–2343. [Google Scholar] [CrossRef]
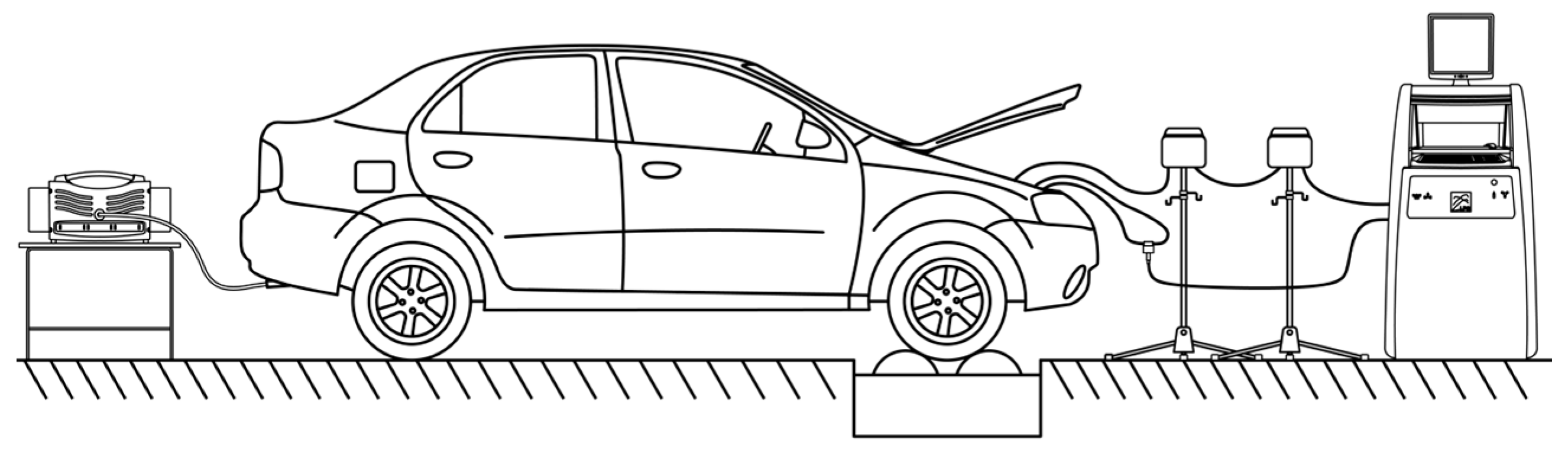
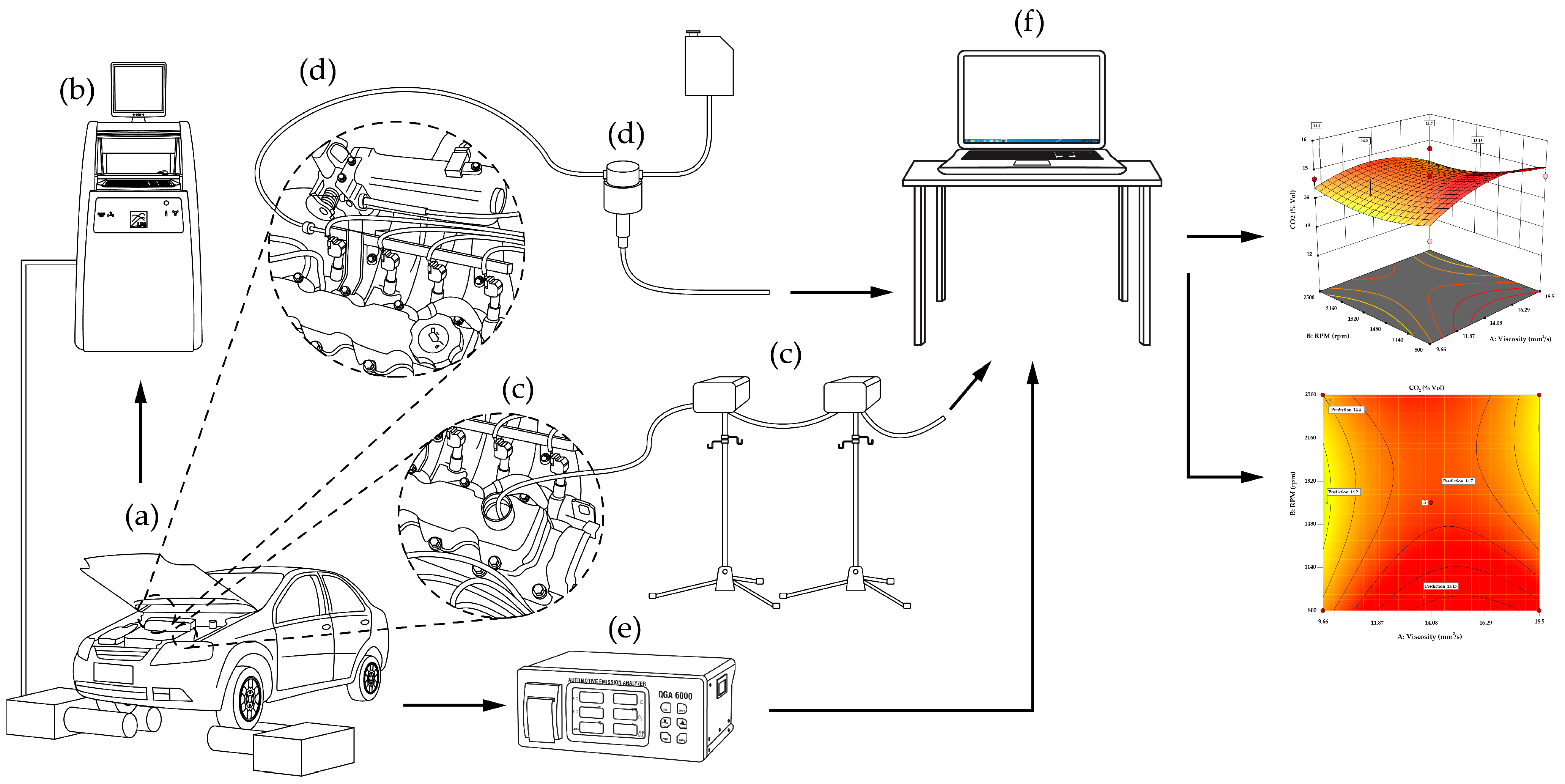



| Technical Specifications | |
|---|---|
| Engine | 1.5 L SOHC |
| Valves | 8 |
| Number of cylinders | 4 |
| Power (hp @ rpm) | 83 @ 5600 |
| Torque (Nm @ rpm) | 128 @ 3000 |
| Fuel supply | Multi-point fuel injection (MPFI) |
| Compression ratio | 9.5 |
| Final ratio | 3.944 |
| Gross vehicle weight | 1365 Kg |
| Load capacity | 325 Kg |
| Measuring Fields | Range | Unit | Resolution |
|---|---|---|---|
| CO | 0–9.99 | % vol | 0.01 |
| CO2 | 0–19.9 | % vol | 0.1 |
| HC hexane | 0–9999 | ppm vol | 1 |
| O2 | 0–25 | % vol | 0.01 |
| NOx | 0–5000 | ppm vol | 1 |
| Revolutions inductance/capacitance | 300–9990 | rpm | 10 |
| Oil temperature | 20–150 | °C | 1 |
| SAE Grade | 5w30 | 10w30 | 20w50 |
|---|---|---|---|
| Specific gravity @ 15 °C | 0.861 | 0.866 | 0.881 |
| Density, g/mL @ 15 °C | 0.859 | 0.864 | 0.878 |
| Color, ASTM D1500 | 3.0 | 3.0 | 3.0 |
| Flash point (COC), °C (°F) | 216 (421) | 229 (444) | 230 (446) |
| Pour point, °C (°F) | −39 (−38) | −39 (−38) | −30 (−22) |
| Kinematic viscosity, mm2/s @ 40 °C | 66.2 | 65.7 | 176 |
| Kinematic viscosity, mm2/s @ 100 °C | 9.66 | 14.08 | 18.5 |
| Viscosity index | 158 | 148 | 128 |
| Cold cranking viscosity, cP @ (°C) | 6150 (−30) | 4550 (−25) | 7200 (−15) |
| High-temp/high-shear viscosity, cP @ 150 °C | 3.1 | 3.0 | 4.9 |
| Factor | Unit | Lower Level | Middle Level | Upper Level |
|---|---|---|---|---|
| Viscosity | mm2/s | 9.66 | 14.08 | 18.5 |
| Engine speed | rpm | 800 | 1650 | 2500 |
| Load | % | 0 | 50 | 100 |
| Std Order | Run Order | Pt Type | Blocks | Viscosity (mm2/s) | rpm | Load (%) | HC (ppm) | CO2 (% vol) | CO (% vol) | NOx (ppm) | Consumption (L/h) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 13 | 1 | 0 | 1 | 14.08 | 1650 | 50 | 8 | 14.7 | 0 | 0 | 4.11 |
| 17 | 2 | 0 | 1 | 14.08 | 1650 | 50 | 8 | 14.7 | 0.01 | 0 | 5.12 |
| 2 | 3 | 2 | 1 | 18.5 | 800 | 50 | 7 | 14.8 | 0.01 | 80 | 6.76 |
| 6 | 4 | 2 | 1 | 18.5 | 1650 | 0 | 17 | 14.9 | 0.01 | 32 | 4.48 |
| 7 | 5 | 2 | 1 | 9.66 | 1650 | 100 | 181 | 12.1 | 4.27 | 25 | 11.03 |
| 9 | 6 | 2 | 1 | 14.08 | 800 | 0 | 7 | 14.9 | 0.01 | 19 | 8.82 |
| 3 | 7 | 2 | 1 | 9.66 | 2500 | 50 | 10 | 14.7 | 0.02 | 458 | 5.22 |
| 12 | 8 | 2 | 1 | 14.08 | 2500 | 100 | 156 | 12.4 | 4.08 | 498 | 11.81 |
| 16 | 9 | 0 | 1 | 14.08 | 1650 | 50 | 6 | 14.8 | 0.02 | 0 | 5.16 |
| 10 | 10 | 2 | 1 | 14.08 | 2500 | 0 | 14 | 14.9 | 0.02 | 59 | 4.95 |
| 15 | 11 | 0 | 1 | 14.08 | 1650 | 50 | 6 | 14.7 | 0.02 | 0 | 6.14 |
| 1 | 12 | 2 | 1 | 9.66 | 800 | 50 | 15 | 14 | 0.02 | 18 | 4.56 |
| 14 | 13 | 0 | 1 | 14.08 | 1650 | 50 | 1 | 14.7 | 0.03 | 0 | 6.22 |
| 5 | 14 | 2 | 1 | 9.66 | 1650 | 0 | 11 | 14.8 | 0.02 | 17 | 5 |
| 8 | 15 | 2 | 1 | 18.5 | 1650 | 100 | 169 | 12.1 | 4.43 | 266 | 11.48 |
| 11 | 16 | 2 | 1 | 14.08 | 800 | 100 | 9 | 14.9 | 0.02 | 81 | 8.26 |
| 4 | 17 | 2 | 1 | 18.5 | 2500 | 50 | 14 | 14.7 | 0.01 | 465 | 5.76 |
| Source | Sum of Squares | Df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 56,264.32 | 9 | 6251.59 | 6.36 | 0.0117 | significant |
| A-Viscosity | 12.50 | 1 | 12.50 | 0.0127 | 0.9134 | |
| B-RPM | 3042.00 | 1 | 3042.00 | 3.09 | 0.1220 | |
| C-Load | 27,144.50 | 1 | 27,144.50 | 27.61 | 0.0012 | |
| AB | 36.00 | 1 | 36.00 | 0.0366 | 0.8537 | |
| AC | 81.00 | 1 | 81.00 | 0.0824 | 0.7824 | |
| BC | 4900.00 | 1 | 4900.00 | 4.98 | 0.0607 | |
| A2 | 3035.46 | 1 | 3035.46 | 3.09 | 0.1223 | |
| B2 | 1883.46 | 1 | 1883.46 | 1.92 | 0.2088 | |
| C2 | 16,107.04 | 1 | 16,107.04 | 16.38 | 0.0049 | |
| Residual | 6881.80 | 7 | 983.11 | |||
| Lack of fit | 6849.00 | 3 | 2283.00 | 278.41 | <0.0001 | significant |
| Pure error | 32.80 | 4 | 8.20 | |||
| Cor total | 63,146.12 | 16 |
| Coefficient of Determination | Value |
|---|---|
| R2 | 0.8910 |
| Adjusted R2 | 0.7509 |
| Predicted R2 | −0.7362 |
| Source | Sum of Squares | Df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 14.13 | 9 | 1.57 | 4.59 | 0.0285 | significant |
| A-Viscosity | 0.1013 | 1 | 0.1013 | 0.2959 | 0.6034 | |
| B-RPM | 0.4513 | 1 | 0.4513 | 1.32 | 0.2886 | |
| C-Load | 8.00 | 1 | 8.00 | 23.38 | 0.0019 | |
| AB | 0.1600 | 1 | 0.1600 | 0.4675 | 0.5161 | |
| AC | 0.0025 | 1 | 0.0025 | 0.0073 | 0.9343 | |
| BC | 1.56 | 1 | 1.56 | 4.57 | 0.0700 | |
| A2 | 0.9904 | 1 | 0.9904 | 2.89 | 0.1327 | |
| B2 | 0.4178 | 1 | 0.4178 | 1.22 | 0.3057 | |
| C2 | 2.43 | 1 | 2.43 | 7.11 | 0.0322 | |
| Residual | 2.40 | 7 | 0.3422 | |||
| Lack of fit | 2.39 | 3 | 0.7958 | 397.92 | < 0.0001 | significant |
| Pure error | 0.0080 | 4 | 0.0020 | |||
| Cor total | 16.52 | 16 |
| Coefficient of Determination | Value |
|---|---|
| R2 | 0.8550 |
| Adjusted R2 | 0.6687 |
| Predicted R2 | −1.3124 |
| Source | Sum of Squares | Df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 39.85 | 9 | 4.43 | 6.57 | 0.0107 | significant |
| A-Viscosity | 0.0021 | 1 | 0.0021 | 0.0031 | 0.9569 | |
| B-RPM | 2.07 | 1 | 2.07 | 3.07 | 0.1232 | |
| C-Load | 20.29 | 1 | 20.29 | 30.09 | 0.0009 | |
| AB | 0 | 1 | 0 | 0 | 10.000 | |
| AC | 0.0072 | 1 | 0.0072 | 0.0107 | 0.9205 | |
| BC | 4.1 | 1 | 4.1 | 6.08 | 0.0431 | |
| A2 | 1.39 | 1 | 1.39 | 2.06 | 0.1942 | |
| B2 | 1.39 | 1 | 1.39 | 2.07 | 0.1936 | |
| C2 | 10.67 | 1 | 10.67 | 15.83 | 0.0053 | |
| Residual | 4.72 | 7 | 0.6742 | |||
| Lack of fit | 4.72 | 3 | 1.57 | 12,100.58 | <0.0001 | significant |
| Pure error | 0.0005 | 4 | 0.0001 | |||
| Cor total | 44.57 | 16 |
| Coefficient of Determination | Value |
|---|---|
| R2 | 0.8941 |
| Adjusted R2 | 0.7579 |
| Predicted R2 | −0.6943 |
| Source | Sum of Squares | Df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 4.95 × 105 | 9 | 54,953.48 | 12.96 | 0.0014 | significant |
| A-Viscosity | 13,203.13 | 1 | 13,203.13 | 3.11 | 0.121 | |
| B-RPM | 2.05 × 105 | 1 | 2.05 × 105 | 48.45 | 0.0002 | |
| C-Load | 69,006.13 | 1 | 69,006.13 | 16.27 | 0.005 | |
| AB | 756.25 | 1 | 756.25 | 0.1783 | 0.6855 | |
| AC | 12,769 | 1 | 12,769 | 3.01 | 0.1263 | |
| BC | 35,532.25 | 1 | 35,532.25 | 8.38 | 0.0232 | |
| A2 | 32,606.32 | 1 | 32,606.32 | 7.69 | 0.0276 | |
| B2 | 1.18 × 105 | 1 | 1.18 × 105 | 27.77 | 0.0012 | |
| C2 | 37.89 | 1 | 37.89 | 0.0089 | 0.9273 | |
| Residual | 29,684.25 | 7 | 4240.61 | |||
| Lack of fit | 29,684.25 | 3 | 9894.75 | significant | ||
| Pure error | 0 | 4 | 0 | |||
| Cor total | 5.24 × 105 | 16 |
| Coefficient of Determination | Value |
|---|---|
| R2 | 0.9434 |
| Adjusted R2 | 0.8706 |
| Predicted R2 | 0.0941 |
| Source | Sum of Squares | Df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 72.69 | 9 | 8.08 | 11.05 | <0.0001 | significant |
| A-Viscosity | 0.0061 | 1 | 0.0061 | 0.0083 | 0.928 | |
| B-RPM | 0.4278 | 1 | 0.4278 | 0.5855 | 0.4493 | |
| C-Load | 22.34 | 1 | 22.34 | 30.58 | <0.0001 | |
| AB | 0.81 | 1 | 0.81 | 1.11 | 0.2996 | |
| AC | 0.2601 | 1 | 0.2601 | 0.3559 | 0.5546 | |
| BC | 1.92 | 1 | 1.92 | 2.63 | 0.1142 | |
| A2 | 12.91 | 1 | 12.91 | 17.67 | 0.0002 | |
| B2 | 6.9 | 1 | 6.9 | 9.44 | 0.0041 | |
| C2 | 20.7 | 1 | 20.7 | 28.33 | <0.0001 | |
| Residual | 25.58 | 35 | 0.7307 | |||
| Lack of fit | 8.8 | 3 | 2.93 | 5.6 | 0.0034 | significant |
| Pure error | 16.78 | 32 | 0.5242 | |||
| Cor total | 98.27 | 44 |
| Coefficient of Determination | Value |
|---|---|
| R2 | 0.7397 |
| Adjusted R2 | 0.6728 |
| Predicted R2 | −0.6143 |
| Name | Goal | Lower Limit | Upper Limit | Lower Weight | Upper Weight | Importance |
|---|---|---|---|---|---|---|
| A: Viscosity (mm2/s) | is in range | 9.66 | 18.5 | 1 | 1 | 3 |
| B: RPM (rpm) | is in range | 800 | 2500 | 1 | 1 | 3 |
| C: Load (%) | is in range | 0 | 100 | 1 | 1 | 3 |
| HC (ppm) | minimize | 1 | 181 | 1 | 1 | 3 |
| CO2 (% vol) | minimize | 12.1 | 14.9 | 1 | 1 | 3 |
| CO (% vol) | minimize | 0 | 4.43 | 1 | 1 | 3 |
| NOx (ppm) | minimize | 0 | 498 | 1 | 1 | 3 |
| Consumption (L/h) | minimize | 3.67 | 11.82 | 1 | 1 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garcia Tobar, M.; Cabrera Ojeda, O.; Crespo Montaño, F. Impact of Oil Viscosity on Emissions and Fuel Efficiency at High Altitudes: A Response Surface Methodology Analysis. Lubricants 2024, 12, 277. https://doi.org/10.3390/lubricants12080277
Garcia Tobar M, Cabrera Ojeda O, Crespo Montaño F. Impact of Oil Viscosity on Emissions and Fuel Efficiency at High Altitudes: A Response Surface Methodology Analysis. Lubricants. 2024; 12(8):277. https://doi.org/10.3390/lubricants12080277
Chicago/Turabian StyleGarcia Tobar, Milton, Oscar Cabrera Ojeda, and Fredy Crespo Montaño. 2024. "Impact of Oil Viscosity on Emissions and Fuel Efficiency at High Altitudes: A Response Surface Methodology Analysis" Lubricants 12, no. 8: 277. https://doi.org/10.3390/lubricants12080277
APA StyleGarcia Tobar, M., Cabrera Ojeda, O., & Crespo Montaño, F. (2024). Impact of Oil Viscosity on Emissions and Fuel Efficiency at High Altitudes: A Response Surface Methodology Analysis. Lubricants, 12(8), 277. https://doi.org/10.3390/lubricants12080277






