The Effect of Plastic Deformation on the Flattening of Friction Surfaces

Abstract

This work aims to demonstrate the discrepancy between the results achieved in the application of ball-on-flat devices. Meanwhile, the interaction between contact parameters and the morphology of friction surfaces will be considered. Flattening depends on the mechanical properties of contact materials and the variation in the deformed structure in surface layers. To evaluate the interaction between roughness parameters and contact pressure, wear, and morphology of the surfaces, a ball-on-disk rig was applied. The average groove sizes were measured on micro- and macroscales. The relation between groove sizes on micro- and macro scales is close to the same. The flattening sinusoidal ball-on-flat model was considered. The real friction and wear tests were used to analyze plastic deformation by accounting for dislocation gliding and the interaction between neighboring asperities. The relation of shear stresses to the interference of rough asperities was established. The effective plastic strain gradient was evaluated. The formation of a highly effective plastic strain gradient is associated with a high dislocation density. The effect of dislocation density on the hardening–softening of surface layers is considered.

1. Introduction

Flattening refers to the process where the highest asperities on the surfaces are gradually flattened or leveled out due to the applied load. Flattening leads to an increase in the contact area between the surfaces, which can increase friction due to energy dissipation during deformation processes. Understanding the interplay between flattening and plastic deformation is essential for predicting and controlling friction and wear behavior in sliding contacts, rolling contacts, and abrasive wear processes. The object of this work is to analyze the interaction between the roughness parameters and the deformed microstructure of surface layers. Some models of the flattening and plasticity of surface layers will be analyzed.

A simple model of roughness surfaces represents a periodic profile projected on one of the contacting surfaces [1,2]. A smooth cylinder is considered to be a smooth surface on a regular wavy surface whose radius and wavelength are specified [2]. The plastic strain at the contact interface can be represented by two components: a compressive and a unidirectional shear component [3]. The contact pressure is increased by increasing the wavelength or decreasing the radius of the tip. Using Nowell and Hill’s model [2], Kapoor et al. showed that the normalized peak pressure (p_max/p₀) depends strongly on the roughness parameters [4]. High contact pressures increase local stresses, resulting in higher roughness parameters and a shorter service life. Finally, it was noted that the calculated normalized peak pressure did not account for plasticity.

Flattening, as well as the deformation and damage development under contact interaction, is a scale-dependent parameter. Scale effects from macro to nanoscales under dry friction were considered by Bhushan and Nosonovsky [5]. A definite relation between hardness parameters and the real area of contact was revealed. Harder surface layers result in smaller real contact areas. Moreover, it was demonstrated that the average shear strength is mainly determined by dislocation-assisted sliding and increases with decreasing geometrical scale. Scale-dependent friction results are dependent on the real contact area and shear strength of the surface layers under elastic or plastic contact conditions. At present, the precise definition and quantification of contact and friction lack the characteristic length parameters, which are responsible for scale effects. The roughness of asperities and the deformation parameters of friction surfaces are scale-dependent. In relation to this theory, the fractal model of asperity surfaces developed by Majumdar and Bhushan [6] does not contain length parameters and is based on the scale-invariant principle. Existing models of contact interaction during inelastic deformation are largely based on the continuum theory (e.g., Persson [7,8], Gong and Komvopoulos [9], Pei et al. [10], and Gao et al. [11]).

As a development of the continuum theory, discrete dislocation models allow us to demonstrate significant deviations from classical plasticity predictions. Concerning existing models of rough contact surfaces described by the continuum theory of plasticity, the discrete dislocation model provides contact pressures significantly higher than those predicted by the continuum theory of plasticity. For this reason, a strain gradient plasticity theory has been proposed for a better understanding of microscale deformation [12,13,14]. The dependence of the scale-dependent strain gradient determines the mechanical properties of contact interaction; the smaller the size of the deformed region, the greater the gradient of the plastic strain. A mechanism-based strain gradient plasticity model, linking strain gradients on the microscale (10–100 nm) and mesoscale (1–10 μm) under plastic deformation, was proposed by Gao H. et al. [15] and Huang et al. [16,17]. The effects of contact size and deformation resistance due to dislocation sliding on the evolution of the mean contact pressure were explored [13]. The response of crystals having dislocation sources in the surface layers to that of dislocation sources in the bulk was compared. Under severe plastic deformation of bulk sources, the mean contact pressure is independent of the friction condition, whereas, for sufficiently small contact sizes, there is a significant dependence on the friction condition. If only surface dislocation sources are considered, the contact pressure increases more rapidly with detachment depth than when bulk sources are present.

The plastic deformation of neighboring contact spots occurs at smaller deformation depths for small contact sizes, and this interaction leads to an increase in the slope of the contact pressure [13,14]. It should be pointed out that the exact location and strength of the sources and obstacles are found in the high-stressed region near the contact. It is concluded that the contact pressure on the macroscale (large contact spots ≥ 1 μm) is independent of the friction between the contacting surfaces, while for contact spot sizes (<1 μm), significant plastic deformation occurs.

Recently, Gao Y.F. et al. [18] provided an analysis of the contact between elastic–plastic solids, where the surface roughness was represented by a Weierstrass profile. Here, a two-dimensional contact model of deformation between two bodies—a flat, rigid platen and an elastic–plastic solid with a sinusoidal surface—was analyzed. The authors characterized the deformation of surface layers by two parameters: α = a/λ, where a is the half-width of the contact and λ is the period of the surface waviness. Plasticity of the surface layers was estimated by a new parameter, the index of plasticity, ψ = E*g/σ_Yλ, where E* and σ_Y are the effective modulus and yield stress of the substrate, respectively, and g is the amplitude of the surface roughness. Based on the analysis of ψ, eight stages of plasticity of asperity contact surfaces were considered: (a) elastic, elastic–plastic, or fully plastic for isolated Hertz contacts; (b) elastic, or elastic–plastic for isolated non-Hertzian contacts; (c) elastic, elastic–plastic, or fully plastic for contact interaction. Interaction between the contact pressure, size of the contact spots, indentation depth, and residual stress were investigated for each loading regime. In addition, the discrete dislocation plasticity theory was used to analyze single crystal indentation [19]. Size-dependent contact pressures calculated by application of the discrete dislocation plasticity theory were several times higher than those predicted by the continuum theory of plasticity. These results were confirmed by simulation of the interaction between neighboring rough asperity surfaces and contact pressure using discrete dislocation plasticity analysis [20]. The simulation was performed using the model of rough surfaces as an array of equispaced asperities with a sinusoidal profile. The asperity density effect is a result of the collective glide of dislocations, the formation of gradient nanocrystalline grains, and the interaction between neighboring plastic zones. Since dislocation-limited plasticity plays a dominant role, the asperity density effect will mainly be relevant for surfaces having a small asperity roughness. It is suggested that the asperity density effect vanishes when the hardening coefficient approaches zero. The real contact area is considered to be the sum of the contact spots in sheared asperities on a microscopic scale [21]. Nevertheless, the real contact area of small asperities and the pressure cannot be described accurately in the macroscopic plasticity of surface layers. In order to analyze the interaction between a rigid platen and an elastoplastic solid with rough rubbed surfaces, the conventional mechanism-based strain gradient plasticity model (CMSGP) was applied.

The flattening behavior of sinusoidal asperities is studied by the application of CMSGP and J2 isotropic plasticity theories. The flattening of strain-gradiented asperities gives rise to a higher flow stress and average contact pressure in the CMSGP model than in under-sized J2 plasticity. In general, all the materials considered increase their contact area nearly linearly with flattened surfaces. In this instance, the asperity distribution is strongly influenced by size-dependent plasticity and shifts toward higher pressure levels. Size-dependent plasticity magnifies the sensitivity of contact pressure to surface roughness; the larger the surface roughness, the bigger the difference between size-independent and size-dependent plasticity. According to the authors, future friction experiments, such as the shear of friction surfaces, and the analysis of gradient structures will be crucial in the development of simulation models and real contact interactions.

The static frictional behavior of a metal asperity in contact with a rigid platen was investigated by discrete dislocation plasticity simulations [22]. Plasticity can delay or inhibit slipping under close static conditions or low friction. Size-independent frictional behavior is observed when asperities of different sizes are flattened to the same depth and sheared. However, asperity sizes can vary under the same contact pressure: smaller asperities continue to slip, but larger asperities deform plastically. In other words, large asperities form during severe plastic deformation, localized in thick surface layers, while contact partial slip is dominant in contact with a smooth surface localized in thin surface layers. Moreover, small asperities can be subjected to higher pressure than large asperities when their contact area is smaller. Consequently, when real multiscale rough surfaces are tangentially loaded, the large macroscale asperities slide before small mesoscale asperities. When the smoothness of the rubbed surfaces is obtained, friction on the atomic scale is dominant.

Recently, Persson et al. investigated the plastic deformation of rough metallic surfaces [23,24]. The nature of plastic deformation on a sandblasted aluminum surface was studied. It is noted that Perrson’s model is less accurate than the discrete dislocation plasticity model, but it is easy to implement. It is expected that the resistance of asperities to severe plastic deformation becomes maximal when the applied stress approaches hydrostatic stress and further plastic deformation is limited. It was shown that the plasticity of deformed roughness depends strongly on work hardening and the stress–strain relation. The results of Persson’s theory were compared with those of discrete dislocation plasticity [25]. The results obtained by theory and by simulations are in good agreement for rough surfaces with a very small root mean square (rms) height. The multi-scale contact theory proposed by Jackson and Streator [26] was developed using a comparison with the finite element simulation analysis of rough surfaces and CMSGP theory [27]. Ghaednia et al. [28] summarize the models of elastic–plastic contacts in a wide range of geometries and loading situations.

Recently, Ta W. et al. [29] considered the interface model, including the mechanical and thermal properties of the friction contact, by establishing a mechanical–thermal contact model. The authors evaluated the contact area, number of contact points, void, and contact force based on the thermal analysis of contact resistance. The proposed model, based on the change in contact volume, allows us to describe the change in the real contact area and the number of contact points. In this model, all micro-contacts are in various states ranging from elastic to severe plastic deformation.

Here, we seek to employ the theoretical models of the deformation process in the analysis of asperity contact interaction (flattening models) published in the literature and the experimental results of the effect of test time on the variation in the parameters of asperity contact, friction, and wear of pure FCC metals. This study investigated the interaction between the plasticity of deformed surface layers of FCC metals and the flattening parameters, hardness, and asperity profiles. The effectivity of plastic strain gradients on the formation of surface profiles will be evaluated. The balance between hardening and softening in surface layers of friction contact on the one hand and the external parameters of loading (contact area, contact pressure, and distribution of asperity contacts) on the other hand will be considered. The interaction between applied external and internal stresses will be evaluated during friction in the steady state. The two-dimensional contact model of a flat, rigid plate and an elastic–perfectly plastic solid with a sinusoidal surface will be analyzed while considering a link between parameters of a gradient nanograined structure and the flattened spots. Multi-asperity contact surfaces subjected to severe plastic deformation will be analyzed as being size- and scale-dependent. The interaction between the asperity parameters and variations in the deformed structure will be performed on macro and mesoscales.

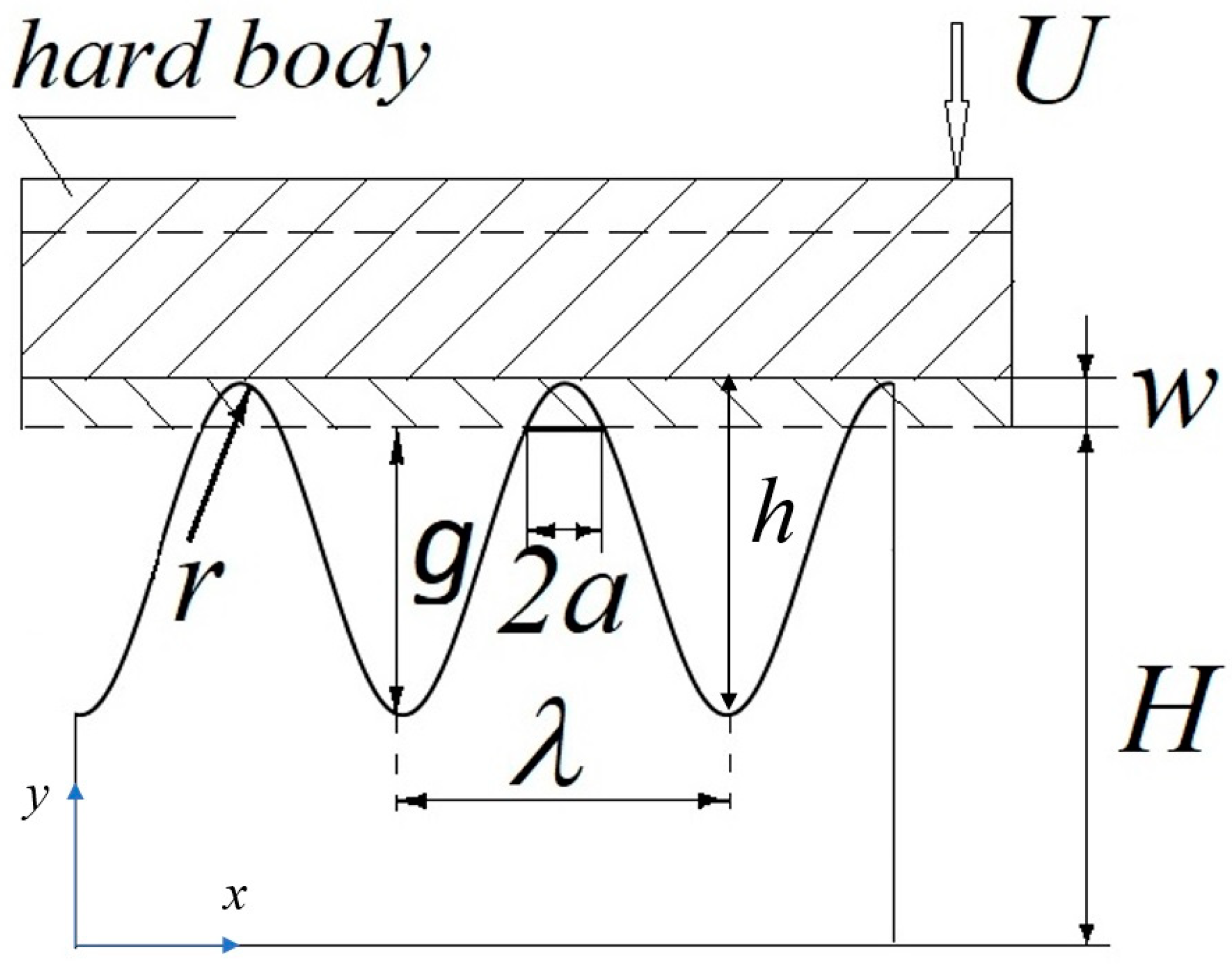
2. Models of Flattening and Discrete Plastic Deformation

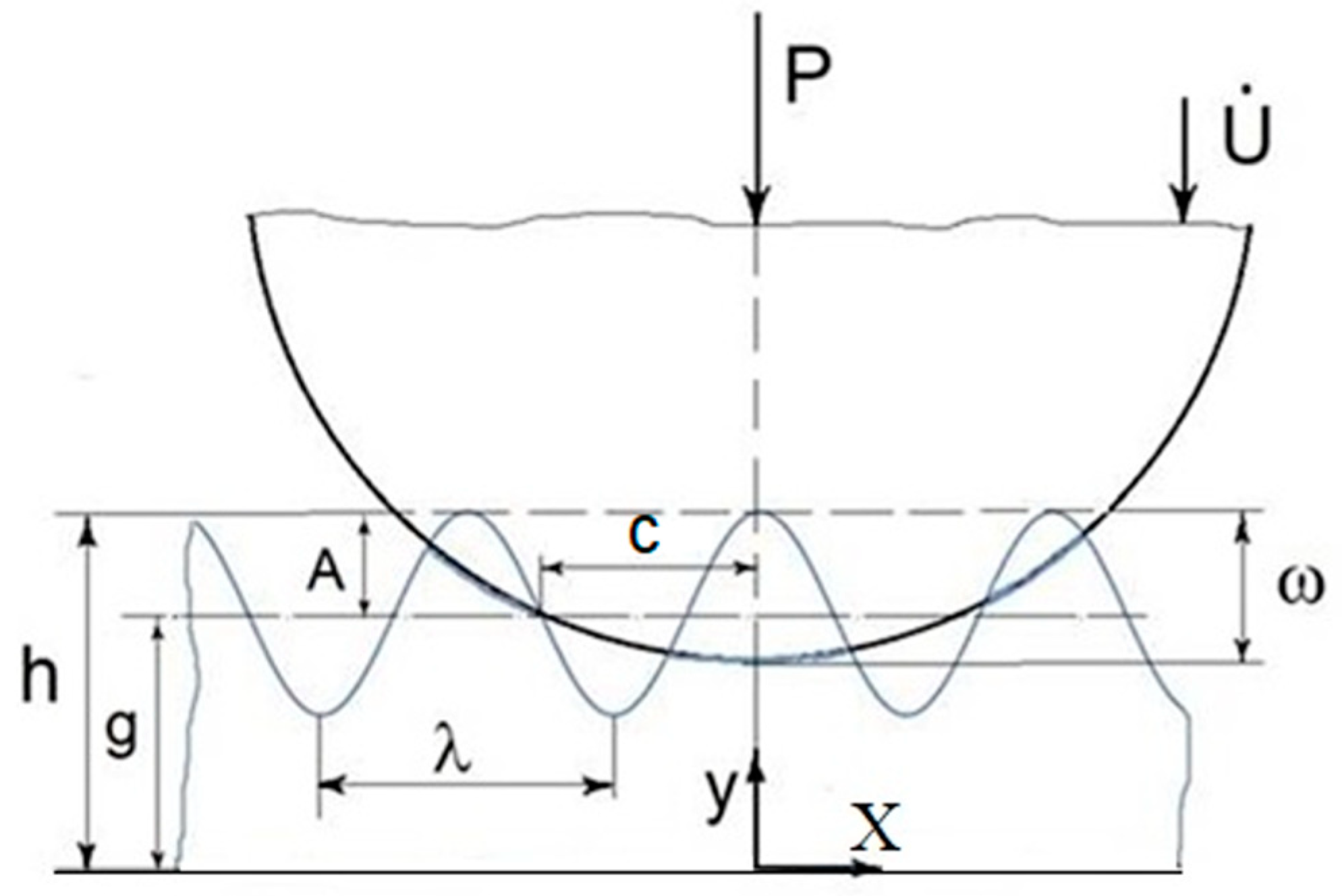
The effect of roughness on sliding contact is the basis of most models of friction and wear, e.g., [30,31,32,33,34]. We will start with the partial contact model for a sinusoidal surface used to develop a relation between the distribution of contact pressure on different scales [35,36,37,38]. In Figure 1, a two-dimensional elastic rigid body with a sinusoidal profile was first considered, where

$$h\left(x\right)=g·\cos \left({\displaystyle \frac{2\pi x}{\lambda }}\right)$$

(1)

Furthermore, the roughness was described by the two-dimensional Weierstrass function as

$$h\left(x_1\right)=g_0{\sum }_{n=0}^{\infty }{\gamma }^{\left(D-2\right)n}\cos \left({\displaystyle \frac{2\pi {\gamma }^n{x}_1}{{\lambda }_0}}\right),$$

(2)

where g₀ and λ₀ are the amplitude and wavelength of the Zeroth scale, respectively, and g and D are dimensionless parameters that characterize the fractal properties. The authors represent the contact area by a fractal set, i.e., contact is limited by set of infinitesimal contact segments with the limit n → ∞. It is clear that the addition of surface contamination, diffusion, and adhesion would also vary the behavior of mesoscale contacts. A.J. Gao et al. [11] developed Ciavarella’s research of elastic–plastic solids. The average contact pressure p_m and nominal contact pressure p were estimated by

$$p_m={\displaystyle \frac{1}{a}}{\int }_0^{a}p\left(x\right)dx, \mathrm{and} \overline{p}={\displaystyle \frac{2}{\lambda }}{\int }_0^{a}p\left(x_1\right)d{x}_1,$$

(3)

where a represents the contact half-width; 0 < $a$ < λ/2. No connection between contact pressure and the parameters of plasticity in the surface layers appeared. Functional relationships between these parameters are defined by

$${\displaystyle \frac{p_m}{{\sigma }_y}}={\prod }_p(\alpha ,{\displaystyle \frac{g}{\lambda }},{\displaystyle \frac{E^{*}}{{\sigma }_y}},\nu ),$$

(4)

where α = α/λ is the fractional contact area. An additional dependent parameter, Ψ, has been introduced [19]:

$$\Psi =g·{\displaystyle \frac{E^{*}}{\lambda ·{\sigma }_y}}$$

(5)

It is suggested that there are substantial regions of parameters where the behavior of the contact depends on α. ψ, g/λ, and E^*/σ_y. E^* = E (1 − ν²). For a large number of materials, 10 < E*/σ_Y < 1000, and for most surfaces, 0.01 < g/λ < 0.1. Thus, ψ comprises a significant amount of parameters, i.e., 0.1 < ψ < 100. The parameter α and the nominal contact pressure p can be regarded as load parameters. However, the analysis of these parameters in the elastic–plastic and plastic regimes indicates that ψ and α do not fully characterize the features of the contact interaction. The maximum value of p_m depends on the properties of the material (E/σ_Y) and the contact geometry (g/λ). The transition from an elastic–plastic to a fully plastic contact occurs for a definite value of α~0.7 [18]. The elastic to elastic–plastic contact is determined only by the parameters α and ψ, and it is independent of the parameter g/λ. When neighboring plastic spots interact, the contact pressure increases abruptly and may reach high values of hardness. To evaluate the effect of surface roughness on the displacement of the hard body, Gao et al. [18] described a difference in the vertical displacements ${\overline{u}}_2^I$ and ${\overline{u}}_2^S$ on the surfaces of the rigid body and the solid, respectively:

$$\delta ={\displaystyle \frac{2}{\lambda }}{\int }_0^{\lambda /2}({\overline{u}}_2^I-{\overline{u}}_2^S)d{x}_1$$

(6)

A sharp increase in both the asperity and the nominal contact pressure begins when δ/g→1 and Ψ > 2. The fraction of direct contact is about 30% higher than in linear elastic regimes under high contact pressure and severe plastic deformation. It was concluded that for most engineering surfaces, only the first few roughness scales (0 < n < 4) will be in the elastic or elastic–plastic regimes of behavior. The scales (n > 4) are characterized as a fully plastic asperity interaction, which occurs at high values of α and ψ. In addition, the average values of asperity contact pressure persists and approaches a fixed asymptote as n→∞.

To compare the results of the simulation with real contact conditions, the value of ψ under real experiments with Cu rubbed in elastohydrodynamic lubrication (EHL) and boundary lubrication (BL) regions were evaluated [39].

According to preliminary results [40,41], the following parameters were used: E*~143 GPa (E = 130 GPa, n = 0.3); σ_y in the steady states of the EHL and BL regions (σ_y = H/3): σ_EHL~0.37 and σ_BL~0.57 GPa; and g/λ was chosen as 0.01 and 0.05 under friction in EHL and BL regions, respectively. The calculated values of Ψ are as follows: Ψ = 3.9 and 12.5 in EHL and BL conditions, respectively. As can be seen, Ψ > 1 in the EHL region, while Ψ > 10 in the plastic region. 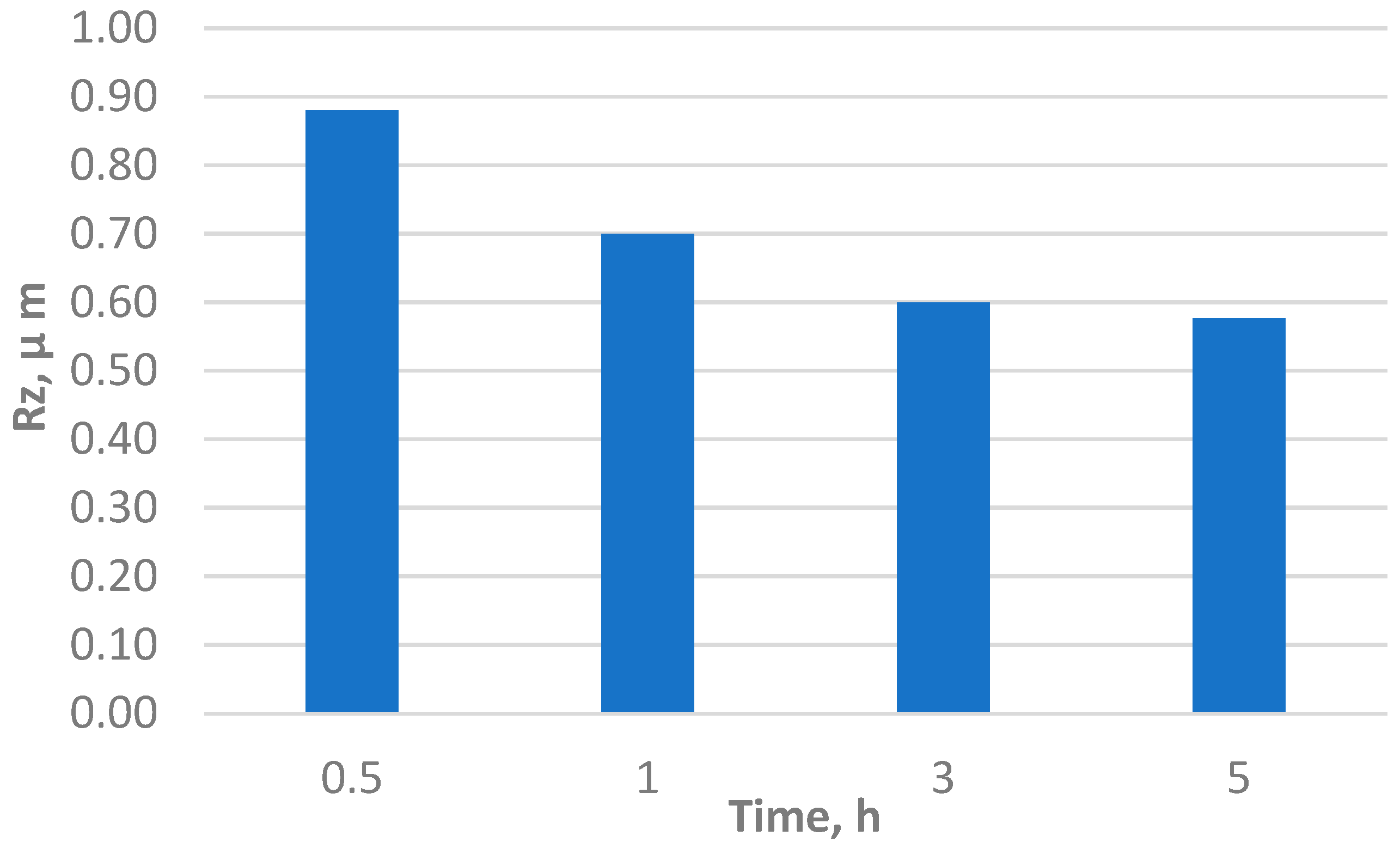Interestingly, when a severe plastic deformation gradient occurs in the BL region, the real value of Ψ is significantly larger than in the simulation. When the hardness of the surface layers was increased from 1100 MPa to 1700 MPa, the roughness parameter, Rz, was raised from ~0.2 to 0.65 μm in the EHL and BL regions, respectively. If H_BL/H_EHL is greater than 1.5, then Rz_BL/Rz_EHL is greater than 3. Hence, we can draw the following conclusion: the idea that “harder is smoother” is convenient in the description of initial hardness only. Moreover, hardening in the BL region does not directly effect a decrease in the roughness of the asperities. It is suggested that flattening is mainly determined by the relation between the applied stress and the deformation resistance stress. During friction in the steady state (μ and H are constant), λ will decrease while δ (and Rz) will increase with loading. The definite correlation can be observed between the vertical displacement δ and the Rz parameter; the larger the δ, the deeper the penetration of the indenter into the surface layers (Rz).

Discrete dislocation plasticity (DDP) simulation investigates the role of interactions between neighboring asperities on the contact pressure induced by a rigid platen on a rough surface. In this instance, the sinusoidal surface asperity model flattened by a rigid platen is considered [20]. A sinusoidal profile of asperities is characterized by the wavelength λ and amplitude A. The spacing asperities are described by the next function:

$$f\left(x_1\right)=h-Acos({\displaystyle \frac{2\pi x_1}{w}}){ x}_1\in (0,w),$$

(7)

where h is the height from the bottom of the crystal to the mean height of the asperity. The contact area, C, is defined as the region of direct contact between the flat platen and the crystal. To evaluate the effect of contact load on the platen surface, the flattening force F (per unit of length) was calculated:

$$F=-{\int }_{x_1\in C}{\sigma }_{22}d{x}_1,$$

(8)

The fundamental equation for shear rate on the slip system α corresponds to the viscoplastic power law [42,43]:

$${\dot{\gamma }}^{\alpha }={\dot{\gamma }}_0^{\alpha }exp({\displaystyle \frac{-F_0}{k_{B}T}}{\{1-{[{\tau }_{eff}^{\alpha }/S^{\alpha }\times G/G_0]}^p\}}^q sgn({\tau }^{\alpha }-{\tau }_b^{\alpha })$$

(9)

Without going into the complexities of this equation, the driving force of plastic deformation as the effective stress, τ^α_eff, will be considered. τ^α_eff = {(τ^α − τ_b^α)/S^α}, where τ^α is the applied stress, τ_b^α is the internal back stress, and S^α is the local athermal stress. The back stress defines the deformation resistance of dislocation pile-ups. The back stress can be screened when the number of piled-up dislocations approaches the critical value. The evolution of back stress increases in fine grains of the surface layers during friction, while it decreases in the softening process. The balance between hardening and softening was considered in our previous works [44,45] and will be analyzed in our future works in more detail. Increasing the hardness of surface layers with the formation of a refined structure decreases the wear rate. On the other hand, ductility is deceased, leading to failure development. Wear properties are best achieved under high work hardening and definite softening values determined by dynamic recovery or dynamic recrystallization at relatively high temperatures. Our experiments showed that τ^α_eff = τ^α − τ_b^α is very low in a steady friction state in the regime of balanced deformation hardening–dynamic recovery [45].

The applied stress can be expressed as τ_α = μL/NA in friction, where μ is the coefficient of friction, N is the number of contact spots, and A is the area of a single contact. Here, τ^α is the applied stress at the macroscale level, where dominant processes are determined by the hardness and wear of contact points. Plastic deformation at the mesoscale is characterized by dislocation gliding as interference decreases. Qualitative analysis of the applied and back stress will allow us to better understand the model of structural balance during friction and the transition to instability. We will investigate the mechanisms of plasticity to characterize the applied stress, back stress, and energy activation during friction.

Song H. et al. [21] analyzed the strengthening of the asperity density effect in the plastic deformation of surface layers and evaluated the effects of different combinations of dislocation interactions under plastic deformation of asperity contact as (a) plastic strain gradient effects, (b) the interaction between plastic zones, or (c) limited dislocation plasticity. It is known that severe plastic deformation of asperity surfaces is accompanied by the formation of inhomogeneous compressive stress in thin surface layers of about two microns of the crystal, according to the DDP simulation. Importantly, stress peaks are remarkably high, up to 200 times the yield strength. Moreover, the effect of the distance between contact spots was analyzed. Simulations were performed for asperities with the following sizes: w = 2 μm and A = 0.1 μm; a constant obstacle spacing, Lobs = 0.18 μm; but different spacings between nucleated spots: Lnuc = 0.09, 0.13, 0.26 and 1 μm. A maximum effect appeared for a spacing between spots of Lnuc = 1 and 0.26 μm. When decreasing the number of spacing sources, the effect of the asperity density decreases until it converges at the plasticity limit. Hence, when plastic deformation was estimated by DDP simulation with a source spacing of about Lnuc = 0.26 μm, the effect of the asperity density was enhanced both in the elastic and the continuum plastic regimes. Finally, it was shown that the asperity density depends significantly both on the hardening and the continuum plasticity. The effect of asperity density on the asperity size was also investigated. Simulation was performed for some asperity parameters: w = 4 μm, spaced at s = 4 μm and s = 16 μm. As expected, the larger the asperities, the easier it is to flatten the contact spots compared with the smaller asperities. When the actual spacing between contacts is twice as large as that for small asperities, the interaction of plastic zones is not expected. Our experiments under friction in lubricant conditions [43,44] and dry friction [46] indicate the complexity of plasticity and flattening in surface layers, demonstrating that the application of continuum plasticity in the analysis of friction and wear mechanisms is limited. Furthermore, Song H. et al. [21] proposed a conventional mechanism-based strain gradient plasticity (CMSGP) model for two-parameter characterizations of rough surfaces using the analysis of the root mean square (rms) height and the surface correlation length ls:

$$rms=\sqrt{{\displaystyle \frac{\sum _1^n{z}_i^2}{n}}}$$

(10)

The average contact pressure of asperity p_m,asp under a definite pre-set displacement U is given as:

$$p_{m, asp}={\displaystyle \frac{1}{C}}{\iint }_C\overline{p}\left(x,y\right)dxdy,$$

(11)

Here, p (x, y) represents the contact pressure of the partial element, and C indicates the contact area between the two surfaces. Furthermore, a strain-like value is described as: ε = U/R_asp, where U is the displacement of the asperity under the deformation and R_asp is the radius of curvature. Three spherical asperities with radii of 50 μm, 5 μm, and 0.5 μm were chosen. Contact pressure and strain change analyses indicate a strong size dependency between asperity parameters and the contact surface deformation; smaller is harder. Similar experiments [15,17] use the Taylor hardening model to describe the deformation shearing:

$$\tau =\alpha Gb\sqrt{{\rho }_s+{\rho }_G},$$

(12)

where μ is the shear modulus, b is the magnitude of the Burgers vector, and α is an empirical coefficient of the order 0.2–0.5. The densities, ρ_s and ρ_G, are the densities of the statistically stored (SSD) and geometrically necessary dislocations (GNDs), respectively. The density of the GND is connected to the effective plastic strain gradient η^p:

$${\rho }_G=\overline{r}{\displaystyle \frac{{\eta }^p}{b}}$$

(13)

If ρ_G = 10¹⁴ m⁻², $\overline{r}$ is the Nye factor, which is close to 1.9 for FCC polycrystals, and if b = 0.25 nm, then η^p = 100 μm⁻¹. The real evaluation of η^p, performed for nanocrystalline Cu (d~100 nm) after friction in the BL region will be considered bellow. Following this line of reasoning, Huang et al. [16,17] proposed an expression for flow stress that holds in the presence of strain gradients. The flow stress, σ_flow, is

$${\sigma }_{flow}={\sigma }_y\sqrt{f^2\left({\epsilon }^p\right)+l{\eta }^p}$$

(14)

where l is the intrinsic material length, l ≈ μ/σ_Y, and it is in the range of micrometers. It is seen from Equation (14) that the flow stress grows with increasing $l{\eta }^p$. Thus, the asperities become harder and smoother as the flow stress increases. The interaction between the microscopic flow stress, σ_flow, and the macroscopic yield stress, σ_y, was formulated as σ_flow = σ_y f(ε^p), where ε^p is the effective plastic strain, and f is the non-dimensional hardening function. f(ε^p) is represented as f(ε^p) = (1 + Eε^p/σ_Y)ⁿ, where E is Young’s modulus, and n is the plastic work-hardening exponent (0 < n < 1).

A lot of length scale parameters are used in the analysis of the interaction between the plasticity of surface layers and the flattening of the asperity contact. There is a constant obstacle spacing (L_obs = 0.18 μm) and different source spacings (L_nuc = 0.26 and 1 μm [18], some micrometers [19], or l = 4.4 μm [25]). The l value was evaluated based on our friction test with Cu and Ni [35]. For instance, l (Cu)~0.4 μm, and ~0.3 μm for Ni. Usually, the real value of l under severe plastic deformation in the nanocrystalline structure is decreased and close to L_nuc = 0.26 μm. Analysis of the material’s length under deformation during friction will be considered in more detail in the part on “Results”.

Furthermore, statistics of the contact pressure were analyzed. The real pressure distribution on the rough surface is difficult to estimate experimentally. It is noted that the change in pressure distribution using the CMSGP model is much more significant. Since A/A₀ and U are strongly related, it is preferable to study the distribution of contact pressures at a particular U value. The contact pressure distribution is insensitive to whether it is computed at the same flattening distance, U = 0.25 μm (when A/A₀ is found to be 0.3), or at the same contact area, A/A₀ = 0.1 (which requires flattening to U = 0.16 μm). Finally, it was concluded that increased surface roughness in a larger strain gradient is mathematically equivalent to a larger material intrinsic length l in CMSGP theory.

The considered relations, A/A₀, were compared under friction in the BL region. The A/A₀ relation in friction tests of FCC metals was calculated based on the results presented in refs. [41]. Interestingly, this relation is significantly lower than in the simulation: A/A₀ = 0.07 and 0.06 for Cu and Ni, respectively. Thus, the number of asperities in direct contact is relatively low under friction in lubrication conditions, i.e., a large part of the load is taken by the lubricant film. It is clear that the U value will be lower in conditions of lubrication in the simulation.

Researchers widely accept the contact model of Kogut and Etsion (KE) [47]. In the KE model, the transition from elastic deformation to elastic–plastic deformation is determined by the critical deformation thickness: δcr = (p_KH/2E)². Based on the KE model, and the multi-scale contact theory of Jackson and Streator [26], the scale effect using a finite element method and CMSGP theory was analyzed [27]. The following relationships of dimensionless contact parameters (contact force, P/Pcr; contact area, A/Acr; and deformation thickness, δ/δcr) were considered. In an elastic regime, where δcr represents the critical interference at the yielding initiation, Pcr and Acr indicate the critical contact force and contact area in the elastoplastic regime. It is suggested that the single asperities are distributed on the surface, and that they have the same geometric parameters for the contact load equally for each scale space i. Thus:

$$P_i={\displaystyle \frac{P}{{\eta }_i{A}_{i-1}}}; {\overline{\delta }}_i=f\left({\overline{P}}_i\right), \mathrm{and} {\overline{A}}_i=f\left({\overline{P}}_i\right),$$

(15)

where Pi, Ai, and ${\overline{\delta }}_i$ are the contact force, contact area, and deformation thickness, respectively, and η_I is a real asperity number density. The fitting parameters d, m, c, and e are varied for different materials and contact conditions and will be estimated in future work.

Finally, the effect of a deformed shape on hardness and the real-time change during the contact process were not considered in this study. Hence, in our future work, we will continue to explore the influence of the above factors on contact behavior with the scale effect to broaden the applicability of the model.

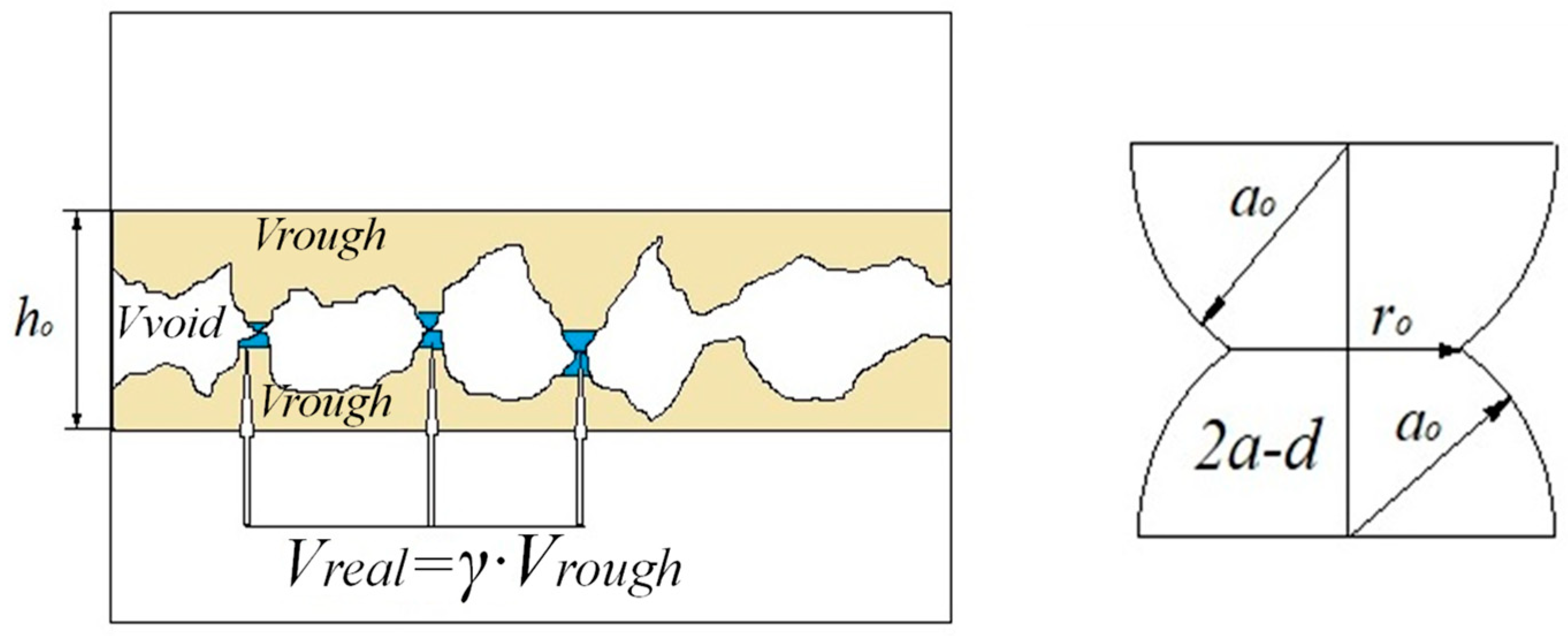
Previously, Ta et al. [29] had proposed a mechanical–thermal contact model based on the reconstruction of the contact interface, as shown in Figure 2.

The volume of the two solid contact parts, V_total, is considered as three volumes by these two parameters, which are the void volume V_void (equal to αV_total), rough volume V_rough (equal to V_total − V_void), and true contact volume V_real (equal to γV_rough). The void volume should gradually decrease, while the actual contact area should gradually increase as the contact is loaded. The void ratio in the initial contact, α₀, and the real contact volume ratio, γ, are close to zero. The relationship between α and γ is described by an exponential function. The authors evaluate the real contact area S_real as a relation between the real contact volume γV_rough and (h₀ − d), where d is the contact depth, d = (α₀ − α)h₀, and the real contact volume change, V_real = [V_total − (α₀ − Δα)V_total]γ, and the void reduction ratio is Δα = d/h₀; α = α₀ − d/h₀. As can be seen, all equations for contact depth, S_real, and V_real include α as a fitting parameter. All parameters determined by α and A are key parameters that depend on the deformation plasticity of surface layers. It is noted that as contact occurs, α gradually decreases to 0, and γ gradually increases to 1. In fact, when γ is close to 1, seizure or galling usually appears. The values of α, A, and γ depend strongly on variations in the mechanical properties and the deformed microstructure, geometrical, and loading parameters of the contact bodies. Such analyses were not considered in the presented work. Therefore, this model cannot present reliable results. The number of contacting asperities n is expressed as n = A^a N_max, where N_max is the number of contact asperities after full contact. However, full contact is not obtained in the conditions of normal friction. The S_real is described as

$$S_{real}^p={\displaystyle \frac{F}{{\sigma }_y}}+{\displaystyle \frac{{\pi }^2{\sigma }_y^2\gamma S_n}{12E^2}}$$

(16)

The correlating contact force F acting on the asperities equals F/n = F/γN_max. The contact force F is the tangential force that depends on the many geometrical and structural parameters. Moreover, σ_Y is an unknown parameter determined by the accumulation of plastic deformation and the formation of the gradient structure. To confirm the results of simulation, the friction from 99.90% copper was studied. Finally, it is concluded that the proposed model provides direct observation of the interface morphology and temperature and stress distributions, which allows us to evaluate the interface performance. This conclusion was not confirmed by physical evidence. Moreover, the loads in the presented results under Cu friction have unreal values (2000–10,000 N) [29]. Some realistic results of loads under friction from Cu or Cu alloys are presented here: 1.5 N [48]; 10 N (Cu-Ag) [49], 10–200 N (Cu-Zn) [50], and 30 N (Cu-Al) [51] (all in dry friction).

Finally, it can be concluded that the interaction between asperity distribution and the deformed structure of surface layers plays a crucial role in the prediction of friction and wear behavior, which warrants further investigation of the interaction between the applied stress and deformation resistance based on modern new models.

3. The Interaction between Roughness Parameters and Morphology of the Friction Surfaces (Experimental Results)

Mechanical properties of materials and variations in deformed structures in surface layers determine flattening. The main aim of the experiments presented here is to examine the interaction between contact parameters and friction and wear processes. To demonstrate the variation in asperity contacts during friction, the time of the tests was varied from 0.5 to 5 h under a definite load and sliding velocity.

3.1. Procedure

To evaluate the interaction between roughness parameters and contact pressure, wear, and morphology of the surfaces, the homemade ball-on-disk rig was loaded under a definite load, 19 N. The sliding velocity was 0.22 m/s. The load and sliding velocity were chosen based on our previous experiments [40,41]. Experimental durations ranged from 0.5 to 5 h. Ball bearings made from stainless steel 302 L with a diameter of 10 mm were moved against a steel disk (AISI 1040, Four Seas Steel Group, Qingdao, China). The ball and disk hardness were ~4300 MPa and 5600 MPa, respectively. The real contact pair does not correspond to the theoretical model of a hardened ball on a soft disk. Therefore, the morphology of the ball and disk as well as the roughness parameters of the disk were evaluated. The initial Hertzian contact pressure under a load of 19 N and a 10 mm ball diameter was ~1 GPa. Microhardness in the wear track was measured at loads of 0.01 N and 0.05 N. The results were repeated 20 times.

The virgin roughness of ball and disk Ra = 0.10 ± 0.02 μm. To diminish surface oxidation during friction, 4–5 drops of synthetic oil (PAO4, Essenza lubricants, Roma, Italy) were applied to the contact. The friction force, wear, and temperature close to the contact were measured during the test. All measurements were performed after 0.5, 1, 3, and 5 h. Wear on the ball sample was measured by SEM image analysis. The wear volume was calculated based on the estimation of geometrical parameters of contact. The standard wear coefficient, mm³/Nm, is the wear volume/load and sliding distance. A linear sensor was also used to evaluate the wear. The microhardness of the wear tracks was determined. The details of the test can be found in our previous works [40,41].

3.2. Results

The experimental results of variations in the mean size of contact spots on the surface of the ball (mm) and the wear coefficient (mm³/Nm) are shown in Figure 3. The average wear rates based on the duration of the test time (μm/min) over 1 h and 5 h were calculated. These were ~13 μm/min and ~1.7 μm/min, respectively. So, high wear is associated with very rough, highly deformed surface layers after friction during the first 0.5 h of the run-in. With time, the wear rate and wear coefficients decreased significantly. Figure 4 depicts SEM images of the wear spots after one (a) and five hours (b) and the magnified images after one (c) and five hours of friction (d).

Meanwhile, the principal difference between the variations in the damaged surface after friction for 1 and 5 h is evident. Wear surfaces are characterized by strong ploughing after friction for 1 h, while pore formation, joining, and delamination are observed after long-term testing. Despite this, the surface profiles also confirm damage development as a function of test time (Figure 5). In this instance, the number and depth of grooves were significantly larger following friction for 1 h.

For comparison, the average distances between the grooves on the surface of the ball are ~4.5 μm and ~14 μm after friction for one (Figure 4c) and five (Figure 4d) hours. These measurements can be related to the microscale level. The average groove sizes are ~80 μm and ~200 μm after friction for 1 h and 5 h, respectively (Figure 6). These are measurements at the macroscale level. It is also noteworthy that the relation between groove sizes at the micro- and macroscales is close to the same: 3.1 and 2.75, respectively. The variation in the mean values of the roughness parameter, R_z, is shown in Figure 6.

It can be seen that the R_z parameter decreases with the time of the test from ~0.9 μm to ~0.6 μm. The rate of roughness variation after friction at time 0.5 h–1 h is ~7 times higher than during the next 2 h (0.36 μm/h–0.05 μm/h, respectively). It is reasonable to deduce that a definite connection exists between the contact length parameters at the micro- and macroscales. Figure 7 shows the dependence of the wear coefficient and contact pressure on time.

There is no correlation between wear variation and the contact pressure. The rate of wear is notably decreased with contact pressure. Furthermore, the microhardness of the wear tracks and the friction coefficient were measured (Figure 8). The nanograin structure is expected to be preserved in these layers. The COF’s variations can be explained by the process of microstructural recovery and the flattening effect developed over the test time. The microhardness and friction coefficient variations are small and similar. Stable microhardness can be explained by the preservation of a high dislocation density over the test time. This supports the idea that shear stress (τ = H/(3√3)) is mainly responsible for the contact interaction during friction.

3.3. Links between the Flattening and Structural Parameters during Friction

An illustration of the ball–sinusoidal rough disk surface is shown in Figure 9. The implications of the hardness of rough surface layers on the deformed structure and contact parameters will be discussed. The real area of contact, A_r = P/H, where P is the load and H is the hardness after friction. As the test progresses, A_r practically does not vary with the duration of the test. However, the nominal area is increased (Figure 6). This situation can be explained by the formation of a strain gradient microstructure at the microscale level during the first hour of friction. The nominal contact area was calculated based on the evaluation of the general diameters of wear spots after friction for 1 h and 5 h: A_nom1~0.116 mm² and A_nom5~0.216 mm², respectively.

The real contact area after severe plastic deformation can be determined as a relation of load to hardness: A = P/H. Then, A_r1~3.2 × 10⁻³ mm² and A_r5~3.6 × 10⁻³ mm² under the test times of 1 h and 5 h, respectively. Then, the relation A_r1/A_r5~0.89~H₅/H₁ was calculated. Nevertheless, the relationship between the nominal areas and pressures is different: A_nom1/A_nom5~0.58. It is known that severe plastic deformation occurs in surface layers under friction. At a steady friction state, the real contact pressure is close to the applied stress: σ_appl~H/3~p_r~2000 MPa and 1730 MPa under friction for 1 and 5 h, respectively. If we take the relation between the nominal and real areas of contact by convention, the general number of contact spots (n) can be determined as follows: n = A_nom5/A_r5~585 spots, while after the first hour, it is ~670 spots. The results presented herein are in full agreement with the roughness profiles, where the distance between grooves (λ) varied as the duration of friction increased.

As shown in Figure 9, the displacement (interference, w) of the hard body in the y-direction is a crucial contact parameter. Nix and Gao [13] proposed a model assuming that the generation of dislocation loops in surface layers is responsible for the value of the displacement under indentation.

$$H=H_0\sqrt{1+{\displaystyle \frac{{\rho }_{GND}}{{\rho }_{ssD}}}}=\sqrt{1+{\displaystyle \frac{w^{*}}{w}}},$$

(17)

where w is the interference, w* is a characteristic length depending on both the indented material and the indenter angle, and H₀ is the macroscopic indentation hardness. In our case, H/H_o~1. Hence, the relationship ρ_GND/ρ_SSD practically does not vary under friction. The values of hardness after friction in a steady friction state is close to the hardness of materials after some processes of SPD [52,53,54,55], and these values of hardness can be used as the preliminary results. Moreover, if we use the connection τ = H/(3·√3) instead of H in Equation (18), the relation of shear stresses can be presented as

$${\displaystyle \frac{\tau }{{\tau }_0}}=\sqrt{1+{\displaystyle \frac{w^{*}}{w}}}$$

(18)

In this instance, the larger the relation of the shear stress, the smaller the interference w. In other words, the harder the material, the smoother it becomes. The evaluation of w* will be considered in our future work.

The strong increase in plastic deformation in the first stage of loading is associated with the formation of nanocrystalline structures and dominant dislocation density in the grain boundaries, ρ_GND [52,53,54,55]. Huang et al. showed that the ρ_GND influences the effective plastic strain gradient η^p [16,17]:

It has been shown (Equation (13)) that η^p is mainly determined by ρ_GND. Generally, the higher the ρ_GND, the wider the effective plastic strain gradient, and the harder the surface. Nevertheless, a balance between deformation hardening and softening due to dynamic recovery (DRV) during steady friction occurs [51,55]. Therefore, the strain hardening caused by dislocation multiplication and the flow softening resulting from DRV-driven dislocation recombination are well considered in the Kocks–Mecking model [56,57]. The revised model of dislocation density evolution is presented as

$${\dot{\rho }}_i=\dot{\rho }{i}^w-\dot{\rho }{i}^{drv}-\dot{\rho }{i}^{dm},$$

(19)

where $\dot{\rho }{i}^w$ represents the strain-hardening portion, $\dot{\rho }{i}^{drv}$ represents the DRV portion, and $\dot{\rho }{i}^{dm}$ is the plastic damage portion. Hence, the application of the real density of the dislocations considers also the improvement in ductility due to the softening of surface layers, which decreases the wear loss and roughness parameters.

As pointed out before, the average nominal area A_nom~0.15 mm², and p_nom = P/A_nom = 133 MPa. p_nom can be considered as P/N × A, where p_nom is the nominal pressure, P is the load, N is the number of direct contacts, and A is the area of a single contact. In our experiment, P = 20 N, p_nom~133 MPa, and there are many direct contacts (~600); then, the average size of contact spots is ~38 nm, which is a little smaller than that observed in the real measurements [41].

Conventional mechanism-based strain gradient plasticity (CMSGP) theory was adopted for the simulations and analyses of the flattening under contact interaction of micrometer-sized metal crystals [20,21,22]. Surface roughness was simplified to a sinusoidal wave function, but plasticity caused by dislocation glide was carefully computed by discrete dislocation simulations.

Two parameters were used to characterize a surface: the rms height and the surface correlation length ls. The ls describes the statistical independence of two points on a surface.

$$ls~18{\alpha }^2({\displaystyle \frac{\mu }{{\sigma }_y}}{)}^{2}b,$$

(20)

where α is an empirical coefficient of ~0.4. The intrinsic material length l_s represents the microstructural and macro-constraint characteristics. In our experiment, l_s~1.5 μm, and it is close to the characteristic material length l. For a smooth surface, l_s = ∞. Within the framework of an isotropic plasticity theory, the GND density is connected to an effective plastic strain gradient η^p, which is mathematically equivalent to a larger l (η^p~1.4 μm, l~1 μm, l_s~1.5 μm).

Recently, Zhang W. et al. [27] confirmed the theory of Jackson and Streator [26] and develop the scale effect using a finite element method and CMSGP theory to analyze the contact interaction between rough surfaces while considering the size-affected deformation behavior of multi-scale asperities. The authors considered the functional relationship among the corresponding dimensionless contact parameters (contact force P/P_cr, contact area A/A_cr, and deformation thickness δ/δ_cr) for elastic contact (Equation (15)):

$${\displaystyle \frac{\overline{P}}{{\overline{P}}_{cr}}}=c{({\displaystyle \frac{\overline{\delta }}{{\overline{\delta }}_{cr}}})}^d {\displaystyle \frac{A}{A_{cr}}}=e{({\displaystyle \frac{\overline{\delta }}{{\overline{\delta }}_{cr}}})}^m,$$

(21)

where δ_cr represents the critical interference at yielding inception and corresponds to the critical contact force and contact area. The value of δ_cr is related to τ_cr~τ_{b cr}. Critical interference indicates the transition to instability associated with the annihilation of dislocation and dynamic recrystallization. A connection between δ_cr and the process of softening will be considered in our future work. The exponents d, m, and the constant coefficients c and e were given specific values in their study. As a result of the B.W. van de Waal cross-twinning model of FCC crystal growth [58], the relationship between the contact pressures and the interferences can be considered:

$${\displaystyle \frac{\overline{P}}{{\overline{P}}_{cr}}}=n{({\displaystyle \frac{\overline{\delta }}{{\overline{\delta }}_{cr}}})}^k,$$

(22)

where n and k are new constant coefficients. The exponential coefficient in Equation (23) was changed for different scales (i). When the scale effect reaches approximately 50–55 μm, the coefficient value approaches the pure elastic boundary. It is expected that in the steady friction state, the following relationship is also preserved:

$${\displaystyle \frac{\overline{\tau }}{{\overline{\tau }}_{cr}}}=r{({\displaystyle \frac{\overline{\delta }}{{\overline{\delta }}_{cr}}})}^s,$$

(23)

where τ can be considered to be the shear stress in a steady state, τ_s, while τ_cr is the critical shear stress (deformation resistance). The lesser the relationship τ/τ_cr, the smaller is the displacement concerning τ_cr.

Further understanding of the interaction of flattening with gradient structural parameters will be considered in our future work.

4. Conclusions

• The interaction between variations in the roughness of asperities and the deformed microstructure of surface layers was considered.
• The models of flattening and the plasticity of surface layers were analyzed.
• The principal difference between the morphology of damaged surfaces after friction for 1 and 5 h was revealed. Strong ploughing was observed after friction for 1 h, while pore formation, joining, and delamination were observed after 5 h.
• The number and depth of grooves under friction for 0.5 h were significantly greater than when under friction for 5 h. The same relationship applies to the average distance between the nearest grooves using roughness profiles (macroscale level) and the ploughing tracks on SEM images (microscale level).
• A small influence of time on hardness and friction coefficient variation appeared. High hardness and relatively low friction coefficient values (f~0.15) with test time can be explained by the preservation of a high density of dislocations in the surface layers. The nominal and real contact areas were determined. The same relationships as A_r0.5/A_r5 = H₅/H_0.5 = A_nom5/A_nom0.5 were established.
• The relation of shear stresses to the interference of rough asperities was established. The larger the shear stress, the smaller the interference. In other words, harder means smoother.
• The effective plastic strain gradient was evaluated. The formation of a highly effective plastic strain gradient was associated with a high dislocation density, ρ_GND. The higher the ρ_GND, the greater the strain gradient. In other words, with an increase in the density of GND dislocations, the asperity surface is smoother. The effect of dislocation density on the hardening–softening of surface layers was considered.