Theoretical Evaluation of Lubrication Performance of Thrust-Type Foil Bearings in Liquid Nitrogen
Abstract
1. Introduction
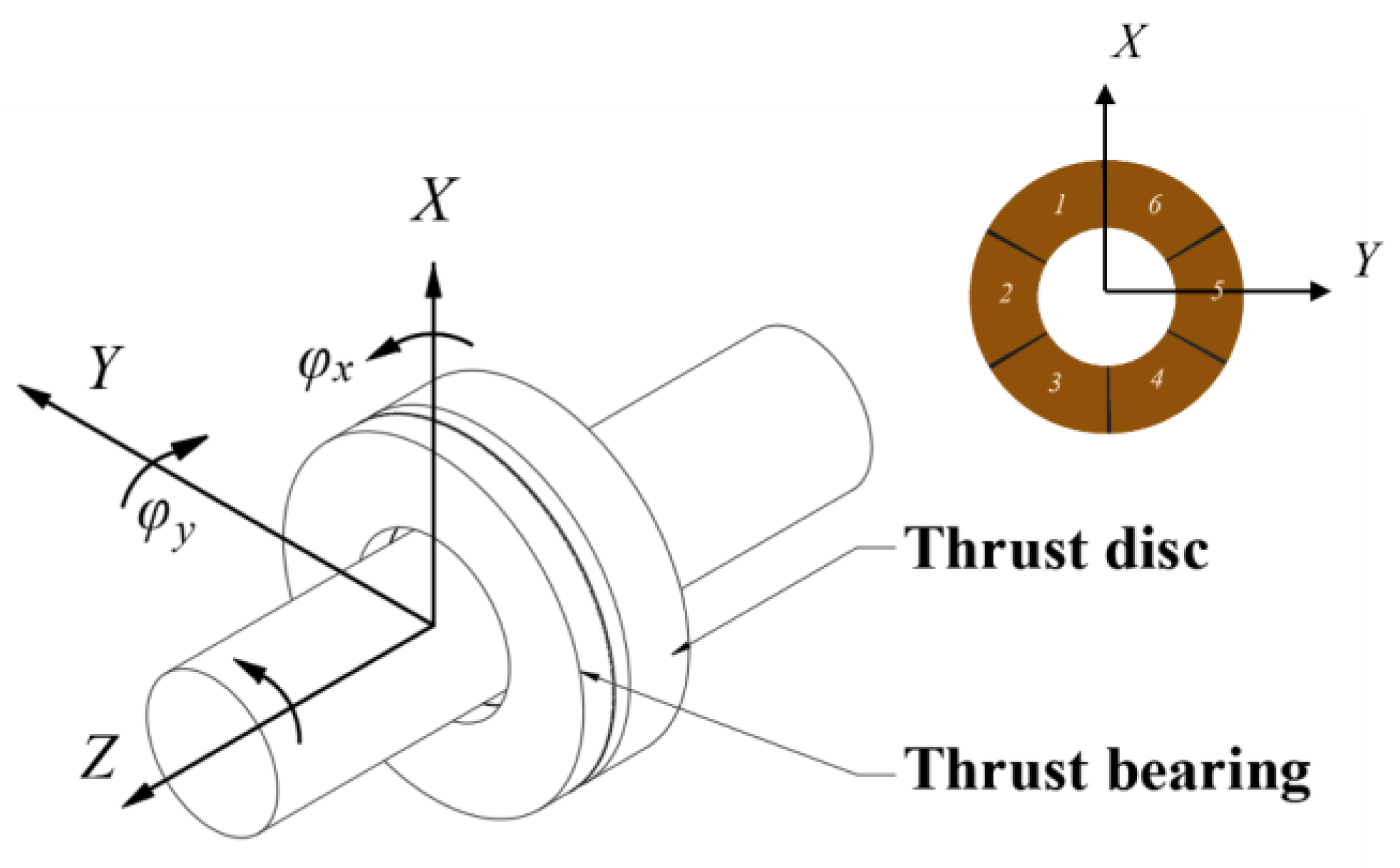
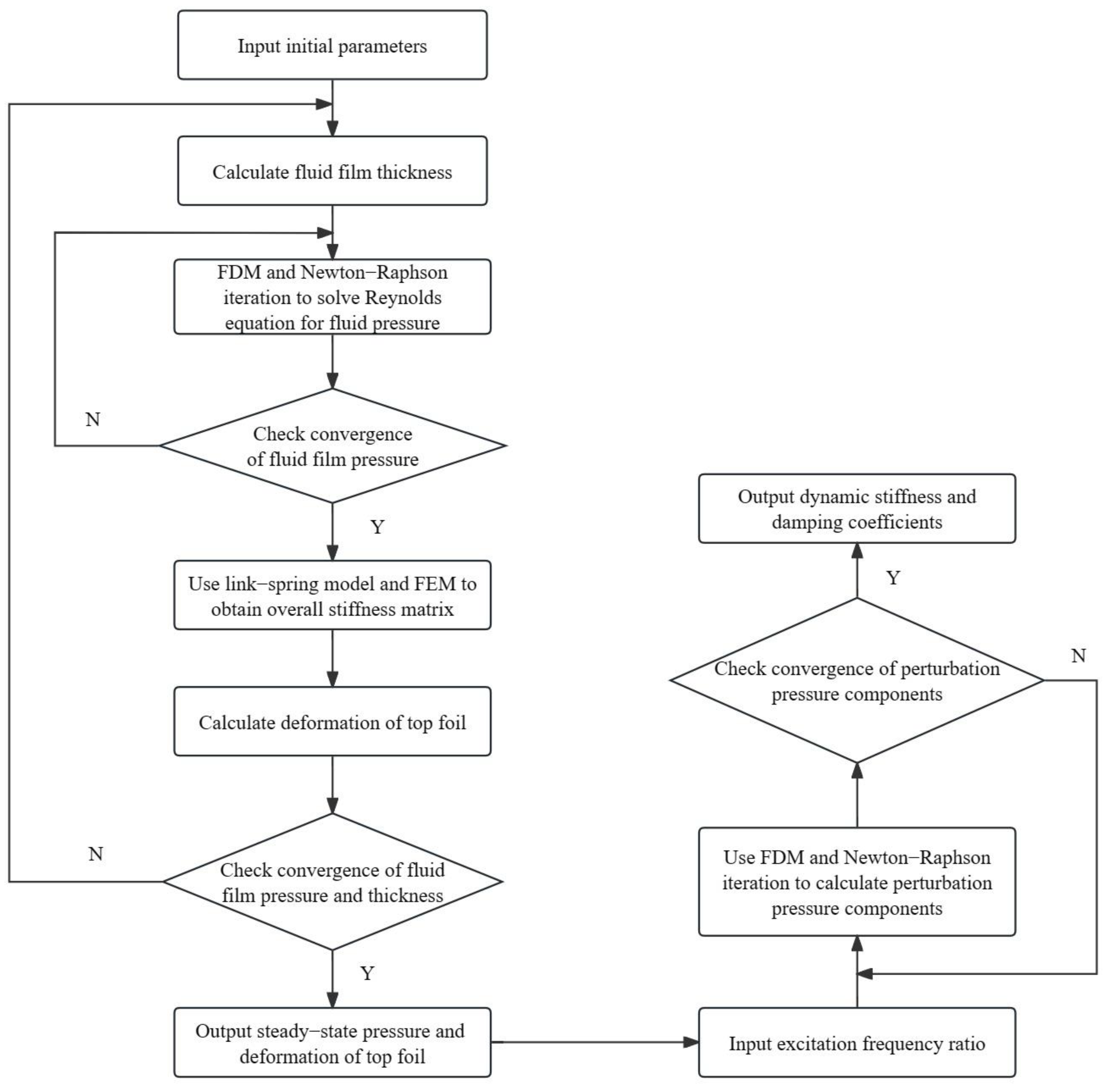
2. Theoretical Analysis Procedures
2.1. Fluid Lubrication Equations
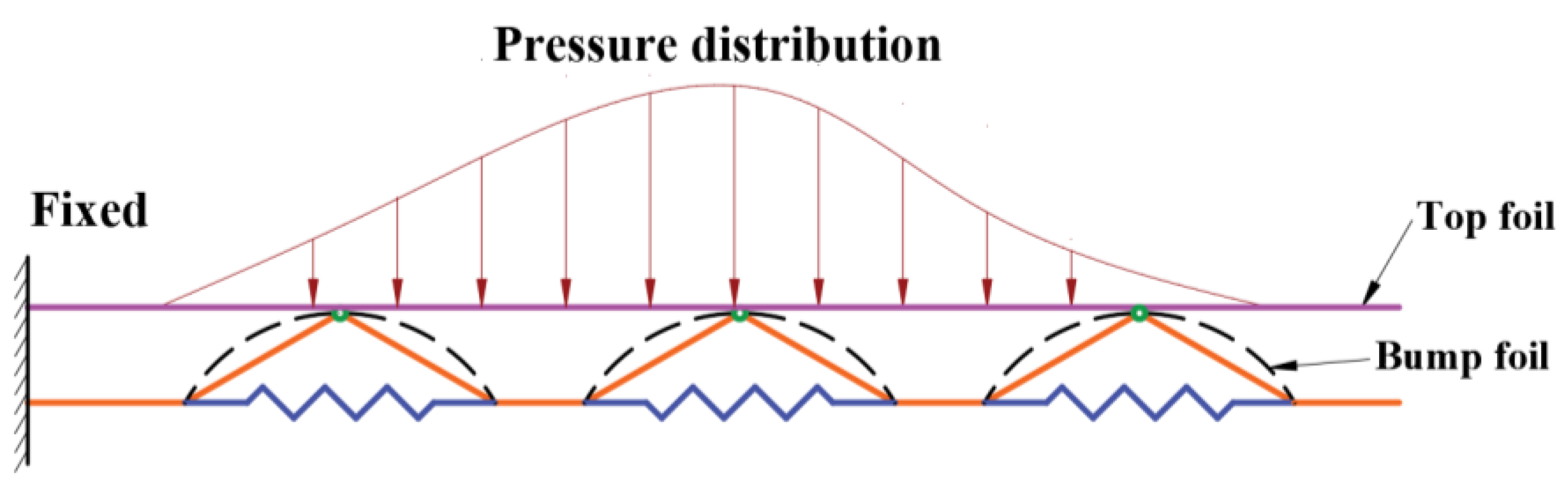
2.2. Foil Deformation Equation
2.3. Calculation of Dynamic Characteristics
3. Results
3.1. Structure Parameters of the Thrust-Type Foil Bearing
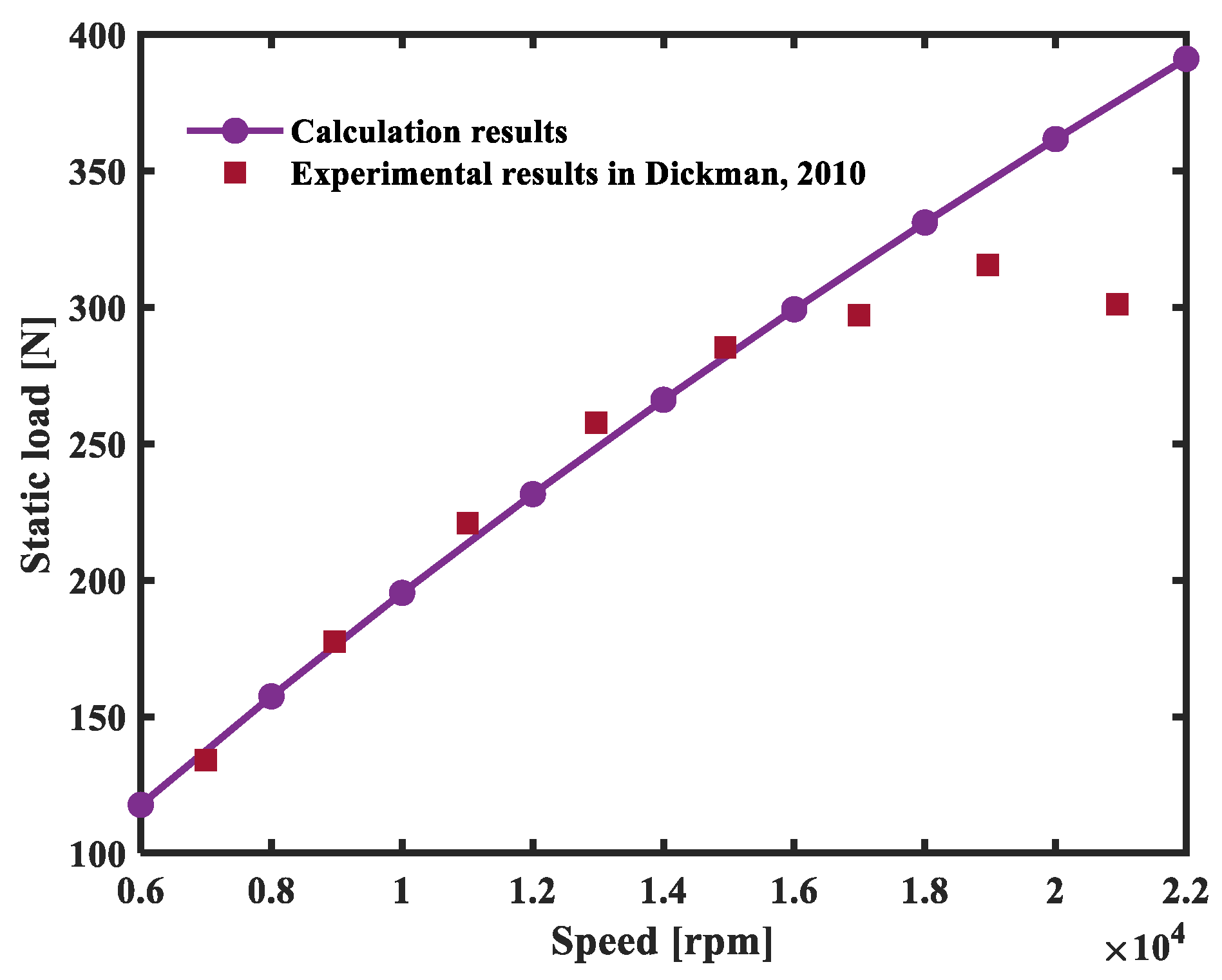
3.2. Validation of Theoretical Analysis Method
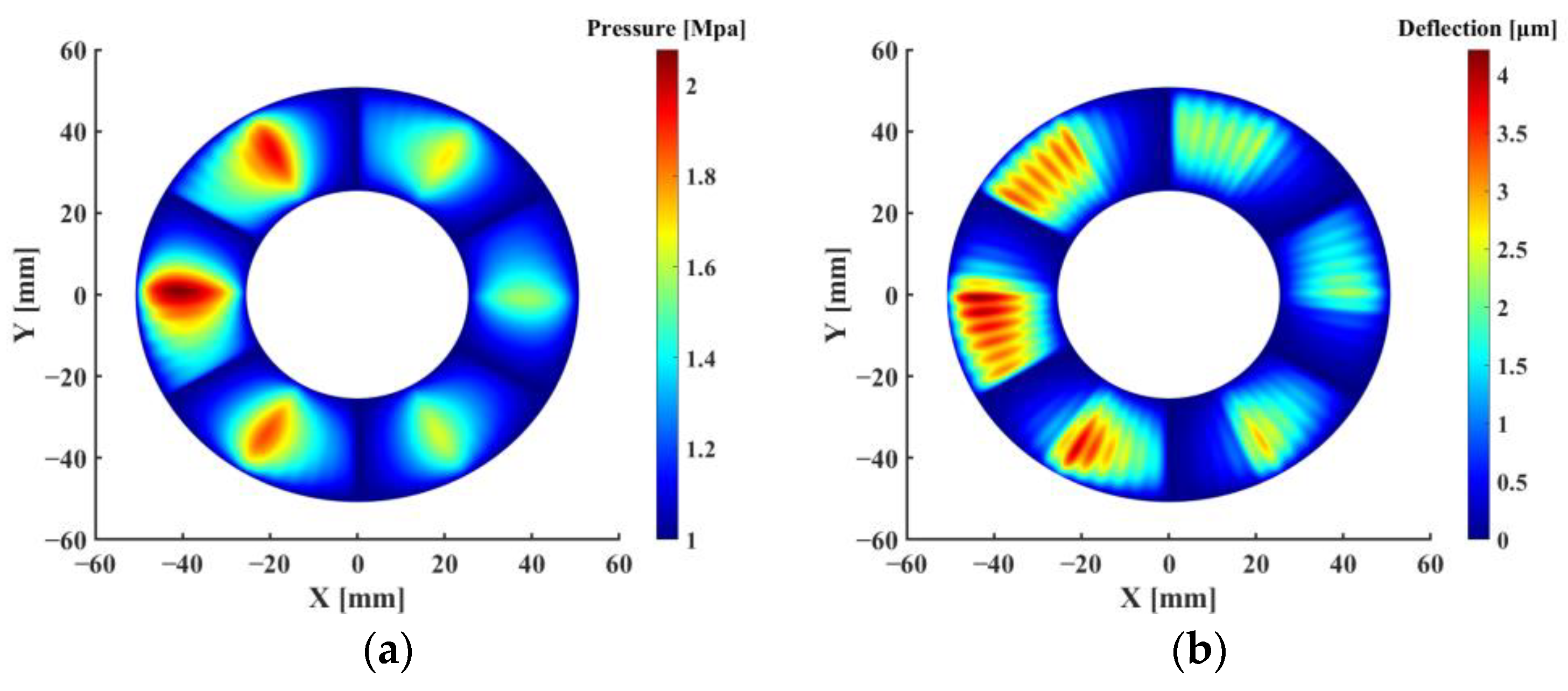
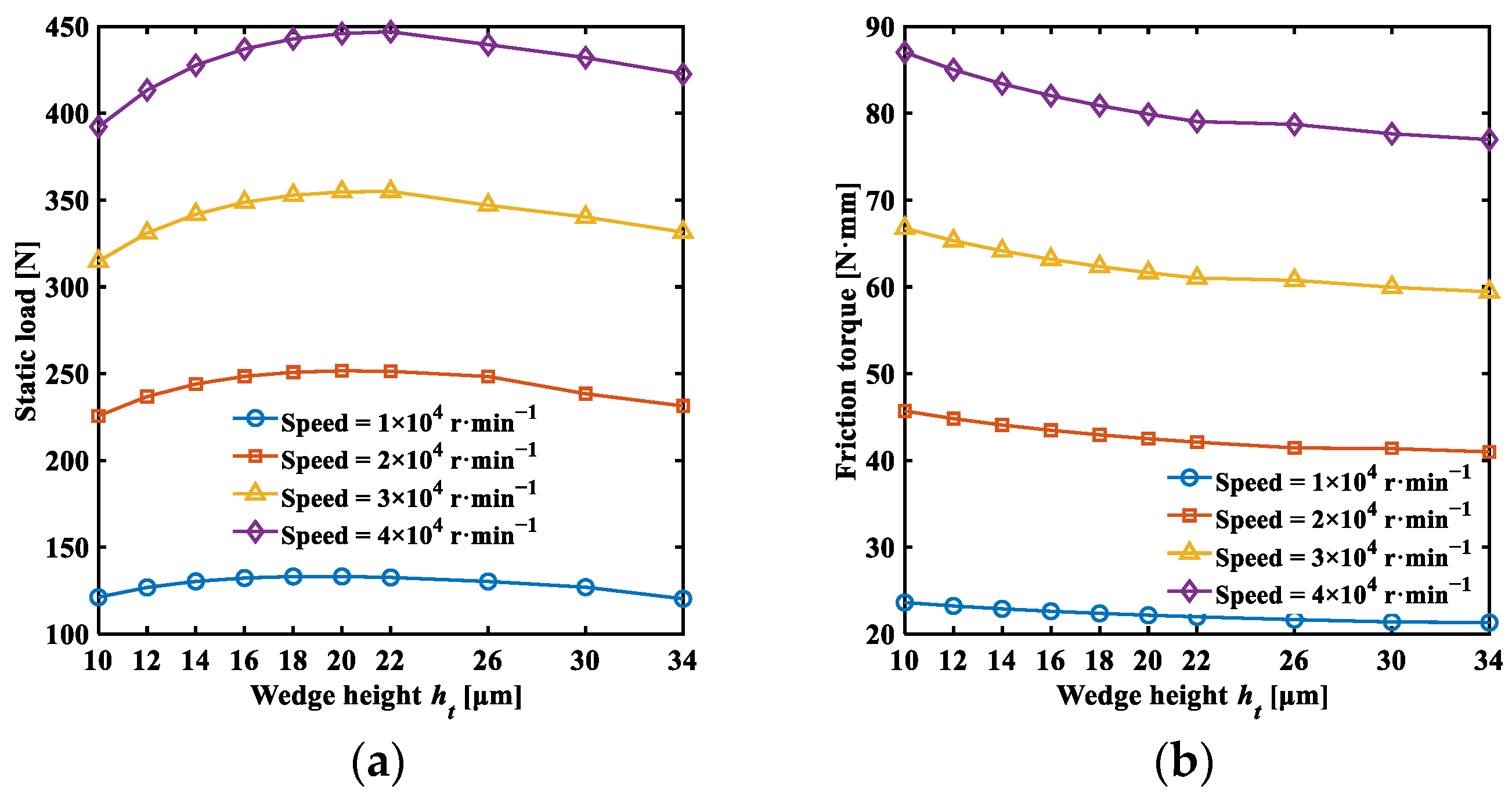
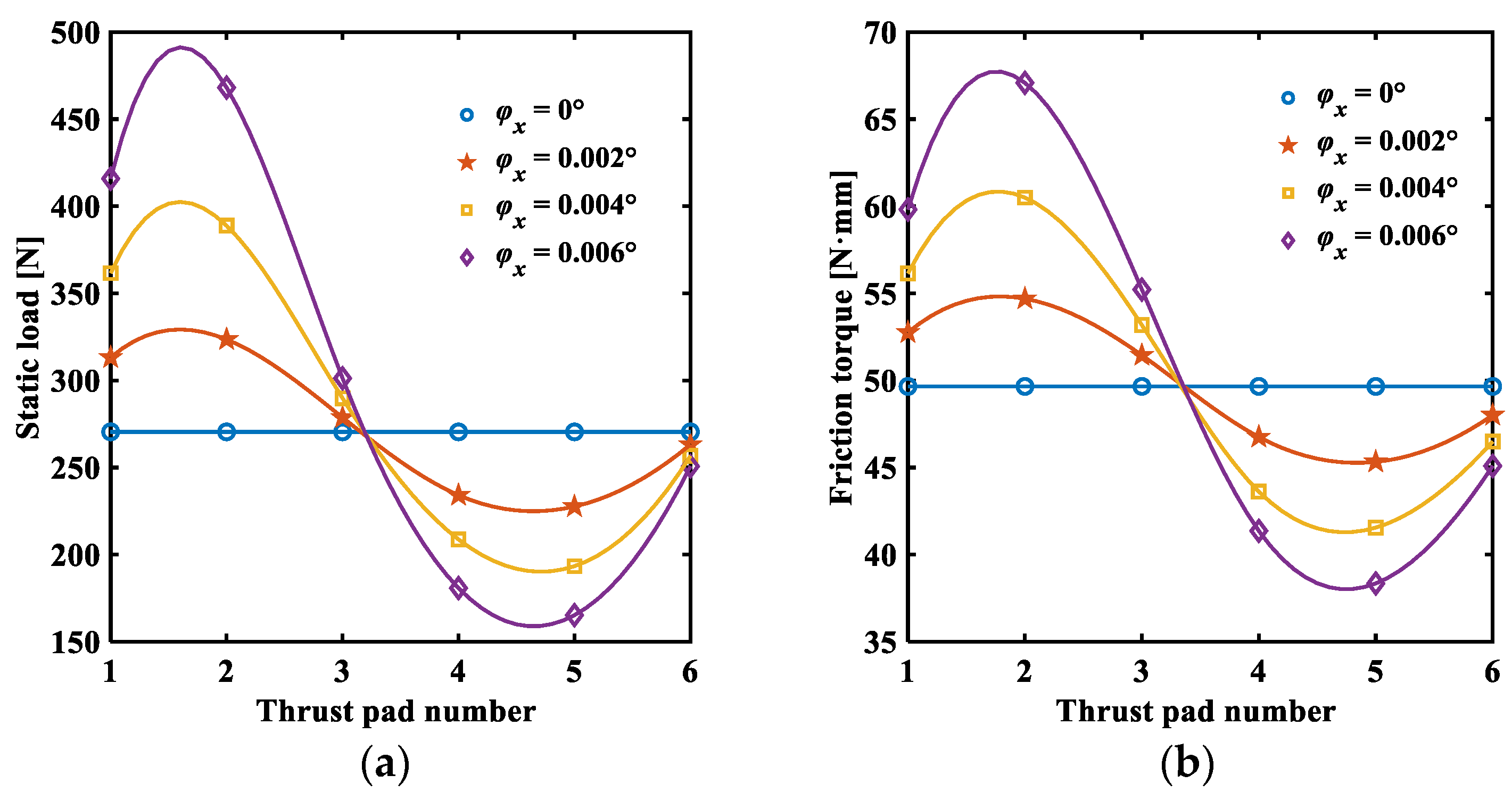
3.3. Analysis Results of Static Characteristics
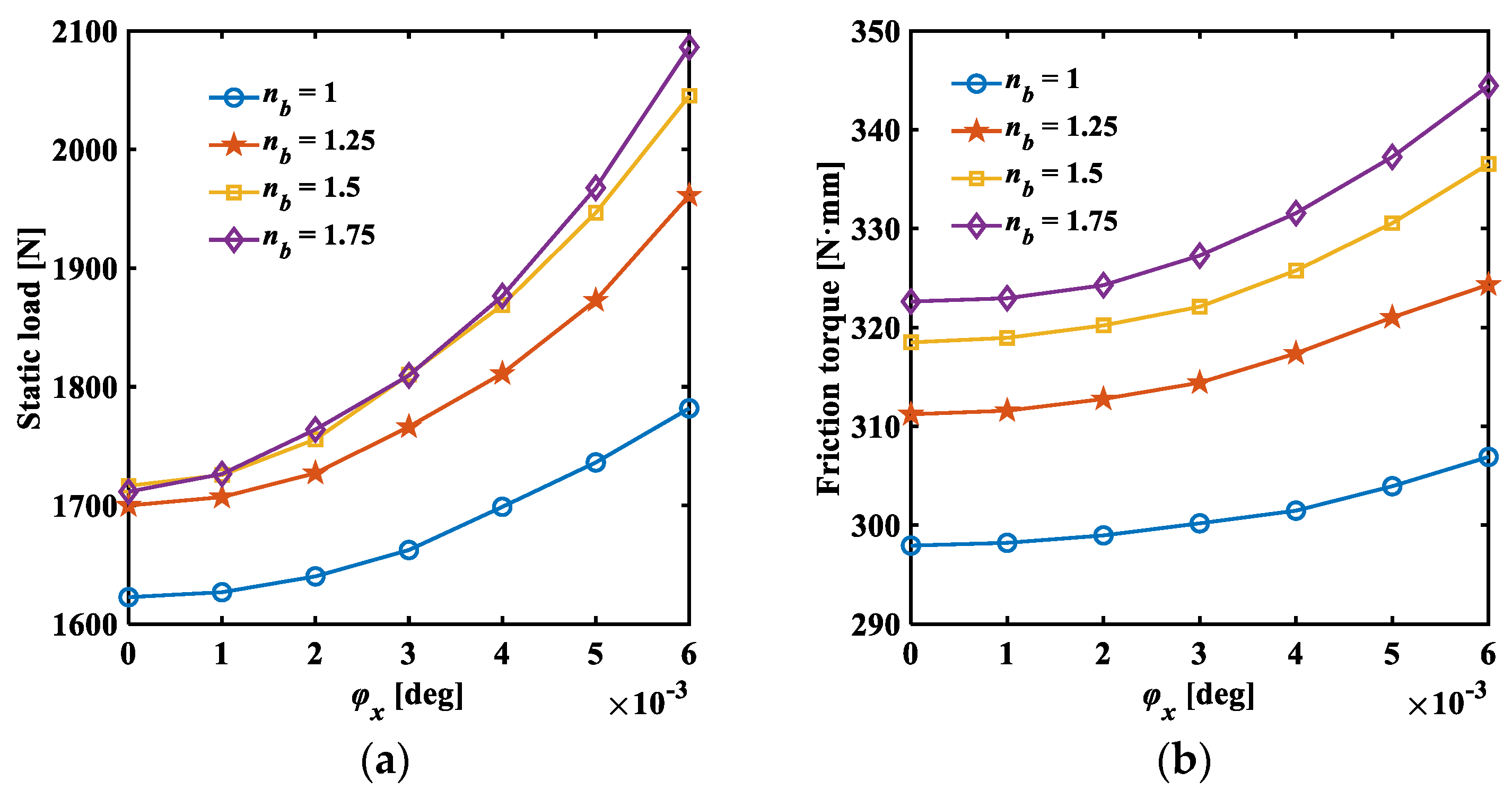
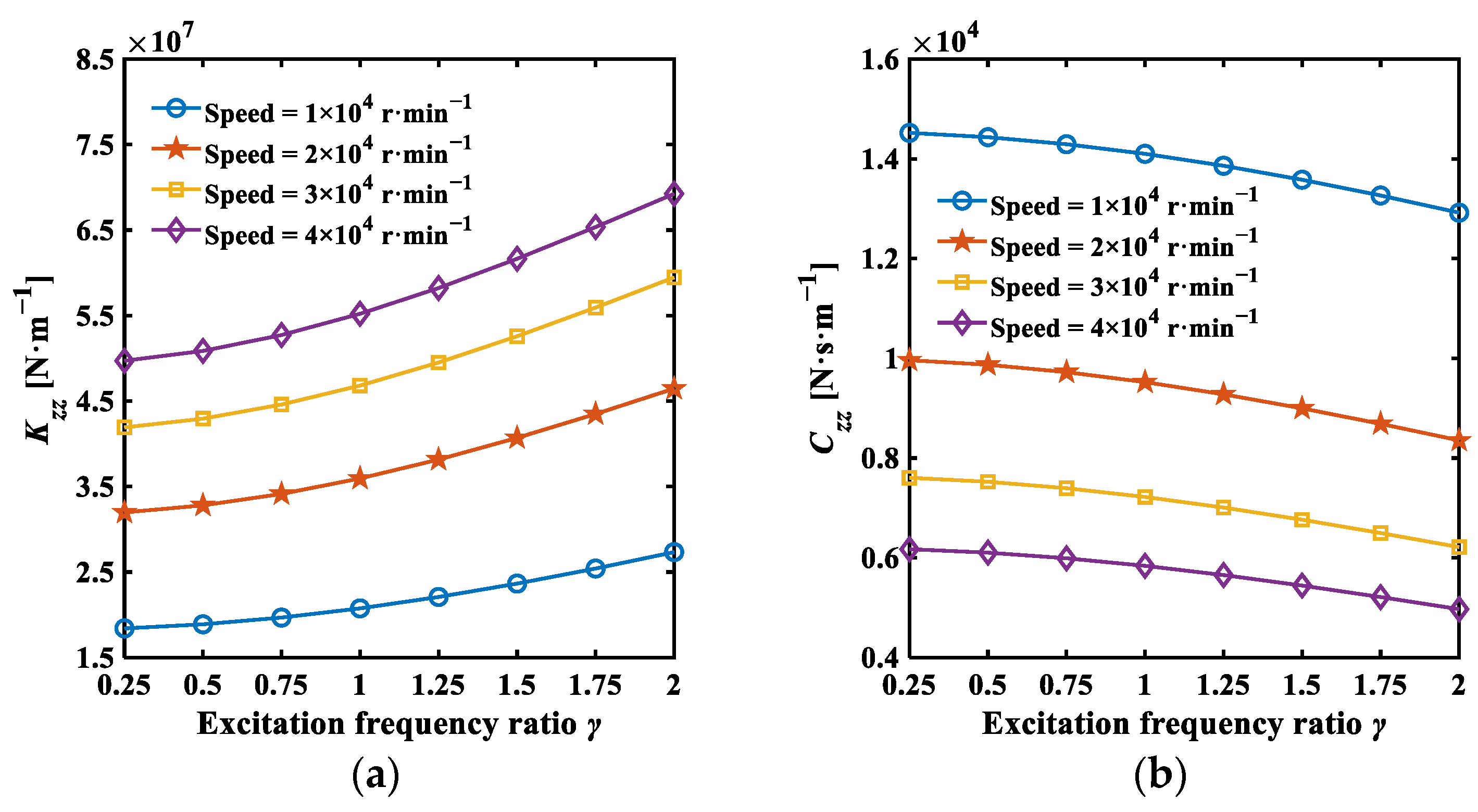
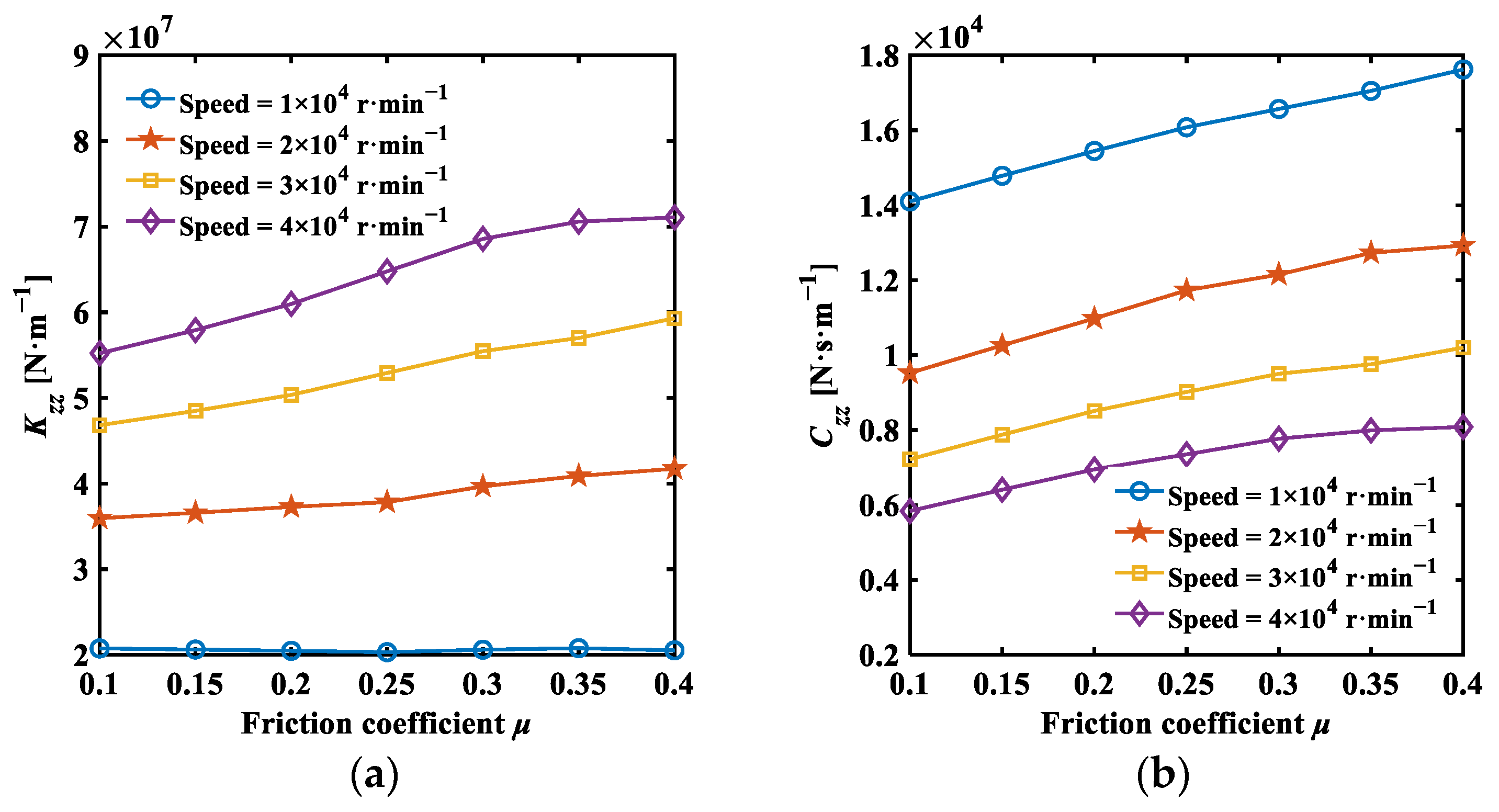
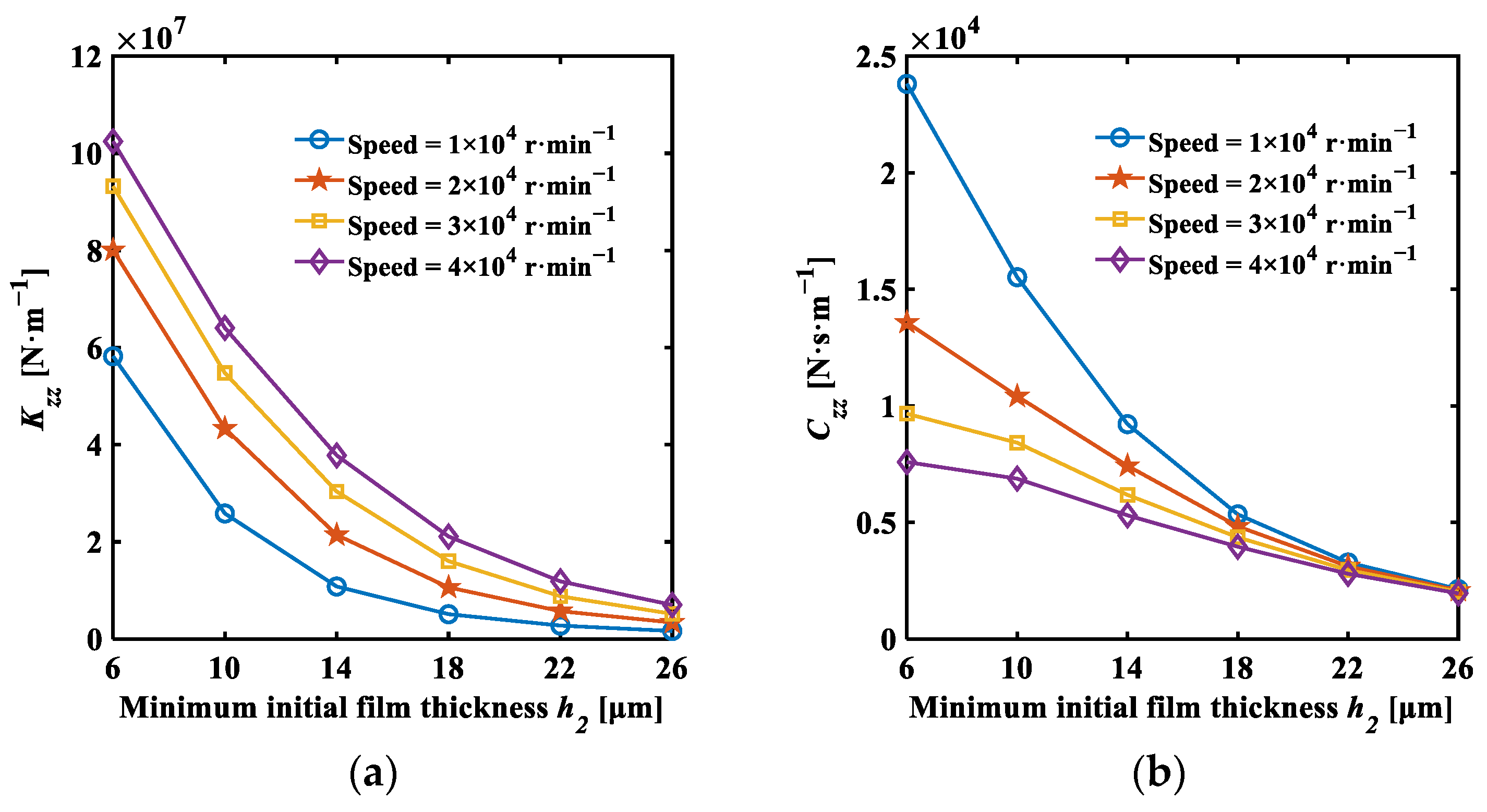
3.4. Analysis Results of Dynamic Characteristics
4. Conclusions
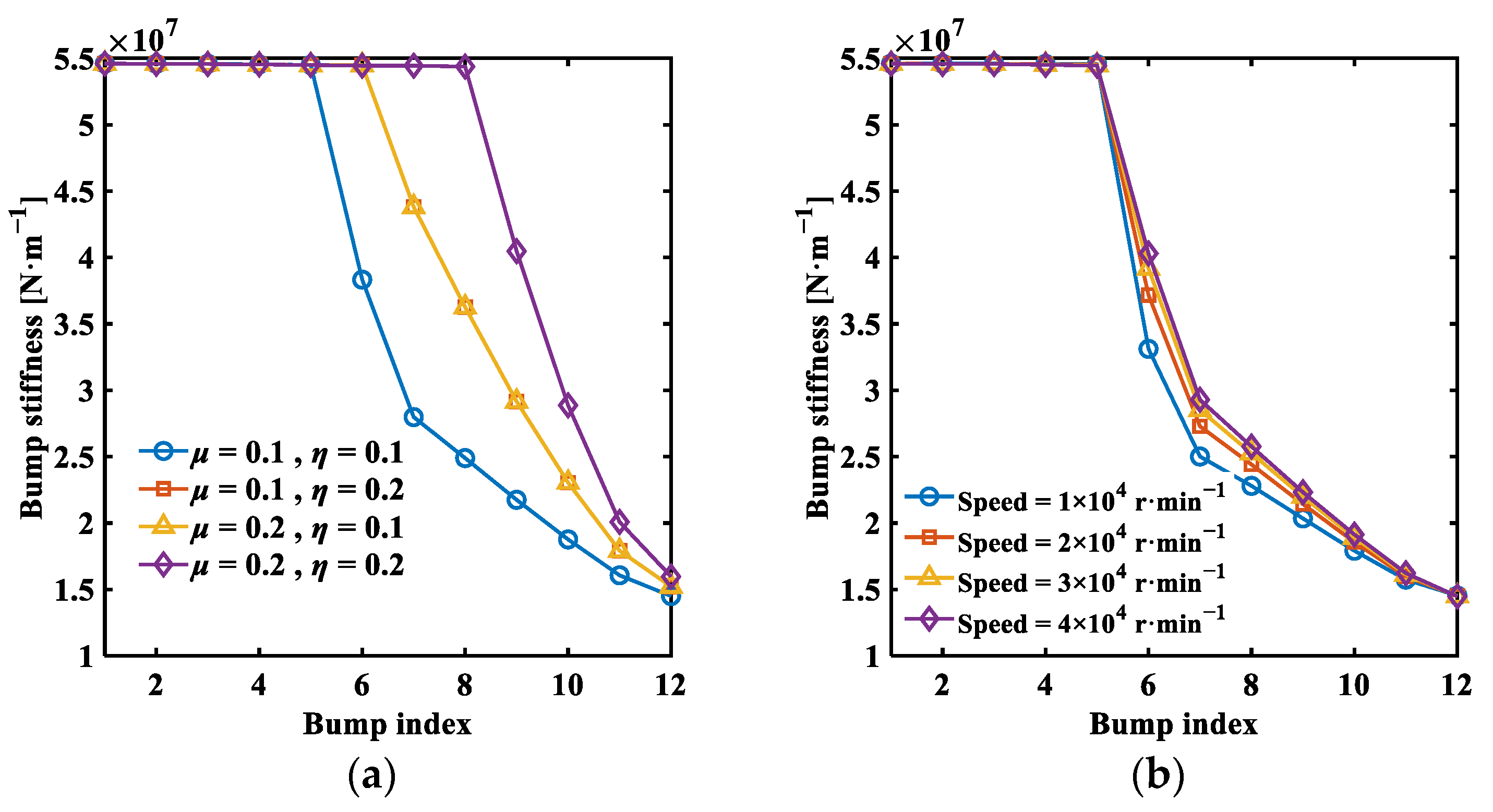
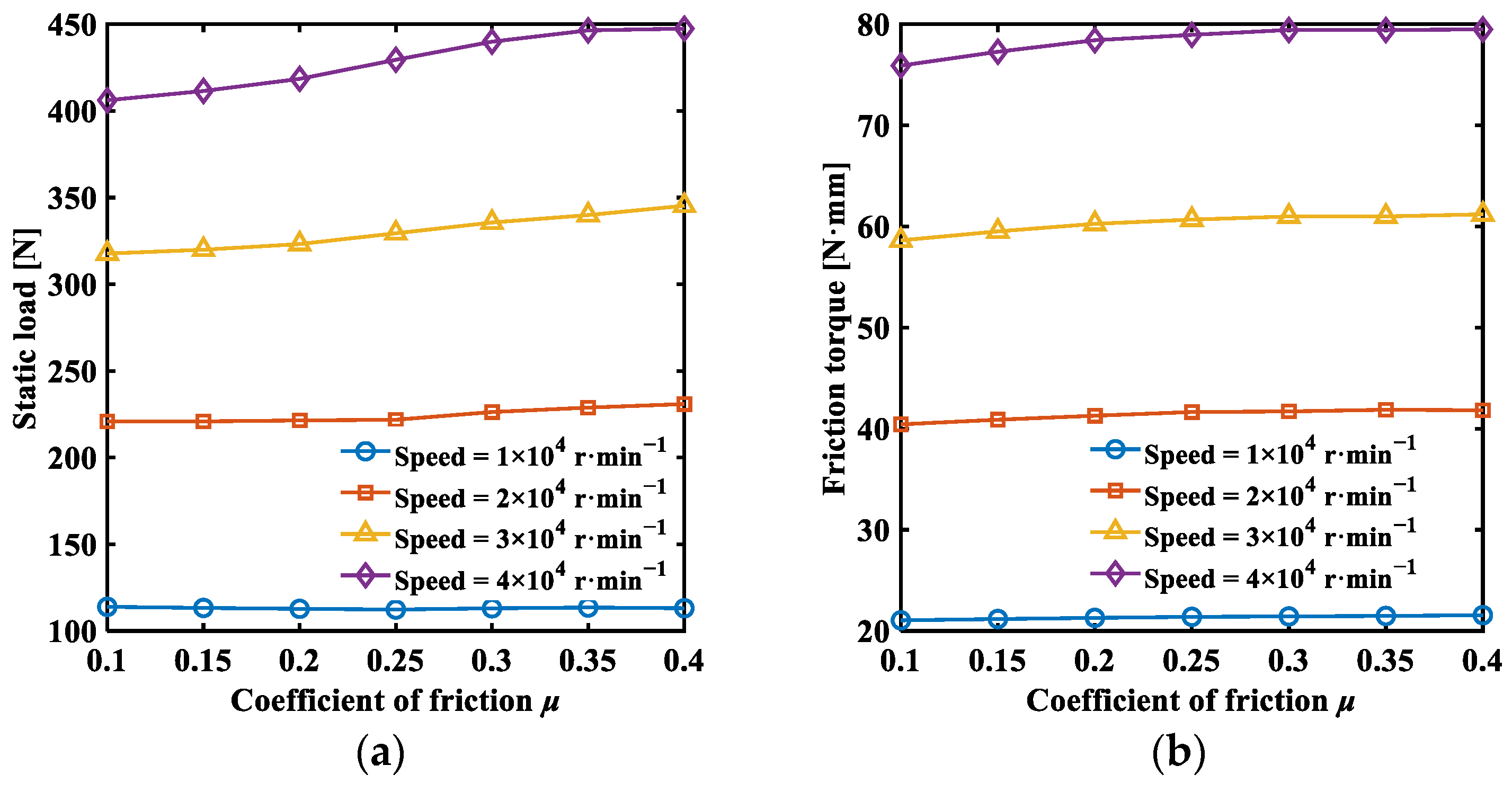
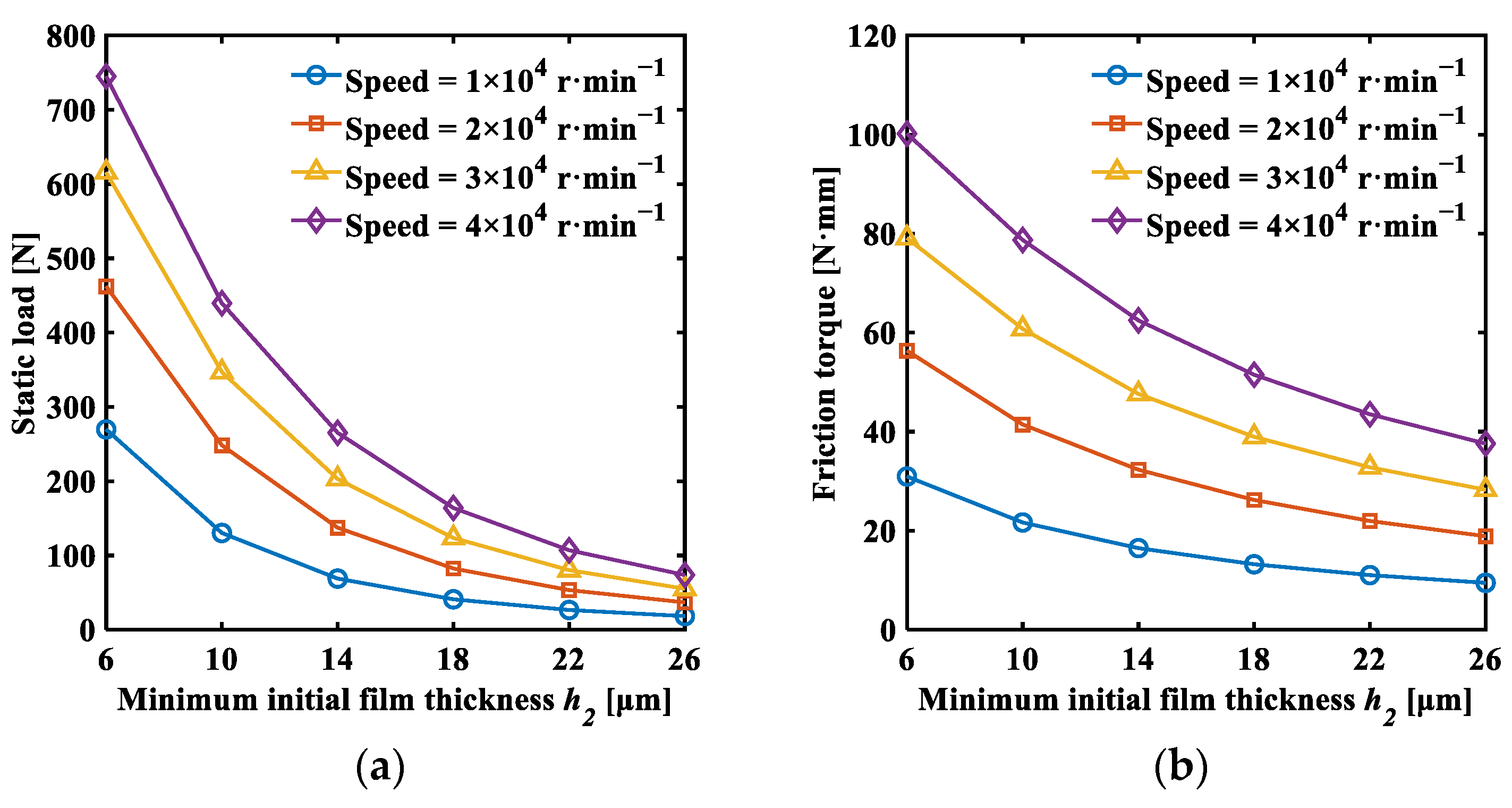
- Through the analysis of static characteristics, it is observed that increasing the friction coefficient and decreasing the initial minimum film thickness enhance the static load and friction torque of the bearing. There is an optimal wedge height that achieves a higher load-carrying capacity while minimizing friction torque and reducing power loss. The severe tilt of the thrust disk causes the uneven distribution of fluid film thickness across the thrust pad, affecting the bearing stability. Reducing the bump foil thickness effectively increases top foil deformation, enhancing the fluid film thickness but decreasing the static load-carrying capacity of the bearing.
- Through the analysis of dynamic characteristics, it is observed that increasing the excitation frequency enhances the direct translational stiffness of the thrust-type foil bearing, while the damping coefficient decreases. Moreover, both the direct translational stiffness and damping coefficients increase with the friction coefficient and the bump foil’s thickness, yet decrease with an increase in the minimum initial film thickness and wedge height. The tilt of the thrust disk notably impacts the cross-coupling stiffness and damping coefficients (), which escalate rapidly with tilt, significantly affecting system stability. Therefore, substantial tilts of the thrust disk should be avoided.
- Different from rolling bearings, thrust-type foil bearings exhibit adaptive response characteristics and operate with completely non-contact lubrication during the working stage, which can reduce the risk of contact and wear between the bearing and rotor. The low-temperature conditions in liquid rocket turbopumps effectively cool the bearings, preventing performance degradation due to thermal effects. Moreover, thrust-type foil bearings are characterized by high operating speeds, a compact structure, maintenance-free operation, and a high load-carrying capacity, all of which meet the requirements for repeated use. Therefore, based on the results in this study, the exceptional performance characteristics of thrust-type foil bearings make them a promising alternative to rolling bearings for the development of reusable liquid rocket turbopumps.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| b | Pitch ratio (proportion of the tilted plane in the sector thrust pad) |
| Cij | Dynamic damping coefficients (i, j = z,,) |
| E | Young’s modulus [Pa] |
| Fload | Static load [N] |
| g | Wedge surface clearance [m] |
| h | Film thickness [m] |
| hb | Foil height [m] |
| h1 | Inlet film thickness [m] |
| h2 | Outlet film thickness [m] |
| ht | Wedge height [m] |
| Tilt clearance thickness caused by rotor misalignment [m] | |
| H | Dimensionless film thickness |
| Kij | Dynamic stiffness coefficients (i, j = z,,) |
| Kf | Overall stiffness matrix [N/m] |
| Kt | Top foil stiffness matrix [N/m] |
| Kv | Effective stiffness matrix of the foil [N/m] |
| lb | Half bump length [m] |
| nb | Bump foil thickness ratio |
| N | Film thickness ratio (h1/h2) |
| p | Film pressure [Pa] |
| P | Dimensionless film pressure |
| Ps | Supply pressure [Pa] |
| P0 | Steady-state dimensionless film pressure |
| Perturbation pressure ( = z,,) | |
| r | Axial coordinate [m] |
| r1 | Inner diameter of the thrust pad [m] |
| r2 | Outer diameter of the thrust pad [m] |
| t | Time variable [s] |
| Dimensionless time variable | |
| Bump foil thickness [m] | |
| Top foil thickness [m] | |
| Tc | Friction torque [N·m] |
| z | Axial coordinate [m] |
| Angular range of the top foil and bump foil [°] | |
| Foil deformation [m] | |
| Dimensionless foil deformation | |
| Coefficient of friction between the bump foil and the top foil | |
| Excitation frequency ratio | |
| Bearing number, | |
| Coefficient of friction between the bump foil and the bearing housing | |
| Dynamic viscosity of liquid nitrogen [Pa·s] | |
| Poisson’s ratio of the top foil and bump foil | |
| Angular speed of the shaft [rad/s] | |
| Excitation frequency [rad/s] | |
| Circumferential coordinate [°] | |
| Tilt angle in the X-axis direction [°] | |
| Tilt angle in the Y-axis direction [°] |
References
- Okayasy, A.; Ohta, T.; Kamijyo, A.; Yamada, H. Key technology for reusable rocket engine turbopump. Acta Astronaut. 2002, 50, 351–355. [Google Scholar] [CrossRef]
- Lance, A.D. First stage recovery. Engineering 2016, 2, 152–153. [Google Scholar]
- Baiocco, P. Overview of reusable space systems with a look to technology aspects. Acta Astronaut. 2021, 189, 10–25. [Google Scholar] [CrossRef]
- Baiocco, P.; Bonnal, C. Technology demonstration for reusable launchers. Acta Astronaut. 2016, 120, 43–58. [Google Scholar] [CrossRef]
- Xu, J.; Li, C.; Miao, X.; Zhang, C.; Yuan, X. An overview of bearing candidates for the next generation of reusable liquid rocket turbopumps. Chin. J. Mech. Eng. 2020, 33, 26. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, C.; Wang, J.; Wang, W. Experimental investigations of novel compound bearing of superconducting magnetic field and hydrodynamic fluid field. IEEE Trans. Appl. Supercond. 2020, 30, 3600407. [Google Scholar] [CrossRef]
- Nosaka, M.; Takada, S.; Kikuchi, M.; Sudo, T.; Yoshida, M. Ultra-high-speed performance of ball bearings and annular seals in liquid hydrogen at up to o 3 million DN (120000 rpm). Tribol. Trans. 2004, 47, 43–53. [Google Scholar] [CrossRef]
- Lv, F.; Shangguan, Y.; Zou, D.; Ji, A. Transient mixed-lubrication analysis of low-viscosity lubricated bearings under impact load with consideration of turbulence. Phys. Fluids 2022, 34, 033108. [Google Scholar] [CrossRef]
- Deng, X. Study of temperature drop region in transitional region in fluid-film thrust bearings. J. Fluids Eng.-Trans. ASME 2024, 146, 121201. [Google Scholar] [CrossRef]
- Deng, X. A mixed zero-equation and one-equation turbulence model in fluid-film thrust bearings. J. Tribol.-Trans. ASME 2024, 146, 034101. [Google Scholar] [CrossRef]
- Deng, X.; Harrison, G.; Roger, F.; Houston, W. Methodology of turbulence parameter correction in water-lubricated thrust bearings. J. Fluids Eng.-Trans. ASME 2019, 141, 070014. [Google Scholar] [CrossRef]
- Deng, X.; Brian, W.; Cori, W.; Michael, B.; Houston, W.; Roger, F. Modeling Reichardt’s formula for eddy viscosity in the fluid film of tilting pad thrust bearings. J. Eng. Gas Turbines Power 2018, 140, 082505. [Google Scholar] [CrossRef]
- Hannum, N.; Nielson, C. The performance and application of high speed long life hybrid bearings for reusable rocket engine turbomachinery. In Proceedings of the 19th Joint Propulsion Conference cosponsored by the AIAA, SAE and ASME, Seattle, WA, USA, 27–29 June 1983. [Google Scholar]
- Ohta, T.; Kitamura, A.; Ogata, H. LH2 turbopump test with hydrostatic bearing. In Proceedings of the 35th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Los Angeles, CA, USA, 20–24 June 1999. [Google Scholar]
- Fayolle, P.; Lambert, P.-A.; Gelain, P.; Fonteyn, P.; Olofsson, H.; Ore, S.; Supie, P.; Dehouve, J. Major achievements reached through TPX LH2-turbopump demonstration program. In Proceedings of the 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, San Diego, CA, USA, 31 July–3 August 2011. [Google Scholar]
- Mertz, D.H. Lift-Off Performance in Flexure Pivot Pad and Hybrid Bearing. Master’s Thesis, Texas A&M University, College Station, TX, USA, 2008. [Google Scholar]
- Xu, J.; Chen, R.; Hong, H.; Yuan, X.; Zhang, C. Static characteristics of high-temperature superconductor and hydrodynamic fluid-film compound bearing for rocket engine. IEEE Trans. Appl. Supercond. 2015, 25, 3601908. [Google Scholar] [CrossRef]
- Xu, J.; Yuan, X.; Zhang, C.; Miao, X. Dynamic characteristics of high-Tc superconductor and hydrodynamic fluid-film compound bearing for rocket engine. IEEE Trans. Appl. Supercond. 2016, 26, 3600505. [Google Scholar]
- Heshmat, H. A feasibility study on the use of foil bearings in cryogenic turbopumps. In Proceedings of the 27th AIAA/SAE/ASME/ASEE Joint Conference, Sacramento, CA, USA, 24–27 June 1991. [Google Scholar]
- Guo, Z.; Feng, K.; Liu, T.; Lyu, P.; Zhang, T. Nonlinear dynamic analysis of rigid rotor supported by gas foil bearings: Effects of gas film and foil structure on subsynchronous vibrations. Mech. Syst. Signal. Pract. 2018, 107, 549–566. [Google Scholar] [CrossRef]
- Gu, A. Cryogenic foil bearing turbopumps. In Proceedings of the 32nd Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 10–13 January 1994. [Google Scholar]
- Guan, H.; Li, J.; Wei, K.; Zou, H. Rotordynamics of a rotor radially and axially supported by active bump-type foil bearings and bump-type thrust bearings. Mech. Syst. Signal. Pract. 2024, 208, 110995. [Google Scholar] [CrossRef]
- Shi, J.; Cao, H.; Jin, X. Investigation on the static and dynamic characteristics of 3-DOF aerostatic thrust bearings with orifice restrictor. Tribol. Int. 2019, 138, 435–449. [Google Scholar] [CrossRef]
- Xu, Z.; Li, C.; Du, J.; Li, J.; Wang, Y. Load-carrying characteristics of bump-type gas foil thrust bearings. Int. J. Mech. Sci. 2023, 244, 108080. [Google Scholar] [CrossRef]
- Chen, R.; Zhao, Y.; Yao, J.; Wang, Z. Research on the performance of foil bearings under dynamic disturbances. Tribol. Int. 2022, 174, 107744. [Google Scholar] [CrossRef]
- Feng, K.; Liu, L.J.; Guo, Z.Y.; Zhao, X.Y. Parametric study on static and dynamic characteristics of bump-type gas foil thrust bearing for oil-free turbomachinery. Proc. Inst. Mech. Eng. J.—J. Eng. 2016, 230, 944–961. [Google Scholar] [CrossRef]
- Somaya, K.; Kishino, T.; Miyatake, M.; Yoshimoto, S. Static characteristics of small aerodynamic foil thrust bearings operated up to 350,000 r/min. Proc. Inst. Mech. Eng. J.—J. Eng. 2014, 228, 928–936. [Google Scholar] [CrossRef]
- Lee, D.; Kim, D. Design and performance prediction of hybrid air foil thrust bearings. J. Eng. Gas Turbines Power 2011, 133, 042501. [Google Scholar] [CrossRef]
- LaTray, N.; Kim, D. Design of novel gas foil thrust bearings and test validation in a high-speed test rig. J. Tribol.-Trans. ASME 2020, 142, 071803. [Google Scholar] [CrossRef]
- Li, C.; Du, J.; Yao, Y. Modeling of a multi-layer foil gas thrust bearing and its load carrying mechanism study. Tribol. Int. 2017, 114, 172–185. [Google Scholar] [CrossRef]
- Guo, Y.; Hou, Y.; Wang, Y.; Zhao, Q.; Zheng, Y.; Lai, T. Numerical analysis of aerodynamic lubricated double-decked protuberant foil thrust bearing. J. Adv. Mech. Des. Syst. 2019, 13, JAMDSM0056. [Google Scholar] [CrossRef]
- Lee, D.; Kim, D. Three-dimensional thermohydrodynamic analyses of Rayleigh step air foil bearing with radially arranged bump foils. Tribol. Trans. 2011, 54, 432–448. [Google Scholar] [CrossRef]
- Gad, A.M.; Kaneko, S. Performance characteristics of gas-lubricated bump-type foil thrust bearing. Proc. Inst. Mech. Eng. J.—J. Eng. 2015, 229, 746–762. [Google Scholar] [CrossRef]
- Gad, A.M. On the performance of foil thrust bearing with misaligned bearing runner. Ind. Lubr. Tribol. 2017, 69, 105–115. [Google Scholar] [CrossRef]
- Feng, K.; Kaneko, S. Analytical model of bump-type foil bearings using a link-spring structure and a finite-element shell mode. J. Tribol.-Trans. ASME 2010, 132, 021706. [Google Scholar] [CrossRef]
- Jang, G.H.; Kim, Y.J. Calculation of dynamic coefficients in a hydrodynamic bearing considering five degrees of freedom for a general rotor-bearing system. J. Tribol.-Trans. ASME 1999, 121, 499–505. [Google Scholar] [CrossRef]
- Dickman, J.R. An Investigation of Gas Foil Thrust Bearing Performance and Its Influencing Factors. Master’s Thesis, Case Western Reserve University, Cleveland, OH, USA, 2010. [Google Scholar]



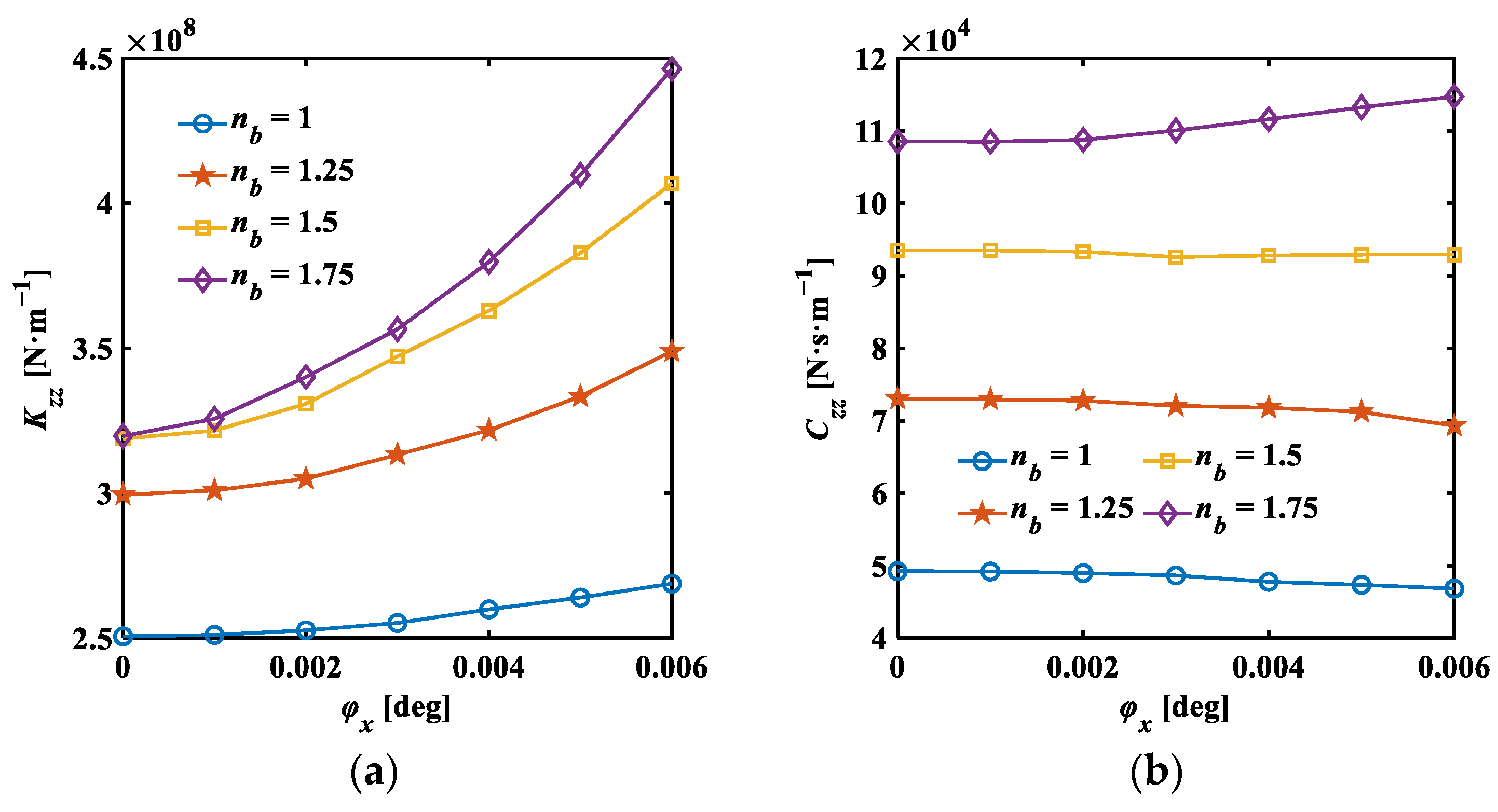
| Parameter | Value |
|---|---|
| /mm | 25.4 |
| /mm | 50.8 |
| Number of bearing pads | 6 |
| Top foil and bump foil angular extent | 60° |
| Proportion of the tilted plane in the sector thrust pad (pitch ratio b) | 0.5 |
| Number of bumps | 12 |
| /mm | 0.9 |
| /mm | 0.4 |
| /mm | 0.1016 |
| /mm | 0.1016 |
| Young’s modulus /GPa | 214 |
| Poisson’s ratio of bump foil and top foil | 0.29 |
| Dynamic viscosity of liquid nitrogen, μ0/μPa·s | 160.7 |
| Supply pressure of liquid nitrogen Ps/MPa | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dou, H.; Jiang, T.; He, L.; Cheng, S.; Fang, X.; Xu, J. Theoretical Evaluation of Lubrication Performance of Thrust-Type Foil Bearings in Liquid Nitrogen. Lubricants 2024, 12, 257. https://doi.org/10.3390/lubricants12070257
Dou H, Jiang T, He L, Cheng S, Fang X, Xu J. Theoretical Evaluation of Lubrication Performance of Thrust-Type Foil Bearings in Liquid Nitrogen. Lubricants. 2024; 12(7):257. https://doi.org/10.3390/lubricants12070257
Chicago/Turabian StyleDou, Hang, Tao Jiang, Longgui He, Shuo Cheng, Xiaoliang Fang, and Jimin Xu. 2024. "Theoretical Evaluation of Lubrication Performance of Thrust-Type Foil Bearings in Liquid Nitrogen" Lubricants 12, no. 7: 257. https://doi.org/10.3390/lubricants12070257
APA StyleDou, H., Jiang, T., He, L., Cheng, S., Fang, X., & Xu, J. (2024). Theoretical Evaluation of Lubrication Performance of Thrust-Type Foil Bearings in Liquid Nitrogen. Lubricants, 12(7), 257. https://doi.org/10.3390/lubricants12070257






