Impact of Interatomic Potentials on Atomic-Scale Wear of Graphene: A Molecular Dynamics Study
Abstract
1. Introduction
2. Methods
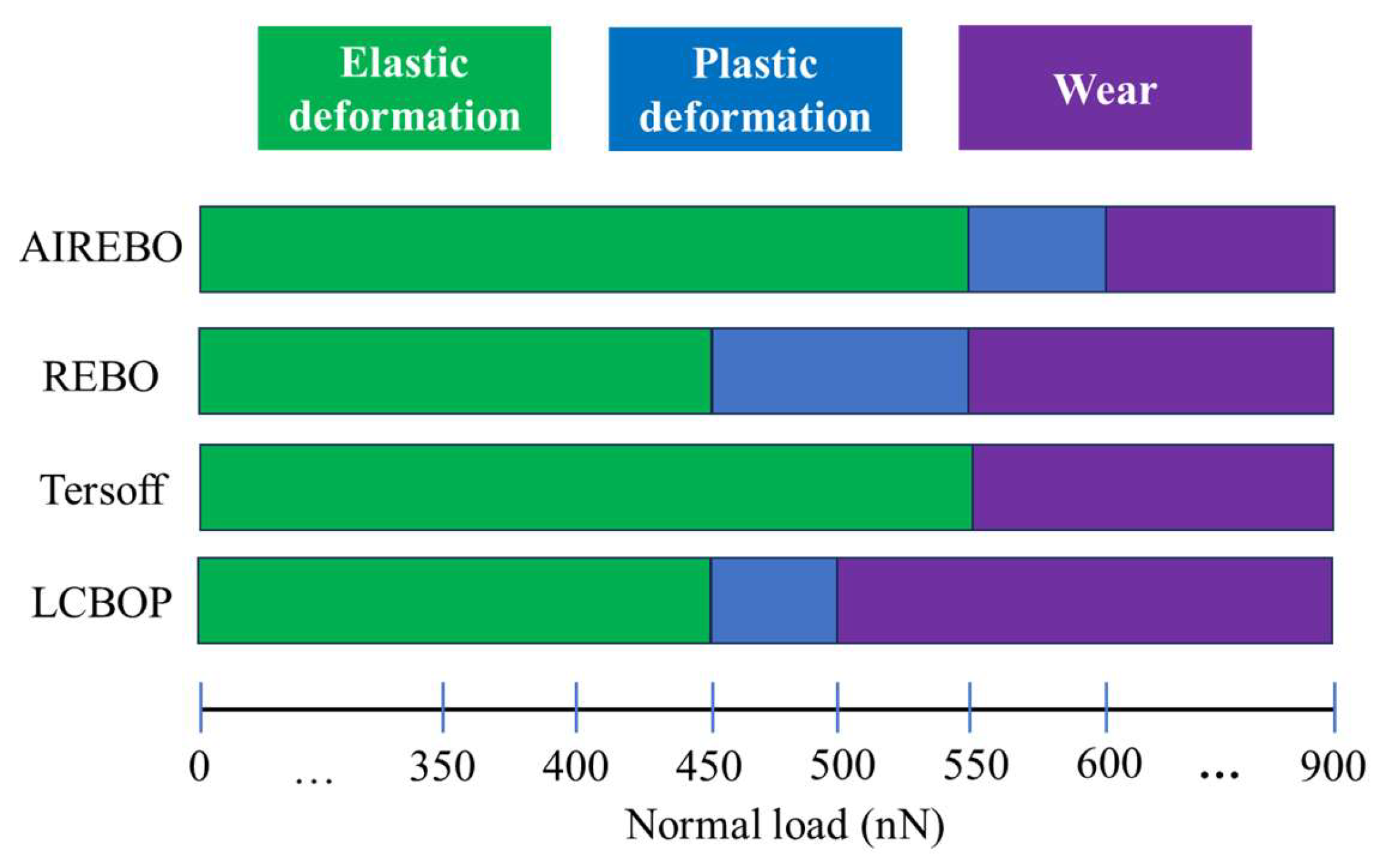
3. Results and Discussion
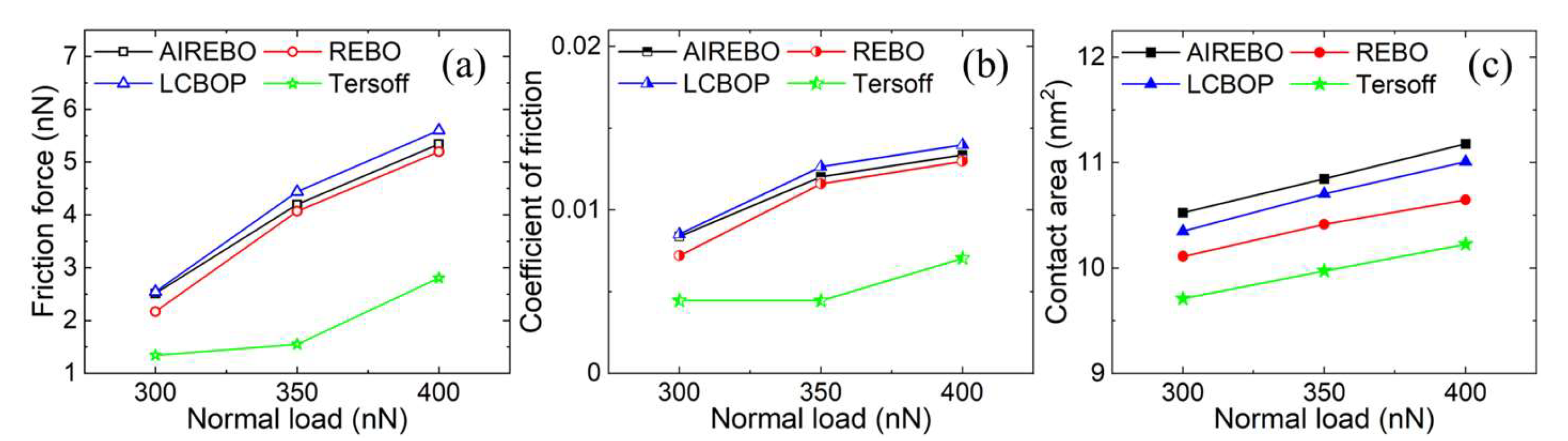
3.1. Elastic Deformation Phase
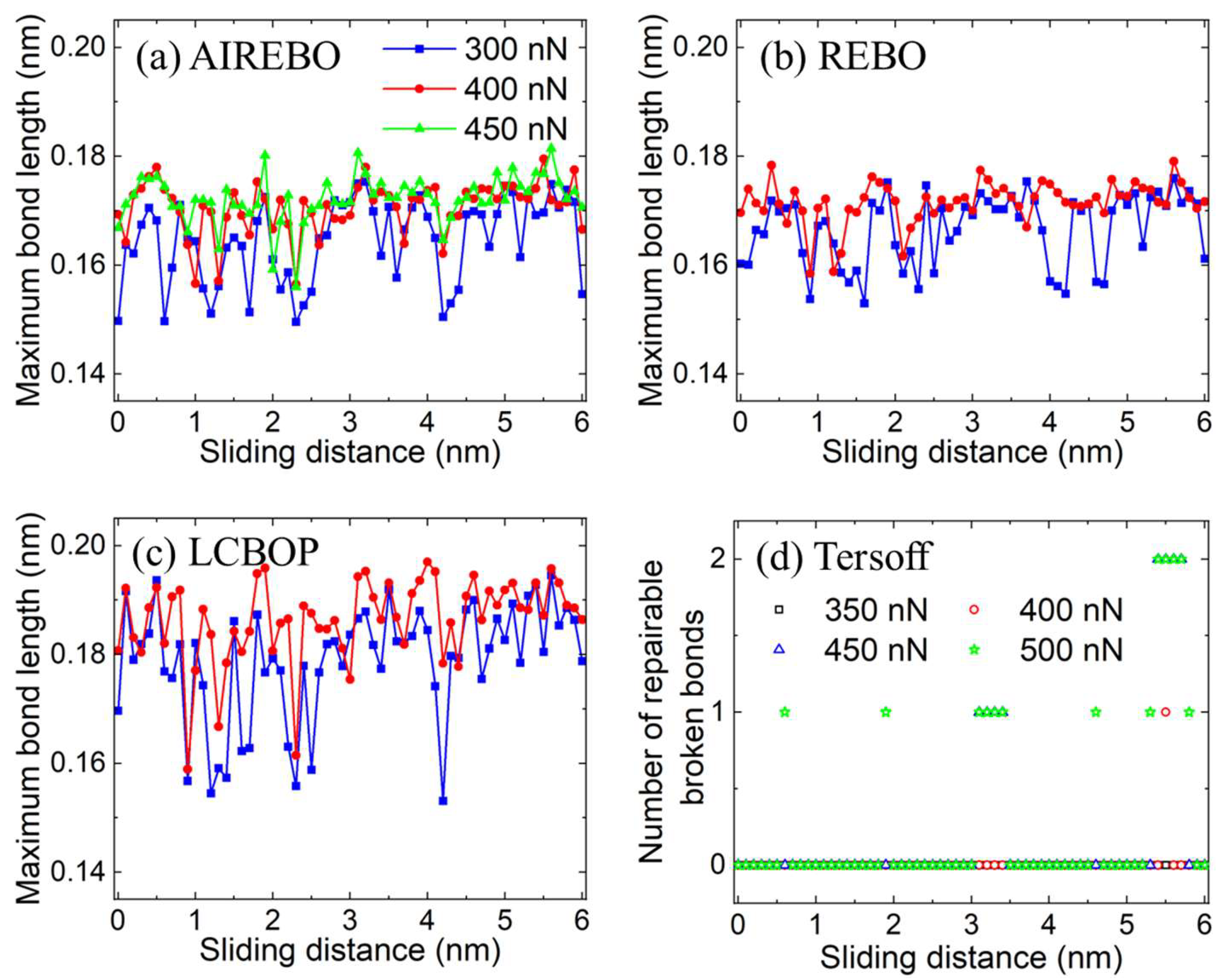
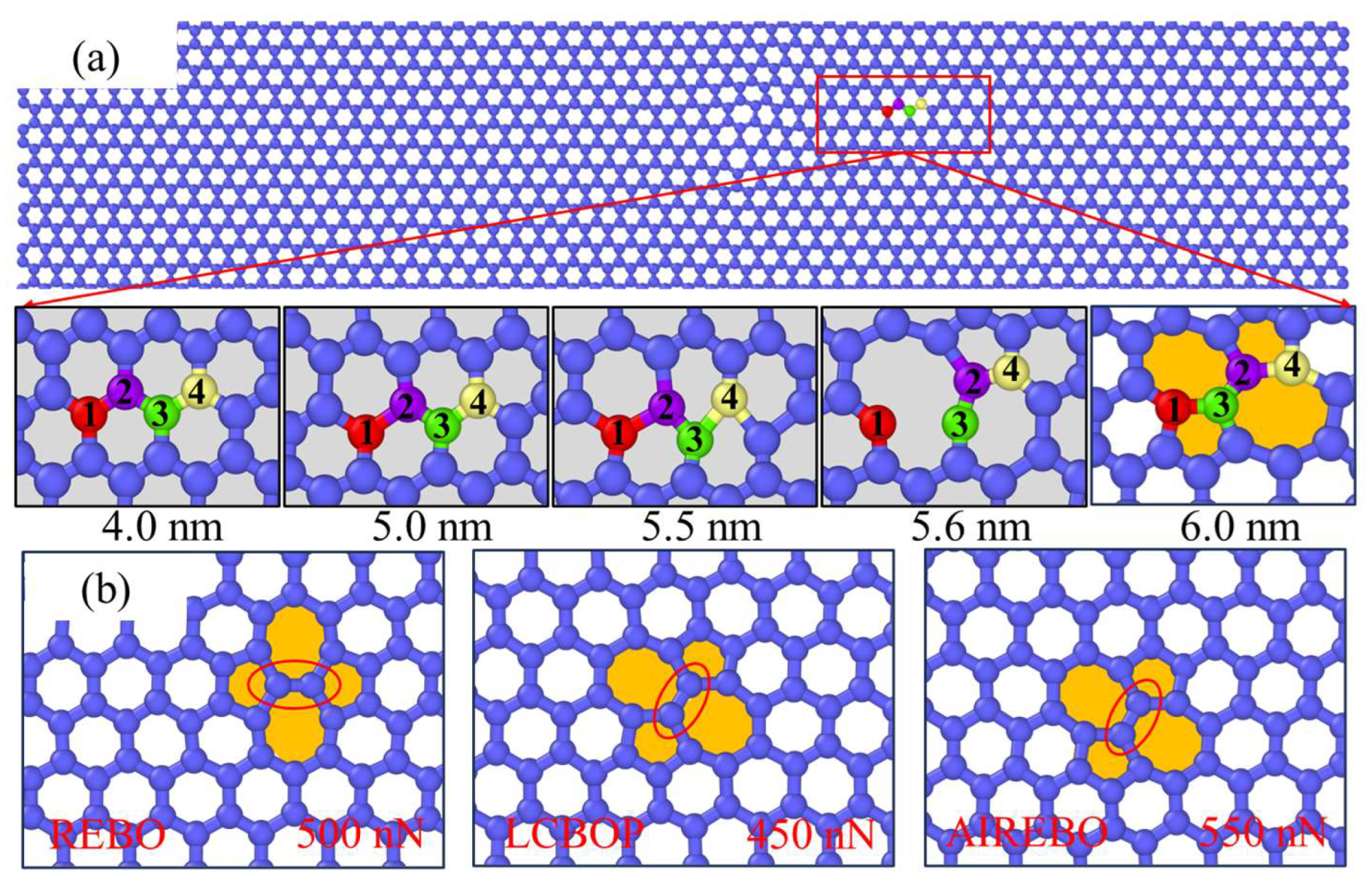
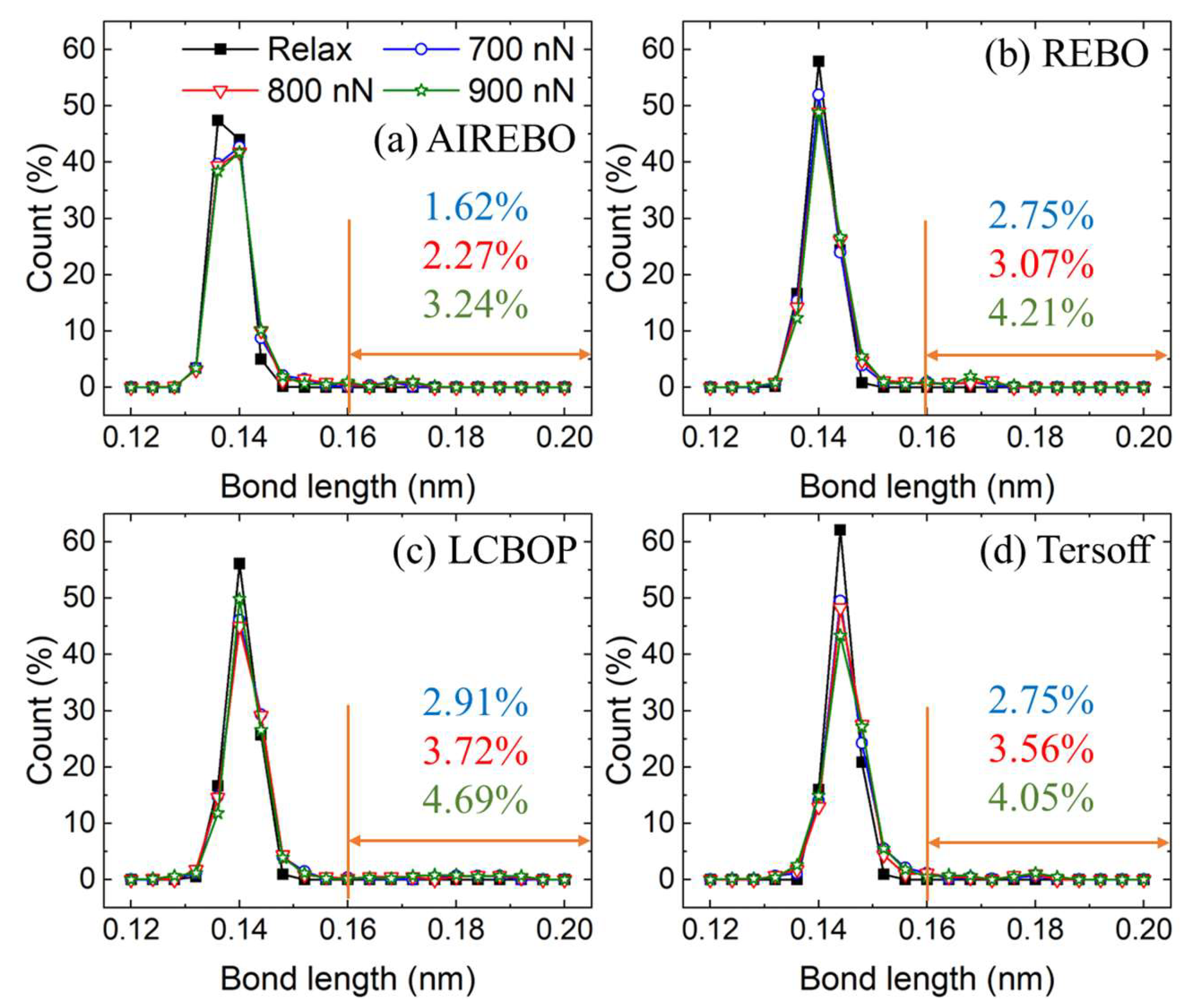
3.2. Plastic Deformation Phase
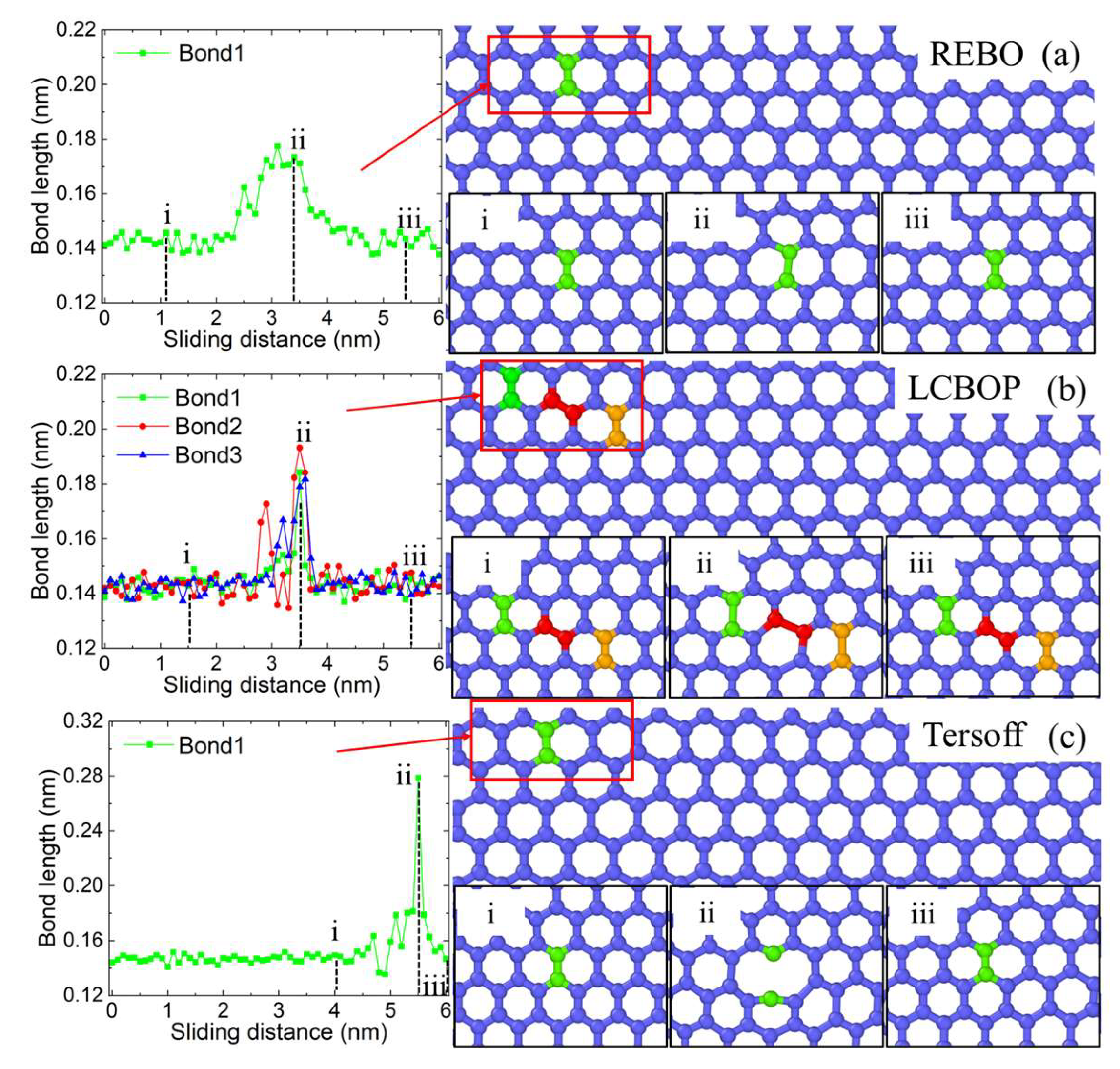
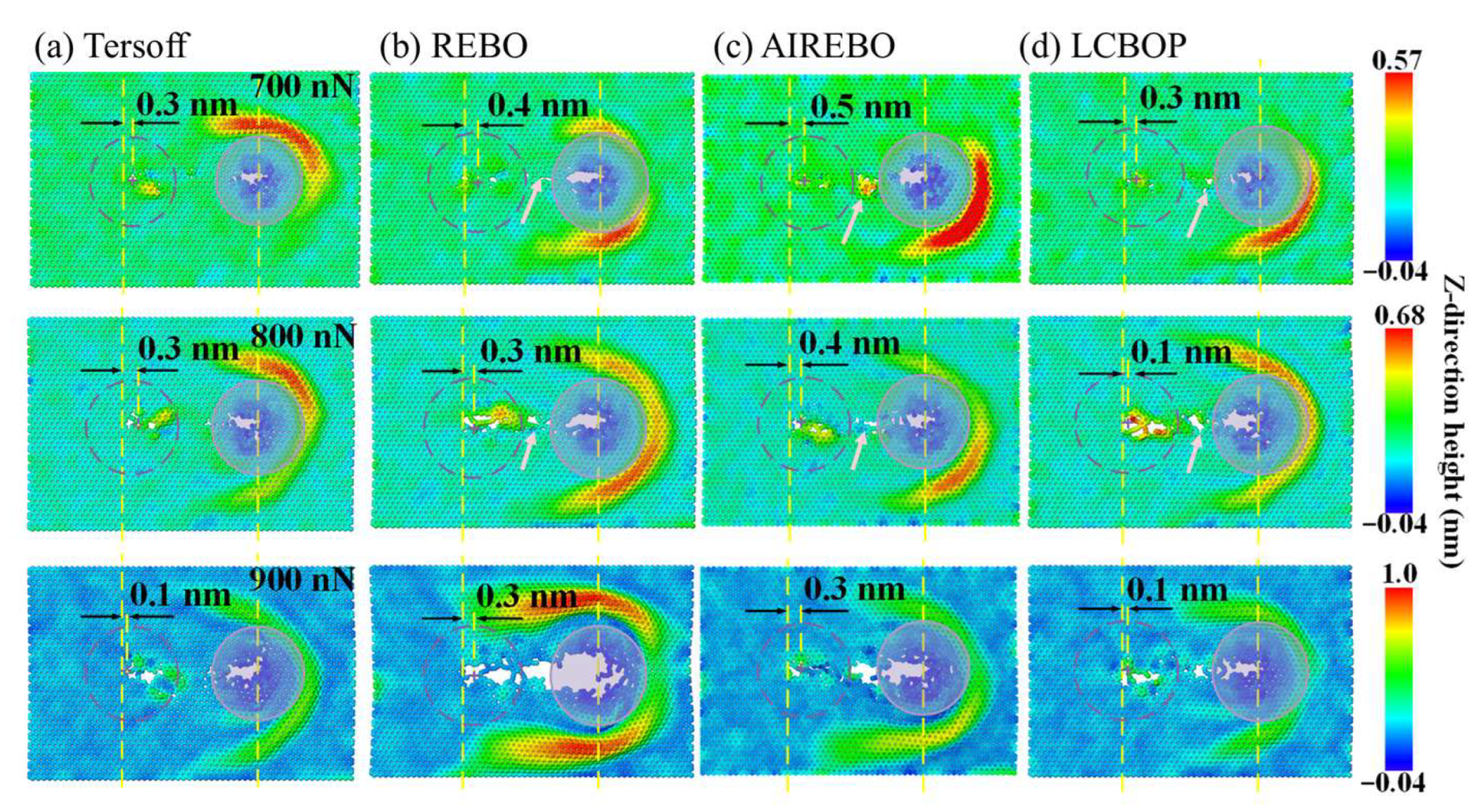
3.3. Wear Phase
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Tan, P.H.; Han, W.P.; Zhao, W.J.; Wu, Z.H.; Chang, K.; Wang, H.; Wang, Y.F.; Bonini, N.; Marzari, N.; Pugno, N.; et al. The shear mode of multilayer graphene. Nat. Mater. 2012, 11, 294–300. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Ge, X.; Li, J. Graphene lubrication. Appl. Mater. Today 2020, 20, 100662. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, S.; Shi, Q.; Ge, X.; Wang, W. Graphene-Family Lubricant Additives: Recent Developments and Future Perspectives. Lubricants 2022, 10, 215. [Google Scholar] [CrossRef]
- Yi, S.; Chen, X.; Li, J.; Liu, Y.; Ding, S.; Luo, J. Macroscale superlubricity of Si-doped diamond-like carbon film enabled by graphene oxide as additives. Carbon 2021, 176, 358–366. [Google Scholar] [CrossRef]
- Wu, G.; Ogata, S.; Gao, L. Atomistic simulations of the frictional properties of 2D materials: A review. J. Phys. D Appl. Phys. 2024, 57, 293001. [Google Scholar] [CrossRef]
- Liu, Y.; Song, A.; Xu, Z.; Zong, R.; Zhang, J.; Yang, W.; Wang, R.; Hu, Y.; Luo, J.; Ma, T. Interlayer Friction and Superlubricity in Single-Crystalline Contact Enabled by Two-Dimensional Flake-Wrapped Atomic Force Microscope Tips. ACS Nano 2018, 12, 7638–7646. [Google Scholar] [CrossRef] [PubMed]
- Yi, S.; Li, J.; Liu, Y.; Ge, X.; Zhang, J.; Luo, J. In-situ formation of tribofilm with Ti3C2Tx MXene nanoflakes triggers macroscale superlubricity. Tribol. Int. 2021, 154, 106695. [Google Scholar] [CrossRef]
- Li, P.; Wang, B.; Ji, L.; Li, H.; Chen, L.; Liu, X.; Zhou, H.; Chen, J. Environmental Molecular Effect on the Macroscale Friction Behaviors of Graphene. Front. Chem. 2021, 9, 679417. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Ouyang, W.; Urbakh, M.; Hod, O. Superlubric polycrystalline graphene interfaces. Nat. Commun. 2021, 12, 5694. [Google Scholar] [CrossRef]
- Gao, X.; Urbakh, M.; Hod, O. Stick-Slip Dynamics of Moiré Superstructures in Polycrystalline 2D Material Interfaces. Phys. Rev. Lett. 2022, 129, 276101. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Xu, Q.; Gao, L.; Ma, T.; Qiu, M.; Hu, Y.; Wang, H.; Luo, J. A molecular dynamics study of lubricating mechanism of graphene nanoflakes embedded in Cu-based nanocomposite. Appl. Surf. Sci. 2020, 511, 145620. [Google Scholar] [CrossRef]
- Li, S.; Li, Q.; Carpick, R.W.; Gumbsch, P.; Liu, X.Z.; Ding, X.; Sun, J.; Li, J. The evolving quality of frictional contact with graphene. Nature 2016, 539, 541–545. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Su, L.; Deng, G. Influence of Nanoparticles in Lubricant on Sliding Contact of Atomic Rough Surfaces—A Molecular Dynamics Study. Lubricants 2024, 12, 160. [Google Scholar] [CrossRef]
- Dmitriev, A.I.; Nikonov, A.Y.; Österle, W. Molecular Dynamics Modeling of the Sliding Performance of an Amorphous Silica Nano-Layer—The Impact of Chosen Interatomic Potentials. Lubricants 2018, 6, 43. [Google Scholar] [CrossRef]
- de Tomas, C.; Suarez-Martinez, I.; Marks, N.A. Graphitization of amorphous carbons: A comparative study of interatomic potentials. Carbon 2016, 109, 681–693. [Google Scholar] [CrossRef]
- Tersoff, J. Empirical Interatomic Potential for Carbon, with Applications to Amorphous Carbon. Phys. Rev. Lett. 1988, 61, 2879–2882. [Google Scholar] [CrossRef] [PubMed]
- Brenner, D.W. Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films. Phys. Rev. B 1990, 42, 9458–9471. [Google Scholar] [CrossRef] [PubMed]
- Brenner, D.W.; Olga, A.S.; Judith, A.H.; Steven, J.S.; Boris, N.; Susan, B.S. A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons. J. Phys. Condens. Matter 2002, 14, 783. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef]
- Los, J.H.; Fasolino, A. Intrinsic long-range bond-order potential for carbon: Performance in Monte Carlo simulations of graphitization. Phys. Rev. B 2003, 68, 024107. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, X.; Xu, Q.; Ma, T.; Hu, Y.; Luo, J. Atomistic insights into friction and wear mechanisms of graphene oxide. Appl. Surf. Sci. 2021, 546, 149130. [Google Scholar] [CrossRef]
- Xu, Q.; Li, X.; Zhang, J.; Hu, Y.; Wang, H.; Ma, T. Suppressing Nanoscale Wear by Graphene/Graphene Interfacial Contact Architecture: A Molecular Dynamics Study. ACS Appl. Mater. Interfaces 2017, 9, 40959–40968. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Klemenz, A.; Pastewka, L.; Balakrishna, S.G.; Caron, A.; Bennewitz, R.; Moseler, M. Atomic Scale Mechanisms of Friction Reduction and Wear Protection by Graphene. Nano Lett. 2014, 14, 7145–7152. [Google Scholar] [CrossRef]
- Vasić, B.; Matković, A.; Ralević, U.; Belić, M.; Gajić, R. Nanoscale wear of graphene and wear protection by graphene. Carbon 2017, 120, 137–144. [Google Scholar] [CrossRef]
- Egberts, P.; Han, G.H.; Liu, X.Z.; Johnson, A.T.C.; Carpick, R.W. Frictional Behavior of Atomically Thin Sheets: Hexagonal-Shaped Graphene Islands Grown on Copper by Chemical Vapor Deposition. ACS Nano 2014, 8, 5010–5021. [Google Scholar] [CrossRef]
- Sandoz-Rosado, E.J.; Tertuliano, O.A.; Terrell, E.J. An atomistic study of the abrasive wear and failure of graphene sheets when used as a solid lubricant and a comparison to diamond-like-carbon coatings. Carbon 2012, 50, 4078–4084. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, X.; Xu, Q.; Ma, T.; Hu, Y.; Wang, H.; Tieu, A.K.; Luo, J. Effects of grain boundary on wear of graphene at the nanoscale: A molecular dynamics study. Carbon 2019, 143, 578–586. [Google Scholar] [CrossRef]
- Pastewka, L.; Pou, P.; Pérez, R.; Gumbsch, P.; Moseler, M. Describing bond-breaking processes by reactive potentials: Importance of an environment-dependent interaction range. Phys. Rev. B 2008, 78, 161402. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, N.; Zhang, L.; Xia, H.; Cheng, D.; Ma, H. Atomistic simulation on frictional response of nanoscratched Al–graphene system. AIP Adv. 2021, 11, 075112. [Google Scholar] [CrossRef]
- Zhang, J.; Deng, G.; Li, W.; Su, L.; Liu, X.; Ma, T.; Gao, L. Impacts of chemical short-range orders on nanotribological properties of CrCoNi medium-entropy alloy at room and cryogenic temperatures. Tribol. Int. 2024, 191, 109191. [Google Scholar] [CrossRef]
- Qi, Y.; Liu, J.; Zhang, J.; Dong, Y.; Li, Q. Wear Resistance Limited by Step Edge Failure: The Rise and Fall of Graphene as an Atomically Thin Lubricating Material. ACS Appl. Mater. Interfaces 2017, 9, 1099–1106. [Google Scholar] [CrossRef] [PubMed]
- Szlufarska, I.; Chandross, M.; Carpick, R.W. Recent advances in single-asperity nanotribology. J. Phys. D Appl. Phys. 2008, 41, 123001. [Google Scholar] [CrossRef]
- Huang, Z.; Chen, S.; Lin, Q.; Ji, Z.; Gong, P.; Sun, Z.; Shen, B. Microscopic Mechanisms behind the High Friction and Failure Initiation of Graphene Wrinkles. Langmuir 2021, 37, 6776–6782. [Google Scholar] [CrossRef]
- Tran-Khac, B.-C.; Kim, H.-J.; DelRio, F.W.; Chung, K.-H. Operational and environmental conditions regulate the frictional behavior of two-dimensional materials. Appl. Surf. Sci. 2019, 483, 34–44. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Zhang, S.; Du, H.; Xue, T.; Kang, Y.; Zhang, Y.; Zhao, P.; Li, Q. Revisiting Frictional Characteristics of Graphene: Effect of In-Plane Straining. ACS Appl. Mater. Interfaces 2022, 14, 41571–41576. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.-Y.; Wu, R.; Xia, R.; Chu, X.-H.; Xu, Y.-J. Effects of Stone-Wales and vacancy defects in atomic-scale friction on defective graphite. Appl. Phys. Lett. 2014, 104, 183109. [Google Scholar] [CrossRef]
- Cao, A.; Shen, B.; Lin, Q.; Chen, S.; Huang, Z.; Ji, Z.; Zhang, Z. Influence of Stone-Wales defect on graphene friction: Pinning effect and wrinkle modification. Comput. Mater. Sci. 2020, 173, 109423. [Google Scholar] [CrossRef]
- Qi, Y.; Liu, J.; Dong, Y.; Feng, X.-Q.; Li, Q. Impacts of environments on nanoscale wear behavior of graphene: Edge passivation vs. substrate pinning. Carbon 2018, 139, 59–66. [Google Scholar] [CrossRef]
- Huang, Y.; Yao, Q.; Qi, Y.; Cheng, Y.; Wang, H.; Li, Q.; Meng, Y. Wear evolution of monolayer graphene at the macroscale. Carbon 2017, 115, 600–607. [Google Scholar] [CrossRef]
- Zhang, J.; Li, W.; Qin, R.; Chen, P.; Liu, Y.; Liu, X.; Gao, L. An atomic insight into the stoichiometry effect on the tribological behaviors of CrCoNi medium-entropy alloy. Appl. Surf. Sci. 2022, 593, 153391. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, X.; Zhang, J.; Chen, P. Impact of Interatomic Potentials on Atomic-Scale Wear of Graphene: A Molecular Dynamics Study. Lubricants 2024, 12, 245. https://doi.org/10.3390/lubricants12070245
Ye X, Zhang J, Chen P. Impact of Interatomic Potentials on Atomic-Scale Wear of Graphene: A Molecular Dynamics Study. Lubricants. 2024; 12(7):245. https://doi.org/10.3390/lubricants12070245
Chicago/Turabian StyleYe, Xueqi, Jie Zhang, and Ping Chen. 2024. "Impact of Interatomic Potentials on Atomic-Scale Wear of Graphene: A Molecular Dynamics Study" Lubricants 12, no. 7: 245. https://doi.org/10.3390/lubricants12070245
APA StyleYe, X., Zhang, J., & Chen, P. (2024). Impact of Interatomic Potentials on Atomic-Scale Wear of Graphene: A Molecular Dynamics Study. Lubricants, 12(7), 245. https://doi.org/10.3390/lubricants12070245





