Fundamental Mechanisms Underlying the Effectiveness of Nanoparticle Additives to Lubricants: 25 Examples Linking Nano- to Macroscale Friction

Abstract

Studies of the fundamental origins of friction have undergone rapid acceleration in recent years by providing valuable information on the nanoscale mechanisms responsible for friction at the macroscopic level. Significant efforts have been directed at developing composite nanofluids and nanoparticle additives to unlock new tribological properties unattainable by traditional lubricants. The studies are now further evolving by developing methods to achieve active control over nano- and/or mesoscale friction through the application of magnetic and electric fields external to the contact. These methods constitute an area of rapidly growing interest, and they also illuminate how the performance of conventional lubricants could be enhanced through the synergistic addition of nanoparticles (NPs). This mini review highlights 25 publications that collectively reveal significant progress, as well as important outstanding challenges, to the fundamental understanding of how the addition of NPs impacts lubricant performance. The first two topics focus on how Quartz Crystal Microbalance (QCM) nanotribological response to solid contacts can be linked to macroscale friction coefficients in the boundary lubrication regime and how QCM response upon immersion into a liquid is linked to macroscale lubricity in the mixed and hydrodynamic regimes. The third and fourth topics highlight the pivotal role of nanoparticle charge and surface treatments, while also indicating that the rolling of nanoparticles is ineffective and/or detrimental. The fifth topic focuses on applications that demonstrate the tuning of friction by varying nanoparticle electric charge and/or an external electric potential. The highlighted literature was selected to demonstrate a range of experimental and theoretical research, to provide direct connections between the nanoscale and macroscale tribological attributes, and to emphasize environmentally friendly lubricating materials such as water-based nanofluids.

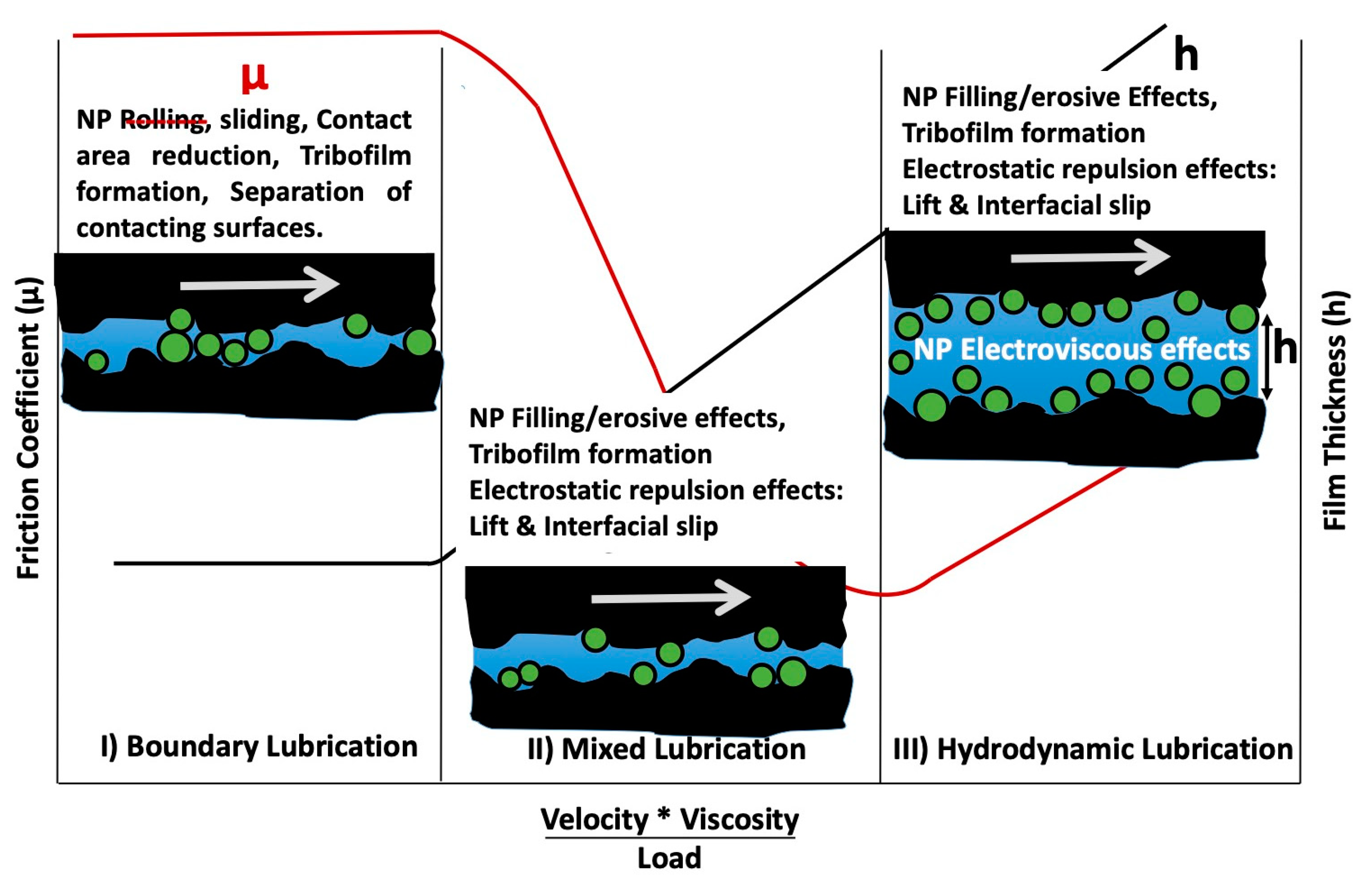
1. Introduction

Close to thirty years ago, in an early nanotribology experiment, Israelachvili and coworkers employed a surface forces apparatus (SFA) to measure the viscosity of toluene between atomically uniform mica surfaces as C₆₀ was added to the liquid [1]. Remarkably, they observed “full-slip” conditions when C₆₀ was present but not for toluene alone. The authors suggested that macroscopic friction might also be profoundly impacted by the addition of C₆₀ to lubricants. They proposed a rolling action of the small, 0.7 nm wide soccer ball-shaped molecules as a possible mechanism, or possibly changes to the slip conditions within one or two molecular layers from the surface.

Although C₆₀ did not subsequently become established as a commercial lubricant additive, the opportunities to reduce macroscale friction using nanoscale additives have sparked intense interest among researchers and industry [2,3,4]. This interest is driven by the importance of tribology and energy efficiency to the burgeoning financial and environmental costs of global energy consumption [5,6,7,8] and the demand for the replacement of fossil fuel lubricants with environmentally friendly and degradable materials [6,9,10]. Current annual global greenhouse gas emission rates (~57 GtCO₂e [8]) correspond to an additional global temperature increase of ~0.5 C within ~15 years if changes are not implemented [7,8]. A 2017 study, meanwhile, found that ~20% of the world’s energy consumption was being used to overcome friction in tribological contacts, and that a ~40% reduction in frictional energy losses was feasible over a 15-year period [5].

Most of the literature reports published to this date find that NP additives generally, but not always, reduce friction. For example, nanodiamonds of ca. 5 nm in diameter when added to oil reduce the macroscale friction coefficients by as much as 75% [11], while aqueous suspensions of nanodiamonds with certain surface treatments substantially increase friction in stainless steel contacts [12]. Titania nanoparticles added to oil, meanwhile, have been found to increase friction by about 20% while reducing wear by about 30% [13]. Clearly, an understanding of such opposite effects amongst very similar NP additives requires fundamental studies of the underlying mechanisms (e.g., rolling, smoothing, film formation, electro-viscous effects, etc.) that give rise to nanoscale and macroscale tribological attributes (Figure 1) [14].

This mini review highlights 25 selected research reports [12,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38], 24 of which were published following the 1996 pioneering work of Israelachvili and coworkers describing “full-slip” conditions achieved via C₆₀ additives to toluene [1]. Collectively, they reveal significant progress, as well as important outstanding challenges, towards the fundamental understanding of how the addition of nanostructures impacts lubricant performance. The first topic of the review focuses on how Quartz Crystal Microbalance (QCM) nanotribological response to solid contacts can be linked to macroscale friction coefficients in the boundary lubrication regime and the second topic describes how QCM response upon immersion into a liquid is linked to macroscale lubricity in the mixed and hydrodynamic regimes. The third and fourth topics, respectively, highlight the applicability of two fundamental nanoscale mechanisms that are commonly invoked to explain changes in macroscale lubricity. Topic three provides examples of the ineffective, and possibly detrimental, effect of nanoparticle rolling while, in contrast, topic four highlights the “astonishing” impact of surface treatments/surface charge. The fifth topic focuses on applications that demonstrate the tuning of friction by varying nanoparticle electric charge and/or external electric potential. Highlights were selected to demonstrate a range of experimental and theoretical research, to provide direct connections between the nanoscale and macroscale tribological attributes, and, when possible, to emphasize environmentally friendly materials such as water-based nanofluids. Given the very limited number of highlights presented here, additional in-depth and extensive topical review articles are also included in the references for follow-up reading and background material [2,3,4,10,14,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60].

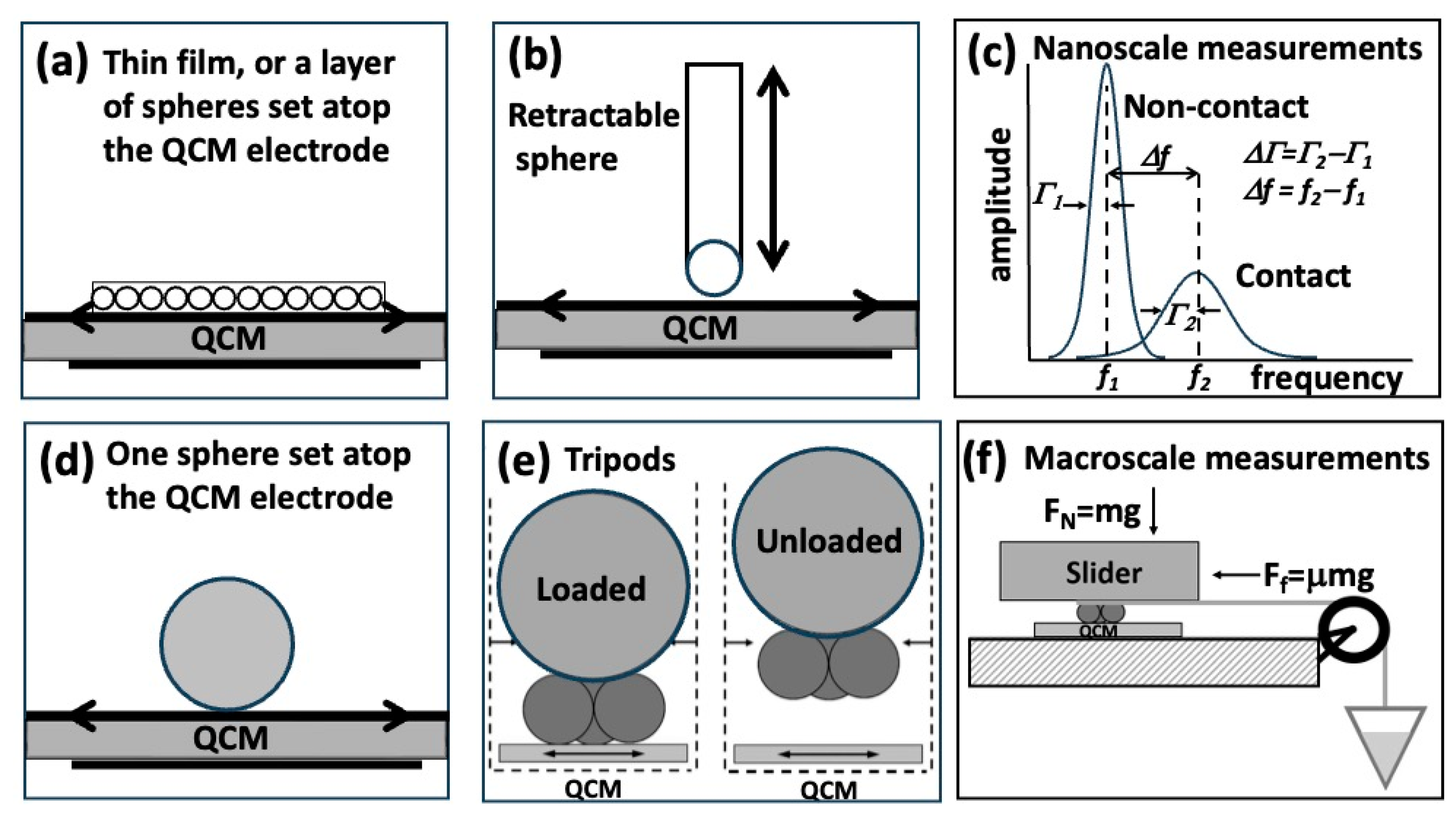
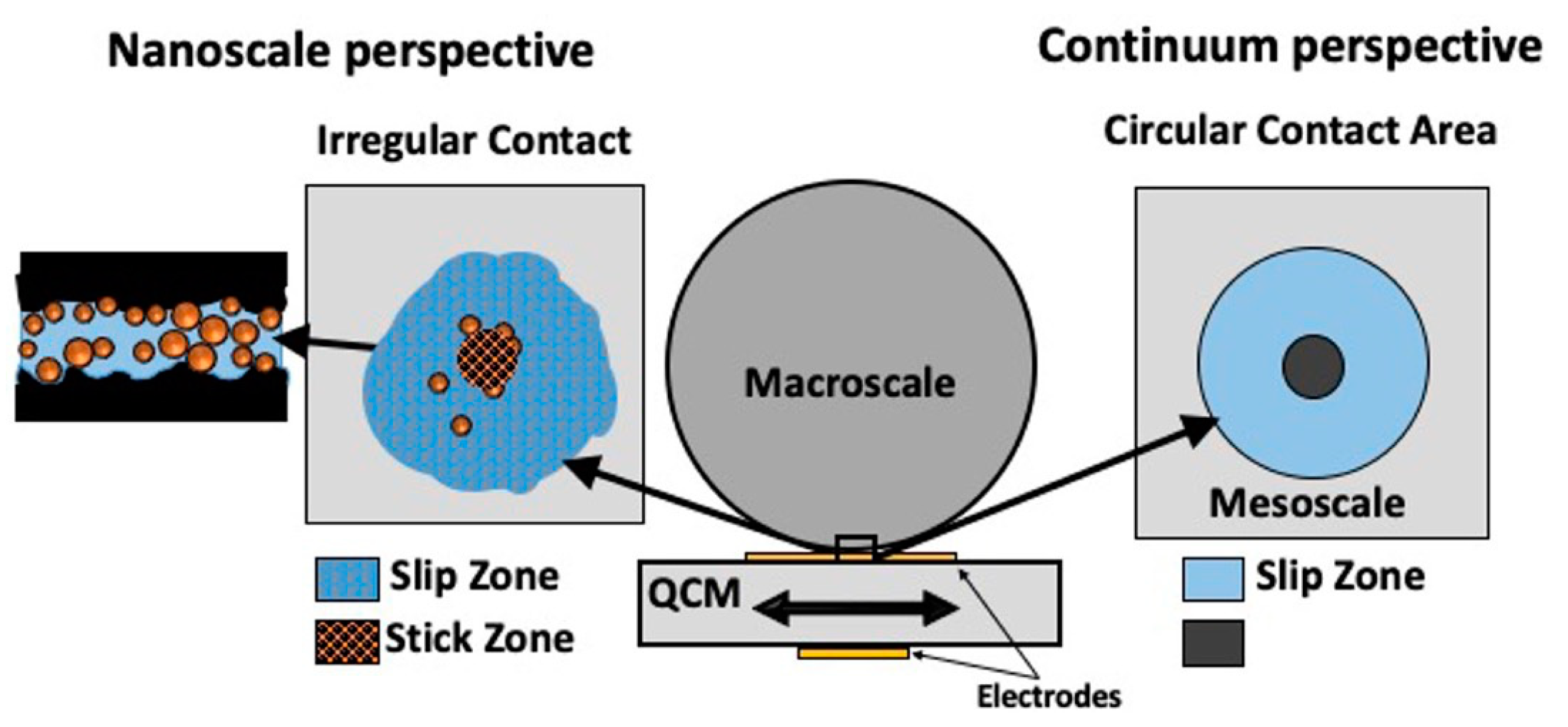
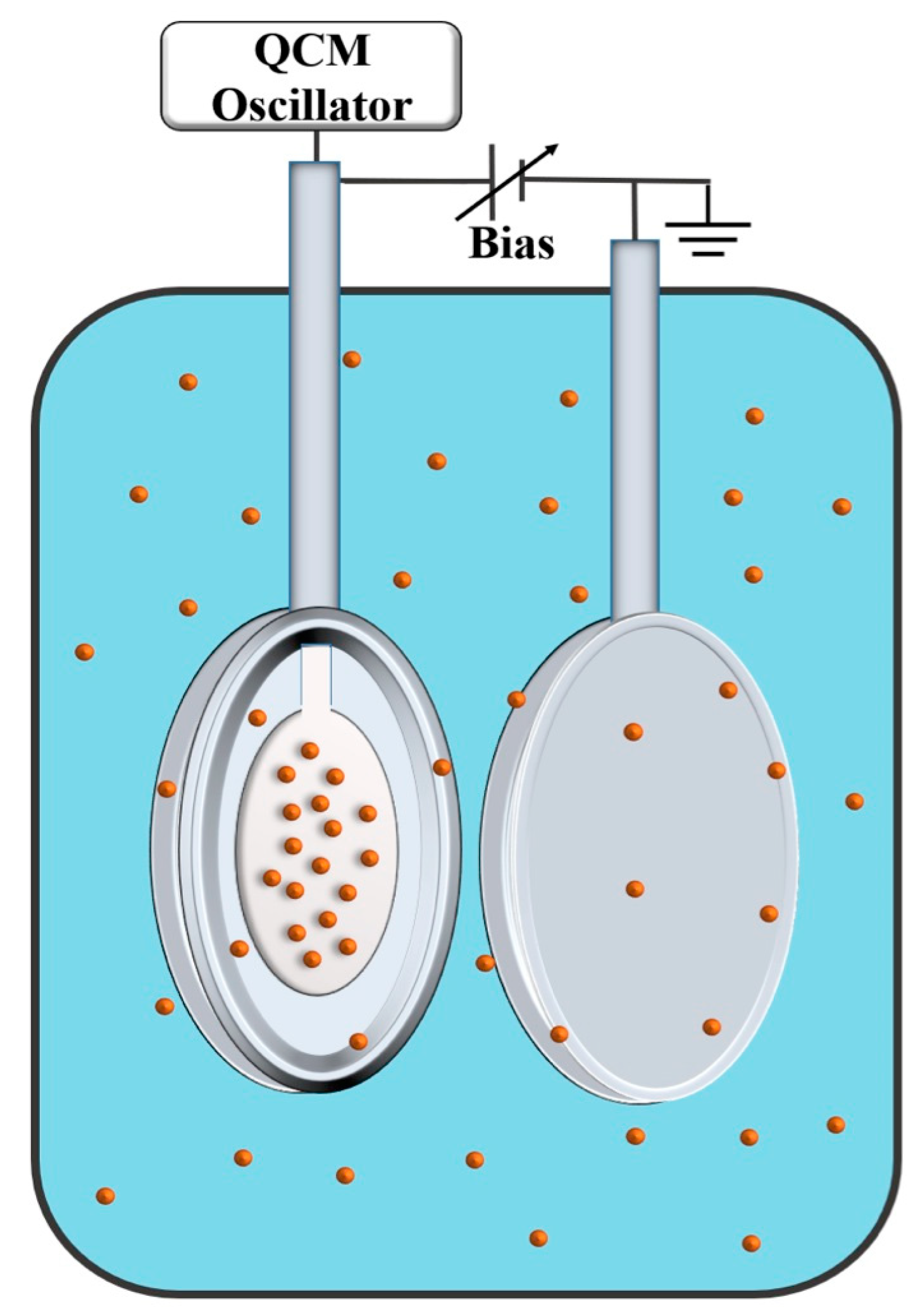
2. Quartz Crystal Microbalance Response to Spherical Contacts Directly Links Nano- and Macroscale Friction

A QCM consists of a thin wafer of single crystal piezoelectric quartz that is cut so as to oscillate in transverse shear motion when an alternating voltage is applied to metal electrodes deposited onto its two planar surfaces. Fundamental resonant frequencies are typically in the 5–10 MHz range, with very low internal dissipation. Initially developed in the 1920s as a tuning fork-shaped time standard, or “quartz clock” [61], its use was extended to deposition rate monitors in the 1950s [62] and to atomic-scale friction measurements in the 1980s [25].

When employed for nanotribology applications, QCM is capable of directly linking nanoscale and macroscale properties because the typical peak electrode velocities of up to several m/s and the shear rates of about 10⁶ s⁻¹ are comparable to those of macroscale systems. The method has been broadly applied to a wide range of soft material systems [41,42] and is sensitive to both mass deposition on its surface electrode and the viscoelastic coupling of fluids it may be in contact with [46]. It has also been used in geometries consisting of bare and lubricated tribological contacts with external objects such as spheres spanning a few μm to cm in diameter. Changes in the QCM frequency and dissipation in response to the external contacts yield information on the contact stiffness and/or friction coefficients [46,47]. Exceptionally high-quality factors Q~10⁶ of QCM allow for precise measurements of shifts in frequency Δf and changes in ΔQ, which are inversely proportional to the half-bandwidth ∆Γ (Figure 2c). To enable a cross-comparison of QCM studies, the highlights selected for this section employ QCMs oscillating in the fundamental mode at or near 5 MHz, with gold or steel electrodes (Figure 2). Further reading on the modeling of contacts at the atomic scale, including QCM response, may be found in refs. [39,40,41,42].

2.1. A Sensitive New Method for the Determination of Adhesive Bonding between a Particle and a Substrate [15]

In this 1985 publication, Dybwad reported frequency shift measurements associated with the placement of one gold microsphere atop a gold electrode of a QCM oscillating in transverse shear motion and inferred the associated particle–substrate adhesive bond strengths for particles of various sizes [15]. For spheres with diameters ranging from 5 to 50 μm, positive QCM frequency shifts in the range of 0.1 to 1.5 ppm were recorded.

For rigidly attached films deposited onto a QCM electrode (Figure 2a), the negative frequency shift is described by equations derived by Sauerbrey in the 1950s [62]:

$$\frac{m_f}{A}={\rho }_f{d}_f=-\frac{∆f\sqrt{{\rho }_q{\mu }_q}}{2{f_0}^2};\mathsf{\Delta }f=-\frac{2{f_0}^2{\rho }_2}{\sqrt{{\rho }_q{\mu }_q}},$$

(1)

In Equation (1), ρ_f and d_f are the film density and thickness, respectively, ρ_q = 2.648 g/cm² and μ_q = 2.947 × 10¹¹ gm cm⁻¹ s⁻² are the density and shear modulus of quartz, f₀ is the fundamental oscillation frequency before the film was deposited, and ρ₂ = m_f/A is the mass per unit area of the film. For f₀ = 5 MHz, Equation (1) simplifies to

$$∆f=-2.263\times {10}^{-6}\left({f_0}^2{\rho }_2\right)=-5.66\times {10}^7{\rho }_2,$$

(2)

where Δf is measured in Hz and ρ₂ is measured in g/cm².

To interpret the positive Δf results, Dybwad employed a coupled oscillator model consisting of a gold particle with mass m attached to a QCM with a spring with stiffness k. Coupling the particle to the QCM changes its resonant frequency in accordance with the following:

$$f^2=\frac{1}{{8\pi }^2}\left(\frac{K}{M}+\frac{k}{M}+\frac{k}{m}\right)\pm {\frac{1}{{8\pi }^2}\left[{\left(\frac{K}{M}+\frac{k}{M}+\frac{k}{m}\right)}^2-4\frac{K}{M}\frac{k}{m}\right]}^{1/2},$$

(3)

where M and K are the effective mass and stiffness of the QCM, and the unloaded resonant frequency f₀ = (2π)⁻¹$\sqrt{K/M}$. The expression in Equation (3) has a positive branch for values of k less than k = Km/M. To the first order, the frequency at k = Km/M is described by $f/f_0=1\pm \sqrt{m/M}$ for m << M. For k = K, Equation (3) reduces to the Sauerbrey result, Equation (1):

$$f=\frac{1}{2\pi }\sqrt{\frac{K}{M+m}}∆f=-\frac{2{f_0}^2{\rho }_2}{\sqrt{{\rho }_q{\mu }_q}}$$

(4)

Meanwhile, for small/weak contact stiffness Equation (3) reduces to

$$f=\frac{1}{2\pi }\sqrt{\frac{K+k}{M}}∆f=+\frac{k{f}_0}{2K}.$$

(5)

Employing Equation (5), Dybwad inferred values of k of the order of 10⁷ dyn/cm for the particles by estimating the effective mass of the QCM as half of the mass in the region of the active oscillations , as only the surfaces oscillate at the full amplitude.

For a QCM electrode with a 5 MHz fundamental resonant frequency, the electrode thickness t is 0.0334 cm and a typical active electrode radius is 0.32 cm. (For cases where a QCM has electrodes with two different radii, the “active electrode radius” is the smaller of the two, designating an area of “active” driven oscillation.) The effective mass M of the active oscillation region ~(ρ_qπr²t)/2 yields M = 0.0142 g, K = 1.4 × 10¹³ dyn/cm, and A = 0.32 cm², where K = (2πf)² M and m = 1.263 μg for the 50 μm sphere, assuming the bulk density of gold (19.3 g/cm³).

If the mass of the microsphere is spread uniformly over the electrode, then ρ₂ = 3.95 mg/cm², corresponding to a 2 nm thick film, and Δf = −223 Hz using Equation (1). For comparison, the frequency shift decreases to Δf = −16.0 Hz for a non-slipping monolayer of close-packed C₆₀ molecules (mass per molecule: 1.19559 × 10⁻²¹ g; area per particle: 0.4244 nm² ; ρ₂ = 0.282 mg/cm² ) and to Δf = −59.8 Hz for a close-packed layer of 5 nm nanodiamonds (ρ₃ = 3.5 g/cm³; mass per particle: 2.29 × 10⁻¹⁹ g; area per particle: 21.65 nm², ρ₂ = 1.058 mg/cm²). Merging all these particles into a single sphere without any voids would yield a 90 mm diameter particle.

Dybwad observed a +1.5 ppm frequency shift upon the placement of the 50 μm gold particle on the electrode. From Equation (5), the corresponding +7.5 Hz shift for a 5 MHz QCM yields k = 42 × 10⁶ dyn/cm, which is well below the transition value of k = Km/M. Dybwad noted that this value was of the order of a few hundred atomic bonds or a few thousand Van der Waals bonds and did not distinguish between viscoelastic resistance to shear and frictional energy dissipation associated with sliding. See also [63] for a general discussion of QCM resonators.

2.2. High-Frequency Tribological Investigations on Quartz Resonator Surfaces [16]

Laschitsch and Johannsmann reported in 1999 a study of QCM response to a macroscopic tribological contact by bringing a 3.5 mm diameter brass sphere in and out of contact with a gold electrode (Figure 2b) [16]. They also studied several other sphere–electrode materials combinations. Given the macroscopic size of the sphere, the QCM was treated as being in oscillatory contact with a hard wall and a local elasticity at the point of contact. Employing the coupled oscillator approach and measuring ∆Γ, these authors found the response to be well described by an increased stiffness of the QCM–sphere system, which, for the full contact, was reflective of the area of contact and the elasticity of the sphere.

In the range of distances where a contact was just being formed, Laschitsch and Johannsmann detected an additional contribution to the dissipation that was highly dependent on the specific materials in the contact. The authors attributed this to frictional processes associated with the transverse shear oscillatory motion of the contact. To test this hypothesis, they performed measurements on materials combinations that were known to exhibit high (gold on brass) and low (fluoropolymer on fluoropolymer) friction at the macroscale.

Using the loss factor ∆Γ/Δf as a metric for friction levels, they successfully linked larger values of ΔΓ/Δf to systems known to exhibit higher macroscale friction coefficients. The work, therefore, provided a direct means to connect QCM frequency and dissipation response to the macroscale friction coefficients. The loss factor metric as a gauge of macroscale lubricity will be further discussed in the highlights presented herein. See also Refs. [64,65] for closely related studies.

2.3. An Integrated Force Probe and Quartz Crystal Microbalance for High-Speed Microtribology [17]

Nearly 20 years after the Laschitsch and Johannsmann study, Borovsky and coworkers employed a similar geometry (Figure 2b) with a 50 μm Al₂O₃ sphere at the tip of a precision-controlled nanoindenter to form a microscopic contact with a gold QCM electrode coated with octadecanethiol (C18) [17]. Their report includes an excellent overview of the various QCM-tip studies inspired by the original Dybwad paper and the evolution of the technique for tribological studies up to 2017.

The QCM apparatus constructed by Borovsky et al. [17] had the capability to measure frictional forces and contact areas over a wide range of applied loads while maintaining microscopic contacts reaching high sliding speeds near 1 m/s. Nanoscale and microscale comparison studies of friction coefficients for identical material contacts were reported for 50 μm diameter spheres pressed into the surface with ~1 mN loads and 2 μm contact diameters. Contact stiffness values consistent with the prior literature data were also reported. Energy dissipation and lateral contact stiffness were monitored with the QCM, allowing direct determination of the friction force, friction coefficients, and contact areas. The authors found that the full-slip threshold force was by about a factor of two larger than the kinetic friction and identified important transition points between the static and kinetic friction.

The work of Borovsky and coworkers provided detailed insights into measurements of the friction coefficients and contact areas in well-defined micro-contacts. Friction coefficients were calculated for the contacts in the full-slip regime achieved at ~0.2 m/s velocity in QCM measurements and compared to measurements performed at 25 μm/s velocity for the same contacts in a microtribometer setup. The authors found an agreement between the two systems with velocities spanning over a significant range. They also found the friction forces F_f to increase sublinearly with the load F_N in close correspondence with the contact area while the shear strengths were relatively insensitive to pressure.

The relation that defines the friction coefficient as the ratio of the friction force to the normal force, F_f = μF_N, is based on multiasperity contact between the macroscale objects. The area of multiscale contact grows in proportion to the applied force, giving rise to a proportionality with the friction force. For this precision microscopic study, the measurements were performed in a regime of full sliding and a single contact.

2.4. Partial Slip in Mesoscale Contacts: Dependence on Contact Size [18]

In a series of publications from 2013 to 2015, Johannsmann and coworkers employed tripod geometry to further establish a link between the QCM nanoscale response to macroscale friction coefficients [18,66]. Their apparatus (Figure 2e) was based on three spherical contacts rigidly attached to a support platform upon which further weights could be added. It has several advantages over single-sphere geometry (Figure 2d) as it prevents the rolling of the spheres and allows for the placing of the contacts away from the center, where the amplitude of the vibration can more reliably be determined. The authors employed glass spheres from 50 to 275 μm in diameter on polymer surfaces and developed a formalism showing how QCM frequency and dissipation respond to the value of the coefficient of friction of the materials in contact. Focusing on the partial-slip regime, they demonstrated that the QCM response had distinct characteristics in the static, partial-slip, and full-slip regimes. In particular, the authors made use of a Cattaneo–Mindlin (CM)-slip model to relate contact stiffness to measurements of the QCM response for a contact with a friction coefficient μ.

The CM model is an approximation that allows for a simplified analysis framework for two curved surfaces that are pressed with a normal load F_N into contact and then sheared tangentially. Such bodies commonly remain stuck to each other in one part of the contact while slipping in other regions. The authors’ approximation treats the contact as a rigid indenter pressed into a flat elastic surface and assumes that the sliding friction in the slip region is governed by a “Coulomb” friction law, F_f = μ_kF_N. For a small amplitude reciprocal motion, the partial-slip regime in this model commences at the contact’s edge in the form of a thin annulus. The annulus progressively grows as the amplitude of vibration increases. The system transitions to the full gross slippage for a sufficiently large applied tangential force. One central result of this study is depicted in Figure 3, showing the QCM response for a non-slipping contact exhibiting viscoelasticity, partial-slip, and full-slip conditions. Characteristic slopes of Δf and ΔΓ versus the amplitude of oscillations allow for the CM regime to be readily determined. The friction coefficient can then be inferred from the following equations:

$$∆f\left(u_o\right)=h-b{u}_o∆\Gamma \left(u_o\right)=\frac{4}{3\pi }{bu}_o$$

(6)

$$h=\frac{n_p\kappa }{2n{\pi }^2{A}_{eff}{Z}_q}b=\frac{n_p{\kappa }^2}{6n{\pi }^2{A}_{eff}{Z}_q{F}_N}\frac{1}{\mu },$$

(7)

where n_p is the number of contacts, $\mu$ is the coefficient of friction, and $u_o$ is the amplitude of oscillation at the center of the QCM.

Vlachová et al. later employed the Hanke methodology by varying the amplitude of oscillation while monitoring Δf and ΔΓ [66]. The analysis yielded reasonable values for the friction coefficient μ but the authors did not compare values obtained from QCM to the results of macroscale measurements for the same set of contacts. See also Ref. [68].

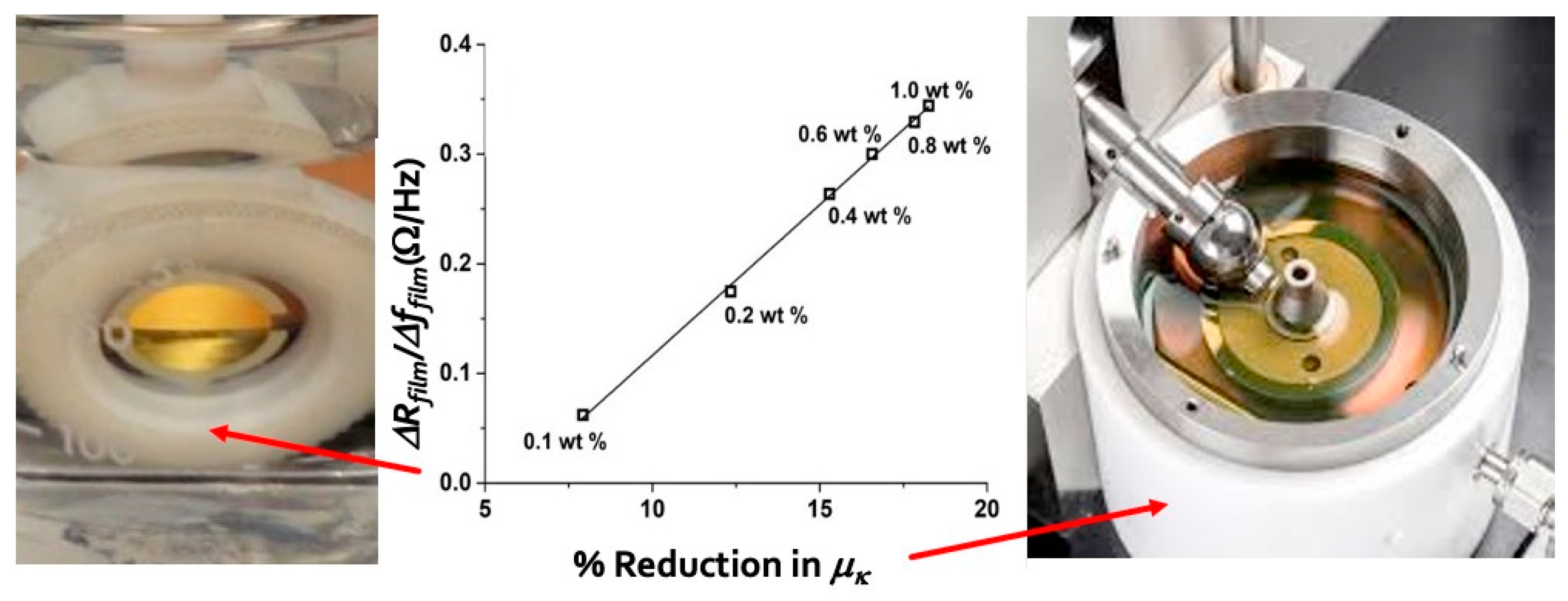
2.5. Correlation of High-Frequency QCM Sphere–Plate Stiffness Measurements with Macroscopic Friction Contacts in Thin Film and Bulk Stainless Steel Materials [19]

In 2020, Seed et al. performed a direct comparison of the QCM response to macroscale friction measurements involving a macroscale ball on a disk tribometer as well as the classic “da Vinci” measurement of μ (Figure 2f) [19]. QCM response measurements were carried out in a tripod geometry (Figure 2e) for 2 mm stainless steel sphere ball bearings on stainless steel QCM electrodes. The values inferred from the two different microscale analysis methods (Example 1.4) were compared with the results of QCM measurements. Because the QCM electrodes are fragile and incompatible with some of the direct macroscale tribometers, a series of intermediate measurements were also performed to allow for all the data to be linked and compared. Overall, the results validated the assumptions collectively employed in the analysis method reported by Vlachová et al. [66] and yielded friction coefficient values that also compared favorably with the macroscale measurements.

Seed et al. [67] later employed the Example 1.4 analysis to infer macroscale friction coefficients μ for QCMs in both dry and lubricated contacts, with a focus on whether a continuum model is applicable to a complex liquid–nanoparticle–solid interface (Figure 4) [66]. While the QCM results for dry and water-lubricated contacts compared favorably with the macroscale friction coefficients, the model failed to adequately describe the contacts lubricated with NP suspensions. The failure, however, was not primarily attributed to the continuum nature of the model but to either the lack of a CM-slip regime when NPs were present at the interface and/or the fact that the amplitude of the QCM vibration was close in size to the individual NP contacting regions, in violation of one key assumption of the model.

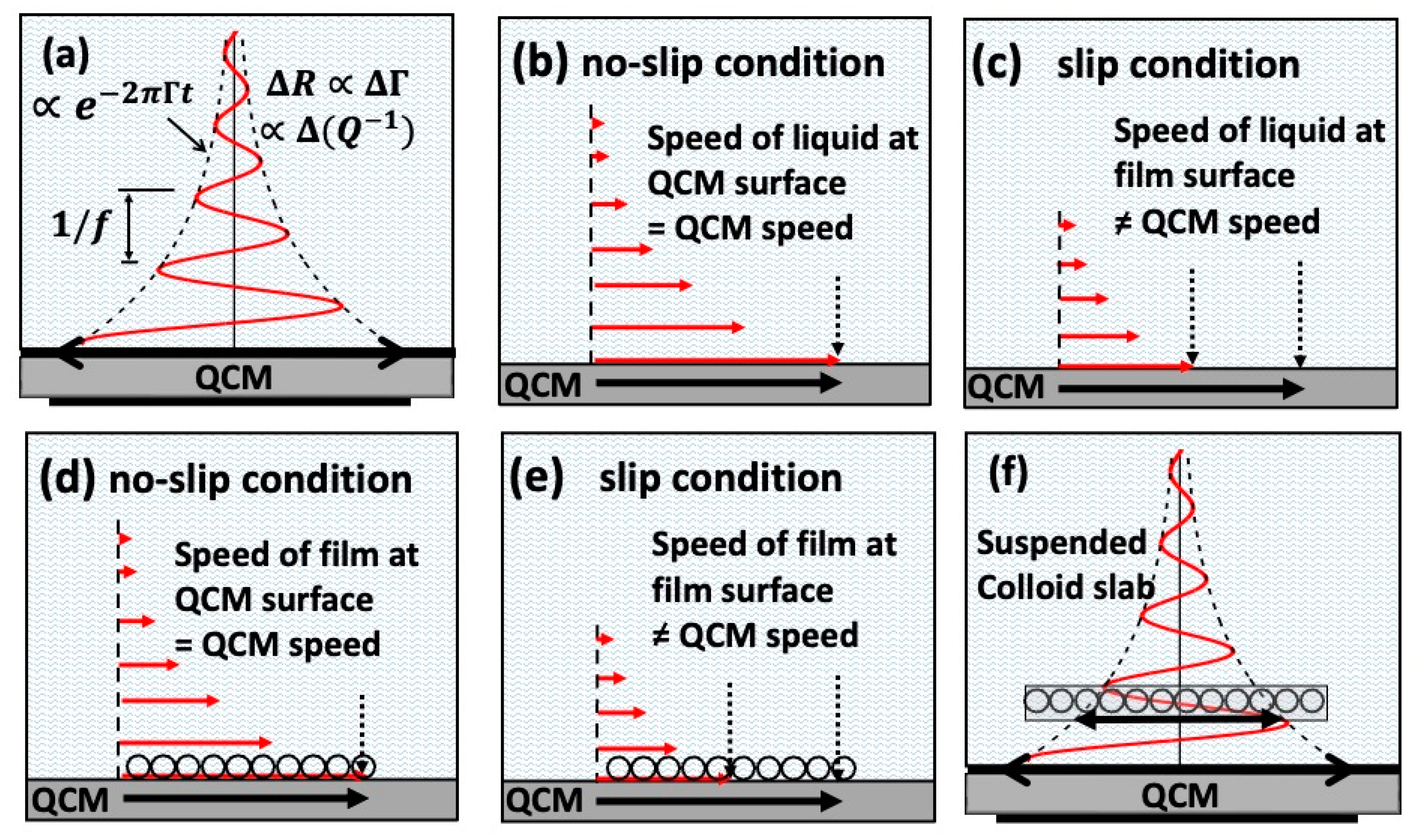
3. Interfacial Slippage Impacts Lubrication in the Mixed and Hydrodynamic Regimes

The examples selected for this section highlight the impact of nanoscale levels of interfacial slippage on macroscale lubricity (Figure 5). QCM response to a slipping film layer, where (V − V_q) is the velocity of film adjacent to the surface, is governed by a viscous friction law F_f/A= −η₂(V − V_q) and can be expressed as follows [69]:

$$\mathsf{\Delta }f=-\frac{2{f_0}^2{\rho }_2}{\sqrt{{\rho }_q{\mu }_q}}\frac{1}{\left(1+{{{(2\pi f}_0)}^2\tau }^2\right)}=\frac{{∆f}_{non-slipping}}{1+{{(2\pi f}_0)}^2{\tau }^2};$$

(8)

$$\mathsf{\Delta }\Gamma =\frac{2{f_0}^2{\rho }_2}{\sqrt{{\rho }_q{\mu }_q}}\frac{{2\pi f}_0\tau }{\left(1+{{{(2\pi f}_0)}^2\tau }^2\right)}=-{2\pi f}_0\tau \frac{{∆f}_{non-slipping}}{1+{{(2\pi f}_0)}^2{\tau }^2},\frac{\mathsf{\Delta }\Gamma }{\mathsf{\Delta }f}=-{2\pi f}_0\tau ,$$

(9)

where τ = ρ₂/η₂ is a “slip time” associated with the interfacial friction coefficient η₂. Equation (8) implies that the magnitude of Δf for a slipping film layer is less than that of a rigidly attached film; see Equation (1). When immersed in liquid, the QCM response is also sensitive to the interfacial slippage (Figure 5c), and the response can be linked to the macroscale lubricity in mixed and hydrodynamic regimes. Further reading may be found in Refs. [43,44,45,46,47,48].

3.1. Slippage at Adsorbate–Electrolyte Interface—Response of Electrochemical Quartz Crystal Microbalance to Adsorption [20]

Daikhin et al. employed a QCM immersed in water or butanol to study the adsorption of pyridine as an additive and reported the results in this 2000 publication [20]. In non-slip conditions (Figure 5d), the total response of the QCM is

$$∆\Gamma =\frac{f_0\sqrt{\pi {\rho }_l{\eta }_l{f}_0}}{\sqrt{{\rho }_q{\mu }_q}};∆f=-\frac{f_0\sqrt{\pi {\rho }_l{\eta }_l{f}_0}}{\sqrt{{\rho }_q{\mu }_q}}-\frac{2{f_0}^2{\rho }_2}{\sqrt{{\rho }_q{\mu }_q}},$$

(10)

where the second term in Δf corresponds to the rigidly attached film as described by Equation (1) and the remaining term accounts for the contribution of the bulk fluid with viscosity η_l and density ρ_l. In practice, the QCM is first immersed in a bulk fluid and then, after a period of stabilization, the response is monitored as an additive is introduced to the bulk. Under these conditions, uptake of pyridine is expected to result in the formation of a rigid film and therefore be described by Equation (1). However, the authors found that the experimentally observed shifts could not be explained in terms of a mass change in the adsorbed layer rigidly coupled to the oscillating surface. The mass-loading term in Equation (10) could not be trivially replaced by Equation (8) to incorporate the boundary slippage, since the slippage of a film in contact with the bulk also impacts the bulk contribution term significantly. Daikhin et al. [20], therefore, developed a model where rigidly attached adsorbate molecules replaced solvent molecules and a slip was allowed at the solvent interface. This “electrolyte” model incorporated both a rigid film and a bulk phase but also allowed for the slip to occur only at the upper boundary of the film with the fluid phase.

Boundary slip was incorporated by inserting the velocity of a monolayer adjacent to the boundary governed by a friction law F_f/A = − η₂(V − V_q) in the place of the no-slip condition V = V_q:

$${\rho }_2\frac{d}{dt}{V}_f\left(t\right)=-{\eta }_2\left[V\left(t\right)-V_q\left(t\right)\right].$$

(11)

The QCM response was then obtained by solving the system of equations of motion. After some rearrangement of terms, the results can be expressed as follows:

$$∆\Gamma =\frac{f_0\sqrt{\pi {\rho }_l{\eta }_l{f}_0}}{\sqrt{{\rho }_q{\mu }_q}}·\left[\frac{1+2a}{{\left(1+a\right)}^2+a^2}\right]∆f=-\frac{f_0\sqrt{\pi {\rho }_l{\eta }_l{f}_0}}{\sqrt{{\rho }_q{\mu }_q}}·\left[\frac{1}{{\left(1+a\right)}^2+a^2}\right]-\frac{2{f_0}^2{\rho }_2}{\sqrt{{\rho }_q{\mu }_q}},$$

(12)

where a is the ratio of the slip length λ_s to the penetration depth δ of the oscillations in a liquid. For fluids with uniform density, the parameter a is related to η₂ as λ_s = η/η₂. Other parameters commonly employed in the literature to represent the boundary slip of a liquid are the slip parameter s = 1/η₂, which is measured in cm²s/g, and the parameter $\chi =1/\tau$, which is measured in s⁻¹. For a no-slip boundary condition at the film–fluid boundary, a = 0, and the response reduces to the sum of the separate non-slipping film and bulk contributions; see Equation (10).

Equation (12) describes a QCM response upon immersion into a liquid and allows one to infer adsorption levels and slip lengths from the experimental data. For pyridine added to water, typical values of surface uptake were about 5 × 10¹⁰ mol/cm² with slip lengths of about 0.8 nm. Slip lengths were larger for water than butanol, approaching 2 nm for the highest concentrations of the adsorbate molecules. See also Refs. [46,69] for further details. Ref. [46] is a book chapter with a comprehensive discussion and an explanation of QCM in liquid with slipping interfaces, while Ref. [69] details examples of slip length calculations and mass uptake for nanoparticle suspensions employing the results of Daikin et al. [20] and related methodologies.

3.2. A Low Friction Bearing Based on Liquid Slip at the Wall [21]

In this 2007 publication, Spikes and colleagues explored the macroscale implications of bearing lubrication when the surfaces in a macroscopic tribological contact were configured so that the lubricating liquid exhibited a slip on one of the contacting surfaces and a no-slip boundary condition on the counterface [21]. They noted that the nanoscale slip had been firmly established in the decade prior to their work and that there was no intrinsic reason why a fluid is forbidden to slip at an interface. Non-wetting fluids, i.e., those in contact with lyophobic surfaces, are expected to exhibit some degree of slippage while surfaces wetted with the lubricant should exhibit non-slip conditions. This publication described a bearing design and demonstrated that a conventional wetted surface draws a lubricant fluid into contact to achieve hydrodynamic lubrication conditions. The counterface is prepared with a treatment that inhibits wetting by the lubricant, in turn giving rise to interfacial slippage at one of the contacts.

The authors cited a previous theoretical work based on a half-wetted bearing principle (i.e., only one of the contacts is wetted by the lubricant), indicating that the friction could be significantly reduced in the lubricated sliding contacts [70,71], and then reported their experimental validation of the theoretical concept, which makes possible the hydrodynamic lubrication of very low-load contacts. They constructed a low load bearing and explored the influence of the surface roughness and the wetting properties of the surfaces on friction over a wide range of sliding speeds to construct Stribeck curves for various conditions (Figure 1). For the materials studied (hexadecane films in the contact between a rotating Pyrex cylinder and a stationary, sapphire flat), the authors concluded that the liquid slip can be used to considerably reduce friction under the full-film hydrodynamic conditions. Based on the friction versus speed curves and numerical modeling of the contact, the authors identified the range of the test conditions resulting in a thick-film hydrodynamic lubrication. They considered three possible origins of the observed tribological behavior and concluded that the most likely explanation was a slippage of the hexadecane along the smooth lyophobized coated sapphire surface. The latter exhibited friction coefficients of ~0.001 at 1 m/s and 0.2 N. This value compares favorably with the friction coefficient of ~0.003 and the slip lengths of ca. 4 μm observed for the smooth uncoated surface of lyophobic sapphire with the non-wetting contact angle measuring 109°.

3.3. A Tribological Study of Aqueous Suspension of γ-Fe₂O₃ Nanoparticles [22]

In this 2018 report, Pardue et al. compared and contrasted the nano- versus macroscale tribological properties of aqueous suspensions of maghemite (γ-Fe₂O₃) nanoparticles in contact with alumina surfaces for various nanoparticle concentrations [22]. A QCM with an alumina electrode was employed for the nanoscale measurements while an alumina ball on alumina disk geometry was employed for the macroscale friction coefficient experiments. The nanoparticle concentrations were increased stepwise and changes in friction and drag forces were monitored using both the QCM and a macroscale tribometer.

Several potential QCM “bulk” and “surface” “performance factors” were selected from functions of Δf and ΔR_m upon the addition of nanoparticles to water surrounding the QCM, where R_m is the motional resistance and $R_m=\mathsf{\Delta }\Gamma /\left(8K_0^2{C}_0^{2}f\right)$, C₀ is the static capacitance between the electrodes, and $K_0^2$ = 7.74 × 10⁻³ is the electromechanical coupling factor for the AT-cut quartz crystal. A number of candidate functions were assessed, and the factor ΔR_film/Δf_film was observed to exhibit a linear correlation with reductions in the macroscale friction coefficient. The authors attributed this to interfacial effects and changes in the glide plane location upon introduction of nanoparticles—the two factors that would impact both nanoscale and macroscale friction (Figure 6). Notably, the macroscale measurements were performed in a mixed lubrication regime, indicating the impact of slippage on the friction coefficient is not confined to the hydrodynamic lubrication regime.

Surface excess quantities were defined as differences between the experimentally measured shifts ΔΓ_exp and Δf_exp and the changes ΔΓ_ns and Δf_ns attributable to an increased viscosity η_ns and density r_ns of the bulk suspension when nanoparticles were added:

$${∆\Gamma }_{ns}=-{∆f}_{ns}{∆f}_{ns}=\frac{f_0\sqrt{\pi f_0}}{\sqrt{{\rho }_q{\mu }_q}}\left(\sqrt{{\rho }_l{\eta }_l}-\sqrt{{\rho }_{ns}{\eta }_{ns}}\right)$$

(13)

Both the average density and viscosity of the bulk fluid increase upon the addition of NPs. Equation (13), therefore, indicates negative frequency shifts and positive bandwidth shifts upon the addition of NPs. The authors observed the “film” loss factor to scale linearly with reductions in the macroscale friction coefficient, with a correlation of 0.999, where the films loss factor was defined as follows:

$$\frac{{\mathsf{\Delta }\Gamma }_{film}}{{\mathsf{\Delta }f}_{film}}=\frac{{\mathsf{\Delta }\Gamma }_{exp}-{\mathsf{\Delta }\Gamma }_{ns}}{{\mathsf{\Delta }f}_{exp}-{\mathsf{\Delta }f}_{ns}}$$

(14)

The factor in Equation (14) was notably observed to be positive since both the numerator and the denominator were observed to be positive; an addition of nanoparticles to the liquid surrounding the QCM caused a decrease in the half bandwidth, which was attributed to slippage.

Atomic force microscopy was also utilized to both qualitatively and quantitatively determine surface roughness before and after the particle uptake. It was observed that the particles were easily removed from the surface without significantly altering surface morphology.

3.4. Nanotribological Performance Factors for Aqueous Suspensions of Oxide Nanoparticles and Their Relation to Macroscale Lubricity [23]

In 2019, Krim, Smirnov, and coworkers extended the initial studies reported by Pardue et al. [22] to a wide range of material system combinations and reported the QCM performance factors along with selected comparisons to macroscale friction coefficients [23]. Aqueous suspensions of four ceramic nanoparticles, TiO₂, SiO₂, Al₂O₃, and maghemite (γ-Fe₂O₃) and ten substrate materials (Au, Al, Cr, Cu, Mo, Ni, Pt, SiO₂, Al₂O₃, and stainless steel SS304) were studied. The variations in QCM response from one nanoparticle composition to another were observed to be far greater than from changes in the substrate material, indicating that the properties of nanoparticles are playing a larger role in determining the frictional drag force levels than the substrates. The results were categorized according to the direction of the frequency, and motional resistance changes and candidate statistical performance factors for the datasets were generated. Shifts in frequency upon the introduction of nanoparticles were observed to be zero, negative, or positive, depending on the degree of decoupling of the bulk fluid attributed to the interfacial slippage.

The performance factors were employed to identify associations between the QCM atomic scale results and the macroscale friction coefficient measurements. Macroscale measurements of friction coefficients for selected systems documented that a reduction or an increase in motional resistance to shear, as measured with the QCM, is linked to a decrease or increase, respectively, in the macroscale friction coefficients. The performance factors identified in the study of a single material combination reported in Section 3.3, therefore, were shown to be applicable to a broader set of statistically diverse samples. The authors concluded that sophisticated treatments are required to analyze the full implication of the results, given the wide-ranging values. The range of applicability for sliding speeds also remained an outstanding question for future studies.

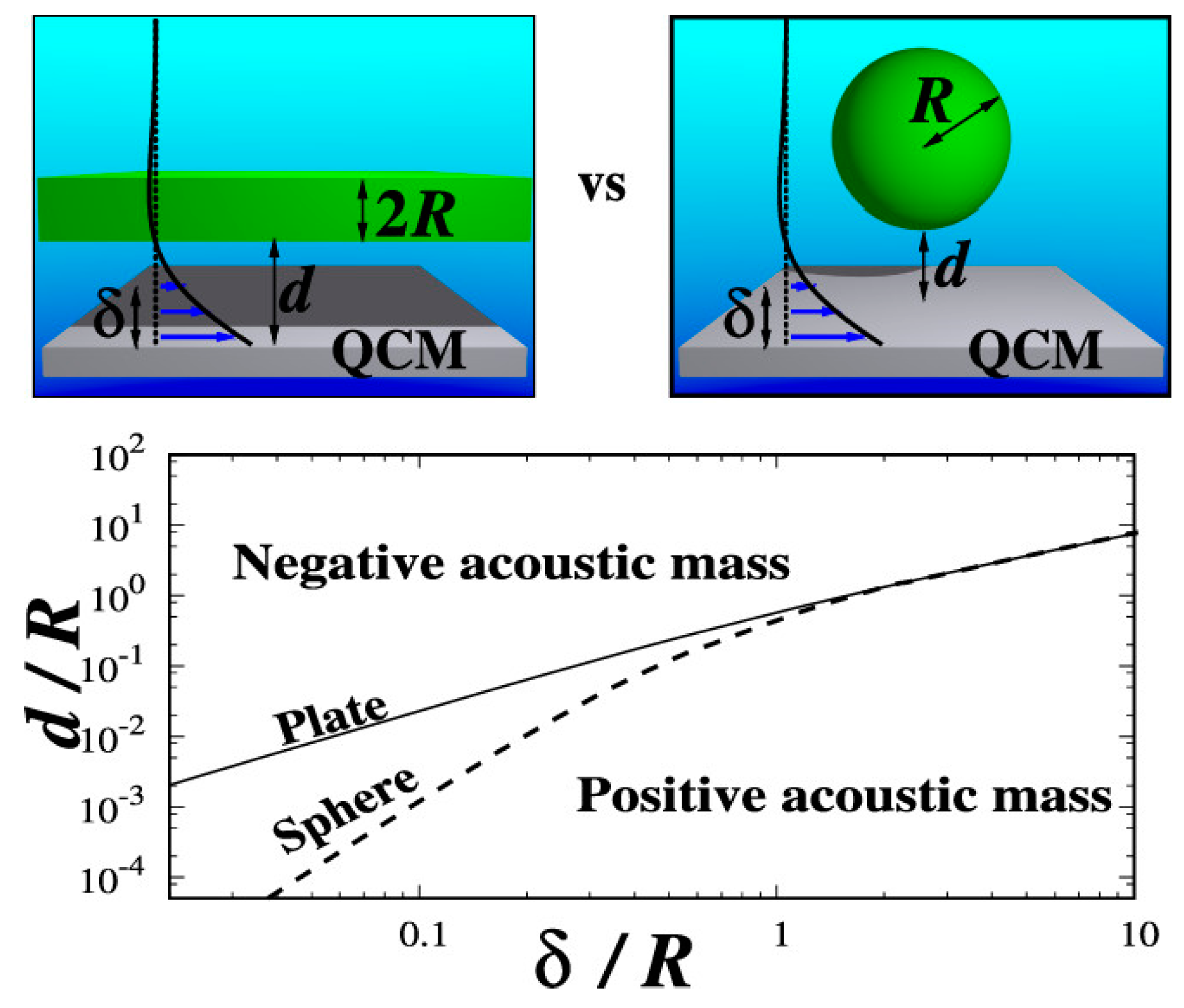
3.5. Load Impedance of Immersed Layers on the Quartz Crystal Microbalance: A Comparison with Colloidal Suspensions of Spheres [24]

In this 2020 publication, Melendez et al. considered a slab suspended at a distance d above an oscillating QCM electrode immersed in a bulk liquid (Figure 5f) [24]. Transverse shear waves propagating into the liquid with heavy damping were characterized by a penetration depth d in the absence of the slab (Figure 2a). The slab was treated as both a continuous plate with thickness a and a density ρ′, and also as an array of spheres with diameter a. The location and dimensions of the slab were found to impact the degree to which it oscillates in a transverse shear motion and the degree to which it changed the acoustic load on the QCM in a slab-free liquid. No-slip boundary conditions were applied to the solid–liquid boundaries at the QCM and the slab surfaces, and an expression was derived for the extra impedance due to the presence of the slab. In employing this no-slip geometry, the authors demonstrated that positive frequency shifts associated with the decoupling of the bulk fluid occur in some regimes.

When an oscillating electrode of the QCM is exposed to a mass-loading and/or a surrounding fluid, the acoustic impedance $\mathcal{Z}=\mathcal{R}-i\mathcal{X}$ results in shifts to Δf and ΔΓ as follows:

$$∆\Gamma =\frac{\mathcal{R}{f}_0}{\pi \sqrt{{\rho }_q{\mu }_q}};∆f=-\frac{f_0\mathcal{X}}{\pi \sqrt{{\rho }_q{\mu }_q}}$$

(15)

The authors derived an expression for an additional impedance arising from the presence of the slab in terms of dimensionless parameters ρ′/ρ, a/δ, and d/δ.

$$\frac{{\mathcal{Z}}_L}{{\mathcal{Z}}_{ref}}=\frac{e^{-2\left(1-i\right)d/\delta }}{\left(\frac{1+i}{2}\right)\frac{{\rho }^{\prime }}{\rho }\frac{a}{\delta }\left(e^{-2\left(1-i\right)d/\delta }-1\right)-1}$$

(16)

where ${\mathcal{Z}}_{ref}=-i2\pi f_0{\rho }_2$ is the impedance of a rigidly attached layer (the Sauerbrey Equation (1)), and ρ₂ is the mass per unit area of the slab or the mass per unit area of the array of spheres with radius R. The analytical solutions derived in this example indicated positive frequency shifts upon introduction of suspended colloids for certain regimes (Figure 7), which the authors referred to as a “negative acoustic mass” because mass-loading according to Equation (1) results in a negative shift.

The authors noted that the Dybwad double oscillator contact methodology of Section 2.1 has been used extensively in studies of colloids and recommended the hydrodynamic approach of their work as a preferable methodology. The authors also compared the one-dimensional immersed plate theory with three-dimensional simulations of rigid and flexible submicron-sized suspended spheres, as well as with experimental results for adsorbed micron-sized colloids in the “negative acoustic mass” regime where frequency shifts are positive. One of the important conclusions of this work was a call for a revision of the existing theories, which are currently based entirely on adhesion forces and elastic contact stiffness, to include hydrodynamics. See also ref. [72] where QCM response to an immersion in a flowing, rather than static, liquid was explored.

4. Nanoparticle Rolling Has Little Influence and When Present May Increase Friction

Close to thirty years have passed since the pioneering work of Campbell et al., who utilized a surface forces apparatus to study intermolecular interactions and the nanotribology of adsorbed C₆₀ monolayers on mica surfaces immersed in toluene [1]. The results have raised speculation that observed molecular “ball-bearing”-like attributes might give rise to macroscale lubricity since C₆₀ molecules are near-perfect spheres, and when contacting crystalline solids, the molecules can rotate rapidly while remaining in their lattice positions (Figure 8). Campbell et al. noted that such lubricity was not observed for C₆₀ alone, including control molecular-scale experiments performed in air using 50 nm C₆₀ films deposited on mica [1]. However, these authors discovered that the deposition of one or two weakly bound monolayers atop mica surfaces resulted in the full-slip (zero interfacial friction, within the detection limit of the apparatus) boundary conditions when immersed in a C₆₀ additive suspension. The observed tribological behavior was dramatically different from that of conventional fluids. The authors concluded that C₆₀ could hold great promise as a macroscale lubricant additive and suggested the interfacial slippage might be linked to a rapid rotation of the molecules that somehow produced an effective boundary of near-zero drag on the adjacent liquid.

While the notion of molecular ball bearings may be intuitive as a nanoscale mechanism for friction reduction for both C₆₀ and NP additives, the current consensus is that the profound changes in interfacial slippage and friction are not attributable to molecular rotation. When present, the rotation may actually increase friction, as highlighted by the examples in this section. Further reading on the topic of carbon materials as lubricant additives and molecular machinery may be found in Refs. [49,50,51].

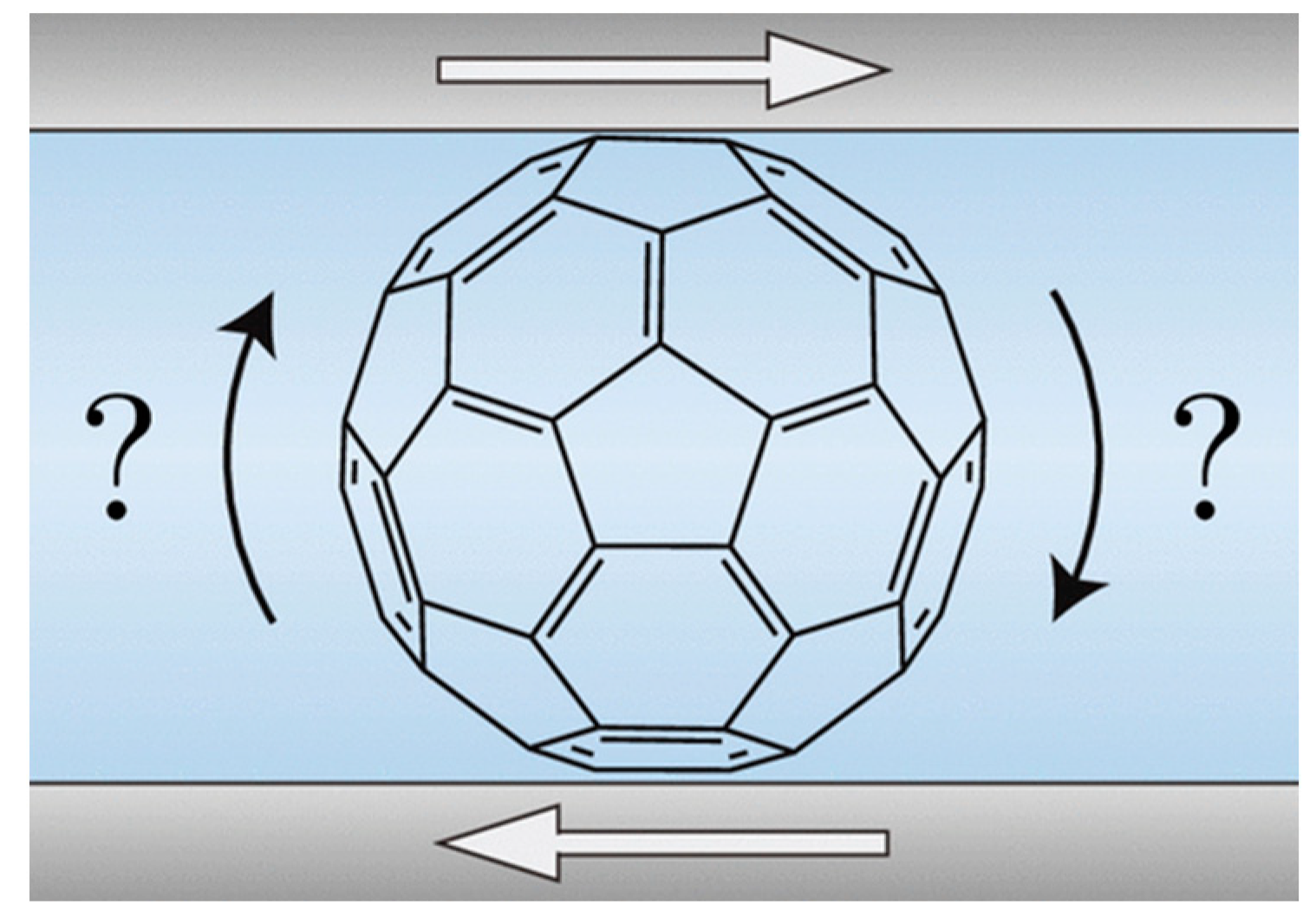
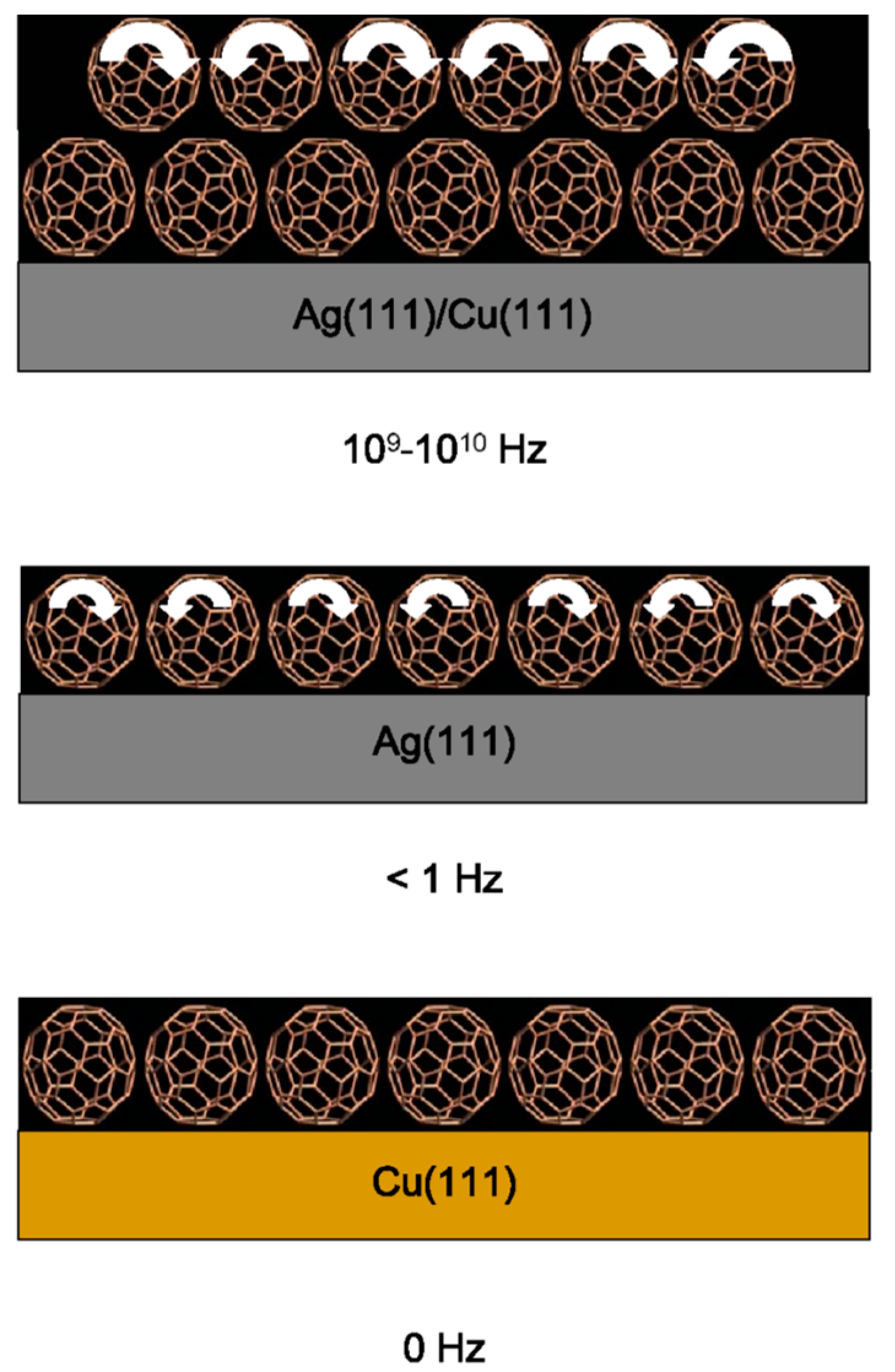
4.1. C₆₀ Molecular Bearings and the Phenomenon of Nanomapping [25]

In 2001 and 2006, Coffey and coworkers reported a set of nanotribological measurements of C₆₀ employing AFM and QCM techniques. AFM failed to detect C₆₀ at the toluene/mica interface by yielding friction levels that were unchanged by the presence of C₆₀ additives. The authors suggested that C₆₀ was easily displaced from the interface by the slow-moving AFM probe tip and, therefore, no effects of the C₆₀ additive on the interfacial friction were observed in such experiments. In contrast, QCM measurements of interfacial friction and slippage for the toluene/Ag(111) interface were highly sensitive to the presence of interfacial C₆₀. The friction, however, doubled when C₆₀ was deposited as a film onto the Ag(111) surface in advance of the tribological experiments.

To explore and isolate the role of molecular rotation on friction, Coffey and Krim measured sliding friction on fixed and rotating C₆₀ layers by preparing substrates upon which the C₆₀ molecules rotated at a high rate (10⁹–10¹⁰ Hz), a slow rate (<1 Hz), or did not rotate at all (Figure 9). Sliding friction for methanol on various substrates was measured at room temperature, and for krypton layers at 77 K. At the latter temperature, all rotations are known to cease. To the best of our knowledge, this was the first experimental report to directly link friction to a documented molecular rotation state. The observed friction was, however, higher when the C₆₀ was rotating, in defiance of the ball-bearing analogy. See also Refs. [73,74] for closely related theoretical and experimental studies.

4.2. Are Buckminsterfullerenes Molecular Ball Bearings [26]?

The topic of rotation by C₆₀ molecules was revisited in 2019 by Lhermerout et al. [26], twenty years after the original Campbell publication. The authors employed a surface force balance method to study C₆₀ additives to tetralin and reported the first quantitative friction force measurements of C₆₀ dispersed in between surfaces in the boundary regime of lubrication. As such, the study was complementary to the hydrodynamic regime measurements reported by Campbell et al. [1] in a system with geometry more directly comparable than the one employed by Coffey et al. [25].

Lhermerout et al. [26] noted that C₆₀ molecules freely rotate at room temperature not only when dissolved in a liquid but also in a solid state and examined whether the molecules could prevent contact in the boundary regime while simultaneously dissipating shear stress through fast rotation. High-resolution shear and normal force measurements between mica sheets separated by 0.1 wt% C₆₀ solutions were performed in a single-asperity contact geometry and with sub-nanometer resolution in film thickness. The authors observed that C₆₀ forms a solid-like amorphous boundary film sustaining a high normal load that suggests that the system undergoes a glass transition when confined. Overall, the C₆₀ films were deemed to be excellent boundary lubricants and, up to moderate applied loads, exhibited low friction coefficients. The fact that the molecules were readily trapped in contacts was attributed to them being close to aggregation while in solution, with the solvent squeezed out when the contact was made.

The authors discussed rotation extensively throughout the publication and suggested that, among other possibilities, a lubrication mechanism involving the molecules rotating while in a glass phase cannot be ruled out because of the available space for such rotations. It was concluded that although rotation may be important, a comparative study of fixed (via chemical grafting) and rotating molecules would be required to clarify the role of rotation. While this study found C₆₀ to be a beneficial lubricant additive for systems in the boundary regime, no specific evidence that molecular rotation impacted friction levels was obtained. See also ref. [75].

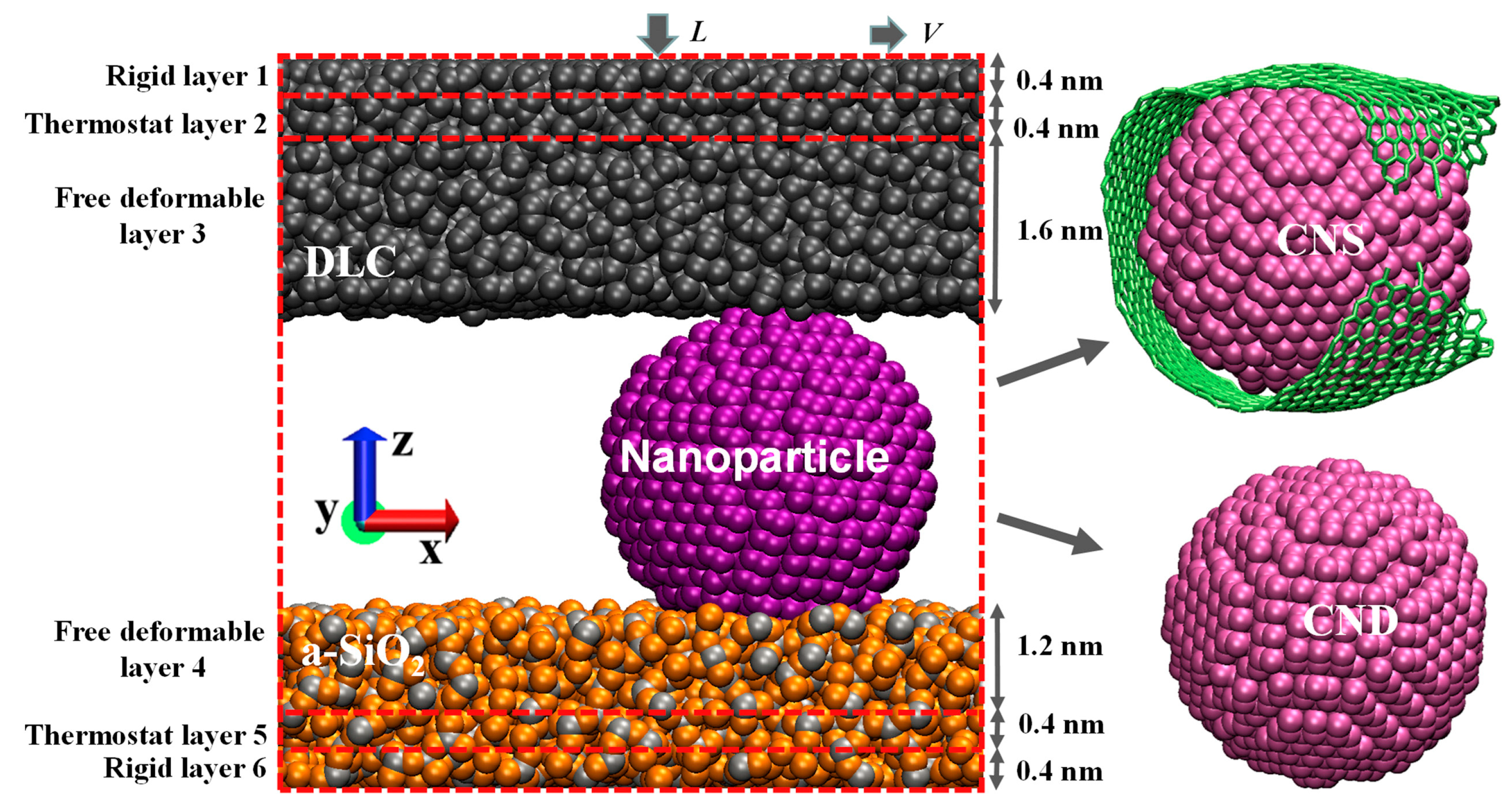
4.3. Friction Properties of Carbon Nanoparticles (Nanodiamonds and Nanoscrolls) Confined between Diamond-like Carbon and a-SiO₂ Surfaces [27]

In this study, Zhao et al. [27] compared the tribological properties of carbon nanoparticles including nanodiamonds (NDs) and nanoscrolls (NSs) formed by wrapping graphene sheets around nanodiamonds. The authors performed nonequilibrium molecular dynamic simulation of sliding diamond-like carbon over the nanoparticles supported by amorphous silica slabs (Figure 10). The friction coefficient for the sliding of nanoscrolls was observed to be 72% lower than that of the nanodiamonds and found to be in a regime of superlubricity (m ≤ 0.01) consistent with the experimental observations.

The lower friction for the nanoscroll–diamond-like carbon combination was attributed to a lower contact area as well as a lack of rolling motion, both attributed to the presence of the graphene patch surrounding the nanodiamond. The authors concluded that, in contrast to the rolling motion of ball bearings at the macroscale, rolling motion of nanoparticles at the nanoscale was linked to increased frictional dissipation. They conclude that nanoscrolls should be more effective as solid lubricants compared to nanodiamonds. Although the study was not performed in suspension, we note that the results should be applicable to the boundary regime of lubrication, in cases where solvents are squeezed out of the contact. See also [76].

4.4. Addition of Solid Oxide Particles for Friction Reduction [28]

Van Sang et al. [28] performed numerical simulations consisting of a combined SPH/DEM method to explore lubrication mechanisms of 20 types of micron-sized oxide particles added to water- or diesel-based fluids in iron contacts. The rough-on-flat iron contacts and spherical iron oxide particles were, respectively, modeled by elastic particle lattice coarse-graining and discrete element methods. The interactions between the iron-oxide surfaces with the various oxide particles, as well as the particle–particle interactions included both Hertz repulsive contacts and attractive van der Waals forces for non-contacting separation distances. Friction was determined by assessing the kinetic energy dissipated into the environment via Stokes damping forces. The authors found that the stability and shear properties of films formed on the iron surfaces dominated friction reduction levels and that denser and/or heavier oxide particles resulted in better lubricity. Friction was also reduced for an increasing number of particles in the tribofilm and the sliding speed. Although the nature of the surrounding fluid and temperature strongly influenced the overall friction levels, the relative ranking of lubricity amongst the various oxides studied was observed to be almost independent of the base fluid. Van der Waals forces were, meanwhile, found to have very little effect on lubricity and the rolling of the particles had almost no effect whatsoever.

The friction coefficient for bare contact was 0.32, and all the particles, including iron oxides, reduced the friction coefficient. The rank ordering of lubricity for the oxides in this study was Bi₂O₃, CeO₂, SnO₂, WO₃, Co₃O₄, CuO, CoO, FeO, ZnO, Cr₂O₃, ZrO₂, Fe₂O₃, Fe₃O_4, Y₂O₃, Al₂O₃, TiO₂, MgO, V₂O₅, BeO, and SiO₂., with Bi₂O₃ providing the largest reduction (m = 0.04) and SiO₂ the least reduction (m = 0.22).

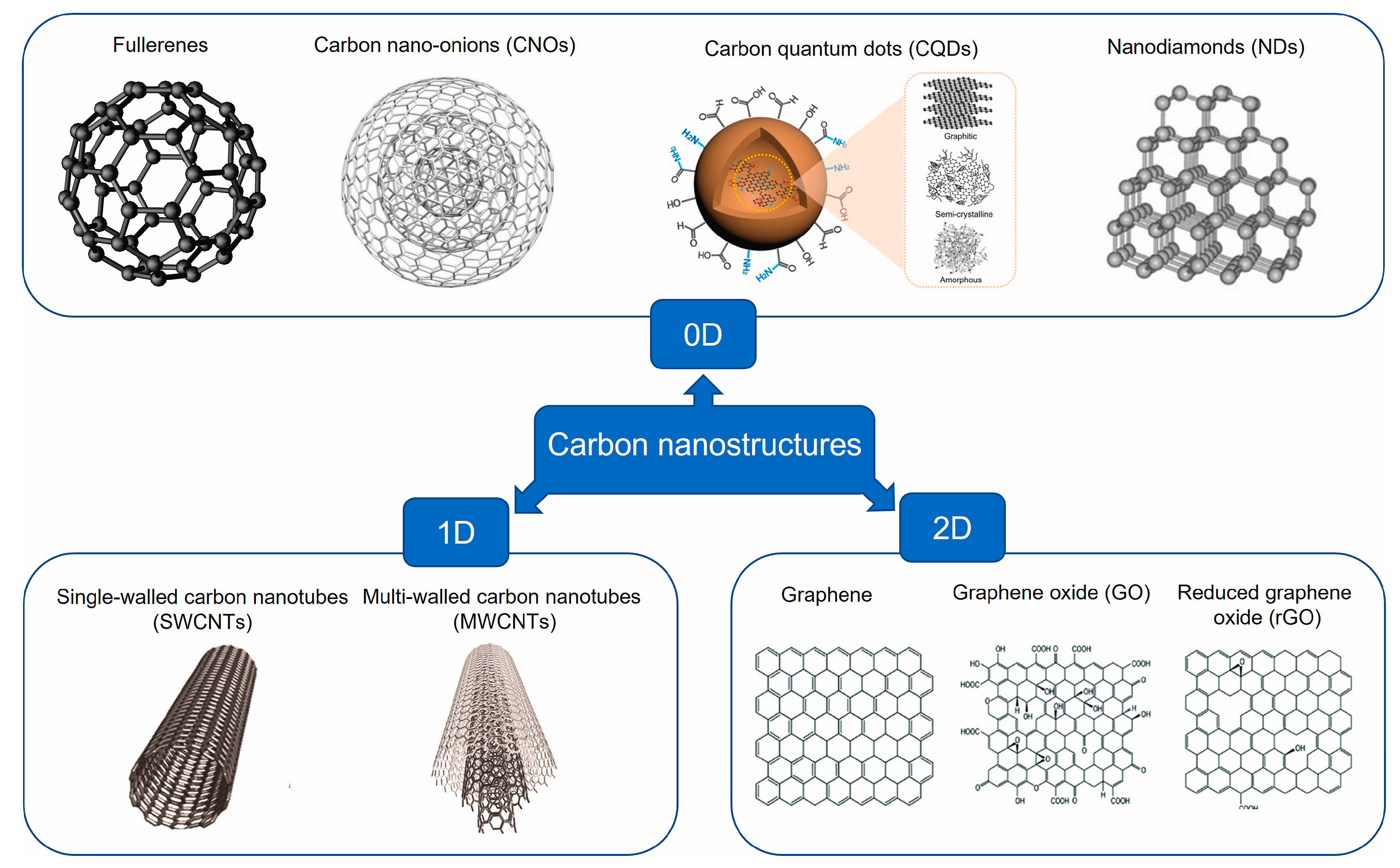
4.5. Functionalized Carbon Nanostructures as Lubricant Additives—A Review [29]

In this comprehensive review of carbon nanostructures as lubricant additives, Nyholm et al. [29] described the state of the field as of 2023 and identified the most promising future research areas. Additive dimensionality, structural integrity, and the nature of chemical interactions were identified as particularly important properties governing tribological behavior. The theoretical basis for fundamental lubrication mechanisms revealed that much was yet to be understood. Nonetheless, the authors concluded that two-dimensional graphene-based nanostructures and carbon quantum dots are likely the most promising candidates for a new generation of lubricant additives due to their excellent properties as carrier materials and the well-established chemistry of carbon (Figure 11). These attributes were identified as particularly important for the customization of additives through surface functionalization to achieve wide-ranging and beneficial surface properties. The authors also commented that the surface functionalization of nanomaterials, a key component of the samples presented in the first highlight of the next section, has the potential to impact both the dispersibility and the inherent lubrication mechanisms of the nanostructure, enabling the development of multifunctional additives.

Notably, after an exhaustive and in-depth discussion and review of carbon-based lubricant additives, the authors found no evidence todocument rolling as a beneficial mechanism to reduce friction and commented on the difficulty of achieving the rolling motion for nanoscale structures, such as 1D carbon nanotubes (CNTs), in the first place. It was concluded that “even though there is some theoretical support for the rolling ability of certain 0D carbon nanostructures, it is uncertain whether this contributes to reducing the interfacial friction between tribosurfaces to any significant extent” [29].

“After critically reviewing the fundamental research available at present date, the roller bearing ability of 1D CNTs is also deemed unlikely for several reasons…, even if all the aforementioned challenges (e.g., entanglement, need for commensurability, structural collapse, etc.) were minimized or eliminated in a way such that rolling motion of CNTs was more plausible, it is still unclear whether this would contribute to friction reduction in any significant way”.

[29]

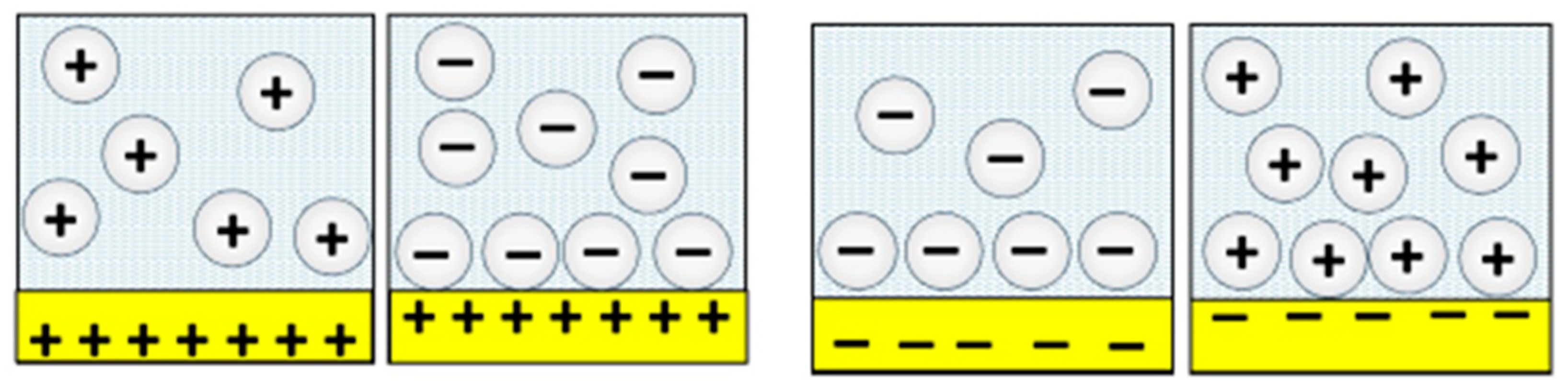
5. Surface Charge on Nanoparticles and Contacting Surfaces and the Surface Groups That Give Rise to the Charge Have an “Astonishing” Impact on Friction

The prior example of the effects of carbon nanostructures on friction highlighted a review article that emphasized a major observation of surface functionalization of nanomaterials having a pivotal role in both particle dispersibility and lubrication mechanisms. It is well documented that the surface charge, causing electrostatic repulsion between the nanoparticles, enables suspension stability [10,51,52,60], and in some cases can be continuously tuned to optimize system properties [77] The repulsive interactions also impact lubrication through changes to slip planes and/or counteracting externally applied normal forces. Some nanoparticle materials, but not all, become charged when added to lubricants (Figure 12) while others require additional surface treatments to render them charged and/or provide steric repulsion. The articles selected for this section highlight the major impact of the nanoparticle surface charge on lubricity.

5.1. A Comparative Study of the Nanoscale and Macroscale Tribological Attributes of Alumina and Stainless Steel Surfaces Immersed in Aqueous Suspensions of Positively or Negatively Charged Nanodiamonds [12]

Curtis et al. monitored the frequency and dissipation of QCMs with stainless steel and alumina electrodes immersed in aqueous suspensions of positively and negatively charged detonation nanodiamonds (NDs) [12] to explore the role of charge on NPs as lubricant additives for conducting and insulating contact materials. Surface charge and nanoparticle end groups were varied by preparing them via either a reduction reaction in the case of the positive (hydroxylated) particles or alternatively an oxidation of soot in ozone-enriched air in the case of the negative (carboxylated) particles.

The group compared QCM nanoscale nanotribological data with the macroscale tribological attributes of alumina and stainless steel surfaces measured using a commercial macroscale tribometer. The immersion of the contacts in −ND suspensions resulted in a decrease in the macroscopic friction coefficients to values in the range of 0.05–0.1 for both stainless steel and alumina, while +ND suspensions caused an increase in friction for stainless steel contacts and little to no increase for the alumina contacts. Quartz crystal microbalance (QCM), atomic force microscopy (AFM), and scanning electron microscopy (SEM) measurements were employed to assess nanoparticle uptake, surface polishing, and resistance to solid–liquid interfacial shear motion. The QCM studies revealed abrupt changes to the surfaces of both alumina and stainless steel upon adding −NDs to lubricating water—the effects consistent with a strong attachment of NDs and/or chemical changes to the surfaces. The authors suggested that carboxylated −NDs in aqueous suspensions may be forming robust lubricious deposits on stainless steel and alumina surfaces that enabled gliding/slippage through the surrounding −NDs. In stark contrast, +ND suspensions not only failed to improve tribological performance but potentially abraded the existing protective boundary layers in the case of stainless steel contacts. To conclude, the authors reported radically different tribological properties at both the nanoscale and macroscale for the two different surface treatments of the same nanoparticles. Such reports are increasingly common, as highlighted in the next example.

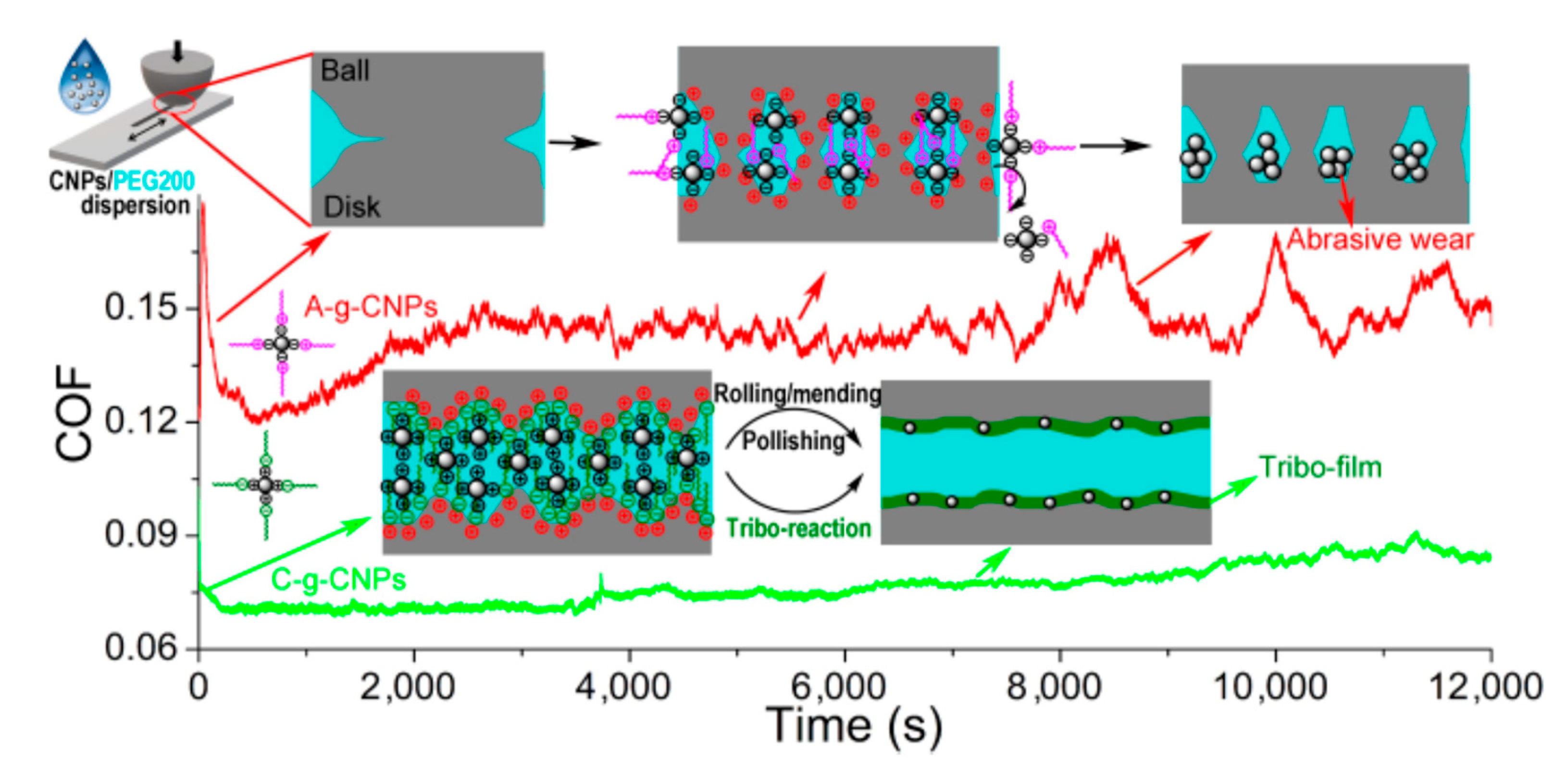
5.2. Astonishingly Distinct Lubricity Difference between the Ionic Liquid Modified Carbon Nanoparticles Grafted by Anion and Cation Moieties [30]

Wang et al. [30] reported macroscale measurements of friction coefficients in a macroscale reciprocating tribometer for another carbon-based nanoparticle additive—carbon nanoparticles (CNPs) prepared via pyrolysis [30]. Like NDs, the CNPs studied were formed from carbon but the latter demonstrated poor crystallinity based on the XRD analysis. The CNPs were further treated to yield oppositely charged end groups. The nanoparticles were employed as 0.7 wt% additives to polyethylene glycol (PEG200)—a synthetic oil with biodegradability—and the difference in lubricity between the two treatments was described by the authors as “astonishingly distinct” (Figure 13).

Positive CNPs, designated as A-g-CNPs, were prepared through the preferential electrostatic adsorption of negatively charged inner parts with repulsive peripheral cation end groups. These additives were found to have little effect and/or actually impair the lubricity of PEG200. Abrasive wear was also reported. Negatively charged peripheral anion end groups and positively charged inner parts of CNPs, designated as C-g-CNPs, meanwhile, absorbed onto the frictional contacts, presumably through electrostatic interactions, to form organic–inorganic electric double-layer structures, “tremendously boosting” the lubricity of PEG200.

A common theme in this and the previous example is the role of electrostatics in determining the impact of surface treatments on system lubricity. Four geometries were employed for the studies at varying length scales (QCM, ball-bearing on QCM, pin-on-disk, and reciprocating pin-on-flat), and a range of contacting materials was studied (e.g., steel on gold, alumina on alumina, stainless steel on stainless steel, etc.). Abrasive wear was observed for positively charged +CNPs and +NDs, while an improved lubricity was reported for −CNPs and −NDs. See also Ref. [78].

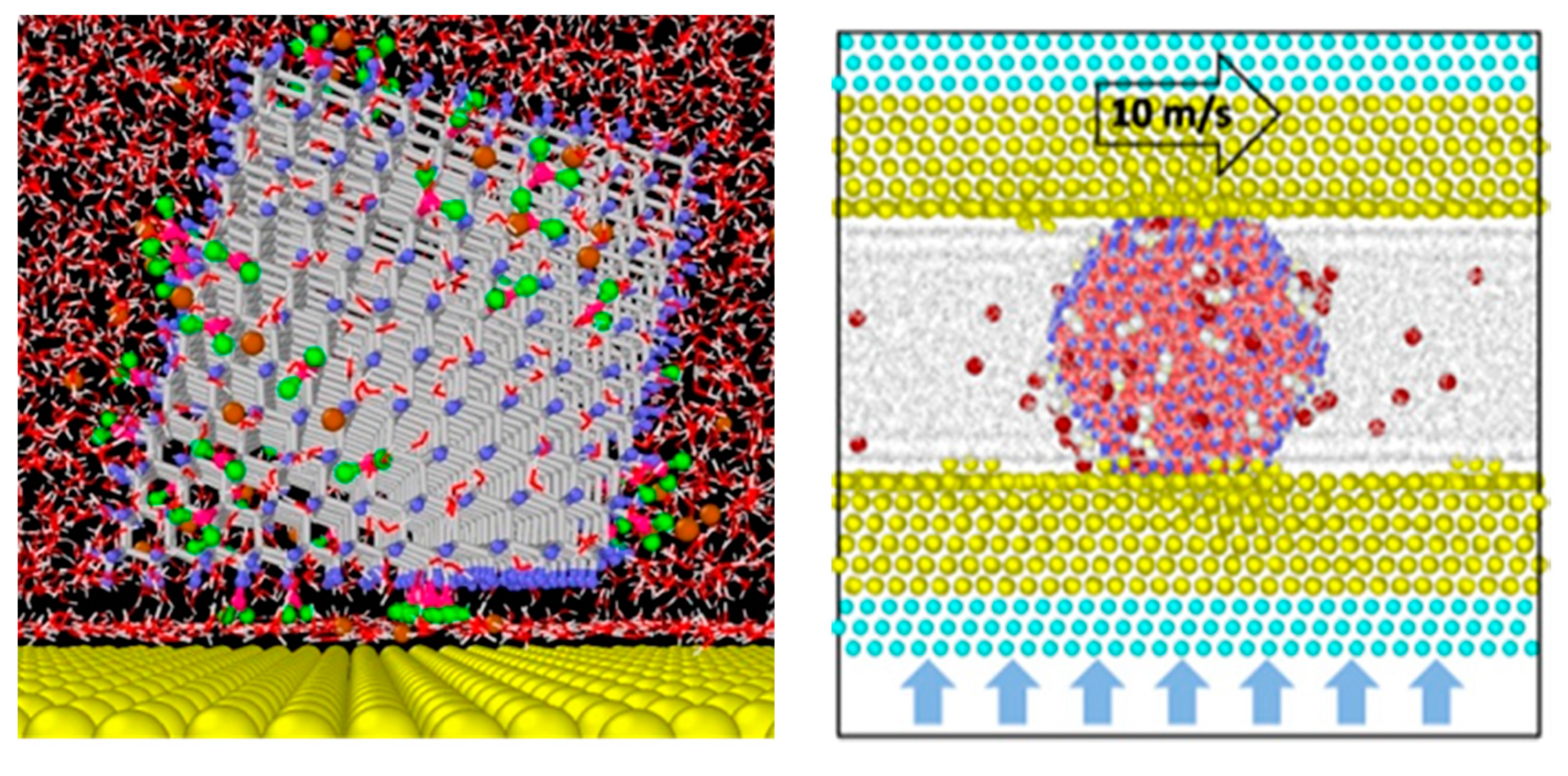
5.3. Interdependent Roles of Electrostatics and Surface Functionalization on the Adhesion Strengths of Nanodiamonds to Gold in Aqueous Environments Revealed via Molecular Dynamics Simulations [31]

It is apparent that both surface functionalization and surface charge play major roles in lubricity. An important fundamental problem is to decipher the individual contributions of each phenomenon, which can be explored through molecular-level simulations of NP systems in the presence and absence of induced image charges to assess the impact of electrostatics. Such simulations were reported for +ND and −ND in aqueous suspensions on gold surfaces by Su et al., who found that adhesion strengths resulted from the interdependence of electrostatics and surface functionalization [31]. The simulations revealed a water layer containing Na⁺ counterions between −NDs with the surface −COO⁻ functional groups, but no such layer for a +ND with −NH₃⁺ functional groups. The closer proximity of the +ND to the gold surface and the lack of cancelation of electrostatic interactions due to counterions and the water layer resulted in an electrostatic adhesion force for +ND that was nearly three times greater than that of a −ND. The authors, therefore, demonstrated how both surface functionalization and electrostatics contribute to determining the adhesive binding strengths (Figure 14).

In a follow-up study, the same group modeled tribological contact between two gold surfaces lubricated with NDs in water to explore friction levels, rolling, and surface deformation [79]. Higher friction levels were notably observed when induced image charges in the gold contacts were present versus when they were absent.

Significant surface deformation was observed when −NDs were placed between gold surfaces under external loads that were sufficient to displace water from the contact. Rolling and relatively high friction levels were also observed under these conditions. This observation is consistent with conclusions drawn from highlight 4.5: friction levels are not necessarily reduced when the normal forces reach the levels to cause rolling of the trapped NPs. Both neutral and +NDs meanwhile exhibited sliding behavior with only minor deformations of the gold surfaces under similar load conditions, suggesting that the size of the surface functional group is a major factor in determining sliding versus rolling.

5.4. Potential-Controlled Boundary Lubrication Using MoS₂ Additives in Diethyl Succinate [32]

In this 2020 publication, Liu et al. [32] demonstrated active friction control by applying an external electric field to 900 nm MoS₂ nanoparticle additives in diethyl succinate base oil lubricating a ZrO₂ sphere in contact with a copper surface [32]. MoS₂ particles displayed a natural negative charge in base oil but can be positively charged through modification with poly(diallyldimethyl-ammonium chloride). In contrast to the prior examples, both charge polarities reduced the friction coefficient, with significant reductions of up to 60–70% (i.e., from 0.18 to ~0.06). The mechanism underlying friction control was investigated by observing the distributions of the particle additives and characterizing the tribofilms formed at different potentials. As expected, charged particles were attracted to the electrically opposite pole, and the effect was reversed by applying the opposite potential. Interfacial slippage was presumed to occur near the interface where NPs were attracted. For locally high concentrations of MoS₂ particles, a MoS₂/MoOx tribofilm with a thickness of 100–500 nm and a loose structure was formed on the lower friction pair, resulting in a significant decrease in the shear force during the friction process. See also Ref. [80].

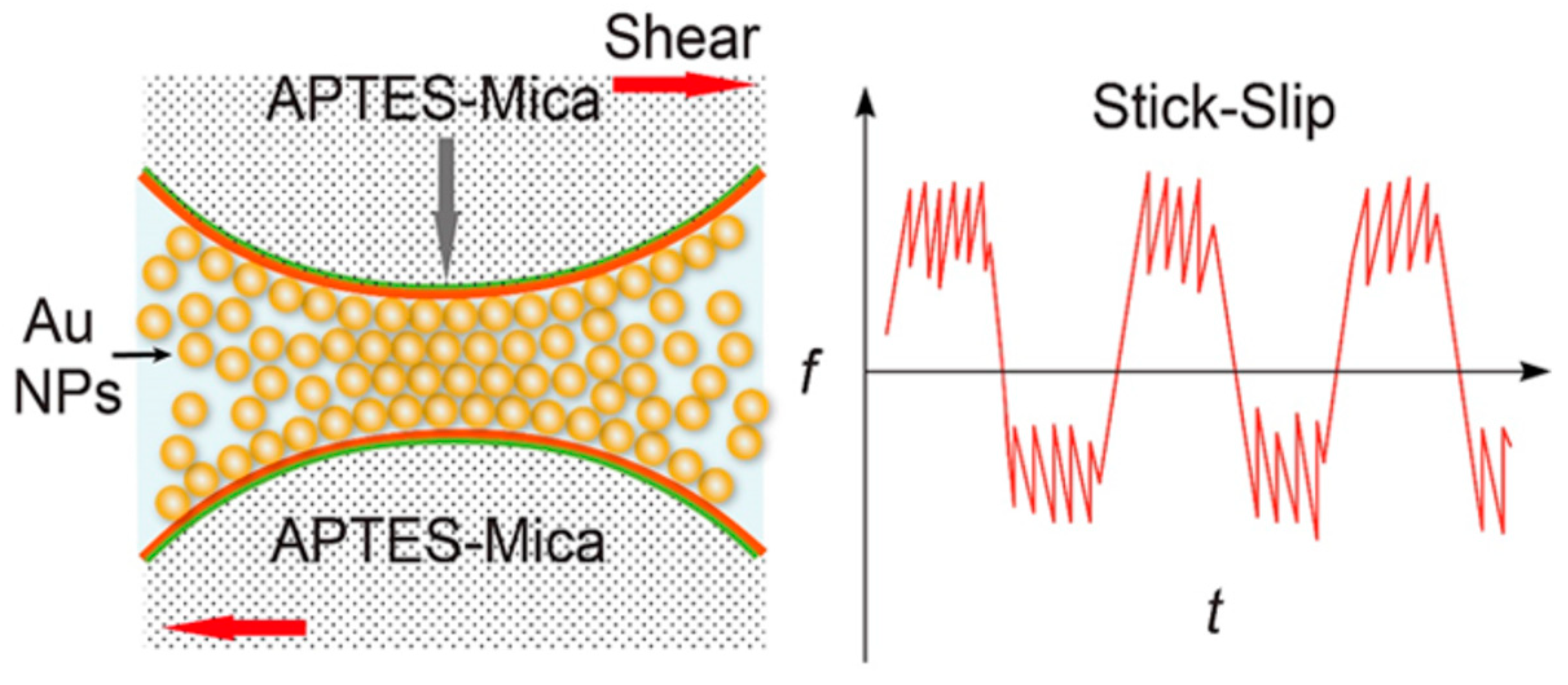
5.5. Probing Self-Assembly and Nonlinear Friction Behavior of Confined Gold Nanoparticles [33]

In this nanotribological study, the authors employed a surface forces apparatus to explore the assembly and associated surface forces for aqueous suspensions of 5 nm gold nanoparticles confined between pairs of mica (negatively charged) and (3-aminopropyl) triethoxysilane-modified mica (APTES-mica, positively charged) surfaces. Notably, in this study, it was the surface charge of the contacts that was reversed and not the surface charge of the NPs. The Au NPs were observed to be squeezed out of the confined gap between the two (negatively charged) mica surfaces during the loading process—an effect attributed to a repulsive electric double-layer force. In contrast, multilayers of Au NPs were observed to remain between the two positively charged APTES-mica surfaces (Figure 15). The authors attributed this observation to an attractive double-layer force between the oppositely charged surfaces of Au NPs and the APTES-mica sheets. It was also noted that the interaction between Au NPs and APTES-mica is stronger than the interactions between Au NPs, which caused a rearrangement of the confined Au NPs under shear motion. The confined nanoparticles did not, however, enhance lubricity: the friction coefficients (μ > 0.7) characterized by a nonlinear stick−slip friction were observed when sliding the two APTES-mica surfaces with thin (~20 nm) confined layers of Au NPs.

The results presented in this example demonstrate the potentially important role of the hydrodynamic glide as a component of the friction-reducing mechanisms associated with the introduction of NP as additives: the oil was not reported to be squeezed out from the interface as in highlight 5.4. Moreover, all examples in this section illuminate the important role of the surface charge, which in turn implies that external control of friction levels can be achieved by applying external electric fields, as demonstrated in highlight 5.4. Tuning the friction via this mechanism is the topic of the next and final section.

6. Tuning Friction through Charge and Potential Variations

Tribotronics involves the design of active control methods for nano- and/or mesoscale friction by typically employing magnetic and/or electric fields external to the contact. A number of approaches to the electromagnetic tuning of friction have been reported in the literature [81]. The tribotronic methods are particularly amenable to charged lubricant additives and have the potential to achieve in situ control of friction levels without removing and replacing lubricant materials situated within the inaccessible confines of a contact. Applications include, but are not limited to, triboelectric generators, electric vehicles, magnetic spintronics, geological drilling, automotive braking and efficiency, spacecraft systems, biological systems, and the rapid recharging of flow batteries. The impact of an external field on the tribological performance of lubricants with charged additives is, however, highly variable, as is the speed with which a lubricant responds to an imposition of an external field (Figure 16). The publications highlighted in this section demonstrate both great potential, as well as great challenges that hold for the field of tribotronics.

6.1. Study of Tribotronic Control in Ionic Liquids and Nanoparticle Suspensions [34]

When combined with an externally applied field, QCM can serve as a rapid screening tool for tribotronic applications, as reported in 2021 by Seed et al. [34]. This work followed up on an earlier work by Acharya et al. by reporting a comparative study of positively and negatively charged NP additives repositioned by external fields [69].

The group employed an experimental setup consisting of a QCM serving as a tribology sensor and an electrode and a nearby counter electrode immersed in a liquid that contained electrically charged constituents. The electric potential applied between the two electrodes produced a well-defined field resulting in electrophoretic forces that repositioned the charged constituents in the surrounding liquid (Figure 17). The resulting changes in the interfacial friction were detected via QCM for both static and alternating (sinusoidal) fields. The latter provided data on the system response time to the external electric field.

The authors employed aqueous suspensions of negatively charged TiO₂ nanoparticles, positively charged Al₂O₃ nanoparticles, and also aqueous solutions of positively and negatively charged constituents of the ionic liquid 1-butyl-3-methylimidazolium hexafluorophosphate, BMIM⁺P ${\mathrm{F}}_6^{-}$. Application of electric fields induced a variety of responses. Positively and negatively charged constituents were attracted or repelled from the surface, depending on the field direction, and the strength and duration of the field determined whether the electrodeposition would occur.

Characteristic response times from ca. 100 to 1000 s showed that the tribotronic tuning of the system studied was not instantaneous. Depending on the particulars of the system, a deposited layer could increase or decrease friction. The overall tribological impact was attributable to how the interfacial layer interacted with the charged constituents in the surrounding liquid and the resulting changes to the slip planes.

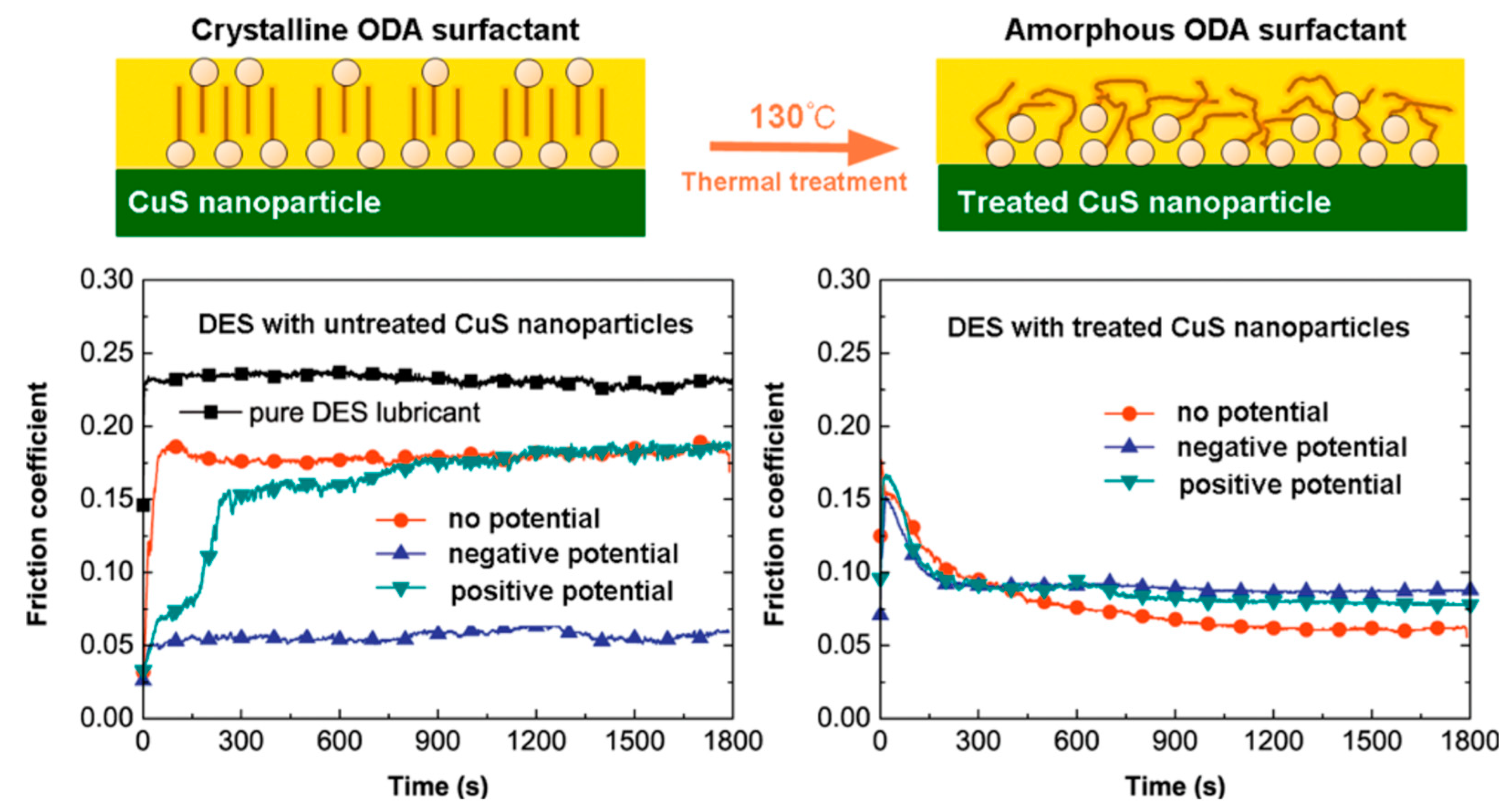
6.2. Electric Response of CuS Nanoparticle Lubricant Additives: The Effect of Crystalline and Amorphous Octadecylamine Surfactant Capping Layers [35]

This 2019 publication by Liu et al. reported on tuning the macroscale friction coefficients by applying an external potential—an effect attributed to a repositioning of nanoparticles added to an ester-based fluid [35]. The results highlighted the interdependent roles of electrostatics and surface functionalization on friction levels reported in highlight 5.3, as well as the rich variety of the responses attainable. Specifically, it was demonstrated that surface treatments resulting in crystalline structures enhanced the tribotronic response while the amorphous treatments essentially eliminated sensitivity to the external fields while still enhancing lubricity (Figure 18).

The measurements were carried out using a macroscale reciprocating tribometer configured with a copper plate, a ZrO₂ ball, and octadecylamine-coated CuS nanoparticles added to an ester-base stock lubricant. Such additives are of great interest in electric vehicle applications because of their capability to maintain electrical conductivity in critical system components. This publication was a follow-up of an earlier study, where the same group observed that for copper plate potentials lower than −14 V, the friction coefficient decreased from 0.18 to 0.05 after an induction period [82]. This reduction in friction coefficients was attributed to an excess of positively charged nanoparticles in the vicinity of the negatively charged plate. The induction periods were shorter for increasingly negative potentials. The latter observation is consistent with an increased rate of nanoparticles’ migration with increasingly negative potentials.

CuS nanoparticles prepared with a crystalline surfactant were positively charged due to the presence of the amino headgroup in octadecylamine. The surface zeta potential was reported to be +18.47 ± 0.99 mV higher than with the amorphous surfactant—an effect attributed to random chain conformations of the octadecylamine molecules. The observed friction coefficient decreased from 0.18 to 0.09 and 0.05, respectively, when the negative potential (for the copper lower pair) was applied. A thermal treatment was employed to destroy the local order in the layer of the surface ligands and the lack of response to the external field was attributed to amino groups being obscured by the disordered carbon chains. The authors concluded that this hindered the electron transfer and, thus, weakened the system response to external fields.

6.3. Tribotronic and Electrochemical Properties of Platinum–Nanofluid Interfaces Formed by Aqueous Suspensions of 5 and 40 nm TiO₂ Nanoparticles [36]

For nanoparticles to be effective as liquid lubricant additives, the nanoparticle suspension must remain stable. This consideration would tend to favor NPs with a higher magnitude of the zeta potential and also smaller in size. However, the smaller NPs may respond differently depending on the material systems: Small particles, for example, may fill voids to render a surface smoother. Larger particles, meanwhile, provide better separation of contacting surfaces and lesser susceptibility to surface roughness. The stronger repulsive forces required to keep larger NPs separated in liquids may also act to counteract normal forces in the contacting surfaces.

The particle size considerations pose a significant design challenge since NPs are generally present in a range of sizes, along with unintentional constituents such as wear particles. In this 2023 publication, Seed et al. [36] employed QCM in combination with cyclic voltammetry to characterize the nanotribological and electrochemical behavior of platinum–nanofluid interfaces formed by aqueous suspensions of negatively charged 5, 40, and 100 nm TiO₂ NPs, including the response to externally applied electric fields [69]. TiO₂ particles gain a negative charge in suspension, and, therefore, do not require additional surface treatments. The particles of all three sizes reduced interfacial frictional drag forces when added to pure water in zero-field conditions. Unfortunately, the 100 nm NPs failed to remain in suspension for longer than 10–20 min. The 5 and 40 nm NPs were readily repositioned by an external electric field in a reversible manner, consistent with no permanent attachment of NPs to the QCM surface. For electric fields of sufficient amplitude and duration, the 40 nm TiO₂ NPs displayed an electrochemical signature consistent with a reversible electrophoretic deposition of the NPs that was accompanied by changes in the electrochemical attributes and increased interfacial drag.

The smallest 5 nm NPs under the same field conditions resulted in progressive reductions in the interfacial drag forces associated with field-induced increases in the concentration of NPs at the surface. The response time to external fields was not significantly different. Slip lengths, which are longer for lower interfacial friction, in zero-field conditions were estimated to be 17 nm (22 nm), respectively, for the 5 nm (40 nm) NPs. Attractive fields increased the slip lengths for the 5 nm NPs but decreased them for the 40 nm, exemplifying the great degree of sensitivity to NP size. The authors attributed this primarily to the greater charge held on the larger NPs.

Overall, the study suggested a method for the active tribological control and optimization of device performance in applications where suspensions of charged nanoparticles are present and can be exposed to external fields, or, alternatively, a method for selecting the best NP size to optimize system performance based on the electrochemical properties of the materials of interest.

6.4. Friction and Adhesion Control between Adsorbed Layers of Polyelectrolyte Brush-Grafted Nanoparticles via pH-Triggered Bridging Interactions [37]

In this 2018 publication, Riley et al. [37] employed multiple nanotribological methods to explore the tuning of friction by changing the pH of a base fluid doped with brush-grafted silica nanoparticles. The main innovation of this work was to employ pH-responsive brush-grafted NPs with annealed polyelectrolyte brushes capable of undergoing controlled changes in surface area coverage through post-adsorption swelling or de-swelling into nonequilibrium layer conformations (Figure 19). The changes in the surface coverage can then switch the particle intercalation on and off. The resulting bridging attractions and an enhanced energy dissipation upon sliding provide for a mechanism to tune friction and adhesion.

In this study, colloidal probe atomic force microscopy was employed to measure normal and frictional forces between negatively charged silica surfaces with adsorbed pH-responsive cationic brush-grafted silica nanoparticles. Complementary QCM and ellipsometry measurements were performed in the swollen and de-swollen states, providing independent measures of the mass density and thickness of the confined NPs.

The study confirmed that adsorbed brush-grafted NPs can be swollen or de-swollen by adjusting pH, thus allowing for direct control of the surface coverage and bridging interactions. Adhesive bridging contacts with high friction (μ ≈ 1.5) were observed for the de-swollen/weakly charged state while non-adhesive contacts with low friction levels (μ ≈ 0.1) were observed for the swollen/highly charged repulsive condition. Overall, this work demonstrated an alternate means to tune friction. See also Refs. [83,84,85].

6.5. High Lubricity and Electrical Responsiveness of Solvent-Free Ionic SiO₂ Nanofluids [38]

Conventional NPs and surface functionalized NPs are, in general, solid-like when not dispersed in a base fluid. The colloidal stability of such particles can be improved via surface functionalization and then the properties of the surface ligands become essential when considering such particles as lubricant additives. “Solvent-free” ionic nanofluids (NFs) are liquid materials composed of NPs whose surface functionalization renders them to behave similarly to ionic liquids [86]. NFs in particular are characterized by Newtonian liquid behavior, macroscopic homogeneity, good thermal stability, and good tribological properties when used alone or as additives.

In this 2018 study, Gou et al. explored the impact of external fields on nanofluids consisting of functionalizing silica nanoparticles with a charged corona and ionically tethered with oligomeric chains as a canopy [38]. The study demonstrated that the as-synthesized nanofluids were both stable and fluid and showed excellent friction-reducing and anti-wear properties both as additives and as pure liquids. Similar to what has been observed for conventional ionic liquids, the authors found that a small fraction of nanofluids blended into a base fluid reduces friction and wear as effectively as the nanofluid alone.

Measurements were performed with a macroscale reciprocating tribometer using a steel ball on steel disk contact. NFs were studied both in pure forms and as additives to polyethylene glycol base oil. For one specific shell structure, μ dropped from about 0.15 to 0.13 for an applied potential of both +3 V (disk as an anode) and −3 V (disk as a cathode). For the second specific shell structure, the friction coefficient dropped from about 0.12 to 0.11 only for −3 V (disk as a cathode), and no change was observed when a positive potential was applied. The formation of a unique double electric layer consisting of both organic and inorganic materials during friction was suggested as the underlying mechanism for the observations, which can be essential for yielding robust lubrication by the adsorption film. The authors also noted that a nanostructured tribofilm comprising a significant fraction of silica and tribo-chemical products of the organic layers had formed, and it was believed to be significant in improving the boundary lubrication performance.

The results reveal both the great promise of such novel lubricants and the challenges associated with the sensitivities to external field conditions. The latter issue must be harnessed in order to optimize lubricant performance.

7. Summary and Concluding Comments

In this mini review, we have highlighted 25 selected research reports that demonstrate major progress and important challenges in the linkage of nanoscale contacts and nanoparticles to macroscale tribological properties. For the pioneering case of C₆₀ additives to toluene, NP rolling and/or changes to interfacial slip conditions were proposed as potential explanations. It is now clear that the second scenario is far more likely for this and a wide range of other systems. Important challenges nonetheless remain in establishing a basic understanding of the impact of nanoparticles on macroscale lubricant performance. These include the rapid screening of materials; the interrelated impacts of surface charge, particle size, and particle dispersiveness; and responsiveness to external fields that both underlie and enable the active control of tribological properties.