Influence of Natural Gas Composition and Operating Conditions on the Steady-State Performance of Dry Gas Seals for Pipeline Compressors
Abstract
1. Introduction
2. Numerical Analysis Models
2.1. Geometrical Model
2.2. Governing Equations
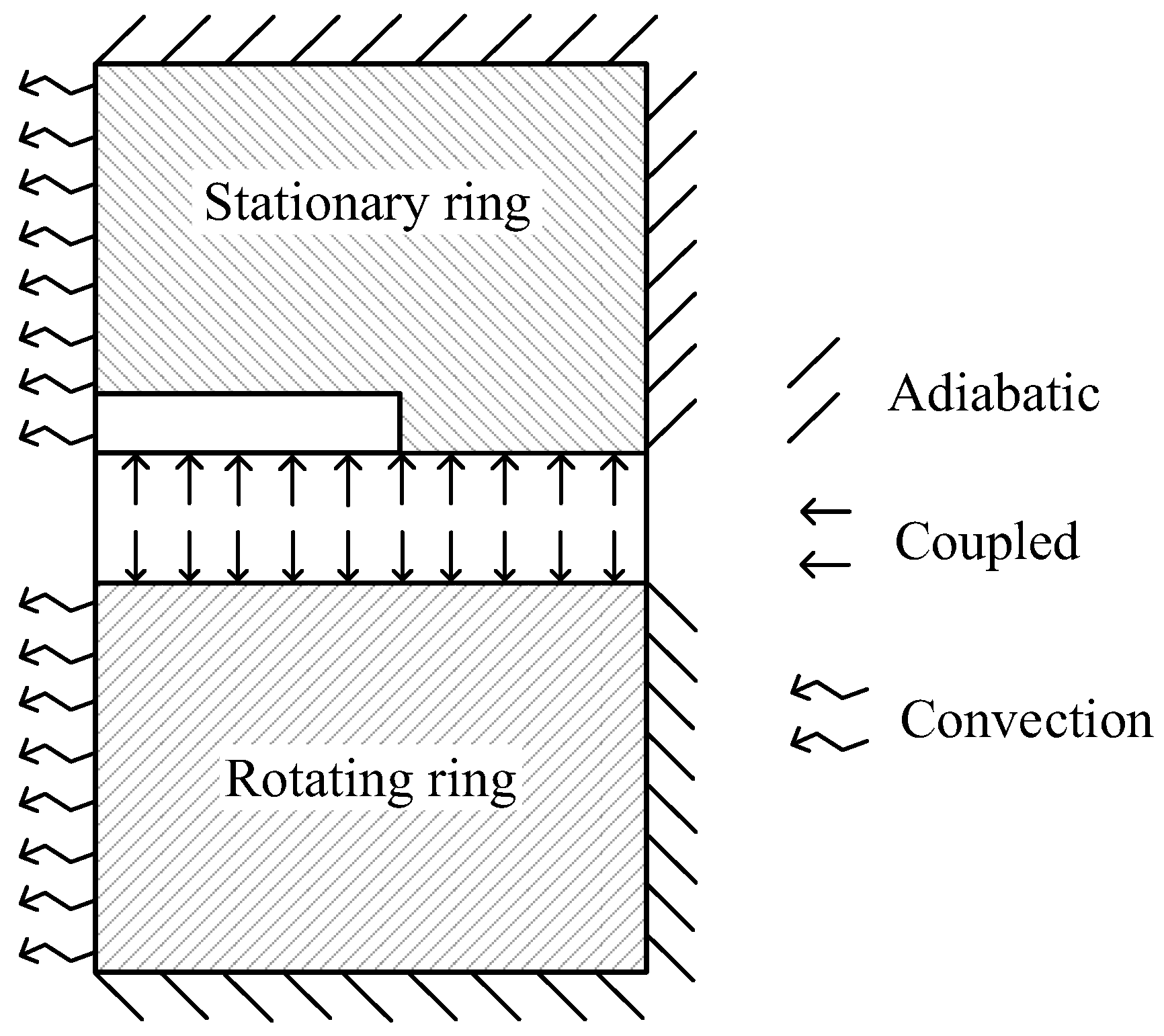
2.3. Boundary Conditions
2.4. Numerical Procedure
3. Result Discussion and Analysis
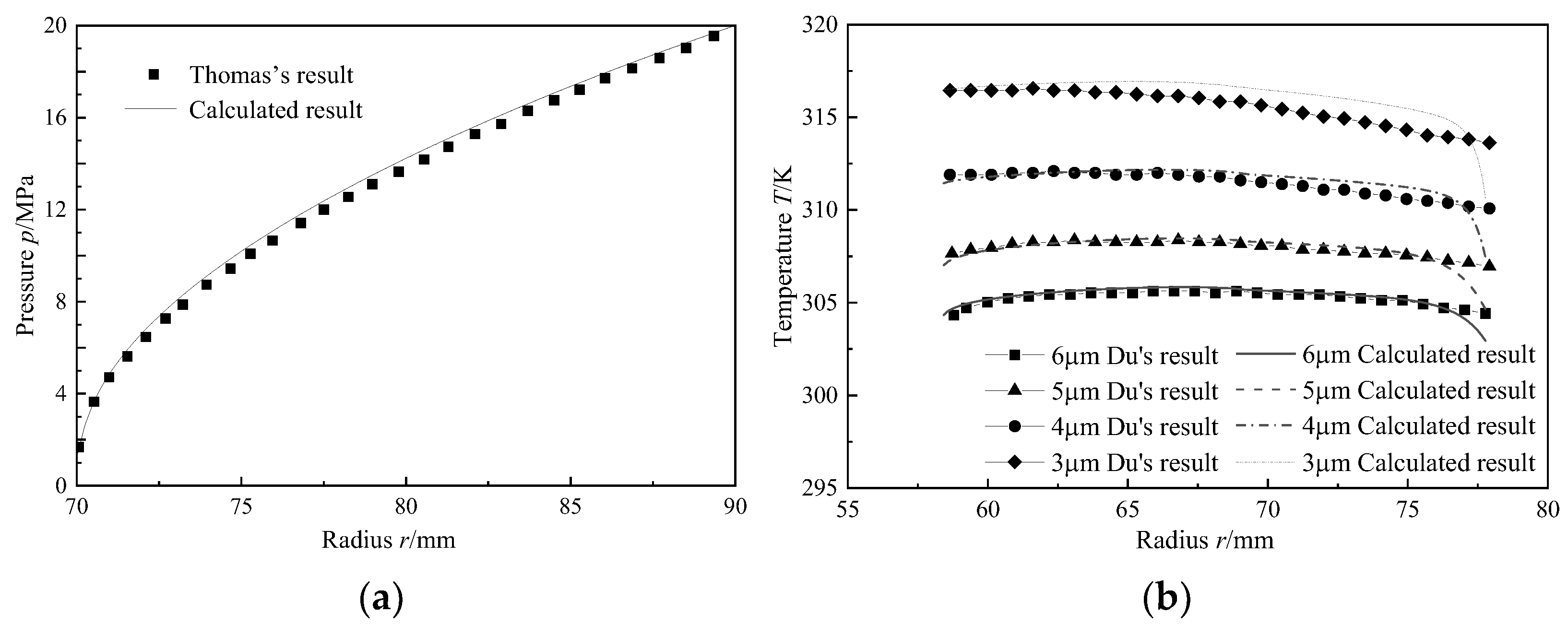
3.1. Numerical Model Validation
3.2. Influence Analysis of Real Fluid Effects
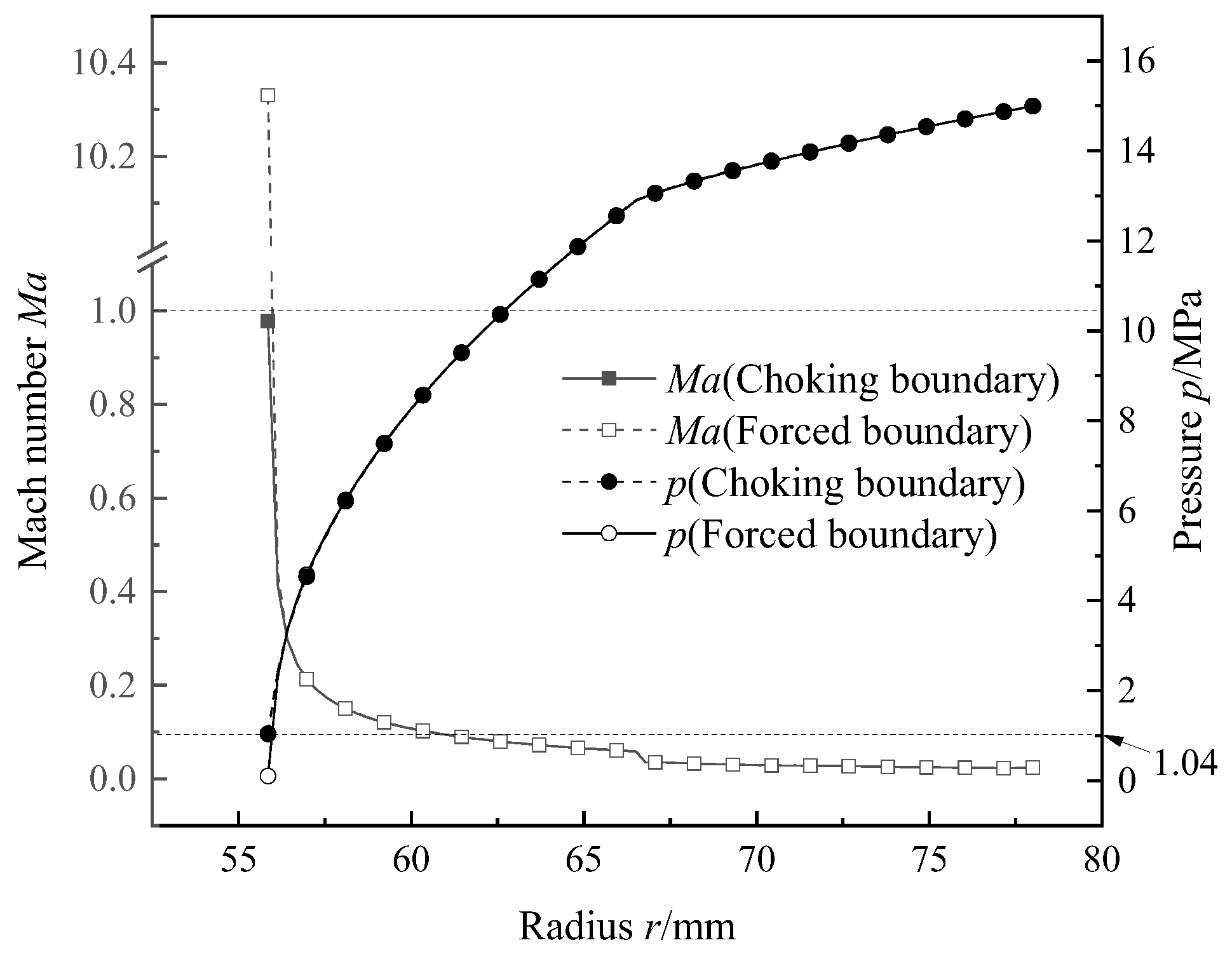
3.2.1. Influence of the Choking Effect
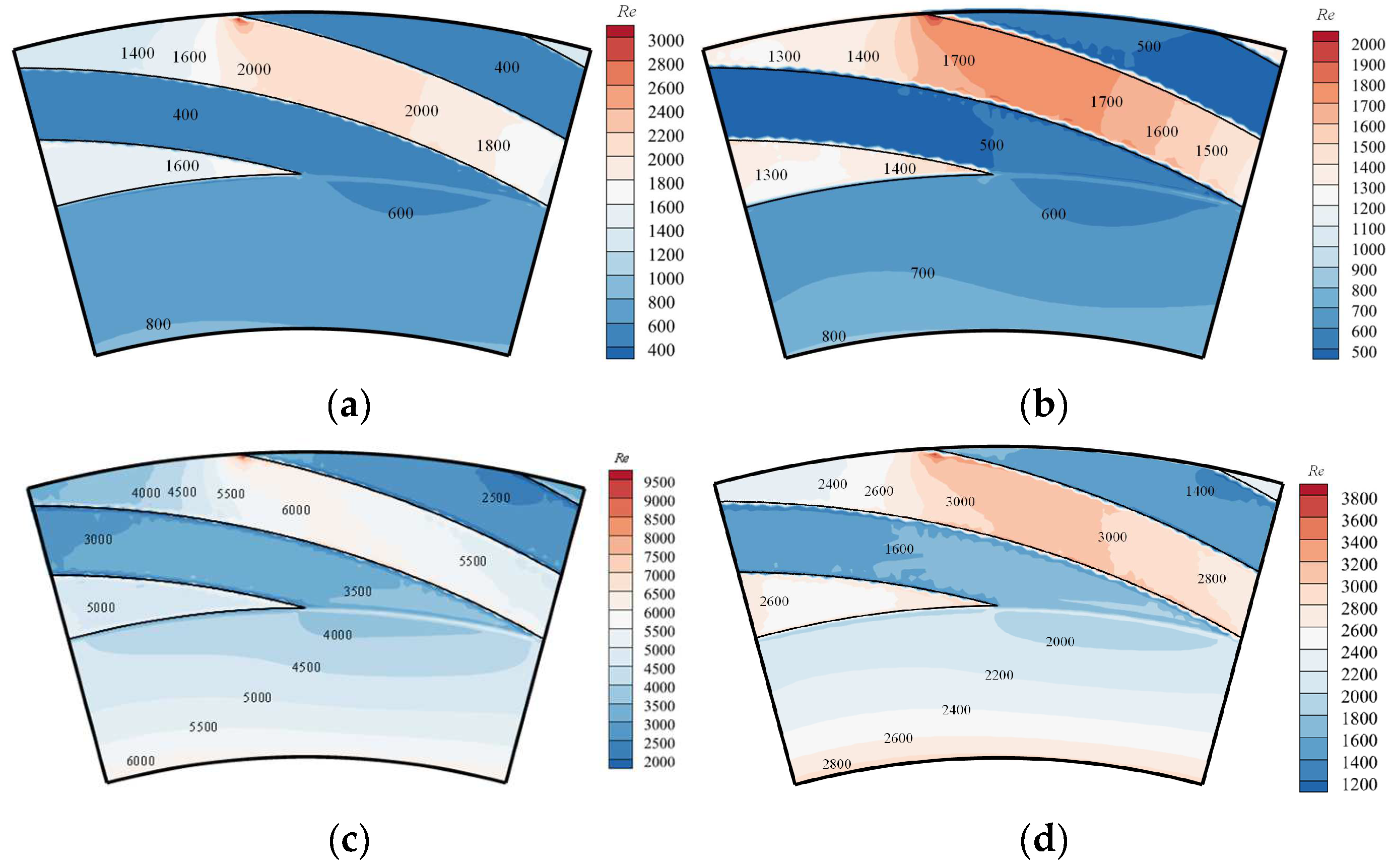
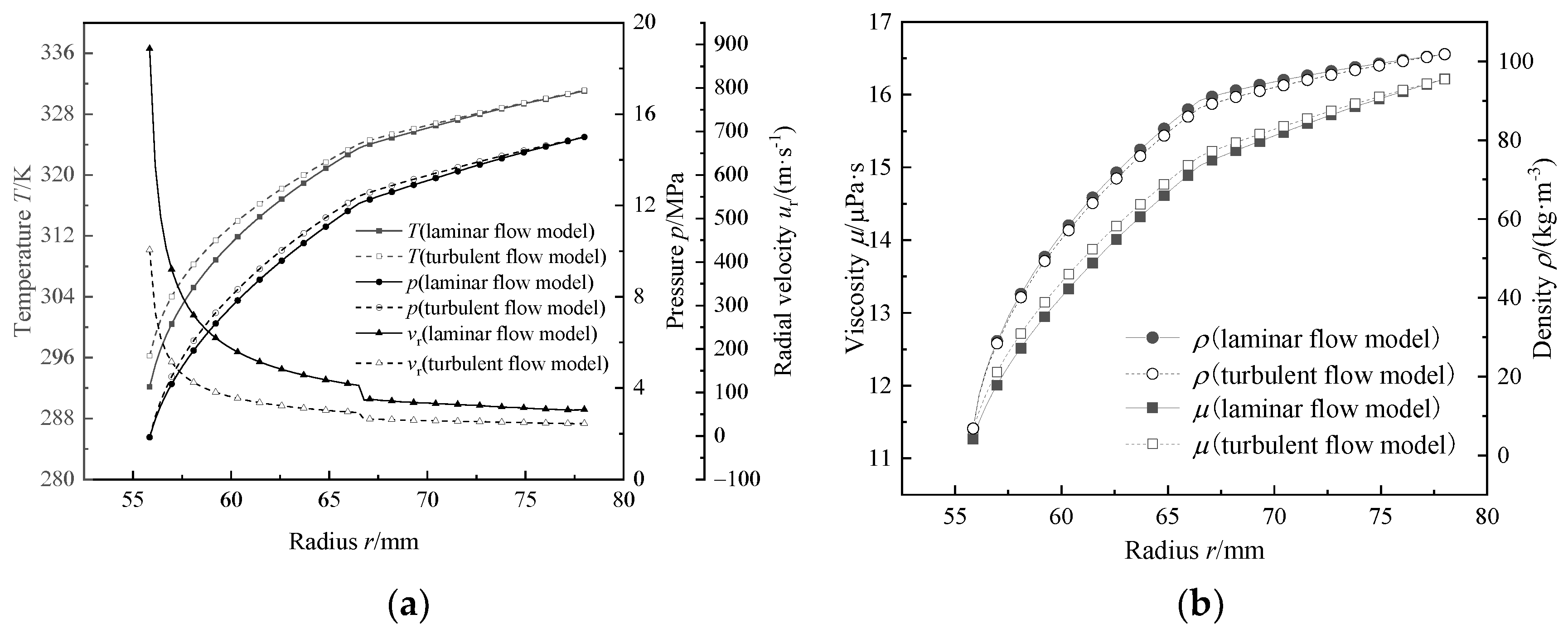
3.2.2. Influence of the Turbulence Effect
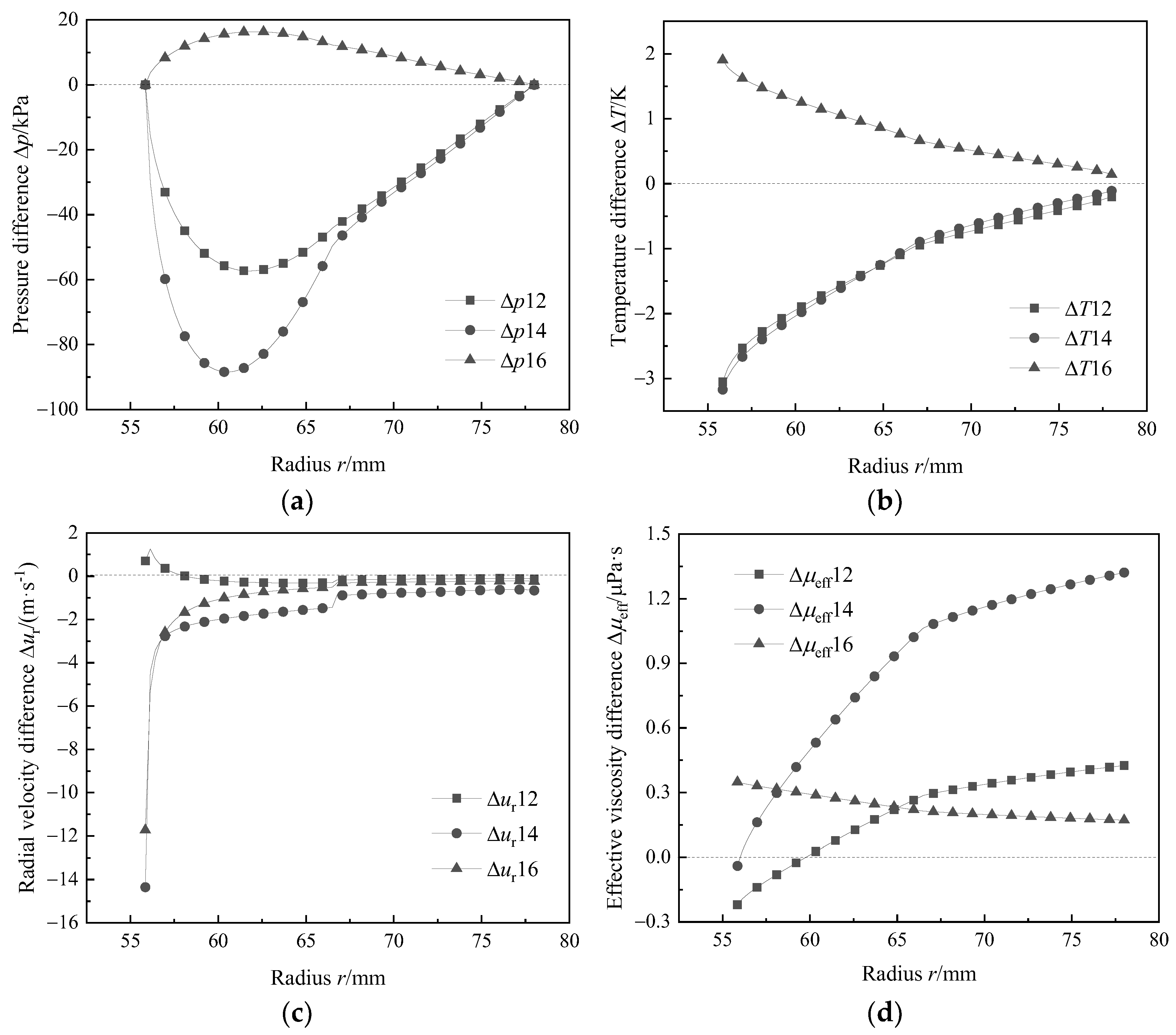
3.3. Influence of Unitary Component and Content of Impurity on Sealing Performance
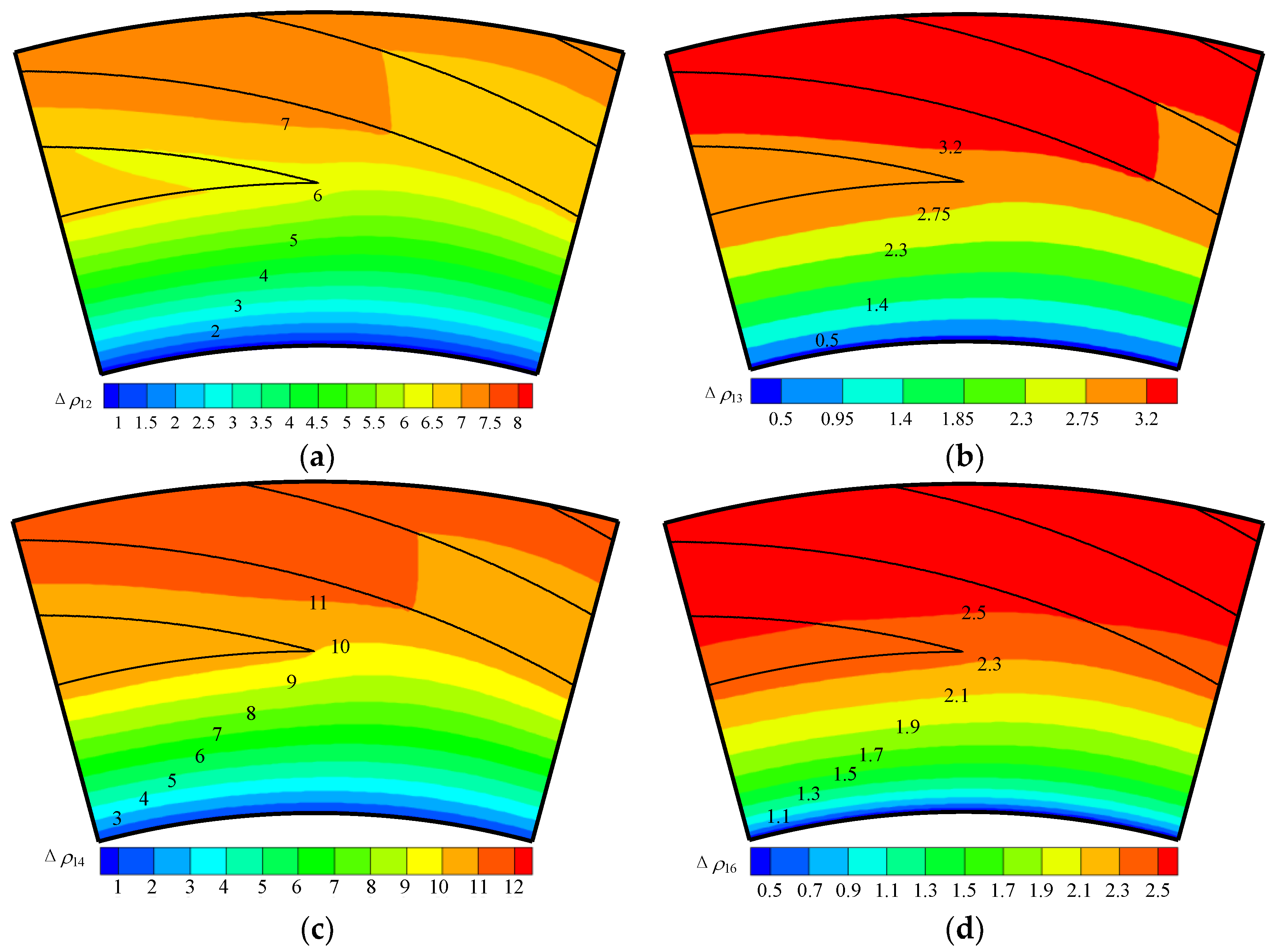
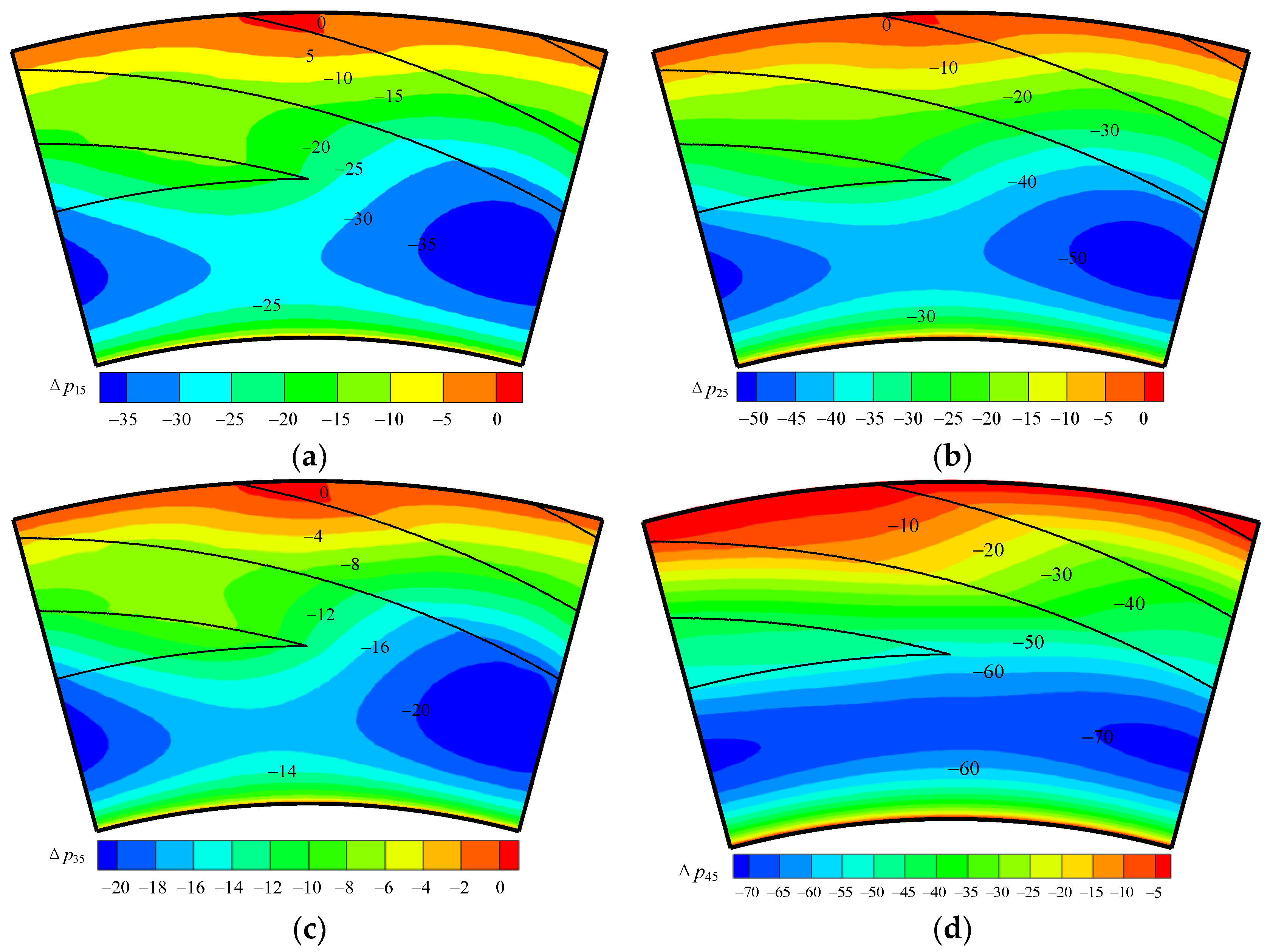
3.4. Influence of Multi-Impurity Components and Working Conditions on the Sealing Performance
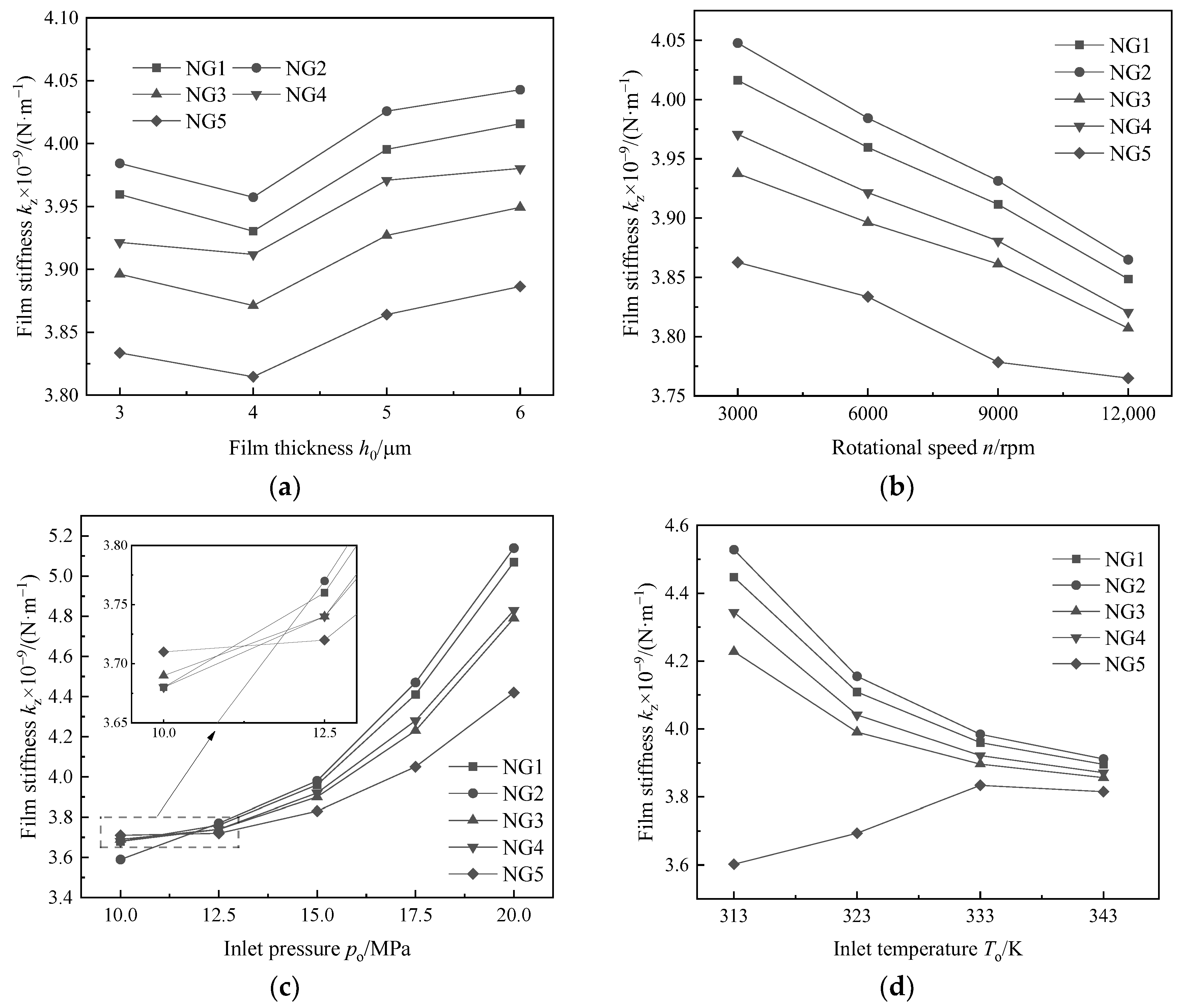
3.4.1. Influence of Components on Opening Force and Gas Film Stiffness
3.4.2. Influence of Components on Leakage Rate
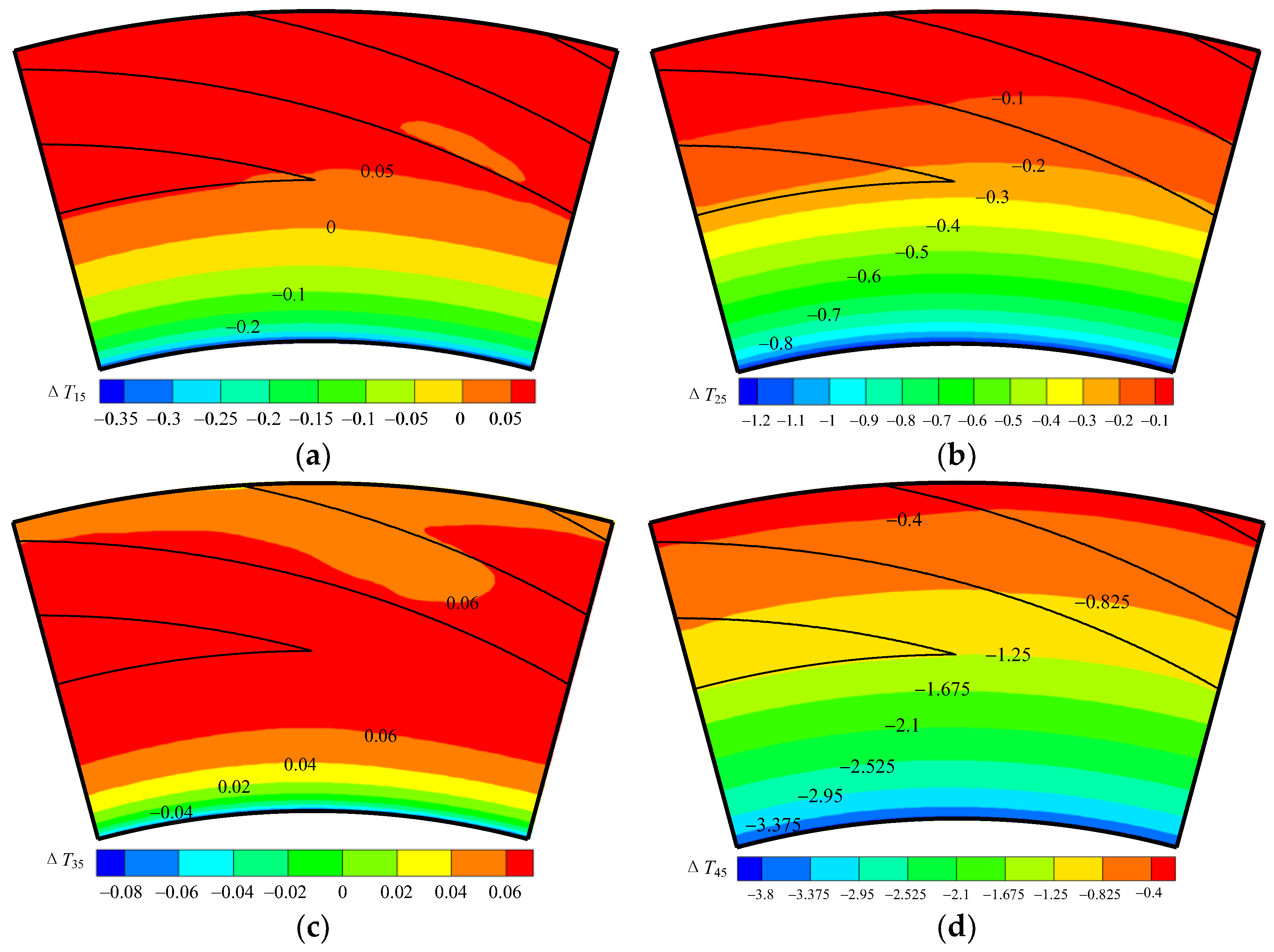
3.4.3. Influence of Components on the Temperature Difference between Inlet and Outlet
4. Conclusions
- (a)
- For the DGS of a natural gas pipeline compressor operating at high pressures, the laminar flow assumption caused a significantly higher mass leakage rate, and the relative error of the leakage rate exceeded 100% when the film thickness was large. Therefore, the influence of the turbulence effect is significant and cannot be ignored, while the choking effect has little influence on the steady-state performance of a natural gas DGS.
- (b)
- The change of impurities, such as light hydrocarbon, heavy hydrocarbon, and non-hydrocarbon in the natural gas mixture and their contents, as well as the interactions between the components, made the thermal physical properties of natural gas different from those of pure CH4 and further affected the flow and heat transfer behavior between the two faces of a DGS, resulting in the sealing performance of the natural gas DGS, which was different from that of the pure CH4 DGS.
- (c)
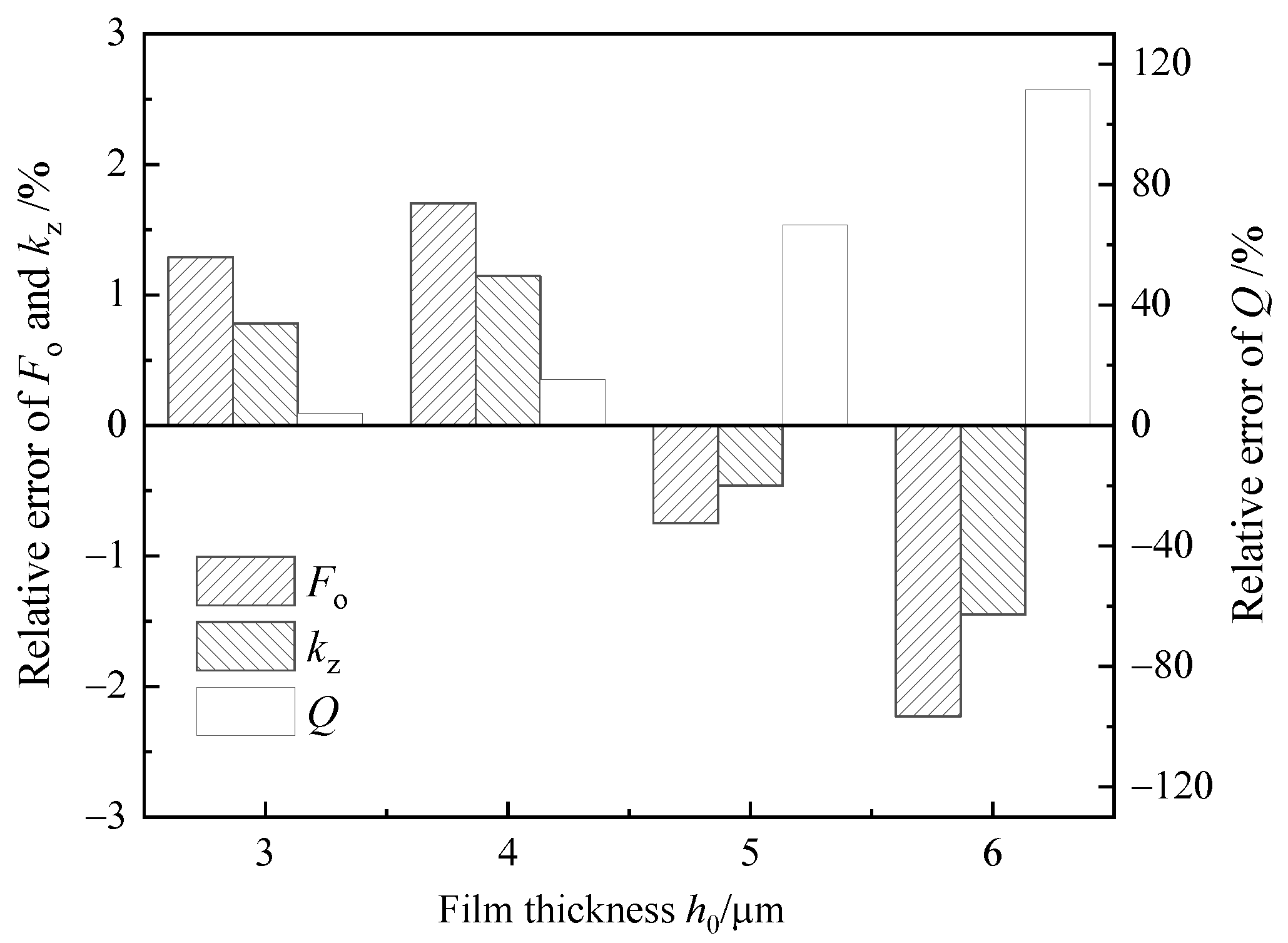
- For natural gas containing unitary impurity component, increasing the content of light and heavy hydrocarbon resulted in the increase of sealing performance, such as the film stiffness, leakage rate, and the temperature difference of both the inlet and outlet of the DGS. When the content of light hydrocarbon or heavy hydrocarbon reached 8%, the influence of impurity could not be neglected. When the impurity content was 10%, the values of the above performance parameters increased by about 1.5~3.5%, 6.5%, and 3 K, respectively. For natural gas containing non-hydrocarbon, when the impurity content reached 10%, the temperature difference between the inlet and outlet of the DGS decreased by 1.8 K, but the influence on the opening force, gas film stiffness, and leakage rate was negligible.
- (d)
- The influence of multiple impurities on the sealing performance is basically the same as that of the unitary impurity, and increasing the content of light or heavy hydrocarbon at lower temperatures is more conducive to the improvement of the gas film stiffness. With the increase of the film thickness and inlet pressure, the leakage rate of the DGS and the temperature difference between inlet and outlet will increase. The increase of rotational speed or inlet temperature will decrease the leakage rate and the temperature difference between the inlet and outlet.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xie, M.H.; Wei, X.N.; Chen, C.L.; Sun, C. China’s natural gas production peak and energy return on investment (EROI): From the perspective of energy security. Energy Policy 2022, 164, 112913. [Google Scholar] [CrossRef]
- Liu, J.; Wang, S.; Wei, N.; Chen, X.; Xie, H.; Wang, J. Natural gas consumption forecasting: A discussion on forecasting history and future challenges. J. Nat. Gas Sci. Eng. 2021, 90, 103930. [Google Scholar] [CrossRef]
- Liu, H.; Tian, Z.; Guo, P.; Li, Q.; Wang, Z.; Wang, W.; Du, J.; Wen, Y. Study the high pressure effect on compressibility factors of high CO2 content natural gas. J. Nat. Gas Sci. Eng. 2020, 87, 103759. [Google Scholar] [CrossRef]
- Hsing, F.C.; Carrano, M.J. Analysis of compressible fluid flow in gas turbine mainshaft seals. ASLE Trans. 1980, 23, 237–243. [Google Scholar] [CrossRef]
- Glienicke, J.; Launert, A.; Schums, H.; Kohring, B. Non-contacting gas lubricated face seals for high p·v-values. In Seals Flow Code Development 1993; IICA Biblioteca Venezuela: San José, Costa Rica, 1994; pp. 367–378. [Google Scholar]
- Hirs, G.G. A Bulk-Flow Theory for Turbulence in Lubricant Films. ASME J. Lubr. Technol. 1973, 95, 137–145. [Google Scholar] [CrossRef]
- Xu, H.; Song, P.; Mao, W.; Deng, Q. The performance of spiral groove dry gas seal under choked flow condition considering the real gas effect. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2019, 234, 554–566. [Google Scholar] [CrossRef]
- Hu, X.P.; Song, P.Y. Theoretic analysis of the effect of carbon dioxide real gas on the performance of the T-groove dry gas seal. Adv. Mater. Res. 2013, 634–638, 3815–3820. [Google Scholar] [CrossRef]
- Fairuz, Z.M.; Jahn, I. The influence of real gas effects on the performance of supercritical CO2 dry gas seals. Tribol. Int. 2016, 102, 333–347. [Google Scholar] [CrossRef]
- Teng, L.; Jiang, J.; Peng, X.; Li, J. Influence of surface grooving methods on steady and dynamic performance of spiral groove gas face seals. Alex. Eng. J. 2023, 64, 55–80. [Google Scholar] [CrossRef]
- Atkinson, S. Robust, gas-lubricated mechanical seal for processing natural gas. Seal. Technol. 2018, 2018, 5–6. [Google Scholar] [CrossRef]
- Jia, W.L.; Ren, Q.Y.; Zhang, H.; Yang, M.; Wu, X.; Li, C. Multicomponent leakage and diffusion simulation of natural gas/hydrogen mixtures in com-pressor plants. Saf. Sci. 2023, 157, 105916. [Google Scholar] [CrossRef]
- Seevam, P.N.; Race, J.M.; Downie, M.J.; Hopkins, P. Transporting the next generation of CO2 for carbon, capture and storage: The impact of impurities on supercritical CO2 pipelines. In Proceedings of the 2008 7th International Pipeline Conference, Calgary, AB, Canada, 29 September–3 October 2008; pp. 39–51. [Google Scholar]
- Li, H.; Yan, J. Impacts of equations of state (EOS) and impurities on the volume calculation of CO2 mixtures in the applica-tions of CO2 capture and storage (CCS) processes. Appl. Energy 2009, 86, 2760–2770. [Google Scholar] [CrossRef]
- Martynov, S.B.; Daud, N.K.; Mahgerefteh, H.; Brown, S.; Porter, R.T.J. Impact of stream impurities on compressor power requirements for CO2 pipe-line transportation. Int. J. Greenh. Gas Control 2016, 54, 652–661. [Google Scholar] [CrossRef]
- Okezue, C.; Kuvshinov, D. A comprehensive study of the effect of chemical impurities on selection and sizing of centrifugal machines for supercritical carbon dioxide transport pipelines. Appl. Energy 2018, 230, 816–835. [Google Scholar] [CrossRef]
- Wang, Z.L.; Wang, Q.Y.; Hao, M.M.; Li, X.; Liu, K. The effect of thermal-elastic deformation on the sealing performance of supercritical CO2 dry gas seal. Ind. Lubr. Tribol. 2023, 75, 950–958. [Google Scholar] [CrossRef]
- Brunetière, N.; Tournerie, B.; Frêne, J. Influence of fluid flow regime on performances of non-contacting liquid face seals. ASME J. Tribol. 2002, 124, 515–523. [Google Scholar] [CrossRef]
- Brunetière, N. A modified turbulence model for low reynolds numbers: Application to hydrostatic seals. ASME J. Tribol. 2005, 127, 130–140. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, J.; Peng, X.; Zhang, X. An investigation on phase transitions in a supercritical CO2 dry gas seal. Tribol. Trans. 2022, 65, 728–748. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, J.; Peng, X.; Meng, X.; Li, J. The influence and a direct judgement method of the flow state in supercritical CO2 dry gas seal. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 486. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, B.; Lin, J.; Ye, C. A thermohydrodynamic analysis of dry gas seals for high-temperature gas-cooled reactor. ASME J. Tribol. 2013, 135, 021701. [Google Scholar]
- Becker, K.M. Measurements of convective heat transfer from a horizontal cylinder rotating in a tank of water. Int. J. Heat Mass Transf. 1963, 6, 1053–1062. [Google Scholar] [CrossRef]
- Jiang, J.; Zhao, W.; Peng, X.; Li, J. A novel design for discrete surface texture on gas face seals based on a superposed groove model. Tribol. Int. 2020, 147, 106269. [Google Scholar] [CrossRef]
- Thomas, S.; Brunetière, N.; Tournerie, B. Thermoelastohydrodynamic behavior of mechanical gas face seals operating at high pressure. ASME J. Tribol. 2007, 129, 841–850. [Google Scholar] [CrossRef]
- Du, Q.; Gao, K.; Zhang, D.; Xie, Y. Effects of grooved ring rotation and working fluid on the performance of dry gas seal. Int. J. Heat Mass Transf. 2018, 126, 1323–1332. [Google Scholar] [CrossRef]
- Taylor, C.M.; Dowson, D. Turbulent lubrication theory application to design. ASME J. Lubr. Technol. 1974, 96, 36–46. [Google Scholar] [CrossRef]
- Yu, C.; Ni, Y.; Dai, J.; He, Y.; Fang, C.; Liao, F. A Comparison of the geochemical characteristics of ultra-deep natural gas in the Kuqa Foreland and Marine Craton Areas in the Tarim Basin, China. Front. Earth Sci. 2022, 10, 884445. [Google Scholar] [CrossRef]
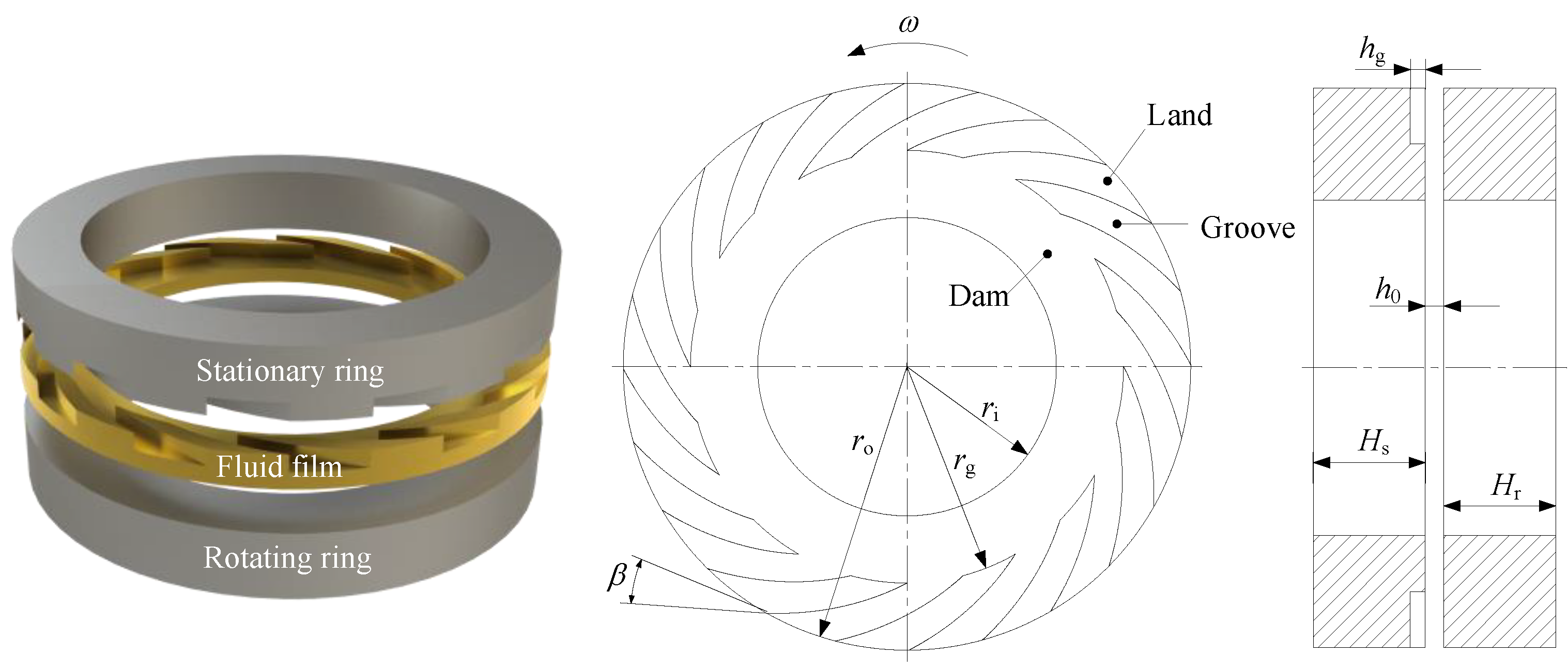





| Item and Symbol | Value | Item and Symbol | Value |
|---|---|---|---|
| Groove root radius rg/mm | 66.65 | Outer diameter pressure po/MPa | 15 |
| Groove depth hg/μm | 5 | Rotational speed n/rpm | 6000 |
| Spiral angle β/° | 15 | Outer diameter temperature To/K | 333 |
| Slot width ratio δ | 1 | Gas film thickness h0/μm | 3 |
| Groove number Ng | 12 |
| Item and Symbol | Value | Item and Symbol | Value |
|---|---|---|---|
| Inner radius ri/mm | 55.85 | Density ρ/kg·m−3 | 3150 |
| Outer radius ro/mm | 78 | Thermal conductivity λ/W·m−1·K−1 | 57 |
| Stationary ring thickness Hs/mm | 12 | Specific Heat Capacity Cp/J·kg−1·K−1 | 710 |
| Rotating ring thickness Hr/mm | 12 |
| Natural Gas Category | Gas Sample | CH4 | C2H6 | C5H12 | N2 |
|---|---|---|---|---|---|
| Ⅰ | ng1 | 100% | |||
| Ⅱ | ng2 | 90% | 10% | ||
| ng3 | 95% | 5% | |||
| Ⅲ | ng4 | 90% | 10% | ||
| ng5 | 95% | 5% | |||
| Ⅳ | ng6 | 90% | 10% | ||
| ng7 | 95% | 5% |
| Gas Sample | hconv (kW·m−2·K−1) | Gas Sample | hconv (kW·m−2·K−1) |
|---|---|---|---|
| ng1 | 5.71 | ng5 | 5.90 |
| ng2 | 5.87 | ng6 | 5.51 |
| ng3 | 5.75 | ng7 | 5.58 |
| ng4 | 6.21 |
| Gas Sample | CH4 | C2H6 | C3H8 | C4H10 | C5H12 | C6H14 | N2 |
|---|---|---|---|---|---|---|---|
| NG1 | 66% | 8% | 4% | 2% | 20% | ||
| NG2 | 66% | 8.3% | 3.5% | 2% | 0.7% | 0.9% | 18.6% |
| NG3 | 75% | 7% | 2% | 1% | 15% | ||
| NG4 | 82% | 10% | 3% | 1% | 4% | ||
| NG5 | 92% | 2% | 1% | 5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, F.; Jiang, J.; Peng, X.; Teng, L.; Meng, X.; Li, J. Influence of Natural Gas Composition and Operating Conditions on the Steady-State Performance of Dry Gas Seals for Pipeline Compressors. Lubricants 2024, 12, 217. https://doi.org/10.3390/lubricants12060217
Wu F, Jiang J, Peng X, Teng L, Meng X, Li J. Influence of Natural Gas Composition and Operating Conditions on the Steady-State Performance of Dry Gas Seals for Pipeline Compressors. Lubricants. 2024; 12(6):217. https://doi.org/10.3390/lubricants12060217
Chicago/Turabian StyleWu, Fan, Jinbo Jiang, Xudong Peng, Liming Teng, Xiangkai Meng, and Jiyun Li. 2024. "Influence of Natural Gas Composition and Operating Conditions on the Steady-State Performance of Dry Gas Seals for Pipeline Compressors" Lubricants 12, no. 6: 217. https://doi.org/10.3390/lubricants12060217
APA StyleWu, F., Jiang, J., Peng, X., Teng, L., Meng, X., & Li, J. (2024). Influence of Natural Gas Composition and Operating Conditions on the Steady-State Performance of Dry Gas Seals for Pipeline Compressors. Lubricants, 12(6), 217. https://doi.org/10.3390/lubricants12060217





