Investigation into the Heat Transfer Behavior of Electrostatic Atomization Minimum Quantity Lubrication (EMQL) during Grinding
Abstract
1. Introduction
2. Experimental Methodology
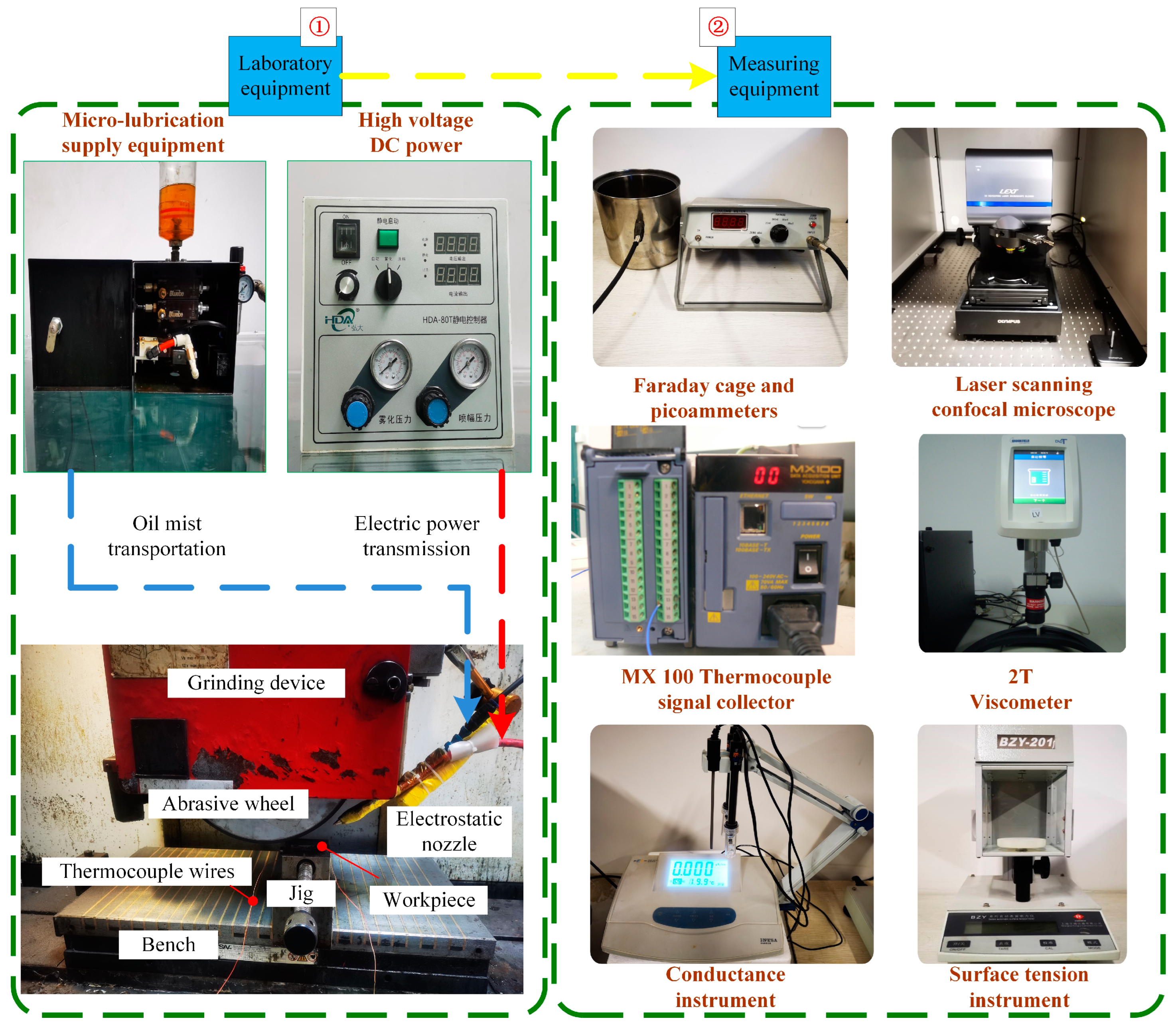
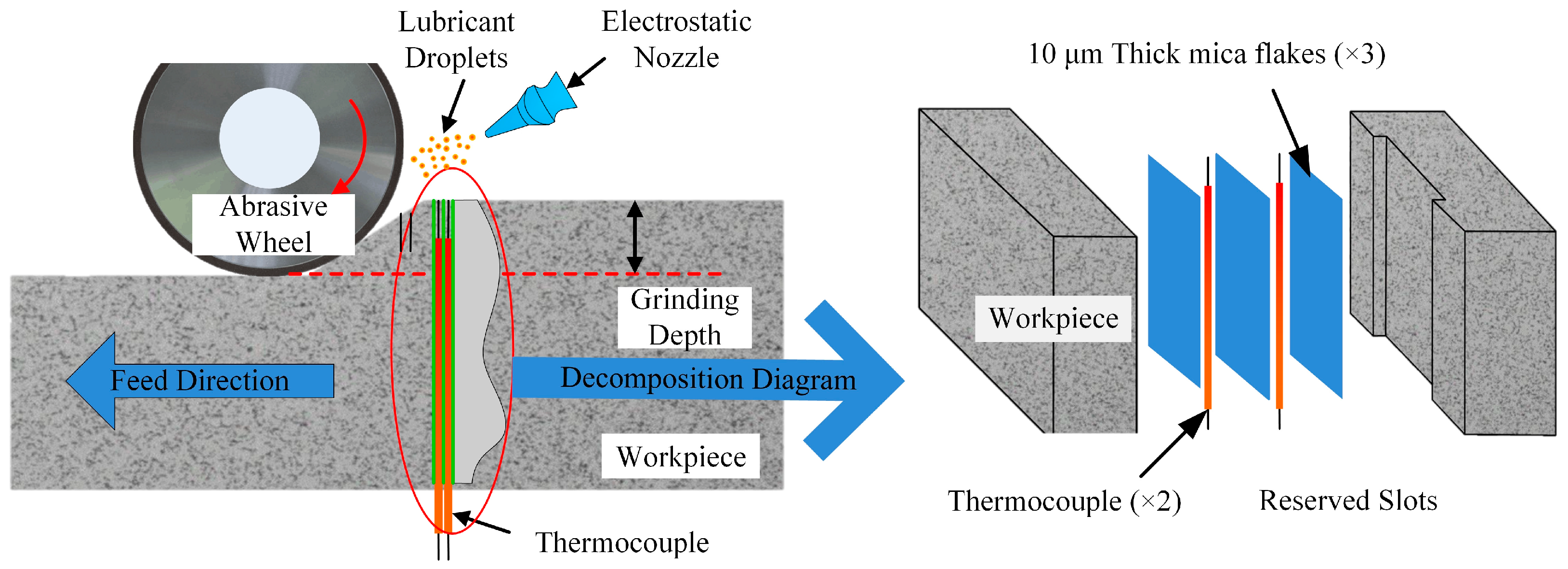
2.1. Experiment and Measuring Device
2.2. Experimental Materials
2.3. Experimental Parameters
3. Results and Discussion
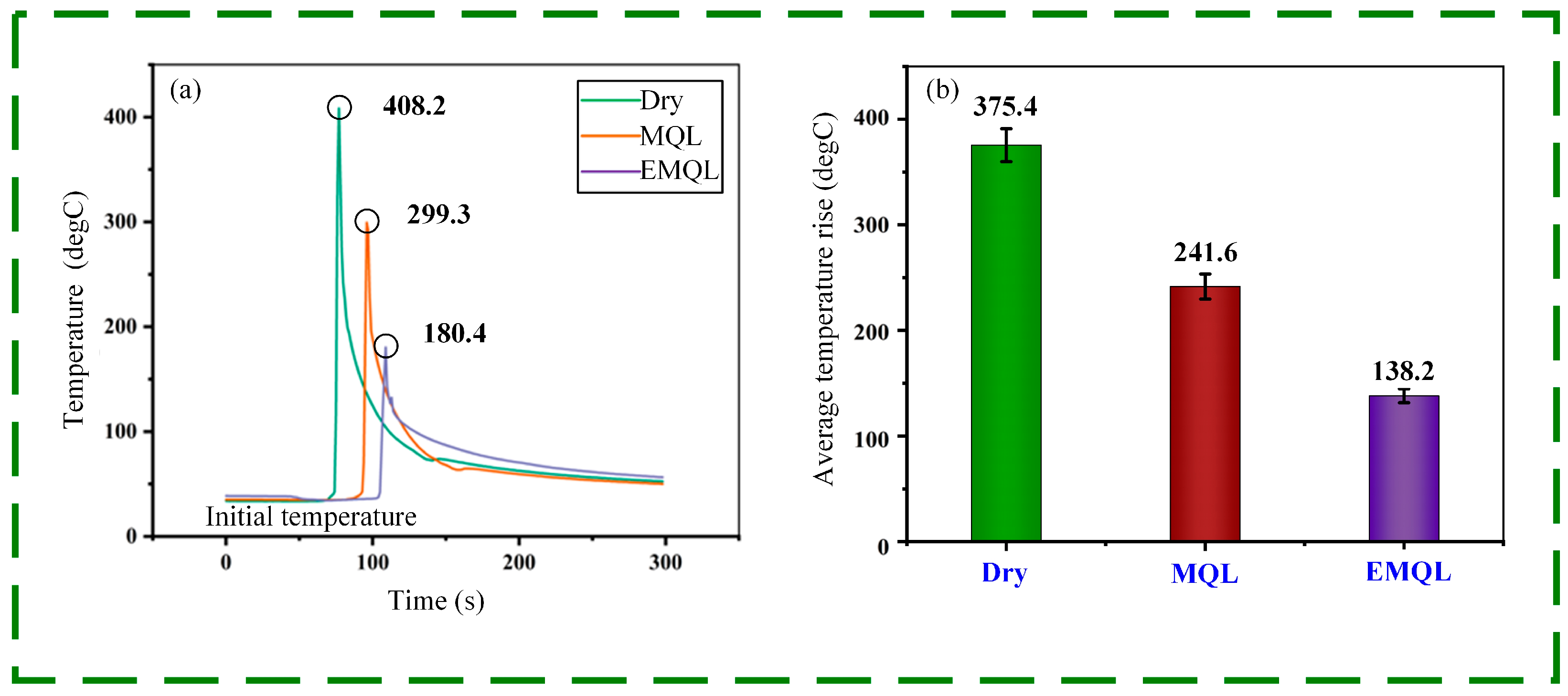
3.1. Grinding Temperature Analysis
3.2. Surface Quality Evaluation
4. Model of Electric Field-Enhanced Heat Transfer
4.1. Theoretical Model of Electric Field-Enhanced Heat Transfer
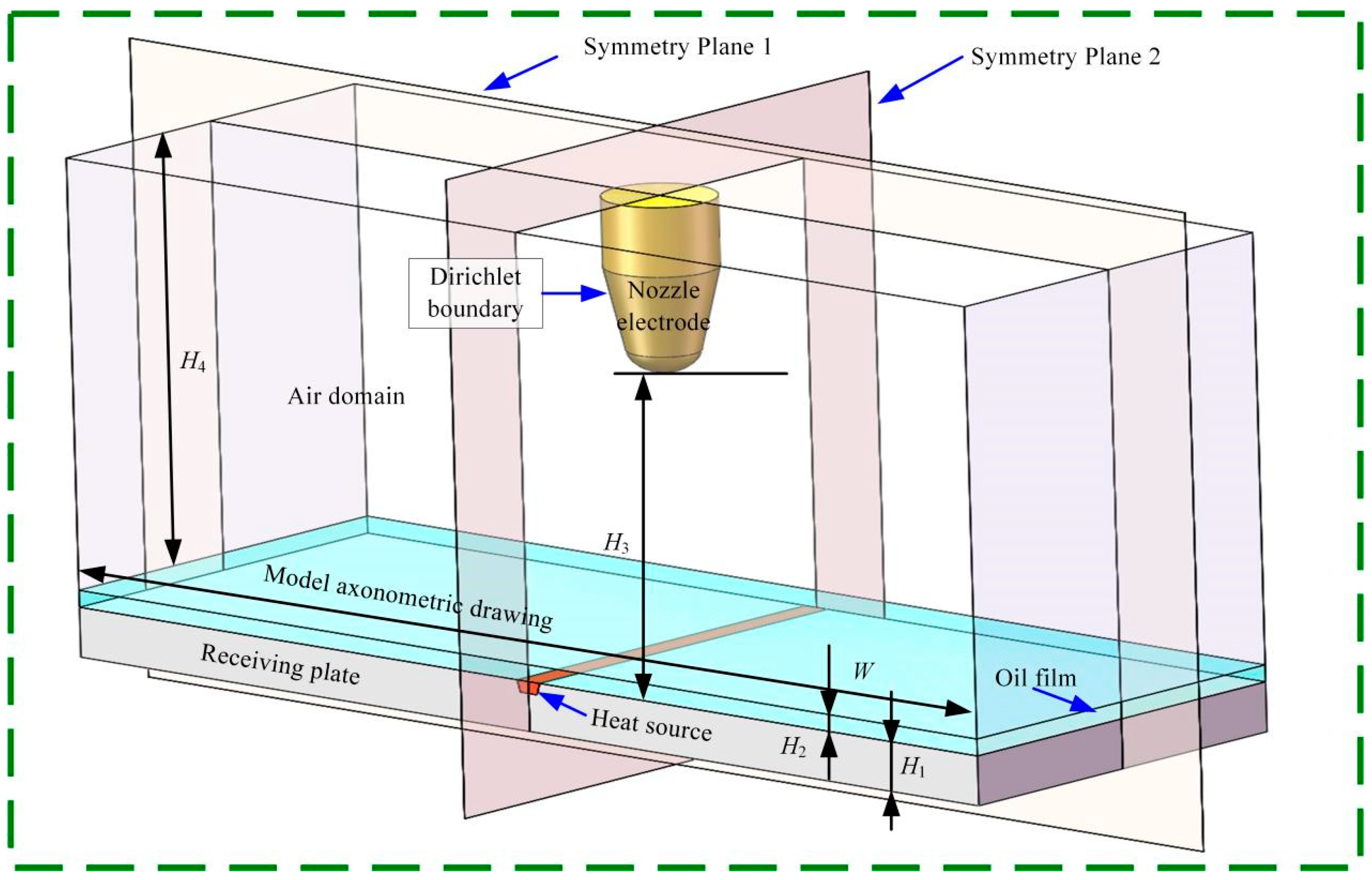
4.2. Geometric Model of Electric Field-Enhanced Heat Transfer
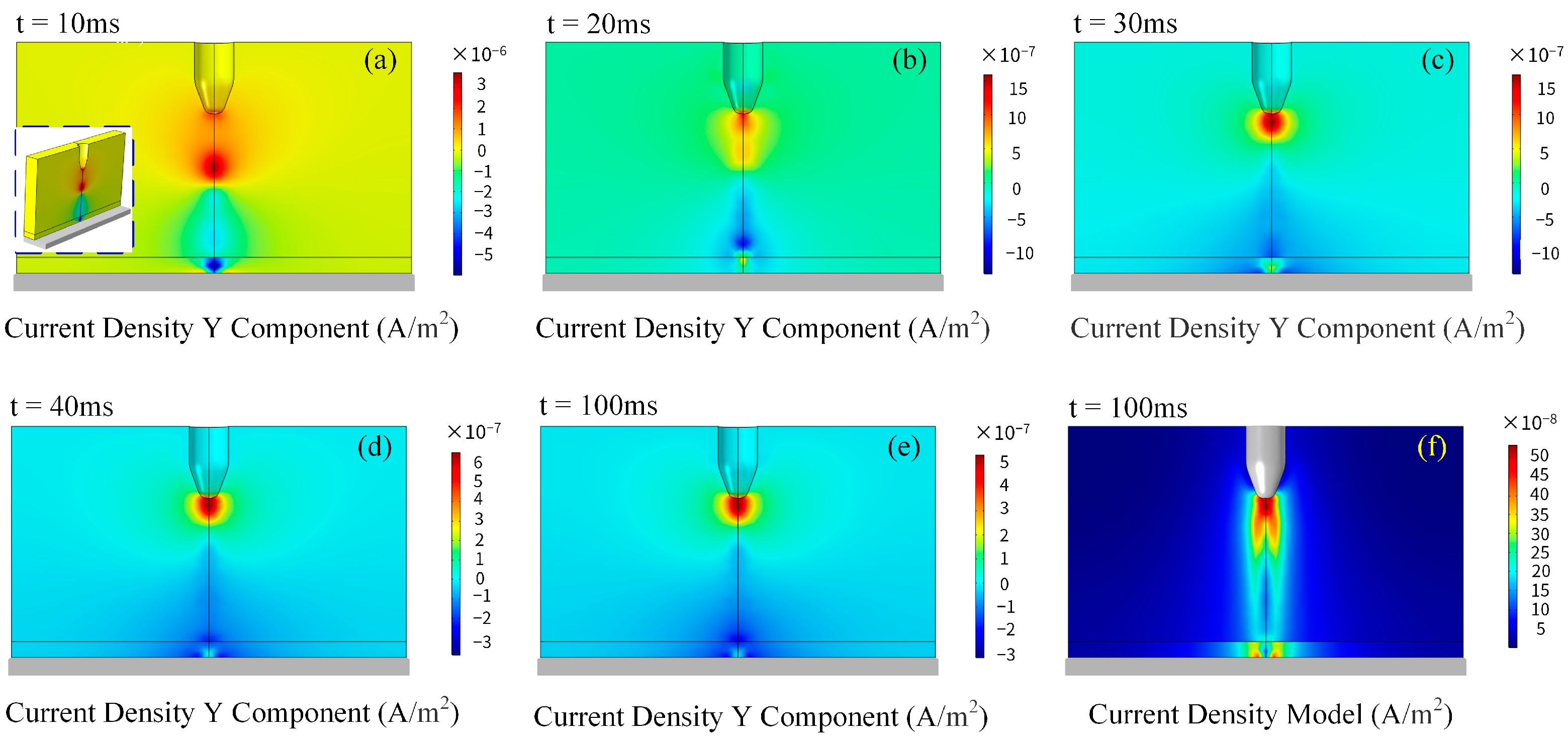
4.3. Current Density Distribution Characteristics Analysis
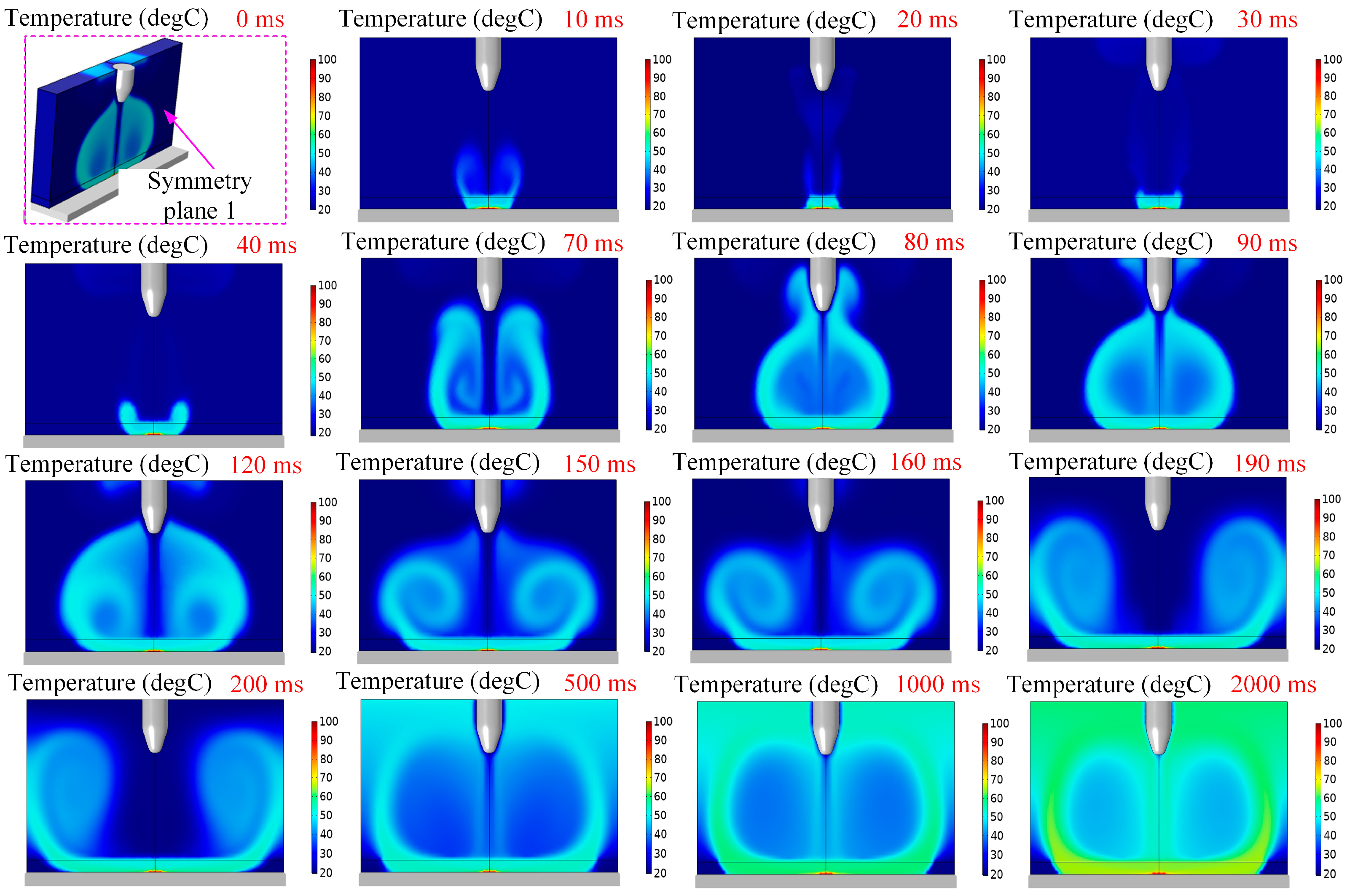
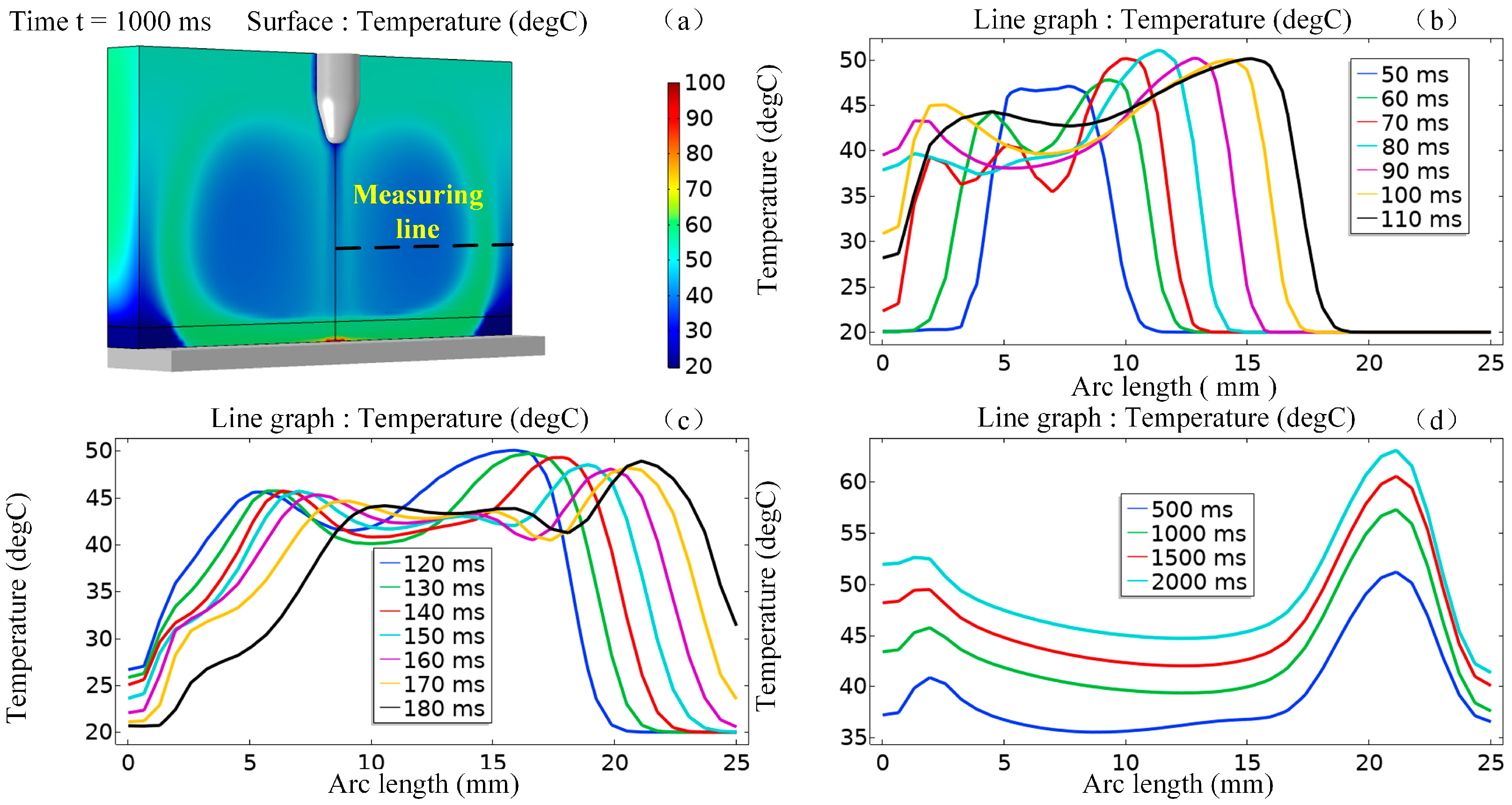
4.4. Study on Temperature Field of Electric Field-Enhanced Heat Transfer
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rao, B.; Dandekar, C.R.; Shin, Y.C. An experimental and numerical study on the face milling of Ti–6Al–4V alloy: Tool performance and surface integrity. J. Mater. Process Technol. 2011, 211, 294–304. [Google Scholar] [CrossRef]
- Cui, C.X.; Hu, B.M.; Zhao, L.C.; Liu, S.J. Titanium alloy production technology, market prospects and industry development. Mater. Des. 2011, 32, 1684–1691. [Google Scholar] [CrossRef]
- Veiga, C.; Davim, J.P.; Loureiro, A.J.R. Review on machinability of titanium alloys: The process perspective. Rev. Adv. Mater. Sci. 2013, 34, 148–164. [Google Scholar]
- Hong, S.Y.; Markus, I.; Jeong, W. New cooling approach and tool life improvement in cryogenic machining of titanium alloy Ti-6Al-4V. Int. J. Mach. Tools Manuf. 2001, 41, 2245–2260. [Google Scholar] [CrossRef]
- Jia, D.Z.; Li, C.H.; Zhang, Y.B.; Yang, M.; Cao, H.J.; Liu, B.; Zhou, Z.M. Grinding performance and surface morphology evaluation of titanium alloy using electric traction bio micro lubricant. Chin. J. Mech. Eng. 2022, 58, 198–211. [Google Scholar]
- Dvivedi, A.; Kumar, P. Surface quality evaluation in ultrasonic drilling through the Taguchi technique. Int. J. Adv. Manuf. Technol. 2007, 34, 131–140. [Google Scholar] [CrossRef]
- Dearnley, P.A.; Grearson, A.N. Evaluation of principal wear mechanisms of cemented carbides and ceramics used for machining titanium alloy IMI 318. Mater. Sci. Technol. 1986, 2, 47–58. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, C.F. State-of-the-art on minimum quantity lubrication in green machining. J. Clean. Prod. 2023, 429, 139613. [Google Scholar] [CrossRef]
- Irani, R.A.; Bauer, R.J.; Warkentin, A. A review of cutting fluid application in the grinding process. Int. J. Mach. Tools Manuf. 2005, 45, 1696–1705. [Google Scholar] [CrossRef]
- Gunter, K.L.; Sutherland, J.W. An experimental investigation into the effect of process conditions on the mass concentration of cutting fluid mist in turning. J. Clean. Prod. 1999, 7, 341–350. [Google Scholar] [CrossRef]
- Shokrani, A.; Dhokia, V.; Muñoz-Escalona, P.; Newman, S.T. State-of-the-art cryogenic machining and processing. Int. J. Comput. Integr. Manuf. 2013, 26, 616–648. [Google Scholar] [CrossRef]
- Gupta, K.; Laubscher, R.F. Sustainable machining of titanium alloys: A critical review. Proceedings of the Institution of Mechanical Engineers. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2017, 231, 2543–2560. [Google Scholar] [CrossRef]
- Kaynak, Y.; Gharibi, A. Progressive tool wear in cryogenic machining: The effect of liquid nitrogen and carbon dioxide. J. Manuf. Mater. Proc. 2018, 2, 31. [Google Scholar] [CrossRef]
- Dhananchezian, M.; Pradeep Kumar, M. Cryogenic Turning of the Ti–6Al–4V Alloy With Modified Cutting Tool Inserts. Cryogenics 2011, 51, 34–40. [Google Scholar] [CrossRef]
- Jebaraj, M.; Pradeep Kumar, M. Effect of cryogenic CO2 and LN2 coolants in milling of aluminum alloy. Mater. Manuf. Process. 2019, 34, 511–520. [Google Scholar] [CrossRef]
- Hong, S.Y.; Ding, Y. Cooling approaches and cutting temperatures in cryogenic machining of Ti-6Al-4V. Int. J. Mach. Tools Manuf. 2001, 41, 1417–1437. [Google Scholar] [CrossRef]
- Shakeel Ahmed, L.; Govindaraju, N.; Pradeep Kumar, M. Experimental investigations on Cryogenic cooling in the drilling of titanium alloy. Mater. Manuf. Process. 2016, 31, 602–607. [Google Scholar]
- Hong, S.Y.; Zhao, Z.B. Thermal aspects, material considerations and cooling strategies in cryogenic machining. Clean Prod. Process. 1999, 1, 107–116. [Google Scholar] [CrossRef]
- Wu, X.F.; Xu, W.H.; Ma, H.; Zhou, Z.M.; Liu, B.; Cui, X.; Li, C.H. Mechanism of Electrostatic Atomization and Surface Quality Evaluation of 7075 Aluminum Alloy under Electrostatic Minimum Quantity Lubrication Milling. Surf. Technol. 2023, 52, 337–350. [Google Scholar]
- Ramana, S.V.; Ramji, K.; Satyanarayana, B. Influence of nano-level variation of solid lubricant particle size in the machining of AISI 1040 steel. Int. J. Mater. Eng. Innov. 2011, 2, 16–29. [Google Scholar] [CrossRef]
- Sun, J.; Wong, Y.S.; Rahman, M.; Wang, Z.G.; Neo, K.S.; Tan, C.H.; Onozuka, H. Effects of coolant supply methods and cutting conditions on tool life in end milling titanium alloy. Mach. Sci. Technol. 2006, 10, 355–370. [Google Scholar] [CrossRef]
- Rahim, E.A.; Sasahara, H. Investigation of tool wear and surface integrity on MQL machining of Ti-6AL-4V using biodegradable oil. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2011, 225, 1505–1511. [Google Scholar] [CrossRef]
- Tascioglu, E.; Gharibi, A.; Kaynak, Y. High speed machining of near-beta titanium Ti-5553 alloy under various cooling and lubrication conditions. Int. J. Adv. Manuf. Technol. 2019, 102, 4257–4271. [Google Scholar] [CrossRef]
- He, T.; Liu, N.C.; Xia, H.Z.; Wu, L.; Zhang, Y.; Li, D.G.; Chen, Y. Progress and trend of minimum quantity lubrication (MQL): A comprehensive review. J. Clean. Prod. 2023, 386, 135809. [Google Scholar] [CrossRef]
- Huang, S.Q.; Lv, T.; Wang, M.H.; Xue, X.F. Enhanced machining performance and lubrication mechanism of electrostatic minimum quantity lubrication-EMQL milling process. Int. J. Adv. Manuf. Technol. 2018, 94, 655–666. [Google Scholar] [CrossRef]
- Lv, T.; Xu, X.F.; Yu, A.B.; Hu, X.D. Oil mist concentration and machining characteristics of SiO2 water-based nano-lubricants in electrostatic minimum quantity lubrication-EMQL milling. J. Mater. Process Technol. 2021, 290, 116964. [Google Scholar] [CrossRef]
- Xu, X.F.; Lv, T.; Luan, Z.Q.; Zhang, Y.Y.; Wang, M.H.; Hu, X.D. Capillary penetration mechanism and oil mist concentration of Al2O3 nanoparticle fluids in electrostatic minimum quantity lubrication (EMQL) milling. Int. J. Adv. Manuf. Technol. 2019, 104, 1937–1951. [Google Scholar] [CrossRef]
- Liu, N.C.; Zou, X.; Yuan, J.; Jiang, H.; Zhang, Y.; Chen, Y. Optimization of MQL turning process considering the distribution and control of cutting fluid mist particles. Int. J. Adv. Manuf. Tech. 2021, 116, 1233–1246. [Google Scholar] [CrossRef]
- Lv, T.; Huang, S.Q.; Hu, X.D.; Feng, B.H.; Xu, X. Study on Aerosol Characteristics of Electrostatic Minimum Quantity Lubrication and Its Turning Performance. Chin. J. Mech. Eng. 2019, 55, 129–138. [Google Scholar] [CrossRef]
- Yuan, S.M.; Zhu, G.Y.; Wang, L. Recent Progress on Lubricant Characteristics of Minimum Quantity Lubrication (MQL) Technology in Green Cutting. Chin. J. Mech. Eng. 2017, 53, 131–140. [Google Scholar]
- Huang, S.Q.; Wang, Z.; Yao, W.Q.; Xue, X.F. Tribological evaluation of contact-charged electrostatic spray lubrication as a new near-dry machining technique. Tribol. Int. 2015, 91, 74–84. [Google Scholar] [CrossRef]
- Bartolomeis, A.D.; Newman, S.T.; Shokrani, A. Initial. investigation on Surface Integrity when Machining Inconel 718 with Conventional and Electrostatic Lubrication. Procedia CIRP 2020, 87, 65–70. [Google Scholar] [CrossRef]
- Shah, P.; Gadkari, A.; Sharma, A.; Shokrani, A.; Khanna, N. Comparison of machining performance under MQL and ultra-high voltage EMQL conditions based on tribological properties. Tribol. Int. 2021, 153, 106595. [Google Scholar] [CrossRef]
- Huang, S.Q. A Study on Lubrication-Cooling Mechanisms and Machining Characteristics of Electrostatic Minimum Quantity Lubrication (EMQL). Ph.D. Thesis, College of Mechanical Engineering Zhejiang University of Technology, Hangzhou, China, June 2018. [Google Scholar]
- Gong, L. Investigation on The Lubricating Performance and Mechanism of Electrostatic Atomization Cutting Using Micro Oil-Based Nanofluids. Ph.D. Thesis, Jiangsu University of Science and Technology, Zhenjiang, China, June 2016. [Google Scholar]
- Lee, P.H.; Kim, J.W.; Lee, S.W. Experimental characterization on eco-friendly micro-grinding process of titanium alloy using air flow assisted electrospray lubrication with nanofluid. J. Clean. Prod. 2018, 201, 452–462. [Google Scholar] [CrossRef]
- Jia, D.Z.; Li, C.H.; Liu, J.H.; Zhang, Y.B.; Yang, M.; Gao, T.; Shubham Sharma, Z.S. Prediction model of volume average diameter and analysis of atomization characteristics in electrostatic atomization minimum quantity lubrication. Friction 2023, 11, 2107–2131. [Google Scholar] [CrossRef]
- Chen, D.D. Research on Cooling Performance and Mechanism of Micro-Waterbased Nanofluid Electrostatic Spray. Ph.D. Thesis, Jiangsu University of Science and Technology, Zhenjiang, China, June 2016. [Google Scholar]
- Ezugwu, E.O.; Wang, Z.M. Titanium alloys and their machinability—A review. J. Mater. Process Technol. 1997, 68, 262–274. [Google Scholar] [CrossRef]
- Sadeghi, M.H.; Haddad, M.J.; Tawakoli, T.; Emami, M. Minimal quantity lubrication-MQL in grinding of Ti–6Al–4V titanium alloy. Int. J. Adv. Manuf. Technol. 2009, 44, 487–500. [Google Scholar] [CrossRef]
- Gajrani, K.K. Assessment of cryo-MQL environment for machining of Ti-6Al-4V. J. Manuf. Process. 2020, 60, 494–502. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Li, C.H.; Yang, M.; Jia, D.Z.; Wang, Y.G.; Li, B.K.; Hou, Y.L.; Zhang, N.Q.; Wu, Q.D. Experimental evaluation of cooling performance by friction coefficient and specific friction energy in nanofluid minimum quantity lubrication grinding with different types of vegetable oil. J. Clean. Prod. 2016, 139, 685–705. [Google Scholar] [CrossRef]
- Guo, S.M.; Li, C.H.; Zhang, Y.B.; Wang, Y.G.; Li, B.K.; Yang, M.; Zhang, X.P.; Liu, G.T. Experimental evaluation of the lubrication performance of mixtures of castor oil with other vegetable oils in MQL grinding of nickel-based alloy. J. Clean. Prod. 2016, 140, 1060–1076. [Google Scholar] [CrossRef]


| Thermal Conductivity (W/m·K) | Specific Heat (J/kg·K) | Density (g/cm3) | Elastic Modulus (GPa) | Poisson Ratio | Yield Strength (MPa) | Tensile Strength (MPa) |
|---|---|---|---|---|---|---|
| 7.955 | 526.3 | 4.42 | 114 | 0.342 | 880 | 950 |
| C14:0 | C16:0 | C18:0 | C18:1 | C18:2 | C18:3 | C20:0 | C20:1 | SFA | MUFA | PUFA |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.06 | 10.30 | 3.78 | 22.30 | 50.84 | 5.90 | 0.29 | 0.36 | 14.92 | 22.87 | 57.83 |
| Lubrication Conditions | Lubrication Parameters |
|---|---|
| Dry cutting | - |
| MQL | Liquid flow rate: 60 mL/h; Pressure: 0.3 MPa; Nozzle angle: 15°; Jet distance: 30 mm |
| EMQL | Liquid flow rate: 60 mL/h; Pressure: 0.3 MPa; Nozzle angle: 15°; Jet distance: 30 mm; Voltage: 30 kV |
| Grinding Parameter | Values |
|---|---|
| Grinding wheel speed vs. (m/s) | 30 |
| Feed rate VW (m/min) | 3.5 |
| Grinding depth ap (μm) | 10 |
| Cutting mode | Rectangular path plane grinding |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z.; Jia, D.; Zhang, Y.; Qu, D.; Lv, Z.; Zeng, E. Investigation into the Heat Transfer Behavior of Electrostatic Atomization Minimum Quantity Lubrication (EMQL) during Grinding. Lubricants 2024, 12, 158. https://doi.org/10.3390/lubricants12050158
He Z, Jia D, Zhang Y, Qu D, Lv Z, Zeng E. Investigation into the Heat Transfer Behavior of Electrostatic Atomization Minimum Quantity Lubrication (EMQL) during Grinding. Lubricants. 2024; 12(5):158. https://doi.org/10.3390/lubricants12050158
Chicago/Turabian StyleHe, Zhiyong, Dongzhou Jia, Yanbin Zhang, Da Qu, Zhenlin Lv, and Erjun Zeng. 2024. "Investigation into the Heat Transfer Behavior of Electrostatic Atomization Minimum Quantity Lubrication (EMQL) during Grinding" Lubricants 12, no. 5: 158. https://doi.org/10.3390/lubricants12050158
APA StyleHe, Z., Jia, D., Zhang, Y., Qu, D., Lv, Z., & Zeng, E. (2024). Investigation into the Heat Transfer Behavior of Electrostatic Atomization Minimum Quantity Lubrication (EMQL) during Grinding. Lubricants, 12(5), 158. https://doi.org/10.3390/lubricants12050158






