Calculation and Validation of Planet Gear Sliding Bearings for a Three-Stage Wind Turbine Gearbox
Abstract
1. Introduction
2. Materials and Methods
2.1. Hydrodynamic Bearing Model
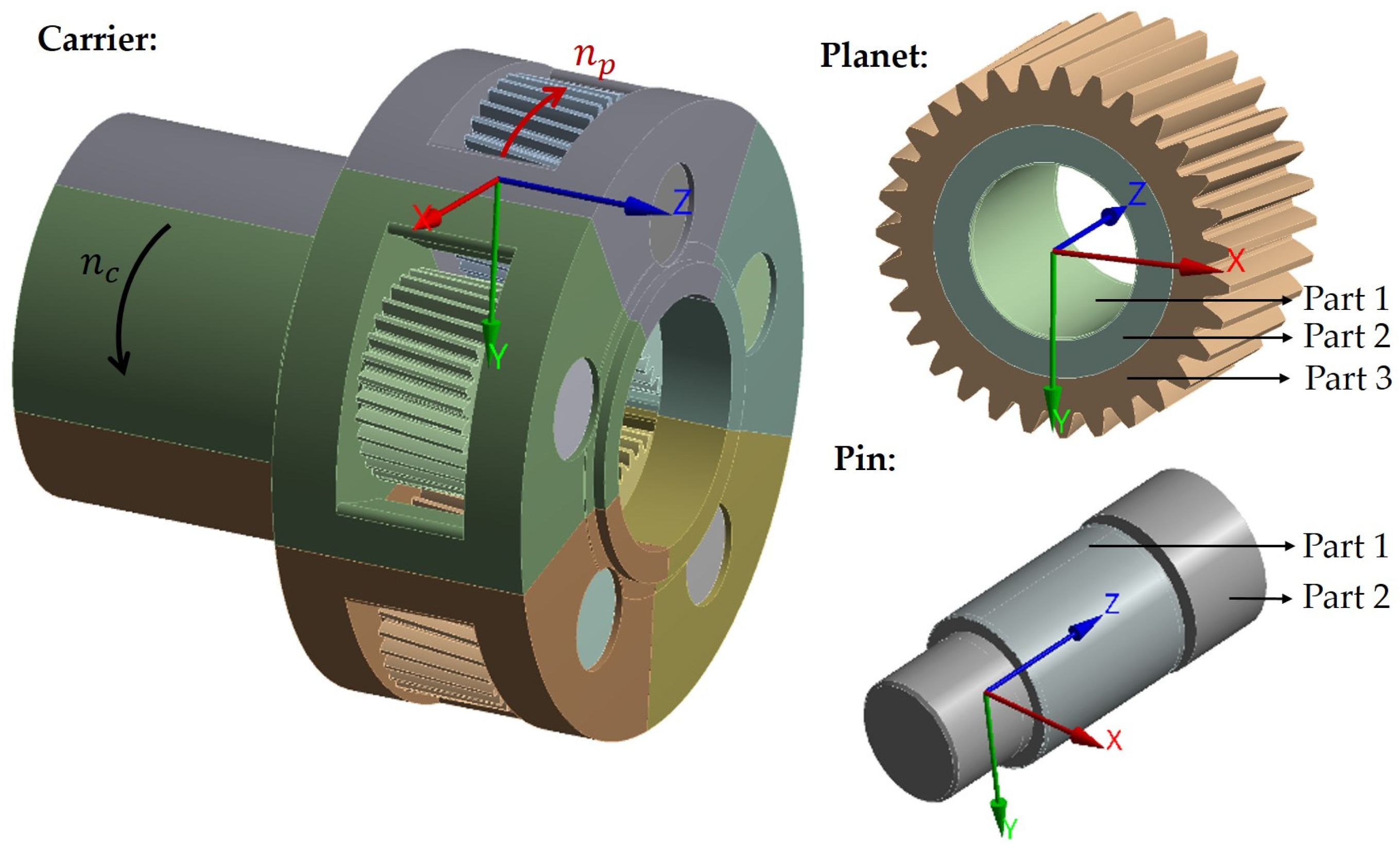
2.2. Method for Calculation of Planet and Pin Deformation
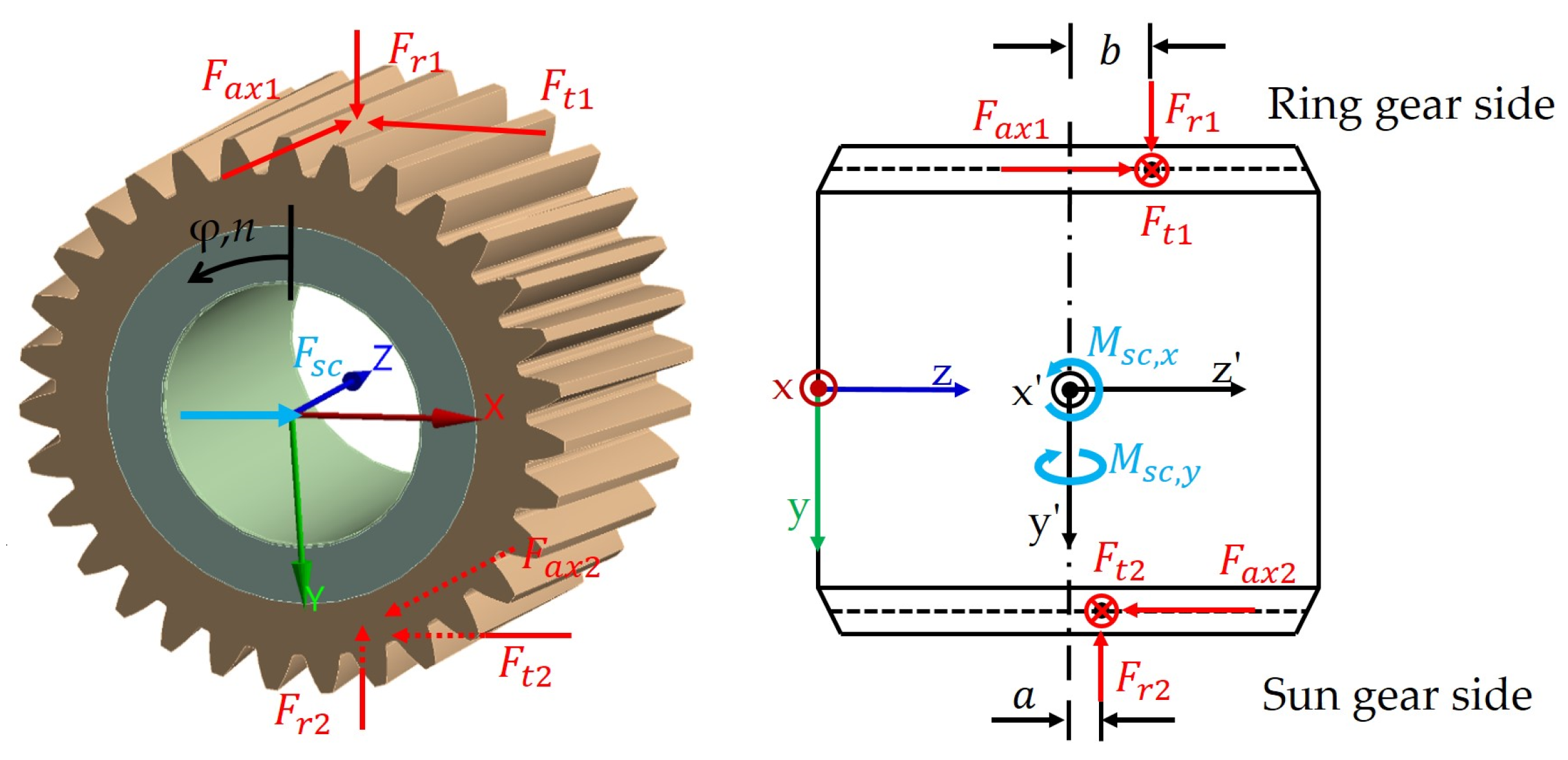
2.3. Investigated Planet Gear Sliding Bearing
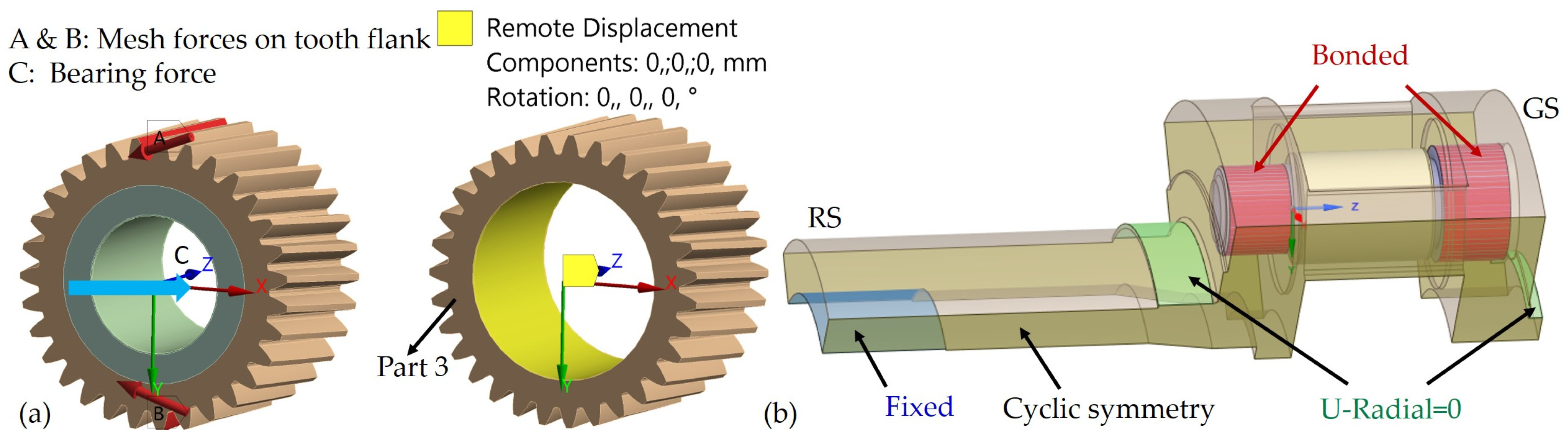
2.4. FEM Model for Structure Analysis: Material, Boundary Condition and Mesh Load
3. Results
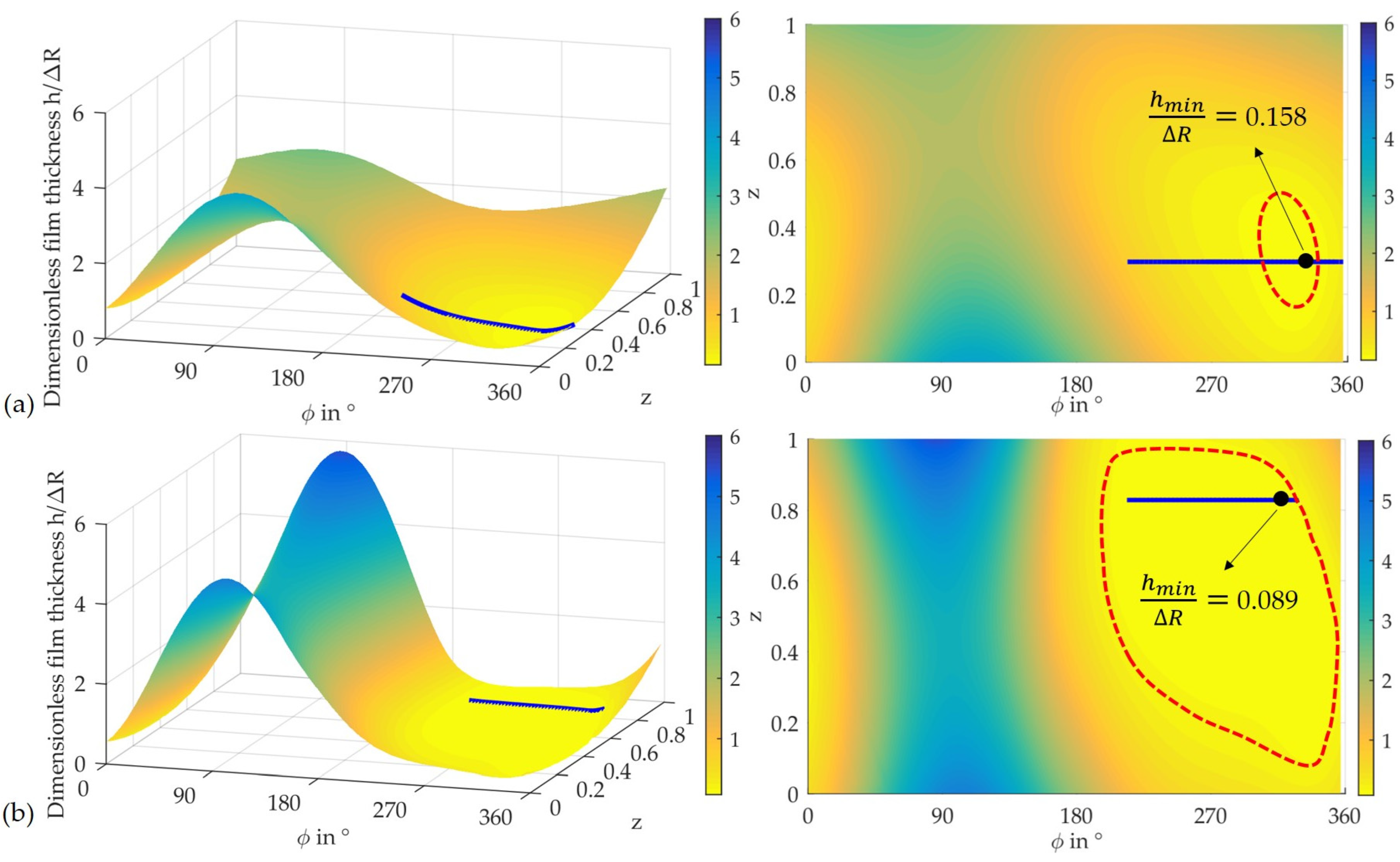
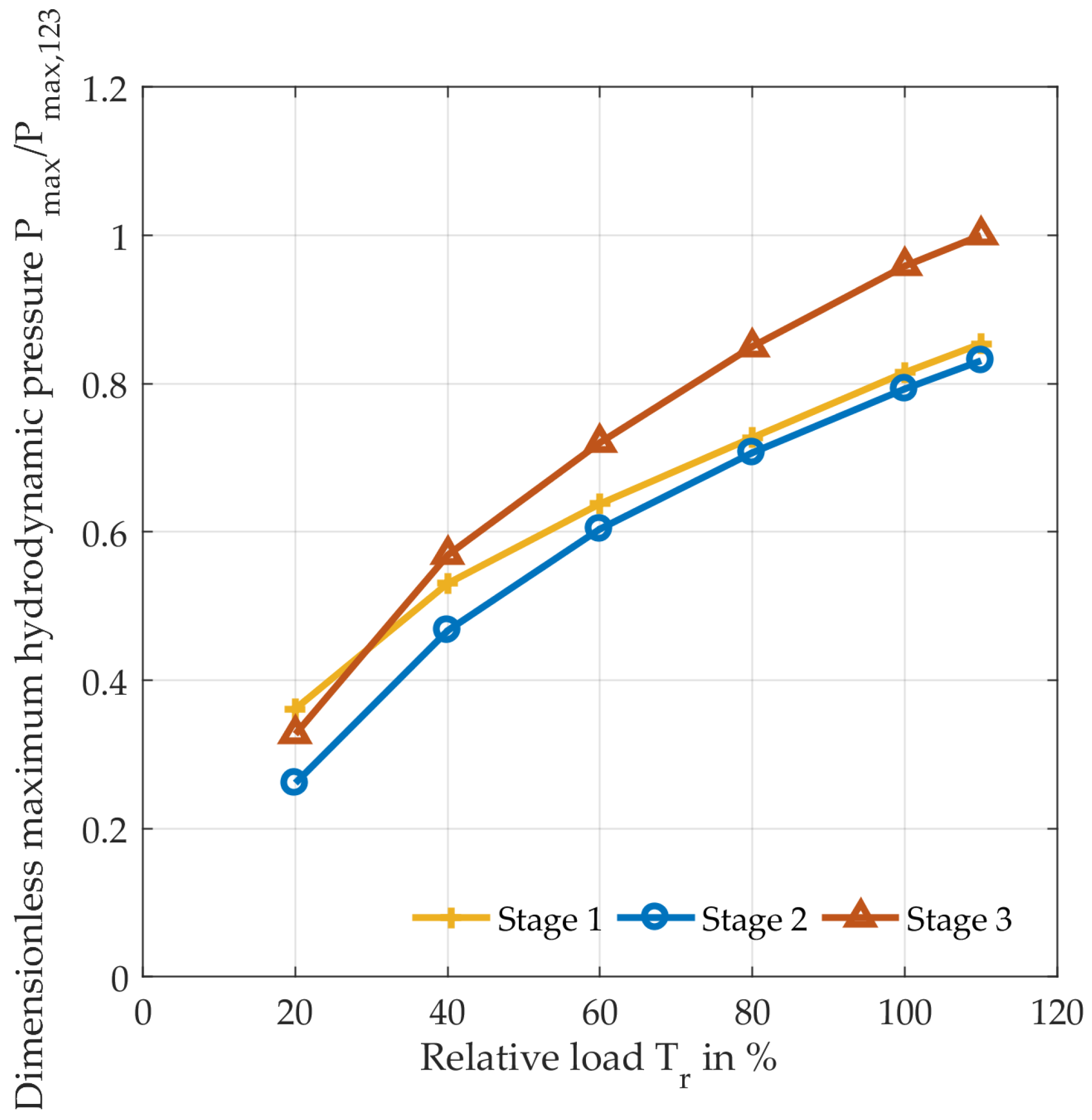
3.1. Predicted Film Thickness and Structure Deformation
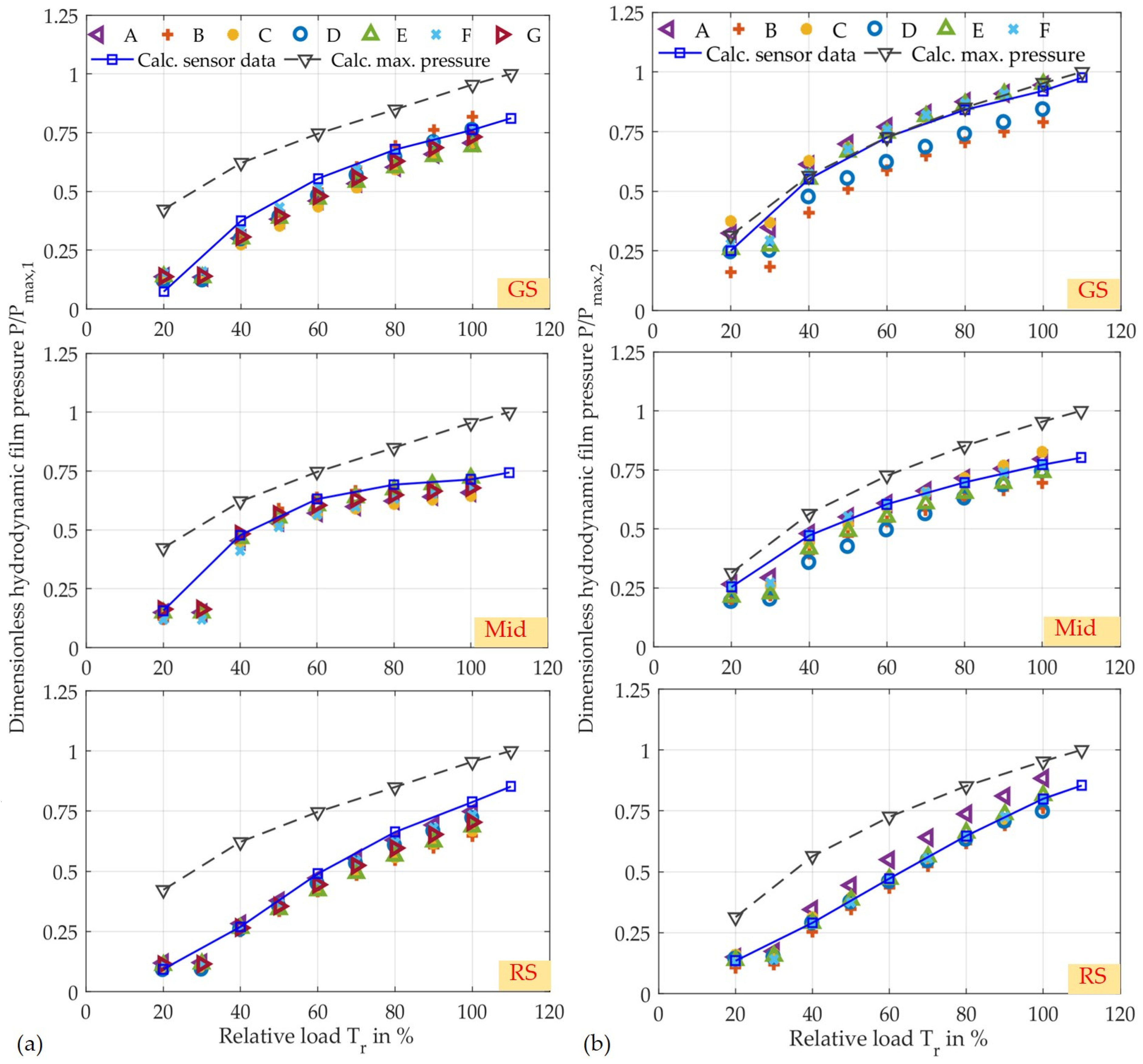
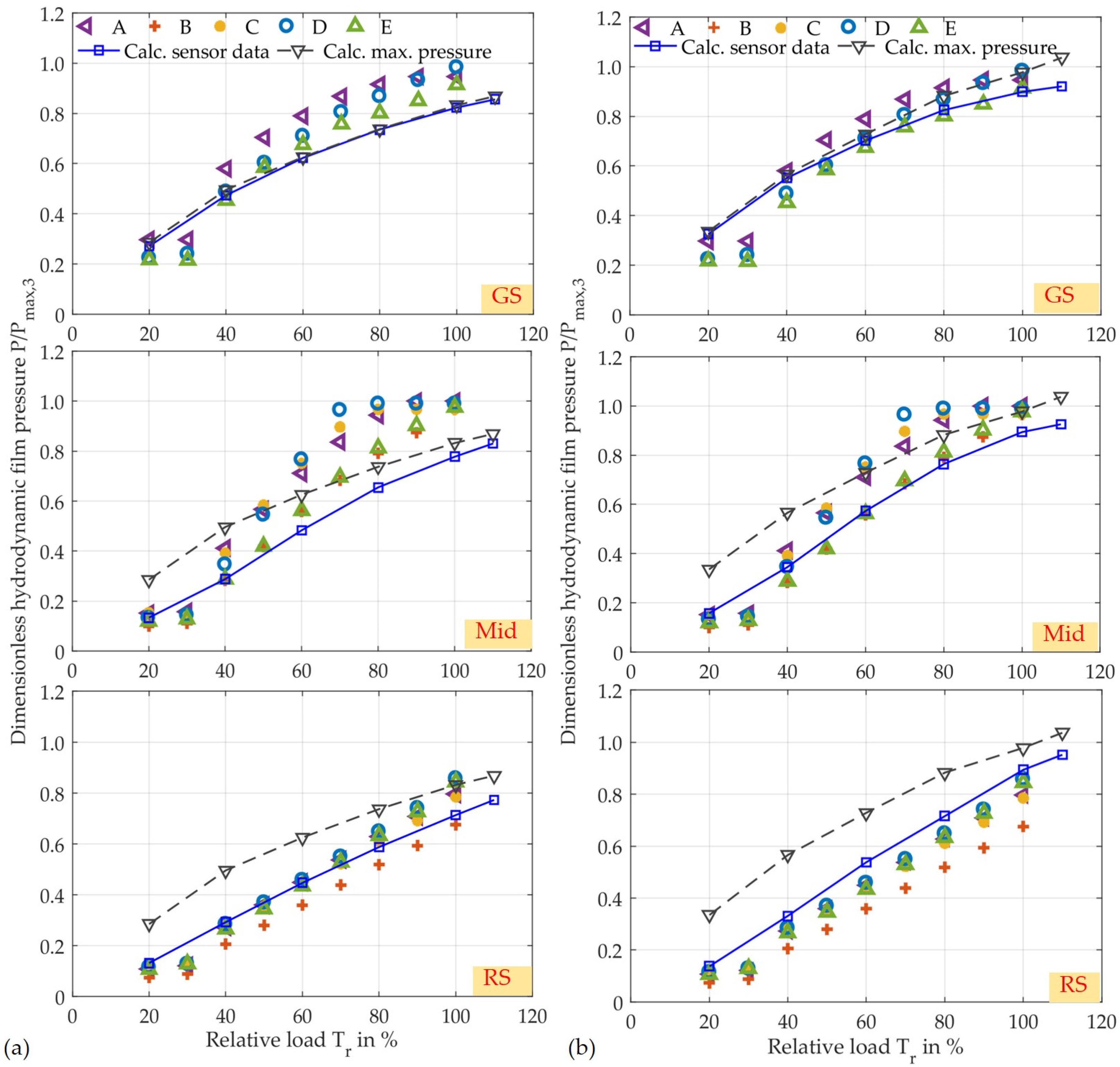
3.2. Validation of Pressure Distribution
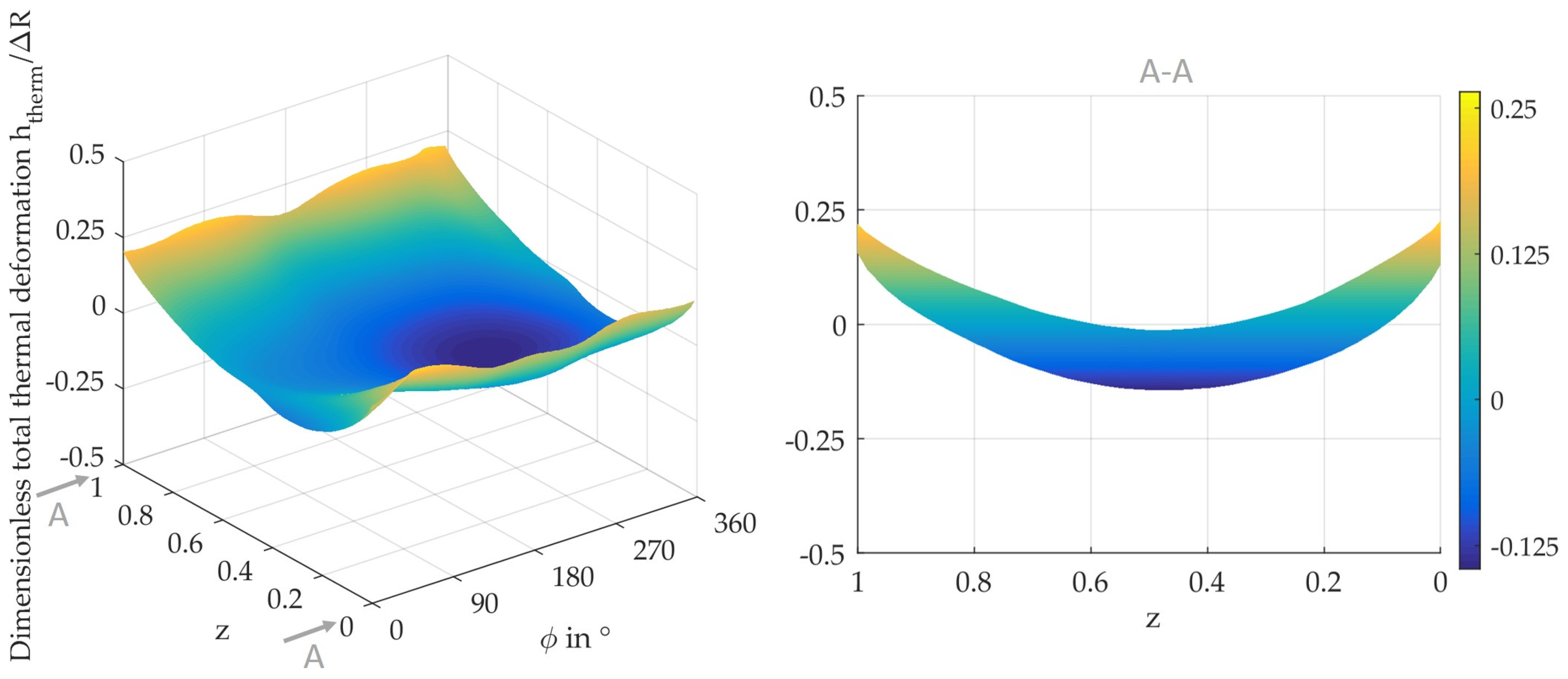
3.3. Extended Thermal Deformation Analysis for the Third Stage
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Grid Convergence Study
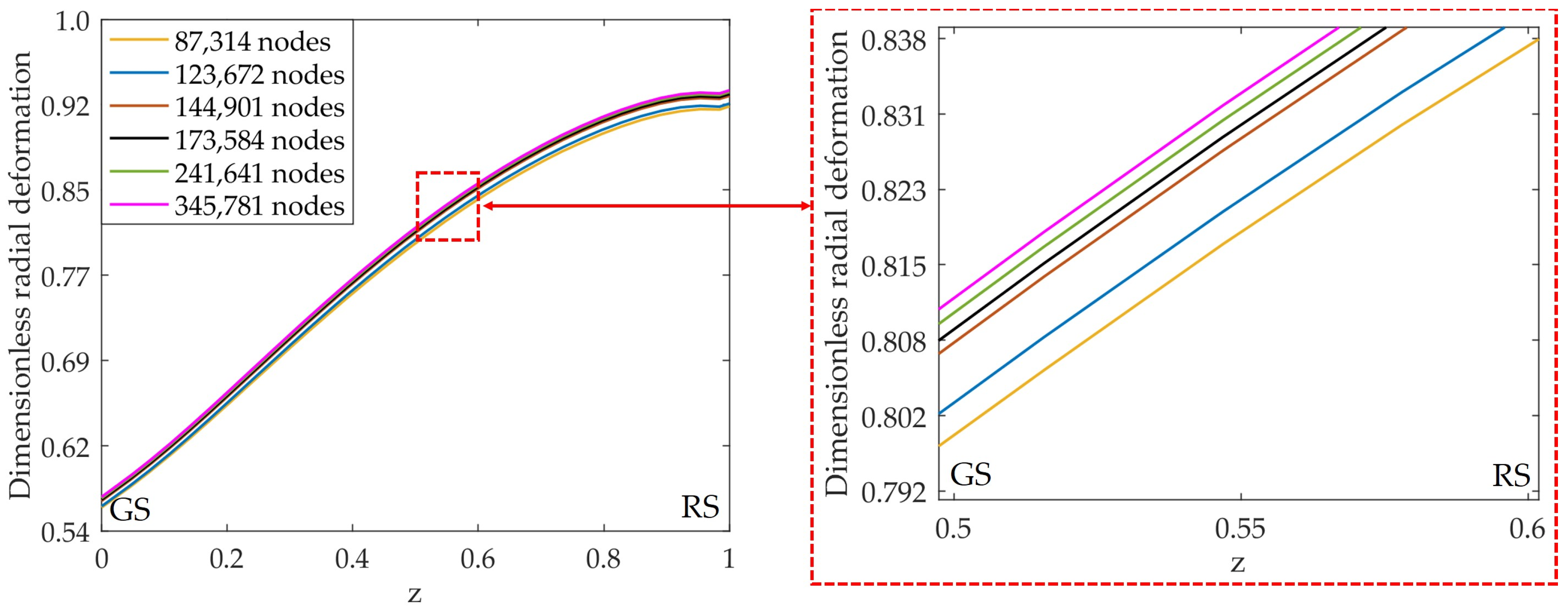
| Nodes Number | Radial Deformation, - | Deviation, % |
|---|---|---|
| 345,781 | 0.8329 | - |
| 241,641 | 0.8314 | 0.18 |
| 173,584 | 0.8297 | 0.39 |
| 144,901 | 0.8283 | 0.55 |
| 123,672 | 0.8220 | 1.30 |
| 87,314 | 0.8187 | 1.70 |
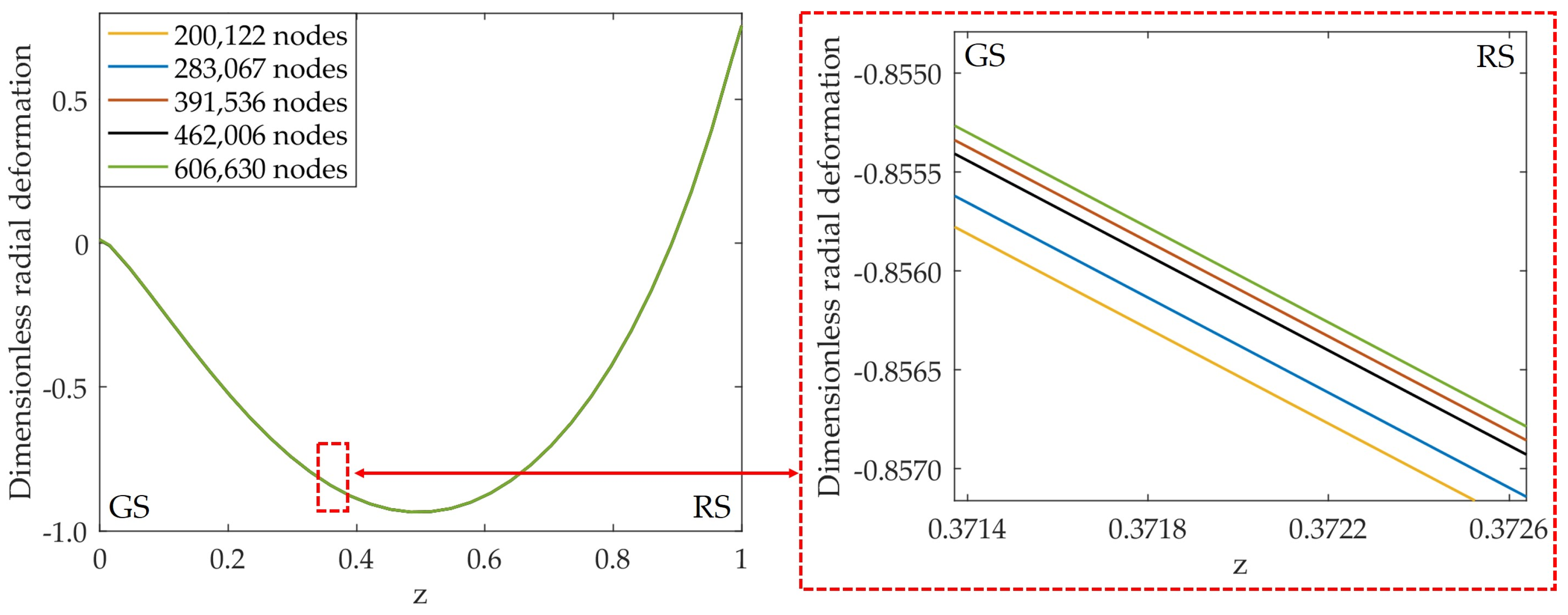
| Nodes Number | Radial Deformation, - | Deviation, % |
|---|---|---|
| 606,630 | −0.8558 | - |
| 462,006 | −0.8559 | 0.02 |
| 391,536 | −0.8559 | 0.01 |
| 283,067 | −0.8561 | 0.04 |
| 200,122 | −0.8563 | 0.06 |
References
- Díaz, H.; Guedes Soares, C. Review of the Current Status, Technology and Future Trends of Offshore Wind Farms. Ocean Eng. 2020, 209, 107381. [Google Scholar] [CrossRef]
- Offshore Wind Turbine SG 14-222 DD|Siemens Gamesa. Available online: https://www.siemensgamesa.com/products-and-services/offshore/wind-turbine-sg-14-222-dd (accessed on 13 February 2024).
- Hagemann, T.; Ding, H.; Radtke, E.; Schwarze, H. Operating Behavior of Sliding Planet Gear Bearings for Wind Turbine Gearbox Applications—Part I: Basic Relations. Lubricants 2021, 9, 97. [Google Scholar] [CrossRef]
- Muzakkir, S.M.; Hirani, H.; Thakre, G.D. Lubricant for Heavily Loaded Slow-Speed Journal Bearing. Tribol. Trans. 2013, 56, 1060–1068. [Google Scholar] [CrossRef]
- Xiang, G.; Han, Y.; Wang, J.; Wang, J.; Ni, X. Coupling Transient Mixed Lubrication and Wear for Journal Bearing Modeling. Tribol. Int. 2019, 138, 1–15. [Google Scholar] [CrossRef]
- Lehmann, B.; Trompetter, P.; Guzmán, F.G.; Jacobs, G. Evaluation of Wear Models for the Wear Calculation of Journal Bearings for Planetary Gears in Wind Turbines. Lubricants 2023, 11, 364. [Google Scholar] [CrossRef]
- Lucassen, M.; Decker, T.; Gutierrez Guzman, F.; Lehmann, B.; Bosse, D.; Jacobs, G. Simulation Methodology for the Identification of Critical Operating Conditions of Planetary Journal Bearings in Wind Turbines. Forsch. Im Ingenieurwesen 2023, 87, 147–157. [Google Scholar] [CrossRef]
- Prölß, M. Berechnung langsam laufender und hoch belasteter Gleitlager in Planetengetrieben unter Mischreibung. Verschleiß Und Deform. 2020. [Google Scholar] [CrossRef]
- Hagemann, T.; Ding, H.; Radtke, E.; Schwarze, H. Operating Behavior of Sliding Planet Gear Bearings for Wind Turbine Gearbox Applications—Part II: Impact of Structure Deformation. Lubricants 2021, 9, 98. [Google Scholar] [CrossRef]
- Dong, P.; Lai, J.; Guo, W.; Tenberge, P.; Xu, X.; Liu, Y.; Wang, S. An Analytical Approach for Calculating Thin-Walled Planet Bearing Load Distribution. Int. J. Mech. Sci. 2023, 242, 108019. [Google Scholar] [CrossRef]
- Jones, A.B.; Harris, T.A. Analysis of a Rolling-Element Idler Gear Bearing Having a Deformable Outer-Race Structure. J. Basic Eng. 1963, 85, 273–278. [Google Scholar] [CrossRef]
- Fingerle, A.; Hochrein, J.; Otto, M.; Stahl, K. Theoretical Study on the Influence of Planet Gear Rim Thickness and Bearing Clearance on Calculated Bearing Life. J. Mech. Des. 2019, 142. [Google Scholar] [CrossRef]
- Hagemann, T.; Kukla, S.; Schwarze, H. Measurement and Prediction of the Static Operating Conditions of a Large Turbine Tilting-Pad Bearing Under High Circumferential Speeds and Heavy Loads. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013. [Google Scholar] [CrossRef]
- Linjamaa, A.; Lehtovaara, A.; Larsson, R.; Kallio, M.; Söchting, S. Modelling and Analysis of Elastic and Thermal Deformations of a Hybrid Journal Bearing. Tribol. Int. 2018, 118, 451–457. [Google Scholar] [CrossRef]
- Zhang, K.; Chen, Q.; Zhang, Y.; Zhu, J.; Wang, M.; Feng, K. Numerical and Experimental Investigations on Thermoelastic Hydrodynamic Performance of Planetary Gear Sliding Bearings in Wind Turbine Gearboxes. Tribol. Int. 2024, 191, 109081. [Google Scholar] [CrossRef]
- Gong, J.; Liu, K.; Zheng, Y.; Meng, F. Thermal-Elastohydrodynamic Lubrication Study of Misaligned Journal Bearing in Wind Turbine Gearbox. Tribol. Int. 2023, 188, 108887. [Google Scholar] [CrossRef]
- Goris, S.; Ooms, M.; Goovaerts, M.; Krieckemans, K.; Bogaert, R. Plain Bearings for Wind Turbine Gearboxes-Trajectory towards Technology Readiness. In Proceedings of the Conference for Wind Power Drives 2017: Tagungsband zur Konferenz, Aachen, Germany, 7–8 March 2017; p. 327. [Google Scholar]
- Meyer, T. Validation of Journal Bearings for Use in Wind Turbine Gearboxes|Wind Systems Magazine. Available online: https://www.windsystemsmag.com/validation-of-journal-bearings-for-use-in-wind-turbine-gearboxes/ (accessed on 31 January 2024).
- Elrod, H.G. A Cavitation Algorithm. J. Lubr. Technol. 1981, 103, 350–354. [Google Scholar] [CrossRef]
- Guyan, R.J. Reduction of Stiffness and Mass Matrices. AIAA J. 1965, 3, 380. [Google Scholar] [CrossRef]




| Parameter | Stage 1 | Stage 2 | Stage 3 |
|---|---|---|---|
| Bearing width/diameter, - | 1.5 | 1.2 | 0.83 |
| Nominal rotational speed, rpm | 30 | 85 | 271 |
| Nominal specific bearing load, MPa | 13.5 | 12.7 | 10.4 |
| Lubricant | ISO VG 320 | ||
| Lubricant density kg/m3 | 853 @ 40 °C | ||
| Lubricant specific heat capacity kJ/(kg·K) | 2.0 @ 20 °C | ||
| Lubricant thermal conductivity, W/(m·K) | 0.13 | ||
| Parameter | Planet | Pin | Carrier |
|---|---|---|---|
| Young’s Modulus, MPa | 210,000 | 210,000 | 176,000 |
| Poisson’s Ratio, - | 0.3 | 0.3 | 0.275 |
| Stage 1 | Stage 2 | Stage 3 | ||||
|---|---|---|---|---|---|---|
| Offset a | Offset b | Offset a | Offset b | Offset a | Offset b | |
| 20% | 0.38 | 0.19 | 0.13 | 0.14 | 0.021 | 0.35 |
| 60% | 0.18 | −0.09 | 0.09 | −0.04 | 0.031 | 0.12 |
| 100% | 0 | −0.22 | 0.03 | −0.11 | 0.021 | 0.021 |
| Stage 1 | Stage 2 | Stage 3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| GS | Mid | RS | GS | Mid | RS | GS | Mid | RS | |
| Avg. exp. , - | 1.13 | 1.1 | 1.13 | 1.34 | 1.37 | 1.42 | 1.67 | 1.74 | 1.76 |
| Calc. , - | 1.18 | 1.17 | 1.15 | 1.4 | 1.38 | 1.36 | 1.64 | 1.69 | 1.65 |
| Deviation , % | 4.4 | 6.2 | 1.8 | 4.6 | 0.6 | 3.7 | 1.4 | 3.0 | 6.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, H.; Mermertas, Ü.; Hagemann, T.; Schwarze, H. Calculation and Validation of Planet Gear Sliding Bearings for a Three-Stage Wind Turbine Gearbox. Lubricants 2024, 12, 95. https://doi.org/10.3390/lubricants12030095
Ding H, Mermertas Ü, Hagemann T, Schwarze H. Calculation and Validation of Planet Gear Sliding Bearings for a Three-Stage Wind Turbine Gearbox. Lubricants. 2024; 12(3):95. https://doi.org/10.3390/lubricants12030095
Chicago/Turabian StyleDing, Huanhuan, Ümit Mermertas, Thomas Hagemann, and Hubert Schwarze. 2024. "Calculation and Validation of Planet Gear Sliding Bearings for a Three-Stage Wind Turbine Gearbox" Lubricants 12, no. 3: 95. https://doi.org/10.3390/lubricants12030095
APA StyleDing, H., Mermertas, Ü., Hagemann, T., & Schwarze, H. (2024). Calculation and Validation of Planet Gear Sliding Bearings for a Three-Stage Wind Turbine Gearbox. Lubricants, 12(3), 95. https://doi.org/10.3390/lubricants12030095







