Transient Simulation Analysis of Needle Roller Bearing in Oil Jet Lubrication and Planetary Gearbox Lubrication Conditions Based on Computational Fluid Dynamics
Abstract
1. Introduction
2. Materials and Methods
2.1. CFD Numerical Calculation Model
2.1.1. Governing Equations
2.1.2. SST k-ω Turbulence Model
2.1.3. Multiphase Model
2.1.4. Dynamic Mesh Model
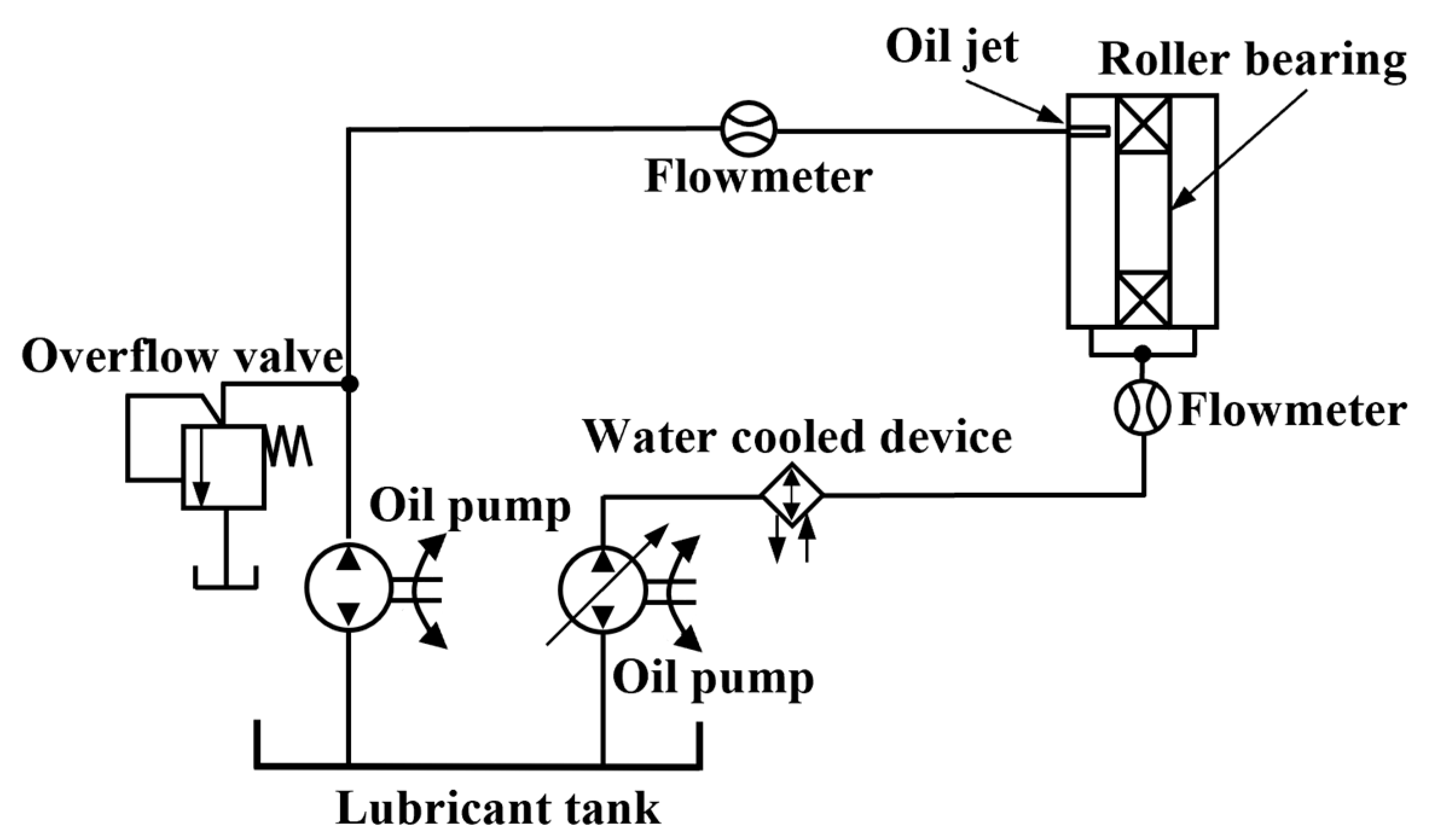
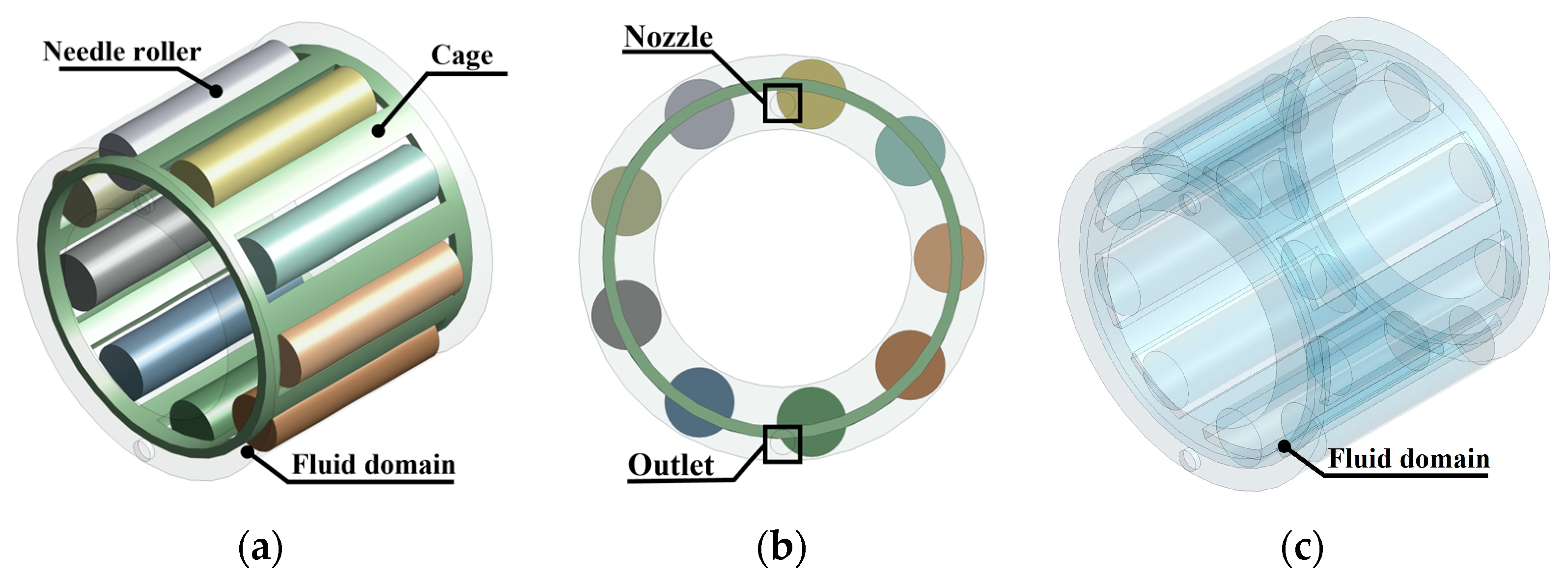
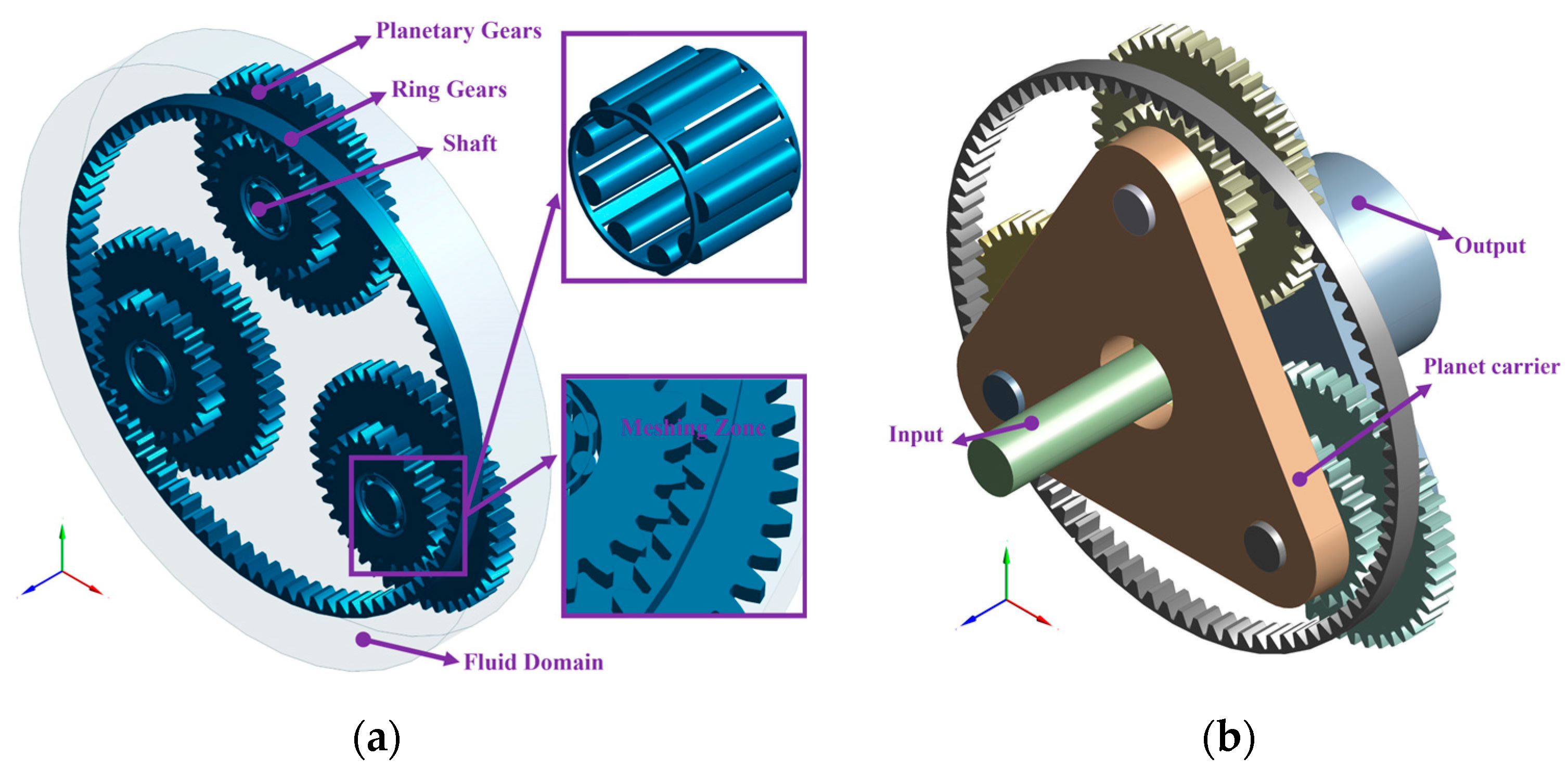
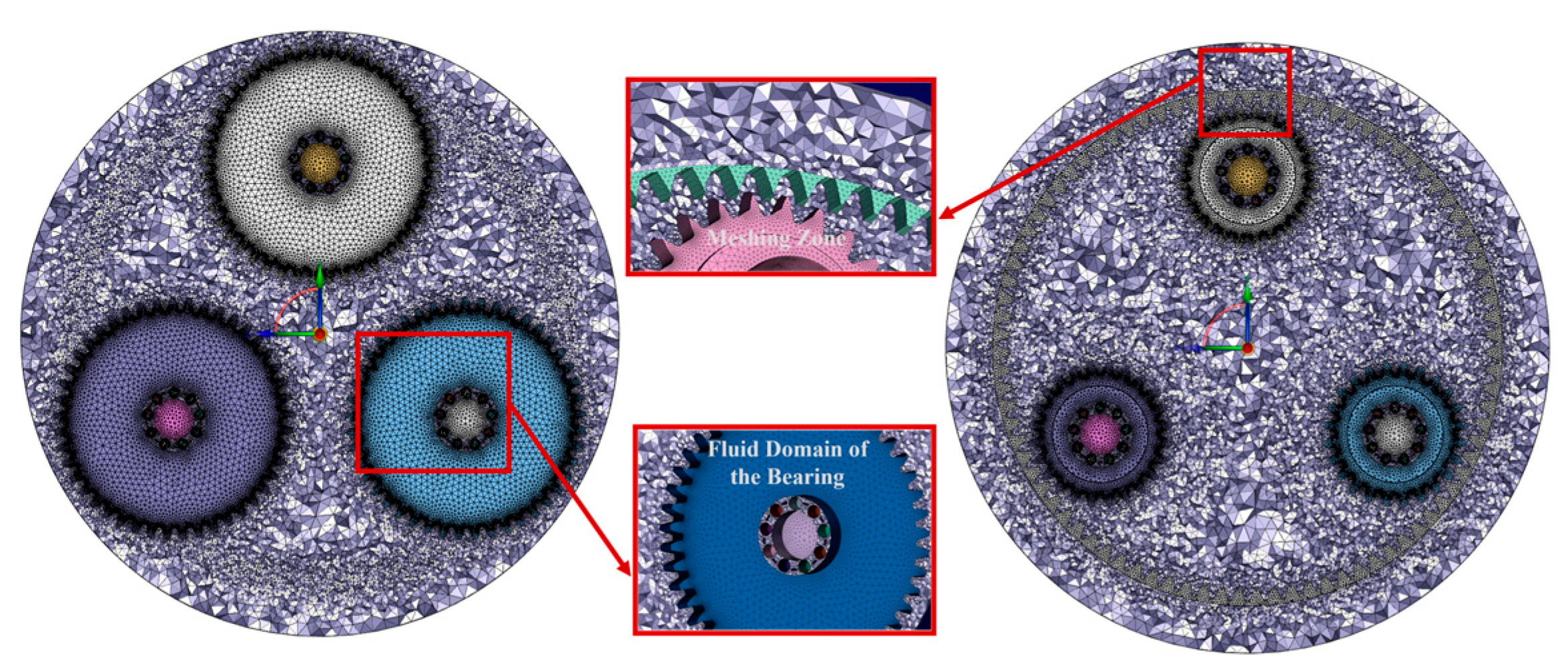
2.2. Computational Domains and Meshing
2.2.1. Computational Domains
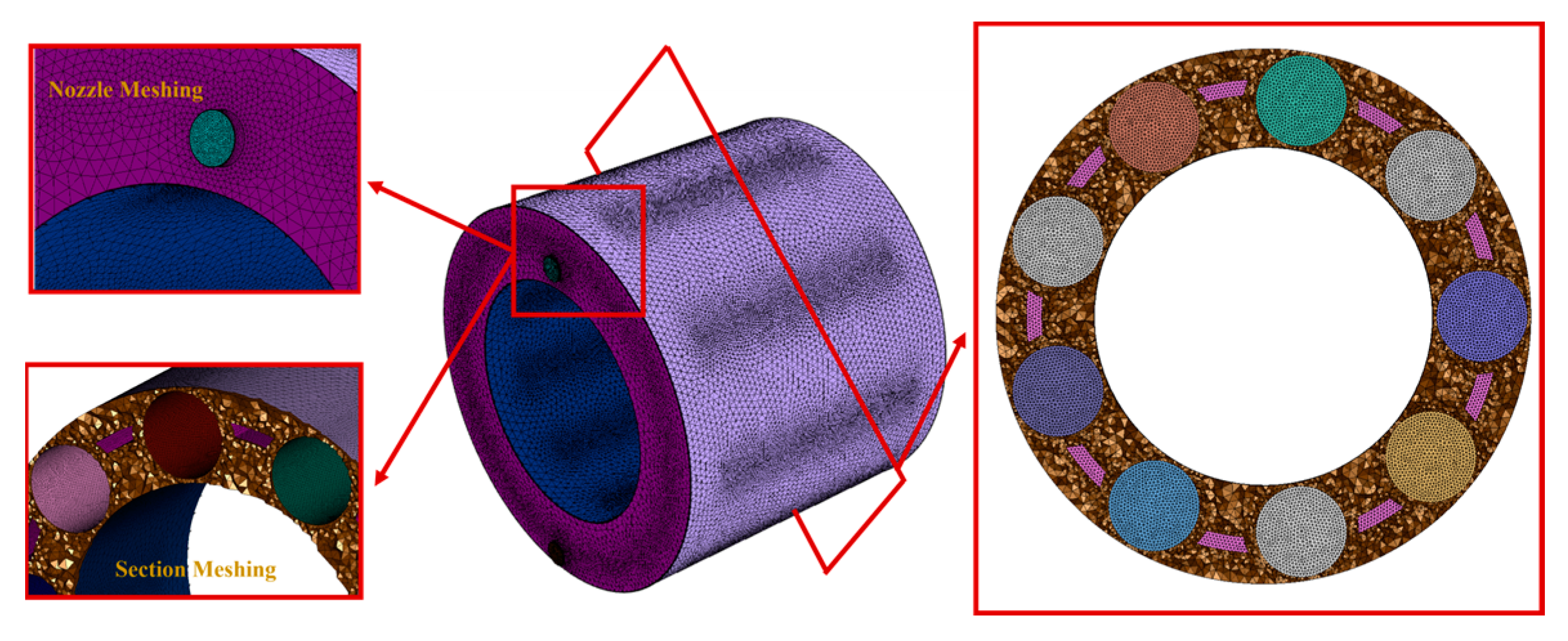
2.2.2. Meshing of Computational Domains
2.2.3. Boundary Conditions and Simulation Parameter Settings
3. Results and Discussion
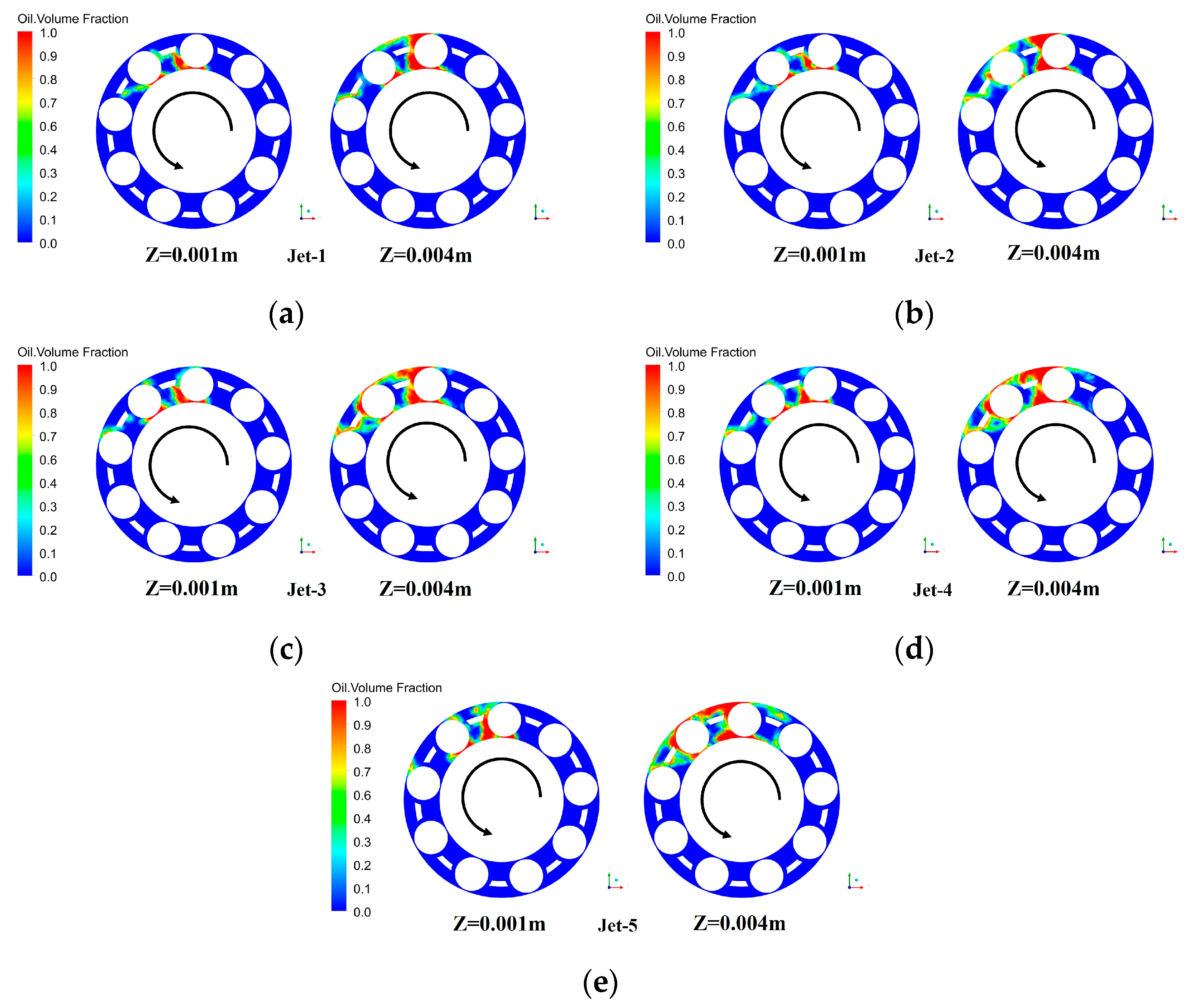
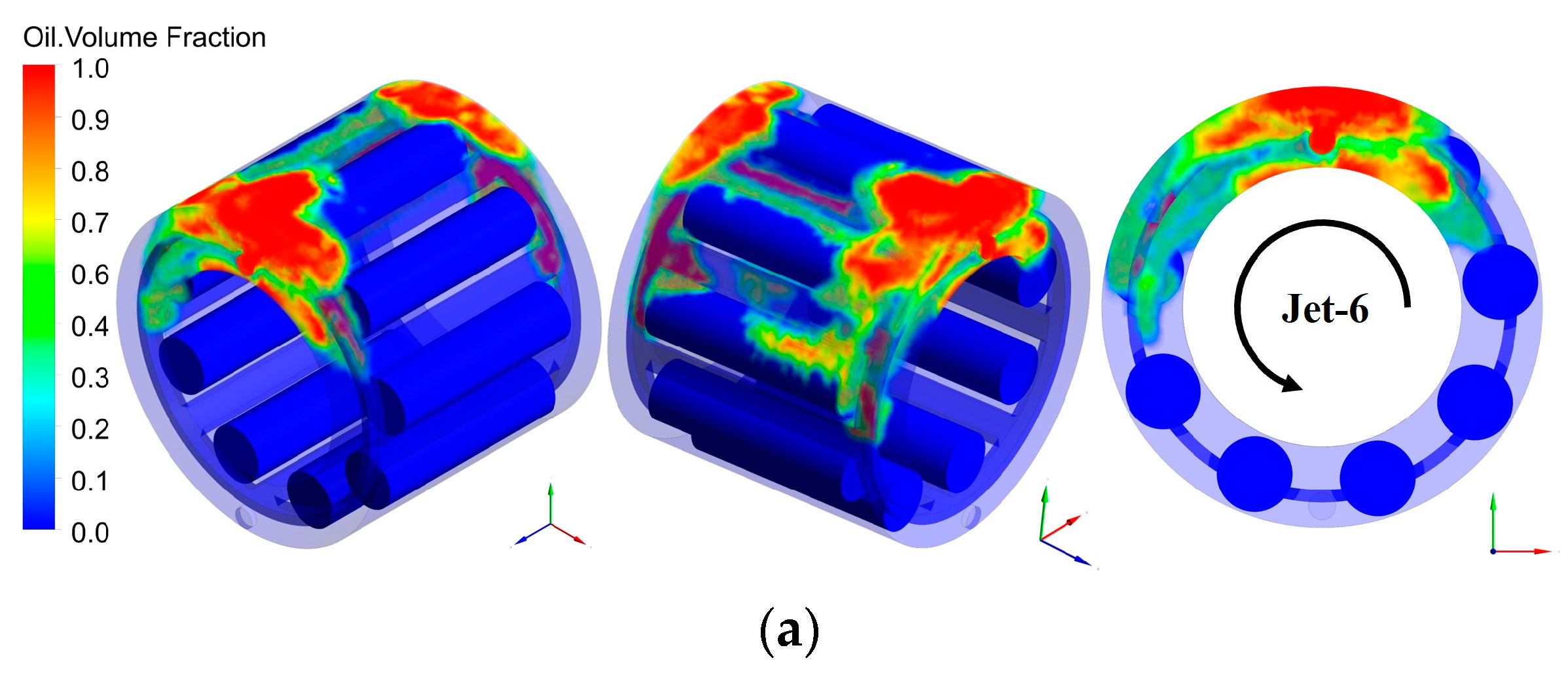
3.1. Simulation Results and Discussion of Oil Jet Lubrication
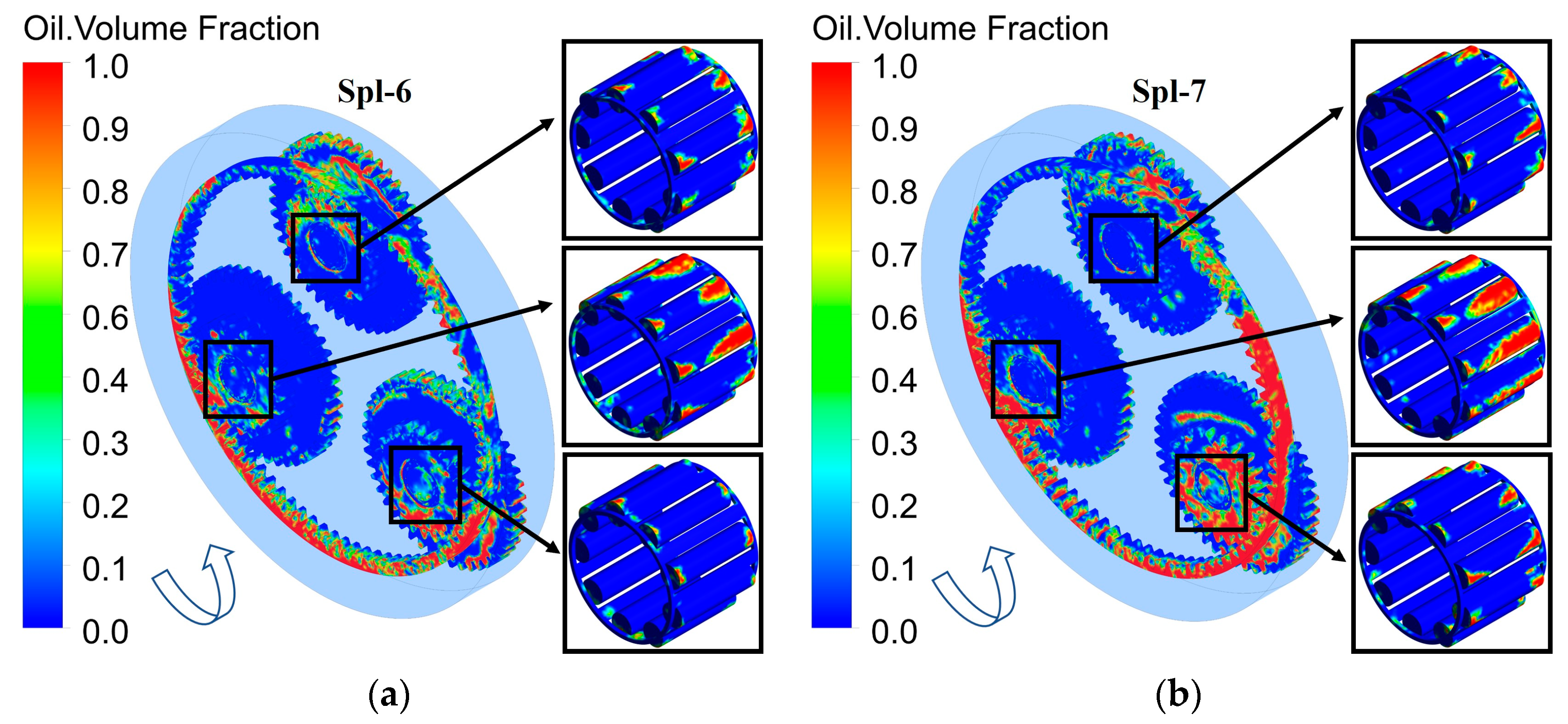
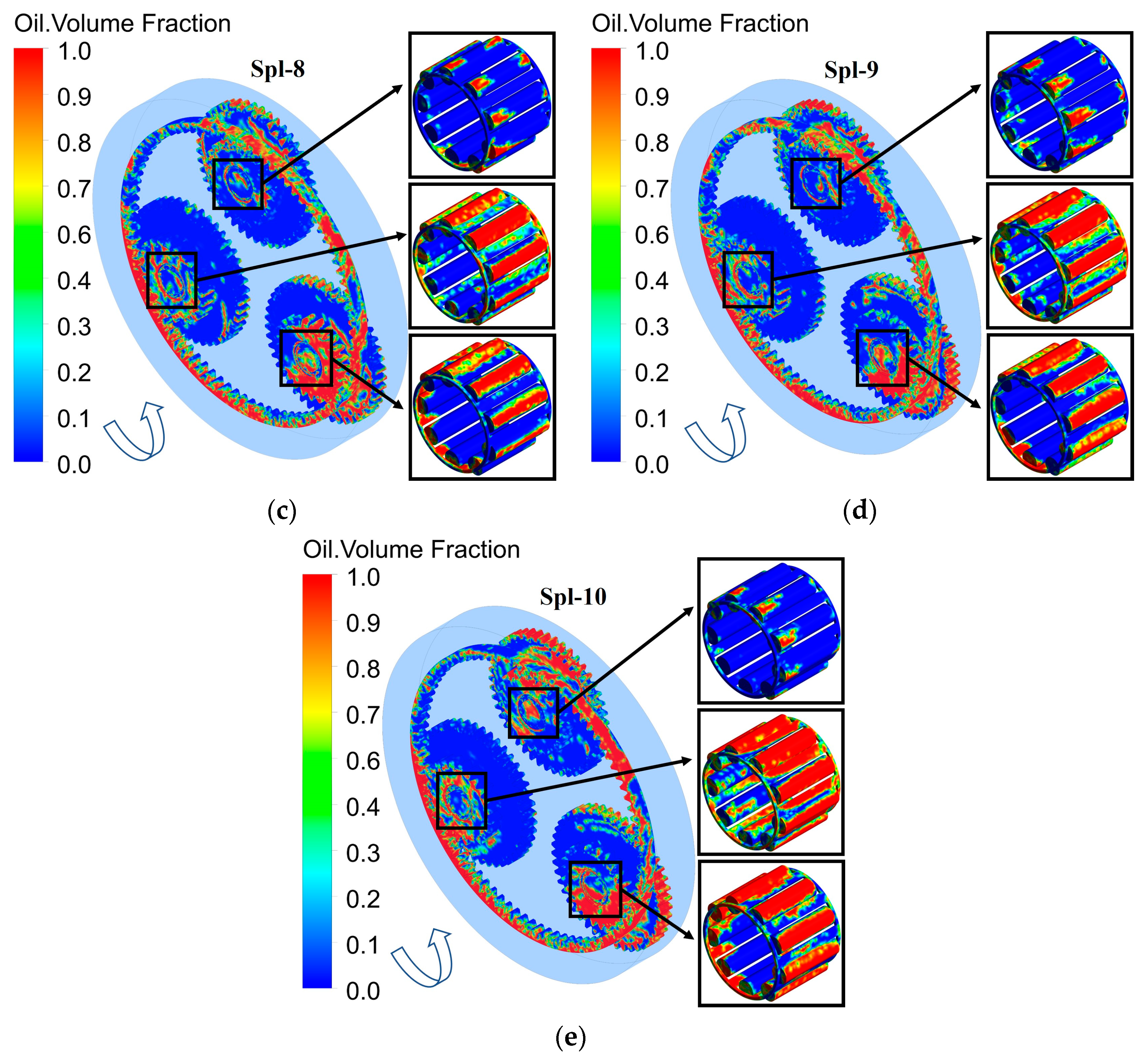
3.2. Simulation Results and Discussion of Splash Lubrication
3.3. Comparative Analysis of Needle Roller Bearings with Two Types of Lubrication
4. Conclusions
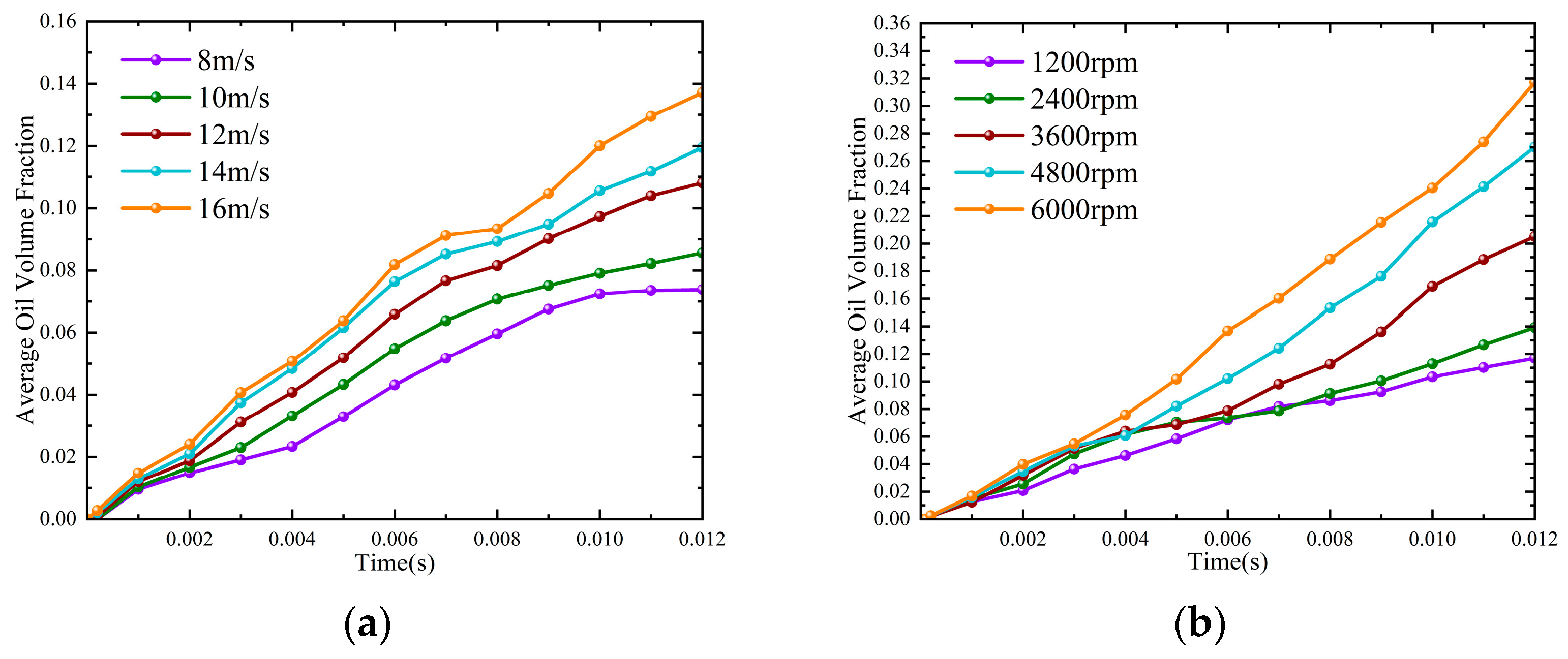
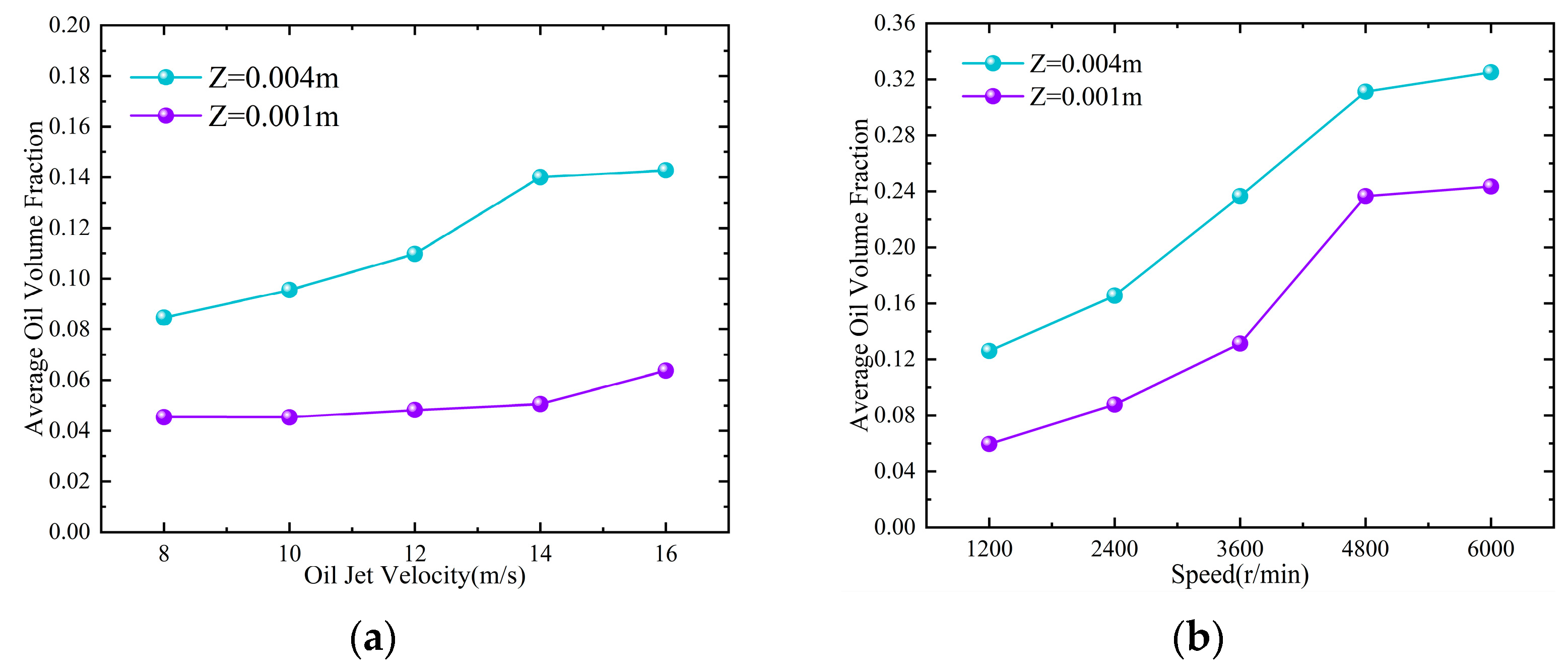
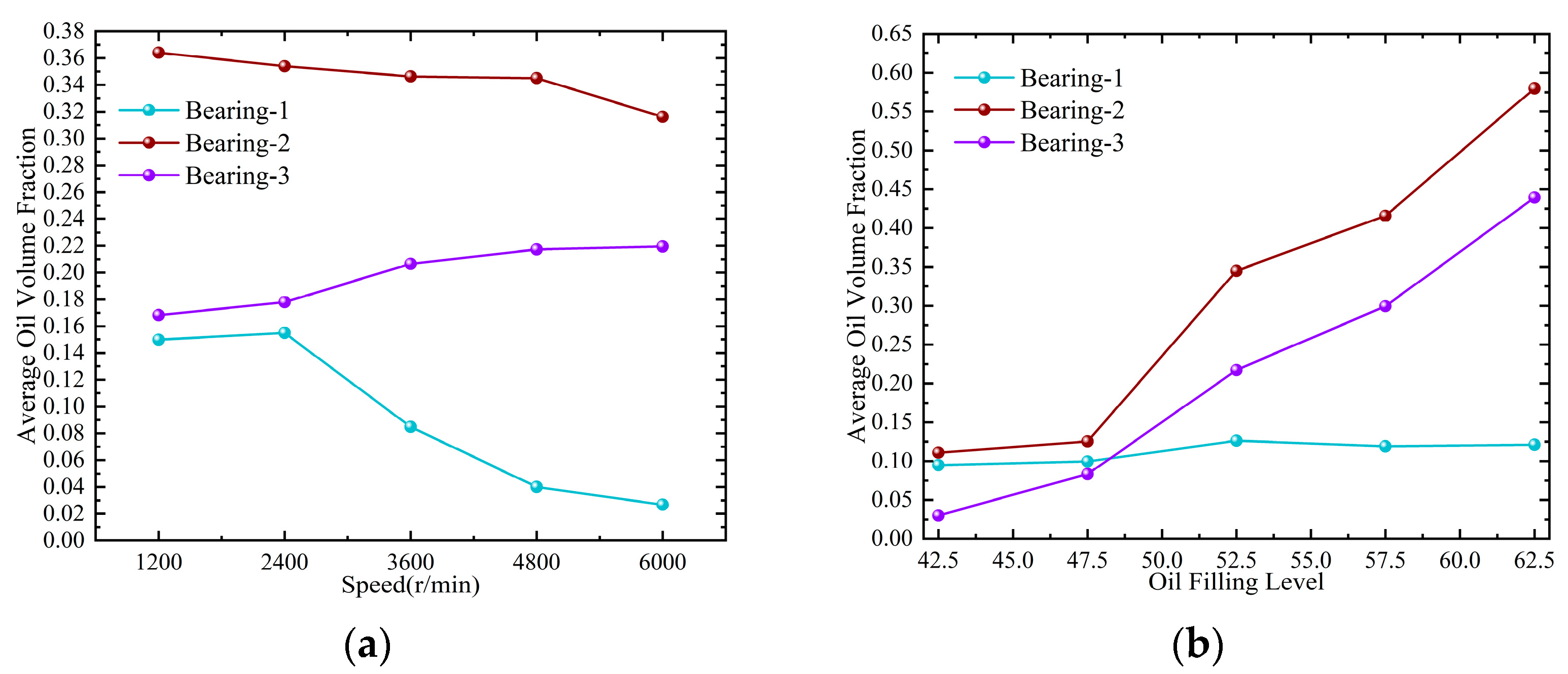
- The rotational speed had a significant effect on the oil jet lubrication of the needle roller bearings. The average oil volume fraction rose by 0.2 with the increase in the bearing speed from 1200 r/min to 6000 r/min and by 0.06 with the increase in the oil jet velocity from 8 m/s to 16 m/s. The oil volume fraction on the bearing at a high speed was not very high, but it was well lubricated due to the constant flow of lubricant through the nozzle. A large amount of oil accumulated near the nozzle at lower speeds. Although the oil jet velocity had a great influence on the lubrication, a large amount of oil accumulated near the nozzle at lower speeds.
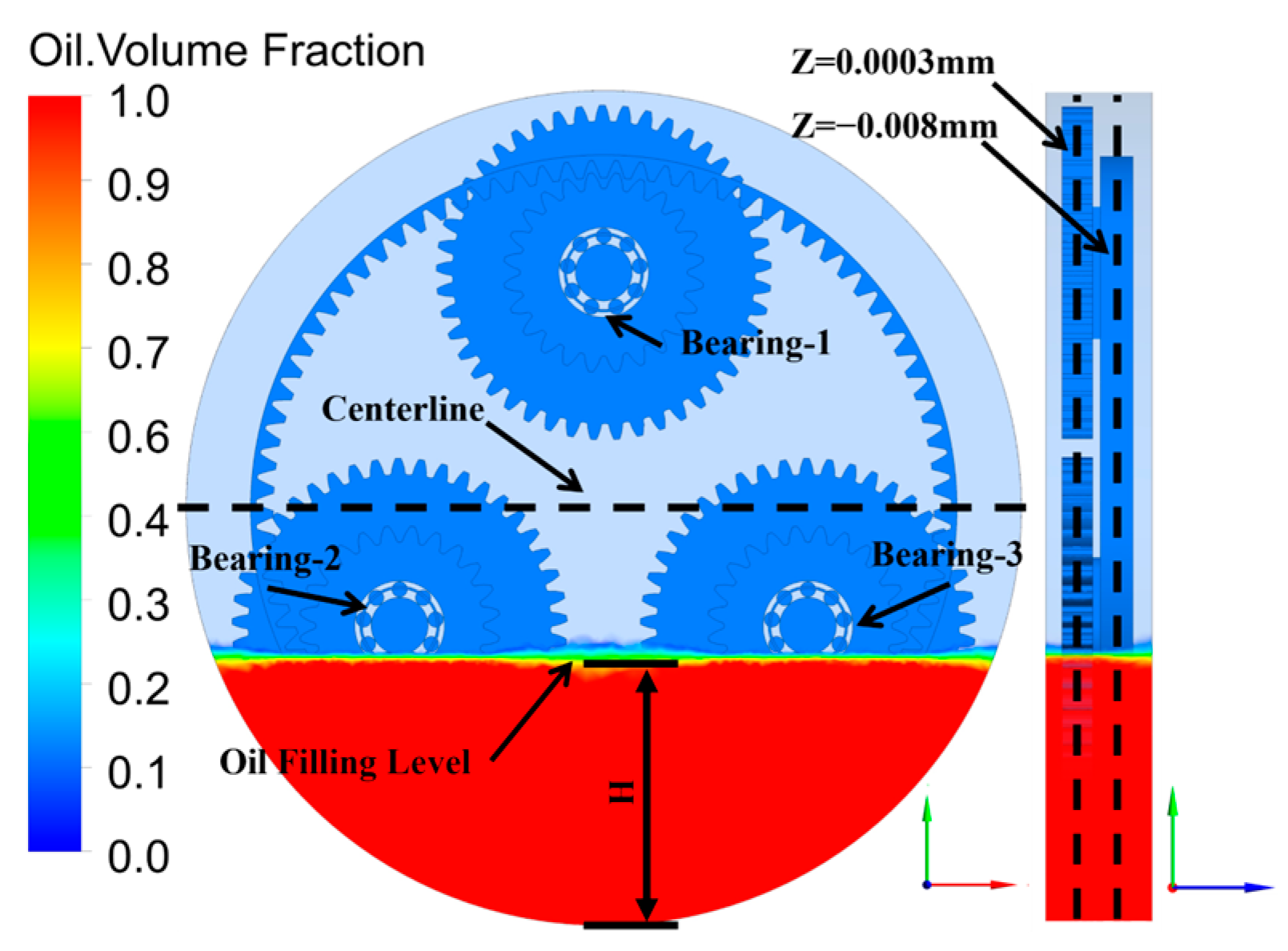
- The splash lubrication of the bearings in the planetary gearbox was directly related to the immersion depth of the bearings in the initial position. The increase in speed from 1200 r/min to 6000 r/min made the bearing lubrication decrease by 4.4%. The average oil volume fraction rose by 0.28 with the increase in the oil filling level. In the simulations from Spl-1 to Spl-10, the bearing above the centerline was under insufficient lubrication. This was caused by the inadequate oil churning of the planetary gears. Moreover, there was no apparent change with the speed and oil filling level increases.
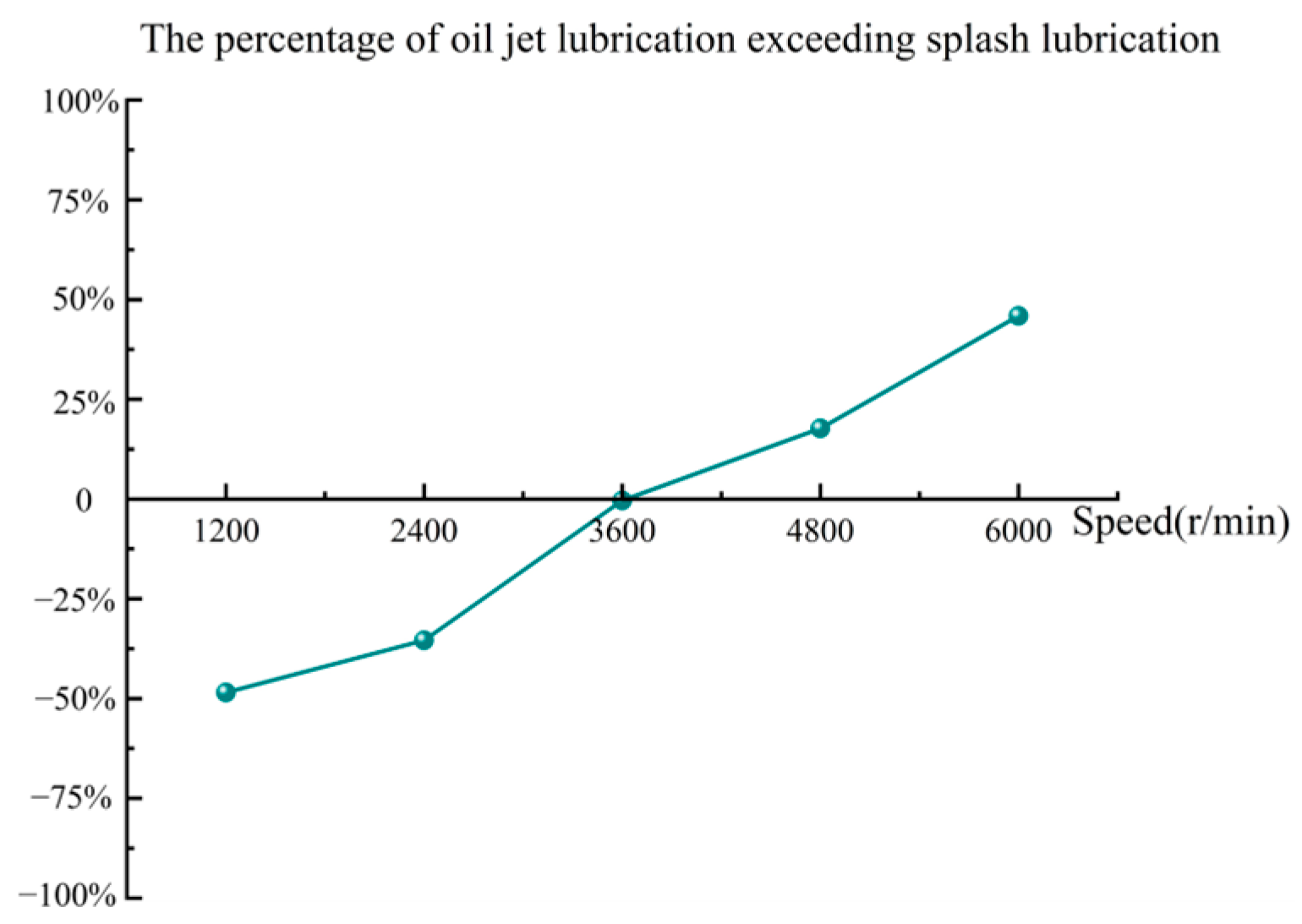
- The average oil volume fraction on the bearings with splash lubrication was better than that with oil jet lubrication by an average of 41.9% when the bearing speed was in the low-speed stage ranging from 1200 r/min to 3600 r/min. On the contrary, the average oil volume fraction on the bearings with oil jet lubrication was better than that with splash lubrication by an average of 31.8% when the bearing speed was in the high-speed stage ranging from 4800 r/min to 6000 r/min.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kumar, S.; Kumar, V.; Singh, A.K. Influence of lubricants on the performance of journal bearings—A review. Tribol. Mater. Surf. Interfaces 2020, 14, 67–78. [Google Scholar] [CrossRef]
- Li, Y.; Ai, Y.; Liu, W.; Pan, W.; Hu, Y. Splash lubrication simulation analysis and verification of a gearbox based on CFD. J. Aerosp. Power 2020, 35, 1482–1488. [Google Scholar] [CrossRef]
- Wittbrodt, M.J.; Pechersky, M.J. Hydrodynamic analysis of fluid flow between meshing spur gear teeth. J. Mech. Des. 1990, 111, 395–401. [Google Scholar] [CrossRef]
- Pinel, S.I.; Signer, H.R.; Zaretsky, E.V. Comparison between oil-mist and oil-jet lubrication of high-speed, small-bore, angular-contact ball bearings. Tribol. Trans. 2001, 44, 327–338. [Google Scholar] [CrossRef]
- Zhong, J.; Dai, Y.; Liang, C.; Zhu, X.; Xu, L. CFD investigation of air-oil two-phase flow in oil jet nozzle. Proc. Inst. Mech. Engineers. Part C J. Mech. Eng. Sci. 2022, 236, 10079–10089. [Google Scholar] [CrossRef]
- Liu, H.; Jurkschat, T.; Lohner, T.; Stahl, K. Determination of oil distribution and churning power loss of gearboxes by finite volume CFD method. Tribol. Int. 2017, 109, 346–354. [Google Scholar] [CrossRef]
- Lu, F.; Wang, M.; Pan, W.; Bao, H.; Ge, W. CFD-based investigation of lubrication and temperature characteristics of an intermediate gearbox with splash lubrication. Appl. Sci. 2021, 11, 352. [Google Scholar] [CrossRef]
- Maccioni, L.; Concli, F. Computational fluid dynamics applied to lubricated mechanical components: Review of the approaches to simulate gears, bearings, and pumps. Appl. Sci. 2020, 10, 8810. [Google Scholar] [CrossRef]
- Keller, M.C.; Kromer, C.; Cordes, L.; Schwitzke, C.; Bauer, H. CFD study of oil-jet gear interaction flow phenomena in spur gears. Aeronaut. J. 2020, 124, 1301–1317. [Google Scholar] [CrossRef]
- Peterson, W.; Russell, T.; Sadeghi, F.; Berhan, M.T.; Stacke, L.; Ståhl, J. A CFD investigation of lubricant flow in deep groove ball bearings. Tribol. Int. 2021, 154, 106735. [Google Scholar] [CrossRef]
- Liu, H.; Hao, J.; Jia, Q.; Yang, M.; Shen, Z. Oil atomization analysis of jet lubrication for high speed angular contact ball bearing. J. Aerosp. Power 2020, 35, 1186–1194. [Google Scholar] [CrossRef]
- Liu, H.; Wang, H.; Zhang, L.; Shi, Y.; Liu, G. Analysis on penetration mechanism of oil jet lubrication for high speed rolling bearing. J. Aerosp. Power 2016, 31, 1766–1776. [Google Scholar] [CrossRef]
- Zheng, D.; Gu, L.; Wang, L.; Wei, Y. Effect of lubrication oil supply parameters on the performance of high-speed rolling bearing. J. Harbin Inst. Technol. 2006, 38, 11–14. [Google Scholar]
- Zhang, R.; Wei, C.; Wu, W.; Yuan, S.H. CFD Investigation on the Influence of Jet Velocity of Oil-jet Lubricated Ball Bearing on the Characteristics of Lubrication Flow Field. In Proceedings of the International Conference on Fluid Power and Mechatronics FPM, Harbin, China, 5–7 August 2015; pp. 1324–1328. [Google Scholar] [CrossRef]
- Liu, J.; Xu, Z. A simulation investigation of lubricating characteristics for a cylindrical roller bearing of a high-power gearbox. Tribol. Int. 2022, 167, 107373. [Google Scholar] [CrossRef]
- Wu, W.; Hu, C.; Hu, J.; Yuan, S. Jet cooling for rolling bearings: Flow visualization and temperature distribution. Appl. Therm. Eng. 2016, 105, 217–224. [Google Scholar] [CrossRef]
- Wu, W.; Hu, C.; Hu, J.; Yuan, S.; Zhang, R. Jet cooling characteristics for ball bearings using the VOF multiphase model. Int. J. Therm. Sci. 2017, 116, 150–158. [Google Scholar] [CrossRef]
- Wu, W.; Hu, J.; Yuan, S.; Hu, C. Numerical and experimental investigation of the stratified air-oil flow inside ball bearings. Int. J. Heat Mass Transf. 2016, 103, 619–626. [Google Scholar] [CrossRef]
- Moshammer, T.; Mayr, F.; Kargl, K.; Honeger, C. Simulation of oil flow in gear box housing. SAE Tech. Pap. Ser. 2006, 1486–1494. [Google Scholar] [CrossRef]
- Concli, F.; Gorla, C. Numerical modeling of the churning power losses in planetary gearboxes: An innovative partitioning-based meshing methodology for the application of a computational effort reduction strategy to complex gearbox configurations. Lubr. Sci. 2017, 29, 455–474. [Google Scholar] [CrossRef]
- Höhn, B.; Michaelis, K.; Otto, H. Influence of immersion depth of dip lubricated gears on power loss, bulk temperature and scuffing load carrying capacity. Int. J. Mech. Mater. Des. 2008, 4, 145–156. [Google Scholar] [CrossRef]
- Mastrone, M.N.; Hildebrand, L.; Paschold, C.; Lohner, T.; Stahl, K.; Concli, F. Numerical and experimental analysis of the oil flow in a planetary gearbox. Appl. Sci. 2023, 13, 1014. [Google Scholar] [CrossRef]
- Liu, H.; Standl, P.; Sedlmair, M.; Lohner, T.; Stahl, K. Efficient CFD simulation model for a Planetary gearbox. Forsch. Im Ingenieurwesen 2018, 82, 319–330. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Li, L.; Versteeg, H.K.; Hargrave, G.K.; Potter, T.; Halse, C. Numerical investigation on fluid flow of gear lubrication. SAE Int. J. Fuels Lubr. 2009, 1, 1056–1062. [Google Scholar] [CrossRef]
- Liu, H.; Jurkschat, T.; Lohner, T.; Stahl, K. Detailed investigations on the oil flow in dip-lubricated gearboxes by the finite volume CFD method. Lubricants 2018, 6, 47. [Google Scholar] [CrossRef]
- Zhu, W.; Zhang, X.; Lu, Y.; Wang, D. Numerical Study for Influence of Lubrication Methods on Lubrication Performance of Ball Bearing. J. Propuls. Technol. 2019, 40, 892–901. [Google Scholar] [CrossRef]
- Boni, J.B.; Changenet, C.; Ville, F. Analysis of flow regimes and associated sources of dissipation in splash lubricated planetary gear sets. J. Tribol. 2021, 143, 111805. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| Outer diameter (mm) | 18 |
| Inner diameter (mm) | 12 |
| Width (mm) | 14 |
| Number of rollers | 9 |
| Parameter | Planetary Gear 1 | Planetary Gear 2 | Ring Gear |
|---|---|---|---|
| Modulus (mm) | 1.5 | 1.5 | 1.5 |
| Number of teeth | 45 | 24 | 87 |
| Pressure angle (°) | 20 | 20 | 20 |
| Tooth width (mm) | 6.5 | 6.5 | 6.5 |
| Parameter | Symbol | FVA4 |
|---|---|---|
| ISO VG | - | 460 |
| Density at 40 °C in kg/m3 | ρ (15 °C) | 882 |
| Kinematic viscosity at 40 °C in mm2/s | ν (40 °C) | 480 |
| Kinematic viscosity at 100 °C in mm2/s | ν (100 °C) | 31.5 |
| Simulation Name | Lubricant | Fluid Domain Temperature in °C | Oil Jet Velocity in m/s | Bearing Speed in rpm |
|---|---|---|---|---|
| Jet-1 | FVA4 | 40 | 8 | 1200 |
| Jet-2 | 10 | |||
| Jet-3 | 12 | |||
| Jet-4 | 14 | |||
| Jet-5 | 16 | |||
| Jet-6 | 12 | 1200 | ||
| Jet-7 | 2400 | |||
| Jet-8 | 3600 | |||
| Jet-9 | 4800 | |||
| Jet-10 | 6000 |
| Simulation Name | Lubricant | Oil Sump Temperature in °C | Bearing Speed in r/min | Oil Filling Level in mm |
|---|---|---|---|---|
| Spl-1 | FVA4 | 40 | 1200 | 52.5 |
| Spl-2 | 2400 | |||
| Spl-3 | 3600 | |||
| Spl-4 | 4800 | |||
| Spl-5 | 6000 | |||
| Spl-6 | 4800 | 42.5 | ||
| Spl-7 | 47.5 | |||
| Spl-8 | 52.5 | |||
| Spl-9 | 57.5 | |||
| Spl-10 | 62.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, S.; Hou, X.; Ma, C.; Yang, Y.; Li, Z.; Yin, R.; Zhu, R. Transient Simulation Analysis of Needle Roller Bearing in Oil Jet Lubrication and Planetary Gearbox Lubrication Conditions Based on Computational Fluid Dynamics. Lubricants 2024, 12, 39. https://doi.org/10.3390/lubricants12020039
Gao S, Hou X, Ma C, Yang Y, Li Z, Yin R, Zhu R. Transient Simulation Analysis of Needle Roller Bearing in Oil Jet Lubrication and Planetary Gearbox Lubrication Conditions Based on Computational Fluid Dynamics. Lubricants. 2024; 12(2):39. https://doi.org/10.3390/lubricants12020039
Chicago/Turabian StyleGao, Shushen, Xiangying Hou, Chenfei Ma, Yankun Yang, Zhengminqing Li, Rui Yin, and Rupeng Zhu. 2024. "Transient Simulation Analysis of Needle Roller Bearing in Oil Jet Lubrication and Planetary Gearbox Lubrication Conditions Based on Computational Fluid Dynamics" Lubricants 12, no. 2: 39. https://doi.org/10.3390/lubricants12020039
APA StyleGao, S., Hou, X., Ma, C., Yang, Y., Li, Z., Yin, R., & Zhu, R. (2024). Transient Simulation Analysis of Needle Roller Bearing in Oil Jet Lubrication and Planetary Gearbox Lubrication Conditions Based on Computational Fluid Dynamics. Lubricants, 12(2), 39. https://doi.org/10.3390/lubricants12020039





