Estimation of Road Wetness from a Passenger Car
Abstract
:1. Introduction
2. Background
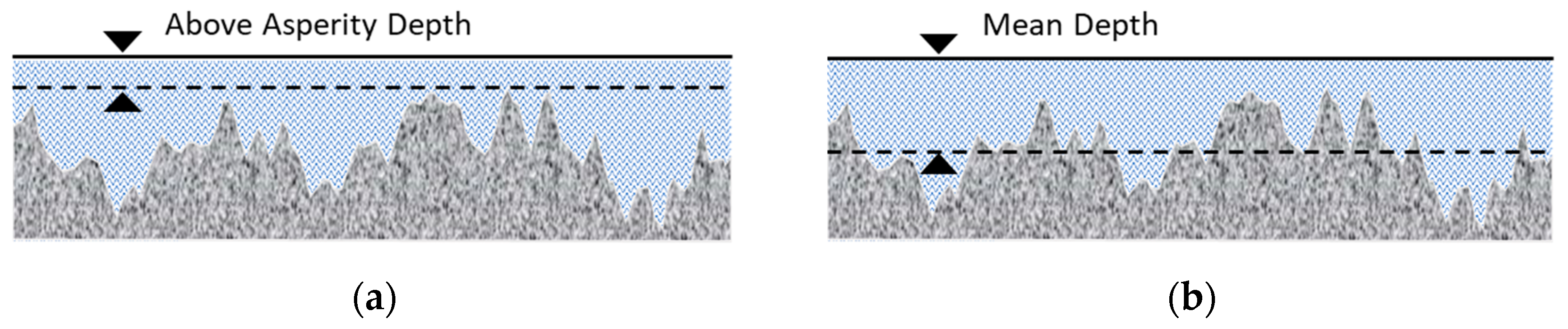
2.1. Measurement and Estimation of Water Depth
2.2. Effect of Water Depth on Skid Resistance
- -
- Ahead of the tire is the “sinkage” zone where the tire floats on a water film.
- -
- In the rear part, the tread elements are in contact with the road surface. As the full-contact condition is not always fulfilled due to the presence of water pockets trapped between the tread elements and the asperity summits, this zone is called the “mixed-contact” zone.
- -
- Between the sinkage and the mixed-contact zones is the “transition” zone.
- -
- The three-zone description is useful because it helps:
- -
- To understand why friction on a wet road, which is generated only in the mixed-contact zone, is lower than on a dry road;
- -
- To study the onset of hydroplaning where the tire is entirely supported by the water film. Many researches have been dedicated to this dangerous situation [24,25,26,27] where, locally, a tread element entering the contact area does not have enough time to go through the water film—sinkage—to be in contact with the road surface asperities. One can see the importance of the water depth, which defines the time to sinkage, and the vehicle speed, which defines the time of traversal that a tread element needs to go through the contact area. Moore [23], among many authors, highlights the role of the road surface macrotexture (surface asperities whose dimensions range between 0.1 mm and 20 mm vertically, and between 0.5 mm and 50 mm horizontally [28]) in reducing the water depth ahead of the tire and the time to sinkage; both mechanisms contributing to mitigate the hydroplaning risk.
- -
- To remind that there can be a loss of contact in the mixed-contact zone if the presence of water pockets is significant. This situation happens when the microtexture (asperities smaller than 0.5 mm in height and in width [28]) is not enough—in terms of height and sharpness—to remove the water pockets. Moore [29] named this situation “viscous” hydroplaning to highlight the fact that the corresponding water depth is low.
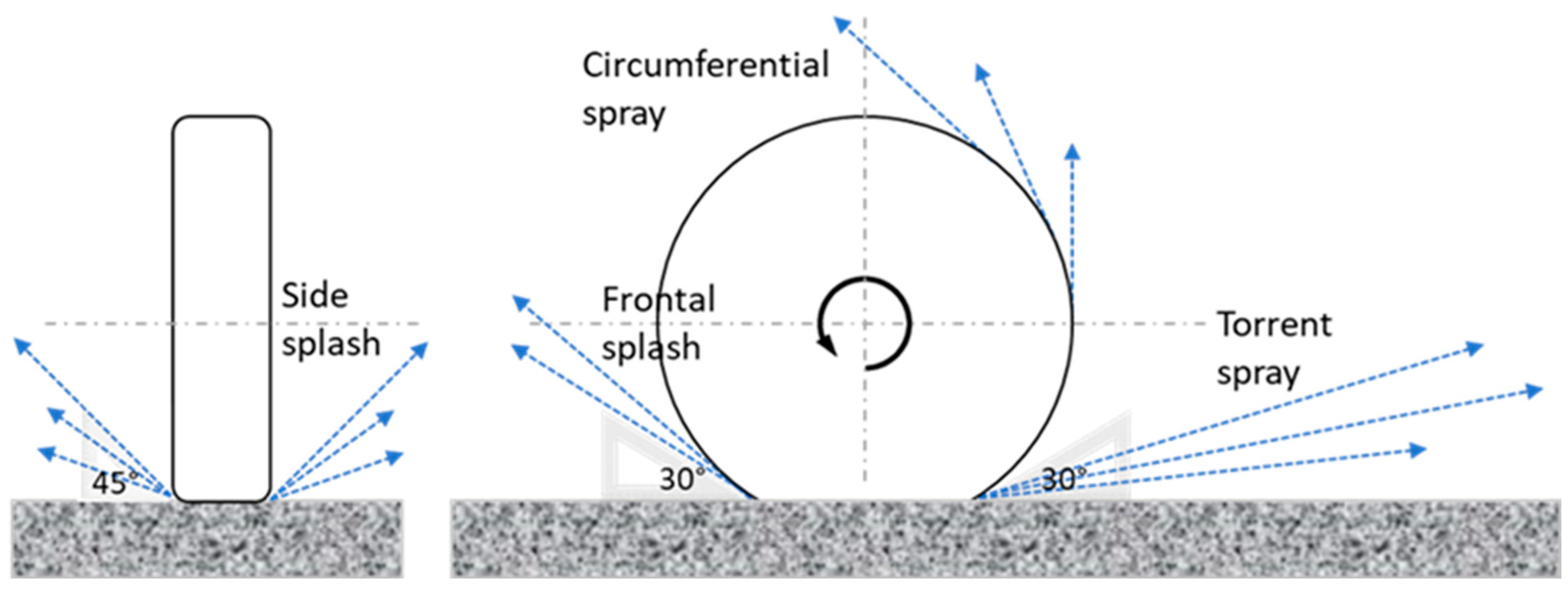
2.3. Tire Splash and Spray
3. Experiments
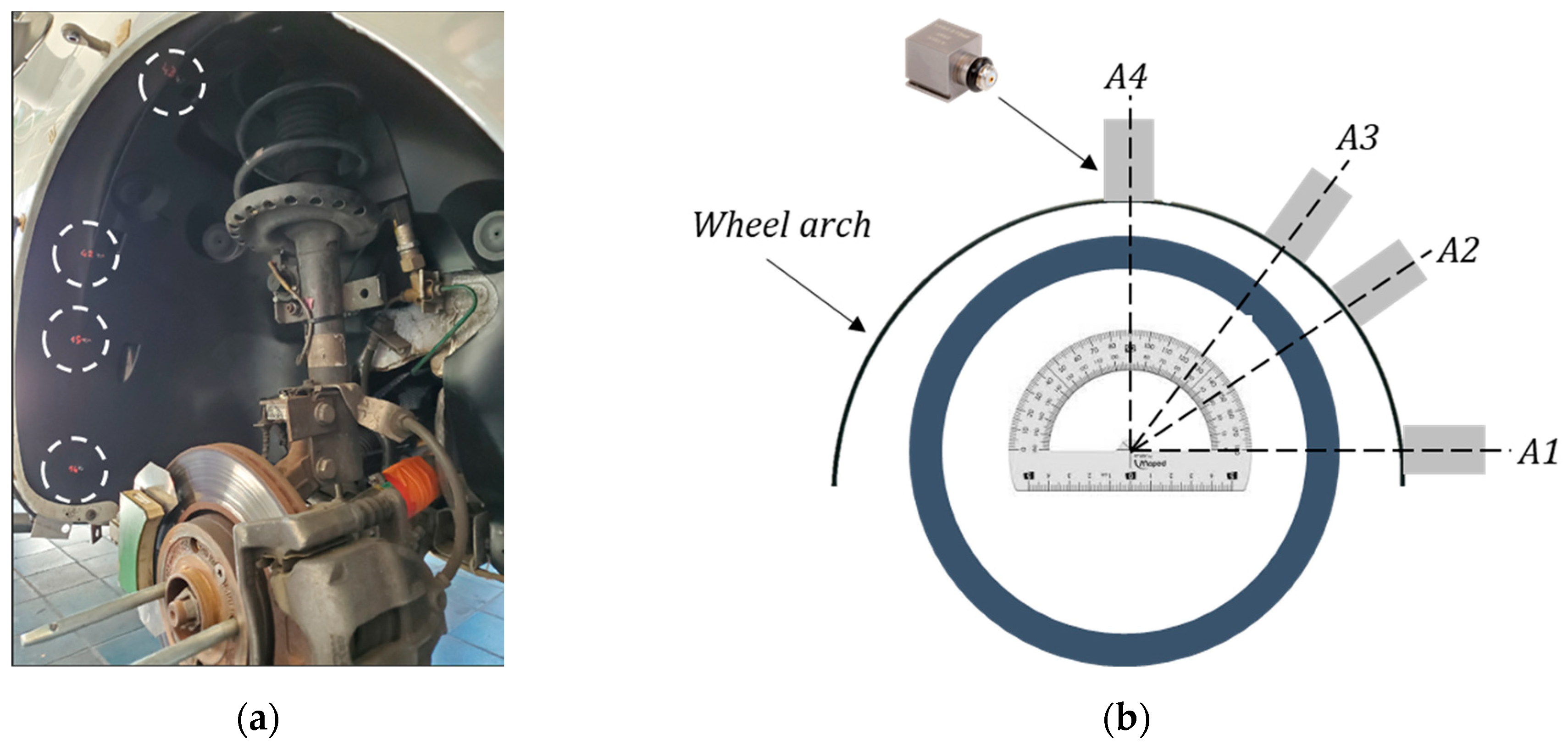
3.1. Instrumentation of a Wheel Arch Liner
3.2. Other Test Equipment
3.3. Test Tracks and Test Protocol
- -
- Passage of the vehicle on the dry surface;
- -
- Wetting of the test section (100 m long) for 5 min to obtain an evenly wetted (checked visually) surface;
- -
- Passage of the vehicle during the wetting process;
- -
- The wetting system is stopped and the vehicle performs successive passages during the drying period.
4. Results
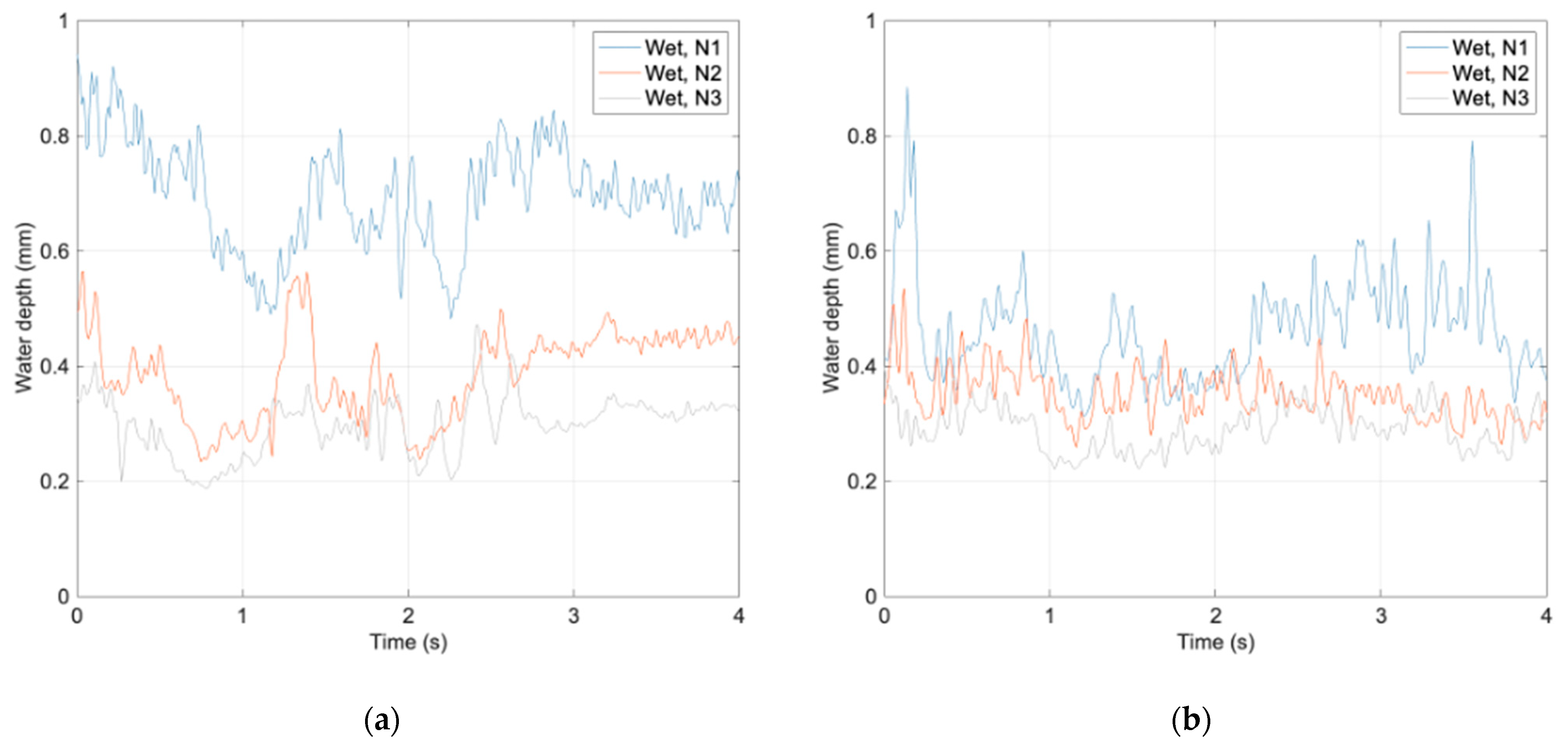
4.1. Determination of the Water Depth
- -
- To the cross slope of the test sections (2%), which facilitates the water runoff and induces a decrease in water depth once the wetting system is stopped;
- -
- To the macrotexture of the test surfaces, which can store water in available voids of the surface. On the fine asphalt concrete, the relative low macrotexture leaves most of the water on the surface and, as soon as the surface wetting stops, a large amount of water is evacuated; this explains the difference between data from the N1 run and the following ones. On the asphalt concrete, the relative high macrotexture allows a more important water storage; this explains the smaller difference between the three runs.
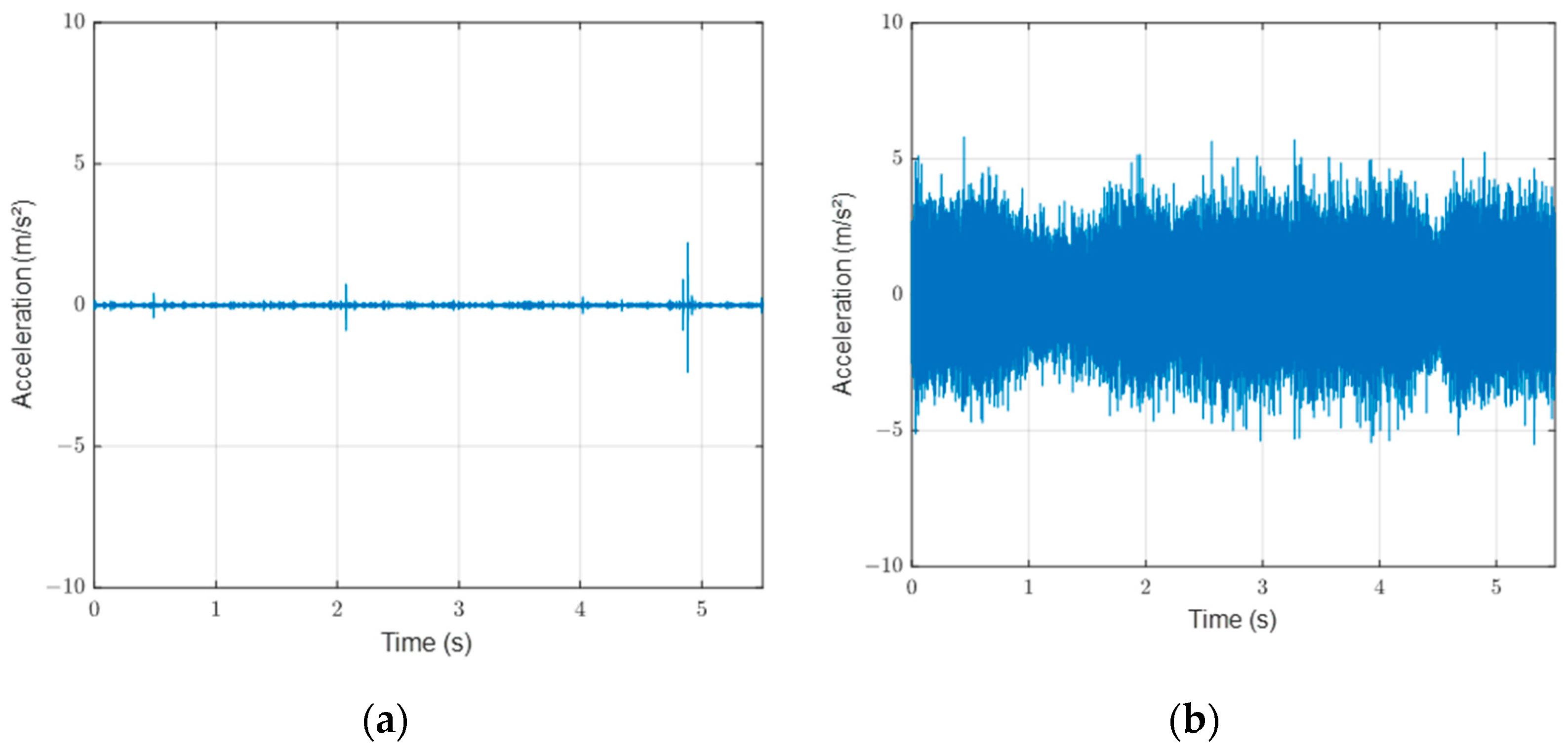
4.2. Processing of Accelerometric Signals
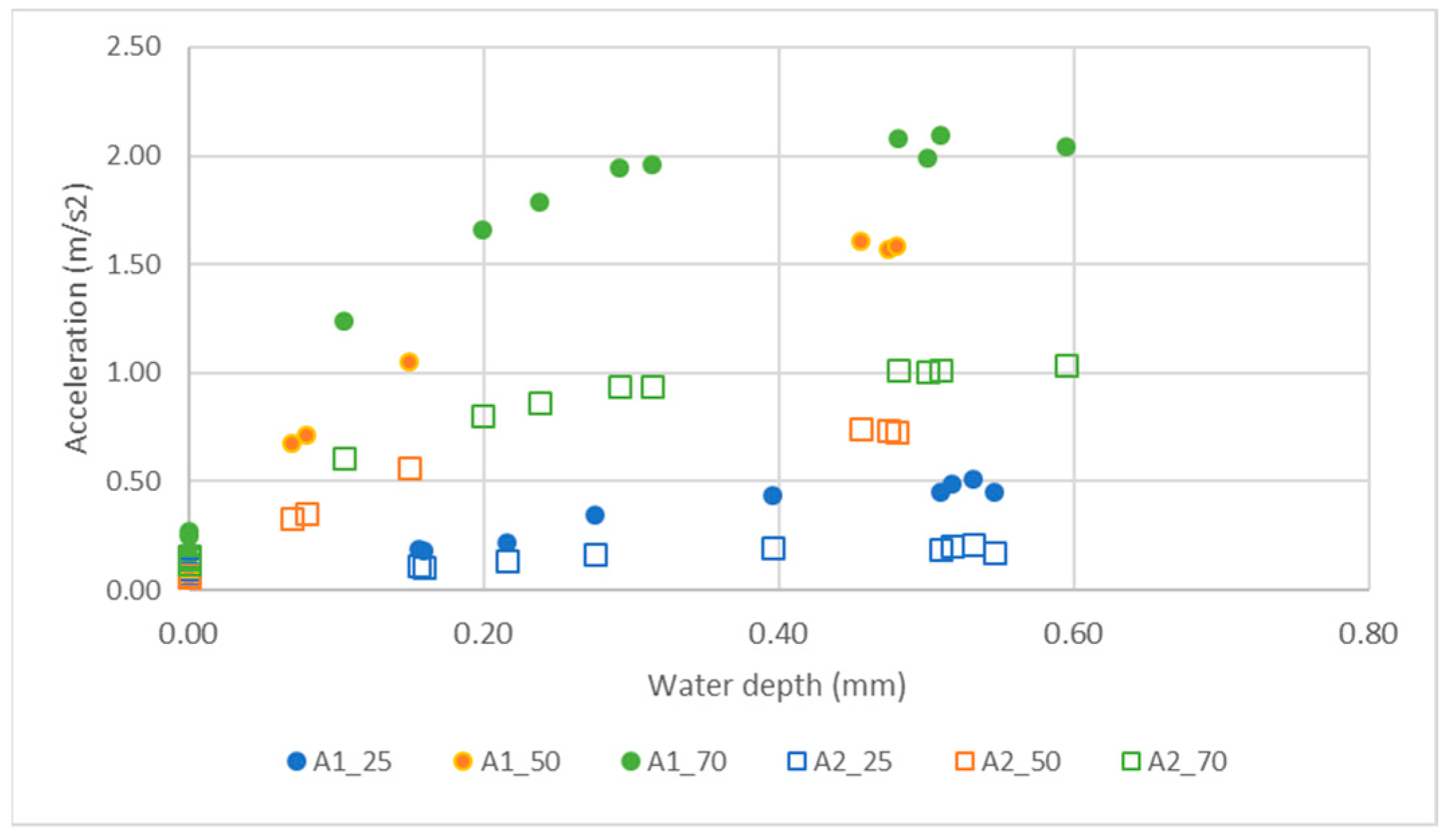
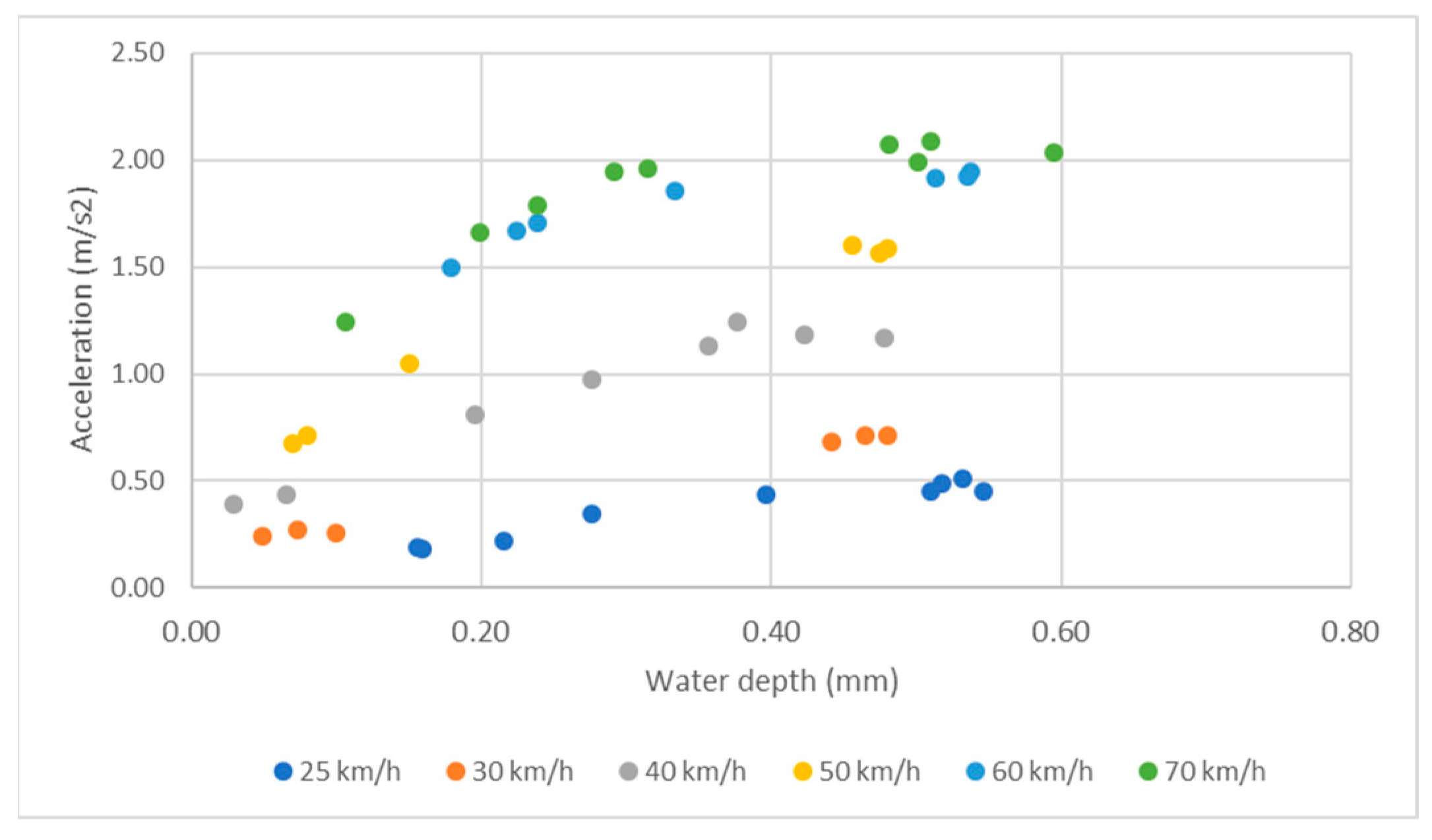
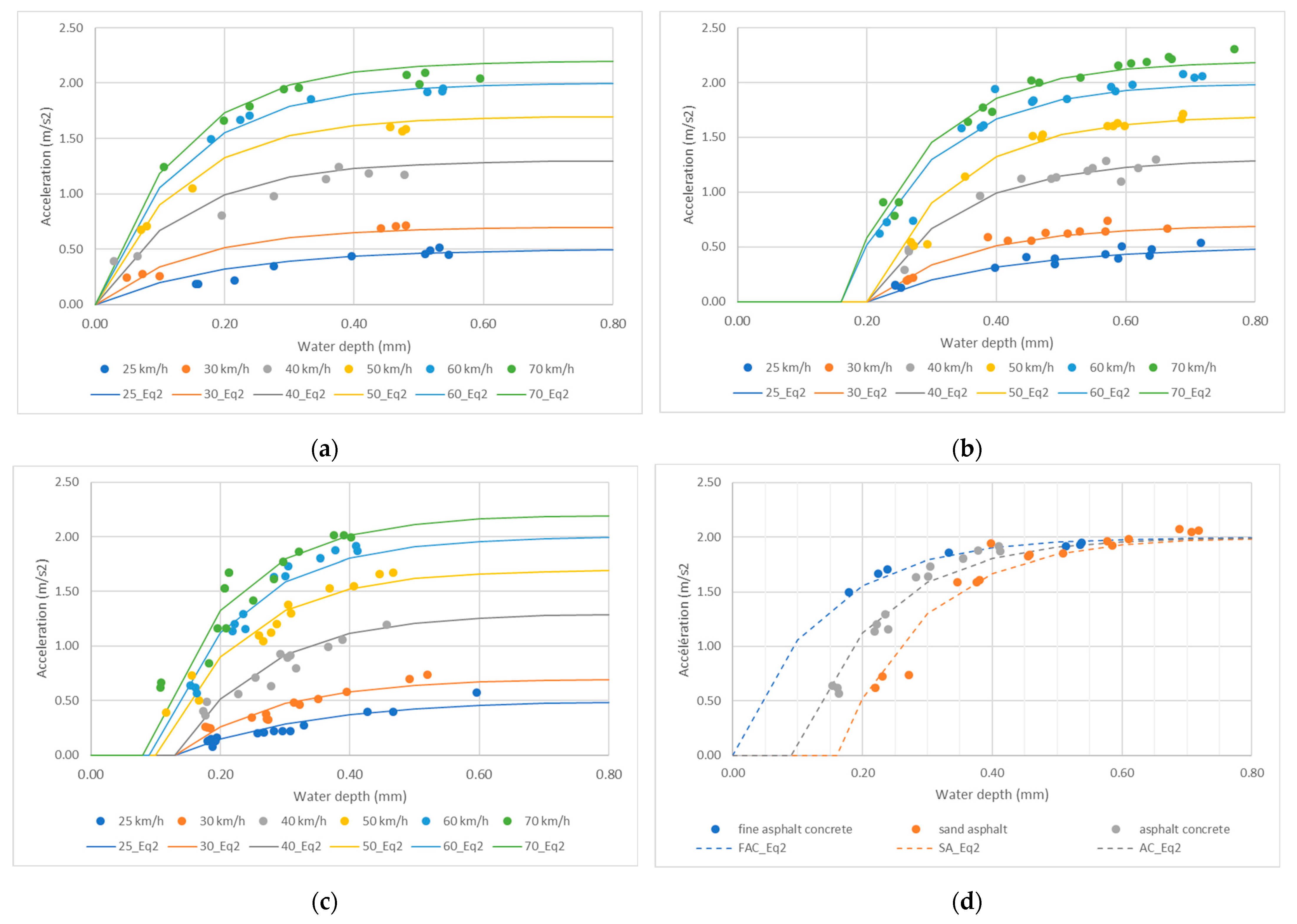
4.3. Variaton of the Acceleration Amplitude with the Water Depth
- -
- At low speed (Figure 10a), the variation is linear and similar for all surfaces;
- -
- At high speed (Figure 10b), the variation depends on the surface for water depths lower than 0.4 mm. For a given water depth, the acceleration amplitude is highest for the surface dressing and lowest for the sand asphalt.
- -
- For water depths higher than 0.4 mm at high speed, there seems to be no difference between the three surfaces. However, as data are limited, this interpretation should be treated with caution.
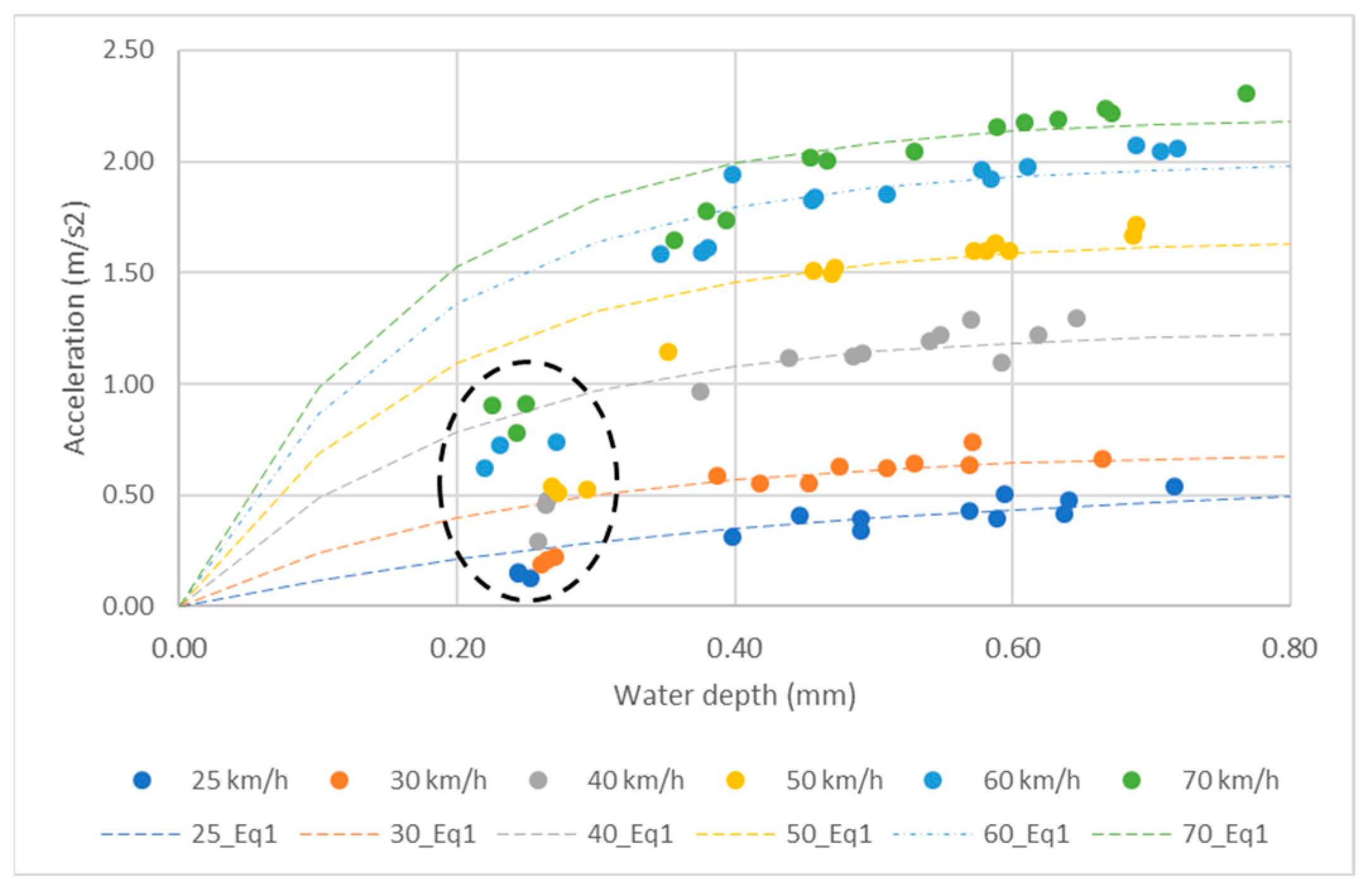
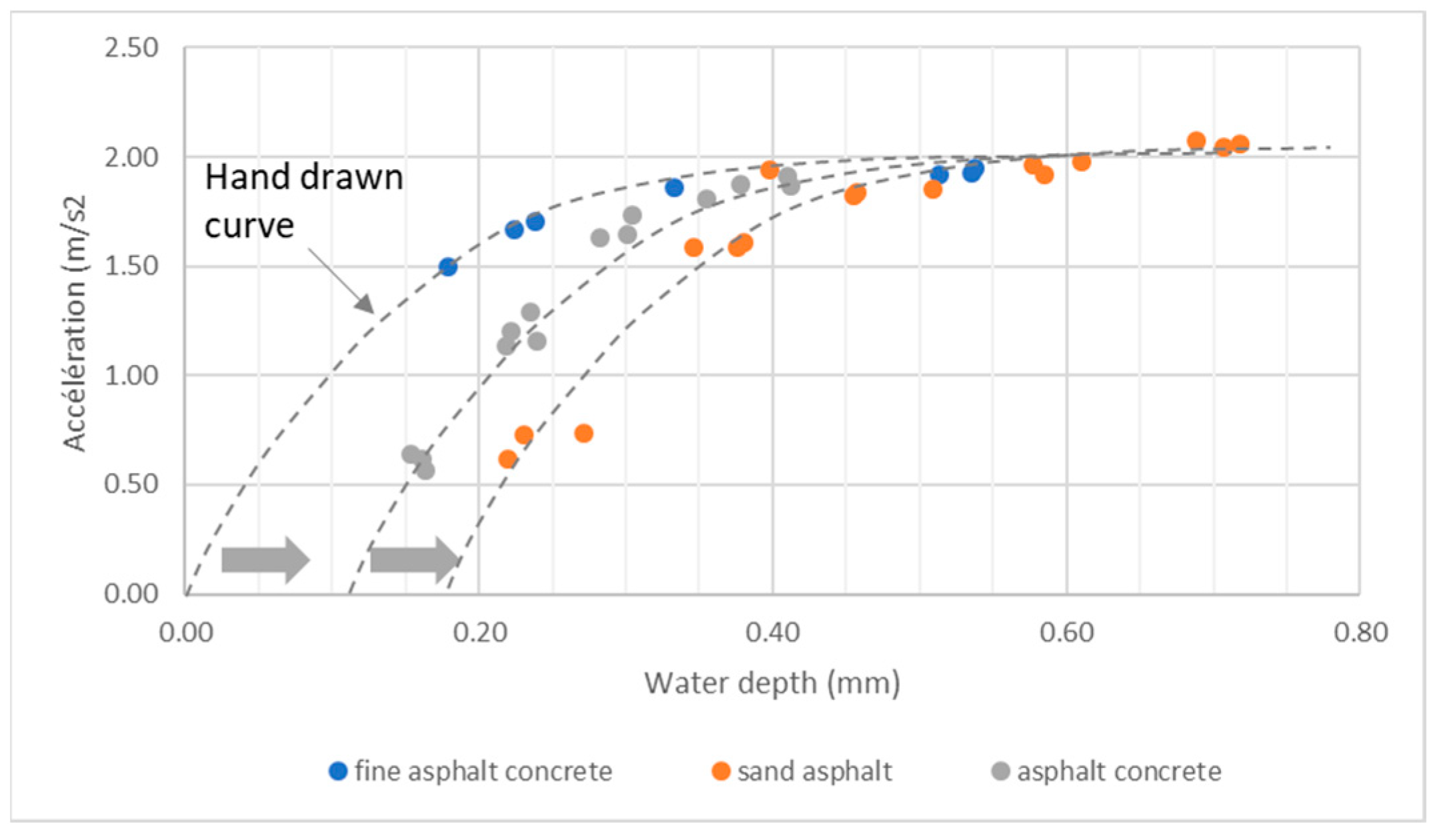
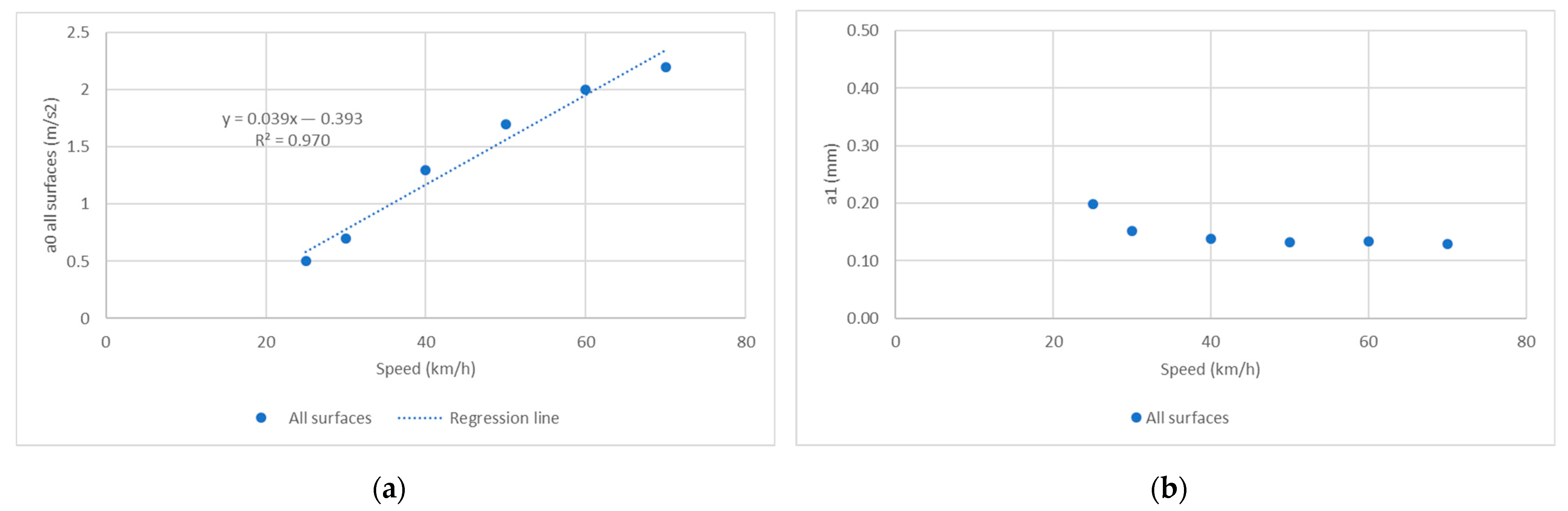
4.4. Relating Acceleration Amplitude to Water Depth
- -
- The same line fits data of all surfaces;
- -
- The lines cross the X axis at three different values of water depth at approximately 0, 0.1 mm, and 0.2 mm for the fine asphalt concrete, the sand asphalt, and the asphalt concrete, respectively.
5. Discussion
5.1. On the Influence of Water Depth
5.2. On the Influence of Speed
5.3. On the Influence of Road Surface Texture
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Do, M.-T.; Cerezo, V.; Beautru, Y.; Kane, M. Modeling of the connection road surface microtexture/water depth/friction. Wear 2013, 302, 1426–1435. [Google Scholar] [CrossRef]
- Warth, G.; Sieberg, P.; Unterreiner, M.; Schramm, D. A Concept for Using Road Wetness Information in an All-Wheel-Drive Control. Energies 2022, 15, 1284. [Google Scholar] [CrossRef]
- Salvi, K.A.; Kumar, M. Rainfall-induced hydroplaning risk over road infrastructure of the continental USA. PLoS ONE 2022, 17, e0272993. [Google Scholar] [CrossRef] [PubMed]
- D’Apuzzo, M.; Evangelisti, A.; Nicolosi, V. An exploratory step for a general unified approach to labelling of road surface and tyre wet friction. Accid. Anal. Prev. 2020, 138, 105462. [Google Scholar] [CrossRef] [PubMed]
- Stevens, S.E.; Schreck, C.J., III; Saha, S.; Bell, J.E.; Kunkel, K. Precipitation and Fatal Motor Vehicle Crashes: Continental Analysis with High-Resolution Radar Data. Bull. Am. Meteorol. Soc. 2019, 100, 1453–1461. [Google Scholar] [CrossRef]
- Black, A.W.; Villarini, G.; Mote, T.L. Effects of Rainfall on Vehicle Crashes in Six U.S. States. Weather Clim. Soc. 2017, 9, 53–70. [Google Scholar] [CrossRef]
- Eisenberg, D. The mixed effects of precipitation on traffic crashes. Accid. Anal. Prev. 2004, 36, 637–647. [Google Scholar] [CrossRef]
- Billet, Y. Detection of wet road conditions in the new generation of the 911. In 10th International Munich Chassis Symposium 2019; Pfeffer, P., Ed.; Springer Vieweg: Wiesbaden, Germany, 2020. [Google Scholar] [CrossRef]
- Riahi, E.; Edjeou, W.; Buisson, S.; Gennesseaux, M.; Do, M.-T. Estimation of water depth on road surfaces using accelerometric signals. Sensors 2022, 22, 8940. [Google Scholar] [CrossRef]
- Ling, J.; Yang, F.; Zhang, J.; Li, P.; Uddin, M.I.; Cao, T. Water-film depth assessment for pavements of roads and airport runways: A review. Constr. Build. Mater. 2023, 392, 132054. [Google Scholar] [CrossRef]
- Xiao, K.; Hui, B.; Qu, X.; Wang, H.; Diab, A.; Cao, M. Asphalt pavement water film thickness detection and prediction model: A review. J. Traffic Transp. Eng. (Engl. Ed.) 2023, 10, 349–367. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, M.; Feng, Q.; He, Z.; Tian, M. Current Non-Contact Road Surface Condition Detection Schemes and Technical Challenges. Sensors 2022, 22, 9583. [Google Scholar] [CrossRef] [PubMed]
- Flintsch, G.W.; Tang, L.; Katicha, S.W.; de León Izeppi, E.; Viner, H.; Dunford, A.; Nesnas, K.; Coyle, F.; Sanders, P.; Gibbons, R.B.; et al. Splash and Spray Assessment Tool Development Program; Final Report, DTFH61-08-C-00030; FHWA: Washington, DC, USA, 2014; Available online: https://vtechworks.lib.vt.edu/handle/10919/50550 (accessed on 26 July 2019).
- Koppa, R.J.; Zimmer, R.A.; Ivey, D.L.; Pendleton, O. Heavy Truck Splash and Spray Testing: Phase I; Texas Transportation Institute, Texas A&M University: College Station, TX, USA, 1984; Available online: https://static.tti.tamu.edu/tti.tamu.edu/documents/TTI-1984-ID19437.pdf (accessed on 9 November 2021).
- Weir, D.H.; Strange, J.F.; Heffley, R.K. Reduction of Adverse Aerodynamic Effects of Large Trucks; Report FHWA-RD-79-84; Federal Highway Administration: Washington, DC, USA, 1978. Available online: https://rosap.ntl.bts.gov/view/dot/753 (accessed on 10 November 2021).
- Maycock, G. The Problem of Water Thrown Up by Vehicles on Wet Roads; Road Research Laboratory: Wokingham, UK, 1966. [Google Scholar]
- Döring, J.; Beering, A.; Scholtyssek, J.; Krieger, K.-L. Road Surface Wetness Quantification Using a Capacitive Sensor System. IEEE Access 2021, 9, 145498–145512. [Google Scholar] [CrossRef]
- Alonso, J.; López, J.M.; Pavón, I.; Recuero, M.; Asensio, C.; Arcas, G.; Bravo, A. On-board wet road surface identification using tyre/road noise and Support Vector Machines. Appl. Acoust. 2014, 76, 407–415. [Google Scholar] [CrossRef]
- Schmiedel, B.; Gauterin, F.; Unrau, H.-J. Study of System Layouts for Road Wetness Quantification via Tire Spray. Automot. Engine Technol. 2019, 4, 63–73. [Google Scholar] [CrossRef]
- Schmiedel, B.; Gauterin, F. Tire Splash and Spray Directly before and during Hydroplaning. Tire Sci. Technol. 2019, 47, 141–159. [Google Scholar] [CrossRef]
- Fwa, T.F. Determination and prediction of pavement skid resistance–connecting research and practice. J. Road Eng. 2021, 1, 43–62. [Google Scholar] [CrossRef]
- Guo, F.; Pei, J.; Zhang, J.; Li, R.; Zhou, B.; Chen, Z. Study on the skid resistance of asphalt pavement: A state-of-the-art review and future prospective. Constr. Build. Mater. 2021, 303, 124411. [Google Scholar] [CrossRef]
- Moore, D.F. A review of squeeze films. Wear 1965, 8, 245–263. [Google Scholar] [CrossRef]
- Ong, G.P.; Fwa, T.F. Prediction of Wet-Pavement Skid Resistance and Hydroplaning Potential. Transp. Res. Rec. 2007, 2005, 160–171. [Google Scholar] [CrossRef]
- Zhu, X.; Yang, Y.; Zhao, H.; Jelagin, D.; Chen, F.; Gilabert, F.A.; Guarin, A. Effects of surface texture deterioration and wet surface conditions on asphalt runway skid resistance. Tribol. Int. 2021, 153, 106589. [Google Scholar] [CrossRef]
- Jiang, B.; Wang, H. An integrated analytical model for friction characteristics of aircraft tire on wet runway pavement. Tribol. Int. 2023, 185, 108501. [Google Scholar] [CrossRef]
- Zhao, L.; Zhao, H.; Cai, J. Tire-pavement friction modeling considering pavement texture and water film. Int. J. Transp. Sci. Technol. 2023, in press. [Google Scholar] [CrossRef]
- ISO 13473-1; Characterization of Pavement Texture by Use of Surface Profiles—Part 1: Determination of Mean Profile Depth. International Standard Organization: Geneva, Switzerland, 1997.
- Moore, D.F. A theory of viscous hydroplaning. Int. J. Mech. Sci. 1967, 9, 797–810. [Google Scholar] [CrossRef]
- Otxoterena, A.F.; Drake, P.; Willstrand, O.; Andersson, A.; Biswanger, H. Physical characteristics of splash and spray clouds produced by heavy vehicles (trucks and lorries) driven on wet asphalt. J. Wind. Eng. Ind. Aerodyn. 2021, 217, 104734. [Google Scholar] [CrossRef]
- Holzwarth, F.; Eichhorn, U. Non-contact sensors for road conditions. Sens. Actuators A Phys. 1993, 37–38, 121–127. [Google Scholar] [CrossRef]
- EN 13036-4:2011; Road and Airfield Surface Characteristics. Test Methods Method for Measurement of Slip/Skid Resistance of a Surface: The Pendulum Test. CENELEC (European Committee for Electrotechnical Standardization): Brussels, Belgium, 2011.
- CEN/TS 15901-6:2009; Road and Airfield Surface Characteristics—Part 6: Procedure for Determining the Skid Resistance of a Pavement Surface by Measurement of the Sideway Force Coefficient (SFCS): SCRIM®. CENELEC (European Committee for Electrotechnical Standardization): Brussels, Belgium, 2009.
- Koppa, R.J.; Pezoldt, V.J.; Zimmer, R.A.; Deliman, M.N.; Flowers, R. Development of a Recommended Practice for Heavy Truck Splash and Spray Evaluation; Texas Transportation Institute, Texas A&M University: College Station, TX, USA, 1990; Available online: https://static.tti.tamu.edu/tti.tamu.edu/documents/TTI-1990-ID19793.pdf (accessed on 26 October 2023).



| Surface | MTD (mm) | MPD (mm) | PTV | SFC |
|---|---|---|---|---|
| Fine asphalt concrete | 0.38 | 0.41 | 62 | 0.84 |
| Sand asphalt | 0.84 | 0.97 | 50 | 0.70 |
| Asphalt concrete | 1.14 | 1.05 | 45 | 0.52 |
| Surface | Aggregates | Bitumen | |||||
|---|---|---|---|---|---|---|---|
| <0/2 mm | 0/2 mm | 0/4 mm | 2/6 mm | 4/10 mm | 6/10 mm | ||
| Fine asphalt concrete | 2.4 | 56.7 | 10.4 | 25.0 | 5.5 | ||
| Sand asphalt | 42.2 | 51.6 | 6.2 | ||||
| Asphalt concrete | 0.9 | 32.0 | 28.3 | 33.0 | 5.8 | ||
| Speed (km/h) | Parameters | ||||
|---|---|---|---|---|---|
| a01 (m/s2) | a11 (mm) | a21 (mm) | |||
| All surfaces | Fine asphalt concrete | Sand asphalt | Asphalt concrete | ||
| 25 | 0.5 | 0.198 | 0 | 0.2 | 0.13 |
| 30 | 0.7 | 0.152 | 0 | 0.2 | 0.13 |
| 40 | 1.3 | 0.139 | 0 | 0.2 | 0.13 |
| 50 | 1.7 | 0.132 | 0 | 0.2 | 0.1 |
| 60 | 2 | 0.133 | 0 | 0.16 | 0.09 |
| 70 | 2.2 | 0.130 | 0 | 0.16 | 0.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Edjeou, W.; Riahi, E.; Gennesseaux, M.; Cerezo, V.; Do, M.-T. Estimation of Road Wetness from a Passenger Car. Lubricants 2024, 12, 2. https://doi.org/10.3390/lubricants12010002
Edjeou W, Riahi E, Gennesseaux M, Cerezo V, Do M-T. Estimation of Road Wetness from a Passenger Car. Lubricants. 2024; 12(1):2. https://doi.org/10.3390/lubricants12010002
Chicago/Turabian StyleEdjeou, Wiyao, Ebrahim Riahi, Manuela Gennesseaux, Veronique Cerezo, and Minh-Tan Do. 2024. "Estimation of Road Wetness from a Passenger Car" Lubricants 12, no. 1: 2. https://doi.org/10.3390/lubricants12010002
APA StyleEdjeou, W., Riahi, E., Gennesseaux, M., Cerezo, V., & Do, M.-T. (2024). Estimation of Road Wetness from a Passenger Car. Lubricants, 12(1), 2. https://doi.org/10.3390/lubricants12010002








