Individual Feature Selection of Rolling Bearing Impedance Signals for Early Failure Detection
Abstract
:1. Introduction
1.1. Condition Monitoring Using Vibration Data
1.2. Feature Engineering
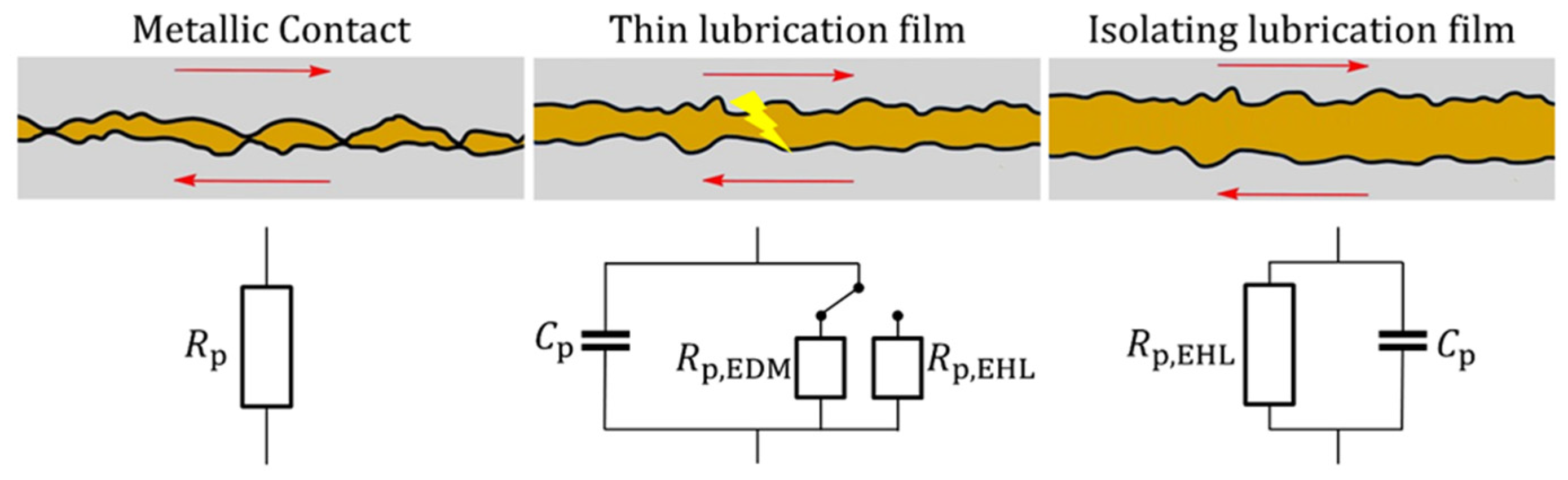
1.3. Electric Behavior of Rolling Bearings
1.4. Research Design
2. Materials and Methods
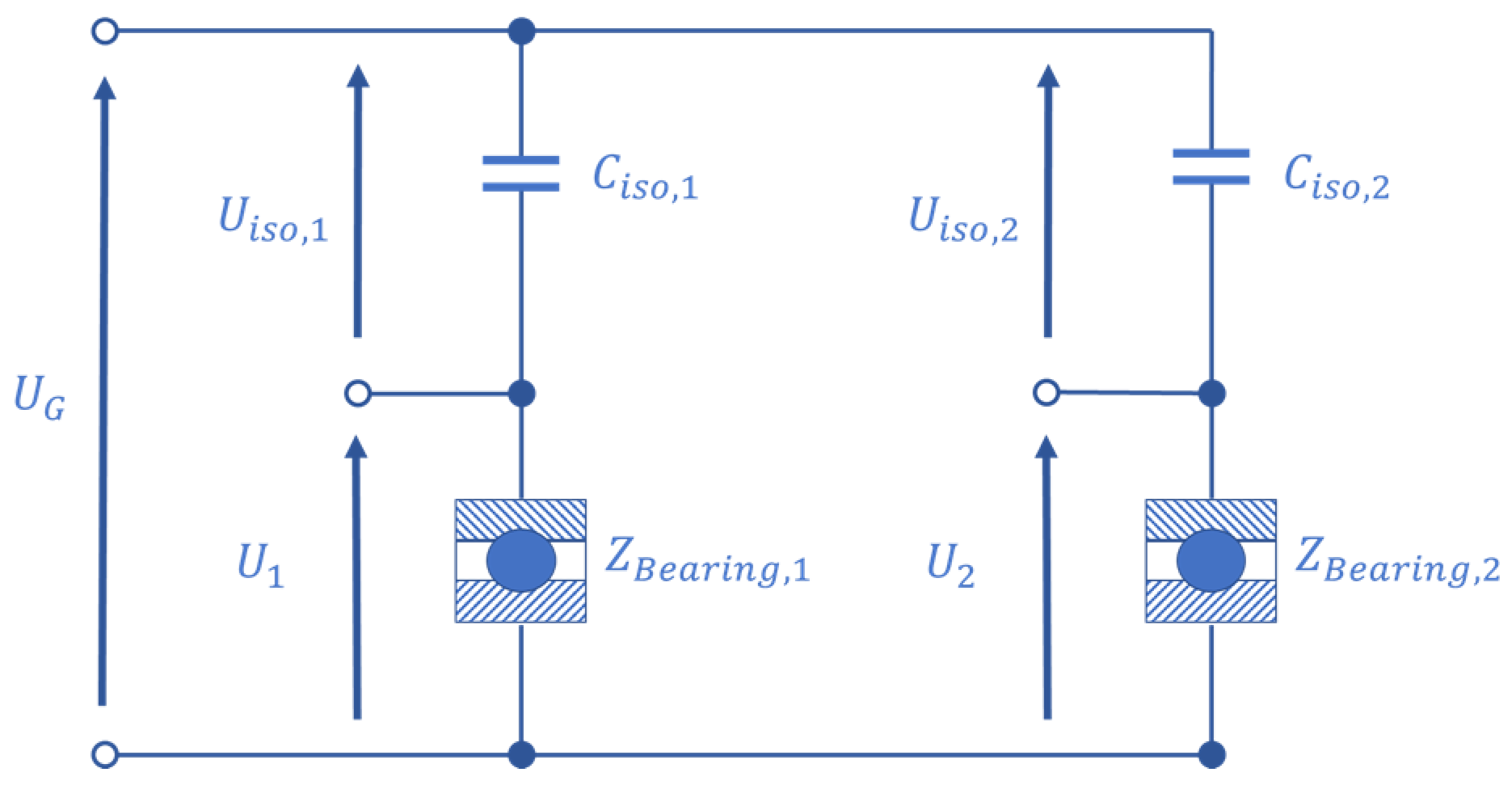
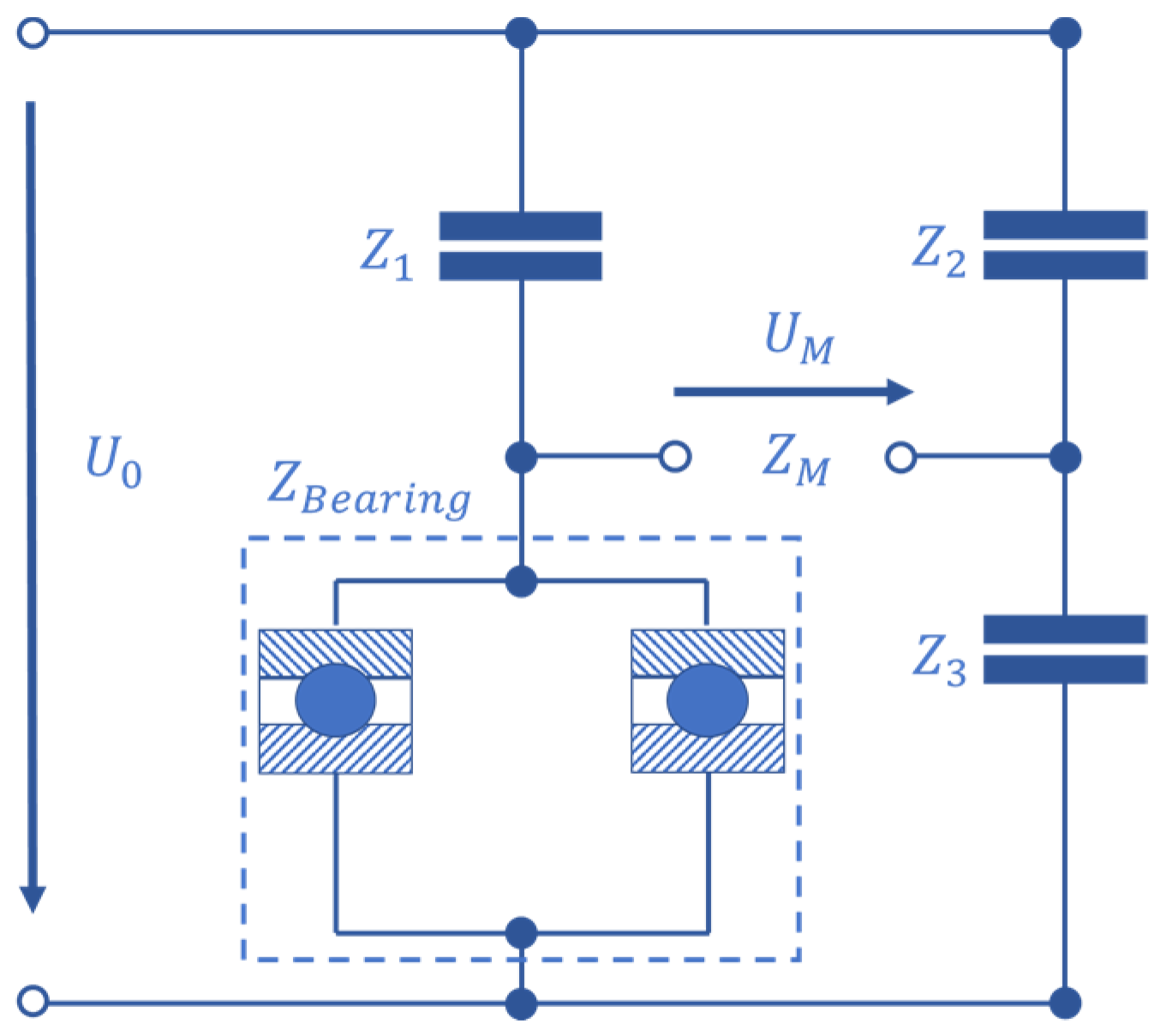
2.1. Impedance Measurement Methods
2.2. Test Rig and Impedance Measurement
2.3. Design and Procedure of the Fatigue Tests
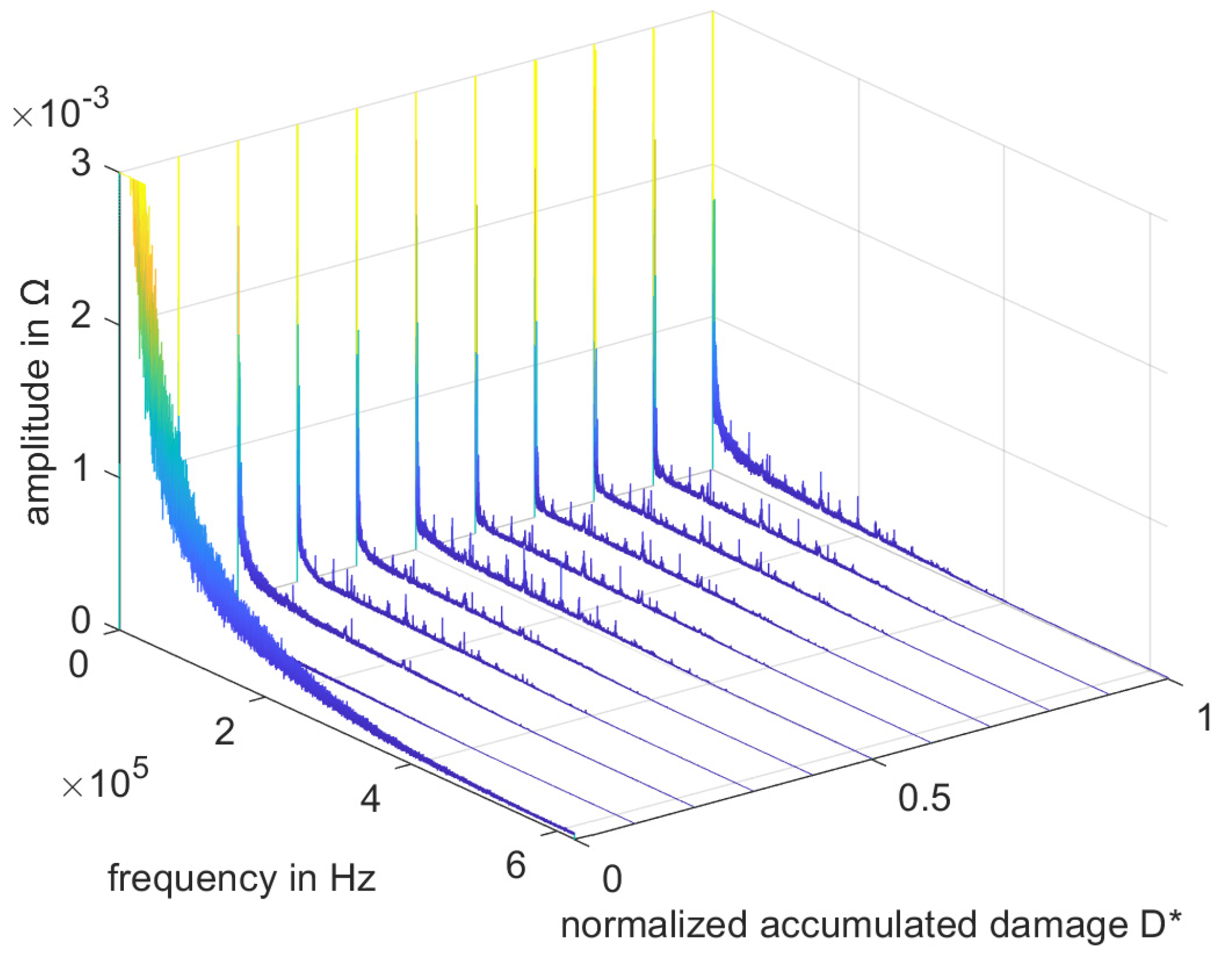
2.4. Preprocessing and Feature Generation
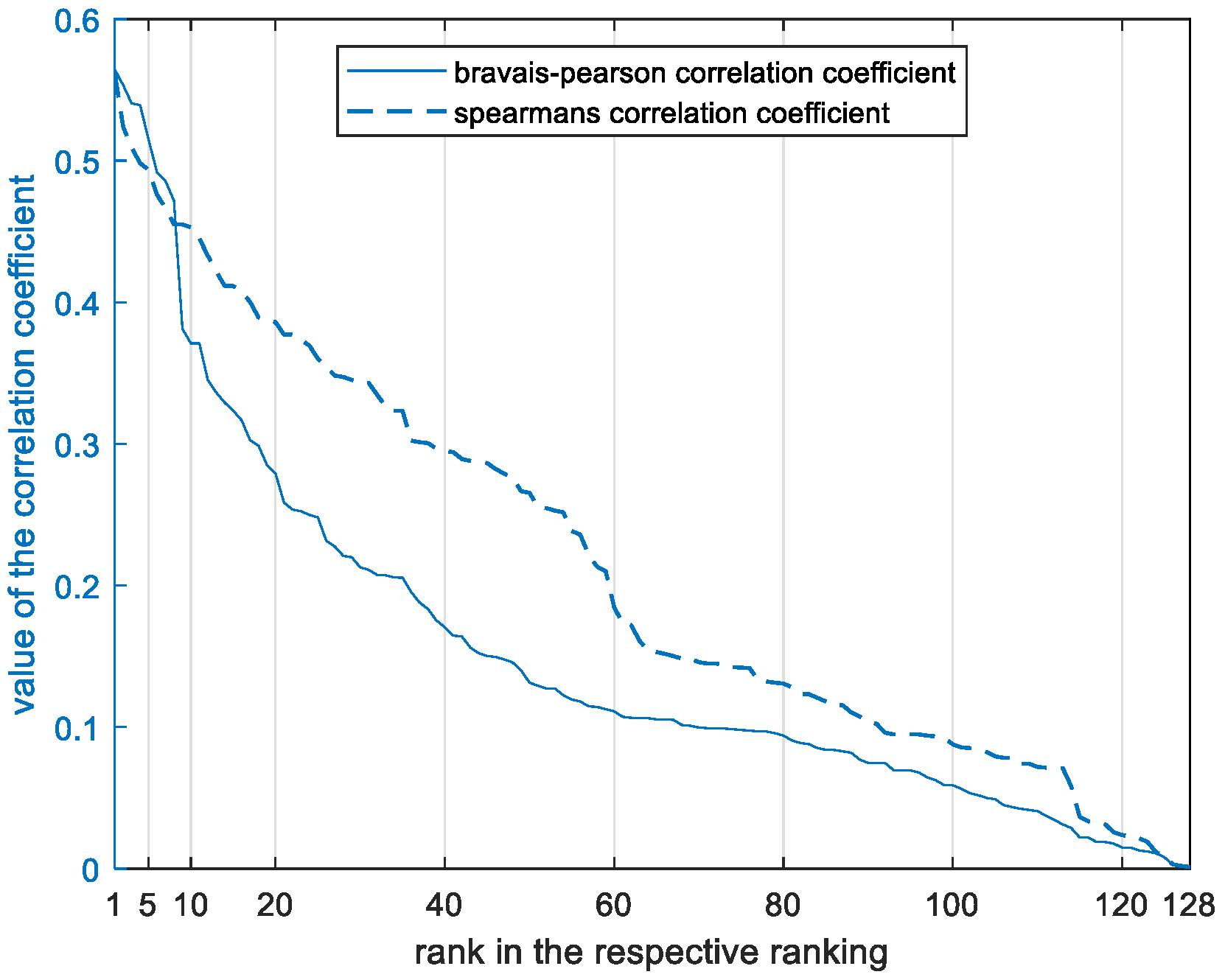
2.5. Individual-Feature Selection
3. Results
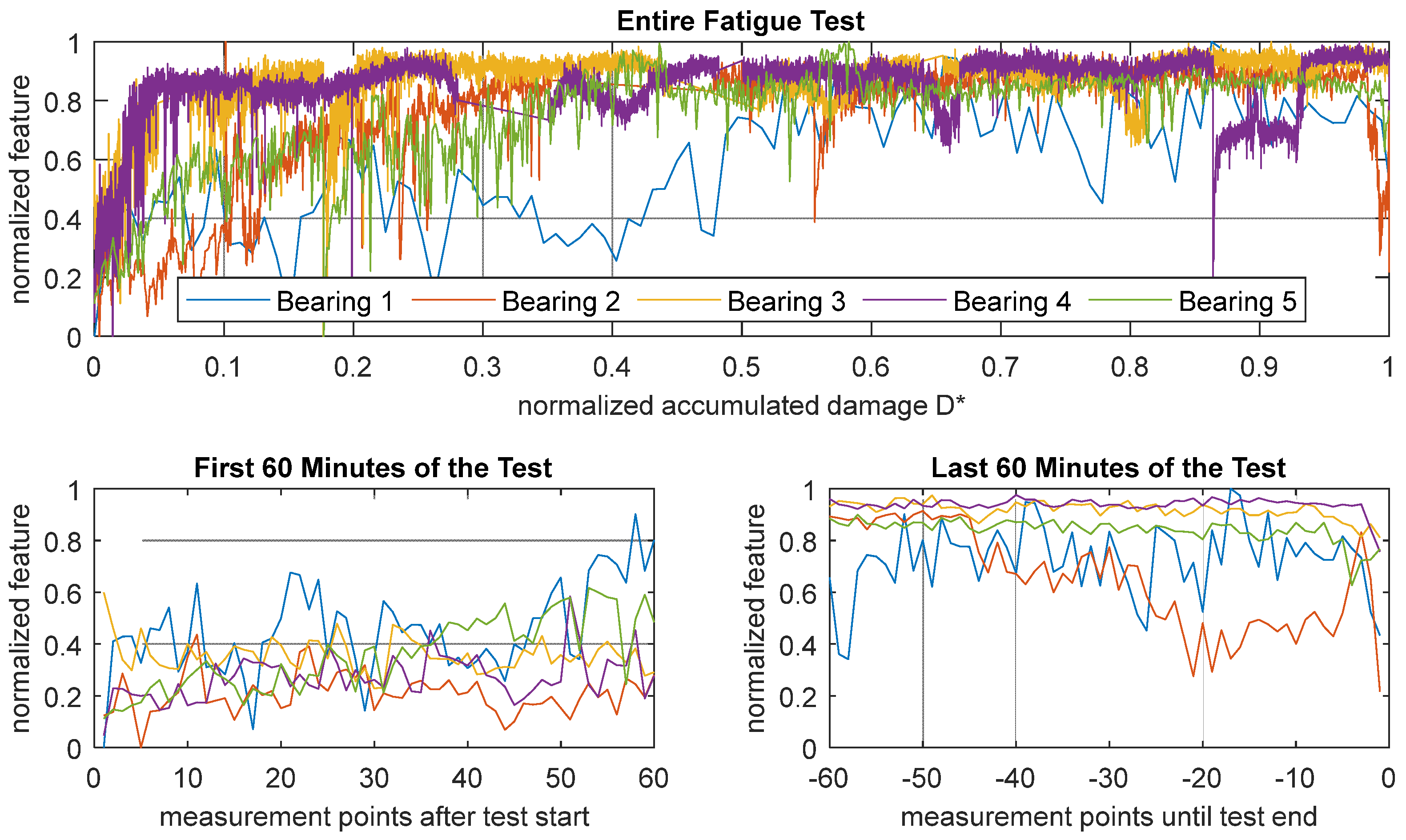
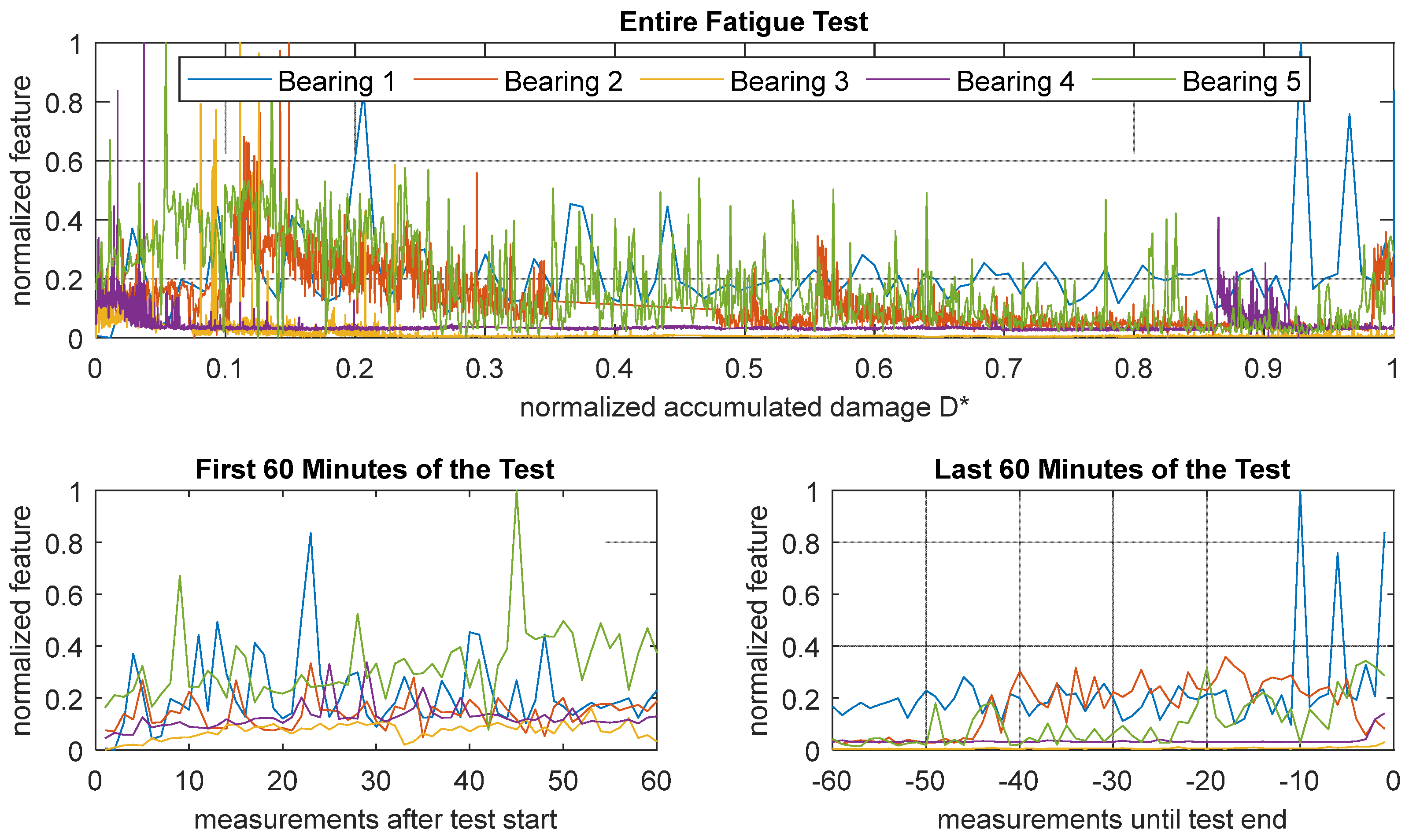
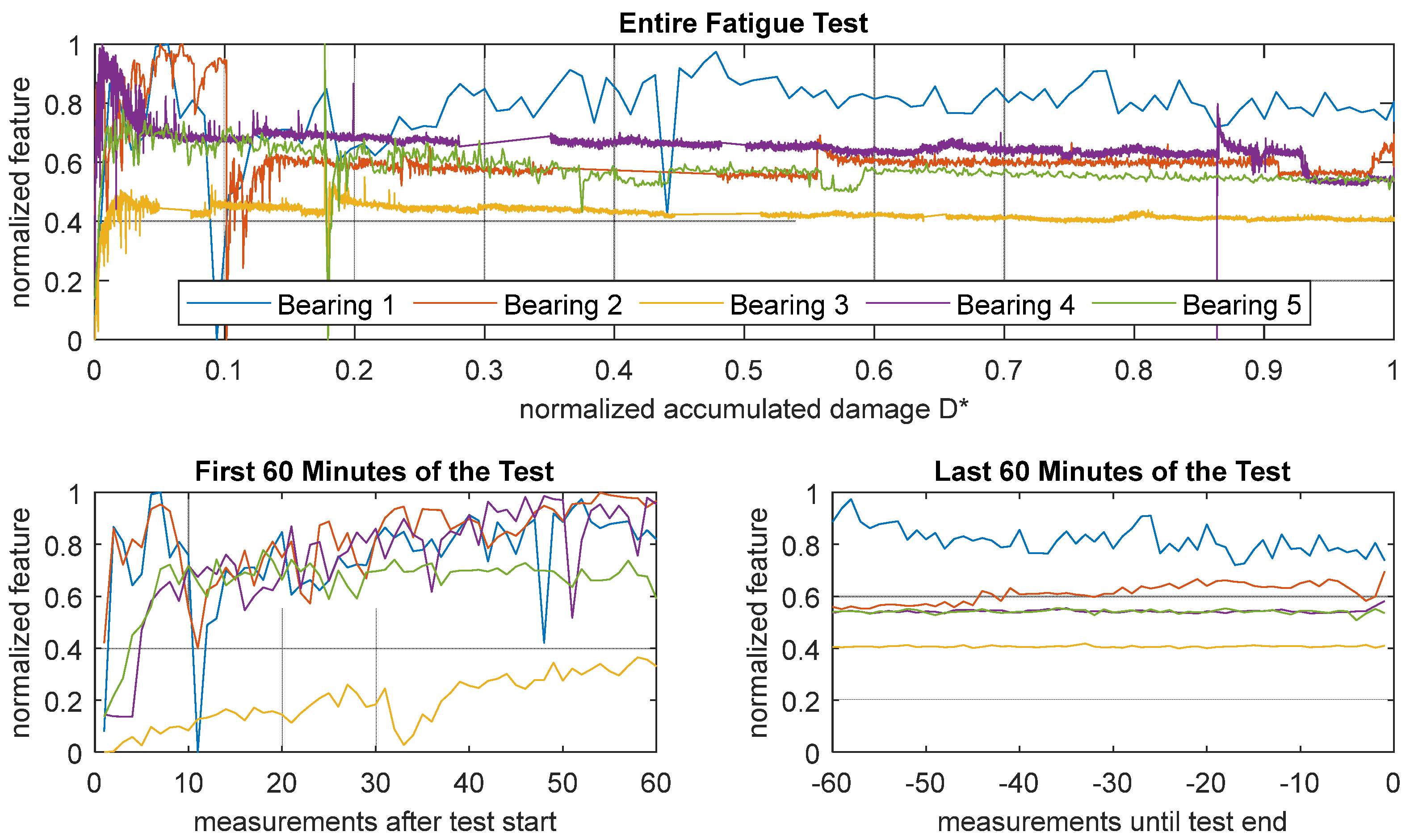
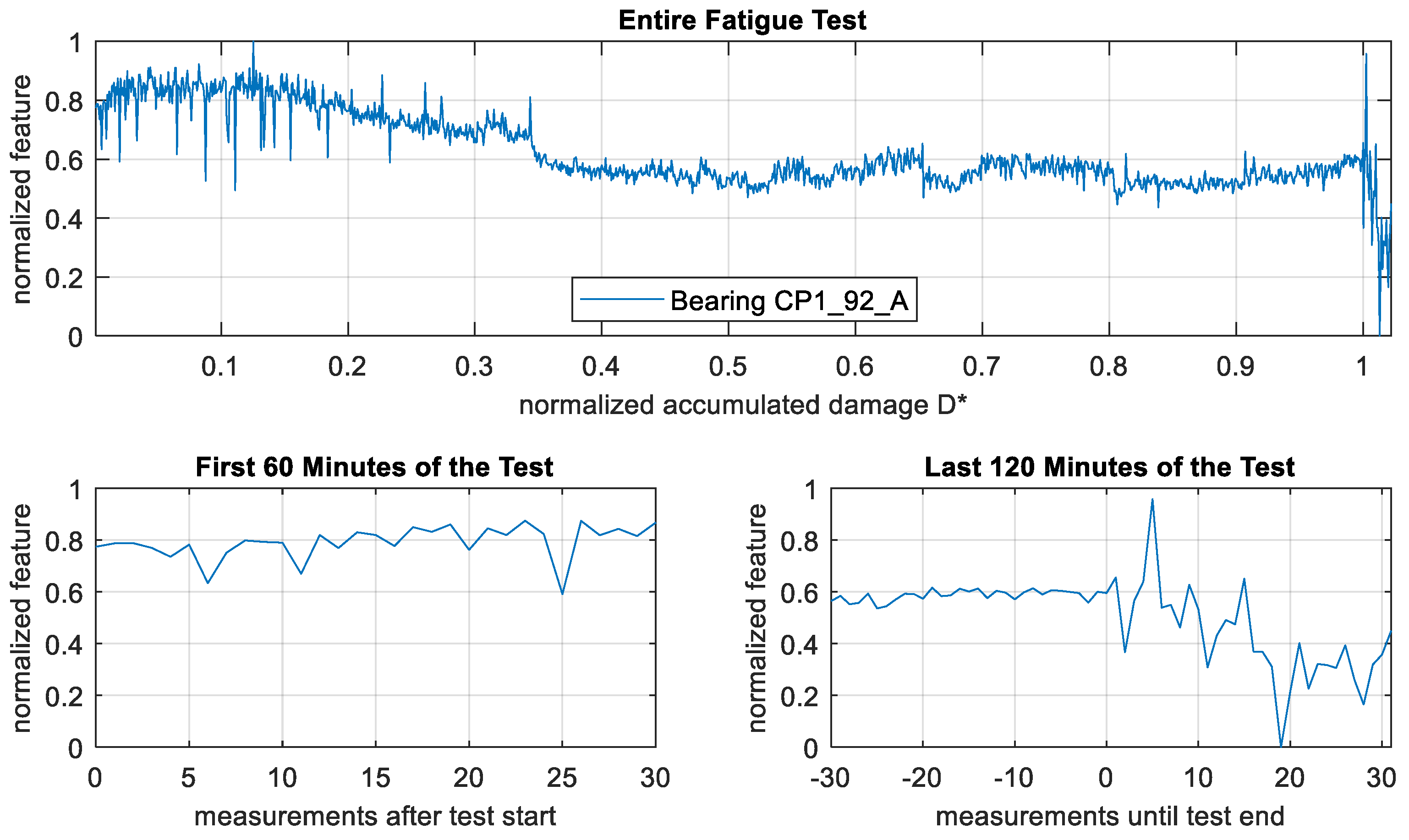
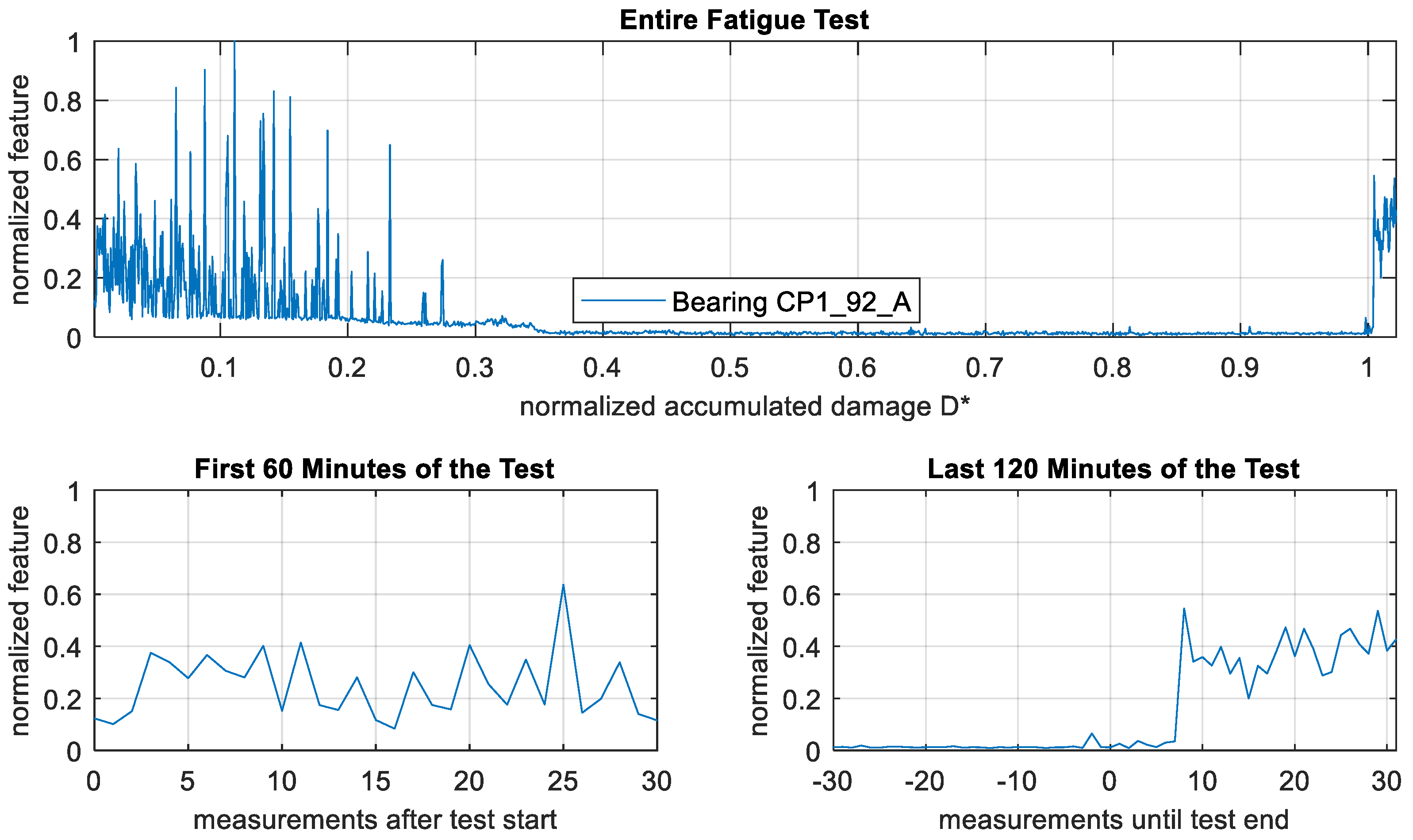
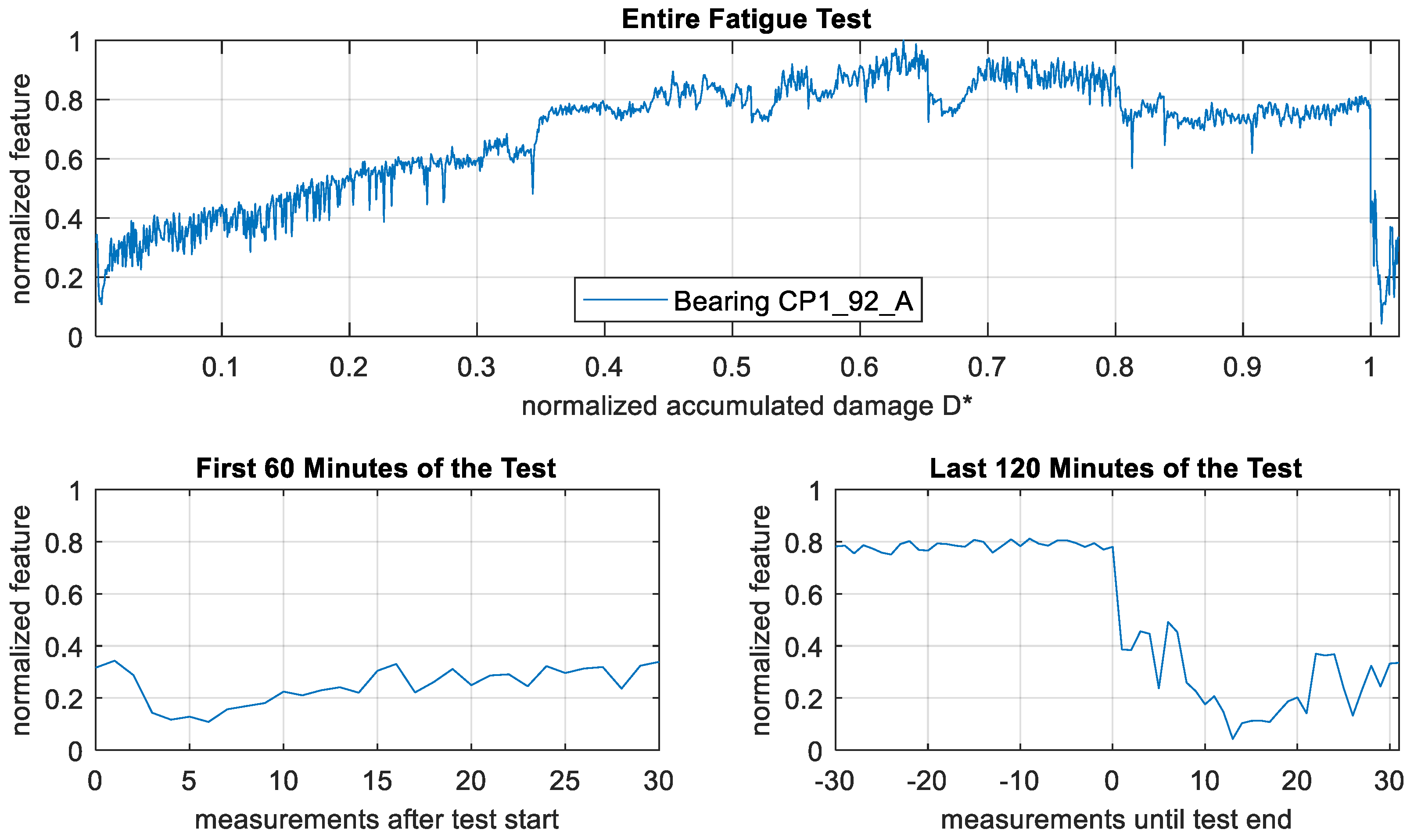
3.1. Description of Individual Features
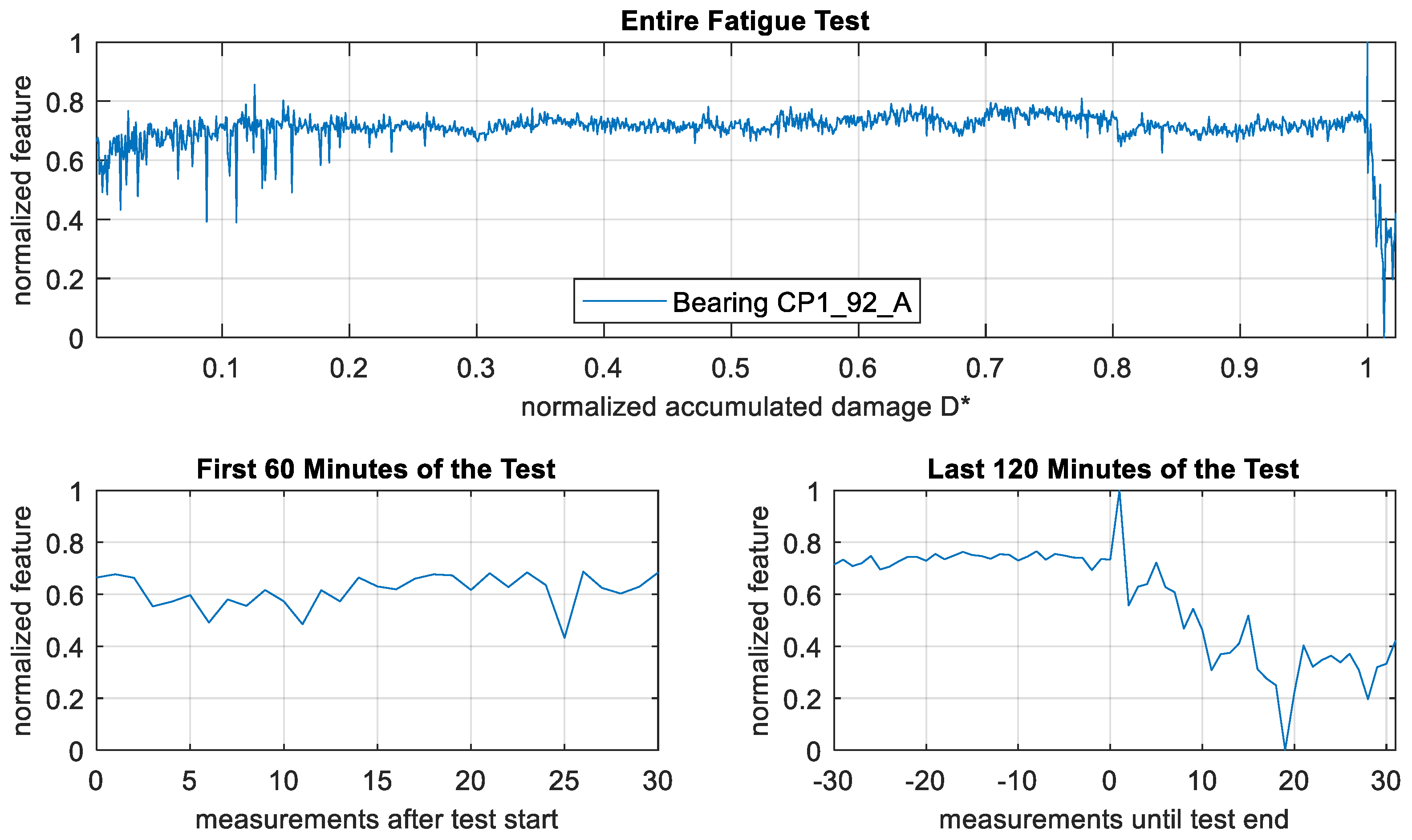
3.2. Validation Fatigue Tests
3.3. Comparison to Vibration Signals
4. Discussion
4.1. Phenomenological Explanation
4.2. Effects Observed in the Validation Test
4.3. Explanation of Delay between Vibration and Impedance Features
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lei, Y. Intelligent Fault Diagnosis and Remaining Useful Life Prediction of Rotating Machinery; Elsevier: Oxford, UK, 2016. [Google Scholar]
- Randall, R.B. Vibration-Based Condition Monitoring: Industrial, Aerospace and Automotive Applications; Wiley: Chichester, UK, 2011. [Google Scholar]
- Schaeffler Monitoring Services GmbH. Condition Monitoring Praxis: Handbuch zur Schwingungs-Zustandsüberwachung von Maschinen und Anlagen, 1st ed; Vereinigte Fachverlage GmbH: Mainz, Germany, 2019. [Google Scholar]
- Schirra, T.; Martin, G.; Vogel, S.; Kirchner, E. Ball Bearings as Sensors for Systematical Combination of Load and Failure Monitoring. In Proceedings of the Design 2018 15th International Design Conference, Dubrovnik, Croatia, 21–24 May 2018; Marjanović, D., Štorga, M., Škec, S., Bojčetić, N., Pavković, N., Eds.; University of Zagreb Faculty of Mechanical Engineering and Naval Architecture: Zagreb, Croatia, 2018; pp. 3011–3022. [Google Scholar]
- Martin, G.; Becker, F.M.; Kirchner, E. A novel method for diagnosing rolling bearing surface damage by electric impedance analysis. In Tribology International 170; Elsevier: Amsterdam, The Netherlands, 2022. [Google Scholar] [CrossRef]
- Martin, G. Die Wälzlagerimpedanz als Werkzeug zur Untersuchung von Oberflächenabweichungen in Wälzlagern. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 2021. [Google Scholar]
- Maruyama, T.; Radzi, F.; Sato, T.; Iwase, S.; Maeda, M.; Nakano, K. Lubrication Condition Monitoring in EHD Line Contacts of Thrust Needle Roller Bearing Using the Electrical Impedance Method. Lubricants 2023, 11, 223. [Google Scholar] [CrossRef]
- Lei, Y.; He, Z.; Zi, Y. A new approach to intelligent fault diagnosis of rotating machinery. Expert Syst. Appl. 2008, 35, 1593–1600. [Google Scholar] [CrossRef]
- Bienefeld, C.; Vogt, A.; Kacmar, M.; Kirchner, E. Feature-Engineering für die Zustandsüberwachung von Wälzlagern mittels maschinellen Lernens. Tribol. und Schmier. 2021, 68, 5–11. [Google Scholar] [CrossRef]
- Prashad, H. Tribology in Electrical Environments; Elsevier: Amsterdam, The Netherlands; London, UK, 2006. [Google Scholar]
- Alpaydin, E. Introduction to Machine Learning, 2nd ed.; The MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Soviany, S.; Soviany, C. Feature Engineering. In Principles of Data Science; Arabnia, H.R., Daimi, K., Stahlbock, R., Soviany, C., Heilig, L., Brüssau, K., Eds.; Springer: Cham, Switzerland, 2020; pp. 79–103. [Google Scholar]
- Schirra, T. Phänomenologische Betrachtung der Sensorisch Nutzbaren Effekte am Wälzlager—Einfluss Unbelasteter Wälzkörper Auf das Elektrische Impedanzmodell. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 2021. [Google Scholar]
- Barz, M. Die Schmierfilmbildung in Fettgeschmierten Schnellaufenden Spindellagern. Ph.D. Thesis, Gottfried Wilhelm Leibniz Universität Hannover, Hannover, Germany, 1996. [Google Scholar]
- Gemeinder, Y. Lagerimpedanz und Lagerschädigung bei Stromdurchgang in Umrichtergespeisten Elektrischen Maschinen. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 2016. [Google Scholar]
- Puchtler, S.; Schirra, T.; Kirchner, E.; Späck-Leigsnering, Y.; de Gersem, H. Capacitance calculation of unloaded rolling elements—Comparison of analytical and numerical methods. Tribol. Int. 2022, 176, 107882. [Google Scholar] [CrossRef]
- Harder, A.; Zaiat, A.; Becker-Dombrowsky, F.M.; Puchtler, S.; Kirchner, E. Investigation of the Voltage-Induced Damage Progression on the Raceway Surfaces of Thrust Ball Bearings. Machines 2022, 10, 832. [Google Scholar] [CrossRef]
- Radnai, B.; Gemeinder, Y.; Kiekbusch, T.; Weber, J.; Hering, J.; Arnold, D. Schädlicher Stromdurchgang: Untersuchung des Schädigungsmechanismus und der zulässigen Lagerstrombelastung von Wälzlagern in E-Motoren und Generatoren verursacht durch parasitäre hochfrequente Lagerströme. In Forschungsvorhaben Nr. 650 I; Forschungsvereinigungs Antriebstechnik: Frankfurt am Main, Germany, 2015. [Google Scholar]
- Muetze, A. Bearing Currents in Inverter-Fed AC-Motors; Technische Universität Darmstadt: Darmstadt, Germany, 2003. [Google Scholar]
- Saucedo-Dorantes, J.J.; Arellano-Espitia, F.; Delgado-Prieto, M.; Osornio-Rios, R.A. Diagnosis Methodology Based on Deep Feature Learning for Fault Identification in Metallic, Hybrid and Ceramic Bearings. Sensors 2021, 21, 5832. [Google Scholar] [CrossRef] [PubMed]
- Shi, H.; Hou, M.; Wu, Y.; Li, B. Incipient Fault Detection of Full Ceramic Ball Bearing Based on Modified Observer. International J. Control. Autom. Syst. 2022, 20, 727–740. [Google Scholar] [CrossRef]
- Liu, H.; Shah, S.; Jiang, W. On-line outlier detection and data cleaning. In Computers and Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2004; Volume 28, pp. 1635–1647. [Google Scholar]
- Pal, S.K.; Mishra, D.; Pal, A.; Dutta, S.; Chakravarty, D.; Pal, S. Digital Twin—Fundamental Concepts to Applications in Advanced Manufacturing; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Preusche, C. Clusterbasierte Zustandsbewertung von Technischen Systemen zur Unterstützung der Prädiktiven Instandhaltung. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 2018. [Google Scholar]
- Kateris, D.; Moshou, D.; Pantazi, X.-E.; Gravalos, I.; Sawalhi, N.; Loutridis, S. A machine learning approach for the condition monitoring of rotating machinery. J. Mech. Sci. Technol. 2014, 28, 61–71. [Google Scholar] [CrossRef]
- Akpudo, U.E.; Hur, J.-W. Towards bearing failure prognostics: A practical comparison between data-driven methods for industrial applications. J. Mech. Sci. Technol. 2020, 34, 4161–4172. [Google Scholar] [CrossRef]
- Slavič, J.; Mršnik, M.; Česnik, M.; Javh, J.; Boltežar, M. Uniaxial vibration fatigue. In Vibration Fatigue by Spectral Methods: From Structural Dynamics to Fatigue; Elsevier: Amsterdam, The Netherlands, 2020; pp. 99–113. [Google Scholar]
- Naunheimer, H.; Bertsche, B.; Ryborz, J.; Novak, W.; Fietkau, P. Fahrzeuggetriebe: Grundlagen, Auswahl, Auslegung und Konstruktion, 3rd ed.; Springer: Berlin Heidelberg, Germandy, 2019. [Google Scholar]
- ISO-281: Referenznummer ISO 281:2007(E); Internationale Organisation für Normung, 2nd ed. International Organization for Standardization: Geneva, Switzerland, 2007.
- Steinhilper, W.; Sauer, B. Konstruktionselemente des Maschinenbaus 2; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Akpudo, U.E.; Hur, J.-W. A feature fusion-based prognostics approach for rolling element bearings. J. Mech. Sci. Technol. 2020, 34, 4025–4035. [Google Scholar] [CrossRef]
- Hedderich, J.; Sachs, L. Angewandte Statistik: Methodensammlung Mit R, 17th ed.; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Fahrmeir, L.; Heumann, C.; Künstler, R.; Pigeot, I.; Tutz, G. Statistik: Der Weg zur Datenanalyse, 8th ed.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Dahlke, H. Handbuch Wälzlager-Technik: Bauarten, Gestaltung, Betrieb, 1994th ed.; Springer Fachmedien: Wiesbaden, Germany, 1994. [Google Scholar]
- Kosfeld, R.; Eckey, H.F.; Türck, M. Deskriptive Statistik: Grundlagen—Methoden—Beispiele—Aufgaben, 6th ed.; Springer Gabler: Wiesbaden, Germany, 2016. [Google Scholar]
- Becker-Dombrowsky, F.M.; Zaiat, A.; Kirchner, E. Impedanzmessung an Wälzlagern—Servicemodelle zur Überwachung technischer Anlagen. In Proceedings of the VDI-Berichte, 2415, 15. VDI-Fachtagung Gleit- und Wälzlagerungen 2023, Schweinfurt, Germany, 13—14 June 2023; VDI Verlag GmbH: Düsseldorf, Germany. ISBN 978-3-18-092415-1. [Google Scholar]
- Becker-Dombrowsky, F.M.; Hausmann, M.; Welzbacher, P.; Harder, A.; Kirchner, E. Systematic identification of disturbance factors on electric characteristics of mechanical gearboxes. In Forschung im Ingenieurwesen 87; SpringerNature: Berlin, Germany, 2023; pp. 399–410. [Google Scholar] [CrossRef]





| Description | Formula | Unit |
|---|---|---|
| Real part (effective resistance) | Ω | |
| Imaginary part (reactance) | Ω | |
| Absolute value (apparent resistance) | Ω | |
| Phase angle | rad |
| Test Parameter | Investigation Tests [6] | Validation Test |
|---|---|---|
| Radial load | ||
| Axial load | ||
| Dynamic safety | ||
| Speed | ||
| Oil temperature | ||
| Time between impedance measurements | ||
| Length of each impedance measurement | ||
| Carrier signal frequency | 2.5 MHz | 20 kHz |
| Carrier signal amplitude | 5 V peak to peak | 5 V peak to peak |
| Sampling rate | 50 MHz | 1 MHz |
| Number | Formula | Number | Formula |
|---|---|---|---|
| T1 | F1 | ||
| T2 | F2 | ||
| T3 | F3 | ||
| T4 | F4 | ||
| T5 | F5 | ||
| T6 | F6 | ||
| T7 | F7 | ||
| T8 | F8 | ||
| T9 | F9 | ||
| T10 | F10 | ||
| T11 | F11 | ||
| T12 | F12 | ||
| T13 | F13 | ||
| T14 | F14 | ||
| T15 | F15 | ||
| T16 | |||
| T17 | with sampling period |
| Rank | Whole Lifespan | Last Hour |
|---|---|---|
| 1. | Feature 88: RMS frequency (F7) of the absolute value | Feature 102: skewness (T6) of the phase angle |
| 2. | Feature 56: RMS frequency (F7) of the imaginary part | Feature 60: skewness of the frequencies (F11) of the imaginary part |
| 3. | Feature 86: central frequency (F5) of the absolute value | Feature 92: skewness of the frequencies (F11) of the absolute value |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Becker-Dombrowsky, F.M.; Koplin, Q.S.; Kirchner, E. Individual Feature Selection of Rolling Bearing Impedance Signals for Early Failure Detection. Lubricants 2023, 11, 304. https://doi.org/10.3390/lubricants11070304
Becker-Dombrowsky FM, Koplin QS, Kirchner E. Individual Feature Selection of Rolling Bearing Impedance Signals for Early Failure Detection. Lubricants. 2023; 11(7):304. https://doi.org/10.3390/lubricants11070304
Chicago/Turabian StyleBecker-Dombrowsky, Florian Michael, Quentin Sean Koplin, and Eckhard Kirchner. 2023. "Individual Feature Selection of Rolling Bearing Impedance Signals for Early Failure Detection" Lubricants 11, no. 7: 304. https://doi.org/10.3390/lubricants11070304
APA StyleBecker-Dombrowsky, F. M., Koplin, Q. S., & Kirchner, E. (2023). Individual Feature Selection of Rolling Bearing Impedance Signals for Early Failure Detection. Lubricants, 11(7), 304. https://doi.org/10.3390/lubricants11070304





