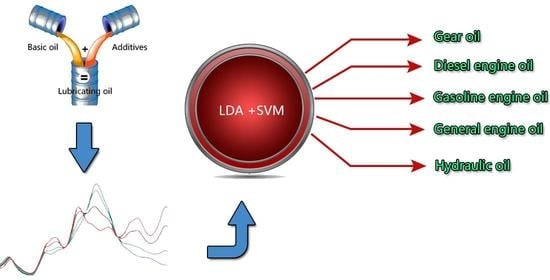
Classification of Lubricating Oil Types Using Mid-Infrared Spectroscopy Combined with Linear Discriminant Analysis–Support Vector Machine Algorithm
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Samples
2.1.2. Experimental Instruments and Parameters
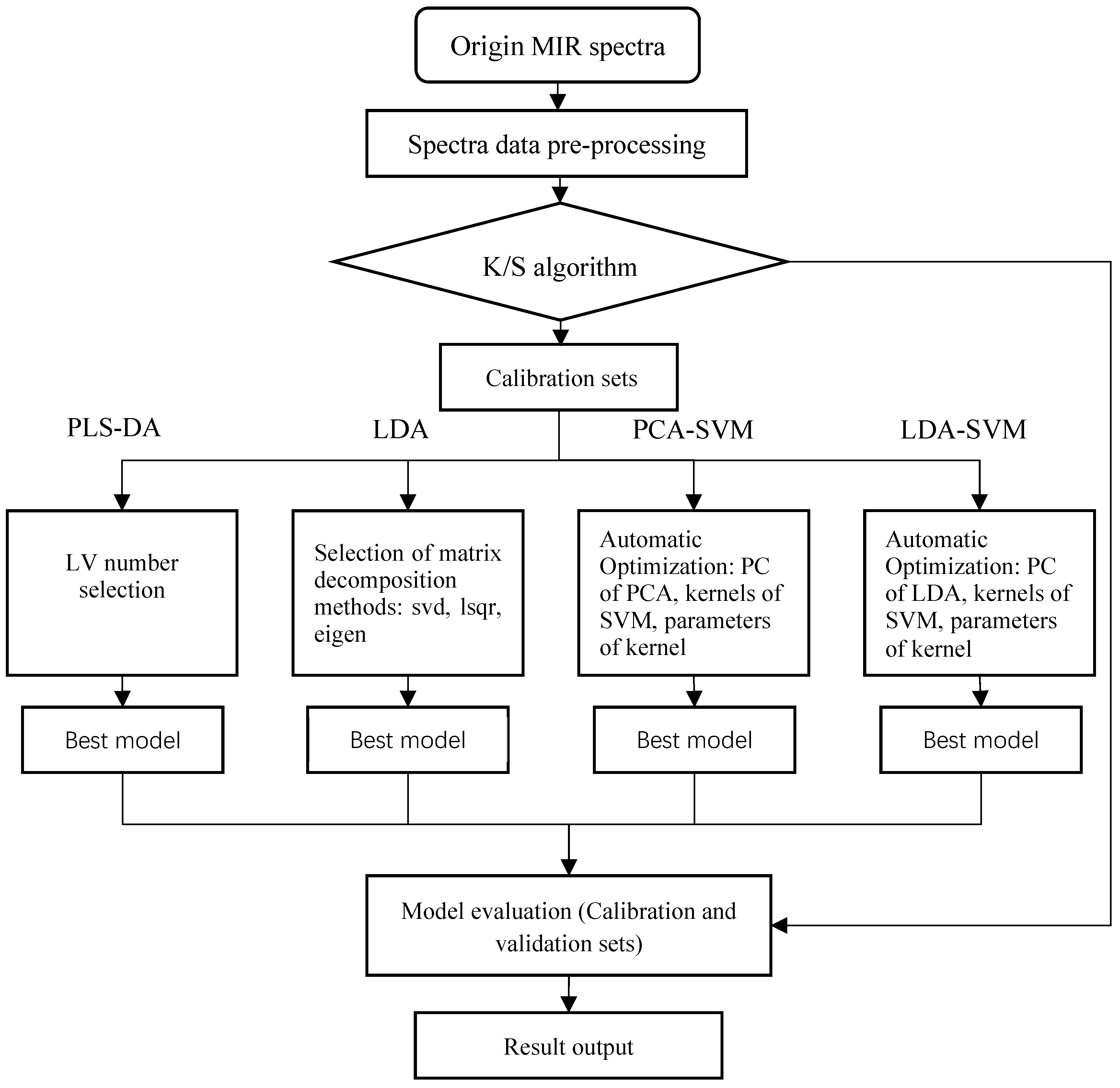
2.2. Methods
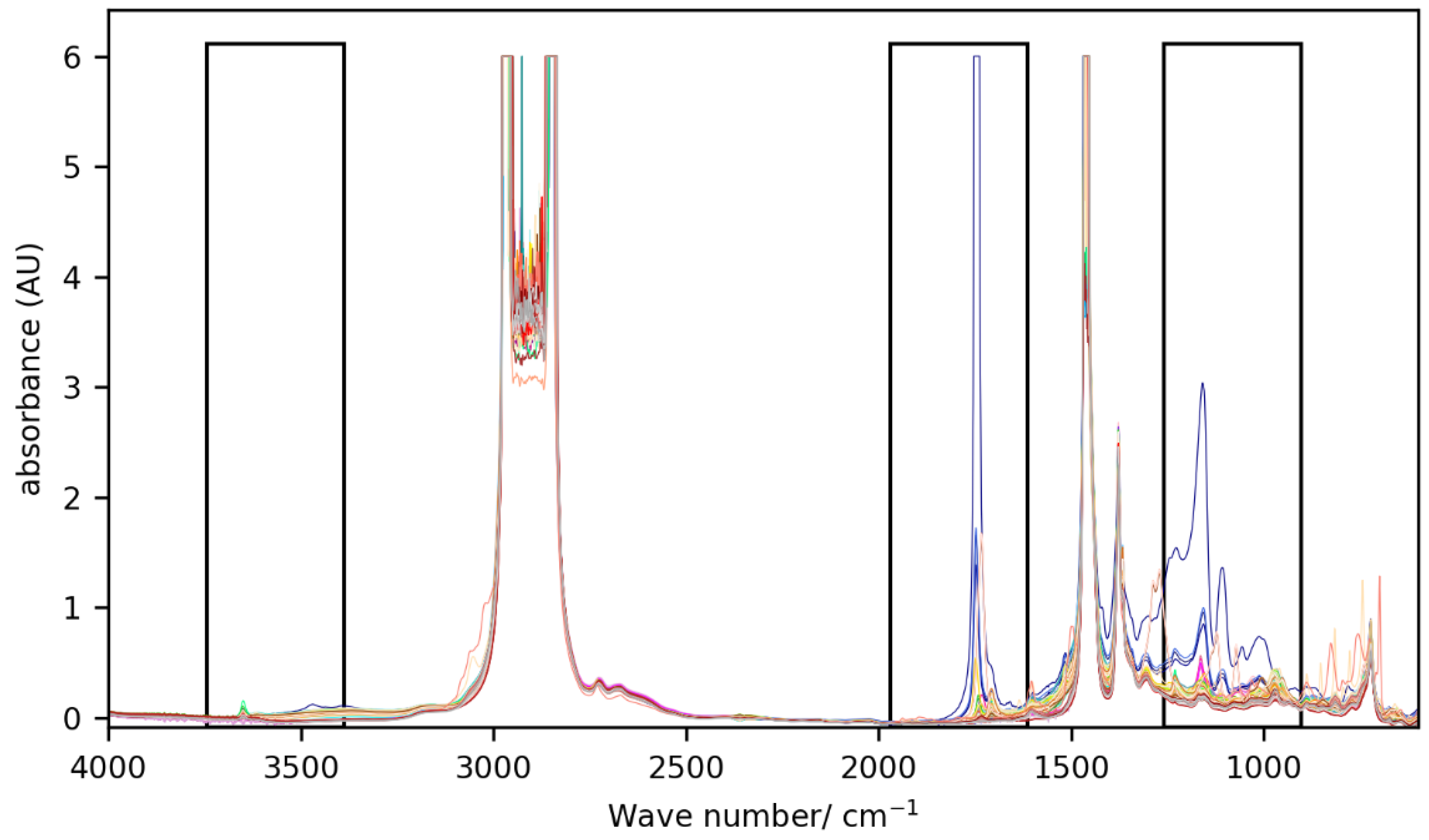
2.2.1. Spectral Data Pre-Processing
2.2.2. Dimensionality Reduction Using LDA Algorithm
2.2.3. SVM Algorithm
2.3. Construction of Calibration Set and Validation Set
2.3.1. K/S Algorithm
2.3.2. Specific Construction of Calibration Set and Validation Set
2.4. LDA-SVM Algorithm Steps
2.5. Experimental Design
3. Results and Discussion
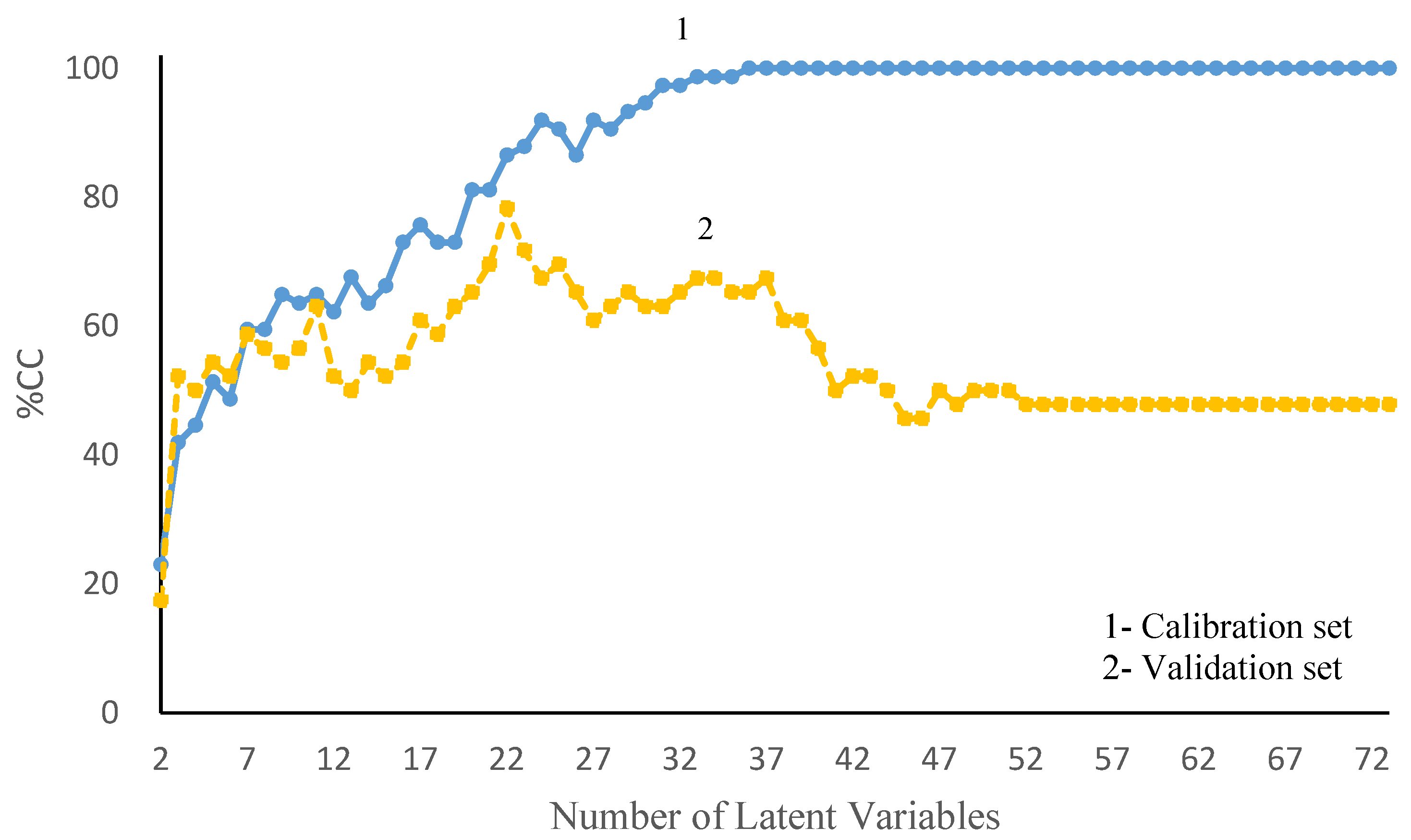
3.1. PLS-DA Model
3.2. LDA Model
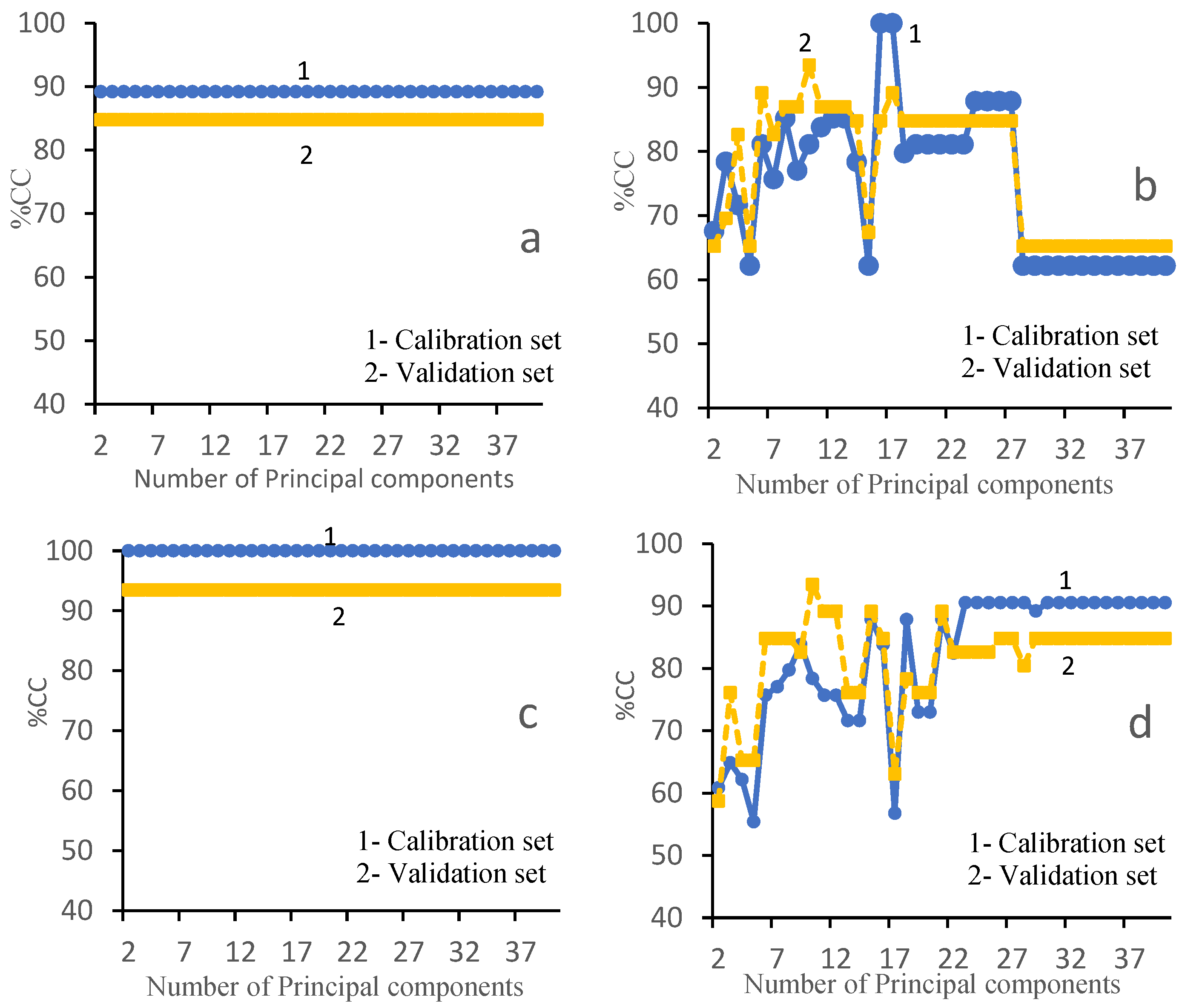
3.3. PCA-SVM Model Recognition Results
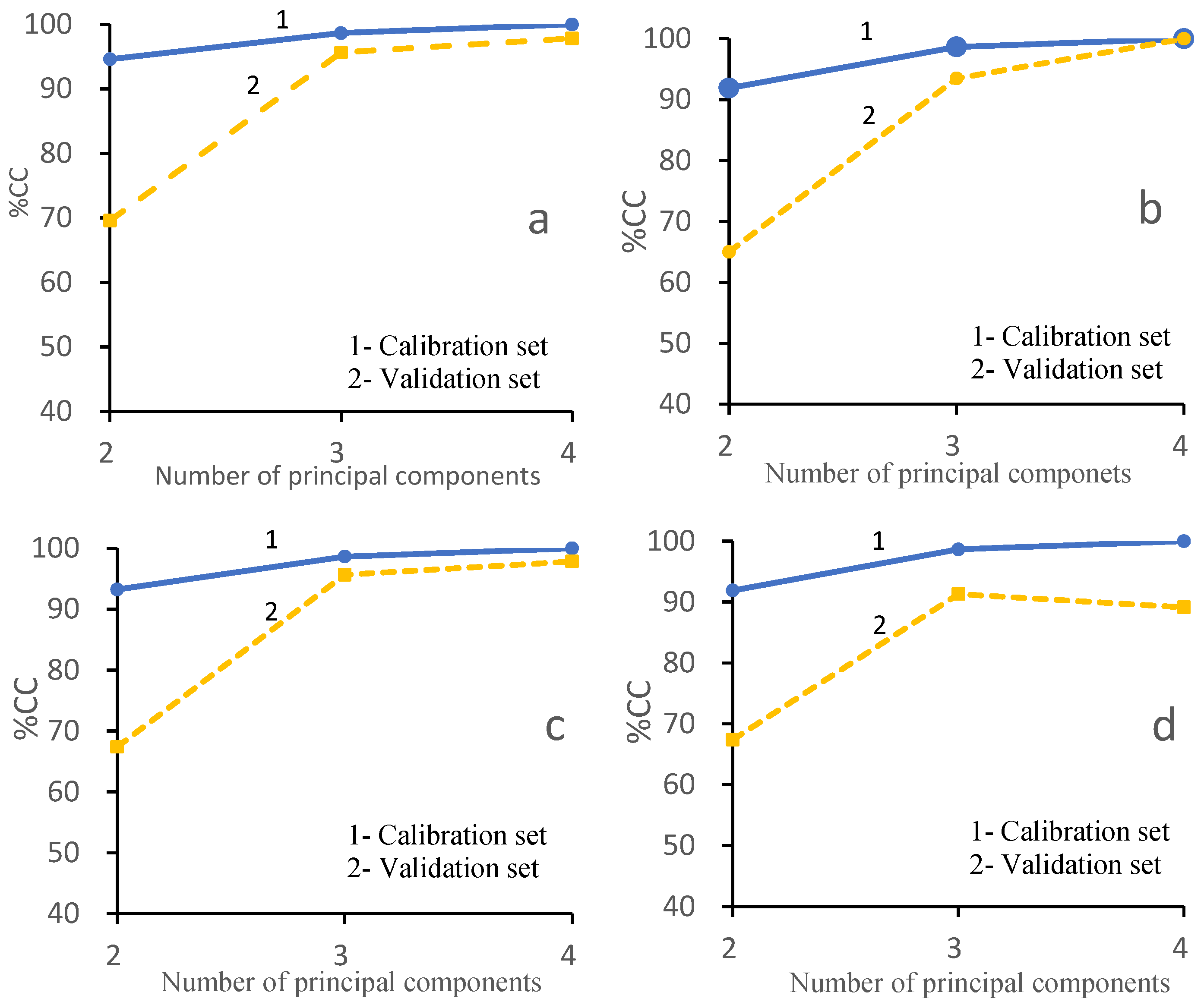
3.4. LDA-SVM Model
3.5. Comparison of Model Classification Results
4. Conclusions and Future Scope
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, H.; Liu, H.; Zhu, C.; Parker, R.G. Effects of lubrication on gear performance: A review. Mech. Mach. Theory 2020, 145, 103707. [Google Scholar] [CrossRef]
- Feng, K.; Pietro, B.; Wade, A.S.; Robert, B.R.; Zhan, Y.C.; Ren, J.; Peng, Z. Vibration-based updating of wear prediction for spur gears. Wear 2019, 426–427, 1410–1415. [Google Scholar] [CrossRef]
- Feng, K.; Ji, J.C.; Ni, Q. A novel gear fatigue monitoring indicator and its application to remaining useful life prediction for spur gear in intelligent manufacturing systems. Int. J. Fatigue 2023, 168, 107459. [Google Scholar] [CrossRef]
- Talbot, D.; Kahraman, A.; Li, S.; Singh, A.; Xu, H. Development and validation of an automotive axle power loss model. Tribol. Trans. 2016, 59, 707–719. [Google Scholar] [CrossRef]
- Fernandes, C.M.; Battez, A.H.; González, R.; Monge, R.; Viesca, J.; García, A.; Martins, R.C.; Seabra, J.H. Torque loss and wear of fzg gears lubricated withwind turbine gear oils using an ionic liquid as additive. Tribol. Int. 2015, 90, 306–314. [Google Scholar] [CrossRef]
- Krantz, T.; Tufts, B. Pitting and bending fatigue evaluations of a new case-carburized gear steel. In Proceedings of the ASME 2007 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Las Vegas, NV, USA, 4–7 September 2007; p. 215009. [Google Scholar]
- Tian, G.Y.; Chu, X.L.; Yi, R.J. Lubrication Oil infrared Spectral Analysis Technology; Chemical Industry Press: Beijing, China, 2014; Volume 20, pp. 119–121. [Google Scholar]
- Martins, R.; Seabra, J.; Magalhães, L. Micropitting of austempered ductile iron gears: Biodegradable ester vs. mineral oil. Rev. Assoc. Port. Anál. Exp. Tensões. 2006, 13, 55–65. [Google Scholar]
- Adebogun, A.; Hudson, R.; Breakspear, A.; Warrens, C.; Gholinia, A.; Matthews, A.; Withers, P. Industrial gear oils: Tribological performance and subsurface changes. Tribol. Lett. 2018, 66, 65. [Google Scholar] [CrossRef]
- Brandão, J.; Meheux, M.; Ville, F.; Seabra, J.; Castro, J. Comparative overview of five gear oils in mixed and boundary film lubrication. Tribol. Int. 2012, 47, 50–61. [Google Scholar] [CrossRef]
- Bhaumik, S.; Prabhu, S.; Singh, K.J. Analysis of tribological behavior of carbon nanotube based industrial mineral gear oil 250 cSt viscosity. Adv. Tribol. 2014, 2014, 341365. [Google Scholar] [CrossRef]
- Song, W.; Yan, J.; Ji, H. Fabrication of GNS/MoS2 composite with different morphology and its tribological performance as a lubricant additive. Appl. Surf. Sci. 2019, 469, 226–235. [Google Scholar] [CrossRef]
- Zhao, Z.Y. The Lubricant Quality Near-Infrared and Raman Spectroscopy Testing Methods; East China Jiaotong University: Shanghai, China, 2013. [Google Scholar]
- Gao, Z.F.; Zeng, L.B.; Shi, L.; Li, K.; Yang, Y.Z.; Wu, Q.S. Development of a portable Mid-Infrared Rapid Analyzer for oil concentration in water Based on MEMS Linear sensor Array. Spectrosc. Spectr. Anal. 2014, 34, 1711–1715. [Google Scholar]
- Yu, H.W.; Wang, X.X.; Li, J.X.; Zhang, Y.X. Study on the structures of New engine oil and used Engine oil by multi-demensional infrared Spectroscopy. LuBricating Oil 2021, 36, 37–41. [Google Scholar]
- Li, H.; Li, J.F.; Xie, L.Q.; Ren, Z.P.; Ding, Y.Q. Analysis of organic component distribution and inorganic mineral composition of tank bottom sludge in change qing oil field. Anal. Instrum. 2021, 52, 52–59. [Google Scholar]
- Zhang, F.Y.; Lang, X.J.; Zhang, D.H.; Liu, J.; Zhang, Y. Determination of soot content in-service Engine oil by Fourier Transform infrared Specrometry. LuBricating Oil 2021, 35, 45–48+59. [Google Scholar]
- Mohammadia, M.; Khorrami, K.M.; Hamid, V.; Karimi, A.; Sadrara, M. Classification and determination of sulfur content in crude oil samples by infrared spectrometry. Infrared Phys. Technol. 2022, 127, 104382. [Google Scholar] [CrossRef]
- Douglas, R.K.; Nawar, S.; Alamar, M.C.; Coulon, F.; Mouazen, A.M. The application of a handheld mid-infrared spectrometry for rapid measurement of oil contamination in agricultural sites. Sci. Total Environ. 2019, 665, 253–261. [Google Scholar] [CrossRef]
- Fatemeh, S.H.N.; Hadi, P. Pattern recognition analysis of gas chromatographic and infrared spectroscopic fingerprints of crude oil for source identification. Microchem. J. 2020, 153, 104326. [Google Scholar] [CrossRef]
- Xia, Y.Q.; Wang, C.; Feng, X. GA-BPSO Hybrid Optimization of Middle Infrared Spectrum Feature Band Selection of Lubricating Oil Additive Type Identification Technology. Tribology 2022, 42, 42–152. [Google Scholar]
- Galtier, O.; Abbas, O.; Le, D.Y. Comparison of PLS1-DA, PLS2-DA and SIMCA for classification by origin of crude petroleum oils by MIR and virgin olive oils by NIR for different spectral regions. Vib. Spectrosc. 2011, 55, 132–140. [Google Scholar] [CrossRef]
- Xia, Y.Q.; Xu, D.W.; Feng, X.; Cai, M.R. Identification and Content Prediction of Lubricating Oil Additives Based on Extreme Learning Machine. Tribology 2020, 40, 97–106. [Google Scholar]
- He, Z.X.; Wu, M.T.; Zhao, X.Y.; Zhang, S.Y.; Tan, J.R. Representative null space LDA for discriminative dimensionality reduction. Pattern Recognit. 2021, 111, 107664. [Google Scholar] [CrossRef]
- Şahin, D.Ö.; Kural, E.O.; Akleylek, S.; Kılıç, E. Permission-based Android malware analysis by using dimension reduction with PCA and LDA. J. Inf. Secur. Appl. 2021, 63, 102995. [Google Scholar] [CrossRef]
- Amiri, V.; Nakagawa, K. Using a linear discriminant analysis (LDA) based nomenclature system and self-organizing maps (SOM) for spatiotemporal assessment of groundwater quality in a coastal aquifer. J. Hydrol. 2021, 603, 127082. [Google Scholar] [CrossRef]
- Xiong, Y.; Cheng, C.H.; Wu, J.H. Research on Premise Selection Technology Based on Machine Learning Classification Algorithm. Netinfo Secur. 2021, 21, 9–16. [Google Scholar]
- Lu, W.P.; Yan, X.F. Balanced multiple weighted linear discriminant analysis and its application to visual process monitoring. Chin. J. Chem. Eng. 2021, 36, 128–137. [Google Scholar] [CrossRef]
- Han, S.; Li, N.; Xue, L.; Hasi, W.L.J. Study on Classification and Identification of Arsenic Mineral Drugs by Raman Spectroscopy Combined with PCA-SVM. J. Anal. Sci. 2022, 38, 224–228. [Google Scholar]
- Chen, C.H.; Zhong, Y.S.; Wang, X.Y.; Zhao, Y.K.; Dai, F. Feature Selection Algorithm for Identification of Male and Female Cocoons Based on SVM Bootstrapping Re Weighted Sampling. Spectrosc. Spectr. Anal. 2022, 72, 1173–1178. [Google Scholar]
- Li, H.; Wang, J.X.; Xing, Z.N.; Shen, G. Influence of Improved Kennard/Stone Algorithm on the Calibration Transfer in Near-Infrared Spectroscopy. Spectrosc. Spectr. Anal. 2011, 31, 362–365. [Google Scholar]


| Sample Types | Calibration Set | Validation Set | Sum of Sample |
|---|---|---|---|
| Gear oil | 8 | 5 | 13 |
| Diesel engine oil | 25 | 16 | 41 |
| Gasoline engine oil | 8 | 5 | 13 |
| All-purpose engine oil | 20 | 13 | 33 |
| Hydraulic oil | 13 | 9 | 22 |
| Total number of samples | 74 | 46 | 120 |
| Sample (Unit) | Data Sets | Number of Samples | Maximum | Minimum | Mean | Standard Deviation |
|---|---|---|---|---|---|---|
| Lubricating oils | Calibration set | 74 | 6.0 | −0.065 | 0.070 | 0.163 |
| Validation set | 46 | 1.732 | −0.063 | 0.064 | 0.117 |
| Decomposition Method | Calibration Sets (%CC) | Validation Sets (%CC) |
|---|---|---|
| SVD | 100 | 95 |
| sqlr | 95 | 97 |
| eigen | 95 | 97 |
| Model | Parameter | Calibration Sets (%CC) | Validation Sets (%CC) |
|---|---|---|---|
| PLS-DA | LV = 22 | 86% | 78% |
| LDA | Decomposition method = SVD | 100% | 95% |
| PCA-SVM | PC = 2, kernel = RBF | 100% | 94% |
| LDA-SVM | PC = 4, kernel = poly | 100% | 100% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Liu, S.; Gao, M.; Zuo, Y. Classification of Lubricating Oil Types Using Mid-Infrared Spectroscopy Combined with Linear Discriminant Analysis–Support Vector Machine Algorithm. Lubricants 2023, 11, 268. https://doi.org/10.3390/lubricants11060268
Xu J, Liu S, Gao M, Zuo Y. Classification of Lubricating Oil Types Using Mid-Infrared Spectroscopy Combined with Linear Discriminant Analysis–Support Vector Machine Algorithm. Lubricants. 2023; 11(6):268. https://doi.org/10.3390/lubricants11060268
Chicago/Turabian StyleXu, Jigang, Shujun Liu, Ming Gao, and Yonggang Zuo. 2023. "Classification of Lubricating Oil Types Using Mid-Infrared Spectroscopy Combined with Linear Discriminant Analysis–Support Vector Machine Algorithm" Lubricants 11, no. 6: 268. https://doi.org/10.3390/lubricants11060268
APA StyleXu, J., Liu, S., Gao, M., & Zuo, Y. (2023). Classification of Lubricating Oil Types Using Mid-Infrared Spectroscopy Combined with Linear Discriminant Analysis–Support Vector Machine Algorithm. Lubricants, 11(6), 268. https://doi.org/10.3390/lubricants11060268